1. Introduction
The study of commuting maps, defined through the commutator
, has been a central topic in the structural theory of rings and algebras for decades. Early investigations by Divinsky established that the existence of non-identity commuting automorphisms forces a ring to be commutative [
1]. Posner proved that every centralizing derivation on a prime ring must vanish [
2]. These pioneering results laid the foundation for a systematic study of commuting and centralizing mappings in algebraic systems.
Subsequent advances were made by Brešar, who characterized commuting maps on prime and semiprime rings in the canonical form
where
lies in the extended centroid and
maps into the center of the ring [
3,
4,
5,
6]. This framework unified several results concerning derivations, automorphisms, and Lie-type maps. Later, several researchers extended these ideas to various settings, including triangular algebras, generalized matrix algebras, and incidence algebras [
7,
8,
9]. Related work on functional identities and Engel-type conditions (
n-commuting maps) was undertaken by Vukman, Brešar, and Beidar et al., highlighting the rich interplay between commutativity conditions and algebraic structure [
10,
11,
12,
13,
14].
In the past decade, attention has shifted toward the graded or
superalgebraic setting, where the underlying algebra
admits a
-grading. For homogeneous elements
, the
supercommutator
generalizes the classical commutator by incorporating a parity-dependent sign. This structure naturally arises in mathematical physics and quantum theory, where even (bosonic) and odd (fermionic) components coexist. Superalgebras thus provide a unified framework for modeling graded symmetries in supersymmetry and representation theory [
15]. Within this framework, supercommuting maps have strong connections to Lie superderivations, superbiderivations, and Jordan superhomomorphisms [
16,
17,
18,
19,
20]. Recent works also relate graded mappings to operator-theoretic and -analytic contexts such as Toeplitz operators and alternative rings [
21,
22].
The structural theory of supercommuting maps has recently gained increased attention. Ghahramani et al. characterized Lie superderivations on unital algebras containing nontrivial idempotents [
23]. Luo et al. examined supercommuting maps deeply under the same settings [
24]. These results exploit the
Peirce decomposition of a unital algebra
A with idempotent
e (
),
which induces a superalgebra structure via
This decomposition allows one to reinterpret many classical ring-theoretic phenomena through the lens of graded algebra.
Parallel to these developments, incidence algebras
, introduced by Ward [
25] and later developed by Rota and Stanley [
26], have emerged as a rich algebraic framework for studying combinatorial and order-theoretic structures. For a locally finite preordered set
, the algebra
consists of functions
satisfying
when
, with convolution
Incidence algebras encode order-theoretic information through algebraic means, serving as a natural setting for derivations, automorphisms, and centralizing maps [
27,
28,
29,
30,
31,
32,
33,
34]. The present paper extends the classical commuting map theory to the
supercommuting context within incidence algebras endowed with a natural
-grading.
Our main result establishes that if the Hasse diagram of a connected locally finite preordered set
satisfies the
cycle condition that any two directed edges in each connected component lie on a common cycle, every homogeneous supercommuting map
on the incidence superalgebra
is
proper; that is,
where
is a homogeneous central element and
is an
R-linear map with an image in the supercenter. This generalizes the theorem of Jia and Xiao [
9] from the commuting to the supercommuting setting and aligns with recent graded studies by Ghahramani at el. [
23] and Luo at el. [
24].
This paper is organized as follows:
Section 2 recalls basic notions of superalgebras and incidence algebras, including
-grading, supercommutators, and supercenters.
Section 3 treats the connected case and proves that every homogeneous supercommuting map is proper under the cycle condition.
Section 4 extends these results to general incidence superalgebras through restriction homomorphisms and multilinear identities.
Section 5 addresses the general case by decomposing the algebra into connected components and establishing the global form of supercommuting maps.
Section 6 concludes with remarks on possible extensions to improper and higher-order supercommuting maps.
2. Preliminaries
Throughout this paper, R denotes a commutative ring with identity, and all algebras are assumed to be associative and unital over R. We begin by recalling essential definitions and establishing the notation used throughout the paper.
2.1. Superalgebras and Supercommutators
An
R-
superalgebra (or
-
graded algebra) is an
R-algebra
where
(the
even part) and
(the
odd part) are
R-submodules satisfying
An element is said to be homogeneous of degree if .
For homogeneous elements
, the
supercommutator is defined by
This operation extends bilinearly to all elements of A. When , it coincides with the ordinary commutator .
Definition 1. An R-linear map is called a supercommuting map if If θ is homogeneous of degree , that is, for each i, then θ is called a homogeneous supercommuting map.
Supercommuting maps generalize the notion of commuting maps by incorporating the parity-dependent sign
, thus capturing the graded antisymmetry intrinsic to superalgebraic structures. This graded modification is crucial in distinguishing the behavior of even and odd components and in extending commutation results to broader algebraic contexts. For further details, see [
15] and the references therein.
2.2. Incidence Algebras
Let
be a locally finite preordered set, that is, every interval
is finite for all
. The
incidence algebra of
over
R is the set of all functions
under pointwise addition and convolution multiplication defined by
This operation is associative and admits the identity element
defined by
For each
with
, we define
by
Then
forms an
R-basis for
, and the multiplication rule is given by
This basis description will be used repeatedly to express and compute the action of linear maps on
. For further details, see [
33] and the references therein.
2.3. Superalgebra Structure on Incidence Algebras
Let
be a finite preordered set and fix an idempotent
, where
. Then
e induces a natural
-grading on
via the Peirce decomposition:
where
Thus, becomes a superalgebra, which we refer to as the incidence superalgebra associated with and e.
This construction generalizes the familiar even–odd decomposition from matrix superalgebras and provides a canonical way to study graded properties in incidence algebras.
Example 1. Let with . Then consists of all upper triangular matrices over R: Choosing , we obtain Hence, is a superalgebra with even elements forming the diagonal subalgebra and odd elements corresponding to the strictly upper triangular part.
2.4. The Supercenter and Proper Maps
The
supercenter of a superalgebra
is defined as
Elements of need not be purely even; rather, they satisfy the graded commutation relation with every homogeneous element of A.
Definition 2. A supercommuting map is called proper
if there exists a homogeneous and an R-linear map such that This definition generalizes the notion of proper commuting maps in the nongraded setting, aligning with the classical forms established for prime and semiprime rings by Brešar [
5,
6]. The central problem addressed in this paper is determining under what structural conditions on
every supercommuting map on the incidence superalgebra
must be proper.
| Summary of notations. | |
| Notation | Description |
| R | Commutative ring with unity that is 2-torsion-free and |
| -torsion-free |
| X | Locally finite preordered set |
| Incidence algebra over X and R |
| Even and odd parts of superalgebra |
| Supercommutator: |
| Supercenter of A |
| Supercommuting map: |
| Basis element of |
| Unity element of |
| Complete Hasse diagram |
| ≈ | Equivalence on directed edges |
3. The Connected Case
Let
R be a 2-torsion-free commutative ring with unity, and let
X be a locally finite preordered set with the complete Hasse diagram
such that any two directed edges in each connected component are contained in one cycle. The incidence algebra
is endowed with a superalgebra structure via a nontrivial idempotent
e, where
is the even part (degree 0), and
is the odd part (degree 1) [
23]. In this section, we study supercommuting maps on
when
X is connected. A map
is called
supercommuting if
for all
, where
for homogeneous
, extended linearly [
19].
Lemma 1. Let A be an R-algebra with a superalgebra structure , and let θ be a supercommuting map on A. Let satisfy for some integer , where b is an idempotent. Then .
Proof. Case 1. First, assume that
a is homogeneous with parity
. Since
is supercommuting, we have
so
Multiplying (
1) on the right by another
a and applying the same identity repeatedly, we obtain by induction
Since
(mod 2), the exponent in the supercommutator satisfies
By assumption,
is idempotent. The above calculation shows that
Case 2. If
a is not homogeneous, write
with
. Expand
as a sum of monomials in
and
. Each monomial is homogeneous, and the calculation above shows that
supercommutes with each such homogeneous monomial. By linearity, the same holds for their sum. Thus,
for general
a, i.e.,
. □
Corollary 1. Let A be an R-algebra with a superalgebra structure, and let θ be a supercommuting map on A. If is an idempotent, then .
Proof. Since e is idempotent (), apply Lemma 1 with , , and . Thus, . □
The set
forms an
R-linear basis of
when
X is finite. For
and
, we write
or
for brevity. Let
be a supercommuting map. We denote
with the convention that
if
.
Lemma 2. The supercommuting map θ satisfiesand Proof. Assume
. Since
is idempotent and even (
), by Corollary 1,
Thus,
implies
for
. Left-multiplying by
, we obtain
This gives
if
or
. For
and
, consider the idempotent
. By Corollary 1,
, so
Multiplying by
on the left and
on the right gives
Combining these results, we obtain .
For
, observe that
is idempotent:
since
,
and
. By Corollary 1,
, so
Since
(as
or
), we have
As
,
is idempotent, this gives
Multiplying appropriately, we obtain
if
,
if
, and
if
. Thus,
□
Lemma 3. Let X be a connected, locally finite preordered set, and let be a supercommuting map on the incidence algebra , where R is a 2-torsion-free commutative ring with unity, and is endowed with a superalgebra structure [23]. Then the coefficients in the expansion satisfy the following relations: - (R1)
, if ;
- (R2)
, if ;
- (R3)
, if and ;
- (R4)
, for all ;
- (R5)
, if .
Proof. Consider the supercommutator relation
for
and any
, derived from the idempotent
(as in Lemma 2). It follows that
Since
(
) and
may have both even and odd components, we write
, where
and
. Thus,
and
Similarly, for
, since
, we have
and therefore
Equating the two expressions, we obtain
This implies the following:
For : , so .
For : , so .
For : .
Thus, for , set in the first case to obtain , proving (R1). For , set and in the second case to obtain , proving (R2). For with , the third case gives , proving (R3).
For (R5), if , from (R2) we have , and from (R1), . By (R3), , and hence .
For (R4), consider
and
with
and
. The element
is idempotent for
. By Lemma 1, we have
, which implies
We find , giving . Similarly, for , we obtain for . For , consider , which satisfies . This yields . For , the element gives . From , we have . Combining these, we obtain for all .
Since X is connected, for any , there exists a sequence , where covers or is covered by . Applying recursively yields , proving (R4). □
Definition 3. For any two directed edges , define if and only if there exists a cycle containing both and . The relation ≈ is an equivalence relation on D.
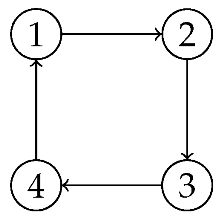
Example 2. Let with partial order relations (or arrows) of , , and . The corresponding Hasse diagram is the Dynkin diagram of type , and the associated complete Hasse diagram is depicted in Figure 1. Thus, , since the directed edges and are contained in the cycle , with , , , and .
Proposition 1. Let R be a 2-torsion-free commutative ring with unity, and let X be a finite, connected, preordered set. Let be endowed with a superalgebra structure via a nontrivial idempotent e [23]. Then every supercommuting map , satisfying for all , which is proper if and only if any two directed edges in the complete Hasse diagram are contained in one cycle. Proof. Assume that any two directed edges in
are contained in one cycle, i.e., the equivalence relation ≈ has a single equivalence class. By Lemma 2, for a supercommuting map
, we have
From Lemma 3, the coefficients satisfy:
- (R1)
, if ;
- (R2)
, if ;
- (R3)
, if and ;
- (R4)
, for all ;
- (R5)
, if .
By (R4),
for all
. Therefore,
Since (the unity element, with ), we have , as for all f. By (R5), for all , since all edges are in the same equivalence class under ≈. For , set . By (R1) and (R2), for any or , we can adjust the coefficients to align with the supercenter.
Define
where
if
. Then
where
and
, since
for fixed
. Thus,
is proper.
Conversely, if some edges
and
are not contained in the same cycle, the equivalence classes under ≈ partition
D. By [
9], a commuting map may be improper in such cases, and similarly, a supercommuting map may fail to be proper due to inconsistent
across equivalence classes, violating the uniformity condition (R5).
This proof extends the results of [
9] to the superalgebra context using the supercenter
[
19]. □
Example 3. Let with relations , , , and . The Hasse diagram of X is four-cycle (a square): In this case, any two directed edges are contained in a cycle. For instance, via the cycle , and via the same cycle. Hence, the condition of Proposition 1 is satisfied.
4. Supercommuting Maps on Incidence Algebras
Let
R be a commutative ring with unity that is both 2-torsion-free and
-torsion-free for some positive integer
n, and let
be a locally finite preordered set, possibly infinite. Denote by
the incidence algebra endowed with a superalgebra structure via a nontrivial idempotent
e, where
is the even part (degree 0), and
is the odd part (degree 1). The supercommutator is defined as
for homogeneous elements
, and extended linearly. A map
is said to be
supercommuting if
Definition 4. Let and . The restriction of f to the interval is defined by Let denote the R-subspace of generated by the elements with . Thus, consists of those functions that are nonzero only for finitely many pairs . For each , the map defined by is an algebra homomorphism.
Definition 5. For a multilinear map , we define its trace
(or diagonal evaluation) by Lemma 4. Let be a supercommuting map on the incidence algebra , where R is -torsion-free for some positive integer n. Then, for any and , we have Proof. Define the map
by
where the polynomial
in noncommutative variables
is defined inductively by
for all
. Since
is supercommuting, we have
. Consider the
n-fold supercommutator
where the supercommutator is applied
n times. The trace of
satisfies
Linearizing
, we obtain
where
is the symmetric group on
. Set
and
, where
is the basis element satisfying
and is zero elsewhere, with
(since
). Substituting into (
3), we obtain
Now replace
f with
, where
Since
is an algebra homomorphism, we apply the same substitution to obtain
The second terms in (
4) and (
5) are identical, as they depend only on
and
. Subtracting (
5) from (
4), we obtain
Since
R is
-torsion-free, we have
We now evaluate both sides at
. For any
, compute the supercommutator with
:
Since
,
unless
, hence
. Iteratively, for
, we have
and higher iterates
yield zero at
. Similarly, for the restricted function,
To refine this, note that for any
and
,
For
, we have
Applying
to both sides of (
6) gives
Since
is an algebra homomorphism and
, evaluating at
yields
because higher supercommutators vanish due to the idempotence and degree zero of
. Similarly,
From (
6), and since
R is
-torsion-free, it follows that
This completes the proof. □
Theorem 1. Let be a supercommuting map on the incidence algebra , where R is 2-torsion-free and -torsion-free, and any two directed edges in the complete Hasse diagram are contained in one cycle. Then θ is proper.
Proof. Assume without loss of generality, as the case corresponds to the supercommuting condition . Restrict to , the subalgebra of functions that are nonzero at finitely many pairs , and denote this restriction by . Since is supercommuting, for all , we have .
By the superalgebra analog of [
9] (Lemma 2.7) adapted to
, if
satisfies
(with
n supercommutators), then
, which is already true since
is supercommuting. By the superalgebra version of [
9] (Theorem 2.5), since
inherits the superalgebra structure and the cycle condition holds,
is proper. Hence, there exist
and an
R-linear map
such that
Since
X is connected and the Hasse diagram satisfies the cycle condition, the supercenter
consists of diagonal functions that are constant on connected components. For a connected
X, we have
(analogous to [
33] (Corollary 1.3.15)). Thus, we may take
.
Define
by
We now show that
is central-valued, i.e.,
for all
. For
, we have
since
is central. For any
and
, by Lemma 4, we have
Hence,
since
and elements of the supercenter are diagonal (i.e., zero off the diagonal), thus,
for all
, and
Next, we show that
for all
, ensuring
. Since
X is connected, it suffices to show
for
. Consider the map
defined by
where
,
, and
. Since
is supercommuting, we have
. Linearizing
, we obtain
Replace
with
, since
and
supercommutes with
f. Set
,
, and
. Then
since terms with
involve
, which is diagonal. This simplifies to
Since
R is
-torsion-free, we have
Since
is diagonal and even (
), while
, we have
Higher supercommutators with
(which is even) yield
Since
X is connected,
for some
, and therefore
Hence,
, and
is proper. The cycle condition ensures the consistency of coefficients, as in [
9]. □
Example 4. Let , which is -torsion-free for all , and let with the natural order . The incidence algebra has the -basiswhere denotes the characteristic function of . Choose the idempotent . Then the induced -grading is Define by That is, is obtained by doubling f and then adding a diagonal function whose entries are all equal to the trace .
Claim: θ is a supercommuting map and hence proper.
Proof. For , writewhere . Since is diagonal with constant diagonal entries, we have . As clearly supercommutes with f, and central elements also supercommute, it follows that Thus, θ is supercommuting. By Theorem 1, θ is proper, with and μ central-valued. □
5. The General Case
In this section, we study supercommuting maps on the incidence algebra
in the general case, i.e., without assuming the connectedness of
X. Let
R be a commutative ring with unity that is
-torsion-free, and let
be endowed with a superalgebra structure via a nontrivial idempotent
e, with an even part
and odd part
The supercommutator is defined as
for homogeneous elements
, and extended linearly. For a positive integer
n, we define the
super-n-center of an
R-algebra
A as follows:
where
and
for
. Clearly,
, the supercenter of
A.
Lemma 5. Let be the family of connected components of a locally finite preordered set X, and letbe the incidence algebra over a commutative ring R that is -torsion-free, endowed with a superalgebra structure. Let θ be a supercommuting map on , i.e., for all . Then, for each , there exists a unique supercommuting map on and a unique mapsuch that the restriction of θ on satisfies Proof. Since
X is a locally finite preordered set, its connected components
partition
X, and the incidence algebra decomposes as
where each
is a subalgebra with the induced superalgebra structure. For each
, let
be the canonical projection onto
, and let
be the canonical projection onto the complementary subalgebra. Define
Clearly, , and this decomposition is unique since and project onto complementary subspaces.
For any
, since
is supercommuting, we have
Write
, where
and
. Since
, we have
for any
with
, because
only if
. Thus,
since
. Hence,
This shows that is a supercommuting map on .
Next, we show that
. Define the map
by
where
,
, and
for all
. Since
is supercommuting,
. For
n-fold supercommuting, we assume that
Linearizing this condition gives
Let
and
for some
. Then,
Since
,
, and
, we have
. Hence,
because
, so
The second term involves
, but we focus on the first term:
Since
R is
-torsion-free, we obtain
Thus, , as has support only in . This completes the proof. □
Proposition 2. Let be a family of -torsion-free R-algebras, each endowed with a superalgebra structure. If for all , then every n-supercommuting map on , satisfying for all , is proper if and only if every n-supercommuting map on is proper for all .
Proof. Let
be an
n-supercommuting map on
, i.e.,
for all
. By the superalgebra analog of Lemma 5, for each
, the restriction satisfies
where
is an
n-supercommuting map and
is an
R-linear map.
Sufficiency: Assume that every
n-supercommuting map on
is proper for all
. Then, for each
, there exists
and an
R-linear map
such that
Define an
R-linear map
by
where
with
. Define
for all
. We need to show that
.
Since
is
n-supercommuting, we have the linearized identity
where
and
. Set
and
for some fixed
. Then,
Since
, it follows that
Since
and
, for
, we have
, because
has no component in
. Hence,
Since
, we have
because
. Therefore,
and hence,
Since
R is
-torsion-free and
for all
, we obtain
Thus,
. However, since
and
, we must have
. Therefore,
Since
and
, we can define
, where
. Thus,
where
and
are
R-linear. Hence,
is proper.
Necessity: Suppose there exists some
such that not every
n-supercommuting map on
is proper. Then there exists an
n-supercommuting map
that is improper. Construct a map
by
where
for the given
i, and for
,
is a proper
n-supercommuting map, say
for some
. For
, we have
since
for
. Because each
is
n-supercommuting, we have
, so
is
n-supercommuting. However, since
is improper,
cannot be proper, as its restriction to
is
. This completes the proof. □
Theorem 2. Let R be a commutative ring with unity that is 2-torsion-free and -torsion-free for some positive integer n. Let X be a locally finite preordered set with connected components , and letbe the incidence algebra endowed with a superalgebra structure via a nontrivial idempotent e. If any two directed edges in each connected component of the complete Hasse diagram are contained in one cycle, then every supercommuting map is proper. Proof. Since
X is a locally finite preordered set, its incidence algebra decomposes as
where each
is a subalgebra with the superalgebra structure induced via
e. By Lemma 5, for a supercommuting map
on
, the restriction to
satisfies
where
is supercommuting, and
.
Since each
satisfies the cycle condition (any two directed edges lie in one cycle), Theorem 1 implies that every supercommuting map
on
is proper. Hence, there exists
and an
R-linear map
such that
Since
R is
-torsion-free, Lemma 5 implies that
. For incidence algebras, the super-
n-center
coincides with the supercenter
, because elements in
must supercommute with all basis elements
up to the
n-th supercommutator, forcing them to be diagonal and constant on connected components (see [
33]).
From the proof of Proposition 2, since
, we have
for all
, because
For any
, define
and
Since
for
, we obtain
As , we have , and is R-linear. Hence, is proper, completing the proof. □
Example 5. Let and equip X with the preorder generated by the directed m-cycle The transitive closure of these relations gives for every pair , so every pair of vertices is comparable (in both directions). Hence,which is the full matrix algebra (identifying f with the matrix ). Choose the nontrivial idempotent (the matrix unit). The induced superalgebra grading isThe (super-)center of is the set of scalar matrices: By Theorem 2, the cycle condition (that any two directed edges lie in one cycle) is clearly satisfied here, since the single cycle contains all edges. Therefore, every supercommuting map is proper; that is, there exists and an R-linear map such that Remark: Conversely, not every map of the form is automatically supercommuting; additional graded constraints may further restrict the admissible λ and μ. The theorem asserts that if θ is supercommuting, then it must be of the above form.
Example 6. Let , where forms a directed 3-cycle and forms a directed 4-cycle. As in Example 5, taking the transitive closure on each makes every pair within comparable. Hence, The superalgebra structure is induced by the same fixed nontrivial idempotent e, which splits each block according to the matrix decomposition.
Let be a supercommuting map. By Lemma 5, we may write, for ,where is supercommuting andtakes values in the super-n-center of the other component. In our matrix algebra components, we have (the scalar matrices of each block). Hence, each is a scalar matrix lying in the other block. We now show that . Fix i and take and arbitrarily. Linearizing the n-fold supercommuting identity (as in the proof of Proposition 2) yields a relation whose first summand equals Since R is -torsion-free, this implies However, is a scalar matrix residing in the other summand, (), so it has zero support on . Therefore, the only possibility consistent with this identity and the disjoint supports is that is the zero scalar. Hence, for both .
Consequently,i.e., there are no cross terms. By Theorem 1, each is proper on its respective block. Combining these, we obtainwhere and are R-linear. Equivalently, for any , Thus, θ is proper on . This verifies Theorem 2 in this concrete two-component case.
6. Conclusions and Future Work
In this paper, we have advanced the theory of commuting maps on incidence algebras [
9] by introducing and characterizing
supercommuting maps in the context of superalgebra structures, as developed by Ghahramani and Heidari Zadeh [
23]. Our main result demonstrates that, under the graph-theoretic condition that any two directed edges in each connected component of the complete Hasse diagram
lie within a single cycle, every supercommuting map on the incidence algebra
, where
R is a 2-torsion-free and
-torsion-free commutative ring with unity, is proper. This finding extends classical results on commuting maps in prime rings, triangular algebras, and generalized matrix algebras [
4,
7,
8] to the superalgebra setting, employing the Peirce decomposition induced by a nontrivial idempotent to separate even and odd components.
The proofs rely on foundational Lemmas that describe the structure of supercommuting maps on basis elements (Lemmas 2 and 3) and their behavior under restrictions to connected components (Lemma 5). The culminating theorems (Theorems 1 and 2) provide a precise characterization: such maps take the form
where
lies in the supercenter
and
is an
R-linear map into
.
Looking ahead, several directions merit further investigation. One may study supercommuting maps on broader classes of algebraic structures, such as generalized matrix algebras or triangular algebras equipped with supergradings, or explore functional identities and multilinear maps within superalgebras [
6]. Moreover, relaxing the cycle condition, examining situations in which improper supercommuting maps arise, or extending the framework to infinite preordered sets lacking local finiteness could reveal new structural phenomena and classifications.
To guide future research, we propose the following open problems:
- (i)
Characterize improper supercommuting maps on incidence algebras when the cycle condition is violated. In particular, construct explicit examples of improper maps on posets whose Hasse diagrams contain multiple equivalence classes under the relation ≈ defined in Definition 3.
- (ii)
Extend the present results to incidence algebras over noncommutative rings R or rings that are not -torsion-free. What modifications to the proper form are required in such settings?
- (iii)
Investigate higher-order supercommuting maps, where the condition is for . Can analogs of Theorems 1 and 2 be established, and what role does the super-k-center play?
- (iv)
Explore potential applications of supercommuting maps to combinatorial structures such as poset cohomology or Möbius inversion in superalgebras. For instance, how do supercommuting automorphisms influence the Möbius function in incidence algebras with supergrading?
- (v)
Examine supercommuting maps on variants of incidence algebras, such as reduced incidence algebras or those arising from categories. Does the cycle condition generalize to categorical Hasse diagrams?