Obstacle Avoidance Algorithm for Multi-Robot Formation Based on Affine Transformation
Abstract
1. Introduction
1.1. Traditional Formation Control Method
1.2. Affine Formation Control Method
2. Formation Control Law
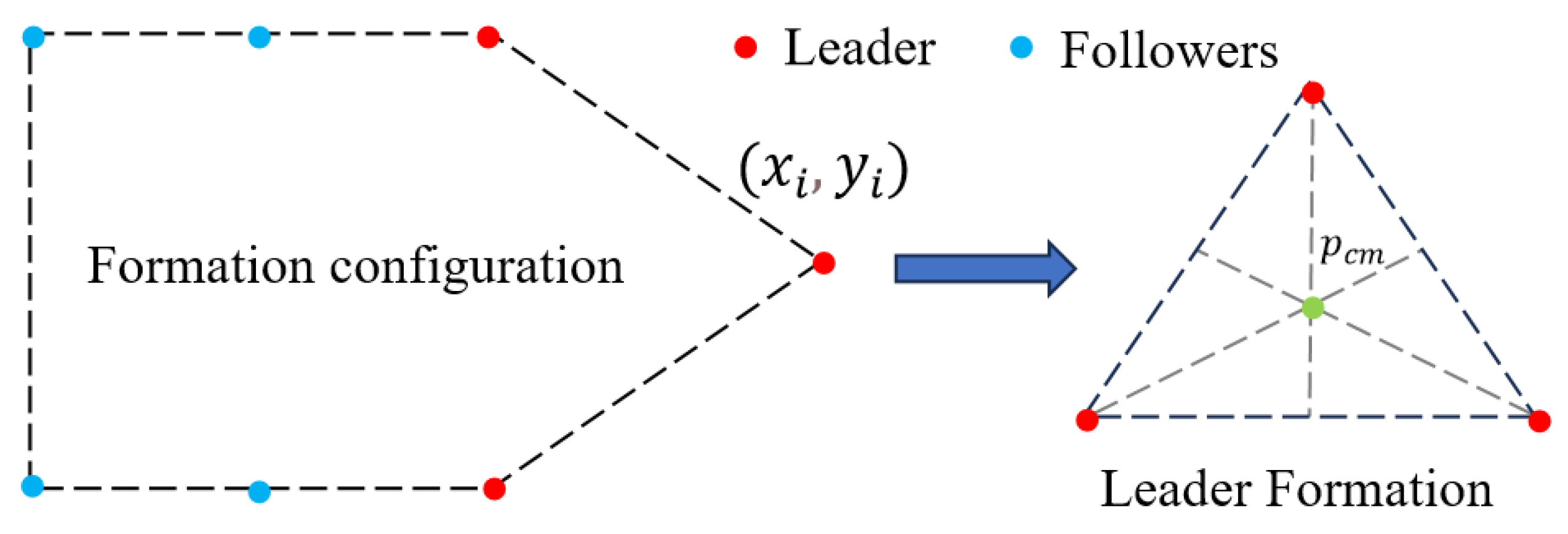
2.1. Fundamentals of Graph Theory
2.2. Control Law
3. Obstacle Avoidance Formation Control
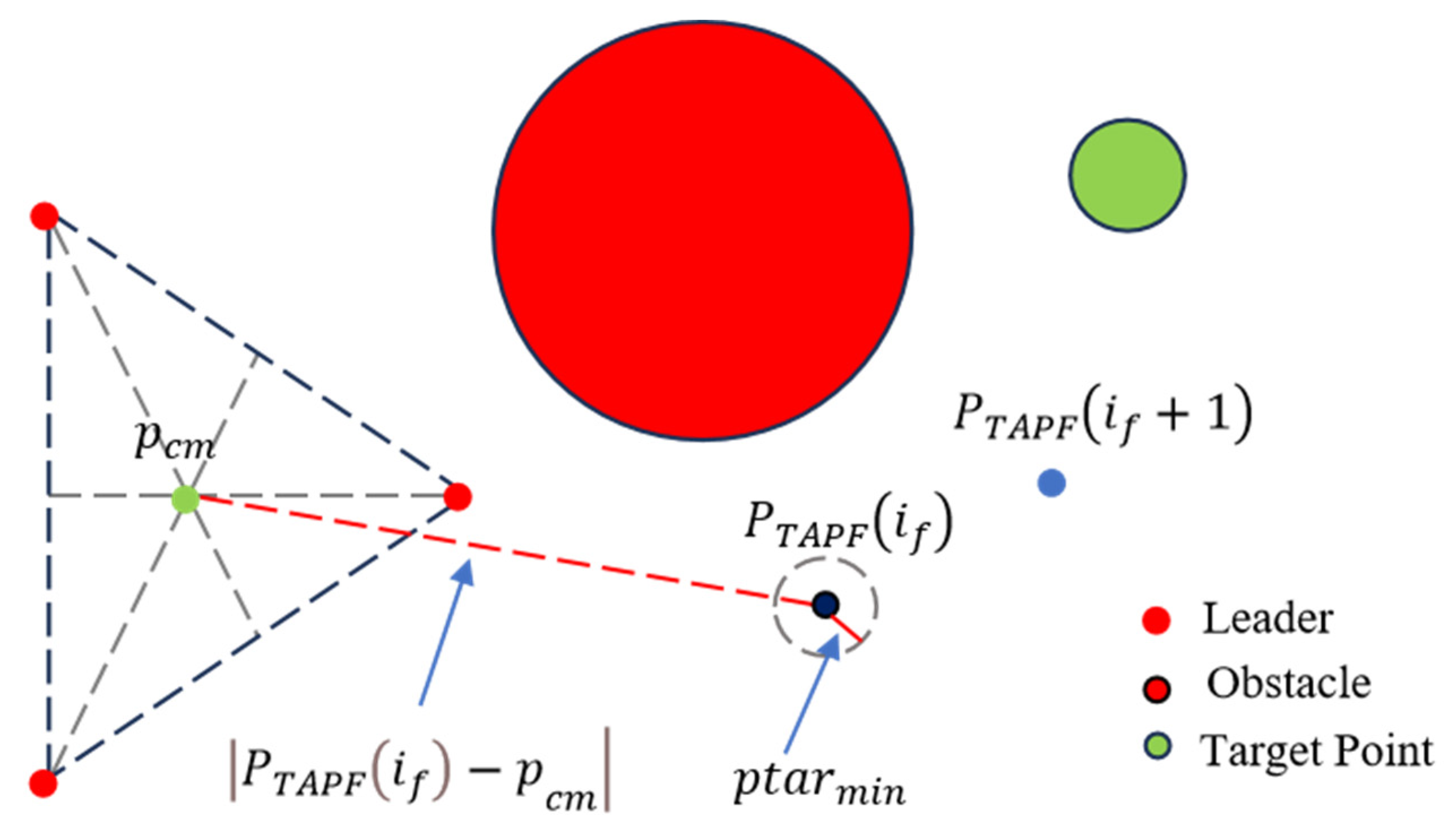
3.1. Affine Transformation
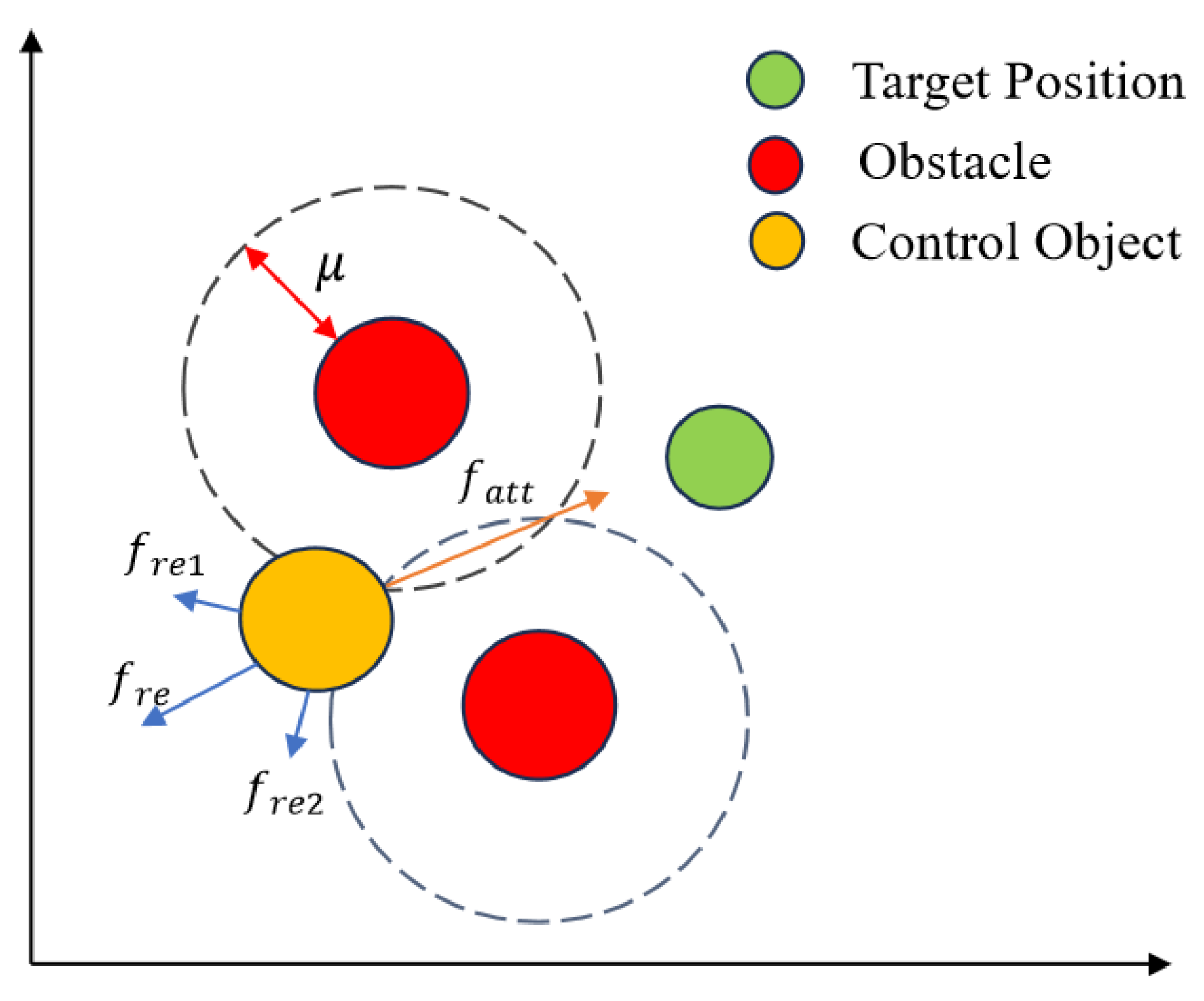
3.2. Artificial Potential Field Method
3.3. Obstacle Avoidance Formation Control
4. Results and Discussion
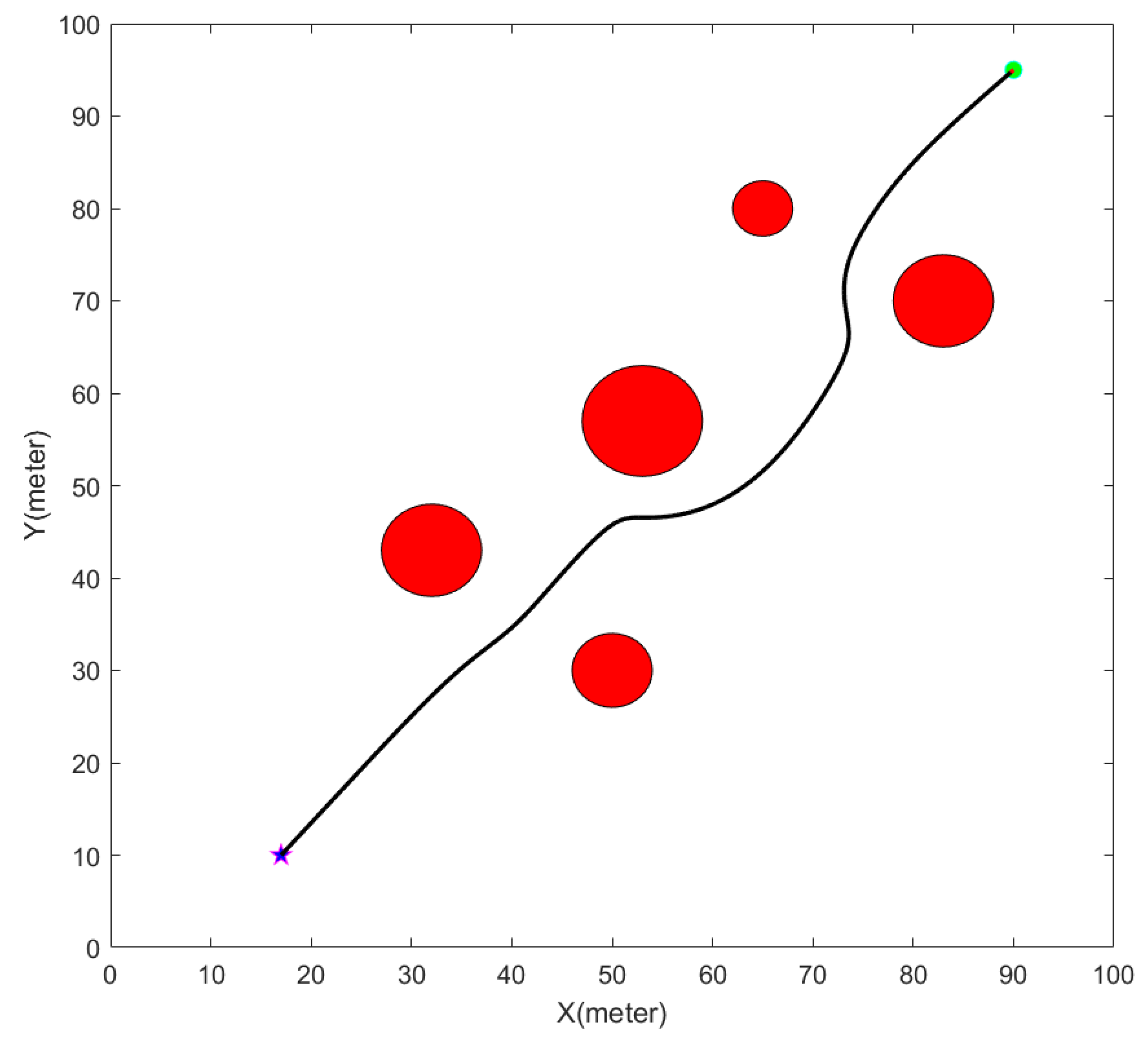
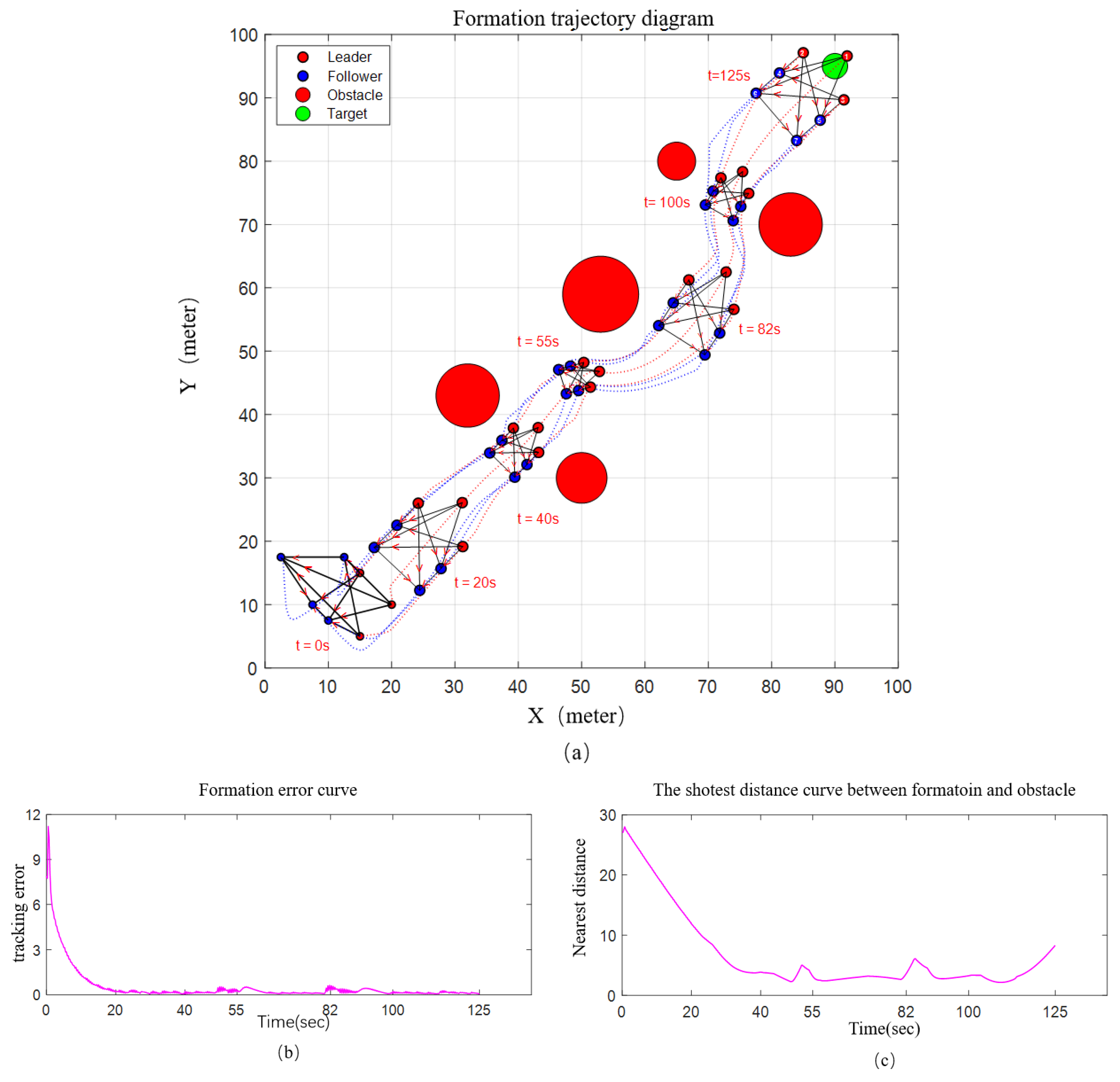
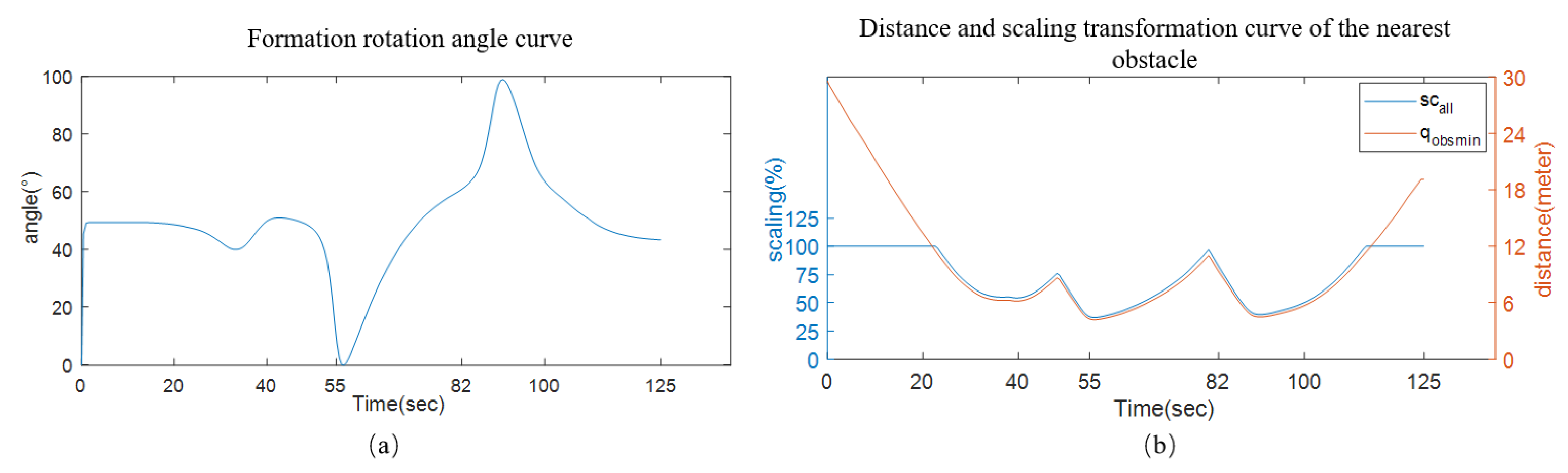
4.1. Simulation Validation
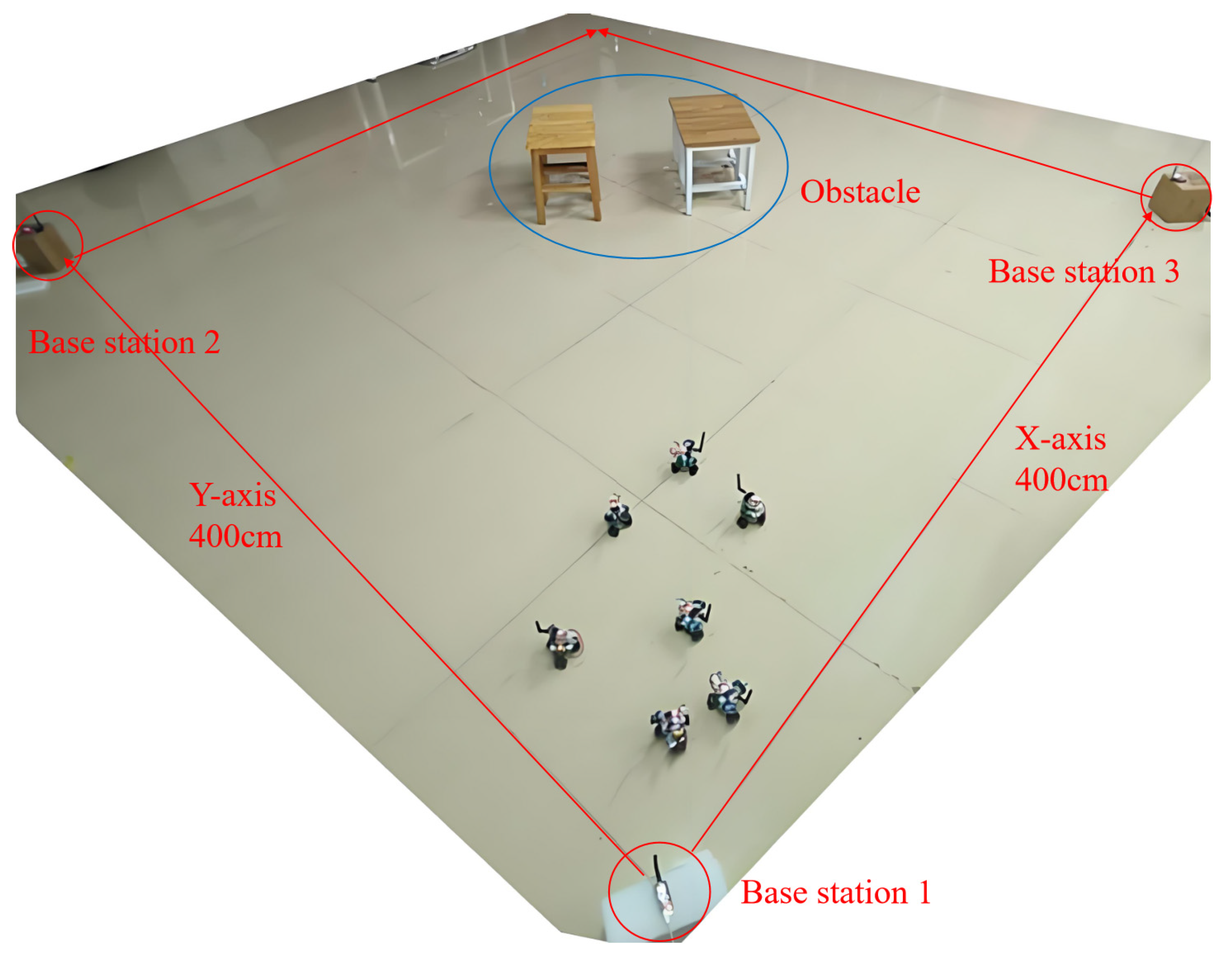
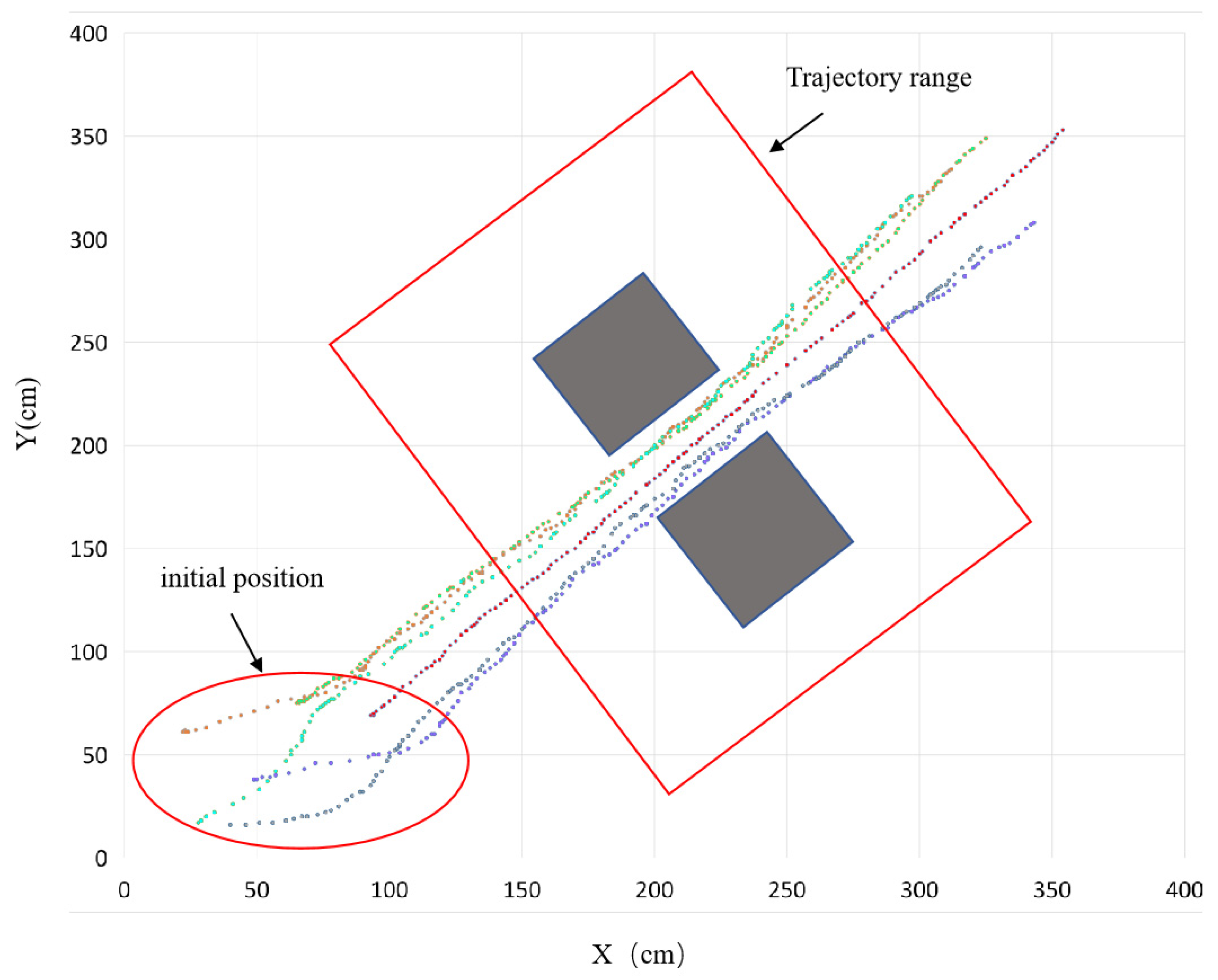
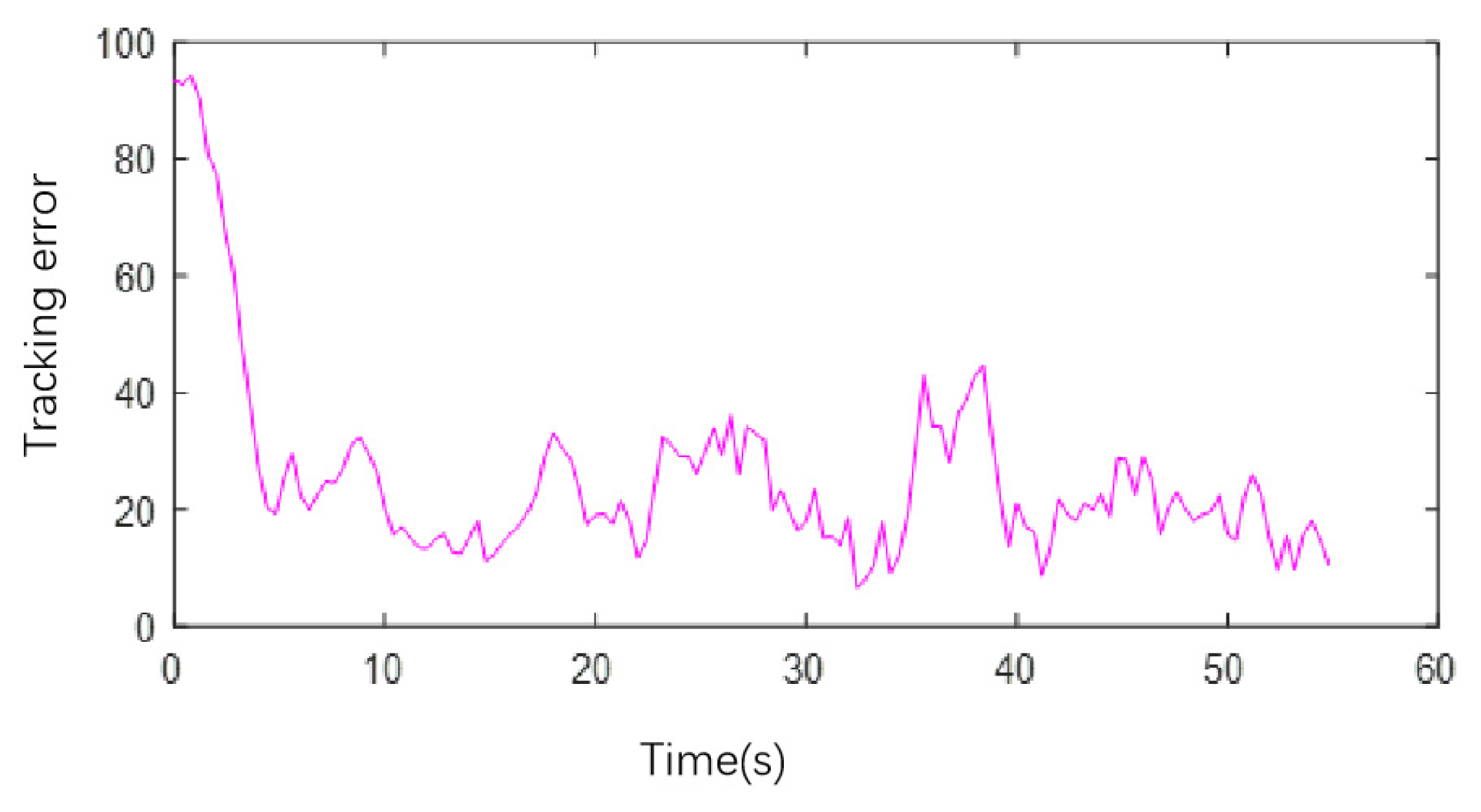
4.2. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Comprehensive Table of Simulation Parameters
| Parameter Category | Parameter Name | Symbol | Function Description |
| Artificial Potential Field (APF) Basic Parameters | Attractive Field Gain Coefficient | katt | Adjusts the gravitational pull of the target point on the formation centroid, ensuring stable movement toward the target without path deviation from insufficient attraction. |
| Repulsive Field Gain Coefficient | kobs | Regulates the repulsive force of obstacles on the formation centroid—sufficient to avoid collisions when approaching obstacles, while preventing path oscillation from excessive repulsion. | |
| Time Step | Δt | Balances simulation efficiency and trajectory smoothness. Too large a step causes discrete trajectories; too small causes increases in computational cost. | |
| Maximum Obstacle Influence Range | μ | Defines the effective range of obstacle repulsion. Beyond this, obstacles exert no force. Set based on simulated obstacle size (≈2 m diameter) to trigger avoidance only when necessary. | |
| APF Path-Related Parameters | Path Data Storage Set | PTAPE | Stores all discrete path coordinates of the formation centroid (from initial to target position), providing a movement reference for the formation. |
| Target Point Coordinates | qobs | Defines the final destination of the formation and acts as the source of the attractive field. | |
| Current Centroid Position | Plo(t) | Describes the real-time position of the formation centroid, used to calculate attraction, repulsion, and path updates. | |
| Control Law—Follower Parameters | Follower Proportional Gain | kp | Accelerates convergence of follower position errors. Larger values speed up correction but may cause overshoot if excessive. |
| Follower Derivative Gain | kv | Suppresses oscillations during follower movement. Larger values enhance stability but may slow response if too high. | |
| Follower Design Parameter | di | Forms the stable diagonal matrix D = \text{diag}(d_i), eliminating non-positive eigenvalues of the signed Laplacian matrix to ensure follower control stability. | |
| Follower Weight Coefficient | ri | Adjusts information interaction intensity between followers and adjacent robots, influencing tracking accuracy. | |
| Control Law—Leader Parameters | Leader Proportional Gain | kj | Ensures leaders move stably along the P_{\text{TAPE}} path, avoiding deviation from weak responsiveness. |
| Current Leader Position | pj | Real-time position of the j-th leader, used to compute leader control inputs. | |
| Target Leader Position | pij | Calculated via the P_{\text{TAPE}} path and affine matrix, serving as the movement target for leaders. | |
| Affine Transformation Core Parameters | Minimum Obstacle Distance Threshold | kmax | Triggers formation scaling when exceeded. Equals the distance from the leader centroid to the farthest robot, ensuring a safe gap between the formation and obstacles. |
| Initial Scaling Coefficient | sc(0) | Sets the formation to its nominal size initially, aligning with theoretical formation design. | |
| Real-Time Scaling Coefficient | sc(t) | Dynamically adjusts based on centroid-obstacle distance to enable adaptive obstacle avoidance. | |
| Initial Rotation Angle | θ(0) | Starts the formation with no rotation (aligned with the X-axis) for stable initial movement. | |
| Real-Time Rotation Angle | θ(t) | Adjusts formation direction via the centroid-target distance vector, ensuring path alignment. |
References
- Wu, X.; Wang, S.; Xing, M. Observer-based leader-following formation control for multi-robot with obstacle avoidance. IEEE Access 2019, 7, 14791–14798. [Google Scholar] [CrossRef]
- Bernardo, J.M.; Bazan, M.H.; Costa, D.G. Formation tracking control and obstacle avoidance of unicycle-type robots guaranteeing continuous velocities. Sensors 2021, 21, 4374. [Google Scholar] [CrossRef] [PubMed]
- Alahmari, S.; Salameh, A.A.; Innab, N.; Alsharif, A.; Alqarni, A.M. Hybrid bio-inspired optimized neural network for real-time evasion of multi-robot systems in dynamic environments. Dyn. Games Appl. 2024; early access. [Google Scholar]
- Liu, Y.; Zhang, J.; Zhang, Y.; Li, Z. Local path planning of unmanned surface vehicles’ formation based on vector field and flow field traction. J. Mar. Sci. Eng. 2024, 12, 1705. [Google Scholar] [CrossRef]
- Nakamura, J.W.G.; de Lima, D.W.B.; Almeida, N.M. Adaptive immune fuzzy quasi-sliding mode control for leader–follower formation of wheeled mobile robots under uncertainties and disturbances with obstacle avoidance. Eng. Comput. 2024, 41, 1697–1739. [Google Scholar]
- Liu, Y.; Chen, C.; Wang, Y.; Xin, B. A fast formation obstacle avoidance algorithm for clustered UAVs based on artificial potential field. Aerosp. Sci. Technol. 2024, 147, 108974. [Google Scholar] [CrossRef]
- Shojaei, K. Neural network formation control of underactuated autonomous underwater vehicles with saturating actuators. Neurocomputing 2016, 194, 372–384. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Ma, X.-W.; Bai, G.-Q.; Sha, Y.; Liu, J. Multi-autonomous underwater vehicle formation control and cluster search using a fusion control strategy at complex underwater environment. Ocean. Eng. 2020, 216, 108048. [Google Scholar] [CrossRef]
- Han, G.; Qi, X.; Peng, Y.; Lin, C.; Zhang, Y.; Lu, Q. Early warning obstacle avoidance-enabled path planning for multi-AUV-based maritime transportation systems. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2656–2667. [Google Scholar] [CrossRef]
- Pham, V.T.; Gonzalez, A.M.; Pena, R.I. Switching formation strategy with the directed dynamic topology for collision avoidance of a multi-robot system in uncertain environments. IET Control Theory Appl. 2020, 14, 2948–2959. [Google Scholar]
- Dai, Y.; Kim, Y.G.; Wee, S.G.; Lee, D.H.; Lee, S.G. A switching formation strategy for obstacle avoidance of a multi-robot system based on robot priority model. ISA Trans. 2015, 56, 123–134. [Google Scholar] [CrossRef] [PubMed]
- Shiyu, Z. Affine formation maneuver control of multiagent systems. IEEE Trans. Autom. Control 2018, 63, 4140–4145. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, D.; You, Y.; Duan, H. Affine transformation based formation maneuvering for discrete-time directed networked systems. Sci. China Technol. Sci. 2020, 63, 73–85. [Google Scholar] [CrossRef]
- Kang, C.; Xu, J.; Bian, Y. Affine formation maneuver control for multi-agent based on optimal flight system. Appl. Sci. 2024, 14, 2292. [Google Scholar] [CrossRef]
- Yao, M.; Guo, K.; Lu, Y.; Sun, Z. Distributed adaptive integral sliding mode affine formation maneuver control for multiple AUVs with event-triggered chattering-reduction mechanism. IEEE Trans. Veh. Technol. 2024, 73, 16341–16350. [Google Scholar] [CrossRef]
- Pang, W.; Zhu, D.; Yang, S.X. A novel time-varying formation obstacle avoidance algorithm for multiple AUVs. Int. J. Robot. Autom. 2023, 38, 194–207. [Google Scholar] [CrossRef]
- Sun, J.; Xie, B.; Xiong, W.; Zhang, Q.; Zhao, Z. Posture algorithm for mobile robot based on ultrawide band. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221115285. [Google Scholar] [CrossRef]




| Transformation Type | Geometric Characteristic | Obstacle Avoidance Flexibility |
|---|---|---|
| Similarity/Helmert transformation | Keep the shape unchanged (angle, side length ratio unchanged) | Low, only the overall scaling |
| Affine transformation | Shape can be changed (parallelism unchanged, non-uniform scaling) | Higher, directional compression/stretching formation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Su, Y.; Zhou, Y.; Sun, J.; Zhou, Z.; Wan, Z.; Deng, W. Obstacle Avoidance Algorithm for Multi-Robot Formation Based on Affine Transformation. Symmetry 2025, 17, 1816. https://doi.org/10.3390/sym17111816
Zhang Q, Su Y, Zhou Y, Sun J, Zhou Z, Wan Z, Deng W. Obstacle Avoidance Algorithm for Multi-Robot Formation Based on Affine Transformation. Symmetry. 2025; 17(11):1816. https://doi.org/10.3390/sym17111816
Chicago/Turabian StyleZhang, Qiaolong, Yanhong Su, Youhang Zhou, Jing Sun, Zhe Zhou, Zilin Wan, and Wenna Deng. 2025. "Obstacle Avoidance Algorithm for Multi-Robot Formation Based on Affine Transformation" Symmetry 17, no. 11: 1816. https://doi.org/10.3390/sym17111816
APA StyleZhang, Q., Su, Y., Zhou, Y., Sun, J., Zhou, Z., Wan, Z., & Deng, W. (2025). Obstacle Avoidance Algorithm for Multi-Robot Formation Based on Affine Transformation. Symmetry, 17(11), 1816. https://doi.org/10.3390/sym17111816






