Symmetry-Guided Numerical Simulation of Viscoelastic Pipe Leakage Based on Transient Inverse Problem Analysis
Abstract
1. Introduction
2. Numerical Simulation
2.1. Viscoelastic Constitutive Equation
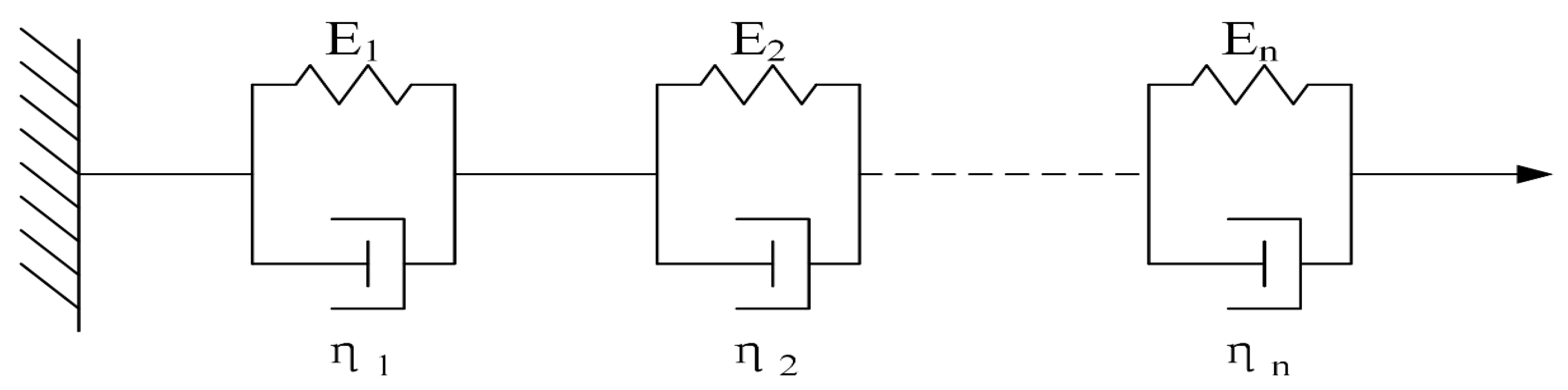
2.1.1. Kelvin–Voigt Model
2.1.2. Strain Equation
2.2. One-Dimensional Transient Flow Model for Viscoelastic Pipelines
2.2.1. Basic Equations
2.2.2. One-Dimensional Unsteady Friction Model
2.2.3. Boundary Conditions
3. Frequency-Domain Analysis of Transient Flow in Viscoelastic Pipelines
3.1. Fourier Transform
3.2. Derivation of the Transfer Matrix
4. Inverse Problem Analysis Method for Transient Flow Leak Detection
5. Model Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| J0 | instantaneous compliance; |
| τk | relaxation time of the k-th dashpot (s); |
| Jk | creep compliance of the k-th element; |
| Ek | elastic modulus of the k-th spring; |
| γ | specific weight (kg/m2·s2); |
| α | a parameter related to whether the pipeline can be displaced and the degree of displacement; |
| e | pipeline wall thickness (m); |
| n | Total number of monitoring points in the flow field; |
| D(t) | inner diameter of the pipeline at time t (m); |
| e (t) | wall thickness of the pipeline at time t (m); |
| Ar | cross-sectional area of the pipeline (m2); |
| R | inner diameter of the pipeline (m); |
| bimax | Widest blade length after unfolding; |
| w (t) | weight function; |
| u | axial flow velocity of the fluid (m/s); |
| λ | friction coefficient; |
| μ | dynamic viscosity (Pa·s); |
| v | kinematic viscosity (m2/s); |
| mi,, ni | constant coefficients related to the dimensionless time; |
| AA*,BB* | revision coefficients that vary with the pipeline smoothness; |
| Hp | piezometric head at the pipeline inlet; |
| Hr | upstream reservoir water level; |
| Qp1 | flow rate at the pipeline inlet at time t; |
| Q0 | flow rate under steady-state conditions; |
| H0 | head loss of the valve under steady-state conditions; |
| (CdAG)0 | product of the valve opening area and discharge coefficient; |
| instantaneous drop of the hydraulic grade line when flowing through the valve; | |
| reflects the influence of the flow rate Q on the pressure head gradient ; | |
| reflects the influence of the flow rate on the pressure head gradient H; | |
| = | propagation constant; |
| Zc = | characteristic impedance; |
| E | represents the objective function; |
| M | number of sensor measurement points; |
| N | denotes the total sampling time; |
| Xj | unknown leak parameters; |
| l | leak location; |
| Ql0 | leak rate; |
| , | weight coefficients. |
| , | water head and flow rate results after filtering and denoising, respectively. |
References
- Tjuatja, V.; Keramat, A.; Pan, B.; Duan, H.F.; Brunone, B.; Meniconi, S. Transient flow modeling in viscoelastic pipes: A comprehensive review of literature and analysis. Phys. Fluids 2023, 35, 081302. [Google Scholar] [CrossRef]
- Rezapour, I.; Shafai Bejestan, M.; Aminnejad, B. Case study of leak detection based on Gaussian function in experimental viscoelastic water pipeline. Water Supply 2021, 21, 3860–3874. [Google Scholar] [CrossRef]
- Khudayarov, B.A.; Turaev, F.Z. Mathematical simulation of nonlinear oscillations of viscoelastic pipelines conveying fluid. Appl. Math. Modell. 2019, 66, 662–679. [Google Scholar] [CrossRef]
- Parvin, C.C.; Manoochehr, F.M.; Sadegh, H. Modeling of Transient Flows in Viscoelastic Pipe Network with Partial Blockage; Aqua-Water Infrastructure Ecosystems Society: London, UK, 2021; Volume 70, pp. 832–844. [Google Scholar]
- Lazhar, A.; Hadj-Taïeb, L.; Hadj-Taïeb, E. Two leaks detection in viscoelastic pipeline systems by means of transient. J. Loss Prev. Process Ind. 2013, 26, 1341–1351. [Google Scholar] [CrossRef]
- Lee, P.J.; Vítkovský, J.P.; Lambert, M.F.; Simpson, A.R.; Liggett, J. Frequency response leak detection using inline valve closures. In Proceedings of the 9th International Conference on Pressure Surges, Chester, UK, 24–26 March 2004; Volume 1, pp. 239–253. [Google Scholar]
- Lee, P.J.; Vítkovský, J.P.; Lambert, M.F.; Simpson, A.J.; Liggett, J.A. Frequency domain analysis for detecting pipeline leaks. J. Hydraul. Eng. 2005, 131, 596–604. [Google Scholar] [CrossRef]
- Duan, H.F.; Lee, P.J.; Ghidaoui, M.S.; Tung, Y.K. System response function–based leak detection in viscoelastic pipelines. J. Hydraul. Eng. 2012, 138, 143–153. [Google Scholar] [CrossRef]
- Pan, B.; Duan, H.F.; Meniconi, S.; Urbanowicz, K.; Che, T.C.; Brunone, B. Multistage frequency-domain transient-based method for the analysis of viscoelastic parameters of plastic pipes. J. Hydraul. Eng. 2020, 146, 04019068. [Google Scholar] [CrossRef]
- Pan, B.; Duan, H.F.; Meniconi, S.; Brunone, B. FRF-based transient wave analysis for the viscoelastic parameters identification and leak detection in water-filled plastic pipes. Mech. Syst. Signal Process. 2021, 146, 107056. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients; Van Nostrand Reinhold: New York, NY, USA, 1987. [Google Scholar]
- Nault, J.D.; Karney, B.W.; Jung, B.S. Generalized flexible method for simulating transient pipe network hydraulics. J. Hydraul. Eng. 2018, 144, 04018031. [Google Scholar] [CrossRef]
- Ranginkaman, M.H.; Haghighi, A.; Samani, H.M.V. Application of the frequency response method for transient flow analysis of looped pipe networks. Int. J. Civ. Eng. 2017, 15, 677–687. [Google Scholar] [CrossRef]
- Kim, S.H. Address-oriented impedance matrix method for generic calibration of heterogeneous pipe network systems. J. Hydraul. Eng. 2008, 134, 66–75. [Google Scholar] [CrossRef]
- Ferrante, M.; Brunone, B. Pipe system diagnosis and leak detection by unsteady-state tests. 1. Harmonic analysis. Adv. Water Resour. 2003, 26, 95–105. [Google Scholar] [CrossRef]
- Weinerowska-Bords, K. Viscoelastic model of waterhammer in single pipeline-problems and questions. Arch. Hydro-Eng. Environ. Mech. 2006, 53, 331–351. [Google Scholar]
- Wineman, A.S.; Rajagopal, K.R. Mechanical Response of Polymers: An Introduction; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Xu, Y.; Zhang, S.; Zhou, L.; Ning, H.; Wu, K. Dynamic Behavior and Mechanism of Transient Fluid–Structure Interaction in Viscoelastic Pipes Based on Energy Analysis. Water 2024, 16, 1468. [Google Scholar] [CrossRef]
- Mohammad, B.; Mahdi, R.A.; Kayvan, S. Numerical analysis of laminar viscoelastic fluid hammer phenomenon in an axisymmetric pipe. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 396. [Google Scholar] [CrossRef]
- Zielke, W. Frequency-dependent friction in transient pipe flow. J. ASME 1968, 90, 109–115. [Google Scholar] [CrossRef]
- Urbanowicz, K. New approximation of unsteady friction weighting functions. In Proceedings of the 11th International Conference on Pressure Surges 2012, Lisbon, Portugal, 24–26 October 2012. [Google Scholar]
- Urbanowicz, K. Analytical expressions for effective weighting functions used during simulations of water hammer. J. Theor. Appl. Mech. 2017, 55, 1029–1040. [Google Scholar] [CrossRef]
- Nash, G.A.; Karney, B.W. Efficient inverse transient analysis in series pipe systems. J. Hydraul. Eng. 1999, 125, 761–764. [Google Scholar] [CrossRef]
- Vítkovský, J.P.; Simpson, A.R.; Lambert, M.F. Leak detection and calibration using transients and genetic algorithms. J. Water Resour. Plan. Manag. 2000, 126, 262–265. [Google Scholar] [CrossRef]
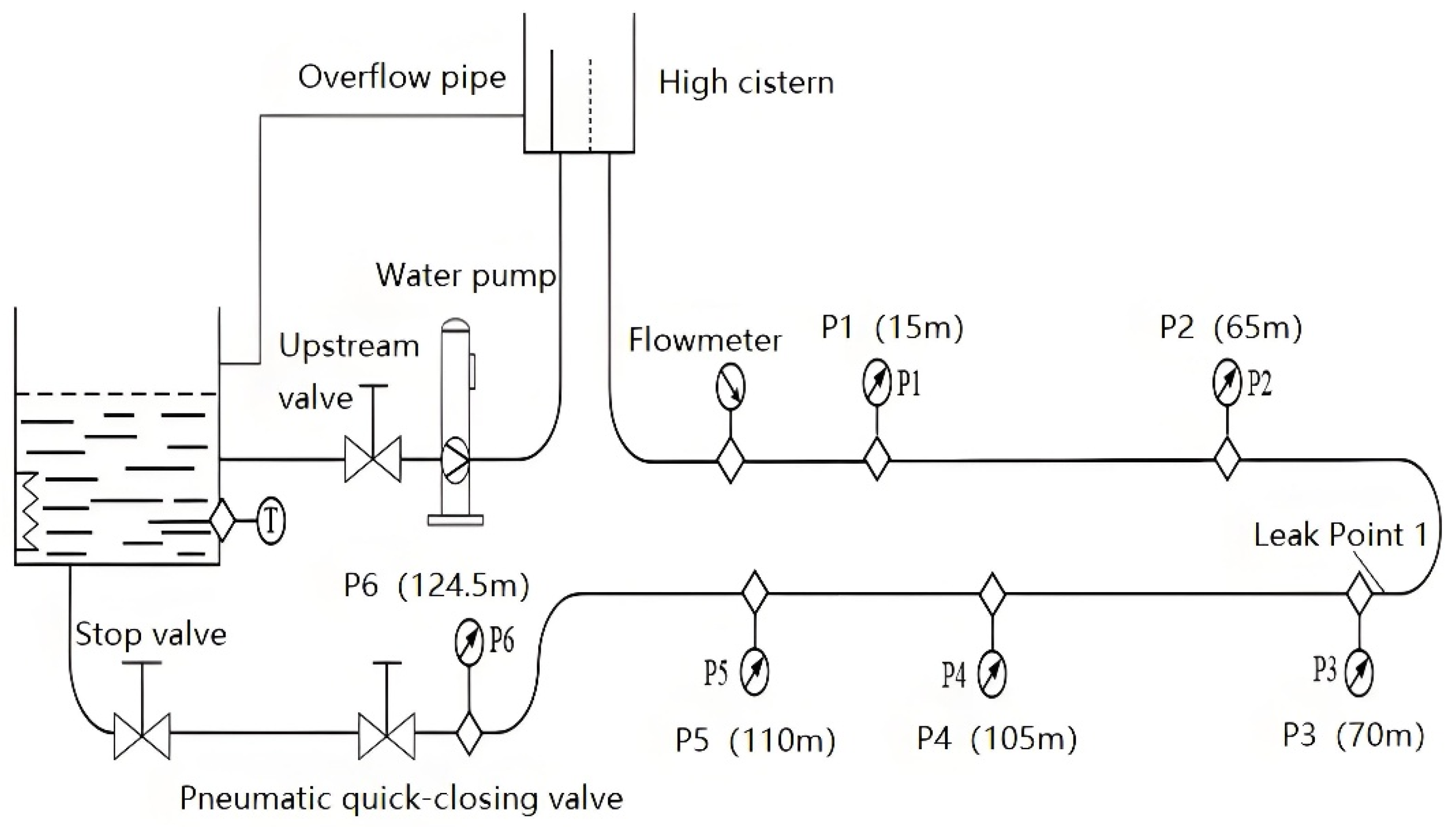

| Position Number | Distance from the Elevated Water Tank (m) |
|---|---|
| 1 | 15 |
| 2 | 65 |
| 3 | 70 |
| 4 | 105 |
| 5 | 110 |
| 6 | 124.5 |
| Comparison | Indicator | Numerical Value | Result |
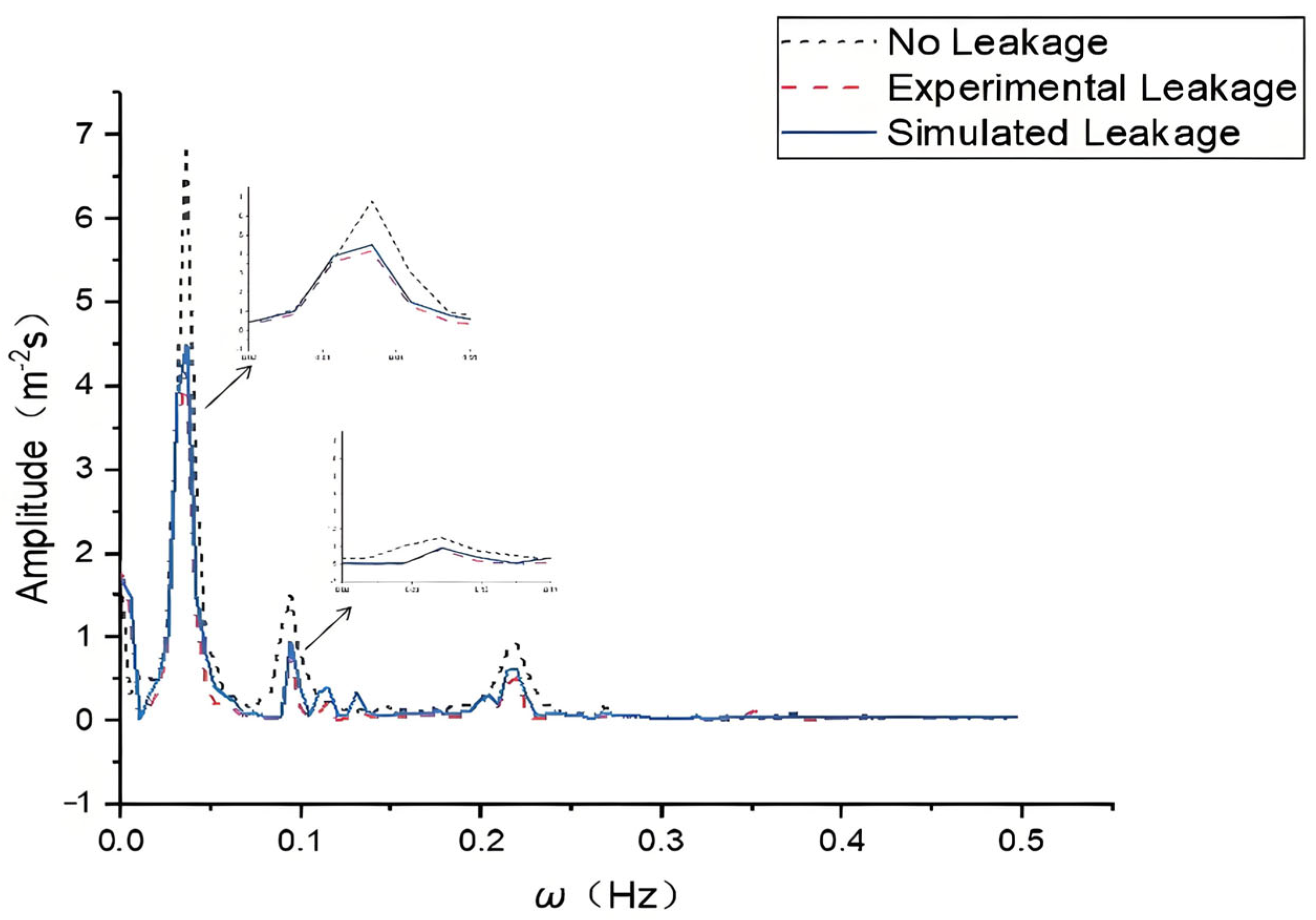
| Experimental leakage- Simulated leakage | RMSE | 0.042 m | The deviation is less than 0.05 m, far lower than the engineering allowable pressure measurement error (±0.1 m), and the simulation value is in high agreement with the experimental value |
| Experimental leakage- Simulated leakage | R2 | 0.968 | The correlation coefficient is close to 1, indicating that the variation trend of the amplitude in the frequency domain is completely consistent, and the model can accurately reproduce the characteristics of the leakage flow field |
| No leakage-Experimental leakage | PAR | 24.2% | The peak attenuation exceeds 20%, and the amplitude attenuation caused by leakage is significant, meeting the threshold requirements for leakage identification criteria |
| No leakage-Simulated leakage | PAR | 26.3% | The PAR deviation between the simulated values and the experimental values was only 2.1%, further verifying the quantification accuracy of the model for leakage disturbances |
| Leakage Parameter | Theoretical Value | Estimated Value | Absolute Error | Relative Error |
|---|---|---|---|---|
| Leakage location l (m) | 69.5 | 69.3~69.7 | ±0.2 m | ±0.29% |
| Leakage rate Ql0 (%) | 20 | 19.6~20.3 | ±0.4% | ±2.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.-Y.; Xu, Y.; Ma, Y.-C.; Qian, J.-F. Symmetry-Guided Numerical Simulation of Viscoelastic Pipe Leakage Based on Transient Inverse Problem Analysis. Symmetry 2025, 17, 1805. https://doi.org/10.3390/sym17111805
Zhang T-Y, Xu Y, Ma Y-C, Qian J-F. Symmetry-Guided Numerical Simulation of Viscoelastic Pipe Leakage Based on Transient Inverse Problem Analysis. Symmetry. 2025; 17(11):1805. https://doi.org/10.3390/sym17111805
Chicago/Turabian StyleZhang, Tian-Yu, Ying Xu, Yu-Chao Ma, and Jian-Feng Qian. 2025. "Symmetry-Guided Numerical Simulation of Viscoelastic Pipe Leakage Based on Transient Inverse Problem Analysis" Symmetry 17, no. 11: 1805. https://doi.org/10.3390/sym17111805
APA StyleZhang, T.-Y., Xu, Y., Ma, Y.-C., & Qian, J.-F. (2025). Symmetry-Guided Numerical Simulation of Viscoelastic Pipe Leakage Based on Transient Inverse Problem Analysis. Symmetry, 17(11), 1805. https://doi.org/10.3390/sym17111805






