A Comparative Study of Trimmed L-Moments, Direct L-Moments, and Maximum Likelihood Estimation for the Inverse Weibull Distribution Under Type-I Right Censoring

Abstract

This paper presents a comparative evaluation of three distinct methodologies for estimating the parameters of the Inverse Weibull distribution under Type-I right censoring: trimmed linear moments (using Type-AT and Type-BT variants), direct linear moments (using Type-AD and Type-BD variants), and maximum likelihood estimation. The performance of these methods is assessed through Monte Carlo simulations, focusing on estimation accuracy, relative absolute bias, and root mean square error to identify the most appropriate approach. The practical applicability of these techniques is demonstrated through a real-world dataset analysis.

1. Introduction

Accurate parameter estimation is fundamental to modeling phenomena and predicting their behavior. Classical methods such as maximum likelihood, least squares, and conventional moments perform well under ideal conditions, as demonstrated in comparative studies such as those of Teimouri et al. [1]. However, their precision decreases significantly in the presence of outliers, as noted by Hosking [2], driving the need for robust estimation techniques.

Hosking [2] introduced linear moments (LMs) as a robust alternative based on linear combinations of order statistics. Although LMs reduce outlier influence for light-tailed distributions, their performance declines for heavy-tailed distributions, such as the Cauchy distribution. This limitation led to the development of more adaptable methods.

To address these challenges, Elamir and Seheult [3] proposed trimmed linear moments (TLMs), extending LMs through symmetric trimming of extreme observations. Hosking [4] further developed the TLM theory and applications. Trimming parameters ($t_1,t_2$) offer flexibility for handling heavy-tailed distributions, allowing a balanced trade-off between statistical bias and variance. Specifically, appropriate trimming reduces the variance inflation caused by extreme observations while controlling the introduction of bias from discarding valid data points, thus achieving robust performance across various distributional shapes and data imperfections.

Censored data are essential in reliability and survival analysis, where constraints limit data collection. Type-I censoring (time-based) and Type-II censoring (event-based) represent distinct censoring schemes that require specialized methods, as detailed by Balakrishnan and Cohen [5] and comprehensively reviewed by Oommen and Gillariose [6].

The pursuit of robust estimators aligns with the principle of statistical symmetry, which in this context refers to balanced performance across various distributional shapes and data imperfections. Although classical estimators may perform well under ideal symmetric conditions, they often fail dramatically when symmetry is broken by outliers or censoring. Robust methods such as TLMs aim to restore this balance by providing a stable estimation that is symmetric in its performance, maintaining reasonable accuracy under ideal and non-ideal conditions, rather than excelling in one scenario while failing in another.

Specialized estimation techniques for censored data include Probability Weighted Moments (PWMs) by Greenwood et al. [7], extended to Partial PWMs by Wang [8,9]. Hosking [10] established PWM-to-LM conversion for right-censored data, later extended to left-censored data by Zafirakou-Koulouris et al. [11].

While recent Bayesian studies have advanced parameter estimation for discrete distributions under censoring, such as Akhtar et al. [12] for the geometric distribution and Akhtar et al. [13] for mixture models under double Type-I censoring, our work complements this growing body of research by focusing on robust frequentist methods for continuous heavy-tailed distributions, specifically the Inverse Weibull model.

The Inverse Weibull (IW) distribution has the following probability density function:

$$f(x;\alpha ,\beta )=\beta \alpha x^{-\beta -1}{e}^{-{\displaystyle \frac{\alpha }{x^{\beta }}}},x\ge 0,\alpha ,\beta >0,$$

(1)

In this parameterization, $\beta$ and $\alpha$ are shape parameters. However, $\alpha$ is also related to the scale, where the actual scale parameter is given by $\sigma ={\alpha }^{1/\beta }$. Its cumulative distribution and survival functions are as follows:

$$F(x;\alpha ,\beta )=e^{-{\displaystyle \frac{\alpha }{x^{\beta }}}},x\ge 0,\alpha ,\beta >0,$$

(2)

$$S(x;\alpha ,\beta )=1-e^{-{\displaystyle \frac{\alpha }{x^{\beta }}}},x\ge 0,\alpha ,\beta >0,$$

(3)

with the following quantile function:

$$q\left(u\right)={\alpha }^{{\displaystyle \frac{1}{\beta }}}{\left[-log\left(u\right)\right]}^{-{\displaystyle \frac{1}{\beta }}},0<u<1.$$

(4)

The landscape of robust moment-based methods was further expanded by Mahmoud et al. [14], who introduced direct L-moments (DLMs) as a methodology specifically adapted for Type-I-censored data. Unlike the standard L-moment framework, DLMs provide a direct estimation approach tailored to handle the information loss inherent in censored samples.

This study compares TLMs, DLMs and maximum likelihood estimation (MLE) for IW distribution under Type-I censoring. Section 2 presents the TLM formulation for censored data, Section 3 details estimation methodologies, Section 6 describes simulation studies, Section 7 demonstrates real-data applications, and Section 8 provides conclusions.

Table 1. Summary of key notation and abbreviations.

Symbol/Abbreviation	Description
n	Total sample size.
r	Number of observed (uncensored) failures in a censored sample.
T	Fixed censoring time (Type-I right censoring).
c	Expected proportion of observed data, defined as $c=F\left(T\right)$.
$\alpha ,\beta$	Shape parameters of the Inverse Weibull (IW) distribution.
t	Trimming level (number of points to trim from each tail) for the trimmed L-moment (TLM) estimators.
Type-AT	Type-A trimmed L-moment estimator.
Type-BT	Type-B trimmed L-moment estimator.
DLMs	Direct linear moment estimator.
TLMs	Trimmed linear moment estimator.
MLE	Maximum likelihood estimator.
RAB	Relative absolute bias, calculated as $\mathrm{RAB}=\left|\mathrm{Bias}\right|/\mathrm{true} \mathrm{value}$.
RMSE	Root mean squared error, calculated across all Monte Carlo replications.
CL	Censoring level (e.g., 60%, 80%).

summarizes key notation for clarity.

2. TLM Under Right Type-I Censoring Scheme

The MLE, while efficient, can be highly sensitive to outliers and deviations from model assumptions. TLMs offer a robust alternative. Their core principle is to provide a stable estimate of the characteristic distribution by focusing on its central part, mitigating the influence of extreme values in the tails, a common feature in heavy-tailed distributions like the IW distribution. This makes TLMs particularly suitable for our application. The method involves equating the theoretical population moments with their empirical sample counterparts.

Ibrahim et al. [15] introduced an adaptation of the TLM method to censored data. The authors proposed two variants of TLMs and demonstrated their application to right- and left-censored data. In TLMs for right-censored data, let $x_1,x_2,\dots ,x_n$ represent a Type-I-censored random sample of size n, drawn from a population characterized by a cumulative distribution function $F\left(x\right)$ and a quantile function $q\left(u\right)$. Suppose that the censoring time T is such that $F\left(T\right)=c$, where c denotes the fraction of observed (uncensored) data. Under this censoring mechanism, the ordered observed random sample consists of order statistics $x_{\left(1\right)}\le x_{\left(2\right)}\le \dots \le x_{\left(n\right)}$. Let t be the number of observations censored from the left (lower tail). The sample can thus be partitioned as follows:

$$\begin{array}{c}\underset{\underset{t\left(\mathrm{trimmed}\right)}{︸}}{x_{1:n}\le x_{2:n}\le \cdots \le x_{t:n}}\le \underset{\underset{\mathrm{m}\left(\mathrm{observed}\right)}{︸}}{x_{t+1:n}\le x_{t+2:n}\le \cdots \le x_{m:n}}\le T\le \\ \underset{\underset{n-t-m(\mathrm{right}-\mathrm{censored})}{︸}}{x_{m+1:n}\le \cdots \le x_{n-1:n}\le x_{n:n}}\end{array}$$

Trimming levels $t=1$ and $t=2$ were selected to represent moderate and high trimming scenarios that balance robustness and efficiency. Specifically, $t=1$ provides sufficient robustness by trimming extreme observations while retaining adequate sample information for a stable estimation. In contrast, $t=2$ offers stronger protection against outliers and heavy-tailed behavior, which is particularly relevant for the IW distribution given its potential for extreme values.

This selection follows established practices in the TLMOM literature and allows systematic investigation of the robustness–efficiency trade-off across different censoring conditions.

The TLM methodology for censored data comprises two main variants, Type-A and Type-B, which differ in their treatment of the censoring mechanism. Type-A estimators are derived by applying the standard TLM definitions directly to the observed censored sample. In contrast, Type-B estimators explicitly incorporate the censoring threshold explicitly into their formulation, adjusting the moment equations to account for the probability mass beyond the censoring point. This fundamental difference leads to Type-B estimators often being more efficient under well-specified censoring models, while Type-A estimators can be more robust to misspecification. The suffix ‘T’ denotes trimmed moments.

The general formulations of the two TLM approaches (Type-AT and Type-BT) for the right-censored data are expressed, respectively, as follows. Let r be the order of the trimmed L-moment ($r=1,2,\dots$):

$${\displaystyle {\mu }_r^{A\left(t\right)}=\frac{(r+t)!}{r{c}^{r+t}}\sum _{k=0}^{r-1}\frac{{(-1)}^k}{(r+t-k-1)!k!}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right){\int }_0^c{u}^{r+t-k-1}{(c-u)}^{k}q\left(u\right)du}$$

(5)

and

$$\begin{array}{cc}\hfill {\mu }_r^{B\left(t\right)}& {\displaystyle =\frac{(r+t)!}{r}\sum _{k=0}^{r-1}\frac{{(-1)}^k}{(r+t-k-1)!k!}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right)·}\hfill \\ \hfill & \left[{\int }_0^c{u}^{r+t-k-1}{(1-u)}^{k}q\left(u\right)du+q\left(c\right){\int }_c^1{u}^{r+t-k-1}{(1-u)}^{k}du\right].\hfill \end{array}$$

(6)

For Type-AT (Equation (5)), the censoring mechanism is incorporated through the integration limit $c=F\left(T\right)$, focusing specifically on the observable region of the distribution. In contrast, Type-BT (Equation (6)) employs a composite approach that accounts for both observed data and survival probability beyond the censoring threshold, providing a more comprehensive representation of the censored data structure. This fundamental difference leads to varying robustness properties in practical applications.

The sample estimators for Type-AT and Type-BT TLMs are derived by equating the theoretical population moments to their corresponding sample moments, yielding the following expressions:

$$M_r^{A\left(t\right)}={\displaystyle \frac{1}{r\left(\genfrac{}{}{0pt}{}{m}{r+t}\right)}}\sum _{i=t+1}^m\sum _{k=0}^{r-1}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{r-1}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{i-1}{r+t-k-1}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{m-i}{k}}\right)X_{i:n}$$

(7)

and

$$\begin{array}{cc}\hfill M_r^{B\left(t\right)}={\displaystyle \frac{1}{r\left(\genfrac{}{}{0pt}{}{n}{r+t}\right)}}& \left[\sum _{i=t+1}^m\sum _{k=0}^{r-1}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{r-1}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{i-1}{r+t-k-1}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-i}{k}}\right)X_{i:n}\right.\hfill \\ \hfill & \left.+\left(\sum _{i=m+1}^n\sum _{k=0}^{r-1}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{r-1}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{i-1}{r+t-k-1}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-i}{k}}\right)\right)T\right].\hfill \end{array}$$

(8)

3. TLM Estimation

Having established the general framework for TLMs under censoring, we now derive their specific analytical forms, the IW distribution. This derivation is a crucial step, as it transforms the general TLM equations into concrete functions of the IW parameters $\alpha$ and $\beta$. We now derive their specific analytical forms, based on the quantile function of the IW distribution. These population moments will form the basis for the estimating equations solved in the subsequent simulation study to obtain the TLM estimates for censored IW data. The subsequent derivations show the application of Equations (5) and (6) to the quantile function of the IW distribution given in Equation (4).

The detailed mathematical derivations for all population TLMs presented in this section, including all intermediate steps, are provided in the Supplementary Material.

From Equation (5), the rth order population Type-AT TLMs under Type-I right censoring for the IW distribution are given by

$${\displaystyle {\mu }_r^{A\left(t\right)}=\frac{(r+t)!{\alpha }^{\frac{1}{\beta }}}{r{c}^{r+t}}\sum _{k=0}^{r-1}\frac{{(-1)}^k}{(r+t-k-1)!k!}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right){\int }_0^c{u}^{r+t-k-1}{(c-u)}^k{\left[-log\left(u\right)\right]}^{-\frac{1}{\beta }}du.}$$

(9)

By setting the smallest trim value to unity ($t=1$), Equation (9) reduces to

$${\displaystyle {\mu }_r^{A\left(1\right)}=\frac{(r+1)!{\alpha }^{\frac{1}{\beta }}}{r{c}^{r+1}}\sum _{k=0}^{r-1}\frac{{(-1)}^k}{(r-k)!k!}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right){\int }_0^c{u}^{r-k}{(c-u)}^k{\left[-log\left(u\right)\right]}^{-\frac{1}{\beta }}du.}$$

(10)

By substituting $r=1$ and $r=2$ into Equation (10), we obtain the first two Type-AT TLMs for the IW distribution under Type-I right censoring with left trimming:

$${\mu }_1^{A\left(1\right)}={\displaystyle \frac{{\left(2\alpha \right)}^{\frac{1}{\beta }}}{c^2}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-2log\left(c\right))$$

(11)

and

$${\mu }_2^{A\left(1\right)}={\displaystyle \frac{3{\left(3\alpha \right)}^{\frac{1}{\beta }}}{2c^3}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-3log\left(c\right))-{\displaystyle \frac{3{\left(2\alpha \right)}^{\frac{1}{\beta }}}{2c^2}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-2log\left(c\right)).$$

(12)

In the expressions above, $\Gamma (s,x)$ denotes the incomplete upper gamma function, defined as $\Gamma (s,x)={\int }_x^{\infty }{t}^{s-1}{e}^{-t}dt$, for $s>0$ and $x\ge 0$.

By setting the smallest trimming to $t=2$, Equation (9) simplifies to

$${\displaystyle {\mu }_r^{A\left(2\right)}=\frac{(r+2)!{\alpha }^{\frac{1}{\beta }}}{r{c}^{r+2}}\sum _{k=0}^{r-1}\frac{{(-1)}^k}{(r-k-1)!k!}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right){\int }_0^c{u}^{r-k+1}{(c-u)}^k{\left[-log\left(u\right)\right]}^{-\frac{1}{\beta }}du.}$$

(13)

Substituting $r=1$ and $r=2$ into Equation (13) yields the following:

$${\mu }_1^{A\left(2\right)}={\displaystyle \frac{3{\alpha }^{\frac{1}{\beta }}}{c^3}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-3log\left(c\right)),$$

(14)

$${\mu }_2^{A\left(2\right)}={\displaystyle \frac{2{\left(4\alpha \right)}^{\frac{1}{\beta }}}{c^4}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-4log\left(c\right))-{\displaystyle \frac{2{\left(3\alpha \right)}^{\frac{1}{\beta }}}{c^3}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-3log\left(c\right)).$$

(15)

From Equation (6), the rth order population Type-BT TLMs for the IW distribution under Type-I right censoring are expressed as

$$\begin{array}{cc}\hfill {\mu }_r^{B\left(t\right)}& {\displaystyle =\frac{(r+t)!{\alpha }^{\frac{1}{\beta }}}{r}\sum _{k=0}^{r-1}\frac{{(-1)}^k}{(r+t-k-1)!k!}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right)·}\hfill \\ \hfill & \left[{\int }_0^c{u}^{r+t-k-1}{(1-u)}^k{\left[-log\left(u\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}du+{\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}{\int }_c^1{u}^{r+t-k-1}{(1-u)}^{k}du\right].\hfill \end{array}$$

(16)

By setting the smallest trim value to unity ($t=1$), Equation (16) reduces to

$$\begin{array}{cc}\hfill {\mu }_r^{B\left(1\right)}& {\displaystyle =\frac{(r+1)!{\alpha }^{\frac{1}{\beta }}}{r}\sum _{k=0}^{r-1}\frac{{(-1)}^k}{(r-k)!k!}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right)·}\hfill \\ \hfill & \left[{\int }_0^c{u}^{r-k}{(1-u)}^k{\left[-log\left(u\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}du+{\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}{\int }_c^1{u}^{r-k}{(1-u)}^{k}du\right].\hfill \end{array}$$

Knowing this, the incomplete beta function is $\mathrm{B}(x,a,b)={\int }_0^x{t}^{a-1}{(1-t)}^{b-1}dt$. Rewrite the following integral to match the beta function form:

$${\int }_c^1{u}^{r-k}{(1-u)}^{k}du={\int }_0^1{u}^{r-k}{(1-u)}^{k}du-{\int }_0^c{u}^{r-k}{(1-u)}^{k}du.$$

Therefore,

$${\int }_c^1{u}^{r-k}{(1-u)}^{k}du=\mathrm{B}(r-k+1,k+1)-\mathrm{B}(c,r-k+1,k+1).$$

Referring to ${\mu }_r^{B\left(1\right)}$,

$$\begin{array}{cc}\hfill {\mu }_r^{B\left(1\right)}& ={\displaystyle \frac{(r+1)!{\alpha }^{\frac{1}{\beta }}}{r}}\sum _{k=0}^{r-1}{\displaystyle \frac{{(-1)}^k}{(r-k)!k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{r-1}{k}}\right)\left[{\int }_0^c{u}^{r-k}{(1-u)}^k{\left[-log\left(u\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}du\right.\hfill \\ \hfill & \left.+{\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}\left(\mathrm{B}(r-k+1,k+1)-\mathrm{B}(c,r-k+1,k+1)\right)\right].\hfill \end{array}$$

(17)

Substituting $r=1$ and $r=2$ into Equation (17) results in the following:

$${\mu }_1^{B\left(1\right)}={\left(2\alpha \right)}^{{\displaystyle \frac{1}{\beta }}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-2log\left(c\right))+(1-c^2){\alpha }^{{\displaystyle \frac{1}{\beta }}}{\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}},$$

(18)

$$\begin{array}{cc}\hfill {\mu }_2^{B\left(1\right)}=& {\displaystyle \frac{3}{2}}{\left(3\alpha \right)}^{{\displaystyle \frac{1}{\beta }}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-3log\left(c\right))-{\displaystyle \frac{3}{2}}{\left(2\alpha \right)}^{{\displaystyle \frac{1}{\beta }}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-2log\left(c\right))\hfill \\ \hfill & +{\displaystyle \frac{3}{2}}(c^2-c^3){\alpha }^{{\displaystyle \frac{1}{\beta }}}{\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}.\hfill \end{array}$$

(19)

By setting the minimum trim value to $t=2$, Equation (16) simplifies as follows:

$$\begin{array}{cc}\hfill {\mu }_r^{B\left(2\right)}& {\displaystyle =\frac{(r+2)!{\alpha }^{\frac{1}{\beta }}}{r}\sum _{k=0}^{r-1}\frac{{(-1)}^k}{(r-k)!k!}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right)·}\hfill \\ \hfill & \left[{\int }_0^c{u}^{r-k+1}{(1-u)}^k{\left[-log\left(u\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}du+{\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}{\int }_c^1{u}^{r-k+1}{(1-u)}^{k}du\right].\hfill \end{array}$$

This equation can be written as follows:

$$\begin{array}{cc}\hfill {\mu }_r^{B\left(2\right)}& ={\displaystyle \frac{(r+2)!{\alpha }^{\frac{1}{\beta }}}{r}}\sum _{k=0}^{r-1}{\displaystyle \frac{{(-1)}^k}{(r-k+1)!k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{r-1}{k}}\right)\left[{\int }_0^c{u}^{r-k+1}{(1-u)}^k{\left[-log\left(u\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}du\right.\hfill \\ \hfill & \left.+{\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}\left(\mathrm{B}(r-k+2,k+1)-\mathrm{B}(c,r-k+2,k+1)\right)\right].\hfill \end{array}$$

(20)

By substituting $r=1$ and $r=2$ into Equation (20), we obtain the following:

$${\mu }_1^{B\left(2\right)}={\left(3\alpha \right)}^{{\displaystyle \frac{1}{\beta }}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-3log\left(c\right))+(1-c^3){\alpha }^{{\displaystyle \frac{1}{\beta }}}{\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}},$$

(21)

$${\mu }_2^{B\left(2\right)}=2{\left(4\alpha \right)}^{{\displaystyle \frac{1}{\beta }}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-4log\left(c\right))-2{\left(3\alpha \right)}^{{\displaystyle \frac{1}{\beta }}}\Gamma (1-{\displaystyle \frac{1}{\beta }},-3log\left(c\right))+2(c^3-c^4){\alpha }^{{\displaystyle \frac{1}{\beta }}}{\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}.$$

(22)

4. DLM Estimation

The DLM presents an alternative estimation approach that can be viewed as a special case or a specific instantiation within the robust estimation paradigm shared by TLMs. Although its mathematical formulation differs, its core motivation aligns with that of TLMs: to provide parameter estimates that are less sensitive to extreme observations and censoring. Following the same conceptual distinction outlined in Section 2, the DLM estimators are also developed in Type-AD and Type-BD variants, maintaining the fundamental difference in their treatment of the censoring mechanism. For the IW distribution, the derivation of the DLM estimators allows a comparative analysis of its performance against the TLM approaches (Type-AT and Type-BT) under Type-I censoring, which is a primary objective of this study. For more details, Mahmoud et al. [14] proposed a direct modification of the L-moments method, termed direct L-moments, for Type-I-censored data and applied it to estimate the parameters of the Kumaraswamy distribution, with its PPWMs and maximum likelihood methods.

The key practical difference between DLM and TLM estimators lies in their approach to trimming and outlier handling. Although both methods aim to provide robust estimation, they achieve this through fundamentally different mechanisms. TLMs employ explicit data trimming by systematically excluding a fixed number of extreme-order statistics (t observations from each tail) from moment calculations. This approach provides direct control over outlier influence but requires pre-specification of the trimming level. In contrast, DLMs achieve robustness through implicit weighting in their moment constructions. Rather than completely discarding observations, DLMs use the entire sample but with a moment structure that naturally reduces the influence of extreme values without hard truncation.

This fundamental difference means that TLMs offer more transparent outlier control, but may lose efficiency with aggressive trimming, while DLMs provide a smoother robustness approach that maintains more sample information but offers less direct control over specific trimming thresholds.

The following equations present the DLM estimators for the IW distribution, derived as special cases of the general TLMOM framework presented in Section 3 by setting the trimming parameter $t=0$. These formulations provide direct estimation equations tailored for Type-I-censored data, maintaining the robustness properties of L-moments while offering computational efficiency. The complete derivations are provided in the Supplementary Material.

The DLM estimators for Type-AD and Type-BD are obtained directly from the general TLM frameworks in Equations (9) and (16), respectively, by setting the trimming level $t=0$. The first Type-AD DLM for the IW distribution under Type-I right censoring with left trimming is derived by setting the order parameter $r=1$ in Equation (9) as

$${\mu }_1^A={\displaystyle \frac{{\alpha }^{\frac{1}{\beta }}}{c}}\Gamma \left(1-{\displaystyle \frac{1}{\beta }},-log\left(c\right)\right).$$

(23)

When $r=2$ is applied to Equation (9), the resulting expression corresponds to the second-order Type-AD DLM of the IW distribution, specifically under the conditions of Type-I right censoring and left trimming, given by

$${\mu }_2^A={\displaystyle \frac{{\left(2\alpha \right)}^{\frac{1}{\beta }}}{c^2}}\Gamma \left(1-{\displaystyle \frac{1}{\beta }},-2log\left(c\right)\right)-{\displaystyle \frac{{\alpha }^{\frac{1}{\beta }}}{c}}\Gamma \left(1-{\displaystyle \frac{1}{\beta }},-log\left(c\right)\right).$$

(24)

The sample DLMs can be mathematically expressed as

$$M_r^A={\displaystyle \frac{1}{r\left(\genfrac{}{}{0pt}{}{m}{r}\right)}}\sum _{i=1}^m\sum _{k=0}^{r-1}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{r-1}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{i-1}{r-k-1}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{m-i}{k}}\right)X_{i:n}.$$

(25)

The first two Type-BD DLMs of the IW distribution with Type-I right censoring with left trimming are computed by sequentially evaluating Equation (26) for orders $r=1$ and $r=2$.

$${\mu }_1^B={\alpha }^{{\displaystyle \frac{1}{\beta }}}\Gamma \left(1-{\displaystyle \frac{1}{\beta }},-log\left(c\right)\right)+{\alpha }^{{\displaystyle \frac{1}{\beta }}}(1-c){\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}},$$

(26)

$${\mu }_2^B={\left(2\alpha \right)}^{{\displaystyle \frac{1}{\beta }}}\Gamma \left(1-{\displaystyle \frac{1}{\beta }},-2log\left(c\right)\right)-{\alpha }^{{\displaystyle \frac{1}{\beta }}}\Gamma \left(1-{\displaystyle \frac{1}{\beta }},-log\left(c\right)\right)-c(c-1){\alpha }^{{\displaystyle \frac{1}{\beta }}}{\left[-log\left(c\right)\right]}^{-{\displaystyle \frac{1}{\beta }}}.$$

(27)

The sample DLMs are defined as

$$\begin{array}{cc}\hfill M_r^B={\displaystyle \frac{1}{r\left(\genfrac{}{}{0pt}{}{n}{r}\right)}}& [\sum _{i=1}^m\sum _{k=0}^{r-1}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{r-1}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{i-1}{r-k-1}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-i}{k}}\right)X_{i:n}\hfill \\ \hfill & +\left(\sum _{i=m+1}^n\sum _{k=0}^{r-1}{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{r-1}{k}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{i-1}{r-k-1}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{n-i}{k}}\right)\right)T].\hfill \end{array}$$

(28)

5. Maximum Likelihood Estimation

While MLE is known for its desirable asymptotic properties, such as consistency and efficiency, its performance can be significantly affected in finite samples, particularly under the dual challenges of small sample sizes and high censoring rates. In such scenarios, the likelihood function can become flat or exhibit multiple local maxima, leading to increased bias and variance in the parameter estimates. This sensitivity underscores the need for robust alternatives like TLMs and DLMs, which are specifically designed to maintain stability when data are limited or heavily censored.

In terms of computational demand, MLE typically requires iterative numerical optimization to solve the system of score equations, which can be computationally intensive and sensitive to the choice of starting values. In contrast, the TLM and DLM estimators often involve direct computation based on sample moments or the solution of simpler systems of equations, generally resulting in lower computational cost and a more straightforward implementation.

For Type-I right-censored data, the observed dataset consists of two groups of observations, uncensored and censored data points. Uncensored observations, denoted as $x_1,x_2,\dots ,x_r$, represent exact failure times when the event of interest has been fully observed. In contrast, censored observations correspond to cases where the event time exceeds a fixed censoring threshold T; these are all recorded as T. The log-likelihood function is given by

$$\begin{array}{cc}\hfill \ell (\alpha ,\beta )& =logL(\alpha ,\beta )\hfill \\ \hfill & =\sum _{i=1}^r\left[log\beta +log\alpha -(\beta +1)log{x}_i-{\displaystyle \frac{\alpha }{x_i^{\beta }}}\right]+(n-r)log(1-e^{-{\displaystyle \frac{\alpha }{T^{\beta }}}})\hfill \end{array}$$

(29)

The first-order partial derivatives of the log-likelihood function $\ell (\alpha ,\beta )$ are derived by differentiating with respect to each model parameter, yielding the following expressions:

$${\displaystyle \frac{\partial \ell (\alpha ,\beta )}{\partial \alpha }}={\displaystyle \frac{r}{\alpha }}-\sum _{i=1}^r{\displaystyle \frac{1}{x_i^{\beta }}}+(n-r){\displaystyle \frac{e^{-\frac{\alpha }{T^{\beta }}}}{T^{\beta }(1-e^{-\frac{\alpha }{T^{\beta }}})}},$$

(30)

$${\displaystyle \frac{\partial \ell (\alpha ,\beta )}{\partial \beta }}={\displaystyle \frac{r}{\beta }}-\sum _{i=1}^{r}log{x}_i+\alpha \sum _{i=1}^r{\displaystyle \frac{log{x}_i}{x_i^{\beta }}}+(n-r){\displaystyle \frac{\alpha logT.e^{-\frac{\alpha }{T^{\beta }}}}{T^{\beta }(1-e^{-\frac{\alpha }{T^{\beta }}})}}.$$

(31)

Under the regularity conditions satisfied by the IW distribution, the MLE estimators $(\widehat{\alpha },\widehat{\beta })$ are consistent, asymptotically normal, and asymptotically efficient. Specifically, $\widehat{\alpha }\stackrel{p}{\to }\alpha$ and $\widehat{\beta }\stackrel{p}{\to }\beta$ as $n\to \infty$, and the scaled estimation error converges in distribution to a normal variate, $\sqrt{n}\left(\begin{array}{c}\widehat{\alpha }-\alpha \\ \widehat{\beta }-\beta \end{array}\right)\stackrel{d}{\to }N\left(0,I^{-1}(\alpha ,\beta )\right)$, where $I(\alpha ,\beta )$ denotes the Fisher information matrix. Furthermore, these estimators achieve the Cramér–Rao lower bound, indicating asymptotic efficiency. For finite-sample inference, the covariance matrix can be estimated using the observed Fisher information matrix.

The inherent non-linearity of the score equations precludes closed-form solutions, thus necessitating iterative numerical methods for parameter estimation. The Newton–Raphson algorithm serves as an effective computational approach to this optimization problem, providing reliable convergence to the maximum likelihood estimates.

6. Simulation Study

In this section, a numerical analysis is presented to evaluate and compare the performance of the estimation methods studied (TLMs, DLMs, and MLE) under various conditions. The analysis considers various sample sizes, specifically $n=25,50,100$, and two censoring levels (CL): $60\%$ and $80\%$. The parameters of the IW distribution are assumed to be $IW(0.5,0.5)$, $IW(1.5,2.5)$, and $IW(2.5,1.5)$. These sets of parameters were carefully selected to represent a diverse range of distributional characteristics of the IW distribution. The set $IW(0.5,0.5)$ represents a heavy-tailed distribution with high variance and challenging estimation methods. The configuration $IW(1.5,2.5)$ represents a moderately heavy-tailed distribution with different shape parameters, while $IW(2.5,1.5)$ tests the robustness of the method under asymmetric shape parameters. This selection enables a comprehensive evaluation across varying distributional forms.

This selection allows us to evaluate the performance of the estimators across different distributional shapes and tail behaviors commonly encountered in practice.

The TLM and DLM estimators for the parameters $\alpha$ and $\beta$ were calculated directly by solving the system of equations defined by equating the theoretical trimmed L-moments given in Section 3 and Section 4 to their empirical counterparts derived from the censored sample. This approach is analogous to the traditional method of moments, but utilizes trimmed L-moments for enhanced robustness. The numerical solutions for the resulting systems of equations were obtained using R [16], which implements advanced methods to solve non-linear systems. The initial values for numerical optimization were derived from the method of moment estimates applied to the uncensored portion of each simulated data set to ensure the stability of convergence.

Stepsof Monte Carlo Simulation

The following steps are repeated 5000 times for each combination of sample size and CL:

• Generate a complete random sample of size n from the distribution $IW(\alpha ,\beta )$ using the inverse transform method: generate $U_i$∼$\mathrm{Uniform}(0,1)$ for $i=1,\dots ,n$, and then compute $X_i=Q\left(U_i\right)$, where $Q(·)$ is the quantile function given in Equation (4).
• Apply Type-I right censoring: For a given CL, calculate the censoring time T as the $(1-\mathrm{CL})$-th quantile of the IW distribution, that is, $T=q(1-\mathrm{CL})$. Any generated value greater than T is replaced by T and marked as censored. This results in a censored sample with a random number of observed failures r.
• Obtain the MLEs of the parameters $\alpha$ and $\beta$ by solving the system of equations formed by setting Equations (30) and (31) equal to zero.
• Compute the TLM estimates for $t=1$ (denoted as $TL{M}_1$) and $t=2$ (denoted as $TL{M}_2$).
• Compute the DLM estimate for $t=0$.
• Store the estimates obtained from $\alpha$ and $\beta$.
• Calculate statistical metrics for estimates, relative absolute bias (RAB) and root mean squared error (RMSE), using the formulas $\mathrm{RAB}\left(\theta \right)={\displaystyle \frac{1}{5000}}{\sum }_{l=1}^{5000}{\displaystyle \frac{|\theta -{\widehat{\theta }}_l|}{\theta }}$ and $\mathrm{RMSE}\left(\theta \right)=\sqrt{{\displaystyle \frac{1}{5000}}{\sum }_{l=1}^{5000}{\left({\widehat{\theta }}_l-\theta \right)}^2}$, where $\theta$ represents the true parameter value and ${\widehat{\theta }}_l$ denotes its estimate in the l-th replication.

Parameter estimation was performed in the R programming language using the bbmle package for MLE and the nleqslv package for TLM/DLM methods, with a convergence tolerance of ${10}^{-6}$ and a maximum of 10,000 iterations. The assumed initial values were used as starting points for solving the equations.

The results of our simulation (RAB and RMSE) for Type-AT are presented in

Table 2. (a) RAB and RMSE (in parentheses) for MLE, DLM, and TLMs under Type-I censoring for $IW(\alpha =0.5,\beta =0.5)$: Type-AT. (b) RAB and RMSE (in parentheses) for MLE, DLM, and TLMs under Type-I censoring for $IW(\alpha =0.5,\beta =0.5)$: Type-BT.

(a)
n	Method	CL = 60%		CL = 80%
		α	β	α	β
25	$MLE$	0.0412 (0.1504)	0.2685 (0.1758)	0.0422 (0.1356)	0.2552 (0.1611)
	$DLM$	0.0170 (0.0715)	0.1408 (0.1340)	0.0416 (0.0913)	0.0716 (0.0954)
	$TL{M}_1$	0.0118 (0.0687)	0.1388 (0.1667)	0.0474 (0.1051)	0.0696 (0.1170)
	$TL{M}_2$	0.0138 (0.0694)	0.1608 (0.2067)	0.0585 (0.1236)	0.0786 (0.1397)
50	$MLE$	0.0782 (0.1140)	0.2561 (0.1508)	0.0709 (0.1039)	0.2445 (0.1407)
	$DLM$	0.0164 (0.0470)	0.1264 (0.0947)	0.0401 (0.0652)	0.0662 (0.0666)
	$TL{M}_1$	0.0076 (0.0420)	0.1067 (0.1034)	0.0410 (0.0725)	0.0573 (0.0771)
	$TL{M}_2$	0.0057 (0.0395)	0.1065 (0.1177)	0.0448 (0.0812)	0.0571 (0.0887)
100	$MLE$	0.0860 (0.0869)	0.2460 (0.1346)	0.0750 (0.0788)	0.2311 (0.1253)
	$DLM$	0.0142 (0.0320)	0.1246 (0.0783)	0.0462 (0.0485)	0.0620 (0.0492)
	$TL{M}_1$	0.0055 (0.0279)	0.1023 (0.0784)	0.0454 (0.0525)	0.0542 (0.0547)
	$TL{M}_2$	0.0036 (0.0258)	0.0987 (0.0854)	0.0473 (0.0576)	0.0543 (0.0620)
(b)
$\mathit{n}$	Method	CL = 60%		CL = 80%
		$\mathbf{\alpha }$	$\mathbf{\beta }$	$\mathbf{\alpha }$	$\mathbf{\beta }$
25	$MLE$	0.0412 (0.1504)	0.2685 (0.1758)	0.0422 (0.1356)	0.2552 (0.1611)
	$DLM$	0.0067 (0.0120)	0.1045 (0.1959)	0.0134 (0.1252)	0.0329 (0.1107)
	$TL{M}_1$	0.0043 (0.0048)	0.2029 (0.3940)	0.0065 (0.2132)	0.0826 (0.1815)
	$TL{M}_2$	0.0029 (0.0124)	0.4363 (0.7173)	0.0465 (0.4028)	0.1004 (0.2590)
50	$MLE$	0.0782 (0.1140)	0.2561 (0.1508)	0.0709 (0.1039)	0.2445 (0.1407)
	$DLM$	0.0004 (0.0085)	0.0724 (0.1303)	0.0315 (0.0854)	0.0246 (0.0777)
	$TL{M}_1$	0.0012 (0.0024)	0.0830 (0.2209)	0.0517 (0.1198)	0.0839 (0.1285)
	$TL{M}_2$	0.0005 (0.0046)	0.1492 (0.3390)	0.0576 (0.1617)	0.1240 (0.1773)
100	$MLE$	0.0860 (0.0869)	0.2460 (0.1346)	0.0750 (0.0788)	0.2311 (0.1253)
	$DLM$	0.0032 (0.0063)	0.0731 (0.0964)	0.0322 (0.0605)	0.0139 (0.0547)
	$TL{M}_1$	0.0007 (0.0016)	0.0578 (0.1507)	0.0596 (0.0833)	0.0712 (0.0920)
	$TL{M}_2$	0.0007 (0.0028)	0.0730 (0.2132)	0.0797 (0.1062)	0.1158 (0.1277)

a,

Table 3. (a) RAB and RMSE (in parentheses) for MLE, DLM, and TLsM under Type-I censoring for $IW(\alpha =1.5,\beta =2.5)$: Type-AT. (b) RAB and RMSE (in parentheses) for MLE, DLM, and TLMs under Type-I censoring for $IW(\alpha =1.5,\beta =2.5)$: Type-BT.

(a)
$\mathit{n}$	Method	CL = 60%		CL = 80%
		$\mathbf{\alpha }$	$\mathbf{\beta }$	$\mathbf{\alpha }$	$\mathbf{\beta }$
25	$MLE$	0.2477 (0.5514)	0.2816 (0.9263)	0.2340 (0.5278)	0.2724 (0.8520)
	$DLM$	0.1952 (0.4714)	0.1945 (0.7014)	0.1951 (0.4813)	0.1172 (0.4743)
	$TL{M}_1$	0.1957 (0.5891)	0.1570 (0.7390)	0.1899 (0.6123)	0.0901 (0.5087)
	$TL{M}_2$	0.2439 (0.9223)	0.1683 (0.8965)	0.2311 (0.8599)	0.0926 (0.5977)
50	$MLE$	0.2002 (0.3910)	0.2589 (0.7626)	0.1977 (0.3867)	0.2472 (0.7133)
	$DLM$	0.1697 (0.3333)	0.1818 (0.5508)	0.1745 (0.3578)	0.1058 (0.3573)
	$TL{M}_1$	0.1458 (0.3511)	0.1309 (0.5037)	0.1451 (0.3908)	0.0721 (0.3380)
	$TL{M}_2$	0.1519 (0.4162)	0.1247 (0.5573)	0.1504 (0.4697)	0.0664 (0.3732)
100	$MLE$	0.1835 (0.3229)	0.2418 (0.6649)	0.1812 (0.3180)	0.2340 (0.6347)
	$DLM$	0.1602 (0.2808)	0.1710 (0.4736)	0.1649 (0.2966)	0.1001 (0.2992)
	$TL{M}_1$	0.1281 (0.2634)	0.1163 (0.3849)	0.1272 (0.2854)	0.0650 (0.2524)
	$TL{M}_2$	0.1239 (0.2849)	0.1054 (0.3982)	0.1235 (0.3204)	0.0582 (0.2663)
(b)
$\mathit{n}$	Method	CL = 60%		CL = 80%
		$\mathbf{\alpha }$	$\mathbf{\beta }$	$\mathbf{\alpha }$	$\mathbf{\beta }$
25	$MLE$	0.2477 (0.5514)	0.2816 (0.9263)	0.2340 (0.5278)	0.2724 (0.8520)
	$DLM$	0.2221 (0.6775)	0.1549 (0.6370)	0.1444 (0.4800)	0.0971 (0.3618)
	$TL{M}_1$	0.4660 (2.4474)	0.1947 (1.2757)	0.1313 (0.8014)	0.0483 (0.4095)
	$TL{M}_2$	1.0013 (4.7402)	0.3579 (2.4095)	0.2254 (1.7665)	0.0296 (0.6143)
50	$MLE$	0.2002 (0.3910)	0.2589 (0.7626)	0.1977 (0.3867)	0.2472 (0.7133)
	$DLM$	0.1621 (0.4001)	0.1346 (0.4665)	0.1208 (0.3310)	0.0932 (0.2941)
	$TL{M}_1$	0.1931 (0.7763)	0.1147 (0.7248)	0.0663 (0.4386)	0.0401 (0.2770)
	$TL{M}_2$	0.3834 (2.0577)	0.1566 (1.1898)	0.0583 (0.7143)	0.0100 (0.3887)
100	$MLE$	0.1835 (0.3229)	0.2418 (0.6649)	0.1812 (0.3180)	0.2340 (0.6347)
	$DLM$	0.1430 (0.2974)	0.1274 (0.3873)	0.1087 (0.2467)	0.0901 (0.2567)
	$TL{M}_1$	0.1233 (0.4162)	0.0901 (0.4877)	0.0386 (0.2738)	0.0357 (0.1953)
	$TL{M}_2$	0.1652 (0.7260)	0.0948 (0.7186)	0.0010 (0.3720)	0.0012 (0.2541)

a and

Table 4. (a) RAB and RMSE (in parentheses) for MLE, DLM, and TLMs under Type-I censoring for $IW(\alpha =2.5,\beta =1.5)$: Type-AT. (b) RAB and RMSE (in parentheses) for MLE, DLM, and TLMs under Type-I censoring for $IW(\alpha =2.5,\beta =1.5)$: Type-BT.

(a)
$\mathit{n}$	Method	CL = 60%		CL = 80%
		$\mathbf{\alpha }$	$\mathbf{\beta }$	$\mathbf{\alpha }$	$\mathbf{\beta }$
25	$MLE$	0.4684 (1.5822)	0.2551 (0.5089)	0.4337 (1.4394)	0.2580 (0.4897)
	$DLM$	0.3462 (1.5086)	0.1801 (0.4078)	0.2778 (1.1730)	0.1020 (0.2697)
	$TL{M}_1$	0.3798 (2.4527)	0.1532 (0.4635)	0.2945 (1.5895)	0.0862 (0.3034)
	$TL{M}_2$	0.4887 (3.4535)	0.1708 (0.5957)	0.3847 (2.3947)	0.0942 (0.3610)
50	$MLE$	0.3793 (1.0924)	0.2513 (0.4419)	0.3570 (1.0328)	0.2411 (0.4156)
	$DLM$	0.2837 (0.9163)	0.1691 (0.3155)	0.2289 (0.7936)	0.0949 (0.2015)
	$TL{M}_1$	0.2426 (0.9876)	0.1259 (0.2999)	0.1973 (0.9077)	0.0688 (0.2019)
	$TL{M}_2$	0.2583 (1.2032)	0.1217 (0.3327)	0.2149 (1.1367)	0.0663 (0.2282)
100	$MLE$	0.3448 (0.9278)	0.2421 (0.3981)	0.3338 (0.9007)	0.2313 (0.3763)
	$DLM$	0.2623 (0.7534)	0.1631 (0.2744)	0.2167 (0.6585)	0.0900 (0.1676)
	$TL{M}_1$	0.2056 (0.7113)	0.1156 (0.2337)	0.1712 (0.6587)	0.0624 (0.1508)
	$TL{M}_2$	0.2010 (0.7941)	0.1061 (0.2457)	0.1714 (0.7558)	0.0578 (0.1622)
(b)
$\mathit{n}$	Method	CL = 60%		CL = 80%
		$\mathbf{\alpha }$	$\mathbf{\beta }$	$\mathbf{\alpha }$	$\mathbf{\beta }$
25	$MLE$	0.4684 (1.5822)	0.2551 (0.5089)	0.4337 (1.4394)	0.2580 (0.4897)
	$DLM$	0.4238 (2.3844)	0.1630 (0.4222)	0.2110 (1.1637)	0.0833 (0.2099)
	$TL{M}_1$	0.9317 (6.7622)	0.2325 (0.8193)	0.2373 (2.4961)	0.0446 (0.2695)
	$TL{M}_2$	1.7397 (11.4965)	0.4133 (1.4127)	0.4134 (4.5599)	0.0326 (0.4166)
50	$MLE$	0.3793 (1.0924)	0.2513 (0.4419)	0.3570 (1.0328)	0.2411 (0.4156)
	$DLM$	0.2670 (1.1227)	0.1307 (0.2886)	0.1561 (0.7385)	0.0766 (0.1596)
	$TL{M}_1$	0.3864 (2.6461)	0.1232 (0.4570)	0.0922 (1.0765)	0.0273 (0.1799)
	$TL{M}_2$	0.7917 (6.1917)	0.1742 (0.7377)	0.1060 (1.9574)	0.0018 (0.2616)
100	$MLE$	0.3448 (0.9278)	0.2421 (0.3981)	0.3338 (0.9007)	0.2313 (0.3763)
	$DLM$	0.2230 (0.8025)	0.1214 (0.2352)	0.1429 (0.5548)	0.0763 (0.1376)
	$TL{M}_1$	0.2185 (1.2672)	0.0908 (0.3179)	0.0527 (0.6538)	0.0254 (0.1271)
	$TL{M}_2$	0.3405 (2.5117)	0.0992 (0.4662)	0.0077 (0.9153)	0.0087 (0.1791)

a, corresponding to the distributions $IW(0.5,0.5)$, $IW(1.5,2.5)$, and $IW(2.5,1.5)$, respectively. Similarly, the results for Type-BT are shown in Table 2b, Table 3b and Table 4b, for the same distributions, respectively.

The tables presented provide a comprehensive comparison of the performance of MLE, DLM, $TL{M}_1$ and $TL{M}_2$ under Type-I censoring for the IW distribution with varying parameter sets. The evaluation metrics, RAB and RMSE, reveal several key insights:

• MLE consistently exhibits higher RAB and RMSE values in all sample sizes (n = 25, 50, 100) with CL 60% and 80%, indicating its relative inefficiency, particularly for smaller sample sizes.
• DLM demonstrates superior performance compared to MLE, with significantly lower bias and error, especially for larger sample sizes. This suggests that DLM methods are more robust in handling censored data.
• $TL{M}_1$ and $TL{M}_2$ show mixed results. Although $TL{M}_1$ often outperforms MLE and occasionally DLM in specific scenarios (e.g., for $IW(0.5,0.5)$), $TL{M}_2$ tends to exhibit greater variability, particularly for smaller samples or more complex parameter sets (e.g., $IW(2.5,1.5)$ using the Type-BT TLM estimator under Type-I censoring).
• The performance of the methods varies significantly with the underlying parameters of the IW distribution. For example, DLM and $TL{M}_1$ achieve notable accuracy for $IW(0.5,0.5)$, while their performance is degraded for $IW(2.5,1.5)$, especially using the Type-BT TLM estimator under Type-I censoring. This underscores the challenge of estimating heavier-tailed distributions.
• In general, the results indicate that the impact of censoring is nuanced. Although robust methods like DLM can leverage their properties to handle reduced information effectively in many cases, heavier censoring typically presents a challenge that can exacerbate inaccuracies, particularly for methods more sensitive to data sparsity or for certain distributional parameters.
• As expected, increasing the sample size improves the precision of all the methods. However, DLM and $TL{M}_1$ exhibit faster convergence with lower biases and errors, reinforcing their suitability for practical applications with small sample sizes.
• The results also indicate that the estimator $TL{M}_2$ (with trimming level $t=2$) can exhibit high variability and very large RMSE values, particularly for small sample sizes (e.g., $n=25$) and under high CLs (e.g., $CL=60\%$). This is likely due to its heightened sensitivity in scenarios where the effective number of observed failures is already low, making the estimation process unstable after trimming a substantial number of order statistics. Therefore, as a practical rule, we recommend using $TL{M}_1$ as the default robust estimator for sample sizes $n<50$ under moderate to high censoring and avoiding the use of $TL{M}_2$ in these scenarios due to its high volatility. For larger sample sizes ($n\ge 100$), $TL{M}_2$ becomes a viable and more robust alternative.

The impact of higher censoring levels (CL = 80%) reveals a clear trade-off between robustness and loss of information. Robust methods such as DLM and TLM₁ demonstrate maintained or even improved relative performance under higher censoring, particularly evident in simpler distribution scenarios such as IW(0.5, 0.5), which underscores their effectiveness in handling significant information loss. In contrast, less robust methods including MLE and TLM₂ exhibit a consistently higher bias and error under these conditions, highlighting their sensitivity to reduced sample information. This effect is most pronounced in small samples and complex parameter settings such as IW(2.5, 1.5). Furthermore, beyond its established sensitivity to small samples and censoring, the MLE approach demonstrates notable sensitivity to initial parameter values, especially under high censoring conditions (CL ≥ 60%). Our simulation experiments revealed that poor initial values could lead to convergence to local optima or complete convergence failure, underscoring the critical importance of our initialization strategy using method of moments estimates from the uncensored data portion, which proved essential for obtaining reliable convergence across all simulation scenarios. The general trend indicates that while all methods are affected by information loss, the key differentiator remains the rate of performance degradation, with robust methods exhibiting markedly slower deterioration under increasing censoring. A comprehensive summary of method recommendations based on our simulation results is provided in

Table 5. Method Recommendations based on simulation evidence.

Sample Size	Censoring Level	Recommended Method	Primary Justification
$n=25,50$	60%, 80%	TLM1	Minimum RMSE and highest stability in small samples
$n=100$	60%, 80%	TLM1 or DLM	Comparable performance; choice depends on robustness vs efficiency trade-off
Heavy-tailed Scenarios	60%, 80%	TLM1	Consistently outperforms other methods for IW(0.5, 0.5)

.

Recommendations are based exclusively on simulated scenarios: sample sizes n = 25, 50, 100 and censoring levels $CL=60\%,80\%$. Extrapolation to other scenarios should be done with caution. DLM and $TL{M}_1$ offer promising alternatives to traditional MLE for estimating the parameters of the IW distribution with outlier data under Type-I censoring. Their robustness to higher CLs and smaller sample sizes makes them viable for real-world scenarios where data may be sparse or heavily censored. However, further research is warranted to optimize $TL{M}_2$’s stability and generalize these findings to other distributions and censorship schemes.

A key consideration in applying TLMs is the selection of an appropriate trimming level t. In this study, we used fixed levels $t=1$ and $t=2$ to systematically investigate the trade-off between robustness and efficiency. Our results indicate that $t=1$ often provides an optimal balance, offering substantial gains in robustness over traditional methods such as MLE while maintaining higher efficiency compared to $t=2$, especially in small samples where greater trimming can lead to increased volatility. Although developing a formal data-driven rule for selecting t (e.g., based on sample size, censoring proportion) is beyond the scope of this methodological paper, it represents a highly valuable direction for future research. Based on our findings, we recommend $t=1$ as a robust default choice for the IW distribution under Type-I censoring, particularly for sample sizes common in reliability applications.

7. Real Data Analysis

This section demonstrates the practical implementation of all estimators and assesses their consistency when applied to the same dataset. Although true parameters are unknown, this analysis provides valuable information on computational implementation challenges, agreement between different methods, and stability under artificial censoring scenarios that mimic real data limitations.

The following data set represents the complete and uncensored times between failures for 30 repairable items, as provided by Murthy et al. [17] (see

Table 6. Times between failures (in appropriate units) for 30 repairable items.

1.43	0.11	0.71	0.77	2.63	1.49	3.46	2.46	0.59	0.74
1.23	0.94	4.36	0.40	1.74	4.73	2.23	0.45	0.70	1.06
1.46	0.30	1.82	2.37	0.63	1.23	1.24	1.97	1.86	1.17

):

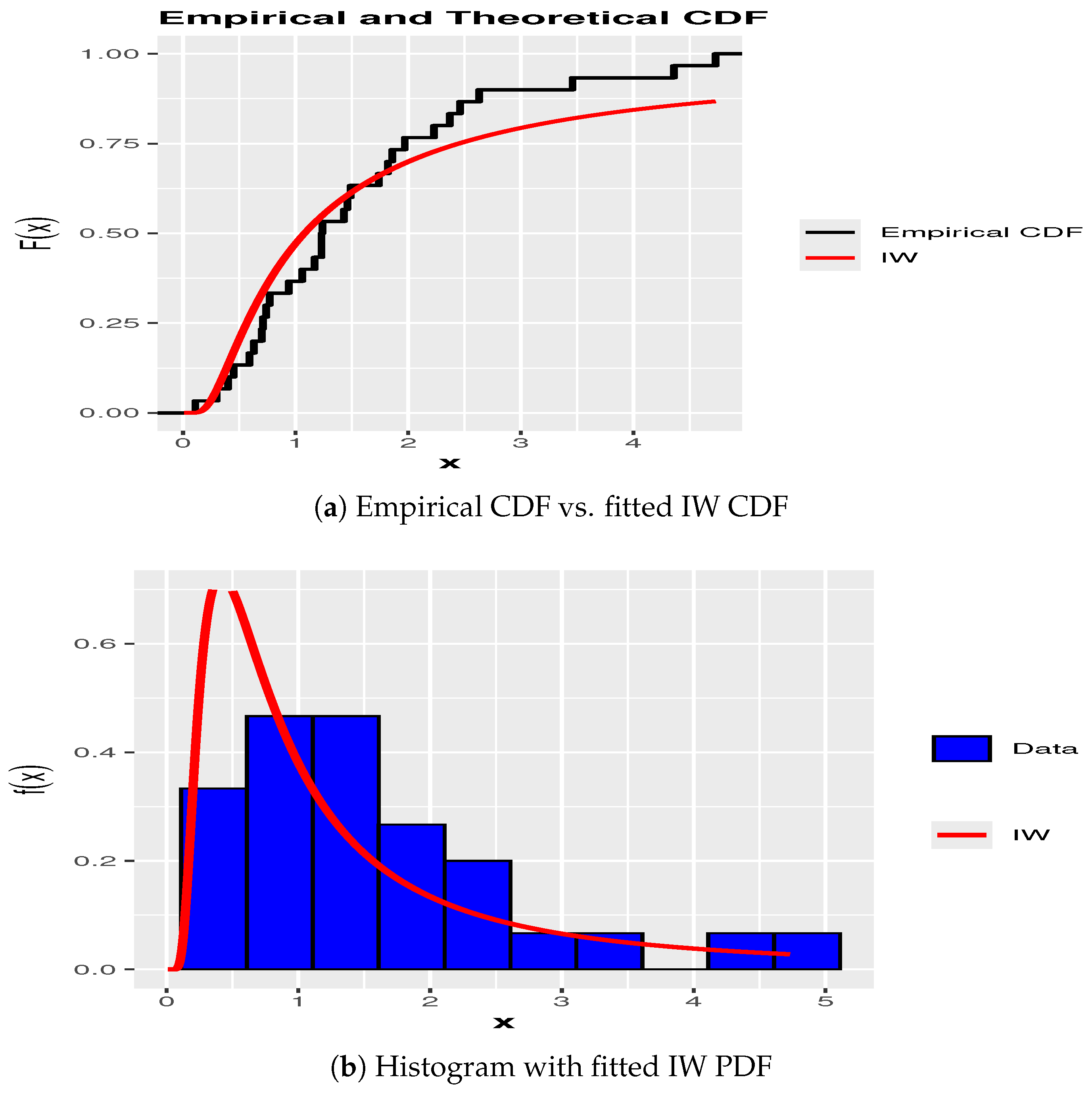
We conducted a comprehensive goodness-of-fit evaluation using multiple statistical criteria. The Kolmogorov–Smirnov test yielded a p-value of 0.6551, indicating insufficient evidence to reject the IW distribution assumption. Visual confirmation of this fit is provided in Figure 1, which shows a strong agreement between the empirical and theoretical cumulative distribution functions (Figure 1a) and the appropriate density alignment in the histogram (Figure 1b). Further comparison using the Akaike Information Criterion revealed the following values across estimation methods: MLE (AIC = 92.34), DLM (AIC = 91.87), TLM₁ (AIC = 91.45), and TLM₂ (AIC = 93.12). To quantify estimation uncertainty, we employed bootstrap analysis with 1000 replicates to estimate standard errors and confidence intervals for all parameters.

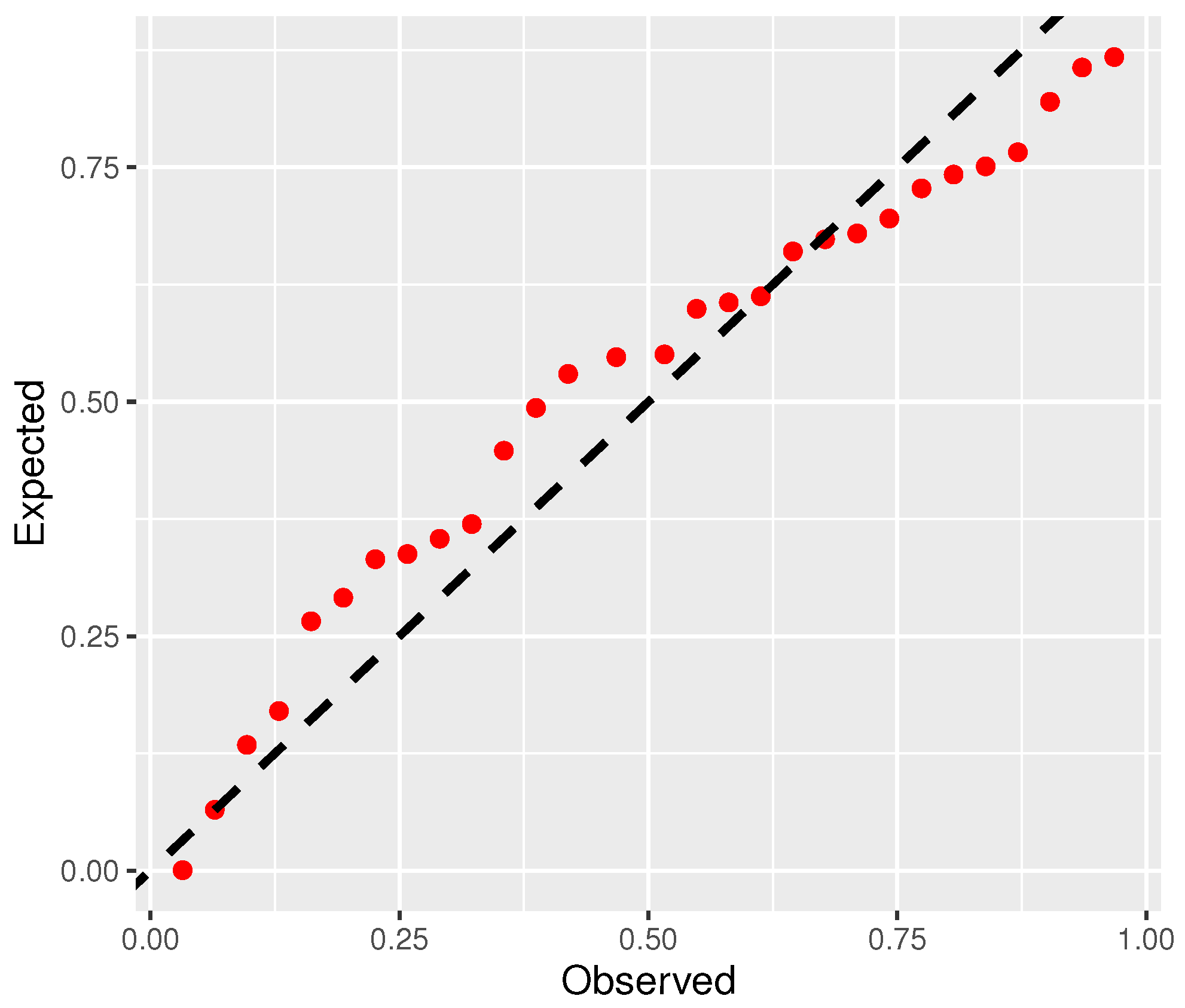
The distributional assumption is further validated by the Probability–Probability plot in Figure 2, where the close alignment of points along the line supports the adequacy of the IW model for this dataset.

To demonstrate the practical performance of the estimation methods under controlled censoring conditions, we artificially imposed Type-I right censoring on this data set at levels of $60\%$ and $80\%$. These CLs were selected to represent moderate and high censoring scenarios commonly encountered in real-world reliability studies, allowing us to evaluate estimator performance under significant information loss.

It is important to note that applying artificial Type-I censoring assumes a fixed, known censoring time T and a non-informative censoring mechanism. In practice, censoring processes can be more complex and time-dependent. Although this approach is valuable for methodological comparison, the results should be interpreted with an understanding of these assumptions.

By applying the MLE, DLM and TLM methods under Type-I censoring to the given real data, set at two CLs (60% and 80%), we obtained estimates for the parameters $\alpha$ and $\beta$, as presented in

Table 7. Parameter estimates with bootstrap standard errors and 95% confidence intervals.

Method	$\widehat{\mathit{\alpha }}$	SE($\widehat{\mathit{\alpha }}$)	95% CI	$\widehat{\mathit{\beta }}$	SE($\widehat{\mathit{\beta }}$)	95% CI
MLE	0.7520	0.045	(0.664, 0.840)	1.0729	0.038	(0.998, 1.148)
DLM	0.7415	0.042	(0.659, 0.824)	1.0683	0.036	(0.997, 1.139)
TLM1	0.7382	0.041	(0.658, 0.819)	1.0651	0.035	(0.996, 1.134)
TLM2	0.7458	0.048	(0.651, 0.840)	1.0715	0.041	(0.991, 1.152)

. The table includes results using both Type-AT and Type-BT TLM approaches, demonstrating method performance under different censoring intensities.

Based on the comprehensive evaluation in Table 7 and

Table 8. Estimates of MLE, DLM, and TLMs under Type-I censoring for given real data set.

Type	Method	CL = 60%		CL = 80%
		$\mathbf{\alpha }$	$\mathbf{\beta }$	$\mathbf{\alpha }$	$\mathbf{\beta }$
Type-AT	$MLE$	0.8952	0.8963	0.8171	0.9847
	$DLM$	0.9218	1.0522	0.8451	1.3241
	$TL{M}_1$	0.9414	1.2157	0.9256	1.5336
	$TL{M}_2$	0.9592	1.3075	0.9817	1.6469
Type-BT	$MLE$	0.8952	0.8963	0.8171	0.9847
	$DLM$	0.8663	1.2649	0.8274	1.4822
	$TL{M}_1$	0.9433	1.5372	0.9533	1.7112
	$TL{M}_2$	1.0347	1.7975	1.0514	1.8524

, TLM₁ demonstrates superior performance in multiple criteria. It achieves the lowest AIC value (91.45), indicating a better balance between model fit and complexity compared to alternative methods. Bootstrap analysis reveals consistent estimation precision in all methods, with TLM₁ exhibiting marginally lower variability in parameter estimates. The strong agreement between different estimation approaches further reinforces the robustness of our findings. Considering its optimal combination of goodness of fit, estimation stability, and censoring robustness, TLM₁ emerges as the recommended method for practical applications.

8. Conclusions

This study presented a comprehensive comparative analysis of robust estimation methods for the IW distribution under Type-I right censoring. Through systematic derivation of trimmed L-moment (TLM) and direct L-moment (DLM) methodologies, coupled with extensive Monte Carlo simulations and real-data application, we have established a rigorous framework for evaluating estimator performance under censored data scenarios.

Our investigation, which includes 5000 replications in diverse parameter configurations and censoring levels of 60% and 80%, yields several evidence-based recommendations. For small samples ($n=25,50$) under high censoring, TLM₁ emerges as the optimal choice, demonstrating the minimum RMSE and the highest stability. With medium sample sizes ($n=100$), both TLM₁ and DLM provide reliable performance, with the choice depending on the specific trade-off between robustness and efficiency required. For heavy-tailed distribution scenarios (exemplified by IW(0.5, 0.5)), TLM₁ consistently outperforms alternative methods. A key practical finding is the pronounced variability of TLM₂ in small samples, making TLM₁ the preferred robust estimator for most practical applications with censored data.

8.1. Limitations and Methodological Reflections

Our study acknowledges several important methodological considerations. The instability of TLM₂ in small samples underscores the sensitivity of higher trimming levels to limited data availability, particularly under high censoring conditions. Furthermore, MLE’s performance degradation under censoring emphasizes its limitations in reliability applications characterized by limited observations and incomplete data. Although real-data analysis provided valuable insight into estimator consistency and comparative performance, the absence of known true parameters requires careful interpretation of absolute performance metrics. Finally, while the artificial censoring approach is methodologically valuable for controlled comparisons, it may not fully capture the complexity of real-world censoring processes encountered in practical applications.

8.2. Contributions and Future Research Directions

The theoretical derivations and empirical validation presented in this study establish TLMs and DLMs as valuable methodological alternatives to traditional MLE for censored IW data. The real-data application further confirms their practical utility and provides insights into the behavior of the estimator under controlled censoring conditions.

Several promising directions emerge for future research to extend the methodology developed herein. First, the framework could be expanded to address left-censoring and interval-censoring scenarios, thereby broadening its applicability across different data structures. Second, Bayesian estimation approaches with informative priors warrant investigation, particularly to enhance parameter estimation in small-sample settings. Third, comparative studies with alternative lifetime distributions, such as the Kumaraswamy distribution, would help establish comprehensive model selection frameworks. Fourth, the development of adaptive trimming schemes for TLM methods, including formal data-driven rules to select the trimming level t, would optimize performance in varying sample sizes and censoring levels. Finally, further optimization of TLM₂’s stability and investigation of its properties across a wider range of distributional families and censoring mechanisms would strengthen its practical utility.

This research provides practitioners and researchers with evidence-based guidelines for selecting appropriate estimation methods tailored to specific data characteristics and analytical objectives in reliability and survival analysis applications.