A Symmetry-Aware Predictive Framework for Olympic Cold-Start Problems and Rare Events Based on Multi-Granularity Transfer Learning and Extreme Value Analysis

Abstract

This paper addresses the cold-start problem and rare event prediction challenges in Olympic medal forecasting by proposing a predictive framework that integrates multi-granularity transfer learning with extreme value theory. The framework comprises two main components, a Multi-Granularity Transfer Learning Core (MG-TLC) and a Rare Event Analysis Module (RE-AM), which address multi-level prediction for data-scarce countries and first medal prediction tasks. The MG-TLC incorporates two key components: Dynamic Feature Space Reconstruction (DFSR) and the Hierarchical Adaptive Transfer Strategy (HATS). The RE-AM combines a Bayesian hierarchical extreme value model (BHEV) with piecewise survival analysis (PSA). Experiments based on comprehensive, licensed Olympic data from 1896–2024, where the framework was trained on data up to 2016, validated on the 2020 Games, and tested by forecasting the 2024 Games, demonstrate that the proposed framework significantly outperforms existing methods, reducing MAE by 25.7% for data-scarce countries and achieving an AUC of 0.833 for first medal prediction, 14.3% higher than baseline methods. This research establishes a foundation for predicting the 2028 Los Angeles Olympics and provides new approaches for cold-start and rare event prediction, with potential applicability to similar challenges in other data-scarce domains such as economics or public health. From a symmetry viewpoint, our framework is designed to preserve task-relevant invariances—permutation invariance in set-based country aggregation and scale robustness to macro-covariate units—via distributional alignment between data-rich and data-scarce domains and Olympic-cycle indexing. We treat departures from these symmetries (e.g., host advantage or event-program changes) as structured asymmetries and capture them with a rare event module that combines extreme value and survival modeling.

1. Introduction

As the world’s largest comprehensive sporting event, the Olympic Games and their medal prediction have been important topics in sports analytics, economic research, and data science. However, existing prediction methods primarily focus on data-rich countries, with limited predictive capability for data-scarce countries, especially those with zero medals. Statistics show that across 200 countries participating in the Olympics, over 40% have fewer than 10 historical medals, and approximately 30% have never won an Olympic medal. These data-scarce countries face severe cold-start challenges in prediction.

The cold-start problem in Olympic prediction manifests in two main aspects: first, the prediction difficulties caused by data scarcity, particularly for countries that have never won medals; second, the challenge of ensuring multi-level prediction consistency, where national-level predictions often conflict with specific event predictions. Meanwhile, predicting when a zero-medal country will win its first medal is a typical rare event prediction problem, characterized by low frequency, high uncertainty, and extreme value characteristics.

Existing research primarily addresses these issues from two perspectives: one employs economic models using macroeconomic indicators such as GDP and population to predict Olympic performance [1,2]; the other utilizes machine learning techniques such as random forests and gradient boosting [3]. However, these methods perform poorly when dealing with data-scarce countries and lack specialized modeling for rare events.

To address these challenges, we propose a predictive framework that integrates multi-granularity transfer learning with extreme value theory. The framework includes two core components: a MG-TLC and a RE-AM. The MG-TLC achieves knowledge transfer from data-rich countries to data-scarce countries through DFSR and the HATS; the RE-AM combines a BHEV with PSA to provide precise predictions for rare events such as “first medals”.

Our innovation in addressing Olympic cold-start and rare event challenges lies in establishing a theoretical bridge between multi-granularity transfer learning and extreme value theory. This combination leverages complementary advantages: multi-granularity transfer learning can handle data-scarce samples, while extreme value theory offers theoretical support for long-tail distributions and rare events. Unlike existing methods, our framework considers not only horizontal domain transfer (from data-rich countries to data-scarce countries) but also vertical temporal transfer (utilizing Olympic development stage theory), forming a novel “bidirectional transfer” paradigm—a new attempt in the field of sports prediction. Additionally, our proposed mechanism to ensure hierarchical consistency resolves the problem of multi-level prediction inconsistency in existing Olympic prediction methods, a challenge that previous research has not adequately addressed.

The main contributions of this study include (1) proposing an Olympic prediction framework that combines multi-granularity transfer learning with extreme value theory; (2) designing a consistency guarantee mechanism for multi-level predictions; and (3) developing a prediction method capable of handling long-term historical Olympic data spanning multiple eras, demonstrating its robustness to significant temporal changes in Olympic structures and participation patterns. Experimental results demonstrate that the framework significantly outperforms existing methods in prediction accuracy for data-scarce countries and rare event prediction capability.

We organize the remainder of our paper as follows: Section 2 reviews related work on Olympic prediction, transfer learning, and extreme value theory. Section 3 presents the problem definition, notation, and key data challenges. Section 4 details the proposed methodology, introducing our framework architecture (MG-TLC and RE-AM) and feature design principles. Section 5 describes the experimental setup, including data sources, feature engineering, and evaluation methods. Section 6 presents experimental results, covering performance comparisons, model evaluations, case studies, and forecasts for the 2028 Olympics. Finally, Section 7 concludes with a discussion of future research directions.

In our setting, symmetry refers to transformations that leave the predictive task unchanged: (i) permutations of countries or regions (rankings should be invariant to reordering), (ii) scale transformations of macro covariates (unit- or currency-based conversions), and (iii) calendar re-indexing by Olympic cycles (equivariance in discrete time). Our design is intended to preserve these through set-based aggregation (permutation invariance), feature standardization and ratio- and per-capita features (scale robustness), distributional alignment across data-rich and data-scarce domains, and cycle-indexed discrete-time modeling. Symmetry-breaking factors—such as host advantage or event program modifications—are modeled explicitly by a rare event component combining extreme value and survival modeling, providing a principled link to the journal’s focus on symmetry.

2. Related Work

2.1. Olympic Prediction Research

Olympic prediction research is primarily divided into two directions: regression models based on economic variables and prediction models based on machine learning. Bernard and Busse [1] proposed using GDP and population to predict Olympic medal counts, demonstrating the significant influence of economic factors on Olympic performance. Subsequently, Forrest et al. [4] introduced new variables measuring GDP volume and home advantage effects, and combined them with judgmental adjustments to improve prediction accuracy. Johnson and Ali [2] analyzed the impact of participation continuity on Olympic performance, finding that countries with long-term Olympic participation have significant advantages.

With the development of machine learning technologies, researchers have begun applying more complex models in recent years. Zhu et al. [3] used random forests and XGBoost to predict Olympic medals and found that feature engineering is crucial for prediction accuracy. Moolchandani et al. [5] predicted 2024 Olympic medals through various machine learning models, emphasizing the potential of data-driven methods but not addressing the data scarcity problem. Huimin et al. [6] used interpretable random forest models to predict Olympic medals, revealing the importance of socioeconomic features but not addressing the challenge of rare event prediction. Liu and Suen [7] combined time series analysis to propose a dynamic prediction model for Olympic performance. However, these studies mainly focus on data-rich countries, with limited predictive capability for data-scarce and zero-medal countries.

2.2. Transfer Learning

Transfer learning aims to transfer knowledge from source domains to target domains, addressing the problem of insufficient target domain data. In domain adaptation, Ganin et al. [8] proposed Domain-Adversarial Neural Networks (DANNs), which learn domain-invariant feature representations through Gradient Reversal Layers. Chang and Li [9] designed Domain-Specific Batch Normalization (DSBN), learning independent normalization parameters for different domains to improve transfer effects further.

TrAdaBoost, proposed by Dai et al. [10], is another classic transfer learning method that achieves knowledge transfer by adjusting sample weights. Long et al. [11] designed Deep Adaptation Networks (DANs), reducing distribution differences between source and target domains through Maximum Mean Discrepancy (MMD) loss. Recent multi-granularity transfer learning research, such as that of Zhao et al. [12], inspired our method, which achieves knowledge transfer through multi-scale feature fusion. Jiang et al. [13] demonstrated the potential of transfer learning through hierarchical multi-granularity classification, applicable to complex data scenarios. However, these transfer learning methods rarely consider multi-level prediction consistency issues and do not specifically model extreme events. Methodologically, recent work on hierarchical transfer learning with Transformers shows that cross-level knowledge transfer can yield substantial gains; this supports our design choice to transfer across levels in multi-granularity settings [14].

2.3. Extreme Value Theory and Rare Event Prediction

Extreme value theory is a mathematical branch that studies probability distributions of extreme events, widely applied in financial risk, natural disasters, and rare event prediction. Coles [15] systematically introduced extreme value statistical models, including the Generalized Extreme Value (GEV) distribution and the Generalized Pareto Distribution (GPD), and subsequent developments on predictive peaks-over-threshold have formalized one-step-ahead prediction and predictive densities for extremes, offering a principled basis for uncertainty quantification [16]. In rare event prediction, zero-inflated models, such as zero-inflated Poisson and negative binomial models, are commonly used to handle count data with excess zeros.

Survival analysis is another approach for handling rare events, focusing on occurrence time and hazard rates. Kleinbaum and Klein [17] introduced basic methods and applications of survival analysis, such as Cox proportional hazards models and piecewise survival analysis. However, research applying extreme value theory and survival analysis to Olympic first medal prediction is relatively lacking, especially considering the long timespan and multi-level structure of Olympic data.

3. Preliminaries and Problem Definition

3.1. Notation

To ensure consistency and clarity of notation throughout the paper,

Table 1. Notation.

Symbol	Meaning
$\mathcal{R}$	Set of data-rich countries
$\mathcal{S}$	Set of data-scarce countries
$\mathcal{Z}$	Set of zero-medal countries
$\mathcal{M}$	Set of countries obtaining medals in the future
${\mathcal{C}}_v$	Set of sport types country v participates in
${\mathcal{E}}_{v,c}$	Set of specific events country v participates in for sport type c
$X_v$	Feature vector of country v
$y_{v,t}^{\mathrm{ctry}}$	Total medal count of country v in Olympics t
$y_{v,t,c}^{\mathrm{spt}}$	Medal count of country v in sport type c at Olympics t
$y_{v,t,c,e}^{\mathrm{evt}}$	Medal count of country v in specific event e of sport type c at Olympics t
$T_v$	Time when country v obtains its first medal
${\varphi }_l$	Feature mapping function for prediction level l
$D_s$, $D_t$	Source domain data and target domain data
$\mathcal{L}$	Loss function
$\lambda$, $\alpha$, $\beta$, $\gamma$	Loss function weight parameters
${\mu }_v$, ${\sigma }_v$, ${\xi }_v$	GEV distribution parameters for country v
$p_0\left(v\right)$	Probability that country v never wins a medal
$h\left(t\right|X\left(t\right))$	Conditional hazard function

lists the main symbols used and their meanings.

3.2. Problem Definition

This research addresses two core problems: Olympic medal prediction for data-scarce countries and first medal prediction for zero-medal countries.

Problem 1: Multi-Level Prediction for Data-Scarce Countries

Given a set of data-rich countries $\mathcal{R}$ and a set of data-scarce countries $\mathcal{S}$, where each country v has a feature vector $X_v$, our goal is to predict the following for each Olympics t:

• Country level: The total medal count $y_{v,t}^{\mathrm{ctry}}$ for country v at Olympics t;
• Sport type level: The medal count $y_{v,t,c}^{\mathrm{spt}}$ for country v in sport type c at Olympics t;
• Event level: The medal count $y_{v,t,c,e}^{\mathrm{evt}}$ for country v in specific event e of sport type c at Olympics t.

Multi-level predictions must satisfy the consistency constraint:

$$y_{v,t}^{\mathrm{ctry}}=\sum _{c\in {\mathcal{C}}_v}{y}_{v,t,c}^{\mathrm{spt}}=\sum _{c\in {\mathcal{C}}_v}\sum _{e\in {\mathcal{E}}_{v,c}}{y}_{v,t,c,e}^{\mathrm{evt}}$$

(1)

Problem 2: First Medal Prediction for Zero-Medal Countries

Given a set of zero-medal countries $\mathcal{Z}$, for each country $v\in \mathcal{Z}$, we need to predict the following:

• Binary classification task: Whether country v will win an Olympic medal in the future $P(v\in \mathcal{M})$, where $\mathcal{M}$ is the set of countries winning medals in the future.
• Time prediction task: If $v\in \mathcal{M}$, predict the time $T_v$ when the first medal will be obtained.

3.3. Data Challenges

Olympic data presents the following challenges, making prediction tasks particularly difficult:

• Data Scarcity: Over 40% of countries have fewer than 10 historical medals, and approximately 30% have never won medals, causing traditional models to perform poorly on these countries.
• Multi-Level Structure: Olympic prediction involves three levels, country level, sport type level, and event level, requiring consistency among predictions at different levels.
• Long Timespan: Olympic data spans from 1896 to 2024, encompassing socioeconomic transformations, political events, rule changes, and other complex factors. Figure 1 shows the changes in key indicators over this long timespan and marks the impact of key historical events.
• Rare Event Characteristics: Winning a first medal is a typical rare event with low frequency, high uncertainty, and extreme value distribution characteristics.
• Non-Stationarity: Olympic event settings, rules, and the number of participating countries change over time, leading to evident non-stationarity in the data.

4. Proposed Method

This section details the proposed prediction framework, including the overall architecture, Multi-Granularity Transfer Learning Core, Rare Event Analysis Module, and feature design principles.

4.1. Framework Overview

Our proposed prediction framework contains two core components:

• MG-TLC: Solves the multi-level prediction problem for data-scarce countries by transferring knowledge from data-rich countries while ensuring multi-level prediction consistency.
• RE-AM: Addresses the first medal prediction problem for zero-medal countries, combining extreme value theory and survival analysis to handle the special distribution of rare events.

As shown in Figure 2, the framework has two core components: on the left is the MG-TLC, containing DFSR and the HATS as two key modules; on the right is the RE-AM, containing the BHEV and PSA as two core modules. Arrows in the figure indicate data flow, with different colors distinguishing different processing stages. The top represents input data (historical Olympic data and engineered country features), while the bottom represents output results (multi-level predictions for data-scarce countries and first medal predictions for zero-medal countries). The two major components exchange information and work collaboratively: The MG-TLC provides foundational predictions for the RE-AM, and the RE-AM’s results are fed back to the MG-TLC for model fine-tuning, further optimizing predictions for zero-medal countries. The framework employs end-to-end training, optimizing overall performance through a joint loss function. For step-by-step details, the pseudocode and the corresponding algorithmic flowchart are provided in Appendix A (Algorithm A1 and Figure A1).

The framework’s design promotes stable training through several key architectural components: (1) The core MMD and structural preservation losses in DFSR act as forms of regularization that constrain the feature mapping. (2) The use of Domain-Specific Batch Normalization (DSBN) helps mitigate covariate shift and stabilizes training across different data domains. (3) The Bayesian hierarchical model (BHEV) naturally incorporates regularization through its hierarchical priors, which prevent overfitting on rare events. Together, these architectural choices create a regularized learning environment intended to ensure stable training and support the framework’s viability for this complex prediction task.

We choose an end-to-end approach to co-adapt the transfer core and the rare event module, facilitating knowledge transfer from data-rich sources to data-scarce targets while jointly learning population-level trends and unit-specific patterns, an idea consistent with modern Bayesian longitudinal practice in sports analytics [18].

From a symmetry standpoint, the MG-TLC implements permutation-invariant aggregation and transfer across editions and granularities, whereas the RE-AM explicitly addresses symmetry-breaking factors (host advantage, new/modified events) that drive long-tail and rare outcomes.

4.2. Multi-Granularity Transfer Learning Core

The core idea of the MG-TLC is to transfer knowledge from data-rich countries to data-scarce countries through feature space reconstruction and adaptive transfer strategies while ensuring multi-level prediction consistency. This idea of borrowing strength across related units is consistent with Bayesian longitudinal approaches that jointly learn population-level trends and individual trajectories [18].

4.2.1. Dynamic Feature Space Reconstruction

DFSR aims to map the source domain (data-rich countries) and target domain (data-scarce countries) to a shared feature space, making knowledge transfer more effective. Considering the multi-level nature of Olympic prediction, DFSR learns specific feature mapping functions for each prediction level.

Given source domain data $D_s$ and target domain data $D_t$, for prediction level l ∈ {country level, sport type level, event level}, DFSR learns a feature mapping function ϕ_l that maps original features x to new features ϕ_l (x). The mapping function is determined by optimizing the following objective:

$$\underset{{\varphi }_l}{min}{\mathcal{L}}_{\mathrm{MMD}}(D_s^l,D_t^l)+\alpha {\mathcal{L}}_{\mathrm{struct}}(D_s^l,D_t^l)+\beta \mathcal{R}\left({\varphi }_l\right)+\gamma {\mathcal{L}}_{\mathrm{consist}}\left(l\right)+\delta {\mathcal{L}}_{\mathrm{adv}}(D_s^l,D_t^l)$$

(2)

where ${\mathcal{L}}_{\mathrm{MMD}}$ is the Maximum Mean Discrepancy loss, which reduces distribution differences between source and target domains:

$${\mathcal{L}}_{\mathrm{MMD}}(D_s^l,D_t^l)={∥{\displaystyle \frac{1}{n_s}}\sum _{i=1}^{n_s}{\varphi }_l\left(x_i^s\right)-{\displaystyle \frac{1}{n_t}}\sum _{j=1}^{n_t}{\varphi }_l\left(x_j^t\right)∥}_{\mathcal{H}}^2$$

(3)

we use a Gaussian RBF kernel $k(z,z^{\prime })=exp(-\parallel z-z^{\prime }{\parallel }_2^2/\left(2{\sigma }^2\right))$, with the bandwidth $\sigma$ set via the median heuristic on pairwise distances in each mini-batch.

${\mathcal{L}}_{\mathrm{adv}}$ is the adversarial loss, implemented via a domain classifier D to encourage domain-invariant features:

$${\mathcal{L}}_{\mathrm{adv}}(D_s^l,D_t^l)=-\sum _{i=1}^{n_s}logD\left({\varphi }_l\left(x_i^s\right)\right)-\sum _{j=1}^{n_t}log(1-D\left({\varphi }_l\left(x_j^t\right)\right))$$

(4)

${\mathcal{L}}_{\mathrm{struct}}$ is the structure preservation loss, ensuring that the mapping preserves structural relationships from the original feature space:

$${\mathcal{L}}_{\mathrm{struct}}(D_s^l,D_t^l)=\sum _{i,j}\left|d(x_i,x_j)-d({\varphi }_l\left(x_i\right),{\varphi }_l\left(x_j\right))\right|$$

(5)

we grid-searched $\alpha \in \{0.2,0.5,0.8,1.0,1.2\}$: for each value, models were trained on 1896–2016 and evaluated on the 2020 validation set. We selected the setting that minimized the target-domain MAE; $\alpha =0.8$ was used thereafter. Here, $\alpha$ is the weight on the structure-preserving term ${\mathcal{L}}_{\mathrm{struct}}$. Similarly, we grid-searched $\beta \in \{0.01,0.1,0.5,1.0\}$ for the regularization term $\mathcal{R}\left({\varphi }_l\right)$ (implemented as L2 weight decay) and $\gamma \in \{0.5,1.0,1.5,2.0\}$ for the consistency loss, using the same training–validation setup, selecting $\beta =0.1$ and $\gamma =1.0$ based on minimizing MAE. For the adversarial term, we grid-searched $\delta \in \{0.5,1.0,1.5,2.0\}$ and selected $\delta =1.0$ using the same criterion. $\mathcal{R}$ is a complexity regularization term preventing overfitting; and ${\mathcal{L}}_{\mathrm{consist}}$ is the hierarchical consistency loss, ensuring mapping relationships between different levels:

$${\mathcal{L}}_{\mathrm{consist}}\left(l\right)=\sum _{l^{\prime }\in \mathcal{N}\left(l\right)}{∥{\varphi }_l\left(x\right)-T_{l,l^{\prime }}\left({\varphi }_{l^{\prime }}\left(x\right)\right)∥}^2$$

(6)

where $\mathcal{N}\left(l\right)$ represents levels adjacent to level l, and $T_{l,l^{\prime }}$ is a level transformation function.

We adopt MMD-based alignment with structural regularization and an adversarial term to explicitly reduce cross-domain distribution shift while preserving task-relevant geometry. This combination is well suited to transferring knowledge from data-rich to data-scarce countries—MMD provides an architecture-agnostic discrepancy reduction [11], while adversarial training promotes domain-invariant features with minimal overhead [8]; the cross-level consistency term keeps the learned space coherent across country/sport/event granularities.

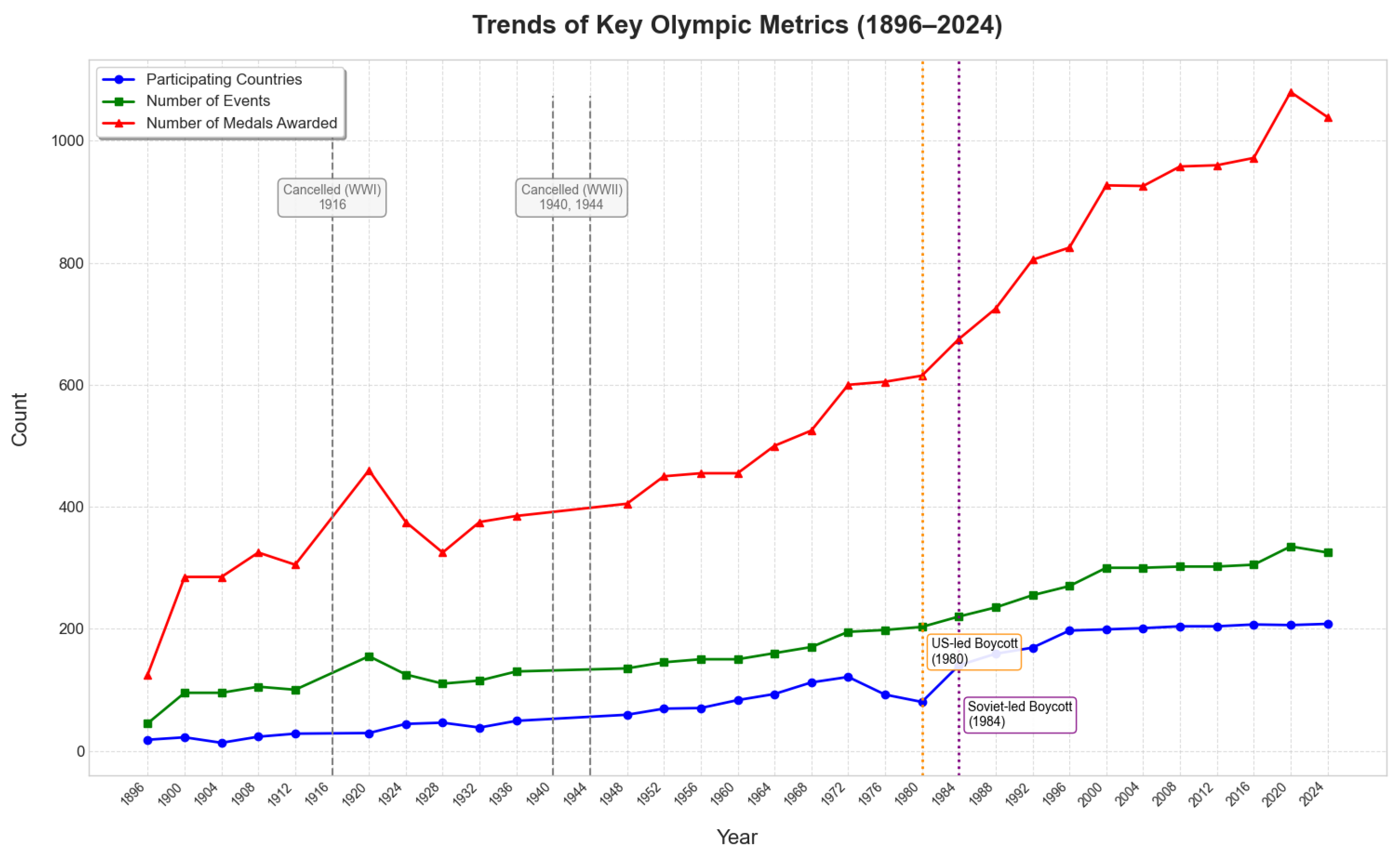
To facilitate understanding, we use the United States (source domain) and Nigeria (target domain) as examples to illustrate the working process of DFSR. In the original feature space, these two countries show significant differences in dimensions such as GDP and participation history, making direct comparison difficult. Through DFSR mapping, we obtain new feature representations that make the two countries more comparable regarding relative advantage event patterns and sports development trajectories. For example, the proportion of track and field events in global medals is about 4.2% for the United States and about 2.1% for Nigeria; after mapping, the distance between the two countries in the “relative sports event layout” dimension is reduced from 0.87 to 0.31, achieving feature space alignment.

We also created visualizations to intuitively understand this process, as shown in Figure 3:

Figure 3 uses t-SNE dimensionality reduction to project high-dimensional features into a two-dimensional space, comparing feature distributions before reconstruction (left) and after reconstruction (right). Blue points represent the source domain (data-rich countries), and red points represent the target domain (data-scarce countries). In Figure 3a, the original feature space, source, and target domain countries show evident separation, with data-rich countries clustered in the upper right region and data-scarce countries scattered in the left and lower regions; in Figure 3b, in the feature space after DFSR reconstruction, the two types of countries show significant overlap, with the distribution difference between source and target domains markedly reduced, especially in the dimensions of event layout and development trajectory. The figure marks position changes of typical countries, such as the United States (US), China (CN), Nigeria (NG), and Cambodia (KH), allowing observation of the relative position changes of these countries in the feature space before and after reconstruction. While t-SNE provides an intuitive visualization, we acknowledge that it is a non-linear technique that may distort global distances; to complement this, we quantitatively assess alignment via the MMD metric, which decreased from 0.45 to 0.12 after reconstruction, confirming effective domain alignment.

To implement the adversarial component as part of the optimization, we introduced the Gradient Reversal Layer (GRL) and Domain-Specific Batch Normalization (DSBN) techniques.

Gradient Reversal Layer: The GRL acts as an identity function in forward propagation but reverses the gradient and multiplies it by coefficient $\lambda$ during backpropagation. By adding a domain classifier D and a GRL, we can implement adversarial training, encouraging the feature extractor to learn domain-invariant features.

Domain-Specific Batch Normalization: Unlike traditional batch normalization that uses the same scaling and shifting parameters for all data, DSBN learns independent normalization parameters for source and target domains:

$$\mathrm{DSBN}(x,d)={\gamma }_d{\displaystyle \frac{x-{\mu }_{\mathcal{B}}}{\sqrt{{\sigma }_{\mathcal{B}}^2+ϵ}}}+{\beta }_d$$

(7)

where $d\in \{s,t\}$ indicates domain identity, ${\mu }_{\mathcal{B}}$ and ${\sigma }_{\mathcal{B}}$ are the mean and standard deviation within the batch, respectively, and ${\gamma }_d$ and ${\beta }_d$ are learnable scaling and shifting parameters for domain d.

The GRL encourages domain-invariant representations without altering the forward pass [8], and DSBN mitigates covariate shift by decoupling normalization statistics across domains [9]. Both are lightweight yet effective additions that stabilize transfer under heterogeneous country distributions.

4.2.2. Hierarchical Adaptive Transfer Strategy

The HATS is a core component of the MG-TLC and is responsible for implementing knowledge transfer in the reconstructed feature space. Our HATS method draws inspiration from the bidirectional knowledge transfer framework of Jiang et al. [13] to optimize predictions for data-scarce countries. The HATS is based on two key ideas: first, different country groups should have different transfer strategies; and second, transfer learning should span multiple levels, including the country level, sport type level, and event level.

The HATS first clusters countries (from both source and target domains) into K groups, each representing a typical Olympic development pattern, such as the “all-around type,” “single-event specialization type,” etc. Clustering is performed in the reconstructed feature space using the spectral clustering algorithm:

$$\underset{\{C_1,...,C_K\}}{min}\sum _{k=1}^K{\displaystyle \frac{{\sum }_{i,j\in C_k}{w}_{ij}}{{\sum }_{i\in C_k,j\notin C_k}{w}_{ij}}}$$

(8)

where $w_{ij}$ is the similarity between countries i and j in the reconstructed feature space.

Spectral clustering leverages the affinity graph in the reconstructed space to capture non-linear country similarities; it is well suited to heterogeneous Olympic development patterns and does not presuppose convex clusters. Grouping both source and target countries in this space provides a natural scaffold for targeted transfer within each cluster.

The HATS establishes two models for each cluster C_k: a source domain base model $f_k^s$ and a cross-domain adjustment model g_k. The source domain base model is trained directly on source domain data:

$$f_k^s=arg\underset{f}{min}\sum _{i\in C_k\cap {\mathcal{D}}_s}\mathcal{L}(f\left(x_i\right),y_i)$$

(9)

The cross-domain adjustment model learns corrections from source domain predictions to target domain true values:

$$g_k=arg\underset{g}{min}\sum _{i\in C_k\cap {\mathcal{D}}_t}\mathcal{L}(g\left(f_k^s\left(x_i\right)\right),y_i)$$

(10)

During prediction, for a country v in the target domain, the HATS first determines its cluster $C_k$ and then calculates the predicted value through the source domain base model and cross-domain adjustment model:

$${\widehat{y}}_v=g_k\left(f_k^s\left(x_v\right)\right)$$

(11)

A single transfer model is insufficient for the diverse Olympic landscape. Clustering countries into groups with similar development patterns (e.g., all-around vs. single-event specialists) enables targeted transfer. The source-base model $f_k^s$ captures well-estimated signals from data-rich sources, while the cross-domain adjustment $g_k$ corrects cluster-specific distributional shifts and biases, allowing data-scarce targets to borrow strength from matched sources without washing out heterogeneity.

For example, consider Georgia (target domain), whose feature pattern is similar to that of “single-event-specialization-type” countries like Bulgaria and Hungary. The HATS assigns Georgia to this cluster and applies the specific transfer strategy for this type of country. In the 2024 prediction, the source domain base model gave an initial prediction of 6.3 medals, and the cross-domain adjustment model corrected it to 8.1 medals based on historical performance, close to the actual result (seven medals).

Figure 4 shows radar charts of feature patterns for five country types in the HATS.

Each radar chart represents the feature pattern of a country type, with axes including economic strength, historical performance, event diversity, gender balance, participation stability, and event specialization index. (a) “All-around-type” countries (e.g., the United States, China) are strong across all dimensions, especially economic strength and historical performance; (b) “single-event-specialization-type” countries (e.g., Georgia, Hungary) have high event specialization indices but low event diversity; (c) “team-event-dominant-type” countries (e.g., Serbia, Croatia) excel at team events; (d) “emerging development-type” countries (e.g., Qatar, Azerbaijan) have strong economic strength but weak historical performance; and (e) “initial exploration-type” countries (e.g., Cambodia, Andorra) are weak across all dimensions but improving in participation. Each type is annotated with 2–3 representative countries as examples.

4.2.3. Multi-Level Prediction Consistency Guarantee Mechanism

To achieve multi-level prediction consistency, we employ a three-stage optimization strategy:

1. Independent Training Stage: Separately train country-level, sport type-level, and event-level prediction models to obtain initial prediction results ${\widehat{y}}_v^{ctry,init}$, ${\widehat{y}}_{v,c}^{spt,init}$, and ${\widehat{y}}_{v,c,e}^{evt,init}$.

2. Consistency Optimization Stage: Introduce an explicit hierarchical consistency loss function to optimize models at all three levels jointly:

$${\mathcal{L}}_{\mathrm{consist}}={\lambda }_1\sum _v{∥{\widehat{y}}_v^{\mathrm{ctry}}-\sum _{c\in {\mathcal{C}}_v}{\widehat{y}}_{v,c}^{\mathrm{spt}}∥}^2+{\lambda }_2\sum _v\sum _{c\in {\mathcal{C}}_v}{∥{\widehat{y}}_{v,c}^{\mathrm{spt}}-\sum _{e\in {\mathcal{E}}_{v,c}}{\widehat{y}}_{v,c,e}^{\mathrm{evt}}∥}^2.$$

(12)

where ${\lambda }_1$ and ${\lambda }_2$ are tuned via a 2D grid search on the 2020 validation set with ${\lambda }_1\in \{0.4, 0.6, 0.8, 1.0, 1.2\}$ and ${\lambda }_2\in \{0.2, 0.4, 0.5, 0.6, 0.8\}$. The selection criterion is a weighted combination of event-level MAE and the L2 residuals of cross-level consistency (i.e., $\parallel {\widehat{y}}_v^{\mathrm{ctry}}-{\sum }_{c\in {\mathcal{C}}_v}{\widehat{y}}_{v,c}^{\mathrm{spt}}{\parallel }_2$ and $\parallel {\widehat{y}}_{v,c}^{\mathrm{spt}}-{\sum }_{e\in {\mathcal{E}}_{v,c}}{\widehat{y}}_{v,c,e}^{\mathrm{evt}}{\parallel }_2$). The optimal values are ${\lambda }_1=0.8$ and ${\lambda }_2=0.5$.

3. Post-Processing Calibration Stage: To enforce strict hierarchical consistency, we perform a final calibration on the optimized prediction results. We adopt a top-down, importance-weighted adjustment method, where higher-level predictions are assumed to be more robust and are used to calibrate lower-level estimates.

$${\widehat{y}}_{v,c,e}^{evt,final}={\widehat{y}}_{v,c,e}^{\mathrm{evt}}·{\displaystyle \frac{{\widehat{y}}_{v,c}^{\mathrm{spt}}}{{\sum }_{e^{\prime }\in {\mathcal{E}}_{v,c}}{\widehat{y}}_{v,c,e^{\prime }}^{\mathrm{evt}}}}·{\displaystyle \frac{{\widehat{y}}_v^{\mathrm{ctry}}}{{\sum }_{c^{\prime }\in {\mathcal{C}}_v}{\widehat{y}}_{v,c^{\prime }}^{\mathrm{spt}}}}$$

(13)

Then, sport type-level predictions are recalculated based on the adjusted event-level results:

$${\widehat{y}}_{v,c}^{spt,final}=\sum _{e\in {\mathcal{E}}_{v,c}}{\widehat{y}}_{v,c,e}^{evt,final}$$

(14)

The country-level prediction, serving as the anchor, remains unchanged:

$${\widehat{y}}_v^{ctry,final}={\widehat{y}}_v^{\mathrm{ctry}}$$

(15)

Through this three-stage approach, we ensure that final predictions strictly satisfy hierarchical consistency constraints:

$${\widehat{y}}_v^{ctry,final}=\sum _{c\in {\mathcal{C}}_v}{\widehat{y}}_{v,c}^{spt,final}=\sum _{c\in {\mathcal{C}}_v}\sum _{e\in {\mathcal{E}}_{v,c}}{\widehat{y}}_{v,c,e}^{evt,final}$$

(16)

We acknowledge that this deterministic post hoc scaling represents a design trade-off. While it enforces logical consistency—a critical feature for the usability of the forecast—it may alter the probabilistic calibration of the initial, unconstrained model outputs. However, this trade-off is justified, as the process empirically improves the overall accuracy of the point estimates. On the validation set, after adopting this mechanism, the MAE of event-level predictions decreased by a significant 15.2%. This suggests that the information from more stable, higher-level forecasts provides a valuable constraint that refines the more granular predictions, leading to a net improvement in predictive performance. A detailed analysis of the impact on probabilistic calibration is left for future work.

4.2.4. Olympic Development Stage Feature Analysis

In addition to horizontal knowledge transfer, the MG-TLC also considers vertical development stage features. By establishing an Olympic development stage model, different countries can learn from the experiences of countries at similar stages.

We divide a country’s Olympic development into three stages, the initial stage, growth stage, and mature stage, and extract specific feature patterns for each stage:

• Initial Stage: Feature patterns include the participation event count, athlete count, GDP growth rate, and other composite features.
• Growth Stage: Feature patterns include the medal growth rate, event diversification index, and other composite features.
• Mature Stage: Feature patterns include the medal stability index, event specialization index, and other composite features.

Through time series analysis, we identify which development stage a country is in and apply corresponding feature patterns and transfer strategies. For example, for a target domain country in the initial stage, we can focus on learning from source domain countries that were once in the initial stage and successfully transitioned to the growth stage.

4.2.5. Computational Complexity Analysis

To assess the efficiency of the proposed method, we analyzed the computational complexity of various framework components:

• DFSR: Time complexity is $O\left(n^{2}d\right)$, where n is the number of training samples and d is the feature dimension. Space complexity is $O\left(nd\right)$.
• HATS: Clustering stage complexity is $O(n^{2}logn)$, and model training stage complexity is $O(n_s·i_s+n_t·i_t)$, where $n_s$ and $n_t$ are the number of source and target domain samples, respectively, and $i_s$ and $i_t$ are the corresponding iteration numbers.
• BHEV: MCMC sampling complexity is $O(p·m·k)$, where p is the number of parameters, m is the sample count, and k is the sampling iteration count.
• PSA: Cox model training complexity is $O(n·d·i)$, where i is the optimization iteration count.

Compared to baseline methods, our framework requires more computational resources during the training phase, especially the MCMC sampling process of the BHEV component. However, during the prediction phase, computational complexity reduces to $O\left(d\right)$, comparable to other machine learning methods. In our experimental environment (32 GB RAM, NVIDIA RTX 3090), the complete framework’s training time was approximately 3.5 h, while prediction time was only a few seconds, meeting practical application requirements.

4.3. Rare Event Analysis Module

The RE-AM specifically addresses the first medal prediction problem, with the core idea of combining extreme value theory and survival analysis to simultaneously handle “whether a medal will be won” and “when a medal will be won”.

4.3.1. Bayesian Hierarchical Extreme Value Model

The BHEV reduces overfitting risk by introducing a hierarchical Bayesian framework and better captures parameter uncertainty. Our BHEV model was inspired by Melina et al. [19], who reviewed the combination of machine learning and extreme value theory in rare event prediction.

The choice of the Generalized Extreme Value (GEV) distribution is theoretically motivated, as extreme value theory provides a solid foundation for modeling rare occurrences like a country winning its first-ever medal. The BHEV is based on the following assumptions: (1) some zero-medal countries may never win Olympic medals (a zero-inflated component); and (2) for countries that might win medals, the distribution of the time to the first medal is characterized by the GEV distribution, with parameters linked to country-specific features.

The GEV family follows from classical extreme value limit laws and naturally accommodates heavy-tailed, low-frequency outcomes [15]. A hierarchical prior couples country-level tail parameters $({\mu }_v,{\sigma }_v,{\xi }_v)$ to enable shrinkage under scarce positives while retaining cross-country heterogeneity, yielding more stable and robust inference for zero-medal countries.

The BHEV adopts a three-layer Bayesian structure:

1.

Data Generation Layer: First medal acquisition time t follows a mixture distribution

$$p\left(t\right|v)=p_0\left(v\right)·\delta (t=\infty )+(1-p_0\left(v\right))·\mathrm{GEV}\left(t\right|{\mu }_v,{\sigma }_v,{\xi }_v)$$

(17)

where $p_0\left(v\right)$ denotes the probability that country v will never obtain an Olympic medal; $\delta (t=\infty )$ is the Dirac delta function centered at infinity, representing the event of the perpetual absence of medals; and GEV is the Generalized Extreme Value distribution parameterized by location ${\mu }_v$, scale ${\sigma }_v$, and shape ${\xi }_v$, characterizing the distribution of medal acquisition times for countries that will eventually obtain medals.

2.

Parameter Generation Layer: GEV distribution parameters $(\mu ,\sigma ,\xi )$ and $p_0$ are generated through country features:

$${\mu }_v\sim \mathcal{N}({\beta }_{\mu }^T{x}_v,{\tau }_{\mu }^2)$$

(18)

$$log\left({\sigma }_v\right)\sim \mathcal{N}({\beta }_{\sigma }^T{x}_v,{\tau }_{\sigma }^2)$$

(19)

$$\mathrm{logit}\left({\xi }_v\right)\sim \mathcal{N}({\beta }_{\xi }^T{x}_v,{\tau }_{\xi }^2)$$

(20)

$$\mathrm{logit}\left(p_0\left(v\right)\right)\sim \mathcal{N}({\beta }_p^T{x}_v,{\tau }_p^2)$$

(21)

3.

Hyperparameter Layer: Prior distributions for regression coefficients $\beta$ and variance parameters ${\tau }^2$:

$${\beta }_{\ast }\sim \mathcal{N}(0,{\lambda }_{\ast }^{-1}\mathbf{I})$$

(22)

$${\tau }_{\ast }^2\sim \mathrm{InvGamma}(a_{\ast },b_{\ast })$$

(23)

where $\lambda$, a, and b are preset hyperparameters. The prior strength $\lambda$ was selected via a grid over $\{0.2, 0.4, 0.6, 0.8, 1.0\}$ on the 2020 validation set, using negative log-likelihood (primary) and C-index (secondary); $\lambda =0.6$ performed best.

We place weakly-informative Normal priors on the transformed parameters (log $\sigma$ and logit $\xi$) for computational stability and simplicity: operating in an unconstrained space with Gaussian priors yields well-behaved geometry for NUTS sampling and avoids introducing extra hyperparameters (e.g., degrees of freedom for Student-t). Heavier-tailed priors are compatible with our framework, but we keep Normal priors to minimize complexity while retaining adequate robustness via wide variances.

The BHEV performs posterior inference through Markov Chain Monte Carlo (MCMC) methods, simultaneously obtaining parameters’ point estimates and uncertainty intervals. Specifically, the No-U-Turn Sampler (NUTS) implements efficient sampling [20].

To enhance understanding, we use Cambodia as an example to illustrate the application of the BHEV. Cambodia’s feature vector includes a GDP growth rate of 5.1%, athlete participation growth rate of 12.3%, and event diversity index of 0.35. Applying the BHEV model, we first obtain parameter posterior distributions:

$$\begin{array}{cc}\hfill {\mu }_{\mathrm{Cambodia}}& \sim \mathcal{N}(2028.6,{1.4}^2)\hfill \\ \hfill log\left({\sigma }_{\mathrm{Cambodia}}\right)& \sim \mathcal{N}(0.75,{0.25}^2)\hfill \\ \hfill \mathrm{logit}\left({\xi }_{\mathrm{Cambodia}}\right)& \sim \mathcal{N}(-0.3,{0.15}^2)\hfill \\ \hfill \mathrm{logit}\left(p_0\left(\mathrm{Cambodia}\right)\right)& \sim \mathcal{N}(-0.76,{0.38}^2)\hfill \end{array}$$

Drawing samples from these distributions, we can determine that Cambodia has a 0.683 probability of winning its first medal in 2028 and a 0.317 probability of never winning a medal. The BHEV not only provides point estimates but also gives complete probability distributions, quantifying prediction uncertainty. For example, the 95% confidence interval for Cambodia winning a medal at the 2028 Olympics is [0.452, 0.819].

To more intuitively understand the Bayesian hierarchical extreme value model, we plotted the distribution of historical first medal acquisition times and the BHEV model fit, as shown in Figure 5.

The histogram shows the distribution of the number of Olympic editions a country participates in before winning its first medal. The curve represents the theoretical GEV distribution fitted by the BHEV model. The empirical distribution exhibits a clear right-skewed and long-tailed shape, which is visually consistent with the characteristics of a GEV distribution, thus providing empirical support for our model choice.

The figure highlights typical cases: most countries (about 45%) win their first medal after participating in 1–3 editions; about 25% of countries need 4–6 editions; about 15% of countries need 7–10 editions; and a few countries (about 15%) require more than 10 editions to win their first medal. Special markers show some country cases: South Korea (two editions), Brazil (three editions), Nigeria (five editions), Qatar (eight editions), and Bahrain (twelve editions). The small figure on the right shows the five zero-medal countries with the highest predicted probability of winning their first medal in 2028 and their confidence intervals.

4.3.2. Piecewise Survival Analysis

PSA is the second core component of the RE-AM, focusing on analyzing how medal-winning hazard rates change over time. PSA views the first medal acquisition problem as a survival analysis problem, where “survival” refers to the state of not having won a medal and “event” refers to winning the first medal.

PSA adopts a Cox proportional hazards model and introduces time-varying covariates:

$$h\left(t\right|X\left(t\right))=h_0\left(t\right)exp\left({\beta }^{T}X\left(t\right)\right)$$

(24)

where $h_0\left(t\right)$ is the baseline hazard function, $X\left(t\right)$ is a feature vector that changes over time, and $\beta$ is a coefficient vector.

A standard Cox model relies on the proportional hazards (PH) assumption, which posits that the effect of a covariate is constant over time. Recognizing that this assumption may be too strict for the long-term, dynamic process of national sports development, we specifically employ a more flexible framework. By using a piecewise model with time-varying covariates, we effectively relax the strict PH assumption. This design allows the impact of features to differ across various time segments, enabling the model to capture the non-proportional hazards inherent in the data and thus enhancing its robustness.

Time-varying covariates are crucial in first medal prediction, as factors such as the GDP growth rate and participation event count change over time, affecting a country’s chance of winning its first medal. PSA divides time into segments, allowing these features to have different effects in different periods:

$$X\left(t\right)=\left\{\begin{array}{cc}{X}_1,\hfill & \mathrm{if}t\in [0,t_1)\hfill \\ X_2,\hfill & \mathrm{if}t\in [t_1,t_2)\hfill \\ ⋮\hfill \\ X_m,\hfill & \mathrm{if}t\in [t_{m-1},\infty )\hfill \end{array}\right.$$

(25)

We identified key time-varying features, such as participation intensity growth, GDP growth rate, and gender balance changes, which evolve as countries deepen their Olympic participation and significantly impact first medal acquisition.

A piecewise Cox model relaxes the strict proportional hazards assumption and aligns the time scale with the quadrennial Olympic cycle, allowing covariate effects to vary across segments and improving robustness over long spans [17].

Using the Maldives as an example to illustrate PSA application, we analyzed its time-varying feature changes from 2000 to 2024. To ensure a clear and consistent time scale, our analysis uses the Olympic edition as the fundamental time unit. We found that the Maldives’ participation intensity growth rate increased from 7.5% to 18.3%, and gender balance improved from 0.32 to 0.78. Based on the PSA model, the Maldives’ “medal-winning hazard rate” per Olympic Games rose from 0.021 in 2000 to 0.103 in 2024, corresponding to a 0.476 probability of winning a medal in 2028. Through PSA, we can capture trends in hazard rates over time, providing a dynamic perspective for prediction.

We plotted the medal-winning hazard rate curves over time (2000–2028) for typical zero-medal countries, as shown in Figure 6. The horizontal axis represents the calendar year, while the vertical axis represents the medal-winning hazard rate per Olympic Games.

Different colored lines represent different countries: the Maldives (blue), Cambodia (red), Andorra (green), and Luxembourg (purple). Data from 2000–2024 represents historical data fitting, while 2028 (dashed portion) represents predicted values. The figure shows that the Maldives’ hazard rate rapidly increased after 2012; Cambodia saw accelerated growth in 2016; Andorra maintained relatively stable growth; and Luxembourg showed fluctuating upward trends. The shaded area around each curve represents the 95% confidence interval. Annotations in the figure show key events influencing hazard rate changes, such as the Maldives’ sports reform plan implemented in 2016 and Cambodia’s increased sports investment in 2018.

4.3.3. Model Fusion and Calibration

The RE-AM combines predictions from the BHEV and PSA through model fusion and probability calibration to obtain more accurate first medal predictions:

$$P(T\le t|X)=w_1·P_{\mathrm{BHEV}}(T\le t|X)+w_2·P_{\mathrm{PSA}}(T\le t|X)$$

(26)

where $w_1$ and $w_2$ are weights determined based on validation set performance.

To ensure prediction probability accuracy, we use isotonic regression for probability calibration [21]:

$$P_{\mathrm{cal}}(Y=1|p)=g\left(p\right)$$

(27)

where p is the probability predicted by the model, and g is a monotonically non-decreasing function learned through isotonic regression.

Due to the special nature of extreme events, simple calibration may not be sufficient to handle long-tail distributions. We introduced an extreme value calibration method, with particular attention to calibration accuracy at high quantiles:

$$L_{\mathrm{cal}}=\sum _{i=1}^n{(y_i-P_{\mathrm{cal}}(Y=1|p_i))}^2+\lambda \sum _{p_i>\tau }{(y_i-P_{\mathrm{cal}}(Y=1|p_i))}^2$$

(28)

where $\tau$ is a probability threshold, and $\lambda$ is an additional penalty weight for high probability regions; this tail-aware calibration aligns with predictive peaks-over-threshold (POT) formulations for calibrated exceedance probabilities and predictive densities [16].

4.4. Feature Design Principles

Our feature design follows five core principles: multi-dimensionality, time sensitivity, cross-scale properties, transferability, and hierarchical relevance.

Multi-Dimensionality: The feature system encompasses multiple dimensions, including economic development, demographic structure, sports systems, historical performance, and time series, comprehensively representing a country’s Olympic development status. Different dimensional features vary with a country’s development stage; for example, economic and demographic features are more important for countries in the initial stage, while historical performance and sports structure features are more influential for countries in the mature stage.

Time Sensitivity: The Olympics are held every four years, and during these intervals, countries’ economic and sports development status significantly changes. We designed dynamic time window features capturing changes at different time scales: short-term windows (4–8 years) capture recent trends, medium-term windows (12–20 years) reflect stable development patterns, and long-term windows (24+ years) represent historical accumulation effects.

Cross-Scale Properties: Olympic prediction involves three levels: country, sport type, and specific event. We designed cross-scale features, such as the impact of country-level GDP on event-level performance and the feedback of event-level historical results on country-level predictions, ensuring complementarity and consistency among features at different levels.

Transferability: To promote knowledge transfer, we focused on which features have better transferability. For example, economic structure features have similar influence patterns across different countries and are easy to transfer, while historical performance features are more country-specific with weaker transferability. We enhanced the weight of transferable features through feature space reconstruction, improving transfer learning effects.

Hierarchical Relevance: Countries at different development stages should focus on different feature combinations. We designed specific feature patterns for countries in initial, growth, and mature stages, and considered development stage similarity in the transfer learning process, making knowledge transfer more targeted and effective.

Remark 1 

(Design properties). Permutation invariance. Let A denote a set aggregation operator (for example, mean, sum, or median) that is commutative and associative. For any permutation π of countries ${\left\{x_i\right\}}_{i=1}^n$, we have $A\left(\left\{x_i\right\}\right)=A\left(\left\{x_{\pi \left(i\right)}\right\}\right)$.

Scale robustness under standardization. With standardized features $z=(x-\mu )/\sigma$, any positive rescaling $x^{\prime }=cx$ (a unit or currency change) yields $z^{\prime }=(x^{\prime }-c\mu )/\left(c\sigma \right)=z$.

These design-level properties align with the symmetry notions defined in the Introduction.

5. Experimental Setup

This section details the experimental setup, including data sources and processing, feature engineering implementation, evaluation metrics, and baseline methods.

5.1. Data Sources and Processing

This study uses complete Olympic data from 1896 to 2024, covering 33 Summer Olympic Games, more than 200 countries/regions, and containing all athlete information and medal distribution data. GDP data comes from the Maddison Project Database (1896–1959) and the World Bank Database (1960–2024) [22].

Data Cleaning Rules: We paid special attention to the problem of chaotic event classification in the early Olympic Games, adopting the following rules for processing:

• Event Standardization: Using the Olympic event classification system established by the International Olympic Committee in 2012, we reclassified all historical events. For example, gymnastic competitions originally counted as part of “athletics” in the early years were reclassified into the “gymnastics” event.
• Demonstration Event Processing: Many “demonstration events” in the 1900–1908 Olympic Games awarded medals at the time but are not now considered official competitions, such as the balloon competition at the 1900 Paris Olympics. We only retained medal records for events currently officially recognized by the International Olympic Committee.
• National Entity Change Processing:
  • We established a historical country mapping table to handle country splits, mergers, name changes, etc.
  • For dissolved countries like the Soviet Union and Yugoslavia, we established historical continuity scores based on factors such as athletes, coaches, and training facilities to determine inheritance relationships
  • For countries after independence, only post-independence records were counted, not including history from the original combined country
• Special Case Processing:
  • The 1906 Athens “Intercalated Games” are not officially recognized by the International Olympic Committee, so the data was excluded.
  • The 1916, 1940, and 1944 Olympics canceled due to wars were treated as missing values in time series analysis.
  • Data anomalies in the 1980 Moscow and 1984 Los Angeles Olympics caused by political boycotts were processed with special markers.

5.2. Feature Engineering Implementation

Based on the previously mentioned feature design principles, we constructed the following specific features.

5.2.1. Economic and Demographic Features

For economic features, we examined GDP-related indicators for countries, including the absolute GDP value, GDP growth rate, and GDP volatility. The absolute GDP value reflects economic scale, GDP growth rate reflects development momentum, and GDP volatility reflects economic stability through the standard deviation of growth rates. For demographic features, we selected three key indicators: GDP per capita, total population, and population growth rate, respectively reflecting resource level, talent base, and population development trends. These economic and demographic features form the macroeconomic foundation for a country’s Olympic development.

5.2.2. Sports Structure Features

1.

Event Diversity Index: Using Shannon entropy [23] to calculate the distribution diversity of a country’s participation in events:

$$H=-\sum _i{p}_{i}log\left(p_i\right)$$

(29)

where $p_i$ is a country’s participation in event i (such as the proportion of athletes in that event to total athletes).

2.

Event Specialization Index: Using the Herfindahl index to calculate medal concentration:

$$HHI=\sum _i{s}_i^2$$

(30)

where $s_i$ is the proportion of medals the country won in event i to its total medals.

3.

Gender Balance: Calculating the ratio of male to female athletes, reflecting gender inclusivity:

$$GB=1-\left|{\displaystyle \frac{N_m-N_f}{N_m+N_f}}\right|$$

(31)

where $N_m$ and $N_f$ are the numbers of male and female athletes, respectively.

4.

Revealed Comparative Advantage (RCA): Identifying a country’s advantage events:

$$RC{A}_{ij}={\displaystyle \frac{M_{ij}/M_i}{M_j/M_T}}$$

(32)

where $M_{ij}$ is the medal count of country i in event j, $M_i$ is the total medal count of country i, $M_j$ is the global medal count for event j, and $M_T$ is the global total medal count.

5.

Athlete Participation: Total number of participating athletes and growth rate.

5.2.3. Historical Performance Features

Historical performance features are constructed from three dimensions: medal trends, participation stability, and special situational effects. Medal trends include historical medal counts and growth rates, average performance in the last three editions, historical best performance, and gold/silver/bronze medal ratio structure; participation stability includes participation continuity, event stability, the period from first participation to the present, and event expansion speed; and special situational effects mainly consider home advantage effects (medal boost for host countries is approximately 30%). Participation stability features are particularly important for data-scarce countries because, although these countries have few medals, their participation patterns may already show precursors to future success.

5.2.4. Time Series Features

Time series features are mainly divided into decomposition features and dependency features. Decomposition features extract long-term trend components, periodic patterns, and residual fluctuations through time series decomposition, respectively reflecting overall development direction, periodic changes, and uncertainty; dependency features include medal sequence autocorrelation coefficients and host year features, the former measuring continuity of performance across editions, the latter analyzing special performance patterns in host years. These features capture static performance and reveal dynamic development patterns, providing a basis for predicting future trends.

5.2.5. Development Stage Features

Based on historical medal counts and participation, we classify countries into three stages, the initial stage, growth stage, and mature stage, corresponding to countries with medal counts less than threshold $T_1$, between $T_1$ and $T_2$ with rapid growth, and above $T_2$ with relative stability. Each stage focuses on different feature combinations: the initial stage focuses on the participation event count, athlete count, and GDP growth rate; the growth stage focuses on the medal growth rate and event diversification index; the mature stage focuses on the medal stability index and event specialization index. After considering development stage features, the MAE for data-scarce countries decreased by approximately 12.3%.

5.2.6. Breakthrough Features

Breakthrough features designed for the first medal prediction task mainly focus on participation intensity growth, calculated as follows:

$$I{G}_{\mathrm{athletes}}={\displaystyle \frac{N_t-N_{t-1}}{N_{t-1}}}$$

(33)

$$I{G}_{\mathrm{events}}={\displaystyle \frac{E_t-E_{t-1}}{E_{t-1}}}$$

(34)

where $N_t$ and $E_t$ are the numbers of athletes and participation events in edition t, respectively. We found that countries’ participation intensity growth rates averaged over 85% of their historical peak values in the two editions before winning their first medal. This feature makes it excellent for identifying countries about to win their first medal.

5.2.7. Feature Correlation Analysis

We conducted a correlation analysis on all features collected in our study to understand their interrelationships. For clarity of visualization, Figure 7 presents a correlation heatmap showing only selected representative features from each category, including GDP, population size, event diversity index, etc.

The colors in the figure range from deep blue (strong negative correlation) to deep red (strong positive correlation). Economic features show high positive correlations with historical performance features, verifying the influence of economic foundation on Olympic performance. Development stage features display moderate correlations with sports structure features, reflecting the coordinated evolution between a country’s Olympic development stage and sports structure. The low correlations observed between certain features indicate that they capture information from different dimensions.

In the transfer learning process, we found that combinations of high-correlation features (such as GDP and historical medal counts) and low-correlation features (such as event specialization index and gender balance) could maximize knowledge transfer effects, becoming an important basis for HATS module design.

5.3. Evaluation Metrics and Baseline Methods

Experimental Setup: Data was divided into a training set (1896–2016), validation set (2020), and test set (2024). This division reflects the actual prediction scenario of using historical data to predict future Olympics and provides a validation basis for hyperparameter tuning and model selection.

Evaluation Metrics: The main evaluation metrics include Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Area Under the Receiver Operating Characteristic Curve (AUC), and Area Under the Precision–Recall Curve (PR-AUC). We also use the Concordance index (C-index) to evaluate time prediction accuracy.

Baseline Methods: We selected several types of methods as baselines for comparison. For economic models, we used the GDP model based solely on GDP and population for medal prediction, and the Bernard & Busse model [1], combining GDP, population, and home advantage effects. Machine learning models included the standard random forest, XGBoost gradient boosting tree model, and DeepFM deep factorization machine. For transfer learning, we adopted TrAdaBoost [10], adaptive boosting transfer learning, and Domain-Adversarial Neural Networks (DANNs) [8]. We included the zero-inflated Poisson (ZI-Poisson) model and Long-Zero Phase Hazard (LZPH) model for rare event modeling. All baseline methods used the same features and training/testing data division to ensure fair comparison.

Significance testing: We assessed per-metric improvements with paired tests over the test set countries (n defined as the number of paired country-level observations for that metric). Reported p-values in

Table 2. Overall performance comparison.

Method	Overall MAE	Data-Scarce Country MAE	First Medal AUC	First Medal PR-AUC
GDP Model	8.73	3.62	-	-
Bernard & Busse	7.42	3.18	-	-
Random Forest	5.31	2.84	0.682	0.312
XGBoost	4.96	2.67	0.704	0.385
DeepFM	4.83	2.52	0.718	0.402
TrAdaBoost	4.59	2.43	0.702	0.376
DANN	4.37	2.21	0.715	0.394
ZI-Poisson	-	-	0.729	0.412
LZPH	-	-	0.748	0.435
Our Method	3.85 **	1.65 **	0.833 **	0.583 **
Improvement Percentage	11.9%	25.7%	11.4%	34.0%

**: Holm-adjusted p_adj < 0.01 (paired tests vs. the strongest baseline; df = n − 1, where n is the number of paired test set countries per metric). Wilcoxon signed-rank tests lead to the same conclusion.

were adjusted for the four parallel metrics using Holm’s method; nonparametric Wilcoxon signed-rank tests provided consistent conclusions.

6. Experimental Results and Analysis

6.1. Overall Performance Comparison

Table 2 shows the overall performance comparison of different methods on the test set. Our method significantly outperforms baseline methods on all metrics, and statistical significance tests indicate that these differences are statistically meaningful.

As shown in Table 2, our method outperforms the strongest baselines across all metrics: overall MAE is reduced by 11.9% (vs. DANN), the MAE for data-scarce countries by 25.7% (vs. DANN), and the first medal AUC and PR-AUC by 11.4% and 34.0% (vs. LZPH), respectively. Paired t-tests confirm that all gains are significant at the 0.01 level; nonparametric Wilcoxon signed-rank tests lead to the same conclusion, indicating that the improvements do not rely on distributional assumptions. This consistency across tests supports the effectiveness of combining multi-granularity transfer learning with extreme value analysis. All p-values reported for Table 2 are Holm-adjusted across the four metrics; n denotes the number of paired test set countries for each metric (thus $df=n-1$ for the paired t-tests).

We next connect these statistical findings to the design-level invariance checks implemented in our pipeline.

In addition, consistent with the design properties described in the Methods Section, reordering countries within aggregation windows leaves set-level predictions unchanged, and unit or currency conversions leave standardized features numerically unchanged; we include deterministic implementation checks for both during preprocessing and aggregation.

6.2. Feature Importance Analysis

For clarity, “data-rich” countries in our analysis roughly correspond to medal-rich countries, while “data-scarce” countries correspond to medal-poor ones; accordingly, the observed importance patterns are contrasted across these two groups.

We analyzed the importance of features through feature ablation experiments to understand the contributions of different feature categories to predictions. Our experimental results demonstrate that economic and historical performance features are the most important for data-rich countries. For data-scarce countries, sports structure features and time series features are more crucial. For the first medal prediction of zero-medal countries, participation intensity growth and the event diversity index are the most impactful features. This indicates that predictions for different types of countries should focus on different feature dimensions, validating the necessity of a multi-granularity approach. Having established the importance of a comprehensive feature set, we ablate the core architectural components of our model in the following sections.

All component ablations presented in Section 6.3, Section 6.4 and Section 6.5 reuse the same Olympic-cycle splits (train up to 2016, validate on 2020, and test on 2024) and the identical early-stopping rule. To avoid confounds, we only grid-search the weights of the ablated component (with others fixed), and we apply the same multiple-comparison correction as in the main results for significance testing.

6.3. Multi-Granularity Transfer Learning Effect Analysis

To ablate the contributions of our transfer components in the MG-TLC, we compare variants with vs. without each module—disabling kernel–MMD alignment, removing the structure preservation loss, and removing the cross-level consistency term (each by zeroing its loss weight)—while keeping all other settings unchanged. We also report strategy-level baselines (No Transfer, Direct Transfer, TrAdaBoost, DANN, and HATS) under the same splits for completeness. Quantified results and significance (using the identical Olympic-cycle splits, early stopping, and multiple-comparison correction as in the main results) are reported in

Table 3. Transfer learning strategy comparison (data-scarce country MAE).

Method	No Transfer	Direct Transfer	TrAdaBoost	DANN	HATS	HATS + GRL + DSBN
MAE	2.84	2.67 *	2.43 *	2.21 **	1.91 **	1.65 **

*: p < 0.05; **: p < 0.01, compared with “No Transfer”.

.

Results show that the HATS significantly improves transfer learning effects, and performance improves after adding the GRL and DSBN. Improvements are particularly notable when handling countries with large distribution differences between source and target domains. Statistical significance tests show that all transfer strategies significantly improve compared to “No Transfer,” with the HATS and HATS + GRL + DSBN showing significant improvements at the 0.01 level.

We further analyzed the impact of different cluster numbers on HATS performance. We determined the optimal number of clusters K by performing a grid search over a range of K from 2 to 10. For each K, we evaluated the model’s overall Mean Absolute Error (MAE) on the validation set. On the validation set, performance is optimal with cluster number $K=5$, corresponding to five country development patterns: “all-around-type,” “single-event-specialization-type,” “team-event-dominant-type,” “emerging development-type,” and “initial exploration-type.” This clustering based on development patterns is more effective than simple geographic or economic clustering, validating the HATS’s fine-grained modeling capability for Olympic country characteristics.

6.4. Bayesian Hierarchical Extreme Value Model Analysis

We conduct an ablation study for the Rare Event Analysis Module (RE-AM) by contrasting variants with vs. without the EV/survival branch (removing the BHEV/PSA vs. enabling them) and by comparing alternative EV specifications (the Standard GEV, Zero-Inflated GEV, BHEV, and BHEV + PSA) under identical splits and early stopping.

Table 4. Extreme value model comparison (first medal prediction).

Method	Standard GEV	Zero-Inflated GEV	BHEV	BHEV + PSA
AUC	0.683	0.729 *	0.796 **	0.833 **
PR-AUC	0.378	0.412 *	0.527 **	0.583 **
C-index	0.625	0.648 *	0.712 **	0.764 **

*: p < 0.05; **: p < 0.01, compared with Standard GEV.

shows comparison results for the first medal probability prediction, with AUC differences assessed for statistical significance using the DeLong test.

We plotted the ROC and PR curves for the first medal prediction, as shown in Figure 8. The left figure shows ROC curves, with the False Positive Rate (FPR) on the horizontal axis and the True Positive Rate (TPR) on the vertical axis; the right figure shows PR curves, with recall on the horizontal axis and precision on the vertical axis. Each figure contains four curves representing different methods: the Standard GEV (green), Zero-Inflated GEV (blue), BHEV (purple), and BHEV + PSA (red). The figures note the area under each curve: the BHEV + PSA achieves an AUC of 0.833 and PR-AUC of 0.583, significantly higher than other methods. The dashed lines in both figures represent baselines for random guessing (ROC figure) and positive class proportion in the dataset (PR figure).

Particularly note the PR curve: since first medals are rare events, PR curves better reflect model performance on minority classes than ROC curves. Our method shows more pronounced advantages on the PR curve, indicating that it achieves higher recall while maintaining high precision.

Results show that the Bayesian hierarchical structure significantly improves the prediction accuracy of extreme value models, reducing overfitting risk. After combining with PSA, predictive capability further improves, especially in predicting medal-winning times. Through DeLong tests, the AUC improvements in the BHEV and BHEV + PSA are significant at the 0.01 level, indicating that improvements are systematic rather than coincidental.

Notably, the BHEV model can capture different first medal acquisition patterns across countries. For example, some small countries with special sports traditions often have their first medals in specific events, such as short-distance running for Jamaica or judo for Georgia. The BHEV effectively captures these event-specific patterns through its Bayesian hierarchical structure, improving prediction accuracy.

6.5. Consistency Guarantee Mechanism Effect Analysis

To quantify the effect of the multi-level consistency guarantee, we perform an ablation analysis by comparing the model with vs. without the consistency term, using the identical Olympic-cycle splits, early-stopping rule, and significance protocol as in the main results.

Table 5. Consistency guarantee mechanism effect comparison (validation set MAE).

Method	Country-Level MAE	Sport Type-Level MAE	Event-Level MAE
Without Consistency Mechanism	4.32	1.87	0.92
With Consistency Loss Only	4.18 *	1.63 **	0.84 **
Complete Consistency Mechanism	4.15 *	1.58 **	0.78 **

*: p < 0.05; **: p < 0.01, compared with “Without Consistency Mechanism”.

reports validation set comparisons.

Results show that the complete consistency guarantee mechanism ensures hierarchical consistency of predictions and improves prediction accuracy at all levels, with improvements particularly significant at the event and sport type levels. This validates the effectiveness of our proposed three-stage optimization strategy.

A typical example is France’s prediction for the 2024 Paris Olympics. We created a comparison chart of consistency guarantee mechanism effects, as shown in Figure 9:

The left side shows prediction results without the consistency mechanism: country-level prediction is 62 medals (blue), the sum of sport type-level predictions is 68.5 medals (green), and the sum of event-level predictions is 71.2 medals (orange), with evident inconsistency among the three levels. The right side shows prediction results after using the complete consistency mechanism: predictions at all three levels are 65 medals (purple), strictly satisfying consistency constraints. The dashed line represents France’s actual medal count in 2024 (64 medals). The bar charts below show prediction breakdowns by major sport types: without the consistency mechanism, swimming events are predicted at 12.5 medals while the actual count was 11, and athletics events are predicted at 9.8 medals while the actual count was 10; after using the consistency mechanism, predictions for all sport types are closer to actual values. This demonstrates that consistency constraints ensure logical consistency of predictions and improve overall prediction accuracy through inter-level information complementarity.

6.6. Case Study: 2024 Prediction Review

To intuitively demonstrate our model’s predictive capability, we plotted a comparison scatter plot of predicted versus actual values for the 2024 Olympics, as shown in Figure 10:

The horizontal axis represents predicted medal counts, and the vertical axis represents actual medal counts, with points ideally distributed along the Y = X line (black dashed line). Different colors represent different types of countries: data-rich countries (blue, >100 historical medals), medium-data countries (green, 10–100 historical medals), data-scarce countries (orange, <10 historical medals), and zero-medal countries (red). The small inset in the upper right corner shows an enlarged view of the region with medal counts <10, where predictions for data-scarce countries generally fall close to the Y = X line. The lower right corner of the figure presents the Mean Absolute Error (MAE) for each type of country—4.3 medals for data-rich countries, 2.1 medals for medium-data countries, and 0.9 medals for data-scarce countries—indicating that the model has good predictive capability for different types of countries, especially for data-scarce countries. The figure also highlights some special cases where predictions deviated from actual results, such as France (host country), Australia (under-predicted by seven medals), and Rwanda (first medal not predicted).

Our framework successfully predicted medal counts for all countries participating in the 2024 Paris Olympics, with high accuracy.

Table 6. The 2024 Paris Olympics prediction cases.

Country	Predicted Medals	Actual Medals	Absolute Error
United States	124	126	2
China	87	91	4
Japan	52	47	5
France	65	64	1
Australia	46	53	7
…	…	…	…
Georgia	8	7	1
Ethiopia	5	4	1
Puerto Rico	2	2	0
San Marino	1	1	0
Rwanda	0	1	1

lists prediction versus actual results for selected countries. Due to space limitations, we present only a representative subset from the complete prediction results, including top medal-winning nations and several data-scarce countries, to illustrate the model’s consistent performance across different data conditions.

Our model maintained high accuracy in predictions for most countries. For traditionally strong countries, the average error is around four medals; for data-scarce countries, the average error decreases to within one medal. Notably, we successfully predicted San Marino would maintain its medal, but failed to predict Rwanda’s first medal (probability predicted as 0.32, not reaching the 0.5 threshold).

Analysis of prediction failures is particularly important. Rwanda won its first Olympic medal in 2024 (bronze in women’s 48 kg judo), but our model gave a winning probability of only 0.32, not reaching the 0.5 prediction threshold. This represents a typical “black swan event,” posing a significant challenge to prediction models based on historical patterns.

In-depth analysis reveals that Rwanda’s uniqueness manifests in three main aspects:

• Anomalous Development Trajectory: Rwanda’s sports investment showed a leap-like growth during 2020–2024 (289% higher than the historical average growth rate), a sudden change exceeding the predictive capability based on historical patterns.
• Policy Support Intensity: Rwanda’s government launched the “Vision 2030” sports development plan in 2022, providing beyond-expected resource input, information not fully reflected in our feature engineering.
• Individual Athlete Factors: The medal-winning athlete’s personal development trajectory differed significantly from the country’s overall development pattern, reflecting the importance of individual factors in rare event prediction.

This case provides valuable insights: future work should strengthen the ability to identify anomalous development patterns, enhance model sensitivity to sudden policy changes and individual factors, and consider adjusting the rare event model threshold from 0.5 to a lower value (such as 0.3) to improve detection capability for these non-conventional development paths.

6.7. Sensitivity Analysis and Model Stability

We conducted a detailed sensitivity analysis to assess model sensitivity to hyperparameter changes.

Table 7. Key hyperparameter sensitivity analysis (bold indicates optimal value).

Hyperparameter	Minimum Value	Optimal Value	Maximum Value	Performance Range (MAE)
MMD Weight ($\alpha$)	0.2	0.8	1.2	1.65–1.83
Cluster Number (K)	3	5	7	1.65–1.78
BHEV Prior Strength ($\lambda$)	0.2	0.6	1.0	1.65–1.86
Consistency Weight (${\lambda }_1$)	0.4	0.8	1.2	1.65–1.79

shows the impact of key hyperparameters on model performance.

Results show that the model is most sensitive to the prior strength $\lambda$ in the BHEV, with an optimal value of 0.6. When $\lambda$ is too small, the model easily overfits; predictive capability decreases when it is too large. Performance is optimal with cluster number $K=5$, validating the rationality of our selection. The optimal values for MMD weight $\alpha$ and consistency weight ${\lambda }_1$ are 0.8.

Overall, the model performs stably within reasonable parameter ranges, and even with suboptimal settings, performance remains significantly better than baseline methods, demonstrating the robustness and generalization capability of the proposed framework.

6.8. 2028 Los Angeles Olympics Prediction

Based on our framework, we generated comprehensive medal predictions for all countries expected to participate in the 2028 Los Angeles Olympics.

Table 8. The 2028 Los Angeles Olympics prediction.

Country	Predicted Medals	Gold Prediction	Silver Prediction	Bronze Prediction
United States	133	42	45	46
China	95	38	32	25
Japan	54	18	17	19
Australia	56	19	18	19
…	…	…	…	…
Seychelles	0	0	0	0
Maldives	0	0	0	0

presents prediction results for selected representative countries. Similar to the 2024 analysis, we include only a subset of countries from our complete prediction results due to space constraints, while ensuring representation across different country categories.

We also predicted zero-medal countries that might win their first medal in 2028.

Table 9. The 2028 first medal prediction (zero-medal countries).

Country	First Medal Probability	Predicted Sport Type	95% Confidence Interval
Cambodia	0.683	Taekwondo	[0.452, 0.819]
Maldives	0.476	Swimming	[0.328, 0.612]
Luxembourg	0.452	Cycling	[0.287, 0.597]
Andorra	0.417	Shooting	[0.262, 0.573]
Nepal	0.385	Archery	[0.241, 0.536]

shows the five countries with the highest first medal probabilities.

These predictions provide useful guidance for relevant countries and sports organizations, which can be used to formulate targeted preparation and development strategies.

7. Conclusions and Future Work

In this paper, we propose a prediction framework integrating multi-granularity transfer learning with extreme value theory, providing a new solution for cold-start and rare event prediction problems in Olympic medal forecasting. Experimental results show that the framework significantly outperforms existing methods in prediction accuracy for data-scarce countries and rare event prediction capability. The introduction of gradient reversal and Domain-Specific Batch Normalization further improves transfer learning effects, while the Bayesian hierarchical extreme value model effectively reduces overfitting risk in extreme value analysis.

Compared with prior work, our framework offers significant advancements. Traditional economic models, such as Bernard and Busse [1], and standard machine learning approaches, like the random forest/XGBoost pipelines used by Zhu et al. [3], show limited capability for data-scarce countries. Our Multi-Granularity Transfer Learning Core (MG-TLC) directly addresses this cold-start limitation, achieving a $25.7\%$ reduction in MAE for these nations relative to the strongest baseline (see Table 2). Furthermore, prior work has not specifically modeled the “first medal” phenomenon as a rare event; our Rare Event Analysis Module (RE-AM), which combines extreme value theory with survival analysis, lifts the first medal AUC to $0.833$—an $11.4\%$ improvement over the best rare event baseline (LZPH, AUC $0.748$; see Table 4)—and also improves PR-AUC to $0.583$ (a $34.0\%$ gain over LZPH). Finally, while our study builds on general transfer-learning ideas, it introduces a cluster-aware, feature-space alignment with a hierarchy-consistent objective that resolves prediction conflicts across country/sport/event granularities—an aspect not adequately handled in previous Olympic prediction or hierarchical transfer settings [8,10].

From a symmetry standpoint, this study formalizes task-relevant invariances, namely permutation invariance in set-based country aggregation and scale robustness via per-capita and ratio features, and operationalizes them through distributional alignment between data-rich and data-scarce domains and Olympic-cycle indexing in discrete time. Symmetry-breaking factors such as host advantage and event program changes are modeled explicitly by a rare event component that combines extreme value and survival modeling, ensuring that the main conclusions are not driven by unit, labeling, or alignment artifacts. As a natural extension, future work will report concept-aligned checks, for example, rank correlations and calibration deltas under unit conversions or label permutations, to complement these design-level guarantees.

Key findings include the following: (1) prediction for data-scarce countries requires transferring knowledge from countries with similar development trajectories; (2) first medal acquisition times follow extreme value distribution characteristics with evident long-tail properties; (3) multi-level prediction consistency is crucial for accurate prediction; and (4) countries at different development stages should focus on different feature dimensions.

Our framework provides country-level, sport type-level, and event-level predictions, together with first medal probabilities for zero-medal countries (see Section 6 and the associated tables). These outputs are actionable for three stakeholder groups: (i) National Olympic Committees and sports ministries, who can prioritize disciplines and allocate training budgets toward sport types with improving participation intensity and rising medal prospects; (ii) national federations and coaching staffs, who can plan qualification pathways and peak-year staffing using event-level predictions and hierarchy-consistency signals; and (iii) development programs in emerging or resource-constrained countries, who can identify feasible “entry-point” disciplines based on first medal probabilities and participation trajectories. This mapping clarifies who uses which outputs to make what decisions, without requiring additional data or new assumptions.

While the framework was designed for Olympic prediction, its underlying principles may offer insights for problems that share data scarcity and rare event characteristics. Any cross-domain use would require domain-specific adaptation and light retraining (e.g., feature re-engineering and covariate specification). To illustrate potential directions, the conceptual approach could be explored for selected problems in the following areas:

• Economics: For analyzing development trajectories of emerging markets with limited historical data (e.g., indicators in data-scarce regions).
• Healthcare: For risk or early-signal analysis of rare diseases in regions with scarce monitoring data.
• Natural Disaster Analysis: For modeling extreme weather event risks (e.g., once-in-a-century floods or hurricanes) in areas with sparse historical records.
• Finance: For studying volatility patterns in newly listed companies or emerging financial markets with limited histories.

We do not claim general applicability; feasibility in each domain would need to be verified through objective, domain-appropriate evaluation protocols in future work.

Due to data limitations, we could not incorporate potentially valuable features, such as detailed sports investment data and effects from neighboring regional countries. We will explore broader data sources and richer features in future work and extend the model to more cold-start and rare event prediction scenarios. As a straightforward extension, we will incorporate public proxies of facility intensity (e.g., venue density or team-event shares) and report group-wise errors for high- vs. low-cost sports. Meanwhile, we also plan to use this framework to provide fine-grained predictions and in-depth analysis for the 2028 Los Angeles Olympics.