Abstract
This study presents a mathematical model to understand the dynamics of eye vision disability, incorporating key physiological and environmental variables such as visual acuity, lens power, pupil diameter, and environmental influence. The novel model developed in this work consists of four state variables that describe their interactions, aiming to simulate changes in visual acuity and the progression of vision disability under different circumstances. Various mathematical aspects including positivity and equilibrium points along with local and global stability are demonstrated. In addition, the sensitivity analysis is also presented to examine the impact of variations in parameters on the model’s outcomes, highlighting the factors that significantly influence visual acuity and pupil adjustments. Furthermore, the phase portraits explore the dynamic interactions between variables, revealing different insights into the stability of the system and adaptive responses. These results provide a thorough understanding of factors influencing eye vision, offering new insights into vision disability dynamics through an integrated, non-autonomous model and practical applications in developing corrective strategies.
1. Introduction
Mathematical modeling is now indispensable for forecasting and managing disease across disciplines, from epidemiology to health system engineering. By converting complex biological processes into structured, quantitative representations through differential equations and agenda-based simulations, systems capture dynamics and project how conditions evolve over time. During the outbreaks such as COVID-19, they informed public health decisions by estimating transmission rates, anticipating health-care demand, and evaluating interventions like physical distancing and vaccination [1,2,3,4,5]. In addition to them, some other works include the use of neural networks, bifurcation approaches on prey–predator population among others [6,7,8,9,10]. Similarly, HIV, tumor immune interactions, and leptospirosis disease are studied in [11,12,13,14]. In the area of disabilities, models can be tailored to specific impairments, enabling the researchers to analyze impact of interventions, identify crucial factors influencing the outcomes, and optimize rehabilitation or treatment plans.
In disability studies, mathematical models offer structured way to simulate the progression of different impairments, like mobility limitations, cognitive decline, and vision disabilities [15,16,17]. Such models enable a deeper understanding of how environmental, physiological, and genetic factors contribute to disabilities. Additionally, they provide important insights into effective prevention policies, long-term prognosis, and improvements of quality of life. In particular, for the vision disabilities, mathematical models can be developed to quantify effects of optical interventions, environmental changes, and age-related factors on visual acuity. By capturing these complex interactions, models assist the researchers and clinicians to refine diagnostic criteria, enhance treatment protocols, and design devices tailored to needs of individuals. Mathematical modeling bridges the gap between theory and practice, which provides evidence-based guidance to improve health outcomes and manage disabilities in an effective manner.
Eye vision disability, including conditions like age-related macular degeneration, glaucoma, cataracts, and refractive errors, is a vital public health concern in the world. Millions of people suffer due to varying degrees of vision impairment, which impacts their ability to perform daily life activities, worsens quality of life, and, in severe cases, leads to blindness. The literature on eye vision disabilities contains clinical research, epidemiological studies, and technological advancement aimed at improving visual function. Such studies often rely on identifying risk factors, such as genetics, age, and environmental influences, which contribute to onset and progression of disabilities. Age-related macular degeneration (AMD), for example, is influenced by genetic and environmental factors, which includes diet and UV exposure. This is the leading cause of loss of vision among older adults [18]. In a similar way, cataracts, clouding of the eye lens mostly due to aging, affect millions and are a leading cause of blindness, though they are often treatable with surgical intervention.
Furthermore, together with risk factors, considerable advancements in diagnostics and imaging technology have enhanced the understanding of eye vision disabilities. Optical coherence tomography and fundus imaging, for instance, allow for visualization of the retinal structures in high resolution, aiding in early diagnosis and the monitoring of diseases. Moreover, development of devices and vision rehabilitation programs opened new avenues for reducing vision loss and supporting individuals with low vision. Recent studies focus on the importance of environmental factors, like lighting and contrast, on visual function, which has implications for designing inclusive spaces for individuals with vision impairments [19,20].
The motivation to develop a mathematical model for eye vision disability stems from the complex and multifactorial nature of visual impairment. The existing literature has extensively documented the physiological, genetic, and environmental factors that contribute to various eye conditions, yet few models integrate these elements into a cohesive framework. Several individuals experience slow visual decline due to age, environmental exposures, or underlying medical conditions, which are not managed alone with standard clinical assessments easily. Therefore, as we know, a mathematical model which captures the dynamics of visual acuity, lens adjustments, pupil responsiveness, and environmental factors could provide important and deeper insights into how these variables interact over time, particularly for the individuals at risk of progressive vision loss [21,22]. Such a model can also aid in the development of tailored interventions, enabling clinicians to predict the likely trajectory of a patient’s visual function and to optimize treatment strategy based on individualized needs.
To model the factors affecting eye vision disability over time, we define the following variables:
denotes visual acuity at time t. represents the lens power (diopters) needed for corrective vision at time t. describes the pupil diameter, affected by environmental conditions. denotes the environmental factors, for instance, light intensity that fluctuate over time. The are constants representing how fast each factor changes as time evolves. The is desired visual acuity, representing ideal vision.
The proposed model is comprises a system of differential equations describing the time-based evolution of visual acuity, corrective lens power, pupil diameter, and environmental influence.
The first state variable shows change in visual acuity over time and is described as
The second state variable shows corrective lens power adjusts to compensate for vision decline and is given by
The pupil diameter changes in response to environmental factors and is expressed as
The environmental factors may fluctuate over time depending on exposure conditions and are given by
The mathematical model is integrated as follows:
The parameters description is given in Table 1.

Table 1.
Model terms and descriptions.
This paper is structured as follows:
Section 2 deals with the mathematical investigation of the considered model, including the positivity of the solution, identification of equilibrium points, and analysis of their local and global stability. Section 3 provides parameter estimations using synthetic data. Section 4 is devoted to the results and discussion, including graphical demonstrations of the considered model. Section 5 concludes this manuscript by summarizing the main findings and outlining directions for future work.
2. Mathematical Analysis of Eye Vision Disability Model
This section presents a mathematical analysis of the proposed model.
Theorem 1
(Positivity of Solutions). Given the initial conditions , , , , the solutions , , , and remain non-negative for all .
Proof.
We prove the positivity of each state variable , , , and individually by analyzing their respective differential equations and ensuring that their values remain non-negative over time under the given initial conditions and parameter constraints.
First, consider as
where and . At , assume momentarily, then,
Since , the term only if dominates . This ensures near , preventing from becoming negative.
Thus, for all . Next, the differential equation for is expressed by
where and . At , if , then . If , , which increases . Since whenever , cannot become negative.
Thus, for all .
Now, the differential equation for is given by
where and . At , assume momentarily, then,
This ensures near , preventing from becoming negative. If , the term ensures decay, but compensates, maintaining non-negativity. Thus, for all .
Now, consider as
where and . At , as long as . Since , cannot decrease below zero.
Thus, for all . As each state variable is proven to remain non-negative under the given conditions, the solutions of the system satisfy positivity for all . □
Disease-Free and Endemic Equilibrium Points and Their Stability Analysis
Disease-Free Equilibrium: The DFE is given by , representing no impairment.
Endemic Equilibrium: The endemic equilibrium represents a stable impairment state:
Note that the model (1) is non-autonomous due to the presence of in the equation for . For , this requires either or . This distinction must be incorporated when considering the stability and behavior of E at equilibrium.
Theorem 2
(Local Stability of Disease-Free Equilibrium). The disease-free equilibrium is locally stable if all eigenvalues of the Jacobian evaluated at this point have negative real parts.
Proof.
The Jacobian Matrix J is given as:
Now, eigenvalues are , , , and .
To ensure local stability, must have a negative real part. Under the assumption of a constant environment or , the equilibrium is stable for small perturbations in and D. □
Theorem 3
(Local Stability of Endemic Equilibrium). The endemic equilibrium is locally stable if all eigenvalues of the Jacobian evaluated at this point have negative real parts.
Proof.
Using similar steps as above, the Jacobian at includes terms that depend on . Stability conditions require that for any perturbation around the endemic equilibrium.
If , the eigenvalues are given as , , , and 0, indicating marginal stability. Additional analysis of is necessary to determine the stability in this case. □
Theorem 4
(Global Stability of Disease-Free Equilibrium). The disease-free equilibrium is globally stable if a Lyapunov function can be constructed such that .
Proof.
Defining the Lyapunov function as
This function is non-negative and reaches zero only at the disease-free equilibrium point . Now, computing the derivative of with respect to t as
Substitute the differential equations into the above expression, we have
Thus,
To ensure , additional constraints on must be imposed to ensure that the term does not introduce positive contributions. For example, if or stabilizes near zero, the equilibrium remains globally stable. □
Theorem 5
(Global Stability of Endemic Equilibrium). The endemic equilibrium is globally asymptotically stable if a suitable Lyapunov function can be found.
Proof.
Defining the Lyapunov function as
This function is non-negative and equals zero only at the endemic equilibrium point . Now, computing the derivative of with respect to t as
Substituting the differential equations in the above equation, we have
We observe that additional constraints on are necessary to ensure global stability of the endemic equilibrium, particularly requiring . □
3. Parameter Estimation for Eye Vision Disability Model
To estimate the parameters of the differential equations modeling eye vision disability, we need empirical data on visual acuity, lens power, pupil diameter, and environmental factors. While comprehensive datasets encompassing all these variables over time are scarce, several studies provide relevant data that can inform our parameter estimation:
3.1. Visual Acuity and Pupil Diameter Across Age Groups
A study [23] examines how pupil size and visual acuity vary with age and refractive errors. The research provides data on pupil diameters and visual acuity measurements across different age groups and refractive statuses.
3.2. Pupil Size Regulation in Natural Vision
The article [24] explores how pupil size is regulated in natural viewing conditions and how it changes with age. This study offers insights into the relationship between environmental factors and pupil diameter.
3.3. Association Between Myopia and Pupil Diameter in Preschoolers
The research [25] investigates the relationship between pupil diameter and myopia in young children. It provides data on pupil sizes and refractive errors, which can be useful for understanding the dynamics between lens power and pupil diameter.
While these studies offer valuable data points, they may not provide a complete time-series dataset required for dynamic modeling. In the absence of comprehensive longitudinal data, we can proceed by synthesizing a dataset based on the available information and reasonable assumptions.
3.4. Synthesizing the Dataset
Based on the insights from the aforementioned studies, we can create a synthetic dataset that captures the typical ranges and relationships between the variables: Visual Acuity (V): measured in logMAR units, with values ranging from 0 (normal vision) to higher positive values indicating worse acuity. Lens Power (L): measured in diopters (D), representing the corrective lens power needed. Pupil Diameter (D): measured in millimeters (mm), with typical values ranging from 2 mm (bright light) to 8 mm (dim light). Environmental Factors (E): quantified as a normalized value between 0 and 1, representing the intensity of external stimuli (e.g., light levels).
3.5. Synthetic Data
We generated a ten-time-point dataset to span plausible dynamics across the four state variables. Values respect physiological ranges: V rises from 0.1 to 0.6 logMAR, L from 0.5 D to 1.5 D, D from 4.0 mm to 6.5 mm, and E varies within 0.1–0.8 after normalization; the full Table 2 shows synthetic data.

Table 2.
Synthetic dataset for the model.
3.6. Parameter Estimation Process
To estimate the parameters, we define an objective function based on the sum of squared errors (SSE) between the observed data and model predictions:
The optimization was performed using numerical methods, with initial guesses for parameters and bounds ensuring non-negative values. The objective function minimized the SSE to obtain the best-fitting parameters. The estimated parameter values for the eye vision disability model are as follows:
The estimated values imply the following:
- -
- Visual acuity is influenced primarily by its natural decline (through ) and the corrective lens power, with minor roles played by pupil diameter and environmental factors.
- -
- Lens power adjusts at a moderate rate toward the target vision level, showing effectiveness without oversensitivity to changes in V.
- -
- Pupil diameter is slightly affected by environmental factors but shows minimal independent decay.
- -
- Environmental factors have a stable impact on D with minor fluctuations over time.
These parameter estimates indicate that the main drivers of vision changes in the model are the natural decline and corrective lens power, while other factors like pupil diameter and environmental influences serve as secondary contributors. This reflects a balanced approach in simulating realistic vision dynamics based on the synthetic data provided.
4. Results and Discussion
The initial values for the state variables were selected based on physiological ranges and a plausible starting point for simulating vision dynamics. The rationale for each is as follows:
The initial value represents mild visual impairment, where could indicate ideal vision, and larger values signify reduced clarity. A starting value of suggests a manageable but noticeable vision limitation.
The lens power diopters was chosen as an initial corrective adjustment, typical in cases of mild refractive error. This implies that a slight corrective lens is already in use.
The pupil diameter mm falls within a common range. Under normal lighting, pupil diameters vary between 2 and 4 mm in bright light and can expand to 6–8 mm in dim light. The choice of 4.0 mm represents a neutral lighting condition.
The environmental factor was chosen to simulate bright starting conditions, which may affect pupil diameter and, indirectly, vision.
These values provide a balanced and plausible starting point for the simulation. For real-world applications, actual measurements or clinically observed initial conditions would be ideal.
The sinusoidal environmental function was selected to simulate periodic changes in environmental conditions, such as daily light cycles or brightness variations. The reasoning behind this choice is as follows:
The sinusoidal form introduces cyclic fluctuations in the environmental factor, modeling repeating patterns like day–night transitions or ambient light changes. This is more realistic than a constant or linear trend, as environmental factors typically exhibit cyclical patterns.
Amplitude and Offset:
The offset of 0.5 ensures that remains positive throughout its cycle.
The amplitude of 0.3 causes to oscillate between 0.2 and 0.8, keeping it within a range that affects pupil diameter without causing extreme fluctuations.
The frequency term (0.5) in the sinusoidal function introduces moderate oscillations over the simulation duration, allowing for noticeable variability in and its impact on D and other model variables.
These selections provide a reasonable simulation setup that allows for meaningful interactions within the model variables.
Figure 1 shows the time evolution of four state variables in the model. Each subplot provides insights into how these variables behave over a specific time period (0 to 50 units of time). The sub figure top left panel shows that visual acuity increases initially, reaching a peak around 20 units of time, and then begins to stabilize slightly below 0.6. This plot may suggest that initial conditions or adjustments (such as lens corrections) help improve visual acuity over time, but the improvement plateaus, likely due to physiological or environmental limitations. The sub figure top left panel shows the lens power rapidly increases from its initial value of 0.5, reaching a peak near 1.5. After the peak, it shows slight oscillations, indicating minor adjustments. This pattern reflects how the lens power is adjusted to correct visual acuity early on and then fine-tuned to maintain or optimize vision quality. The oscillations could represent minor fluctuations due to environmental or internal factors in the system. The sub figure at bottom left demonstrates that the pupil diameter increases linearly over time from 5 to approximately 15. This linear trend suggests that pupil diameter is expanding, possibly due to reduced light sensitivity or gradual adaptation to environmental factors. This could indicate a response to changing light levels or other external stimuli. In the sub figure at the bottom right, we see that environmental factors show a slight upward trend with small fluctuations, rising from 0.8 to around 0.83. This suggests a dynamic but relatively stable environmental influence. The small oscillations could represent periodic changes in the external environment, such as daily light cycles or other fluctuations that impact vision.
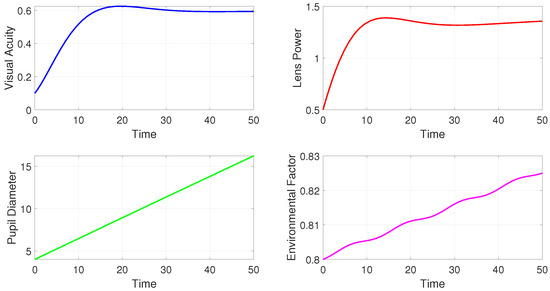
Figure 1.
Simulations of the model for a periodic environment.
Figure 2 demonstrates the sensitivity of each variable to changes in specific parameters: , and . Each subplot shows how altering a parameter value affects the trajectory of a particular variable over a time period of 10 units. Figure 2a shows how different values of (0.1, 0.26, and 0.4) impact visual acuity. We see a rapid increase in visual activity reaching higher levels with lower values, suggesting that a lower (rate of visual degradation) positively influences visual clarity. Higher values lead to slower improvements in acuity.
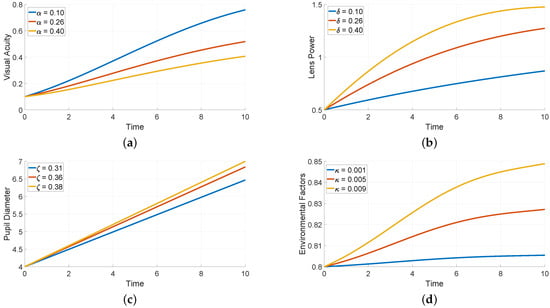
Figure 2.
Numerical simulations with respect to different values of parameter.
Figure 2b demonstrates how varying (0.1, 0.26, and 0.4) affects lens power. Higher values of lead to faster and greater increases in lens power, which enhances corrective adjustments. This suggests that strongly influences how quickly and effectively lens power compensates for visual acuity changes. Figure 2c displays the effect of different values (0.31, 0.36, and 0.38) on pupil diameter. Higher values result in a faster increase in pupil diameter, indicating that governs the responsiveness of pupil size to environmental factors or internal demands. This may correspond to pupil dilation in response to low light or other external stimuli. Figure 2d shows how changes in (0.001, 0.005, and 0.009) affect the environmental factor, which rises more quickly with higher values, showing that controls the intensity of environmental changes. Higher values more sensitive, potentially imitating conditions with rapid changes in light or other external influences.
Figure 3 shows 3D phase portraits to explore the relation among three state variables. It provides insights into the dynamics of the system over time by examining how variables interact rather than simply tracking individual trajectories. Figure 3a shows the trajectory of the path which starts from an initial point and evolves over time. This view suggests how the changes in , , and interact dynamically. The trajectory indicates adaptation to environmental factors, where adjustments in pupil size and the acuity are influenced by fluctuations. Similarly Figure 3b shows the path of the system, with and influencing . This illustrates the combined effect of adjustments in lens and diameter of the pupil on maintaining visual acuity. It reflects the model’s balance in correcting vision and adapting pupil size to optimize vision quality under varying conditions.
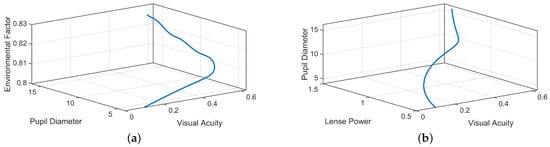
Figure 3.
Phase portraits of the considered model.
Compared to the previous studies, which fundamentally focused on individual aspects of vision disability like the lens power adjustments or the environmental effects, this work provides an integrated model which captured the dynamic interplay among visual acuity, lens power, pupil diameter, and environmental factors. The incorporation of a non-autonomous framework allows the model to account for environmental fluctuations as time evolves, which was absent in earlier works. Additionally, the sensitivity analysis presented in this work offers new insights into the parameters that significantly influence visual acuity and pupil adjustments, paving the way for targeted interventions. These contributions not only extend the theoretical understanding of vision disability dynamics but also provide practical applications for developing corrective strategies and adaptive devices.
5. Conclusions
The developed mathematical model presents a detailed demonstration of eye vision disability dynamics by examining the interplay among visual acuity, lens power, pupil diameter, and environmental factors. Various mathematical properties like positivity, equilibrium points, and local and global stability have been demonstrated in detail. The estimation of the parameters for synthetic data has been presented. The simulations include time series plots for state variables, showing their evolution and equilibrium behaviors. The sensitivity analysis shows how changes in the specific parameters impact variables, helping to identify critical factors for the control of the model. The results show that visual acuity can be improved effectively by optimization of these parameters, and the model’s adaptive behavior suggests potential for applications in vision disability management and correction strategies.
This study presents several new findings, including the integration of environmental factors into vision dynamics, the application of non-autonomous systems for modeling visual impairment, and insights into parameter sensitivities that guide corrective strategies. These advancements contribute to both theoretical knowledge and practical approaches in managing vision disabilities.
Future Research Directions
The findings lay a foundation for future research to further refine models and improve interventions for vision-related challenges. A particularly compelling direction for future research involves exploring the concept of symmetry in binocular vision disability. The current model provides a powerful toolkit to investigate balanced patterns of vision loss between both eyes. In the future, symmetry in eye disability disease can be studied using a mathematical model that analyzes balanced patterns of vision loss between both eyes. This would involve adapting the framework to a coupled system of equations representing the left and right eyes, linked by neurological and compensatory mechanisms. Investigating such symmetry can reveal whether certain conditions promote symmetrical deterioration or if asymmetry is a hallmark of specific diseases. Understanding these patterns is crucial for diagnosing systemic versus localized ocular issues and for developing balanced, bilateral treatment approaches, ultimately leading to more holistic and effective management of vision disabilities.
Funding
The authors extend their appreciation to the King Salman Center For Disability Research for funding this work through Research Group no KSRG-2024-065.
Data Availability Statement
The datasets used during the current study are available from the corresponding author on reasonable request.
Acknowledgments
The authors extend their appreciation to the King Salman Center For Disability Research for funding this work through Research Group no KSRG-2024-065.
Conflicts of Interest
Author Ibrahim Al-Dayel was employed by the company Imam Mohammad Ibn Saud Islamic University. The author declares that this study received funding from King Salman Center for Disability Research. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
References
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.A.P. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis, and Interpretation; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Beijing, China, 2011. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematical Models in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Mandal, S.; Bhatnagar, T.; Arinaminpathy, N.; Agarwal, A.; Chowdhury, A.; Murhekar, M. A model-based study on the dynamics of COVID-19: Implications for the control of the disease in India. Med. J. Armed Forces India 2020, 76, 315–325. [Google Scholar]
- Zhao, Y.; Xu, C.; Xu, Y.; Lin, J.; Pang, Y.; Liu, Z.; Shen, J. Mathematical exploration on control of bifurcation for a 3D predator-prey model with delay. AIMS Math. 2024, 9, 29883–29915. [Google Scholar] [CrossRef]
- Lin, J.; Xu, C.; Xu, Y.; Zhao, Y.; Pang, Y.; Liu, Z.; Shen, J. Bifurcation and controller design in a 3D delayed predator–Prey model. AIMS Math. 2024, 9, 33891–33929. [Google Scholar] [CrossRef]
- Maharajan, C.; Sowmiya, C.; Xu, C. Lagrange stability of inertial type neural networks: A Lyapunov-Krasovskii functional approach. Evol. Syst. 2025, 16, 63. [Google Scholar] [CrossRef]
- Xu, C.; Liao, M.; Farman, M.; Shehzad, A. Hydrogenolysis of glycerol by heterogeneous catalysis: A fractional order kinetic model with analysis. MATCH Commun. Math. Comput. Chem. 2024, 91, 635–664. [Google Scholar] [CrossRef]
- Baber, M.Z.; Yasin, M.W.; Xu, C.; Ahmed, N.; Iqbal, M.S. Numerical and analytical study for the stochastic spatial dependent prey–predator dynamical system. J. Comput. Nonlinear Dyn. 2024, 19, 101003. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Partohaghighi, M.; Saifullah, S.; Akgül, A.; Jarad, F. Oscillatory and complex behaviour of Caputo-Fabrizio fractional order HIV-1 infection model. AIMS Math. 2022, 7, 4778–4792. [Google Scholar] [CrossRef]
- Xu, C.; Alhejaili, W.; Saifullah, S.; Khan, A.; Khan, J.; El-Shorbagy, M.A. Analysis of Huanglongbing disease model with a novel fractional piecewise approach. Chaos Solitons Fractals 2022, 161, 112316. [Google Scholar] [CrossRef]
- Saifullah, S.; Ahmad, S.; Jarad, F. Study on the dynamics of a piecewise tumor–Immune interaction model. Fractals 2022, 30, 2240233. [Google Scholar] [CrossRef]
- Qu, H.; Saifullah, S.; Khan, J.; Khan, A.; Ur Rahman, M.; Zheng, G. Dynamics of leptospirosis disease in context of piecewise classical-global and classical-fractional operators. Fractals 2022, 30, 2240216. [Google Scholar] [CrossRef]
- Sallah, K.; Giorgi, R.; Bengtsson, L.; Lu, X.; Wetter, E.; Adrien, P.; Rebaudet, S.; Piarroux, R.; Gaudart, J. Mathematical models for predicting human mobility in the context of infectious disease spread: Introducing the impedance model. Int. J. Health Geogr. 2017, 16, 42. [Google Scholar] [CrossRef] [PubMed]
- Chow, S.M.; Nesselroade, J.R. General slowing or decreased inhibition? Mathematical models of age differences in cognitive functioning. J. Gerontol. Ser. Psychol. Sci. Soc. Sci. 2004, 59, P101–P109. [Google Scholar] [CrossRef] [PubMed]
- Akbar, S.; Shah, S.R.; Alshehri, M.M.; Sharma, S.K.; Gupta, P. A mathematical study for promoting disability inclusion in glaucoma: A comprehensive approach. J. Disabil. Res. 2024, 3, 20230062. [Google Scholar] [CrossRef]
- Wong, T.Y.; Cheung, C.M.; Larsen, M.; Sharma, S.; Simo, R. Global prevalence of age-related macular degeneration and visual impairment. Lancet Glob. Health 2014, 2, e106–e116. [Google Scholar] [CrossRef] [PubMed]
- Labiris, G.; Panagiotopoulou, E.K.; Taliantzis, S.; Perente, A.; Delibasis, K.; Doulos, L.T. Lighting standards revisited: Introduction of a mathematical model for the assessment of the impact of illuminance on visual acuity. Clin. Ophthalmol. 2021, 15, 4553–4564. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhao, J.; Wang, L.; Hu, W.; Yan, F. A Mathematical Model for the Action Spectrum of Steady-State Pupil Size in Photopic Vision with Insight into Healthful Lighting. Buildings 2023, 13, 781. [Google Scholar] [CrossRef]
- Edwards, D.A.; Emerick, B.; Kondic, A.G.; Kiradjiev, K.; Raymond, C.; Zyskin, M. Mathematical models for the effect of anti-vascular endothelial growth factor on visual acuity. J. Math. Biol. 2020, 81, 1397–1428. [Google Scholar] [CrossRef] [PubMed]
- Ye, H. A Mathematic Model to Correct Myopic Astigmatism. In Proceedings of the 2010 4th International Conference on Bioinformatics and Biomedical Engineering, Chengdu, China, 18–20 June 2010; pp. 1–4. [Google Scholar]
- Dumbleton, K.; Guillon, M.; Theodoratos, P.; Wooley, C.B.; Moody, K. The effects of age and refraction on pupil size and visual acuity: Implications for multifocal contact lens design and fitting. Contact Lens Anterior Eye 2018, 41, S23. [Google Scholar] [CrossRef]
- Lazar, R.; Degen, J.; Fiechter, A.S.; Monticelli, A.; Spitschan, M. Regulation of pupil size in natural vision across the human lifespan. R. Soc. Open Sci. 2024, 11, 191613. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Li, L.; Han, W.; Zhu, Y.; Hu, Y.; Li, Z.; Ruan, Z.; Zhou, Z.; Zhuo, Y.; Fu, M.; et al. Association Between Myopia and Pupil Diameter in Preschoolers: Evidence from a Machine Learning Approach Based on a Real-World Large-Scale Dataset. Ophthalmol. Ther. 2024, 13, 2009–2022. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).