Predicting the Forest Fire Duration Enriched with Meteorological Data Using Feature Construction Techniques

Abstract

The spread of contemporary artificial intelligence technologies, particularly machine learning, has significantly enhanced the capacity to predict asymmetrical natural disasters. Wildfires constitute a prominent example, as machine learning can be employed to forecast not only their spatial extent but also their environmental and socio-economic impacts, propagation dynamics, symmetrical or asymmetrical patterns, and even their duration. Such predictive capabilities are of critical importance for effective wildfire management, as they inform the strategic allocation of material resources, and the optimal deployment of human personnel in the field. Beyond that, examination of symmetrical or asymmetrical patterns in fires helps us to understand the causes and dynamics of their spread. The necessity of leveraging machine learning tools has become imperative in our era, as climate change has disrupted traditional wildfire management models due to prolonged droughts, rising temperatures, asymmetrical patterns, and the increasing frequency of extreme weather events. For this reason, our research seeks to fully exploit the potential of Principal Component Analysis (PCA), Minimum Redundancy Maximum Relevance (MRMR), and Grammatical Evolution, both for constructing Artificial Features and for generating Neural Network Architectures. For this purpose, we utilized the highly detailed and publicly available symmetrical datasets provided by the Hellenic Fire Service for the years 2014–2021, which we further enriched with meteorological data, corresponding to the prevailing conditions at both the onset and the suppression of each wildfire event. The research concluded that the Feature Construction technique, using Grammatical Evolution, combines both symmetrical and asymmetrical conditions, and that weather phenomena may provide and outperform other methods in terms of stability and accuracy. Therefore, the asymmetric phenomenon in our research is defined as the unpredictable outcome of climate change (meteorological data) which prolongs the duration of forest fires over time. Specifically, in the model accuracy of wildfire duration using Feature Construction, the mean error was 8.25%, indicating an overall accuracy of 91.75%.

1. Introduction

In this section, we begin with a brief reference to the dual role that fire has played in shaping human civilization. Historically, fire has possessed the capacity to either elevate civilizations or bring about their destruction. Fire has served as a weapon capable of unleashing unspeakable natural disasters, while simultaneously acting as a catalyst for technological advancement. For instance, the Great fire of London in 1666 devastated the city and reshaped the political, social, demographic, and economical landscape [1]. On the other hand, the ability to harness fire for cooking, metallurgy, and warmth played a crucial role in the development of early industrial processes and human societies [2]. This duality underscores fire’s paradoxical role in human progress: a force capable of both creation and destruction.

This belief is also evident in ancient Greek mythology, particularly in the tale of Prometheus, who defied the gods by stealing fire and gifting it to humanity. This act symbolizes the transfer of divine knowledge and power to humans, enabling progress and civilization. The myth underscores fire’s dual role as a tool for human advancement and as a source of conflict, illustrating the tension between progress and its ethical implications as well as the costs of rebellion and innovation [3]. In other words, fire has played multiple roles in human history, both through myths and its diverse impacts.

Thus, in the modern era, wildfires are ranked highly among the most significant natural hazards [4], with immense effects on Earth’s ecosystems and human societies. Beyond that, according to the Chair of ISO/TC 92 fire safety, Mr. P. Van Hees, ‘With losses caused by fire estimated at 1% of the global GDP each year, fire safety must be viewed in the broader perspective of risk management and disaster mitigation’ [5].

Through a graphical representation in Figure 1, the economic burden from forest fires on the annual GDP is illustrated.

The following numbers show the extent of the destruction caused by fires:

• The cost of fire is estimated at about 1% to 2% of the annual GDP.
• About 1% of fires are responsible for more than 50% of the costs.
• The number of people that die in fires is estimated at 2.2 deaths per 100,000 inhabitants (based on 35 countries) [5].

In other words, wildfires and climate change fuel each other’s intensity. Climate change interacts synergistically with wildfires by increasing drought, high temperatures, low humidity, lightning, asymmetrical patterns, and strong winds, leading to more severe and prolonged fire seasons. Conversely, wildfires contribute to reinforcing climate change [6]. Thus, wildfires (along with the extraction and burning of fossil fuels, and volcanic eruptions) mutually enhance climate change, by further releasing carbon dioxide into the atmosphere [7]. Concerning this, the Mediterranean region is recognized as a key “hot-spot” for the forceful impacts of climate change [8]. At the same time, the critical need to address climate change and the effects on wildfire asymmetrical patterns is crucial for protecting both the environment and public health in Greece [9].

In Figure 2, we observe the continuous increase in carbon dioxide levels, beginning in 1751.

In this regard, the United Nations Environment Programme are calling on governments “to radically shift their investments in wildfires to focus on prevention and preparedness” [6]. On that ground, despite the challenging conditions posed by climate change, driven by endless human expansion and technological progress, we attempt to transform this disadvantage into an advantage, from asymmetrical to symmetrical, by focusing our efforts on rising technology itself. That is to say, artificial intelligence, particularly machine learning, has emerged as a helpful ally in addressing this global issue, offering innovative solutions and aiding sustainable development [10,11].

Machine learning can be applied to a collection of techniques and algorithms that make it easier for systems to identify symmetrical/asymmetrical patterns and make decisions based on data enriching their performance over time without explicitly being programmed for specific tasks [12]. This was the vision of Alan Turing, when, in 1936, he wrote his PhD ‘On Computable Numbers, with an application to the Entscheidung problem’ [13]. That is to say, machine learning is a vital branch of artificial intelligence, presenting golden opportunities for businesses and society alike. Beyond its countless advantages, it plays a critical role in driving innovative advancements in climate change, adaptation, and mitigation. By accelerating the development of resolutions to some of the most urgent asymmetrical challenges facing the planet, machine learning is transforming the process of addressing global environmental issues [12]. That being said, modeling multiplex environmental variables repeatedly presents challenges on account of the significant computation resources required and the diverseness or complexity of data formats [14]. Machine learning algorithms, nevertheless, can bypass these asymmetrical challenges by deriving mappings and relationships straight from the data, eliminating the need for prespecified expert rules. This ability is particularly helpful when dealing with frameworks involving numerous parameters with complex asymmetrical physical properties, such as in forest fires. Therefore, adopting a machine learning technique to fire management can help defeat many of the barriers associated with traditional physics-based simulation models.

Concerning this, in the current literature, noteworthy interest has developed in the role of machine learning in the domain of fire management [15]. Forest fires, though, have not been extensively studied, as research on forest fires represents only 2.9% of the global literature, according to a study conducted between 2017 and 2021 [16]. More specifically, floods draw the most attention in research (20.3%), followed by earthquakes and hurricanes, each accounting for 18.8%. Studies on general disaster types make up 15.9%, while landslides account for 10.1%. Remarkably, depending on the area of focus, researchers apply corresponding algorithms to address specified challenges.

Figure 3 sums up the machine learning methods used in several fields of fire management, as obtained from the relevant literature. At this point, we present a number of recent publications which utilize machine learning techniques for forest fire management. For example, Bayesian networks have been broadly applied in the context of forest fires, in particular “ A Bayesian network model for prediction and analysis of possible forest fire causes” [17]. Additionally, a recent study “ Modeling of the cascading impacts of drought and forest fire based on a Bayesian network” [18]. Also, Bayesian networks were integrated with deep learning techniques: “A Bayesian network-based information fusion combined with DNNs for robust video fire detection” [19].

Naïve Bayes has also been employed to face fire-related challenges in many studies. For instance, Nugroho developed a forest fire prevention system, “Peatland Forest Fire Prevention Using Wireless Sensor Network Based on Naïve Bayes Classifier” [20]. Zainul’s work proposes a method for classifying hotspots responsible for forest fires: “Classification of Hotspots Causing Forest and Land Fires Using the Naive Bayes Algorithm” [21]. Karo presented a method for wildfire classification that incorporates feature selection and employs Naïve Bayes alongside other machine learning techniques: “Wildfires Classification Using Feature Selection with K-NN, Naïve Bayes, and ID3 Algorithms” [22].

Moreover, Logistic Regression has been deployed various forest fire-related issues, including estimating human-caused wildfire risk “Logistic regression models for human-caused wildfire risk estimation: analyzing the effect of the spatial accuracy in fire occurrence data” [23], predicting wildfire vulnerability “Predicting wildfire vulnerability using logistic regression and artificial neural networks: a case study in Brazil’s Federal District” [24], probabilistic modeling of wildfire occurrence “Probabilistic modeling of wildfire occurrence based on logistic regression, Niassa Reserve, Mozambique” [25], and analyzing wildfire danger “Analysis of Wildfire Danger Level Using Logistic Regression Model in Sichuan Province, China” [26].

Numerous studies have utilized Artificial Neural Networks (ANNs) in the area of forest fire prediction and monitoring. For instance, Hossain employed ANNs to detect flames and smoke “Wildfire flame and smoke detection using static image features and artificial neural network” [27]. Lall and Mathibela applied neural networks to predict wildfire risk “The application of artificial neural networks for wildfire risk prediction” in Cape Town [28]. Likewise, Sayad utilized neural networks along with other machine learning techniques for wildfire predictive modeling, using data from NASA’s Land Processes Distributed Active Archive Center (LP DAAC) “Predictive modeling of wildfires: A new dataset and machine learning approach” [29]. Similarly, Gao recently published a case study on predicting wildfires in a Chinese province, “ Using multilayer perceptron to predict forest fires in Jiangxi province, southeast China” using neural networks [30].

In addition, Random Forests have been widely employed in forest fire prediction. For instance, Latifah applied Random Forest to predict forest fires in “Evaluation of Random Forest model for forest fire prediction based on climatology over Borneo” [31]. In parallel, Malik proposed the usage of Random Forest to estimate “ Data-driven wildfire risk prediction in northern California” [32]. Song demonstrated the superiority of the Random Forest model, over SVM, XGBoost, and LightGBM, in predicting forest lightning fires “Interpretable artificial intelligence models for predicting lightning prone to inducing forest fires” [33]. As well, Gao conducted a forest fire risk prediction study in China, “Forest-fire-risk prediction based on random forest and back propagation neural network of Heihe area in Heilongjiang province, China” [34]. Hu developed and validated results related to fire events in fuel tanks, employing Particle Swarm Optimization with a back propagation neural network: “Development and Validation of a Novel Method to Predict Flame Behavior in Tank Fires Based on CFD Modeling and Machine Learning” [35].

This paper examines a key issue in forest fire management, such as predicting the duration of fires using data from already-happened forest fires in combination with the weather conditions that prevailed during the development of this phenomenon. Concerning this topic, a series of research papers have been published during the past years, like the work of Xiao et al. [15], who designed a wildfire duration prediction model, based on historical fire data and geospatial information. The algorithms employed included RF (Random Forest), KNN, and XGBoost regression model, as well as image-based approaches such as CNN and Encoder. The model achieved an accuracy exceeding 80% for fires lasting longer than 10 days. In the same vein, Andela validated the fire data from the Global Fire Atlas, utilizing independent datasets from the United States. The study employed satellite data and highlighted that the duration of fires is significantly influenced by the fire season, among other things: “The Global Fire Atlas of individual fire size, duration, speed and direction” [36]. Ujjwal settled a surrogate model to capture the dynamic spread of a wildfire over time. The mathematical model, designed to simulate the relationship between the burned area and key meteorological parameters (such as relative humidity, temperature, and wind speed), provides valuable insights into fire behavior “A surrogate model for rapidly assessing the size of a wildfire over time” [37]. Zi-Cong also leveraged the capabilities of a Deep Learning Surrogate Model, designed to predict the temperature evolution within a tunnel in the event of a fire outbreak: “A deep learning--based surrogate model for spatial-temporal temperature field prediction in subway tunnel fires via CFD simulation” [38]. Liang investigated the capability of yielding results for predicting wildfire duration, primarily focused on forecasting the scale of a forest fire. The research “A neural network model for wildfire scale prediction using meteorological factors” utilized neural network algorithms, including Back propagation Neural Network (BPNN), Recurrent Neural Network (RNN), and Long Short-Term Memory (LSTM). Among them, LSTM demonstrated the highest accuracy, achieving 90.9% [39]. Subsequently, researchers also highlighted the LSTM method in a study concerning fires in enclosed and industrial environments: “ Prediction method and application of temperature distribution in typical confined space spill fires based on deep learning” [40]. Xi established a framework for jointly modeling fire duration and size using a bivariate finite mixture model, “Modeling the duration and size of wildfires using joint mixture models”. Four subpopulations (normal or extreme in duration and size) were analyzed, incorporating variables such as location, month, and environmental factors. The research revealed a strong connection between duration and size, and identified key predictors influencing these subpopulations [41].

Predicting the duration of a fire is crucial, as it allows for the estimation of the potential risk to the affected area and determining the necessary human resources for its suppression. Additionally, forest fires and asymmetrical climate change are commonly “inflamed”, highlighting their interconnection. The Western fire chief’s association from the U.S. emphasizes that climate change is drastically impacting the fire season. Therefore, fire seasons now last six to eight months, compared to the four months they previously spanned. Face the Facts USA reports that in the U.S., the average duration of wildfires increased from 8 days before 1986, to 37 days by 2013 [42].

On this subject, regarding the asymmetric effects and phenomena brought about by climate change, we will indicatively refer to certain studies. In 2001, Flato & Boer introduced the paper “Warming asymmetry in Climate Change simulations” [43]. In 2009, Whitmarsh published the article “Behavioural responses to climate change: Asymmetry of intentions and impacts” [44]. In 2012, Xu & Ramanathan published “Latitudinally asymmetric response of global surface temperature: Implications for regional climate change” [45]. In 2018, Shunchuan released “A symmetrical CO₂ peak and asymmetrical climate change during the middle Miocene” [46]. In 2021, Gao issued “Asymmetrical lightning fire season expansion in the boreal forest of Northeast China” [47].

The current work employs a series of feature construction and selection methods in order to improve the ability of various machine learning techniques to predict the duration of forest fires. These methods involve creating new, meaningful variables by combining or transforming existing symmetrical and asymmetrical data attributes [48]. For example, integrating material resources deployed during a forest fire event into a single metric constitutes Feature Construction, enabling models to better capture the complexity of fire incidents and resource allocation. Another example of Feature Construction during a forest fire is combining weather attributes in order to form a fire risk index. Such approaches enhance data representation, facilitating more robust and interpretable predictive models, in disaster management. The Feature Construction or selection methods were applied to data collected for the Greek case that contained weather information.

The main contributions of the current work can be summarized as the following highlights:

• The incorporation of Greek Forest Fire data from the years 2014–2021 (57,904 entries).
• The inclusion of meteorological data for each fire event.
• The classification of forest fires according to their duration.
• The usage of Feature Construction techniques.
• The prediction of the forest fire duration.
• Main contributions: Estimating fire duration and analyzing the interaction between environmental conditions and fire duration.

The remaining of this manuscript is divided as follows: Section 2 describes the used dataset and provides a detailed discussion on the used methods, Section 3 outlines the conducted experiments and some statistical tests on them, and finally Section 4 discusses some conclusions on the experimental results.

2. Materials and Methods

This section initiates with a description of the used datasets and continues with a detailed description of the used feature construction and selection techniques that will be applied to the datasets incorporated in the conducted experiments.

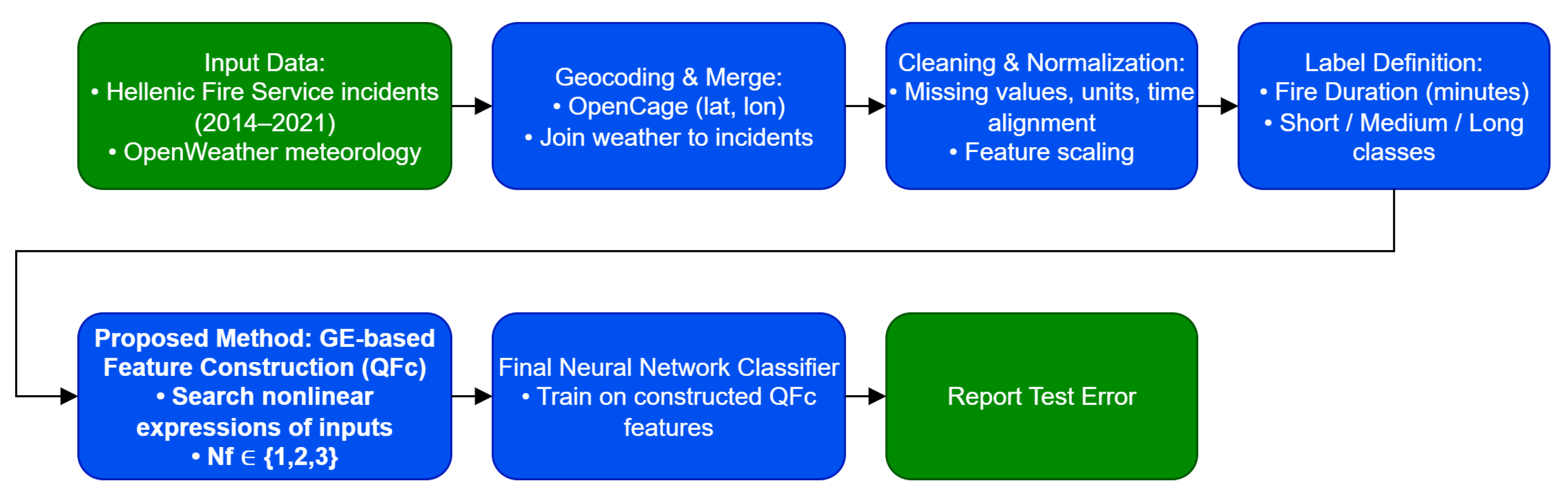
2.1. The Used Dataset

In this research, open data provided by the Hellenic Fire Service were utilized, available at the link https://www.fireservice.gr/en_US/synola-dedomenon (accessed on 15 October 2025). The datasets used included information on all fires that occurred in Greece during the years 2014–2021. The data encompassed the location of the fire, the date and time of ignition and extinguishment, the burned areas categorized by land type, and the firefighting forces deployed for suppression efforts.

The datasets comply with the European transparency legislation (Directive 2013/37/EU), ensuring that the data are unbiased in terms of type and location, and represent all fires in the Hellenic region. The information provided by the Hellenic Fire Service is easily accessible, regularly updated, accurate, and comprehensive, facilitating analysis and covering all involved entities. Regarding burned areas, the dataset included measurements for the following categories: forests, forested areas, groves, grasslands, reed beds and wetlands, agricultural lands, crop residues, and landfills.

As for the firefighting units deployed, the dataset included measurements for the following resources: firefighters, ground-based teams, volunteers, military forces, other supporting units, fire trucks, service vehicles, tankers, machinery, CL-215 aircraft, PZL aircraft, and GRU aircraft, as well as contracted helicopters and aircraft. From the raw data obtained from the Hellenic Fire Service, we removed all records that lacked essential values such as the date, fire ignition time, or fire extinguishing time, as it would not be possible to proceed with predicting the duration of a fire without these fundamental parameters. This data preprocessing step ensured the retention of complete and consistent information, establishing a symmetric and reliable basis for subsequent analyses, while mitigating potential asymmetric data gaps. The original number of patterns for every year and the deleted patterns (due to missing data) are presented in

Table 1. The original size of datasets and the eliminated rows.

Year	Raw Data	Deleted	Final Data
2014	6834	1158	5676
2015	8117	1358	6759
2016	10,258	1642	8616
2017	10,355	1678	8677
2018	8005	1363	6642
2019	9499	2280	7219
2020	11,798	4579	7096
2021	9513	2417	7096
TOTAL	74,379	16,475	57,904

.

2.1.1. Data Preprocessing and Weather Feature Extraction

The first step in data preprocessing involved removing rows with missing values. Subsequently, using the OpenCage Geocoding API, the location data, initially formatted as “Municipality, Area, Address,” were converted into geolocation data in the form of latitude and longitude coordinates.

Next, weather information was extracted for each fire event using the OpenWeather API, capturing data for both the ignition and extinguishment times. OpenWeather is a widely used service that provides detailed weather data, including historical, real-time, and forecasted weather information. The extracted weather features included the following:

• Temperature at 2 m: The air temperature near the ground level.
• Relative Humidity at 2 m: The percentage of moisture in the air relative to its maximum capacity.
• Dew Point at 2 m: The temperature at which air reaches saturation and moisture condenses.
• Precipitation: The amount of rainfall during the specific time interval.
• Weather Code: A classification of the general weather conditions (e.g., clear, cloudy, rainy).
• Cloud Cover: The percentage of the sky obscured by clouds.
• Evapotranspiration (ET0): The potential evapotranspiration measured using the FAO Penman–Monteith method, indicating water loss from the surface and vegetation.
• Vapour Pressure Deficit (VPD): The difference between the amount of moisture in the air and the maximum it can hold.
• Wind Speed at 10 m and 100 m: Wind velocity measured at heights of 10 m and 100 m.
• Wind Direction at 10 m and 100 m: The directional angle of the wind at the respective heights.

Additionally, daily-level weather data were included, such as the following:

• Daylight Duration: The total hours of daylight during the day.
• Sunshine Duration: The total hours of direct sunlight during the day.

These features were aggregated and matched with each fire record, ensuring comprehensive weather context for both the ignition and extinguishment phases of the fires. In this context, incorporating meteorological variables from both the ignition and extinguishment periods captures the asymmetric evolution of weather conditions throughout the fire’s duration. Forest fires in Greece often evolve under rapidly changing meteorological patterns, where factors such as wind speed, temperature, and humidity fluctuate significantly between ignition and suppression. Therefore, integrating both sets of meteorological data allows for a more comprehensive and symmetric representation of the fire event, enhancing the model’s ability to approximate real world dynamics. However, the primary aim of this study is not real-time operational prediction, but rather the post-event modelling and understanding of the duration of forest fires under realistic and dynamic environmental conditions.

2.1.2. Definition of the Output Variable

To define the output variable, the duration of each forest fire was converted from hours or other time units into minutes, ensuring greater precision in classification. A logarithmic transformation of fire duration in minutes was then applied to manage the wide range of values effectively, preventing excessive influence from extreme durations. Based on this transformation, three distinct categories were established, serving as target values for experimental analysis. This approach enabled the classification of forest fires according to their duration. For the Greek forest fire data used in this study, the following classification scheme was adopted:

• Up to 360 min (6 h) is considered to be a fire, of short duration.
• From 361–7200 min (6 h–5 days) is a fire of medium duration.
• More than 7201 min (5 days- and more), which is considered a long duration fire.

The specific temporal categorization was determined based on the distribution of forest fire duration data across the Greek territory, as observed in the dataset we processed. This data-driven approach ensured that the selected cut-points (≤360 min, 361–7200 min, >7201 min) accurately reflected the natural groupings present within the observed fire duration patterns. It should be noted that in Greek territory, the combination of fuel types (such as pine and fir forests), geomorphological features (including mountainous terrain, ravines, and steep slopes), and climatic conditions (temperature, humidity, and wind speed) are particularly distinctive. As a result, if a wildfire is not brought under control within the first few hours, it tends to spread rapidly beyond containment, potentially burning for several days.

2.2. The Used Feature Construction and Selection Methods

2.2.1. The PCA Method

The Principal Component Analysis (PCA) technique was introduced by mathematician Karl Pearson in 1901 [49], and developed by Harold Hotelling (1933). This technique operates on the principle that when data from a higher-dimensional space is transformed into a lower-dimensional space, the resulting lower-dimensional representation should retain the maximum variance of the original data.

Notably, it is worth mentioning that the use of PCA, on larger datasets, became practical only after the advent of electronic computers, which made it computationally feasible to handle datasets beyond trivial sizes [50]. Continuing, with the applications of PCA, it is a widely utilized technique in exploratory data analysis and machine learning, particularly in building predictive models. It is an unsupervised learning method, designed to analyze the relationships among a set of variables. Often referred to as a form of general factor analysis, it involves regression to determine a line of best fit. The primary objective of PCA is to reduce the dimensionality of a dataset while retaining the most significant patterns and relationships among the variables, all without requiring prior knowledge of the target variables [51].

Next, we will briefly reference studies that have utilized PCA, covering different areas such as statistical physics, genetic improvement, face recognition, economic and environmental sciences, medical prediction, etc. Explicitly, the research conducted by Park [52] highlights the reasons behind the success of the PCA technique for lattice systems. The study’s primary limitation lies in the dependency of the proposed formula’s accuracy on the dataset size. Specifically, the results achieve full precision only under the condition of an infinite dataset. This constraint restricts the practical applicability of the method when working with finite or limited data, a common scenario in real-world analyses.

Additionally, the work of Sarma et al. [53] utilizes PCA in order to evaluate morphometric traits under a multivariate approach. The findings suggest that PCA could significantly enhance genetic improvement. Noteworthy is the fact that 64.29%, of the total variance explained can be considered relatively low. This suggests that a significant amount of unexplained information remains which is not captured by the four principal components. Moreover, Gambardella et al. used the PCA technique for monitoring the cultivation of cannabis in Albania. Specifically, with PCA they remove redundant spectral information from multiband datasets [54]. The article by Slavkovic and Jevtic [55] presents the implementation of a face-recognition system based on the Principal Component Analysis (PCA) algorithm. The PCA technique was utilized by Hargreaves [56] for stock selection, specifically to identify a limited number of stock variables that could effectively aid in determining winning stocks.

Moreover, Xu et al. presents an interesting example of a modified application of Principal Component Analysis (PCA), utilizing both linear and non-linear methods, through Kernel PCA (KPCA), in combination, with the Adaptive Boosting (AdaBoost) algorithm [57]. In the study by Zhang [58], a neural network model combining PCA and Levenberg–Marquardt [59] was developed to efficiently and accurately analyze and predict the interaction between IAQ and its influencing factors, in particular indoor air quality (IAQ) and its relationship with building features and environmental conditions.

In the work of Akinnuwesi et al. [60], a hybrid approach was suggested combining Principal Component Analysis (PCA) and Support Vector Machine (SVM) [61]. They created the Breast Cancer Risk Assessment and Early Diagnosis (BC-RAED) model, designed to accurately detect BCa in its early stages. PCA was initially applied to extract features during the first preprocessing stage, followed by further feature reduction in the second stage. The multi-preprocessed data were analyzed for breast cancer risk and diagnosis using SVM. The BC-RAED model achieved an accuracy of 97.62%, a sensitivity of 95.24%, and a specificity of 100% in assessing and diagnosing breast cancer risk.

Subsequently, we will briefly mention certain studies that have been conducted in the field of forest fires. Guan’s research focuses on forest fire prediction using PCA-preprocessed data. The preprocessing step removed irrelevant information, simplifying analysis. Linear regression and random forest methods were then applied, revealing temperature, relative humidity, wind, and rain as the most influential factors in forest fire occurrence [62].

A novel model was developed by Nikolov, using meteorological forecast data as input. Principal Component Analysis (PCA) with orthogonal rotation was applied to reduce 195 meteorological variables from the NARR dataset to a smaller set of significant fire-ignition predictors, later used in logistic regression to calculate wildfire ignition probabilities [63]. Also, a recent publication focuses on predicting wildfire ignitions caused by lightning strikes, which account for the largest area burned annually in the extratropical Northern Hemisphere. Principal Component Analysis (PCA) played a key role in reducing 611 potential predictors to 13 principal components, which were used in logistic regression to identify the primary factors influencing lightning occurrence [64].

2.2.2. The MRMR Method

The min-redundancy max-relevance (MRMR) algorithm, introduced by Chris Ding and Hanchuan Peng [65]. This method aims to optimize feature selection by minimizing redundancy and maximizing relevance [66]. In sum, MRMR enhances relevance-only methods, such as using an f-test between the target and the features. When two features are similar, MRMR prioritizes only the one with the highest relevance.

The study by Zhao extends traditional MRMR methods by introducing a non-linear feature redundancy measure and a model-based feature relevance measure, which are tested on synthetic and real-world datasets. Based on its empirical success, MRMR is integrated into Uber’s marketing machine learning platform to automate the creation and deployment of scalable targeting and personalization models [67].

Moreover, Wu et al. proposed that the MRMR algorithm is utilized in conjunction with a Random Forest model [68] to perform feature selection in the context of air quality prediction. MRMR is employed to determine which variables have the most significant impact on the air quality index (AQI), while minimizing redundancy among them [69].

The article by Elbeltagi is an innovative approach for estimating maize chlorophyll by integrating hyperspectral indices with six cutting-edge advanced machine learning techniques. The MRMR algorithm was incorporated into the process to enhance feature selection by pinpointing the most significant spectral bands, minimizing data redundancy and boosting model efficiency [70].

In the energy sector, Liu conducted the following research offering an improved method for predicting transient stability in power systems. The MRMR algorithm is applied for feature selection with minimal redundancy and maximum relevance, providing an enhanced approach for forecasting transient stability in power systems. This approach addresses the limitations of previous methods, such as low accuracy, difficult applicability, and high computational cost, while incorporating the “winner take all” (WTA) technique for ensemble learning and enhanced precision [71].

Eristi also refers to the energy sector. Specifically, this paper presents a new PD detection system that combines spectral analysis, spectrogram analysis, deep learning algorithms, MRMR, and ensemble machine learning (EML) [72]. The most impactful features are identified by performing MRMR feature selection analysis on the extracted deep features [73].

Zhang employed an Acoustic Emission (AE) technique to monitor inaccessible areas of large storage tank floors utilizing AE sensors positioned externally to the tank. The implemented algorithm effectively distinguishes corrosion signals from interference signals, particularly drop-back signals induced by condensation. Experimental studies were conducted both in laboratory settings and in field environments, focusing on Q235 steel. Seven characteristic AE features derived from signal hits and frequency were extracted and subsequently selected for pattern recognition using the MRMR method [74].

Additionally, Karamouz et al., proposed a methodology to examine the effects of climate change on sea level variations in coastal areas using an artificial neural network model. Feature selection techniques, including MRMR and Mutual Information (MI), are employed to identify the most suitable predictors for the neural network input [75].

2.2.3. The Neural Network Construction Method

Another machine learning method introduced recently that is based on Grammatical Evolution [76] is the construction of artificial neural networks [77]. In this work, the architecture of the neural network is produced through a series of generations of the underlying genetic algorithm by reducing the training error of the neural network. Furthermore, the method is able to identify the best set of parameters for the neural network. This method can also retain only a small portion of features from the original objective problem, significantly reducing the information required to reduce the training error. This method was used in a series of practical problems, such as the identification of amide I bonds [78], solutions of differential equations [79], incorporation in the detection of Parkinson’s disease [80], usage in the estimation of performance of students [81], autism screening [82], etc.

The used grammar for the construction of neural networks expressed in Backus–Naur (BNF) form [83] is shown in Figure 4. Numbers in parentheses represent the sequence number of each production rule. The constant n stands for the number of input features.

This grammar produces artificial neural networks in the following form:

$$\mathbf{NN}\left(\overrightarrow{x},\overrightarrow{w}\right)=\sum _{i=1}^H{w}_{(n+2)i-(n+1)}\sigma \left(\sum _{j=1}^n{x}_j{w}_{(n+2)i-(n+1)+j}+w_{(n+2)i}\right)$$

(1)

The symbol H defines the number of processing nodes (weights). The sigmoid function $\sigma \left(x\right)$ is used as the activation function of the neural network and it is defined as:

$$\sigma \left(x\right)={\displaystyle \frac{1}{1+exp(-x)}}$$

(2)

The main steps of the algorithm are as follows:

• Initialization step.

  (a)

  Set the number of used chromosomes $N_c$. Each chromosome is a set of randomly selected integers. These integer values represent rule number in the extended BNF grammar previously presented.

  (b)

  Set the maximum number of allowed generations $N_g$.

  (c)

  Set the selection rate $p_s\in [0,1]$ and the mutation rate $p_m\in [0,1]$.

  (d)

  Set $k=0$, the generation number.

• Fitness calculation step.

  (a)

  For each chromosome $g_i,$$i=1,\dots ,N_c$,

  • Create using the grammar of Figure 4 the corresponding neural network ${\mathrm{N}\mathrm{N}}_i\left(\overrightarrow{x},\overrightarrow{w}\right)$
  • Set as $f_i={\sum }_{j=1}^M{\left({\mathrm{N}\mathrm{N}}_i\left({\overrightarrow{x}}_j,\overrightarrow{w_i}\right)-y_j\right)}^2$ the fitness of chromosome i. The set $\left(\overrightarrow{x_j},y_j\right),j=1,\dots ,M$ stands for the train set of the objective problem.

  (b)

  End

• Genetic operations step.

  (a)

  Application of Selection operator. The chromosomes of the population are sorted according to their fitness values and the best $\left(1-p_s\right)\times N_c$ chromosomes are copied to the next generation. The remaining are replaced by new chromosomes produced during crossover and mutation.

  (b)

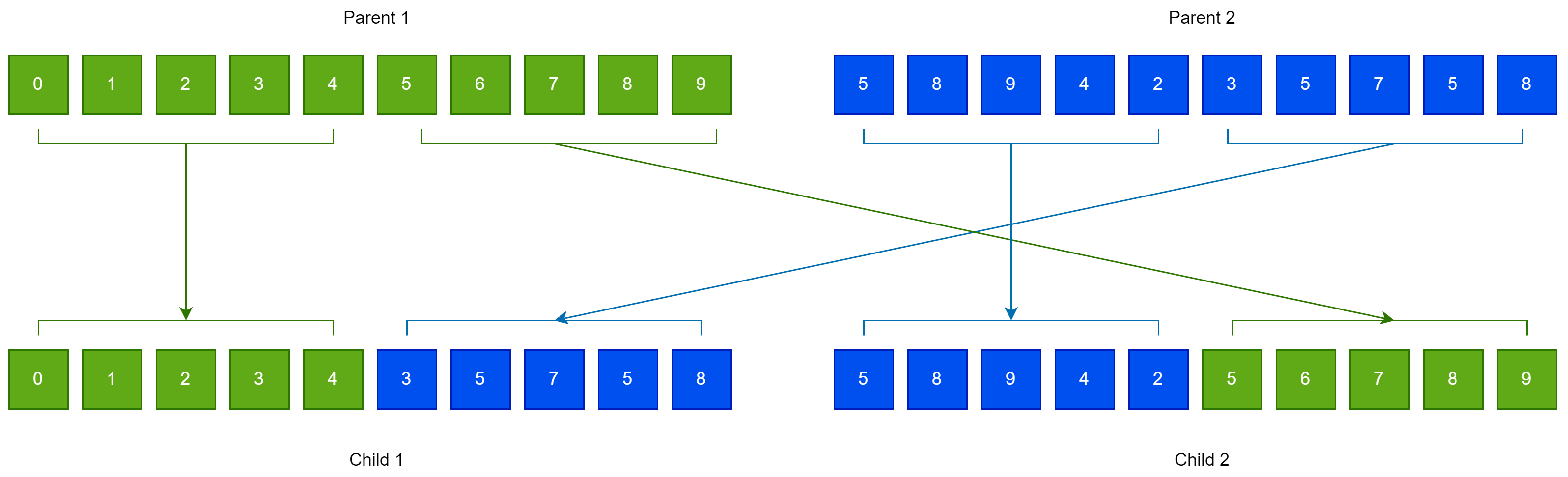
  Application of Crossover operator. In this step $p_s\times N_c$ new chromosomes will be created from the original ones. For each set $c_1,c_2$ of new chromosomes that will be created, two chromosomes $g_a$ and $g_b$ are selected from the old population using tournament selection. The new chromosomes are created using one-point crossover between $g_a$ and $g_b$. An example of this operation is shown graphically in Figure 5.

  (c)

  Application of Mutation operator. For each element of every chromosome, a random number $r\in [0,1]$ is selected. The corresponding element is changed randomly when $r\le p_m$.

• Termination check step.

  (a)

  Set $k=k+1$

  (b)

  If $k\le N_g$ then go to Fitness Calculation Step.

• Application to the test set.

  (a)

  Obtain the best chromosome $g^{*}$ from the genetic population.

  (b)

  Create the corresponding neural network ${\mathrm{N}\mathrm{N}}^{*}\left(\overrightarrow{x},\overrightarrow{w}\right)$.

  (c)

  Apply this neural network to the test set of the objective problem and report the corresponding error (test error).

2.2.4. The Feature Construction Method

Another approach discussed here and used in the conducted experiments is the feature construction technique initially proposed in [84]. This approach creates artificial features from the original ones using the Grammatical Evolution procedure. The new features are non-linear mappings of the original ones. This method has been used in a series of practical cases during recent years, such as Spam Identification [85], Fetal heart classification [86], EEG signal processing [87,88], etc. The extended version of BNF grammar used during the feature construction process is outlined in Figure 6.

The main steps of the used algorithm are as follows:

• Initialization step.

  (a)

  Define the number of used chromosomes $N_c$.

  (b)

  Define the maximum number of allowed generations $N_g$.

  (c)

  Set the selection rate $p_s\in [0,1]$ and the mutation rate $p_m\in [0,1]$.

  (d)

  Set $N_f$ as the number of desired features that will be created.

  (e)

  Set $k=0$, the generation number.

• Fitness calculation step.
• For $i=1,\dots ,N_c$,

  (a)

  Create, with the assistance of Grammatical Evolution, a set of $N_f$ artificial features from the original ones, for chromosome $g_i$.

  (b)

  Transform the original train set using the previously produced features. Represent the new set as $\mathrm{T}\mathrm{R}=\left(x_{g_i,j},t_j\right),j=1,\dots M$

  (c)

  Apply a machine learning model denoted as C on set TR and train this model and denote $C\left(x\right)$ as the output of this model for any input pattern x.

  (d)

  Calculate the fitness $f_i$ as:

  $$f_i=\sum _{j=1}^M{\left(C\left(x_{g_i,j}\right)-t_j\right)}^2$$

  The Radial Basis Function (RBF) networks [89,90] were used as the machine learning models $C\left(x\right)$ in the current work. This machine learning model was chosen because of the significantly shorter training time it requires compared to other machine learning models.

• End
• Genetic operations step. Perform the same genetic operators as in the case of construction neural networks, discussed previously.
• Termination check step.

  (a)

  Set $k=k+1$

  (b)

  If $k\le N_g$ then go to Fitness Calculation Step.

• Application to the test set.

  (a)

  Obtain the chromosome $g^{*}$ with the lowest fitness value.

  (b)

  Create the $N_f$ artificial features that correspond to this chromosome.

  (c)

  Apply the $N_f$ features to the train set and produce the mapped training set $\mathrm{T}\mathrm{R}=\left(x_{g_i,j},t_j\right),j=1,\dots M$

  (d)

  Train a machine learning model on the produced training set. An artificial neural network [91,92] with $H=10$ processing nodes is used in the current work. This neural network was trained using a BFGS variant of Powell [93].

  (e)

  Apply the new features to the test set of the objective problem and create the set $\mathrm{T}\mathrm{T}=\left(x_{g_i,j},t_j\right),j=1,\dots K$

  (f)

  Apply the machine learning model on set TT and report the test error.

The diagram in Figure 7 depicts the proposed FC scheme, from raw data to statistically substantiated results. Incident records from the Hellenic Fire Service (2014–2021) are combined with meteorological data from OpenWeather at ignition and extinguishment times. Each incident is geocoded with OpenCage (latitude/longitude) and merged with the corresponding weather measurements, yielding a consistent spatiotemporal profile per event. The unified dataset is then cleaned and normalized (handling missing values, harmonizing units and timing, and applying feature scaling). The target variable is defined as fire duration in minutes and categorized into Short, Medium, and Long according to the thresholds specified in the manuscript. Feature Construction is performed by the proposed GE-based FC (QFc), which searches for nonlinear expressions of the original variables and produces a compact set of constructed features $\left(N_f\right)$ tailored to the classification task. These features feed the final neural-network classifier, which is trained and evaluated using classification error (%) as the primary metric.

3. Results

The experiments were executed using the freely available optimization environment of Optimus [94], which can be downloaded from https://github.com/itsoulos/GlobalOptimus.git (accessed on 11 October 2025). as well as the WEKA programming tool [95]. The WEKA software has been incorporated in a series of problems [96,97,98,99]. Each experiment was conducted 30 times and the average classification error is reported, using different seed for the random generator each time and the ten-fold cross validation procedure was used to validate the experimental results. The values of parameters for the used methods are shown in

Table 2. The values for each parameter of the proposed method.

Name	Meaning	Value
$N_c$	Chromosomes	500
$N_g$	Generations	200
$p_s$	Selection rate	0.1
$p_m$	Mutation rate	0.05
$N_f$	Number of features	2
H	Number of weights	10
$B_I$	Iterations for BFGS	2000
$A_I$	Iterations for ADAM	2000
${\beta }_1$	Parameter for ADAM	0.9
${\beta }_2$	Parameter for ADAM	0.999

.

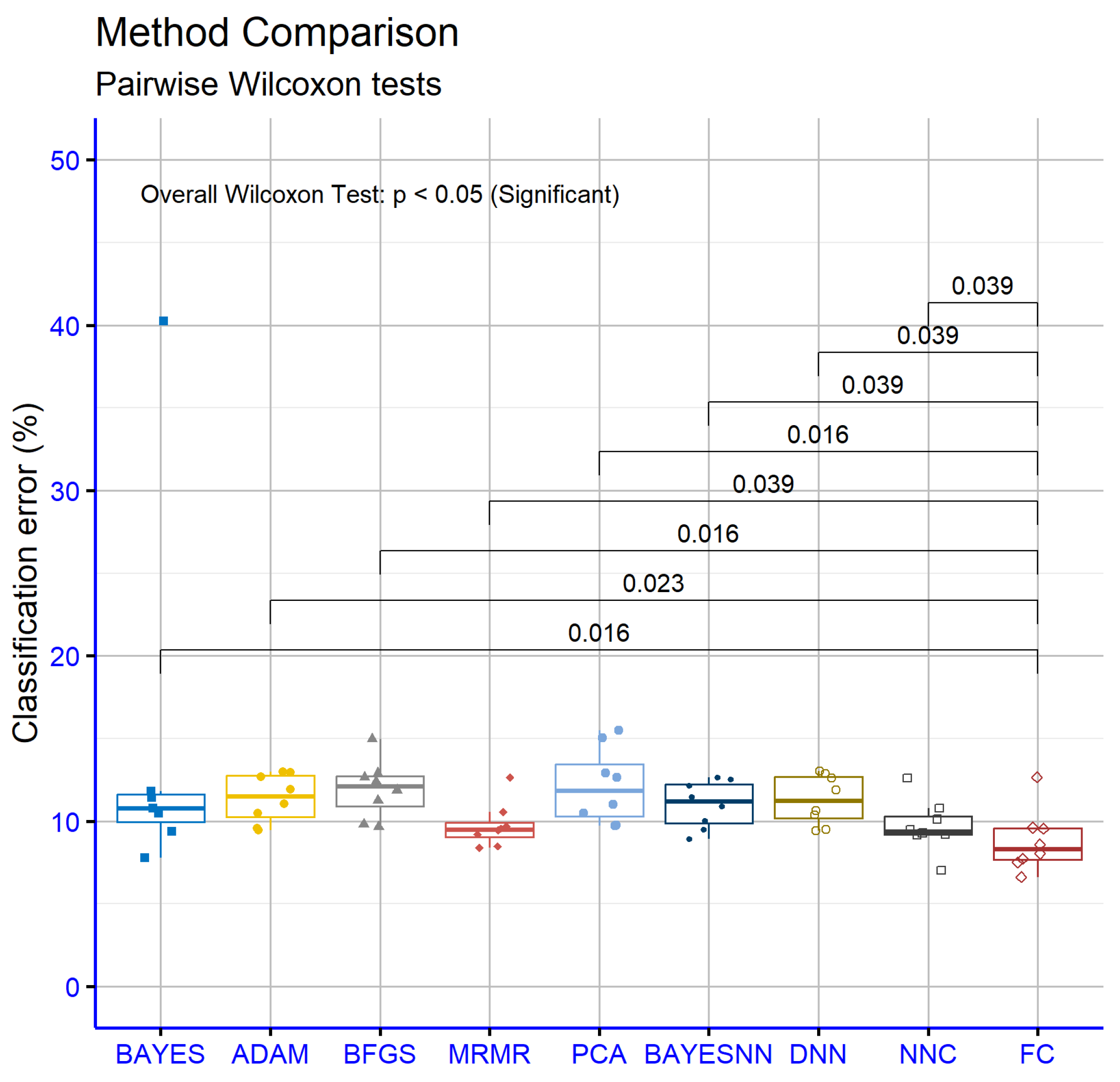
The following notation is used in the tables presenting the experimental results:

• The column YEAR denotes the year of recording.
• The column BAYES the application of the Naive Bayes [100] method to the corresponding dataset.
• The column ADAM represents the usage of the ADAM optimizer [101] for the training of a neural network with $H=10$ processing nodes.
• The column BFGS denotes the incorporation of the BFGS optimizer [93] to train a neural network with $H=10$ processing nodes.
• The column MRMR denotes the results obtained by the application of a neural network trained with the BFGS optimizer on two features selected using the MRMR technique.
• The column PCA stands for the results obtained by the application of a neural network trained with the BFGS optimizer on two features created using the PCA technique. The PCA variant implemented in MLPACK software [102] was incorporated to create these features.
• The column BAYESNN presents results using the Bayesian optimizer from the open-source BayesOpt library [103]. This method was used to train a neural network with 10 processing nodes.
• The column DNN denotes the usage of a deep neural network as implemented in the Tiny Dnn library, which can be downloaded freely from https://github.com/tiny-dnn/tiny-dnn (accessed on 10 October 2025). The optimization method AdaGrad [104] was used to train the neural network in this case.
• The column NNC denotes the usage of the method of Neural Network Construction on the proposed datasets. The software that implements this method was obtained from [105].
• The column FC represents the usage of the previously mentioned method for constructing artificial features. For the purposes of this article, two artificial features were created. These features were produced and evaluated using the QFc software version 1.0 [106].

Year-wise results show that the proposed FC method achieves the lowest average classification error (8.25%), outperforming NNC (9.38%), MRMR (9.25%), BAYESNN (10.50%), DNN (10.75%), ADAM (10.88%), BFGS (11.25%), and PCA (11.63%) (

Table 3. Experimental results using a series of machine learning methods for the prediction of forest fire duration.

Year	BAYES	ADAM	BFGS	MRMR	PCA	BAYESNN	DNN	NNC	FC
2014	11.41%	13.00%	12.38%	9.68%	15.50%	12.14%	13.01%	9.21%	8.04%
2015	10.49%	11.94%	11.25%	8.49%	15.03%	11.48%	11.89%	9.17%	7.51%
2016	10.79%	12.95%	11.88%	9.45%	12.93%	12.53%	12.89%	10.12%	8.60%
2017	53.36%	12.68%	12.65%	12.65%	12.64%	12.65%	12.62%	12.61%	12.66%
2018	9.39%	10.48%	14.97%	9.21%	10.49%	10.02%	10.38%	9.29%	7.72%
2019	7.79%	9.44%	9.66%	8.39%	9.72%	8.94%	9.41%	7.03%	6.62%
2020	40.26%	9.56%	9.80%	9.55%	9.76%	9.50%	9.50%	9.50%	9.61%
2021	11.81%	11.06%	12.90%	10.57%	11.03%	10.90%	10.62%	10.80%	9.55%
AVERAGE	18.88%	10.88%	11.25%	9.25%	11.63%	10.50%	10.75%	9.38%	8.25%

). FC attains the best annual score in 6 out of 8 years (2014, 2015, 2016, 2018, 2019, 2021), with two exceptions: in 2017, NNC is marginally better (12.61% vs. 12.66%), and in 2020 other methods tie at the lowest error (BAYESNN/DNN/NNC = 9.50% vs. 9.61% for FC). Notable anomalies appear for BAYES in 2017 (53.36%) and 2020 (40.26%), suggesting that this classifier is sensitive to the data characteristics in those years. Regarding stability, standard deviations indicate high variability for NNC (e.g., 0.99 in 2014) and elevated dispersion for BFGS in some years (up to 0.51), whereas FC maintains moderate and consistent variability (≈0.04–0.19), offering a robust accuracy–reliability balance. Overall, the evidence supports FC as the top performer, with consistently lower errors, especially in recent years, apart from specific edge cases in 2017 and 2020.

The standard deviation for the experimental results is also depicted in

Table 4. Standard deviation values for all used methods.

Year	ADAM	BFGS	MRMR	PCA	BAYESNN	DNN	NNC	FC
2014	0.06	0.47	0.07	0.10	0.33	0.06	0.99	0.17
2015	0.08	0.19	0.12	0.06	0.22	0.11	0.70	0.17
2016	0.04	0.12	0.07	0.03	0.20	0.06	0.57	0.19
2017	0.05	0.03	0.06	0.14	0.05	0.04	0.11	0.04
2018	0.06	0.51	0.16	0.05	0.20	0.08	0.47	0.17
2019	0.07	0.45	0.12	0.03	0.29	0.05	0.49	0.18
2020	0.05	0.07	0.03	0.04	0.04	0.04	0.12	0.19
2021	0.08	0.12	0.14	0.13	0.26	0.08	0.48	0.18

.

In Figure 8 the average execution time for all methods participated in the experiments is outlined.

As expected, the proposed method requires significantly more time than other techniques since it consists of a Genetic Algorithm that in each iteration minimizes the error in a large series of RBF networks in order to calculate the corresponding fitness values.

Using paired Wilcoxon signed-rank tests across the classification datasets, the proposed FC method exhibits a consistent statistical advantage over all competing models. The pairwise comparisons FC vs. BAYES (p = 0.016), ADAM (p = 0.023), BFGS (p = 0.016), MRMR (p = 0.039), PCA (p = 0.016), BAYESNN (p = 0.039), DNN (p = 0.039), and NNC (p = 0.039) are all significant at $\alpha =0.05$. None of the p-values fall below 0.01; therefore, the evidence corresponds to “significant” rather than “highly” or “extremely” significant according to the Figure 9 legend. The uniform pattern of p < 0.05 across all pairs substantiates that FC attains systematically lower error than every alternative model on the evaluated datasets, with the strongest statistical indication against BAYES, BFGS, and PCA (p = 0.016).

The data in

Table 5. Experiments with different numbers of constructed features for the procedure that creates artificial features with Grammatical Evolution.

Year	${\mathit{N}}_{\mathit{f}}=1$	${\mathit{N}}_{\mathit{f}}=2$	${\mathit{N}}_{\mathit{f}}=3$
2014	8.36%	8.04%	7.95%
2015	8.10%	7.51%	7.24%
2016	8.61%	8.60%	8.15%
2017	12.68%	12.66%	12.46%
2018	7.68%	7.72%	7.51%
2019	6.77%	6.62%	6.49%
2020	9.50%	9.61%	9.58%
2021	10.53%	9.55%	9.62%
AVERAGE	8.50%	8.25%	8.13%

present the classification error rates for the “FC” machine learning model across different numbers of constructed features ($N_f=1$, $N_f=2$, and $N_f=3$) generated using Grammatical Evolution, spanning the years 2014 to 2021. These results provide insights into the impact of the number of features on the model’s performance over time. For $N_f=1$, the classification error rates exhibit variability across the years, ranging from a minimum of 6.77% in 2019 to a maximum of 12.68% in 2017. The average error rate for this configuration is 9.03%, indicating a relatively moderate level of accuracy overall. The peak error in 2017 suggests possible challenges in that year’s data or specific interactions between the model and the constructed feature set. For $N_f=2$, the classification error rates show a slightly improved overall performance compared to $N_f=1$, with an average error of 8.25%. The error rates range from 6.62% in 2019, marking the lowest rate for this configuration, to 12.66% in 2017, the highest. These results indicate that adding one more feature generally leads to improved accuracy, although the improvement is not uniform across all years. For $N_f=3$, the classification error rates demonstrate further improvement, with an average error of 8.13%, which is the lowest among the three configurations. The error rates range from a minimum of 6.49% in 2019 to a maximum of 12.46% in 2017. The slightly lower peak error compared to $N_f=1$ and $N_f=2$ suggests that the inclusion of a third constructed feature enhances the model’s ability to capture data patterns more effectively. Across all configurations, the year 2017 consistently exhibits the highest classification error rates, irrespective of the number of features. This outlier suggests specific data-related challenges or unique model behavior during that year. Conversely, 2019 consistently shows the lowest error rates, indicating favorable conditions for accurate classification during that period. The trend in the average classification error rates decreasing from 9.03% for $N_f=1$ to 8.50% for $N_f=3$ demonstrates that the addition of constructed features through Grammatical Evolution positively impacts the model’s accuracy. However, the diminishing returns between $N_f=2$ and $N_f=3$ suggest that the incremental benefit of adding more features may plateau after a certain point. In conclusion, the analysis reveals that increasing the number of constructed features generally improves the accuracy of the “FC” model. The results highlight the importance of balancing feature complexity and model performance while considering the specific characteristics of the data across different years.

For Table 5, a statistical analysis was conducted using the Wilcoxon Test (Figure 10) to compare classification error rates among configurations with different numbers of constructed features ($N_f=1,N_f=2$, and $N_f=3$). The results of the test provide valuable insights into the statistical significance of the differences in the performance of these configurations. The overall result of the Wilcoxon Test, with p < 0.5, indicates that statistically significant differences exist in at least one of the pairwise comparisons between the configurations. Specifically, the comparison between $N_f=1$ and $N_f=2$ yields p = 0.15, which is not statistically significant. This suggests that adding a second constructed feature does not lead to a significant improvement in the model’s performance. On the other hand, the comparison between $N_f=1$ and $N_f=3$ shows p = 0.016, a statistically significant value. This indicates that the inclusion of a third constructed feature substantially enhances the model’s accuracy compared to using only one feature. The comparison between $N_f=2$ and $N_f=3$ also reveals a statistically significant difference, with p = 0.023. This result suggests that even the transition from $N_f=2$ to $N_f=3$ leads to an improvement in performance, although the difference is less pronounced than between $N_f=1$ and $N_f=3$. Overall, the analysis demonstrates that increasing the number of constructed features from $N_f=1$ to $N_f=3$ results in a statistically significant improvement in the model’s accuracy. The comparison between $N_f=1$ and $N_f=2$ is not statistically significant, possibly due to the limited impact of adding only one additional feature. In contrast, the difference between $N_f=2$ and $N_f=3$ highlights that further increasing the number of features continues to enhance performance, albeit to a lesser degree.

Furthermore, to study the accuracy of the measurements in relation to the number of chromosomes ($N_c)$, another experiment was conducted using only the techniques based on Grammatical Evolution and with a variable number of chromosomes, and the results are presented in

Table 6. The effect of the number of chromosomes $N_c$ on the accuracy of methods based on Grammatical Evolution.

	NNC			FC
Year	${\mathit{N}}_{\mathit{c}}=\mathbf{100}$	${\mathit{N}}_{\mathit{c}}=\mathbf{200}$	${\mathit{N}}_{\mathit{c}}=\mathbf{500}$	${\mathit{N}}_{\mathit{c}}=\mathbf{100}$	${\mathit{N}}_{\mathit{c}}=\mathbf{200}$	${\mathit{N}}_{\mathit{c}}=\mathbf{500}$
2014	9.90%	9.78%	9.21%	8.74%	8.77%	8.04%
2015	9.13%	9.07%	9.17%	8.24%	8.30%	7.51%
2016	9.98%	10.18%	10.12%	8.98%	8.92%	8.60%
2017	12.63%	12.63%	12.61%	12.66%	12.71%	12.66%
2018	8.58%	8.80%	9.29%	7.96%	7.85%	7.72%
2019	7.40%	7.48%	7.03%	6.55%	6.69%	6.62%
2020	9.43%	9.51%	9.50%	9.50%	9.50%	9.61%
2021	10.97%	10.98%	10.80%	9.65%	9.90%	9.55%
AVERAGE	9.13%	9.25%	9.38%	8.38%	8.39%	8.25%

.

Studying this table, one finds that there are no large deviations in the average classification error regardless of the number of chromosomes used in Grammatical Evolution.

4. Conclusions

The study examines the application of feature construction techniques for predicting the duration of forest fires using data collected in Greece over a ten-year period. The methods utilized include Principal Component Analysis (PCA), Minimum Redundancy Maximum Relevance (MRMR), and Grammatical Evolution for constructing artificial features and generating neural networks. The analysis focused on meteorological parameters such as temperature, humidity, wind, and rainfall, which significantly influence the behavior of forest fires. The research concluded that the feature construction technique, using grammatical evolution, outperforms other methods in terms of stability and accuracy. The results indicated that this technique achieved the lowest error rate in predicting fire duration compared to other approaches such as PCA, MRMR, and traditional algorithms like Bayes and Adam. While PCA proved effective for dimensionality reduction, it often led to a loss of critical information. MRMR, though capable of identifying relevant features, did not exhibit consistent performance across all datasets. Traditional algorithms like Bayes showed significant variability, with their performance heavily influenced by the data characteristics. Statistical analysis using the Wilcoxon test demonstrated the clear superiority of feature construction over other methods. This advantage can be attributed to the technique’s ability to adapt to the peculiarities of the data, avoiding the information loss observed with other approaches. Specifically, the method excelled in both accuracy and robustness. The study’s findings underscore the potential of advanced machine learning techniques in addressing critical environmental challenges such as forest fires. Future research could focus on integrating data from diverse geographical regions or climatic conditions, developing automated real-time monitoring systems, and combining advanced algorithms for even more efficient analysis. Incorporating social and environmental factors into predictive models could also offer a multidimensional understanding of the causes and spread of fires. Overall, this study highlights the importance of scientific approaches and technology in tackling contemporary challenges posed by climate change and natural disasters.