Capturing the Asymmetry of Pitting Corrosion: An Interpretable Prediction Model Based on Attention-CNN

Abstract

Fossil fuels are crucial to the global energy supply, with pipelines being a vital transportation method. However, these vital assets are highly susceptible to pitting corrosion, an insidious form of degradation that can lead to catastrophic failures. Unlike uniform corrosion, which represents a symmetric form of material loss, pitting corrosion is a highly asymmetric and localized phenomenon. The inherent complexity and asymmetry of this process make its prediction a significant challenge. To address this, this study presents SSA-CNN-Attention, a deep learning model specifically designed to analyze the complex, nonlinear interactions among environmental factors. The model employs a Convolutional Neural Network (CNN) to extract local features, while a crucial attention mechanism allows it to asymmetrically weight the importance of these features, enhancing its ability to recognize intricate interactions. Additionally, the Sparrow Search Algorithm (SSA) optimizes the model’s hyperparameters for improved accuracy and stability. Furthermore, a post hoc interpretability analysis using the LIME framework validates that the model’s learned feature relationships are consistent with established corrosion science, revealing how the model accounts for the asymmetric influence of key variables. The experimental results demonstrate that the proposed model reduces mean squared error (MSE) by 61.3% and mean absolute error (MAE) by 26.6%, while improving the coefficient of determination (R²) by 28.2% compared to traditional CNNs. These findings highlight the model’s superior performance in predicting a fundamentally asymmetric process and provide valuable insights into the underlying corrosion mechanisms.

1. Introduction

Although renewable energy has surged forward in recent years, fossil fuels still command the lion’s share of the world’s energy supply. According to the Energy Institute’s Annual Edition of the Statistical Review of World Energy, coal, oil, and natural gas still supplied about 80% of global energy consumption in 2024 and remain essential to industrial production [1]. In the oil and gas sector, pipeline transport is widely regarded as the most economical, efficient, and technologically mature method, conveying more than 60% of the world’s oil and gas each year [2]. Nevertheless, despite pipeline transportation offering considerable economic advantages, its accompanying safety hazards must not be overlooked. Statistics show that from 1994 to 2013, the United States recorded roughly 745 major pipeline incidents, resulting in 278 deaths, 1059 injuries, and about 110 million USD in direct economic losses. Data from the Pipeline and Hazardous Materials Safety Administration (PHMSA) attributes nearly 20% of these incidents to corrosion [3]. Additionally, analysis by the European Gas Pipeline Incident Data Group (EGIG) also revealed that corrosion was responsible for approximately one-quarter of pipeline incidents [4]. Therefore, corrosion has emerged as one of the primary factors leading to pipeline failures, posing a long-term threat to the safety of pipeline operations. Consequently, it is particularly important to develop an accurate and efficient corrosion prediction model for assessing the current safety conditions of pipelines. Such a model will aid in the timely identification of potential corrosion risks, guide maintenance and inspection decisions, and thereby ensure the stability and safety of oil and gas transportation, preventing major incidents.

Pipeline corrosion manifests in two primary forms: symmetric and asymmetric. Uniform corrosion represents a symmetric process, where material loss occurs evenly across the surface. In contrast, pitting corrosion is a fundamentally asymmetric phenomenon, characterized by localized, stochastic attacks that break the spatial symmetry of the material’s surface. This symmetry breaking makes pitting corrosion far more insidious and difficult to predict than its uniform counterpart, as a single, localized pit can lead to catastrophic failure.

This challenging asymmetry arises from the interplay of chemical, electrochemical, mechanical, and environmental influences. Chemically, the composition of the fluids moving through the pipeline can accelerate degradation. Electrochemically, cathodic and anodic reactions at the pipe surface weaken the metal. Environmentally, factors such as temperature, humidity, and soil characteristics further intensify material loss. Because these elements interact in complex ways, scholars have explored a range of strategies for monitoring buried pipelines under challenging service conditions. Prior to the emergence of artificial intelligence and machine-learning approaches, prediction efforts relied mainly on physical models, empirical equations, and conventional statistical analyses.

In terms of physical models, Nesic et al. proposed an electrochemical model specifically targeting CO₂ corrosion [5], which predicts corrosion rates based on reaction kinetics. Empirical models typically involve fitting equations to experimental or field data without explicitly simulating underlying electrochemical processes. A classic example is the de Waard–Milliam model, which provides a correlation formula relating parameters such as CO₂ partial pressure, temperature, and flow velocity to pipeline corrosion rates. Statistical methods generally employ regression analysis and statistical inference to establish predictive relationships for corrosion rates. Although these traditional methods are straightforward to implement, they exhibit limitations in capturing highly nonlinear interactions among multiple corrosion factors. Empirical models are often only valid within the specific data ranges from which they were developed, making it difficult to extrapolate to new conditions. Regression analyses, while capable of handling large volumes of corrosion data and making predictions based on trend fitting, typically treat input factors as independent variables and rely on simplistic functional forms, failing to accurately reflect the complexity of real-world corrosion phenomena. Thus, traditional models possess significant limitations.

With rapid advancements in computational technology and the continuous accumulation of corrosion data, researchers have gradually shifted their attention toward artificial intelligence and machine learning algorithms to enhance the accuracy and reliability of pipeline corrosion prediction. The primary motivation for adopting machine learning algorithms is to overcome traditional physical and empirical models’ inability to capture complex nonlinear relationships and dynamic features among corrosion factors while simultaneously improving model generalizability. Current research in pipeline corrosion prediction based on artificial intelligence technologies can be categorized into three main types: traditional machine learning models, deep learning models, and hybrid models. Regarding traditional machine learning approaches, Ji et al. applied least squares support vector machines (LS-SVM) to predict stress-concentration factors under elliptical corrosion [6], achieving close agreement with numerical simulations. Li et al. introduced a multi-kernel SVM approach for ranking CO₂/H₂S corrosion severity within natural gas gathering pipelines [7], integrating linear, polynomial, and Gaussian kernels to address data nonlinear separability. Their results showed a prediction accuracy of 66%, significantly outperforming single-kernel methods. Dia et al. comparatively studied gradient boosting machine (GBM) [8], support vector machine (SVM), random forest (RF), K-nearest neighbors (KNN), and multilayer perceptron (MLP), finding RF, SVM, and GBM to yield superior performance. However, despite achieving favorable results under certain conditions, these traditional machine learning methods heavily depend on manual feature extraction, making it challenging to capture complex nonlinearity and time-varying characteristics of corrosion processes, thereby limiting their extrapolation capabilities under conditions involving multi-factor coupling or significant noise fluctuations [9,10].

Compared to traditional machine learning models, deep learning methods can automatically capture complex nonlinear relationships within data, more accurately reflecting pipeline corrosion phenomena. Liu et al. compared classification trees, artificial neural networks, and Bayesian networks [11], demonstrating that Bayesian networks performed best, providing strong interpretability. Du et al. proposed an automatic machine learning (AML)-based corrosion depth prediction model, achieving promising results in pipeline corrosion prediction [12]. Akhlaghi et al. employed deep learning models (generalization model and generalization memory model) to predict maximum pit depth in oil and gas pipelines [13], considering multiple soil characteristics and various protective coating types. Their results indicated superior performance by deep neural networks over previously applied empirical and traditional machine learning models. Additionally, Guang et al. significantly improved prediction accuracy by combining deep neural networks with attention mechanisms. Nevertheless, deep learning models are not without drawbacks [14], exhibiting high data dependency during training, complex training processes, limited interpretability, and vulnerability to local optima during parameter tuning, thus affecting overall model performance [15]. To further enhance predictive performance, researchers have proposed hybrid ensemble models that leverage the advantages of multiple algorithms. Peng et al. introduced a hybrid model for predicting corrosion rates in multiphase pipelines [16], combining Principal Component Analysis (PCA), Chaotic Particle Swarm Optimization (CPSO), and Support Vector Regression (SVR). Li et al. developed a data-driven corrosion prediction model based on the Sparrow Search Algorithm (SSA) and Long Short-Term Memory (LSTM) networks [17]. This approach excels at modeling corrosion as a time-series problem, utilizing LSTM’s powerful ability to capture long-term dependencies from historical monitoring data. Zhu et al. presented a novel pipeline pitting depth prediction model integrating Sparrow Search Algorithm (SSA) [18], Regularized Extreme Learning Machine (RELM), Principal Component Analysis (PCA), and residual correction. This framework effectively capitalizes on the high computational efficiency and strong generalization performance of RELM, making it a rapid and robust predictive tool. Compared with the SSA-RELM model, this new model significantly reduced mean squared error (MSE), mean absolute percentage error (MAPE), and mean absolute error (MAE), demonstrating outstanding performance. Despite the significant improvements in prediction accuracy achieved by these hybrid models, their “black box” nature makes it challenging for engineers to interpret their decision-making processes, thus limiting their practical applicability in engineering scenarios. As Coelho et al. emphasized in their review of machine learning-based corrosion prediction methods [19], interpretability techniques are crucial in corrosion prediction research. Engineers require not only accurate predictions of corrosion severity but also insights into critical factors influencing corrosion to develop effective protective measures and maintenance strategies.

While the predictive accuracy of recent hybrid models has been impressive, their practical adoption in critical engineering fields is often hindered by a significant research gap: their inherent difficulty in interpretation. This challenge does not mean they are completely unexplainable, but rather that their internal decision-making processes are highly opaque. The core of the issue lies in their complex architecture. As input data (e.g., soil properties, operational parameters) passes through multiple nonlinear layers, the original, human-understandable features are transformed into abstract, high-dimensional representations. The final prediction is derived from these complex, learned features, making it exceedingly difficult to trace the output back and quantify the direct influence of any single original input variable. Consequently, these models function as ‘black boxes,’ leaving engineers unable to answer the crucial question of why a certain area is predicted to be at high risk.

In response to the challenge of explaining complex models, Ribeiro et al. introduced the model-agnostic interpretability framework LIME [20], providing a powerful tool for interpreting complex models. This framework generates locally interpretable surrogate models for any classifier, enabling engineers to intuitively understand the decision-making process of the model. The research by Yan et al. further demonstrated that LIME excels in handling features transformed through convolution and pooling layers [21], especially when explaining highly nonlinear models such as CNNs. Compared to SHAP, LIME offers superior advantages in the field of pipeline corrosion. Furthermore, Ben Seghier et al. incorporated a hybrid model with interpretability techniques in their study of predicting the maximum pitting corrosion depth in pipeline external corrosion [22], which not only improved prediction accuracy but also helped engineers understand the model’s prediction logic and feature contributions, further advancing the field. Based on the current state of research, to address the limitations in feature extraction, feature importance evaluation, and model interpretability, a hybrid prediction model is proposed, which integrates Convolutional Neural Networks (CNN), attention mechanisms, the Sparrow Search Algorithm (SSA), and the LIME interpretability framework. Specifically, the model utilizes CNN to automatically capture deep features of corrosion data, thus avoiding the incompleteness of traditional manual feature extraction. The introduced attention mechanism enhances the model’s ability to select features, not only improving prediction accuracy but also enhancing interpretability. SSA is employed to efficiently optimize the model’s hyperparameters, effectively avoiding local optima and further improving the model’s generalization performance and stability. Finally, the LIME framework is applied not to explain inherent mechanisms but to provide post hoc local explanations. This allows for a crucial validation step: verifying whether the data-driven relationships learned by the ‘black-box’ model are physically meaningful and align with established corrosion science, thereby increasing the model’s transparency and trustworthiness for engineering applications.

In this study, a pipeline-corrosion prediction framework was constructed by sequentially integrating deep learning, attention enhancement, swarm-based hyperparameter optimization and local interpretability. A Convolutional Neural Network (CNN) first generated an initial estimate of corrosion severity from raw chemo-electro-mechanical and environmental variables. An attention mechanism was then embedded to heighten the network’s sensitivity to the intricate feature interactions that underpin corrosion processes, thereby refining the preliminary forecast. The Sparrow Search Algorithm (SSA) subsequently tuned convolutional, attention, and learning parameters in a data-adaptive manner, improving generalization and predictive accuracy under complex operating conditions. Finally, the Local Interpretable Model-agnostic Explanations (LIME) technique quantified the influence of each input attribute on the model’s predictions, providing engineers with transparent, mechanism-oriented insight into the model’s decisions.

The remainder of this paper is organized as follows: Section 2 provides an overview of the methods employed—namely the Sparrow Search Algorithm (SSA), Convolutional Neural Network (CNN), attention mechanism, and Local Interpretable Model-agnostic Explanations (LIME). Section 3 introduces the evaluation criteria. Section 4 presents a case study demonstrating the feasibility and effectiveness of the proposed approach. The paper is concluded in Section 5.

2. Developed Methodology

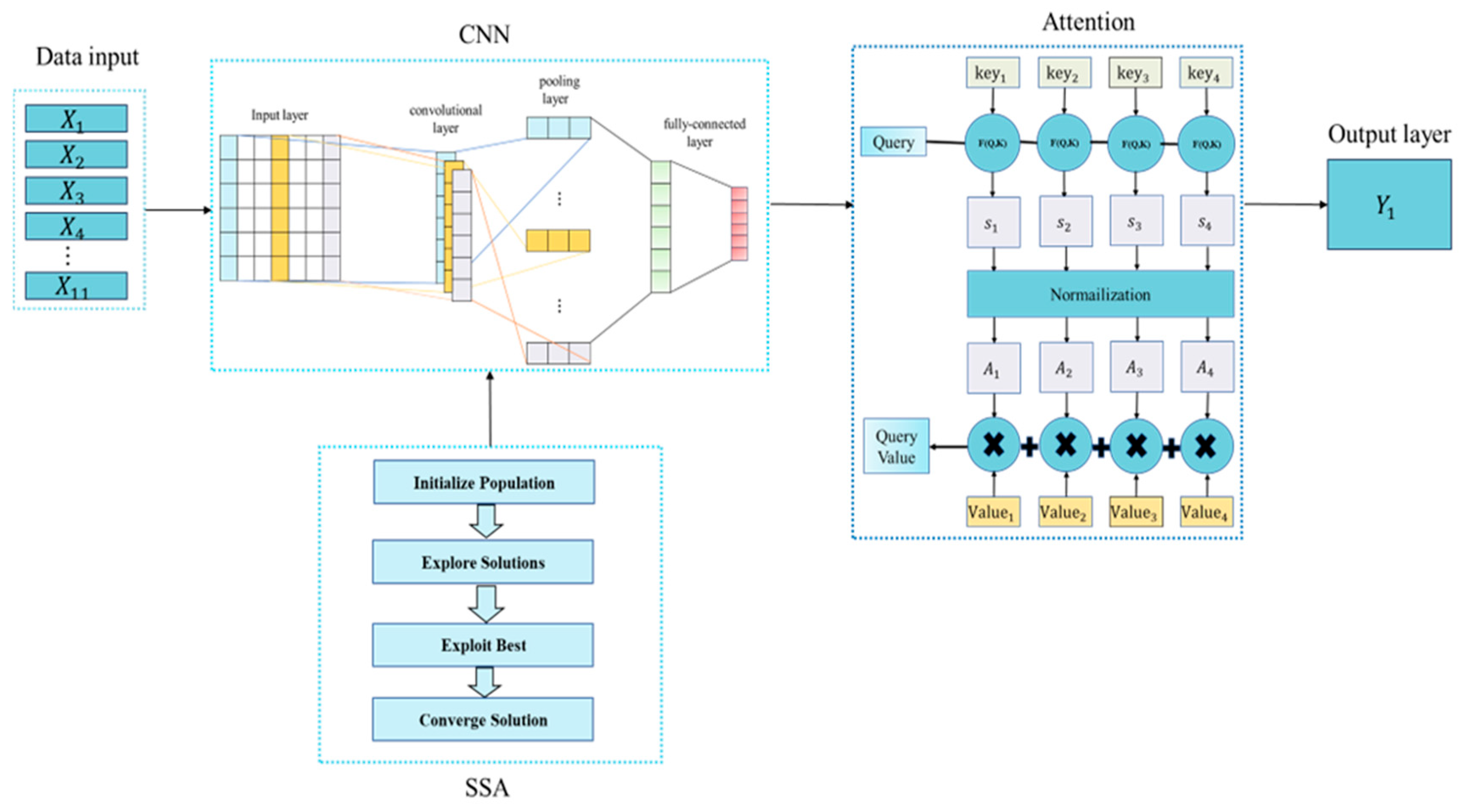
This section proposes a hybrid intelligent framework for pipeline-pitting-depth prediction, as illustrated in Figure 1. The framework first employs a CNN to mine high-level corrosion features from the multivariate monitoring data, then inserts an attention module to adaptively highlight the most influential feature maps. To further improve accuracy and stability, the Sparrow Search Algorithm (SSA) is wrapped around the CNN-Attention model to autonomously tune key hyperparameters such as learning rate, filter number, and batch size. The detailed structure is shown below.

2.1. SSA

The Sparrow Search Algorithm (SSA) simulates the foraging behavior of sparrow populations in nature, treating each sparrow’s position as a candidate solution. During foraging, sparrows assume three roles:

Discoverers: These individuals actively search for food sources and lead the group to them.

Joiners: They follow the discoverers to obtain food, enhancing their own fitness by exploiting the discovered resources.

Sentinels: These sparrows monitor the environment for potential threats, alerting the group to danger.

The roles of discoverers and joiners are dynamic and can interchange during the search process, maintaining a constant ratio within the population. Discoverers, as the group’s leaders, typically possess higher fitness levels and explore broader areas. Joiners, by following discoverers, improve their own fitness, with some even observing and opportunistically competing for resources to enhance their foraging success. Additionally, approximately 10–20% of the population is designated as sentinels. These individuals continuously monitor the environment, and upon detecting potential threats, they issue alarm signals, prompting the group to take evasive actions to mitigate predation risks [23].

During the iterative update phase of the algorithm, the position of the discoverer can be adjusted using the following formula:

$$X_{i,j}^{t+1}=\left\{\begin{array}{l}{X}_{i,j}^t\cdot \exp (-{\displaystyle \frac{i}{\alpha \cdot ite{r}_{\max }}})\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{1em}{R}_2<ST\\ X_{i,j}^{t+1}+Q\cdot L\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{1em}{R}_2\ge ST\end{array}\right.$$

(1)

In the formula, t represents the current iteration number; $ite{r}_{\max }$ represents a constant, indicating the maximum number of iterations; $X_{i,j}$ represents the position of the i-th sparrow in the j-th dimension at iteration; $\alpha \in \left(0, 1\right]$ represents a random number; $R_2$ and $ST$ represent the alarm value and safety value, respectively.

Q is a random number following a normal distribution, and L is a row vector with all elements equal to 1. When $R_2<ST$, it indicates that there are no predators in the current foraging environment, and the discoverer can perform an extensive search. When $R_2\ge ST$, it indicates that some sparrows have detected predators and have alerted the group, prompting all sparrows to quickly fly to safer places to forage.

The position update formula for the joiner is as follows:

$$X_{i,j}^{t+1}=\left\{\begin{array}{l}Q\cdot \exp ({\displaystyle \frac{X_{\mathrm{worst}}^t-X_{i,j}^t}{i^2}})\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{1em}i>P/2\\ X_b^{t+1}+\left|X_{i,j}^t-X_b^{t+1}\right|\cdot A^{+}\cdot L\hspace{1em}\hspace{1em} \mathrm{otherwise}\end{array}\right.$$

(2)

In the formula, $X_b$ represents the optimal position of the current discoverer; $X_{worst}^t$ represents the global worst position; A is a row vector with elements randomly assigned as 1 or −1. When $i>P/2$, the joiner will randomly update its position following a normal distribution; otherwise, the joiner will move towards the current optimal position and participate in searching for positions with better fitness values.

The randomly selected sentinel position update is described as follows:

$$X_{i,j}^{t+1}=\left\{\begin{array}{l}{X}_{\mathrm{best}}^t+\beta \cdot \left|X_{i,j}^t-X_{\mathrm{best}}^t\right|\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} if\hspace{1em}{f}_i>f_g\\ X_{i,j}^t+K\cdot \left({\displaystyle \frac{\left|X_{i,j}^t-X_{\mathrm{worst}}^t\right|}{(f_i-f_w)+\epsilon }}\right)\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{1em}{f}_i=f_g\end{array}\right.$$

(3)

In the formula, $X_{\mathrm{best}}^t$ is the current global optimal position; $X_{worst}^t$ is the current global worst position; $\beta$ is the step size control parameter; $f_i$ is the fitness value of the current sparrow individual; $f_g$ and $f_w$ are the current best and worst fitness values, respectively; and $\epsilon$ is a constant that is infinitesimally close to zero. The sentinels move from poorer fitness positions toward the current best fitness position.

2.2. CNN

Convolutional Neural Networks (CNN) are deep learning models known for their efficient feature extraction capabilities [24]. In the context of pipeline corrosion prediction, the task is characterized by complex, nonlinear interactions among multivariate environmental parameters such as soil resistivity, pH, and temperature. To address this, our study introduces a novel approach by conceptualizing the one-dimensional vector of 11 environmental parameters as a “feature pseudo-sequence”. This conceptualization allows the convolutional kernel to operate along this feature dimension, effectively discerning local “combinatorial effects” and “interaction patterns” among adjacent features.

To operationalize this concept, a tailored CNN architecture was developed, as illustrated in Figure 2. The architecture is composed of an input layer, a convolutional layer, a global average pooling layer, and a fully connected layer. Within this framework, the convolutional layers operate synergistically to distill highly informative, high-level features from the input data. Subsequently, the global average pooling and fully connected layers aggregate these features to generate the final prediction for pitting depth.

The Rectified Linear Unit (ReLU) function is used as the activation function for the network, and pooling layers are employed to reduce the dimensionality of the data, thus extracting effective features and mitigating the risk of model overfitting. When the input data is denoted as X, the computation in the convolutional layer can be expressed as Equation (4):

$$h_i=f\left(W_i\odot X+b_i\right)$$

(4)

where $h_i$ is the feature map output of the i-th layer; $f(·)$ is the activation function; $W_i$ is the weight vector of the convolutional kernel; and $b_i$ is the bias vector.

The pooling layer is used to reduce the dimensionality and computational load of the feature map while retaining important features. The pooling operation is defined as:

$$O=maxCo{n}_k$$

(5)

where O represents the output of the pooling layer, and ${Con}_k$ is the input to the pooling layer. By utilizing CNN, complex nonlinear mappings in the data can be accurately captured through local convolution operations, allowing for a more precise reflection of pipeline corrosion phenomena. The performance of the CNN is shown in Figure 2:

2.3. Attention

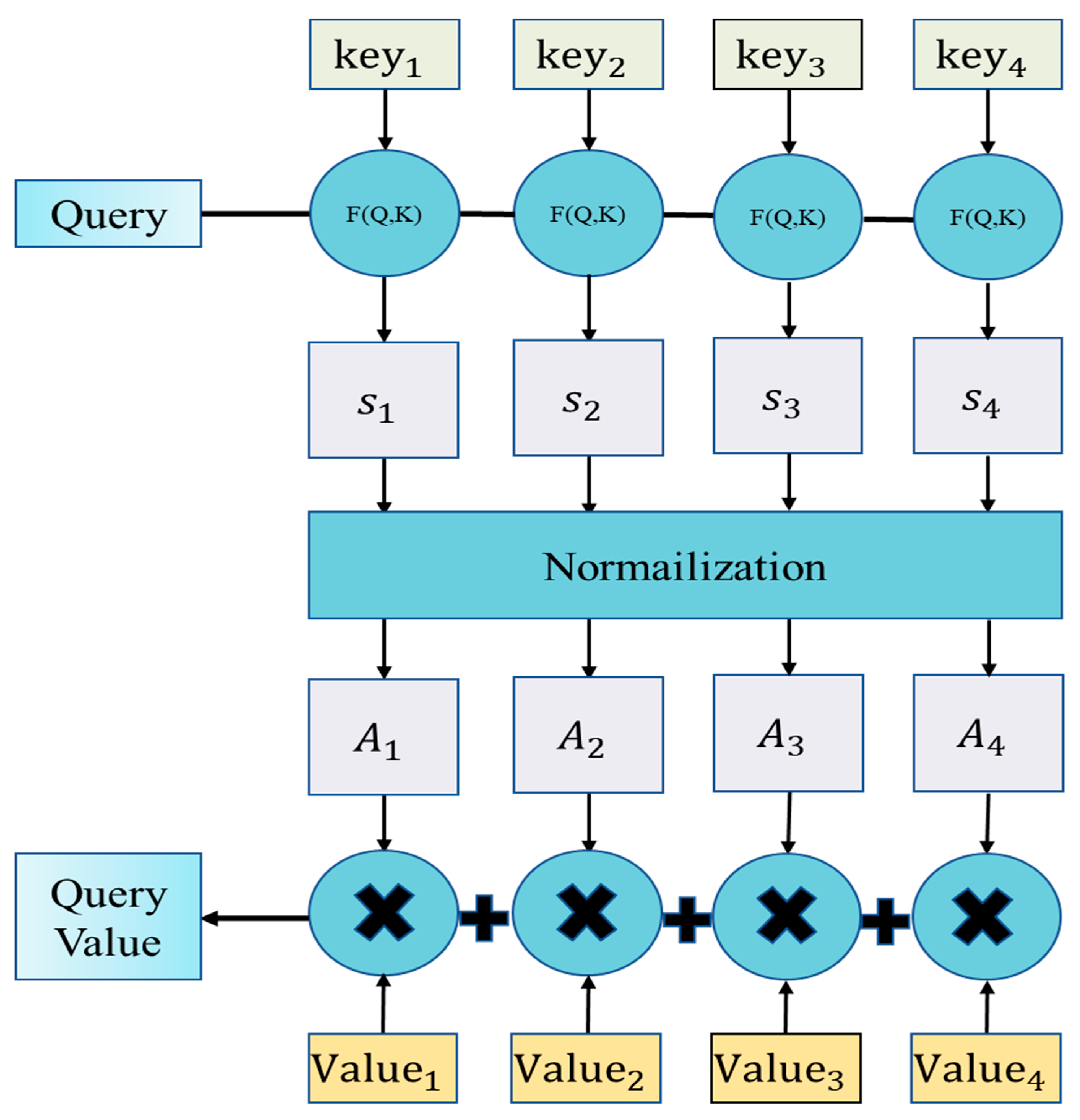
The attention mechanism aims to simulate the selective focus of human perception, enabling the model to assign weights to different features or channels of input data, thereby enhancing the overall performance of the model. In the model proposed in this study, an attention mechanism is introduced that combines global average pooling and multi-layer fully connected neural networks to weight the importance of input features [25]. The process is as follows:

First, let the output of the convolutional layers be the feature map $X\in R^{L*C}$, where L is the sequence length and C is the number of feature channels. Q, K, and V are all derived from this same input feature map X through linear projections:

$$Q=X{W}_Q,K=X{W}_K,V=X{W}_V$$

(6)

where $W_Q$, $W_K$, and $W_V$ are learnable weight matrices implemented as dense layers.

The attention scores, which measure the compatibility between each Query and all Keys, are then computed. This is achieved using the scaled dot-product operation, as formulated in Equation (7):

$$\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}={\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}$$

(7)

The dot product is scaled by the square root of the key dimension, $d_k$, a technique employed to prevent the gradients from becoming too small during training and thus stabilize the learning process. Subsequently, a SoftMax function is applied along the key dimension of the scores to convert them into attention weights, denoted as α. This normalization creates a probability distribution, ensuring the weights are positive and sum to one. The calculation is defined as follows:

$$\alpha =\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}\right)$$

(8)

The output of the attention layer $X_{att}$, is computed as the weighted sum of the Value vectors, formulated as:

$$X_{att}=\alpha V=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V$$

(9)

Finally, the attention-enhanced feature map $X_{att}$ is passed to a prediction head to generate the final output. This process is executed in a sequence of steps. First, a global average pooling layer aggregates the feature map into a fixed-size vector, denoted as $h_{pool}$. Subsequently, this vector is transformed by a hidden fully connected layer with a ReLU activation function, yielding an intermediate feature representation, $h_{hidden}$. Finally, an output fully connected layer with a linear activation maps this hidden representation to the final pitting depth prediction, $d_{pred}$. This sequence of computations is defined by Equation (10):

$$\begin{array}{c}{h}_{pool}=\mathrm{G}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}\mathrm{A}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{P}\mathrm{o}\mathrm{o}\mathrm{l}\left(X_{att}\right)\\ h_{hidden}=\mathrm{ReLU}\left(h_{pool}{W}_h+b_h\right)\\ d_{pred}=h_{hidden}{W}_f+b_f \end{array}$$

(10)

In these equations, $W_h$ and $b_h$ are the weight matrix and bias vector for the hidden layer, while $W_f$ and $b_f$ are those for the final output layer. It is important to note that these parameters are not predefined constants; they are learnable parameters that are automatically optimized during the model training process through backpropagation to minimize the loss function.

During training, the model’s parameters are optimized by minimizing the MSE, which serves as the loss function, as defined in Equation (10):

$$\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N} (d_{true}^{\left(i\right)}-d_{pred}^{\left(i\right)}{)}^2$$

(11)

The proposed attention mechanism is illustrated in Figure 3.

2.4. SSA-CNN-Attention

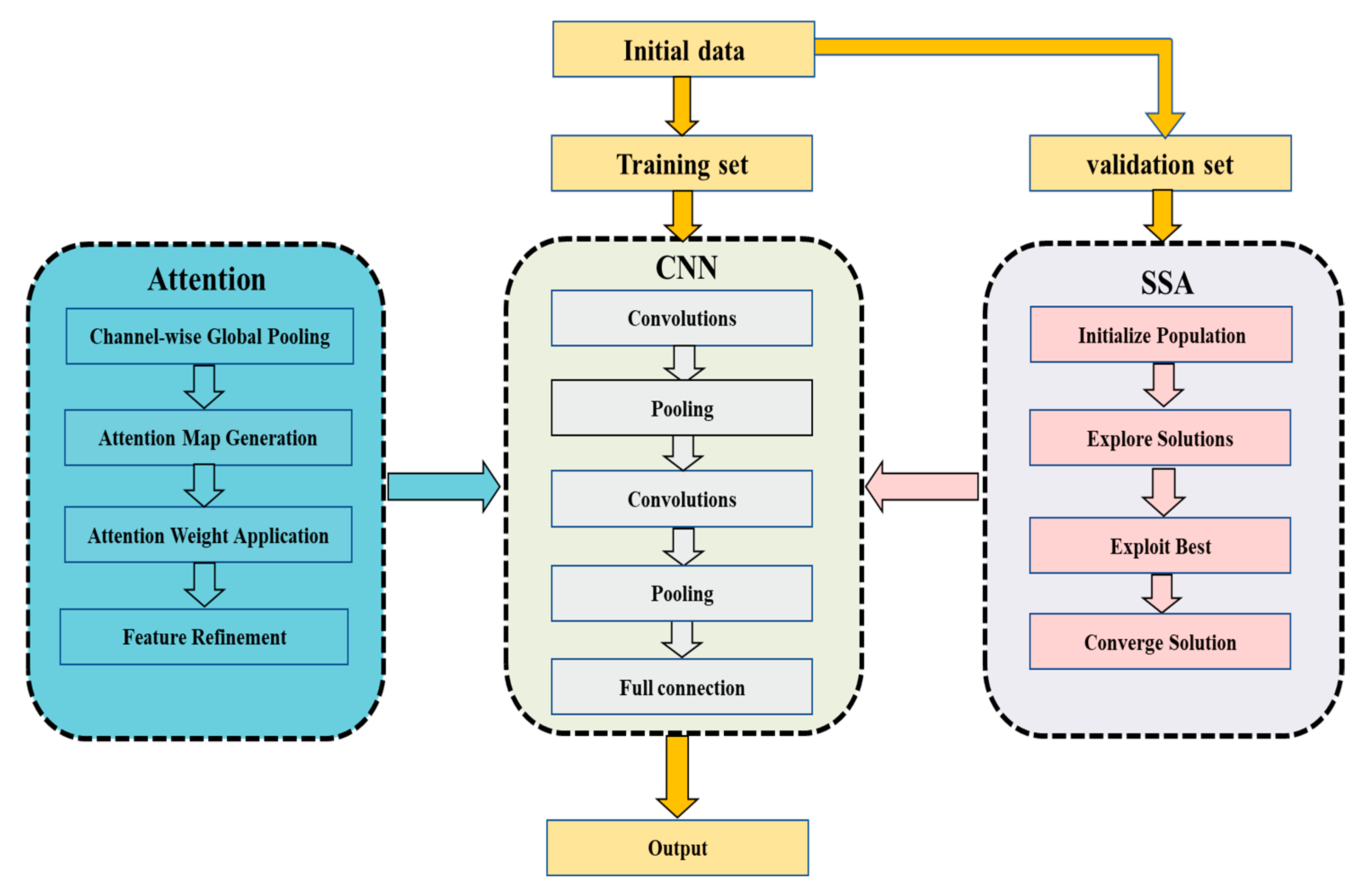
Based on the foregoing theory, this paper proposes the SSA-CNN-Attention model by integrating three data-driven methods: SSA, CNN, and Attention. The detailed procedure is as follows:

Step 1: Key environmental factors—redox potential, pH value, moisture content, and resistivity—are selected as input features according to relevant standards and measured data, with corrosion rate or corrosion depth defined as the model’s output variable. The raw data are then cleaned and normalized, and split into training, validation, and test sets in a 6:2:2 ratio.

Step 2: A convolutional neural network (CNN) automatically extracts deep features from the processed data. An attention mechanism subsequently adaptively adjusts the weights of these features, enabling the network to emphasize the most critical factors for corrosion prediction and thereby enhance overall predictive performance.

Step 3: The Sparrow Search Algorithm (SSA) is employed to automatically optimize key hyperparameters of the CNN-Attention model—such as the number of convolutional kernels, network depth, and learning rate—to avoid convergence to local optima and further improve the model’s generalization ability.

Step 4: The trained SSA-CNN-Attention model is applied to the test set to generate predictions of corrosion rate or corrosion depth.

Step 5: Model performance is comprehensively evaluated using mean squared error (MSE), mean absolute error (MAE), and the coefficient of determination (R²). Results are compared against those from existing benchmark models to validate the accuracy and robustness of the proposed SSA-CNN-Attention approach.

Figure 4 presents the full workflow—data processing, model optimization and training, sequential modeling, and prediction—underlying the SSA-CNN-Attention framework.

Based on the framework, the prediction model is outlined in Algorithm 1.

Algorithm 1: Predict the pitting corrosion based on the SSA-CNN-Attention

Input: The corrosion dataset Output: ${d }_{pred}$ 1. Divide the dataset into train, validation, and test set 2. Construct the CNN -Attention Model 3. Optimize the CNN-Attention model using the SSA to find the best hyperparameters on the validation set 4. Train the optimized CNN-Attention Model 5. for epoch from 1 to Total_Epochs do 6.       for each batch in train set do 7.             Compute the predicted pitting depth in Equation (10); 8. //**Loss Calculation & Backward Pass** 9.             Compute the loss function in Equation (11); 10.           Update model weights using backpropagation based on ‘loss’ 11.      end for 12. end for 13. //**Final predication** 14. Apply the trained model to the test set to obtain the final predictions ${d }_{pred}$ 15. return ${d }_{pred}$

2.5. Local Interpretable Model-Agnostic Explanations

The Local Interpretable Model-Agnostic Explanations (LIME) method provides explanations for complex machine learning model predictions by constructing local surrogate models. The core idea is to perturb samples and fit interpretable proxy models, revealing the decision logic of a black-box model within the local neighborhood of specific samples. Specifically, the workflow of LIME can be divided into the following three stages [26]:

First, perturbation sampling is performed n times within the feature space of the target sample x, generating a synthetic sample set $D=\left\{\begin{array}{c}(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\end{array}\right\}$, where n represents the specified number of perturbations. Perturbed sample $x_i^{\prime }$ is represented using an interpretable data representation method, with weights assigned based on its similarity to x to reflect its local importance.

Next, an optimization algorithm is applied to select the best surrogate model g from the interpretable model space G (such as linear regression, decision trees, etc.). The generated dataset from the perturbed features of the target sample is fitted using the model g, thereby approximating a prediction model for the perturbed dataset. The fitted model g is then analyzed; for instance, in the case of a linear model, its non-zero dimensional coefficients are analyzed. By utilizing the interpretability of the surrogate model itself, the feature importance of the target user’s perturbed dataset is predicted, which is then used to analyze the feature importance of model f within the current local neighborhood. The objective function is expressed as follows:

$$\xi \left(x\right)=arg \underset{g\in G}{lim} L(f,g,{\pi }_x)+\Omega (g)$$

(12)

In this formula, ${\pi }_x\left(z\right)$ is a proximity measure between a perturbed instance z and x, f represents the original model (i.e., the model to be explained); g is a simple model, and G is a set of simple models, such as all possible linear models. Ω(g) represents the complexity of model. L(f, g, π_x) is a measure of the inaccuracy of g approximating f in the local neighborhood defined by x. The specific workflow diagram is shown in Figure 5.

3. Comparative Criteria

Performance metrics are crucial for evaluating its overall performance. These metrics provide a means to measure how well the model performs and allow for meaningful comparisons between different models. In this study, Mean Squared Error (MSE), Mean Absolute Error (MAE), and Coefficient of Determination (R²) are chosen as the key performance indicators.

$$MSE={\displaystyle \frac{1}{m}}{\displaystyle \sum _{i=1}^m} (y_i-{\widehat{y}}_i{)}^2$$

(13)

$$MAE={\displaystyle \frac{1}{m}}{\displaystyle \sum _{i=1}^m} \left|y_i-{\widehat{y}}_i\right|$$

(14)

$$R^2=1-{\displaystyle \frac{{\displaystyle {\sum }_{i=1}^m} (y_i-{\widehat{y}}_i{)}^2}{{\displaystyle {\sum }_{i=1}^m} (y_i-\overline{y}{)}^2}}.$$

(15)

In the formula, $y_i$ represents the observed value for the i-th sample; ${\widehat{y}}_i$ represents the model’s predicted value for that same sample; $\overline{y}$ denotes the arithmetic mean of all observed values; m is the total number of observations.

4. Case Study

4.1. Data Description

A comprehensive and scientifically rigorous dataset is crucial for enhancing the accuracy of pipeline pitting corrosion prediction models. Velázquez et al. developed a publicly available corrosion database that has been widely recognized and applied in related fields due to its thorough and scientific data records [27]. This dataset encompasses 259 sets of actual observations of maximum pitting corrosion depths in buried pipelines, along with corresponding soil properties and other pipeline attribute information. Key features include soil resistivity (re), water content (wc), bulk density (bd), dissolved chloride (cc), bicarbonate (bc), sulfate (sc) ion concentrations, pipeline age (t), redox potential (rp), pH value, and the field-measured maximum pitting depth (dmax). A detailed description of each feature is provided in

Table 1. Descriptive statistical table of the database.

	t	ph	pp	re	wc	bd	cc	bc	sc	rp	dmax
Unit	years	-	mV	Ω·m	%	g/cm3	(ppm)	(ppm)	(ppm)	mV	mm
Xmax	50	9.88	−0.42	399.5	66	1.56	672.7	195.2	1370.2	348	13.44
Xmin	5	4.14	−1.97	1.9	8.8	1.1	1	1	1	2.1	0.41
Xmean	22.99	6.13	−0.88	50.15	23.90	1.30	47.73	19.67	152.97	167.04	2.02

.

In this database, soil resistivity (re) serves as an important indicator of soil conductivity. Lower values typically indicate higher moisture and dissolved ion content, facilitating electrochemical reactions and accelerating the oxidation of metal surfaces. Soil moisture content (wc) provides the necessary aqueous medium for these chemical reactions, promoting the migration and local accumulation of corrosive ions, such as chloride ions. Bulk density (bd) describes the compaction of soil. Under high-density conditions, reduced porosity may limit oxygen diffusion, altering the rate of localized electrochemical reactions. Dissolved chloride (cc), a primary factor in disrupting the metal passivation layer, directly weakens the protective properties of the metal surface, leading to pitting corrosion. Bicarbonate (bc) and sulfate (sc) ions play dual roles in regulating soil buffering capacity and chemical stability. Under specific conditions, they can either promote the formation of protective passive films or disrupt existing protective layers, potentially generating more corrosive sulfides under the influence of sulfate-reducing bacteria. Additionally, pipeline service life (t) reflects the extent of cumulative corrosion effects. Over time, the passivation film on the pipeline surface may gradually degrade, increasing corrosion risk. Redox potential (rp) reveals the oxidative or reductive characteristics of the environment, directly influencing the dominant corrosion mechanism. Soil pH regulates the acid-base balance of the surrounding environment, determining the intensity of the corrosion process. The dataset is complete and contains no missing values. Therefore, no preprocessing steps, such as data imputation or normalization, were performed, and the raw data was used directly for model training and evaluation. The data were randomly divided into training, validation, and test sets in a 6:2:2 ratio, with 60% allocated to the training set, 20% to the validation set, and 20% to the test set.

4.2. Hyperparameter Setting

To achieve optimal performance of the CNN model, we systematically calibrated its hyperparameters using the Sparrow Search Algorithm (SSA). Recognizing the prohibitive computational cost of a comprehensive search, we identified and selected five hyperparameters with the most significant influence on model accuracy for targeted optimization. These five parameters were: the number of filters in the first convolutional layer (conv1_filters), the number of filters in the second convolutional layer (conv2_filters), the number of neurons in the dense layer (dense_units), the learning rate (learning_rate), and the batch size (batch_size). After determining the core model hyperparameters that need to be optimized, we then need to configure a set of effective parameters for the Sparrow Search Algorithm (SSA) itself, which is responsible for performing this optimization. The performance of the SSA is quite sensitive to its parameter settings. Therefore, choosing a suitable set of parameters for SSA is a key prerequisite for ensuring the success of the entire hyperparameter optimization process.

The SSA was configured with the following parameters to ensure a robust and efficient search of the hyperparameter space

A maximum generation number (MaxIter) of 500 was set to allow sufficient time for the algorithm to explore the complex search space and converge to a global optimum, as preliminary tests indicated this provided a good balance between computational expense and solution quality. A population size (POP) of 20 was chosen to maintain adequate genetic diversity while remaining computationally feasible for the defined number of generations. The discoverer ratio (DR) was set to 0.2, following recommendations from the foundational SSA literature, to balance global exploration and local exploitation

A high awareness sparrow ratio (SR) of 0.8 and a low safety threshold (ST) of 0.1 were employed to enhance the algorithm’s ability to escape local optima by making the population highly sensitive to stagnation threats and triggering frequent anti-predation dispersal behavior. The complete set of optimization parameters is summarized in

Table 2. Initial parameters of the optimization algorithm.

Parameter	Value
Max generations (Maxtier)	500
Population size (POP)	20
Discoverer ratio (DR)	0.2
Aware Sparrow Ratio (SR)	0.8
Safety threshold (ST)	0.1

.

Beyond the five optimized parameters of CNN mentioned above, the remaining architectural hyperparameters of the Convolutional Neural Network (CNN) were selected based on widely adopted best practices in deep learning for computer vision tasks to establish a strong and comparable baseline

A small 3 × 3 convolution kernel size was used, as it is the standard and most efficient size in modern CNNs (e.g., VGGNet), capable of capturing fine-grained features while keeping the number of parameters manageable. The convolution stride was fixed at 1 to process all spatial locations of the input feature map. For pooling layers, a 2 × 2 kernel with a stride of 2 was adopted to downsample feature maps effectively, reducing computational complexity and introducing a degree of spatial invariance. Max pooling was selected over average pooling for its effectiveness in capturing the most salient features (the highest activation). The ReLU activation function was chosen for its ability to combat the vanishing gradient problem and its computational efficiency. Network weights were initialized using the Xavier (Glorot) method to promote stable gradient flow during training. The Adam optimizer was selected for its adaptive learning rate capabilities, which typically lead to faster convergence. The model was trained for 10 epochs, as validation performance plateaued beyond this point, indicating convergence and mitigating the risk of overfitting. These fixed hyperparameters are detailed in

Table 3. Hyperparameter settings for CNN model.

Hyperparameter	Setting
Convolution kernel size	3 × 3
Convolution stride size	1
Pooling kernel size	2 × 2
Pooling stride size	2
Pooling type	Max
Activation function	ReLU
Weight initialization	Xavier
Optimization function	Adam
Training epochs	10

.

The optimization process begins by initializing a population of sparrows, where each sparrow’s position in the search space represents a unique set of hyperparameters for the CNN-Attention model. The initial values for these hyperparameters are randomly sampled from the predefined ranges specified in

Table 4. Hyperparameter ranges for the optimization problem.

Hyperparameter	Range
conv1_filters	[16, 32, 64]
conv2_filters	[32, 64, 128]
dense_units	[64, 128, 256, 512]
Learning rate	[0.0001, 0.01]
batch_size	[16, 32, 64, 128]

.

In each iteration, the fitness of every sparrow (i.e., each hyperparameter set) is evaluated. The fitness function is defined by the performance of the corresponding CNN-Attention model on a validation dataset; in our case, we use model accuracy as the primary fitness metric. The SSA then updates the positions of the sparrows according to their roles (producers, scroungers, or scouts), guiding the search towards more promising regions of the hyperparameter space. This iterative process continues until the maximum number of generations is reached. The final output of the algorithm is the set of hyperparameters that yielded the best fitness value throughout the search, which is then used to construct the final, optimized model for testing. The initial parameters governing the behavior of the SSA are detailed in Table 2.

To formalize this optimization workflow, the complete procedure for leveraging the SSA to optimize the optimal hyperparameters for our SSA-CNN-Attention model is detailed in Algorithm 2. This algorithm provides a step-by-step blueprint of the entire process, from initialization to the final selection of the best hyperparameter set.

Algorithm 2: Optimization of CNN-Attention model using the SSA metaheuristic

Input: Bounds ← Hyperparameter ranges list/* From Table 4 */ Maxtier, POP, DR, SR, ST/∗ Initial SSA parameters from Table 2 ∗/ Output: $X_{best}$ (the best hyperparameters obtained) ${\mathrm{P}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}^0$← Initialize POP individuals randomly within Bounds. Evaluate the fitness of each individual in ${\mathrm{P}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}^0$. $X_{best}$, $f_{best}$ ← Find the individual with the best (minimum) fitness in ${\mathrm{P}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}^0$. for g = 0 to Maxtier—1 do Sort ${\mathrm{P}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}^g$ by fitness to identify the current best ($X_{currentbest}$) and worst ($X_{worst}$). /* Update positions based on roles/ Update the top DR × POP individuals (Discoverers) using Equation (1). Update the remaining individuals (Joiners) using Equation (2). Randomly select SR × POP individuals (Sentinels) and update their positions using Equation (3). /Evaluate the new generation and update global best */ ${\mathrm{P}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}^{g+1}$ ← The set of all newly updated positions. Clip all positions in ${\mathrm{P}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}^{g+1}$ to stay within Bounds. Evaluate the fitness of each individual in ${\mathrm{P}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}^{g+1}$. $f_{currentmin}$, $X_{currentmin}$ ← Find the best individual in the new ${\mathrm{P}\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}^{g+1}$. if $f_{currentmin}$ < $f_{bestthen}$   $f_{best}$ ← $f_{currentmin}$   $X_{best}$ ← $X_{currentmin}$ end if end for return $X_{best}$

4.3. Comparison of Model Prediction

In this study, comparative experiments against multiple alternative models were performed to verify the effectiveness of the proposed SSA-CNN-Attention hybrid prediction model. These included three individual models (ANN, XGBoost, CNN) and three hybrid models (SSA-CNN, CNN-Attention, SSA-CNN-Attention). The hyperparameters optimized by the SSA include the number of filters in convolution layer 1, the number of filters in convolution layer 2, the number of units in the fully connected layer, the batch size, and the learning rate.

Three evaluation metrics (MSE, MAE, R²) were used to comprehensively assess the model’s predictive performance, which effectively displayed the differences between predicted and actual values.

Table 5. Comparison of Corrosion Prediction Capabilities.

Model	MSE	MAE	${\mathbf{R}}^2$
ANN	1.261	0.711	0.539
XGBOOST	0.991	0.599	0.638
CNN	0.862	0.621	0.685
SSA-CNN	0.502	0.532	0.817
CNN-Attention	0.414	0.478	0.849
SSA-CNN-Attention	0.334	0.456	0.8783

compares the prediction results of the six models. According to the evaluation results, traditional models such as the fully connected neural network (ANN) and the tree-based model XGBoost performed relatively poorly, with higher MSE and MAE values compared to the CNN-based models, and lower R² values, indicating limitations in capturing the inherent complex relationships within the data. In contrast, while CNN was originally used for image processing, its convolutional layers effectively extract local features and capture implicit spatiotemporal dependencies, demonstrating strong modeling capability in this numerical regression task.

Building upon this, introducing SSA for hyperparameter optimization (SSA-CNN) further reduced the model’s error. After automatic tuning, the model’s MSE and MAE significantly decreased, and the R² value increased notably, reflecting the crucial role of tuning key parameters, such as architecture and learning rate, in enhancing prediction accuracy. Furthermore, by combining the attention mechanism with CNN, the model not only extracted effective features globally but also adaptively assigned different weights to each feature, thereby emphasizing the most crucial information affecting the prediction results.

When both SSA hyperparameter optimization and the attention mechanism were integrated (SSA-CNN-Attention), the model achieved optimal performance, with the lowest MSE, smallest MAE, and highest R². This shows that SSA optimization improved the model parameters, enhancing overall fitting capability, while the attention mechanism further strengthened the model’s ability to capture key data patterns at the feature extraction level. Overall, using CNN as the base architecture and incorporating attention mechanisms and parameter optimization techniques effectively addressed the model’s deficiencies in feature weighting and hyperparameter sensitivity, resulting in the best performance on complex numerical regression problems. This result further validates that combining optimization algorithms, attention mechanisms, and deep learning methods can significantly improve the accuracy of pipeline corrosion prediction.

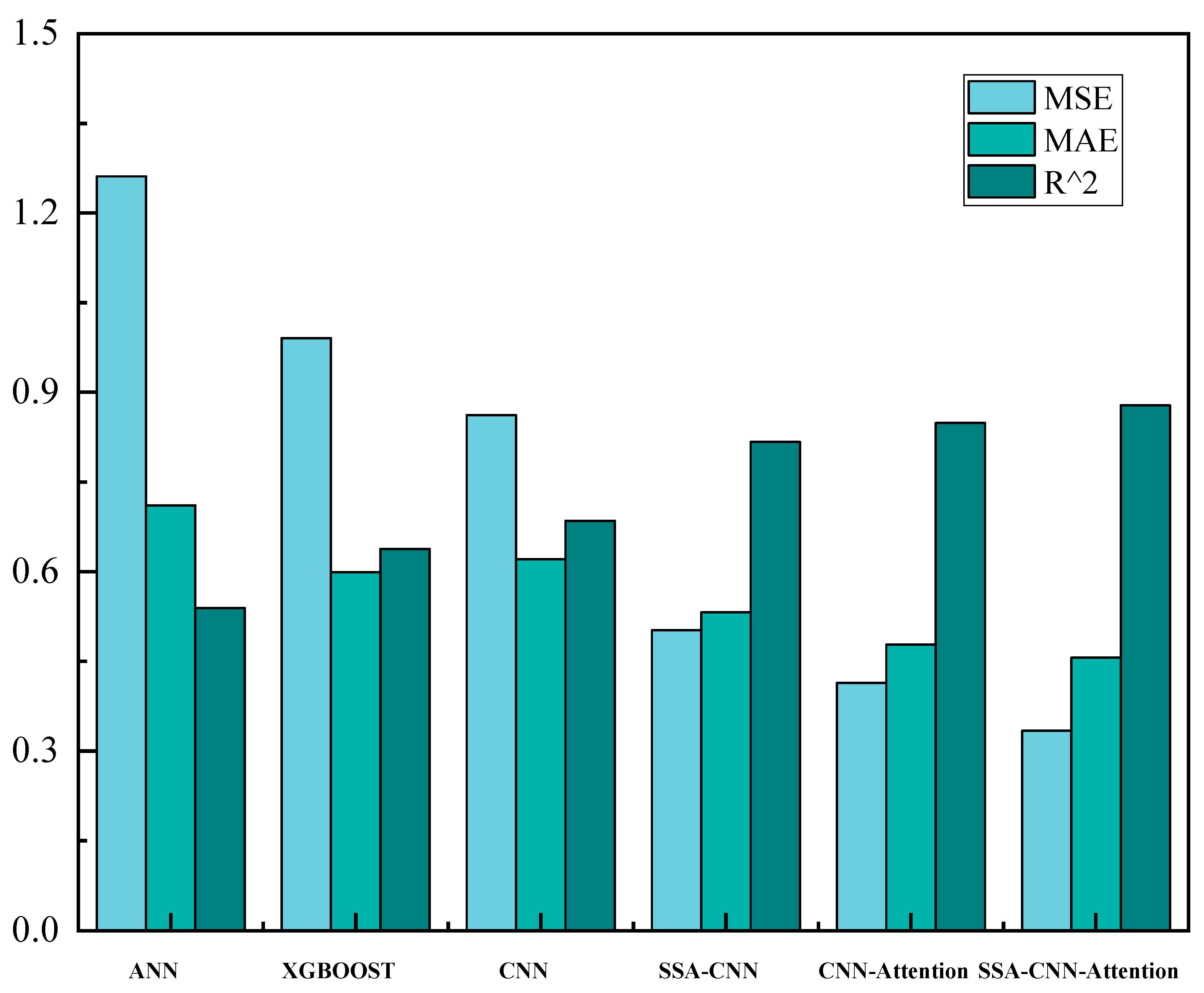
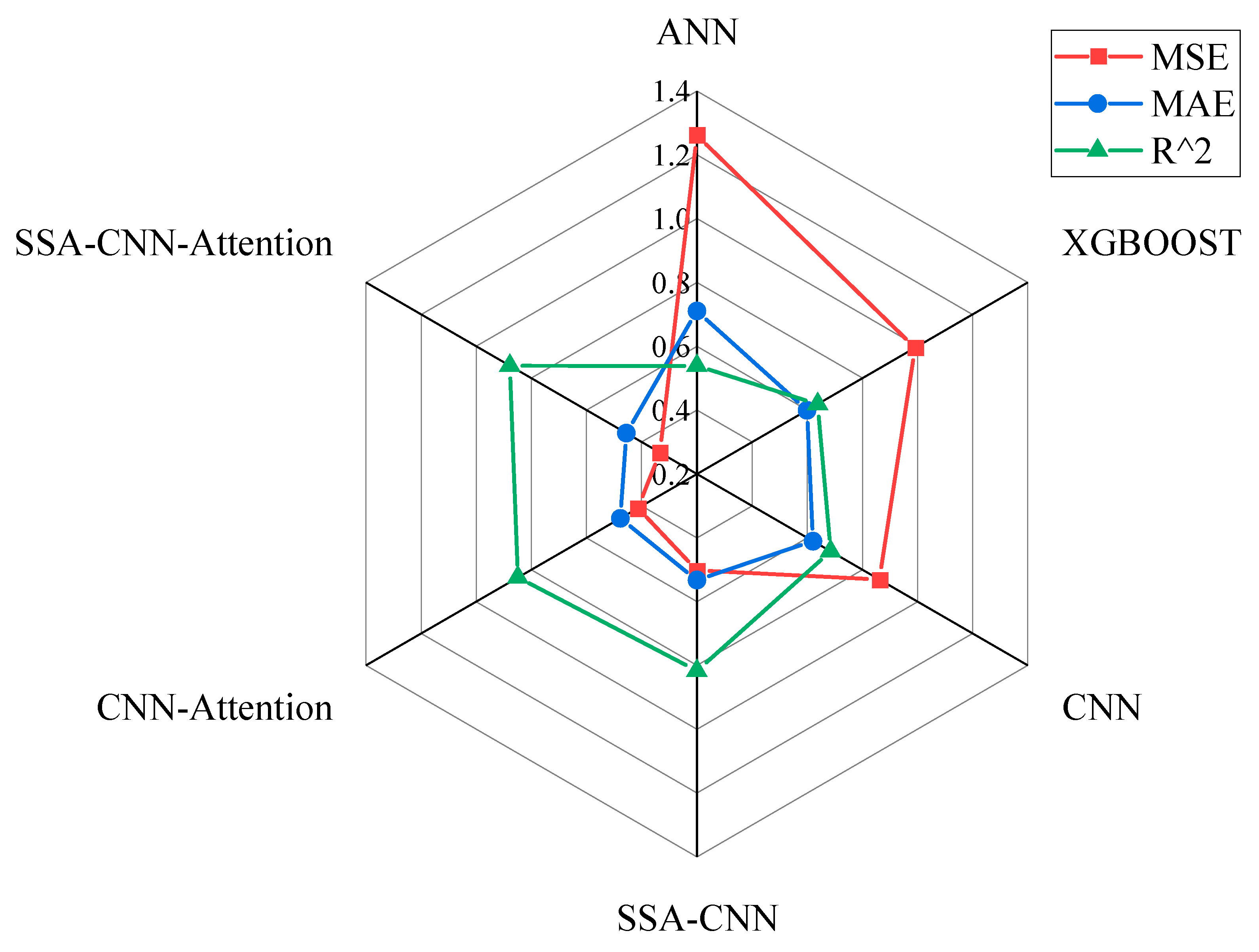
The bar chart in Figure 6 and the radar chart in Figure 7 present a comprehensive evaluation of various models’ performance in predicting pitting corrosion depth of buried pipelines. The bar chart offers a clear comparison of each model’s performance based on Mean Squared Error (MSE), Mean Absolute Error (MAE), and the coefficient of determination (R²). Among these, the SSA-CNN-Attention model demonstrates superior performance with the lowest MSE (0.334), MAE (0.456), and the highest R² (0.8783), indicating its effectiveness in corrosion depth prediction. Conversely, the radar chart consolidates these three metrics into a single coordinate system, providing a multidimensional comparison of the models. The SSA-CNN-Attention model exhibits the most balanced and extensive “radiation” across all axes, signifying its overall excellence in performance and stability.

From the perspectives of MSE and MAE, the SSA-CNN-Attention model effectively minimizes prediction errors, reflecting its robust capacity to capture the complex nonlinear interactions inherent in the corrosion process. Additionally, the elevated R² value indicates that the model accounts for a significant portion of the variance in the data, suggesting a deeper understanding of the underlying corrosion mechanisms. In contrast, other models such as ANN, XGBoost, CNN, SSA-CNN, and CNN-Attention either exhibit higher error metrics or lower R² values, highlighting their limitations in balancing these evaluation criteria.

4.4. Stability and Statistical Significance Analysis

Machine learning models can be sensitive to random factors such as data partitioning and initial weightings. To ensure that our findings are robust and not an artifact of a single favorable run, we performed 10 independent runs for each of the four key models: CNN, SSA-CNN, CNN-Attention, and our proposed SSA-CNN-Attention.

The results of these runs are quantitatively summarized in

Table 6. Mean and Standard Deviation of R² Scores from 10 Independent Runs.

Model	Mean R2	Standard Deviation (R2)
CNN	0.629	0.039
SSA-CNN	0.799	0.013
CNN-Attention	0.815	0.008
SSA-CNN-Attention	0.855	0.0025

. In this analysis, we use two key indicators: the mean R² and its standard deviation. The R² quantifies the proportion of the variance in the pitting depth that is predictable from the model’s inputs; a higher R² value indicates a better goodness-of-fit. The standard deviation of the R² scores, conversely, serves as a direct measure of the model’s stability, with a lower value indicating more consistent performance.

The data in Table 6 reveals a clear and consistent performance hierarchy. The proposed SSA-CNN-Attention model achieves the highest mean R² (0.855), signifying that it consistently provides a superior fit to the data. More importantly, the table shows a distinct trend in model stability. The baseline CNN model exhibits the highest standard deviation (0.039), indicating that its ability to fit the data is highly variable and unreliable. In stark contrast, the proposed SSA-CNN-Attention model has the lowest standard deviation (0.0025), signifying that its excellent fitting performance is highly consistent across different experimental conditions. This dual evidence—a consistently better fit to the data (high mean R²) and minimal variance in that fit (low standard deviation)—strongly supports the stability and reliability of our proposed framework.

A closer analysis of the mean values in Table 6 reveals how this top-tier performance is constructed. The impact of hyperparameter optimization alone is substantial, improving the mean R² from approximately 0.629 (CNN) to 0.799 (SSA-CNN), an absolute improvement of 17.0%. However, the most significant performance gain is attributable to the attention mechanism. Adding attention to the baseline CNN boosts the mean R² to ~0.815, an absolute improvement of 18.6%, making it the single most impactful enhancement to the model’s architecture. The synergy of these components culminates in our final model, where adding attention to the optimized SSA-CNN provides the final push from ~0.799 to 0.855. This step-by-step analysis confirms that while hyperparameter optimization builds a robust foundation, it is the attention mechanism that provides the crucial leap in predictive power.

4.5. Local Interpretability Analysis Based on LIME

Machine-learning models are often criticized for their opaque “black-box” nature, making it difficult for engineers to trust and apply their predictions in practice. To improve transparency, the Local Interpretable Model-Agnostic Explanations (LIME) algorithm was used to analyze predictions over the entire dataset, quantifying the influence of each input feature on the model’s output. A negative contribution value indicates that the feature suppresses the predicted corrosion rate (larger feature values lead to lower predictions), whereas a positive value signifies that the feature amplifies the output (larger values yield higher predictions).

Table 7. LIME-based Feature Contribution Scores.

Feature	ANN	XGboost	CNN	SSA-CNN	CNN-Attention	SSA-CNN-Attention
pp (mV)	0.17869	0.16236	0.15863	0.11745	−0.17133	−0.10362
rp (mV)	0.00277	−0.00963	−0.12543	−0.10431	−0.15315	−0.12693
t (years)	−0.07169	−0.04298	−0.12304	−0.13334	0.07812	0.08028
bc (ppm)	−0.04586	0.052	0.11474	0.12385	−0.05034	−0.04937
wc (%)	−0.01527	0.07901	0.11169	0.09629	0.03195	0.02936
bd (g/cm3)	−0.0192	−0.00593	0.10412	0.07534	0.031	0.037
sc (ppm)	−0.04722	0.036	−0.05712	−0.04345	0.02007	0.02396
re (Ω·m)	−0.04717	0.03007	0.02842	0.01749	−0.0129	−0.0237
cc (ppm)	0.01292	−0.13155	0.02331	−0.00445	0.01008	0.02106
pH	−0.21881	−0.16784	−0.01167	−0.04449	−0.00886	−0.00826

summarizes the feature-contribution scores derived from LIME for each model.

Based on the information presented in Figure 8, it is evident that different models exhibit markedly different understandings of the corrosion mechanism. Corrosion itself is an extremely complex electrochemical process influenced jointly by multiple factors—soil resistivity, moisture content, bulk density, dissolved chloride, bicarbonate, sulfate, pipeline service life, redox potential, and pH. In real-world environments, these features do not act in isolation but interact in intricate, interdependent ways. For example, under certain conditions, a higher voltage (pp(A)(V)) may trigger a protective reaction that slows the corrosion rate; however, other models (such as ANN, XGBoost, and traditional CNN) typically treat it as a purely corrosive, positive contributor. By contrast, the SSA-CNN-Attention model—through deep feature extraction and its attention mechanism—accurately captures the nonlinear interplay between this voltage feature and other indicators, assigning it a negative contribution that aligns with the protective effects observed in actual electrochemical reactions.

A particularly telling example is the interpretation of pipeline service life (t). While traditional models (such as ANN, XGBoost) treat this variable as a negative contributor—a physically counter-intuitive conclusion—our model correctly identifies service life as a positive driver. This is because corrosion is a cumulative process; the longer a pipeline serves, the more severe the damage becomes. By leveraging its attention mechanism, our model accurately reflects this fundamental principle of corrosion science, a nuance missed by other approaches.

Similarly, the model provides a physically accurate interpretation of soil resistivity. Traditional models like XGBoost assign it a positive contribution, incorrectly suggesting that higher resistivity (less conductive soil) accelerates corrosion. This conclusion directly contradicts well-established electrochemical principles, where low-resistivity environments are known to facilitate ionic current and thus promote corrosion. These models likely mistake a spurious correlation—where high-resistivity soils in datasets sometimes happen to be dry and less corrosive—for a causal relationship. In contrast, our SSA-CNN-Attention model correctly identifies soil resistivity as a negative contributor. This aligns perfectly with physical reality. The attention mechanism does not assess resistivity in isolation; it understands that its role is conditional on other factors like water content and ion concentration, correctly identifying it as a facilitator of corrosion in conductive, moist conditions. Because this model recognizes these subtle and intricate feature interactions, it achieves the best performance in MSE, MAE, and R², demonstrating a deeper and more accurate understanding of the corrosion mechanism.

In summary, the SSA-CNN-Attention model not only leads in predictive accuracy but also shows clear advantages in feature extraction and importance assessment. It unveils the complex interactions and bidirectional control effects among real-world influencing factors, providing a solid scientific basis and theoretical support for corrosion protection and maintenance strategies in engineering practice. This ability to faithfully capture intricate corrosion mechanisms—where traditional models fall short—underpins its significance and practical value.

4.6. Practical Implications for Preventive Maintenance

The feature contribution scores generated by LIME offer more than just model transparency; they provide actionable intelligence that can directly inform and optimize preventive maintenance strategies for pipeline integrity management. By moving beyond global feature importance, these local explanations allow engineers to understand why a specific pipeline segment is predicted to be at high risk, enabling a more targeted and efficient response.

The practical applications can be summarized as follows:

(1)

Risk-Based Inspection (RBI) Prioritization: Instead of relying on fixed inspection schedules, engineers can use the model’s predictions to flag high-risk pipeline segments. The LIME explanation then acts as a diagnostic tool. For example, if the model predicts severe pitting for Segment A, LIME might reveal that the primary drivers are high soil conductivity and low pH. For Segment B, the key factors might be pipe age and operational pressure fluctuations. This allows maintenance teams to prioritize Segment A for immediate inspection and soil analysis, while scheduling a different type of integrity check for Segment B, thereby optimizing resource allocation.

(2)

Enhanced Data Collection and Monitoring: The explanations can also guide future data collection efforts. If LIME indicates that a certain parameter is consistently a decisive factor in high-risk predictions, it underscores the importance of ensuring high-quality, high-frequency measurements for that parameter. This feedback loop can help justify investments in new sensors or more frequent soil sampling campaigns in critical areas, continuously improving the accuracy and reliability of future predictive models.

In essence, the interpretability framework transforms the model from a “black box” predictor into a sophisticated decision-support tool. It empowers engineers to not only trust the model’s predictions but also to leverage them to make smarter, data-driven decisions that enhance safety and extend the operational life of pipeline assets.

4.7. Computational Complexity Analysis

A thorough evaluation of the proposed SSA-CNN-Attention model necessitates a discussion of its computational complexity and feasibility for large-scale applications. The computational load of our technique can be analyzed in two distinct phases: the training phase and the inference (prediction) phase.

Training Phase Complexity: The most computationally intensive part of our framework is the training phase, which is dominated by the Sparrow Search Algorithm (SSA) used for hyperparameter optimization. The total computational cost of this phase can be approximated as G × P × T_model, where:

G is the maximum number of generations for SSA. As specified in Table 2, G = 500.

P is the population size of the sparrows. As specified in Table 2, P = 20.

T_model represents the computational cost of training a single CNN-Attention model for one set of hyperparameters.

It is crucial to note that T_model is a variable cost, dependent on the specific hyperparameter combination being evaluated for each individual “sparrow”. The cost of each training session, T_model, is determined by

T_model = E × (N/B) × C_batch

where:

E is the number of training epochs, fixed at 10 (from Table 3).

N is the total number of samples in the training set.

B is the batch size, a hyperparameter optimized by SSA within the range [16, 32, 64, 128] (from Table 4).

C_batch is the cost of a single forward and backward pass for one batch. This cost is a function of the model’s architecture, which varies during optimization based on the number of filters and dense units selected from their respective ranges in Table 4.

Therefore, the total training process involves G × P = 10,000 individual model training evaluations, where the cost of each evaluation varies. This extensive search is a one-time, offline investment.

Inference Phase Complexity: In stark contrast, the inference phase is highly efficient. Once trained, making a prediction for a new data point only requires a single forward pass through the fixed, optimized architecture. The complexity is constant for each prediction:

Complexity_Inference = O(1)per sample.

The cost of a forward pass is determined by the final architecture and involves a fixed sequence of tensor operations (e.g., convolutions, activations, dense layer multiplications), allowing the model to generate predictions in near real-time.

Applicability for Large-Scale Setups: Our analysis confirms that while the one-time training is resource-intensive, the final model is lightweight for inference. This separation between a demanding offline training phase and an efficient online inference phase makes our technique viable for large-scale deployments.

5. Limitations and Future Work

While the proposed SSA-CNN-Attention model demonstrates superior performance and interpretability on the current dataset, this study has several limitations that open avenues for future research.

First, the model was developed and validated using the Velázquez et al. dataset [27], which, despite being a widely recognized benchmark in this field, is relatively small with 259 samples. Although we have taken rigorous measures to mitigate overfitting, such as a strict division of training, validation, and test sets and systematic hyperparameter optimization, the model’s generalization capability on larger and more diverse datasets remains to be fully validated. Future work should focus on applying and fine-tuning the proposed framework on multi-source datasets from different geographical locations and operational conditions to further assess its robustness and generalization performance.

Second, the current study focuses on predicting the maximum pitting depth, which is a critical indicator for pipeline integrity. However, a comprehensive corrosion assessment also involves other geometric parameters, such as pit density and shape. Future research could extend the model’s predictive capabilities to a multi-output framework if datasets containing such rich information become available.

Third, our study successfully leveraged the Sparrow Search Algorithm (SSA) for hyperparameter optimization. However, a systematic comparison of different optimization algorithms—such as Particle Swarm Optimization (PSO), Genetic Algorithms (GA), or Bayesian Optimization—was not conducted. Investigating the relative performance and computational efficiency of these optimizers for this specific application would be a highly valuable endeavor.

Fourth, our comparative analysis was primarily designed as an ablation study to validate the contributions of our model’s components. Consequently, a broader comparison against other advanced deep learning architectures was beyond the scope of this paper. Exploring how our model performs against sequence-based architectures like LSTMs or graph-based models like Graph Neural Networks (GNNs) is a promising and valuable direction for future research.

Finally, while the interpretability analysis using LIME provided valuable insights, we acknowledge that a formal sensitivity analysis of the explanation method itself was not performed. Future studies could build upon our findings by systematically investigating the stability of LIME’s explanations with respect to its parameterization and stochastic sampling, thereby further strengthening the reliability of the model’s interpretations.

6. Conclusions

In conclusion, this study successfully developed an interpretable deep learning model that not only accurately predicts pipeline pitting depth but also effectively captures the inherent asymmetry of the corrosion process. The key findings demonstrate that:

(1)

The SSA-CNN-Attention model attained a mean squared error (MSE) of 0.334, a mean absolute error (MAE) of 0.456, and a coefficient of determination (R²) of 0.8783. Relative to a baseline CNN, these figures correspond to reductions of 61.3% in MSE and 26.6% in MAE, along with a 28.2% gain in R², demonstrating markedly improved accuracy and reduced over-fitting under complex corrosion conditions.

(2)

The embedded attention mechanism adaptively re-weights convolutional features, enabling the model to capture the bidirectional regulatory effects of service life, redox potential, and other factors. Local Interpretable Model-agnostic Explanations (LIME) were used to analyze the model’s predictions. The results confirm that the feature contributions identified by the model are consistent with established electrochemical principles—for example, recognizing the protective influence of elevated potentials in certain soils—relationships that conventional ANN, XGBoost, and unenhanced CNN models fail to reveal.

(3)

By providing transparent local explanations within the deep feature space generated after convolution and pooling, the LIME framework alleviates the “black-box” nature of deep networks. The resulting visualizations clarify the physical meaning of critical features and their interactions, facilitating mechanism-oriented refinement of predictive models.

Collectively, these findings demonstrate that the proposed SSA-CNN-Attention model not only excels in quantitative metrics but also provides qualitative insights into the intricate electrochemical mechanisms governing external pitting corrosion, thereby furnishing a robust scientific basis for data-driven pipeline integrity management.