A Symmetry-Informed Multimodal LLM-Driven Approach to Robotic Object Manipulation: Lowering Entry Barriers in Mechatronics Education

Abstract

The integration of Large Language Models (LLMs), particularly Visual Language Models (VLMs), into robotics promises more intuitive human–robot interactions; however, challenges remain in efficiently translating high-level commands into precise physical actions. This paper presents a novel architecture for vision-based object manipulation that leverages a VLM’s reasoning capabilities while incorporating symmetry principles to enhance operational efficiency. Implemented on a Yahboom DOFBOT educational robot with a Jetson Nano platform, our system introduces a prompt-based framework that uniquely embeds symmetry-related cues to streamline feature extraction and object detection from visual data. This methodology, which utilizes few-shot learning, enables the VLM to generate more accurate and contextually relevant commands for manipulation tasks by efficiently interpreting the symmetric and asymmetric features of objects. The experimental results in controlled scenarios demonstrate that our symmetry-informed approach significantly improves the robot’s interaction efficiency and decision-making accuracy compared to generic prompting strategies. This work contributes a robust method for integrating fundamental vision principles into modern generative AI workflows for robotics. Furthermore, its implementation on an accessible educational platform shows its potential to simplify complex robotics concepts for engineering education and research.

1. Introduction

In recent years, with the rapid development of artificial intelligence and robotics, manipulator robot technology has increasingly been applied across various emerging technological domains. ChatGPT (Chat + Generative Pre-trained Transformer), developed by OpenAI [1], has demonstrated significant potential in diverse contexts—most notably in natural language processing, with essential applications in robotics [2,3]. ChatGPT utilizes machine learning techniques, including deep learning and natural language processing, to comprehend and produce human-like text. Trained by vast amounts of internet data, it produces responses that are both contextually relevant and accurate. This conversational interface enables users to interact with AI through prompts utilizing OpenAI’s large language model. The primary objective of ChatGPT is to simplify access to information and support users in accomplishing tasks by providing accurate and helpful responses. Its ability to generate answers in a manner that resembles human conversation makes it particularly useful for tasks such as answering questions [4,5,6,7,8]. Although ChatGPT is typically categorized as a Large Language Model (LLM) designed for text-based reasoning, the OpenAI API used in this study supports multimodal interaction. Our system functions as a Visual Language Model (VLM), processing both textual prompts and visual data.

The emergence of LLMs (and VLMs) has opened new possibilities for natural language–based robotic control. These models can interpret high-level, often ambiguous human instructions and decompose them into logical sequences of actions, thereby bridging the gap between user intent and robotic execution [9]. Many existing approaches rely on extensive fine-tuning or computationally expensive processes, which limit their scalability and applicability in practical educational and experimental settings.

Symmetry is a fundamental organizing principle of the physical world that serves as a powerful heuristic in computer vision and robotics. By providing geometric priors, symmetry simplifies object detection, pose estimation, and grasp planning [10,11]. Despite this potential, the explicit integration of symmetry principles into the reasoning process of generative AI models applied in robotics remains underexplored.

This study addresses this gap by introducing a hybrid architecture that combines the semantic reasoning of multimodal LLMs with symmetry-informed visual processing. Implemented on an accessible educational robotic arm (the Yahboom DOFBOT with Jetson Nano), the system allows learners to command the robot through natural language rather than low-level programming, thus bridging generative AI reasoning with deterministic robotic control.

Research Contributions

This study makes three primary contributions:

• A hybrid symmetry-informed architecture that integrates multimodal Visual Language Models (VLMs) with deterministic geometric reasoning for robotic object manipulation. This design bridges natural language understanding and precise motion control through an explicit separation of semantic and computational processes, introducing a lightweight and interpretable software workflow that connects VLM reasoning with deterministic algorithms for real-time, human–GenAI–robot interaction.
• An experimental validation demonstrating the technical feasibility of this architecture on an accessible educational robotic platform (Yahboom DOFBOT with Jetson Nano). The results show that the proposed approach is both reproducible and robust under realistic conditions.
• An educational contribution, showing how the system can lower the entry barrier for learning mechatronics and AI-driven robotics by abstracting low-level programming and kinematic complexity through natural language interaction.

The novelty of this work lies in a symmetry-informed hybrid reasoning framework that couples a multimodal VLM (as a semantic sensor) with a deterministic, geometry-preserving control layer. By using standard kinematic and dynamic formulations our contribution focuses on the integration-by-design of deterministic and generative reasoning within a symmetry-aware workflow.

2. Related Works

Recent research has explored how Large Language Models (LLMs) and, more recently, multimodal Visual Language Models (VLMs) can support robotic task execution and human–robot interaction. While early studies focused on text-only LLMs for planning and reasoning, recent studies have extended these capabilities to multimodal contexts that integrate vision, perception, and control. For example, LLMs have been applied to assembly and construction tasks using virtual robots [12]. They are becoming increasingly essential in robotic systems, leveraging their extensive knowledge of task execution and planning. In [13], an LLM-driven look-ahead mechanism is introduced to enhance real-time robotic performance by minimizing latency and optimizing path planning without requiring expensive training data. Wang et al. provide a comprehensive overview of the opportunities and challenges of LLMs in robotics [9]. Similarly, ref. [14] described the integration of multimodal LLM in robot-assisted virtual surgery for autonomous blood aspiration. In this case, the LLM handles high-level reasoning and task prioritization, whereas motion planning relies on a low-level deep reinforcement learning model, enabling distributed decision-making. LLMs have also been incorporated into Virtual Reality environments to generate context-aware interactions, enhancing embodied human–AI experiences [15]. Other studies have employed LLMs to generate skill dependency graphs and optimize task allocation through probabilistic modeling and linear programming [16]. Furthermore, reasoning–action frameworks have been tested in simulated environments, where humanoid robots equipped with vision, locomotion, manipulation, and communication modules interact with LLMs through natural language interfaces [17].

Beyond the industrial and experimental contexts, LLMs are being investigated for life support and healthcare applications. These include robots capable of interpreting verbal instructions, responding to greetings or demonstrations, and executing patient care tasks in dynamic clinical environments [18]. The development of intelligent medical service robots remains challenging owing to the need to integrate multiple knowledge sources while maintaining autonomous operation in unpredictable settings. In [19], a Robotic Health Attendant was presented that combined ChatGPT with healthcare-specific knowledge to interpret both structured protocols and unstructured human input, thereby generating context-aware robotic actions.

Conventional robotic intelligence systems based on supervised learning often struggle to adapt to changing environments. By contrast, LLMs enhance generalization, enabling robots to perform effectively in complex, real-world scenarios. They play a crucial role in improving behavior planning and execution [20] and supporting human–robot collaboration in diverse domains. Unlike rigid, conventional interaction methods, natural language communication offers a more flexible and intuitive approach. By leveraging LLMs, non-expert users can command robots to execute sophisticated tasks such as aerial navigation, obstacle avoidance, and path planning [21]. Current efforts primarily rely on prompt-based systems through online APIs or high-level offline planning and decision-making. However, such approaches are limited in scenarios with weak connectivity and insufficient integration with low-level robotic control [22].

Although the above literature mainly discusses text-based LLMs, our work differs in that it employs a multimodal VLM. Specifically, we used the OpenAI API not only for textual reasoning but also for image-based few-shot prompting. This distinction is critical; related works provide the foundation for how LLMs are applied to robotics, whereas our system extends these concepts into the multimodal domain through a VLM that integrates visual inputs with symmetry-informed reasoning.

3. System Foundations: Robotic Platform and Kinematic Model

This section describes the standard kinematic and dynamic models used as the deterministic foundation of our approach.

3.1. Kinematic Model

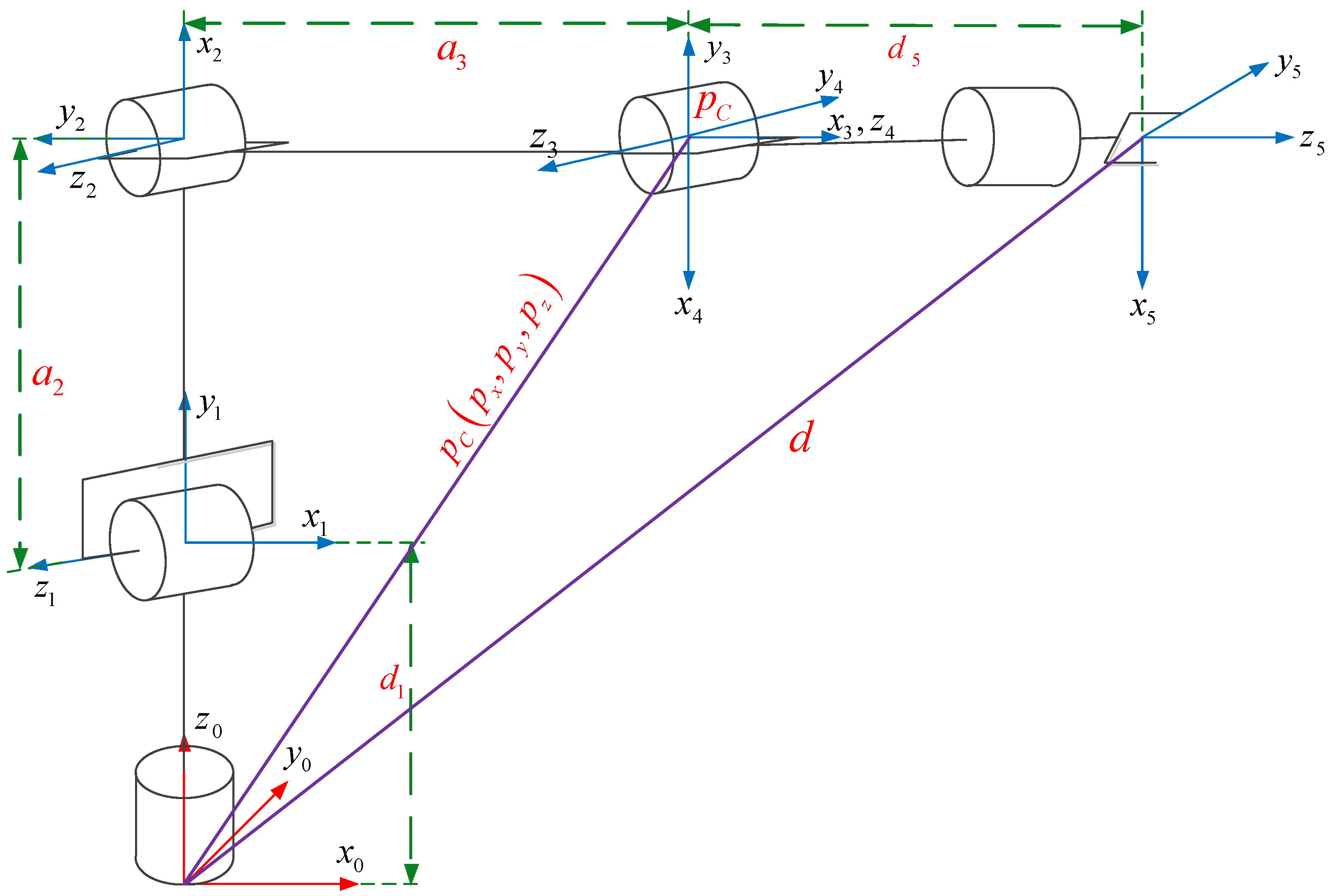
The Denavit–Hartenberg (DH) method was used to calculate the forward kinematics of the open-chain and chain-link manipulators. The DOFBOT robot is a five-degree-of-freedom (DOF) manipulator with direct-current motors. Figure 1 shows the structure of the manipulator under study, with reference frames selected according to the DH convention, which is widely adopted in robotics [23,24].

For students, deriving forward and inverse kinematics involves multiple trigonometric relationships and matrix transformations, which often obscure an intuitive understanding of robotic motion. This mathematical complexity, detailed in

Table 1. Denavit–Hartenberg (DH) parameters of the manipulator robot.

$\mathbf{Joint} \mathit{i}$	${\mathit{\theta }}_{\mathit{i}}$	${\mathit{\alpha }}_{\mathit{i}}$	${\mathit{a}}_{\mathit{i}}$	${\mathit{d}}_{\mathit{i}}$
1	${\theta }_1$	$90°$	$0$	$d_1$
2	${\theta }_2+90°$	$0°$	$a_2$	$0$
3	${\theta }_3$	$0°$	$a_3$	$0$
4	${\theta }_4-90°$	$-90°$	$0$	$0$
5	${\theta }_5$	$0°$	$0$	$d_5$

and Equations (1)–(5), represents a significant learning barrier for novices. The VLM-driven architecture described in the following section was designed to abstract this complexity, enabling learners to focus on robotic behavior and control rather than on the intricacies of kinematic derivations.

Table 1 lists the DH parameters, where ${\theta }_1, {\theta }_2, {\theta }_3, {\theta }_4 \mathrm{and} {\theta }_5$ represent the joint positions.

The transformation matrix relating the two links is defined as:

$${}^{i-1}A_i=\left[\begin{array}{cccc}\cos {\theta }_i& -\sin {\theta }_i\cos {\alpha }_i& \sin {\theta }_i\sin {\alpha }_i& a_i\cos {\theta }_i\\ \sin {\theta }_i& \cos {\theta }_i\cos {\alpha }_i& -\cos {\theta }_i\sin {\alpha }_i& a_i\sin {\theta }_i\\ 0& \sin {\alpha }_i& \cos {\alpha }_i& d_i\\ 0& 0& 0& 1\end{array}\right].$$

(1)

The homogeneous transformation matrix ${}^{0}A_5$ of the DOFBOT robot, representing the mapping from the base coordinate system to the end-effector coordinate system, is obtained by multiplying the transformation matrices of the individual links as follows:

$${}^{0}A_5=\left[\begin{array}{cc}{}^{0}R_5& {}^{0}p_5\\ 0& 1\end{array}\right]$$

(2)

where ${}^{0}R_5$ denotes the 3 × 3 rotation matrix of the end-effector with respect to the base coordinate system, ${}^{0}p_5$ is a 3 × 1 position vector representing the spatial coordinates of the end-effector in the base coordinate system, 0 is the 1 × 3 zero vector, and 1 is a scalar. By substituting the DH parameters from Table 1 into the transformation matrix (1), the homogeneous transformation matrix for each link can be derived as:

• Link 1: ${}^{0}A_1=\begin{array}{cccc}cos\left({\theta }_1\right)& 0& sin\left({\theta }_1\right)& 0\\ sin\left({\theta }_1\right)& 0& -cos\left({\theta }_1\right)& 0\\ 0& 1& 0& d_1\\ 0& 0& 0& 1\end{array}$
• Link 2: ${}^{1}A_2=\begin{array}{cccc}cos\left({\theta }_2\right)& -sin\left({\theta }_2\right)& 0& a_2·cos\left({\theta }_2\right)\\ sin\left({\theta }_2\right)& cos\left({\theta }_2\right)& 0& a_2·sin\left({\theta }_2\right)\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}$
• Link 3: ${}^{2}A_3= \begin{array}{cccc}cos\left({\theta }_3\right)& -sin\left({\theta }_3\right)& 0& a_3·cos\left({\theta }_3\right)\\ sin\left({\theta }_3\right)& cos\left({\theta }_3\right)& 0& a_3·sin\left({\theta }_3\right)\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}$
• Link 4: ${}^{3}A_4= \begin{array}{cccc}cos\left({\theta }_4\right)& 0& -sin\left({\theta }_4\right)& 0\\ sin\left({\theta }_4\right)& 0& cos\left({\theta }_4\right)& 0\\ 0& -1& 0& 0\\ 0& 0& 0& 1\end{array}$
• Link 5: ${}^{4}A_5=\begin{array}{cccc}cos\left({\theta }_5\right)& -sin\left({\theta }_5\right)& 0& 0\\ sin\left({\theta }_5\right)& cos\left({\theta }_5\right)& 0& 0\\ 0& 0& 1& d_5\\ 0& 0& 0& 1\end{array}$

Multiplying the transformation matrices of all links yields the forward kinematics of the manipulator, which is expressed as

$${}^{0}A_5={}^{0}A_1{}^{1}A_2{}^{2}A_3{}^{3}A_4{}^{4}A_5=\left[\begin{array}{cccc}{\mathrm{c}}_1{\mathrm{c}}_{234}{\mathrm{c}}_5-{\mathrm{s}}_1{\mathrm{s}}_5& -{\mathrm{c}}_1{\mathrm{c}}_{234}{\mathrm{s}}_5-{\mathrm{s}}_1{\mathrm{c}}_5& -{\mathrm{c}}_1{\mathrm{s}}_{234}& {\mathrm{c}}_1(a_2{\mathrm{c}}_2+a_3{\mathrm{c}}_{23}-d_5{\mathrm{s}}_{234})\\ {\mathrm{s}}_1{\mathrm{c}}_{234}{\mathrm{c}}_5+{\mathrm{c}}_1{\mathrm{s}}_5& -{\mathrm{s}}_1{\mathrm{c}}_{234}{\mathrm{s}}_5+{\mathrm{c}}_1{\mathrm{c}}_5& {\mathrm{s}}_1{\mathrm{s}}_{234}& {\mathrm{s}}_1(a_2{\mathrm{c}}_2+a_3{\mathrm{c}}_{23}-d_5{\mathrm{s}}_{234})\\ {\mathrm{s}}_{234}{\mathrm{c}}_5& -{\mathrm{s}}_{234}{\mathrm{s}}_5& {\mathrm{c}}_{234}& d_1+a_2{\mathrm{s}}_2+a_3{\mathrm{s}}_{23}+d_5{\mathrm{c}}_{234}\\ 0& 0& 0& 1\end{array}\right]$$

(3)

where ${\mathrm{c}}_i=\cos {\theta }_i$, ${\mathrm{c}}_{ij}=\cos \left({\theta }_i+{\theta }_j\right)$, ${\mathrm{c}}_{ijk}=\cos \left({\theta }_i+{\theta }_j+{\theta }_k\right)$, $s_i=\sin {\theta }_i$, $s_{ij}=\sin \left({\theta }_i+{\theta }_j\right)$, $s_{ijk}=\sin \left({\theta }_i+{\theta }_j+{\theta }_k\right)$. The ${}^{0}A_5$ matrix provides the position of the end-effector in the base coordinate system with respect to the joint position, and is given by:

$$\begin{array}{l}{p}_x=\cos {\theta }_1\left[a_2\cos {\theta }_2+a_3\cos \left({\theta }_2+{\theta }_3\right)-d_5\sin \left({\theta }_2+{\theta }_3+{\theta }_4\right)\right]\\ p_y=\sin {\theta }_1\left[a_2\cos {\theta }_2+a_3\cos \left({\theta }_2+{\theta }_3\right)-d_5\sin \left({\theta }_2+{\theta }_3+{\theta }_4\right)\right]\\ p_z=d_1+a_2\sin {\theta }_2+a_3\sin \left({\theta }_2+{\theta }_3\right)+d_5\cos \left({\theta }_2+{\theta }_3+{\theta }_4\right)\end{array}$$

(4)

3.2. Inverse Kinematics

The inverse kinematics problem involves determining the joint variables ${\theta }_1, {\theta }_2, {\theta }_3, {\theta }_4, \mathrm{and} {\theta }_5$ in terms of the position and orientation of the end-effector, expressed in the base coordinate system. The DOFBOT manipulator robot has five joints, with the last two intersecting at the center of the wrist. This configuration allows the inverse kinematics to be decoupled into two sub-problems: inverse position kinematics and inverse orientation kinematics. 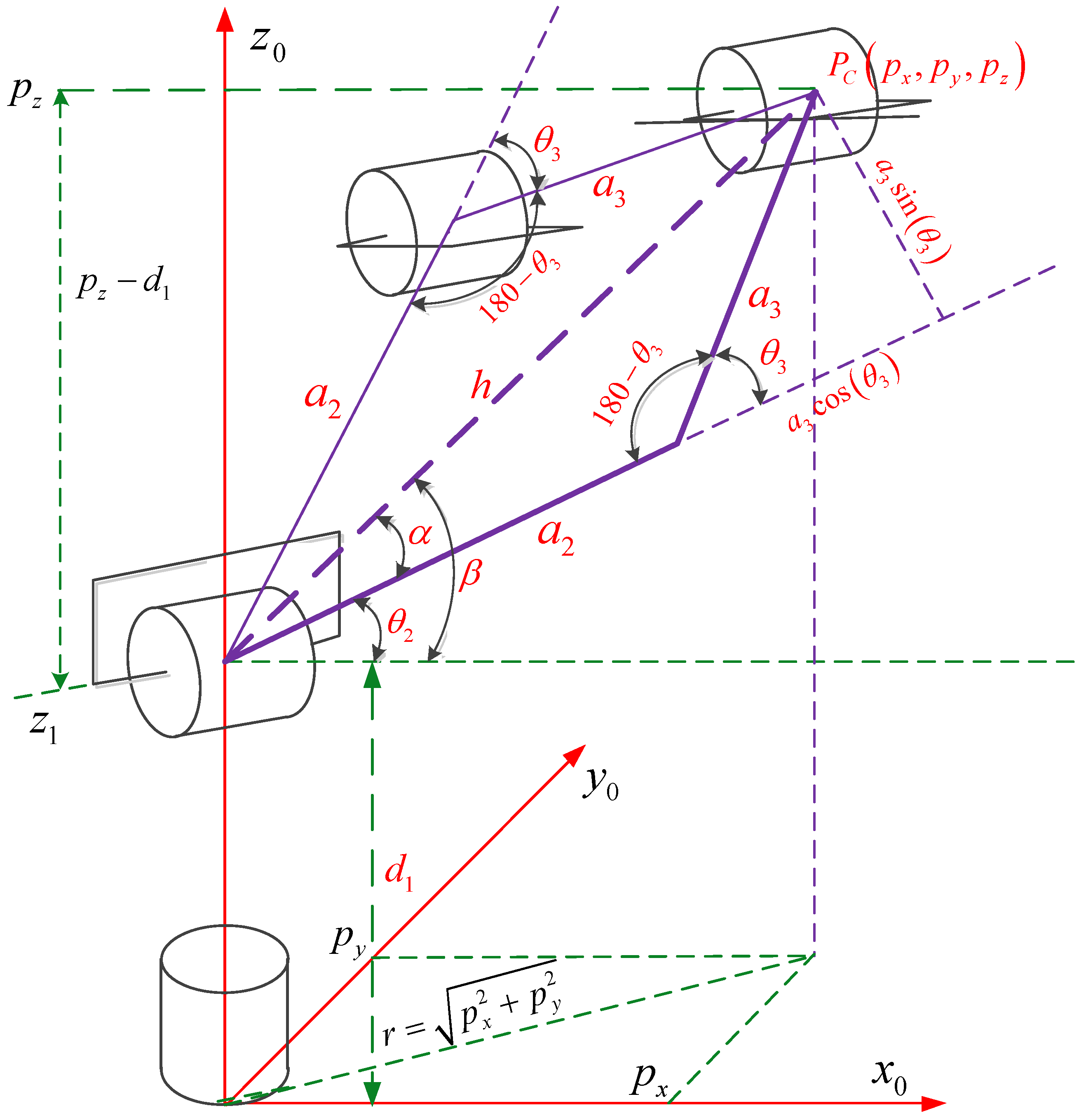Inverse position kinematics focuses on the position of the end-effector of the robot and is determined by the first three joints, as illustrated in Figure 2.

As illustrated in Figure 2, $P_c$ corresponds to the wrist center, serving as the kinematic decoupling point, and is expressed as:

$$P_C=d-d_{5}Rk$$

(5)

where

$$P_C={\left[p_x,p_y,p_z\right]}^T$$

• $d\backslash$ is the desired position of the end-effector, measured with respect to the robot base coordinate system.
• $d_5$ is the distance between the robot’s end-effector and its wrist center.
• $R$ is the desired orientation matrix of the end-effector relative to the robot base.

  $$K={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T$$

To address this problem, a geometric method is employed to determine the first three joint variables using trigonometric functions. As inverse kinematics generally admits two possible solutions, elbow up and elbow down, the geometric method ensures that the robot can achieve its angular position in either configuration.

3.2.1. Elbow Down Configuration

Figure 3 illustrates the solution for the elbow down configuration using the geometric method.

Angle ${\theta }_1$ is obtained from the projection of the end effector $P_C\left(p_x,p_y,p_z\right)$ onto the plane $x_0-y_0$.

$${\theta }_1={\tan }^{-1}\left({\displaystyle \frac{p_y}{p_x}}\right)$$

(6)

Links 2 and 3 form triangles and angles (purple), and angle ${\theta }_2$ is given by:

$${\theta }_2=\beta -\alpha ,$$

(7)

where $\beta$ is

$$\beta =ta{n}^{-1}\left({\displaystyle \frac{p_z-d_1}{r}}\right)$$

(8)

where $r$ is the projection of the $({\left\{p\right\}}_x, p_y)$ coordinates; therefore $r=\sqrt{p_x^2+p_y^2}$. By substituting r into (8),

$$\beta =ta{n}^{-1}\left({\displaystyle \frac{p_z-d_1}{\sqrt{p_x^2+p_y^2}}}\right).$$

(9)

Similarly, to obtain $\alpha$, the distance h is needed

$$h^2={\left(p_z-d_1\right)}^2+r^2,$$

(10)

and substituting r in (10) gives

$$h=\sqrt{p_x^2+p_y^2+{\left(p_z-d_1\right)}^2}$$

(11)

By applying the Law of Cosines and performing the corresponding mathematical operations, the following expression is obtained:

$$a_3^2=a_2^2+h^2-2a_{2}h\cos \left(\alpha \right)$$

(12)

and after applying the corresponding mathematical transformations

$$\cos \left(\alpha \right)={\displaystyle \frac{a_3^2-a_2^2-h^2}{2a_{2}h}}=au{x}_1,$$

(13)

The preferred approach to determine $\alpha$ is to express it using the tangent function

$$\alpha ={\tan }^{-1}\left[{\displaystyle \frac{\pm \sqrt{1-{\cos }^2\left(\alpha \right)}}{\cos \left(\alpha \right)}}\right] \mathrm{or} \alpha ={\tan }^{-1}\left[{\displaystyle \frac{\pm \sqrt{1-au{x}_1^2}}{au{x}_1}}\right]$$

(14)

An alternative approach to determine the angle $\alpha$ is as follows:

$$\alpha ={\tan }^{-1}\left[{\displaystyle \frac{a_3\sin \left({\theta }_3\right)}{a_2+a_3\cos \left({\theta }_3\right)}}\right]$$

(15)

Substituting Equations (9) and (14) into (7), the following expression is obtained:

$${\theta }_2=\beta -\alpha ={\tan }^{-1}\left({\displaystyle \frac{p_z-d_1}{\sqrt{p_x^2+p_y^2}}}\right)-{\tan }^{-1}\left[{\displaystyle \frac{a_3\sin \left({\theta }_3\right)}{a_2+a_3\cos \left({\theta }_3\right)}}\right]$$

(16)

or

$${\theta }_2=\beta -\alpha ={\tan }^{-1}\left({\displaystyle \frac{p_z-d_1}{\sqrt{p_x^2+p_y^2}}}\right)-{\tan }^{-1}\left({\displaystyle \frac{\pm \sqrt{1-au{x}_1^2}}{au{x}_1}}\right)$$

(17)

Finally, to determine ${\theta }_3$, the Law of Cosines is applied, as illustrated in Figure 3:

$$h^2=a_2^2+a_3^2+2a_2{a}_3\cos \left({\theta }_3\right)$$

$$\cos \left({\theta }_3\right)={\displaystyle \frac{h^2-a_2^2-a_3^2}{2a_2{a}_3}}=au{x}_2$$

(18)

Or:

$$\cos \left({\theta }_3\right)={\displaystyle \frac{p_x^2+p_y^2+{\left(p_z-d_1\right)}^2-a_2^2-a_3^2}{2a_2{a}_3}}=au{x}_2$$

(19)

Therefore:

$${\theta }_3={\tan }^{-1}\left({\displaystyle \frac{\pm \sqrt{1-au{x}_2^2}}{au{x}_2}}\right)$$

(20)

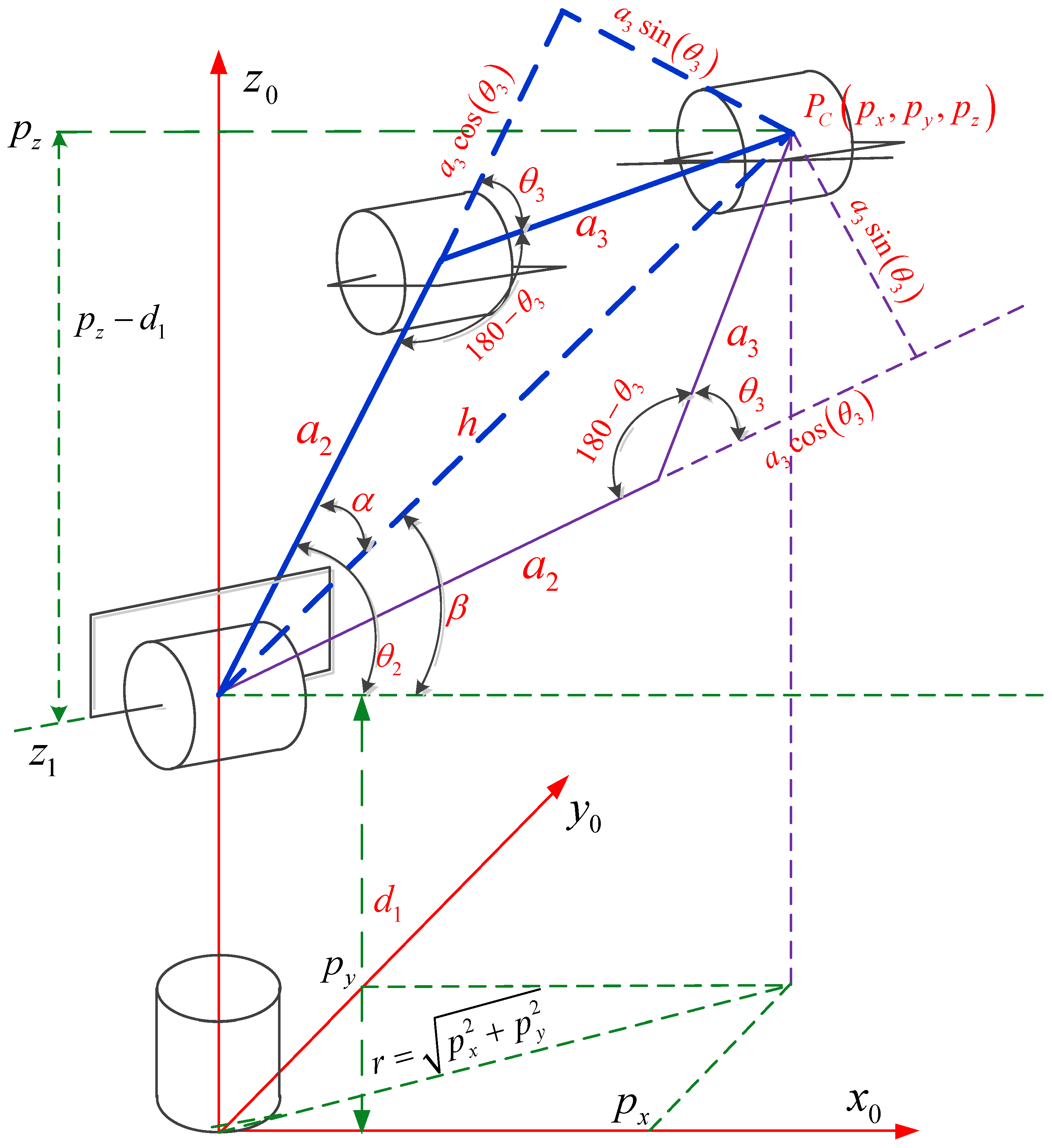
3.2.2. Elbow Up Configuration

The solution for the elbow up configuration was derived using a geometric method, as shown in Figure 4.

By applying the same analysis used for the elbow down configuration, ${\theta }_2$ can be determined from Figure 4.

$${\theta }_2=\beta +\alpha ,$$

(21)

where

$$\beta =Ta{n}^{-1}\left({\displaystyle \frac{p_z-d_1}{\sqrt{p_x^2+p_y^2}}}\right),$$

(22)

and by applying the Law of Cosines, we obtain:

$$\cos \left(\alpha \right)={\displaystyle \frac{a_2^2+h^2-a_3^2}{2a_{2}h}}=au{x}_3,$$

(23)

$$\alpha ={\tan }^{-1}\left[{\displaystyle \frac{\pm \sqrt{1-{\cos }^2\left(\alpha \right)}}{\cos \left(\alpha \right)}}\right]$$

(24)

Or

$$\alpha ={\tan }^{-1}\left({\displaystyle \frac{a_3\sin \left({\theta }_3\right)}{a_2+a_3\cos \left({\theta }_3\right)}}\right)$$

(25)

By substituting Equations (22) and (24) into (25), the expression for ${\theta }_2$ can be derived as:

$${\theta }_2=\beta +\alpha ={\tan }^{-1}\left({\displaystyle \frac{p_z-d_1}{\sqrt{p_x^2+p_y^2}}}\right)+{\tan }^{-1}\left({\displaystyle \frac{\pm \sqrt{1-au{x}_3^2}}{au{x}_3}}\right)$$

(26)

Following the same reasoning:

$${\theta }_2=\beta +\alpha ={\tan }^{-1}\left({\displaystyle \frac{p_z-d_1}{\sqrt{p_x^2+p_y^2}}}\right)+{\tan }^{-1}\left[{\displaystyle \frac{a_3\sin \left({\theta }_3\right)}{a_2+a_3\cos \left({\theta }_3\right)}}\right]$$

(27)

From the geometric construction in Figure ${\theta }_3$, it is derived that:

$$\cos \left({\theta }_3\right)={\displaystyle \frac{h^2-a_2^2-a_3^2}{2a_2{a}_3}}=au{x}_4$$

$${\theta }_3={\tan }^{-1}\left({\displaystyle \frac{\pm \sqrt{1-au{x}_4^2}}{au{x}_4}}\right)$$

(28)

3.2.3. Inverse Orientation Kinematics

The orientation of the end-effector is determined by the last two joints of the robot. To compute ${\theta }_4$ and ${\theta }_5$, we assumed the following:

$${}^{0}R_5={}^{0}R_1{}^{1}R_2{}^{2}R_3{}^{3}R_4{}^{4}R_5={}^{0}R_3{}^{3}R_5$$

(29)

where

$${}^{0}R_3={}^{0}R_1{}^{1}R_2{}^{2}R_3$$

$${}^{3}R_5={}^{3}R_4{}^{4}R_5$$

The rotation matrix ${}^{0}R_3$ obtained from (29) is equal to the desired rotation matrix U:

$${}^{3}R_5\left({\theta }_4,{\theta }_5\right)={}^{0}R_3^T{}^{0}R_5=U=\left[\begin{array}{ccc}u\left(1,1\right)& u\left(1,2\right)& u\left(1,3\right)\\ u\left(2,1\right)& u\left(2,2\right)& u\left(2,3\right)\\ u\left(3,1\right)& u\left(3,2\right)& u\left(3,3\right)\end{array}\right]$$

(30)

The matrix ${}^{3}R_5\left({\theta }_4,{\theta }_5\right)$ is calculated from the forward kinematics (3); therefore:

$${}^{3}R_5\left({\theta }_4,{\theta }_5\right)=\left[\begin{array}{ccc}\cos {\theta }_4\cos {\theta }_5& -\cos {\theta }_4\sin {\theta }_5& -\sin {\theta }_4\\ \sin {\theta }_4\cos {\theta }_5& -\sin {\theta }_4\sin {\theta }_5& \cos {\theta }_4\\ -\sin {\theta }_5& -\cos {\theta }_5& 0\end{array}\right]=\left[\begin{array}{ccc}u\left(1,1\right)& u\left(1,2\right)& u\left(1,3\right)\\ u\left(2,1\right)& u\left(2,2\right)& u\left(2,3\right)\\ u\left(3,1\right)& u\left(3,2\right)& u\left(3,3\right)\end{array}\right]$$

(31)

From Equation (31), the angle ${\theta }_4$ can be determined provided that u(2,3) ≠ 0

$${\displaystyle \frac{{}^{3}R_5\left(1,3\right)}{{}^{3}R_5\left(2,3\right)}}={\displaystyle \frac{-\sin {\theta }_4}{\cos {\theta }_4}}=\tan {\theta }_4=-{\displaystyle \frac{u\left(1,3\right)}{u\left(2,3\right)}}$$

Then,

$${\theta }_4={\tan }^{-1}\left[-{\displaystyle \frac{u\left(1,3\right)}{u\left(2,3\right)}}\right]$$

(32)

By applying the same procedure, ${\theta }_5$ is derived under the condition that $u\left(3,2\right) \ne 0$

$${\displaystyle \frac{{}^{3}R_5\left(3,1\right)}{{}^{3}R_5\left(3,2\right)}}={\displaystyle \frac{-\sin {\theta }_5}{\cos {\theta }_5}}=\tan {\theta }_5=-{\displaystyle \frac{u\left(3,1\right)}{u\left(3,2\right)}}$$

Hence, the rotation matrix can be written as:

$${\theta }_5={\tan }^{-1}\left[-{\displaystyle \frac{u\left(3,1\right)}{u\left(3,2\right)}}\right]$$

(33)

This kinematic model establishes the mathematical foundation for the DOFBOT manipulator and illustrates the inherent complexity of the robotic motion analysis. For students in mechatronics, understanding forward and inverse kinematics can be conceptually challenging, which often hinders their ability to intuitively grasp how robots move and interact with their environment. Although complete derivations of these equations are available in the cited literature [23,24], here, we include a summarized version to contextualize their application in the DOFBOT educational platform. The inclusion of the kinematic model in our system is therefore not merely descriptive but directly functional, and the forward and inverse kinematics equations are applied to convert the quadrant coordinates identified by the VLM into specific joint angles for the manipulator to execute. In this manner, abstract mathematical formulations are transformed into executable motor commands, bridging theory and practice. From an educational perspective, this integration demonstrates how theoretical formulations can be operationalized in real experiments, reinforcing students’ understanding of both mathematics and its practical application. Therefore, in the following section, shifts from abstract derivations to their concrete implementation in an experimental setup, where a VLM and symmetry-informed strategies are employed to lower the entry barrier and make the learning of vision, kinematics, and control more accessible.

4. System Architecture and Methodology

Building on these theoretical foundations, this section introduces an experimental platform that operationalizes kinematic concepts through a VLM-driven, symmetry-informed control architecture. This setup enables students to directly experience how abstract equations translate into robotic movements, reinforcing their understanding of both mathematics and its real-world applications.

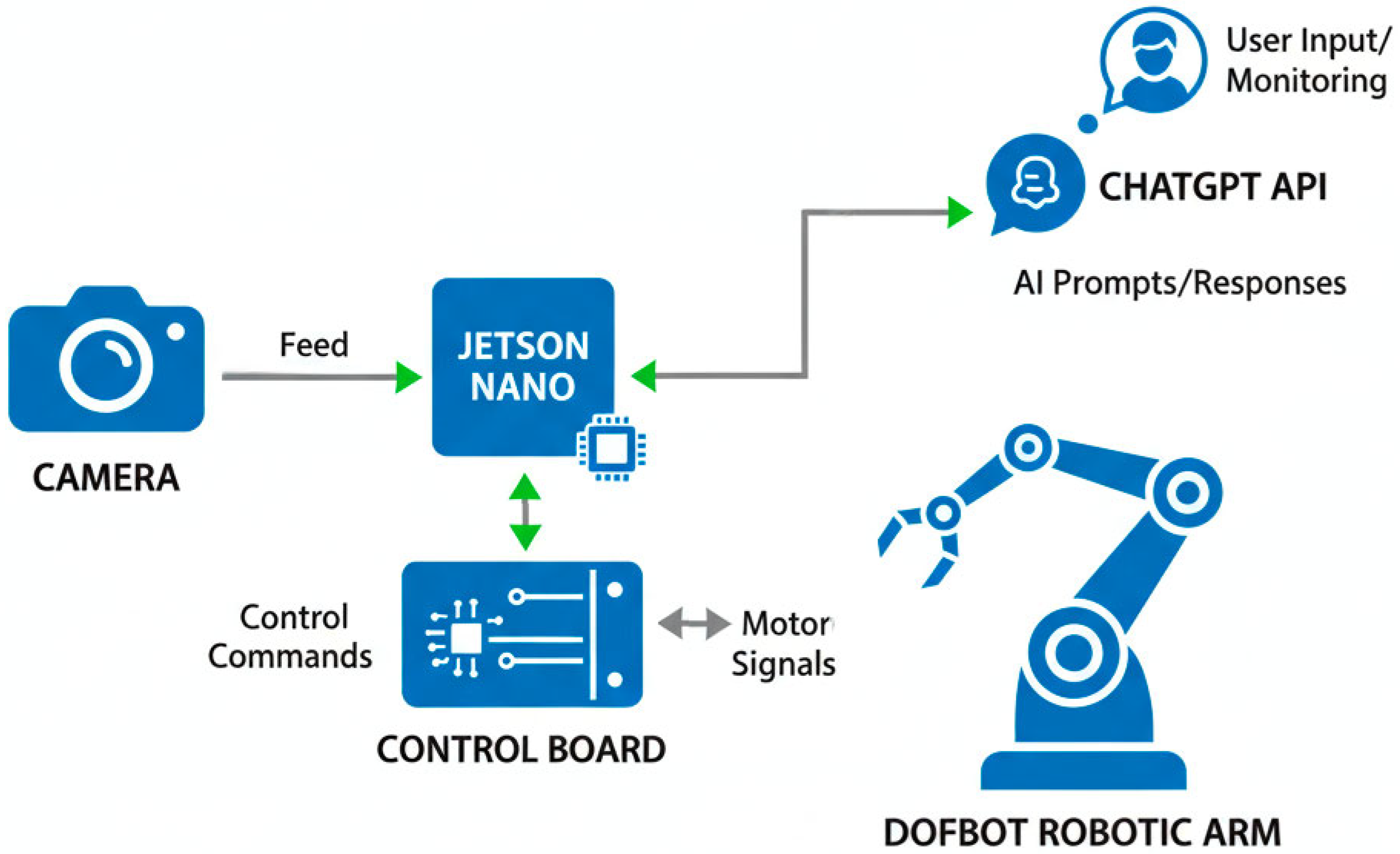
4.1. Experimental Platform

The system is built upon the Yahboom DOFBOT, a 5-DOF educational robotic arm that serves as the primary manipulation device. The core of the system’s processing is the Jetson Nano platform, leveraging an NVIDIA GPU for real-time image processing. A standard USB camera connected to the Jetson Nano provided visual input to the system. The experimental workspace consisted of a circular color map, as shown in Figure 5, which was used as the target object for localization and manipulation tasks.

To provide a more straightforward overview of the experimental platform,

Table 2. Physical and technical parameters of the DOFBOT robotic arm.

Parameter	Specification
Master control	Jetson Nano 4 GB
Operating system	Ubuntu + ROS
Programming language	Python
Communication method	Wi-Fi network
Robotic arm material	Anodized aluminum
Size	272 × 135 × 473 mm
Gripper open-close	60 mm
Total weight of the robot	1256 g (without controller)
Power solution	12 V 5 A power adapter
Degrees of freedom (DOF)	5 DOF + gripper
Payload	200 g
Repeatable positioning accuracy	±0.5 mm
Servo accuracy	≤0.1 degree

summarizes the main physical and technical parameters of the DOFBOT 5-DOF robotic arm used in this study. These specifications contextualize the platform’s capabilities and ensure the transparency and reproducibility of the experimental setup.

The choice of DOFBOT, an educational robotic arm, highlights the platform’s accessibility and suitability for engineering education contexts. This design decision highlights the dual contribution of the system: not only a research prototype for VLM-driven interaction, but also a teaching tool that reduces entry barriers for mechatronics students learning robotics concepts such as kinematics, vision, and control.

4.2. System Workflow

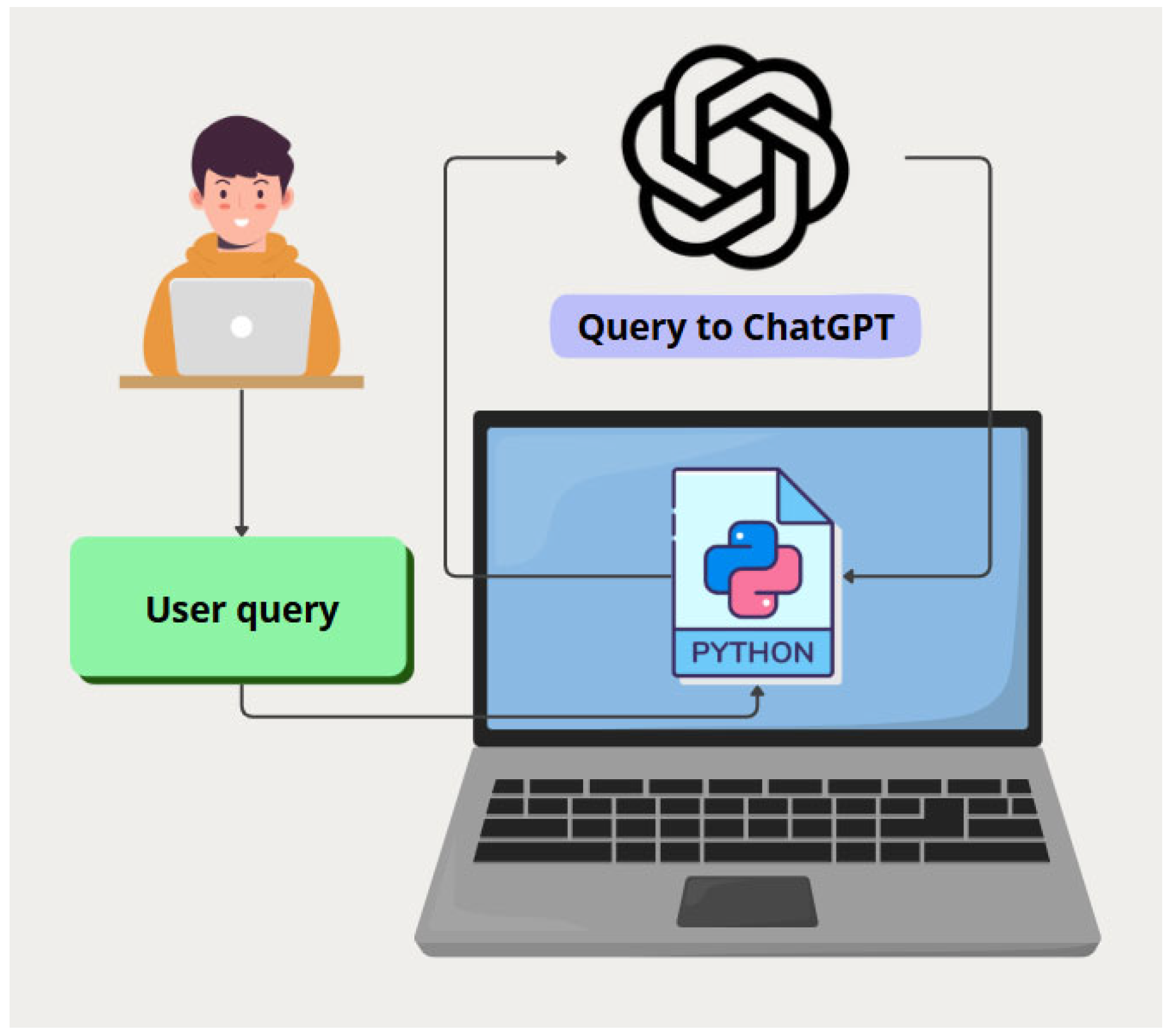
The operational workflow illustrated in Figure 6 facilitates the interaction between the user and the robotic arm. The process begins when a user provides a high-level command in natural language (e.g., “point to the orange color”) on a host computer. This command is transmitted via a socket connection to a Python 3.13.8 script running on the Jetson Nano.

The script executes two key functions: (i) it captures a real-time image of the workspace and (ii) it integrates the user’s command into an engineered prompt for the language model. Instead of directly returning pixel-level coordinates, the VLM identifies the relevant quadrant of the symmetrical color wheel where the target color is located. The system then associates the quadrant with its geometric center, which is used as the reference position. Finally, Jetson Nano translated this reference position into joint commands for the DOFBOT control board, driving the arm to the specified location. The interaction with VLM was implemented using the OpenAI API, specifically GPT-4o.

Figure 7 presents a schematic representation of the system workflow, complementing the textual description above. The diagram illustrates the interaction between the user, VLM, deterministic geometric calculation, and the robotic execution pipeline.

4.3. Hybrid Symmetry-Informed Localization Strategy

Our methodology employs a hybrid, symmetry-informed strategy that leverages the respective strengths of the VLM and traditional algorithmic processing. This approach was explicitly designed to exploit the inherent geometric properties of an experimental workspace. The localization task is decoupled into semantic identification and symmetry-based calculation phases.

4.3.1. VLM-Based Semantic Identification

The primary role of the VLM is to achieve high-level scene understanding. A Python script sent the captured image along with a direct and minimal conversational prompt to the VLM. The prompt asks the VLM to identify which quadrant of the color wheel corresponds to a given color name (e.g., “blue-green”). The VLM’s strength in natural language and contextual reasoning enables it to accurately interpret visual information and return a semantic label for the target region (e.g., “the lower-left quadrant”).

To ensure robustness and reproducibility, the prompt design followed a few-shot prompting strategy that combined the user’s request with contextual instructions. This approach was applied only at the textual level, using exemplar prompts to guide the VLM, whereas visual data were processed directly without additional few-shot training. The prompts explicitly framed the workspace as a color wheel divided into four quadrants. In this way, symmetry-related information is embedded at the semantic level to guide the VLM’s disambiguation of the user command. Simultaneously, the actual exploitation of symmetry for precise localization is systematically automated in the subsequent geometric calculation stage.

The semantic disambiguation process was implemented using a socket-based connection to a Python script. The script transmits the prompt and image to the VLM, which returns a semantic label indicating the target quadrant. This label serves as an intermediate bridge between the natural language input and the subsequent geometric stage, where the centroid coordinates and joint angles are computed. In this way, the VLM output is used exclusively as semantic guidance, while all geometric reasoning is performed deterministically in the following stage.

To ensure consistency and facilitate integration with deterministic algorithms, the prompt design constrains the VLM output to a predefined set of quadrant labels. This closed structure minimizes ambiguity and prevents open-ended responses. In cases where the VLM returned an output outside the expected domain, the system activated a “not recognized” state and prompted the user to provide new input. This mechanism maintains robustness and ensures reliable communication between the semantic and geometric stages.

4.3.2. Symmetry-Based Geometric Calculation

Once the VLM returns the semantic quadrant identifier, a deterministic function within the Python script is executed. This function leverages the predefined symmetry of the color wheel. Because the workspace object and its quadrants are geometrically regular, the script can use a simple hard-coded model of these symmetrical shapes. Based on the VLM’s semantic input, the script selects the appropriate quadrant and algorithmically calculates its precise geometric center (centroid).

The implementation of this hybrid symmetry-informed architecture is realized through a modular communication pipeline that integrates the semantic reasoning of the Visual Language Model (VLM) with the deterministic geometric computation layer. As shown in Figure 6, Figure 7 and Figure 8, the workflow begins when the user issues a natural language command accompanied by an image captured by the robot’s camera. The VLM, accessed through the OpenAI API, interprets this multimodal input and returns a symbolic label (e.g., “lower-left quadrant”) that represents the target region within the symmetrical workspace.

This output is then processed by a Python-based deterministic module, which calculates the centroid coordinates of the identified region and applies inverse kinematics to determine the required joint angles for robotic movement. The Jetson Nano executes these motor commands in real time through a socket-based connection, ensuring synchronized communication between semantic reasoning, geometric precision, and robotic control.

The overall algorithm of this hybrid architecture is summarized in

Table 3. Symmetry-Informed Hybrid Localization and Control Workflow.

Step	Description
Input:	user_prompt, scene_image
Output:	joint_angles [θ1 … θ5]
1. Capture workspace image	The Jetson Nano captures a real-time image from the DOFBOT’s camera.
2. Compose multimodal prompt	The user’s natural-language instruction and the captured image are integrated into a structured multimodal prompt with symmetry context.
3. Semantic reasoning	The prompt is sent to the Visual Language Model (VLM) via API for semantic disambiguation and quadrant identification. Expected output: one of {upper_left, upper_right, lower_left, lower_right}
4. Validate VLM output	The output is checked for consistency; if the label is outside the expected domain, the system requests new input.
5. Symmetry-based geometric computation	The system calculates the centroid of the identified quadrant using the predefined symmetry of the color wheel.
6. Deterministic inverse kinematics	Using the DH parameters, the deterministic layer computes the corresponding joint angles.
7. Command packaging and transmission	The joint-angle command is formatted and transmitted via TCP to the DOFBOT control server.
8. Robotic execution	The DOFBOT executes the command in real time through the control library.
9. End process	The operation status is returned after successful motion execution.

, which formalizes the interaction between the VLM-based semantic reasoning and the deterministic geometric control layers.

This division of labor between the VLM and the deterministic computation layer embodies the essence of the proposed hybrid methodology. By assigning the VLM to handle high-level semantic disambiguation and the deterministic script to enforce geometric symmetry and control accuracy, the system achieves reproducibility and interpretability while maintaining low computational cost. This workflow demonstrates how symmetry can be imposed by design, providing a practical bridge between multimodal generative reasoning and classical kinematic control in educational robotics.

This hybrid strategy effectively uses the VLM as a semantic sensor to handle the ambiguous part of the task while relying on robust deterministic code to perform efficient calculations based on the object’s known symmetry. Here, the notion of a “semantic sensor” is metaphorical. Unlike a physical sensor, which measures environmental variables and produces quantitative data, the VLM provides a contextual interpretation that complements rather than replaces traditional sensing.

This deliberate division of labor makes the system both intelligent and reliable, representing a novel design choice compared with prior approaches that rely exclusively on end-to-end training or purely algorithmic methods. From an educational perspective, it also exemplifies how combining generative AI with deterministic algorithms can provide students with practical insight into building hybrid intelligent systems. In this way, the proposed architecture is not only technically robust and lightweight but also creative and pedagogically valuable, as it makes advanced robotics concepts more approachable in accessible learning environments. Importantly, this integration of symmetry is imposed by the design rather than learned by the VLM, and the entire process is automated within the Python script, eliminating the need for manual preprocessing.

5. Results

This section presents a case study that demonstrates the effectiveness of the proposed hybrid symmetry-informed localization strategy. The experiments validated the system’s ability to translate high-level natural language commands from a user into precise robotic actions. Four representative colors were selected from the color map—blue-green, orange, yellow, and purple—allowing us to illustrate the workflow and assess the consistency and ease of use of the system.

In the first experiment, the user initiated the process with a conversational command, following the hybrid strategy described in Section 4.3. The query was forwarded to the VLM, which correctly performed semantic identification by associating color with the right quadrant. This label was then processed by the local Python script, which used the predefined symmetry of the workspace to calculate the geometric center of the identified quadrant (see Figure 8). The coordinates were translated into motor commands, enabling the DOFBOT arm to precisely point to the target position.

The procedure was repeated for orange color. Once again, the VLM successfully identified the correct region of the color map, returning the label to the upper-right quadrant. The local script then computed the centroid of this quadrant, and DOFBOT executed the pointing action accurately, demonstrating the robustness of the pipeline (Figure 9).

The final two cases involved yellow and purple colors. In both trials, VLM reliably identified the correct quadrants (lower right for yellow and upper left for purple). The deterministic geometric calculation ensured the accurate localization of the quadrant centers, which were consistently reached by the robotic arm (Figure 10). The successful execution of all four commands across symmetrical regions of the workspace confirms the reliability of the hybrid strategy in handling natural language instructions.

To complement the qualitative case study presented earlier, we conducted a series of 30 experiments involving participants from diverse educational backgrounds, including undergraduate and high school students, as well as faculty members from the School of Electromechanical Engineering. The evaluation focuses on the effectiveness, usability, and latency of the proposed hybrid strategy.

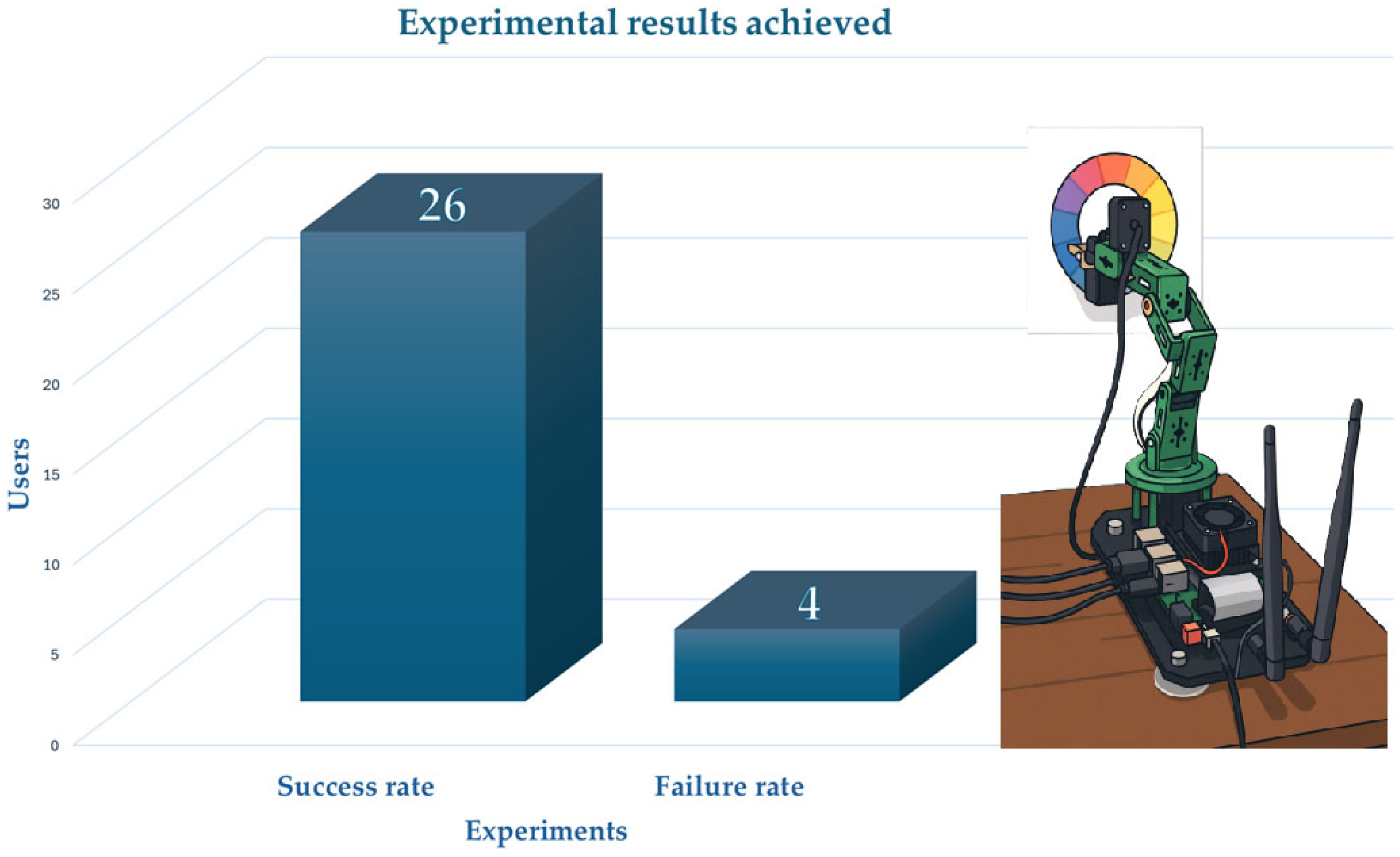
The results (see Figure 11) show a success rate of 86.7% (26 of 30 trials), indicating that the manipulator robot successfully reached the color requested by the user. In the remaining 13.3% of the trials (4 of 30), the objective was not achieved. These failures were primarily attributed to inadequate lighting conditions and, in some cases, to the formulation of unstructured prompts during interaction.

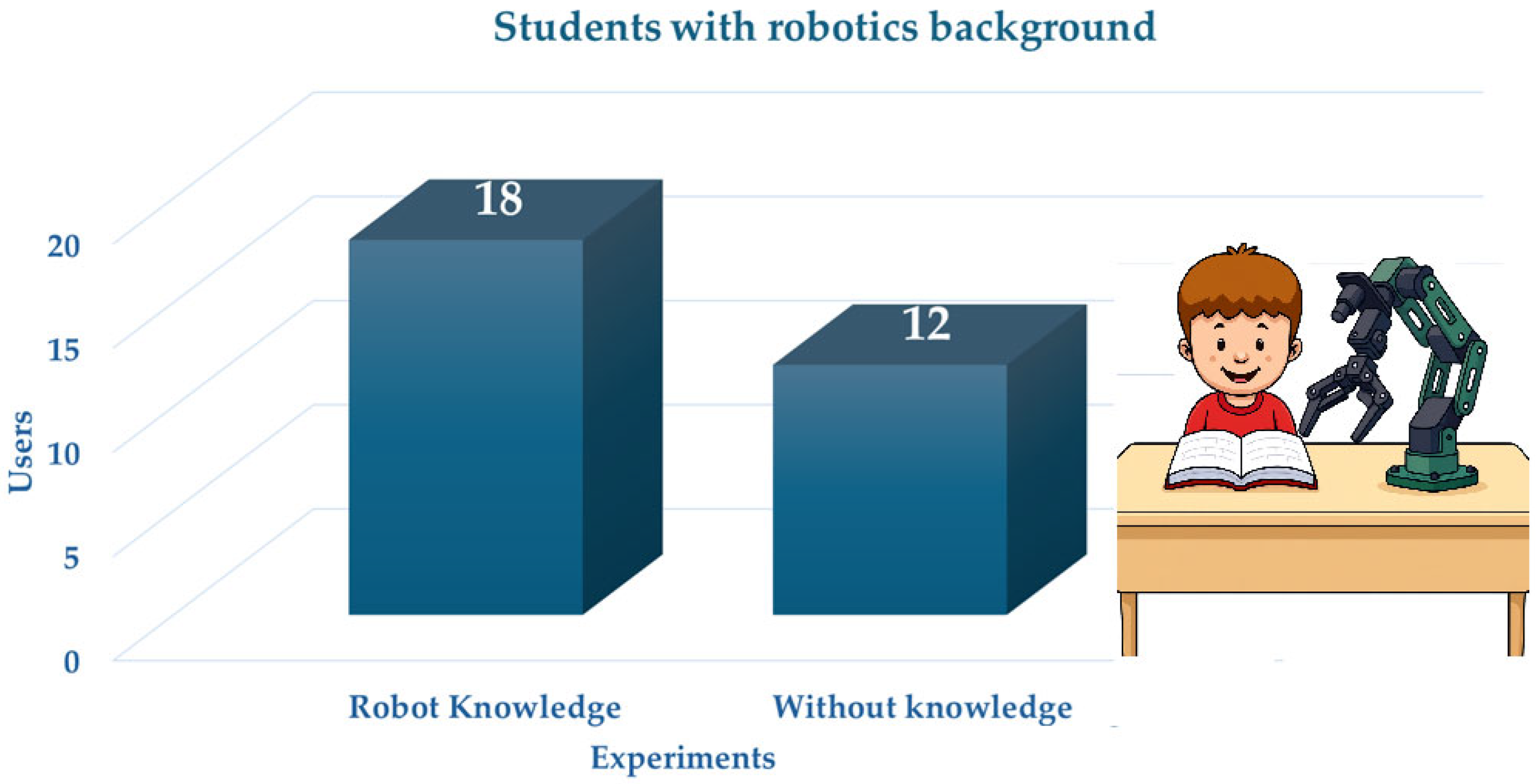
Regarding participant profiles, 60% (18 out of 30) reported having general knowledge of manipulator kinematics, whereas 40% (12 out of 30) had only basic notions of manipulator applications without formal knowledge of kinematic modeling. This distribution (see Figure 12) highlights the accessibility of the system to users with limited prior technical expertise.

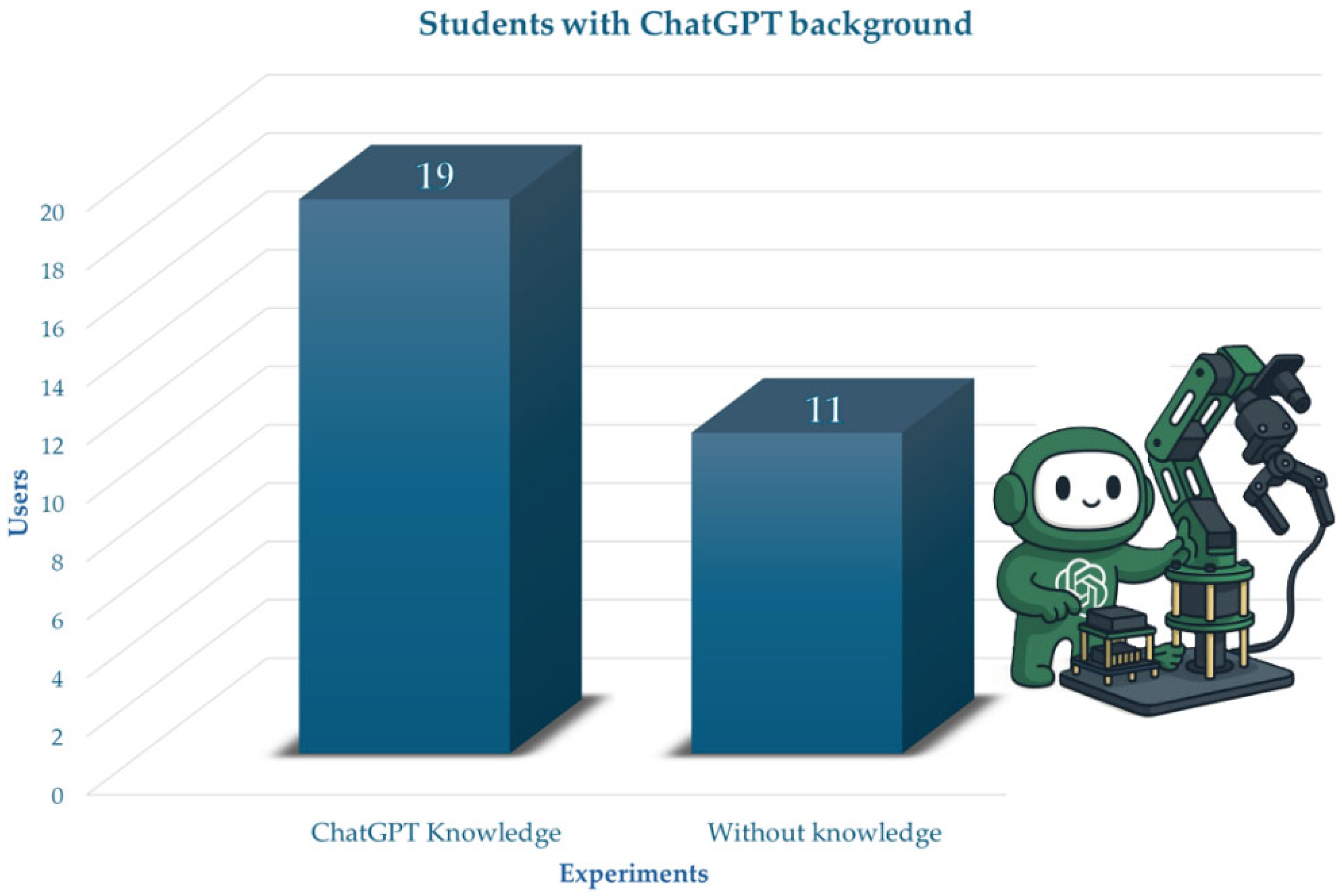
The same sample revealed that 19 participants habitually used ChatGPT for both information retrieval and program development related to robotic applications. In comparison, 11 participants reported using it primarily as an information search tool, as shown in Figure 13. These findings demonstrate that the natural language interface enables intuitive interaction without requiring prior specialization in robotics or experience with ChatGPT.

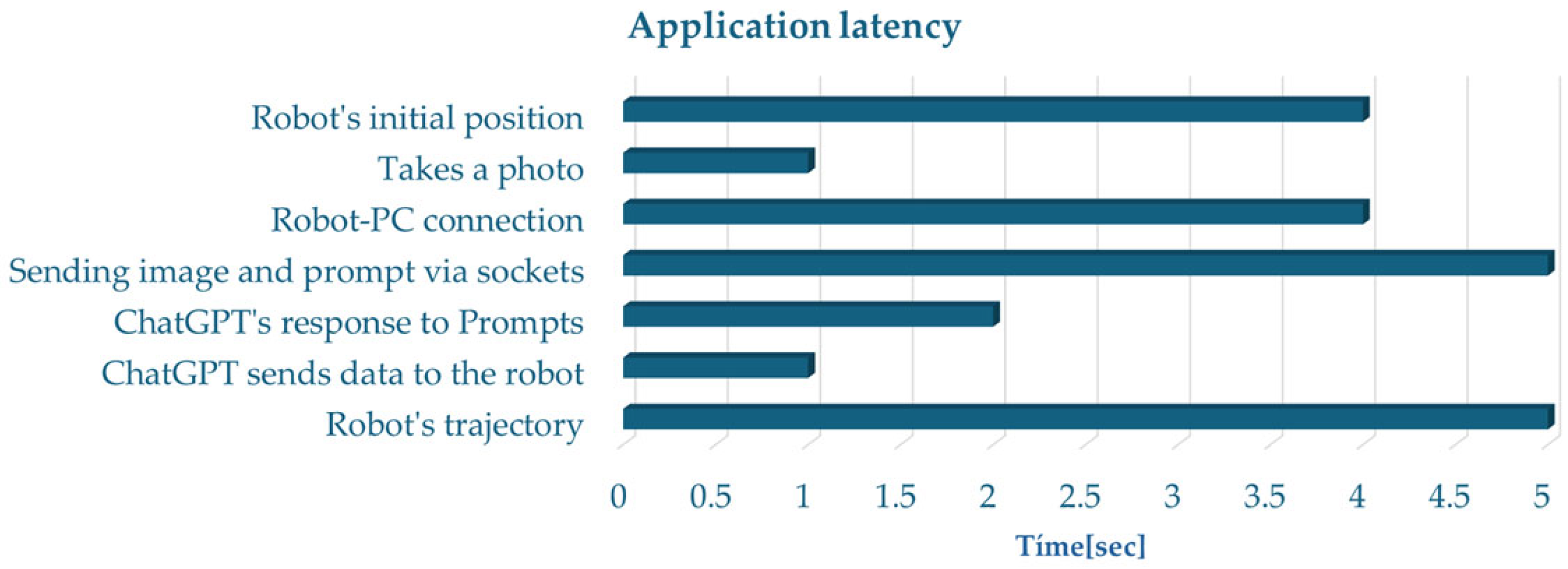
Finally, we measured the system’s latency across the entire perception–action loop (see Figure 14). The average total execution time was 22 s, which included prompt processing, visual analysis, and robotic motion. When only prompt updates are required, the latency decreases to 13 s, reflecting the efficiency of the pipeline under repeated interactions.

To further assess the robustness of the proposed methodology, we compared its performance with that of a baseline implementation using OpenCV. The OpenCV-based method requires manual color calibration for each tone and is highly sensitive to changes in illumination, often resulting in inconsistent results. By contrast, the hybrid VLM and symmetry-informed strategies proved to be more resilient under different lighting conditions and eliminated the need for manual calibration.

Table 4. Comparative analysis between the OpenCV baseline and the proposed method.

Condition/Metric	OpenCV (Baseline)	Proposed Method
Programming effort	Major	Minor
Robustness to illumination	No	Yes
Need for color calibration	Required	Not required

summarizes the most significant differences between the two approaches, demonstrating that our method substantially reduces the programming effort while enhancing robustness and usability.

Beyond verifying operational feasibility, these quantitative results demonstrate the methodological soundness of the proposed hybrid reasoning pipeline. The consistent success rate and low latency confirm that the deterministic geometric layer and the VLM-based semantic reasoning module interact effectively and reproducibly, validating the integration of symmetry-informed computation with generative AI reasoning as a robust and scalable approach for educational robotics.

Overall, this extended evaluation provides robust evidence for the feasibility of the proposed approach. The system demonstrates technical effectiveness by demonstrating how simple conversational prompts can be transformed into accurate robotic actions through the integration of VLM-based semantic identification and symmetry-based deterministic computation. From an educational perspective, the results underscore the teaching value of the system: students or novice users can experience a complete perception–action loop without needing to understand the underlying programming of the kinematics or vision processes. This abstraction of technical complexity enables learners to shift their focus from debugging code to understanding higher-level robotics concepts such as task sequencing, logical reasoning, and the interplay between natural language and robotic control. Thus, the study confirms both the feasibility of the hybrid strategy and its potential to enhance the teaching and learning of mechatronics and artificial intelligence.

6. Discussion

The innovation of this study resides not in the mechanical design of the robotic components or the conventional kinematic formulations themselves, but in their methodological integration within a hybrid architecture that combines deterministic and generative approaches. As detailed in Section 4.3 and illustrated in Figure 6, Figure 7 and Figure 8, the proposed framework establishes a modular communication pipeline connecting the VLM reasoning module with the deterministic inverse kinematics layer. This real-time interaction (where semantic outputs from the VLM are transformed into precise robotic actions) demonstrates the methodological novelty of the approach.

By explicitly coupling symmetry-informed geometric reasoning with multimodal VLM-based semantic understanding, the system introduces a reproducible and lightweight architecture that bridges classical robotics principles and modern generative AI reasoning. This design ensures transparency, scientific rigor, and educational value, exemplifying how hybrid AI–robot integration can be achieved without the complexity of end-to-end training.

The results confirm the efficacy of the proposed symmetry-informed strategy in translating high-level user commands into precise robotic actions. The strength of this approach lies in its explicit division of labor: semantic reasoning is handled by VLM, whereas deterministic algorithms perform geometry-based calculations. This design makes symmetry an integral part of the system rather than a property that must be inferred or approximated.

In contemporary robotics research, a central challenge is to enable agents to exploit symmetry through learned invariant policies. For instance, Mittal et al. [11] explored task-symmetric reinforcement learning, aiming to teach robots to generalize behaviors under transformations such as mirrored locomotion. Although conceptually powerful, these approaches often require complex model architectures, large datasets, and significant computational resources to ensure that the agent consistently internalizes symmetry.

This paper presents a pragmatic alternative. Instead of relying on end-to-end training for symmetry-aware behavior, symmetry is imposed by the design. The VLM is used only for the semantic disambiguation of natural language commands, while the deterministic script exploits the perfect geometric regularity of the workspace to compute precise targets. This hybrid approach deliberately bypasses the difficulties of learning symmetry, yielding a lightweight and reliable solution, particularly in structured environments.

Furthermore, this study highlights the originality of the proposed symmetry-informed prompting strategy. By deliberately combining VLM-based semantic reasoning with deterministic, symmetry-informed computation, the system introduces a hybrid architecture that differs from prior approaches, which rely solely on data-intensive training or algorithmic methods. This contribution advances LLM/VLM research by demonstrating a lightweight and pragmatic approach to multimodal reasoning while also benefiting robotics education through its accessible and reproducible implementation. This dual contribution underscores the originality of the work and clarifies its value for both technical innovation and pedagogical practice.

Importantly, this distinction has substantial implications in educational contexts. Although learning symmetric policies through deep reinforcement learning (DRL) is a long-term research objective, our method demonstrates to students how fundamental geometric principles can be integrated with modern AI tools to achieve robust, symmetrically consistent robotic behavior. This design situates our work within the emerging paradigm of human–GenAI–robot interaction, where generative AI acts as a cognitive bridge between natural human commands and robotic execution. This illustrates the pedagogical value of combining explicit mathematical models with generative AI, demonstrating that effective interaction can be realized without the overhead of complex training pipelines.

In addition to validating technical feasibility, the experimental outcomes also provide empirical evidence of the effectiveness of the hybrid reasoning pipeline. The consistent success rate and low latency observed across trials demonstrate not only the robustness of the deterministic layer but also the reliability of VLM-based semantic reasoning under real-world interaction. These results go beyond confirming functional correctness; they validate the practical advantages of integrating generative reasoning and geometric computation, supporting the proposed framework as both a scientific and educational contribution.

Beyond the technical feasibility, the results also reveal preliminary insights into the educational dimensions of the system. The distribution of participants’ knowledge levels and their consistent ability to successfully interact with the robot through natural language indicate that the proposed interface reduces the dependence on prior technical expertise. This supports the claim that the system lowers the entry barrier for learning robotic concepts, such as vision and kinematics. Nevertheless, these findings should be interpreted as initial indicators rather than definitive evidence of educational outcomes. Future work will therefore focus on formal pedagogical evaluation, incorporating metrics such as learning gains, cognitive load, and student engagement to quantitatively measure their impact on mechatronics education.

A key limitation of the present system is its reliance on a structured and symmetrical environment. Deterministic geometric stages cannot be directly applied to scenarios with irregular objects or unstructured layouts. Addressing such conditions will require additional perception modules, adaptive learning methods, or integration with general vision-based localization strategies. We acknowledge this boundary as an inherent limitation of the current design and identify it as an important direction for future research.

7. Conclusions and Future Work

This study successfully designed, implemented, and demonstrated a robotic manipulation system that leveraged a novel hybrid, symmetry-informed strategy. The core contribution lies in the methodological decoupling of a complex vision-based task: a VLM provides a high-level semantic scene understanding. Simultaneously, a deterministic local script ensures precise geometric calculations, grounded in the symmetry of the workspace. This division of labor effectively positions the VLM as a semantic sensor while preserving the reliability and efficiency of the traditional algorithmic control.

The illustrative case study confirmed that our system can translate simple, natural language commands into accurate robotic actions. Implemented on the DOFBOT educational platform, the system serves a dual purpose. On the one hand, it provides a robust proof of concept for the technical viability of hybrid architectures. On the other hand, it demonstrates strong pedagogical potential by lowering the entry barrier in mechatronics. By abstracting the intricacies of kinematics and low-level coding, the system enables students to engage more directly with advanced concepts, such as AI-driven interaction, task sequencing, and the integration of perception and action. In this way, the platform contributes to the broader vision of human–GenAI–robot interaction, where natural language and generative AI mediate the learning and control of robotic systems.

Future studies will focus on two main tracks. From a technical perspective, we aim to enhance the robustness of the system by extending it to asymmetrical objects and dynamic, unstructured environments. From an educational standpoint, the next step is to conduct controlled user studies with mechatronics students, comparing traditional programming-based methods with the proposed natural language interaction. These studies will include measurable educational metrics such as knowledge acquisition, reductions in cognitive load, and engagement levels. Such evaluations will provide substantial evidence of the system’s ability to lower entry barriers and enhance learning outcomes in engineering education.

Taken together, these directions underscore the dual significance of this work: advancing research in hybrid AI-robotics integration, while contributing to more accessible and practical approaches for engineering education.