Predefined Time Transient Coordination Control of Power-Split Hybrid Electric Vehicle Based on Adaptive Extended State Observer
Abstract
1. Introduction
- (1)
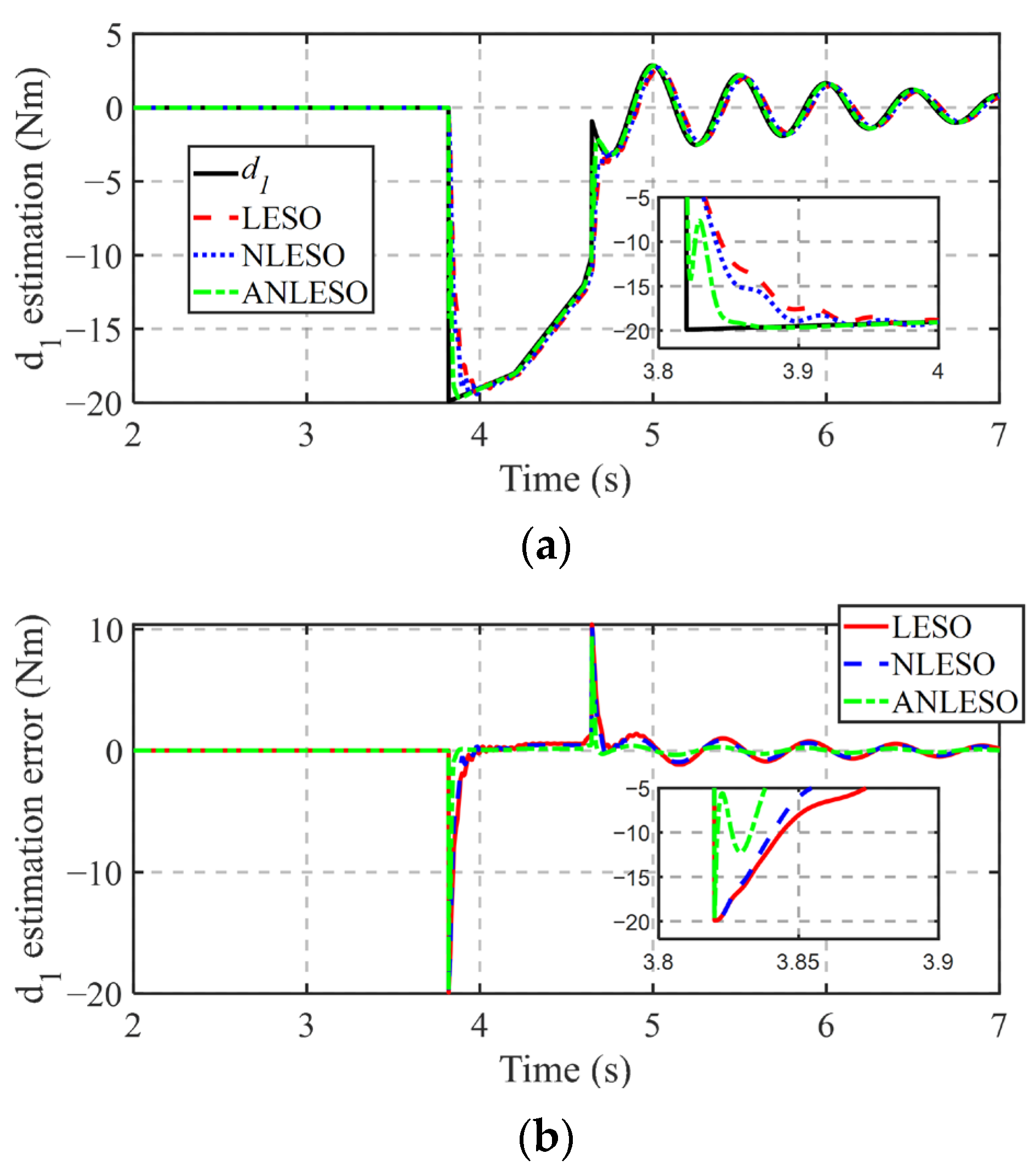
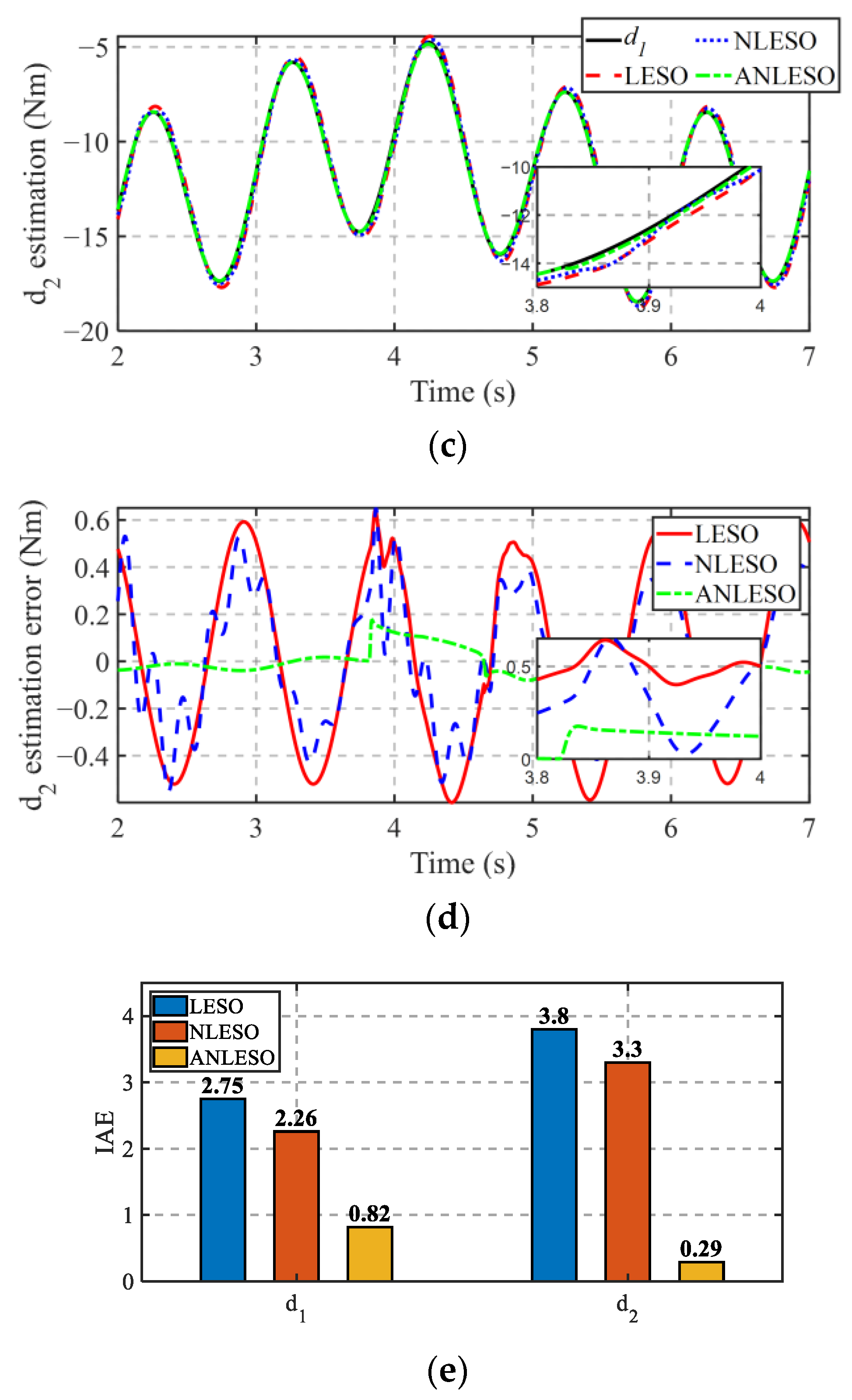
- This paper proposes an ANLESO. An adaptive nonlinear parameter regulator is designed based on adaptive control theory to dynamically adjust the observer gain, thereby achieving high-precision tracking of maximum torque fluctuations. Compared with the conventional LESO, the proposed ANLESO improves the convergence accuracy by 70.2%, while ensuring symmetric convergence of both the sign and magnitude of the estimation error.
- (2)
- Compared to existing transient coordinated control strategies, a predefined-time speed tracking controller dependent on acceleration conditions is designed based on predefined-time control theory. Additionally, external disturbances are compensated to achieve high-quality transient coordinated control for PS-HEVs.
2. Mode Transition Modeling and Problem Description of PS-HEV
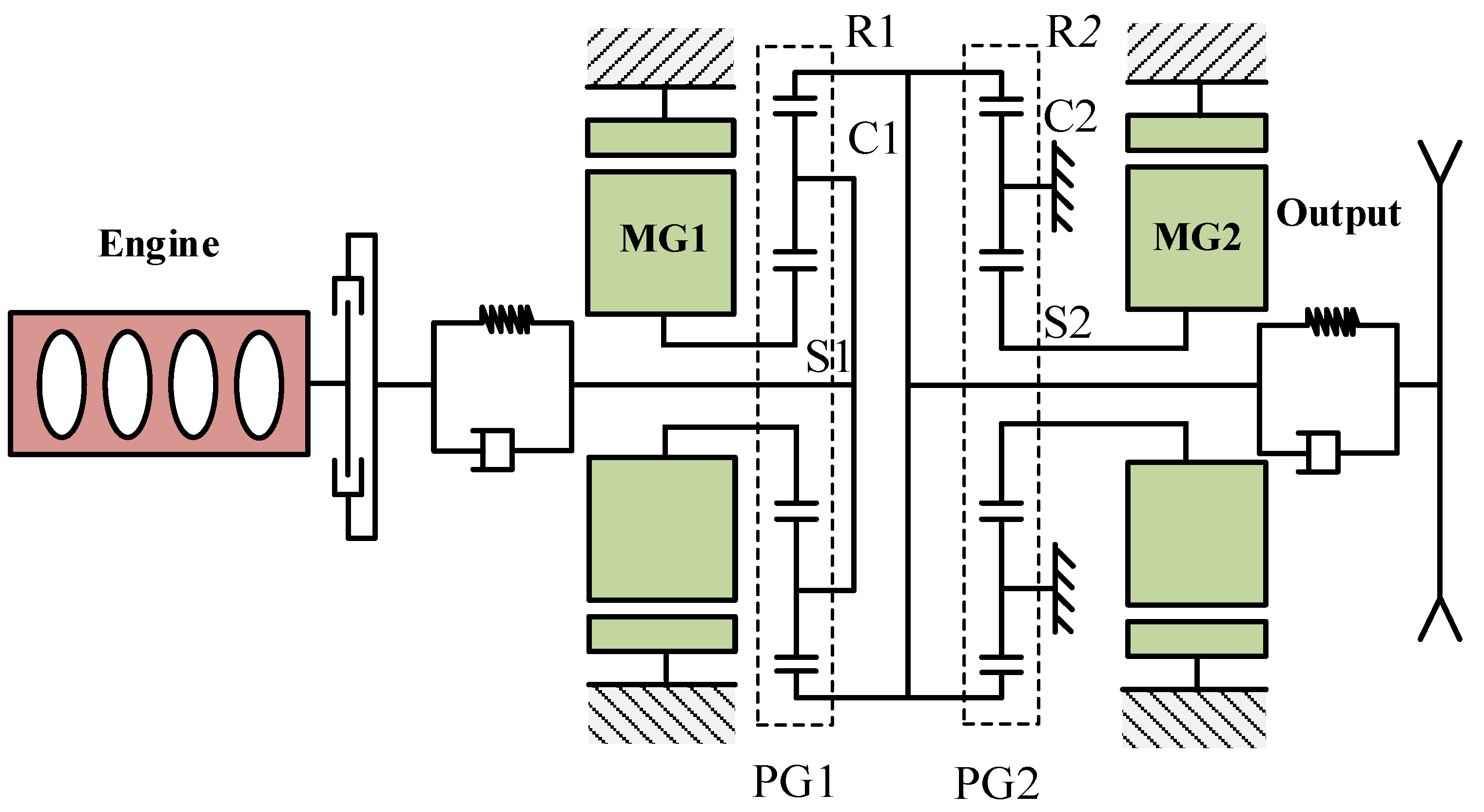
2.1. PS-HEV Drivetrain Model
2.2. Mode Transition Problem Description for PS-HEV
- (1)
- Design an MTP disturbance observer capable of adaptively adjusting the observer gain during mode transition phases to enhance observation accuracy.
- (2)
- Design an MTP controller whose convergence time does not depend on the initial value of the state and can converge at the expected time.
3. Predefined Time Transient Coordination Control of PS-HEV Based on Adaptive Nonlinear Extended State Observer
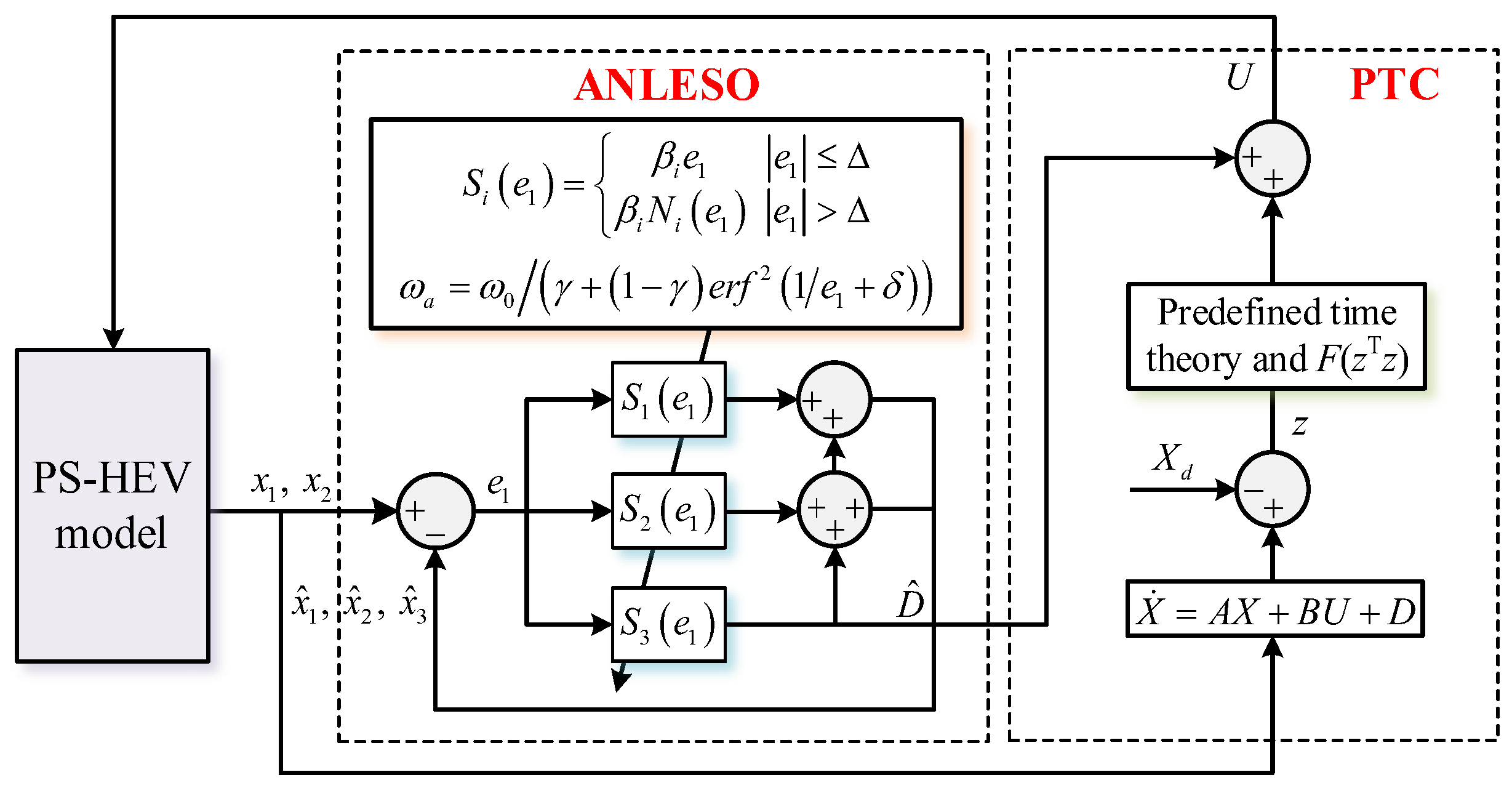
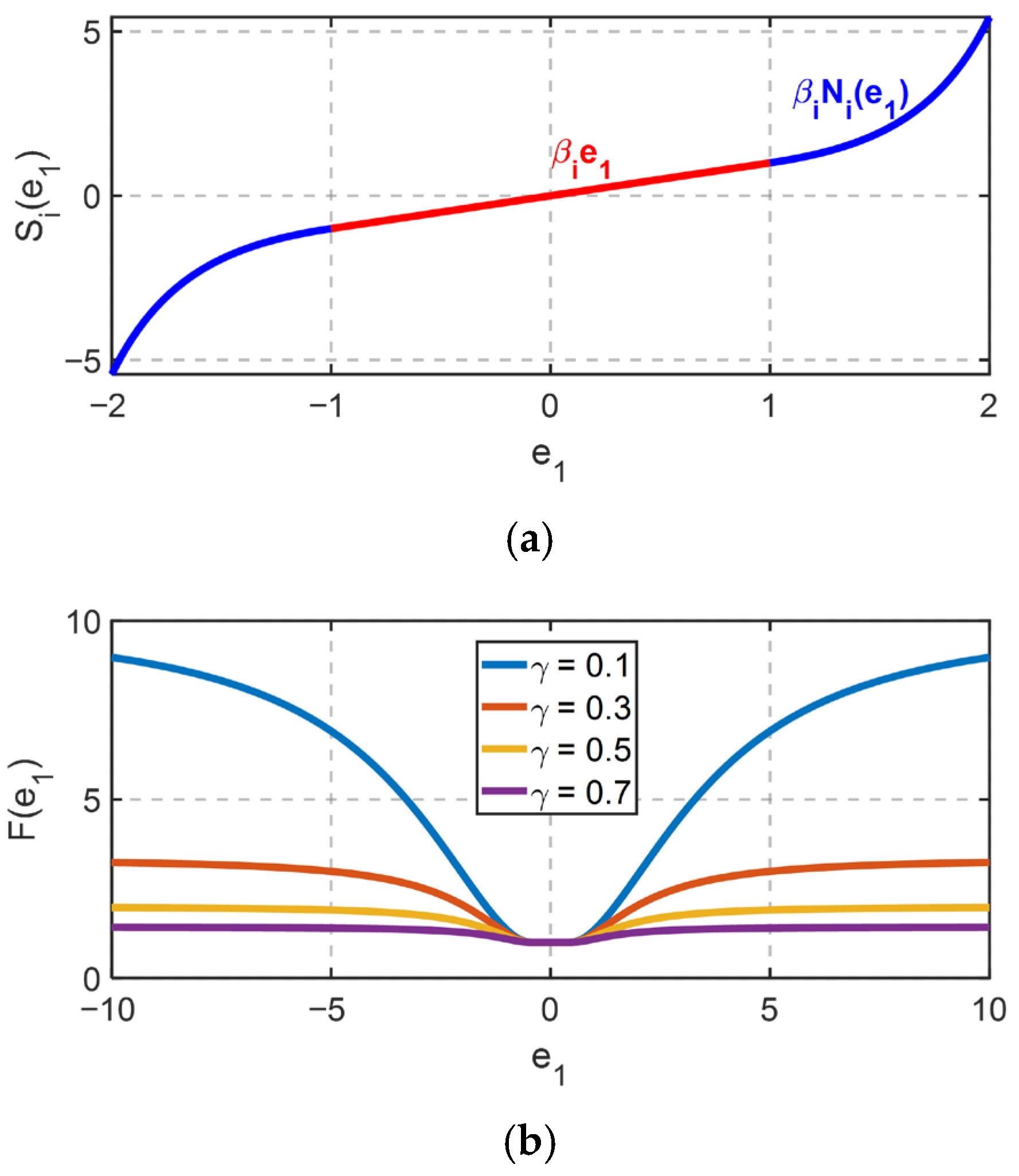
3.1. Design of Adaptive Nonlinear Extended State Observer
3.2. Design of MTP Predefined-Time Controller
4. Results and Discussion
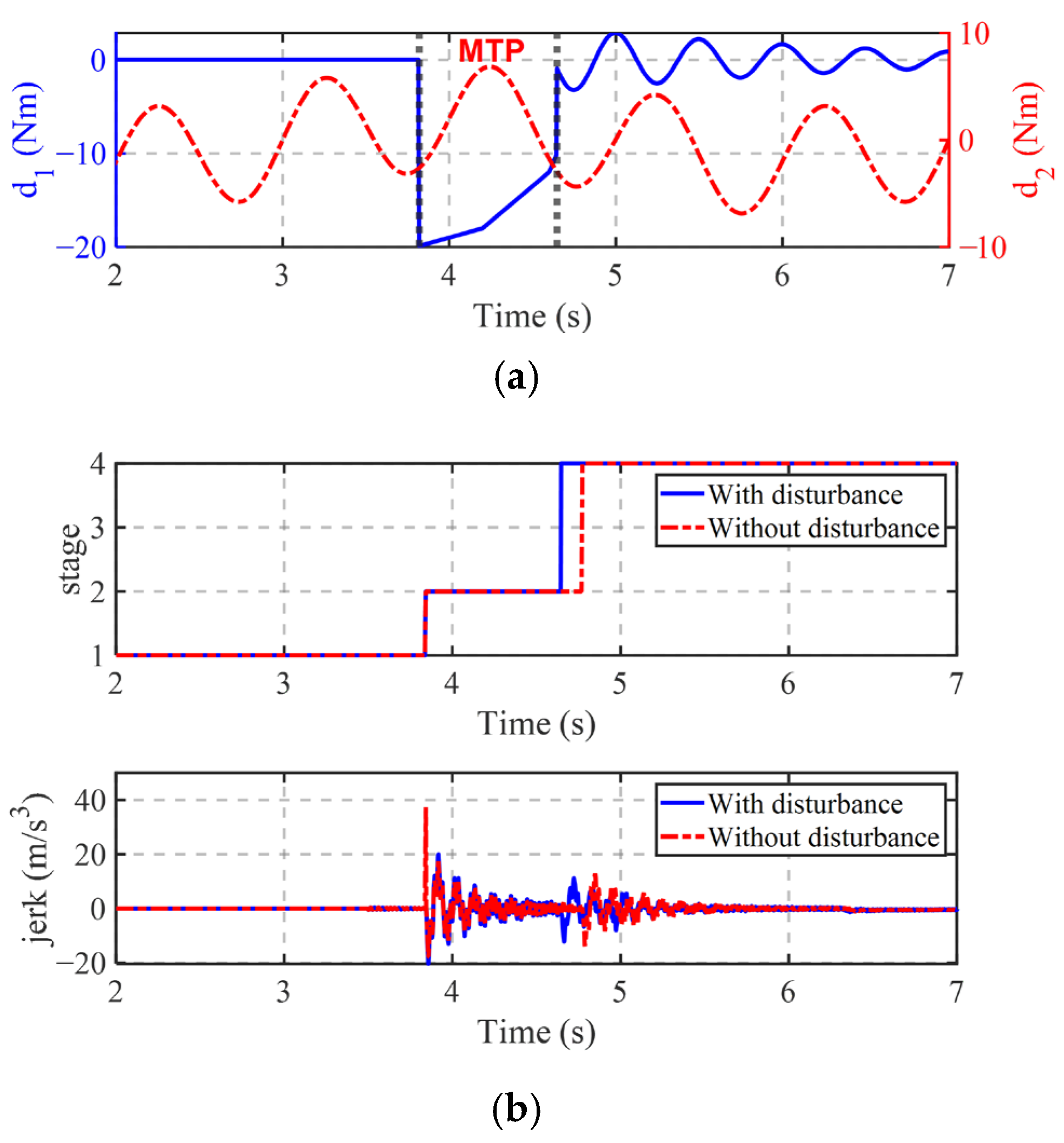
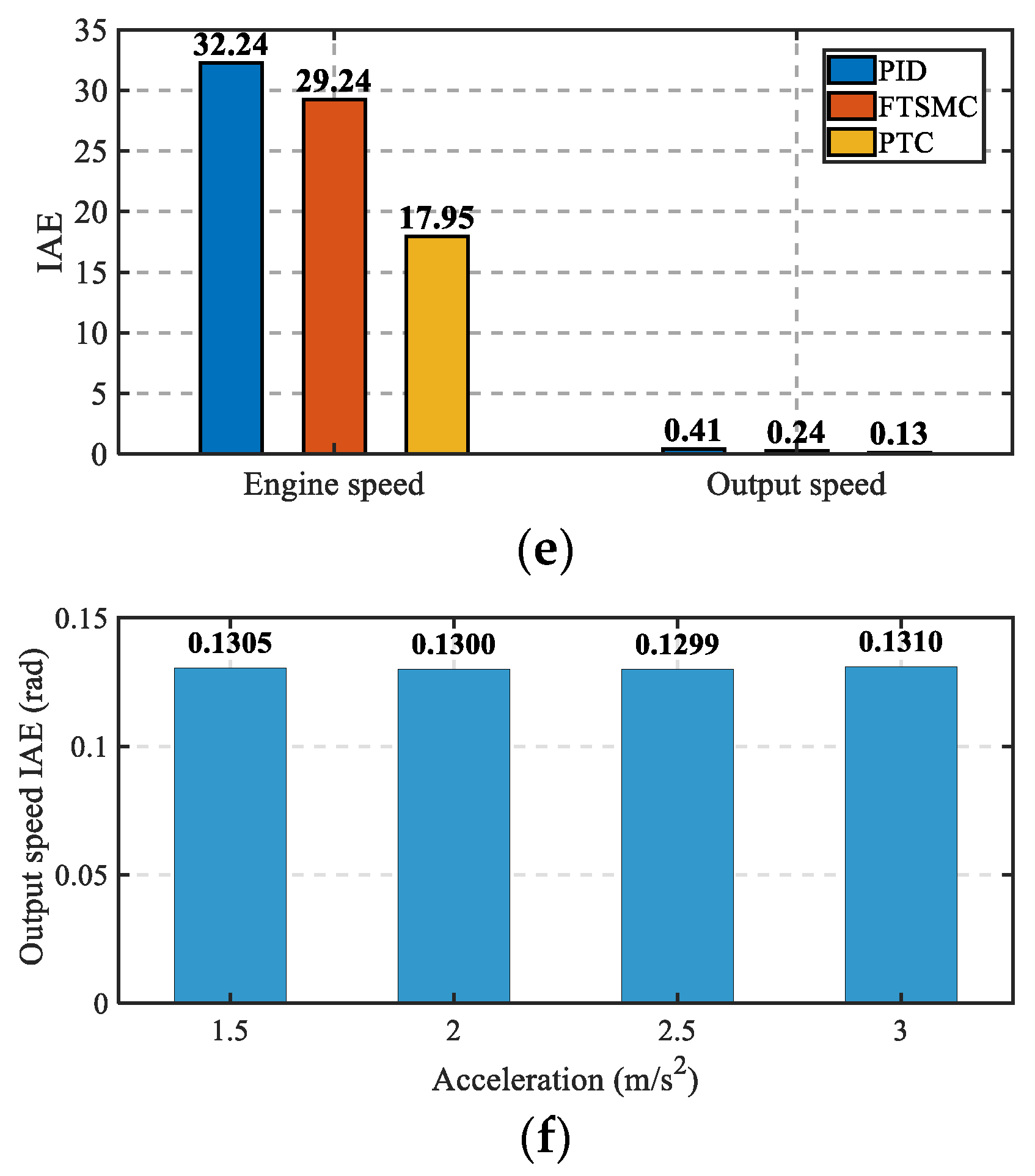
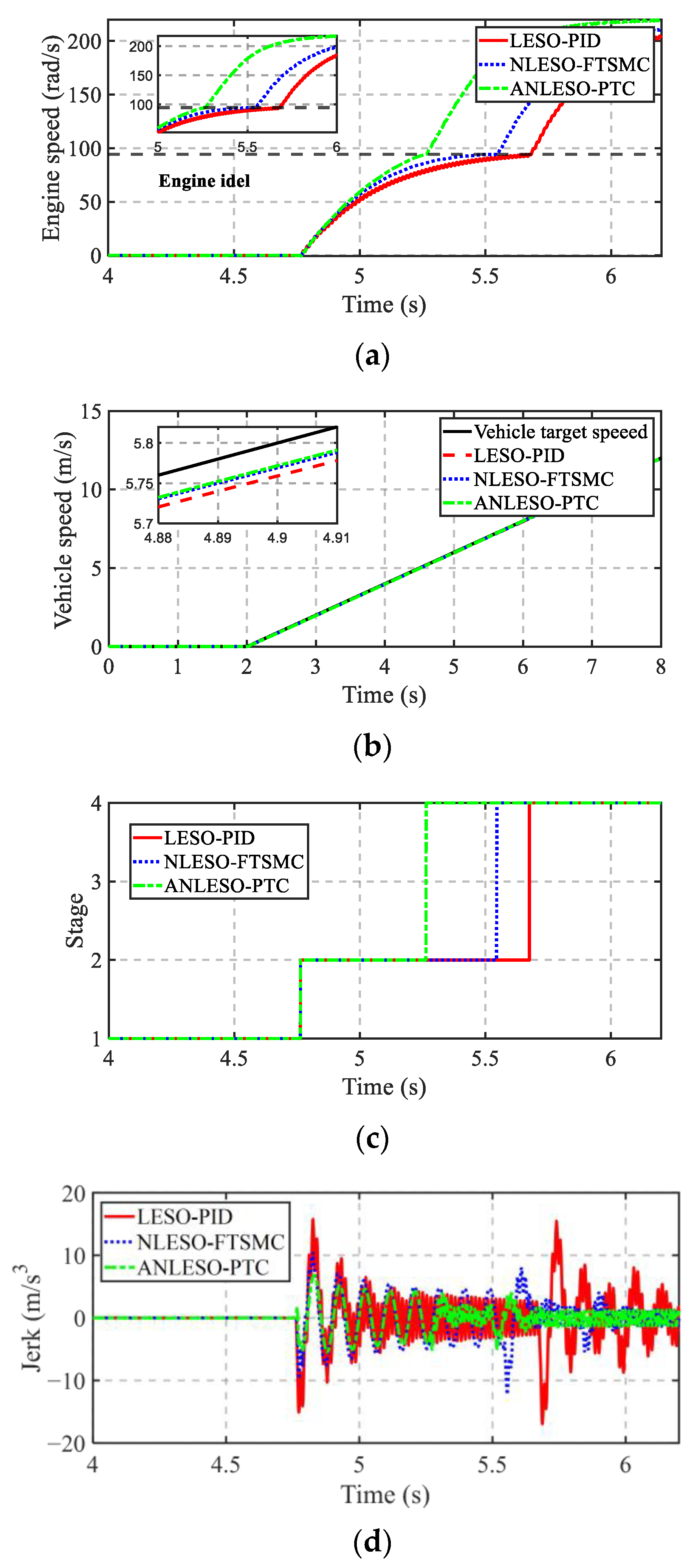
4.1. HIL Test Results and Analysis
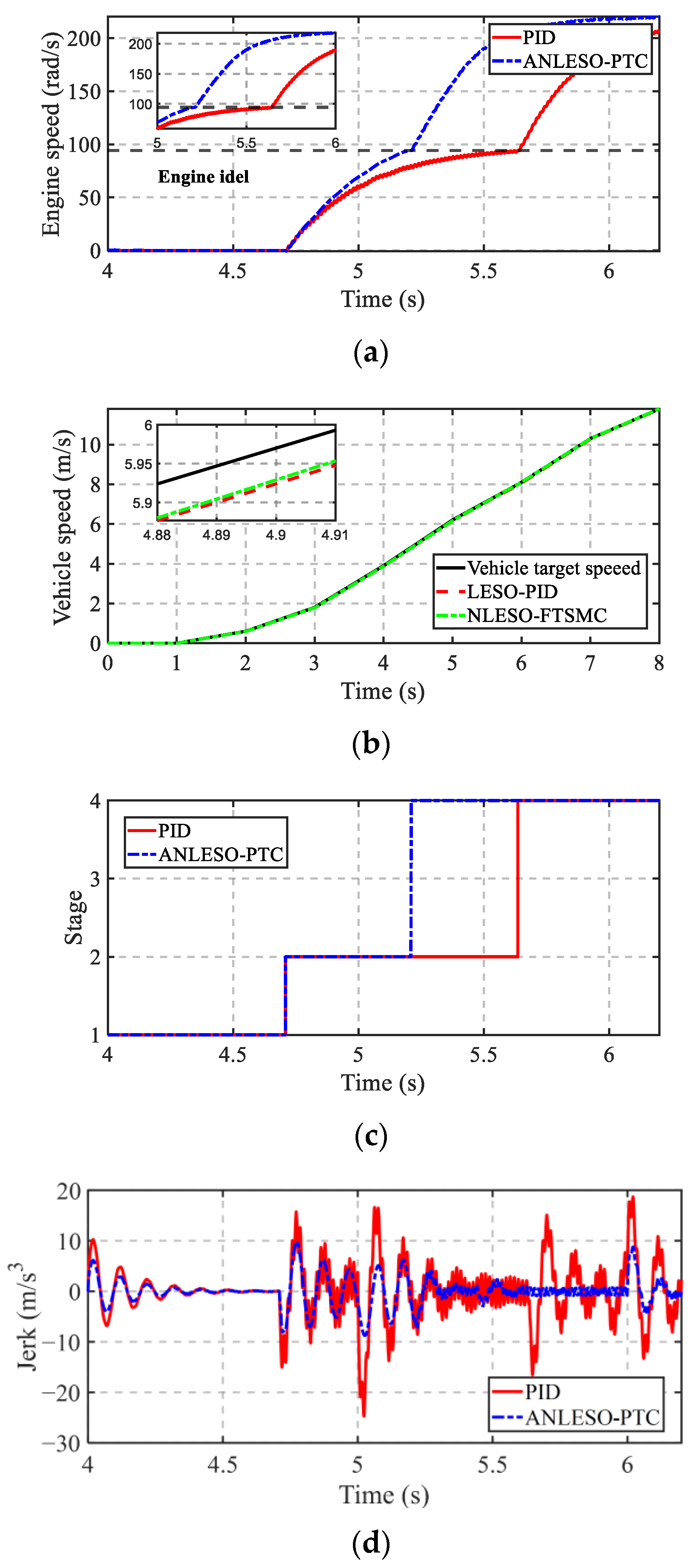
4.2. Experimental Results and Analysis
5. Conclusions
- (1)
- Based on the conventional dynamic coordinated control framework and extended state observer (ESO), this study analyzes the impact of different types of disturbances, revealing that they can severely degrade estimation accuracy and transition performance.
- (2)
- The proposed adaptive nonlinear extended state observer enhances the global convergence speed and accuracy of maximum torque pulsation (MTP) disturbance estimation, while guaranteeing symmetric convergence with respect to both positive/negative and large/small estimation errors. Furthermore, the predefined-time controller is designed to ensure that both engine speed and output shaft speed converge to their equilibrium points within a predefined time frame, regardless of the initial conditions.
- (3)
- The HIL tests conducted under three different control strategies demonstrate that the proposed ANLESO-PTC technique reduces the mode transition time by 45.7% and decreases the driving jerk by 59.2%. Furthermore, real vehicle validation confirms that the proposed control strategy can effectively limit the mode transition jerk within 10 m/s3. Overall, the proposed control strategy significantly improves the quality of mode transitions and enhances driving smoothness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ANLESO | Adaptive nonlinear extended state observer |
| ANLESO-PTC | Predefined-time control based on an adaptive nonlinear extended state observer |
| CVT | Continuously variable transmission |
| DHT | Dedicated hybrid transmission |
| FTSMC | Finite-time terminal sliding mode control |
| HEV | Hybrid electric vehicle |
| HIL | Hardware-in-the-Loop |
| IAE | Integral of absolute error |
| LESO | Linear extended state observer |
| LESO-PID | Proportional integral derivative based on a linear extended state observer |
| MTP | Mode transition process |
| NLESO | Nonlinear extended state observer |
| NLESO-FTSMC | Finite-time terminal sliding mode control based on a nonlinear extended state observer |
| PS-HEV | Power-split hybrid electric vehicle |
| PTC | Predefined-time controller |
| SOC | State of charge |
| TSM | Terminal sliding mode |
References
- Bai, S.; Liu, C. Overview of energy harvesting and emission reduction technologies in hybrid electric vehicles. Renew. Sustain. Energy Rev. 2021, 147, 111188. [Google Scholar] [CrossRef]
- Wang, J.; Cai, Y.; Chen, L.; Shi, D.; Wang, R.; Zhu, Z. Review on multi-power sources dynamic coordinated control of hybrid electric vehicle during driving mode transition process. Int. J. Energy Res. 2020, 44, 6128–6148. [Google Scholar] [CrossRef]
- Rong, X.; Shi, D.; Wang, S.; Yin, C.; Li, C. Control allocation-based adaptive dynamic coordinated control of compound power-split hybrid electric vehicles. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2025, 239, 8192–8208. [Google Scholar] [CrossRef]
- Zhao, Q.; Rong, X.; Shi, D. Research on switching control based sliding mode coordination strategy of hybrid electric vehicle. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2024, 238, 1872–1887. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Cai, Y.; Shi, D.; Wang, R. Mode transition control of a power-split hybrid electric vehicle based on improved extended state observer. IEEE Access 2020, 8, 207260–207274. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Lee, H. Mode transition control using disturbance compensation for a parallel hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2011, 225, 150–166. [Google Scholar] [CrossRef]
- Gao, A.; Fu, Z.; Tao, F. Dynamic coordinated control based on sliding mode controller during mode switching with ICE starting for an HEV. IEEE Access 2020, 8, 60428–60443. [Google Scholar] [CrossRef]
- Wang, J.; Cai, Y.; Chen, L.; Shi, D.; Wang, S.; Zhu, Z. Research on compound coordinated control for a power-split hybrid electric vehicle based on compensation of non-ideal communication network. IEEE Trans. Veh. Technol. 2020, 69, 14818–14833. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Ding, R.; Han, Q.; Yang, W. Dynamic switching control of power-split hybrid electric vehicles based on time delay prediction and interference compensation. IEEE Trans. Power Electron. 2023, 38, 13521–13534. [Google Scholar] [CrossRef]
- Yang, C.; Jiao, X.; Li, L.; Zhang, Y.; Chen, Z. A robust H∞ control-based hierarchical mode transition control system for plug-in hybrid electric vehicle. Mech. Syst. Signal Process. 2018, 99, 326–344. [Google Scholar] [CrossRef]
- Peng, C.; Chen, L. Model reference adaptive control based on adjustable reference model during mode transition for hybrid electric vehicles. Mechatronics 2022, 87, 102894. [Google Scholar] [CrossRef]
- Huang, C.; Du, C.; Li, L.; Gongye, X.; Zhao, Y. Torsional vibration suppression during mode transition process in a parallel hybrid electric vehicle based on multiple model predictive control. IEEE Access 2024, 12, 197400–197411. [Google Scholar] [CrossRef]
- Yin, C.; Xie, Y.; Shi, D.; Wang, S.; Zhang, K.; Li, M. Sliding mode coordinated control of hybrid electric vehicle via finite-time control technique. ISA Trans. 2024, 146, 541–554. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Vázquez, A.J.; Fernández-Anaya, G.; Sánchez-Torres, J.D.; Meléndez-Vázquez, F. Predefined-time control of distributed-order systems. Nonlinear Dyn. 2021, 103, 2689–2700. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.; Liu, W.; Hu, J. Adaptive fuzzy predefined-time control for third-order heterogeneous vehicular platoon systems with dead zone. IEEE Trans. Ind. Inform. 2022, 19, 9525–9534. [Google Scholar] [CrossRef]
- Pan, J.; Han, T.; Xiao, B.; Yan, H. Predefined-time bipartite time-varying formation tracking control of networked autonomous surface vehicles via hierarchical control approach. IEEE Trans. Veh. Technol. 2024, 73, 9536–9545. [Google Scholar] [CrossRef]
- Yang, Y.; Li, P.; Pei, H.; Zou, Y. Design of all-wheel-drive power-split hybrid configuration schemes based on hierarchical topology graph theory. Energy 2022, 242, 122944. [Google Scholar] [CrossRef]
- Rong, X.; Shi, D.; Wang, S. Adaptive anti-saturation fixed-time control for PS-HEV mode transition with predefined performance. IEEE Trans. Power Electron. 2025, 40, 13852–13865. [Google Scholar] [CrossRef]
- Liang, C.; Xu, X.; Wang, F.; Zhou, Z. Coordinated control strategy for mode transition of DM-PHEV based on MLD. Nonlinear Dyn. 2021, 103, 809–832. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Y.; Ma, X.; Liu, L. Sensorless control of dual three-phase IPMSM based on frequency adaptive linear extended state observer. IEEE Trans. Power Electron. 2023, 38, 14492–14503. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, X.; Peretti, L.; Bai, J.; Gao, X.; Li, Z.; Huang, S. Smooth Nonlinear ESO-based Model-Free Predictive Current Control with an Extended Control Set for SPMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 2565–2579. [Google Scholar] [CrossRef]
- Shaohua, W.; Xiangwei, R.; Dehua, S.; Chunfang, Y. Research on fixed-time robust control allocation of the mode transition for CPS-HEV considering actuator uncertainties. IEEE Trans. Transp. Electrif. 2025, 1. [Google Scholar] [CrossRef]
- Xie, S.; Chen, Q. Adaptive nonsingular predefined-time control for attitude stabilization of rigid spacecrafts. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 189–193. [Google Scholar] [CrossRef]


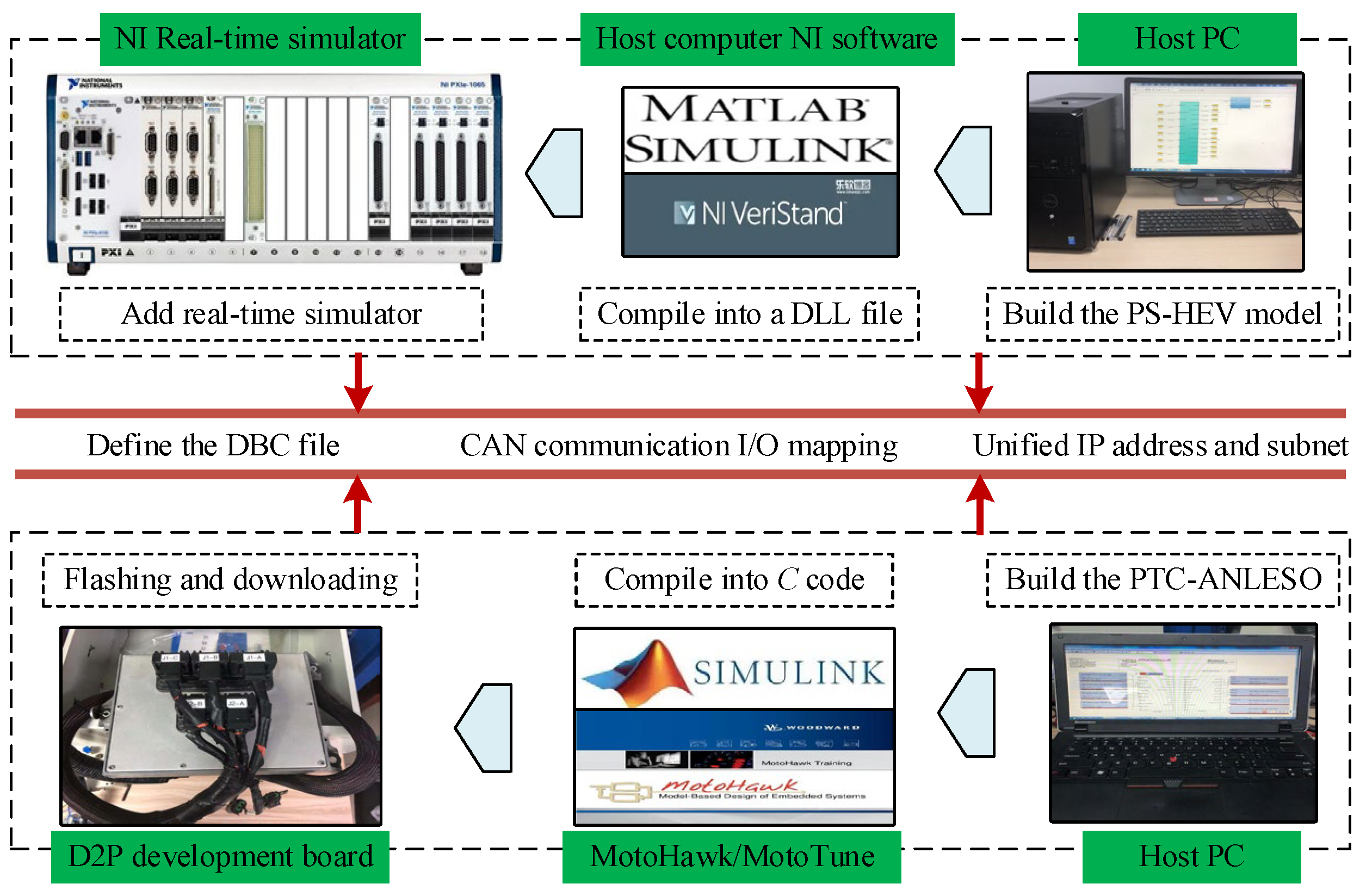


| Parameters | Value |
|---|---|
| Vehicle mass m | 1525 kg |
| Air resistance coefficient Cd | 0.31 |
| Air density ρv | 1.23 m3/kg |
| Frontal area A | 2.02 m2 |
| Rolling resistance coefficient f | 0.008 |
| The radius of wheel Rr | 0.317 m |
| The ratio of the final drive i0 | 3.269 |
| Characteristic parameter of PG1 and PG2 η1/η2 | 2.6/2.639 |
| Engine maximum power Pe | 73 kW |
| MG1 maximum power PMG1 | 23 kW |
| MG2 maximum power PMG2 | 60 kW |
| Engine rotational inertia Ie | 0.13 Kg·m2 |
| Rotational inertia of MG1 and MG2 Img1/Img2 | 0.0226/0.0326 Kg·m2 |
| Output rotational inertia Iout | 15.8841 Kg·m2 |
| Rotational inertia of R1 and R2 Ir1/Ir2 | 0.1/0.105 Kg·m2 |
| Rotational inertia of S1 and S2 Is1/Is2 | 0.0045/0.0045 Kg·m2 |
| Rotational inertia of C1 and C2 Ic1/Ic2 | 0.05/0.052 Kg·m2 |
| Engine and output shaft end damping cec1/cr2out | 0.2/12 N/(m/s) |
| Engine and output shaft end stiffness kec1/kr2out | 10,000/2000 N/m |
| Parameters | Value |
|---|---|
| γ | [0.5, 0.5, 0.5, 0.5] |
| ω0 | [100, 0, 0, 100] |
| Δ | [2, 0, 0, 2] |
| ε | [1, 1, 1, 1, 1, 1] |
| Tc | [0.5, 0.5, 0.5, 0.5, 0.5, 0.5] |
| r | [0.01, 0.01, 0.01, 0.01, 0.01, 0.01] |
| Strategy | MTP Time | Improve | Jerk | Improve |
|---|---|---|---|---|
| LESO-PID | 0.92 s | - | 16.9 m/s3 | - |
| NLESO-FTSMC | 0.79 s | 14.1% | 12.2 m/s3 | 27.8% |
| ANLESO-PTC | 0.5 s | 45.7% | 6.9 m/s3 | 59.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yang, H.; Zhang, F.; Zuo, Y. Predefined Time Transient Coordination Control of Power-Split Hybrid Electric Vehicle Based on Adaptive Extended State Observer. Symmetry 2025, 17, 1751. https://doi.org/10.3390/sym17101751
Zhang H, Yang H, Zhang F, Zuo Y. Predefined Time Transient Coordination Control of Power-Split Hybrid Electric Vehicle Based on Adaptive Extended State Observer. Symmetry. 2025; 17(10):1751. https://doi.org/10.3390/sym17101751
Chicago/Turabian StyleZhang, Hongdang, Hongtu Yang, Fengjiao Zhang, and Yanyan Zuo. 2025. "Predefined Time Transient Coordination Control of Power-Split Hybrid Electric Vehicle Based on Adaptive Extended State Observer" Symmetry 17, no. 10: 1751. https://doi.org/10.3390/sym17101751
APA StyleZhang, H., Yang, H., Zhang, F., & Zuo, Y. (2025). Predefined Time Transient Coordination Control of Power-Split Hybrid Electric Vehicle Based on Adaptive Extended State Observer. Symmetry, 17(10), 1751. https://doi.org/10.3390/sym17101751




