Achieving Computational Symmetry: A Novel Workflow Task Scheduling and Resource Allocation Method for D2D Cooperation

Abstract

With the rapid advancement of mobile edge computing and Internet of Things (IoT) technologies, device-to-device (D2D) cooperative computing has garnered significant attention due to its low latency and high resource utilization efficiency. However, workflow task scheduling in D2D networks poses considerable challenges, such as severe heterogeneity in device resources and complex inter-task dependencies, which may result in low resource utilization and inefficient scheduling, ultimately breaking the computational symmetry—a balanced state of computational resource allocation among terminal devices and load balance across the network. To address these challenges and restore system-level symmetry, a novel workflow task scheduling method tailored for D2D cooperative environments is proposed. First, a Non-dominated Sorting Genetic Algorithm (NSGA) is employed to optimize the allocation of computational resources across terminal devices, maximizing the overall computing capacity while achieving a symmetrical and balanced resource distribution. A scoring mechanism and a normalization strategy are introduced to accurately assess the compatibility between tasks and processors, thereby enhancing resource utilization during scheduling. Subsequently, task priorities are determined based on the calculation of each task’s Shapley value, ensuring that critical tasks are scheduled preferentially. Finally, a hybrid algorithm integrating Q-learning with Asynchronous Advantage Actor–Critic (A3C) is developed to perform precise and adaptive task scheduling, improving system load balancing and execution efficiency. Extensive simulation results demonstrate that the proposed method outperforms state-of-art methods in both energy consumption and response time, with improvements of 26.34% and 29.98%, respectively, underscoring the robustness and superiority of the proposed method.

1. Introduction

With the rapid development of informatization, both the number of terminal devices and the demand for computational power have grown exponentially, rendering traditional centralized computing architectures increasingly inadequate for handling the rising complexity of computational tasks. Driven by the proliferation of 5G networks and artificial intelligence, computational workloads have become significantly more complex, and the volume of data has increased substantially. These trends have positioned device-to-device (D2D) cooperation, with its distributed nature and low-latency advantages, as a promising solution to modern computational challenges [1,2]. By offloading computing tasks to edge devices located closer to data sources, D2D collaboration not only reduces data transmission latency and alleviates bandwidth pressure but also substantially enhances real-time system responsiveness and reliability [3]. Nevertheless, the heterogeneity of computing resources and the diversity of tasks in D2D environments significantly complicate the task scheduling process. Terminal devices typically possess limited and highly dynamic computational capabilities, with substantial variability in processing power, storage capacity, and energy availability across different devices. These inherent asymmetries disrupt the symmetry and balance of resource distribution, collectively increasing the complexity of scheduling and making it challenging to achieve computational symmetry and load balancing across the network [4]. Furthermore, with the widespread adoption of application scenarios such as intelligent transportation, smart homes, and smart cities, the nature of distributed system tasks has become increasingly diverse. These range from simple data collection tasks to complex deep learning model training, imposing higher demands on the design of scheduling algorithms [5]. Moreover, as individual service requests are often decomposed into multiple subtasks that must be executed in parallel across different terminal processors, it is imperative to employ globally optimized scheduling strategies to ensure that each task is assigned to the most appropriate device at the most suitable time [6]. Efficiently managing the scheduling of such complex computational resources—so as to maximize resource utilization, minimize task completion time, and enhance overall system performance—has become a central research focus in the field [7,8,9].

Task scheduling has a direct impact on system performance and user experience. Inefficient scheduling strategies may lead to resource wastage, task delays, or even system failures. Therefore, devising effective task allocation mechanisms to optimize overall system performance is of paramount importance. Although extensive research has been conducted on task scheduling in distributed environments, the current approaches still exhibit critical limitations that lead to their failure in addressing the complexities of modern D2D environments. Specifically, prior methods often fail due to several key reasons, including suboptimal resource utilization, ambiguous task prioritization, and insufficient dynamic scheduling capabilities [10,11]. For instance, many existing studies focus solely on a single optimization objective, such as minimizing latency or energy consumption, while overlooking the need to balance resource distribution across the system [12,13]. This single-dimensional optimization fails to capture the multi-objective trade-offs required in heterogeneous and dynamic settings, resulting in imbalanced resource allocation and degraded overall efficiency. Moreover, traditional approaches often rely on simplistic heuristic rules for task ordering, lacking quantitative assessments of task importance and contribution [14,15]. Consequently, these methods fail to prioritize tasks effectively, leading to increased latency for critical tasks and inefficient use of available resources. Additionally, current scheduling algorithms struggle to adapt to complex and dynamically changing resource environments, which can lead to decreased resource efficiency and degraded system performance. Many state-of-the-art algorithms are designed under static assumptions and lack the adaptive mechanisms necessary to respond to real-time fluctuations in device availability, network conditions, and task demands, thereby failing in practical dynamic scenarios. These challenges highlight the urgent need for a novel scheduling framework that can holistically consider multiple optimization criteria, incorporate task prioritization, and support adaptive dynamic scheduling in heterogeneous and volatile environments.

To address the aforementioned challenges, this study proposes an efficient and flexible distributed task scheduling framework with three algorithmically synergistic components that overcome the limitations of standalone methods: First, the NSGA-II is employed to assign tasks to the most appropriate processors, leveraging its multi-objective optimization capability to balance computational resources and task compatibility with conflicting objectives like latency and energy consumption. Second, task priorities are determined by quantifying the contribution of each task using Shapley values, which uniquely capture marginal contributions in dynamic task dependencies, outperforming heuristic-based prioritization in complex workflows. Finally, a hybrid reinforcement learning algorithm that integrates Q-learning with A3C is developed to perform dynamic scheduling. This algorithm enables macro-level adjustments to processor selection and task execution timing in response to changing system conditions. This specific integration creates a closed-loop optimization framework, and the components collectively achieve superior performance in reducing task completion time and energy consumption while enhancing resource utilization and system robustness. The main contributions of this paper are summarized as follows:

• A multi-objective optimization model based on NSGA-II is proposed, which comprehensively considers various resource attributes of terminal devices, including CPU capacity, GPU performance, and storage capability. To enhance both resource utilization and systemic symmetry, the computational capabilities of terminal devices and the requirements of tasks are normalized to a unified dimensionless scale, enabling more accurate and fair resource matching;
• A cooperative game-theoretic model is introduced, in which the Shapley value is employed to quantify each task’s contribution to the overall system performance while satisfying the constraints of DAG structures. Based on the computed Shapley values, task priorities are dynamically adjusted to optimize the scheduling sequence and, consequently, improve the global scheduling efficiency;
• A novel QVAC (Q-learning Value Actor–Critic) algorithm is proposed, wherein the traditional Critic component in the A3C framework is replaced by a Q-learning module. This modification enhances the stability and global search capability of the scheduling strategy. The proposed method simultaneously optimizes the task execution order while achieving low latency, reduced energy consumption, effective load balancing, and improved rationality in task allocation;
• Extensive experiments are conducted on various task models to evaluate the proposed method. The results demonstrate that the approach significantly improves resource utilization and reduces both task execution delay and overall energy consumption in complex heterogeneous computing environments while maintaining robust performance in dynamic scheduling scenarios.

The remainder of this paper is organized as follows: Section 2 reviews the related work. Section 3 presents the system model and problem formulation. Section 4 proposes a dynamic scheduling algorithm for optimal allocation of complex computational resources. Section 5 demonstrates the experimental setup and results. Finally, Section 6 concludes the paper.

2. Related Work

With the rapid advancement of edge computing technologies, task scheduling has emerged as a critical challenge affecting both computational resource utilization and processing efficiency [16]. In scenarios characterized by multi-tasking and heterogeneous resource environments, the efficient allocation of computing resources to enhance system performance, reduce energy consumption, and achieve load balancing and system symmetry has become a key research focus in both academia and industry [17,18]. Existing studies primarily concentrate on leveraging heuristic algorithms, optimization techniques, and reinforcement learning approaches to improve task scheduling performance, and workflow scheduling—a subfield targeting tasks with logical precedence dependencies—is also a crucial research direction that has accumulated rich results, yet its classic algorithms have not been sufficiently discussed in existing reviews.

Traditional task scheduling approaches include heuristic algorithms such as Shortest Processing Time [19] and Earliest Deadline First, as well as metaheuristic algorithms such as Particle Swarm Optimization (PSO) and Genetic Algorithms (GAs). While these methods offer simplicity in computation, their performance is often limited in scenarios involving complex task dependencies and heterogeneous computing resources [20,21,22]. In the domain of workflow scheduling, two classic and widely used heuristic algorithms—Heterogeneous Earliest Finish Time (HEFT) and Critical Path On a Processor (CPOP)—have been extensively studied and applied: HEFT is a greedy workflow scheduling algorithm designed for heterogeneous environments; it calculates the “upward rank” of each task to determine task priority and assigns each task to the resource that minimizes its earliest finish time, effectively shortening the overall workflow makespan and exhibiting good scalability for small-to-medium-scale workflows [23,24], but its greedy decision-making lacks global optimization consideration, leading to suboptimal resource allocation for large-scale workflows with tight deadlines; CPOP, by contrast, first identifies the critical path and assigns all critical-path tasks to the resource with the fastest average processing speed, while non-critical tasks are scheduled using a strategy similar to HEFT, which allows it to outperform HEFT in workflows with long critical paths by concentrating core tasks on high-performance resources [25], yet it struggles with load balancing across non-critical resources, easily causing resource bottlenecks when non-critical task volumes surge.

To overcome the limitations of traditional heuristics in complex environments, recent research has explored intelligent optimization and machine learning-based scheduling strategies. While these methods have shown promising results, they often incur high computational overhead and struggle to adapt to dynamic resource constraints, particularly in large-scale task environments. Ye et al. proposed a dynamic task prioritization method based on urgency evaluation, which is combined with a firefly optimization mechanism for task allocation. Although this approach effectively improves scheduling efficiency, reduces task completion time, and achieves good load balancing under large-scale scenarios, its lack of global optimization limits applicability in more complex scheduling contexts [26]. Liu et al. addressed the problem of scheduling tasks with deadline constraints by introducing a method based on an improved Apriori algorithm. While this method enhances task classification and constructs a scheduling model to optimize execution time and cost, it may suffer from significant computational overhead when applied to large and complex task sets [27]. Yang et al. proposed a workflow task scheduling model that integrates machine learning with greedy optimization. Their method uses a multi-layer perceptron to predict task execution time and relaxes non-preemptive constraints to optimize the scheduling order, ultimately yielding near-optimal solutions for utility-based task completion. A key limitation, however, is its heavy reliance on historical data, which restricts adaptability when facing unexpected or bursty tasks [28]. In contrast, deep reinforcement learning (DRL) methods have gained significant attention in task scheduling due to their adaptability and decision optimization capabilities, offering a more dynamic approach to handling complex scheduling scenarios compared to traditional machine learning methods. Shi et al. reformulated the task offloading problem as a mixed-integer linear programming (MILP) model and employed a Double Deep Q-network (DDQN) to optimize decision-making. Their approach is well-suited to complex edge environments with strict real-time requirements, achieving superior performance in both task latency and execution efficiency. Nevertheless, the approach may suffer from slow convergence under constrained computational resources [29]. Xu et al. developed a mathematical model to perform online task scheduling via DRL, aiming to minimize task response time. By adopting an adaptive exploration strategy, they improved task completion rates; however, the method incurs high training costs and exhibits limited generalization in highly dynamic environments [30]. Li et al. introduced a joint task scheduling and resource allocation approach based on a multi-action adaptive environment algorithm. The method first generates task offloading decisions and assigns task priorities to reduce the completion time. Then, it dynamically adjusts transmission power according to the communication distance to minimize energy consumption. The approach shows strong performance in minimizing both task delay and energy consumption while adapting to dynamic conditions. However, the complexity of state-space adjustments and a slow convergence rate hinder scheduling efficiency [31].

In summary, existing studies on resource scheduling and task allocation often rely on a limited set of evaluation metrics, which fail to comprehensively reflect the overall performance of the system. Moreover, given the diverse characteristics of heterogeneous computing resources, current approaches to resource modeling remain inadequate, as they are unable to fully capture the variations among resources and their practical implications for task scheduling [32,33]. Additionally, many existing methods lack in-depth analysis of task interdependencies regarding fairness-aware allocation and dynamic adjustment strategies, which restricts the accuracy and adaptability of scheduling outcomes [34,35]. To address these limitations, this paper proposes a holistic solution based on multiobjective optimization and fairness-aware resource allocation, offering a novel perspective on task scheduling in complex computing environments.

3. Problem Formulation and System Model

In heterogeneous environments, task scheduling is a key factor affecting system performance. Due to the varying computational demands of different tasks and significant disparities in the computational, storage, and communication capabilities of terminal devices, efficient task scheduling presents a considerable challenge. This paper proposes an effective scheduling strategy that not only considers rational resource allocation but also incorporates game-theoretic concepts to optimize the task scheduling order, thereby improving system symmetry and energy efficiency. The key notations used in this section are defined in

Table 1. Main notations in this study.

Notation	Description
$D(E,A,X)$	DAG workflow
$T_i$	The i-th computational task in the workflow
$C_j$	The j-th terminal processor
$E_{ij}$	Transmission delay between task i and task j
$A_{ij}$	Processing delay of task i on processor j
$X_{ij}$	Computing resource demand of task i for the j-th type of resource
$R_{ij}$	The j-th computing resource of processor i
M	Number of processors
N	Number of tasks
$p{r}_i$	Predecessor tasks of task i
$s{u}_i$	Successor tasks of task i
$t{m}_{sta}^{t\left(i\right)}$	Start time of task i
$t{m}_{end}^{t\left(i\right)}$	End time of task i
$h_i$	State of the processor
${\alpha }_k$	Weight of the k-th computing resource
$P_i^{CPU/GPU}$	Power consumption for executing task i on CPU/GPU
$D_i$	Total computation cycles required by task i

.

3.1. Problem Formulation

In heterogeneous computing environments, the core objective of task scheduling is to appropriately allocate tasks to different terminal devices to maximize resource utilization and optimize system performance. However, task scheduling is not a single problem but consists of multiple interrelated decision processes, mainly involving task-to-processor mapping, the task execution order, and global scheduling optimization.

First, each task $T_i$ needs to select an appropriate processor $C_j$ for execution. Due to the heterogeneity in the computational capabilities of different processors, such as significant differences in the CPU, GPU, and storage capacity, and the varying computational requirements of various tasks, the matching between tasks and processors needs to be optimized based on the compatibility between computational capabilities and task demands. This optimization ensures proper resource allocation, improves overall computational resource utilization, and prevents processor overload or resource idle time.

Secondly, once the execution device for each task has been determined, it is essential to optimize the execution order of tasks on the same processor [36]. Given that functions often exhibit interdependencies—particularly those constrained by Directed Acyclic Graphs (DAGs)—the execution sequence directly impacts the task completion time and the overall system throughput [37]. Therefore, effective scheduling of task execution orders on each processor can significantly reduce task waiting times, enhance parallel computation efficiency, and ultimately improve overall scheduling performance.

Finally, after determining the task-to-processor mapping and execution sequence, it remains essential to further refine the global scheduling strategy by jointly considering task completion time, communication overhead, and energy consumption. As task scheduling is inherently a multi-objective optimization problem, focusing solely on a single performance metric may lead to degradation in others. Therefore, a trade-off must be made among low latency, energy efficiency, and load balancing to achieve optimal system performance across multiple objectives.

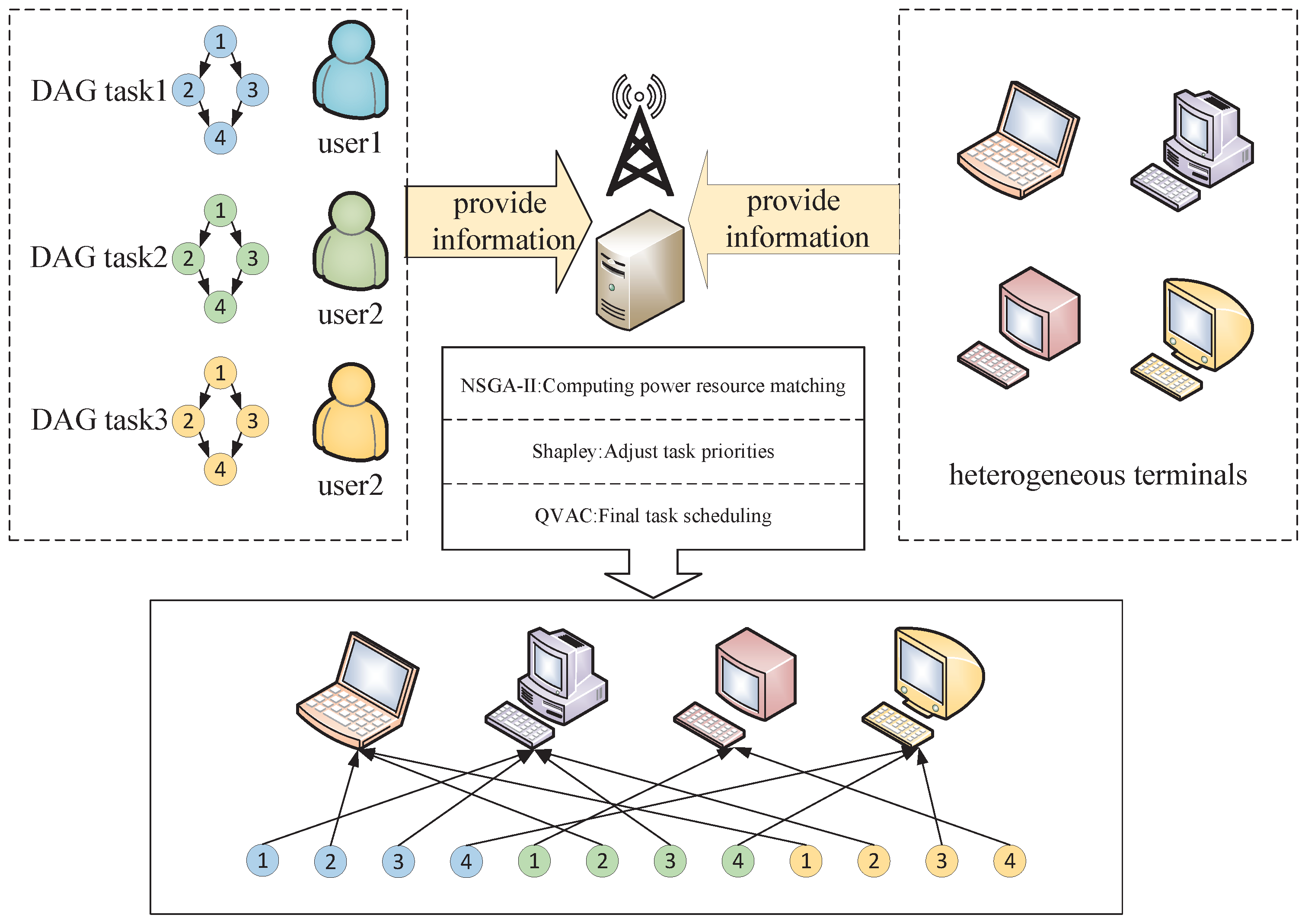
To address these challenges, this paper designs a task scheduling framework aimed at optimizing task allocation and execution workflows in heterogeneous computing environments. Figure 1 illustrates the architecture of the proposed task scheduling system. In this framework, tasks submitted by different users are modeled as DAGs and forwarded to a centralized scheduler. The scheduling server performs task allocation and execution order optimization based on task requirements, device capabilities, and task dependencies. The resulting scheduling scheme is then distributed to heterogeneous edge devices for execution.

3.2. Workflow Task Model

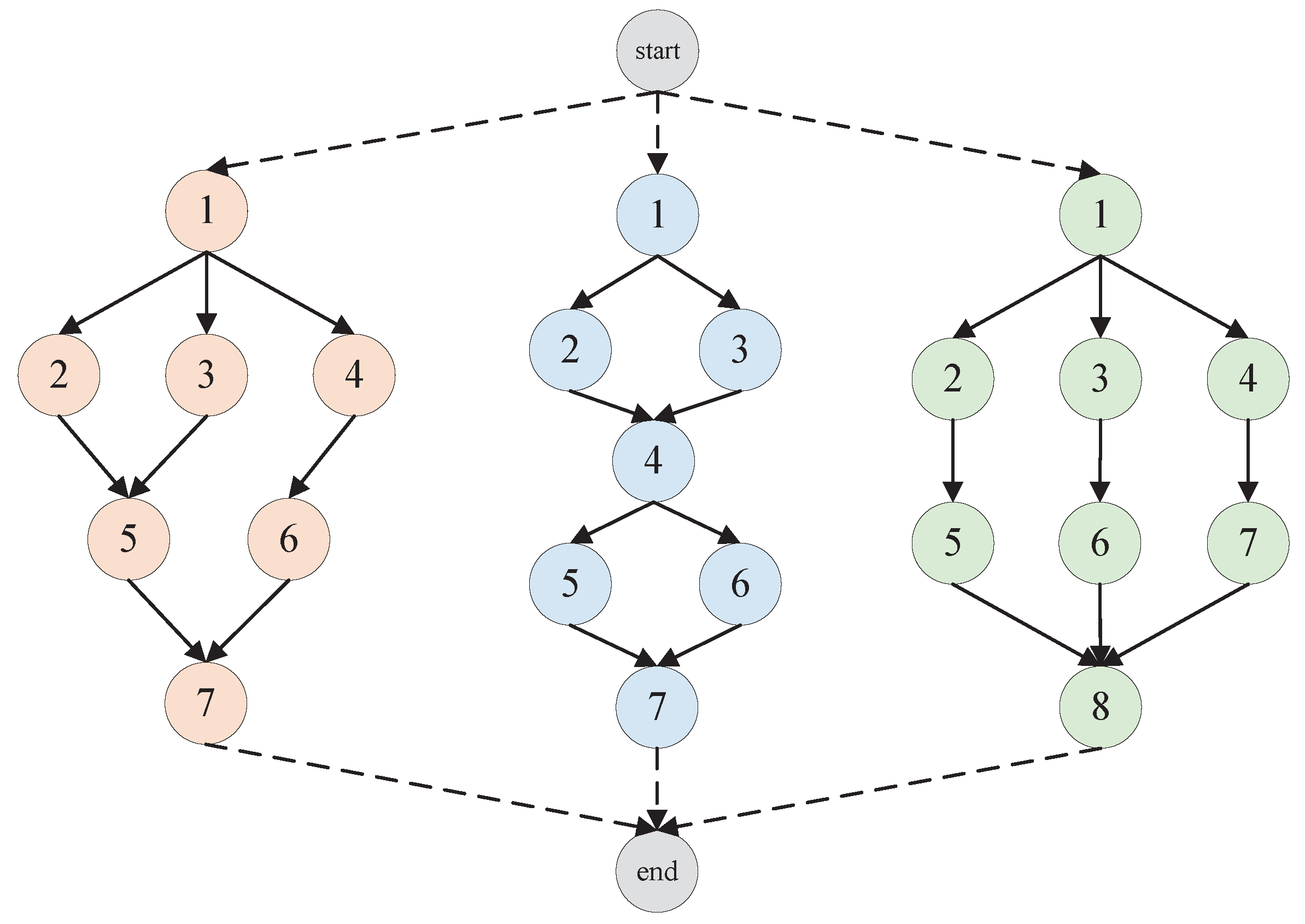
In a heterogeneous computing environment, task scheduling typically involves the coordinated execution of multiple computational tasks with interdependencies across various heterogeneous computing terminals. Let the set of computational tasks be denoted as $T=\{T_1,T_2,\dots ,T_N\}$, where N represents the total number of tasks; the set of computing terminals is denoted as $C=\{C_1,C_2,\dots ,C_M\}$, where M represents the number of available heterogeneous terminals. The scheduling process can be modeled as a DAG and is denoted by $D(E,A,X)$, where E represents the task propagation matrix, which defines the dependency relationships between tasks and the data transmission latency. When $E_{ij}>0$, it indicates that task $T_i$ is a predecessor of task $T_j$, and the value corresponds to the transmission delay from $T_i$ to $T_j$. Matrix A denotes the task execution time matrix, where $A_{ij}$ indicates the time required by computing terminal $C_j$ to process task $T_i$. Matrix X denotes the resource demand matrix, representing the computational resource requirements of each task during execution. Due to differences in hardware configurations and network connectivity among computing terminals, the computation time $A_{ij}$ for processing the same task and the transmission delay $E_{ij}$ between different terminals vary accordingly, which significantly impacts the overall performance of task scheduling.

Figure 2 presents an example of a DAG model. In this graph, each node represents a task, and each directed edge indicates a precedence constraint and the associated communication delay between tasks. If there exists a directed edge from task $T_i$ to task $T_j$, then $T_i$ is referred to as the predecessor of $T_j$, and $T_j$ is the successor of $T_i$. Assuming that node $T_i$ represents the current task, its set of predecessor tasks is denoted as $p{r}_i$, and its set of successor tasks is denoted as $s{u}_i$. A task may have multiple predecessors and successors. Task $T_i$ can only be executed after all of its predecessor tasks in $p{r}_i$ have been completed. This constraint can be formally expressed as

$$t{m}_{end}^{t\left(i\right)}\ge max\left(t{m}_{end}^{pr\left(i\right)}+E_{T\left(i\right),pr\left(i\right)}+A_{ij}\right)$$

(1)

At the same time, each task can be executed on one and only one processor, subject to the following constraint:

$$\sum _{j=1}^M{x}_{i,j}=1,\forall i=1,\dots ,N$$

(2)

In a DAG, a task with no predecessor is referred to as an entry task, while a task with no successor is called an exit task. If the DAG contains multiple entry or exit tasks, virtual entry or exit nodes with zero weight can be added to ensure that the system has a single entry and a single exit point. Let the first task $T_1$ be designated as the entry task and the last task $T_N$ as the exit task. All tasks are assumed to share the same deadline and are executed in a non-preemptive manner.

3.3. Resource Matching Model

In a heterogeneous computing environment, processors exhibit significant differences in computational capabilities, including basic computing power, intelligent computing power, and storage capacity. Specifically, basic computing power refers to the CPU’s ability to handle general-purpose tasks, where computational performance and processing speed can serve as indicators of computing capacity. Intelligent computing power typically refers to the GPU’s capacity for handling tasks such as deep learning and graphical rendering. Storage capacity encompasses both random-access memory (RAM) and disk storage, reflecting the system’s memory size and persistent storage capacity, respectively. Together, these constitute five computing power indicators that define a processor’s comprehensive capability. To achieve efficient task scheduling, it is essential to construct a resource matching model that aligns task demands with these processor capabilities for optimal allocation. Given that these five computing power indicators have different physical dimensions, normalization is required to allow for comparisons on a unified scale. The min–max normalization method is adopted, mapping all computational resources and task demands into the interval [0,1], thereby balancing the influence weights of different resource types. The normalization formula is as follows:

$$X_{ij}^{\prime }={\displaystyle \frac{X_{ij}-X_{\min }}{X_{\max }-X_{\min }}}$$

(3)

To measure the degree of matching between tasks and processors, the normalized task computational demands and processor capabilities are evaluated using the Euclidean distance. A weight factor, ${\alpha }_k$, is introduced to adjust the importance of different computing resources. The matching degree is calculated as follows:

$$\mathrm{Dist}(X_i,R_i)=\sqrt{\sum _{k=1}^5{\alpha }_k{\left(X_{ik}^{\prime }-R_{ik}^{\prime }\right)}^2}$$

(4)

Here, ${\alpha }_k$ represents the importance weight of the k-th type of computing resource, which can be adjusted based on specific system requirements. A smaller computed distance indicates a closer match between the task’s requirements and the processor’s capabilities. Therefore, each task is assigned to the device with the minimum matching distance, which is denoted as $R_i^{*}$, where

$$R_i^{*}=arg\underset{R_i}{min}\mathrm{Dist}(X_i,R_i)$$

(5)

Through this resource matching model, the rationality of task allocation can be effectively improved, enabling the system to achieve efficient and balanced resource utilization in a heterogeneous computing environment.

3.4. Energy Consumption and Latency Models

The total energy consumption is represented as the sum of the CPU energy consumption and the GPU energy consumption, which can be mathematically expressed as

$$W_{\mathrm{all}}=W_{\mathrm{cpu}}+W_{\mathrm{gpu}}=\sum _{i=1}^M{w}_{\mathrm{cpu}}^i+\sum _{i=1}^M{w}_{\mathrm{gpu}}^i$$

(6)

For a DAG workflow, the task delay consists of two components: communication delay and computation delay. Specifically, the communication delay between relevant tasks, such as from a predecessor task $T_i$ to its successor task $T_i$, is denoted as $E_{ij}$. The delay primarily arises from the data transmission overhead incurred during inter-task communication within the DAG workflow. The computation delay of task $T_i$, denoted as $A_{ij}$, refers to the execution time required by the processor to complete the task. The total delay of the entire DAG workflow is determined by the latest finishing time among all tasks. This is because the DAG workflow has task dependencies; some tasks can only start execution after their predecessor tasks are completed and data is transmitted. Consequently, the overall completion time of the workflow is constrained by the task with the longest “communication + computation” time chain.

When task $T_i$ is assigned to the CPU processor, the power consumption of the CPU is $P_{\mathrm{CPU}}^i$, and its computation delay is given by

$$A_{ij}={\displaystyle \frac{D_i}{R_{j,1}}}$$

(7)

Thus, the energy consumed by the task is

$$W_{\mathrm{cpu}}=P_i^{\mathrm{CPU}}\times A_{ij}$$

(8)

If the task is assigned to a GPU processor for execution, the GPU power consumption is denoted as $P_i^{\mathrm{GPU}}$, and the computation delay is

$$A_{ij}={\displaystyle \frac{D_i}{R_{j,3}}}$$

(9)

At this point, the CPU is typically at a certain level of activity, though its power consumption is not as high as that of the GPU. Let $\beta$ denote CPU utilization, which represents the busy level of the CPU during task execution and is expressed as a percentage; then the energy consumption of the task can be expressed as

$$W_{\mathrm{gpu}}=\left(P_i^{\mathrm{GPU}}+\beta ·P_i^{\mathrm{CPU}}\right)·A_{ij}$$

(10)

The total energy consumption is the sum of the energy consumed by all tasks, and the overall completion time is determined by the latest finishing time among all tasks. Optimizing these two objectives contributes to enhancing the overall system performance, ensuring efficient resource utilization and timely task completion.

4. Task Scheduling Algorithm

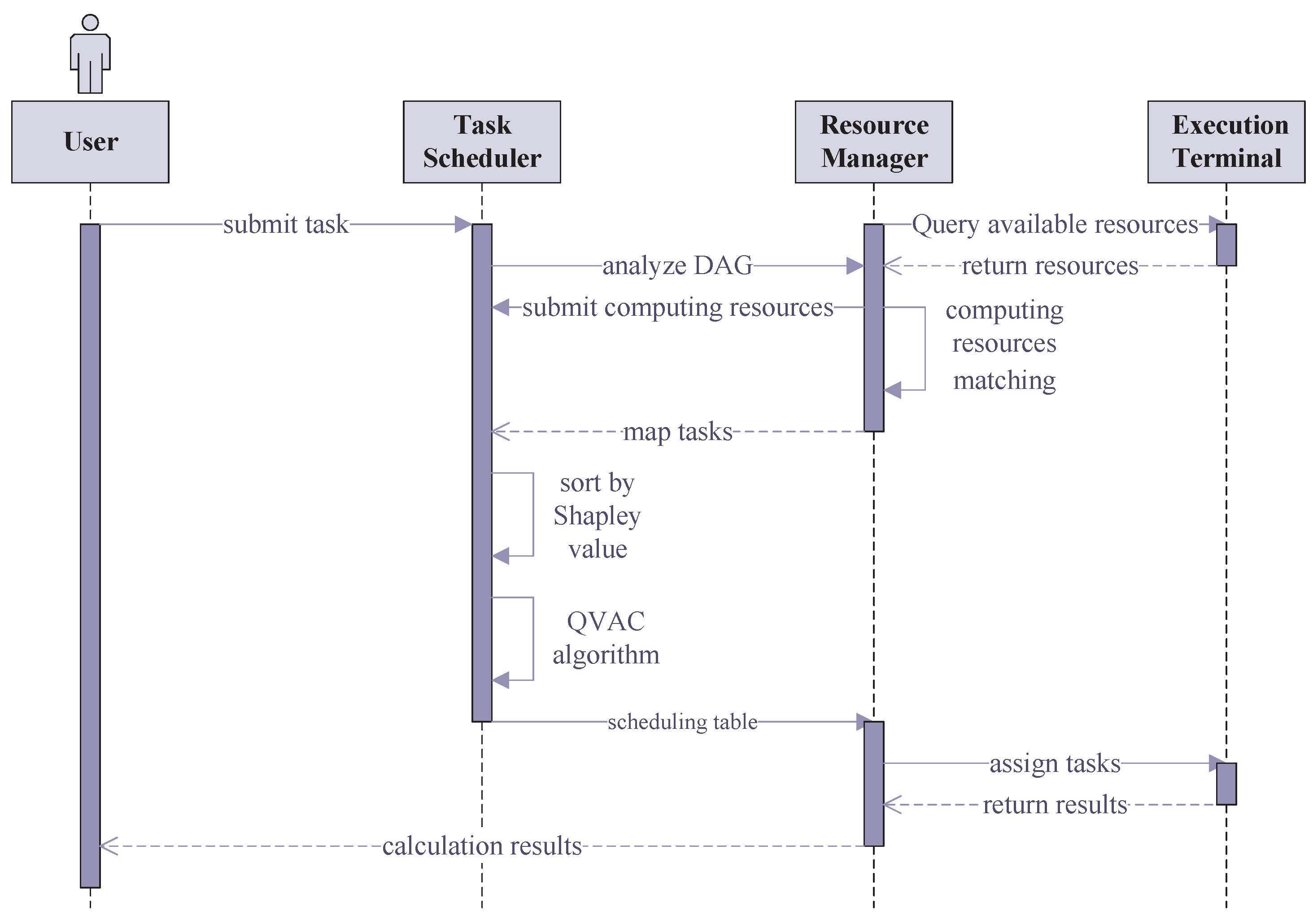
To address the aforementioned challenges, this paper presents a task scheduling algorithm that integrates NSGA-II for multi-objective optimization to match computational resources, incorporates the Shapley value to adjust task priorities, and utilizes the QVAC algorithm to optimize the task execution order. Through the synergistic combination of these three components, the proposed approach enables low energy consumption, low latency, and effective load balancing in heterogeneous computing environments, thereby enhancing overall system performance and symmetry; a sequence diagram is provided in Figure 3.

4.1. Heterogeneous Computing Resource Matching Algorithm

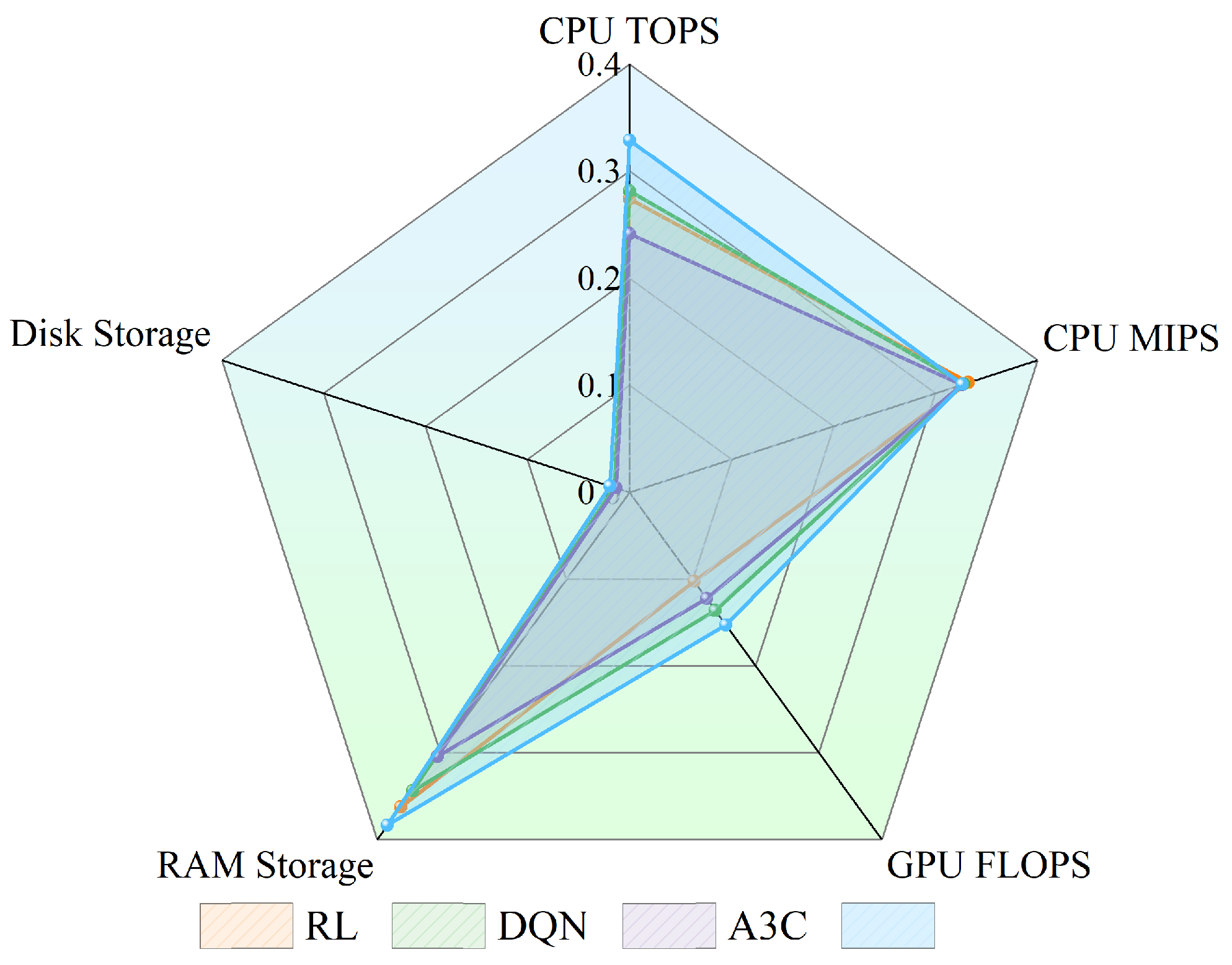
In this study, an efficient heterogeneous computing resource matching algorithm is proposed to address the problem of resource allocation in a multi-objective optimization environment. The core idea of the algorithm is to achieve efficient utilization and fair distribution of computing resources by comprehensively considering multiple optimization objectives. Specifically, three key objectives are defined: maximizing the total computational power to ensure full utilization, minimizing the standard deviation of resource utilization to achieve load balancing among resources, and minimizing the difference in weights to ensure fairness in resource allocation.

In terms of computing resource metrics, this study comprehensively considers three aspects, basic computing power, intelligent computing power, and storage capability, to fully reflect the performance of computing nodes. Basic computing power refers to a node’s ability to handle general-purpose computational tasks and is measured by the CPU’s computational performance at a fixed operating frequency. Metrics such as TOPS (Tera Operations Per Second) and MIPS (Million Instructions Per Second) are adopted as indicators of basic computing power. Intelligent computing power, which is mainly relevant for compute-intensive tasks such as deep learning, relies heavily on the GPU and is evaluated using FLOPS (Floating Point Operations Per Second) to reflect its computational capability. Storage capability includes both RAM and disk storage, where RAM affects the ability to execute concurrent tasks, while disk capacity determines the upper limit for data access and storage. During the resource matching process, in order to eliminate dimensional differences among the above objectives, all types of computing resources are normalized. This allows the optimization algorithm to evaluate basic, intelligent, and storage capacities on a common scale, ensuring fairness and rationality in resource allocation. Subsequently, the NSGA-II algorithm is employed to solve the multi-objective problem and determine the corresponding weight distribution scheme for each objective. Based on this, the normalized values of task requirements and available system resources are compared using a weighted Euclidean distance. A smaller distance indicates a higher degree of matching between the task and the resource, which maximizes resource utilization while avoiding excessive waste. The specific scheduling algorithm is shown in Algorithm 1.

Algorithm 1: Computing Resource Matching Algorithm

The Pareto front is a critical concept for evaluating the quality of solution sets in multi-objective optimization problems. In such problems, conflicting objectives often prevent the simultaneous optimization of all targets through a single solution. Consequently, the goal shifts from identifying a unique global optimum to discovering a set of Pareto-optimal solutions. These are solutions for which no objective can be improved without degrading at least one other objective. Formally, let the objective vector of a multi-objective optimization problem be defined as $F=(f1,f2,\dots ,fn)$. For two solutions, $X_1$ and $X_2$,$X_1$ is said to dominate $X_2$ if the following conditions are satisfied:

$$\forall i\in \{1,2,\dots ,m\},f_i\left(X_1\right)\le f_i\left(X_2\right)$$

(11)

$$\exists j\in \{1,2,\dots ,m\},f_j\left(X_1\right)\le f_j\left(X_2\right)$$

(12)

Then $X_1$ is said to dominate $X_2$. Conversely, if no solution exists that dominates $X^{*}$, then $X^{*}$ is referred to as a Pareto-optimal solution.

4.2. Task Prioritization Algorithm

In the task scheduling process, tasks often exhibit complex dependency relationships, and different tasks contribute unequally to the overall system performance. To allocate task execution orders more rationally, this study introduces a cooperative game-theoretic model. It employs the Shapley value to measure each task’s marginal contribution to system performance, thereby optimizing the scheduling strategy.

Specifically, tasks are regarded as players in a cooperative game, and collaboration is achieved by sharing system resources, with the goal of minimizing the system’s total completion time. Each task is associated with its own computational load and communication demands, thus contributing differently during the scheduling process. The Shapley value is employed to fairly allocate the benefits of cooperation by evaluating each task’s impact on overall system performance across all possible task scheduling combinations. The Shapley value is calculated using the following formula:

$${\varphi }_i\left(v\right)=\sum _{S\subseteq N}{\displaystyle \frac{\left|S\right|!\left(\right|N|-|S|-1)!}{\left|N\right|!}}\left[v(S\cup \{i\left\}\right)-v\left(S\right)\right]$$

(13)

where S is a subset of tasks, N denotes the set of all tasks, $v\left(S\right)$ represents the system utility under the task set S, and ${\varphi }_i\left(v\right)$ is the Shapley value of task i, indicating the contribution of task i to the overall system performance. The specific scheduling algorithm is shown in Algorithm 2.

Algorithm 2: Prioritization Algorithm

In Algorithm 2, within the DAG-constrained task framework, priorities are distinguished among tasks with no direct precedence or succession and belonging to the same scheduling tier. For a selected task i, its contribution is evaluated in each possible task ordering $\{1,2,\dots ,i-1,i+1,\dots ,n\}$. This contribution is typically measured by the change in system performance resulting from the inclusion of task i into the sequence. Finally, the average of these contributions across all possible orderings is calculated to obtain the Shapley value of task i. A larger Shapley value indicates a greater marginal gain brought by the task, suggesting that it should be scheduled earlier with a higher priority. This approach enables an effective assessment of each task’s importance to system performance and facilitates optimization of the task scheduling sequence accordingly.

4.3. QVAC Task Scheduling Algorithm

To address the task scheduling problem under complex computational resources, this study designs a reinforcement learning-based approach that progressively learns the optimal scheduling policy through interaction with the environment. Specifically, the initial step leverages the results from Algorithms 1 and 2 to identify the preferred processor for each task and sorts the tasks according to their computational requirements and priority relations. Subsequently, a hybrid reinforcement learning method is proposed, integrating Q-learning with the A3C algorithm. In this approach, the traditional A3C architecture is enhanced by adopting an Actor–Critic structure to optimize the scheduling policy. The Actor network is responsible for policy updates and continuously adjusts the scheduling strategy using policy gradient methods. Meanwhile, the Critic network applies Q-learning to evaluate the value function of each action—the expected return for taking a specific action in a given state. This evaluation serves as feedback to the Actor network, enabling more accurate policy refinement. The use of Q-learning to replace the traditional Critic component is primarily driven by several reasons: First, Q-learning directly evaluates the value of Q without relying on state transition probability estimates, which is crucial for addressing highly dynamic heterogeneous environments, where stable-state transition modeling is difficult. Next, D2D task scheduling has a discrete action space, and Q-learning excels at distinguishing the value of discrete actions, avoiding the over-generalization of action values that often occurs with traditional Critic components in discrete scenarios. Then, Q-learning supports more stable value updates through mechanisms like Bellman equation iteration and potential experience replay, which help reduce the interference of random fluctuations in dynamic scheduling environments on value assessments, ensuring that the Actor network receives reliable feedback to stably adjust scheduling policies. The specific scheduling algorithm is shown in Algorithm 3.

In Algorithm 3, the task scheduling problem is modeled as a Markov Decision Process (MDP), where the state space includes the statuses of both tasks and processors and the action space represents the decision to assign tasks to processors. The optimization objective is to minimize total completion time and energy consumption. A discount factor $\gamma$ and a learning rate $\alpha$ are set. The Actor network outputs a probability distribution over server-task assignments. Using the policy gradient method, the Actor network updates its policy based on feedback from the Critic network to achieve more efficient task allocation. The updated formula is as follows:

$${\nabla }_{\theta }J\left(\theta \right)=\mathbb{E}\left[{\nabla }_{\theta }log{\pi }_{\theta }(a\mid s)·A(s,a)\right]$$

(14)

The Critic network employs the Q-learning method to evaluate the action-value function $Q(s,a)$, providing optimization guidance for the Actor network. By updating $Q(s,a)$ using the Bellman equation, the Critic can more accurately estimate the long-term return of actions, thereby improving policy quality. Here, $Q(s,a)$ specifically describes the expected long-term return of assigning a particular task to a target processor under the current system state, where the system state integrates the key task attributes and processor attributes, as defined in Table 1 of this study. For the update process, the learning rate $\alpha$ is set to ${10}^{-4}$ to avoid parameter oscillations during training, and the discount factor $\gamma$ is set to $0.9$ to balance near-term optimization effects and long-term system performance. This update is expressed as

$$Q(s,a)\leftarrow Q(s,a)+\alpha \left[r+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime })-Q(s,a)\right]$$

(15)

Overall, Q-learning is a value iteration method known for its convergence stability, making it particularly effective in discrete action spaces, as it updates Q-values for each state–action pair using a simple lookup table without complex gradient computations. In contrast, A3C excels by employing multiple parallel agents to train asynchronously, which enhances learning efficiency and reduces sampling bias due to correlation. The QVAC approach integrates the strengths of both—leveraging Q-learning’s stability and A3C’s parallelism—to address challenges in stability and exploration, enabling more efficient training of reinforcement learning agents in complex heterogeneous environments.

Algorithm 3: QVAC Algorithm

Through the QVAC approach, this study effectively balances the computational demands of tasks with processor resources in complex scheduling scenarios, maximizing overall scheduling performance while gradually enhancing system efficiency and reducing energy consumption. Furthermore, leveraging the self-optimizing nature of reinforcement learning, the method continuously learns optimal scheduling strategies in dynamic computing environments, offering a highly efficient and flexible solution for real-world resource management and task scheduling.

4.4. Time Complexity Analysis

In Algorithm 1, different types of computing resources are first normalized. For N tasks, the normalization has a time complexity of $O\left(N\right)$. Then, the NSGA-II algorithm is used to assign weights to multiple optimization objectives. The main operations include non-dominated sorting, crowding distance calculation, selection, crossover, and mutation. Among these, non-dominated sorting is the most time-consuming, with a time complexity of $O\left(N^2\right)$. Assuming the algorithm runs for T iterations, the total time complexity of the NSGA-II phase is $O(T\times N^2)$. Finally, the weighted Euclidean distance between tasks and resources is calculated during the resource matching stage, with each task requiring $O\left(1\right)$, giving a total of $O\left(N\right)$. Therefore, the overall time complexity of Algorithm 1 is $O(N+T\times N^2)$.

For Algorithm 2, suppose there are Pvalid task permutations. Each permutation requires checking task dependencies, with a complexity of $O\left(N^2\right)$, leading to a total complexity of $O(P\times N^2)$. Then, for each task i, the algorithm calculates its contribution across all permutations. This step has a complexity of $O(N\times P)$. Lastly, computing the Shapley value requires averaging these contributions, with a complexity of $O\left(P\right)$. Therefore, the total time complexity of Algorithm 2 is $O(P\times N^2)$.

In Algorithm 3, the task scheduling problem is modeled as an MDP. Let the batch size be B, the number of training iterations be T, and the state space dimension be $S=O(N+M)$, with an action space of $A=M^N$. The Actor network outputs a probability distribution over task–server assignments and is updated using policy gradient methods. Its time complexity is $O(N\times M\times T\times P\times B)$. The Critic network, based on Q-learning, evaluates Q-values and updates them using the Bellman equation, with a time complexity of $O(S\times A\times T)$. Therefore, the total time complexity of Algorithm 3 is $O(N\times M\times T\times P\times B)+O((N+M)\times M^N\times T)$.

In summary, the overall time complexity of the entire system is $O(N+T\times N^2)+O(P\times N^2)+O(N\times M\times T\times P\times B)+O((N+M)\times M^N\times T)$. The complexity reflects the computational cost of model training during task scheduling. As the number of tasks and processors increases, the computational overhead grows accordingly but remains within a controllable range.

5. Experimental Results and Algorithm Evaluation

The experimental comparisons and results are presented in this section, along with an analysis of the algorithm’s scalability. The experimental parameters and evaluation metrics are provided to assess the performance of the proposed method from multiple perspectives. The experimental environment is configured as shown in

Table 2. Configuration of the experimental environment.

Experimental Environment	Parameter
Operating system	64-bit Windows 11
Processor	AMD Ryzen 5 5600H with Radeon Graphics
CPU frequency	3.3GHz
Memory	32GB RAM
Simulation environment	MATLAB R2023a
Toolbox	MATLAB Basic Toolbox, Optimization Toolbox, Deep Learning Toolbox, Reinforcement Learning Toolbox, Parallel Computing Toolbox, etc.

.

5.1. Baseline Comparison Experiment

In this section, several experiments are conducted to validate and compare the proposed scheduling method. To comprehensively evaluate its performance, several classical and state-of-the-art scheduling algorithms are selected as baselines. The primary objective of the experiments is to compare the effectiveness of different algorithms in heterogeneous computing environments by analyzing key metrics such as energy consumption, task latency, and resource utilization. To ensure the generality and representativeness of the experiments, a set of complex workflow tasks—reflecting typical multi-task heterogeneous computing scenarios in real-world applications—is designed. The main workflow tasks involved are listed in

Table 3. Main workflow tasks we use.

Task	Model	Model Size	GFLOPS
Image Classification	VGG-16	528	15.5
Image Segmentation	UNet	40	30
Machine Translation	Transformer	200	15.7
Question Answering	BERT	440	189
Text Generation	GPT-2	500	172
Text Summarization	BART	500	120
Image Classification	ResNet-101	170	7.6
Object Detection	YOLOv8	150	130
Video Classification	SlowFast-50	230	36
Object Tracking	DERT	350	86
Anomaly Detection	LightGCN	75	2.5

.

In the baseline comparison experiments, the proposed scheduling method is systematically compared with traditional RL algorithms, the conventional A3C algorithm, as well as state-of-the-art methods—specifically the EPT algorithm from [31] and the DE-HEFT algorithm from [24]. The comparison focuses on four key performance metrics: energy consumption, task latency, device utilization, and resource utilization. 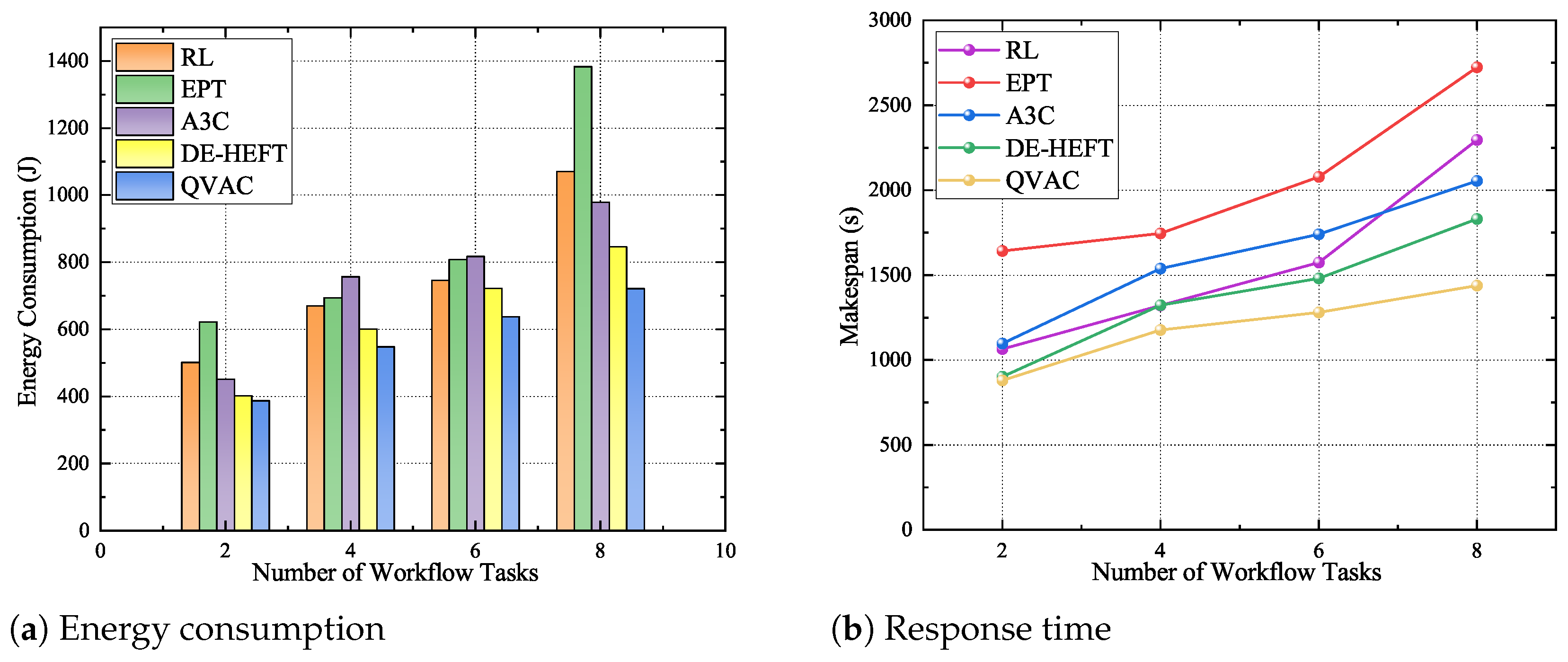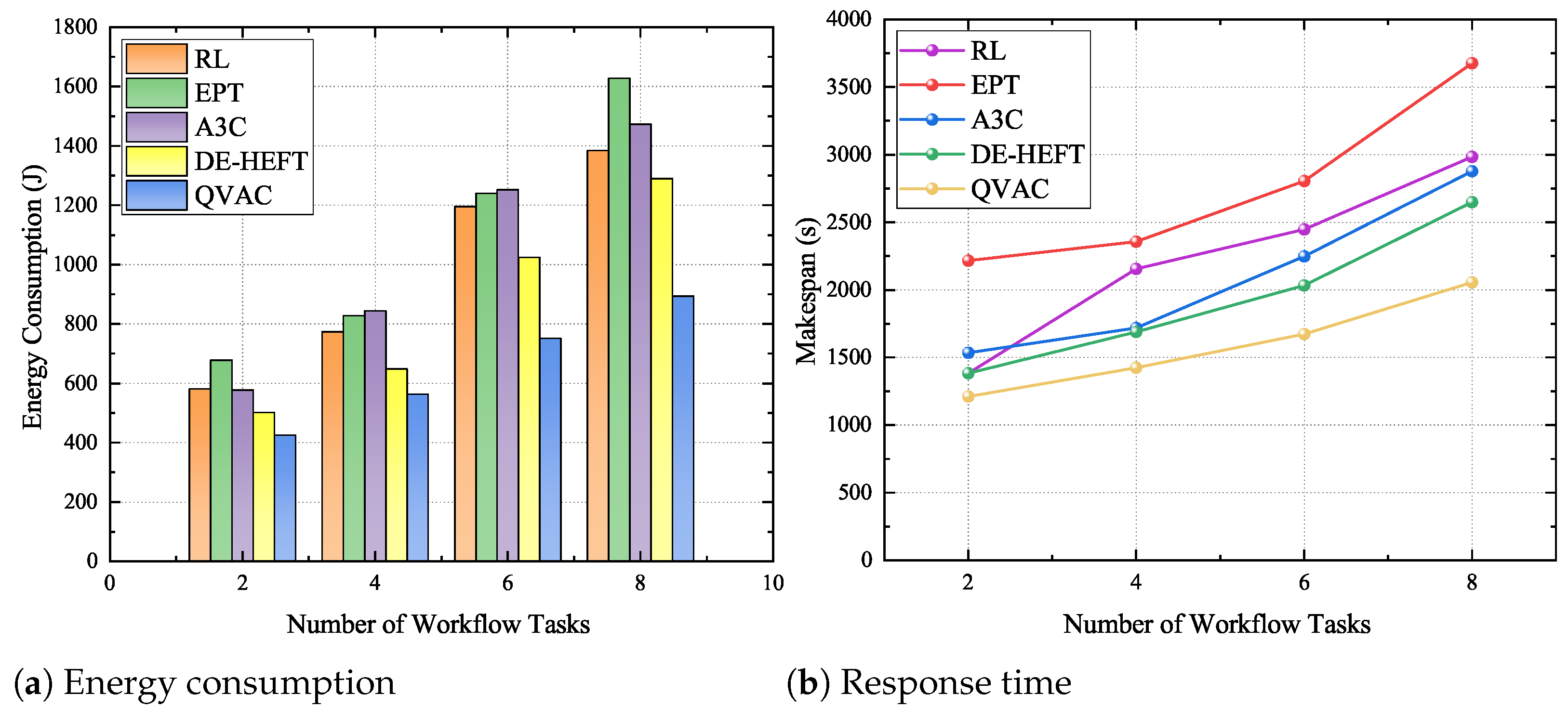As shown in Figure 4, energy consumption and delay increase linearly with task scale across all algorithms. This trend reflects the fact that a growing number of tasks directly increases the system’s computational load, thereby impacting both energy use and response time. However, the impact of optimized scheduling strategies becomes more pronounced with increasing task numbers, particularly in mitigating communication delays between tasks. Specifically, as the number of workflow tasks increases, the proposed method demonstrates clear advantages over the others. Despite the rise in inter-task communication delay, the proposed strategy effectively utilizes these communication periods to process additional tasks, reducing processor idle time and enhancing scheduling efficiency.

To better illustrate the effectiveness of the scheduling method in utilizing processors, this study also considers device utilization as a key performance metric. Device utilization reflects the ratio of a processor’s actual working time to its total active time, and it is calculated as follows:

$$\mathrm{Equipment}\mathrm{Utilization}={\displaystyle \frac{{\sum }_{i=1}^M\mathrm{Working}{\mathrm{Time}}_i}{{\sum }_{i=1}^M\mathrm{Available}{\mathrm{Time}}_i}}$$

(16)

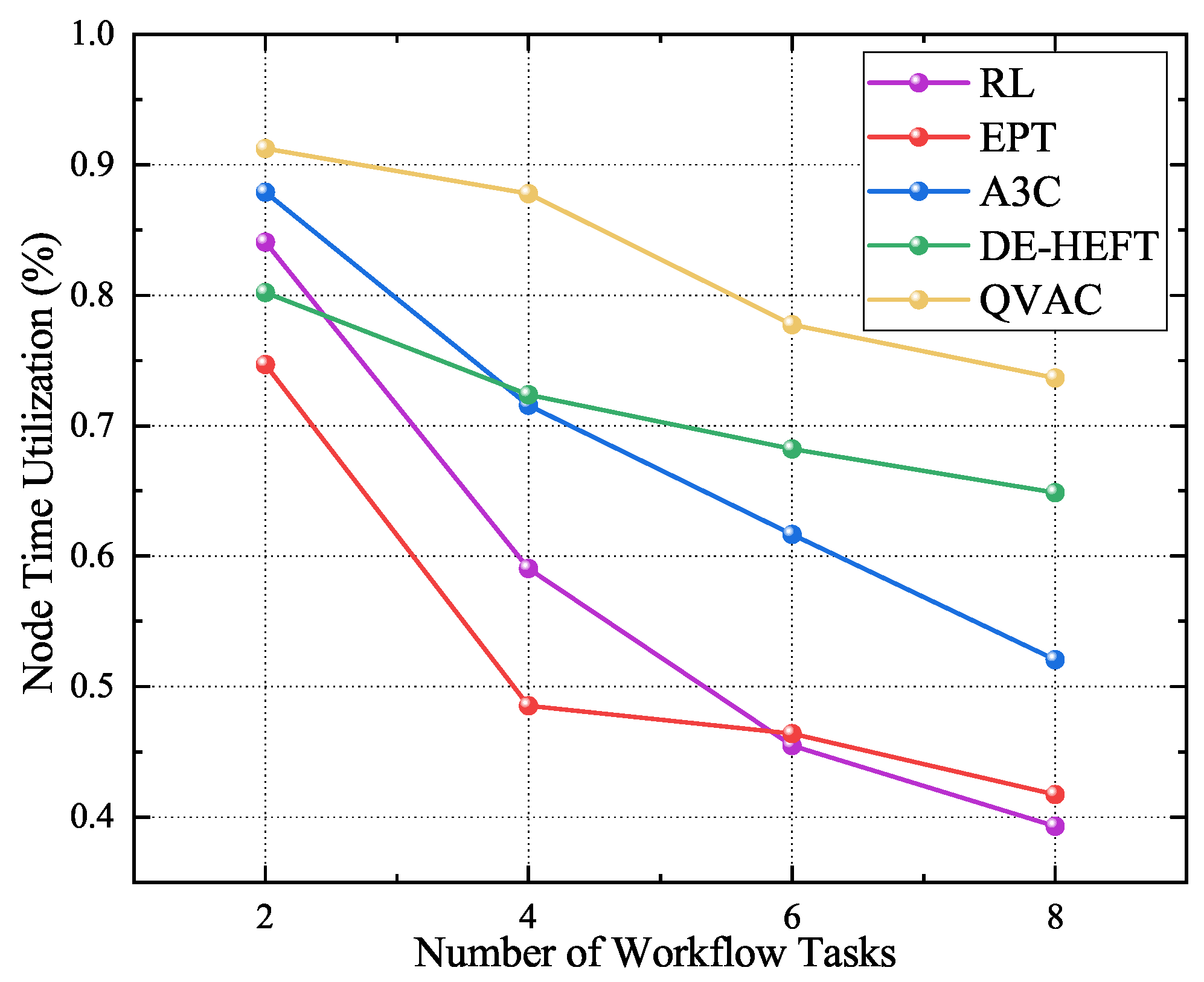
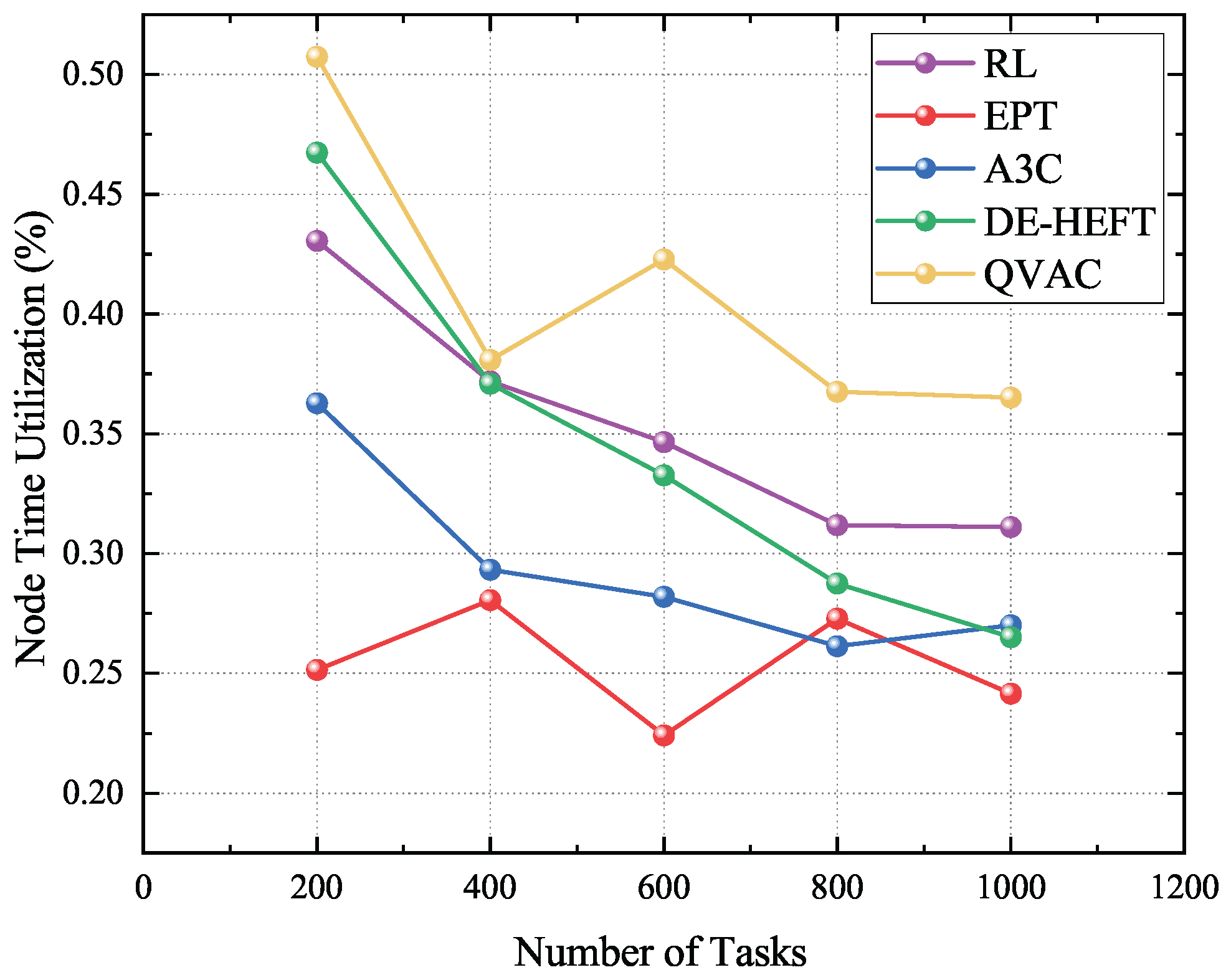
As shown in Figure 5, although device utilization generally declines as the number of tasks increases, the proposed method consistently achieves the best resource utilization across all experimental scenarios. It minimizes idle resources through intelligent scheduling and precise task allocation, especially in multi-task environments, significantly improving computational resource efficiency. 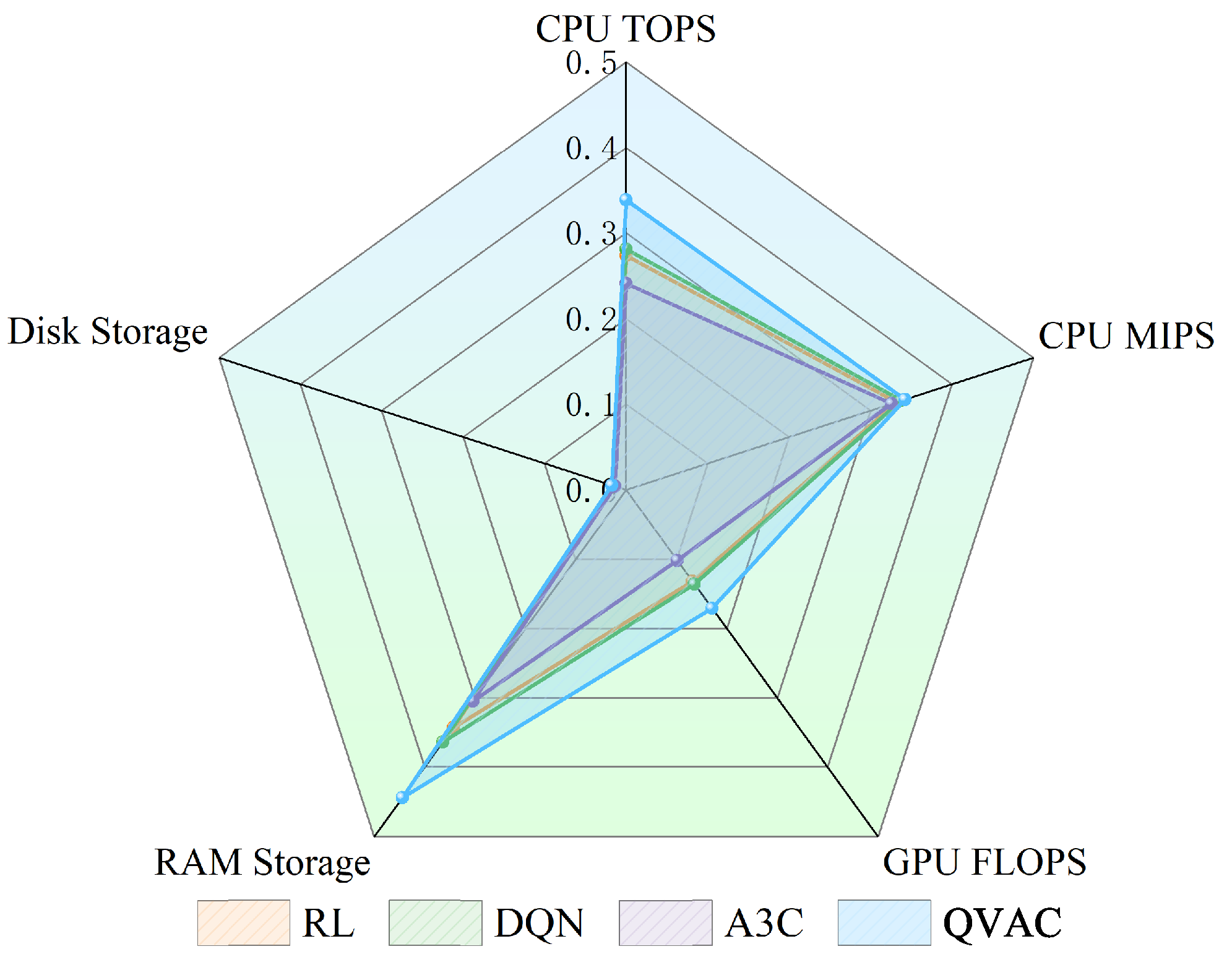In terms of resource utilization, as illustrated in Figure 6, the proposed method also demonstrates clear advantages. Calculating the Euclidean distance between processor capability and task demand ensures that each task is assigned to the most suitable processor, effectively reducing resource waste while maintaining load balance.

Through this fine-grained resource scheduling strategy, the proposed method effectively optimizes the matching between tasks and resources in complex heterogeneous computing environments. This not only improves overall system resource utilization but also reduces energy consumption and execution latency during task processing. Consequently, it offers a more efficient solution for task scheduling and resource allocation.

5.2. Ablation Experiments

To explicitly isolate the contribution of each core component, the ablation experiments are designed to remove one module at a time while keeping all other experimental settings strictly consistent with the complete method. This controlled design ensures that any performance variation can be uniquely attributed to the absence of the targeted module, avoiding interference from confounding factors.

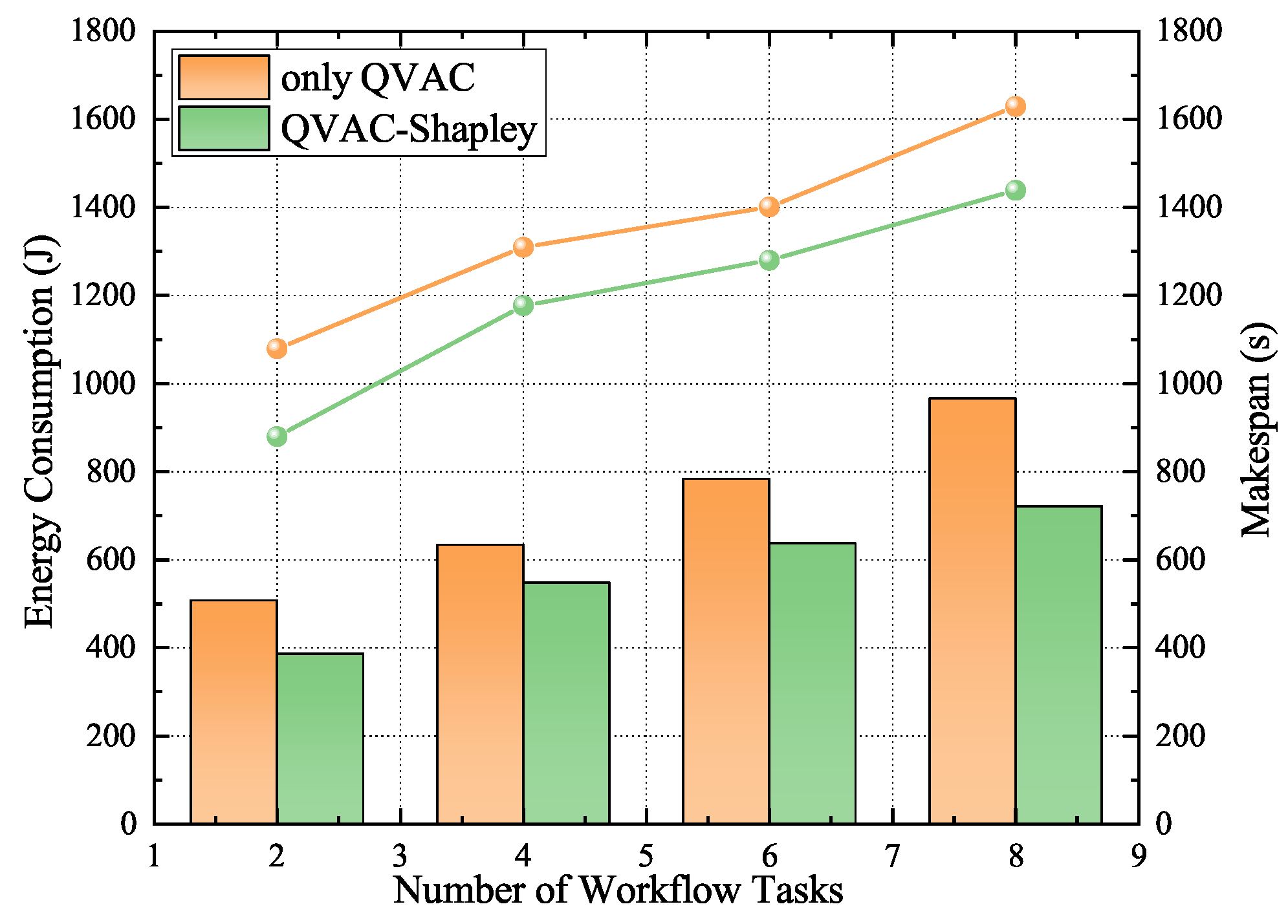
First, the performance of the method without Algorithm 2 is compared with that of the complete method, as illustrated in Figure 7, where the bar chart represents energy consumption and the line chart shows latency. Without incorporating the Shapley value, task priorities are assigned based on static rules. In this case, the scheduling sequence relies solely on the basic characteristics of the tasks, lacking a dynamic mechanism to adjust priorities based on task contributions. This omission leads to weaker performance, especially when tasks exhibit strong interdependencies, as it fails to account for their impact on overall system efficiency. Although the QVAC algorithm can still optimize the task execution order to some extent, the lack of appropriate priority settings prevents optimal resource allocation and task execution efficiency. As a result, both system latency and energy consumption increase, with performance degradation becoming more significant when communication delays between tasks are considerable.

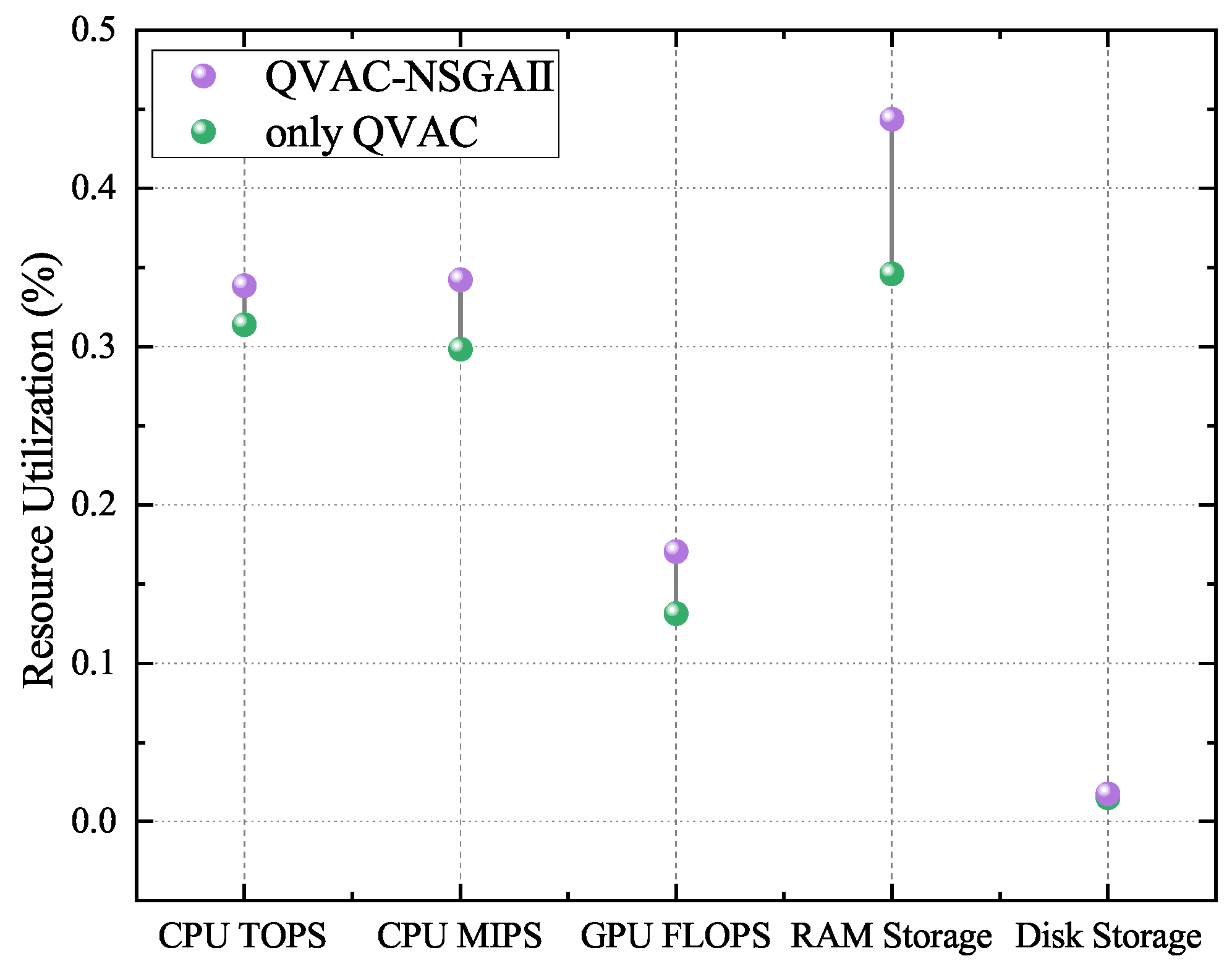
Secondly, a comparison is made between the method without the NSGA-II optimization model and the complete model, as shown in Figure 8. Without this model, the accuracy and fairness of resource allocation decrease significantly. The computational power of devices such as CPUs, GPUs, and memory cannot be accurately matched with task requirements, especially under resource-constrained conditions, resulting in lower resource utilization. Some devices suffer from wasted computing resources, while others cannot meet task demands due to insufficient resources. Moreover, lacking a multi-objective optimization strategy leads to poor system load balancing. Resource allocation becomes short-sighted and localized, causing frequent resource bottlenecks during task execution and further degrading the overall performance of the system.

The ablation experiments clearly demonstrate the significant roles of the NSGA-II optimization model and Shapley value-based priority adjustment in enhancing scheduling performance. The NSGA-II model effectively balances multiple objectives during optimization, thereby maximizing resource utilization while maintaining fairness in allocation. Meanwhile, the Shapley value-based priority adjustment improves the overall efficiency and performance of the system by optimizing the task execution order in a more informed and dynamic manner.The removal of either module leads to a noticeable decline in resource scheduling efficiency, further validating that each component in the proposed method is essential and plays a critical role in achieving optimal task scheduling and resource management.

5.3. Scalability Analysis

With the rapid development of the IoT and edge computing, massive volumes of computational tasks and data processing demands follow, posing unprecedented challenges to task scheduling and resource allocation [38]. This section provides a detailed analysis of the scalability of the proposed method.

In the extreme scenario where device capabilities are highly imbalanced and a single heavy-load task exists, both overall energy consumption and execution latency increase significantly, underscoring the challenges imposed by severe resource heterogeneity and workload skewness. As shown in Figure 9, the performance of baseline methods degrades notably with the increase in task numbers, particularly at scales of six and eight tasks, where energy consumption and makespan exhibit sharp growth. This indicates that their scheduling strategies lack robustness when facing single-node bottlenecks and heavy-task-induced blocking. In contrast, QVAC demonstrates much smaller performance degradation, consistently maintaining the lowest energy consumption and shortest execution time. This superiority is mainly attributed to its advantages in task–resource matching and critical-task identification, which effectively mitigate node overloading and reduce the delay caused by heavy tasks, thereby exhibiting stronger robustness and adaptability under extreme conditions.

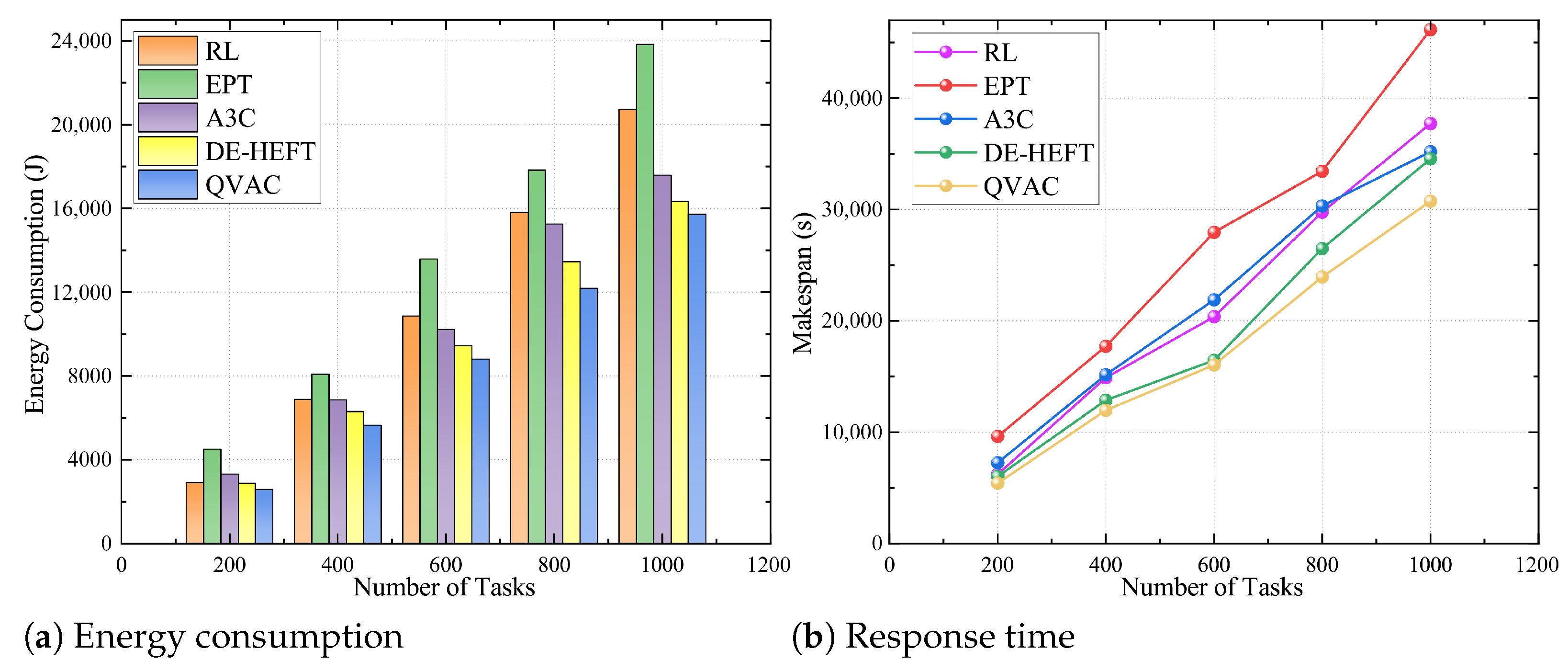
Figure 10, Figure 11 and Figure 12 evaluate the scheduling performance of the proposed method as the task scale increases. The results show that the proposed method can still effectively maintain low energy consumption and latency when handling large-scale tasks. Moreover, as the number of tasks grows, the performance gap between the proposed method and other approaches gradually widens. When the number of tasks increases from 100 to 1000, the system’s energy consumption and latency remain stable, and the proposed method begins to outperform others more significantly. Specifically, compared with state-of-art algorithms, the proposed method reduces energy consumption by 16.17% and latency by 13.86%. This demonstrates that the method retains strong energy control and scheduling efficiency under large-scale workloads. In addition, the proposed method also exhibits good scalability in terms of device utilization and resource usage. As the number of tasks increases, it more efficiently utilizes heterogeneous computing resources, avoiding issues such as overloading a single device or idling computational resources. Compared with other algorithms, the proposed method better incorporates multi-device collaborative computing and computing power matching, further improving task execution efficiency.

The experimental results demonstrate that the proposed method exhibits strong scalability in large-scale task environments. By leveraging parallel processing of the optimization algorithm, dynamic scheduling, and incremental computation, the system can effectively handle the increasing number of tasks while maintaining low computational complexity and high resource utilization efficiency, making the proposed approach highly adaptable and promising for large-scale heterogeneous computing environments.

6. Conclusions

This study investigates task scheduling methods for complex computational resources, integrating NSGA-II, cooperative game theory, and the QVAC algorithm to improve the efficiency and systemic symmetry of task scheduling in heterogeneous computing environments. First, a multi-objective optimization model based on the NSGA-II algorithm is introduced, which comprehensively considers various resource attributes of edge devices and applies dimensionless processing to ensure the accuracy, fairness, and symmetrical distribution of resource allocation. Second, a cooperative game model is incorporated, and the Shapley value is employed to quantify each task’s contribution to overall system performance. By dynamically adjusting task priorities based on their marginal contributions, our method optimizes the scheduling order, significantly improving scheduling efficiency and system performance while maintaining task-level symmetry. Subsequently, the QVAC algorithm is proposed, in which the traditional Critic component in the A3C framework is replaced with Q-learning. This enhancement strengthens the stability and global search capability of the scheduling strategy. Compared with conventional reinforcement learning approaches, the QVAC algorithm achieves lower latency, reduced energy consumption, and better load balancing. Finally, several experiments validate the effectiveness of the method in dynamic task scheduling, with specific metrics showing a 26.34% reduction in energy consumption, a 29.98% reduction in latency, and a 21.6% improvement in device utilization. In summary, the proposed multi-objective optimization model and the novel scheduling algorithm offer a new perspective for solving task scheduling problems in heterogeneous computing environments, holding substantial theoretical and practical value. Future research may extend their applicability and explore additional innovations in resource scheduling and optimization technologies.