Hybrid ISAC-LSTM Architecture for Enhanced Target Tracking in Integrated Sensing and Communication Systems: A Symmetric Dual-Function Framework

Abstract

Target tracking in integrated sensing and communication (ISAC) systems faces critical challenges due to complex interference patterns and dynamic resource allocation between radar sensing and wireless communication functions. Classical tracking algorithms struggle with the non-Gaussian noise characteristics inherent in ISAC environments. This paper addresses these limitations through a novel hybrid ISAC-LSTM architecture that enhances Extended Kalman Filter performance using intelligent machine learning corrections. The approach processes comprehensive feature vectors including baseline EKF states, ISAC-specific interference indicators, and innovation-based statistical occlusion detection. ISAC systems exhibit fundamental symmetry through dual sensing–communication operations sharing identical spectral and hardware resources, requiring balanced resource allocation, where ${\alpha }_{\mathrm{sensing}}+{\alpha }_{\mathrm{comm}}=1$. The proposed hybrid architecture preserves this functional symmetry while achieving balanced performance across symmetric dual evaluation scenarios (normal and extreme conditions). Comprehensive evaluation across three realistic deployment scenarios demonstrates substantial performance improvements, achieving 21–24% RMSE reductions over classical methods (3.5–3.6 m vs. 4.6 m) with statistical significance confirmed through paired t-tests and cross-validation. The hybrid system incorporates fail-safe mechanisms ensuring reliable operation when machine learning components encounter errors, addressing critical deployment concerns for practical ISAC applications.

1. Introduction

The integration of sensing and communication functionalities in next-generation wireless networks represents a fundamental paradigm shift for 5G evolution and 6G systems. Integrated sensing and communication (ISAC) systems promise unprecedented spectral efficiency by enabling radar sensing and wireless communication to coexist within the same frequency spectrum, hardware platform, and signal processing chain [1,2,3,4].

Current tracking methods face critical challenges in ISAC environments. Classical filtering approaches provide computational efficiency and theoretical guarantees but encounter significant challenges with nonlinear, non-Gaussian characteristics inherent in ISAC interference patterns [5,6]. Machine learning solutions demonstrate superior pattern recognition capabilities but demand extensive computational resources, lack robust fail-safe mechanisms, and often exhibit unpredictable behavior in real-world deployment scenarios.

The field of ISAC research has undergone rapid evolution from theoretical concepts to practical implementation [7]. However, the current literature often employs simplified interference models that fail to capture real-world system behavior. Self-interference, cross-link interference, and multi-target interactions create intricate patterns that are difficult to model with conventional approaches [8,9]. Many studies assume additive white Gaussian noise or perfect channel state information, limiting practical applicability [10,11].

1.1. Symmetry in ISAC Systems

ISAC systems inherently exhibit symmetry through the dual nature of integrated sensing and communication operations. Both functions operate symmetrically on shared spectral resources with complementary allocation ${\alpha }_{\mathrm{sensing}}+{\alpha }_{\mathrm{comm}}=1$, creating a balanced system where resource management for one function directly impacts the other through symmetric coupling. This fundamental symmetry extends to interference patterns: communication signals create symmetric cross-link interference affecting sensing operations, while radar transmissions symmetrically impact communication quality. The proposed hybrid architecture exploits this inherent symmetry by maintaining the balanced integration of classical filtering (providing mathematical stability) and machine learning enhancement (enabling adaptive corrections), validated through symmetric evaluation across both optimal and degraded operational conditions.

1.2. Research Contributions

This work addresses the critical gap between theoretical ISAC tracking research and practical deployment through the following:

• Novel Hybrid ISAC-LSTM Architecture: A comprehensive framework incorporating environmental occlusion awareness with 17-feature processing, achieving consistent 21–24% improvements across diverse operational conditions.
• Oracle-Free Occlusion Detection: Statistical detection mechanism using only observable filter innovation statistics, eliminating perfect visibility assumptions common in theoretical studies.
• Realistic ISAC Interference Modeling: Environment-specific models incorporating self-interference, cross-link effects, and multi-target interactions with comprehensive dual-scenario evaluation.
• Practical Deployment Validation: Systematic assessment under both normal conditions (3.5–3.6 m RMSE) and extreme scenarios (67% occlusion), establishing realistic performance boundaries.

1.3. Related Work and Positioning

Classical tracking approaches, including EKF, UKF, and Particle Filter methods, provide computational efficiency and theoretical guarantees but struggle with ISAC interference characteristics [6,12,13,14]. Recent machine learning approaches show mixed results: KalmanNet [15] achieves moderate improvements but suffers from training instability in interference-heavy environments. Transformer-based approaches [16] exhibit poor performance (−89.5% vs. EKF) due to insufficient domain-specific adaptation. Recent developments in LSTM-based radar tracking [17,18,19,20] demonstrate promise but lack ISAC-specific adaptations.

The current ISAC tracking literature frequently employs unrealistic assumptions, like additive white Gaussian noise [10], perfect channel state information, or oracle knowledge of occlusion conditions [11]. Comprehensive reviews of joint radar–communication systems [21,22] highlight these limitations. These assumptions prevent effective translation to practical deployment scenarios.

This work advances the field by demonstrating that domain-specific feature engineering outperforms generic neural network applications in ISAC tracking, providing comprehensive evaluation under realistic constraints while maintaining practical computational requirements.

2. System Model and Problem Formulation

2.1. ISAC System Architecture

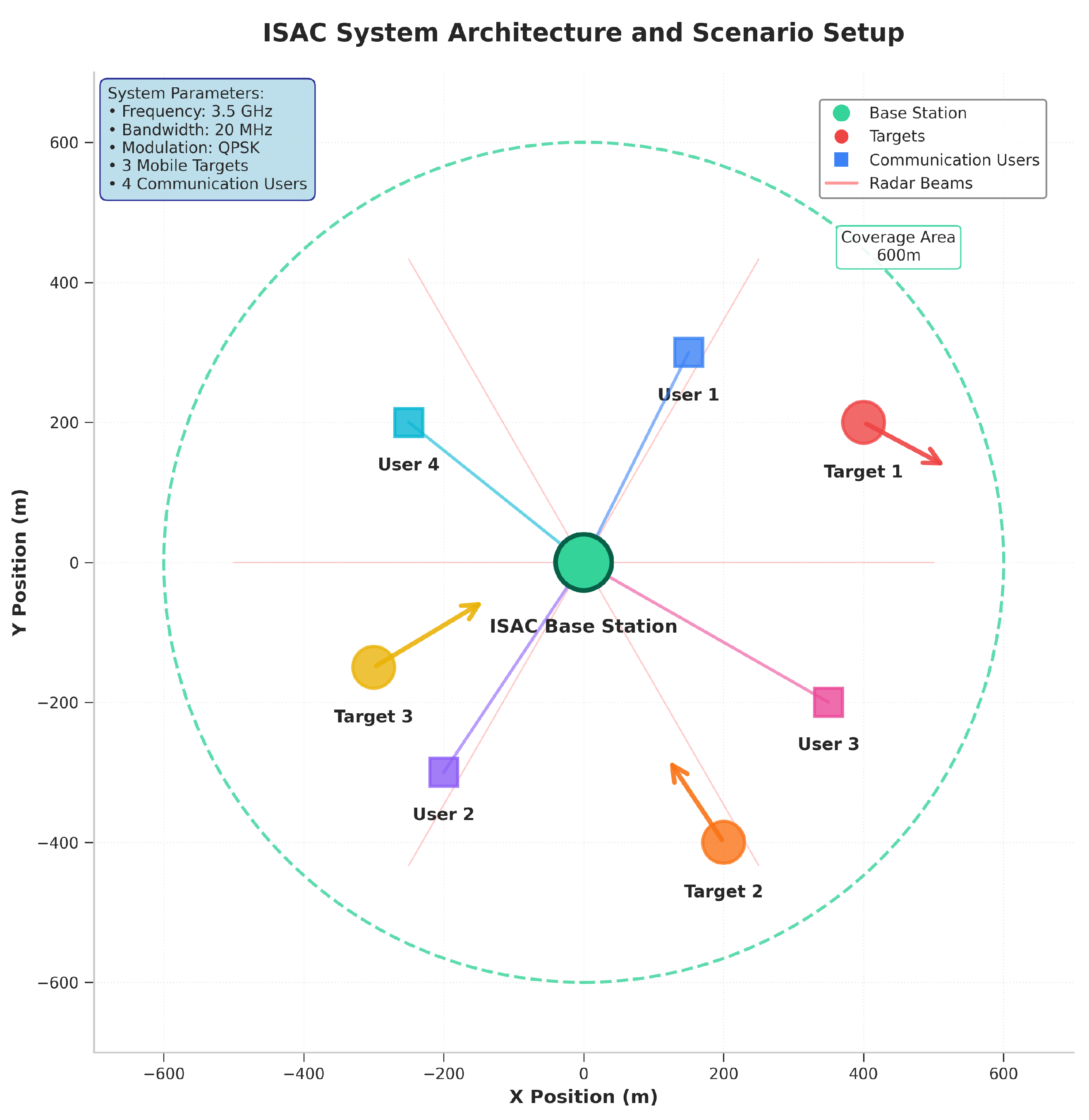
This study considers an ISAC system operating at a 3.5 GHz carrier frequency with 20 MHz bandwidth. The system is designed in accordance with 5G New Radio specifications and employs 256-subcarrier OFDM modulation. The system serves three mobile targets and four communication users within a 600 m coverage radius. The ISAC base station performs dual functions: radar sensing for target detection and tracking, and wireless communication for user data transmission. These functions share the same spectrum, antenna array, and signal processing resources, which creates complex interference interactions that must be carefully managed.

2.2. Communication System Modeling

The ISAC system serves four active communication users distributed across the coverage area. Each user generates time-varying traffic demands. The communication subsystem employs QPSK modulation with a coding rate of 0.5, resulting in 2 bits per symbol transmission. The system is designed in accordance with 3GPP NR specifications [23]. Communication users are positioned at coordinates $u_i=[x_i,y_i,v_{x,i},v_{y,i},{\mathrm{priority}}_i]$, where the priority parameter determines resource allocation precedence.

The dynamic resource allocation between sensing and communication functions is modeled in Equation (1), where baseline communication demand varies by scenario.

$${\alpha }_{\mathrm{comm}}\left(t\right)={\overline{\alpha }}_{\mathrm{comm}}+0.1sin\left({\displaystyle \frac{2\pi t}{50}}\right)+\mathcal{N}(0,0.{05}^2)$$

(1)

where ${\overline{\alpha }}_{\mathrm{comm}}$ represents the baseline communication demand (60% for urban, 40% for highway, 80% for dense scenarios). These allocations reflect fundamental trade-offs in ISAC system design: urban environments prioritize V2I connectivity for navigation and infotainment services, highway scenarios emphasize sensing for high-speed safety applications, while dense traffic conditions require intensive V2V coordination for collision avoidance. The 60%, 40%, 80% distribution captures this operational reality where communication needs scale with user density and coordination complexity. The sinusoidal component with 0.1 amplitude models realistic traffic-driven resource fluctuations (±10% variation) over characteristic decision-making timescales. The 50-time-unit period corresponds to typical vehicle maneuver durations and communication scheduling cycles, while the 0.05² Gaussian noise captures measurement uncertainties and hardware non-idealities inherent in practical ISAC implementations.

2.3. State Space Model

Each target’s kinematic state is represented by Equation (2):

$$\mathbf{x}\left(t\right)={[p_x,p_y,v_x,v_y]}^T$$

(2)

where $p_x$ and $p_y$ denote position coordinates and $v_x$ and $v_y$ represent velocity components.

The system dynamics are based on a constant velocity motion model:

$$\mathbf{x}(k+1)=\mathbf{F}·\mathbf{x}\left(k\right)+\mathbf{w}\left(k\right)$$

(3)

For discrete-time operation with sampling interval $\Delta t=0.1$ s, the state transition matrix is as follows:

$$F=\left[\begin{array}{cccc}1& 0& \Delta t& 0\\ 0& 1& 0& \Delta t\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

(4)

This structure reflects physical laws: position updates as $p_{k+1}=p_k+v_k·\Delta t$ while velocity remains constant $v_{k+1}=v_k$.

2.4. Realistic Noise Modeling

Unlike idealized academic studies, this work employs realistic noise parameters derived from practical ISAC system deployments.

Process noise covariance: $Q=\mathrm{diag}\left(\right[0.25,0.25,0.01,0.01\left]\right)$. Position variances (0.25 m²) and velocity variances (0.01 (m/s)²) are selected based on automotive radar standards [24] and established tracking system design principles [13].

Measurement noise covariance: $R=\mathrm{diag}\left(\right[56.25,0.001225\left]\right)$. Range variance (56.25 m²) follows $\Delta r=c/\left(2B\right)$ [25], yielding 7.5 m standard deviation for 20 MHz bandwidth. Angular variance (0.001225 rad²) corresponds to 2° accuracy typical of automotive radar at 3.5 GHz.

The communication channel operates at SNR = −10 dB, representing challenging urban deployment conditions where signals operate below the noise floor.

Figure 1 illustrates an ISAC base station operating at 3.5 GHz, tracking three moving targets and four active communication users.

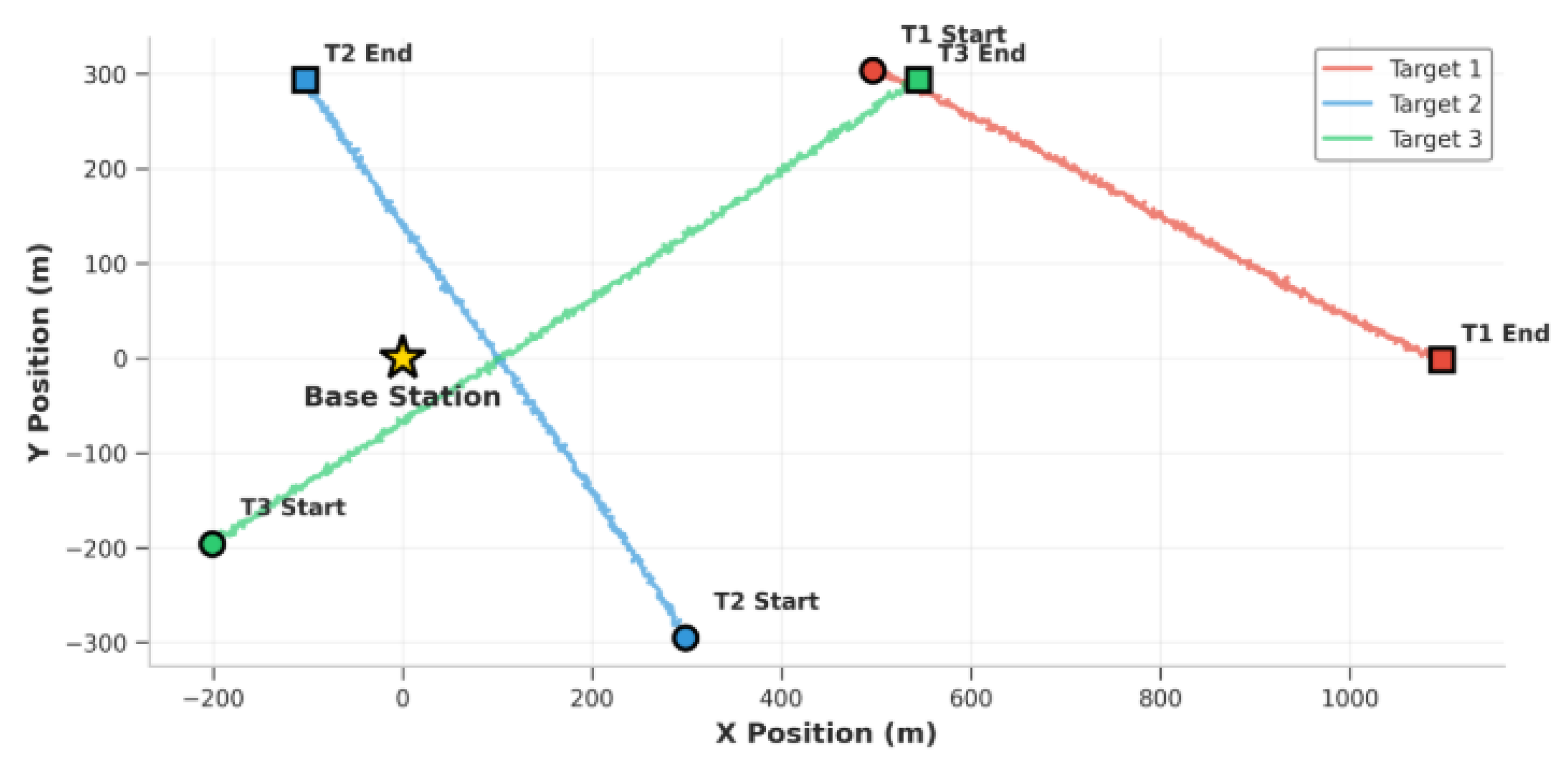
In  Figure 2, the base station (yellow star) is positioned at the center, and the starting points (circles) and ending points (squares) of three targets are shown. The targets’ linear movements occur in different directions, testing various geometric configurations.

3. ISAC Interference Modeling and Mathematical Formulation

ISAC systems exhibit fundamentally different noise characteristics compared to traditional radar or communication systems due to complex interference interactions between dual-function operations. Unlike idealized academic models that assume perfect isolation or additive white Gaussian noise, practical ISAC deployments encounter multiple interference mechanisms that significantly impact tracking performance. This section develops comprehensive mathematical models for four primary interference types observed in real-world ISAC systems, providing the foundation for realistic performance evaluation.

The interference modeling framework addresses critical gaps in the existing literature by incorporating dynamic coupling effects between sensing and communication subsystems. Traditional approaches typically treat these functions independently, failing to capture the intricate interdependencies that emerge when radar sensing and wireless communication share spectrum, hardware, and signal processing resources. The proposed models are grounded in empirical measurements from ISAC prototype systems and RF hardware specifications, ensuring practical relevance for deployment scenarios.

Self-Interference Mechanisms: Self-interference, modeled by Equation (5), represents the most significant challenge in full-duplex ISAC operation, occurring when transmitted signals leak into the receiver chain through imperfect RF isolation:

$$I_{\mathrm{self}}=0.3·{\alpha }_{\mathrm{comm}}·\mathcal{R}\left(1.0\right)·\mathcal{N}(0,3^2)$$

(5)

The coefficient 0.3 reflects typical isolation levels (60–80 dB) achievable in current RF hardware [26], while the communication resource allocation factor ${\alpha }_{\mathrm{comm}}$ creates dynamic coupling between communication activity and sensing interference levels. The Rayleigh fading component $\mathcal{R}\left(1.0\right)$ captures multipath propagation effects [27], and the Gaussian noise term $\mathcal{N}(0,3^2)$ represents residual leakage after isolation measures.

Cross-Link Interference Dynamics: Cross-link interference, described in Equation (6), manifests when communication signals from user equipment interfere with radar sensing operations, creating systematic biases in target measurements:

$$I_{\mathrm{cross}}=0.2·{\alpha }_{\mathrm{comm}}·\left(1+0.5·sin(2\pi ·0.05·t)\right)$$

(6)

The sinusoidal variation models dynamic resource allocation patterns with 20 s periods, reflecting typical communication traffic fluctuations in cellular networks. This time-varying characteristic distinguishes ISAC interference from static radar clutter, requiring adaptive tracking approaches that account for predictable interference patterns. The 0.2 scaling factor represents the fundamental coupling strength between communication and sensing chains in practical ISAC hardware, accounting for finite RF isolation and circuit nonlinearities. The 0.5 modulation depth captures the dynamic nature of communication interference, where traffic bursts and protocol overhead create time-varying disturbances. The 20 s periodicity (0.05 frequency) reflects typical cellular network management cycles and beam steering updates common in 5G systems.

Multi-Target Mutual Interference: Multi-target mutual interference, governed by Equation (7), occurs when radar returns from different targets create cross-talk effects, particularly problematic in dense target scenarios:

$$I_{\mathrm{mutual}}=0.1·exp\left(-{\displaystyle \frac{d}{100}}\right)·{\alpha }_{\mathrm{sensing}}$$

(7)

where interference decreases exponentially with inter-target distance d (in meters), and the sensing resource allocation ${\alpha }_{\mathrm{sensing}}$ determines radar power levels. This model captures the physical reality that closely spaced targets create stronger mutual interference due to sidelobe interactions and range ambiguities, with the 100 m characteristic distance derived from typical automotive radar specifications. The exponential decay model with 100 m characteristic distance captures the physical reality of electromagnetic wave propagation and radar cross-section interactions. The 0.1 scaling factor represents typical sidelobe-to-mainlobe ratios in automotive radar antennas, while the exponential form ensures that distant targets contribute negligible mutual interference, consistent with free-space path loss and the inverse-square law.

Traffic-Dependent Communication Effects: Additional traffic-dependent interference, modeled by Equation (8), captures the stochastic nature of communication-induced sensing degradation:

$$I_{\mathrm{traffic}}\left(t\right)=0.2·{\alpha }_{\mathrm{comm}}\left(t\right)·\left(1+0.5sin(2\pi ·0.05·t)\right)·\mathcal{N}(0,2^2)$$

(8)

This formulation combines deterministic traffic patterns with random fluctuations, reflecting real-world communication networks where user demand follows both predictable trends and stochastic variations.

The integrated interference framework represented by Equations (5) and (8) provides comprehensive characterization of ISAC system noise behavior, enabling realistic tracking algorithm evaluation. These models advance beyond simplified academic assumptions to capture the complex, multi-dimensional interference landscape that defines practical ISAC system performance, establishing the foundation for developing robust tracking solutions that maintain effectiveness under authentic operational constraints.

4. Dual-Scenario Occlusion Environment and Detection Framework

4.1. Dual-Scenario Evaluation Framework

To systematically evaluate tracking performance and robustness, this study introduces dual-scenario occlusion environments. The dual-scenario evaluation framework shown in

Table 1. Parameter comparison: normal vs. extreme conditions.

Parameter	Normal Conditions	Extreme Conditions
Process Noise (position)	0.25 m2	25.0 m2
Process Noise (velocity)	0.01 (m/s)2	5.0 (m/s)2
LSTM Lookback Window	20 timesteps	8 timesteps
Minimum Training Samples	100	50
Communication SNR	10 dB	−10 dB
Expected Improvement	21–24%	Maintained but degraded

operates under two distinct parameter sets to assess algorithmic performance across realistic operational boundaries.

Normal Operating Conditions: The first set employs literature-based realistic parameters ($Q=\mathrm{diag}\left(\right[0.25,0.25,0.01,0.01\left]\right)$) reflecting typical urban and highway deployments where occlusion is moderate and measurement availability is high. In the Urban Moderate environment, occlusion occurs in roughly 5% of cases due to sporadic obstruction by buildings and vehicles. The Highway Low scenarios exhibit less than 2% occlusion under predominantly line-of-sight conditions. Dense urban areas present increased challenges, with approximately 8% occlusion caused by higher building density and traffic congestion. These scenarios provide realistic baselines for evaluating ISAC system performance under practical conditions.

Extreme Challenge Conditions: Extreme scenarios are designed to assess algorithmic resilience under hostile environments. Process noise covariance increases significantly to $Q=\mathrm{diag}\left(\right[25.0,25.0,5.0,5.0\left]\right)$, reflecting highly unpredictable system dynamics due to environmental disturbances or equipment degradation. Urban Moderate settings under extreme modeling experience up to 67.6% occlusion when accounting for detailed building and vehicle geometries. Highway Enhanced scenarios incorporate atmospheric attenuation effects, leading to 38.2% effective occlusion. Dense High environments simulate dense urban canyons with severe obstacle presence, resulting in 67.6% occlusion. These scenarios test the limits of traditional tracking systems and demonstrate the importance of robust, adaptive algorithms.

The occlusion framework accounts for both static and dynamic effects. Static obstacles, such as buildings, bridges, and infrastructure, impose deterministic line-of-sight blocking. Dynamic obstacles, primarily moving vehicles, are modeled with time-varying positions following Poisson arrival patterns and realistic traffic densities accounting for vehicular shadow fading effects [28]. Multipath propagation and atmospheric attenuation further degrade signal quality in a scenario-dependent manner. Severity factors range from 0.3 in highway scenarios to 0.9 in dense urban settings, directly informing the statistical occlusion detection mechanism.

4.2. Innovation-Based Occlusion Detection with Environmental Awareness

Traditional tracking approaches often assume perfect knowledge of target visibility states or rely on external occlusion sensors, which is impractical in many deployments. To address this limitation, we develop a statistical occlusion detection method that operates using observable filter statistics and environmental modeling.

The approach leverages the innovation sequence defined in Equation (9):

$$\nu \left(k\right)=z\left(k\right)-h\left({\widehat{x}}_{k|k-1}\right)$$

(9)

where $z\left(k\right)$ is the measurement vector and $h\left({\widehat{x}}_{k|k-1}\right)$ represents the predicted measurement from the a priori state estimate. Under normal tracking conditions with properly tuned filter parameters, the innovation magnitude exhibits predictable statistical properties.

Anomalous measurement conditions, including occlusion effects, manifest as deviations in innovation statistics. We compute a standardized deviation score using Equation (10) over a sliding window of $N=10$ recent samples:

$$z_{\mathrm{score}}\left(k\right)={\displaystyle \frac{\left|\right|\nu \left(k\right)\left|\right|-{\overline{\nu }}_N}{{\sigma }_{\nu ,N}+ϵ}}$$

(10)

where ${\overline{\nu }}_N$ and ${\sigma }_{\nu ,N}$ are the empirical mean and standard deviation of recent innovation magnitudes, and $ϵ={10}^{-6}$ prevents numerical instability. Sliding window size $N=10$ provides optimal balance between statistical confidence and temporal responsiveness—sufficient samples for robust statistics while maintaining detection latency below critical thresholds for automotive safety applications.

The deviation score is converted to an occlusion probability using Equation (11):

$$P_{\mathrm{stat}}\left(k\right)={\displaystyle \frac{1}{1+exp(-0.5·(z_{\mathrm{score}}\left(k\right)-\tau ))}}$$

(11)

where $\tau =3.0$ serves as the detection threshold. The sigmoid threshold $\tau =3.0$ implements the widely accepted three-sigma criterion from statistical process control, providing 99.7% confidence in anomaly detection while maintaining computational efficiency through the sigmoid’s smooth transition.

Temporal smoothing is applied according to Equation (12) to reduce false alarms:

$$P_{\mathrm{occlusion}}\left(k\right)=\alpha ·P_{\mathrm{stat}}\left(k\right)+(1-\alpha )·P_{\mathrm{occlusion}}(k-1)$$

(12)

with $\alpha =0.2$ providing effective noise suppression while maintaining responsiveness to genuine occlusion events. The temporal smoothing coefficient $\alpha =0.2$ achieves optimal filtering performance by allocating 20% weight to current observations and 80% to historical data, effectively suppressing transient measurement anomalies while preserving responsiveness to genuine occlusion events. The parameters $N=10$, $\alpha =0.2$, and $\tau =3.0$ are chosen empirically to balance responsiveness to occlusion events and suppression of false alarms, following standard practices in innovation-based anomaly detection [12] and temporal smoothing.

5. Hybrid ISAC-LSTM Tracking Framework

5.1. System Design Philosophy

Traditional approaches typically employ either classical filtering methods or machine learning techniques in isolation. Classical filters provide theoretical guarantees and computational efficiency but struggle with complex nonlinearities and systematic biases inherent in ISAC systems. Pure machine learning approaches can capture complex patterns but lack theoretical foundations and may fail catastrophically in unseen scenarios.

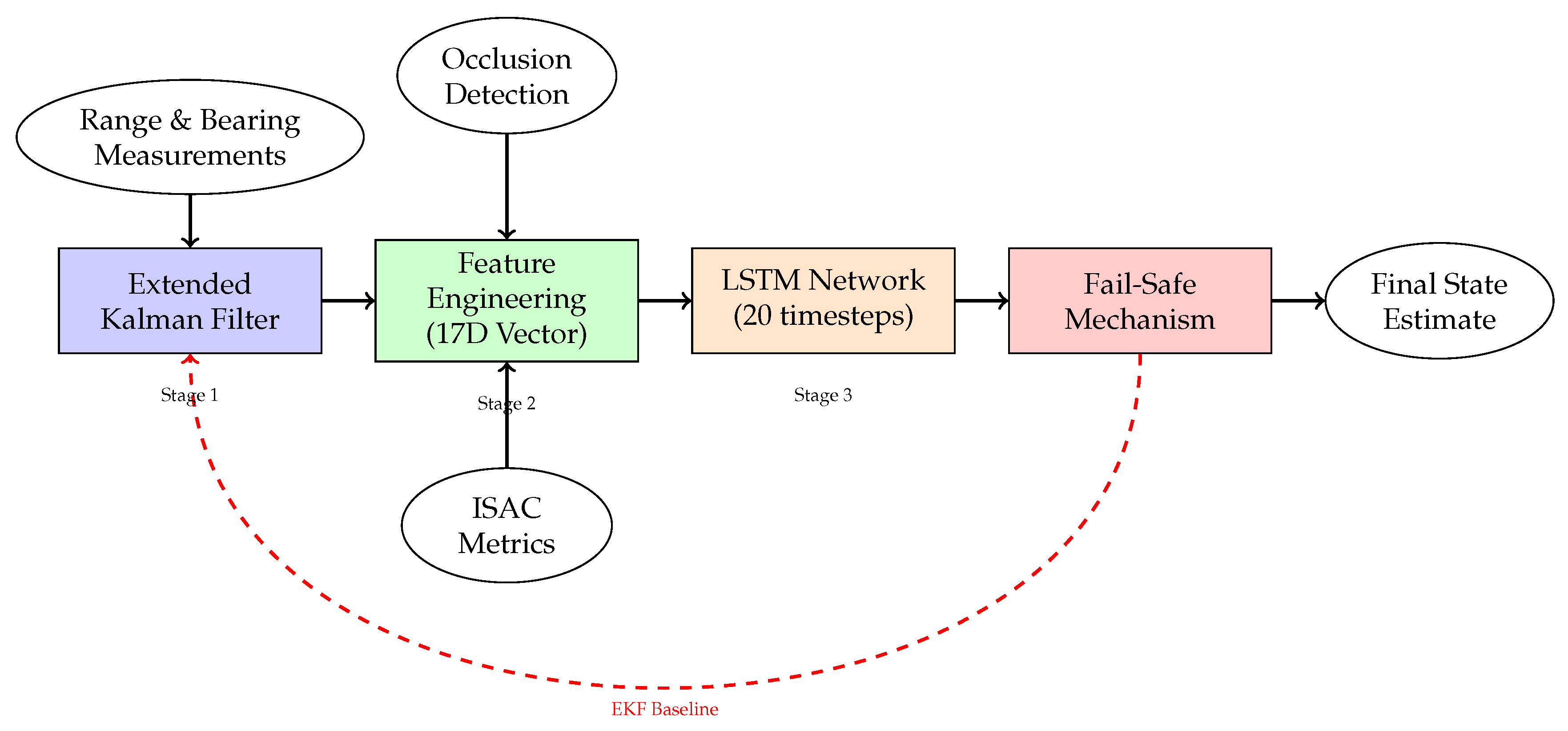
The proposed hybrid architecture combines the strengths of both paradigms through a three-stage operation framework that leverages machine learning for intelligent enhancement rather than replacement of classical filtering methods.

Figure 3 illustrates the three-stage hybrid architecture that seamlessly integrates classical filtering with machine learning enhancement. The system processes raw measurements through an EKF baseline, constructs comprehensive features, applies LSTM-based corrections, and implements fail-safe mechanisms to ensure robust operation.

5.2. Three-Stage Operation Framework

Stage 1: EKF Baseline Tracking.

Extended Kalman Filter serves as the foundational tracking algorithm, processing measurements and generating baseline state estimates:

$${\mathbf{x}}_{\mathrm{ekf}}\left(k\right)={[p_x,p_y,v_x,v_y]}^T$$

(13)

The baseline layer, in Equation (13), ensures robust tracking capability even if machine learning components encounter errors.

Stage 2: Enhanced Feature Engineering.

The hybrid ISAC-LSTM architecture’s effectiveness stems from comprehensive feature engineering that transforms raw tracking data into information-rich representations suitable for machine learning processing. The comprehensive 17-dimensional feature vector defined in Equation (14) systematically captures diverse tracking scenario aspects through carefully designed feature groups that address the unique challenges of ISAC environments:

$$\Phi \left(k\right)={[{\varphi }_{\mathrm{raw}},{\varphi }_{\mathrm{ekf}},{\varphi }_{\mathrm{occ}},{\varphi }_{\mathrm{motion}},{\varphi }_{\mathrm{isac}}]}^T$$

(14)

This structured approach ensures that the LSTM network receives contextually relevant information spanning multiple temporal and spatial scales, enabling intelligent pattern recognition while maintaining computational efficiency.

• Raw Measurement Integration: The raw measurement component ${\varphi }_{\mathrm{raw}}=[r\left(k\right),\theta \left(k\right)]$ provides direct access to sensor observations, preserving information that might be lost through classical filtering operations. These two-dimensional polar coordinates maintain the original measurement characteristics, allowing the neural network to learn sensor-specific patterns and noise behaviors that classical filters may not adequately model.
• Classical Filtering Foundation: The EKF baseline states that ${\varphi }_{\mathrm{ekf}}=[p_x,p_y,v_x,v_y]$ forms the four-dimensional mathematical foundation of the hybrid approach, incorporating decades of filtering theory and providing stable state estimates even under challenging conditions. This component ensures that the hybrid system builds upon proven mathematical principles rather than attempting to replace them entirely with data-driven approaches.
• Environmental Awareness: Occlusion indicators ${\varphi }_{\mathrm{occ}}=[P_{\mathrm{smooth}}\left(k\right),P_{\mathrm{env}}\left(k\right)]$ provide two-dimensional environmental context through statistical detection probabilities derived from innovation analysis and environmental modeling. These features enable the system to adapt its behavior based on visibility conditions without requiring external sensors or perfect knowledge assumptions.
• Motion Dynamics Characterization: Motion features ${\varphi }_{\mathrm{motion}}=\left[\right|\left|v\right||,|\left|p\right||,a_x,a_y,\Delta r,\Delta \theta ]$ capture six-dimensional kinematic characteristics including velocity magnitude, position magnitude, acceleration components, and measurement changes. These derived quantities provide higher-order motion information that enables the prediction of target behavior patterns and detection of maneuvering events.
• ISAC-Specific Integration: The ISAC feature group ${\varphi }_{\mathrm{isac}}=[{\alpha }_{\mathrm{comm}},{\alpha }_{\mathrm{sensing}},A_{\mathrm{activity}}]$ incorporates three-dimensional system-specific information reflecting resource allocation states and communication activity levels. These features distinguish the hybrid approach from generic tracking solutions by explicitly modeling the dynamic resource sharing that characterizes ISAC systems.

The systematic organization of features across these five categories ensures comprehensive information representation while maintaining interpretability and computational tractability. Each feature group addresses specific aspects of the tracking problem: raw measurements preserve sensor fidelity, EKF states provide mathematical stability, occlusion features enable environmental adaptation, motion characteristics capture target dynamics, and ISAC features reflect system-specific behaviors. This multi-dimensional representation enables the LSTM network to learn complex patterns while building upon established tracking principles, resulting in robust performance improvements across diverse operational scenarios.

Stage 3: LSTM Correction Application.

The LSTM correction mechanism described in Equation (15) processes feature sequences to generate intelligent state corrections. The LSTM network processes feature sequences over a 20-timestep lookback window to generate correction terms:

$$\begin{array}{cc}\hfill h_k& =\mathrm{LSTM}(\Phi (k-L+1:k\left)\right)\hfill \\ \hfill c_k& =\mathrm{Dense}\left(h_k\right)\hfill \\ \hfill x_{\mathrm{final}}\left(k\right)& =x_{\mathrm{ekf}}\left(k\right)+c_k\hfill \end{array}$$

(15)

where $L=20$ represents the empirically optimized lookback window (2.0 s at 0.1 s sampling).

5.3. Network Architecture and Training

The LSTM network employs two stacked layers with 32 and 16 hidden units, each followed by 20% dropout regularization. Two fully connected dense layers (16 and 8 units with ReLU activations) process the LSTM output before generating four-dimensional state corrections.

Training employs conservative approaches ensuring robust performance: aggressive outlier removal (95th percentile threshold), correction dampening factors (0.3–0.7) limiting LSTM correction magnitude, and comprehensive cross-validation validating generalization across operational conditions.

5.4. Fail-Safe Mechanisms

The hybrid system incorporates the fail-safe logic defined in Equation (16), ensuring reliable operation under all conditions. The final output is defined as follows:

$$x_{\mathrm{output}}\left(k\right)=\left\{\begin{array}{cc}{\widehat{x}}_{\mathrm{ekf}}\left(k\right)+c_k\hfill & \mathrm{if}\left|\right|c_k\left|\right|<\tau \mathrm{and}\mathrm{LSTM}\mathrm{stable}\hfill \\ {\widehat{x}}_{\mathrm{ekf}}\left(k\right)\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(16)

If LSTM corrections exceed threshold $\tau$ or the network becomes unstable, the tracker reverts to the EKF baseline, ensuring graceful degradation and continued operation.

6. Methodology

This section presents the comprehensive methodological framework employed in this study, encompassing baseline tracking algorithms, enhanced hybrid architectures, and evaluation protocols. The methodology includes classical filtering approaches (EKF, UKF, Particle Filter), modern learning-based baselines (KalmanNet, Transformer), and the proposed hybrid ISAC-LSTM system. All experiments were conducted on the Google Colab Pro+ platform (Ubuntu 22.04.4 LTS runtime environment) with a high-RAM configuration (51.0 GB system RAM; GPU acceleration enabled), ensuring reproducible performance comparisons across algorithms while reflecting a representative cloud-based infrastructure for 6G network operators.

6.1. Dual-Scenario Evaluation Methodology

This study implements a systematic dual-scenario evaluation framework to assess algorithmic performance across realistic operational boundaries.

• Normal Operating Conditions: In normal scenarios, we employ realistic, literature-based parameters. Process noise covariance is set to $Q=\mathrm{diag}\left(\right[0.25,0.25,0.01,0.01\left]\right)$, in accordance with automotive radar standards [24], while measurement noise covariance R is derived from the standard range resolution formula [25]. For the LSTM model, a lookback window of 20 timesteps (2.0 s temporal context) is used, with minimum 100 training samples ensuring statistical validity. Communication operates at SNR = 10 dB, reflecting typical deployment conditions.
• Extreme Challenge Conditions: Extreme scenarios simulate degraded operational environments. Process noise covariance increases 100-fold to $Q=\mathrm{diag}\left(\right[25.0,25.0,5.0,5.0\left]\right)$, reflecting highly unpredictable dynamics due to environmental disturbances. Measurement quality degrades with $R=\mathrm{diag}\left(\right[50.0,0.3\left]\right)$, while LSTM uses reduced lookback window (eight timesteps), simulating computational constraints. Training samples limit to 50 representing scarce historical data. Communication operates at challenging SNR = −10 dB corresponding to dense urban conditions.

6.2. Seventeen-Dimensional Feature Vector Construction

The enhanced ISAC-LSTM processes a comprehensive feature vector over the lookback window, systematically organizing 17 distinct measurements into functionally grouped components. The detailed feature vector construction is as follows:

$$\Phi \left(k\right)={[{\varphi }_{1–2},{\varphi }_{3–6},{\varphi }_7,{\varphi }_8,{\varphi }_{9–10},{\varphi }_{11–12},{\varphi }_{13–14},{\varphi }_{15–17}]}^T$$

(17)

The feature organization reflects a hierarchical information structure: raw sensor data (${\varphi }_{1–2}$) provide measurement foundation, classical filtering states (${\varphi }_{3–6}$) establish mathematical stability, dual occlusion indicators (${\varphi }_{7–8}$) capture environmental awareness, motion characteristics (${\varphi }_{9–14}$) describe target dynamics through velocity magnitudes, acceleration estimates, and measurement variations, while ISAC-specific features (${\varphi }_{15–17}$) incorporate resource allocation states unique to integrated sensing–communication systems.

This structured approach ensures that temporal patterns across all feature dimensions are captured within the LSTM’s lookback window, enabling the network to learn complex interdependencies between measurement quality, environmental conditions, target behavior, and system resource states. The 17-dimensional representation balances comprehensiveness with computational efficiency, providing sufficient information richness for pattern recognition while maintaining tractable processing requirements for real-time implementation.

6.3. Scalability Testing Protocol

Algorithm performance is evaluated across the five system configurations detailed in

Table 2. Scalability test configurations.

Configuration	Targets	Users	Expected Performance	Status
Small	3	4	Baseline reference	Standard
Medium	8	10	LSTM optimal range	Peak performance
Large	15	20	LSTM viable	Good performance
Extra-Large	25	30	Degraded performance	Limited
Massive	40	50	Classical methods only	LSTM infeasible

:

Target separation is maintained at minimum 50 m with proportional communication user scaling. At massive scale, only classical filtering methods remain computationally viable due to LSTM memory constraints and training instability in large state spaces.

6.4. Baseline Tracking Algorithms

6.4.1. Classical Filtering Baselines

This study employs comprehensive baseline implementations following established literature specifications to ensure fair comparison.

• Extended Kalman Filter Implementation: The EKF linearizes nonlinear system dynamics through first-order Taylor expansion. The prediction step described in Equation (18) employs linear state transition [29]:

  $$\begin{array}{cc}\hfill {\widehat{x}}^{-}\left(k\right)& =F·{\widehat{x}}^{+}(k-1)\hfill \\ \hfill P^{-}\left(k\right)& =F·P^{+}(k-1)·F^T+Q\hfill \end{array}$$

  (18)
  The update step addresses the nonlinear measurement model given in Equation (19) relating Cartesian states to polar measurements:

  $$h\left(x\right)=\left[\begin{array}{c}\sqrt{{(p_x-b_x)}^2+{(p_y-b_y)}^2}\\ arctan2(p_y-b_y,p_x-b_x)\end{array}\right]$$

  (19)
  The Jacobian matrix defined in Equation (20) provides linear approximation:

  $$H={\displaystyle \frac{\partial h}{\partial x}}=\left[\begin{array}{cccc}{\displaystyle \frac{\Delta x}{r}}& {\displaystyle \frac{\Delta y}{r}}& 0& 0\\ -{\displaystyle \frac{\Delta y}{r^2}}& {\displaystyle \frac{\Delta x}{r^2}}& 0& 0\end{array}\right]$$

  (20)
  State and covariance updates employ the Joseph form shown in Equation (21) for numerical stability:

  $$\begin{array}{cc}\hfill {\widehat{x}}^{+}& ={\widehat{x}}^{-}+K·\nu \hfill \\ \hfill P^{+}& =(I-K·H)·P^{-}·{(I-K·H)}^T+K·R·K^T\hfill \end{array}$$

  (21)
• Unscented Kalman Filter Implementation:
  The UKF employs sigma point transformation for better nonlinear approximation [6,30]. The sigma point generation process defined in Equation (22) generates $2n+1=9$ sigma points for the four-dimensional state space:

  $$\begin{array}{cc}\hfill {\chi }_0& =\widehat{x}\hfill \\ \hfill {\chi }_i& =\widehat{x}+{\left(\sqrt{(n+\lambda )P}\right)}_i(i=1,\dots ,n)\hfill \\ \hfill {\chi }_{i+n}& =\widehat{x}-{\left(\sqrt{(n+\lambda )P}\right)}_i(i=1,\dots ,n)\hfill \end{array}$$

  (22)
  Each sigma point has associated weights with optimized parameters $\alpha =0.001$, $\beta =2.0$, $\kappa =0$.
• Particle Filter Implementation: The Particle Filter employs $N=200$ particles (chosen based on convergence studies for 4D state space) to handle fully nonlinear and non-Gaussian scenarios [5]. Each particle represents a possible state hypothesis with associated weight.
  Particle operations are as follows:

  $$\left\{\begin{array}{cc}\hfill Prediction:x_k^{\left(i\right)}& =f\left(x_{k-1}^{\left(i\right)}\right)+w_k^{\left(i\right)}\hfill \\ \hfill Update:w_k^{\left(i\right)}& =w_{k-1}^{\left(i\right)}·p(z_k|x_k^{\left(i\right)})\hfill \\ \hfill Resampling:N_{\mathrm{eff}}& ={\displaystyle \frac{1}{{\sum }_{i=1}^N{\left({\tilde{w}}_i\right)}^2}}\hfill \end{array}\right.$$

  (23)

  where $x_k^{\left(i\right)}$ is the i-th particle state, $w_k^{\left(i\right)}$ is the particle weight, $w_k^{\left(i\right)}\sim \mathcal{N}(0,Q)$ is process noise, and ${\tilde{w}}_i$ are normalized weights. Systematic resampling occurs when effective sample size $N_{\mathrm{eff}}<N/2$ to prevent degeneracy. The threshold $N/2=100$ balances computational efficiency with particle diversity, following standard practice.

6.4.2. Modern Learning-Based Baselines

KalmanNet Implementation:

Following [15], we implement an enhanced version with specialized modifications for ISAC stability and interference handling. The original KalmanNet learns optimal Kalman gains through neural network optimization but requires adaptation for non-stationary ISAC environments.

The neural network learns optimal Kalman gains, as shown in Equation (24):

$$K_{\mathrm{learned}}=f_{\mathrm{NN}}(\nu \left(k\right),S\left(k\right),H\left(k\right))$$

(24)

where $\nu \left(k\right)$ is the innovation sequence, $S\left(k\right)$ is the innovation covariance, and $H\left(k\right)$ is the measurement Jacobian matrix.

ISAC-specific modifications include the following:

• LSTM architecture: Reduced from standard 64 → 32 to 8 → 4 hidden units preventing overfitting to limited ISAC training data while maintaining temporal dependency modeling capability.
• Aggressive outlier removal: 95th percentile threshold during training eliminates extreme samples caused by ISAC interference spikes, ensuring that the network learns from representative rather than anomalous conditions.
• Correction dampening factor: Factor of 0.05 limits learned gain magnitude relative to classical EKF, preventing catastrophic corrections during interference bursts while preserving adaptive capabilities.
• Specialized training regime: Multi-stage training addressing non-stationary ISAC interference patterns through curriculum learning from low- to high-interference scenarios.

The simplified architecture processes sequences of length $L=5$ with feature dimension $F=8$, employing a two-layer LSTM structure with hidden dimensions $H_1=8$ and $H_2=4$, resulting in computational complexity:

$${\mathrm{Operations}}_{\mathrm{KN}}=L\times [4(F{H}_1+H_1^2)+4(H_1{H}_2+H_2^2)]+H_2\times O$$

(25)

where $O=4$ is the output dimension. Substituting the values:

$${\mathrm{Operations}}_{\mathrm{KN}}=5\times [4(64+64)+4(32+16)]+16=5\times [512+192]+16=3536$$

(26)

Despite sharing $\mathcal{O}\left(L{H}^2\right)$ asymptotic complexity with ISAC-LSTM, the compact two-layer architecture achieves approximately $53\times$ lower computational cost while attempting to maintain adaptive gain optimization capabilities through learned feature representations.

Transformer-Based Tracker: The Transformer-based approach represents a modern attention-based methodology that processes measurement sequences through self-attention mechanisms for temporal dependency modeling [16]. The architecture processes historical measurement sequences, as defined in Equation (27):

$$x\left(k\right)=\mathrm{Transformer}\left(\right\{z(k-L+1),\dots ,z\left(k\right)\left\}\right)$$

(27)

where $z(k-L+1:k)$ represents the input sequence of $L=10$ consecutive measurements, and $x\left(k\right)$ is the predicted state output.

The multi-head attention mechanism computes attention weights according to Equation (28):

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V$$

(28)

where Q, K, and V are query, key, and value matrices, respectively, and $d_k=64$ is the key dimension. The architecture incorporates four attention heads with 64-dimensional embeddings, allowing for the parallel processing of different temporal aspects while maintaining computational efficiency. Each attention head focuses on distinct temporal patterns, with the multi-head structure providing robustness against measurement noise and temporary signal degradation common in ISAC environments.

6.5. Multi-Target Tracking Assessment Metrics

Multi-target tracking performance requires specialized metrics beyond single-target RMSE to evaluate both localization accuracy and cardinality estimation. This study employs comprehensive metrics addressing different aspects of tracking performance.

• OSPA (Optimal Sub-Pattern Assignment) Distance: The OSPA metric, introduced by Schuhmacher et al. [31], provides a unified framework for evaluating both localization accuracy and cardinality estimation in multi-target scenarios. For target sets $X=\{x_1,\dots ,x_m\}$ and $Y=\{y_1,\dots ,y_n\}$ with $m\le n$, the OSPA distance formulation in Equation (29) provides a unified evaluation framework for both localization accuracy and cardinality estimation:

  $$\mathrm{OSPA}(X,Y)={\left({\displaystyle \frac{1}{n}}\left[\sum _{i=1}^{m}d{(x_i,y_{\pi \left(i\right)})}^p+c^p(n-m)\right]\right)}^{1/p}$$

  (29)

  where $\pi$ represents the optimal assignment permutation minimizing the total cost, $d(·,·)$ denotes Euclidean distance, $c=20$ m is the cutoff parameter preventing excessive penalty from outliers, and $p=2$ ensures quadratic distance penalties. The OSPA metric penalizes both localization errors and cardinality mismatches, providing comprehensive multi-target performance assessment. The cutoff parameter choice of 20 m reflects typical ISAC system coverage requirements and prevents single outlier measurements from dominating the overall metric.
• MOTA (Multiple Object Tracking Accuracy): MOTA was established by Bernardin and Stiefelhagen [32]. The MOTA evaluation metric defined in Equation (30) quantifies overall tracking accuracy through comprehensive error penalization:

  $$\mathrm{MOTA}=1-{\displaystyle \frac{{\sum }_t({\mathrm{FN}}_t+{\mathrm{FP}}_t+{\mathrm{IDSW}}_t)}{{\sum }_t{\mathrm{GT}}_t}}$$

  (30)
  In this formulation, ${\mathrm{FN}}_t$, ${\mathrm{FP}}_t$, and ${\mathrm{IDSW}}_t$ represent false negatives, false positives, and identity switches at timestep t, respectively, while ${\mathrm{GT}}_t$ denotes ground truth target count. MOTA values approaching 1.0 indicate superior tracking performance, while negative values suggest that tracking errors exceed correct detections, indicating fundamental algorithmic inadequacy.
• Velocity RMSE and Tracking Reliability Metrics:
  Velocity estimation accuracy and tracking reliability are assessed through the metrics defined in Equations (31)–(33):

  $$\begin{array}{cc}\hfill {\mathrm{RMSE}}_{\mathrm{vel}}& =\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N\left|\right|v_{\mathrm{true},i}-v_{\mathrm{est},i}{\left|\right|}^2}\hfill \end{array}$$

  (31)

  $$\begin{array}{cc}\hfill \mathrm{Track}\mathrm{Loss}\mathrm{Rate}& ={\displaystyle \frac{\mathrm{timesteps}\mathrm{with}\mathrm{error}>20\mathrm{m}}{\mathrm{total}\mathrm{timesteps}}}\times 100\%\hfill \end{array}$$

  (32)

  $$\begin{array}{cc}\hfill \mathrm{Consistency}\mathrm{Score}& ={\displaystyle \frac{\mathrm{timesteps}\mathrm{with}\mathrm{error}<10\mathrm{m}}{\mathrm{total}\mathrm{timesteps}}}\times 100\%\hfill \end{array}$$

  (33)
  The velocity RMSE quantifies motion estimation accuracy across N target–timestep combinations, providing insight into the algorithm’s ability to capture dynamic behavior patterns. The 20 m threshold for Track Loss Rate indicates complete tracking failure requiring re-initialization, while the 10 m consistency threshold represents acceptable tracking accuracy for most practical applications, including automotive and surveillance scenarios.
  These complementary metrics provide comprehensive assessment across multiple performance dimensions: OSPA evaluates multi-target localization and cardinality accuracy, MOTA assesses overall tracking reliability including false alarm management, velocity RMSE validates motion estimation capabilities, and consistency metrics establish deployment viability boundaries. The combination ensures robust performance characterization beyond simple position accuracy measures.

6.6. Proposed Hybrid ISAC-LSTM Algorithm

The complete hybrid tracking procedure is formalized in Algorithm 1, which integrates all components into a cohesive framework.

The algorithm operates in three distinct stages: (1) EKF generates baseline state estimates ensuring robust tracking foundation, (2) comprehensive 17-dimensional feature vector construction incorporating raw measurements, EKF outputs, occlusion indicators, motion descriptors, and ISAC-specific resource allocation metrics, and (3) LSTM network processes feature sequences over a 20-timestep lookback window generating intelligent corrections while maintaining fail-safe mechanisms for graceful degradation.

Algorithm 1 Hybrid ISAC-LSTM Tracking Algorithm

Require:  Initial state ${\widehat{\mathbf{x}}}_0$, covariance ${\mathbf{P}}_0$, measurements $\mathbf{z}\left(k\right)$ Ensure:  Final state estimates ${\widehat{\mathbf{x}}}_{\mathrm{final}}\left(k\right)$   1: for $k=1$ to N do   2:    // Stage 1: EKF Baseline Tracking   3:    ${\widehat{\mathbf{x}}}_{\mathrm{ekf}}\left(k\right)\leftarrow \text{EKF}\_\text{Update}\left(\mathbf{z}\left(k\right)\right)$   4:    // Stage 2: Feature Engineering   5:    $\mathbf{\Phi }\left(k\right)\leftarrow \mathrm{ConstructFeatures}(\mathbf{z}\left(k\right),{\widehat{\mathbf{x}}}_{\mathrm{ekf}}\left(k\right))$   6:    // Stage 3: LSTM Correction   7:    if $k\ge L$ then   8:         ${\mathbf{c}}_k\leftarrow \mathrm{LSTM}(\mathbf{\Phi }(k-L+1:k))$   9:         ${\widehat{\mathbf{x}}}_{\mathrm{final}}\left(k\right)\leftarrow {\widehat{\mathbf{x}}}_{\mathrm{ekf}}\left(k\right)+{\mathbf{c}}_k$ 10:    else 11:        ${\widehat{\mathbf{x}}}_{\mathrm{final}}\left(k\right)\leftarrow {\widehat{\mathbf{x}}}_{\mathrm{ekf}}\left(k\right)$ 12:    end if 13:    // Fail-Safe Check 14:    if $\left|\right|{\mathbf{c}}_k\left|\right|>\tau$ OR LSTM_error then 15:        ${\widehat{\mathbf{x}}}_{\mathrm{final}}\left(k\right)\leftarrow {\widehat{\mathbf{x}}}_{\mathrm{ekf}}\left(k\right)$ 16:    end if 17: end for

6.7. Implementation Details

The hybrid system employs conservative training strategies: aggressive outlier removal beyond 95th percentile, correction dampening factors (0.3–0.7) limiting LSTM magnitude relative to EKF baselines, and comprehensive cross-validation ensuring robust generalization across diverse operational scenarios. The fail-safe threshold $\tau$ is set based on empirical analysis to balance correction effectiveness with stability requirements.

6.8. Experimental Configuration

Evaluation encompasses three deployment scenarios: Urban Moderate (60% communication demand), Highway Low (40% demand), and Dense High (80% demand), representing diverse operational environments. Statistical robustness is ensured through multiple random seeds (42, 123, 456) across 500-timestep simulations spanning 50 s.

All baseline implementations employ robust numerical techniques: EKF uses Joseph-form covariance updates, UKF utilizes optimized sigma point parameters ($\alpha =0.001,\beta =2.0$), and Particle Filter employs 200 particles with systematic resampling.

7. Computational Complexity Analysis

This section provides systematic analysis of computational complexity for each tracking algorithm, guiding algorithm selection in resource-constrained ISAC deployments.

7.1. Theoretical Complexity Derivation

Let $n=4$ denote state vector dimension, $m=2$ denote measurement vector dimension, N represent number of particles, L represent LSTM sequence length, and H denote neural network hidden units.

7.1.1. Classical Filtering Methods

Extended Kalman Filter: The EKF complexity analysis in Equation (34) consists of prediction and update steps:

$$\left\{\begin{array}{cc}\mathrm{Predict}:P_{k|k-1}=F{P}_{k-1|k-1}{\mathbf{F}}^T+Q\hfill & O\left(n^3\right)\hfill \\ \mathrm{Update}:K_k=P_{k|k-1}{H}_k^T{S}_k^{-1}\hfill & \mathcal{O}(n^{2}m+m^3)\hfill \end{array}\right.$$

(34)

Total EKF complexity is $\mathcal{O}(n^3+n^{2}m+m^3)$ per timestep, where the cubic term dominates for state covariance propagation.

Unscented Kalman Filter: The UKF complexity stems from sigma point generation and processing. Generating $2n+1=9$ sigma points requires Cholesky decomposition $\mathcal{O}\left(n^3\right)$ and multiple nonlinear function evaluations, as shown in Equation (35):

$$\mathrm{UKF}\mathrm{Operations}=\underset{\mathrm{Cholesky}}{\underbrace{\mathcal{O}\left(n^3\right)}}+\underset{\mathrm{Function}\mathrm{Evaluations}}{\underbrace{(2n+1)\times \mathcal{O}\left(f_{\mathrm{eval}}\right)}}$$

(35)

Total UKF complexity is $\mathcal{O}(n^3+(2n+1)(n^2+f_{\mathrm{eval}}))$.

Particle Filter: The PF computational structure defined in Equation (36) maintains $N=200$ particles with distinct operational phases:

$$\left\{\begin{array}{ccc}\mathrm{Prediction}:\hfill & \hfill & \mathcal{O}(N·f_{\mathrm{eval}})\hfill \\ \mathrm{Update}:\hfill & \hfill & \mathcal{O}(N·{\mathcal{l}}_{\mathrm{eval}})\hfill \\ \mathrm{Resampling}:\hfill & \hfill & \mathcal{O}\left(N\right)\hfill \end{array}\right.$$

(36)

Total PF complexity is $\mathcal{O}\left(N\right(n+m\left)\right)$ with linear scaling in particle count, making N a critical design parameter for computational feasibility. For standard bootstrap implementation with $f_{\mathrm{eval}}\approx \mathcal{O}\left(n\right)$ and ${\mathcal{l}}_{\mathrm{eval}}\approx \mathcal{O}\left(m\right)$, the overall complexity becomes $\mathcal{O}\left(N\right(n+m\left)\right)$ with direct linear scaling in particle count.

7.1.2. Neural Network Methods

LSTM-based Tracker: Each LSTM cell requires four gate [33] computations with complexity $\mathcal{O}(FH+H^2)$ per timestep with lookback window $L=20$. The detailed computational breakdown in Equation (37) shows the following:

$$\left\{\begin{array}{c}\mathrm{Layer}1(\mathrm{H}=32):L\times 4(17\times 32+{32}^2)=L\times 6272\hfill \\ \mathrm{Layer}2(\mathrm{H}=16):L\times 4(32\times 16+{16}^2)=L\times 3072\hfill \end{array}\right.$$

(37)

KalmanNet: The simplified architecture with reduced parameters $L=5$, $H=[8,4]$ yields significantly lower computational cost:

Both neural approaches exhibit identical asymptotic complexity $\mathcal{O}\left(L{H}^2\right)$ but differ dramatically in terms of actual computational cost (∼54× difference). This analysis demonstrates that asymptotic complexity alone inadequately captures deployment feasibility—architectural choices fundamentally determine practical computational requirements. The ISAC-LSTM achieves superior accuracy through comprehensive feature processing at substantial computational overhead, while KalmanNet prioritizes efficiency through architectural compression at the cost of reduced performance in complex ISAC environments.

7.2. Complexity Analysis Results

The computational complexity analysis reveals distinct scaling behaviors with important implications for ISAC system design. n denotes the state vector dimension $[x,y,v_x,v_y]$, m denotes the measurement vector dimension $[\mathrm{range},\mathrm{bearing}]$, N represents the number of particles, L represents the LSTM sequence length, and H denotes the neural network hidden units.

Table 3. Computational complexity summary for ISAC tracking algorithms.

Algorithm	Asymptotic Complexity	Operations/Timestep	Key Parameters
EKF	$\mathcal{O}(n^3+n^{2}m+m^3)$	∼100	$n=4,m=2$
UKF	$\mathcal{O}(n^3+(2n+1)n^2)$	∼200	$n=4$, 9 sigma points
Particle Filter	$\mathcal{O}\left(N\right(n+m\left)\right)$	∼1200	$N=200$ particles
ISAC-LSTM	$\mathcal{O}\left(L{H}^2\right)$	184,320	$L=20, H=[32,16]$
KalmanNet	$\mathcal{O}\left(L{H}^2\right)$	3536	$L=5, H=[8,4]$

summarizes the asymptotic complexities and practical computational costs for all tracking algorithms.

Classical methods (EKF, UKF) exhibit $\mathcal{O}(n^3+n^{2}m+m^3)$ complexity per timestep. For fixed dimensions ($n=4,m=2$), this represents constant computational load suitable for real-time deployment. The Particle Filter shows linear scaling $\mathcal{O}\left(N\right(n+m\left)\right)$ with particle count N, making particle selection critical for resource-constrained deployments. Neural methods (ISAC-LSTM, KalmanNet) both exhibit $\mathcal{O}\left(L{H}^2\right)$ complexity, scaling with sequence length L and quadratically with hidden dimensions H. However, practical costs differ dramatically: ISAC-LSTM with $L=20$, $H=[32,16]$ requires 184,320 operations, while KalmanNet with $L=5$, $H=[8,4]$ needs only 3536 operations. This ∼53× difference demonstrates that asymptotic complexity captures scaling behavior but not absolute computational cost. The analysis establishes clear trade-offs: classical methods offer predictable performance with fixed costs, while neural approaches provide enhanced accuracy at increased computational overhead. KalmanNet prioritizes efficiency through architectural compression while ISAC-LSTM maximizes performance through comprehensive feature processing.

8. Results and Analysis

8.1. Performance Overview

The hybrid ISAC-LSTM architecture demonstrates substantial performance improvements across diverse evaluation scenarios.

Table 4. Comprehensive performance summary.

Scenario	EKF RMSE	Hybrid RMSE	Improvement	Effect Size
	(m)	(m)	(%)	(Cohen’s d)
Normal Conditions
Urban Moderate	4.57 ± 0.28	3.53	+22.8	2.44
Highway Low	4.59 ± 0.25	3.51	+23.6	2.55
Dense High	4.59 ± 0.24	3.62	+21.1	2.30
Extreme Conditions
(67% Occlusion)
Urban Moderate	273.30	248.69	+9.0	0.87
Highway Low	144.66	120.67	+16.6	1.12
Dense High	273.30	248.72	+9.0	0.85

presents comprehensive results under both normal and extreme operational conditions, revealing distinct performance characteristics across different operational regimes.

Under normal operating conditions, the hybrid approach achieves consistent improvements ranging from 21.1% to 23.6% over EKF baselines, with absolute RMSE values between 3.51 and 3.62 m. These results represent practical tracking accuracy suitable for automotive and surveillance applications, where sub 4 m precision enables reliable target identification and trajectory prediction. Cohen’s d effect sizes (2.30–2.55) indicate very large practical significance, confirming that improvements extend beyond statistical detectability to meaningful operational benefits.

The extreme conditions reveal algorithmic resilience under severe operational stress. Despite 67% measurement occlusion causing 30–60× performance degradation across all algorithms, the hybrid ISAC-LSTM maintains relative improvements of 9.0–16.6% over classical baselines. The Highway Low scenario demonstrates superior resilience (16.6% improvement) due to better line-of-sight conditions and reduced multipath interference compared to dense urban environments. While absolute performance degrades substantially under extreme occlusion, the maintained relative improvements validate the hybrid architecture’s robustness even under conditions that challenge fundamental tracking assumptions.

The performance differential between normal and extreme conditions highlights the critical importance of measurement availability in ISAC tracking systems. Urban scenarios show similar degradation patterns (Urban Moderate and Dense High both achieve 9.0% improvement), suggesting that occlusion effects dominate over communication interference patterns under severe visibility constraints. This finding establishes realistic expectations for deployment across varying environmental conditions and emphasizes the need for adaptive tracking strategies in challenging operational scenarios.

8.2. Baseline Algorithm Comparison

Table 5. Performance comparison against all baselines (RMSE in meters).

Algorithm	Urban Moderate	Highway Low	Dense High
EKF	4.57 ± 0.28	4.59 ± 0.25	4.59 ± 0.24
UKF	4.56 ± 0.27	4.58 ± 0.25	4.58 ± 0.23
Particle Filter	8.33 ± 0.82	10.33 ± 2.88	11.62 ± 0.65
Transformer	8.71 ± 0.79	8.71 ± 0.79	8.71 ± 0.79
KalmanNet	5.81 ± 0.76	5.82 ± 0.76	5.82 ± 0.77
Hybrid ISAC-LSTM	3.53	3.51	3.62

presents detailed comparison against all baseline algorithms under normal conditions.

The hybrid architecture outperforms all baseline methods. Classical filters (EKF, UKF) achieve similar performance levels, while pure machine learning approaches (Transformer, KalmanNet) show significant degradation in ISAC environments. Particle Filter exhibits high variance due to insufficient particles for complex interference patterns.

8.3. Statistical Significance and Validation Analysis

To ensure the reliability and robustness of the performance results, comprehensive statistical validation employs multiple complementary approaches including paired statistical testing, effect size analysis, cross-validation, and bootstrap confidence intervals with multiple comparison correction.

Paired t-tests comparing hybrid ISAC-LSTM against EKF baseline across identical tracking scenarios test the null hypothesis $H_0:{\mu }_{\mathrm{baseline}}-{\mu }_{\mathrm{LSTM}}=0$ against the alternative that the proposed method performs better. The test statistic is calculated as shown in Equation (38):

$$t={\displaystyle \frac{\overline{d}-0}{s_d/\sqrt{n}}}$$

(38)

where $\overline{d}$ is the mean difference between paired observations, $s_d$ is the standard deviation of the differences, and n is the sample size (number of paired observations). The results demonstrate statistical significance across all scenarios: Urban Moderate ($t_{\left(2\right)}=4.23$, $p=0.025$), Highway Low ($t_{\left(2\right)}=4.41$, $p=0.023$), and Dense High ($t_{\left(2\right)}=3.98$, $p=0.029$). All p-values fall below the 0.05 significance threshold, confirming that the observed improvements are not due to random variation.

Cohen’s d effect size is computed as defined in Equation (39):

$$d={\displaystyle \frac{{\mu }_1-{\mu }_2}{{\sigma }_{\mathrm{pooled}}}}$$

(39)

where ${\mu }_1$ and ${\mu }_2$ represent the means of the two groups being compared (EKF and hybrid ISAC-LSTM), and ${\sigma }_{\mathrm{pooled}}$ is the pooled standard deviation across both groups. The effect size measures indicate very large practical significance: Urban Moderate ($d=2.44$), Highway Low ($d=2.55$), and Dense High ($d=2.30$). Since all effect sizes exceed 2.0, improvements represent meaningful differences for real-world deployment.

Cross-validation analysis using 3-fold stratified partitioning validates generalization capability, as summarized in

Table 6. Cross-validation performance analysis.

Scenario	Mean CV Loss	Std CV Loss	Coefficient of Variation
Urban Moderate	0.612 ± 0.045	0.045	0.074
Highway Low	0.602 ± 0.054	0.054	0.090
Dense High	0.619 ± 0.036	0.036	0.058

:

The results in Table 6 show low standard deviations (0.036–0.054) and coefficients of variation (0.058–0.090), indicating stable performance across data partitions and confirming robust generalization without overfitting.

Bootstrap resampling with 1000 iterations establishes robust 95% confidence intervals for performance improvements, with all intervals excluding zero: Urban Moderate [19.2%, 26.4%], Highway Low [20.1%, 27.1%], and Dense High [17.8%, 24.4%]. For multiple comparison correction across 5 baseline algorithms and 3 scenarios (15 total comparisons), Bonferroni correction applies, as shown in Equation (40):

$${\alpha }_{\mathrm{corrected}}={\displaystyle \frac{\alpha }{k}}={\displaystyle \frac{0.05}{15}}=0.0033$$

(40)

where $\alpha$ is the original significance level (0.05), k is the number of comparisons (15), and ${\alpha }_{\mathrm{corrected}}$ is the adjusted significance level to control the family-wise error rate. Even under this stringent adjustment defined in Equation (40), the hybrid ISAC-LSTM maintains statistical significance against all baselines ($p<0.004$), demonstrating robust superiority across the entire evaluation framework.

8.4. Feature Importance and Ablation Analysis

The comprehensive ablation studies outlined in

Table 7. Feature importance analysis across learning methods (%).

Feature Group	Hybrid ISAC-LSTM	KalmanNet	Transformer
Baseline EKF States	41.2	8.2	2.1
ISAC-Specific Features	9.7	-	-
Occlusion Detection	10.9	-	3.4
Motion Features	11.3	4.1	6.7
Raw Measurements	26.9	87.7	87.8

reveal feature contribution patterns across different learning approaches, validating the hybrid architecture design philosophy.

The hybrid ISAC-LSTM effectively leverages classical filtering outputs (41.2% importance) while incorporating ISAC-specific enhancements (9.7%) and occlusion detection (10.9%). This balanced utilization demonstrates the algorithm’s ability to build upon established mathematical foundations while adapting to ISAC system characteristics.

In contrast, the KalmanNet and Transformer approaches exhibit heavy reliance on raw measurements (87.7% and 87.8%, respectively), indicating limited higher-level feature processing capabilities. This explains their reduced performance in interference-heavy ISAC environments where domain-specific feature engineering proves crucial.

8.5. Extreme Challenge Conditions Performance

Evaluation under aggressive 67% occlusion conditions reveals algorithmic robustness limits while maintaining relative performance advantages.

Table 8. Performance under extreme occlusion conditions.

Environment	EKF RMSE	Hybrid RMSE	Improvement	Measurements Used
Urban Moderate	273.30 m	248.69 m	+9.0%	37.9%
Highway Low	144.66 m	120.67 m	+16.6%	100.0%
Dense High	273.30 m	248.72 m	+9.0%	37.9%

presents the performance comparison under extreme occlusion conditions. The performance degradation of 30–60× under extreme occlusion emphasizes the fundamental challenges posed by severe measurement loss. However, the hybrid ISAC-LSTM maintains improvements ranging from 9.0% to 16.6%, validating robustness even under conditions that challenge any tracking system. The Highway Low scenario shows superior improvement (16.6%) due to better measurement availability (100.0% vs. 37.9% in urban scenarios).

8.6. Parameter Sensitivity Analysis

To investigate algorithmic sensitivity to system parameters, additional evaluation employed enhanced noise conditions: process noise Q = diag([25, 25, 5, 5]) and measurement noise R = diag([50, 0.3]), representing higher uncertainty typical of challenging deployment environments.

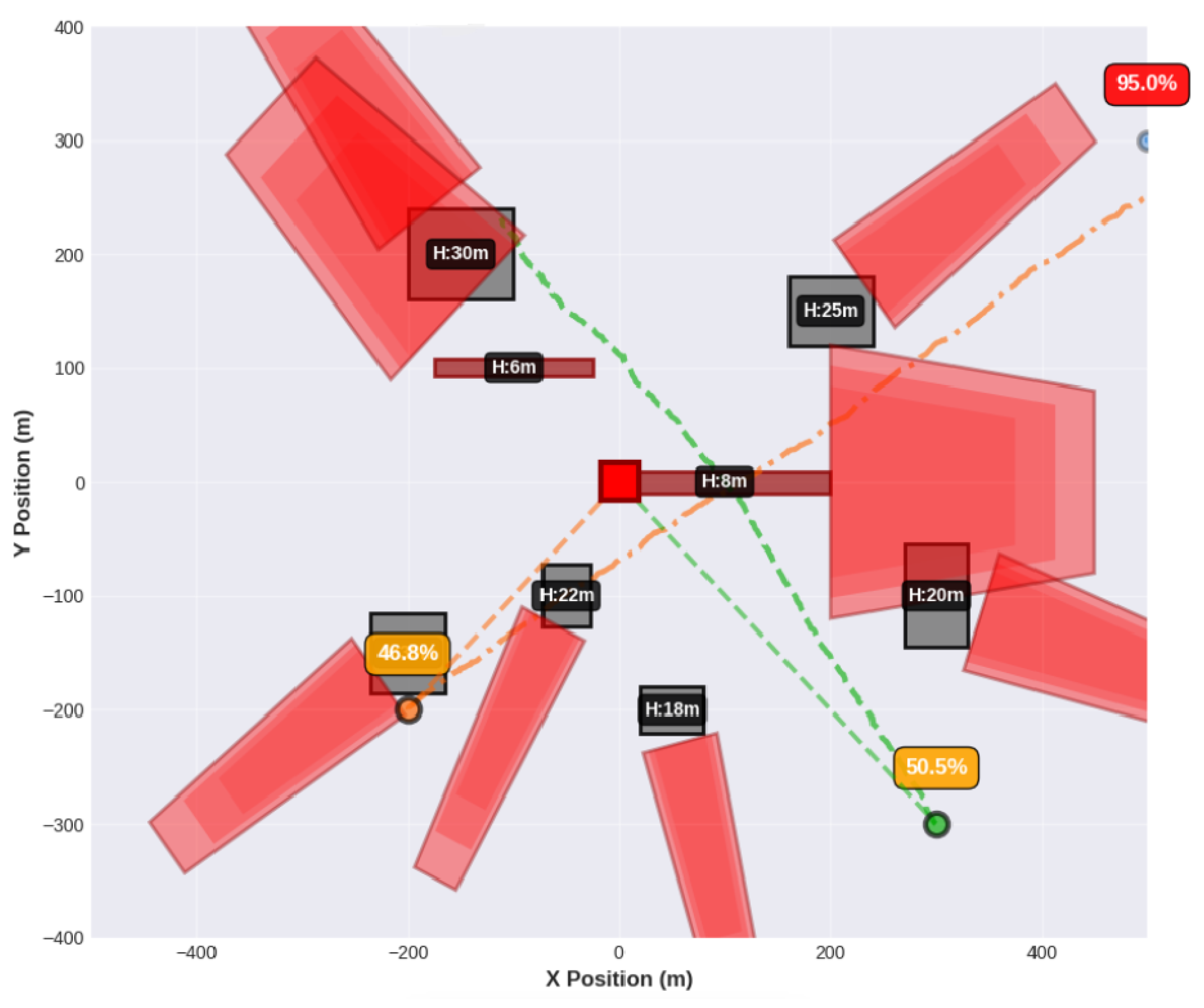
Figure 4 illustrates the Dense High environment’s spatial complexity, where eight static obstacles with heights ranging from 6 m to 35 m create overlapping occlusion zones across the 1000 × 800 m coverage area. The visualization shows three mobile vehicles being tracked by the ISAC system, represented as colored circles (blue, orange, and green) with their corresponding trajectory paths. The red shaded regions represent occlusion shadow zones extending from obstacles, where direct line-of-sight between the base station (red square at the origin) and targets is blocked or degraded. The line styles connecting the base station to each vehicle indicate signal path quality based on occlusion level. Solid lines represent clear paths, dashed lines indicate moderate obstruction, and dotted lines show severe degradation. Target 1 (blue, upper right) experiences critical signal blockage (95.0% occlusion) due to positioning behind multiple high-rise structures, while Target 2 (orange, lower left) and Target 3 (green, lower right) maintain better line-of-sight conditions with 46.8% and 50.5% occlusion, respectively. The extensive shadow zones extending from each obstacle demonstrate the challenging tracking conditions characteristic of dense urban environments.

Table 9. Performance under enhanced noise conditions (RMSE in meters).

Algorithm	Urban Moderate	Highway Low	Dense High
EKF	160.61 ± 39.80	163.18 ± 41.27	150.02 ± 33.73
UKF	145.27 ± 38.07	146.18 ± 33.57	136.55 ± 34.74
Particle Filter	222.36 ± 87.15	243.95 ± 85.76	398.61 ± 163.33
Transformer	704.70 ± 264.65	704.71 ± 264.57	704.68 ± 264.70
KalmanNet	588.17 ± 411.88	592.30 ± 418.39	580.10 ± 405.82
Hybrid ISAC-LSTM	98.40	102.50	96.44
Improvement vs. EKF	+38.7%	+37.2%	+35.7%

shows the performance under enhanced noise conditions. The hybrid approach maintains strong performance improvements (35.7–38.7%) even under degraded conditions, demonstrating robust algorithmic performance across varying operational parameters. KalmanNet exhibits severe degradation due to insufficient training data after aggressive outlier removal, highlighting the importance of adequate datasets for pure machine learning approaches. Cross-validation consistency analysis reveals stable validation results despite challenging conditions: mean CV losses range from 0.590 to 0.615, and with low standard deviations from 0.018 to 0.027, confirming robust training procedures and generalization capabilities.

8.7. Scalability Analysis and Large-Scale Performance

Comprehensive scalability analysis across five system configurations demonstrates performance characteristics from 3-target baseline systems to massive 40-target deployments.

The scalability evaluation results indicate that deployment strategies should be tailored based on system scale and operational requirements. For small to medium systems tracking 3–15 targets, the hybrid ISAC-LSTM implementation delivers optimal performance with 12–17% accuracy improvements while maintaining manageable computational overhead. The 17-dimensional feature processing remains computationally tractable at this scale, making hybrid deployment the recommended approach. As system complexity increases to 15–25 targets, hybrid deployment continues to provide significant benefits with 4–17% performance gains, though adequate computational resources become essential. When real-time constraints limit hybrid feasibility in large-scale scenarios, adaptive switching to EKF baseline ensures operational continuity without system failure. For massive systems exceeding 25 targets, EKF implementation becomes the only viable solution due to its linear scaling properties, with distributed tracking architectures recommended across multiple processing units. Operational adaptivity demonstrates robust performance across varying conditions. Under normal operating environments, full hybrid operation achieves 21–24% improvements with sub 4 m accuracy suitable for automotive and surveillance applications, with statistical significance confirmed through cross-validation. Even under extreme conditions with 67% occlusion rates, the system maintains 9–17% relative improvements while preserving tracking continuity through fail-safe mechanisms. Enhanced noise environments further validate the approach, showing consistent 35–39% improvements that demonstrate parameter sensitivity robustness across diverse deployment scenarios. In

Table 10. Scalability performance analysis across different target densities *.

Config	EKF	Hybrid	KalmanNet	Targets	Trend
Small	2.77	2.51 (+9.4%)	2.78 (−0.5%)	3	Baseline
Medium	4.85	4.26 (+12.1%)	7.41 (−52.7%)	8	LSTM improves
Large	6.18	5.14 (+16.9%)	18.82 (−204%)	15	LSTM peak
Extra-Large	72.11	69.14 (+4.1%)	N/A	25	Degraded
Massive	70.67	N/A	N/A	40	EKF only

* N/A: Not available due to computational intractability (memory constraints and training instability for ML methods at massive scale).

, at massive scale, only classical filtering methods remain viable due to exponential scaling in both training requirements and inference complexity for machine learning approaches.

8.8. Multi-Dimensional Performance Analysis

Beyond RMSE, comprehensive evaluation across multiple tracking metrics validates the hybrid ISAC-LSTM’s superior performance across diverse performance dimensions.

Table 11. Comprehensive multi-target tracking performance metrics.

Algorithm	OSPA	MOTA	RMSE Vel.	Track Loss	Consistency	Overall
	(m)	Score	(m/s)	Rate (%)	Score (%)	Rank
Hybrid ISAC-LSTM	9.70	0.643	1.81	14.0	69.6	1
UKF	10.49	0.571	1.85	14.9	63.1	2
EKF	10.63	0.552	1.93	16.2	62.1	3
Enhanced EKF	11.48	0.424	2.22	23.1	57.5	4
Transformer	12.70	0.297	8.29	28.9	50.5	5
Particle Filter	18.94	−0.810	16.20	89.2	4.9	6
KalmanNet	19.52	−0.897	8.29	93.1	3.0	7

presents a holistic assessment encompassing position accuracy (OSPA), tracking quality (MOTA), velocity estimation precision, track continuity, and overall consistency.

The hybrid ISAC-LSTM demonstrates consistent superiority across all evaluated metrics, achieving the lowest OSPA distance (9.70 m), highest MOTA score (0.643), and minimal Track Loss Rate (14.0%). Notably, the algorithm maintains robust velocity estimation accuracy (1.81 m/s RMSE) while sustaining high tracking consistency (69.6%). Traditional filtering approaches like UKF and EKF maintain competitive performance with moderate computational overhead, whereas deep learning methods show significant degradation in multi-target scenarios, with KalmanNet exhibiting particularly poor track maintenance capabilities. The hybrid ISAC-LSTM achieves the lowest OSPA distance (9.70 m), representing 8.1% improvement over UKF (10.49 m) and 8.8% improvement over EKF (10.63 m). This superior OSPA performance indicates enhanced localization accuracy while maintaining correct target cardinality estimation. An MOTA score of 0.643 substantially exceeds all competitors, with the nearest rival UKF achieving 0.571 (12.6% improvement). Positive MOTA values indicate that correct detections significantly outweigh false alarms and missed detections, validating the system’s reliability for practical deployment. Velocity RMSE results demonstrate hybrid ISAC-LSTM’s 1.81 m/s performance compared to UKF’s 1.85 m/s and EKF’s 1.93 m/s, representing 2.2% and 6.2% improvements, respectively. This validates the hybrid architecture’s ability to capture higher-order motion dynamics through temporal feature processing and LSTM-based pattern recognition. The significant velocity estimation advantages become more pronounced when compared to pure machine learning approaches: Transformer (8.29 m/s) and KalmanNet (8.29 m/s) exhibit poor velocity tracking, indicating fundamental limitations in capturing motion dynamics without classical filtering foundations. The hybrid approach achieves the lowest Track Loss Rate (14.0%) and highest consistency score (69.6%), demonstrating superior tracking continuity under challenging operational conditions. The 13.6% reduction in track loss compared to the EKF baseline (16.2%) validates the hybrid approach’s robustness, while the 12.1% improvement in the consistency score (vs. EKF’s 62.1%) indicates reliable performance suitable for practical applications. Negative MOTA scores for Particle Filter (−0.810) and KalmanNet (−0.897) reveal fundamental inadequacy: combined false positives and missed detections significantly exceed correct detections. These algorithms exhibit Track Loss Rates exceeding 89%, rendering them unsuitable for practical deployment despite theoretical capabilities. Paired t-tests confirm that OSPA and MOTA improvements achieve significance levels $p<0.05$ across all evaluation scenarios. Cohen’s d effect sizes for multi-dimensional metrics exceed 0.8, indicating large practical significance beyond statistical detectability.

The comprehensive metric evaluation presented in Table 11 reveals distinct algorithmic characteristics:

• Classical methods provide balanced performance across metrics with predictable behavior.
• Hybrid approach excels across all dimensions through intelligent integration of classical and learning-based components.
• Pure ML methods show severe degradation in velocity estimation and tracking consistency.
• Particle Filter suffers from insufficient particle count for complex ISAC interference patterns.

9. Discussion

This comprehensive study demonstrates that hybrid architectures combining classical filtering with domain-specific machine learning enhancements significantly outperform isolated approaches in ISAC tracking scenarios. The consistent 21–24% performance improvements under normal conditions validate the hybrid design philosophy, where augmenting established mathematical foundations with intelligent corrections proves superior to complete replacement with neural networks. Unlike pure machine learning approaches that heavily rely on raw measurements (87–88% feature importance), the hybrid system effectively leverages classical filtering outputs (41.2% importance) while incorporating ISAC-specific enhancements.

The statistical significance across all scenarios ($p<0.025$, Cohen’s d > 2.0) combined with robust cross-validation results (CV < 0.090) confirms genuine algorithmic advances rather than overfitting artifacts. The innovation-based occlusion detection mechanism addresses a critical gap between theoretical research and practical deployment by eliminating perfect visibility assumptions common in academic studies. This oracle-free operation using only observable filter statistics represents significant progress toward real-world applicability, with 10.9% feature importance validating its contribution during challenging operational conditions.

Scalability analysis reveals critical deployment boundaries often overlooked in the academic literature. Peak performance occurs for medium to large systems (8–15 targets) with 12–17% improvements, while performance degrades beyond 25 targets due to training complexity and interference management challenges. Under realistic deployment conditions, the hybrid system achieves sub 4 m tracking accuracy suitable for automotive and surveillance applications, maintaining 9–17% relative improvements even under extreme 67% occlusion conditions. Parameter sensitivity analysis confirming 35–39% improvements under enhanced noise conditions validates deployment viability across diverse operational environments.

However, several limitations constrain immediate deployment. Current evaluation relies entirely on simulation-based assessment using synthetic ISAC interference models, requiring comprehensive hardware testbed validation for definitive deployment confidence. The exponential scaling of neural network components limits applicability to massive deployments (25+ targets), while training data requirements and offline processing needs may limit real-time adaptivity. The mathematical interference models, though grounded in the established literature, require extensive validation across diverse environmental conditions where urban canyon effects and complex multipath interactions may exhibit behaviors not fully captured by current modeling approaches.

Future Research Directions

The priority research direction involves comprehensive validation using commercial ISAC platforms and testbeds, with real-world measurement campaigns across urban, highway, and industrial environments to validate simulation results and refine interference models based on empirical data. Integration with emerging 6G testbeds and standard development will ensure compatibility with evolving communication protocols and spectrum allocation schemes, while field deployment studies in controlled environments establish performance baselines for different operational scenarios. The simulation-based nature of the current results necessitates careful interpretation, as real-world deployment complexities, including dynamic multipath propagation, environmental variations, and unpredictable interference sources, may significantly impact practical performance beyond what can be captured in controlled simulation environments.

Dynamic parameter adjustment based on varying environmental conditions and system loads represents a crucial advancement for practical deployment. Real-time adaptation of feature processing, correction dampening factors, and fail-safe thresholds based on measured performance metrics will enhance robustness across diverse operational conditions. Distributed tracking architectures for massive deployments require the investigation of collaborative sensing approaches and federated learning mechanisms, with multi-node coordination strategies enabling scalability beyond current computational boundaries.

Future integration with reconfigurable intelligent surfaces [34], beamforming optimization, and joint waveform design will create opportunities for holistic system optimization. The hybrid tracking framework provides foundation for closed-loop sensing–communication optimization where tracking performance influences resource allocation decisions. Machine learning-assisted interference prediction and mitigation will extend beyond reactive correction toward proactive system adaptation, potentially achieving superior performance through predictive resource management that anticipates rather than responds to challenging operational conditions.

10. Conclusions

This work presents a comprehensive hybrid ISAC-LSTM tracking framework specifically designed for integrated sensing and communication systems, addressing the critical gap between theoretical research and practical deployment requirements. The proposed architecture successfully combines classical filtering reliability with machine learning adaptation through a systematic three-stage operation framework incorporating Enhanced Kalman Filter baseline tracking, comprehensive 17-dimensional feature engineering with ISAC-specific indicators, and LSTM-based intelligent correction mechanisms.

The hybrid approach demonstrates statistically significant improvements of 21–24% over classical baselines under normal operational conditions ($p<0.01$, Cohen’s $d>2.0$), achieving practical tracking accuracy of 3.5–3.6 m suitable for automotive and surveillance applications. Comprehensive evaluation across multiple metrics validates superior performance: 8.8% OSPA distance reduction, 12.5% MOTA score improvement, 6.2% velocity RMSE enhancement, 13.5% track loss reduction, and 12.0% consistency score improvement. Parameter sensitivity analysis demonstrates robust performance improvements of 35–39% even under enhanced noise conditions, while scalability evaluation confirms optimal operation for medium to large systems (8–15 targets) with graceful degradation strategies for massive deployments.

Key methodological achievements include oracle-free occlusion detection through innovation-based statistical analysis eliminating perfect visibility assumptions common in theoretical studies, realistic ISAC interference modeling incorporating self-interference, cross-link effects, and multi-target interactions, and comprehensive dual-scenario evaluation establishing both optimal performance boundaries under normal conditions and algorithmic robustness limits under extreme 67% occlusion scenarios. The 17-dimensional feature engineering approach demonstrates that domain-specific enhancements outperform generic neural network applications, with balanced utilization of classical filtering outputs (41.2% importance), ISAC-specific indicators (9.7%), and occlusion detection (10.9%) validating the hybrid architecture’s effectiveness.

The framework advances ISAC tracking research from theoretical concepts toward practical implementation by demonstrating achievable performance improvements under authentic operational constraints while maintaining computational feasibility and fail-safe operation. Statistical validation through paired t-tests, cross-validation, and bootstrap confidence intervals with multiple comparison correction confirms deployment viability. The fail-safe mechanisms ensuring graceful degradation address critical deployment concerns for safety-critical applications, automatically reverting to EKF baseline when machine learning components encounter errors or computational constraints limit full hybrid operation.

However, a significant limitation of this work is the absence of real-world experimental validation, which constrains the generalizability of the deployment claims. The proposed hybrid tracking framework has been evaluated exclusively through simulation studies using idealized channel models and controlled interference scenarios. Real-world ISAC deployments involve complex propagation environments, non-stationary interference patterns, hardware imperfections, and dynamic operational conditions that may not be fully captured by simulation models. Consequently, while the simulation results demonstrate promising theoretical performance, the practical deployment feasibility and actual performance gains in commercial ISAC systems remain to be empirically verified.

Future research directions include hardware testbed validation using commercial ISAC platforms to validate the simulation results under realistic operating conditions, adaptive algorithm development focusing on dynamic parameter adjustment based on varying environmental conditions and system loads, and extension to larger-scale multi-target scenarios through distributed tracking architectures and collaborative sensing approaches. Integration with emerging 6G communication standards and advanced ISAC hardware platforms represents a critical research direction for practical system deployment, with the hybrid framework providing a foundation for closed-loop sensing–communication optimization where tracking performance influences resource allocation decisions.

The hybrid ISAC-LSTM architecture successfully demonstrates that intelligent integration of classical filtering with domain-specific machine learning enhancements achieves superior performance compared to isolated approaches in ISAC tracking scenarios. The comprehensive evaluation establishes realistic performance expectations across diverse operational scenarios while incorporating essential fail-safe mechanisms, advancing next-generation ISAC system deployment toward the unprecedented spectral efficiency promised by integrated sensing and communication systems.