Quantum-Inspired Hybrid Metaheuristic Feature Selection with SHAP for Optimized and Explainable Spam Detection
Abstract
1. Introduction
- A Robust Hybrid Metaheuristic Algorithm: the EHQ-FABC extends the current literature on feature selection in spam detection with a novel hybrid Firefly-Bee Colony optimization approach based on Quantum techniques.
- Transparent and Trustworthy Detection: The integration of SHAP-based explainability within the detection framework ensures that both feature selection and classification are interpretable, fostering regulatory compliance and operational trust.
- Empirical Validation: The rigorous evaluation of EHQ-FABC on the ISCX-URL2016 benchmark data demonstrated improved feature reduction and competitive accuracy.
- Addressing Practical and Theoretical Gaps: The proposed algorithm directly confronts longstanding challenges related to feature redundancy, irrelevance, computational overhead, and interpretability, bridging critical gaps in current spam detection literature.
2. Related Work
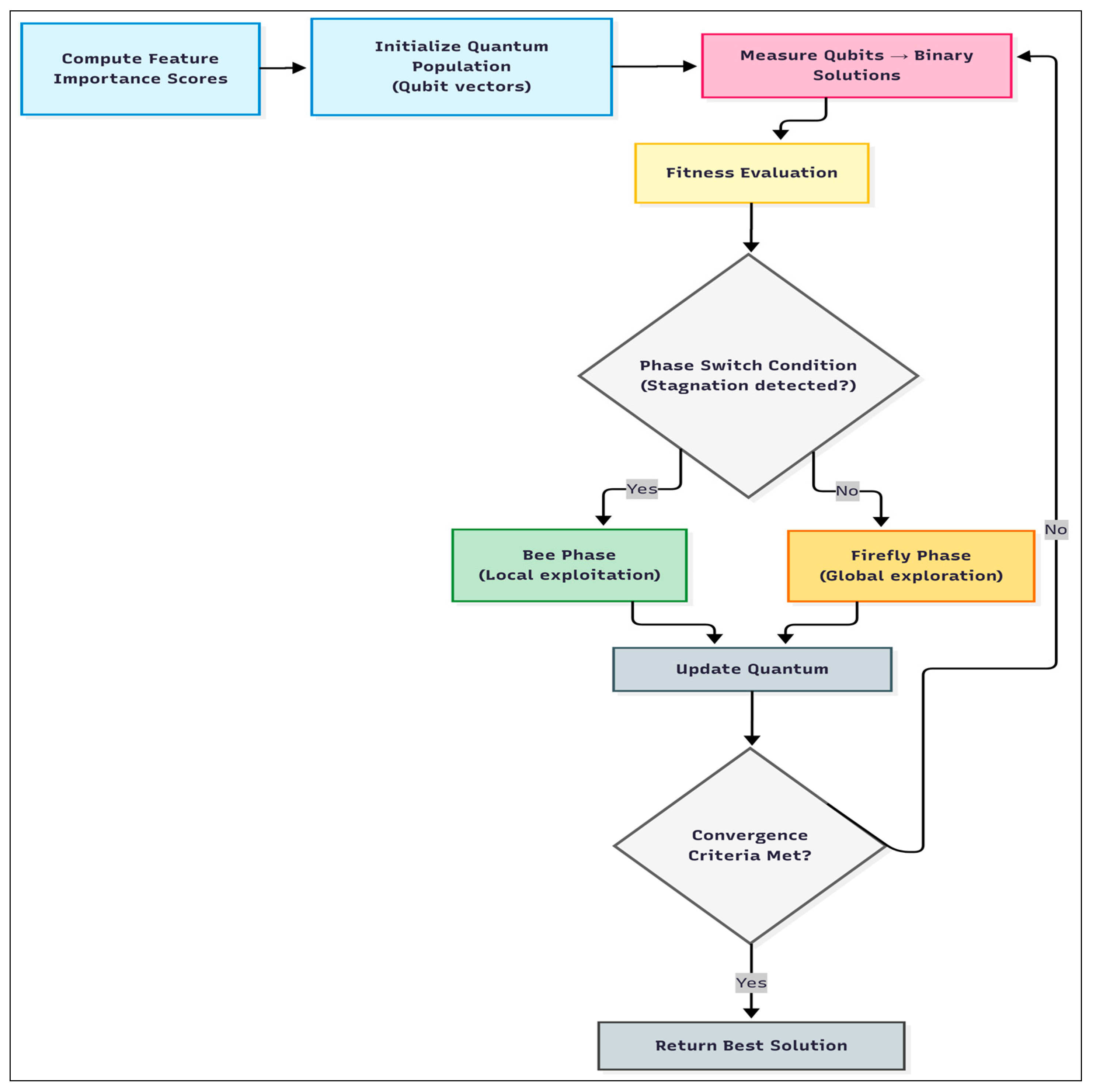
3. The Proposed EHQ-FABC Algorithm
3.1. Methodological Rationale and Overview
| Algorithm 1: The EHQ-FABC Algorithm |
| Input: X, y, params Output: z_best (Set of selected features) 1: Initialize quantum-inspired population Θ(0) using Equation (3) 2: Evaluate initial fitness using Equation (8) 3: For t = 1 to Tmax do 4: Generate binary solutions Zt via quantum measurement (Equation (4)) 5: Evaluate fitness F(Zt) (Equation (8)) 6: Update the global best solution and stagnation counter 7: For each candidate θi in Θt 8: If random number < adaptive chaos factor pc(t): 9: Perform Firefly-inspired update (Equation (5)) 10: else: 11: Perform Bee-inspired update (Equation (6)) 12: Apply the Metropolis criterion based on simulated annealing schedule 13: End for 14: If stagnation is detected (Equation (7)): 15: Trigger phase transition and introduce diversity enhancement 16: Update adaptive parameters (thresholds, chaos factor, Lévy flight scale) 17: If termination conditions met: Break 18: End for 19: Return best-selected feature subset z_best |
3.2. Quantum-Inspired Representation
3.2.1. Quantum Bit (Qubit) Encoding
3.2.2. Importance-Guided Initialization
3.3. Adaptive Quantum Measurement
3.4. Hybrid Optimization Cycle
3.4.1. Firefly Phase (Global Exploration)
3.4.2. Bee Phase (Local Exploitation)
3.4.3. Stagnation Detection and Dynamic Phase Switching
3.5. Multi-Objective Fitness Evaluation
3.6. Termination Criteria
- Maximum iterations: t ≥ Tmax = 100.
- Early-stop: No improvement in Fbest for 25 consecutive iterations.
- Subset stability: the average pairwise Jaccard overlap among the top-q elites exceeds 95% for five consecutive iterations (indicating reproducible convergence).
3.7. Computational Cost and Complexity
4. Experiments and Results
4.1. Dataset Description and Selection
4.2. Dataset Preprocessing
4.3. Experimental Setup
4.3.1. Classification Algorithms
- CatBoost (CB): We include CB, a gradient boosting method optimized for categorical features. CB introduces techniques like ordered boosting and target-based encoding that effectively combat overfitting due to target leakage. These innovations make CB highly robust on structured data and have been shown to outperform other boosting implementations on many datasets [27].
- XGBoost (XGB): We utilize XGB, a scalable tree-boosting system known for its speed and accuracy in classification tasks. XGB implements advanced techniques (e.g., second-order optimization, cache-aware block structures) that allow it to efficiently handle large-scale data. It is widely used in data science competitions and real-world applications for its ability to achieve state-of-the-art results while maintaining computational efficiency [28].
- Random Forest (RF): We include the RF ensemble classifier, which constructs an ensemble of decision trees using random feature subsets and bagging. This approach improves accuracy by averaging multiple deep trees, reducing variance, and mitigating individual tree overfitting. Random Forests also provide useful estimates of feature importance (e.g., via permutation importance) [25].
- Extra Trees (ET): Also known as Extremely Randomized Trees, this is a variant of the random forest that introduces additional randomness in tree construction. Unlike standard RF, Extra Trees chooses split thresholds randomly for each candidate feature, rather than optimizing splits. This extra randomness tends to further reduce overfitting by decorrelating the trees, often improving generalization performance marginally over RF [29].
- Decision Tree (DT): As a baseline interpretable model, we use a single DT classifier. Decision trees greedily partition the feature space into regions, forming a tree of if-then rules. They are easy to interpret but prone to overfitting in high-dimensional spaces without pruning. Despite their tendency to memorize training data, decision trees provide a useful point of reference for model complexity [30].
- K-Nearest Neighbors (KNN): We employ KNN as a lazy learning classifier that predicts labels based on the majority class of the k most similar instances in the feature space. Renowned for its simplicity and effectiveness in applications like recommender systems and pattern recognition [31,32,33], KNN is adept at capturing local data patterns and complex decision boundaries, as it makes no strong parametric assumptions. However, KNN can suffer in high-dimensional feature spaces (the curse of dimensionality), which dilutes the notion of “nearest” neighbors, potentially degrading its performance as the feature count grows [34].
- Logistic Regression (LR): We include LR, a linear model that estimates class probabilities using the logistic sigmoid function. LR is well-suited for binary classification and produces calibrated probability outputs. It is fast and interpretable, but as a linear model, it may struggle to capture complex nonlinear relationships in high dimensions unless feature engineering or kernelization is used. Regularization (e.g., L2) is often applied to mitigate overfitting when the feature space is large [35].
- Multi-Layer Perceptron (MLP): We evaluate an MLP, i.e., a feed-forward artificial neural network with one or more hidden layers, trained with backpropagation. MLPs can model complex nonlinear relationships given sufficient hidden units, making them very flexible classifiers. In our context, the MLP can learn intricate feature interactions that linear models might miss. However, neural networks require careful tuning (architecture, regularization) to generalize well, especially with limited data [36].
4.3.2. Hyperparameter Optimization
4.3.3. Baseline Comparisons
- Full Feature Set: As a primary baseline, we first consider using all 72 extracted features (after preprocessing) with no feature selection. This represents the upper bound in terms of information available to the classifiers. Comparing other methods to this full-set baseline allows us to assess whether feature selection sacrifices any predictive accuracy or, ideally, improves it by removing noise/redundancy.
- Filter Methods: We employ the chi-square filter, which scores each feature by measuring its statistical independence from the class label (for classification, via a χ2 contingency test). Features with higher chi-square scores are more strongly associated with the class. This method is fast and simple, as it evaluates each feature individually. However, because it ignores feature inter-dependencies, the chi-square filter may select redundant features or miss complementary sets. We include it to represent univariate filter techniques that rank features by class relevance [38].
- Wrapper Methods: We use Recursive Feature Elimination (RFE) as a wrapper-based feature selector. RFE iteratively trains a classifier (in our case, we used a tree-based or linear estimator) and removes the least important feature at each step, based on the model’s importance weights, until a desired number of features remains. By evaluating feature subsets using an actual classifier, RFE can account for feature interactions and find a subset that optimizes predictive performance. The trade-off is higher computational cost, since multiple models must be trained. RFE is known to yield strong results, especially when using robust base learners [39].
- Embedded Methods: We include the LASSO (Least Absolute Shrinkage and Selection Operator) as an embedded feature selection approach. LASSO is a linear model with an L1 penalty on weights, which drives many feature coefficients to exactly zero during training. This performs variable selection as part of the model fitting process. We applied LASSO logistic regression to the full feature set; the features with non-zero coefficients after regularization are considered selected. LASSO tends to select a compact subset of the most predictive features, balancing accuracy with sparsity [40].
- Metaheuristic Methods: In addition to the above, we compare EHQ-FABC against a suite of population-based metaheuristic feature selection algorithms. These methods treat feature selection as a global optimization problem–typically maximizing an evaluation metric (e.g., classification accuracy or a fitness function)–and use bio-inspired heuristics to search the combinatorial space of feature subsets. We implemented the following well-known metaheuristics for comparison:
- ○
- Firefly Algorithm (FA): A swarm optimization inspired by fireflies’ flashing behavior. Candidate solutions (feature subsets) are “fireflies” that move in the search space, attracted by brighter (better) fireflies. FA is effective in the global search for multimodal optimization problems [41].
- ○
- Artificial Bee Colony (ABC): An algorithm mimicking the foraging behavior of honey bees in a colony. It maintains populations of employed bees, onlooker bees, and scout bees that explore and exploit candidate feature sets, sharing information akin to waggle dances. ABC excels at local exploitation and has shown strong performance on numeric optimization tasks [42].
- ○
- Particle Swarm Optimization (PSO): A socio-inspired optimization where a swarm of particles (feature subsets) “flies” through the search space, updating positions based on personal best and global best found so far. PSO balances exploration and exploitation through its velocity and inertia parameters and has been widely applied to feature selection problems for its simplicity and speed [43].
4.4. Evaluation Metrics
- Accuracy: This is the simplest metric, defined as the proportion of correctly classified instances among all instances. Accuracy gives an overall sense of how often the classifier is correct. While easy to interpret, accuracy can be misleading in imbalanced datasets (where one class dominates); a high accuracy might simply reflect predicting the majority class. In our balanced evaluation scenarios; however, accuracy provides a useful first indicator of performance.
- Precision: Precision is the ratio of true positives to the total predicted positives, i.e., the fraction of instances predicted as positive that are positive. High precision means that when the model predicts an instance as the positive class (e.g., “spam” URL), it is usually correct. This metric is crucial when the cost of false positives is high, for example, in our context, a low precision would mean many benign URLs are being misclassified as spam, which could burden a security system with false alarms. Precision helps evaluate how trustworthy positive predictions are.
- Recall: Recall is the ratio of true positives to all actual positives, i.e., the fraction of positive class instances that the model successfully identifies. High recall means the model catches most of the positive instances (e.g., it identifies most of the spam URLs). This metric is vital when a missing positive instance has a large cost, in security, failing to detect a spam URL (false negative) could be dangerous. There is often a trade-off between precision and recall; we report both to give a balanced view of classifier performance.
- F1-macro: The F1-macro score is the unweighted average of F1-scores across all classes, where each class’s F1-score is the harmonic mean of its precision and recall. It treats all classes equally, regardless of their frequency, making it ideal for imbalanced datasets. A high F1-macro score indicates strong performance across both spam and benign classes, balancing false positives and false negatives. In our evaluation, the F1-macro score summarizes the classifier’s ability to handle both classes effectively, accounting for errors without bias toward the majority class.
- Matthews Correlation Coefficient (MCC): MCC is a single summary metric that takes into account all four entries of the confusion matrix (TP, TN, FP, FN). It is essentially the correlation coefficient between the predicted and true labels, yielding a value between −1 and +1. An MCC of 1 indicates perfect predictions, 0 indicates random performance, and −1 indicates total disagreement. MCC is particularly informative for imbalanced datasets because it remains sensitive to changes in minority class predictions, unlike accuracy. In our case, MCC provides a balanced assessment of performance, taking into account both positive and negative classifications. A higher MCC means the classifier is making accurate predictions on both classes (spam and benign) in a balanced way.
- ROC-AUC: The Receiver Operating Characteristic Area Under the Curve (ROC-AUC) measures the classifier’s ability to distinguish between classes by plotting the true positive rate against the false positive rate across various thresholds. Ranging from 0 to 1, an ROC-AUC of 1 indicates perfect separation, while 0.5 suggests random guessing. It is robust for imbalanced datasets, as it focuses on ranking predictions rather than absolute thresholds. In our evaluation, ROC-AUC assesses the classifier’s capability to differentiate spam from benign instances, with a higher score indicating better discriminative power.
- Log loss: Log loss evaluates the probabilistic confidence of the classifier’s predictions. It is defined as the negative log-likelihood of the true class given the predicted probability distribution. In practice, a classifier that assigns higher probability to the correct class will have a lower log loss. Log loss increases sharply for predictions that are both confident and wrong. This metric is important because it rewards classifiers that are not only correct but also honest about their uncertainty. In our evaluation, we use log loss to measure how well-calibrated the classifier’s probability outputs are–lower log loss indicates that the model’s confidence levels align well with reality, and it heavily penalizes any overly confident misclassifications.
- Feature Reduction Ratio (FRR): This metric quantifies the extent of dimensionality reduction achieved by a feature selection method. We define FRR as , where Ntotal = 72 is the original number of features and Nselected is the number of selected features, quantifying the extent of dimensionality reduction. FRR thus represents the percentage of features eliminated. For example, an FRR of 50% means the feature selection halved the dimensionality (selected 36 out of 72 features). A higher FRR is generally desirable as it means more feature reduction (simpler models), but it must be balanced against the impact on predictive performance. We report FRR to compare how aggressively each method trims features. Combined with the accuracy metrics, FRR helps illustrate the trade-off each feature selector makes between model simplicity and accuracy.
4.5. Experimental Results
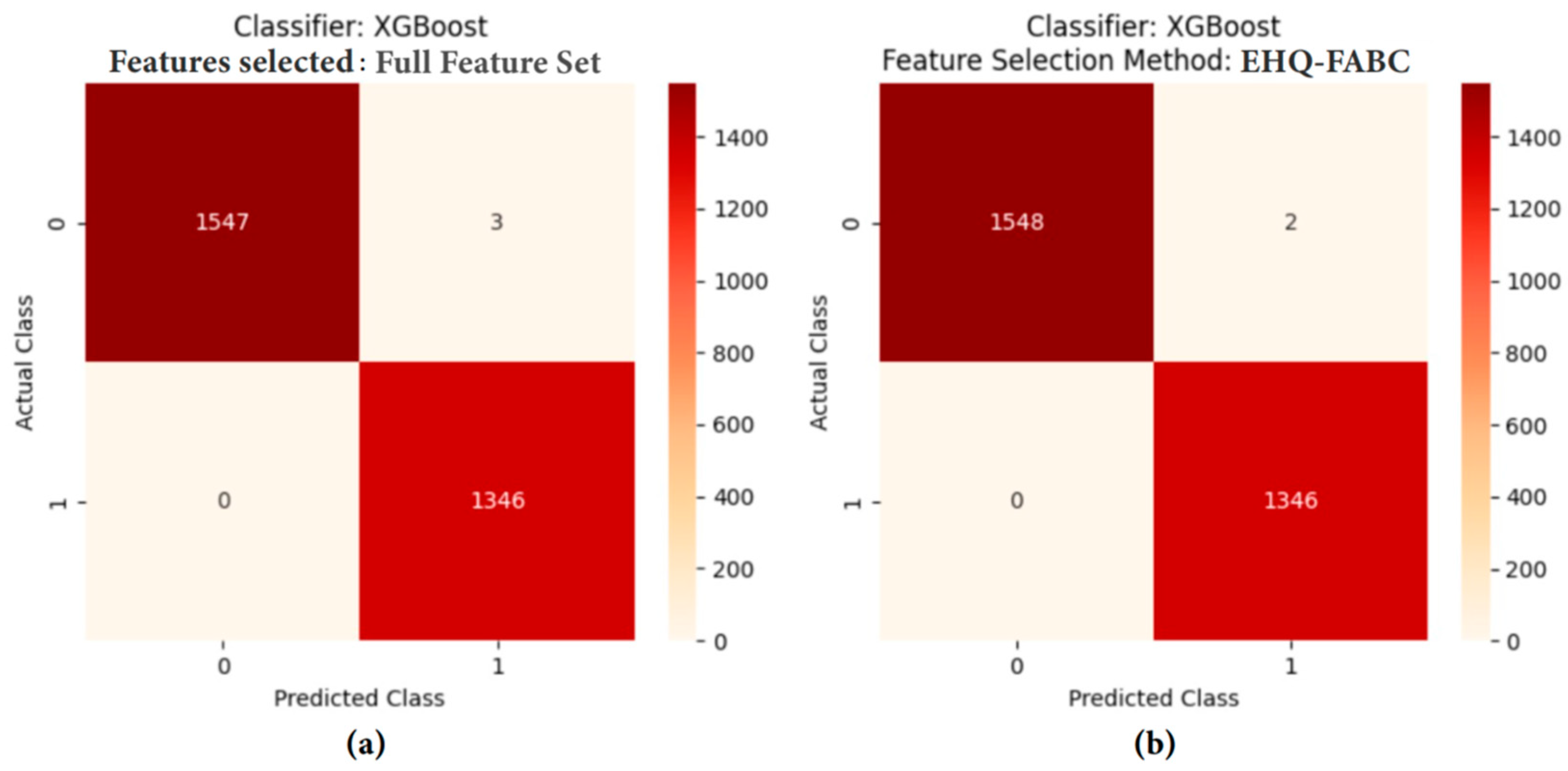
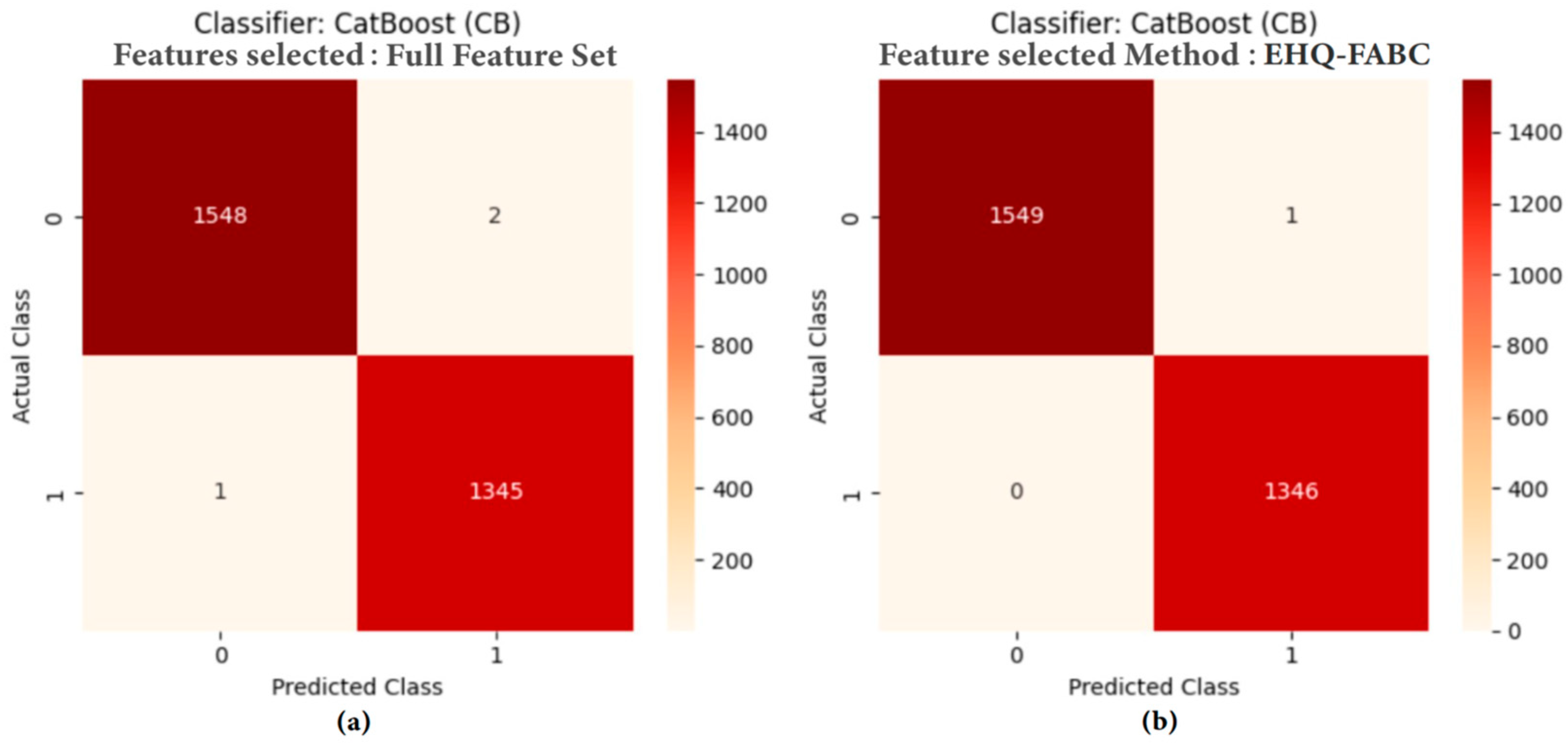
4.5.1. Performance Comparison Analysis
4.5.2. Feature Reduction Analysis
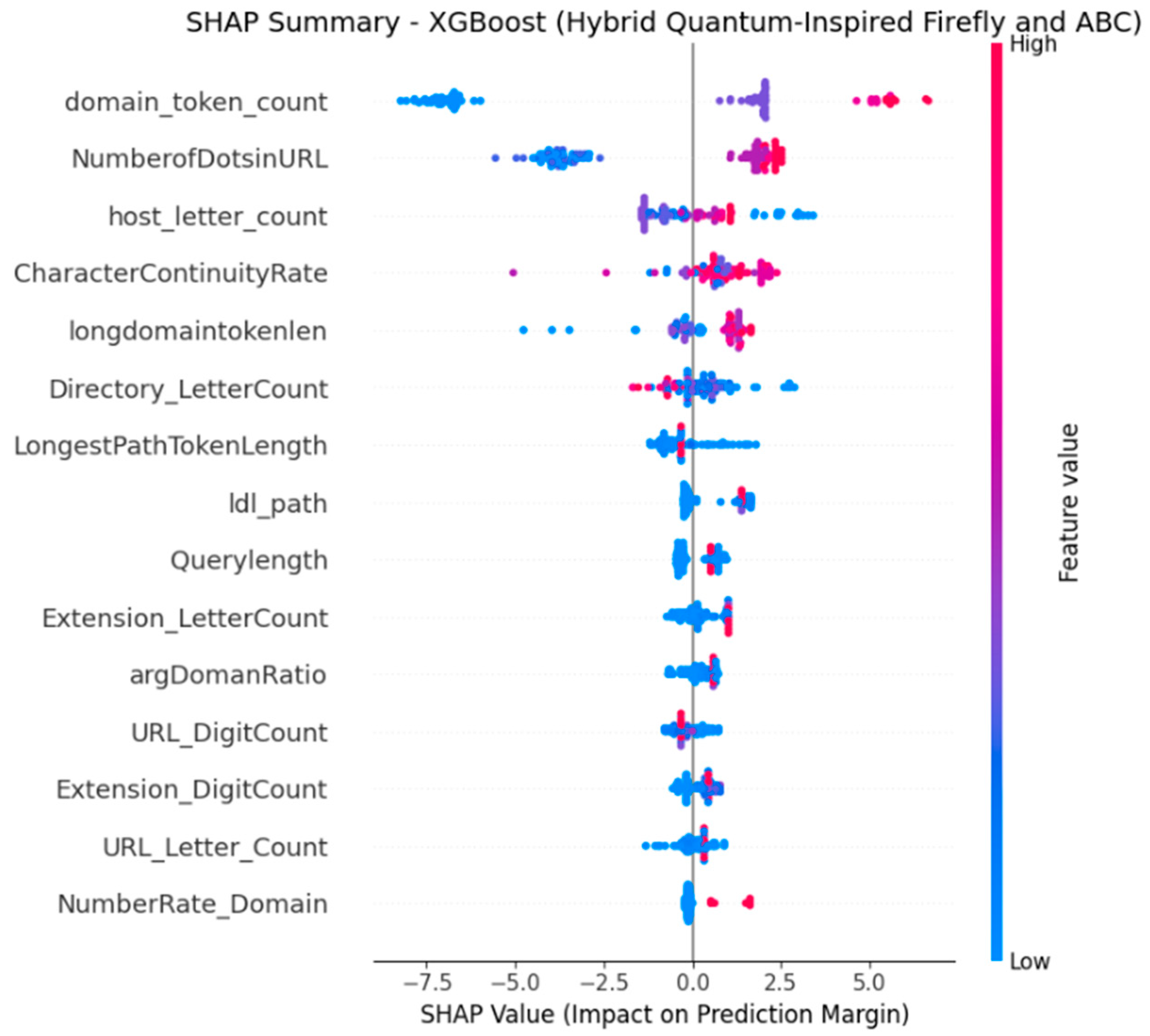
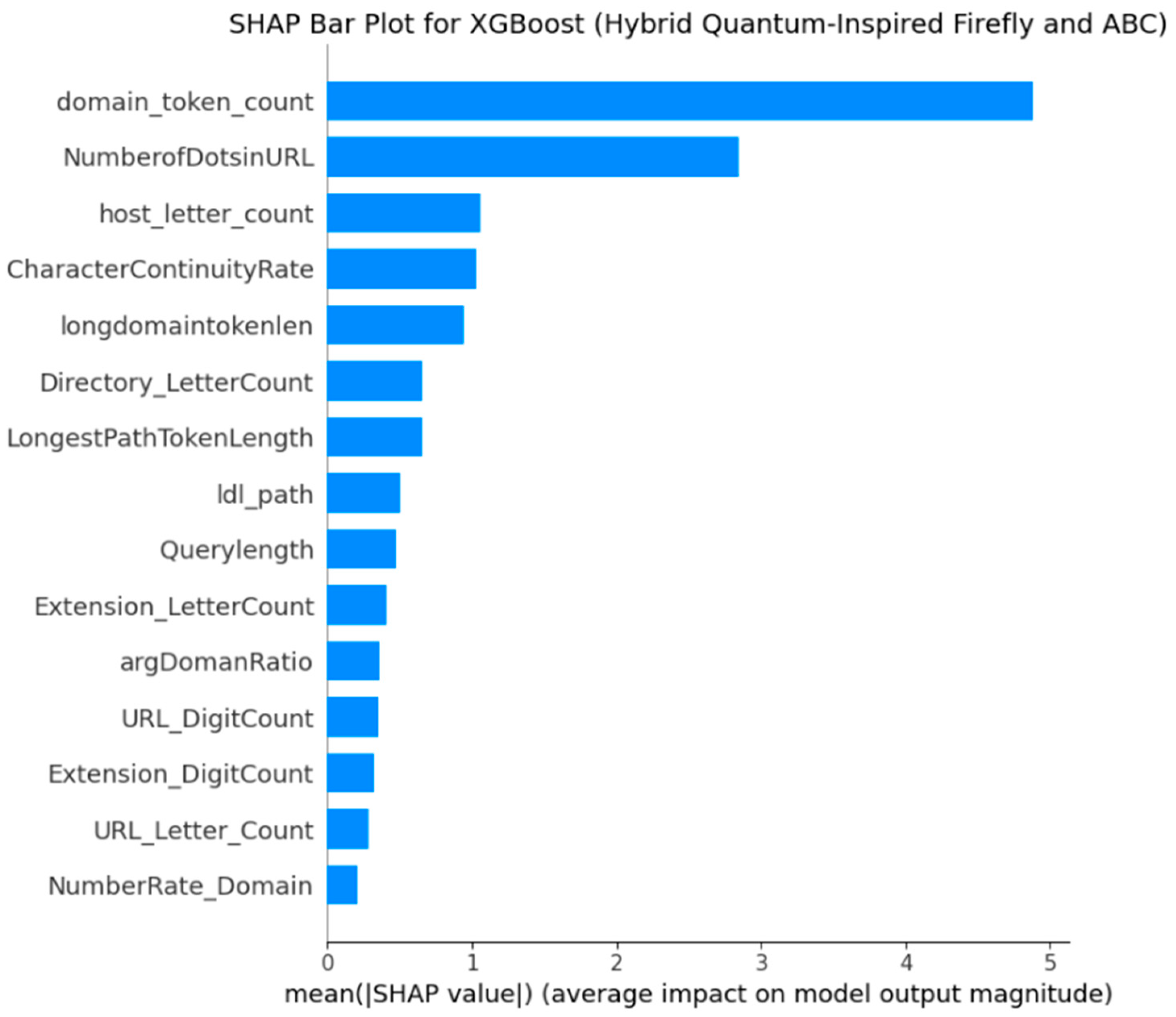
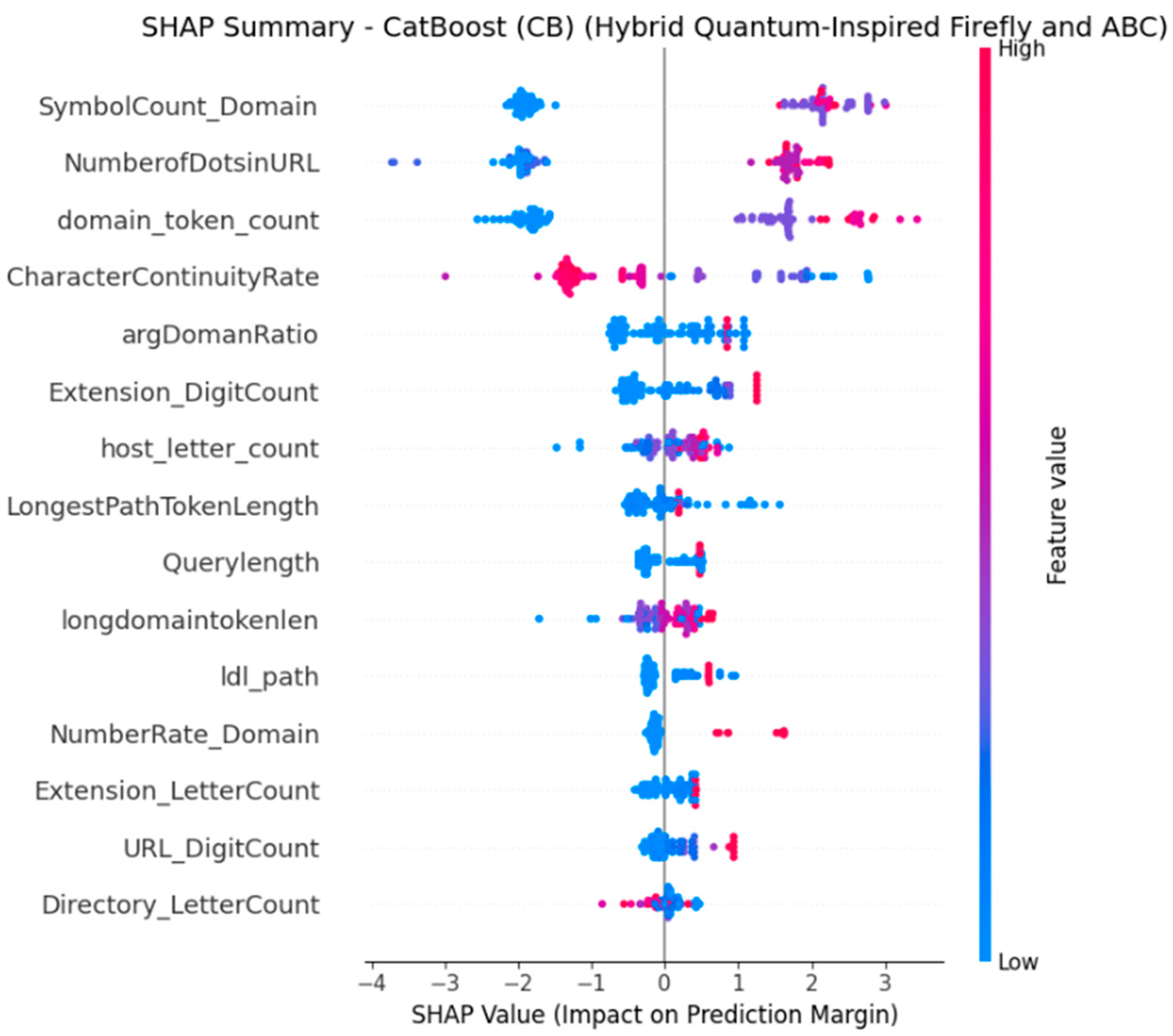
4.5.3. SHAP-Based Explainability Analysis
- SHAP Analysis for XGB with EHQ-FABC Features
- SHAP Analysis for CB with EHQ-FABC Features
- Insights and Comparison with Traditional Importance Rankings
4.5.4. Comparison with Previous Studies
4.6. Discussion
- Why EHQ-FABC works
- Predictive Power and Robustness
- Generalization Capability
- Efficiency and Model Simplicity
- Explainability and Insights into Spam Detection
4.7. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EHQ-FABC | Enhanced Hybrid Quantum-Inspired Firefly and Artificial Bee Colony |
| ML | Machine Learning |
| SHAP | Shapley Additive Explanations |
| QIEAs | Quantum-Inspired Evolutionary Algorithms |
| CatBoost | CB |
| XGBoost | XGB |
| RF | Random Forest |
| ET | Extra Trees |
| DT | Decision Tree |
| KNN | K-Nearest Neighbors |
| LR | Logistic Regression |
| MLP | Multi-Layer Perceptron |
| RFE | Recursive Feature Elimination |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| FA | Firefly Algorithm |
| ABC | Artificial Bee Colony |
| PSO | Particle Swarm Optimization |
| MCC | Matthews Correlation Coefficient |
References
- Tusher, E.H.; Ismail, M.A.; Mat Raffei, A.F. Email spam classification based on deep learning methods: A review. Iraqi J. Comput. Sci. Math. 2025, 6, 2. [Google Scholar] [CrossRef]
- Patil, A.; Singh, P. Spam Detection Using Machine Learning. Int. J. Sci. Technol. 2025, 16, 1–10. [Google Scholar] [CrossRef]
- Mamun, M.S.I.; Rathore, M.A.; Lashkari, A.H.; Stakhanova, N.; Ghorbani, A.A. Detecting Malicious URLs Using Lexical Analysis. In Lecture Notes in Computer Science; Chen, J., Piuri, V., Su, C., Yung, M., Eds.; Network and System Security; Springer International Publishing: Cham, Switzerland, 2016; pp. 467–482. [Google Scholar]
- Ghalechyan, H.; Israyelyan, E.; Arakelyan, A.; Hovhannisyan, G.; Davtyan, A. Phishing URL detection with neural networks: An empirical study. Sci. Rep. 2024, 14, 25134. [Google Scholar] [CrossRef]
- Abualhaj, M.; Al-Khatib, S.; Hiari, M.; Shambour, Q. Enhancing Spam Detection Using Hybrid of Harris Hawks and Firefly Optimization Algorithms. J. Soft Comput. Data Min. 2024, 5, 161–174. [Google Scholar] [CrossRef]
- Almomani, O.; Alsaaidah, A.; Abu-Shareha, A.A.; Alzaqebah, A.; Amin Almaiah, M.; Shambour, Q. Enhance URL Defacement Attack Detection Using Particle Swarm Optimization and Machine Learning. J. Comput. Cogn. Eng. 2025, 4, 296–308. [Google Scholar] [CrossRef]
- Almomani, O.; Alsaaidah, A.; Abualhaj, M.M.; Almaiah, M.A.; Almomani, A.; Memon, S. URL Spam Detection Using Machine Learning Classifiers. In Proceedings of the 2025 1st International Conference on Computational Intelligence Approaches and Applications (ICCIAA), Amman, Jordan, 28–30 April 2025; pp. 1–6. [Google Scholar]
- Abualhaj, M.M.; Hiari, M.O.; Alsaaidah, A.; Al-Zyoud, M.; Al-Khatib, S. Spam Feature Selection Using Firefly Metaheuristic Algorithm. J. Appl. Data Sci. 2024, 5, 1692–1700. [Google Scholar] [CrossRef]
- Harahsheh, K.; Al-Naimat, R.; Chen, C.-H. Using Feature Selection Enhancement to Evaluate Attack Detection in the Internet of Things Environment. Electronics 2024, 13, 1678. [Google Scholar] [CrossRef]
- Panliang, M.; Madaan, S.; Babikir Ali, S.A.; Gowrishankar, J.; Khatibi, A.; Alsoud, A.R.; Mittal, V.; Kumar, L.; Santhosh, A.J. Enhancing feature selection for multi-pose facial expression recognition using a hybrid of quantum inspired firefly algorithm and artificial bee colony algorithm. Sci. Rep. 2025, 15, 4665. [Google Scholar] [CrossRef]
- Abualhaj, M.M.; Abu-Shareha, A.A.; Alkhatib, S.N.; Shambour, Q.Y.; Alsaaidah, A.M. Detecting spam using Harris Hawks optimizer as a feature selection algorithm. Bull. Electr. Eng. Inform. 2025, 14, 2361–2369. [Google Scholar] [CrossRef]
- Abualhaj, M.M.; Alkhatib, S.N.; Abu-Shareha, A.A.; Alsaaidah, A.M.; Anbar, M. Enhancing spam detection using Harris Hawks optimization algorithm. TELKOMNIKA (Telecommun. Comput. Electron. Control) 2025, 23, 447–454. [Google Scholar] [CrossRef]
- Mandal, A.K.; Chakraborty, B. Quantum computing and quantum-inspired techniques for feature subset selection: A review. Knowl. Inf. Syst. 2025, 67, 2019–2061. [Google Scholar] [CrossRef]
- Zhang, Z.; Hamadi, H.A.; Damiani, E.; Yeun, C.Y.; Taher, F. Explainable Artificial Intelligence Applications in Cyber Security: State-of-the-Art in Research. IEEE Access 2022, 10, 93104–93139. [Google Scholar] [CrossRef]
- Mohale, V.Z.; Obagbuwa, I.C. A systematic review on the integration of explainable artificial intelligence in intrusion detection systems to enhancing transparency and interpretability in cybersecurity. Front. Artif. Intell. 2025, 8, 1526221. [Google Scholar] [CrossRef]
- Rehman, J.U.; Ulum, M.S.; Shaffar, A.W.; Hakim, A.A.; Mujirin; Abdullah, Z.; Al-Hraishawi, H.; Chatzinotas, S.; Shin, H. Evolutionary Algorithms and Quantum Computing: Recent Advances, Opportunities, and Challenges. IEEE Access 2025, 13, 16649–16670. [Google Scholar] [CrossRef]
- Han, K.-H.; Kim, J.-H. Quantum-inspired evolutionary algorithm for a class of combinatorial optimization. IEEE Trans. Evol. Comput. 2002, 6, 580–593. [Google Scholar] [CrossRef]
- Adadi, A.; Berrada, M. Peeking Inside the Black-Box: A Survey on Explainable Artificial Intelligence (XAI). IEEE Access 2018, 6, 52138–52160. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. SHAP: A Unified Approach to Explainability. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Haripriya, C.; Prabhudev, J. An Explainable and Optimized Network Intrusion Detection Model using Deep Learning. Int. J. Adv. Comput. Sci. Appl. 2024, 15, 482–488. [Google Scholar] [CrossRef]
- Sarker, S.K.; Bhattacharjee, R.; Sufian, M.A.; Ahamed, M.S.; Talha, M.A.; Tasnim, F.; Islam, K.M.N.; Adrita, S.T. Email Spam Detection Using Logistic Regression and Explainable AI. In Proceedings of the 2025 International Conference on Electrical, Computer and Communication Engineering (ECCE), Chittagong, Bangladesh, 13–15 February 2025; pp. 1–6. [Google Scholar]
- Adnan, M.; Imam, M.O.; Javed, M.F.; Murtza, I. Improving spam email classification accuracy using ensemble techniques: A stacking approach. Int. J. Inf. Secur. 2024, 23, 505–517. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspired Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of Artificial Bee Colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 6638–6648. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Shambour, Q.; Lu, J. A Framework of Hybrid Recommendation System for Government-to-Business Personalized E-Services. In Proceedings of the 2010 Seventh International Conference on Information Technology: New Generations, Las Vegas, NV, USA, 12–14 April 2010; pp. 592–597. [Google Scholar]
- Shambour, Q.; Lu, J. Integrating Multi-Criteria Collaborative Filtering and Trust filtering for personalized Recommender Systems. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence in Multicriteria Decision-Making (MDCM), Paris, France, 11–15 April 2011; pp. 44–51. [Google Scholar]
- Shambour, Q.Y.; Al-Zyoud, M.M.; Hussein, A.H.; Kharma, Q.M. A doctor recommender system based on collaborative and content filtering. Int. J. Electr. Comput. Eng. 2023, 13, 884–893. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest Neighbor Pattern Classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Cox, D.R. The Regression Analysis of Binary Sequences. J. R. Stat. Soc. Ser. B (Methodol.) 1958, 20, 215–232. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Zhai, Y.; Song, W.; Liu, X.; Liu, L.; Zhao, X. A Chi-Square Statistics Based Feature Selection Method in Text Classification. In Proceedings of the 2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 23–25 November 2018; pp. 160–163. [Google Scholar]
- Li, F.; Yang, Y. Analysis of recursive feature elimination methods. In Proceedings of the 28th annual international ACM SIGIR conference on Research and development in information retrieval, Salvador, Brazil, 15–19 August 2005; pp. 633–634. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B (Methodol.) 2018, 58, 267–288. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization. In Stochastic Algorithms: Foundations and Applications; Watanabe, O., Zeugmann, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Naidu, G.; Zuva, T.; Sibanda, E.M. A Review of Evaluation Metrics in Machine Learning Algorithms. In Artificial Intelligence Application in Networks and Systems; Silhavy, R., Silhavy, P., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 15–25. [Google Scholar]
- Anne, W.R.; CarolinJeeva, S. Performance analysis of boosting techniques for classification and detection of malicious websites. In Proceedings of the First International Conference on Combinatorial and Optimization (ICCAP 2021), Chennai, India, 7–8 December 2021; pp. 405–415. [Google Scholar]

| No. | Feature Name | Format | No. | Feature Name | Format |
|---|---|---|---|---|---|
| 1 | Querylength | Integer | 41 | Directory_DigitCount | Integer |
| 2 | domain_token_count | Integer | 42 | File_name_DigitCount | Integer |
| 3 | path_token_count | Integer | 43 | Extension_DigitCount | Integer |
| 4 | avgdomaintokenlen | Float | 44 | Query_DigitCount | Integer |
| 5 | longdomaintokenlen | Integer | 45 | URL_Letter_Count | Integer |
| 6 | avgpathtokenlen | Float | 46 | host_letter_count | Integer |
| 7 | tld | Categorical | 47 | Directory_LetterCount | Integer |
| 8 | charcompvowels | Integer | 48 | Filename_LetterCount | Integer |
| 9 | charcompace | Integer | 49 | Extension_LetterCount | Integer |
| 10 | ldl_url | Integer | 50 | Query_LetterCount | Integer |
| 11 | ldl_domain | Integer | 51 | LongestPathTokenLength | Integer |
| 12 | ldl_path | Integer | 52 | Domain_LongestWordLength | Integer |
| 13 | ldl_filename | Integer | 53 | Path_LongestWordLength | Integer |
| 14 | ldl_getArg | Integer | 54 | sub-Directory_LongestWordLength | Integer |
| 15 | dld_url | Integer | 55 | Arguments_LongestWordLength | Integer |
| 16 | dld_domain | Integer | 56 | URL_sensitiveWord | Integer |
| 17 | dld_path | Integer | 57 | URLQueries_variable | Integer |
| 18 | dld_filename | Integer | 58 | spcharUrl | Integer |
| 19 | dld_getArg | Integer | 59 | delimeter_Domain | Integer |
| 20 | urlLen | Integer | 60 | delimeter_path | Integer |
| 21 | domainlength | Integer | 61 | delimeter_Count | Integer |
| 22 | pathLength | Integer | 62 | NumberRate_URL | Float |
| 23 | subDirLen | Integer | 63 | NumberRate_Domain | Float |
| 24 | fileNameLen | Integer | 64 | NumberRate_DirectoryName | Float |
| 25 | this.fileExtLen | Integer | 65 | NumberRate_FileName | Float |
| 26 | ArgLen | Integer | 66 | NumberRate_Extension | Float |
| 27 | pathurlRatio | Float | 67 | NumberRate_AfterPath | Float |
| 28 | ArgUrlRatio | Float | 68 | SymbolCount_URL | Integer |
| 29 | argDomainRatio | Float | 69 | SymbolCount_Domain | Integer |
| 30 | domainUrlRatio | Float | 70 | SymbolCount_Directoryname | Integer |
| 31 | pathDomainRatio | Float | 71 | SymbolCount_FileName | Integer |
| 32 | argPathRatio | Float | 72 | SymbolCount_Extension | Integer |
| 33 | executable | Integer | 73 | SymbolCount_Afterpath | Integer |
| 34 | isPortEighty | Integer | 74 | Entropy_URL | Float |
| 35 | NumberOfDotsinURL | Integer | 75 | Entropy_Domain | Float |
| 36 | ISIpAddressInDomainName | Integer | 76 | Entropy_DirectoryName | Float |
| 37 | CharacterContinuityRate | Float | 77 | Entropy_Filename | Float |
| 38 | LongestVariableValue | Integer | 78 | Entropy_Extension | Float |
| 39 | URL_DigitCount | Integer | 79 | Entropy_Afterpath | Float |
| 40 | host_DigitCount | Integer | Label | URL_Type_obf_Type | Categorical (benign, spam) |
| Parameter | Description | Value | Justification |
|---|---|---|---|
| N | Population size | 50 | Balances diversity and computation cost; typical for swarm/metaheuristic search |
| Tmax | Max iterations | 100 | Sufficient for convergence in high-dimensional problems; avoids overfitting. |
| γ | Light absorption coefficient | 1.7706 | Optimized for feature-space distances; controls Firefly attraction |
| λ0 | Initial Lévy step size | 0.6370 | Optimized; promotes effective global exploration in early iterations |
| W | Stagnation window | 10 | Window for stagnation detection in phase switching |
| ε | Stagnation threshold | 0.001 | Sensitivity for detecting stagnation; prevents premature or late switching |
| Tstop | Early stopping window (patience) | 29 | Limits computation if no improvement; avoids unnecessary evaluations |
| ρ | Chaos/adaptive exploration factor | 0.8143 | Controls global vs. local search; best found by optimization |
| αSA | Simulated annealing cooling rate | 0.9454 | Regulates acceptance of worse solutions; improves escape from local minima |
| |A| | Elite solution archive size | 15 | Number of top solutions stored; balances exploitation and memory efficiency |
| ML Model | Optimized Parameters |
|---|---|
| XGB | n_estimators: 236, max_depth: 3, learning_rate: 0.29500875327999976 |
| CB | iterations: 510, depth: 13, learning_rate: 0.06790539682592432, l2_leaf_reg: 8 |
| RF | n_estimators: 432, max_depth: 16, min_samples_split: 5, min_samples_leaf: 1 |
| ET | n_estimators: 476, max_depth: 21, min_samples_split: 2 |
| DT | max_depth: 27, criterion: ‘entropy’, splitter: random, min_samples_split: 9, min_samples_leaf: 2 |
| KNN | metric: ‘manhattan’, n_neighbors: 3, weights: ‘distance’ |
| LR | C: 746.5701064197558, penalty: ‘l2’, solver: ‘liblinear’, max_iter: 473, l1_ratio: 0.0995374802589899 |
| MLP | layers: 2, activation: ‘tanh’, alpha: 0.0006103726304159704, learning_rate: ‘constant’, solver: ‘lbfgs’, max_iter: 437 |
| CLASSIFIER | FEATURE SELECTION METHOD | ACCURACY | PRECISION | RECALL | MACRO-F1 | MCC | ROC-AUC SCORE | LOG LOSS | FRR (%) | # OF FEATURES |
|---|---|---|---|---|---|---|---|---|---|---|
| XGB | Full Feature Set | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9979 | 1 | 0.0026 | 72 | |
| Chi-Square | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9979 | 1 | 0.0040 | 59.72 | 29 | |
| LASSO | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9979 | 1 | 0.0021 | 48.61 | 37 | |
| RFE | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9979 | 1 | 0.0018 | 62.50 | 27 | |
| FA | 0.9976 | 0.9976 | 0.9976 | 0.9976 | 0.9951 | 1 | 0.0070 | 65.28 | 25 | |
| ABC | 0.9983 | 0.9983 | 0.9983 | 0.9983 | 0.9965 | 1 | 0.0040 | 68.06 | 23 | |
| PSO | 0.9993 | 0.9993 | 0.9993 | 0.9993 | 0.9986 | 1 | 0.0025 | 80.56 | 14 | |
| Proposed EHQ-FABC | 0.9993 | 0.9993 | 0.9993 | 0.9993 | 0.9986 | 1 | 0.0030 | 76.39 | 17 | |
| CB | Full Feature Set | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9979 | 1 | 0.0037 | 72 | |
| Chi-Square | 0.9983 | 0.9983 | 0.9983 | 0.9983 | 0.9965 | 1 | 0.0044 | 59.72 | 29 | |
| LASSO | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9979 | 1 | 0.0032 | 48.61 | 37 | |
| RFE | 0.9979 | 0.9979 | 0.9979 | 0.9979 | 0.9958 | 1 | 0.0038 | 62.50 | 27 | |
| FA | 0.9983 | 0.9983 | 0.9983 | 0.9983 | 0.9965 | 1 | 0.0062 | 65.28 | 25 | |
| ABC | 0.9983 | 0.9983 | 0.9983 | 0.9983 | 0.9965 | 1 | 0.0047 | 68.06 | 23 | |
| PSO | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9979 | 1 | 0.0037 | 80.56 | 14 | |
| Proposed EHQ-FABC | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9993 | 1 | 0.0026 | 76.39 | 17 | |
| RF | Full Feature Set | 0.9976 | 0.9976 | 0.9976 | 0.9976 | 0.9951 | 1 | 0.0083 | 0.00 | 72 |
| Chi-Square | 0.9979 | 0.9979 | 0.9979 | 0.9979 | 0.9958 | 1 | 0.0084 | 59.72 | 29 | |
| LASSO | 0.9976 | 0.9976 | 0.9976 | 0.9976 | 0.9951 | 1 | 0.0079 | 48.61 | 37 | |
| RFE | 0.9979 | 0.9979 | 0.9979 | 0.9979 | 0.9958 | 1 | 0.0065 | 62.50 | 27 | |
| FA | 0.9972 | 0.9972 | 0.9972 | 0.9972 | 0.9945 | 1 | 0.0110 | 65.28 | 25 | |
| ABC | 0.9969 | 0.9969 | 0.9969 | 0.9969 | 0.9938 | 1 | 0.0090 | 68.06 | 23 | |
| PSO | 0.9972 | 0.9972 | 0.9972 | 0.9972 | 0.9944 | 1 | 0.0100 | 80.56 | 14 | |
| Proposed EHQ-FABC | 0.9983 | 0.9983 | 0.9983 | 0.9983 | 0.9965 | 1 | 0.0073 | 76.39 | 17 | |
| ET | Full Feature Set | 0.9976 | 0.9976 | 0.9976 | 0.9976 | 0.9951 | 1 | 0.0102 | 72 | |
| Chi-Square | 0.9959 | 0.9959 | 0.9959 | 0.9959 | 0.9917 | 1 | 0.0155 | 59.72 | 29 | |
| LASSO | 0.9983 | 0.9983 | 0.9983 | 0.9983 | 0.9965 | 1 | 0.0107 | 48.61 | 37 | |
| RFE | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9979 | 1 | 0.0069 | 62.50 | 27 | |
| FA | 0.9965 | 0.9965 | 0.9965 | 0.9965 | 0.9931 | 1 | 0.0256 | 65.28 | 25 | |
| ABC | 0.9976 | 0.9976 | 0.9976 | 0.9976 | 0.9951 | 1 | 0.0154 | 68.06 | 23 | |
| PSO | 0.9955 | 0.9955 | 0.9955 | 0.9955 | 0.9910 | 1 | 0.0278 | 80.56 | 14 | |
| Proposed EHQ-FABC | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9979 | 1 | 0.0117 | 76.39 | 17 | |
| DT | Full Feature Set | 0.9941 | 0.9941 | 0.9941 | 0.9941 | 0.9882 | 0.9969 | 0.0602 | 72 | |
| Chi-Square | 0.9924 | 0.9924 | 0.9924 | 0.9924 | 0.9847 | 0.9948 | 0.1747 | 59.72 | 29 | |
| LASSO | 0.9927 | 0.9927 | 0.9927 | 0.9927 | 0.9854 | 0.9955 | 0.1054 | 48.61 | 37 | |
| RFE | 0.9941 | 0.9941 | 0.9941 | 0.9941 | 0.9882 | 0.9969 | 0.0599 | 62.50 | 27 | |
| FA | 0.9931 | 0.9931 | 0.9931 | 0.9931 | 0.9861 | 0.9952 | 0.0872 | 65.28 | 25 | |
| ABC | 0.9931 | 0.9931 | 0.9931 | 0.9931 | 0.9861 | 0.9942 | 0.1312 | 68.06 | 23 | |
| PSO | 0.9962 | 0.9962 | 0.9962 | 0.9962 | 0.9924 | 0.9964 | 0.0862 | 80.56 | 14 | |
| Proposed EHQ-FABC | 0.9965 | 0.9965 | 0.9965 | 0.9965 | 0.9931 | 0.9978 | 0.0803 | 76.39 | 17 | |
| KNN | Full Feature Set | 0.9883 | 0.9883 | 0.9883 | 0.9883 | 0.9764 | 0.9973 | 0.1033 | 72 | |
| Chi-Square | 0.9986 | 0.9986 | 0.9986 | 0.9986 | 0.9972 | 0.999 | 0.0388 | 59.72 | 29 | |
| LASSO | 0.9969 | 0.9969 | 0.9969 | 0.9969 | 0.9938 | 0.9993 | 0.0297 | 48.61 | 37 | |
| RFE | 0.9979 | 0.9979 | 0.9979 | 0.9979 | 0.9958 | 0.9993 | 0.0279 | 62.50 | 27 | |
| FA | 0.9959 | 0.9959 | 0.9959 | 0.9959 | 0.9917 | 0.9986 | 0.0553 | 65.28 | 25 | |
| ABC | 0.9976 | 0.9976 | 0.9976 | 0.9976 | 0.9951 | 0.9985 | 0.0532 | 68.06 | 23 | |
| PSO | 0.9965 | 0.9965 | 0.9965 | 0.9965 | 0.9931 | 0.9989 | 0.0428 | 80.56 | 14 | |
| Proposed EHQ-FABC | 0.9990 | 0.9990 | 0.9990 | 0.9990 | 0.9979 | 1 | 0.0016 | 76.39 | 17 | |
| LR | Full Feature Set | 0.8802 | 0.8801 | 0.8802 | 0.8801 | 0.7590 | 0.9516 | 0.3128 | 72 | |
| Chi-Square | 0.9855 | 0.9855 | 0.9855 | 0.9855 | 0.9709 | 0.9986 | 0.0511 | 59.72 | 29 | |
| LASSO | 0.9952 | 0.9952 | 0.9952 | 0.9952 | 0.9903 | 0.9997 | 0.0209 | 48.61 | 37 | |
| RFE | 0.9931 | 0.9931 | 0.9931 | 0.9931 | 0.9862 | 0.9997 | 0.0235 | 62.50 | 27 | |
| FA | 0.9713 | 0.9713 | 0.9713 | 0.9713 | 0.9424 | 0.995 | 0.0825 | 65.28 | 25 | |
| ABC | 0.9900 | 0.9900 | 0.9900 | 0.9900 | 0.9800 | 0.999 | 0.0363 | 68.06 | 23 | |
| PSO | 0.9807 | 0.9811 | 0.9807 | 0.9807 | 0.9617 | 0.9958 | 0.0635 | 80.56 | 14 | |
| Proposed EHQ-FABC | 0.9900 | 0.9901 | 0.9900 | 0.9900 | 0.9800 | 0.9992 | 0.0403 | 76.39 | 17 | |
| MLP | Full Feature Set | 0.9931 | 0.9932 | 0.9931 | 0.9931 | 0.9862 | 0.9997 | 0.0285 | 72 | |
| Chi-Square | 0.9907 | 0.9909 | 0.9907 | 0.9907 | 0.9815 | 0.9998 | 0.0325 | 59.72 | 29 | |
| LASSO | 0.9979 | 0.9979 | 0.9979 | 0.9979 | 0.9958 | 1 | 0.0068 | 48.61 | 37 | |
| RFE | 0.9983 | 0.9983 | 0.9983 | 0.9983 | 0.9965 | 1 | 0.0048 | 62.50 | 27 | |
| FA | 0.9976 | 0.9976 | 0.9976 | 0.9976 | 0.9952 | 0.9998 | 0.0122 | 65.28 | 25 | |
| ABC | 0.9948 | 0.9949 | 0.9948 | 0.9948 | 0.9896 | 1 | 0.0155 | 68.06 | 23 | |
| PSO | 0.9945 | 0.9945 | 0.9945 | 0.9945 | 0.9889 | 0.9997 | 0.0185 | 80.56 | 14 | |
| Proposed EHQ-FABC | 0.9979 | 0.9979 | 0.9979 | 0.9979 | 0.9958 | 1 | 0.0075 | 76.39 | 17 |
| Refs | Feature Selection Method | Hyper-Parameter Optimization | ML Model | Model Explainability | Highest Accuracy |
|---|---|---|---|---|---|
| [45] | LightGBM | No | RF | No | 99% |
| [11] | Harris Hawks optimization algorithm | Yes | XGB | No | 99.60% |
| [12] | Harris Hawks optimization algorithm | Yes | DT | No | 99.75% |
| [8] | Firefly optimization algorithm | Yes | DT | No | 99.81% |
| [5] | Hybrid Firefly and Harris Hawks optimization algorithm | Yes | ET | No | 99.83% |
| Proposed work | EHQ-FABC algorithm | Yes | CB | Yes | 99.97% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shambour, Q.; Al-Zyoud, M.; Almomani, O. Quantum-Inspired Hybrid Metaheuristic Feature Selection with SHAP for Optimized and Explainable Spam Detection. Symmetry 2025, 17, 1716. https://doi.org/10.3390/sym17101716
Shambour Q, Al-Zyoud M, Almomani O. Quantum-Inspired Hybrid Metaheuristic Feature Selection with SHAP for Optimized and Explainable Spam Detection. Symmetry. 2025; 17(10):1716. https://doi.org/10.3390/sym17101716
Chicago/Turabian StyleShambour, Qusai, Mahran Al-Zyoud, and Omar Almomani. 2025. "Quantum-Inspired Hybrid Metaheuristic Feature Selection with SHAP for Optimized and Explainable Spam Detection" Symmetry 17, no. 10: 1716. https://doi.org/10.3390/sym17101716
APA StyleShambour, Q., Al-Zyoud, M., & Almomani, O. (2025). Quantum-Inspired Hybrid Metaheuristic Feature Selection with SHAP for Optimized and Explainable Spam Detection. Symmetry, 17(10), 1716. https://doi.org/10.3390/sym17101716







