Abstract
Federated Learning (FL) has been proposed as a new machine learning paradigm to ensure data privacy by training the model in a decentralized manner. However, FL is challenged by device heterogeneity, asymmetric data contribution, and imbalanced datasets, which complicate system control and hinder performance due to long waiting times for aggregation. To tackle the FL challenges, we propose Adaptive Time Threshold Client Selection using DRL (ATCS-FL) to adjust the time threshold (α) in each communication round based on computing and resource capacity of each device and the volume of data updates. The Double Deep Q-Network (DDQN) model determines the appropriate α, according to the variations in local training time that achieves performance improvement alongside latency reduction. Based on the α, the server selects a subset of clients with adequate resources that can finish training within the α for participating in the training process. Our approach dynamically adjusts the α and adaptively selects the number of clients, effectively mitigates the impact of heterogeneous training speeds and significantly enhances communication efficiency. Our experiment utilizes CIFAR-10 and MNIST benchmarked datasets for image classification training with convolutional neural networks across non-IID distributed levels in FL. Specifically, ATCS-FL demonstrates performance improvement and latency reduction of 77% and 75%, respectively, compared to FedProx and FLASH-RL.
1. Introduction
Data has become increasingly valuable, and simultaneously, data privacy is required for the data-based learning scheme. To mitigate the challenges, General Data Protection Regulation (GDPR) was introduced and various privacy-preserving techniques, such as Federated Learning (FL), were proposed to protect sensitive information [1], especially from IoT devices [2,3,4]. FL is an advanced machine learning paradigm that solves privacy issues by training the model locally without sharing raw dataset. Only model parameters are transmitted to a central server for aggregation and global model updates.
However, the random selection of clients in traditional FL methods remains challenging due to heterogeneous client training times, imbalanced dataset updates [5], dynamic client participation, varying resource and computing capacities [6], and high communication costs. It significantly impacts FL convergence and efficiency. The heterogeneity of clients leads to diverse training times for clients, resulting in delays and inefficient use of resources [7,8]. Furthermore, imbalanced data size updates are dynamically changing every round, resulting in varying times for completing the training, which causes more delays [9,10]. As IoT devices typically operate in diverse network conditions, the inconsistency in bandwidth, latency, and reliability tend to occur. Furthermore, asymmetric data contribution every round result in differing communication patterns with the server. In cases where the connection is slow or drops out, it increases communication costs or generates a straggler problem [9,11]. To mitigate the challenges in traditional FL, the author in [12] introduced an innovative FL framework, named FLASH-RL, where the clients selected to participate are generated using Deep Reinforcement Learning (DRL). By observing clients’ hardware conditions, the reputation-based utility function learned the clients’ performance and priority high scores for participation and then selected clients with high-reputation scores to distribute the training. However, this method is faced in a fairness issue selection manner. To address the challenge of the straggler, in [13], the FL protocol called FedCS was proposed, where the FL server obtains the resource condition of clients and selects a subset of clients to distribute the training and those clients transmits back the model update within a fixed deadline. However, resource conditions and client data’s size updates are dynamically changed, so adaptive deadline time is required to guarantee performance improvement and low communication costs in the dynamic environment.
Although many proposed approaches have addressed traditional challenges such as long waiting times, stragglers, and system crashes, these issues have not been fully resolved, and several critical problems remain to be tackled. To address the issues, we will divide the statement of federated client selection limitation into four main issues:
- Asymmetric data contribution: Devices update in varying amounts of data at different times, such as in IoT, smart thermostats update a large amount of data and remain active for an extended period. Meanwhile, smartwatch only updates a slight amount of data and with the most active updating period during the daytime, while a few exceptions during sleep time [14].
- Automatically federated strategy: Traditional strategy adapts with environment is limited. To adapt to the dynamic changes in device conditions over time, the automatic strategy is a suitable approach.
- Adaptive number of client selections: Most of the existing federated client selection schemes select a fixed number of clients. However, to adapt to the dynamic change in the FL environment, the number of client selections should be dynamically adjusted based on the real-time environment.
- Fairness selection: Most existing approaches select devices to participate based on resources and computing capacity as well as data contribution, which creates another issue of fairness selection as those approaches prioritize devices with strong capacity or high contribution to the training. As a result, devices with limited capacity may be excluded from participation throughout the training process.
This paper aims to design a state-of-the-art adaptive time threshold client selection FL mechanism, namely ATCS-FL. In this framework, the server dynamically adjusts the time threshold using Double Deep Q-Network (DDQN), enabling the system to effectively handle data imbalance, heterogeneous client capabilities, and fluctuating resource availability. In each communication round, the server obtains a time threshold from the DDQN agent, which adapts in response to environmental changes. Clients who are expected to complete their local training within the specified time threshold are selected to participate in that round. By doing so, ATCS-FL ensures fair client participation and adapts to resource dynamics, thereby mitigating issues such as prolonged waiting times and inefficient aggregation. The key contributions of this research are as follows:
- Automatic deep reinforcement learning models: We propose DRL-based algorithms to determine optimal time thresholds for each round adaptively. Our model learns to recognize dynamic changes in situations to provide optimal times that can dynamically adjust to adapt to the FL environment. Then, the server identifies and selects a subset of clients who take less time than the time threshold to participate.
- Adaptive number of client selection: Our model dynamically adjusts the number of selected clients in each round based on the time threshold provided by the DRL agent, enabling efficient adaptation to resource and data variability.
- ATCS-FL design efficiency, low latency and alongside with long waiting time for aggregation: DRL-optimized time threshold and selection of a subset of clients enables effective time management to reflect the reward function effective that prioritized the subset of clients that take less time threshold in every communication round. Also reflecting from using the time threshold setting that of our maximum threshold equals the average time of random selection approach in the same environment setup result in reducing latency by avoiding long waiting times. The clients that finish training within the limited time threshold are chosen.
- Our proposed experiment typically reduces latency and improves accuracy under non-IID datasets. Specifically, ATCS-FL can reduce latency by approximately 75 percents in dynamic situations compared to the baseline algorithm and state-of-the-art solutions. With the increasing level of non-IID, our proposed approach can learn adaptively in the non-IID environment.
2. Related Works
In 2017, FL approach was introduced by Google research team to address privacy concerns and reduce the need for centralized data storage by enabling separate local training on distributed devices [1]. FL operates the training in only model parameters which are transmitted to a central server for global aggregation performance. In traditional FL, one key challenge is the long waiting for slow clients called straggler issue. When participants are randomly selected, both fast and slow devices may be randomly chosen simultaneously. Slow devices or clients can result from a poor network connection, limited computing power, or a combination of both [15], as well as from processing a larger volume of data updates. As a result, faster devices complete their local training quickly but must wait for slower devices, resulting in inefficiencies and prolonged aggregation times. Due to the diversity of training time, the system has difficulty controlling client selection. While clients spend varying amounts of time on training, the fastest client waits too long for the server to start aggregating, which can result in a system straggler or crash [16,17,18]. To address the traditional problems, numerous research studies have been proposed and detailed focusing on time-based and DRL-based solutions.
2.1. Time-Based Client Selection FL
To address the straggler issue, ref. [19] proposed a Multi-Armed Bandit-based client scheduling approach for FL. This method accounts for the presence of a large number of clients and the limited availability of wireless channels by intelligently scheduling which clients can access the channel for parameter updates in each communication round. The approach leverages statistical information gathered from client performance during previous rounds to improve decision-making in subsequent rounds. To reduce the waiting time caused by straggler clients, a maximum time threshold is introduced to cap their delays. In [13], the authors proposed the FedCS protocol, which selects clients based on their computational capabilities and wireless channel conditions. The aggregation deadline is determined using client-specific information, such as computation and communication resource constraints. Only clients expected to complete their local training and model upload before the deadline are selected. FedCS requires collecting resource information from a subset of randomly chosen clients to estimate overall training time, schedule updates, and manage model uploads effectively. To address the dynamic nature of mobile devices (MDs), the authors in [20] proposed ADD, a method in which the FL server utilizes device-specific information such as available computational resources and wireless channel conditions to learn the performance discrepancies among MDs. Based on this information, the server estimates the expected transmission time for model parameters, including download, training, and upload durations. Using these estimates, the server sets an appropriate deadline for accepting model updates from MDs, effectively minimizing long waiting times and improving training efficiency. To address the limitations of unstable convergence in FL, the authors in [21] proposed the AWTAFL algorithm, which leverages DRL. In this approach, the central server dynamically adjusts the aggregation waiting time to stabilize the training process. AWTAFL enhances traditional global aggregation by improving global accuracy, reducing convergence time, and lowering energy consumption, thereby ensuring a more efficient and reliable FL process.
Although time-based client selection helps mitigate long waiting times and straggler issues, a fixed time threshold may not be sufficient in dynamics FL environments. These environments are subject to frequent changes [22,23] including data size updates, fluctuations in computing resources, and variations in device capacities. Therefore, the time threshold should be adaptive and flexible, enabling the system to respond more effectively to dynamics environment and optimize the training process accordingly.
2.2. DRL-Based Client Selection
To address issues such as uneven data quality, heterogeneous equipment, and high communication costs, ref. [24] proposed a DRL-assisted FL method for selecting high-quality Industrial Internet of Things (IIoT) devices in each communication round. The approach focuses on managing large-scale heterogeneous data in IIoT environments. By leveraging the Deep Deterministic Policy Gradient (DDPG) algorithm, the FL system intelligently selects device nodes with higher data quality. In [25], the authors proposed FedPPO, the deep reinforcement learning-based approach that optimizes client selection in FL under heterogeneous data distributions. FedPPO aims to improve performance and ensure convergence within a limited training time. The method filters noisy clients to reduce the action space and applies model parameter compression followed by hierarchical clustering. Each client’s contribution is then evaluated based on both global and local model performance, and a contribution score is assigned. Clients with the highest scores are selected to participate in the training. To address challenges such as data imbalance, edge dynamics, and resource constraints, the authors in [26] proposed the AAFL mechanism. In this approach, the FL server adaptively selects a fraction of edge nodes to participate in each training epoch. The selection fraction is dynamically adjusted based on real-time system conditions, including network resource availability and data imbalance levels. The DRL technique is employed to enable the server to adapt effectively to the dynamic environment and varying resource limitations. To address the challenges of statistical heterogeneity where client data is non-IID and system heterogeneity caused by diverse hardware and network conditions, the authors in [12] proposed the FLASH-RL approach. In this method, the federated server optimizes client selection by choosing a subset of clients to participate in each communication round. The server defines a reputation-based utility function that evaluates each client’s model performance, taking into account computational resources and system-level heterogeneity. By learning from client experiences across communication rounds, the system prioritizes clients with higher utility scores to contribute to the training.
Most existing studies prioritize clients with strong computational and resource capabilities, which leads to fairness issues as some clients may never be selected throughout the training process [27,28]. Furthermore, the dynamic nature of data size updates across rounds that contribute to client heterogeneity is a factor often overlooked in prior works. These limitations motivate the design of a novel, efficient, and adaptable approach that can flexibly respond to changing environmental conditions, reduce long waiting times, and enhance overall performance. To address these challenges, our proposed method integrates DRL with time-based client selection, aiming to adapt to dynamic system states while promoting fair client participation.
3. System Model and Problem Formulation
3.1. Basic Setup of FL
In this section, Table 1 describes the denotation of correlation FL (server and client) in system models utilizing in this manuscript. Scenario involved two entities in FL: Central server and clients . Each client train a local dataset with number of sample size of represent as . T is the total number of training rounds. At round , system considers selecting clients to participate in the training in each round. The server sends the global model parameter to all participating clients. Participating clients train the local model of the deep neural network using their own data, update the local model, and then upload the local model parameters to the central server for global aggregation. The local loss function of client training local update is define as which is the loss function for computing data sample , the main objective in FL is to optimize minimize global loss function . The following optimization objective is , where is the aggregation weight of clients , . Stochastic optimization is used to solve this problem. In the current round t-th, participating clients separately calculate a local update by with learning rate and send to the central server. The central server receives local updates from all participated clients and perform global model parameter update as . The following process continues till FL training achieves convergence or finished total training round .

Table 1.
Notation of system models.
3.2. System Heterogeneous
Our study aims to minimize total time training by the total latency that involves computing time and transmission time that is spent on each communication round.
Latency is the objective function in the heterogeneous system, and we define the latency of each client at training round by sum of local computing time and transmission time :
- Local computing time: During the iteration of training gradient descent, the required time is estimated based on client-specific resources: CPU frequency , number of cores , CPU cycles process , and the size of local data in bits , and the calculated local computing is then given by
- Transmission time: During communication with the central server, each client takes time to transfer local model parameters to the server; the transmission time is calculated based on the bandwidth of clients at round t, and size of local model . The transmission time is defined as
3.3. Problem Formulation
Considering the limitations of previous studies, particularly the high training latency caused by device heterogeneity in terms of resource capacity, computational power, and dynamic data size updates. This study aims to identify the optimal subset of clients to participate in each communication round. The primary goal is to achieve the target model accuracy with minimal latency while ensuring stable model convergence. To accomplish this, we define as the total training time, which accounts for both computation time and transmission time overall the communication rounds.
From Equation (1), we calculate the total training time as
The first inequality expresses the time threshold that identifies the range value to find the suitable limit time for our environment. The second inequality expresses the number of clients selected to participate in the training, ranging from at least 1 to N clients, in every communication round. The last inequality expresses the convergence required for the global parameter where the difference between the global loss value and optimal loss value is close to 0.
4. Proposed ATCS-FL Approach
4.1. Adaptive Time Threshold Client Selection for Federated Learning
We propose an ATCS-FL mechanism that utilizes the DRL algorithm to optimize the time threshold in each communication round. This approach is designed to adapt to dynamic environments and system heterogeneity, including variations in hardware, resource capacity, asymmetric data contribution, and data size updates, which makes client participation difficult to manage.
ATCS-FL addresses these challenges by dynamically adjusting the time threshold based on system conditions, allowing the selection of clients that can complete training within the specified time. This adaptive time-based strategy minimizes latency and improves overall system efficiency. Importantly, all clients have a fair opportunity to participate as long as they can finish training within the threshold, enhancing fair selection. Furthermore, the number of selected clients is not fixed and adaptively changes in each round, ensuring flexibility in response to environmental changes. To better illustrate our proposed approach, Figure 1 compares existing approach (a) with ATCS-FL (b) under the same time period.
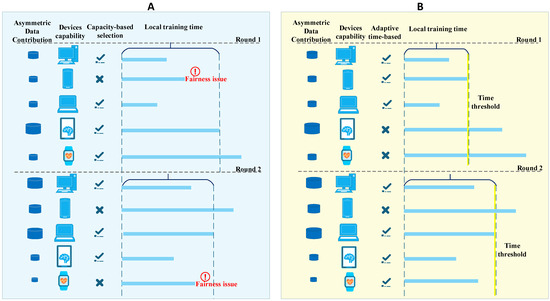
Figure 1.
Comparison between (A) reference scheme and (B) ATCS-FL.
With the existing approaches illustrated in Figure 1, client selection is primarily based on hardware and resource capacity, with a fixed number of participants chosen per round. However, in dynamic environments, this fixed selection strategy lacks flexibility, as the number of suitable clients should vary based on current system conditions. Moreover, the fairness issue becomes a concern, the selection process often favors high-capacity clients, yet large data updates can increase their training time, reducing efficiency. At the same time, lower-capacity clients with smaller data updates that can complete training more quickly are excluded from participation. This results in a fairness issue, as capable yet less powerful clients are overlooked despite being ready and able to contribute effectively to the training.
In Figure 1A, a fourth client with a strong computational capacity is selected to participate in the training. However, due to a large data update, this client requires a longer time to complete training. In contrast, the second client, which has lower computational capacity, is excluded despite having a smaller data update that would allow it to finish training within the required time. This highlights a missed opportunity for more efficient participation. Moreover, the fifth client, with a very limited capacity, is likely to be excluded entirely from the training process or may never contribute until convergence, raising concerns about fairness in client selection.
In Figure 1B, the proposed ATCS-FL approach selects clients based on an adaptive time threshold for participation in training. Clients that can complete their local training within the specified time limit are selected for aggregation. The time threshold is dynamically adjusted in each communication round by the DRL-based model, which learns and adapts to changing environmental conditions. As a result, the number of participating clients also varies adaptively in response to the current threshold. This strategy ensures fair client selection, as all clients, regardless of their capacity, have an opportunity to participate, provided they can complete training within the threshold, promoting both efficiency and fair selection in the system.
Our ATCS-FL leverages DRL by optimizing the time threshold by automatically learning from the environment. This enables the system to dynamically adjust the threshold based on current conditions, flexibly adapting to the environment’s capabilities. As a result, it avoids prolonged waiting times and efficiently reduces latency in each communication round, leading to improved system performance.
The ATCS-FL process will be described in detail in Algorithm 1. For the central server, in every communication round , the server prepares global parameter and time threshold (received from DRL training result) at the beginning of the training (Line 1). After preparing the initialization parameters, we calculate the expected training time of all clients based on the available information state of each client and then compare the expected training time with the limit time threshold received from DRL training; if the clients spent training time less than time threshold, we selected those clients to participate in the training (Line 3–6). After identifying the selected participant clients, the server sends global parameters to the selected participant clients and waits for them to perform local training and update their local model parameters. Then, the central server receives all the local parameters from the participating clients, and the server performs the global aggregate update (Line 7–10). Next, the server updates the global parameter for the next communication round and updates the time threshold parameter for the next round (Line 11–12).
| Algorithm 1 Adaptive time threshold client selection federated learning | |||
| Central server: | |||
| 1 | Initialization: Global parameter , Threshold time | ||
| 2 | Fordo | ||
| 3 | Compute expected training time | ||
| 4 | If clients have , considered as ; is the selected client current round | ||
| 5 | ; is subset of selected clients | ||
| 6 | End if | ||
| 7 | Sent global parameter to | ||
| 8 | Waiting for all client in update | ||
| 9 | Received all local parameter update | ||
| 10 | Perform global model aggregation | ||
| 11 | Update for next round | ||
| 12 | Update | ||
| End for | |||
| Client: | |||
| 1 | Initialization: | ||
| 2 | Receive global parameter from server | ||
| 3 | For | ||
| 4 | Perform local training | ||
| 5 | Update to server | ||
| 6 | End for | ||
For clients, after receiving the global parameter from the central server, participant clients download the global parameter and perform local training. After finishing the training, the clients update the local parameter to the central server to perform global aggregation (Line 1–6). The process will continue till it reaches rounds.
4.2. DRL-Based Adaptive Time Threshold
Our study employs a time-based client selection strategy in FL to achieve model convergence with reduced training time. Specifically, we utilize DDQN to optimize an adaptive time threshold in each communication round. This DRL-based model is integrated with the FL central server, enabling dynamic and efficient client selection based on the current state of the system.
We illustrate the DRL system architecture, which connects to the central server, in Figure 2.
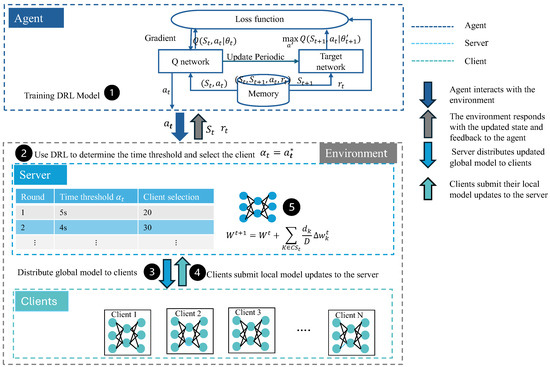
Figure 2.
The architecture of the DRL system in ATCS-FL.
- (1)
- DDQN training: This stage is responsible for determining the optimal time threshold. The agent interacts with the environment by observing the current state input and receiving a reward as feedback to evaluate the quality of its actions. The Q-network, deep neural network (DNN), takes the state as input and estimates Q-values to determine the optimal actions. A separate target network periodically updated with the parameters of the Q-network to provide more stable target Q-values to guide learning and improve convergence. By learning to maximize expected cumulative rewards, the agent ultimately selects the optimal action (i.e., the best time threshold) that can improve training performance in dynamic environments.
- (2)
- Client selection: After receiving the optimal time threshold from the DDQN agent, the server estimates the training time for each client. Clients that expect to finish the training time within the threshold are selected to participate in the training round.
- (3)
- Distribute global model: After identifying the selected clients, the server processes the global model parameter and sends it to the selected clients for computing the local model.
- (4)
- Local training: After receiving the global model parameter, participants start local training and update their local model to the server.
- (5)
- Global aggregation: After receiving local model parameter updates from all selected clients, the server processes global aggregation updates for the subsequent communication round.
In more detail on the agent and environment of DRL, we will explain what we consider in our environment study, state information, action, and reward design for our architecture system. The agent primarily consists of three components: state, action, and deep Q-network. In each training round, the deep Q-network in the agent receives a state (e.g., hardware capacity, resource information) and outputs the q-value of action, which maps from state to action . Then, an action picked from according to policy . In return, the agent receives the next state and a scalar reward . The total accumulated return reward for every round is with a discount factor . The goal of the agent is to maximize the expected reward for every state . We describe the state, action, and reward in our system in detail in the following:
- State: We use vector to denote the state of round . Here is training round index. is the local parameter of client at round , and denotes the data amount of client at round . denote as number of cores, CPU cycles process , CPU frequency of client at round , is bandwidth of client at round .
- Action: At each round , a threshold time , which is used as a limit threshold time for aggregation, will be determined by the agent, called an action . Given the current state, the DDQN agent chooses an action based on its policy, which is expressed as a probability distribution over the entire action space. We use neural networks to represent the policy , where mapping from state to action. -greedy is the probability of taking the action at the state .
- Reward: When an action is applied at round , the agent will receive a reward as a combination of threshold time and difference loss value. , . Our reward function combines negative time threshold emphasizes to the subset of clients that spend less training time every communication round and negative of loss value to ensure the performance improving resulted in less total training time and accuracy improvement.
The DDQN model is described in Algorithm 2.
Following Algorithm 2, we input the main network, target network, and discount factor and the resulting output is the time threshold that will be used in Algorithm 1. We initialize experience replay , mini-batch , main network model , parameter , target network model , parameter at the beginning of DDQN training. While receiving the current state from the environment, the system randomly selects based on a policy with probability and selects the optimal action according to the model. After selected an action, agent performs the action by sending to environment to achieve and reward . The reward will be used for evaluating the action by considering it good if it provides a high reward score (Line 4–6). In every round, experience will be deposited into replay buffer (Line 7). While exceeds the fixed maximum number of iterations or is full, experience is sampled from and used for calculating the target Q-value to update the target network, following in case is not the final state and then perform gradient descent on the loss function by calculate MSE (mean squared error) and update the main network parameter (Line 8–11). Next, update the target network parameter in every fix round (Line 12). The training will continue till convergence. The resulting output will be updated to line 12 of Algorithm 1.
To summarize our proposed approach, we combine Algorithms 1 and 2 as procedure call in Figure 3.
| Algorithm 2 DRL-based adaptive time threshold | |||
| Input: Main network, Target network, Discount factor | |||
| Output: Time threshold | |||
| 1 | Initialization: Experience replay , Mini-batch , Main network model , parameter , Target network model , parameter ψ | ||
| 2 | Set the probability value in the -greedy policy and updating rate | ||
| 3 | For do | ||
| 4 | Obtain current state , action space based on environment | ||
| 5 | Random select action with probability , or select the current optimal action according to the model | ||
| 6 | Perform action to obtain and reward | ||
| 7 | Deposit experience into | ||
| 8 | While exceeds the maximum number of iteration or is full do | ||
| 9 | Sampling experience from | ||
| 10 | Calculate the target -value | ||
| 11 | Perform gradient descent on the loss function and update the main network parameter | ||
| 12 | Update the target network parameter every round | ||
| 13 | End while | ||
| 14 | End for | ||
| 15 | Output the time threshold update to line 12 of Algorithm 1 in every round | ||
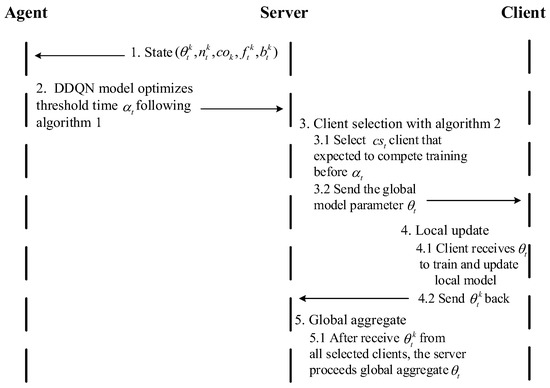
Figure 3.
The procedure call of ATCS-FL will describe the connected Algorithms 1 and 2.
First, the central server has all the information of the client called state , which will be provided to an agent as an input of DDQN model training. The DDQN model processes this state and returns an optimal time threshold , which the server uses to set the time limit for client selection in the current round. Next, the server estimates the expected training time of each client based on the state and selects clients whose training time is less than or equal to the threshold. The selected clients receive the global model parameters, perform local training, and send their updated models back to the server.
Once all updates are received, the server performs global aggregation to update the global model. This process repeats in each communication round until the model converges or the total number of rounds is reached.
5. Simulation Evaluation
5.1. Evaluation Setting
To evaluate our model, we train it on two open-source datasets, MNIST [29] and CIFAR-10 [30], which are constructed for image classification tasks. MNIST consists of 28 × 28 grayscale images with handwritten digits, comprising 70,000 images across 10 categories, with 7000 images per category. The dataset is split into training and testing sets, with 60,000 images allocated for training and 10,000 images reserved for testing. CIFAR-10 is a public dataset that contains 10 classes of images with 6000 images per class. 50,000 images were split for training, and 10,000 images were prepared for testing. We train local model image classification with convolutional neural network (CNN) [31] using two layers with kernel 5 × 5 followed by ReLU activation and 2 × 2 max pooling under non-IID imbalance label with Dirichlet distribution [32,33] with , , Label imbalance (MNIST), and Shard (CIFAR-10).
We use Python (version 3.11) in our simulation and employ all models with the Python library and PyTorch framework (version 2.5.0) [34] for deep learning and FL. We create a federated environment using FedLab [35] to build a federated simulation framework, which involves setting up the central server and clients. In an FL environment, to effectively simulate the training process in FL, a total of 100 clients is generated in the simulation, and the participating clients are selected based on the time threshold to distribute across the model training. The local training client will use 1 epoch to train the local model CNN with two 5 × 5 convolution layers with the batch size of 32 and a learning rate of 0.01 during local training. In the heterogeneous system, ref. [12], they utilize edged equipment and transfer protocols including Intel Core processors, TPUs, Raspberry Pi, Jetson Nano, Jetson TX2, Jetson Xavier NX, and FPGA Xilinx ZCU102 to conduct state for environment simulation. For DRL parameters, we use discount factor , , update rate , and learning rate 0.01 to train our model.
5.2. Simulation Result
To evaluate our model’s performance, we are comparing our proposed model system, ATCS-FL, with baselines including FedProx and FLASH-RL. FedProx is a random client selection approach and FLASH-RL is high-capacity and passed high-performance device selection approach. This comparison demonstrates our model’s performance, achieving good accuracy and latency reduction in the non-IID FL environment.
- Latency
ATCS-FL outperforms FLASH-RL and FedProx in reducing latency across all three non-IID settings using the MNIST dataset under (a) hetero Dirichlet 0.6, (b) hetero Dirichlet 0.3, and (c) non-IID label, as shown in Figure 4. The DDQN model optimizes the time threshold by priority short threshold and improv performance every communication round that effect by reword designed. Specifically, it achieves around 80% latency reduction under the non-IID label distribution, demonstrating its effectiveness in handling data heterogeneity.

Figure 4.
Latency of MNIST dataset under (A) hetero Dirichlet 0.6, (B) hetero Dirichlet 0.3, and (C) non-IID label.
As shown in Figure 5, ATCS-FL significantly reduces latency on the CIFAR-10 dataset across the (a) hetero Dirichlet 0.6, (b) hetero Dirichlet 0.3 and (c) Shard. Resulting by reward function that optimize the flexible time threshold by identified the short time and power each round. It achieves around 77% latency reduction under the non-IID setting compared to FLASH-RL and FedProx. These results confirm the robustness and efficiency of ATCS-FL in handling heterogeneous data distributions.
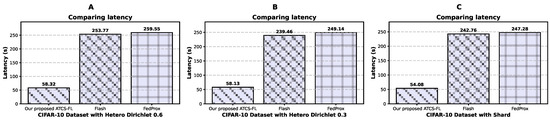
Figure 5.
Latency of CIFAR-10 dataset under (A) hetero Dirichlet 0.6, (B) hetero Dirichlet 0.3 and (C) Shard.
- Accuracy
As Figure 6, our proposed ATCS-FL outperforms state-of-the-art methods, including FLASH-RL and FedProx, in both accuracy and stability on the MNIST dataset across (a) hetero Dirichlet 0.6, (b) hetero Dirichlet 0.3 and (c) non-IID label. The effective from the reward function that selected the subset of client to enhance performance improving each communication round and alongside with latency reduction. The power of correct selection of clients each round results in increased accuracy from the beginning to con-vergence as a highlight of highest performance that indicates fast speed of convergence of our model. Under the non-IID setting, the orange line (ATCS-FL) consistently stays above the blue (FLASH-RL) and green (FedProx) lines, indicating superior accuracy. As the non-IID level increases, ATCS-FL maintains the highest accuracy, while FLASH-RL and FedProx show increased fluctuations. In contrast, ATCS-FL exhibits a smoother trend, demonstrating its enhanced stability and adaptability in highly heterogeneous FL environments.
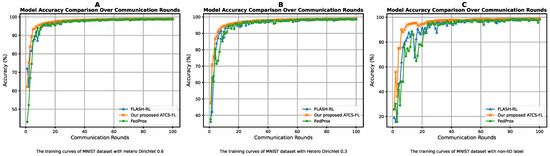
Figure 6.
Accuracy of MNIST dataset under (A) hetero Dirichlet 0.6, (B) hetero Dirichlet 0.3 and (C) non-IID label.
As illustrated Figure 7, the CIFAR-10 dataset being color-based and more complex than the grayscale MNIST generally leads to lower accuracy under non-IID settings. Despite this, our proposed ATCS-FL consistently achieves higher accuracy and greater stability than FLASH-RL and FedProx across (a) hetero Dirichlet 0.6, (b) hetero Dirichlet 0.3, and (c) Shard. Result from correct selection clients of reward function to identify the best subset to participate in the training in each round. The robustness of the DDQN model becomes flexible with a dynamic environment by choosing a subset of clients that can improve performance. Under non-IID distributions, the orange line (ATCS-FL) fast increases accuracy and stays above the green (FedProx) and blue (FLASH-RL) lines from the beginning till the end of training to enhance fast convergence rate of our model, with no-ticeably fewer fluctuations. In contrast, FLASH-RL and FedProx show steeper accuracy drops and increased instability. These results confirm the robustness and adaptability of ATCS-FL in handling complex and highly heterogeneous FL environments.
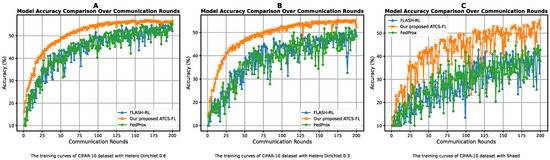
Figure 7.
Accuracy of CIFAR-10 dataset under (A) hetero Dirichlet 0.6, (B) hetero Dirichlet 0.3, and (C) Shard.
- Non-IID level
Figure 8 presents a comparative analysis of how different models adapt to increasing levels of non-IID environments. This includes our proposed ATCS-FL (a) alongside state-of-the-art methods FLASH-RL (b) and FedProx (c), using the MNIST dataset. ATCS-FL demonstrates strong adaptability, maintaining stable performance as the non-IID level increases from hetero Dirichlet 0.6 (blue line) to 0.3 (orange line) and then to the non-IID label setting (green line). The close alignment of ATCS-FL’s lines indicates minimal impact from rising data heterogeneity. In contrast, FLASH-RL and FedProx show notable accuracy drops and increased fluctuations, highlighting their reduced robustness under more skewed data distributions.
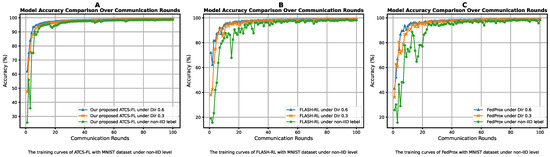
Figure 8.
The accuracy of the MNIST datasets of (A) ATCS-FL, (B) FLASH-FL, and (C) FedProx compares the difference at three levels of non-IID.
As shown in Figure 9, our proposed ATCS-FL (a) outperforms FLASH-RL (b) and FedProx (c) on the more complex CIFAR-10 dataset, even under varying non-IID data distributions. ATCS-FL exhibits only a slight decline in accuracy and moderate fluctuations as the data heterogeneity increases from hetero Dirichlet 0.6 (blue line) to 0.3 (orange line) and then to the non-IID label distribution (green line). In contrast, FLASH-RL and FedProx experience significant drops in accuracy and increased instability, highlighting ATCS-FL’s superior robustness and adaptability in highly non-IID FL environments.
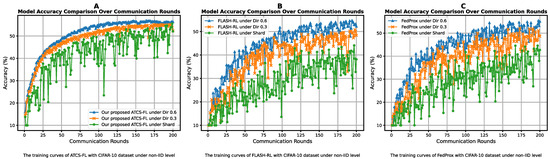
Figure 9.
The accuracy of the CIFAR-10 dataset of (A) ATCS-FL, (B) FLASH-FL, and (C) FedProx compares the difference at three levels of non-IID.
Our ATCS-FL demonstrates performance improvement and latency reduction of 77% and 75%, respectively, compared to FedProx and FLASHRL under the non-IID setting of MNIST and CIFAR-10 dataset. ATCS-FL highlight robustness and adaptability of non-IID FL environments and efficiency latency.
6. Conclusions and Future Work
Based on the heterogeneity capacity of the device, heterogeneity hardware, and the dynamic amount of data updates, we proposed an adaptive time threshold client selection according to the DRL model to optimize the limit time threshold for each communication round and consider the selected subset of participants’ clients to be distributed in the training. We calculated the expected training time for each client based on the state information and compared it with the time threshold. The client that spent less time than the threshold was selected to participate in the training. Every round, the time limit threshold adaptively changed according to the dynamic changes in the environment, and the number of clients selected to participate in each communication round also adaptively changed based on the change in the time limit threshold. Our study solved the fairness issue of selection and avoid long waiting time for aggregation, as all clients have an equal chance to participate in the training if they can meet the training requirements before the time limit. We trained the local CNN model for image classification using the MNIST and CIFAR-10 datasets under three levels of non-IID environment settings. DDQN model manages the time threshold and selection client by optimizing the suitable time threshold every round then identified the subset of selected clients to enhance the effective aggregation. After gathering state information, the main network generates possible time threshold action and target network evaluate the time threshold selected then optimize suitable action selection. Our reward function and threshold setting ensure the latency effectiveness in our simulation environment. Our model achieved an outperforming accuracy and reduced latency by approximately 80% compared to the baseline approach, FedProx, and the state-of-the-art solution, the FLASH-RL method.
Future work: In our study, all clients had the opportunity to participate in the training if they could reach the local training before the time limit. Under the asymmetric updating, some clients participated in the training with low quality updates, which could make them noisy clients. Additionally, when noisy clients are involved in the training, it wastes resources. Following this study, we should further consider excluding noisy clients and selecting only clients who possess quality updates to enhance symmetric training performance and latency reduction.
Author Contributions
Conceptualization, S.S. and S.K. (Seokhoon Kim); methodology, T.I., S.R. (Seyha Ros) and S.S.; software, S.S. and S.R. (Sovanndoeur Riel); validation, S.K. (Seungwoo Kang) and I.S.; formal analysis, R.M. and T.I.; investigation, S.K. (Seokhoon Kim); resources, S.K. (Seokhoon Kim); data curation, S.S.; writing—original draft preparation, S.S. and T.I.; writing—review and editing, S.S. and S.R. (Seyha Ros); visualization, T.I. and R.M.; supervision, S.K. (Seokhoon Kim); project administration, S.K. (Seokhoon Kim); funding acquisition, S.K. (Seokhoon Kim). All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Institute of Information & Communications Technology Planning and Evaluation (IITP) grant funded by the Korean government (MSIT) (No. RS-2022-00167197), in part by BK21 FOUR (Fostering Outstanding Universities for Research) under Grant 5199990914048; and in part by the Soonchunhyang University Research Fund.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated learning: Challenges, methods, and future directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Wang, D.; Shi, S.; Zhu, Y.; Han, Z. Federated analytics: Opportunities and challenges. IEEE Netw. 2021, 36, 151–158. [Google Scholar] [CrossRef]
- Berkani, M.R.; Chouchane, A.; Himeur, Y.; Ouamane, A.; Miniaoui, S.; Atalla, S.; Mansoor, W.; Al-Ahmad, H. Advances in federated learning: Applications and challenges in smart building environments and beyond. Computers 2025, 14, 124. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, Y.; Shi, S.; He, X.; Han, B.; Chu, X. Virtual homogeneity learning: Defending against data heterogeneity in federated learning. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, ML, USA, 17–23 July 2022; pp. 21111–21132. [Google Scholar]
- Deng, Y.; Lyu, F.; Ren, J.; Wu, H.; Zhou, Y.; Zhang, Y.; Shen, X. AUCTION: Automated and quality-aware client selection framework for efficient federated learning. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 1996–2009. [Google Scholar] [CrossRef]
- Lim, W.Y.; Luong, N.C.; Hoang, D.T.; Jiao, Y.; Liang, Y.C.; Yang, Q.; Niyato, D.; Miao, C. Federated learning in mobile edge networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2020, 22, 2031–2063. [Google Scholar] [CrossRef]
- Ye, M.; Fang, X.; Du, B.; Yuen, P.C.; Tao, D. Heterogeneous federated learning: State-of-the-art and research challenges. ACM Comput. Surv. 2023, 56, 1–44. [Google Scholar] [CrossRef]
- Li, J.; Chen, T.; Teng, S. A comprehensive survey on client selection strategies in federated learning. Comput. Netw. 2024, 251, 110663. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, H.; Gao, G.; Zhang, M.; Liu, X. Client selection in federated learning: Principles, challenges, and opportunities. IEEE Internet Things J. 2023, 10, 21811–21819. [Google Scholar] [CrossRef]
- Mayhoub, S.; Shami, T.M. A review of client selection methods in federated learning. Arch. Comput. Methods Eng. 2024, 31, 1129–1152. [Google Scholar] [CrossRef]
- Bouaziz, S.; Benmeziane, H.; Imine, Y.; Hamdad, L.; Niar, S.; Ouarnoughi, H. Flash-rl: Federated learning addressing system and static heterogeneity using reinforcement learning. In Proceedings of the 2023 IEEE 41st International Conference on Computer Design (ICCD), Washington, DC, USA, 6–8 November 2023; pp. 444–447. [Google Scholar]
- Nishio, T.; Yonetani, R. Client selection for federated learning with heterogeneous resources in mobile edge. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20 May 2019; pp. 1–7. [Google Scholar]
- Liu, X.; Chen, T.; Qian, F.; Guo, Z.; Lin, F.X.; Wang, X.; Chen, K. Characterizing smartwatch usage in the wild. In Proceedings of the 15th Annual International Conference on Mobile Systems, Applications, and Services, Niagara Falls, NY, USA, 16 June 2017; pp. 385–398. [Google Scholar]
- Zhang, T.; Gao, L.; He, C.; Zhang, M.; Krishnamachari, B.; Avestimehr, A.S. Federated learning for the internet of things: Applications, challenges, and opportunities. IEEE Internet Things Mag. 2022, 5, 24–29. [Google Scholar] [CrossRef]
- Saputra, Y.M.; Nguyen, D.N.; Hoang, D.T.; Pham, Q.V.; Dutkiewicz, E.; Hwang, W.J. Federated learning framework with straggling mitigation and privacy-awareness for AI-based mobile application services. IEEE Trans. Mob. Comput. 2022, 22, 5296–5312. [Google Scholar] [CrossRef]
- Hard, A.; Girgis, A.M.; Amid, E.; Augenstein, S.; McConnaughey, L.; Mathews, R.; Anil, R. Learning from straggler clients in federated learning. arXiv 2024, arXiv:2403.09086. [Google Scholar] [CrossRef]
- Lang, N.; Cohen, A.; Shlezinger, N. Stragglers-aware low-latency synchronous federated learning via layer-wise model updates. IEEE Trans. Commun. 2024, 73, 3333–3346. [Google Scholar] [CrossRef]
- Xia, W.; Quek, T.Q.; Guo, K.; Wen, W.; Yang, H.H.; Zhu, H. Multi-armed bandit-based client scheduling for federated learning. IEEE Trans. Wirel. Commun. 2020, 19, 7108–7123. [Google Scholar] [CrossRef]
- Lee, J.; Ko, H.; Pack, S. Adaptive deadline determination for mobile device selection in federated learning. IEEE Trans. Veh. Technol. 2021, 71, 3367–3371. [Google Scholar] [CrossRef]
- Liu, W.; Cui, T.; Shen, B.; Huang, X.; Chen, Q. Adaptive waiting time asynchronous federated learning in edge computing. In Proceedings of the 2023 International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 2–4 November 2023; pp. 540–545. [Google Scholar]
- Zhai, S.; Jin, X.; Wei, L.; Luo, H.; Cao, M. Dynamic federated learning for GMEC with time-varying wireless link. IEEE Access 2021, 9, 10400–10412. [Google Scholar] [CrossRef]
- Chen, B.; Ivanov, N.; Wang, G.; Yan, Q. DynamicFL: Balancing communication dynamics and client manipulation for federated learning. In Proceedings of the 2023 20th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Madrid, Spain, 11–14 September 2023; pp. 312–320. [Google Scholar]
- Zhang, P.; Wang, C.; Jiang, C.; Han, Z. Deep reinforcement learning assisted federated learning algorithm for data management of IIoT. IEEE Trans. Ind. Inform. 2021, 17, 8475–8484. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, A.; Li, R.; Yang, L.; Xu, X. FedPPO: Reinforcement learning-based client selection for federated learning with heterogeneous data. IEEE Trans. Cogn. Commun. Netw. 2025, 1. [Google Scholar] [CrossRef]
- Liu, J.; Xu, H.; Wang, L.; Xu, Y.; Qian, C.; Huang, J.; Huang, H. Adaptive asynchronous federated learning in resource-constrained edge computing. IEEE Trans. Mob. Comput. 2021, 22, 674–690. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, Z.; Shi, Z.; Yu, H. Fairness-aware client selection for federated learning. In Proceedings of the 2023 IEEE International Conference on Multimedia and Expo (ICME), Brisbane, Australia, 10–14 July 2023; pp. 324–329. [Google Scholar]
- Zhang, M.; Zhao, H.; Ebron, S.; Xie, R.; Yang, K. Ensuring fairness in federated learning services: Innovative Approaches to Client Selection, Scheduling, and Rewards. In Proceedings of the 2024 IEEE 44th International Conference on Distributed Computing Systems (ICDCS), Jersey City, NJ, USA, 23–26 July 2024; pp. 762–773. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 2002, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated learning with non-iid data. arXiv 2018, arXiv:1806.00582. [Google Scholar] [CrossRef]
- O’shea, K.; Nash, R. An introduction to convolutional neural networks. arXiv 2015, arXiv:1511.08458. [Google Scholar] [CrossRef]
- Yurochkin, M.; Agarwal, M.; Ghosh, S.; Greenewald, K.; Hoang, N.; Khazaeni, Y. Bayesian nonparametric federated learning of neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 7252–7261. [Google Scholar]
- Wang, H.; Yurochkin, M.; Sun, Y.; Papailiopoulos, D.; Khazaeni, Y. Federated learning with matched averaging. arXiv 2020, arXiv:2002.06440. [Google Scholar] [CrossRef]
- Steiner, B.; DeVito, Z.; Chintala, S.; Gross, S.; Paske, A.; Massa, F.; Lerer, A.; Chanan, G.; Lin, Z.; Yang, E.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Zeng, D.; Liang, S.; Hu, X.; Wang, H.; Xu, Z. Fedlab: A flexible federated learning framework. J. Mach. Learn. Res. 2023, 24, 1–7. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).