Oscillator Algebra in Complex Position-Dependent Mass Systems

Abstract

This work introduces non-Hermitian position-dependent mass Hamiltonians characterized by complex ladder operators and real, equidistant spectra. By imposing the Heisenberg–Weyl algebraic structure as a constraint, we derive the corresponding potentials, ladder operators, and eigenfunctions. The method provides a systematic procedure for constructing exactly solvable models for arbitrary mass profiles. Specific cases are illustrated for quadratic, cosinusoidal, and exponential mass functions.

1. Introduction

The study of position-dependent mass (PDM) systems has been extensive since 1966, when BenDaniel–Duke (BDD), investigating charge carrier behavior in semiconductor heterostructures, proposed a Hermitian Hamiltonian that incorporates the spatial variation of the electron’s effective mass across material interfaces [1]. This variation is particularly relevant in systems such as the compositionally graded alloy ${\mathrm{Al}}_x{\mathrm{Ga}}_{1-x}\mathrm{As}$ or in abrupt heterojunctions like $\mathrm{InAs}/\mathrm{GaSb}$ [2,3,4]. These PDM models find applicability in the design of quantum dots, quantum wells, superlattices, and more general heterostructures [4,5,6,7,8,9]. In such systems, the effective mass profile $m\left(x\right)$ often reflects the underlying material composition and can, in principle, be engineered through epitaxial growth techniques and related methods [10]. Interestingly, PDM systems also connect with the Liénard-II class of nonlinear equations, some of which admit isochronous oscillations and equidistant spectra [11], highlighting the possibility of engineering non-linear systems with predictable energy spacings. Achieving arbitrary spatial profiles remains experimentally challenging. This limitation motivates an alternative theoretical question: given a fixed mass profile, regardless of its intricacy, what forms of the potential $V\left(x\right)$ allow the system to exhibit a desired energy spectrum? Addressing this inverse problem opens the door to spectral engineering within constrained material platforms. Traditional approaches fix the mass and potential profiles; for example, ref. [12] explores a particular exponential mass with three different potentials. Other works use supersymmetric quantum mechanics to factorize the Hamiltonian via intertwining operators and corresponding superpartners [13,14,15,16,17]. Alternative treatments rely on point canonical transformations that map the PDM to a position-independent mass (PIM) Schrödinger equation; once in the regime of PIM, standard exactly solvable techniques can be applied [18,19].

The determination of the spectral profile of PDM systems is a challenging problem in its own right. To date, non-Hermitian, position-dependent, and exactly solvable systems remain largely unexplored, with notable exceptions such as Mostafazadeh, who introduced $\eta$-pseudo-Hermiticity generators for such Hamiltonians [20,21,22].

While the present work focuses on constructing complex ladder operators compatible with such configurations, future extensions could incorporate tools such as supersymmetric quantum mechanics to systematically manipulate the spectrum.

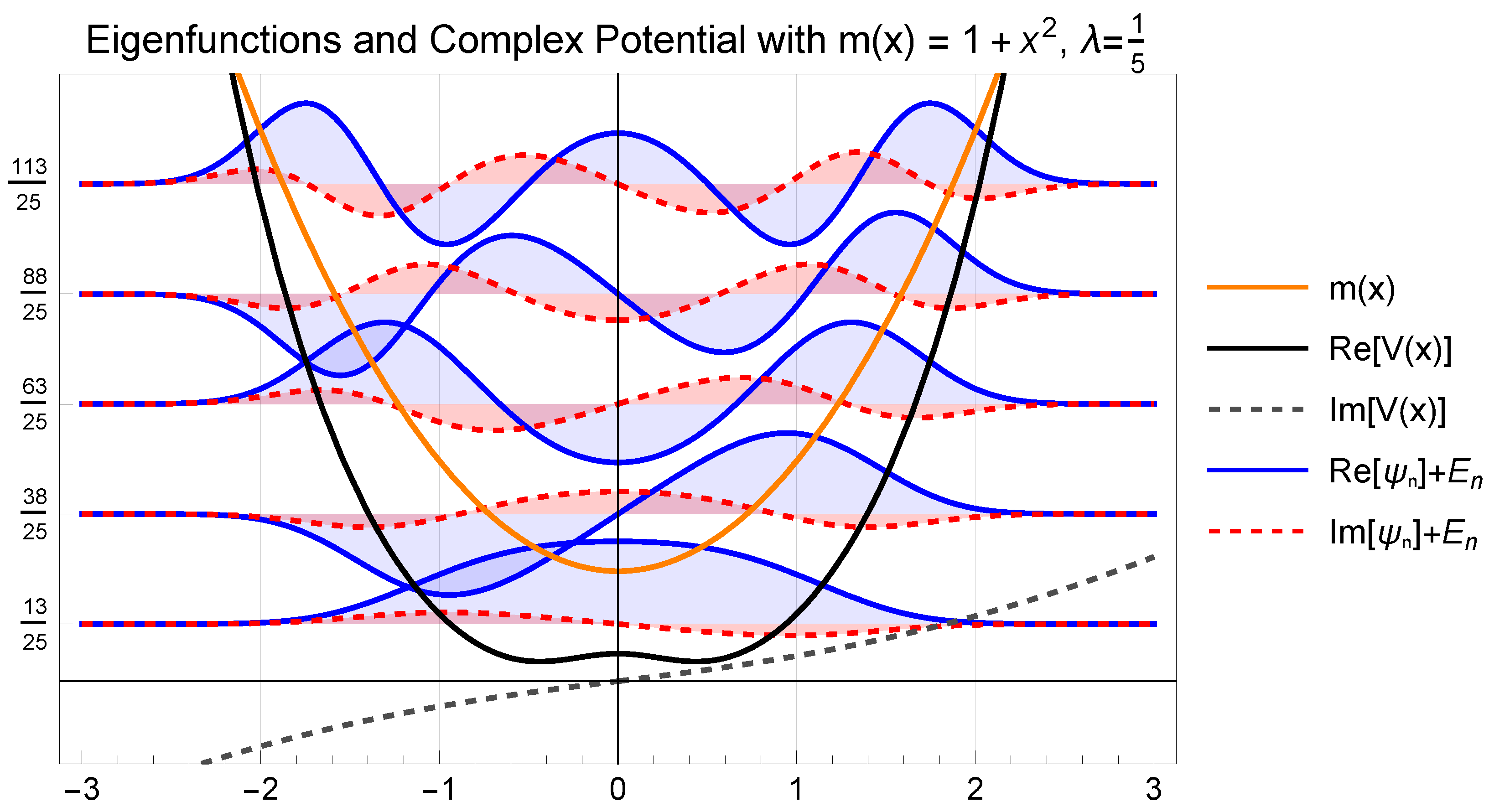
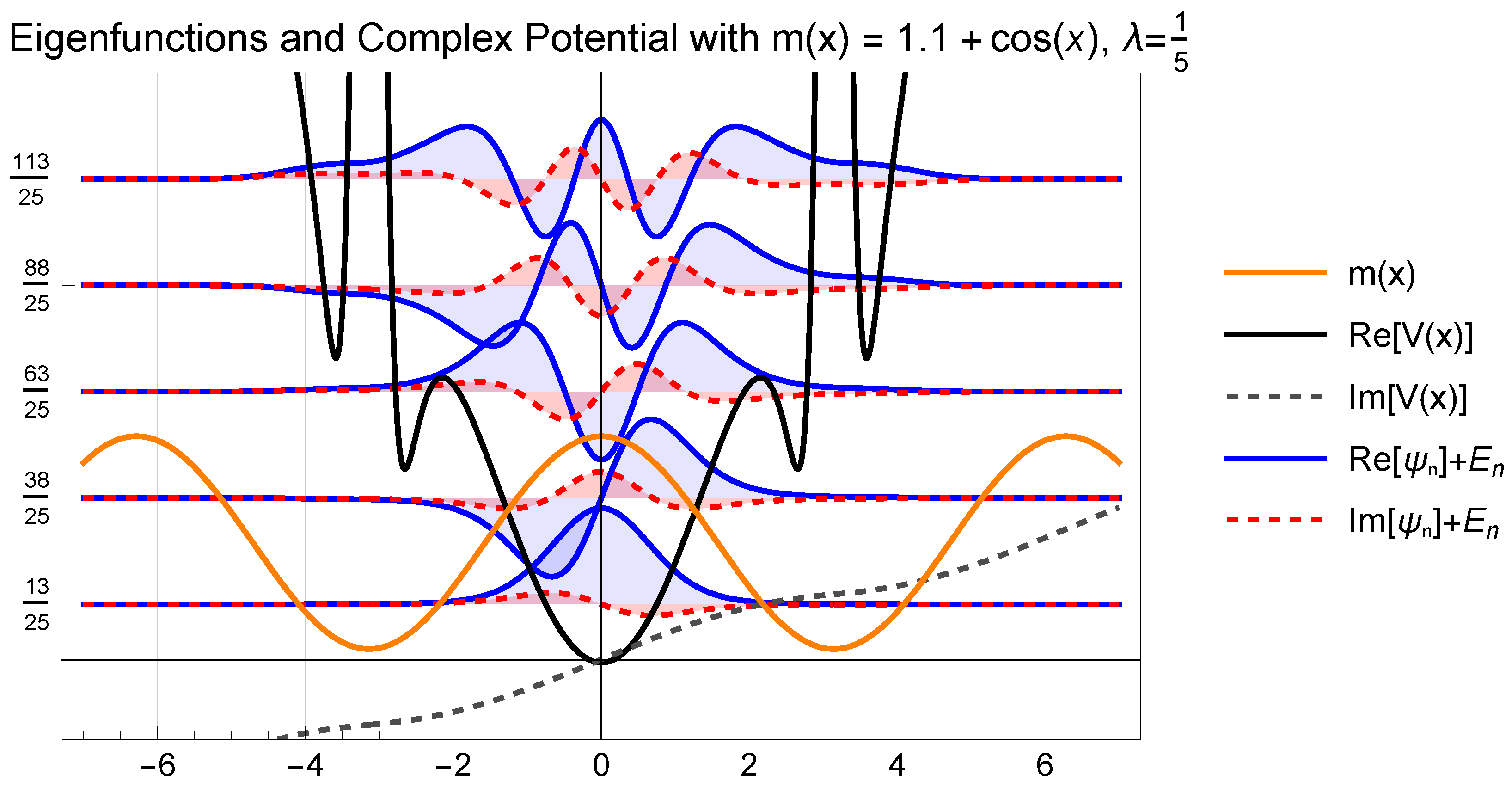
This paper is organized as follows: Section 2 and Section 3 provide a brief review of PDM Hamiltonians and the Heisenberg–Weyl algebra, respectively. In Section 4, we construct a complex first-order ladder operator and the associated non-Hermitian Hamiltonian, present the factorization of H and $H^{†}$, describe their commutation relations, and analyze the biorthogonality of the systems. Section 5 presents illustrative applications involving three distinct mass profiles. In Section 6, we numerically evaluate the expectation values of $\widehat{x}, \widehat{p}, \mathrm{and} \widehat{T}$ for the ground and first excited states, as well as the probability current of the ground state. In Section 7, we contrast the PT-symmetric, pseudo-Hermitian, and anti-pseudo-Hermitian cases with our construction. Finally, Section 8 offers concluding remarks.

2. Position-Dependent Mass Systems

One of the most general and Hermitian approaches to quantum PDM systems is the one proposed by von Ross in 1983 [1]:

$$H_{VR}={\displaystyle \frac{1}{4}}\left(m^{\alpha }\widehat{p}{m}^{\beta }\widehat{p}{m}^{\gamma }+m^{\gamma }\widehat{p}{m}^{\beta }\widehat{p}{m}^{\alpha }\right)+V,$$

(1)

where the mass, $m\left(x\right)$, varies with position. The parameters $\alpha$, $\beta$, and $\gamma$ are real constants that satisfy $\alpha +\beta +\gamma =-1$. Hermiticity is maintained as long as $V\left(x\right)$ is real.

BenDaniel–Duke Hamiltonians

It is possible to manipulate the expression in Equation (1) so that an effective potential emerges. The resulting expression is as follows:

$$H_{VR}=-{\displaystyle \frac{{\hslash }^2}{2m\left(x\right)}}{\displaystyle \frac{d^2}{d{x}^2}}+{\displaystyle \frac{{\hslash }^2{m}^{\prime }\left(x\right)}{2m^2\left(x\right)}}{\displaystyle \frac{d}{dx}}+V_{\mathrm{eff}}\left(x\right),$$

(2)

where

$$V_{\mathrm{eff}}\left(x\right)=V\left(x\right)+{\hslash }^2\left({\displaystyle \frac{(1+\beta )m^{″}\left(x\right)}{4m^2\left(x\right)}}-{\displaystyle \frac{{\left[m^{\prime }\left(x\right)\right]}^2}{2m^3\left(x\right)}}({\alpha }^2+\alpha \beta +\alpha +\beta +1)\right).$$

(3)

Notice that Equation (2) is the one proposed by BenDaniel–Duke in 1966 [1].

Given the equivalence between the von Ross Hamiltonian and the BDD Hamiltonian, from now on, this work will focus on the BDD Hamiltonian form, keeping in mind that the connection between the BDD and von Ross Hamiltonians, as well as any other Hamiltonian derived from it, is straightforward. Importantly, unlike other treatments that explicitly address the operator ordering ambiguity (see, e.g., [23]), this work avoids the issue altogether by employing an effective potential that already accounts for all ordering-related contributions. This allows us to proceed without fixing specific values of the ordering parameters, maintaining flexibility in the mass profile without complicating the formulation.

3. The Heisenberg–Weyl Algebra

The harmonic oscillator satisfies the well-known Heisenberg–Weyl algebra, where a Hamiltonian, H, and two ladder operators, $a^{\pm }$, satisfy the following algebraic relationships:

$$[H,a^{\pm }]=\pm a^{\pm },[a^{+},a^{-}]=1.$$

(4)

When working with the prototypical example of the harmonic oscillator, this algebraic relationship allows for the determination of the ground state, which is annihilated by $a^{-}$ and satisfies

$$a^{-}|\psi \rangle =0.$$

(5)

Using the previously mentioned commutation relation, all excited states can be generated through the iterative operation of $a^{+}$.

4. Complex First-Order Ladder Operators on the BDD Hamiltonian

The search for a general PDM system, specifically a BDD Hamiltonian possessing first-order ladder operators, was already initiated in [17]. However, that work was restricted to Hermitian Hamiltonians and real ladder operators. In this paper, we aim to generalize this study to include non-Hermitian Hamiltonians and complex ladder operators, satisfying a Heisenberg–Weyl algebra. To this end, we begin with the aforementioned Hamiltonian:

$$H=-{\displaystyle \frac{{\hslash }^2}{2m\left(x\right)}}{\displaystyle \frac{d^2}{d{x}^2}}+{\displaystyle \frac{{\hslash }^2{m}^{\prime }\left(x\right)}{2m^2\left(x\right)}}{\displaystyle \frac{d}{dx}}+V\left(x\right).$$

(6)

Here, $V\left(x\right)$ is allowed to be a complex potential. We also need to construct a first-order differential operator,

$$A^{-}={\displaystyle \frac{1}{\sqrt{2}}}\left(\alpha \left(x\right){\displaystyle \frac{d}{dx}}+{\beta }_R\left(x\right)+i{\beta }_I\left(x\right)\right),$$

(7)

following the same idea presented in [17], but allowing for a complex $\beta \left(x\right)$ function such that $\beta \left(x\right)={\beta }_R\left(x\right)+i{\beta }_I\left(x\right)$. This operator is meant to act as a complex ladder operator, specifically an annihilator operator $A^{-}$. For this to hold, a commutation relation, similar to the one presented in Equation (4), must be satisfied:

$$[H,A^{-}]=-\Delta E{A}^{-},\Delta E\in \mathbb{R}.$$

(8)

After imposing this commutativity condition, the following equations arise:

$${\alpha }^{\prime }\left(x\right)+{\displaystyle \frac{m^{\prime }\left(x\right)}{2m\left(x\right)}}\alpha \left(x\right)=0,$$

(9)

$${\beta }_R^{\prime }\left(x\right)={\displaystyle \frac{\alpha \left(x\right){\left[m^{\prime }\left(x\right)\right]}^2}{m^2\left(x\right)}}+{\displaystyle \frac{m^{\prime }\left(x\right){\alpha }^{\prime }\left(x\right)-\alpha \left(x\right)m^{″}\left(x\right)}{2m\left(x\right)}}+{\displaystyle \frac{\Delta \mathrm{E}m\left(x\right)\alpha \left(x\right)}{{\hslash }^2}}-{\displaystyle \frac{{\alpha }^{″}\left(x\right)}{2}},$$

(10)

$${\beta }_I^{\prime }\left(x\right)=0,$$

(11)

$$V^{\prime }\left(x\right)={\displaystyle \frac{1}{2m^2\left(x\right)\alpha \left(x\right)}}\left[2\Delta E{m}^2\left(x\right)\left[{\beta }_R\left(x\right)+i{\beta }_I\left(x\right)\right]+{\hslash }^2{m}^{\prime }\left(x\right)\left[{\beta }_R^{\prime }\left(x\right)+i{\beta }_I^{\prime }\left(x\right)\right]+{\hslash }^{2}m\left(x\right)\left[-{\beta }_R^{″}\left(x\right)-i{\beta }_I^{″}\left(x\right)\right]\right].$$

(12)

We can solve Equation (9) to find $\alpha \left(x\right)$ as a function of the mass as follows:

$$\begin{array}{c}\hfill \alpha \left(x\right)={\displaystyle \frac{a}{\sqrt{m\left(x\right)}}}.\end{array}$$

(13)

From (11), it is concluded that ${\beta }_I=\lambda$, where $\lambda$ is an integration constant. Subsequently, the substitution of $\alpha \left(x\right)$ as a function of $m\left(x\right)$ leads to a general expression for ${\beta }_R\left(x\right)$ as a function of the mass.

$$\begin{array}{c}\hfill {\beta }_R\left(x\right)={\displaystyle \frac{a}{2}}{\left({\left[m\left(x\right)\right]}^{-1/2}\right)}^{\prime }+{\displaystyle \frac{a\Delta E}{{\hslash }^2}}F\left(x\right),F\left(x\right)=\int \sqrt{m\left(x\right)}dx.\end{array}$$

(14)

The previous equation greatly resembles the $\beta$ function presented in [17] when the ladder operator $A^{-}$ was real.

Incorporating all of the above expressions, the potential is determined as

$$V\left(x\right)=V_R\left(x\right)+i{V}_I\left(x\right),$$

(15)

where the real and imaginary parts are given by

$$V_R\left(x\right)={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\Delta E}{\hslash }}\right)}^2{F}^2\left(x\right)-{\displaystyle \frac{{\hslash }^2}{8}}\left({\displaystyle \frac{7{\left[m^{\prime }\left(x\right)\right]}^2}{4m^3\left(x\right)}}-{\displaystyle \frac{m^{″}\left(x\right)}{m^2\left(x\right)}}\right),$$

(16)

$$V_I\left(x\right)={\displaystyle \frac{\Delta E}{a}}\lambda F\left(x\right).$$

(17)

It is worth noting that the presence of a complex component in the ladder operator, introduced through a constant $\lambda$, results in a nontrivial modification of the potential.

Looking for the ground state, at least a mathematical one, we should look for a function that is annihilated by $A^{-}$. Such an eigenfunction is given as follows:

$${\psi }_0=c_0{\left[m\left(x\right)\right]}^{1/4}\exp \left(-{\displaystyle \frac{\Delta E}{2{\hslash }^2}}{F}^2\left(x\right)\right)\left(\cos \left(\lambda F\right(x\left)\right)-i\sin \left(\lambda F\right(x\left)\right)\right).$$

(18)

Let us remark that the current Hamiltonian H is not Hermitian; therefore, the operator ${\left(A^{-}\right)}^{†}$ acts as a creation operator for $H^{†}$, but not, as desired, for H. Thus, we need to begin the search for the corresponding creation operator.

We propose the existence of a creation operator $A^{+}$ that is akin to the dagger of $A^{-}$ but not exactly the same:

$$A^{+}={\displaystyle \frac{1}{\sqrt{2}}}\left(-\alpha \left(x\right){\displaystyle \frac{d}{dx}}-{\alpha }^{\prime }\left(x\right)+\gamma \left(x\right)\right),$$

(19)

where $\gamma \left(x\right)={\gamma }_R\left(x\right)+i{\gamma }_I\left(x\right)$. With this proposition of $A^{+}$ and after the imposition of the corresponding commutation relation $[H,A^{+}]=\Delta E{A}^{+}$, we end up with the following creation operator:

$$A^{+}={\displaystyle \frac{1}{\sqrt{2}}}\left(-\alpha \left(x\right){\displaystyle \frac{d}{dx}}-{\alpha }^{\prime }\left(x\right)+{\beta }_R\left(x\right)+i{\beta }_I\left(x\right)\right).$$

(20)

It is worth noticing that the only difference with respect to the adjoint of $A^{-}$ is a sign in the complex part.

Since the creation operator has been constructed, we are now prepared to build the possible excited states by repeatedly applying $A^{+}$ to the ground state; thus

$${\psi }_n=c_n{\left(A^{+}\right)}^n{\psi }_0.$$

(21)

The eigenvalues associated with these states, and possibly the physical energies once the boundary conditions are satisfied, are given as follows:

$$E_n=\left(n+{\displaystyle \frac{1}{2}}\right)\Delta E+{\displaystyle \frac{1}{2}}{\lambda }^2{\hslash }^2,n=0,1,2,\dots$$

(22)

Finally, the commutator between the two ladder operators $A^{+}$ and $A^{-}$ can be readily calculated as

$$\left[A^{-},A^{+}\right]={\displaystyle \frac{a^2\Delta E}{{\hslash }^2}}.$$

(23)

This commutation relation corresponds to the zero-degree polynomial Heisenberg algebra, where the commutator reduces to a constant.

4.1. Factorization

Since $H^{†}\ne H$, the system is no longer Hermitian. This implies that orthogonality is no longer guaranteed.

Let us point out that the following commutation relation is satisfied:

$$[H,A^{\pm }]=\pm \Delta E{A}^{\pm },$$

(24)

after defining the adjoint ladder operators as

$${\left(A^{\pm }\right)}^{†}=B^{\mp }.$$

(25)

It follows straightforwardly that $B^{\pm }$ is indeed the ladder operator of $H^{†}$:

$$\begin{array}{ccc}\hfill {\left[H,A^{\pm }\right]}^{†}& =& \pm \Delta E{\left(A^{\pm }\right)}^{†},\hfill \\ \hfill \left[H^{†},B^{\mp }\right]& =& \mp \Delta E{B}^{\mp },\hfill \\ \hfill \left[H^{†},B^{\pm }\right]& =& \pm \Delta E{B}^{\pm }.\hfill \end{array}$$

(26)

At this point, we have two Hamiltonians with their respective ladder operators, and, as is expected, both can be factorized in terms of their respective ladder operators as follows:

$$H=A^{+}{A}^{-}+E_0,$$

(27)

$$H^{†}=B^{+}{B}^{-}+E_0.$$

(28)

The eigenstates of $H^{†}$ are constructed analogously:

$$B^{-}{\varphi }_0=0,{\varphi }_n=\overline{c_n}{\left(B^{+}\right)}^n{\varphi }_{0}n\in \mathbb{N},$$

(29)

where ${\varphi }_n$ represents the eigenfunctions of $H^{†}$. After simplification, it is easy to verify that

$${\varphi }_n={\psi }_n^{*},$$

(30)

and that both sets share the same real eigenvalues.

4.2. Biorthogonality

From the mathematical relations established above, it follows that

$$\begin{array}{ccc}\hfill \langle {\varphi }_m|H{\psi }_n\rangle & =& E_n\langle {\varphi }_m|{\psi }_n\rangle ,\hfill \\ \hfill \langle H^{†}{\varphi }_m|{\psi }_n\rangle & =& E_m\langle {\varphi }_m|{\psi }_n\rangle ,\hfill \\ \hfill (E_n-E_m)\langle {\varphi }_m|{\psi }_n\rangle & =& 0.\hfill \end{array}$$

(31)

Hence, the inner product $\langle {\varphi }_m|{\psi }_n\rangle$ must vanish for all $m\ne n$. Nevertheless, according to [24,25], the biorthogonal inner product—distinct from the conventional one—is defined as follows:

$$\langle {\varphi }_m|{\psi }_n\rangle ={\int }_{\Omega }\varphi \left(x\right)\psi \left(x\right)dx,$$

(32)

but, since we have already stated that ${\varphi }_n={\psi }_n^{*}$, we surprisingly recover a more familiar relation:

$$\langle {\varphi }_m|{\psi }_n\rangle ={\int }_{\Omega }{\psi }_m^{*}\left(x\right){\psi }_n\left(x\right)dx={\delta }_{mn}.$$

(33)

It is important to note that we are restricted to an arbitrary, but suitable, choice of a non-negative $m\left(x\right)$, with the requirement that this choice, together with appropriate boundary conditions, generates well-defined and normalizable eigenfunctions as described above.

5. Implementation

In this section, we illustrate the theoretical framework by applying it to specific mass profiles usually found in the literature [8,12,17], thus highlighting its practical implications. To this end, we present the following mass profiles:

$$m\left(x\right)=m_0(\sigma +\delta x^2),$$

(34)

$$m\left(x\right)=m_0+\cos \left(x\right),$$

(35)

$$m\left(x\right)={\displaystyle \frac{m_0\zeta }{1-e^{-\zeta }}}{e}^{-\zeta x},$$

(36)

where $m_0,\sigma ,\delta$, and $\zeta$ are constants. The constants in each expression are chosen solely for illustrative purposes. Accordingly, natural units are employed in the examples, such that $\hslash =\Delta E=a=1$.

5.1. Normalization Constants

All normalization constants in the examples were obtained by numerical integration of Equation (33). However, it is worth noting that, under certain conditions, they can be approximated by ${\pi }^{-1/4}$.

To this end, let us rewrite Equation (18):

$${\psi }_0\left(x\right)=c_0{m}^{1/4}\left(x\right)\exp \left(-{\displaystyle \frac{\Delta E}{2{\hslash }^2}}{F}^2\left(x\right)\right)\exp \left(-i\lambda F\left(x\right)\right).$$

(37)

With this expression in mind, we compute

$$\int {\psi }_0^{*}{\psi }_{0}dx={\left|c_0\right|}^2{\int }_{x_0}^{x_1}{m}^{1/2}\left(x\right)\exp \left(-{\displaystyle \frac{\Delta E}{{\hslash }^2}}{F}^2\left(x\right)\right)dx.$$

(38)

Note that, as long as $m\left(x\right)>0$, $F\left(x\right)$ is monotonally increasing, $F^{-1}$ exists for all x:

$$F\left(x\right)=\int \sqrt{m\left(x\right)}dx\Rightarrow {\displaystyle \frac{dF}{dx}}=\sqrt{m\left(x\right)}.$$

(39)

Using this property, we apply the change in variable $u=\frac{\sqrt{\Delta E}}{\hslash }F\left(x\right)$. It follows that

$$\int {\psi }_0^{*}{\psi }_{0}dx={\displaystyle \frac{\hslash }{\sqrt{\Delta E}}}|c_0{|}^2{\int }_{u_0}^{u_1}{e}^{-u^2}du={\displaystyle \frac{\hslash }{\sqrt{\Delta E}}}{\left|c_0\right|}^2{\displaystyle \frac{\sqrt{\pi }}{2}}\left[\mathrm{erf}\left(u_1\right)-\mathrm{erf}\left(u_0\right)\right].$$

(40)

If $u_1\gg 1$ and $u_0\ll -1$, then

$$\int {\psi }_0^{*}{\psi }_{0}dx\approx {\left|c_0\right|}^2{\displaystyle \frac{\hslash }{\sqrt{\Delta E}}}\sqrt{\pi }.$$

(41)

Therefore, the ground-state normalization constant could be approximated by

$$c_0\approx {\displaystyle \frac{1}{\sqrt{\hslash }}}{\left({\displaystyle \frac{\Delta E}{\pi }}\right)}^{1/4}.$$

(42)

In the illustrative examples, we set $\hslash =\Delta E=1$ for visualization purposes, which leads to the numerical value 0.751126.

5.2. Quadratic Mass Profile

We consider a mass profile similar to that presented in [8]. In this example, we use $m\left(x\right)=1+x^2$ and $\lambda ={\displaystyle \frac{1}{5}}$. Given this mass profile, the following functions are calculated:

$$\alpha (x)={\displaystyle \frac{1}{\sqrt{x^2+1}}},$$

(43)

$${\beta }_R\left(x\right)={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{(x^2+2)x^3}{{(x^2+1)}^{3/2}}}+{\sinh }^{-1}\left(x\right)\right),$$

(44)

$${\beta }_I\left(x\right)={\displaystyle \frac{1}{5}},$$

(45)

$$\begin{array}{cc}\hfill V\left(x\right)& ={\displaystyle \frac{1}{8}}{\left(\sqrt{x^2+1}x+{\sinh }^{-1}\left(x\right)\right)}^2+{\displaystyle \frac{1}{8}}\left({\displaystyle \frac{2}{{(x^2+1)}^2}}-{\displaystyle \frac{7x^2}{{(x^2+1)}^3}}\right)\hfill \\ & +{\displaystyle \frac{1}{10}}i\left(\sqrt{x^2+1}x+{\sinh }^{-1}\left(x\right)\right),\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill {\psi }_0\left(x\right)& =0.751126e^{-{\displaystyle \frac{1}{8}}{\left(\sqrt{x^2+1}x+{\sinh }^{-1}\left(x\right)\right)}^2}{(x^2+1)}^{1/4}\hfill \\ & \times \left[\cos \left({\displaystyle \frac{1}{10}}\left(\sqrt{x^2+1}x+{\sinh }^{-1}\left(x\right)\right)\right)-i\sin \left({\displaystyle \frac{1}{10}}\left(\sqrt{x^2+1}x+{\sinh }^{-1}\left(x\right)\right)\right)\right].\hfill \end{array}$$

(47)

As mentioned previously, the corresponding excited states can be found by iteratively applying the creation operator. The mass profile, potential, ground, and first excited states are visualized in Figure 1.

Notice that the parameter $\lambda$ controls the imaginary parts of the potential and, consequently, the eigenfunctions. The higher the $\lambda$ parameter is, the higher the number of oscillations that we can encounter, even in the ground state. Next, the real and imaginary parts of ${\psi }_0(x,\lambda )$ are shown in Figure 2.

5.3. Cosinusoidal Mass Profile

Let us consider the cosinusoidal mass profile (35). After implementing it, we obtain the following functions:

$$\alpha (x)={\displaystyle \frac{1}{\sqrt{\cos \left(x\right)+1.1}}},$$

(48)

$${\beta }_R\left(x\right)=2.89828E\left(0.5x\right|0.952381)+{\displaystyle \frac{\sin \left(x\right)}{4{(\cos \left(x\right)+1.1)}^{3/2}}},$$

(49)

$${\beta }_I\left(x\right)={\displaystyle \frac{1}{5}},$$

(50)

$$\begin{array}{cc}\hfill V\left(x\right)& ={\displaystyle \frac{1}{8}}\left(-{\displaystyle \frac{\cos \left(x\right)}{{(\cos \left(x\right)+1.1)}^2}}-{\displaystyle \frac{7{\sin }^2\left(x\right)}{4{(\cos \left(x\right)+1.1)}^3}}\right)\hfill \\ & +4.2E{\left(0.5x\right|0.952381)}^2+\left(0.579655i\right)E\left(0.5x\right|0.952381),\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill {\psi }_0\left(x\right)& =0.751126{(\cos \left(x\right)+1.1)}^{1/4}{e}^{-4.2E{\left(0.5x\right|0.952381)}^2}(\cos \left(0.579655E\left(0.5x\right|0.952381)\right)\hfill \\ & -i\sin \left(0.579655E\right(0.5x\left|0.952381\right)\left)\right).\hfill \end{array}$$

(52)

Here, $E\left(\varphi \right|k)$ denotes the elliptic integral of the second kind. We again obtain a complex potential and the corresponding eigenstates by applying the creation operator (See Figure 3).

In the cosinusoidal mass profile, the effect of the $\lambda$ parameter is once again evident. As $\lambda$ increases, the number of oscillations increases, even in the ground state. In Figure 4, the real and imaginary components of the ground state ${\psi }_0(x,\lambda )$ are displayed.

5.4. Exponential Mass Profile

The exponential mass profile (36) illustrated in Figure 5 was previously analyzed in [12]. Applying this profile in our framework yields a complex potential, as well as the ground state of the system. The corresponding functions obtained from this mass profile are presented below:

$$\alpha (x)={\displaystyle \frac{\sqrt{1-\frac{1}{e}}}{\sqrt{e^{-x}}}},$$

(53)

$${\beta }_R\left(x\right)={\displaystyle \frac{e^{-x}\left(-e^x+e^{x+1}-8e\right)}{4\sqrt{e-1}\sqrt{e^{1-x}}}},$$

(54)

$${\beta }_I\left(x\right)={\displaystyle \frac{2}{5}},$$

(55)

$$V(x)=-{\displaystyle \frac{3}{32}}\left(1-{\displaystyle \frac{1}{e}}\right)e^x+{\displaystyle \frac{2e^{1-x}}{e-1}}-{\displaystyle \frac{4i\sqrt{e^{1-x}}}{5\sqrt{e-1}}},$$

(56)

$${\psi }_0\left(x\right)=1.19134e^{-{\displaystyle \frac{2e^{1-x}}{e-1}}}{\left(e^{-x}\right)}^{1/4}\left(\cos \left({\displaystyle \frac{4\sqrt{e^{1-x}}}{5\sqrt{e-1}}}\right)+i\sin \left({\displaystyle \frac{4\sqrt{e^{1-x}}}{5\sqrt{e-1}}}\right)\right).$$

(57)

The complex potential, as well as the ground and first excited states of the system, are shown in Figure 5.

Figure 6 illustrates the effect of the $\lambda$ parameter on the ground state, modulating the imaginary part of the potential and its corresponding eigenfunction. As $\lambda$ increases, the number of oscillations in the ground state also increases.

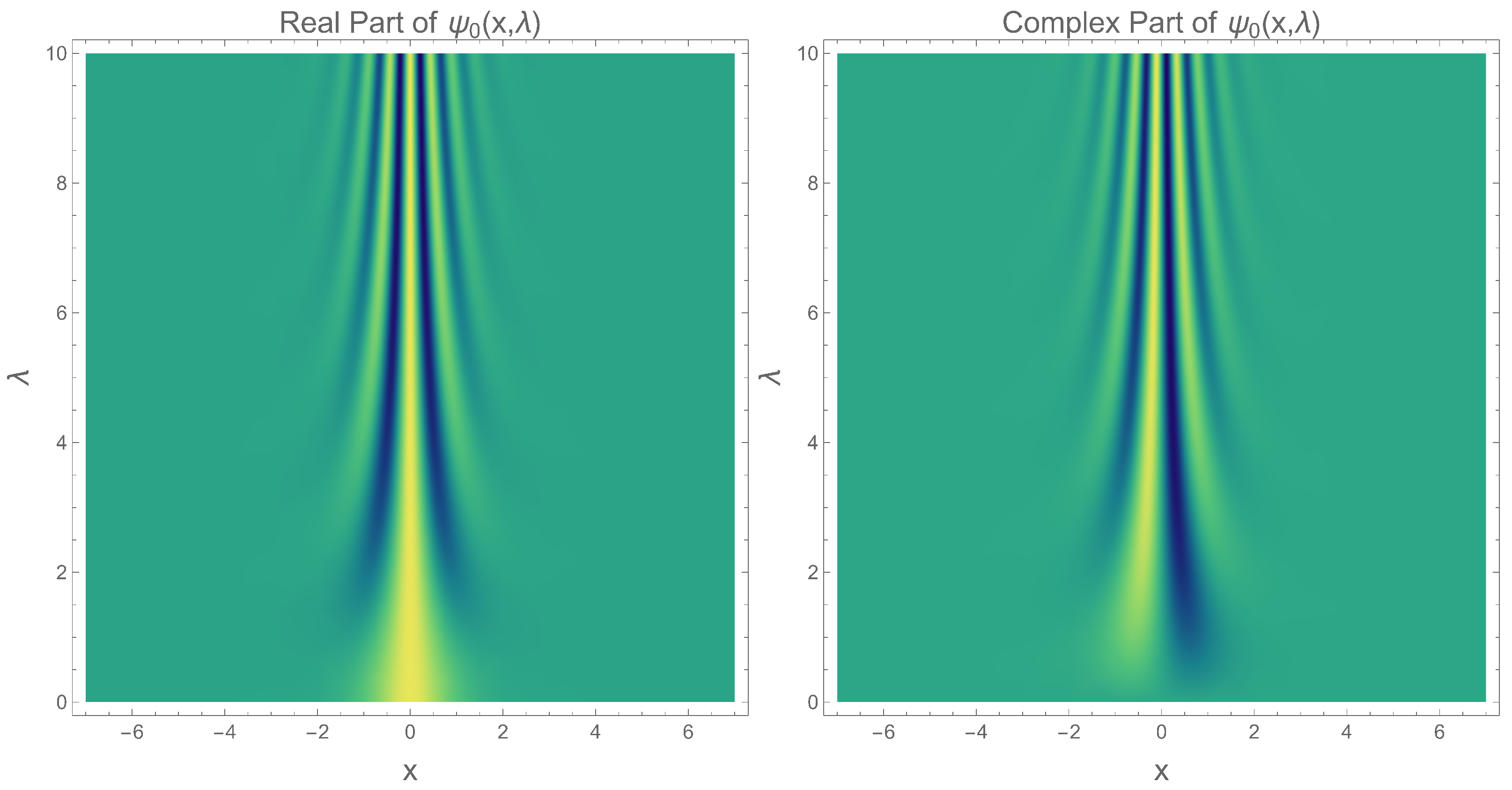
6. Physical Interpretation of $\mathit{\lambda }$

The first appearance of $\lambda$ is as an unbounded, real integration constant, which arises when integrating Equation (11). This parameter modulates the complex part of the ladder operators as well as the complex contribution to the potential. Moreover, $\lambda$ ultimately controls the phase and, consequently, the positions of the zeros of the real and imaginary parts of the eigenfunctions. Another notable effect is that the entire spectrum exhibits an upward shift proportional to ${\lambda }^2$, while the spacing between adjacent levels remains unchanged.

The following discussion is based on numerical insights that give clues regarding the direct physical implications of $\lambda$. However, we were unable to derive exact formulas applicable to the entire spectrum; thus, we restricted our analysis to the ground and first excited states.

6.1. Expectation Values

We investigate the expectation values of $\widehat{x}$, $\widehat{p}$, and $\widehat{T}$ for the ground state, as well as the corresponding probability density. The expectation value of the position operator $\langle \widehat{x}\rangle$ involves ${\left|\psi \right|}^2$, so any phase contribution cancels out; hence, it is completely independent of $\lambda$.

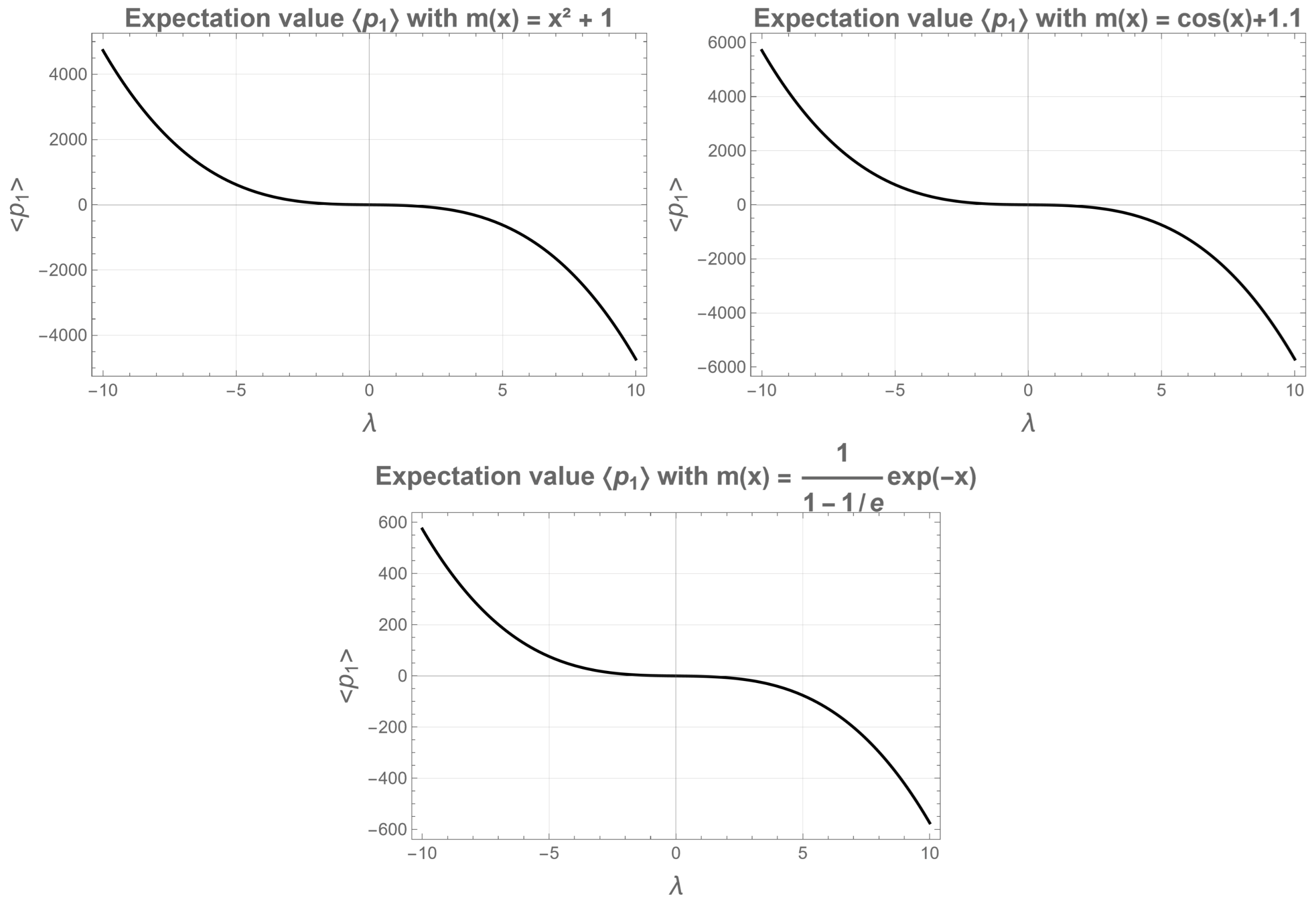
The expectation value of the canonical momentum $\langle \widehat{p}\rangle$ is a different story. Since the operator involves a derivative with respect to position, a linear dependence on $\lambda$ naturally arises. One may ask whether an appropriate position-dependent mass, momentum, or pseudo-momentum operator could be defined. Some examples can be found in the literature [26,27]; however, these operators have been reported to be non-Hermitian or possess a predefined ordering. Additionally, they fail to reproduce the kinetic term of the BDD Hamiltonian, which is necessary for our analysis. Therefore, we restrict ourselves to a qualitative rather than quantitative analysis using the canonical momentum.

6.2. The Expectation Values of the Canonical Momentum $\widehat{p}$

The expectation value of the canonical momentum for the eigenstate ${\psi }_i$ is calculated as follows:

$$\langle {\widehat{p}}_i\rangle ={\int }_{x_i}^{x_f}{\psi }_i^{*}(x,\lambda )\widehat{p}{\psi }_i(x,\lambda )dx={\int }_{x_i}^{x_f}{\psi }_i^{*}(x,\lambda )\left(-i\hslash {\displaystyle \frac{d}{dx}}\right){\psi }_i(x,\lambda )dx.$$

(58)

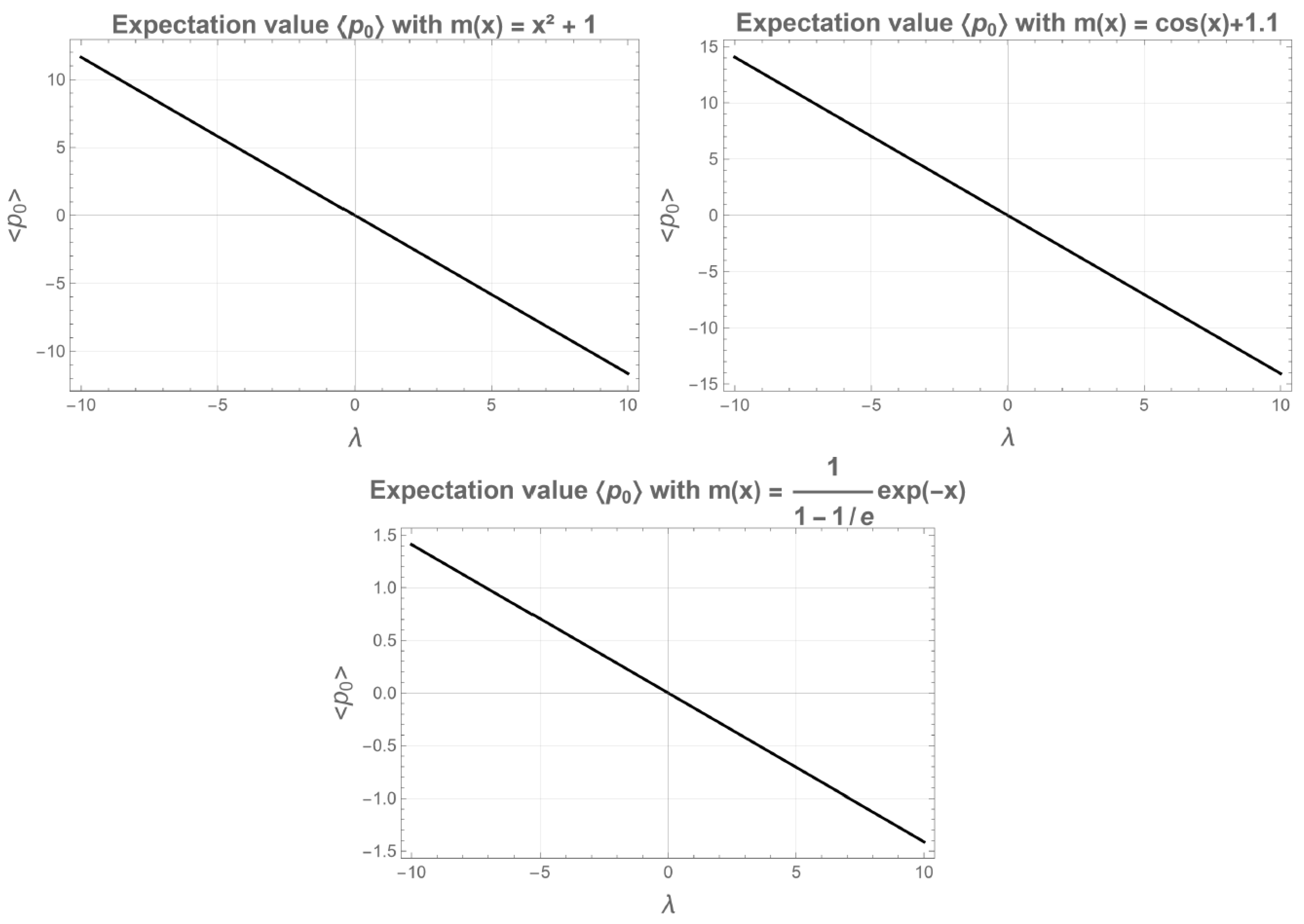
If we focus on the derivative of the ground state, it is evident that the derivative brings down one $\lambda$; hence, we expect $\langle {\widehat{p}}_0\rangle$ to follow a linear dependence on $\lambda$.

This integral was evaluated numerically for $x\in (-\infty ,\infty )$ and $\lambda \in [-10,10]$. The aforementioned linear dependence is observed, the higher the $\lambda$, the lower $\langle {\widehat{p}}_0\rangle$ (see Figure 7).

For the first excited state, the expectation value $\langle {\widehat{p}}_1\rangle$ exhibits a non-linear dependence. This arises because ${\psi }_1$ is obtained from ${\psi }_0$ via the operator $A^{+}$, which introduces a factor of $\lambda$. Consequently, the overall contribution is of order ${\lambda }^3$: two powers come from $A^{+}{\psi }_0$ and its complex conjugate, and the third from the derivative (see Figure 8).

6.3. The Expectation Values of the Kinetic Energy $\widehat{T}$

The expectation value of the BDD kinetic operator is as follows:

$$\langle {\widehat{T}}_i\rangle ={\int }_{x_0}^{x_1}{\psi }_i^{*}\widehat{T}{\psi }_{i}dx={\int }_{x_0}^{x_1}{\psi }_i^{*}\left(x\right)\left[-{\displaystyle \frac{{\hslash }^2}{2}}{\displaystyle \frac{d}{dx}}{\displaystyle \frac{1}{m\left(x\right)}}{\displaystyle \frac{d}{dx}}\right]{\psi }_i\left(x\right)dx$$

(59)

Following the same reasoning as before, we expect $\langle T_0\rangle$ to exhibit a quadratic dependence on $\lambda$, since the second derivative extracts two powers of $\lambda$ from the phase.

Upon numerical integration over $\lambda \in [-10,10]$, we find that $\langle {\widehat{T}}_0\rangle$ follows indeed a quadratic dependence on $\lambda$ (see Figure 9).

Meanwhile, $\langle {\widehat{T}}_1\rangle$ exhibits a quartic dependence, ${\psi }_1$ and its complex conjugate contribute with one lambda each; then, the second derivative will bring down two more (see Figure 10).

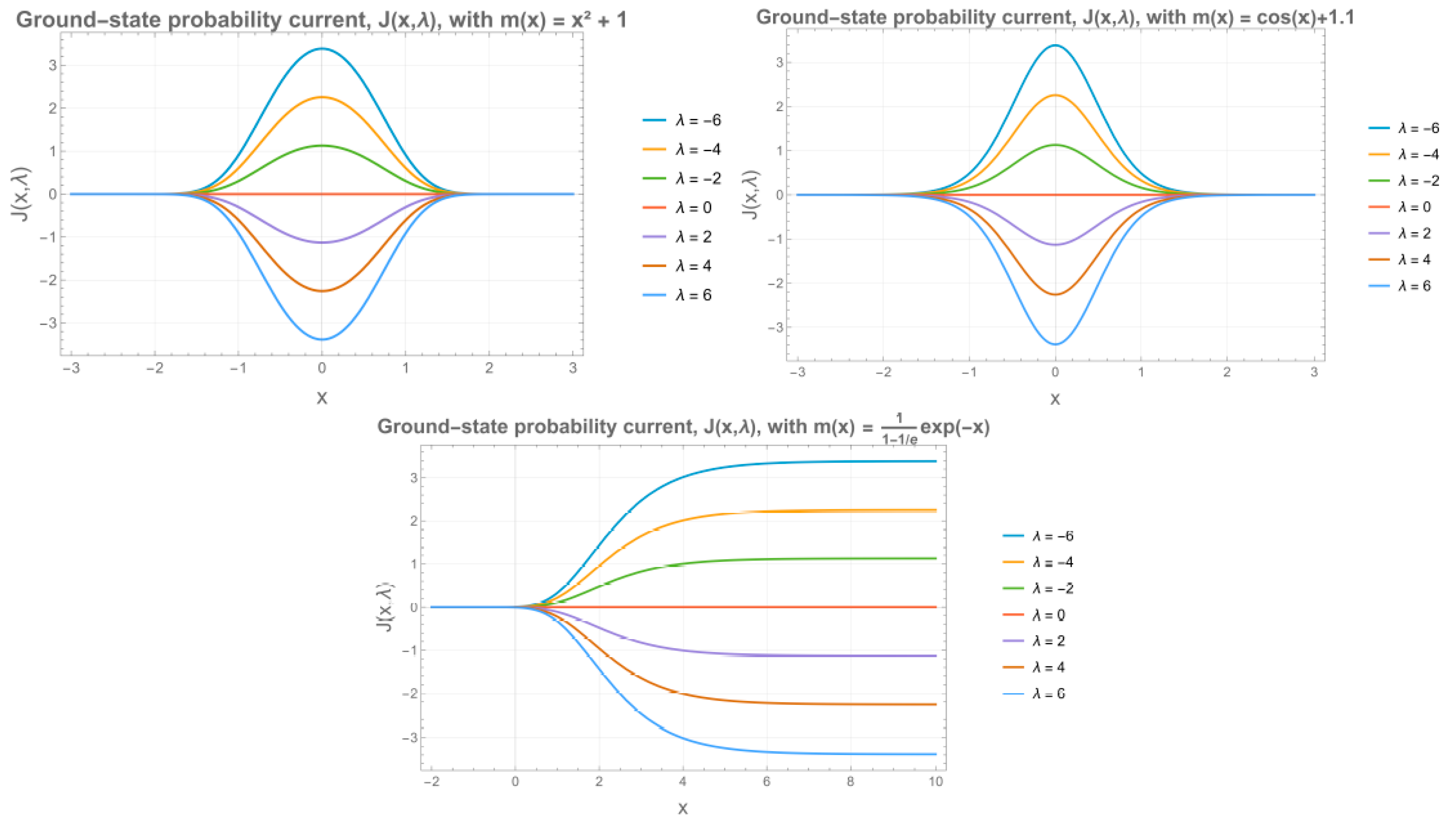
6.4. The Probability Current

The probability current for the BDD Hamiltonian is well known and can be found in [28]. It can be derived from the time-dependent Schrödinger equation and its complex conjugate by multiplying the first by ${\psi }^{*}$ and the second by $\psi$, adding the two to eliminate the potential term, and grouping terms to identify $\rho$ and j. The resulting expression is as follows:

$$J\left(x\right)={\displaystyle \frac{\hslash }{2im\left(x\right)}}\left[{\psi }^{*}\left(x\right){\displaystyle \frac{d\psi \left(x\right)}{dx}}-\psi \left(x\right){\displaystyle \frac{d{\psi }^{*}\left(x\right)}{dx}}\right]$$

(60)

By using this equation, the probability currents associated with the ground states of each of the three problems were calculated:

$$J\left(x\right)=-{\displaystyle \frac{\lambda e^{-\frac{1}{4}{\left(x\sqrt{x^2+1}+{\sinh }^{-1}\left(x\right)\right)}^2}}{\sqrt{\pi }}}$$

(61)

$$J\left(x\right)=-{\displaystyle \frac{0.817588\lambda \sqrt{0.47619\cos \left(x\right)+0.52381}{e}^{-8.4E{\left(0.5x\right|0.952381)}^2}}{\sqrt{\cos \left(x\right)+1.1}}}$$

(62)

$$J\left(x\right)=-{\displaystyle \frac{\lambda e^{-\frac{4e^{1-x}}{e-1}}}{\sqrt{\pi }}}$$

(63)

For the three examples discussed, the probability currents are non-zero for $\lambda \ne 0$. Since these currents correspond to the flow of charge carriers, they are directly related to the electrical current: larger values of $\lambda$ lead to higher currents, and a positive $\lambda$ produces a current in the negative direction (see Figure 11).

7. PT Symmetry, Pseudo-Hermiticity, and Related Properties

When dealing with non-Hermitian systems, one often encounters complex spectra or relies on PT symmetry or pseudo-Hermiticity to ensure real eigenvalues; see, for example, [29,30]. Interestingly, in our system, the spectrum remains entirely real despite the absence of an obvious PT-symmetric or pseudo-Hermitian structure.

7.1. PT Symmetry

PT symmetry is a property that requires a Hamiltonian H to be invariant under parity–time transformations:

$$[H,\mathcal{PT}]=0.$$

(64)

This relation alone is not sufficient to guarantee the reality of the spectrum. The eigenfunctions of H must also be eigenfunctions of the $\mathcal{PT}$ operator; otherwise, the PT symmetry is said to be broken, and some eigenvalues may become complex [31,32,33].

The first step, therefore, is to check whether H is invariant under parity–time transformations, defined as $\mathcal{P}:(x,p)\to (-x,-p)$ and $\mathcal{T}:(x,p,i)\to (x,-p,-i)$.

These definitions have some implications for the potential: the real part must be even, and the imaginary part odd. More importantly, when we examine the kinetic term of the BDD Hamiltonian, we find that PT symmetry requires $m\left(x\right)=m(-x)$. This is not a restriction in our mathematical framework, and we can easily choose a mass profile that does not satisfy this condition; therefore, our systems are not necessarily PT-symmetric.

7.2. Pseudo-Hermiticity and Anti-Pseudo-Hermiticity

PT-symmetric systems belong to a broader class of Hamiltonians, known as Pseudo-Hermitian. Pseudo-Hermiticity ensures the reality of the spectrum by imposing the following intertwining relation [20,21,22,34]:

$$H^{†}\eta =\eta H,$$

(65)

which is equivalent to

$$H^{†}=\eta H{\eta }^{-1}.$$

(66)

This definition of Pseudo-Hermiticity requires $\eta$ to be linear.

Let us take a look to our H and $H^{†}$, both of which can be expressed as a kinetic plus a potential part:

$$H=K+V,H^{†}=T+V^{*}.$$

(67)

The kinetic part is hermitian; meanwhile, the potential parts are related by the complex conjugation operation, which we denote K. This complex conjugation operation has the property $K^2\psi \left(x\right)=K{\psi }^{*}\left(x\right)=\psi \left(x\right)$, so that $K^2=\mathbb{1}$ and $K=K^{-1}$.

Now, consider the following expression:

$$KT{K}^{-1}\psi \left(x\right)=KT{\psi }^{*}\left(x\right)=K\left(-{\displaystyle \frac{{\hslash }^2}{2m\left(x\right)}}{\displaystyle \frac{d^2{\psi }^{*}\left(x\right)}{d{x}^2}}+{\displaystyle \frac{{\hslash }^2{m}^{\prime }\left(x\right)}{2m^2\left(x\right)}}{\displaystyle \frac{d{\psi }^{*}\left(x\right)}{dx}}\right),$$

(68)

$$KT{K}^{-1}\psi \left(x\right)=\left(-{\displaystyle \frac{{\hslash }^2}{2m\left(x\right)}}{\displaystyle \frac{d^2\psi \left(x\right)}{d{x}^2}}+{\displaystyle \frac{{\hslash }^2{m}^{\prime }\left(x\right)}{2m^2\left(x\right)}}{\displaystyle \frac{d\psi \left(x\right)}{dx}}\right)=T\psi \left(x\right).$$

(69)

This shows that $KT{K}^{-1}=K$. Next, let us see what happens with $V\left(x\right)$:

$$KV\left(x\right)K^{-1}\psi \left(x\right)=K^{-1}V\left(x\right){\psi }^{*}\left(x\right)=V^{*}\left(x\right)\psi \left(x\right).$$

(70)

Hence, $KV{K}^{-1}=V^{*}$.

Finally, we can identify that

$$KH{K}^{-1}=K(T+V)K^{-1}=KT{K}^{-1}+KV{K}^{-1}=T+V^{*}=H^{†},$$

(71)

which is precisely Equation (66).

We also need to remember that the complex conjugate operator is not linear, but an antilinear operator:

$$K(a\psi \left(x\right)+b\varphi \left(x\right))=a^{*}K\psi +b^{*}K\varphi$$

(72)

This allows us to conclude that our system belongs to the class of anti-pseudo-Hermitian operators [22].

8. Discussion

Non-Hermitian, position-dependent mass Hamiltonians with complex ladder operators and real, equidistant spectra have been presented. A first-order differential operator satisfying the Heisenberg–Weyl algebra was constructed based on the BenDaniel–Duke Hamiltonian. To illustrate the method, three distinct mass profiles were examined: quadratic, cosinusoidal, and exponential. It was found that the parameter $\lambda$, which introduces a displacement in the energy spectrum and governs the imaginary part of the Hamiltonians, significantly affects the behavior of the eigenfunctions. In particular, as $\lambda$ increases, the number of oscillations rises, and the positions of the nodes shift, even in the ground state. Notably, the ground state may exhibit oscillatory behavior solely due to variations in the $\lambda$ parameter.

To quantify the impact of $\lambda$, we numerically calculated expectation values of the momentum and kinetic energy operators, as well as the corresponding probability currents. For the ground state, the momentum expectation value $\langle p_0\rangle$ and probability currents $J\left(x\right)$ exhibit a linear dependence on $\lambda$, while the ground-state kinetic energy $\langle T_0\rangle$ shows an approximately quadratic dependence. For the first-excited state, $\langle p_1\rangle$ displays a cubic dependence on $\lambda$, and $\langle T_1\rangle$ exhibits a quartic dependence, illustrating how higher-order contributions emerge in excited states. These results demonstrate that the parameter $\lambda$ systematically controls not only the eigenfunctions but also the dynamical observables of the system.

Since the Hamiltonians are non-Hermitian, the eigenstates are not orthogonal in the conventional sense. However, we demonstrate that the eigenstates of H and $H^{†}$ form a biorthogonal system and belong to the class of anti-pseudo-Hermitian systems. This structure preserves a generalized version of the superposition principle and supports a well-defined ladder operator formalism.

A natural extension of the present work could involve using supersymmetric quantum mechanics (SUSY QM) to generate new Hamiltonian systems that possess higher-order ladder operators. In this approach, an intertwining operator connects a known Hamiltonian to a new partner system through appropriate seed solutions, allowing for the construction of complex spectra with controlled features. Importantly, the parameter $\lambda$ could continue to modulate both systems, while the resulting higher-order ladder operators may provide connections to analogs of nonlinear systems that naturally emerge within the SUSY formalism. This perspective opens a potential avenue for exploring richer non-Hermitian structures and spectral engineering possibilities.

Furthermore, complex potentials have optical analogs in photonic systems, where spatially varying complex refractive indices can simulate non-Hermitian Hamiltonians. As far as we know, direct analogs of position-dependent mass systems have not yet been explored, but it is conceivable that spatially varying effective masses could be implemented using engineered photonic lattices or waveguide arrays. Such optical realizations might provide a versatile platform for testing higher-order ladder operators and exploring spectral engineering possibilities that could emerge from SUSY-inspired constructions, representing an interesting avenue for future investigation.