Revisiting the Origin of the Universe and the Arrow of Time
Abstract
1. Introduction
2. Creation of the Universe from Nothing
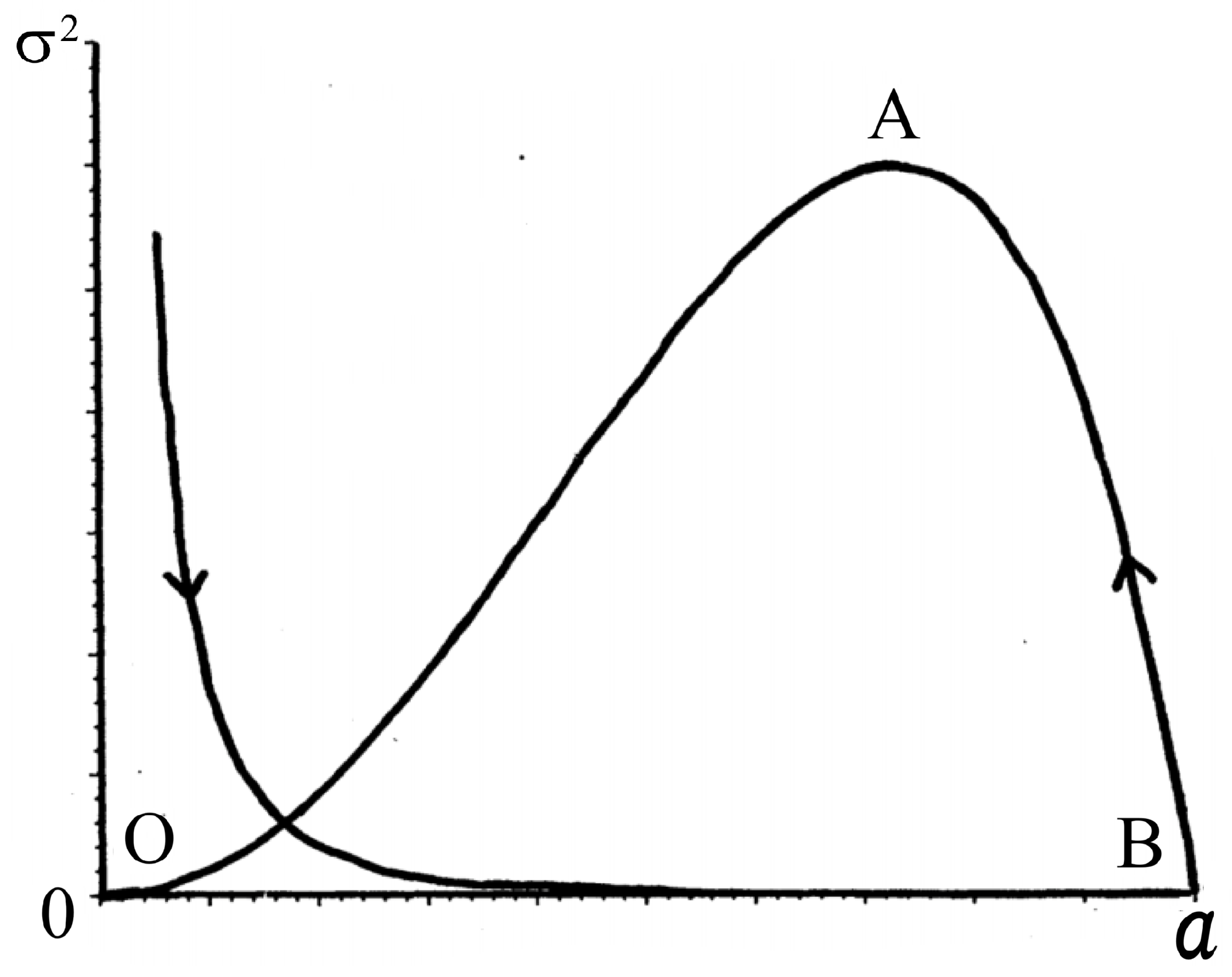
3. The Dynamical Arrow of Time
4. Thermodynamic Arrow of Time
5. Discussions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hawking, S.W. Singularities in the universe. Phys. Rev. Lett. 1966, 17, 444–445. [Google Scholar] [CrossRef]
- Hawking, S.W.; Penrose, R. The Singularities of gravitational collapse and cosmology. Proc. R. Soc. Lond. 1970, 314, 529–548. [Google Scholar]
- Tryon, E.P. Is the Universe a vacuum fluctuation? Nature. 1973, 246, 396–397. [Google Scholar] [CrossRef]
- Vilenkin, A. Creation of universes from nothing. Phys. Lett. 1982, 117, 25–28. [Google Scholar] [CrossRef]
- Vilenkin, A. Quantum creation of universes. Phys. Rev. D 1984, 30, 509–511. [Google Scholar] [CrossRef]
- Atkatz, D.; Pagels, H. Origin of the Universe as a quantum tunneling event. Phys. Rev. D 1982, 25, 2065–2073. [Google Scholar] [CrossRef]
- Hawking, W.; Moss, I.G. Supercooled Phase Transitions in the Very Early Universe. Phys. Rev. Lett B 1982, 110, 35–38. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Wave Function of the Universe. Phys. Rev. D 1983, 28, 2960–2975. [Google Scholar] [CrossRef]
- Carroll, S.M.; Chen, J. Does Inflation Provide Natural Initial Conditions for the Universe? Gen. Rel. Grav. 2005, 37, 1671–1674. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The theory of gravitation in Hamiltonian form. Proc. Roy. Soc. (Lond.) 1958, 246, 333–334. [Google Scholar]
- Wheeler, J.A. Relativity Groups and Topology; 1963 Les Holches Lectlres; Gordon and Breach Science Publishers, Inc.: New York, NY, USA, 1964. [Google Scholar]
- DeWitt, B. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113–1148. [Google Scholar] [CrossRef]
- Kiefer, C.; Sandhoefer, B. Quantum Cosmnology. Z. für Naturforschung A 2022, 77, 543–559. [Google Scholar] [CrossRef]
- Fukuyama, T.; Kamimura, K. Dynamical time variable in cosmology. Mod. Phys. Lett. A 1988, 3, 333–343. [Google Scholar] [CrossRef]
- Fukuyama, T.; Morikawa, K. Directions of dynamical and thermodynamic arrows of time. Phys. Rev. D 1989, 39, 462–469. [Google Scholar] [CrossRef] [PubMed]
- Hawking, S.W.; Laflamme, R.; Lyons, G.W. Origin of time asymmetry. Phys. Rev. D 1993, 47, 5342–5356. [Google Scholar] [CrossRef]
- Jackiw, R. Quantum Theory of Gravity; Christensen, S., Ed.; Adam Hilger: Bristol, UK, 1984. [Google Scholar]
- Teitelboim, C. Quantum Theory of Gravity; Christensen, S., Ed.; Adam Hilger: Bristol, UK, 1984. [Google Scholar]
- Fukuyama, T.; Kamimura, K. Gauge Theory of Two-dimensional Gravity. Phys. Lett. 1985, 160, 259–262. [Google Scholar] [CrossRef]
- Feynman, R.P.; Vernon, F.L., Jr. The Theory of a general quantum system interacting with a linear dissipative system. Ann. Phys. 1963, 24, 118–173. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Legget, A.J. Path integral approach to quantum Brownian motion. Physica 1983, 121, 587–616. [Google Scholar] [CrossRef]
- Chou, K.; Su, Z.; Hao, B.; Yu, L. Equilibrium and Nonequilibrium Formalisms Made Unified. Phys. Rep. 1985, 118, 1–131. [Google Scholar] [CrossRef]
- de Cesare, M. Time and Timelessness in Fundamental Physics and Cosmology; Springer: Berlin/Heidelberg, Germany, 2024; pp. 253–267. [Google Scholar]
- Fukuyama, T. De Sitter Invariant Gravity Coupled with Matters and Its Cosmological Consequences. Ann. Phys. 1984, 157, 321–341. [Google Scholar] [CrossRef]
- Macdowell, S.W.; Mansouri, F. Unified Geometric Theory of Gravity and Supergravity. Phxs. Rev. Lett. 1977, 38, 739–742. [Google Scholar] [CrossRef]
- Loll, R. The Emergence of Spacetime, or, Quantum Gravity on Your Desktop. Class. Quant. Grav. 2008, 25, 114006. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational Collapse and Space-Time Singularities. Phys. Rev. Lett. 1965, 14, 57–59. [Google Scholar] [CrossRef]
- Rubakov, V.A. The Null Energy Condition and its violation. Uspekhi 2014, 57, 128–142. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Time in the Quantum Theory and the Uncertainty Relation for Time and Energy. Phys. Rev. 1961, 122, 1649–1658. [Google Scholar] [CrossRef]
- Aharanov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics; Pergamon Press: Oxford, UK, 1974; Section 44. [Google Scholar]
- Gurzadyan, V.G.; Penrose, R. On CCC-predicted concentric low-variance circles in the CMB sky. Eur. Phys. J. Plus 2013, 128, 22. [Google Scholar] [CrossRef]
- Perna, M.; Arribas, S.; Lamperti, I.; Circosta, C.; Bertola, E.; Pérez-González, P.G.; D’Eugenio, F.; Übler, H.; Cresci, G.; Volonteri, M.; et al. GA-NIFS: High number of dual active galactic nuclei at z ≈ 3. Astron. Astrophys. 2025, 696, A59. [Google Scholar] [CrossRef]
- Fukuyama, T. Axion and the SuperMassive Black Holes at high z. Int. J. Mod. Phys. Lett. A 2023, 38, 2350191. [Google Scholar] [CrossRef]
- Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Becsy, B.; Blecha, L.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; et al. The NANOGrav 15-year Data Set: Evidence for a Gravitational-Wave Background. Astrophys. J. Lett. 2023, 951, 1. [Google Scholar] [CrossRef]
- Afzal, A.; Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Becsy, B.; Blanco-Pillado, J.J.; Blecha, L.; Boddy, K.K.; et al. The NANOGrav 15-year Data Set: Search for Signals from New Physics. Astrophys. J. Lett. 2023, 964, 1. [Google Scholar]
- Antoniadis, J.; Arumugam, P.; Arumugam, S.; Babak, S.; Bagchi, M.; Bak Nielsen, A.-S.; Bassa, C.G.; Bathula, A.; Berthereau, A.; Bonetti, M.; et al. The second data release from the European Pulsar Timing Array III. Search for gravitational wave signals. Astron. Astrophys. 2023, 678, A50. [Google Scholar] [CrossRef]
- Reardon, D.J.; Zic, A.; Shannon, R.M.; Hobbs, G.B.; Bailes, M.; Di Marco, V.; Kapur, A.; Rogers, A.F.; Thrane, E.; Askew, J.; et al. Search for an Isotropic Gravitational-wave Background with the Parkes Pulsar Timing Array. Astrophys. J. Lett. 2023, 951, L6. [Google Scholar] [CrossRef]
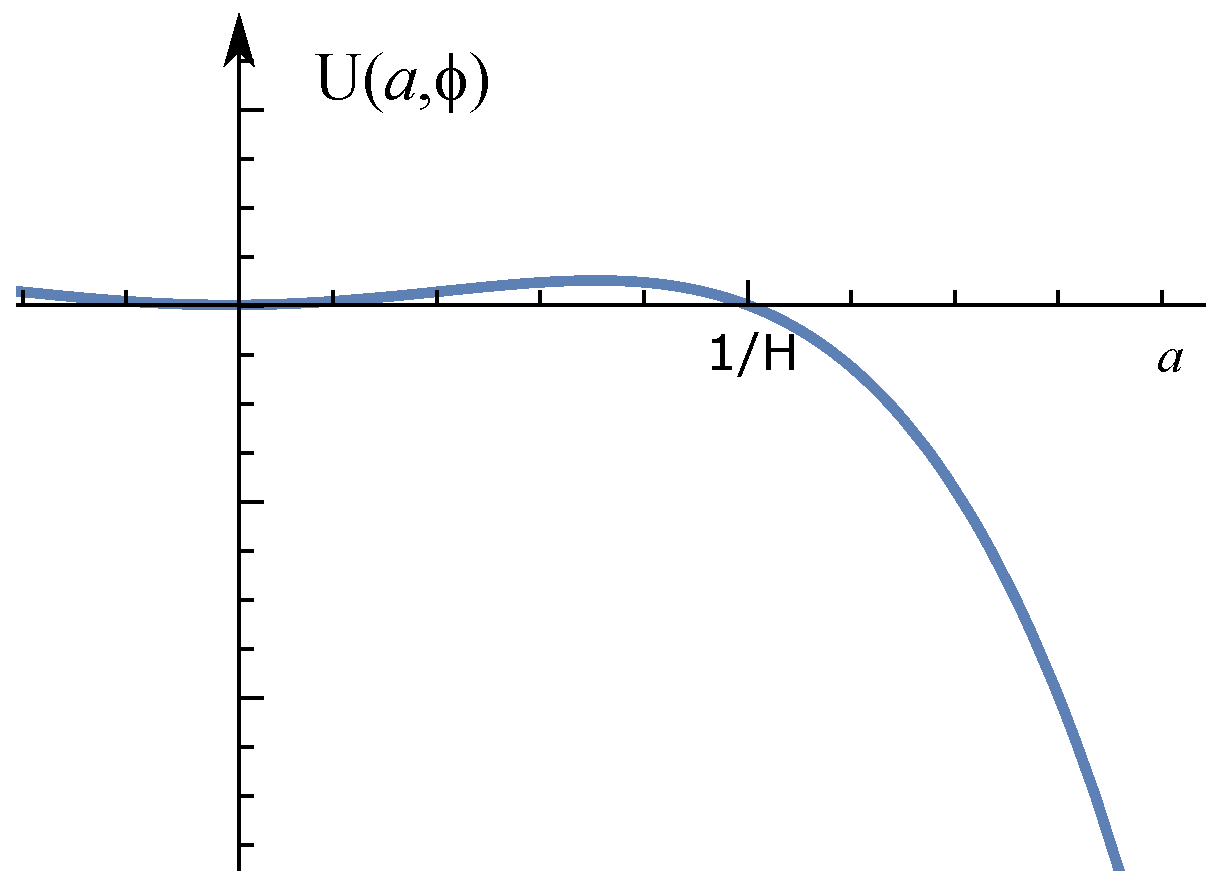

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fukuyama, T. Revisiting the Origin of the Universe and the Arrow of Time. Symmetry 2025, 17, 1688. https://doi.org/10.3390/sym17101688
Fukuyama T. Revisiting the Origin of the Universe and the Arrow of Time. Symmetry. 2025; 17(10):1688. https://doi.org/10.3390/sym17101688
Chicago/Turabian StyleFukuyama, Takeshi. 2025. "Revisiting the Origin of the Universe and the Arrow of Time" Symmetry 17, no. 10: 1688. https://doi.org/10.3390/sym17101688
APA StyleFukuyama, T. (2025). Revisiting the Origin of the Universe and the Arrow of Time. Symmetry, 17(10), 1688. https://doi.org/10.3390/sym17101688