Cooperative Differential Game-Based Modular Unmanned System Approximate Optimal Control: An Adaptive Critic Design Approach
Abstract
1. Introduction
- It is the first paper to use cooperative differential games for MUSs via ACD to guarantee accuracy and optimality. The developed control method is verified on the actual platform.
- The experimental results are verified via tracking error and control torque under the developed cooperative game method using ACD.
Notation
2. Dynamic Model of MUS
- (1)
- Coupling joint torque measurement
- (2)
- Concentrated joint friction torque
- (3)
- Coupling term
3. Approximate Optimal-Control-Based Cooperative Differential Game via ACD
3.1. Problem Description
3.2. An Approximate Solution of Decentralized Approximate Optimal Control in a Cooperative Differential Game Based on a Critic Network
3.3. Fulfillment of Policy Iteration
4. Experiment
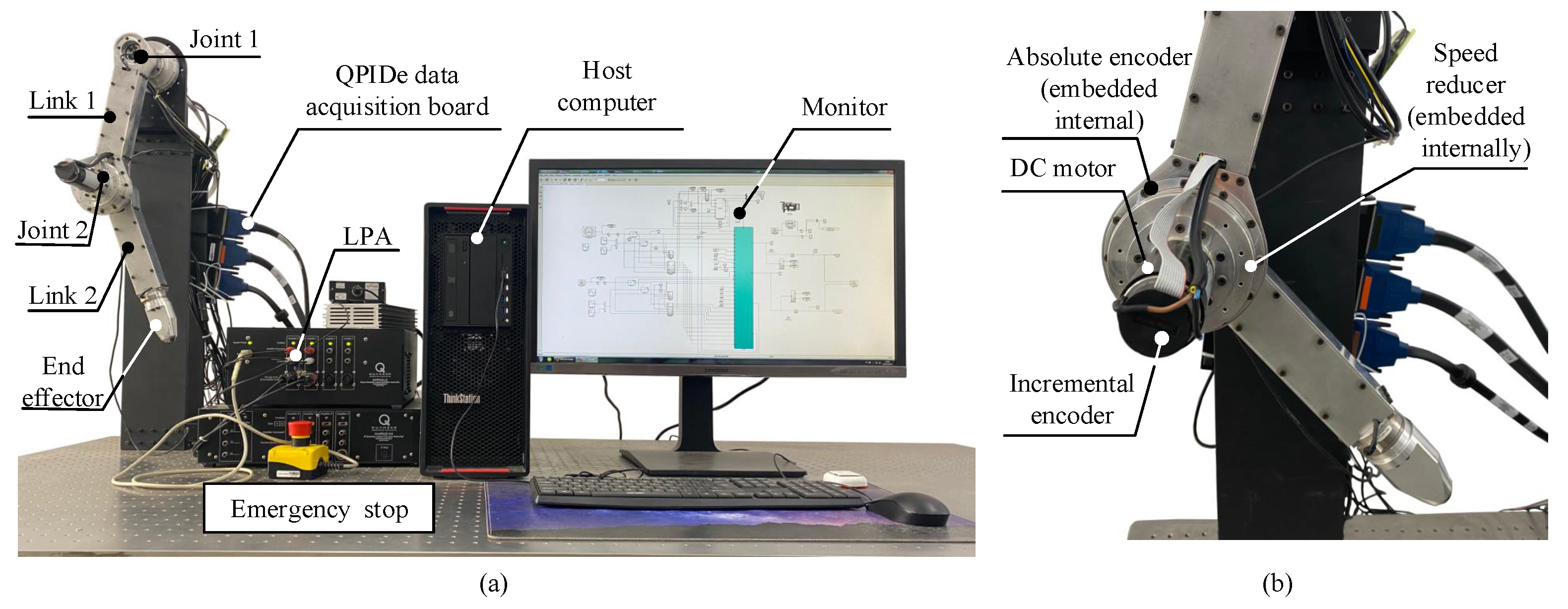
4.1. Experimental Setup
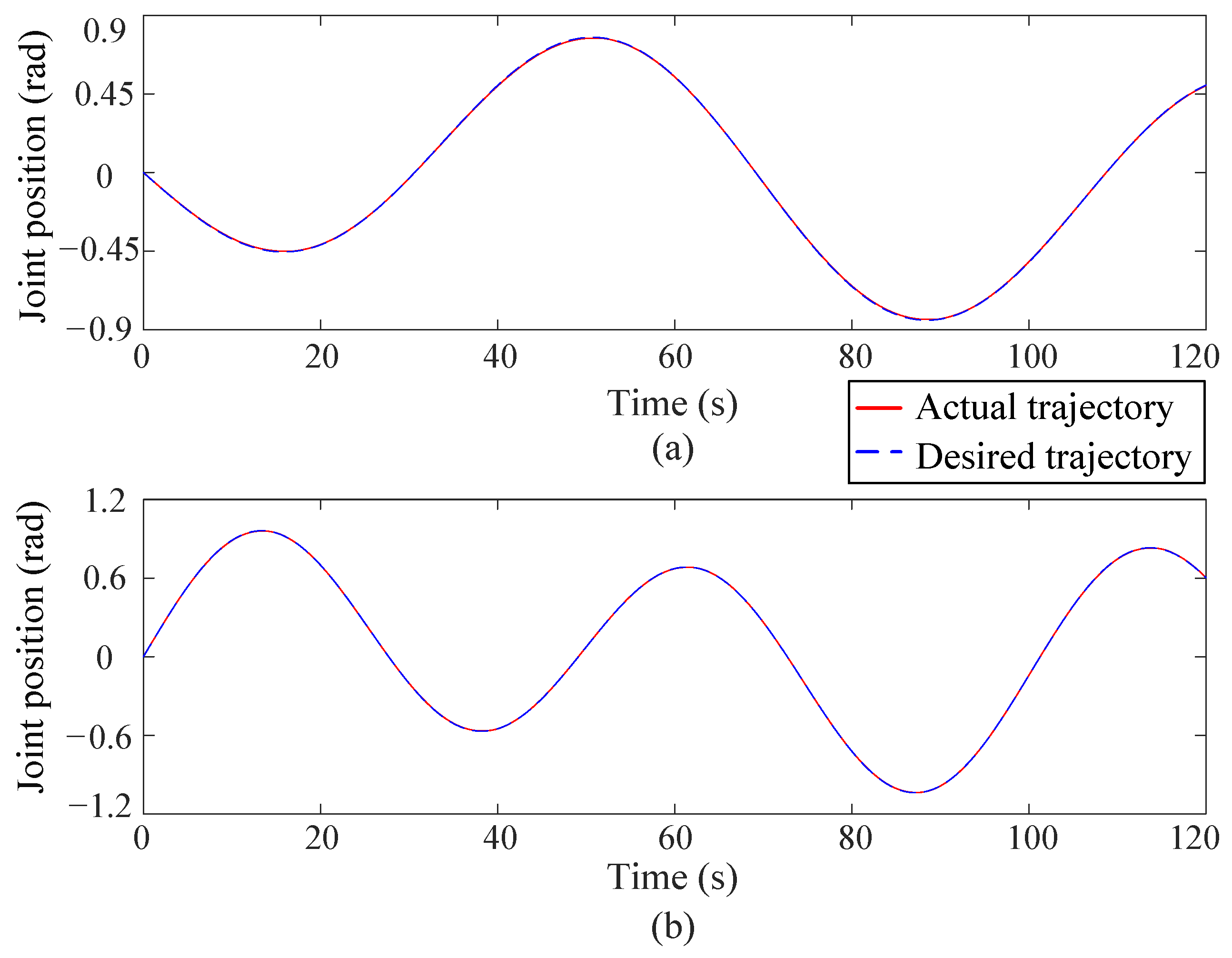
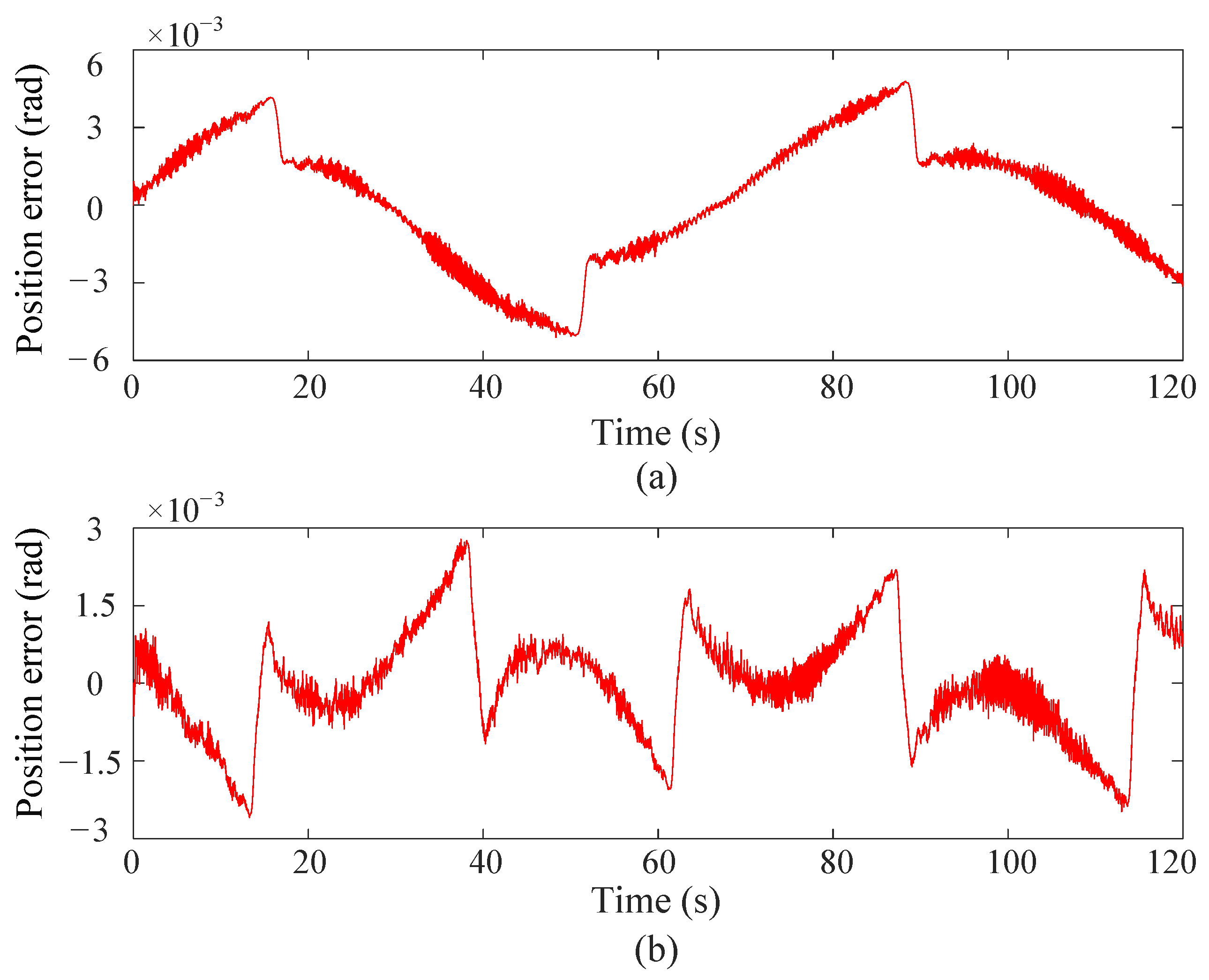
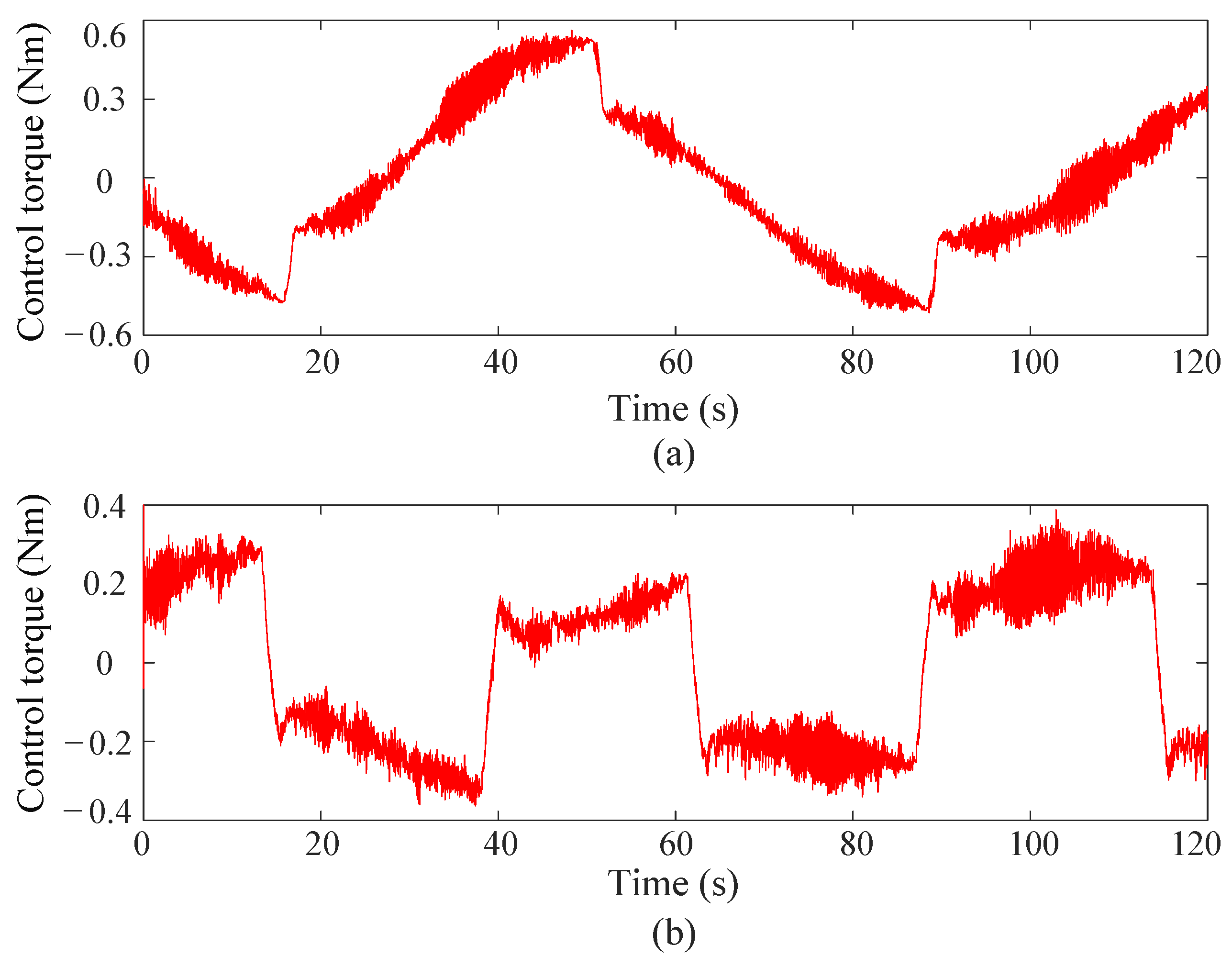
4.2. Experimental Results
- (1)
- Position tracking performance
- (2)
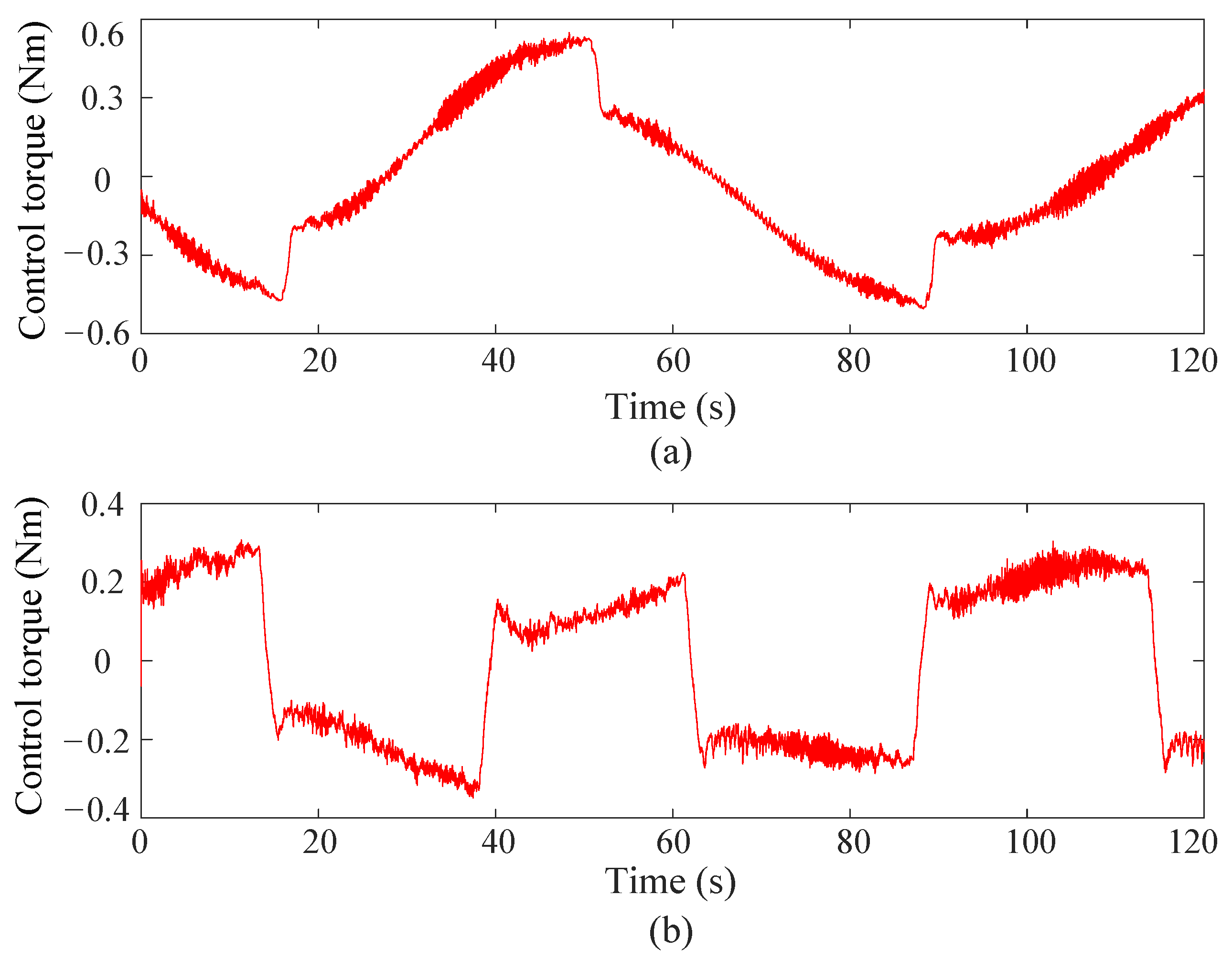
- Control torque
- (3)
- Critic NN weight
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.-J.; Gao, B.; Yu, D.; Li, D.; Liu, L. Neuro-Adaptive Fault-Tolerant Attitude Control of a Quadrotor UAV with Flight Envelope Limitation and Feedforward Compensation. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 3143–3151. [Google Scholar] [CrossRef]
- Xue, S.; Zhao, N.; Zhang, W.; Luo, B.; Liu, D. A Hybrid Adaptive Dynamic Programming for Optimal Tracking Control of USVs. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 9961–9969. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, X.; Meng, Z.; Sun, J. A Smooth Distributed Formation Control Method for Quadrotor UAVs under Event-Triggering Mechanism and Switching Topologies. IEEE Trans. Veh. Technol. 2025, 74, 10081–10091. [Google Scholar] [CrossRef]
- Xue, S.; Zhang, W.; Luo, B.; Liu, D. Integral Reinforcement Learning-Based Dynamic Event-Triggered Nonzero-Sum Games of USVs. IEEE Trans. Cybern. 2025, 55, 1706–1716. [Google Scholar] [CrossRef]
- Luo, D.; Wang, Y.; Li, Z.; Song, Y.; Lewis, F.L. Asymptotic Leader-Following Consensus of Heterogeneous Multi-Agent Systems with Unknown and Time-Varying Control Gains. IEEE Trans. Autom. Sci. Eng. 2025, 22, 2768–2779. [Google Scholar] [CrossRef]
- Huang, Y.; Kuai, J.; Cui, S.; Meng, Z.; Sun, J. Distributed Algorithms via Saddle-Point Dynamics for Multi-Robot Task Assignment. IEEE Robot. Autom. Lett. 2024, 9, 11178–11185. [Google Scholar] [CrossRef]
- Liu, Y.; An, T.; Chen, J.; Zhong, L.; Qian, Y. Event-trigger Reinforcement Learning-based Coordinate Control of Modular Unmanned System via Nonzero-sum Game. Sensors 2025, 25, 314. [Google Scholar] [CrossRef]
- Ren, J.; Wang, D.; Li, M.; Qiao, J. Discounted Stable Adaptive Critic Design for Zero-Sum Games with Application Verifications. IEEE Trans. Autom. Sci. Eng. 2025, 22, 11706–11716. [Google Scholar] [CrossRef]
- Wang, D.; Hu, L.; Li, X.; Qiao, J. Online Fault-Tolerant Tracking Control with Adaptive Critic for Nonaffine Nonlinear Systems. IEEE/CAA J. Autom. Sin. 2025, 12, 215–227. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.-Y. Reinforcement Learning-Based Distributed Robust Bipartite Consensus Control for Multispacecraft Systems with Dynamic Uncertainties. IEEE Trans. Ind. Inform. 2024, 20, 13341–13351. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, S.; Liu, D. Self-Triggered Approximate Optimal Neuro-Control for Nonlinear Systems Through Adaptive Dynamic Programming. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 4713–4723. [Google Scholar] [CrossRef]
- Lin, M.; Zhao, B.; Liu, D. Optimal Learning Output Tracking Control: A Model-Free Policy Optimization Method with Convergence Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 5574–5585. [Google Scholar] [CrossRef]
- Liu, N.; Zhang, K.; Xie, X.; Yue, D. UKF-Based Optimal Tracking Control for Uncertain Dynamic Systems with Asymmetric Input Constraints. IEEE Trans. Cybern. 2024, 54, 7224–7235. [Google Scholar] [CrossRef]
- Wang, K.; Mu, C.; Ni, Z.; Liu, D. Safe Reinforcement Learning and Adaptive Optimal Control with Applications to Obstacle Avoidance Problem. IEEE Trans. Autom. Sci. Eng. 2024, 21, 4599–4612. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Z.; Lv, Y.; Na, J.; Liu, C.; Zhao, Z. Data-Driven Learning for H∞ Control of Adaptive Cruise Control Systems. IEEE Trans. Veh. Technol. 2024, 73, 18348–18362. [Google Scholar] [CrossRef]
- Ding, C.; Zhang, Z.; Miao, Z.; Wang, Y. Event-Based Finite-Time Formation Tracking Control for UAV with Bearing Measurements. IEEE Trans. Ind. Electron. 2025, 72, 7482–7492. [Google Scholar] [CrossRef]
- Wang, K.; Mu, C. Learning-Based Control with Decentralized Dynamic Event-Triggering for Vehicle Systems. IEEE Trans. Ind. Inform. 2023, 19, 2629–2639. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, B.; Liu, D.; Zhang, Y. Event-Triggered Decentralized Integral Sliding Mode Control for Input-Constrained Nonlinear Large-Scale Systems with Actuator Failures. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1914–1925. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, B.; Liu, D.; Zhang, S. Distributed Fault Tolerant Consensus Control of Nonlinear Multiagent Systems via Adaptive Dynamic Programming. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 9041–9053. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Miao, Z.; Jiang, Y.; Feng, Y. Asymptotic Stability Analysis and Stabilization Control for General Fractional-Order Neural Networks via an Unified Lyapunov Function. IEEE Trans. Netw. Sci. Eng. 2024, 11, 2675–2688. [Google Scholar] [CrossRef]
- Xia, H.; Hou, J.; Guo, P. Two-Level Local Observer-Based Decentralized Optimal Fault Tolerant Tracking Control for Unknown Nonlinear Interconnected Systems. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1779–1790. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, H.; Ming, Z.; Wang, S.; Agarwal, R.K. Dynamic Event-Triggered Safe Control for Nonlinear Game Systems with Asymmetric Input Saturation. IEEE Trans. Cybern. 2024, 54, 5115–5126. [Google Scholar] [CrossRef]
- Xia, H.; Wang, X.; Huang, D.; Sun, C. Cooperative-Critic Learning-Based Secure Tracking Control for Unknown Nonlinear Systems with Multisensor Faults. IEEE Trans. Cybern. 2025, 55, 282–294. [Google Scholar] [CrossRef]
- Qin, C.; Qiao, X.; Wang, J.; Zhang, D.; Hou, Y.; Hu, S. Barrier-Critic Adaptive Robust Control of Nonzero-Sum Differential Games for Uncertain Nonlinear Systems with State Constraints. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 50–63. [Google Scholar] [CrossRef]
- Wei, Q.; Jiang, H. Event-/Self-Triggered Adaptive Optimal Consensus Control for Nonlinear Multiagent System with Unknown Dynamics and Disturbances. IEEE Trans. Cybern. 2025, 55, 1476–1485. [Google Scholar] [CrossRef]
- An, T.; Dong, B.; Yan, H.; Liu, L.; Ma, B. Dynamic Event-Triggered Strategy-Based Optimal Control of Modular Robot Manipulator: A Multiplayer Nonzero-Sum Game Perspective. IEEE Trans. Cybern. 2024, 54, 7514–7526. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhang, Z.-X.; Xie, X.P.; Rubio, J.d.J. An Unknown Multiplayer Nonzero-Sum Game: Prescribed-Time Dynamic Event-Triggered Control via Adaptive Dynamic Programming. IEEE Trans. Autom. Sci. Eng. 2024, 22, 8317–8328. [Google Scholar] [CrossRef]
- Mu, C.; Wang, K.; Ni, Z.; Sun, C. Cooperative Differential Game-Based Optimal Control and Its Application to Power Systems. IEEE Trans. Ind. Inform. 2020, 16, 5169–5179. [Google Scholar] [CrossRef]
- An, T.; Wang, Y.; Liu, G.; Li, Y.; Dong, B. Cooperative Game-Based Approximate Optimal Control of Modular Robot Manipulators for Human–Robot Collaboration. IEEE Trans. Cybern. 2023, 53, 4691–4703. [Google Scholar] [CrossRef]
- Belhenniche, A.; Chertovskih, R.; Gonçalves, R. Convergence Analysis of Reinforcement Learning Algorithms Using Generalized Weak Contraction Mappings. Symmetry 2025, 17, 750. [Google Scholar] [CrossRef]



| Joint 1 | Joint 2 | |
|---|---|---|
| Position error of proposed method | 1.88 × rad | 1.23 × rad |
| Position error of existing method | 2.56 × rad | 1.79 × rad |
| Control torque of proposed method | 0.36 Nm | 0.19 Nm |
| Control torque of existing method | 0.42 Nm | 0.22 Nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, L.; Liu, Y.; Zhong, L.; Qian, Y. Cooperative Differential Game-Based Modular Unmanned System Approximate Optimal Control: An Adaptive Critic Design Approach. Symmetry 2025, 17, 1665. https://doi.org/10.3390/sym17101665
Si L, Liu Y, Zhong L, Qian Y. Cooperative Differential Game-Based Modular Unmanned System Approximate Optimal Control: An Adaptive Critic Design Approach. Symmetry. 2025; 17(10):1665. https://doi.org/10.3390/sym17101665
Chicago/Turabian StyleSi, Liang, Yebao Liu, Luyang Zhong, and Yuhan Qian. 2025. "Cooperative Differential Game-Based Modular Unmanned System Approximate Optimal Control: An Adaptive Critic Design Approach" Symmetry 17, no. 10: 1665. https://doi.org/10.3390/sym17101665
APA StyleSi, L., Liu, Y., Zhong, L., & Qian, Y. (2025). Cooperative Differential Game-Based Modular Unmanned System Approximate Optimal Control: An Adaptive Critic Design Approach. Symmetry, 17(10), 1665. https://doi.org/10.3390/sym17101665






