Asymmetric Structural Response Characteristics of Transmission Tower-Line Systems Under Cross-Fault Ground Motions Revealed by Shaking Table Tests
Abstract
1. Introduction
2. Experimental Tower-Line System Model Design
3. Instrumentation Arrangement and Test Scheme
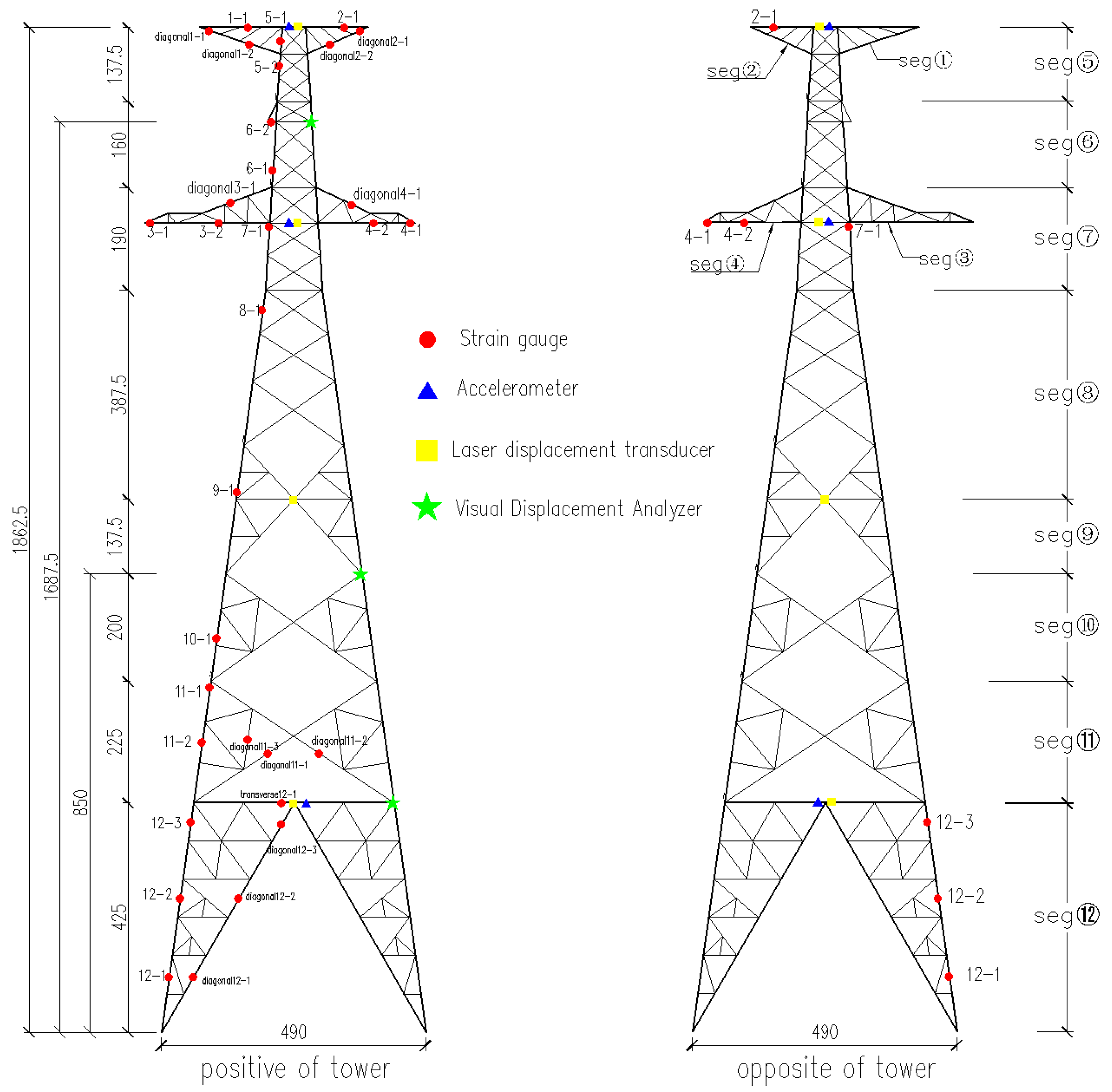
3.1. Instrumentation Arrangement
3.2. Test Scheme
3.3. Structural Dynamic Characterization Test
4. System Response Under Cross-Fault Inputs in the Out-of-Plane Direction
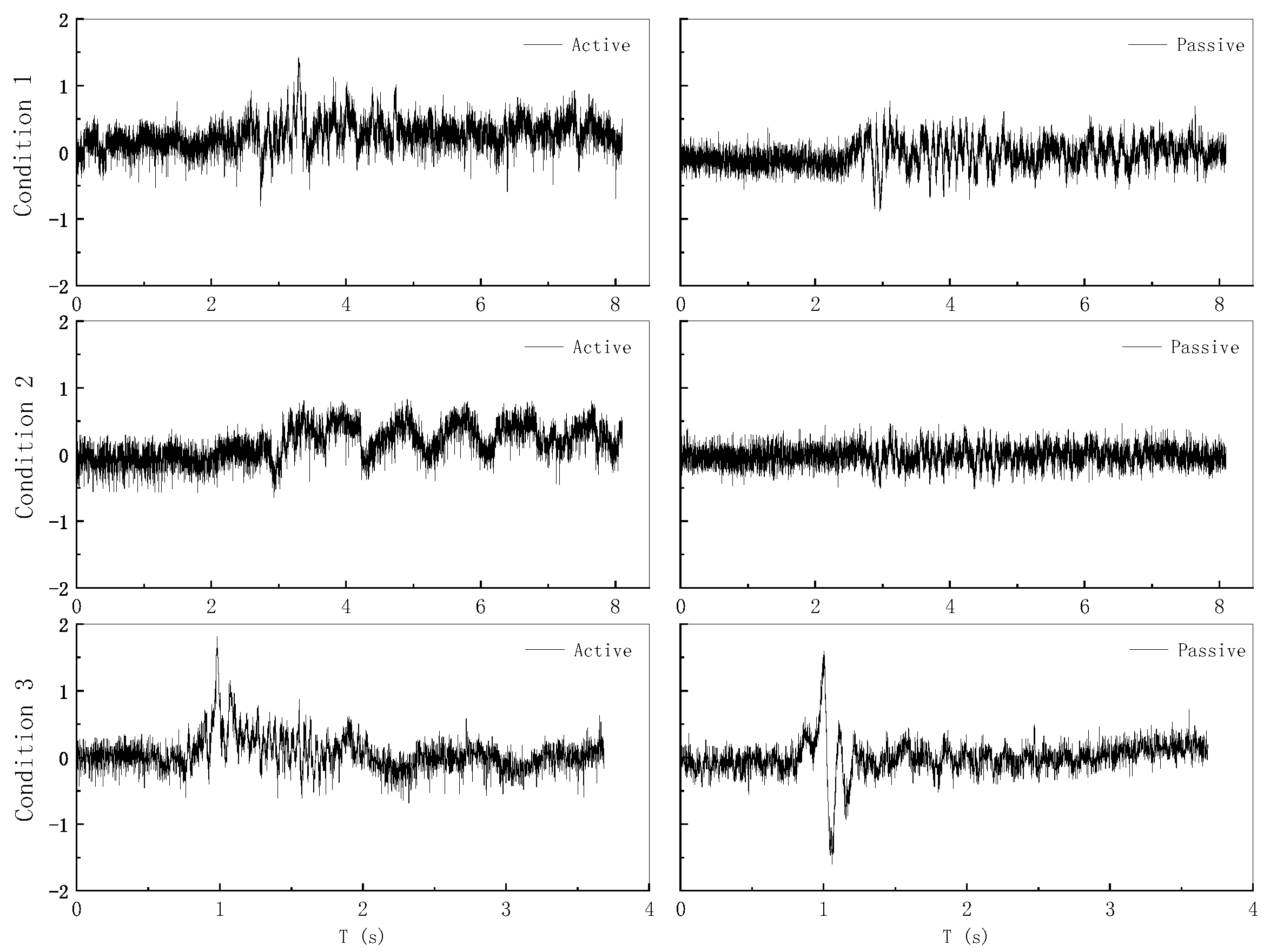
4.1. Influence of Displacement Processes on Tower-Line System Under Identical Permanent Displacement
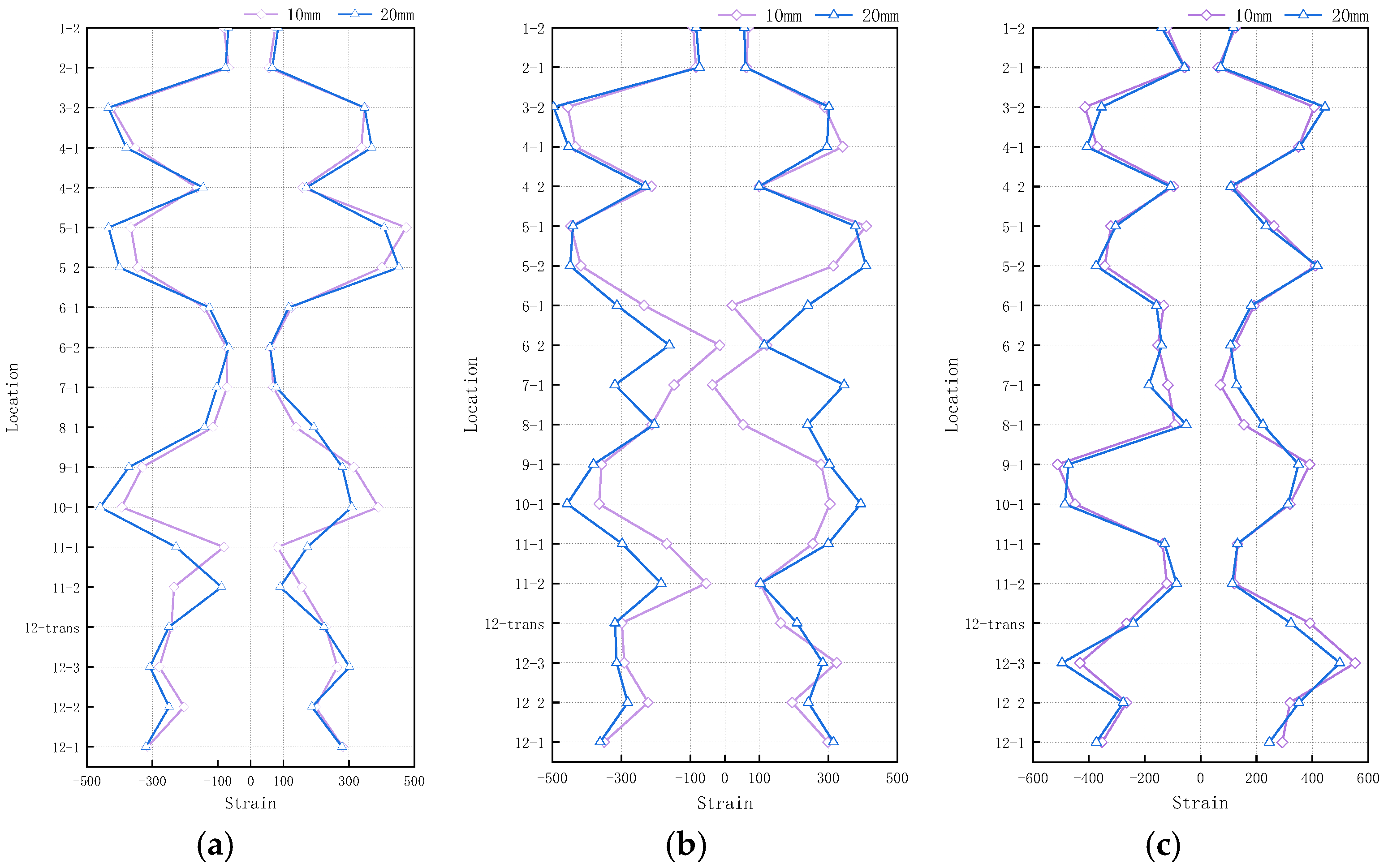
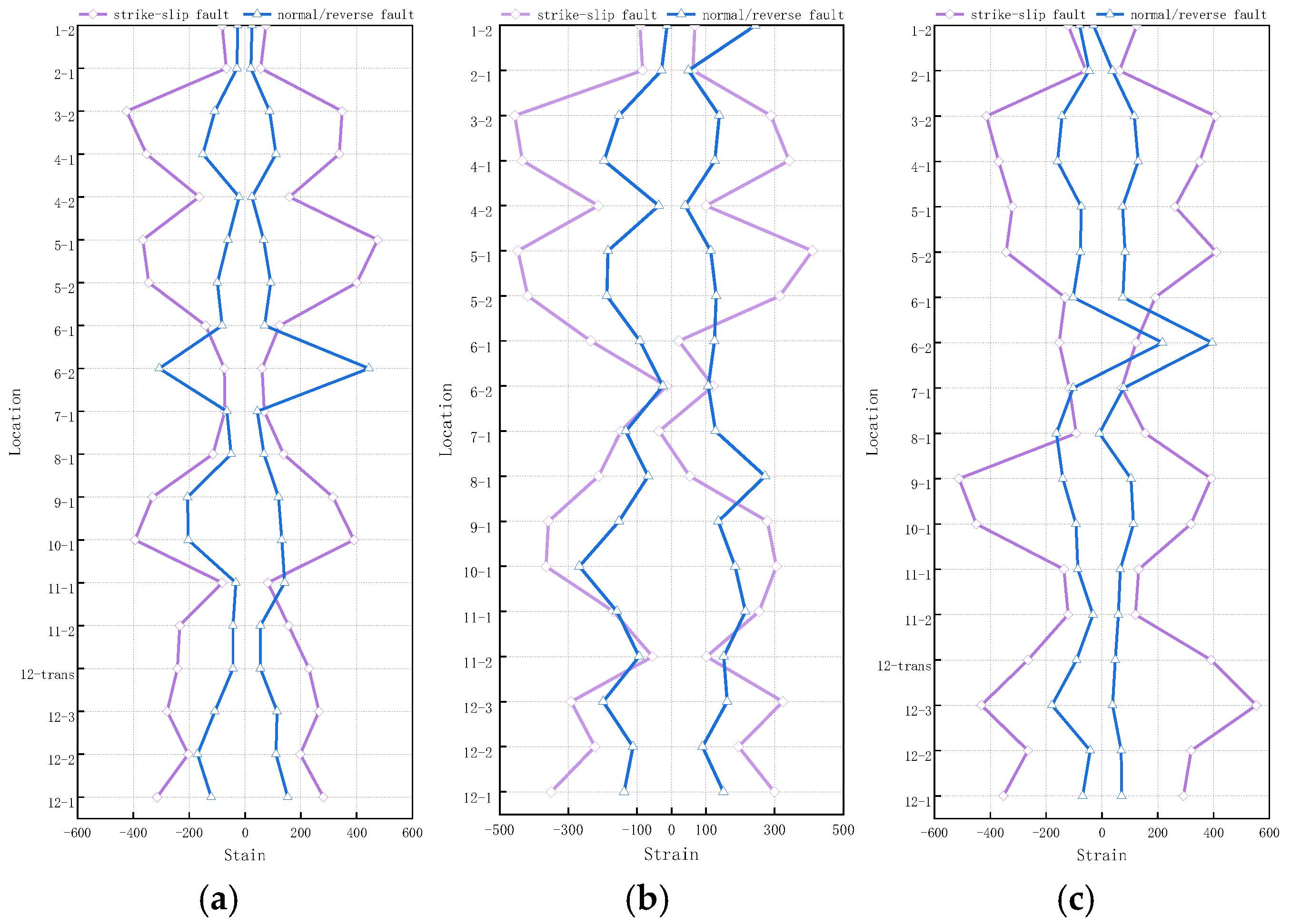
4.1.1. Strain Response Characteristics
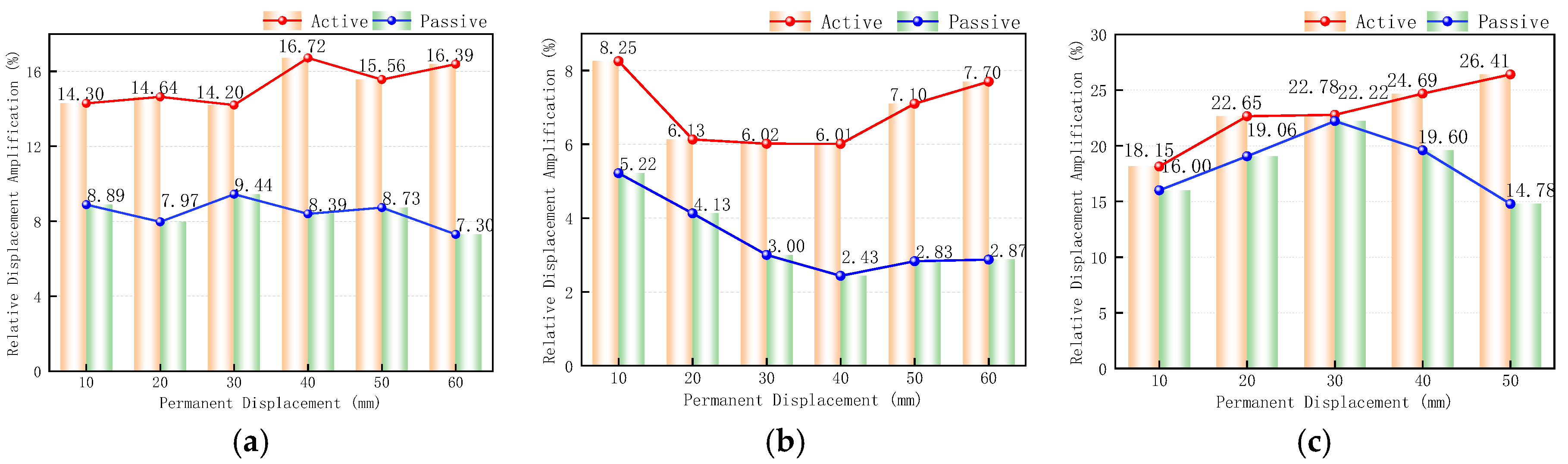
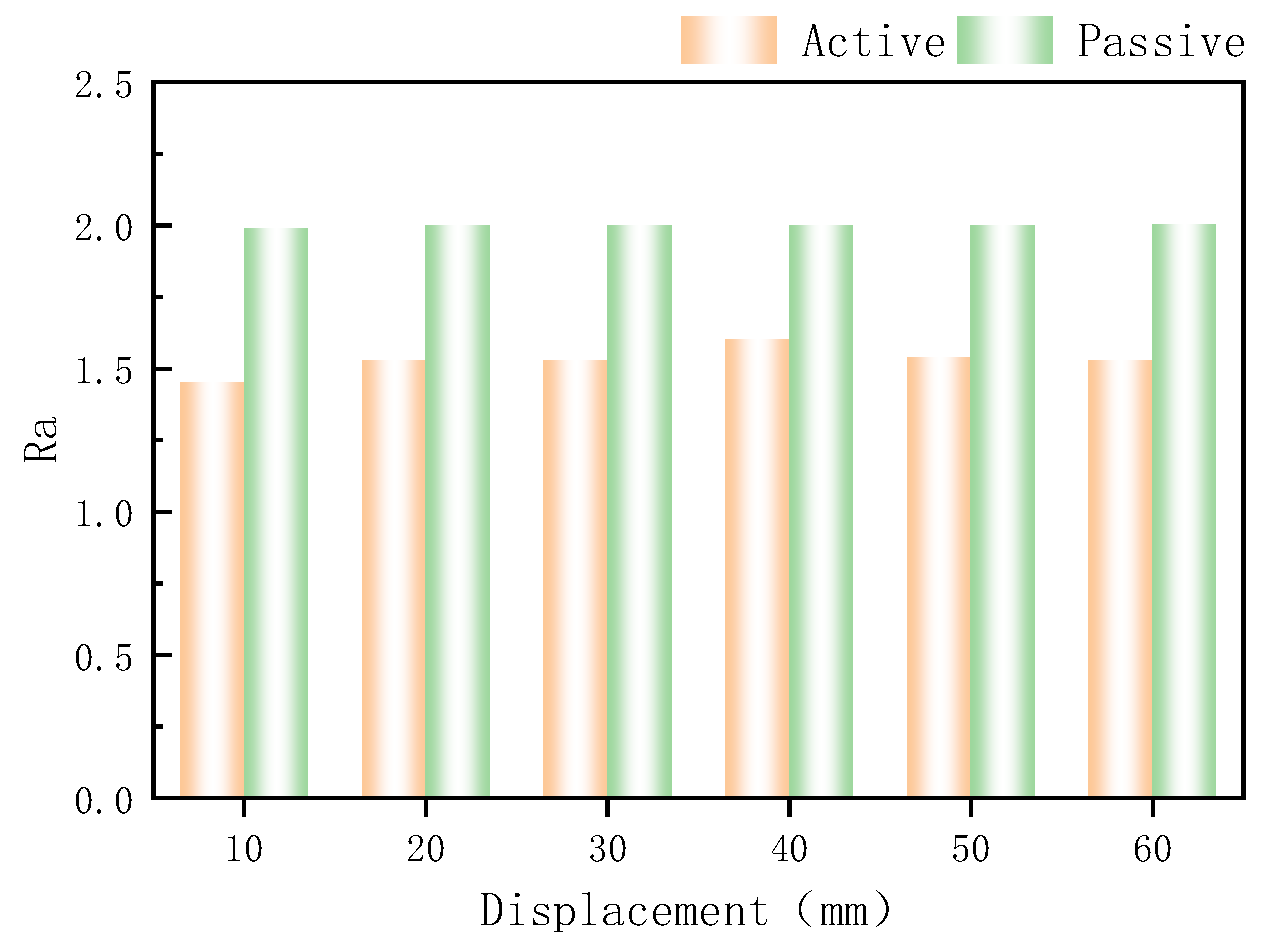
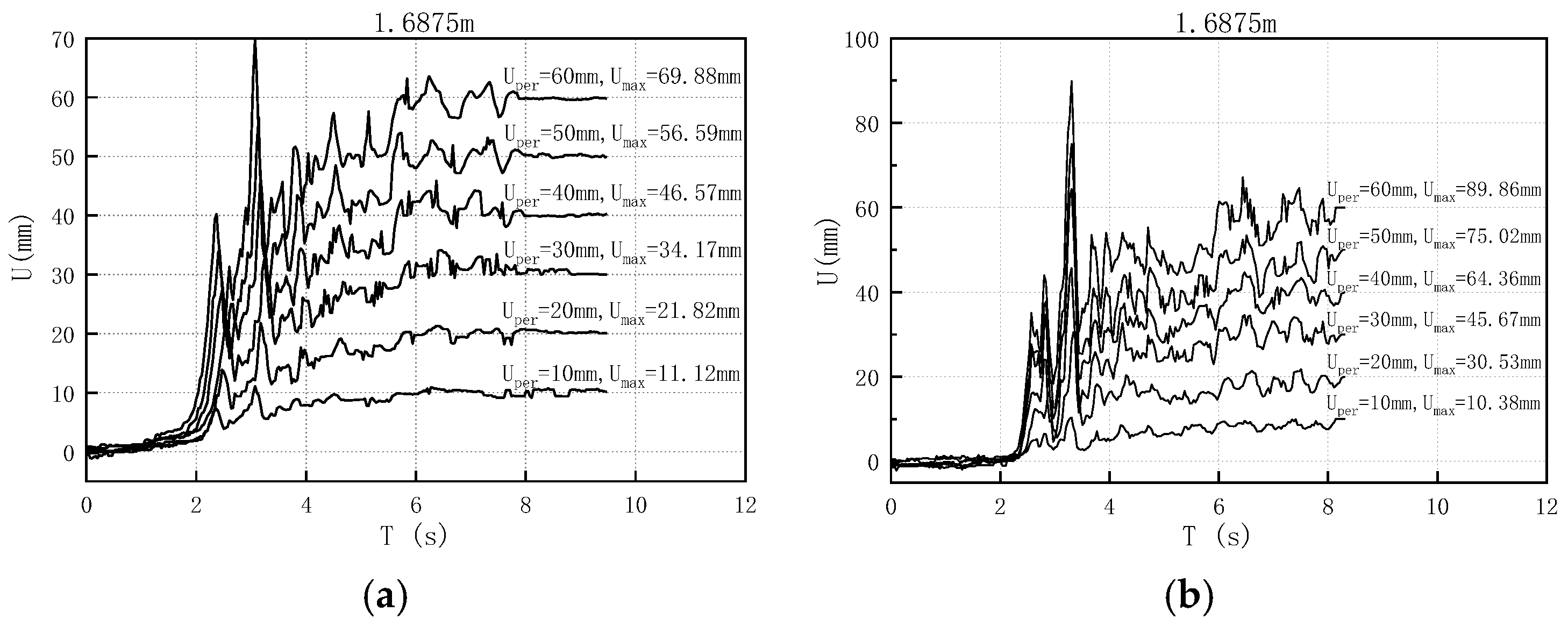
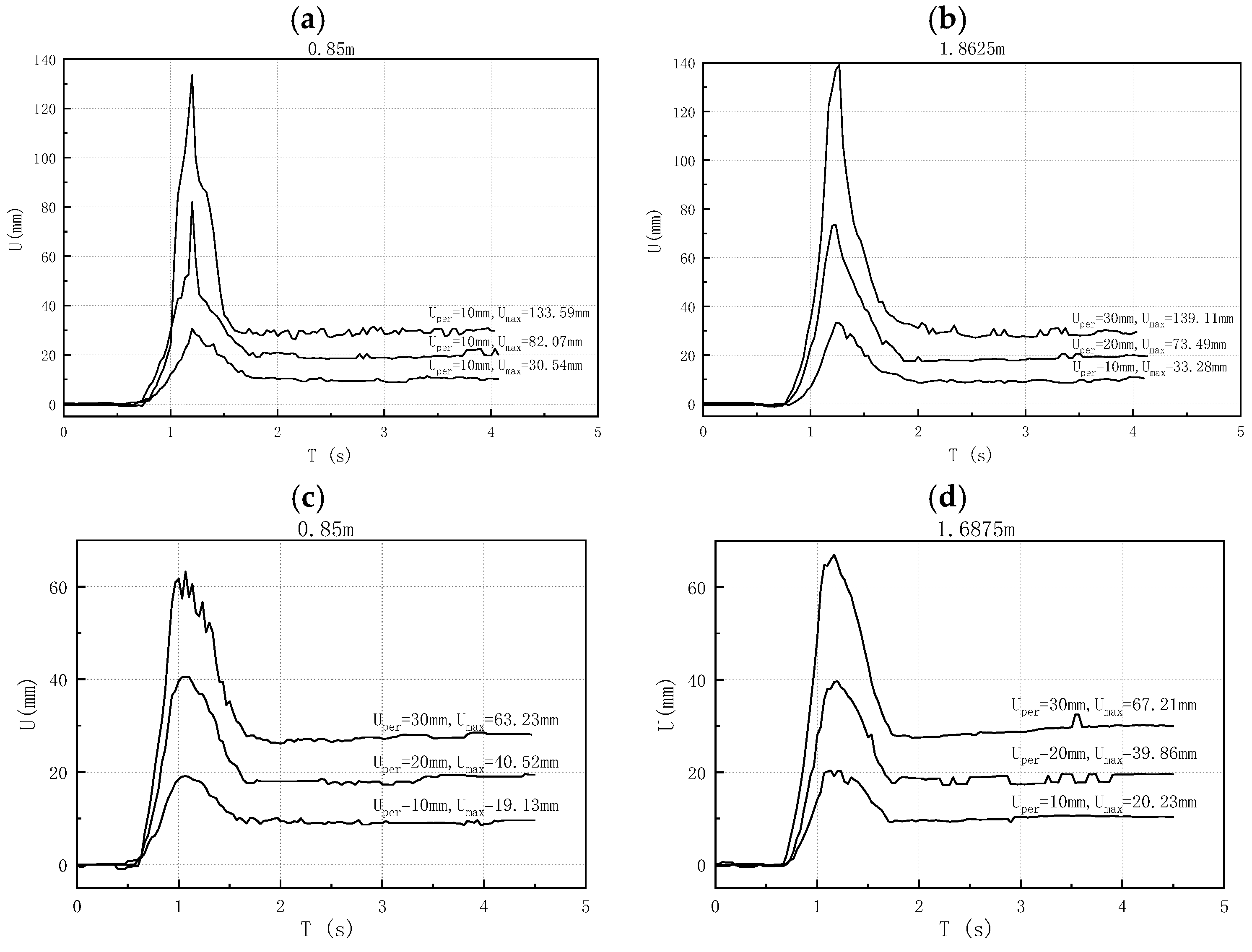
4.1.2. Displacement Response Characteristics
4.1.3. Acceleration Response Characteristics
4.1.4. Analysis of Dynamic Response Results
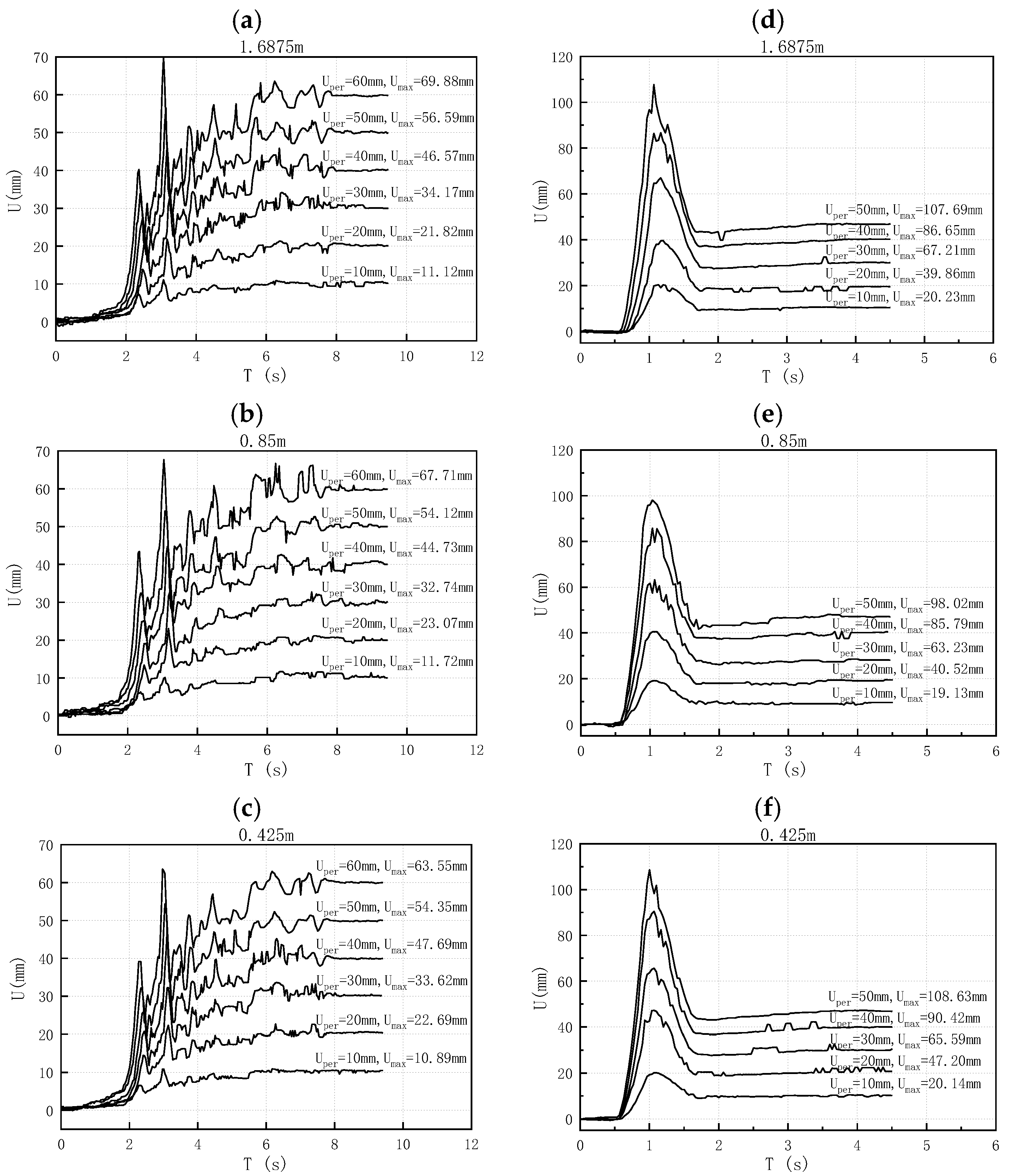
4.2. Influence of Different Permanent Displacement on Tower-Line System
4.2.1. Strain Response Characteristics
4.2.2. Displacement Response Characteristics
4.2.3. Acceleration Response Characteristics
5. System Response Under Cross-Fault Input in the Parallel Tower-Line Direction
5.1. Strain Response Characteristics
5.2. Displacement Response Characteristics
6. Conclusions
- The acceleration response of the tower-line system is dominated by the spectral characteristics of the ground motion, while exhibiting negligible correlation with the amplitude of input displacement. A spatiotemporally asymmetric distribution of acceleration among structural components was observed, indicating a clear deviation from ideal symmetric dynamic behavior. Notably, the acceleration fluctuation in passive plate towers was found to be 35–50% lower than that in active plate towers during seismic excitation, suggesting a significant reduction in the symmetry of the system’s inertial response.
- Distinct damage patterns were identified in transmission towers subjected to horizontal motions from normal/reverse faults versus strike-slip faults. Nevertheless, Segments 9–10 consistently emerged as a critical vulnerable region across fault types. Under identical permanent displacement conditions, peak displacements induced by normal/reverse fault motions exceeded those from strike-slip motions by 50–100%. Accordingly, a fault-type-specific amplification factor of 1.5 is recommended for the design of towers in normal/reverse fault zones. For maintenance prioritization, special attention should be given to inspections within Segments 9–10.
- The displacement responses of the active and passive plates demonstrated strong synchronization. As the excitation frequency approaches the natural frequency of the structure, the dynamic amplification effect is enhanced in the active plate, corroborating the mechanism of resonance response. Increased instantaneous displacement in the active plate leads to greater variability in tower displacement, whereas abrupt displacement changes in the passive plate alter the response mode of the coupled tower-line system. Additionally, step-like changes in ground motion were found to modify the dynamic characteristics of the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, L.; Li, H.; Hou, H. Response Analysis of Transmission Tower-Line System Under Smart-1 Seismic Ground Motion Excitation. Eng. Mech. 2013, 30, 273–278. [Google Scholar]
- GB 50011-2010; Code for Seismic Design of Buildings, 2016 ed. China Architecture Building Press: Beijing, China, 2016. (In Chinese)
- Kim, J.; Nguyen, T.D.; Suleymanzade, A.; An, H.; Hong, S. Learning probabilistic symmetrization for architecture agnostic equivariance. Adv. Neural Inf. Process. Syst. 2023, 36, 18582–18612. [Google Scholar]
- Goel, R.K.; Chopra, A.K. Linear analysis of ordinary bridges crossing fault-rupture zones. J. Bridge Eng. 2009, 14, 203–215. [Google Scholar] [CrossRef]
- Gazetas, G.; Zarzouras, O.; Drosos, V.; Anastasopoulos, I. Bridge-pier caisson foundations subjected to normal and thrust faulting: Physical experiments versus numerical analysis. Meccanica 2015, 50, 341–354. [Google Scholar] [CrossRef]
- Yang, S.; Mavroeidis, G.P.; Ucak, A.; Tsopelas, P. Effect of ground motion filtering on the dynamic response of a seismically isolated bridge with and without fault crossing considerations. Soil Dyn. Earthq. Eng. 2017, 92, 183–191. [Google Scholar] [CrossRef]
- Yang, S.; Mavroeidis, G.P.; Ucak, A. Analysis of bridge structures crossing strike-slip fault rupture zones: A simple method for generating across-fault seismic ground motions. Earthq. Eng. Struct. Dyn. 2020, 49, 1281–1307. [Google Scholar] [CrossRef]
- Zeng, C.; Jiang, H.; Huang, L.; Guo, H.; Ma, X.; Song, G. Nonlinear seismic response characteristics of a single-tower cable-stayed bridge across a fault. China J. Highw. Transp. 2021, 34, 230–245. [Google Scholar]
- Hu, J.J.; Sheng, Z.Q.; Xie, L.L.; Zou, Y.L. Simulation of input ground motion and seismic response of fault-crossing structure. Earthq. Eng. Eng. Dyn. 2024, 44, 1–13. [Google Scholar]
- Jia, H.; Cheng, W.; Kang, W.; Zhai, Y.; Zheng, S.; Hui, Y. BPNN-predicted fault permanent dislocation and seismic response analyses of long-span suspension bridges crossing dip-slip faults. Soil Dyn. Earthq. Eng. 2024, 182, 108712. [Google Scholar]
- Cheng, W.; Tang, Q.H.; Jia, H.Y.; Zhong, Y.; Xu, Z.; Zheng, S.X. A prediction of fault displacement and study of seismic response of suspension bridge across fault. J. Railw. Sci. Eng. 2024, 21, 204–214. (In Chinese) [Google Scholar]
- Han, J.; El Naggar, M.H.; Zhao, M.; Zhong, Z.; Hou, B.; Du, X. Longitudinal response of buried pipeline under non-uniform seismic excitation from multi-point shaking table tests. Soil Dyn. Earthq. Eng. 2021, 140, 106440. [Google Scholar] [CrossRef]
- Guo, W.; Chen, W.Q.; He, C.J.; Jiang, L.; Wang, Y.; Guo, Z.; Yan, Q.; Zhao, L.; Lin, Y. Shaking table test research on shear behavior of cross-fault geosynthetics reinforced and pile-supported embankment. Soil Dyn. Earthq. Eng. 2022, 155, 107197. [Google Scholar]
- Zhang, X.; Shen, Y.; Chang, M.; Su, W.; Tao, W. Dynamic response and failure mode of a novel seismic structure for fault-crossing tunnel: Theoretical analysis and shaking table test verification. Eng. Fail. Anal. 2025, 177, 109671. [Google Scholar] [CrossRef]
- Li, L.; Chen, Z.; Lu, P.; Huang, Y. Dynamic response analysis of cross-fault tunnel considering source-to-structure seismic input and near-fault effect. Tunn. Undergr. Space Technol. 2025, 162, 106674. [Google Scholar] [CrossRef]
- Zhang, T. Effect of Sma-Utmd On Seismic Performance of Transmission Tower Line System. Master’s Thesis, Northeast Electric Power University, Changchun, China, 2023. (In Chinese). [Google Scholar]
- Tian, L.; Li, H.N.; Liu, G.H. Seismic Response of Power Transmission Tower-Line System Subjected to Spatially Varying Ground Motions. Math. Probl. Eng. 2010, 2010, e587317. [Google Scholar]
- Tian, L. Experimental Research and Response Analysis of Transmission Tower-Line System Under Multi-Component and Multi-Support Earthquake Excitations. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2011. (In Chinese). [Google Scholar]
- Tian, L.; Li, H.N.; Liu, G.H. Seismic Response of Power Transmission Tower-Line System Under Multi-Component Multi-Support Excitations. J. Earthq. Tsunami 2012, 6, 1250025. [Google Scholar]
- Tian, L.; Liu, J.C.; Pan, H.Y.; Niu, Y.H.; Guo, W. Research on shaking table test of transmission tower-line system under near-fault earthquake. China Civ. Eng. J. 2018, 51, 127–132. (In Chinese) [Google Scholar]
- Xie, Q.; Bai, J.; Xue, S.T. Shake table test on UHV AC double circuit transmission tower. High Volt. Eng. 2012, 38, 1410–1419. [Google Scholar]
- Xie, Q.; Bai, J.; Xue, S.T.; Qin, Q.Z. Shaking table test on nonlinear vibration responses of UHV transmission tower-line coupling system. Earthq. Eng. Eng. Vib. 2012, 32, 103–110. [Google Scholar]
- Bai, J.; Xie, Q.; Xue, S.T. Design theory and method of shaking table test model for a UHV double circuit transmission tower-line coupled system. J. Vib. Shock. 2013, 32, 47–52. [Google Scholar]
- Bai, J.; Xie, Q.; Xue, S.T.; Shen, D.M. Shaking table test model design for UHV latticed transmission tower-line coupling system. J. Hunan Univ. Nat. Sci. 2013, 40, 20–25. [Google Scholar]
- Xiong, Z.H. Experimental Study on Tower-Lines System of Ultra-High Voltage Glass-Shaped Transmission Under Multiple Array Shaking Tables. Master’s Thesis, Fuzhou University, Fuzhou, China, 2017. (In Chinese). [Google Scholar]
- Xin, A.Q. Experimental Research on the Cross-Fault Transmission Tower-Line System. Master’s Thesis, Shandong University, Jinan, China, 2019. (In Chinese). [Google Scholar]
- Wei, W.H.; Yuan, C.; Wang, H.; Hu, Y. Seismic response of transmission tower-line system under coupled horizontal and tilt ground motion. J. Build. Struct. 2019, 40, 79–88. (In Chinese) [Google Scholar]
- Tian, L.; Fu, Z.Y.; Pan, H.Y.; Ma, R.; Liu, Y. Experimental and numerical study on the collapse failure of long-span transmission tower-line systems subjected to extremely severe earthquakes. Earthq. Struct. 2019, 16, 513–522. [Google Scholar]
- Tian, L.; Dong, X.; Pan, H.; Gao, G.; Xin, A. Critical seismic incidence angle of transmission tower based on shaking table tests. Struct. Eng. Mech. 2020, 76, 251–267. [Google Scholar]
- Tian, L.; Bi, W.; Liu, J.; Dong, X.; Xin, A. Seismic and collapse analysis of a UHV transmission tower-line system under cross-fault ground motions. Earthq. Struct. 2020, 19, 445–457. [Google Scholar]
- Gai, X.; Tian, L. Collapse Analysis of Transmission Towers under Multi-dimensional Seismic Excitation Considering Hysteretic Behavior of Components. China Earthq. Eng. J. 2020, 42, 352–359. [Google Scholar]
- Yuan, G.Y.; Pan, H.Y.; Ma, R.S.; Tian, L. Collapse analysis of transmission tower-line system under multi-dimensional seismic excitation based on different failure criteria. World Earthq. Eng. 2019, 35, 184–192. [Google Scholar]
- Barenblatt, G.I. Scaling, Self-Similarity, and Intermediate Asymptotics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Harris, H.; Sabnis, G.M. Structural Modeling and Experimental Techniques; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Krawinkler, H.; Seneviratna, G.D.P.K. Pros and cons of a pushover analysis of seismic performance evaluation. Eng. Struct. 1998, 20, 452–464. [Google Scholar] [CrossRef]
- Moncarz, P.D.; Krawinkler, H. Theory and Application of Experimental Model Analysis in Earthquake Engineering; Stanford University: Stanford, CA, USA, 1981. [Google Scholar]
- Zhang, M.Z. Study on Similitude Laws for Shaking Table Tests. Earthq. Eng. Eng. Dyn. 1997, 17, 52–58. [Google Scholar]
- Liu, W.P. Shaking Table Test of Transmission Tower-Line System Under Different Input Directions of Multi-Dimensional Ground Motions. Master’s Thesis, Shandong University, Jinan, China, 2022. (In Chinese). [Google Scholar]
- Tian, L.; Li, H.N.; Huang, L.Z. Non-proportional problem in shaking table model of a power transmission tower-line system. Vib. Shock. 2012, 31, 114–118. [Google Scholar]
- Xie, J.J.; Wen, Z.P.; Gao, M.T. Recovery of co-seismic deformation from strong motion records during the Wenchuan earthquake. Acta Seismol. Sin. 2013, 35, 369–379. (In Chinese) [Google Scholar]








| Type | Similarity Ratio | Formula | Value |
|---|---|---|---|
| Geometric | * Length | 1/40 | |
| * Elastic modulus | 1/2 | ||
| Cross-sectional area | 1/261.3 | ||
| Physical | Density | 6.67 | |
| Mass | 1/1567 | ||
| Dynamic | Time | 0.09 | |
| Frequency | 10.95 | ||
| * Acceleration | 3 |
| Name | Section | Material | Unit | Size |
|---|---|---|---|---|
| Transmission Tower | Primary members | Angle copper | mm | L15 × 1 |
| diagonal members | L7 × 0.5 | |||
| Others | L5 × 0.5 | |||
| Transmission Line | Conductors | Steel wire | mm | D3 |
| Ground | D1.5 | |||
| Insulator string | Conductors wire | Steel rods | mm | 263 |
| Ground wire | 20 |
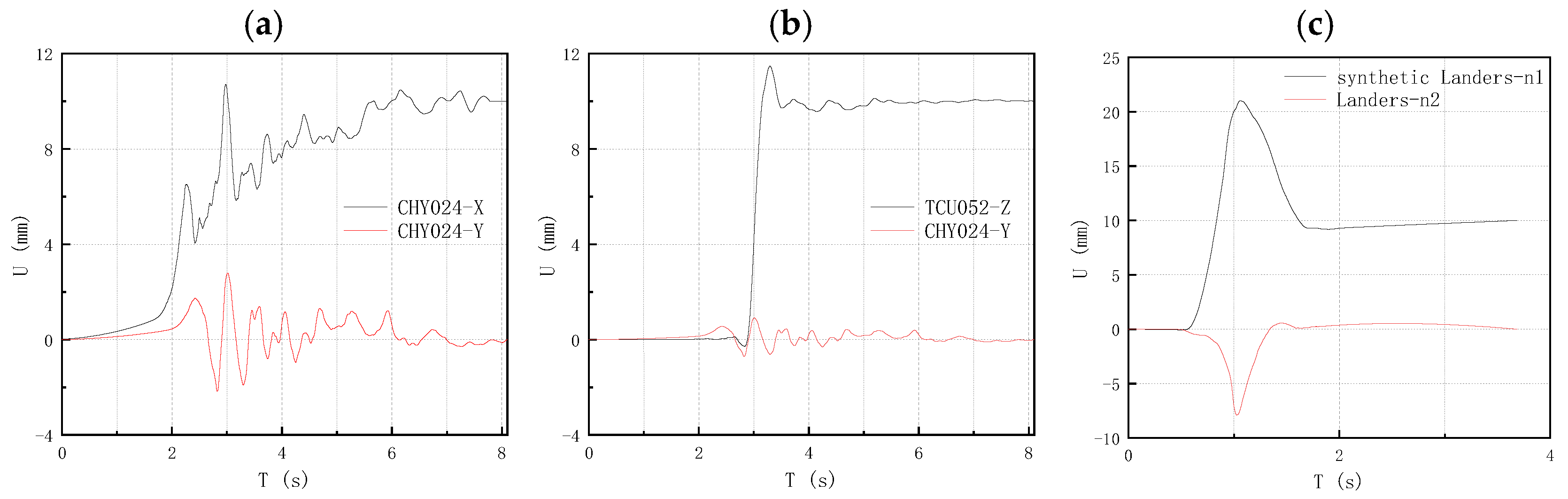
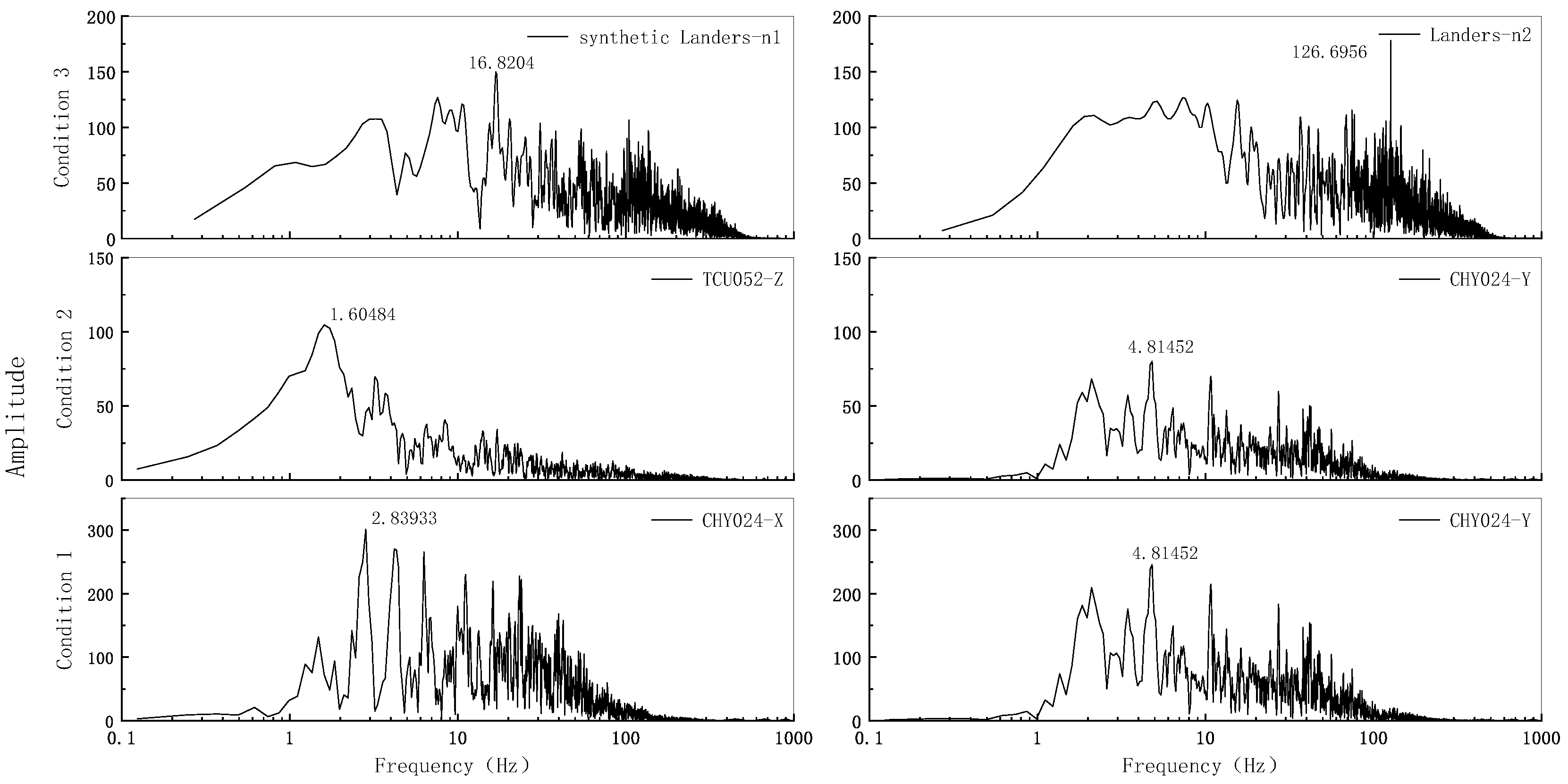
| Name | Direction | Condition | With Permanent Displacement | Seismic Wave |
|---|---|---|---|---|
| The horizontal component of a strike-slip fault | X-direction (vertical line) | Condition 1 | Yes (active plate) | CHY024-X |
| No (passive plate) | CHY024-Y | |||
| Condition 2 | Yes (active plate) | TCU052-Z | ||
| No (passive plate) | CHY024-Y | |||
| Condition 3 | Yes (active plate) | synthetic landers-n1 | ||
| No (passive plate) | landers-n2 | |||
| The horizontal component of a normal-reverse fault | Y-direction (Parallel line) | Condition 1 | Yes (active plate) | CHY024-X |
| No (passive plate) | CHY024-Y | |||
| Condition 2 | Yes (active plate) | TCU052-Z | ||
| No (passive plate) | CHY024-Y | |||
| Condition 3 | Yes (active plate) | synthetic landers-n1 | ||
| No (passive plate) | landers-n2 |
| NGA | Earthquake Name | Year | Station Name | Mw | Vs30 (m/s) | PGA (g) | Rx (km) | Site Condition |
|---|---|---|---|---|---|---|---|---|
| 1193 | Chi-Chi_Taiwan | 1999 | CHY024 | 7.62 | 427.73 | 0.23 | 9.62 | C |
| 1492 | Chi-Chi_Taiwan | 1999 | TCU052 | 7.62 | 579.1 | 0.40 | 1.2 | C |
| 879 | Landers | 1992 | Barstow | 7.28 | 1369 | 0.727 | 2.19 | B |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, X.; Wang, X.; Rong, M. Asymmetric Structural Response Characteristics of Transmission Tower-Line Systems Under Cross-Fault Ground Motions Revealed by Shaking Table Tests. Symmetry 2025, 17, 1646. https://doi.org/10.3390/sym17101646
Wang Y, Li X, Wang X, Rong M. Asymmetric Structural Response Characteristics of Transmission Tower-Line Systems Under Cross-Fault Ground Motions Revealed by Shaking Table Tests. Symmetry. 2025; 17(10):1646. https://doi.org/10.3390/sym17101646
Chicago/Turabian StyleWang, Yu, Xiaojun Li, Xiaohui Wang, and Mianshui Rong. 2025. "Asymmetric Structural Response Characteristics of Transmission Tower-Line Systems Under Cross-Fault Ground Motions Revealed by Shaking Table Tests" Symmetry 17, no. 10: 1646. https://doi.org/10.3390/sym17101646
APA StyleWang, Y., Li, X., Wang, X., & Rong, M. (2025). Asymmetric Structural Response Characteristics of Transmission Tower-Line Systems Under Cross-Fault Ground Motions Revealed by Shaking Table Tests. Symmetry, 17(10), 1646. https://doi.org/10.3390/sym17101646






