Abstract
The result of accelerated development and technological progress is manifested through numerous changes in the labor market, primarily concerning the competencies of future employees. Many of those competencies have symmetrical character. The determinants that may influence the development of specific competencies are variable and dynamic, yet they share the characteristic of transcending temporal and spatial boundaries. In this paper we propose the use of a combination of Principal Component Analysis (PCA) and Fuzzy Analytic Hierarchy Process (FAHP) to rank 21st-century competencies that are developed independently of the formal educational process. Ability to organize and plan, appreciation of diversity and multiculturalism, and ability to solve problems appeared to be the highest-ranked competencies. The development of key competencies is symmetrical to the skills for the labor market. Also, the development of key competencies is symmetrical to the right selection of the quality of media content. The paper proves that the development of key competencies is symmetrical to the level of education of both parents. One of the key findings is that participants with higher levels of media literacy express more readiness for the contemporary labor market. Moreover, the family, particularly parents, exerts a highly significant positive influence on the development of 21st-century competencies. Parents with higher levels of education, in particular, provide a stimulating environment for learning, foster critical thinking, and encourage the exploration of diverse domains of knowledge.
1. Introduction
This study on the development of 21st-century competencies represents a continuation of previous research [1], which examined the competencies that young, recently graduated students developed during their studies, as well as those acquired independently of formal higher education. The study also analyzes the influence of various factors on the development of these competencies, including parental education, place of upbringing, exposure to media content, and the degree of personal responsibility, all with the aim of assessing their preparedness for the labor market. The study considers the strategic directions of the education system in the Republic of Serbia, approaching it holistically and seeking to harmonize all partial segments with the system as a whole, thereby ensuring coherence in development. By connecting formal, non-formal, and informal acquisition of knowledge and skills, a bidirectional feedback loop is created between what educational institutions provide and the demands of the labor market. This study also concerns and detects symmetrical properties and correlations between key competencies and skills, between the development of key competencies and media content quality, as well as between the development of key competencies and the level of education of parents.
The competencies for 21st-century, analyzed in this study, include: (C1) Creativity and innovation, (C2) Critical thinking, (C3) Ability to solve problems, (C4) Ability to make decisions, (C5) Flexibility and adaptability—the ability to adapt to a new situation, (C6) Cooperation—the ability to work in a team, (C7) Communicativeness, (C8) Oral and written communication in a foreign language, (C9) Basic computer skills, (C10) Ability to manage information—gathering and analyzing information from various sources, (C11) Research and inquiry—research skills, (C12) Ethical commitment and orientation, (C13) Ability to apply knowledge in practice, (C14) Leadership ability—leadership and responsibility, (C15) Appreciation of diversity and multiculturalism, (C16) Initiative and self-management, (C17) Ability to learn, (C18) Ability to organize and plan, (C19) Ability to criticize and self-criticize, (C20) Self-motivation to work.
Objectives of the Study
One of the objectives of the research was to demonstrate that, through the combination of two methods—statistical analysis and fuzzy logic—it is possible to identify clusters of competencies, determine the leading competencies within each cluster, and develop a conceptual model to support effective career positioning strategies for individuals in the labor market. In addition, the study aimed to examine the influence of media on the perception and development of all three identified groups of skills, to analyze which skills are most valued in the labor market in order to help individuals formulate their own positioning strategies, and to explore the interrelation and interdependence between the media, the labor market, and the development of professional and social competencies.
This study aims to identify the most relevant competencies for labor market integration that are developed outside the formal education system, examine the role of media literacy and exposure to media content in the development of these competencies, assess the influence of family background, particularly parental education levels, on the formation of key competencies, apply PCA to reduce dimensionality and highlight the most influential factors, use FAHP and SFAHP to rank competencies based on expert judgments and compare the results between the two fuzzy approaches, and demonstrate the symmetrical relationships between media quality, family factors, and key competencies needed in the labor market.
All the previously mentioned goals of the study were formulated as the following hypothesis:
H1.
Young people with higher levels of media literacy are better prepared for the labor market, demonstrating the ability to critically analyze information and adapt their skills to market needs.
H2.
The level of parental education has symmetrical property to the development of key competencies and has a positive effect on the development of 21st-century competencies.
H3.
Ranking of competencies according to the AHP and FAHP methods (eight variants) gives similar results.
2. Sample, Data, and Attitude Analysis
Data collection was implemented using a Google Forms questionnaire. The research sample was purposive, consisting of recent graduates from two private faculties in the Republic of Serbia. The pilot study included 45 respondents. Based on the analysis of the pilot study (which involved verifying the content validity of all aspects measured in this research), the final version of the questionnaire was constructed, and the main study was conducted with a new group of 252 respondents (n = 252).
The first part of the questionnaire contained general demographic information. In the second part, for the purposes of the study, respondents rated on a scale the extent to which particular competencies had been developed independently of their studies, i.e., to what extent the competencies had been acquired outside the formal educational process. In this section, respondents also assessed their own readiness for the labor market and the employment process after graduation. The third part of the questionnaire included questions related to the significance of the media for the educational process and personal development.
A portion of the data was processed using the SPSS 19.0 software package, while AHP, FAHP, and SFAHP analyses were conducted using Microsoft Excel software.
3. Fuzzy AHP Methodology
The selection of the most appropriate assessment for criteria and indicators is effectively addressed using multicriteria decision-making methods, which are integral to various aspects of decision-making. One such method, the Analytic Hierarchy Process (AHP), developed by Thomas L. Saaty in the early 1980s, is a widely utilized multicriteria approach designed to assist in decision-making where conflicting criteria and alternatives are present. AHP has been rigorously examined and enhanced in numerous scholarly publications. The method is founded on several key axioms, namely: the reciprocity axiom, the homogeneity axiom, the dependency axiom, and the axiom of expectations. At its core, AHP decomposes complex problems into a hierarchical structure, with the goal placed at the top, followed by criteria, sub-criteria, and alternatives at lower levels. This versatile framework enables the analysis of problems involving multiple criteria and alternatives, facilitating the identification of interrelationships among factors and the evaluation of their relative importance in real-world contexts. A central feature of AHP is its ability to present issues within a mutual hierarchical framework, wherein the highest level represents the primary objective, and the lower levels contain the supporting criteria essential to the decision-making process. The method is particularly effective for performing pairwise comparisons among the elements of the hierarchy, such as goals, criteria, and alternatives. When experts tend to establish the comparison matrix quantifying the importance of one criterion over another, uncertainty can arise, especially when multiple decision-makers are involved [2]. A valuable tool for addressing uncertainty and imprecise linguistic expressions, providing significant support in decision-making problems has been known in fuzzy sets theory [3,4]. The primary objective of fuzzy sets, as a generalization of classical set theory, was to mathematically represent linguistic variables, allowing decision-makers to model situations involving partially unknown or incomplete information. In classical set theory, an element either belongs to a set, or it does not [5]. In contrast, fuzzy set theory introduces the membership function (MF), typically denoted by , which maps each element of the universal set to the interval indicating the degree to which an element belongs to a fuzzy set.
3.1. Triangular Fuzzy Numbers
In this section basic characteristics of triangular fuzzy numbers will be mentioned.
Definition 1.
A triangular fuzzy number (TFN) is a special fuzzy set denoted by , where is a continuous function presented in the form of [6].
with condition satisfied. The membership function of a TFN is characterized by a triangular shape with a , and illustrating the lower bound, the peak, and the upper bound, respectively. From to the membership function increases linearly, while after the highest value in , it decreases.
Some other well-known and frequently used membership functions are Gaussian curve and Bell curve .
Definition 2.

Let and be two TFNs and scalar , . Basic fuzzy arithmetic operations (see Table 1) are defined as follows [6,7].

Table 1.
Basic fuzzy arithmetic operations using TFNs.
Definition 3.
The left and right side of the membership function of TFN
, denoted by
and
, as can be seen in Figure 1, are defined as = and = , while their inverse functions are of the form [8,9]
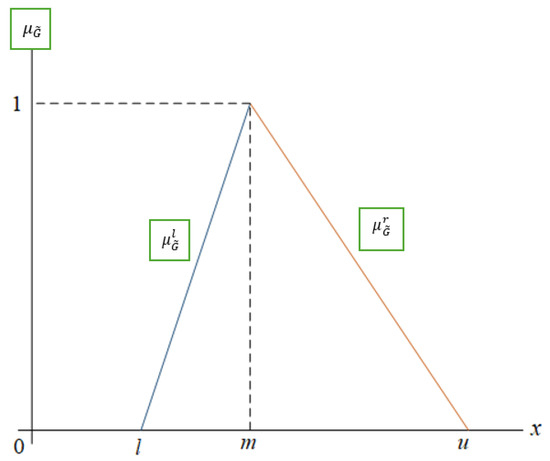
Figure 1.
The representation of a triangular membership function.
Definition 4.
The left and right integral values of a TFN
are equal.
and
The total integral value, combining the left and right integral values, is specified as follows [10]:
with representing an optimism index. This index shows the perspective of the decision-maker, reflecting the degree of optimism. For instance, when = 1, the optimistic point of view is given, and , while the value = 0 shows the pessimistic attitude with . If , then , and if then . When , it is said that .
Definition 5.
Let be a given TFN. The synthetic triangular fuzzy number denoted by is calculated as follows [9]:
with
and
The meaning of TFNs and their notation could be expressed as in Table 2.

Table 2.
Marks, linguistic terms, and notation of TFNs [6].
3.2. Spherical Fuzzy Sets
In this section basic information about spherical fuzzy sets will be mentioned.
Definition 6.
Let be a non-empty universe of discourse. A spherical fuzzy set of the non-empty universe of discourse is defined as follows [11,12]:
where
:
,
:
, and
:
, are the membership, non-membership, and hesitancy functions, satisfying the condition as follows:
Definition 7.
Let and be two spherical fuzzy sets defined on the non-empty universal set , and scalar. The basic unary and binary operations are defined as follows [11,12]:
Intersection:
Union:
Addition:
Multiplication:
Multiplication by a scalar :
Power:
Definition 8.
Let and be two spherical fuzzy sets defined on the non-empty universal set , and and are positive scalars. Then, the following characteristics are valid [13]:
Definition 9.
Let and be two spherical fuzzy sets defined on the non-empty universal set . To compare these fuzzy sets, the score function (SC) and accuracy function (AC) are defined as follows [11]:
After calculating the and functions, the comparison rules are as follows:
Definition 10.

Let be a spherical fuzzy set. The score indices (SI) corresponding to a set are defined as follows [12]:
where are explained in Table 3.

Table 3.
Linguistic measures of importance of criteria and spherical fuzzy sets [11,12,13].
Definition 11.
Spherical Fuzzy Weighted Arithmetic Mean (SFAM) with respect to , , and , is the value calculated as follows [12]:
The selection of fuzzy parameters, specifically the definition of fuzzy comparison scales, is a critical aspect of any fuzzy AHP application. In this study, we employed the widely accepted TFNs presented in Table 2 to represent the relative importance between criteria in pairwise comparisons. The fuzzy numbers were selected to ensure both consistency with existing fuzzy AHP frameworks and interpretability by experts, who were asked to provide judgments using verbal categories, which were then converted into TFNs. The use of these numbers is made by literature validation (commonly used and validated in previous FAHP studies across domains), expert comprehension (simpler fuzzy numbers were preferred over more complex sets to facilitate ease of understanding by non-technical experts), and comparability (using standardized fuzzy parameters allows for easier comparison with results from similar studies and ensures methodological consistency). In addition to classical fuzzy AHP, this study also employs the spherical SAHP to evaluate and rank key competencies. SFAHP, as an extension of the classical fuzzy AHP, is based on spherical fuzzy sets (presented in Table 3), which offer a more generalized and flexible way to express uncertainty by considering membership, non-membership, and hesitation degrees, constrained by the condition that the sum of their squares is less than or equal to 1. This feature enables a richer and more nuanced representation of expert opinions compared to traditional fuzzy numbers. Since spherical fuzzy sets can represent uncertainty more expressively than traditional fuzzy numbers, SFAHP may produce slightly different rankings due to better handling of hesitation or indecisiveness among experts. This is particularly useful when analyzing subjective or abstract criteria, such as media influence, creativity, or intercultural awareness.
3.3. The AHP, Fuzzy AHP, and Spherical Fuzzy AHP Algorithms
In this section a brief overview of the above-mentioned algorithms AHP, FAHP, and SFAHP will be given.
The steps of the well-known AHP algorithm are given in Figure 2.

Figure 2.
The steps of the AHP method.
In the sequel, the steps of the FAHP and SFAHP methods are presented [8,14,15,16].
Step 1: Establishing the hierarchical structure and construction of evaluation matrices.
The vertically constituted hierarchical structure with few levels of organization, with the most significant component (goal) at level 1, contributing criteria, sub-criteria, and sub-sub-criteria at the following levels, and, eventually, alternatives at the last level, is built. The evaluation matrices with pairwise comparisons are conducted for all considered preference criteria and sub-criteria, where and = (), respectively, for the FAHP and SFAHP. Corresponding marks, their meanings, score indices, and denotations are presented in Table 2 and Table 3. The mark E corresponding to is equal in the FAHP and (0.5, 0.5, 0.5) in the SFAHP. The aggregation of different experts’ opinions is calculated by the averaging method, based on the corresponding linguistic assessments of (), (), , respectively, rounding to the nearest integer.
Step 2: Matrices consistency examination.
The matrix consistency index , and consistency index , for the greatest eigenvalue of the matrix and random index depending on the number of criteria are used for each pairwise comparison matrix consistency evaluation. The value of the consistency index is acceptable; otherwise, the experts should revise their evaluation to make the comparison matrix consistent.
Step 3: Calculation of fuzzy weights and global fuzzy weights of criteria.
Using definition 5, the fuzzification process in the case of FAHP is performed. In the case of SFAHP, definition 11 is used.
Step 4: The defuzzification process is conducted.
Applying score function formulas from definition 9, the weights for all criteria and sub-criteria were obtained. Crisp numbers were calculated in two different ways in the SFAHP, while definition 4 and total integral value are used in FAHP.
Step 5: Normalization of the weight vector is calculated.
Using the formula the normalization of the vector is performed.
This study combines Principal Component Analysis (PCA) and the Fuzzy Analytic Hierarchy Process (FAHP) to improve the objectivity and clarity of competency evaluation. PCA reduces redundancy and reveals underlying structures in the data, forming meaningful clusters of competencies. FAHP then builds on these results, integrating expert judgment to ensure practical relevance. This hybrid method balances data-driven analysis with contextual insight, making it valuable for fields like education, labor economics, and media studies.
4. Results
The study included 252 respondents, of whom 41.3% were male and 58.7% were female. The largest proportion of respondents (56.7%) live in a large city (more than 100,000 inhabitants), 17.4% in a city (up to 100,000 inhabitants), 12.4% in a smaller city (up to 50,000 inhabitants), 7.5% in a town (up to 10,000 inhabitants), and the smallest proportion (6.0%) in a village (up to 5000 inhabitants).
With regard to the educational background of the respondents’ parents/guardians, the distribution is as follows:
- Father: 5.5%—Elementary school; 43.3%—Secondary school (3 or 4 years); 10.4%—College (3 years of study); 22.4%—Faculty (4 years of study); 14.9%—Magister or master’s degree (5 years of study); 3.5%—Doctor of Science (Ph.D.).
- Mother: 3.0%—Elementary school; 37.2%—Secondary school (3 or 4 years); 9.5%—College (3 years of study); 30.7%—Faculty (4 years of study); 17.1%—Magister or master’s degree (5 years of study); 2.5%—Doctor of Science (Ph.D.).
4.1. Principal Component Analysis
For the purpose of explaining the shared variance of the variable set, i.e., the variability within groups of variables, factor analysis PCA was applied. PCA is based on a mathematical model in which factors are derived as standardized principal components. By analyzing the correlation matrix among the variables, and in order to assess data suitability, 20 variables were included in the analysis, representing both positive and negative opinions of the respondents.
The general factor model has the following form:
where
X—variable with a mean of zero and variance of one;
i—variable index;
F—mutually independent factors;
m—factor index;
a—factor loading;
e—specific factor associated only with the given variable.
The factor loading indicates the relative importance of each characteristic in defining the factor.
The validity of factor analysis is confirmed by meeting all the criteria: the Kaiser-Meyer-Olkin (KMO) Measure of Sampling Adequacy was 0.750, and Bartlett’s test of sphericity reached statistical significance (Sig < 0.001). Principal Component Analysis revealed the presence of five components with eigenvalues greater than 1 (5.256, 2.052, 1.773, 1.291, and 1.224), which together accounted for 57.98% of the variance. The scree plot indicated the first break point between the third and fourth components (see graph in Figure 3).
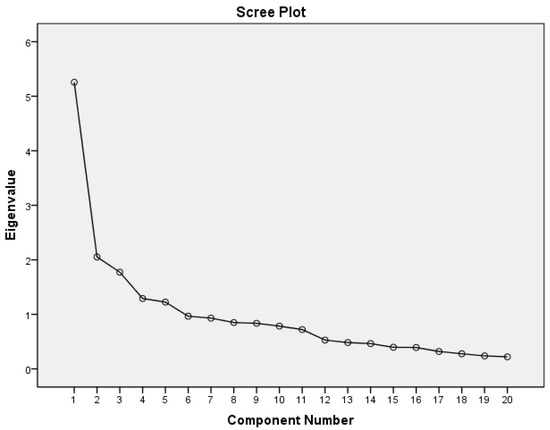
Figure 3.
Graph with diagram.
To determine the number of components to be retained, a parallel analysis was conducted. Based on the results of the parallel analysis and the SPSS Component Matrix table, it was concluded that a three-factor solution was more appropriate. These three components explained a total of 45.40% of the variance.
After performing the Varimax rotation, the following results were obtained (the order of variables within each component is presented according to their factor loadings within the group):
Component 1 (Group Work Competencies): Appreciation of diversity and multiculturalism; ability to apply knowledge in practice; Ethical commitment and orientation; cooperation—the ability to work in a team; Flexibility and adaptability—the ability to adapt to a new situation; communicativeness; oral and written communication in a foreign language, initiative and self-management; ability to criticize and self-criticize.
Component 2 (Cognitive and Analytical Skills): Ability to solve problems; ability to manage information—gathering and analyzing information from various sources; research and inquiry—research skills; ability to make decisions; critical thinking; basic computer skills; creativity/innovation.
Component 3 (Management Skills, including Self-Management): Ability to organize and plan; self-motivation to work; ability to learn; leadership ability—leadership and responsibility.
4.2. Results for the AHP, FAHP, and SFAHP Algorithms
In this section, the outlined algorithms, FAHP [8,17] with the following five degrees of optimism: pessimistic (), semi-pessimistic (), balanced (), semi-optimistic (), and optimistic (), SFAHP, as well as the crisp AHP method, are used to compare the obtained results and sub-criteria ranking. A group of experts from the areas of social sciences, media, economics and statistics, management, and education selected groups of criteria and sub-criteria and expressed their opinion based on the meaning of linguistic measures, TFNs, and SFSs presented in Table 2 and Table 3. The assessments experts gave were aggregated based on the first step of the presented algorithm, securing partial consensus [18].
Firstly, the main criteria groups were discussed. The experts agreed on the equal significance of the following groups: group work competencies (G), cognitive and analytical skills (C), and management skills (including self-management) (M) (CI = CR = 0, = 3). In the AHP case, the weights of main criteria G, C, and M are equal to 0.33, as can be seen in Figure 4.

Figure 4.
The weights of the main criteria G, C, and M.
The dominance of cognitive and analytical skills is especially pronounced in the case of the optimistic FAHP case, with a corresponding weight of 0.42, being 1.27 and 1.75 times higher than criteria M and G, respectively. The same quotients for 0.5 are 1.21 and 1.55, respectively, showing the decision-makers’ balanced point of view. Pessimistic point of view shows the smallest quotient numbers, while the ratios obtained for 0.25 and 0.75 are similar to the ones obtained in the balanced case. The use of spherical fuzzy sets and two different accuracy functions gives uniformly distributed values with the smallest ratios in all cases. The average values of criteria weights are as follows: = 0.38, = 0.333, and = 0.286.
The ranking of sub-criteria is managed in the same manner as the ranking of the main criteria. The fuzzy comparison matrix of sub-criteria belonging to group G is presented in Table 4. This matrix is consistent, with CI = 0.051 and CR = 0.042, calculated as follows:

Table 4.
Fuzzy comparison matrix for sub-criteria from group G.
In all cases, the sub-criterion G1, named appreciation of diversity and multiculturalism, ranked first, with the weights 0.462, 0.416, 0.385, and 0.371 in the AHP and three basic cases of the FAHP algorithm. It is followed by the ability to apply knowledge in practice, having 1.84 times smaller weight than G1 (AHP). In the case of the SFAHP, those ratios are 1.2 and 1.23, using AC1 and AC2, respectively. The sub-criteria G4 and G5 have the same weight equal to 0.062 in the AHP case, while also being in the fourth and fifth positions; their values ascend from the pessimistic to the optimistic point of view. In the SFAHP, the sub-criterion G4 has a slightly higher weight, between 4% and 6%. At the end of the group work competencies group lies the sub-criterion communicativeness, being approximately 15.3, 12.6, 2.4, and 2.9 times less important than the highest ranked sub-criterion G1 (AHP, balanced FAHP, and SFAHP).
Out of six sub-criteria, there are two pairs of equal rankings in the AHP case in the group cognitive and analytical skills. In the highest rank, with the corresponding weight of 0.337, are ability to solve problems, ability to manage information, and, at the end, critical thinking and basic computer skills, with a corresponding weight of 0.039. Using fuzzy algorithms, no two sub-criteria are ranked the same. The C1 still has the highest ranking, with a weight less than in the AHP, with a similar situation in the case of sub-criteria C2. Middle part of the ladder is taken by sub-criteria C3 and C4, with a little bit higher weights than in the AHP case: 0.188, 0.195, and 0.198 are the weights of sub-criteria in the pessimistic, balanced, and optimistic FAHP, while the corresponding weights for C4 are 0.093, 0.106, and 0.111. Applying the SFAHP, the leading sub-criteria have average weights of 0.242 and 0.239, while the average weights for the sub-criteria at the bottom, C5 and C6, are equal to 0.117 and 0.108. The corresponding TFNs for the sub-criteria are as follows: (0.145, 0.316, 0.713), (0.140, 0.316, 0.671), (0.076, 0.193, 0.461), (0.032, 0.102, 0.266), (0.023, 0.037, 0.120), and (0.023, 0.037, 0.120). The matching consistent comparison fuzzy matrix and weights can be seen in Table 5 and Figure 5.

Table 5.
Fuzzy comparison matrix for sub-criteria from group C (CI = 0.034, CR = 0.028, ).
Figure 5.
The weights of sub-criteria from group C.
Management skills (including self-management) group consists of four sub-criteria. The highly influential ability to organize and plan, with a weight of 0.575, is twice as important as the sub-criterion self-motivation to work and more than eight times as important as the sub-criterion ability to learn and leadership ability, all in the AHP case. The weights in the FAHP case are given in Figure 6, where one can observe that ratios M1/M2 and M1/M4 in the optimistic case are equal to 1.529 and 8.784. In the balanced case, the weights of all sub-criteria are equal: = 0.52, = 0.334, = 0.084, and = 0.062.

Figure 6.
The weights of sub-criteria from group M with different degrees of optimism in the FAHP case.
Using spherical fuzzy sets (0.708, 0.299, 0.266), (0.603, 0.405, 0.316), (0.403, 0.579, 0.366), and (0.372, 0.612, 0.365), one can obtain that in the SFAHP case, averaged weights of sub-criteria are, respectively, equal to 0.334, 0.286, 0.198, and 0.183.
The final ranking of sub-criteria is presented in Figure 7, and their weights in the case of AHP, five degrees of optimism in FAHP, and SFAHP are given in Table 6. It can be observed that the sub-criteria from group M, namely M1, is still ranked highest; however, the remaining sub-criteria from the management skills group, M2, M3, and M4, ranked fifth, tenth, and eleventh, respectively. Furthermore, the highest-ranked sub-criteria from group work competencies, namely G1, corresponding to appreciation of diversity and multiculturalism, ranked second overall is 1.84 times higher than G2 and 3.47 times higher than G3 for the AHP case, and 1.45 and 2.44 higher than G2 and G3 in the case of FAHP, respectively (averaged over all points of view). When applying the SFAHP, previously described relations are equal to 1.96 and 1.96 with the first defuzzification method and 1.23 and 1.27 using the second way of defuzzification. The first two sub-criteria from the group cognitive and analytical skills, C1 and C2, are placed third and fourth in all eight different rankings, showing the importance of solving problems and analyzing the information gathered. Ethical commitment and research skills are in the middle of the ladder, being 4.32 and 6.85 times (AHP) and 4.081 and 4.051 times (balanced FAHP) less important than G1. The smallest values in the ranking procedure, being of smaller importance, are determined by the sub-criteria basic computer skills and communicativeness.

Figure 7.
The final ranking of sub-criteria.

Table 6.
Ranking of sub-criteria with final weights by triangular fuzzy AHP method, fuzzy AHP method with five degrees of optimism, and spherical fuzzy AHP method.
The Surface Fuzzy AHP [19], using surface instead of sphere to ensure a higher degree of freedom to a decision-maker, could also be applied in similar situations. The operation with geodesic mappings and tensor calculus [20,21] might be adopted to obtain stronger results.
During the sub-criteria ranging process, eight different variants were used, possibly leading to inconsistencies. To estimate and analyze ranking similarities applying the AHP, the FAHP (five different situations), and the SFAHP (two different situations) to all influencing sub-criteria, as well as to assess the accuracy and validity of the proposed model, the Spearman rank correlation coefficient [22] is applied as follows:
where represents the number of elements in ranking, and and stand for the element in the rankings used for comparison.
Applying Equation (18), it can be observed that min{} = 0.93529, as can be seen in Figure 8, yielding that all rankings have high similarity [23]. The lowest value of the coefficient for SFAHP is obtained when it is compared with optimistic and pessimistic FAHP and AHP, while the value is reached when comparing AHP and FAHP ().

Figure 8.
Ranking similarity.
The classical crisp AHP and FAHP methods were applied. In all cases, from pessimistic to optimistic (FAHP) and two variants of SFAHP, the most influential sub-criteria was ability to organize and plan. Differences can be seen in the second ranking sub-criteria: favoring appreciation of diversity and multiculturalism (AHP and pessimistic FAHP), ability to solve problems (majority of FAHP cases), and self-motivation to work (SFAHP). A similar situation holds for sub-criteria placed third, fourth, and fifth, while in the middle of the ladder stand ethical commitment and orientation and ability to make decisions. Sub-criteria of least importance for AHP, FAHP, and SFAHP are basic computer skills and communicativeness. Considering the ranking of criteria in the AHP compared to all five rankings in the FAHP, it can be concluded that there are no significant differences, with complete overlap with pessimistic FAHP. Semi-pessimistic and semi-optimistic FAHP differ only in four ranking places, while FAHP () and FAHP () have just two differences, yielding to the coefficient . The ranking results between two SFAHP methods, favoring sub-criteria from the management (and self-management) skills group, differ in six ranking places, obtaining approximately 99% similarity ranking.
The competencies within Component 2 (the most significant in terms of importance), namely ability to solve problems and ability to manage information—gathering and analyzing information from various sources—ranked the highest. These findings suggest that young people are capable of identifying challenges, handling unforeseen situations, selectively approaching information, recognizing what is relevant, and applying this knowledge in decision-making. This is of key importance for employers, as it allows them to rely on their employees.
Among the highest-ranked competencies in Component 1, appreciation of diversity and multiculturalism and ability to apply knowledge in practice indicate that young people in Serbia are oriented toward diverse (including international) labor markets. They value diversity, which ultimately enhances their tolerance and their ability to work in international and multicultural teams and companies. Moreover, the capacity to transfer knowledge into practice strengthens their self-confidence and work efficiency, thereby fostering business development and growth.
Within Component 3, the best-ranked competencies were ability to organize and plan and self-motivation to work. these suggest that young people who are able to organize and plan their activities are more likely to achieve goals within set deadlines and tasks. Similarly, those who are self-motivated often maintain stronger focus in reaching their objectives, which leads to greater job satisfaction and personal success and consequently contributes to the overall success of the company, an aspect equally valuable to employers.
4.3. Readiness for the Labor Market and the Employment Process—Challenges
The respondents expressed the view that the family has a very strong influence on the development of competencies. The modes for all items (variables) were either six or seven, while the mean scores ranged from 5.33 (leadership ability—leadership and responsibility) to 5.89 (basic computer skills). For all variables, the median values were within the interval of five to six. The variables demonstrated relatively low variability (coefficients of variation ranged from 19.61% to 30.61%) and strong negative skewness, with the exception of creativity/innovation, which exhibited slight negative skewness (Skewness = −0.219).
When considering the competencies with the highest factor loadings from each of the three previously examined components—ability to solve problems, appreciation of diversity and multiculturalism, and ability to organize and plan—the Mann–Whitney U test revealed a statistically significant difference only in the assessment of ability to organize and plan between male (Me = 2.0, n = 109) and female respondents (Me = 3.0, n = 85), U = 3572.50, z = −2.811, p = 0.005. The effect size is as follows:
i.e., it can be said that the impact is small [24]. The variable shows a higher mean rank for male respondents (indicating a better assessment of ability to organize and plan).
Respondents whose fathers attained the level of magister or master’s degree and doctor of science (Ph.D.) awarded the highest score for the development of the ability to solve problems in 29.6% and 42.9% of cases, respectively. Similarly, the largest proportion of respondents whose mothers had achieved the level of the doctor of science (Ph.D.) (40%) assigned the maximum score (7) for the development of ability to solve problems.
Regarding the development of the competency of appreciation of diversity and multiculturalism, mothers with higher levels of education exert a greater influence. Specifically, 50% and 40% of respondents whose mothers had attained a magister or master’s degree or a doctor of science (Ph.D.), respectively, awarded the highest score (7) for the development of this competency.
Although young people assessed that the family has a significant influence on the development of competencies, it can be concluded that fathers exert a somewhat greater influence than mothers (no differences were found between fathers’ and mothers’ educational levels). The Kruskal–Wallis test revealed a statistically significant difference in the evaluation of ability to solve problems across six groups of fathers categorized by educational level (Gp1, n = 11: elementary school; Gp2, n = 87: secondary school, 3 or 4 years; Gp3, n = 21: college, 3 years of study; Gp4, n = 45: faculty, 4 years of study; Gp5, n = 27: magister or master’s degree, 5 years of study; Gp6, n = 7: doctor of science—Ph.D.), χ2(5, n = 163) = 12.276, p = 0.015. The highest mean ranks were recorded for fathers with a magister or master’s degree and a doctor of science (Ph.D.), indicating a stronger influence on the development of the competency ability to solve problems.
It is particularly interesting to note that the Kruskal–Wallis test revealed a statistically significant difference in the assessment of ability to solve problems across five groups of respondents categorized by their permanent or temporary place of residence (Gp1, n = 12: village, up to 5000 inhabitants; Gp2, n = 15: town, up to 10,000 inhabitants; Gp3, n = 25: smaller city, up to 50,000 inhabitants; Gp4, n = 34: city, up to 100,000 inhabitants; Gp5, n = 112: large city, more than 100,000 inhabitants), χ2(4, n = 198) = 10.379, p = 0.035. The highest mean ranks were observed among respondents whose fathers had attained a magister or master’s degree (5 years of study) and a doctor of science (Ph.D.), suggesting a stronger influence on the development of the competency ability to solve problems.
As for the reasons behind insufficient preparedness for the labor market, the respondents identified the following, in order:
- Unfair practices in the job market (bribery, corruption, and nepotism);
- Personal irresponsibility (lack of interest and laziness);
- Lack of awareness of job market demands;
- Development and education strategies of the Republic of Serbia;
- The country’s poverty;
- None of the above/I consider myself prepared for the labor market;
- An uninspiring social and family environment.
From the previously outlined sequence, it can be observed that young people also demonstrate the characteristic of self-criticism, as they identify personal irresponsibility (lack of interest, laziness) as the second most important reason for their insufficient readiness for the labor market.
After graduation, the most frequently cited reason for difficulties in gaining employment is insufficient knowledge of young people about employment opportunities (31.2%). An equal proportion of respondents (23.7% each) reported a lack of adequate employment programs and a lack of competence with regard to the requirements of employers, while 21.5% identified an insufficient number of jobs in the labor market as the key barrier.
The chi-square test of independence revealed a statistically significant association between the perceived reasons for difficulties in finding employment after graduation and gender, χ2(3, n = 186) = 10.511, p = 0.015. The value of Cramer’s V was 0.238, indicating a medium effect size [25]. For female respondents, the greatest barriers were an insufficient number of jobs in the labor market and a lack of adequate employment programs, whereas for male respondents, the main obstacles were insufficient knowledge of young people about employment opportunities and a lack of competence with regard to the requirements of employers.
4.4. Media Shaping of Key Competencies for the Labor Market
The media, as a mirror of society, are not the primary source of responsibility for the lack of adequate competencies required by the contemporary labor market. Educational institutions, particularly universities, should take the initiative in more rapidly and comprehensively adapting curricula to labor market demands, acknowledging the changing context and the implementation of new technologies, strongly reinforced by the application of artificial intelligence. In this regard, the media industry should be considered one of the most dynamic and demanding sectors, given that the daily use of AI in media strongly influences media business activities. Consequently, curricular changes in the education of media professionals are imperative [26]. Newly acquired competencies and/or the upgrading of existing ones may contribute to strengthening competitiveness and employability while also accelerating career development and mobility among those already employed.
The increasingly pervasive and influential media discourse and information channels exert a strong impact on lifelong learning, requiring individuals to make continuous investments of available resources in acquiring new knowledge and skills related to the functions of both traditional and digital media, as well as to modes of media consumption. Precisely through the lens of these needs emerges the necessity of information and media literacy, achieved through the transfer of knowledge and skills to a broad audience. To minimize potential risks, the media industry is under dual scrutiny: that of state regulation and that of established systems of self-regulation [27].
The development of competencies is not a matter of a single moment but represents a dynamic process in which required competencies are continuously redefined in relation to the labor market. Supporting this claim is a long-term trend that illustrates decision-making regarding job location, where companies prioritize the availability of qualified labor and rank it first, with 74% of respondents identifying this factor as crucial. Labor costs (64%) occupy the second position, while all other determinants—such as the flexibility of labor legislation or the effects of industrial capacity concentration in a single location—are considered less relevant. Indicators from the World Economic Forum [28] unambiguously suggest that workforce transformation is accelerating, while the opportunity for proactive management of these changes is closing, serving as a clear signal to governments and workers that proactive planning and action within the framework of the new architecture of the global labor market are imperative.
Some studies indicate that students identify mass media as the most important source of career guidance, despite the fact that they most frequently perceive them as manipulative, while significantly fewer recognize their informative and educational functions. Mass media indirectly shapes students’ aspirations by reinforcing values such as social recognition, mobility, and identity. Although the influence of media culture is substantial, the media have not assumed a dominant role in the career orientation process, particularly when compared with mechanisms of self-evaluation and the influence of the family [29].
When examining media channels that contribute to the development of key competencies for positioning in the labor market, the majority of respondents identified social networks as the main contributors (69.5%), followed by television (23.2%), printed media (5.8%), and radio (1.5%).
Among social networks, those with the highest reported contribution to the competency development for the labor market were as follows:
- YouTube, with a mean score of 5.53, a median of 6, and a mode of 7, the variable exhibits a very strong negative skewness (Skewness = −1.081) and relatively low variability (CV = 27.88%).
- Instagram, with a mean score of 5.11, a median of 5, and a mode of 7, the variable shows strong negative skewness (Skewness = −0.743) and relatively low to moderate variability (CV = 34.85%).
- LinkedIn, with a mean score of 4.83, a median of 5, and a mode of 7, the variable indicates very strong negative skewness (Skewness = −0.563) and relatively low variability (CV = 38.98%).
Social networks with the highest contribution to the development of competencies required in the labor market (LinkedIn, Instagram, and YouTube) display (see Table 7) a significant direct linear interrelationship, with correlation coefficients falling within the interval .

Table 7.
Correlation.
5. Discussion
Based on the results obtained, a conceptual model can be developed, as illustrated in the scheme in Figure 9. All elements within the conceptual model need to be balanced and mutually reinforced. The evaluation of the functionality and organization of each individual element, as well as their mutual interaction, serves as a criterion for the successful and efficient development of competencies, primarily in terms of meeting the needs of the labor market and employers, which in turn generates positive outcomes in the short, medium, and long term.

Figure 9.
Conceptual model.
Drawing on the research findings and the proposed conceptual model, it is possible to formulate sound business policies, that is, to design effective strategies for ensuring strong positioning of individuals in the labor market. This study may encourage all stakeholders to acquire new knowledge about concepts and approaches of strategic models in the process of building successful labor market positioning.
The media play an important role in the development of 21st-century skills among young people. Through interaction with various types of media content (informational, educational, and digital), respondents develop the following: cognitive and analytical skills (the ability to analyze, interpret, and critically reflect on information); managerial skills (learning to manage time, information, personal behavior, and emotions); and teamwork competencies—through participation in online communities, teams, forums, or student projects. Labor market demands directly shape which skills are required of employees. Employers expect candidates to demonstrate critical thinking and problem-solving abilities, as well as teamwork skills in multidisciplinary and international contexts.
There is a reciprocal relationship between the media and the labor market: media shape perceptions of which professions are desirable and which skills are in demand, while the labor market influences media content by promoting topics related to careers, digital skills, and entrepreneurship.
The conceptual model illustrates the dynamic and mutual relationship among media, the labor market, and key 21st-century competencies. These three components continuously shape and influence one another, while education and individual initiative play an important role in maximizing their potential.
Based on the research results and the proposed conceptual model, it is possible to formulate effective business policies and strategies for successful positioning of individuals in the labor market. This study may also encourage all stakeholders to acquire new knowledge of concepts and approaches to strategic models that contribute to building effective pathways for individual labor market positioning.
We can notice that the development of key competencies is, in some sense, symmetrical to the skills for the labor market. Also, it is obvious that the development of key competencies is symmetrical to the right selection of the quality of media content. The development of key competencies is also symmetrical to the level of education of both parents.
The integration of Principal Component Analysis and the Fuzzy Analytic Hierarchy Process within the same analytical framework is motivated by the need to enhance both the objectivity and interpretability of the competency evaluation process. This hybrid approach leverages the strengths of statistical data analysis and expert-driven decision-making to improve the accuracy and consistency of the final results. The use of PCA in this study helped us to eliminate redundancy among overlapping competencies, reveal hidden structures and interrelationships between variables, and group competencies into interpretable clusters, ensuring that the FAHP, implemented in the next step, is applied to a more manageable and statistically meaningful set of factors. This framework represents a synergistic integration of quantitative and qualitative reasoning since PCA provides a data-driven foundation that captures empirical patterns in the dataset, while FAHP incorporates human expertise and contextual judgment, ensuring that statistical outputs align with real-world relevance, all being useful in interdisciplinary fields such as education, labor economics, and media studies, where both statistical rigor and human interpretation are critical.
6. Conclusions
In a multicultural environment, the aspiration of every individual in the labor market is to secure the opportunity to build a career within a company that is regarded as a desirable workplace, where working conditions and motivation are maintained at a level that prevents high employee turnover. Given the abundance of learning opportunities and the accessibility of data and information, such career objectives appear realistic and attainable for younger generations. Nevertheless, the demands of the labor market are constantly changing, requiring lifelong learning and the harmonization of curricula in order to reduce the gap between existing competencies and those in demand.
An effective and sustainable educational system should provide reformed and flexible models of both initial and lifelong education to minimize the disparity between current competencies and labor market needs. Recognizing that this is a complex and gradual process, integrating the interests of students and parents, universities, employers, ministries of education, labor and social policy, trade unions, chambers of commerce, employment institutes and agencies, as well as the media, achieving 21st-century competencies necessitates a shared consensus on the implementation of new working methods and the structure of the future education system. Within this framework, the role of interactive media and readily accessible digital materials becomes indispensable.
Respondents with higher levels of media literacy demonstrate greater readiness for the contemporary labor market. Their ability to critically analyze information from various sources, including both digital and traditional media, enables them to identify relevant, accurate, and useful data, which is of particular importance in a rapidly changing business environment. In addition to analytical skills, media-literate young people are more adept at recognizing current trends, employer needs, and expectations, and accordingly adjust and further develop their skills. Whether in digital communication, problem-solving, teamwork, or flexibility, they actively build upon their knowledge and competencies in order to remain competitive. This finding confirms Hypothesis H1.
The level of parental education exerts a significant positive influence on the development of 21st-century competencies among young people. Parents with higher levels of education provide a stimulating learning environment, foster curiosity and critical thinking, encourage exploration across diverse fields of knowledge, are more engaged in their children’s educational processes, and promote development through daily activities, communication, and extracurricular content. Twenty-first-century competencies, such as digital literacy, teamwork, problem-solving, creativity, and adaptability, are not acquired exclusively within the higher education system. To a large extent, they are shaped by family values, habits, and interaction with the environment. Young people whose parents have higher educational attainment enjoy greater access to resources such as books, technology, courses, and cultural activities, all of which further contribute to the development of these skills. There is some kind of symmetrical correlation between the development of key competencies and the level of education of parents, a little more of the father than the mother. This finding confirms Hypothesis H2.
Although the combined application of PCA and AHP presented in this manuscript gives a new insight into the determination of 21st-century competencies and their possible inference in the labor market, there are paper shortcomings.
One important limitation of this study is the specificity of the sampled population, which may not fully represent the broader demographic spectrum. The sample primarily consisted of final-year students of two large private universities in the Republic of Serbia, which may introduce a level of selection bias. As such, the generalizability of the findings is limited. Future studies should consider applying the proposed methodology to more diverse populations across different educational, regional, and professional backgrounds to validate the robustness of the results.
PCA outcomes are sensitive to the initial dataset and variable correlations. A different sample or time period may yield a different component structure, affecting the downstream analysis. The combined use of PCA, FAHP, and SFAHP provides robust analytical insights but also increases methodological complexity. The interpretation of the results may require advanced understanding of fuzzy logic-based decision-making models.
Future research should consider a more comprehensive comparative analysis of different MCDM techniques, such as TOPSIS, VIKOR, or the Analytic Network Process (ANP), in combination with data reduction methods like PCA. This would allow for a deeper understanding of how various methodological integrations influence the prioritization and grouping of competencies and whether certain approaches offer greater consistency or interpretability across different datasets. Moreover, future studies could benefit from implementing longitudinal designs to monitor the development of competencies over time, particularly in response to changing labor market demands and evolving media landscapes. Such research would help determine whether the influence of media on competency perception and development is sustained or shifts over time. Additionally, expanding the sample beyond a single educational context—by including respondents from various academic disciplines, institutions, and countries—would enhance the external validity and generalizability of the findings. Finally, future work might focus more specifically on the role of digital and social media in shaping not only perceptions of employability but also in facilitating or hindering the development of both technical and transversal (soft) skills. This line of inquiry could be especially relevant in the context of increasing digitalization and the growing importance of media literacy in professional development.
Author Contributions
Conceptualization, B.S., A.P., D.J.S. and B.M.R.; methodology, D.J.S. and A.P.; software, A.P. and D.J.S.; validation, D.J.S., M.M. and B.M.R.; formal analysis, A.P., D.J.S. and O.B.; investigation, M.M., O.B., A.P. and B.S.; resources, B.S. and B.M.R.; data curation, D.J.S. and A.P.; writing—original draft preparation, A.P., B.S. and D.J.S.; writing—review and editing, D.J.S., A.P. and B.S.; visualization, M.M., O.B. and B.S.; supervision, B.M.R.; project administration, B.M.R., O.B., B.S. and M.M.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by Ministry of Information and Telecommunications of the Republic of Serbia, grant number 001788842 2025 13460 003 005 000 001. This research was also partly funded by Ministry of Science, Innovations and Technological Development of Serbia, through the grants 451-03-137/2025-03/200251 and 451-03-137/2025-03/200102 and funded by Faculty of Teacher’s Education, Leposavic, through the grant IMP-003.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
During the preparation of this manuscript, the authors used ChatGPT 4.0 only for the purposes of better translation. The authors have reviewed and edited the output and take full responsibility for the content of this publication. Authors did not use any GenAI tools for generating text, data, graphics, study design, data collection, analysis, or interpretation of data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sančanin, B.; Penjišević, A.; Simjanović, D.J.; Ranđelović, B.M.; Vesić, N.O.; Mladenović, M. A Fuzzy AHP and PCA Approach to the Role of Media in Improving Education and the Labor Market in the 21st Century. Mathematics 2024, 12, 3616. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Chou, J.S.; Pham, A.D.; Wang, H. Bidding strategy to support decision-making by integrating fuzzy AHP and regression-based simulation. Autom. Constr. 2013, 35, 517–527. [Google Scholar] [CrossRef]
- Wang, W.M.; Lee, A.H.I.; Chang, D.T. An integrated FA-FEAHP approach on the social indicators of Taiwan’s green building. Glob. Bus. Econ. Rev. 2009, 11, 304–316. [Google Scholar] [CrossRef]
- Kulak, O.; Durmusoglu, B.; Kahraman, C. Fuzzy multi-attribute equipment selection based on information axiom. J. Mater. Process. Technol. 2005, 169, 337–345. [Google Scholar] [CrossRef]
- Domínguez, S.; Carnero, M.C. Fuzzy Multicriteria Modelling of Decision Making in the Renewal of Healthcare Technologies. Mathematics 2020, 8, 944. [Google Scholar] [CrossRef]
- Chang, D.Y. Application of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Kahraman, C.; Cebeci, U.; Ruan, D. Multi-attribute comparison of catering service companies using fuzzy AHP: The case of Turkey. Int. J. Prod. Econ. 2004, 87, 171–184. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Kutlu Gündoğdu, F.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
- Kutlu Gündoğdu, F.; Kahraman, C. A novel VIKOR method using spherical fuzzy sets and its application to warehouse site selection. J. Intell. Fuzzy Syst. 2019, 37, 1197–1211. [Google Scholar] [CrossRef]
- Kutlu Gündoğdu, F.; Kahraman, C. A novel spherical fuzzy analytic hierarchy process and its renewable energy application. Soft Comput. 2020, 24, 4607–4621. [Google Scholar] [CrossRef]
- Kutlu Gündoğdu, F.; Kahraman, C. Spherical fuzzy analytic hierarchy process (AHP) and its application to industrial robot selection. In Intelligent and Fuzzy Techniques in Big Data Analytics and Decision Making: Proceedings of the INFUS 2019 Conference, Istanbul, Turkey, 23–25 July 2019; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 988–996. [Google Scholar] [CrossRef]
- Nguyen, P.-H.; Tsai, J.-F.; Lin, M.-H.; Hu, Y.-C. A Hybrid Model with Spherical Fuzzy-AHP, PLS-SEM and ANN to Predict Vaccination Intention against COVID-19. Mathematics 2021, 9, 3075. [Google Scholar] [CrossRef]
- Milošević, M.R.; Milošević, D.M.; Stanojević, A.D.; Stević, D.M.; Simjanović, D.J. Fuzzy and Interval AHP Approaches in Sustainable Management for the Architectural Heritage in Smart Cities. Mathematics 2021, 9, 304. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Chen, T.-C.T. A Partial-Consensus Posterior-Aggregation FAHP Method—Supplier Selection Problem as an Example. Mathematics 2019, 7, 179. [Google Scholar] [CrossRef]
- Simjanović, D.J.; Vesić, N.O.; Ignjatović, J.M.; Ranđelović, B.M. A novel surface fuzzy analytic hierarchy process. Filomat 2023, 37, 3357–3370. [Google Scholar] [CrossRef]
- Vesić, N.O.; Velimirović, L.S.; Stanković, M.S. Some invariants of equitorsion third type almost geodesic mappings. Mediterr. J. Math. 2016, 13, 4581–4590. [Google Scholar] [CrossRef]
- Stanković, M.S.; Zlatanović, M.L.; Vesić, N.O. Some properties of ET-projective tensors obtained from Weyl projective tensor. Filomat 2015, 29, 573–584. [Google Scholar] [CrossRef]
- Ceballos, B.; Lamata, M.T.; Pelta, D.A. A comparative analysis of multi-criteria decision-making methods. Prog. Artif. Intell. 2016, 5, 315–322. [Google Scholar] [CrossRef]
- Vinogradova-Zinkevič, I.; Podvezko, V.; Zavadskas, E.K. Comparative Assessment of the Stability of AHP and FAHP Methods. Symmetry 2021, 13, 479. [Google Scholar] [CrossRef]
- Cohen, J.W. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Gravetter, F.J.; Wallnau, L.B. Statistics for the Behavioral Sciences, 10th ed.; Wadsworth: Belmont, CA, USA, 2012. [Google Scholar]
- Babacan, H.; Arik, E.; Bili, Y.; Akgun, H.; Ozkara, Y. Artificial Intelligence and Journalism Education in Higher Education: Digital Transformation in Undergraduate and Graduate Curricula in Turkiye. J. Media 2025, 6, 52. [Google Scholar] [CrossRef]
- Wilson, C.; Grizzle, A.; Tuazon, R.; Akyempong, K.; Cheung, C.K. (Eds.) Media and Information Literacy Curriculum for Teachers; UNESCO: Paris, France, 2011; Available online: https://unesdoc.unesco.org/ark:/48223/pf0000192971 (accessed on 31 July 2025).
- World Economic Forum. The Future of Jobs Report; World Economic Forum: Geneva, Switzerland, 2018; Available online: http://www3.weforum.org/docs/WEF_Future_of_Jobs_2018.pdf (accessed on 31 July 2025).
- Coman, C.; Dalban, C.M.; Pitea, I.; Iordache, M.; Bucs, A. Influence of Mass Media on Career Choices of Final-Year High School Students in Brașov County, Romania. J. Media 2025, 6, 126. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).