DRBoost: A Learning-Based Method for Steel Quality Prediction

Abstract

Steel products play an important role in daily production and life as a common production material. Currently, the quality of steel products is judged by manual experience. However, various inspection criteria employed by human operators and complex factors and mechanisms in the steelmaking process may lead to inaccuracies. To address these issues, we propose a learning-based method for steel quality prediction, which is named DRBoost,based on multiple machine learning techniques, including Decision tree, Random forest, and the LSBoost algorithm. In our method, the decision tree clearly captures the nonlinear relationships between features and serves as a solid baseline for making preliminary predictions. Random forest enhances the model’s robustness and avoids overfitting by aggregating multiple decision trees. LSBoost uses gradient descent training to assign contribution coefficients to different kinds of raw materials to obtain more accurate predictions. Five key chemical elements, including carbon, silicon, manganese, phosphorus, and sulfur, which significantly influence the major performance characteristics of steel products, are selected. Steel quality prediction is conducted by predicting the contents of these chemical elements. Multiple models are constructed to predict the contents of five key chemical elements in steel products. These models are symmetrically complementary, meeting the requirements of different production scenarios and forming a more accurate and universal method for predicting the steel product’s quality. In addition, the prediction method provides a symmetric quality control system for steel product production. Experimental evaluations are conducted based on a dataset of 2012 samples from a steel plant in Liaoning Province, China. The input variables include various raw material usages, while the outputs are the content of five key chemical elements that influence the quality of steel products. The experimental results show that the models demonstrate their advantages in different performance metrics and are applicable to practical steelmaking scenarios.

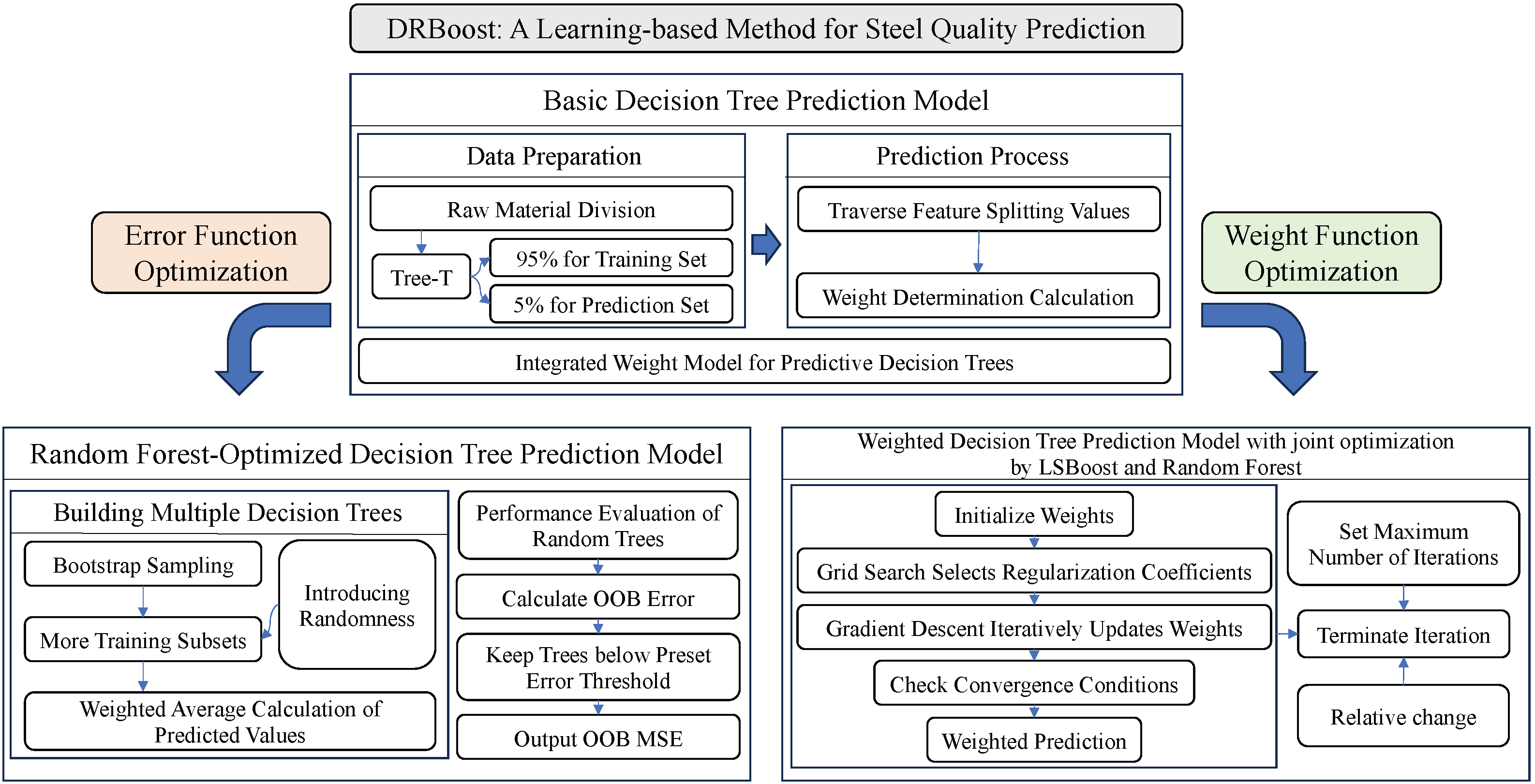
1. Introduction

Steel products, as one of the common production materials, play an important role in daily production and life. The steel industry has a crucial impact on the development of a country as an important indicator of a country’s comprehensive national strength and level of industrialization. In recent years, steel production technology in countries around the world has developed rapidly, and production has increased significantly. According to statistical data from the World Steel Association, in October 2024, the global crude steel production of 71 countries/regions included in the statistics of the World Steel Association reached 152.1 million tons [1]. Among them, China’s crude steel production was 81.88 million tons. In large-scale steel manufacturing, it is essential to ensure the quality of steel products while increasing output, which is crucial for reprocessing steel products, energy savings, and emission reduction.

It is a prerequisite to design an effective method for predicting steel quality in the production process to better control the quality of steel products. In the production process, the quality of steel products is still judged by manual experience, which has many shortcomings. On the one hand, the inspection of steel products carried out by human operators may lead to inaccuracies due to different inspection criteria [2]. On the other hand, multiple factors, such as thermal and compositional factors, influence the quality of steel products [3]. There are many complex factors and mechanisms in the steelmaking process that affect the product quality, and these may remain unclear even for domain experts. In the steelmaking process, different raw materials are involved in various physicochemical reactions, such as oxidation, slag–metal interactions, and deoxidation, containing complex, interdependent feature relationships that are difficult to describe using simple mathematical formulas. Therefore, leveraging machine learning techniques to train models on production data is essential for characterizing these complex, interdependent feature relationships. Machine learning techniques can provide a solution for constructing experience from complex data, gain new information from process measurements, and make predictions about new data samples [4]. Currently, many studies apply intelligent technologies, including operations research, intelligent optimization methods, and machine learning, to process industries represented by steel production [5,6,7,8,9]. However, in the field of steel quality prediction, there is still a lack of data-driven or intelligence-driven methods for steel quality prediction.

The steelmaking process is one of the most important processes in steel production. Pig iron has a high content of carbon, sulfur, and phosphorus elements, which leads to lower hardness, toughness, and poor weldability, resulting in a limited range of applications and an inability to be processed. Therefore, it is necessary to conduct the steelmaking process by adding silicon and manganese elements to re-smelt pig iron to remove impurities, adjust its composition, and improve its properties, making it a steel product with higher hardness and elasticity. In the steelmaking process, the amount of raw materials added determines the final elemental content of the steel, thereby altering the properties of the steel. By adjusting the amount of added raw materials, harmful elements (such as phosphorus, sulfur, etc.) can be controlled, and other elements (such as carbon, manganese, etc.) can be regulated to improve the quality of steel. Therefore, the elemental composition of steel products can be used to predict their quality. Based on this, we design a data-driven method for steel quality prediction.

Considering that various raw materials in the steel production process have a crucial impact on the final chemical content of steel products, the delay caused by traditional chemical analysis methods makes it difficult to meet the requirements of real-time process optimization. Therefore, our method, named DRBoost, utilizes several machine learning techniques, including Decision tree, Random forest, and the LSBoost algorithm, to predict the chemical contents of steel products, thereby predicting the quality of steel products.

Our method builds a three-level prediction framework, including base prediction, ensemble optimization, and weighted correction, to meet diverse prediction requirements in practical production scenarios. Firstly, we construct decision trees through dynamically optimizing the feature links to build relationships among features; thereby, the preliminary predictions of chemical element contents are achieved. To reduce the errors generated by the preliminary predictions, we improve the random forest algorithm through bias–variance balancing using bootstrap resampling with replacements for a more accurate prediction. Moreover, different raw material usages have different influences on the chemical element contents. For example, iron-based materials have more influence on basic elements like carbon, whereas slag-forming materials have more influence on harmful elements like sulfur and phosphorus. Therefore, we employ gradient descent to train an optimized LSBoost model. Based on the model, dynamic contribution coefficients are assigned to different kinds of raw materials to achieve more accurate predictions. The contributions of our method are as follows:

• Our method firstly uses real steelmaking raw material data from steel plants to train a basic decision tree model for predicting the content of several key chemical elements in steel products. The model is referred to as the Basic Decision Tree Prediction Model.
• To address the overfitting problem that may caused by a single decision tree, the random forest algorithm is introduced to optimize the Basic Decision Tree Prediction Model. By incorporating randomness and feature selection, a set of decision trees is constructed, and the prediction results of all decision trees are evaluated collectively to obtain the final prediction results. The model is referred to as the Random Forest-Optimized Decision Tree Prediction Model.
• To improve prediction accuracy, our method employs the LSBoost algorithm, which uses gradient descent training to assign contribution coefficients to the prediction result of each chemical element’s content from each decision tree, thereby optimizing the prediction results. This model is referred to as the Weighted Decision Tree Prediction Model with joint optimization by LSBoost and random forest.
• Through experimental evaluations, we thoroughly analyze the performances of the Basic Decision Tree Prediction Model, the Random Forest-Optimized Decision Tree Prediction Model, and the Weighted Decision Tree Prediction Model with joint optimization by LSBoost and random forest. The experimental results show that three models demonstrate their advantages in different performance metrics. In actual industrial production, we need to choose the appropriate method based on specific requirements.

In our method, three models are constructed to predict the contents of five key chemical elements in steel products. These models are symmetrically complementary to meet the requirements of different production scenarios, forming a more accurate and universal method for predicting a steel product’s quality. In addition, the prediction method provides a symmetric quality control system for steel product production. On the one hand, the method can predict the steel product’s quality in a forward manner based on raw material data. On the other hand, the quality prediction results can guide the use of raw materials in the steel production process in a reverse manner. In practice, operators or engineers compare the predicted contents of various chemical elements to the acceptable ranges specified in relevant standards. If the prediction result falls outside the reasonable range, the model is used in reverse tracing to identify the influencing raw materials, and operators or engineers can evaluate and adjust the quantities of those raw materials accordingly.

Our method has good model interpretability, and the selected input features are important in steel quality prediction. With respect to model interpretability, we employ decision trees to intuitively illustrate the relationships between input features and output results by their clear branch logic. In manufacturing environments, one can directly trace which changes in raw materials contribute to the contents of chemical elements in steel product. Meanwhile, both random forests and LSBoost reflect the influence of different input features on model training through assigning contribution coefficients, enabling operators to verify whether the model’s predictions align with the physicochemical laws of steelmaking. Furthermore, the prediction results can guide raw material usage, offering suggestions for real-world deployment. With respect to feature importance analysis, to evaluate the influence of raw materials in actual production scenarios, we categorize raw materials into five groups containing iron-based materials, slag-forming materials, ore-based materials, alloying materials, and carbon-enhancing and desulfurizing agents. The raw materials in each group have a distinct effect on specific chemical elements during steelmaking. Based on this categorization, our method can quantify the influence of each raw material on the contents of chemical elements, facilitating reasonable material allocations in actual production and thereby achieving more efficient and accurate product quality control.

The structure of our paper is as follows: In Section 2, we introduce some related work on product quality prediction across various areas, especially the steelmaking industry. In Section 3, we provide an overview of our method. Section 4, Section 5 and Section 6 present detailed descriptions of our proposed prediction methods. Section 7 shows the experimental results. Section 8 summarizes our work.

2. Related Work

Recently, data-driven models and machine learning techniques have been utilized for product quality prediction. There exist various methods for predicting the quality of different categories of products [10,11,12,13]. Pilania et al. [14] explored how machine learning techniques can predict the properties of materials, such as metals, semiconductors, and ceramics. Ramprasad et al. [15] provided a comprehensive overview of how machine learning techniques are used to predict material properties and highlighted several successful applications of machine learning in materials informatics. Wu et al. [16] integrated data mining, machine learning, and multi-objective optimization to optimize the hot strip rolling process of microalloyed steels. Zhang et al. [17] employed LightGBM, a gradient-boosting decision tree algorithm for the prediction of chemical toxicity. Xu et al. [18] introduced a novel approach to predict the mechanical properties of hot-rolled alloy steel by training convolutional neural networks. Liu et al. [19] presented a data-driven approach to predict the glass-forming ability of multicomponent metallic alloys by training a backpropagation neural network model. Jiang et al. [20] combined machine learning techniques with multiscale simulations to predict the tensile strength of pearlitic steel wires using real-world industrial datasets. Khedr et al. [9] applied machine learning algorithms, specifically a Random Forest Regressor (RFR) and Gradient Boosting Regressor (GBR), to predict key outcomes of the friction drilling of A356 aluminum alloy.

Machine learning techniques are also applied in steelmaking processes, including predicting defects in steel products, predicting microstructure and mechanical properties, and predicting steel yields. To predict defects in the steelmaking process, Chu et al. [21] proposed a multi-class classifier using quantile-based hyper-spheres to identify different steel surface defects. Nieto et al. [22] designed a hybrid optimized Support Vector Machine (SVM) model via Particle Swarm Optimization for predicting centerline segregation in continuous steel casting. Wu et al. [23] introduced a hybrid deep learning model, named MCRNN, which employs multiscale convolution and recurrent layers to time series data for the prediction of the quality of continuous cast slabs. Thakkar et al. [24] effectively predicted the occurrence of longitudinal facial cracks, enabling early defect detection, by training various machine learning models, such as SVM and gradient boosting. Takalo-Mattila [4] developed a quality prediction system for predicting surface defects in steelmaking plants by training gradient boosting decision trees. For predicting the microstructure and mechanical properties of produced steel, Lieber et al. [25] presented a machine learning-based framework for a rolling mill to predict product quality by identifying key operational patterns affecting intermediate product quality. Li et al. [26] designed an ensemble machine learning framework to predict steel quality parameters in manufacturing workflows and offer a robust practical tool for industrial steel quality control tasks. Guo et al. [27] proposed a multi-property prediction model by combining ordinary least square, SVM, regression trees, and random forest methods to predict the properties of steel products. Orta et al. [28] developed an analytical model-integrated neural network to predict the yield strength, tensile strength, and elongation of cold-rolled and continuously annealed steels. Xie et al. [29] developed LSTM-based time series neural networks to predict hot-rolled steel plates’ properties, such as yield strength, ultimate tensile strength, elongation, and impact energy. In addition, to carry out steel yield predictions, Laha et al. [30] utilized support vector regression to predict key steelmaking outcomes, particularly output yields.

Although machine learning techniques have been applied in product quality predictions across various domains, there is no research work that considers the impact of different raw materials used in the steelmaking processes on the quality of steel products and builds a machine learning model to predict steel product quality. Therefore, this paper focuses on how various raw materials used during the steelmaking process affect the properties of produced steel and builds a model to predict steel product quality by machine learning techniques.

3. Overview of Methods

Our method is introduced from three levels. Firstly, based on real steelmaking data collected from a steel plant, we categorize raw materials into five groups based on their impact on steel products. Then, we construct our proposed decision tree model to predict the contents of chemical elements in each steel product sample according to the impact of different raw materials on the content of each chemical element. For each decision tree, we traverse all samples, and with the goal of minimizing the Mean Squared Error (MSE), we select the node that minimizes the total MSE as the splitting node to build the basic decision tree prediction model. For a given test sample, it is passed along the path of the decision tree to determine the leaf node it belongs to. Once the leaf node is determined, the value of that leaf node is returned as the sample’s predicted content of the current chemical element. The model is named the Basic Decision Tree Prediction Model.

To address the overfitting issue that may arise from relying on a single decision tree in the Basic Decision Tree Prediction Model, our method introduces the random forest algorithm to optimize the model. Specifically, by introducing randomness and feature selection, multiple decision trees are constructed, and the average of all tree predictions is taken as the final predicted content of the chemical element. The optimized model is named the Random Forest-Optimized Decision Tree Prediction Model.

In addition to utilizing the random forest algorithm to construct multiple decision trees to predict the content of each chemical element in steel products, we use the LSBoost algorithm to further improve prediction accuracy. We apply the LSBoost algorithm to assign a dynamic contribution coefficient to the prediction of each decision tree. Specifically, by defining a regularized loss function, setting the learning rate and regularization coefficient, and using gradient descent for iterative updates until convergence, we obtain the trained LSBoost model and dynamic contribution coefficients, resulting in a more accurate prediction model, which is named the Weighted Decision Tree Prediction Model with joint optimization by LSBoost and random forest.

Figure 1 illustrates an overview of our method.

4. Basic Decision Tree Prediction Model

In our method, we construct the basic decision tree model based on several groups of raw materials to predict the content of five representative chemical elements (including S, P, Si, C, and Mn) in steel products, thereby predicting the quality of steel products. In this section, we focus on the construction of the Basic Decision Tree Prediction Model.

4.1. Model Construction

Based on the converter steelmaking process, we selected representative raw materials used in steel production and utilized their quantities as attributes to predict the content of five representative chemical elements in steel products. In steelmaking processes, different raw materials participate in various physicochemical reactions, such as oxidation, slag–metal interactions, and deoxidation, which significantly influence the contents of chemical elements in steel products. For example, molten iron, pig iron, and scrap steel affect the content of key chemical elements, such as C, Si, Mn, S, and P, during refining. Alloy materials are used in the later stages to adjust the contents of chemical elements, while fluxes and slag-forming materials are employed in desulfurization and dephosphorization, directly affecting the contents of S and P. Therefore, it is important to categorize raw materials to train machine learning models for a more accurate characterization of how different reaction types influence the contents of chemical elements, thereby improving prediction accuracy. To ensure the effectiveness of decision trees, the selected raw materials are categorized into five groups to construct multiple decision trees:

• Iron-based materials (e.g., hot metal): These materials can reflect the influence of metallic raw material ratios on steel compositions.
• Slag-forming materials (e.g., slag steel): These materials are crucial for controlling slag-related reactions.
• Ore-based materials (e.g., sintered ore): These materials help analyze the impact of ore compositions on the final steel product.
• Alloying materials (e.g., ferrosilicon): These materials track the reaction dynamics of alloying elements.
• Carbon-enhancing and desulfurizing agents (e.g., coke breeze, carburizers): These materials can capture the effectiveness of desulfurizers and other auxiliary materials.

In our method, we utilize these five groups of raw materials to construct decision trees for predicting the five representative chemical elements. The five groups are denoted as A, B, C, D, and E, and decision trees are trained based on the quantities of these materials in each group and their corresponding contents of the five chemical elements. Each decision tree is denoted as $T_{PQ}$, where $P\in \{A,B,C,D,E\}$ represents the raw material category and $Q\in \{S,P,Si,C,Mn\}$ represents the target chemical element. For example, the decision tree trained on Group A (Iron-based materials) to predict the content of S is denoted as $T_{AS}$.

For each decision tree, we denote the number of raw materials in each group, which are used in the construction of the decision tree (that is, the number of features), as n. For example, if the decision tree $T_{AS}$ for predicting the content of S is trained using the quantities of four raw materials in Group A containing hot metal, steelmaking pig iron, external scrap steel, and in-house scrap steel, then $n=4$.

The total number of feature vectors (i.e., training samples composed of the quantities of each raw material) used to construct the decision tree is denoted as N. The i-th sample can then be represented as follows:

$${\mathbf{X}}_i^{(T_{PQ})}=(X_{i,1}^{(T_{PQ})},X_{i,2}^{(T_{PQ})},\dots ,X_{i,n}^{(T_{PQ})}).$$

All feature vectors constitute the sample space ${\mathbf{R}}^{(T_{PQ})}$, which can be represented as follows:

$${\mathbf{R}}^{(T_{PQ})}=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \dots & x_{1n}\\ x_{21}& x_{22}& \dots & x_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ x_{N1}& x_{N2}& \dots & x_{Nn}\end{array}\right].$$

Meanwhile, each sample includes the contents of five representative chemical elements as the output. The chemical element contents corresponding to the i-th sample are denoted as $Y_i^Q$. Therefore, the i-th sample containing both the input and the output, which is used for training the decision tree, can be represented as

$$({\mathbf{X}}_i^{(T_{PQ})},Y_i^Q),$$

and the whole training set can be represented as

$${\mathbf{D}}^{(T_{PQ})}=\left\{\left({\mathbf{X}}_i^{(T_{PQ})},Y_i^Q\right)|i=1,2,\dots ,N\right\},$$

where $P\in \{A,B,C,D,E\}$, $Q\in \{S,P,Si,C,Mn\}$, and $i\in \{1,2,\dots ,N\}$.

For simplicity, in subsequent descriptions, decision trees are denoted by T, and the sample space, the i-th input feature vector (the quantities of each raw material), the i-th output true value (the actual content of each chemical element), and the i-th output predicted value (the predicted content of each chemical element) are denoted by ${\mathbf{R}}^{(T)}$, ${\mathbf{X}}_i^T$, $Y_i$, and ${\widehat{Y}}_i$, respectively, where $i\in \{1,2,\dots ,N\}$.

In our method, we aim to utilize training data to construct decision trees for predicting the content of each chemical element. That is, we construct a decision tree T that maps the input feature vector ${\mathbf{X}}_i^T$ to a predicted value ${\widehat{Y}}_i$.

Let the feature space ${\mathbf{R}}^{(T)}$ be partitioned into M non-overlapping regions, where each region corresponds to a leaf node of the decision tree. ${\mathbf{R}}^{(T)}$ can be represented as follows:

$${\mathbf{R}}^{(T)}=\bigcup _{m=1}^M{\mathbf{R}}_m^{(T)},$$

where $m\in \{1,2,\dots ,M\}$ and ${\mathbf{R}}_m^{(T)}\cap {\mathbf{R}}_{m^{\prime }}^{(T)}=\varnothing$$(m\ne m^{\prime })$. For the m-th leaf node region ${\mathbf{R}}_m^{(T)}$, which contains a subset of training samples ${\mathbf{D}}^{(T)}=\left\{\left({\mathbf{X}}_i^{(T)},Y_i\right)|{\mathbf{X}}_i^{(T)}\in {\mathbf{R}}_m^{(T)}\right\}$, we compute the predicted value $c_m$ as the mean of the true output values of all samples $Y_i$ within the region ${\mathbf{R}}_m^{(T)}$. This approach minimizes the squared error loss, serving as the optimal predicted constant for the region, which can be represented as follows:

$$c_m={\displaystyle \frac{1}{|{\mathbf{R}}_m^{(T)}|}}\sum _{i:{\mathbf{X}}_i^{(T)}\in {\mathbf{R}}_m^{(T)}}{Y}_i.$$

And the prediction model can be represented as:

$$T({\mathbf{X}}_i^{(T)})=\sum _{m=1}^M\left(c_m·\mathbb{I}\left({\mathbf{X}}_i^{(T)}\in {\mathbf{R}}_m^{(T)}\right)\right),$$

where $\mathbb{I}(·)$ is the indicator function that takes the value of 1 if ${\mathbf{X}}_i^{(T)}$ falls within the region ${\mathbf{R}}_m^{(T)}$ and 0 otherwise.

4.2. Model Training

During the training phase, the decision tree recursively splits nodes starting from the root, with each splitting decision aimed at minimizing the Mean Squared Error (MSE) of the samples after the split. For samples within a given region ${\mathbf{R}}_m^{(T)}$, we aim to identify a set of splitting parameters $(j,\gamma )$, where $j\in \{1,2,$…$,n\}$ denotes the feature index and $\gamma$ represents the threshold for the predicted chemical element, to partition the region into two sub-regions:

$$R_{\mathrm{l}}=\left\{{\mathbf{X}}_i^{(T)}\in {\mathbf{R}}_m^{(T)}|X_{ij}^{(T)}\le \gamma \right\},$$

and

$$R_{\mathrm{r}}=\left\{{\mathbf{X}}_i^{(T)}\in {\mathbf{R}}_m^{(T)}|X_{ij}^{(T)}\le \gamma \right\}.$$

With respect to $(j,\gamma )$, the local loss function is defined as follows:

$$L(j,\gamma )=\sum _{j:X_{ij}^{(T)}\in R_{\mathrm{l}}}{\left(Y_i-c_{\mathrm{l}}\right)}^2+\sum _{j:X_{ij}^{(T)}\in R_{\mathrm{r}}}{\left(Y_i-c_{\mathrm{r}}\right)}^2,$$

where the predicted constants within the leaf nodes are

$$c_{\mathrm{l}}={\displaystyle \frac{1}{|R_{\mathrm{l}}|}}\sum _{i:{\mathbf{X}}_i^{(T)}\in R_1}{Y}_i,$$

and

$$c_{\mathrm{r}}={\displaystyle \frac{1}{|R_{\mathrm{r}}|}}\sum _{i:{\mathbf{X}}_i^{(T)}\in R_{\mathrm{r}}}{Y}_i.$$

By traversing all candidate $(j,\gamma )$ pairs, the split point minimizing the total MSE $L(j,\gamma )$ is selected, which can be represented as follows:

$$(j^{*},{\gamma }^{*})=arg\underset{j,\gamma }{min}L(j,\gamma ).$$

After selecting $(j^{*},{\gamma }^{*})$, the region is divided into $R_{\mathrm{l}}$ and $R_{\mathrm{r}}$ based on the optimal split point. The above splitting process is then repeated for each newly formed pair $R_{\mathrm{l}}$ and $R_{\mathrm{r}}$ until every subspace contains only one definitive sample and its corresponding predicted value of the content of chemical element.

The prediction model of the decision tree can be represented as follows:

$$T({\mathbf{X}}_i^{(T)})=\sum _{m=1}^M\left(c_m·\mathbb{I}({\mathbf{X}}_i^{(T)}\in {\mathbf{R}}_m^{(T)})\right),$$

where M is the number of leaf nodes, ${\mathbf{R}}_m^{(T)}$ is the m-th non-overlapping region (the “coverage” of the leaf node), $c_m$ is the predicted output value when the sample falls within this region, and $\mathbb{I}(·)$ is the indicator function, determining whether ${\mathbf{X}}_i^{(T)}$ belongs to the m-th leaf node.

After model training is completed, for a new input sample ${\mathbf{X}}_i^{(T)}$, we pass it along the decision tree’s path to determine which leaf node ${\mathbf{R}}_m^{(T)}$ it belongs to. Once the corresponding leaf node is identified, we return the predicted value $c_m$ of the leaf node as ${\widehat{Y}}_i$.

5. Random Forest-Optimized Decision Tree Prediction Model

Relying on a single decision tree to predict the content of each chemical element tends to result in significant errors and localized overfitting issues. Therefore, we propose constructing multiple decision trees and employing the random forest approach for weight settings to optimize the predictive model.

In our method, g decision trees are constructed to predict the content of each chemical element, denoted as $T_1,T_2,$…$,T_g$. To train g decision trees, we perform sampling with replacements from the original training set each time, selecting $N_s$ training samples to form g training subsets. The reason for using sampling with replacement is that it ensures each training subset is different while avoiding excessive divergence between them, effectively balancing the model’s bias and variance. The value of g is determined based on the size of the original training set. Theoretically, a larger number of decision trees leads to greater improvements in model performance. However, too many decision trees will cause greater computational costs. Therefore, in practice, our method adopts an empirical approach to select an appropriate value of g based on the scales of the model and the training set.

Although different training subsets lead to variations in the structures and predictions of multiple decision trees, the Law of Large Numbers ensures that

$${\widehat{Y}}_i={\displaystyle \frac{1}{g}}\sum _{k=1}^g{T}_k({\mathbf{X}}_i^{(T_k)})\to \mathbb{E}\left[T({\mathbf{X}}_i^{(T)})\right],$$

Therefore, as the number of decision trees increases, the prediction results tend to stabilize.

The training process yields multiple decision trees, each associated with its own leaf node regions and predictive constants. For the k-th tree ($k\in \{1,2,$…$,g\}$), the final number of leaf nodes is denoted as $M_{T_k}$, and its leaf node regions are sequentially labeled as ${\mathbf{R}}_m^{T_k}(m\in \{1,2,$…$,M_{T_k}\})$. For any input sample ${\mathbf{X}}_i^{(T_k)}$, the prediction model can be expressed as follows:

$$T_k\left({\mathbf{X}}_i^{(T_k)}\right)=\sum _{m=1}^{M_{T_k}}{c}_{m,k}\mathbb{I}\left({\mathbf{X}}_i^{(T_k)}\in {\mathbf{R}}_m^{T_k}\right).$$

After training these g decision trees, we determine the final predicted value by averaging the prediction results of all decision trees. Therefore, the optimized prediction result can be expressed as

$${\widehat{Y}}_i={\displaystyle \frac{1}{g}}\sum _{k=1}^g\sum _{m=1}^{M_{T_k}}{c}_{m,k}\mathbb{I}\left({\mathbf{X}}_i^{(T_k)}\in {\mathbf{R}}_m^{T_k}\right).$$

6. Weighted Decision Tree Prediction Model with Joint Optimization by LSBoost and Random Forest

Based on the previous description, the representative raw materials are categorized into five groups to construct multiple decision trees. Each group of raw materials yields the content of various elements as prediction results. In fact, different raw materials have different influences on the content of chemical elements in the steel products. Therefore, to improve prediction accuracy, we assign a dynamic contribution coefficient to the prediction results of each group of raw materials, which quantifies its influence.

The vector of the contribution coefficient is denoted as follows:

$$\mathbf{w}=[w_1,w_2,w_3,w_4,w_5].$$

For any given sample, its predicted results obtained from the five groups of raw materials are denoted as a vector:

$$\widehat{\mathbf{Y}}=[{\widehat{Y}}_1,{\widehat{Y}}_2,{\widehat{Y}}_3,{\widehat{Y}}_4,{\widehat{Y}}_5].$$

The weighted prediction result using contribution coefficients is calculated as follows:

$${\widehat{\mathbf{Y}}}^{\prime }={\mathbf{w}}^{\mathrm{T}}\widehat{\mathbf{Y}}.$$

During the model training process, we continuously adjust the weights to improve prediction accuracy. To achieve this, the method defines a loss function with a regularization term:

$$L(\mathbf{w})={\left(Y_i-{\mathbf{w}}^{\mathrm{T}}\widehat{\mathbf{Y}}\right)}^2+\lambda {\parallel \mathbf{w}\parallel }^2,$$

where $\lambda$ is the regularization coefficient used to avoid overfitting in the model. The contribution coefficients of five raw material groups are uniformly initialized as 0.2.

The optimal regularization coefficient $\lambda$ is determined using a grid search approach. The gradient descent is used to iteratively update the weight vector $\mathbf{w}$ until convergence. The values of the loss function $L(\mathbf{w})$ are computed, and the final regularization coefficient $\lambda$ is selected to minimize the loss.

Let the iteration step be denoted by $k=0,1,2,\dots$. At the k-th step, the gradient of the loss function with respect to $\mathbf{w}$ is given by the following:

$$\nabla L\left({\mathbf{w}}^{(k)}\right)=-2\widehat{\mathbf{Y}}\left(Y_i-{\left({\mathbf{w}}^{(k)}\right)}^T\widehat{\mathbf{Y}}\right)+2\lambda {\mathbf{w}}^{(k)}.$$

Gradient descent is adopted to update the model. The learning rate is set to $\eta$, and the update rule is

$${\mathbf{w}}^{(k+1)}={\mathbf{w}}^{(k)}-\eta \nabla L\left({\mathbf{w}}^{(k)}\right).$$

The learning rate $\eta$ is determined using the Lipschitz constant estimation method. From the loss function $L(\mathbf{w})$, its Hessian matrix can be derived as

$$\mathbf{H}=2\widehat{\mathbf{Y}}{\widehat{\mathbf{Y}}}^T+2\lambda \mathbf{I},$$

for which its maximum eigenvalue is given by the following:

$${\lambda }_{max}(\mathbf{H})=2{\lambda }_{max}\left(\widehat{\mathbf{Y}}{\widehat{\mathbf{Y}}}^T\right)+2\lambda =2{\Vert \widehat{\mathbf{Y}}\Vert }^2+2\lambda ,$$

where $L_H={max[2\Vert \mathbf{Y}\Vert }^2+2\lambda ]$. That is, the learning rate $\eta$ is guaranteed to achieve global convergence to the optimal solution when satisfying $0<\eta <{\displaystyle \frac{2}{L_H}}$. We set $\eta ={\displaystyle \frac{1}{L_H}}$ based on the predicted contents range of chemical elements $[0,1]$, and it can be obtained that $\Vert \widehat{\mathbf{Y}}{\Vert }^2\le 5$ and $L_H=10+2\lambda$. And the value of $\eta$ can be computed based on the value of $\lambda$.

Based on the previous derivation, we obtain the gradient update formula:

$${\mathbf{w}}^{(k+1)}={\mathbf{w}}^{(k)}+2\eta \widehat{\mathbf{Y}}\left(Y_i-{\left({\mathbf{w}}^{(k)}\right)}^T\widehat{\mathbf{Y}}\right)-2\eta \lambda {\mathbf{w}}^{(k)}.$$

Repeat the iteration process until either convergence is achieved or the maximum iteration count is reached. We employ the relative change method to determine convergence, with a threshold of $\epsilon$. Specifically, when

$${\displaystyle \frac{\Vert {\mathbf{w}}^{(k+1)}-{\mathbf{w}}^{(k)}\Vert }{\Vert {\mathbf{w}}^{(k)}\Vert }}<\epsilon ,$$

the model is considered sufficiently converged, and the training process is terminated. Simultaneously, we set a maximum iteration limit $K_{max}=1000$. If the iteration count $k\ge K_{max}$, the training process is terminated.

7. Experimental Results

In this section, we provide a concise and precise description of the experimental results.

7.1. Experimental Setup

7.1.1. Dataset

The dataset used in the paper is sourced from a steel plant in Liaoning Province, China, and contains 2012 samples, and the dataset represents static batch data. To evaluate the proposed models’ performances, we split the dataset into approximately 95% for training (1900 samples) and 5% for testing (112 samples).

Each sample corresponds to a production batch and includes raw material usage data along with the chemical element contents measured in the corresponding batch products. All input features are continuous variables, with no categorical or discrete data involved. The prediction targets are the contents of five key chemical elements in the steel products, including sulfur, phosphorus, silicon, carbon, and manganese. Their concentration ranges are as follows. The contents of sulfur are in the 0.007–0.02% range. The contents of phosphorus are in the 0.011–0.024% range. The contents of silicon are in the 0.01–0.9% range. The contents of carbon are in the 0.03–0.8% range. The contents of manganese are in the 0.14–1.5% range. Since the contents of chemical elements are continuous values, the prediction task is formulated as a regression problem.

7.1.2. Data Preprocessing

To deal with outliers, we set constraints on value ranges based on the domain knowledge of steelmaking processes and the statistical distributions of the contents of chemical elements. Approximately 0.69% of samples (14 samples) were considered as extreme outliers, and they were directly removed. Approximately 4.2% of samples (85 samples) showed minor deviations but remained within reasonable range, and they were retained. Approximately 2.05% of the samples (41 samples) in the original dataset were missing, and we applied median imputation to fill these gaps.

In our method, we employ data normalization techniques to preprocess the data. For features with significantly different numeric magnitudes, such as the proportion of iron-based raw materials (30–50%) versus the content of trace element sulfur (0.001–0.05%), we apply Min–Max normalization to map their values into the [0, 1] range. Some features are further standardized using Z-score normalization to remove the effects caused by different numeric magnitudes. However, for features with relatively balanced numerical ranges, such as the contents of primary elements like carbon and silicon, we preserve their original values.

7.1.3. Model Training and Parameter Setting

We employ k-fold validation ($k=5$) to train our proposed models. The training data are randomly shuffled at the batch level, and the target variable is stratified to reduce sampling bias. We then perform 5-fold cross-validation. In each fold, four subsets train the model and one validates it, yielding a validation Mean Squared Error (MSE) for that fold. We average the five fold MSEs to obtain the cross-validated MSE (CV_MSE) and record their standard deviation to measure stability. To reduce randomness, we repeat this 5-fold process under 10 different random seeds. Finally, we select the model parameters that minimize the mean CV_MSE and exhibit low variance.

During model training, the hyperparameters are systematically configured and fine-tuned, and the training stop condition is set.

In the Basic Decision Tree Prediction Model, we determined the maximum tree depth using the “Tree depth-validation MSE” curve. By scanning from 5 to 50 in steps of 5, the errors decrease when the depth is less than 20, which indicates underfitting. The errors in the 25–35 range are stable, which indicates that the results are well-fitted, and when errors increase beyond 35, this indicates overfitting. Considering feature nonlinearity, the maximum tree depth is set to 31, as it covers 98% of the nonlinear features while avoiding overfitting. For the leaf node’s minimum size, by scanning in the 5–30 range, it is sensitive to noise when the value is less than 10. Moreover, oversmoothing occurs when the value is greater than 20. Through cross-validation, the value is set to 16. The training process terminates when the node size is less than 16 or the Gini information gain is less than 0.001.

In the Random Forest-Optimized Decision Tree Prediction Model, we conduct experiments ranging from 2 to 20 base learners. When there are fewer than five base learners, the OOB error dropped rapidly, indicating an insufficient ensemble effect. When there are 6 to 10 base learners, the error becomes flat. When there are more than 10 base learners, the error does not decrease significantly, but the computational cost increased by more than 30%. To ensure efficiency, the number of base learner is set to eight.

In the Weighted Decision Tree Prediction Model with joint optimization by LSBoost and random forest, the learning rate is first constrained by the upper bound derived from the Lipschitz constant. Since the contents of chemical elements are in range [0, 1], the Lipschitz constant L of the objective function is estimated as 20. To ensure the convergence of gradient descent, the learning rate $\eta$ should be less than $1/L$ (0.05). Subsequently, a grid search is conducted within the range [0.01, 0.02, 0.03, 0.04, 0.05]. When $\eta$ is set to 0.01, the model converged slowly, requiring more than 800 iterations. When $\eta$ is set to 0.05, convergence is accelerated, requiring around 250 iterations, and the validation error is comparable to that with $\eta =0.01$. Therefore, the learning rate $\eta$ is set to 0.05, achieving a balance between convergence efficiency and prediction accuracy.

The regularization coefficient $\lambda$ is determined via grid search, aiming to minimize the regularized loss function. Specifically, a 5-fold cross-validation is conducted with $\lambda \in \{0.00001,0.0001,0.001,0.01,0.1\}$. The results show that when $\lambda =0.01$, the validation error reached its minimum (0.028), and the L2-norm of the weight vector is reduced by 40% compared with $\lambda =0$, effectively suppressing overfitting. Therefore, the regularization coefficient $\lambda$ is set to 0.01.

For training iterations, convergence is determined, and the training process is terminated when the decrease in the loss function over five consecutive iterations is less than 0.0001. If this condition is not satisfied after 1000 iterations, the training process is terminated to avoid infinite loops caused by extreme samples. In practice, the LSBoost model typically meets the termination condition after 230–280 iterations, ensuring sufficient convergence while keeping computational costs in control.

7.1.4. Experimental Environment

The experiment was conducted on a Windows operating system, with an AMD Ryzen 7 8845H processor. This processor has 8 cores and 16 threads, with a base clock speed of 2.3 GHz. The system is equipped with 16 GB of DDR4 RAM and a 512 GB SSD. The experiment was conducted on Matlab R2020b.

7.1.5. Evaluation Metrics

We select several metrics to evaluate our proposed methods as follows:

• Overall Accuracy: The proportion of correctly predicted instances among all predictions, reflecting the general performance of the model in predicting the contents of key chemical elements in steel products.
• Precision: The ratio of true positive predictions to the total positive predictions made by the model, indicating the reliability of the model when it predicts a sample as having a specific element content.
• Recall: The ratio of true positive predictions to the total actual positive instances, measuring the model’s ability to identify all samples with the specific element content.
• F1 Score: The harmonic mean of precision and recall, providing a balanced measure that combines both metrics to evaluate the model’s performance, which is especially useful when there is an imbalance in the data.
• Prediction Time: The average time taken by the model to generate predictions for a single sample, reflecting the computational efficiency of the model in practical applications.
• Peak Memory Usage: The maximum amount of memory consumed by the model during the prediction process, indicating the memory requirements for deploying the model in industrial environments.
• Training Time: The average time to train the prediction model, reflecting the training efficiency of the model in practical applications.
• Mean Squared Error on Training Set (TrainMSE): The Mean Squared Error on the training set measures the average squared difference between the actual values and the predicted values on the training data. The smaller the MSE, the better the model fits the training data. Therefore, the MSE provides an indication of how well the model captures the patterns in the training data, with smaller values indicating a better fit.
• Cross-Validation MSE (CV_MSE): The CV_MSE is calculated using 10-fold cross-validation. In this process, the data is divided into 10 subsets, with 9 subsets used for training and the remaining subset used for testing, and the average MSE is computed. Cross-validation MSE helps provide a more reliable estimate of the model’s performance, reducing the risk of overfitting, and offers a more robust evaluation of the model’s generalization ability by testing it on different subsets of the data.
• Coefficient of Determination (${\mathbf{R}}^{\mathbf{2}}$):${\mathrm{R}}^2$ measures how well the model explains variance in the target variable. It reflects the proportion of variability in the dependent variable that can be accounted for by the independent variables in the model. A higher ${\mathrm{R}}^2$ value indicates that the model does a better job of explaining variations in the data. Essentially, it shows how well the model fits the data, with a value closer to 1 indicating a stronger fit and a value closer to 0 suggesting that the model does not explain much of the variability.
• Out-of-Bag MSE (OOB MSE): The Out-of-Bag MSE is calculated using out-of-bag samples, which are the training samples that were not selected during the bootstrapping process in a random forest model. OOB MSE provides an evaluation of the model’s performance without the need for additional cross-validation or test set splitting, which is particularly useful in ensemble methods like random forests, offering a way to assess the model’s performance without requiring extra data.
• Root Mean Squared Error (RMSE): RMSE is the square root of the MSE, representing the standard deviation of the residuals (errors), and it is in the same units as the target variable, making it more interpretable than MSE. RMSE quantifies the error of the model’s predictions, and lower RMSE values indicate smaller prediction errors, reflecting better model performance.
• Mean Absolute Error (MAE): MAE measures the average absolute difference between the predicted values and the actual values, disregarding the direction of the error. Unlike MSE and RMSE, MAE does not penalize larger errors excessively, making it a more robust measure when dealing with outliers. It provides a straightforward average error metric.

7.2. Evaluation of Basic Decision Tree Prediction Model

By testing the Basic Decision Tree Prediction Model, it shows an overall accuracy of 63.16% when predicting the contents of chemical elements. However, the average error rates differ significantly among elements: sulfur has the highest error rate at 52.1%, phosphorus at 27.8%, silicon at 47.9%, carbon at 39.4%, and manganese at 18.7%. The average error rates of the chemical elements are listed in

Table 1. Average error rate of the Basic Decision Tree Prediction Model.

Chemical Element	Average Error Rate
Sulfur	0.52143
Phosphorus	0.27831
Silicon	0.47874
Carbon	0.39432
Manganese	0.1873

.

Sulfur and phosphorus are typically present in steel only as trace elements, with concentration levels much lower than other major elements. The exceptionally low values make it difficult for our proposed models to learn the subtle correlations between raw material usages and the contents of chemical elements when data is limited. As a result, even small variations in these trace element concentrations among samples can lead to significant prediction inaccuracies. Moreover, in steelmaking processes, the removal and control of sulfur and phosphorus are more complex and influenced by numerous dynamic factors, such as slagging reaction efficiency and temperature fluctuations. These factors introduce strong nonlinearity between process parameters and raw material usage. Our proposed models, when handling such highly complex mappings, are prone to overfitting, which consequently increases prediction errors.

With respect to other metrics, TrainMSE is close to CV_MSE. For silicon and carbon, TrainMSE values are 0.00093387 and 0.0025319, while CV_MSE values are 0.0011862 and 0.0036208. Their corresponding values of ${\mathrm{R}}^2$ are 0.9535 and 0.9615, indicating the model’s strong fitting ability. The model also performs well when predicting the content of manganese, while TrainMSE and CV_MSE values are 0.0082831 and 0.0086268, respectively. In contrast, the performances when predicting the contents of sulfur and phosphorus predictions are relatively weak, while the values of ${\mathrm{R}}^2$ are only 0.1582 and 0.2037, but the CV_MSE values are higher than TrainMSE. The results of the evaluation metrics are summarized in

Table 2. Evaluation metrics of the Basic Decision Tree Prediction Model.

Chemical Element	TrainMSE	CV_MSE	${\mathbf{R}}^2$
Sulfur	$1.7463\times {10}^{-5}$	$1.9296\times {10}^{-5}$	0.15821
Phosphorus	$1.4338\times {10}^{-5}$	$1.6021\times {10}^{-5}$	0.20368
Silicon	0.00093387	0.0011862	0.95351
Carbon	0.0025319	0.0036208	0.96152
Manganese	0.0082831	0.0086268	0.93315

.

The model predicts very quickly, with an average prediction time of 0.0029 s.

Overall, the model predicts the contents of silicon, carbon, and manganese most accurately, while its prediction of the contents of sulfur and phosphorus is weaker with a relatively larger error. There is still room for improvement with respect to the model’s prediction accuracy.

7.3. Evaluation of Random Forest-Optimized Decision Tree Prediction Model

Compared to the Basic Decision Tree Prediction Model, the Random Forest-Optimized Decision Tree Prediction Model demonstrates higher accuracy. The experimental results indicate that the model achieves an overall accuracy of 75.69% when predicting the contents of chemical element contents, which is higher than the Basic Decision Tree Prediction Model. The average error rates for the predictions of all chemical elements’ contents have decreased, suggesting that the model is more reliable in classifying threshold boundary samples compared to the Basic Decision Tree Prediction Model. The average error rates of the chemical elements are listed in

Table 3. Average error rate of the Random Forest-Optimized Decision Tree Prediction Model.

Chemical Element	Average Error Rate
Sulfur	0.43521
Phosphorus	0.24329
Silicon	0.36214
Carbon	0.29421
Manganese	0.15329

.

The Random Forest-Optimized Decision Tree Prediction Model exhibits superior generalization capabilities across several evaluation metrics compared to the Basic Decision Tree Prediction Model. Firstly, OOB MSE has decreased, especially for sulfur, phosphorus, and manganese, which demonstrates that introducing random forest can effectively reduce both bias and variance, thereby enhancing the model’s predictive ability. For silicon and carbon, the values of ${\mathrm{R}}^2$ reached 0.97821 and 0.9832, respectively, indicating an excellent fitting performance and high accuracy. Additionally, RMSE and MAE also highlight the advantages of the model. Lower RMSE and MAE values suggest better error control, maintaining small errors. Notably, for phosphorus, both RMSE and MAE values are significantly lower than those of other elements, with their errors being the lowest, indicating more accurate predictions for the contents of phosphorus. The results of the evaluation metrics are summarized in

Table 4. Evaluation metrics of the Basic Decision Tree Prediction Model.

Chemical Element	OOB MSE	${\mathbf{R}}^2$	RMSE	MAE
Sulfur	$1.257\times {10}^{-5}$	0.34921	0.0051158	0.0042266
Phosphorus	$1.3006\times {10}^{-5}$	0.47832	0.0036079	0.0030711
Silicon	0.0014302	0.97821	0.11178	0.039049
Carbon	0.0023182	0.9832	0.042593	0.023821
Manganese	0.014506	0.96532	0.1202	0.088941

.

The average prediction time of the model is 0.11 s, slightly higher than that of the Basic Decision Tree Prediction Model, but it still sufficient for meeting practical application requirements.

7.4. Evaluation of Weighted Decision Tree Prediction Model with Joint Optimization by LSBoost and Random Forest

By introducing contribution coefficients, the Weighted Decision Tree Prediction Model with joint optimization by the LSBoost and random forest models demonstrates strong fitting abilities after optimizing the weight function. The model achieves an overall accuracy of 83.33%, though with an average prediction time of 0.39 s. The average error rates of the chemical elements are listed in

Table 5. Average error rate of the Random Forest-Optimized Decision Tree Prediction Model.

Chemical Element	Average Error Rate
Sulfur	0.21925
Phosphorus	0.17203
Silicon	0.20127
Carbon	0.13923
Manganese	0.11209

.

Compared to the Random Forest-Optimized Decision Tree Prediction Model, the model effectively minimizes the loss function and assigns adaptive weights to each weak learner constructed by decision trees. It not only effectively corrects model residuals and reduces bias but also avoids the overfitting problems caused by the high correlations among features, resulting in lower errors and higher accuracies.

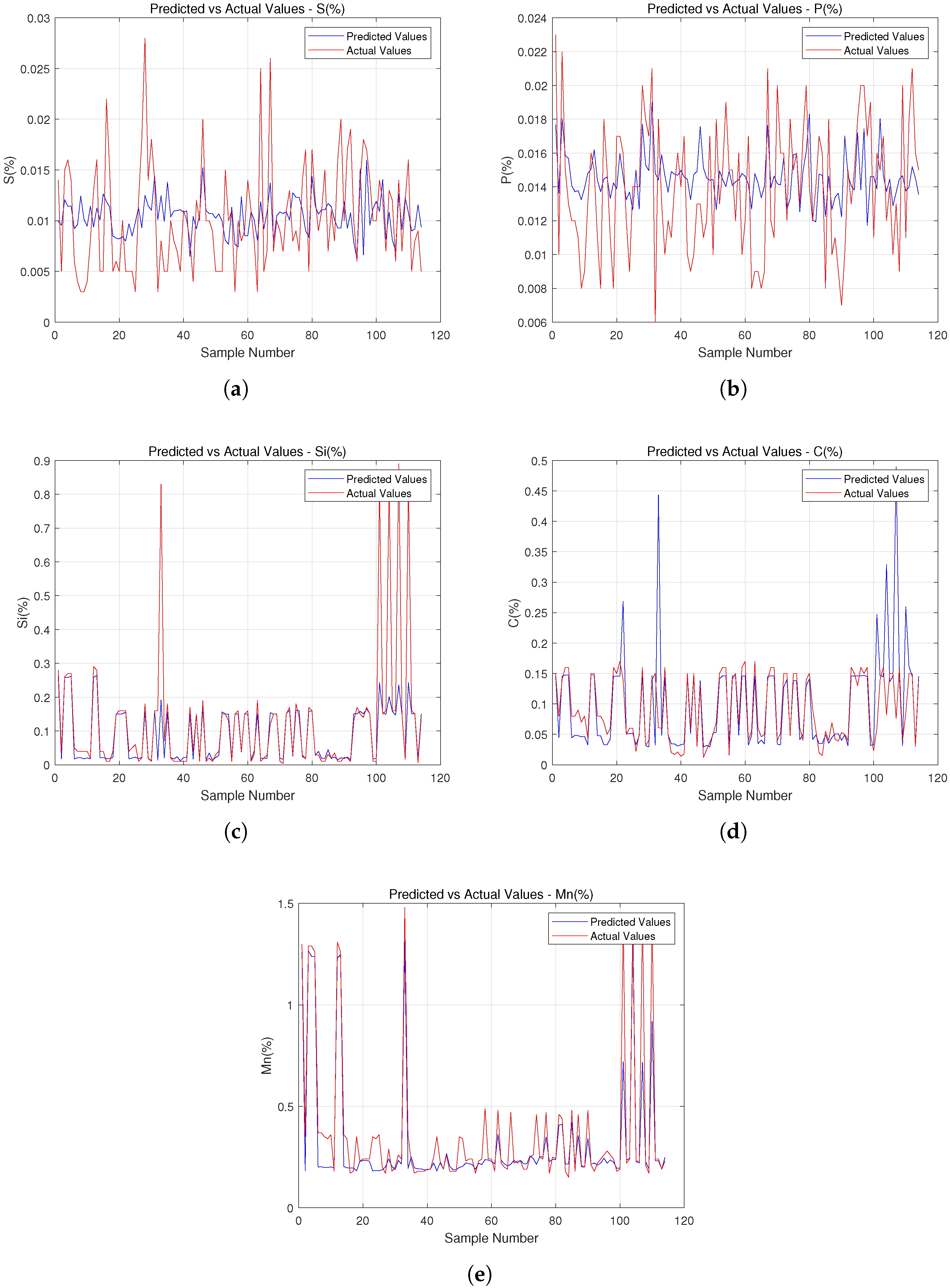
Figure 2 shows the comparisons between the predictions (blue line) and the actual values (red line) using the model. From the experimental results, the trend in prediction is generally consistent with that of actual values, with small errors. Especially in many areas, the fluctuations are consistent, indicating the model’s good performance. However, there are also some samples with large errors, especially at some discrete extreme points, where the predictions deviate significantly from the actual values, indicating that the model has certain shortcomings in predicting these discrete extreme fluctuations. Overall, the model can predict well in most cases, but further improvements in prediction accuracy are required in some special cases.

In Figure 2, the prediction deviations at isolated extreme points are large, and they are directly linked to process anomalies during steelmaking. These extreme points often arise from unexpected operational exceptions, such as interruptions or overdosing during raw material addition, or they result from the deviation of key parameters like temperature and pressure in the converter or refining furnace from standard ranges. Such anomalies disrupt the normal balance of metallurgical reactions, causing the mapping between raw material usage and the contents of chemical elements to diverge from regular patterns. Existing models, trained primarily on stable production data, exhibit limited adaptability to these rare abrupt scenarios and lead to significant prediction errors at extreme points.

To address this issue of poor prediction performance at isolated extremes, we propose enriching the dataset with anomalous samples by collecting real-world batches exhibiting sudden elemental fluctuations over recent years. Additionally, we can simulate abnormal scenarios, such as excessively high temperatures or shortened slagging duration, by generative adversarial networks and augment the training set with these synthetic samples to enhance the model’s adaptability in extreme conditions.

To demonstrate the efficiency of LSBoost, we conducted further experimental evaluations on three metrics, including prediction time, training time, and peak memory usage. The results indicate that LSBoost outperforms XGBoost, Gradient Boosting, and AdaBoost across all these metrics. The experimental results are shown in

Table 6. Comparison between LSBoost, XGBoost, Gradient Boosting, and AdaBoost.

Model	Prediction Time (s)	Training Time (s)	Peak Memory Usage (GB)
LSBoost	0.39	8.2	1.5
XGBoost	0.76	15.4	2.8
Gradient Boosting	0.68	13.1	2.3
Carbon	0.81	16.7	2.5

.

7.5. Comparison with Baseline Models

We selected four baseline algorithms, including single decision tree, linear regression, logistic regression, and naive Bayes, for comparison with our three proposed models. The evaluation metrics include overall accuracy, precision, recall, F1 score, prediction time, and peak memory usage, providing a comprehensive evaluation of each model’s prediction performance. The experimental results are presented in

Table 7. Comparison with baseline models.

Model	Overall Accuracy	Precision	Recall	F1 Score	Prediction Time (s)	Peak Memory Usage (GB)
SDT	58.21%	0.57	0.55	0.56	0.0012	0.6
LinR	60.47%	0.59	0.58	-	0.0015	0.7
LogR	61.4%	0.60	0.58	0.59	0.002	0.7
NB	57.89%	0.56	0.54	0.55	0.001	0.5
DT	63.16%	0.61	0.59	0.6	0.0029	0.8
RFDT	75.69%	0.74	0.73	0.72	0.11	1.2
LRFDT	83.33%	0.82	0.81	0.8	0.39	1.5

. In the table, single decision tree, linear regression, logistic regression, and naive Bayes are, respectively, abbreviated as SDT, LinR, LogR, and NB. Our proposed Basic Decision Tree Prediction Model, Random Forest-Optimized Decision Tree Prediction Model, and Weighted Decision Tree Prediction Model with joint optimization by LSBoost and random forest are, respectively, abbreviated as DT, RFDT, and LRFDT.

The experimental results show that the baseline models exhibited relatively limited performances. Single decision tree, linear regression, logistic regression, and naive Bayes achieve overall accuracies below 62%, with F1 scores ranging from 0.55 to 0.59. This indicates that these models struggle to accurately capture the complex nonlinear relationships between raw material usage and the contents of chemical elements despite their advantages in prediction times and peak memory usage.

In contrast, our proposed Basic Decision Tree Prediction Model achieves a modest improvement, reaching 63.16% on overall accuracy. Benefiting from ensemble learning, the Random Forest-Optimized Decision Tree Prediction Model increases the overall accuracy to 75.69%. And the precision, recall, and F1 score reach 0.74, 0.73, and 0.72, respectively, while maintaining reasonable resource consumption (1.2 GB memory and 0.11s runtime), demonstrating good performance. Among all methods, the proposed Weighted Decision Tree Prediction Model with joint optimization by LSBoost and random forest delivers the best performance, with overall accuracy, precision, recall, and F1 score values of 83.33%, 0.82, 0.81, and 0.8, respectively. Although its computational time (0.39 s) and memory usage (1.5 GB) are higher, they remain within acceptable industry limits. This demonstrates that the model offers significant advantages and is suitable for industrial applications requiring accurate predictions.

7.6. Statistical Significance Analysis

To further analyze statistical significance, we conducted 30 independent repeated experiments for the Basic Decision Tree Prediction Model, Random Forest-Optimized Decision Tree Prediction Model, and Weighted Decision Tree Prediction Model with joint optimization by LSBoost and random forest, which are, respectively, abbreviated as DT, RFDT, and LRFDT, on the testing set. We calculated the mean, standard deviation, and 95% confidence interval (CI) for key performance metrics to systematically evaluate each model’s stability and consistency. The results are show in

Table 8. Statistical significance analysis.

Model	Overall Accuracy	Precision	Recall	F1 Score	CI
DT	$63.16\pm 1.24\%$	$0.61\pm 0.02$	$0.59\pm 0.02$	$0.6\pm 0.02$	$[62.73\%,63.59\%]$
RFDT	$75.69\pm 0.87\%$	$0.74\pm 0.01$	$0.73\pm 0.01$	$0.72\pm 0.01$	$[75.41\%,75.97\%]$
LRFDT	$83.33\pm 0.65\%$	$0.82\pm 0.01$	$0.81\pm 0.01$	$0.8\pm 0.01$	$[83.12\%,83.54\%]$

.

The statistical results show that the models demonstrate high stability across 30 independent experiments. The Basic Decision Tree Prediction Model achieves an overall accuracy of 63.16%, with a standard deviation of 1.24% and a 95% confidence interval of [62.73%, 63.59%], indicating consistent but modest prediction performance due to the limitations of a single decision tree structure in modeling complex relationships. The Random Forest-Optimized Decision Tree Prediction Model improved substantially, reaching 75.69% in overall accuracy with a reduced standard deviation of 0.87% and a narrowed 95% confidence interval of [75.41%, 75.97%]. Its precision, recall, and F1 score range between 0.72 and 0.74, with a minimal standard deviation of 0.01. This suggests that the ensemble strategy effectively enhances accuracy and reduces variability. The Weighted Decision Tree Prediction Model with joint optimization by LSBoost and random forest performs best, with an overall accuracy of 83.33%, standard deviation of 0.65%, and a tight 95% confidence interval of [83.12%, 83.54%]. Its precision, recall, and F1 score values are 0.82, 0.81, and 0.8, respectively, with standard deviations all at 0.01, demonstrating strong stability and consistency in predictions.

8. Conclusions and Future Work

In this paper, we propose a learning-based method for steel quality prediction, which is named DRBoost, based on multiple machine learning techniques, including decision tree, random forest, and the LSBoost algorithm. In our method, the Basic Decision Tree Prediction Model, the Random Forest-Optimized Decision Tree Prediction Model, and the Weighted Decision Tree Prediction Model with joint optimization by LSBoost and random forest are constructed to predict the contents of five key chemical elements in steel products, thereby predicting the quality of steel products. The experimental results show that our models can provide prediction results within a time range of approximately 0.0029 to 0.39 s, achieving overall accuracies of up to 80%, which demonstrates our models’ good performances.

In future work, more process parameters will be considered to propose more applicable prediction models. And we will propose a deployment framework for factory MESs or IoT platforms to enhance the applicability of our proposed prediction models. In addition, the application of explainable AI techniques to steel product quality prediction will also be considered to gain users’ trust.