A Survey of Maximum Entropy-Based Inverse Reinforcement Learning: Methods and Applications
Abstract
1. Introduction
- (1)
- We offer a critical analysis of ME-IRL and systematically examine the evolutionary trajectory of ME-IRL methodologies, comparing the strengths and weaknesses of different approaches.
- (2)
- The benchmark experiments and domain-specific applications in ME-IRL are summarized, laying the foundation for the development of ME-IRL algorithms in various fields.
- (3)
- We provide an identification of future research frontiers, move beyond a summary of existing work, and critically evaluate the current state of the field and pinpoint promising yet underexplored directions.
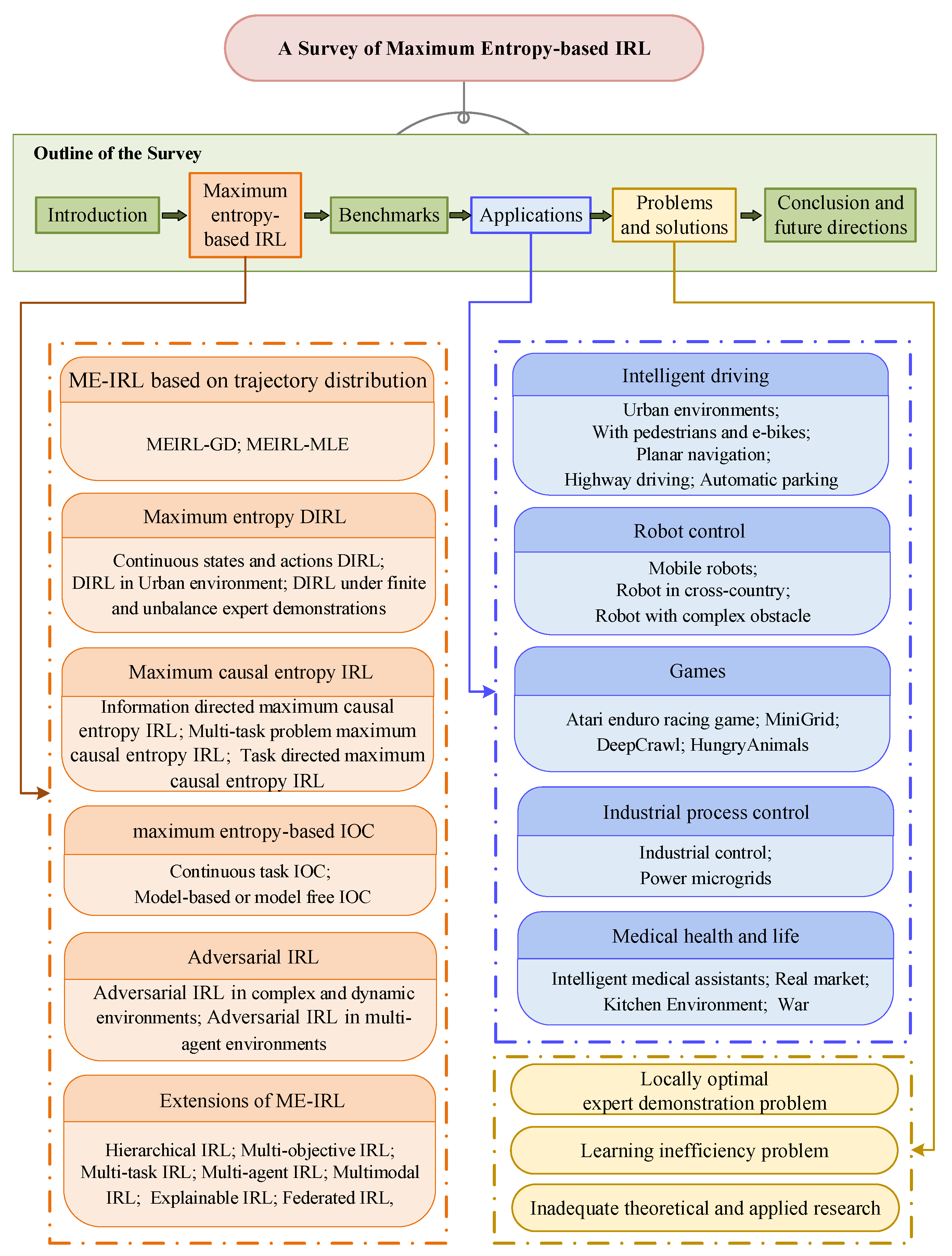
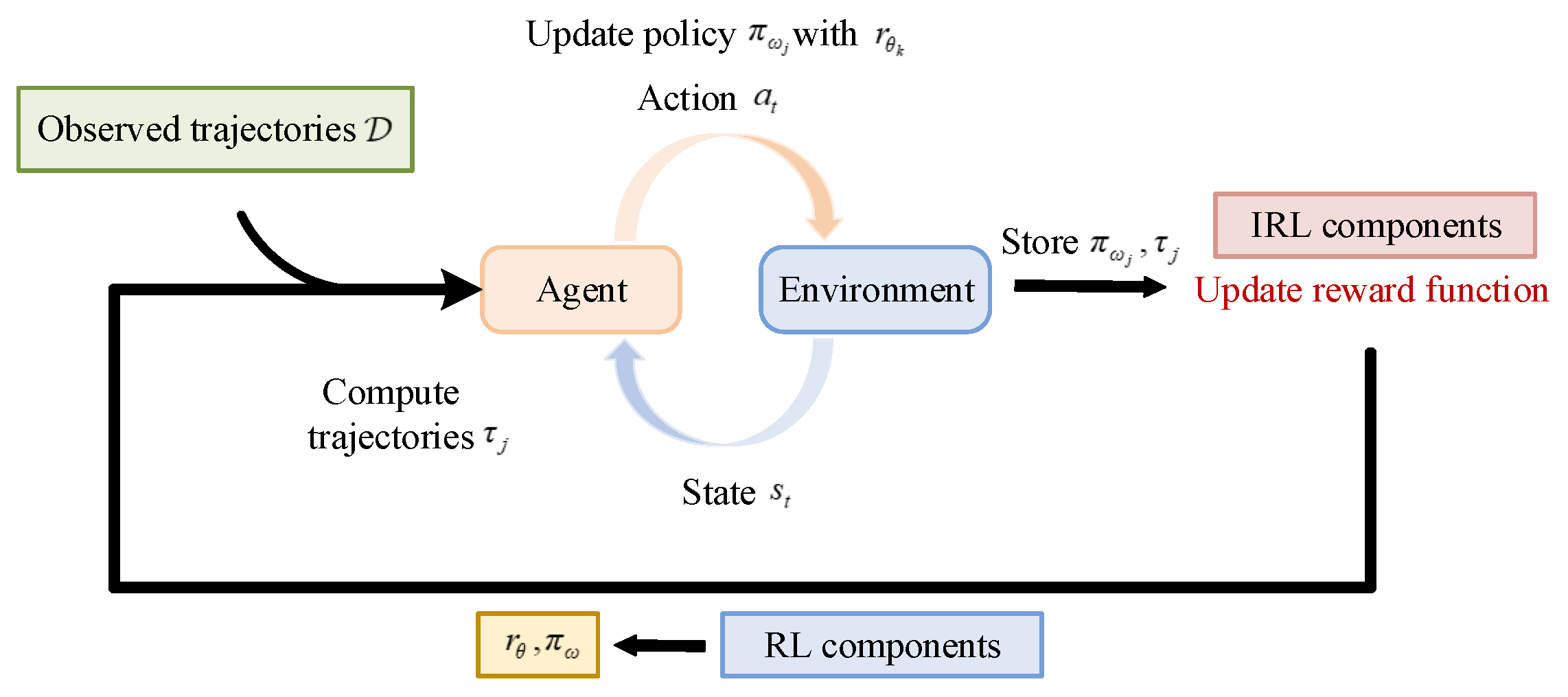
2. Problem Description of Maximum Entropy-Based IRL
3. Foundational Methods of IRL Based on Maximum Entropy
3.1. Maximum Entropy IRL Based on Trajectory Distribution
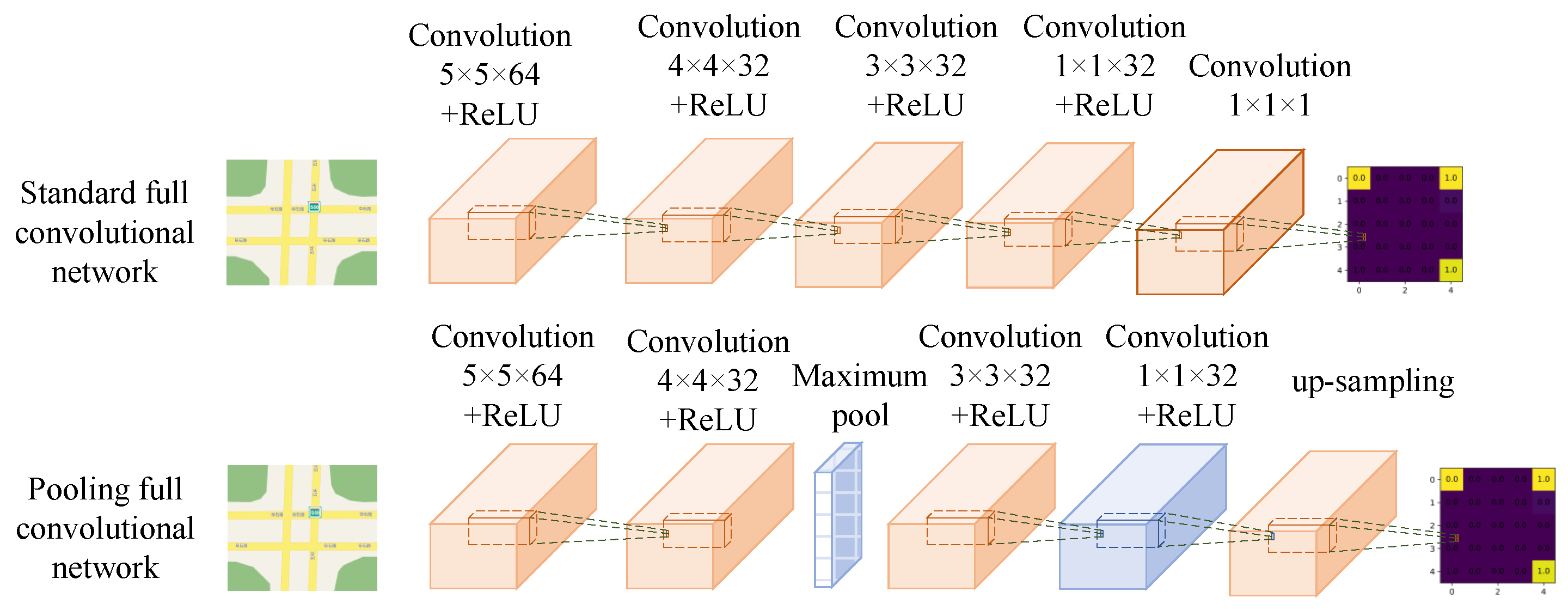
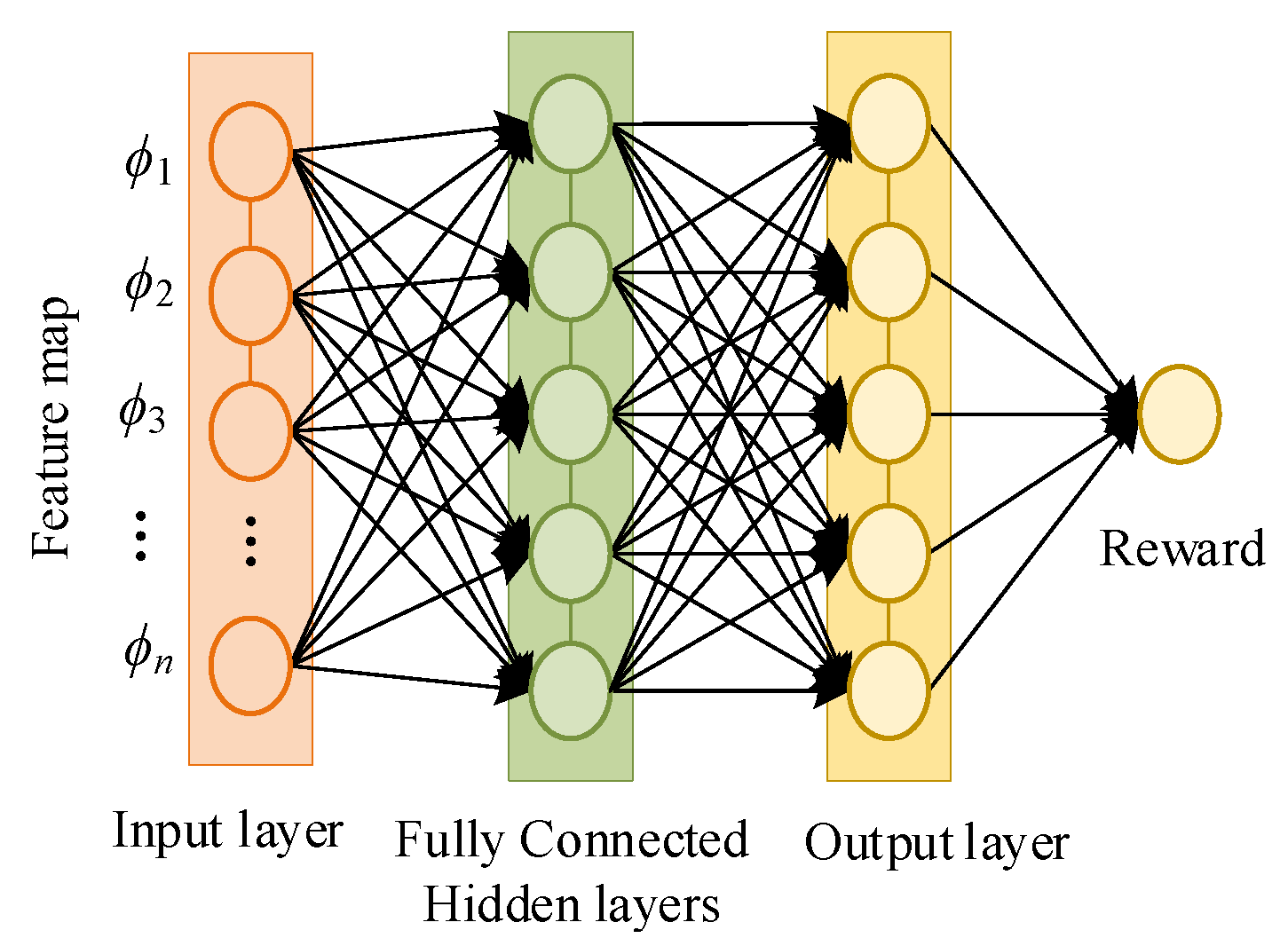
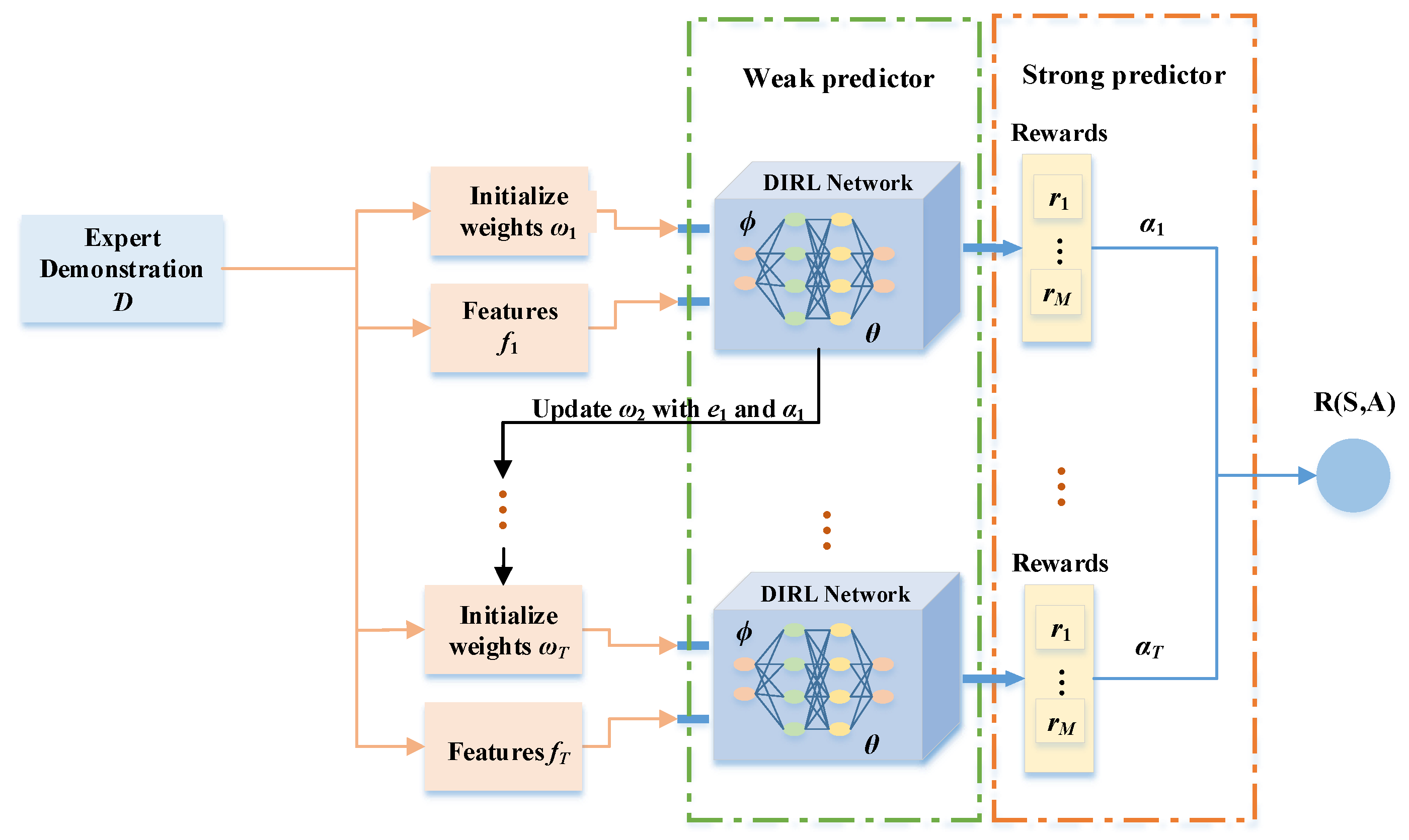
3.2. Maximum Entropy-Based Deep IRL
3.3. Maximum Causal Entropy-Based IRL
3.4. Maximum Entropy-Based Inverse Optimal Control
3.5. Adversarial IRL and Multi-Agent Adversarial IRL
3.6. Extension of Maximum Entropy-Based IRL
4. Benchmark Test Platform
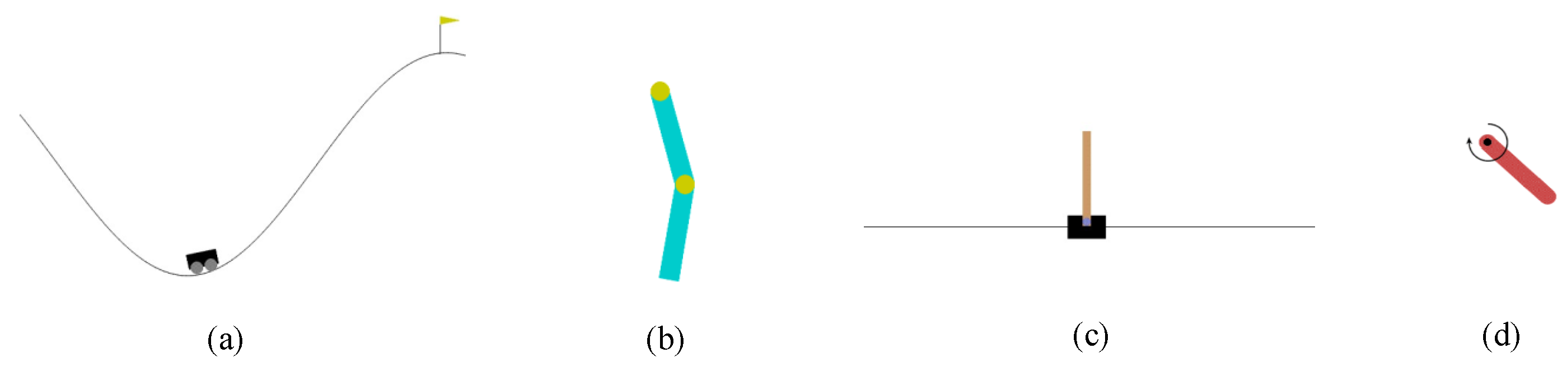
4.1. Four Classic Control
- (1)
- Mountain car environment: The Mountain car environment is comprised of a car that is randomly located at the bottom of a sinusoidally curved valley, and the ultimate goal is to climb to the small yellow flag located on the right-hand peak, as shown in Figure 8a.
- (2)
- Acrobot environment: As shown in Figure 8b, the Acrobot environment proposed in [107] is composed of two linearly connected chains, one of which is fixed at one end. The aim is to achieve the target height by applying a torque to the drive joints that causes the free end of the outer linkage to oscillate.
- (3)
- Cart pole environment: In this setting, a pole gets linked to a cart traveling along a frictionless rail by means of a non-driven joint. Aim of the cart is to help hold the pole in an upright position by moving itself from side to side.
- (4)
- Pendulum environment: An inverted pendulum system contains a pendulum with one end fixed and the other end free to swing. By applying a torque to the free end, a pendulum aims to swing itself to an upright position.
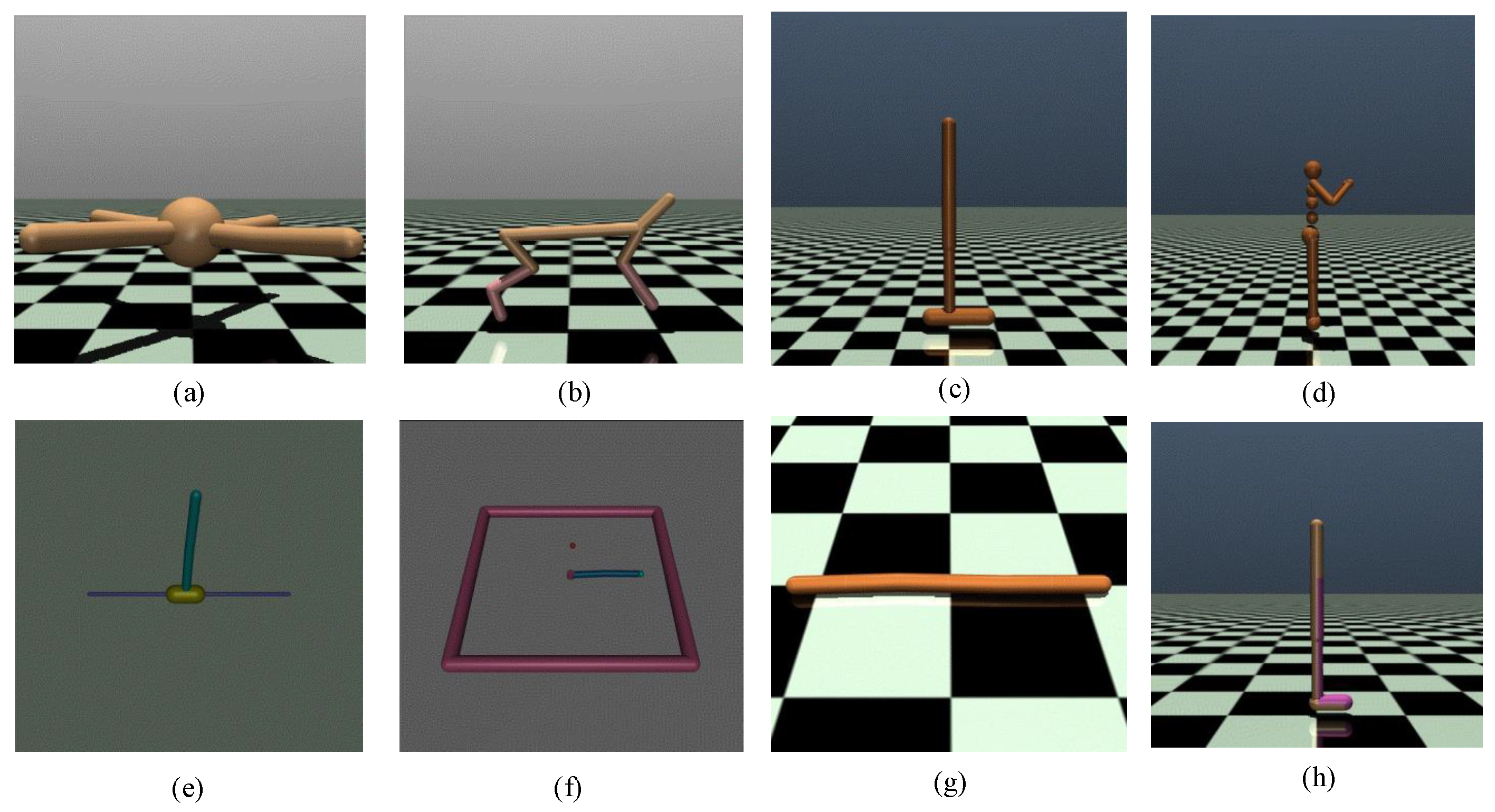
4.2. MuJoCo
- (1)
- Ant experiment: The ant proposed in the [108] is a 3D robot composed of a torso and four legs. By applying torque to the connecting part of the robot, it aims to move forward.
- (2)
- HalfCheetah experiment: A HalfCheetah proposed in [109] is a 2D made of nine links and eight connected joints. By putting torque on the joints, the cheetah is enabled to run forward as quickly as possible.
- (3)
- Hopper experiment: A hopper proposed in [110] contains a torso, a thigh and a calve, a single foot, and three links connecting these four parts. The aim is to achieve a forward-moving jump by applying torque on the hinges.
- (4)
- Humanoid experiment: A humanoid 3D robot proposed in [111] has a torso, two legs, and two arms. In Humanoid experiments include the Humanoid standup experiment and Humanoid experiment. The Humanoid standup environment is designed to allow a lying humanoid to stand up and remain standing through the application of torque on the links. In the Humanoid environment, the robot moves forward as fast as possible without falling.
- (5)
- Inverted pendulum experiment: The Inverted pendulum experiments proposed in [112] conclude two sub-experiments: Inverted double pendulum experiment and Inverted pendulum experiment. The Inverted double pendulum environment comprises a cart, a long pole connected together with two short poles. One end of the long pole is fixed to the cart and the other end is free to move. The long pole is balanced on top of the cart through placing a constant side-to-side shifting force on the cart. The inverted pendulum environment contains a cart and a pole with one end attached to the cart. The pole is kept upright by moving the trolley from side to side.
- (6)
- Reacher environment: A Reacher includes a robotic arm with two joints. By moving the end effector of the arm, it aims to reach the designed goal position.
- (7)
- Swimmer environment: A Swimmer environment proposed in [112] consists of three segments and two articulation joints. The goal is achieved through exerting torque and exploiting friction to make the swimmer move to the right as fast as possible.
- (8)
- Walker2D environment: A walker proposed in [110] is made up of a torso, two thighs, two calves two feet. The feet, calves, and thighs are coordinated to walk forward through applying torque to the hinges linking six parts of the walker.
4.3. Other Benchmark Environments
5. Application Study of Maximum Entropy-Based IRL
5.1. Intelligent Driving
5.2. Robot Control
5.3. Games
5.4. Industrial Process Control
5.5. Medical Health and Life
6. Faced Problems by Maximum Entropy-Based IRL and Solution Ideas
6.1. Locally Optimal Expert Demonstration Problem and Solution Ideas
6.2. Learning Inefficiency and Solutions
6.3. Inadequate Theoretical and Applied Research
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Wang, S.; Liang, X.X.; Zhao, D.W.; Huang, J.C.; Xu, X.; Dai, B.; Miao, Q.G. Deep reinforcement learning: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 5064–5078. [Google Scholar] [CrossRef] [PubMed]
- Rafailov, R.; Hatch, K.B.; Singh, A.; Kumar, A.; Smith, L.; Kostrikov, I.; Hansen-Estruch, P.; Kolev, V.; Ball, P.J.; Wu, J.J.; et al. D5RL: Diverse datasets for data-driven deep reinforcement learning. In Proceedings of the first Reinforcement Learning Conference, Vienna, Austria, 7–11 May 2024; pp. 1–20. [Google Scholar]
- Zhang, X.L.; Jiang, Y.; Lu, Y.; Xu, X. Receding-horizon reinforcement learning approach for kinodynamic motion planning of autonomous vehicles. IEEE Trans. Intell. Veh. 2022, 7, 556–568. [Google Scholar] [CrossRef]
- Pateria, S.; Subagdja, B.; Tan, A.; Quek, C. End-to-end hierarchical reinforcement learning with integrated subgoal discovery. IEEE Trans. Neural Networks Learn. Syst. 2022, 33, 7778–7790. [Google Scholar] [CrossRef]
- Lian, B.; Kartal, Y.; Lewis, F.L.; Mikulski, D.G.; Hudas, G.R.; Wan, Y.; Davoudi, A. Anomaly detection and correction of optimizing autonomous systems with inverse reinforcement learning. IEEE Trans. Cybern. 2023, 53, 4555–4566. [Google Scholar] [CrossRef]
- Gao, Z.H.; Yan, X.T.; Gao, F. A decision-making method for longitudinal autonomous driving based on inverse reinforcement learning. Aut. Eng. 2022, 44, 969–975. [Google Scholar]
- Zhang, T.; Liu, Y.; Hwang, M.; Hwang, K.; Ma, C.Y.; Cheng, J. An end-to-end inverse reinforcement learning by a boosting approach with relative entropy. Inform. Sci. 2020, 520, 1–14. [Google Scholar] [CrossRef]
- Samak, T.V.; Samak, C.V.; Kandhasamy, S. Robust behavioral cloning for autonomous vehicles using end-to-end imitation learning. SAE Int. J. Connect. Autom. Veh. 2021, 4, 279–295. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, H.; Chen, S.P.; Ye, J.; He, R.Q.; Sun, Z.Z. Integrating dijkstra’s algorithm into deep inverse reinforcement learning for food delivery route planning. Transp. Res. E Logist. Transp. Rev. 2020, 142, 102070. [Google Scholar] [CrossRef]
- Adams, S.; Cody, T.; Beling, P.A. A survey of inverse reinforcement learning. Artif. Intell. Rev. 2022, 55, 4307–4346. [Google Scholar] [CrossRef]
- Chen, X.; Abdelkader, E.K. Neural inverse reinforcement learning in autonomous navigation. Robot. Auton. Syst. 2016, 84, 1–14. [Google Scholar] [CrossRef]
- Li, D.C.; He, Y.Q.; Fu, F. Nonlinear inverse reinforcement learning with mutual information and gaussian process. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics, Bali, Indonesia, 5–10 December 2014; pp. 1445–1450. [Google Scholar]
- Yao, J.Y.; Pan, W.W.; Doshi-Velez, F.; Engelhardt, B.E. Inverse reinforcement learning with multiple planning horizons. In Proceedings of the First Reinforcement Conference, Amherst, MA, USA, 9–12 August 2024; pp. 1–30. [Google Scholar]
- Russel, S. Learning agents for uncertain environments. In Proceedings of the Eleventh Annual Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998; pp. 101–103. [Google Scholar]
- Choi, D.; Min, K.; Choi, J. Regularising neural networks for future trajectory prediction via inverse reinforcement learning framework. IET Comput. Vis. 2020, 14, 192–200. [Google Scholar] [CrossRef]
- Huang, W.H.; Braghin, F.; Wang, Z. Learning to drive via apprenticeship learning and deep reinforcement learning. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence, Portland, OR, USA, 4–6 November 2019; pp. 1536–1540. [Google Scholar]
- Lee, D.J.; Srinivasan, S.; Doshi-Velez, F. Truly batch apprenticeship learning with deep successor features. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 5909–5915. [Google Scholar]
- Abbeel, P.; Ng, A.Y. Apprenticeship learning via inverse reinforcement learning. In Proceedings of the Twenty-First International Conference on Machine Learning, New York, NY, USA, 4–8 July 2004; pp. 1–8. [Google Scholar]
- Ratliff, N.D.; Bagnell, J.A.; Zinkevich, M.A. Maximum margin planning. In Proceedings of the 23rd International Conference on Machine Learning, New York, NY, USA, 25–29 June 2006; pp. 729–736. [Google Scholar]
- Ziebart, B.D.; Maas, A.; Bagnell, J.A.; Dey, A.K. Maximum entropy inverse reinforcement learning. In Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence, Chicago, IL, USA, 13–17 July 2008; pp. 1433–1438. [Google Scholar]
- Ziebart, B.D. Modeling Purposeful Adaptive Behavior with the Principle of Maximum Causal Entropy. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2010. [Google Scholar]
- Wulfmeier, M.; Wang, D.Z.; Posner, I. Watch this: Scalable cost-function learning for path planning in urban environments. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems, Daejeon, Republic of Korea, 9–14 October 2016; pp. 2089–2095. [Google Scholar]
- Finn, C.; Levine, S.; Abbeel, P. Guided cost learning: Deep inverse optimal control via policy optimization. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 49–58. [Google Scholar]
- Fu, J.; Luo, K.; Levine, S. Learning robust rewards with adversarial inverse reinforcement learning. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–15. [Google Scholar]
- Donge, V.S.; Lian, B.; Lewis, F.L.; Davoudi, A. Multiagent graphical games with inverse reinforcement learning. IEEE Trans. Control Netw. Syst. 2023, 10, 841–852. [Google Scholar] [CrossRef]
- Bighashdel, A.; Meletis, P.; Jancura, P.; Dubbelman, G. Deep adaptive multi-intention inverse reinforcement learning. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Bilbao, Spain, 13–17 September 2021; pp. 206–221. [Google Scholar]
- Krishnan, S.; Garg, A.; Liaw, R.; Miller, L.; Pokorny, F.T.; Goldberg, K. Hirl: Hierarchical inverse reinforcement learning for long-horizon tasks with delayed rewards. arXiv 2016, arXiv:1604.06508. [Google Scholar] [CrossRef]
- Sun, L.T.; Zhan, W.; Tomizuka, M. Probabilistic prediction of interactive driving behavior via hierarchical inverse reinforcement learning. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems, Maui, HI, USA, 4–7 November 2018; pp. 2111–2117. [Google Scholar]
- Kiran, R.; Sobh, I.; Talpaert, V.; Mannion, P.; Sallab, A.A.; Yogamani, S.; Pérez, P. Deep reinforcement learning for autonomous driving: A survey. IEEE Trans. Intell. Transp. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- García, J.; Fernández, F. A comprehensive survey on safe reinforcement learning. J. Mach. Learn. Res. 2015, 16, 1437–1480. [Google Scholar]
- Fischer, J.; Eyberg, C.; Werling, M.; Lauer, M. Sampling-based inverse reinforcement learning algorithms with safety constraints. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems, Prague, Czech Republic, 27 September–1 October 2021; pp. 791–798. [Google Scholar]
- Shiarlis, K.; Messias, J.; Whiteson, S. Inverse reinforcement learning from failure. In Proceedings of the 2016 International Conference on Autonomous Agents and Multiagent Systems, Singapore, 9–13 May 2016; pp. 1060–1068. [Google Scholar]
- Wu, Z.; Sun, L.T.; Zhan, W.; Yang, C.Y.; Tomizuka, M. Efficient sampling-based maximum entropy inverse reinforcement learning with application to autonomous driving. IEEE Rob. Autom. Lett. 2020, 5, 5355–5362. [Google Scholar] [CrossRef]
- Huang, Z.Y.; Wu, J.D.; Lv, C. Driving behavior modeling using naturalistic human driving data with inverse reinforcement learning. IEEE Trans. Intell. Transp. 2022, 23, 10239–10251. [Google Scholar] [CrossRef]
- Fang, P.Y.; Yu, Z.P.; Xiong, L.; Fu, Z.Q.; Li, Z.R.; Zeng, D.Q. A maximum entropy inverse reinforcement learning algorithm for automatic parking. In Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence, Tianjin, China, 29–31 October 2021; pp. 1–6. [Google Scholar]
- Huang, C.Y.; Srivastava, S.; Garikipati, K. Fp-irl: Fokker-planck-based inverse reinforcement learning-a physics-constrained approach to markov decision processes. arXiv 2023, arXiv:2306.10407. [Google Scholar]
- Geissler, D.; Feuerriegel, S. Analyzing the strategy of propaganda using inverse reinforcement learning: Evidence from the 2022 russian invasion of ukraine. arXiv 2023, arXiv:2307.12788. [Google Scholar] [CrossRef]
- You, C.X.; Lu, J.B.; Filev, D.; Tsiotras, P. Advanced planning for autonomous vehicles using reinforcement learning and deep inverse reinforcement learning. Robot. Auton. Syst. 2019, 114, 1–18. [Google Scholar] [CrossRef]
- Rosbach, S.; James, V.; Großjohann, S.; Homoceanu, S.; Roth, S. Driving with style: Inverse reinforcement learning in general-purpose planning for automated driving. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems, Macau, China, 3–8 November 2019; pp. 2658–2665. [Google Scholar]
- Zhou, Y.; Fu, R.; Wang, C. Learning the car-following behavior of drivers using maximum entropy deep inverse reinforcement learning. J. Adv. Transport. 2020, 2020, 4752651. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Li, N.; Sun, R.Y.; Xu, D.H.; Zhao, H.J. Off-road autonomous vehicles traversability analysis and trajectory planning based on deep inverse reinforcement learning. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium, Las Vegas, NV, USA, 19 October–13 November 2020; pp. 971–977. [Google Scholar]
- Fahad, M.; Chen, Z.; Guo, Y. Learning how pedestrians navigate: A deep inverse reinforcement learning approach. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018; pp. 819–826. [Google Scholar]
- Li, X.J.; Liu, H.S.; Dong, M.H. A general framework of motion planning for redundant robot manipulator based on deep reinforcement learning. IEEE Trans. Ind. Inform. 2022, 18, 5253–5263. [Google Scholar] [CrossRef]
- Gan, L.; Grizzle, J.W.; Eustice, R.M.; Ghaffari, M. Energy-based legged robots terrain traversability modeling via deep inverse reinforcement learning. IEEE Rob. Autom. Lett. 2022, 7, 8807–8814. [Google Scholar] [CrossRef]
- Liu, X.; Yu, W.; Liang, F.; Griffith, D.; Golmie, N. On deep reinforcement learning security for industrial internet of things. Comput. Commun. 2022, 168, 20–32. [Google Scholar] [CrossRef]
- Guo, H.Y.; Chen, Q.X.; Xia, Q.; Kang, C.Q. Deep inverse reinforcement learning for objective function identification in bidding models. IEEE Trans. Power. Syst. 2021, 36, 5684–5696. [Google Scholar] [CrossRef]
- Hantous, K.; Rejeb, L.; Hellali, R. Detecting physiological needs using deep inverse reinforcement learning. Appl. Artif. Intell. 2022, 36, 2022340. [Google Scholar] [CrossRef]
- Adam, G.; Oliver, H. Multi-task maximum causal entropy inverse reinforcement learning. arXiv 2018, arXiv:1805.08882. [Google Scholar]
- Zouzou, A.; Bouhoute, A.; Boubouh, K.; Kamili, M.E.; Berrada, I. Predicting lane change maneuvers using inverse reinforcement learning. In Proceedings of the 2017 International Conference on Wireless Networks and Mobile Communications, Rabat, Morocco, 1–4 November 2017; pp. 1–7. [Google Scholar]
- Martinez-Gil, F.; Lozano, M.; García-Fernández, I.; Romero, P.; Serra, D.; Sebastián, R. Using inverse reinforcement learning with real trajectories to get more trustworthy pedestrian simulations. Mathematics 2020, 8, 1479. [Google Scholar] [CrossRef]
- Navyata, S.; Shinnosuke, U.; Mohit, S.; Joachim, G. Inverse reinforcement learning with explicit policy estimates. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; pp. 9472–9480. [Google Scholar]
- Levine, S.; Koltun, V. Continuous inverse optimal control with locally optimal examples. In Proceedings of the 29th International Conference on International Conference on Machine Learning, Edinburgh, UK, 26 June 2012–1 July 2012; pp. 475–482. [Google Scholar]
- Lian, B.; Xue, W.Q.; Lewis, F.L.; Chai, T.Y. Inverse reinforcement learning for adversarial apprentice games. IEEE Trans. Neural Networks Learn. Syst. 2023, 34, 4596–4609. [Google Scholar] [CrossRef]
- Huang, D.; Kitani, K.M. Action-reaction: Forecasting the dynamics of human interaction. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 489–504. [Google Scholar]
- Sun, J.K.; Yu, L.T.; Dong, P.Q.; Lu, B.; Zhou, B.L. Adversarial inverse reinforcement learning with self-attention dynamics model. IEEE Rob. Autom. Lett. 2021, 6, 1880–1886. [Google Scholar] [CrossRef]
- Bagdanov, A.D.; Sestini, A.; Kuhnle, A. Demonstration-efficient inverse reinforcement learning in procedurally generated environments. arXiv 2020, arXiv:2012.02527. [Google Scholar] [CrossRef]
- Shi, H.B.; Li, J.C.; Chen, S.C.; Hwang, K.A. A behavior fusion method based on inverse reinforcement learning. Inform. Sci. 2022, 609, 429–444. [Google Scholar] [CrossRef]
- Song, Z.H. An automated framework for gaming platform to test multiple games. In Proceedings of the 2020 IEEE/ACM 42nd International Conference on Software Engineering: Companion Proceedings, Seoul, Republic of Korea, 27 June–19 July 2020; pp. 134–136. [Google Scholar]
- Mehr, N.; Wang, M.Y.; Bhatt, M.; Schwager, M. Maximum-entropy multi-agent dynamic games: Forward and inverse solutions. IEEE Trans. Rob. 2023, 39, 1801–1815. [Google Scholar] [CrossRef]
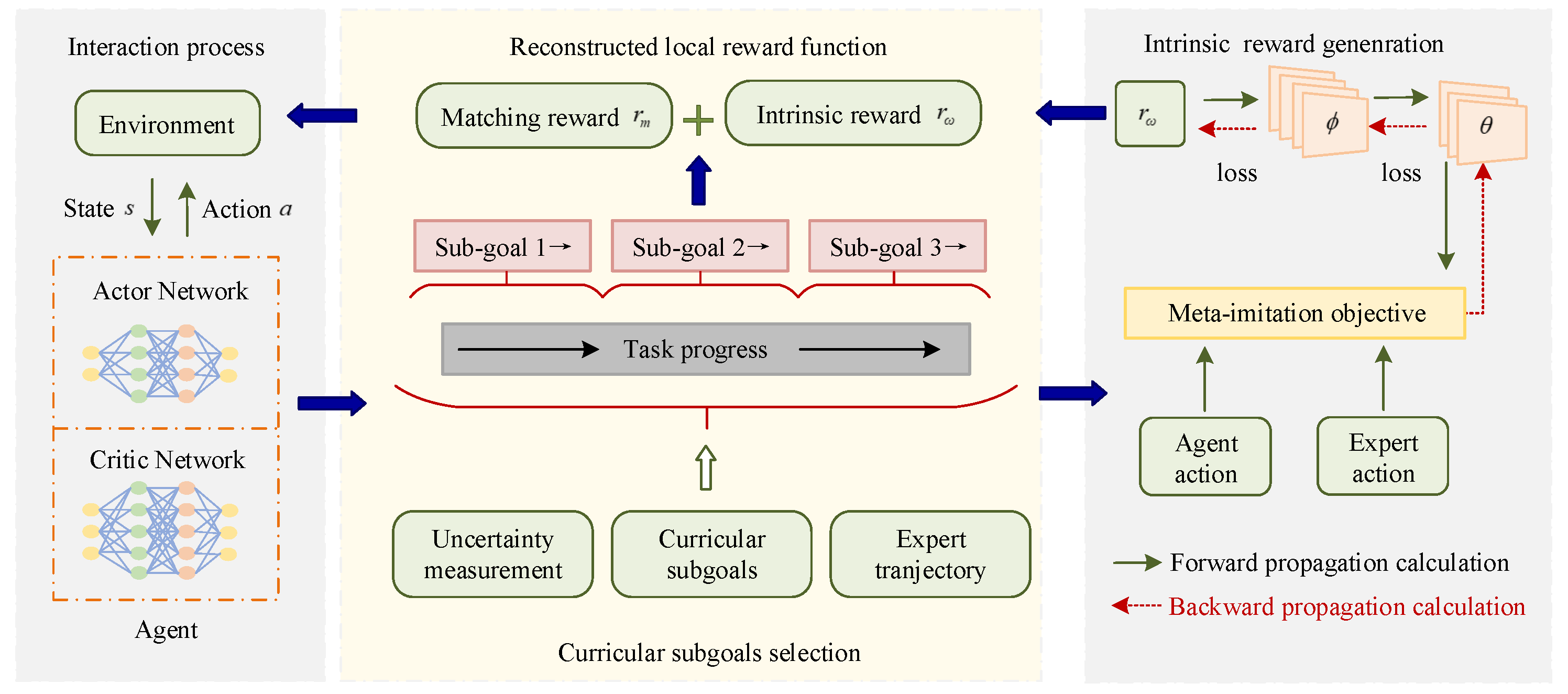
- Xu, S.Q.; Wu, H.Y.; Zhang, J.T.; Cong, J.Y.; Chen, T.H.; Liu, Y.F.; Liu, S.Y.; Qing, Y.P.; Song, M.L. Curricular subgoals for inverse reinforcement learning. arXiv 2023, arXiv:2306.08232. [Google Scholar] [CrossRef]
- Das, N.; Chattopadhyay, A. Inverse reinforcement learning with constraint recovery. arXiv 2023, arXiv:2305.08130. [Google Scholar] [CrossRef]
- Aghasadeghi, N.; Bretl, T. Maximum entropy inverse reinforcement learning in continuous state spaces with path integrals. Proceedings of 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 1561–1566. [Google Scholar]
- Song, L.; Li, D.Z.; Xu, X. Sparse online maximum entropy inverse reinforcement learning via proximal optimization and truncated gradient. Knowl.-Based Syst. 2022, 252, 1–15. [Google Scholar] [CrossRef]
- Li, D.Z.; Du, J.H. Maximum entropy inverse reinforcement learning based on behavior cloning of expert examples. In Proceedings of the 2021 IEEE 10th Data Driven Control and Learning Systems Conference, Suzhou, China, 14–16 May 2021; pp. 996–1000. [Google Scholar]
- Wang, Y.J.; Wan, S.W.; Li, Q.; Niu, Y.C.; Ma, F. Modeling crossing behaviors of e-bikes at intersection with deep maximum entropy inverse reinforcement learning using drone-based video data. IEEE Trans. Intell. Transp. 2023, 24, 6350–6361. [Google Scholar] [CrossRef]
- Snoswell, A.J.; Singh, S.P.N.; Ye, N. Revisiting maximum entropy inverse reinforcement learning: New perspectives and algorithms. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence, Canberra, Australia, 1–4 December 2020; pp. 241–249. [Google Scholar]
- Wulfmeier, M.; Rao, D.; Wang, D.Z.; Ondruska, P.; Posner, I. Large-scale cost function learning for path planning using deep inverse reinforcement learning. Int. J. Robot Res. 2017, 36, 1073–1087. [Google Scholar] [CrossRef]
- Chen, X.L.; Cao, L.; Xu, Z.X.; Lai, J.; Li, C.X. A study of continuous maximum entropy deep inverse reinforcement learning. Math. Probl. Eng. 2019, 2019, 4834516. [Google Scholar] [CrossRef]
- Silva, J.A.R.; Grassi, V.; Wolf, D.F. Continuous deep maximum entropy inverse reinforcement learning using online pomdp. In Proceedings of the 2019 19th International Conference on Advanced Robotics, Belo Horizonte, Brazil, 2–6 December 2019; pp. 382–387. [Google Scholar]
- Fernando, T.; Denman, S.; Sridharan, S.; Fookes, C. Neighbourhood context embeddings in deep inverse reinforcement learning for predicting pedestrian motion over long time horizons. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1179–1187. [Google Scholar]
- Rosbach, S.; Li, X.; Großjohann, S.; Homoceanu, S.; Roth, S. Planning on the fast lane: Learning to interact using attention mechanisms in path integral inverse reinforcement learning. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 25–29 October 2020; pp. 5187–5193. [Google Scholar]
- Memarian, F.; Xu, Z.; Wu, B.; Wen, M.; Topcu, U. Active task-inference-guided deep inverse reinforcement learning. In Proceedings of the 2020 59th IEEE Conference on Decision and Control, Jeju Island, Republic of Korea, 14–18 December 2020; pp. 1932–1938. [Google Scholar]
- Song, L.; Li, D.Z.; Wang, X.; Xu, X. Adaboost maximum entropy deep inverse reinforcement learning with truncated gradient. Inform. Sci. 2022, 602, 328–350. [Google Scholar] [CrossRef]
- Fernando, T.; Denman, S.; Sridharan, S.; Fookes, C. Deep inverse reinforcement learning for behavior prediction in autonomous driving: Accurate forecasts of vehicle motion. IEEE Signal Process. Mag. 2021, 38, 87–96. [Google Scholar] [CrossRef]
- Lee, K.; Isele, D.; Theodorou, E.A.; Bae, S. Spatiotemporal costmap inference for mpc via deep inverse reinforcement learning. IEEE Rob. Autom. Lett. 2022, 7, 3194–3201. [Google Scholar] [CrossRef]
- Ziebart, B.D.; Bagnell, J.A.; Dey, A.K. Modeling interaction via the principle of maximum causal entropy. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 1255–1262. [Google Scholar]
- Ziebart, B.D.; Bagnell, J.A.; Dey, A.K. The principle of maximum causal entropy for estimating interacting processes. IEEE Trans. Inf. Theory 2013, 59, 1966–1980. [Google Scholar] [CrossRef]
- Gleave, A.; Toyer, S. A primer on maximum causal entropy inverse reinforcement learning. arXiv 2022, arXiv:2203.11409. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Bloem, M.; Bambos, N. Infinite time horizon maximum causal entropy inverse reinforcement learning. IEEE Trans. Autom. Control 2018, 63, 2787–2802. [Google Scholar] [CrossRef]
- Mattijs, B.; Pietro, M.; Sam, L.; Pieter, S. Maximum causal entropy inverse constrained reinforcement learning. arXiv 2023, arXiv:2305.02857. [Google Scholar] [CrossRef]
- Viano, L.; Huang, Y.T.; Kamalaruban, P.; Weller, A.; Cevher, V. Robust inverse reinforcement learning under transition dynamics mismatch. In Proceedings of the 35th Conference on Neural Information Processing Systems, Online, 6–14 December 2021; pp. 1–5. [Google Scholar]
- Lian, B.; Xue, W.Q.; Lewis, F.L.; Chai, T.Y.; Davoudi, A. Inverse reinforcement learning for multi-player apprentice games in continuous-time nonlinear systems. In Proceedings of the 2021 60th IEEE Conference on Decision and Control, Austin, TX, USA, 14–17 December 2021; pp. 803–808. [Google Scholar]
- Lian, B.; Xue, W.Q.; Lewis, F.L.; Chai, T.Y. Inverse reinforcement learning for multi-player noncooperative apprentice game. Automatica 2022, 145, 110524. [Google Scholar] [CrossRef]
- Boussioux, L.; Wang, J.H.; Doina, G.M.; Venuto, P.D.; Chakravorty, J. oirl: Robust adversarial inverse reinforcement learning with temporally extended actions. arXiv 2002, arXiv:2002.09043. [Google Scholar]
- Wang, P.; Liu, D.P.; Chen, J.Y.; Li, H.H.; Chan, C. Decision making for autonomous driving via augmented adversarial inverse reinforcement learning. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 2021; pp. 1036–1042. [Google Scholar]
- Gruver, N.; Song, J.M.; Kochenderfer, M.J.; Ermon, S. Multi-agent adversarial inverse reinforcement learning with latent variables. In Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems, Auckland, New Zealand, 9–13 May 2020; pp. 1855–1857. [Google Scholar]
- Alsaleh, R.; Sayed, T. Markov-game modeling of cyclist-pedestrian interactions in shared spaces: A multi-agent adversarial inverse reinforcement learning approach. Transp. Res. Part C Emerg. Technol. 2021, 128, 103191. [Google Scholar] [CrossRef]
- So, S.; Rho, J. Designing nanophotonic structures using conditional deep convolutional generative adversarial networks. Nanophotonics 2019, 8, 1255–1261. [Google Scholar] [CrossRef]
- Ghasemipour, S.K.; Gu, S.X.; Zemel, R. SMILe: Scalable meta inverse reinforcement learning through context-conditional policies. In Proceedings of the 33rd Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 7879–7889. [Google Scholar]
- Peng, P.; Wang, Y.; Zhang, W.J.; Zhang, Y.; Zhang, H.M. Imbalanced process fault diagnosis using enhanced auxiliary classifier gan. In Proceedings of the 2020 Chinese Automation Congress, Shanghai, China, 6–8 November 2020; pp. 313–316. [Google Scholar]
- Yan, K.; Su, J.Y.; Huang, J.; Mo, Y.C. Chiller fault diagnosis based on vae-enabled generative adversarial networks. IEEE Trans. Autom. Sci. Eng. 2022, 19, 387–395. [Google Scholar] [CrossRef]
- Lan, T.; Chen, J.Y.; Tamboli, D.; Aggarwal, V. Multi-task hierarchical adversarial inverse reinforcement learning. arXiv 2023, arXiv:2305.12633. [Google Scholar] [CrossRef]
- Giwa, B.H.; Lee, C. A marginal log-likelihood approach for the estimation of discount factors of multiple experts in inverse reinforcement learning. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems, Prague, Czech Republic, 27 September–1 October 2021; pp. 7786–7791. [Google Scholar]
- Pan, X.L.; Shen, Y.L. Human-interactive subgoal supervision for efficient inverse reinforcement learning. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 1380–1387. [Google Scholar]
- Kitaoka, A.; Eto, R. A proof of convergence of inverse reinforcement learning for multi-objective optimization. arXiv 2023, arXiv:2305.06137. [Google Scholar] [CrossRef]
- Waelchli, P.W.D.; Koumoutsakos, P. Discovering individual rewards in collective behavior through inverse multi-agent reinforcement learning. arXiv 2023, arXiv:2305.10548. [Google Scholar] [CrossRef]
- Zhang, Y.X.; DeCastro, J.; Cui, X.Y.; Huang, X.; Kuo, Y.; Leonard, J.; Balachandran, A.; Leonard, N.; Lidard, J.; So, O.; et al. Game-up: Game-aware mode enumeration and understanding for trajectory prediction. arXiv 2023, arXiv:2305.17600. [Google Scholar]
- Luo, Y.D.; Schulte, O.; Poupart, P. Inverse reinforcement learning for team sports: Valuing actions and players. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence Main Track, Yokohama Yokohama, Japan, 7–15 January 2020; pp. 3356–3363. [Google Scholar]
- Chen, Y.; Lin, X.; Yan, B.; Zhang, L.; Liu, J.; Özkan, T.N.; Witbrock, M. Meta-inverse reinforcement learning for mean field games via probabilistic context variables. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; pp. 11407–11415. [Google Scholar]
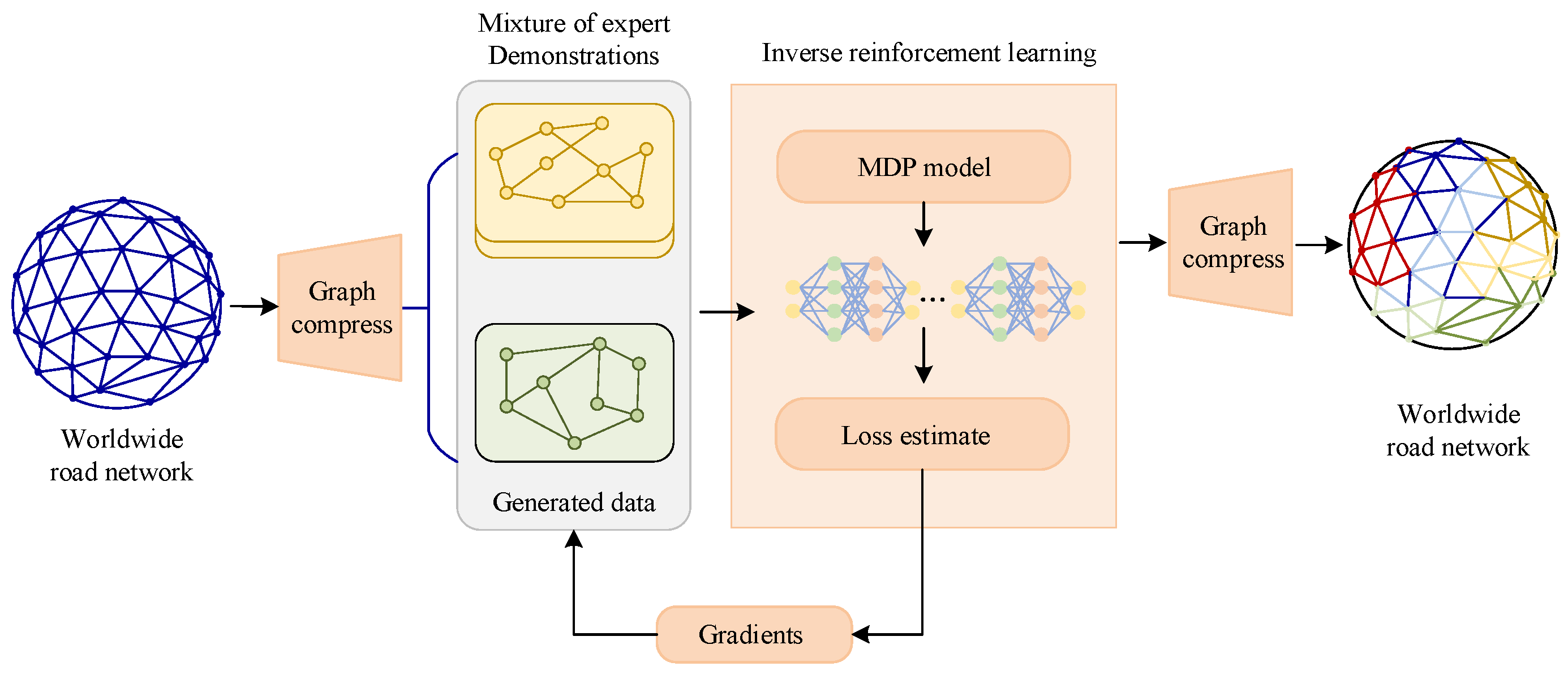
- Barnes, M.; Abueg, M.; Lange, O.F.; Deeds, M.; Trader, J.; Molitor, D.; Wulfmeier, M.; O’Banion, S. Massively scalable inverse reinforcement learning in google maps. arXiv 2023, arXiv:2305.11290. [Google Scholar]
- Qiao, G.R.; Liu, G.L.; Poupart, P.; Xu, Z.Q. Multi-Modal Inverse Constrained Reinforcement Learning from a Mixture of Demonstrations. In Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; pp. 1–13. [Google Scholar]
- Yang, B.; Lu, Y.A.; Yan, B.; Wan, R.; Hu, H.Y.; Yang, C.C.; Ni, R.R. Meta-IRLSOT plus plus: A meta-inverse reinforcement learning method for fast adaptation of trajectory prediction networks. Expert Syst. Appl. 2024, 240, 122499. [Google Scholar] [CrossRef]
- Gong, W.; Cao, L.; Zhu, Y.; Zuo, F.; He, X.; Zhou, H. Federated inverse reinforcement learning for smart ICUs with differential privacy. IEEE Internet Things J. 2023, 10, 19117–19124. [Google Scholar] [CrossRef]
- Zeng, S.L.; Li, C.L.; Garcia, A.; Garcia, A. Maximum-likelihood inverse reinforcement learning with finite-time guarantees. In Proceedings of the 36th Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; pp. 1–14. [Google Scholar]
- Gu, M.R.; Croft, E.; Kulic, D. Demonstration based explainable AI for learning from demonstration methods. IEEE Rob. Autom. Lett. 2025, 10, 6552–6559. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, H.B.; Yang, L.P.; Zhang, B.; Ward, T.E.; Snásel, V. Unraveling human social behavior motivations via inverse reinforcement learning-based link prediction. Computing 2024, 106, 1963–1986. [Google Scholar] [CrossRef]
- Sutton, R.S. Generalization in reinforcement learning: Successful examples using sparse coarse coding. In Proceedings of the 8th International Conference on Neural Information Processing Systems, Denver, CO, USA, 27–30 November 1995; pp. 1038–1044. [Google Scholar]
- Levine, S.; Jordan, M.; Schulman, J.; Moritz, P.; Abbeel, P. High-dimensional continuous control using generalized advantage estimation. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016; pp. 1–14. [Google Scholar]
- Wawrzyński, P. A cat-like robot real-time learning to run. In Proceedings of the 9th International Conference on Adaptive and Natural Computing Algorithms, Kuopio, Finland, 23–25 April 2009; pp. 380–390. [Google Scholar]
- Durrant-Whyte, H.; Roy, N.; Abbeel, P. Infinite-horizon model predictive control for periodic tasks with contacts. In Robotics: Science and Systems VII; MIT Press: Cambridge, MA, USA, 2012; pp. 73–80. [Google Scholar]
- Tassa, Y.; Erez, T.; Todorov, E. Synthesis and stabilization of complex behaviors through online trajectory optimization. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, Portugal, 7–12 October 2012; pp. 4906–4913. [Google Scholar]
- Coulom, R. Reinforcement Learning Using Neural Networks, with Applications to Motor Control. Ph.D. Thesis, Laboratoire IMAG, Institute National Polytechnique de Grenoble, Grenoble, Rhone-Alpes region, France, 2002. [Google Scholar]
- Li, J.; Wu, H.; He, Q.; Zhao, Y.; Wang, X. Dynamic QoS prediction with intelligent route estimation via inverse reinforcement learning. IEEE Trans. Serv. Comput. 2024, 17, 509–523. [Google Scholar] [CrossRef]
- Nan, J.; Deng, W.; Zhang, R.; Wang, Y.; Zhao, R.; Ding, J. Interaction-aware planning with deep inverse reinforcement learning for human-like autonomous driving in merge scenarios. IEEE Trans. Intell. Veh. 2024, 9, 2714–2726. [Google Scholar] [CrossRef]
- Baee, S.; Pakdamanian, E.; Kim, I.; Feng, L.; Ordonez, V.; Barnes, L. Medirl: Predicting the visual attention of drivers via maximum entropy deep inverse reinforcement learning. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, Virtual Conference, 11–17 October 2021; pp. 13158–13168. [Google Scholar]
- Fu, Q.M.; Gao, Z.; Wu, H.J.; Chen, J.P.; Chen, Q.Q.; Lu, Y. Maximum entropy inverse reinforcement learning based on generative adversarial networks. Comput. Eng. Appl. 2019, 55, 119–126. [Google Scholar]
- Wooldridge, M. An Introduction to Multiagent Systems, 2nd ed.; Wiley Publishing: New York, NY, USA, 2009; pp. 1–27. [Google Scholar]
- Wang, P.; Li, H.H.; Chan, C. Meta-adversarial inverse reinforcement learning for decision-making tasks. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 2021; pp. 12632–12638. [Google Scholar]
- Lin, J.-L.; Hwang, K.-S.; Shi, H.B.; Pan, W. An ensemble method for inverse reinforcement learning. Inform. Sci. 2020, 512, 518–532. [Google Scholar] [CrossRef]
- Munikoti, S.; Agarwal, D.; Das, L.; Halappanavar, M.; Natarajan, B. Challenges and opportunities in deep reinforcement learning with graph neural networks: A comprehensive review of algorithms and applications. IEEE Trans. Neural Netw. Learn. Syst. 2023, 15051–15071. [Google Scholar] [CrossRef]
- Pan, W.; Qu, R.P.; Hwang, K.-S.; Lin, H.-S. An ensemble fuzzy approach for inverse reinforcement learning. Int. J. Fuzzy Syst. 2018, 21, 95–103. [Google Scholar] [CrossRef]
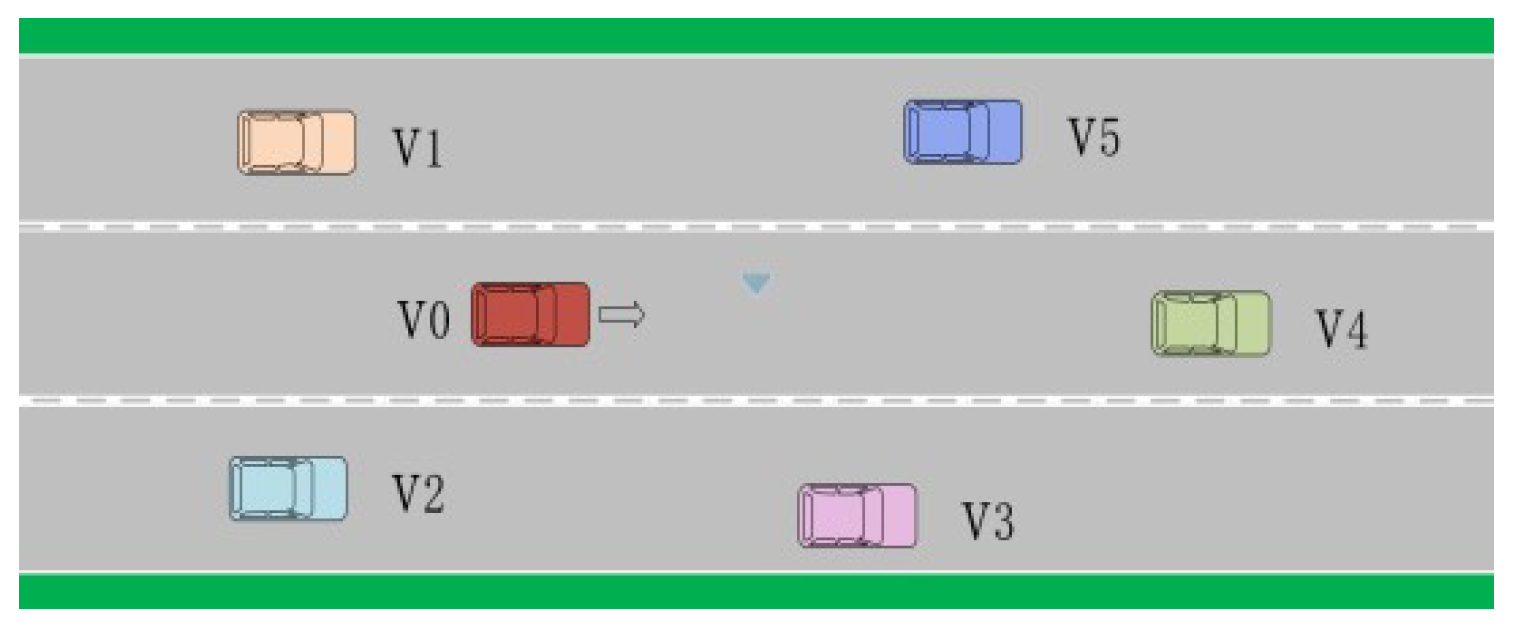
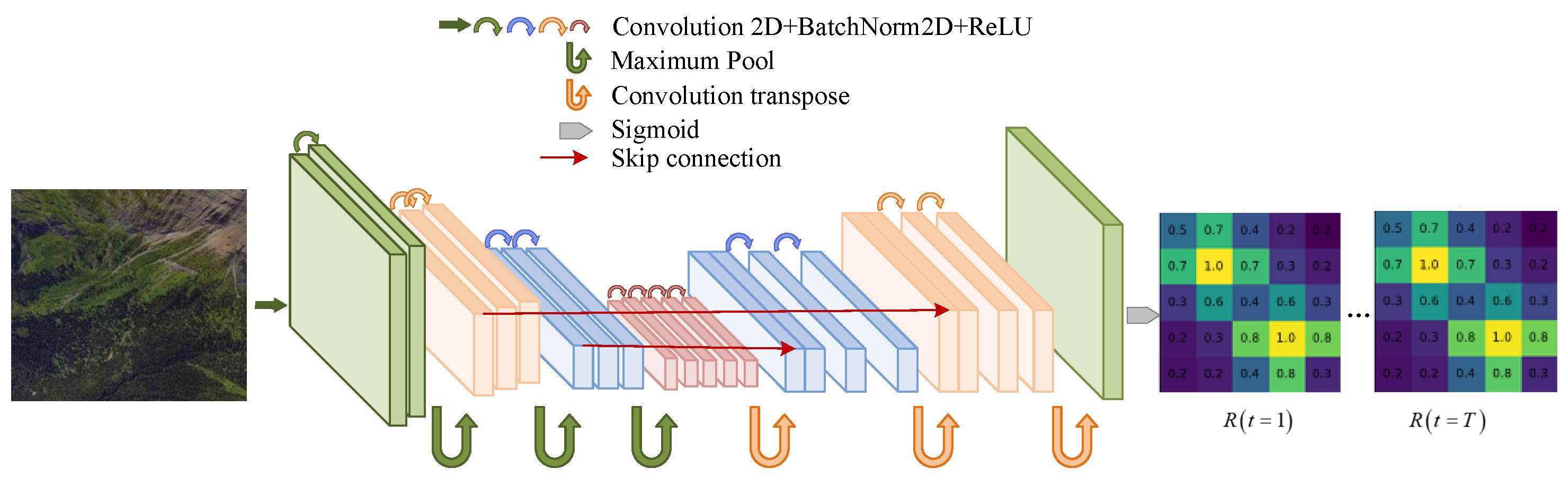
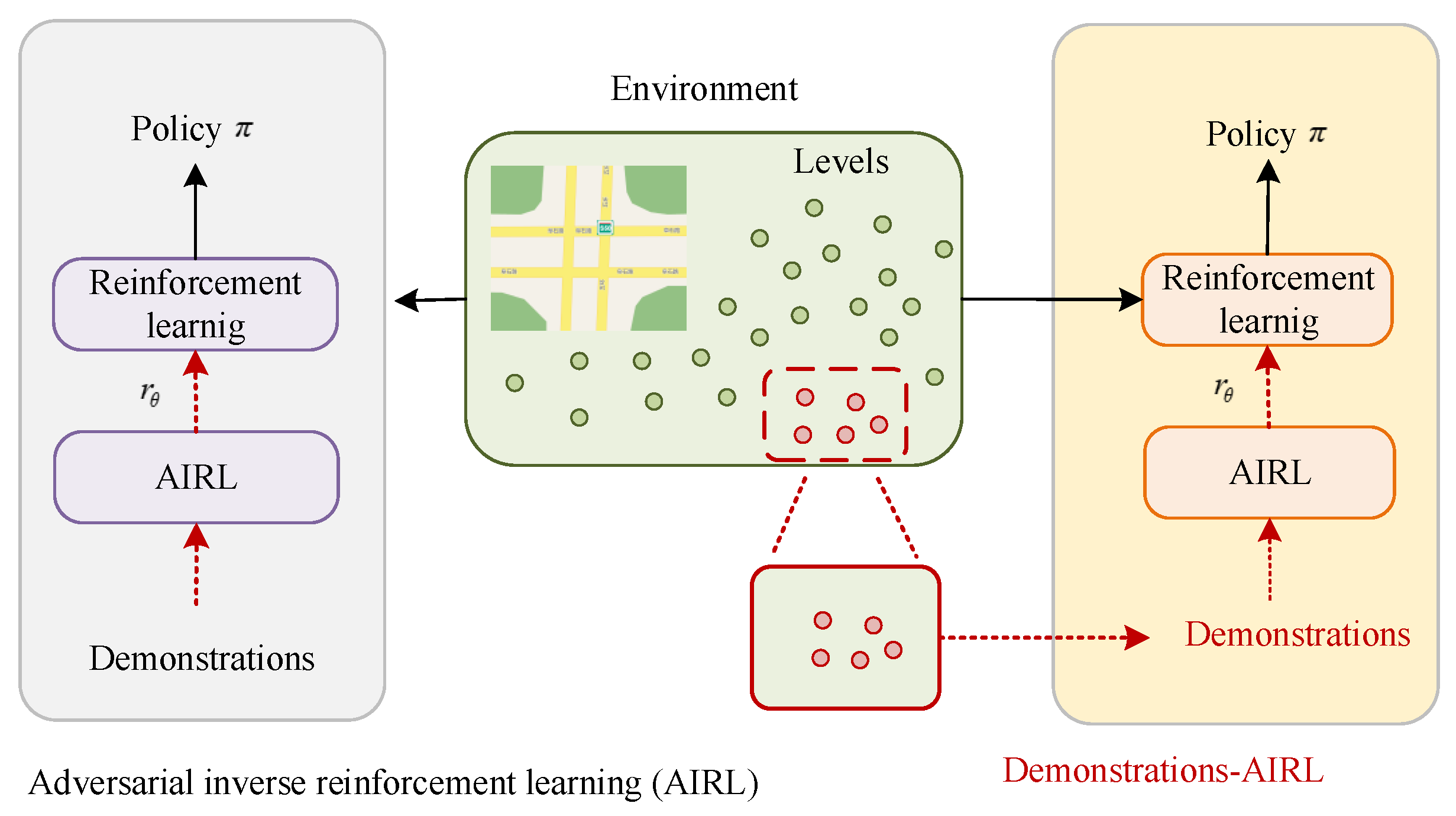
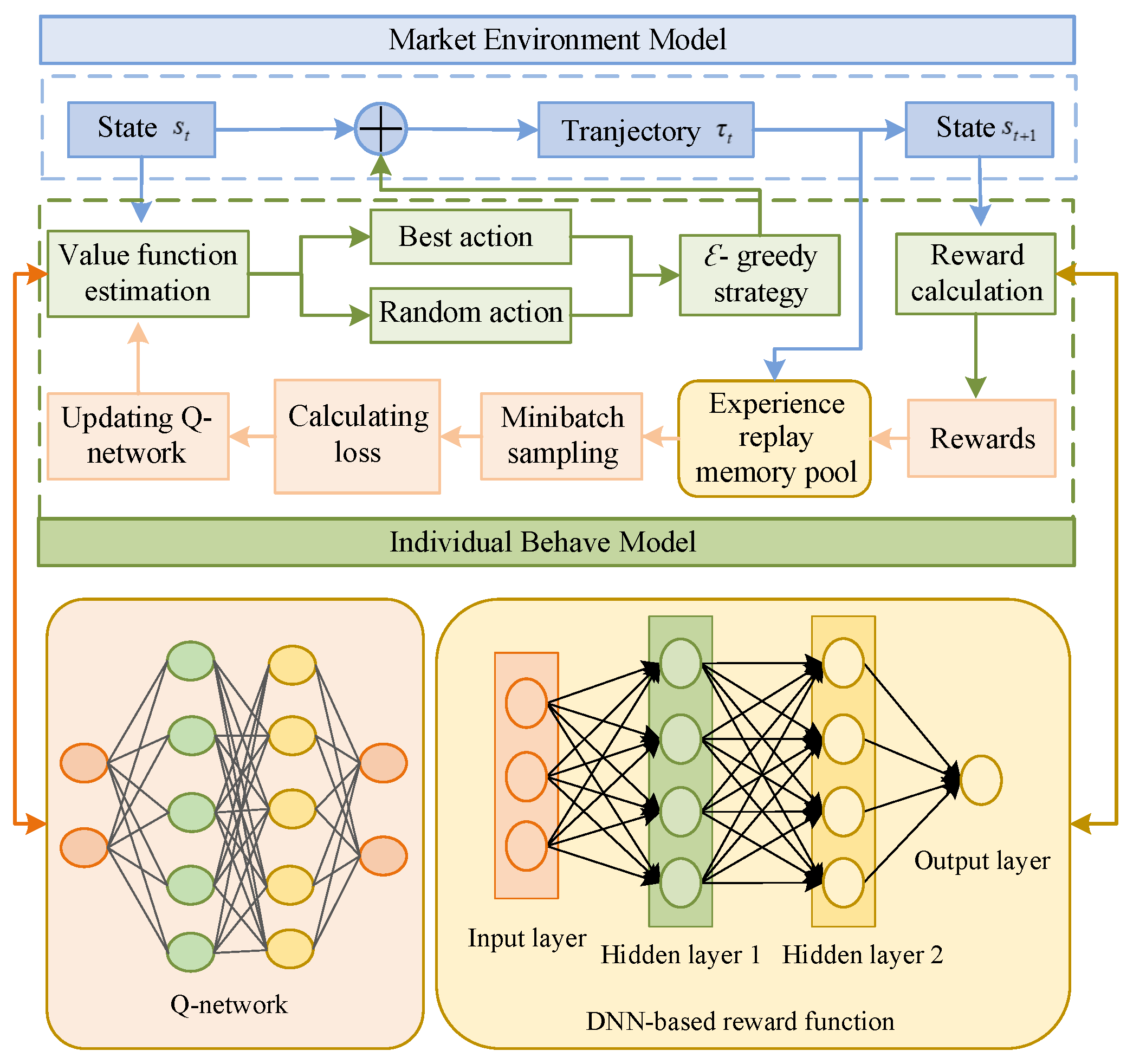
| Methods | Problems Solved | Advantages | Computational | Generalization | Application |
|---|---|---|---|---|---|
| Complexity | Performance | Areas | |||
| Gradient-based feature | |||||
| matching problem | Computationally | Intelligent driving | |||
| ME-IRL | under maximum | efficient, maintaining | [20,33,34,35], | ||
| based on | entropy constraints | critical performance | industrial control | ||
| trajectory | Low | Moderate | [36], | ||
| distribution | Maximum likelihood-based | medical care and life | |||
| feature matching | Good convergence | [37] | |||
| problem under maximum | |||||
| entropy constraints | |||||
| Continuous action and | Fast training speed | ||||
| state space problems | Intelligent driving | ||||
| Maximum | [22,38,39,40], | ||||
| entropy-based | Intelligent driving | Good robustness | High | High | robot control |
| deep | problems in complex | and high prediction | [41,42,43,44], | ||
| IRL | urban | accuracy | industrial control [45], | ||
| medical care and life | |||||
| Problem of non-optimal | High learning | [46,47] | |||
| expert demonstration | accuracy | ||||
| Nonlinear matching | Computationally | ||||
| Maximum | problems under causal | efficient, fast | Intelligent driving | ||
| causal | entropy constraints | convergence, good | [48,49,50], | ||
| entropy | generalization | Moderate | High | robot control [32], | |
| IRL | Matching instability | financial trade [51] | |||
| under causal | Good stability | ||||
| entropy constraints | |||||
| Algorithmic complexity | |||||
| problems in the | Good algorithmic | ||||
| unknown dynamics, | performance | ||||
| Maximum | high-dimensional, | Intelligent driving [52], | |||
| entropy-based | continuous case | High | Moderate | robot control [23,52], | |
| IOC | High learning | industrial control [53], | |||
| Model-based and | accuracy for | medical care and life | |||
| model-free | rewards | [54] | |||
| game problems | |||||
| Model-based | |||||
| adversarial IRL | Robust and stable | ||||
| Adversarial | Very high | High | Robot control [55], | ||
| IRL | games [56], | ||||
| Multi-intelligent | Stable training | [57,58] | |||
| generative adversarial | process and good | ||||
| IRL problem | accuracy | ||||
| Multi-task, multi- | Good explanations | ||||
| objective maximum | and rewards for | ||||
| entropy IRL problem | learning accuracy | Intelligent driving [59], | |||
| Extensions of | Moderate | High | robot control [27,57], | ||
| ME-IRL | Multi-agent maximum | Good sparsity | to High | industrial control [25], | |
| entropy IRL Problem | and accuracy | medical care and life [60] | |||
| Large-scale dataset | Easy control | ||||
| models |
| Methods | Applicable | Data | Reward | Success |
|---|---|---|---|---|
| Environment | Requirements | Recovery | Rate | |
| Accuracy | ||||
| ME-IRL based on | Simple environments | |||
| trajectory | with discrete state/action spaces | High | Low | Moderate |
| distribution | and linear reward structures | |||
| Maximum | Continuous high-dimensional spaces | |||
| entropy-based | and complex | Moderate | High | High |
| deep IRL | urban driving environments | |||
| Maximum | Sequential decision-making | |||
| causal | and temporally | Moderate | Moderate | High |
| entropy IRL | structured environments | |||
| Maximum | Unknown dynamics | |||
| entropy-based | and model-based | High | High | High |
| IOC | control systems | |||
| Adversarial | Multi-agent and | Low | Very High | Very high |
| IRL | game-theoretic environments | |||
| Extensions | Multi-task, multi-agent and | Moderate to high | Moderate to high | High |
| of ME-IRL | large-scale problem environments |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, L.; Guo, Q.; Channa, I.A.; Wang, Z. A Survey of Maximum Entropy-Based Inverse Reinforcement Learning: Methods and Applications. Symmetry 2025, 17, 1632. https://doi.org/10.3390/sym17101632
Song L, Guo Q, Channa IA, Wang Z. A Survey of Maximum Entropy-Based Inverse Reinforcement Learning: Methods and Applications. Symmetry. 2025; 17(10):1632. https://doi.org/10.3390/sym17101632
Chicago/Turabian StyleSong, Li, Qinghui Guo, Irfan Ali Channa, and Zeyu Wang. 2025. "A Survey of Maximum Entropy-Based Inverse Reinforcement Learning: Methods and Applications" Symmetry 17, no. 10: 1632. https://doi.org/10.3390/sym17101632
APA StyleSong, L., Guo, Q., Channa, I. A., & Wang, Z. (2025). A Survey of Maximum Entropy-Based Inverse Reinforcement Learning: Methods and Applications. Symmetry, 17(10), 1632. https://doi.org/10.3390/sym17101632






