Emergence and Localization of Exceptional Points in an Exactly Solvable Toy Model
Abstract
1. Introduction
2. The Model
3. Specific Features of Boundary-Controlled Dynamics
3.1. The Even Models
3.2. Odd Problem
4. Solvability: Sturmians
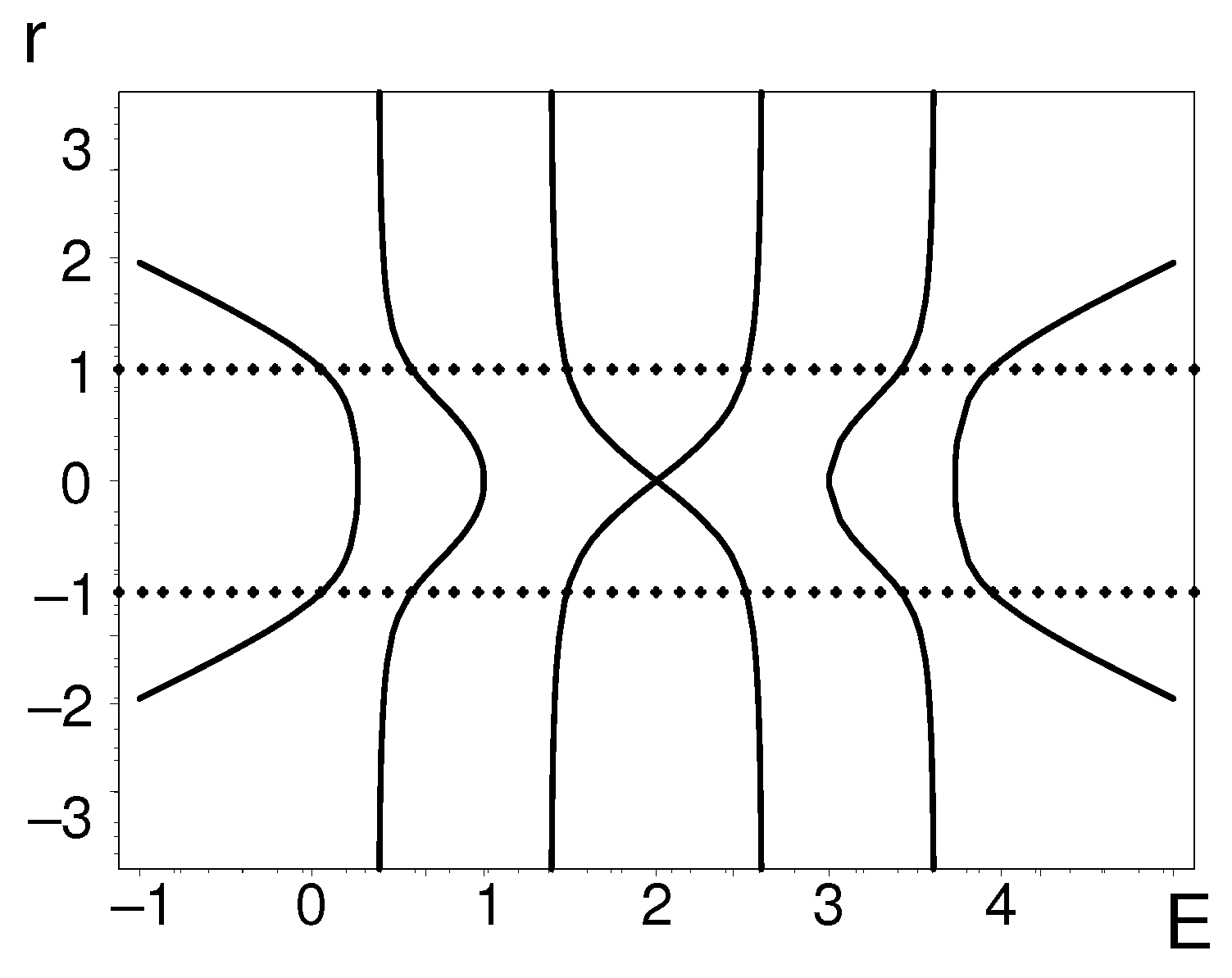
4.1. Non-Numerical Localizations of EPs
4.2. Example
5. Analytically Solvable Benchmark Models
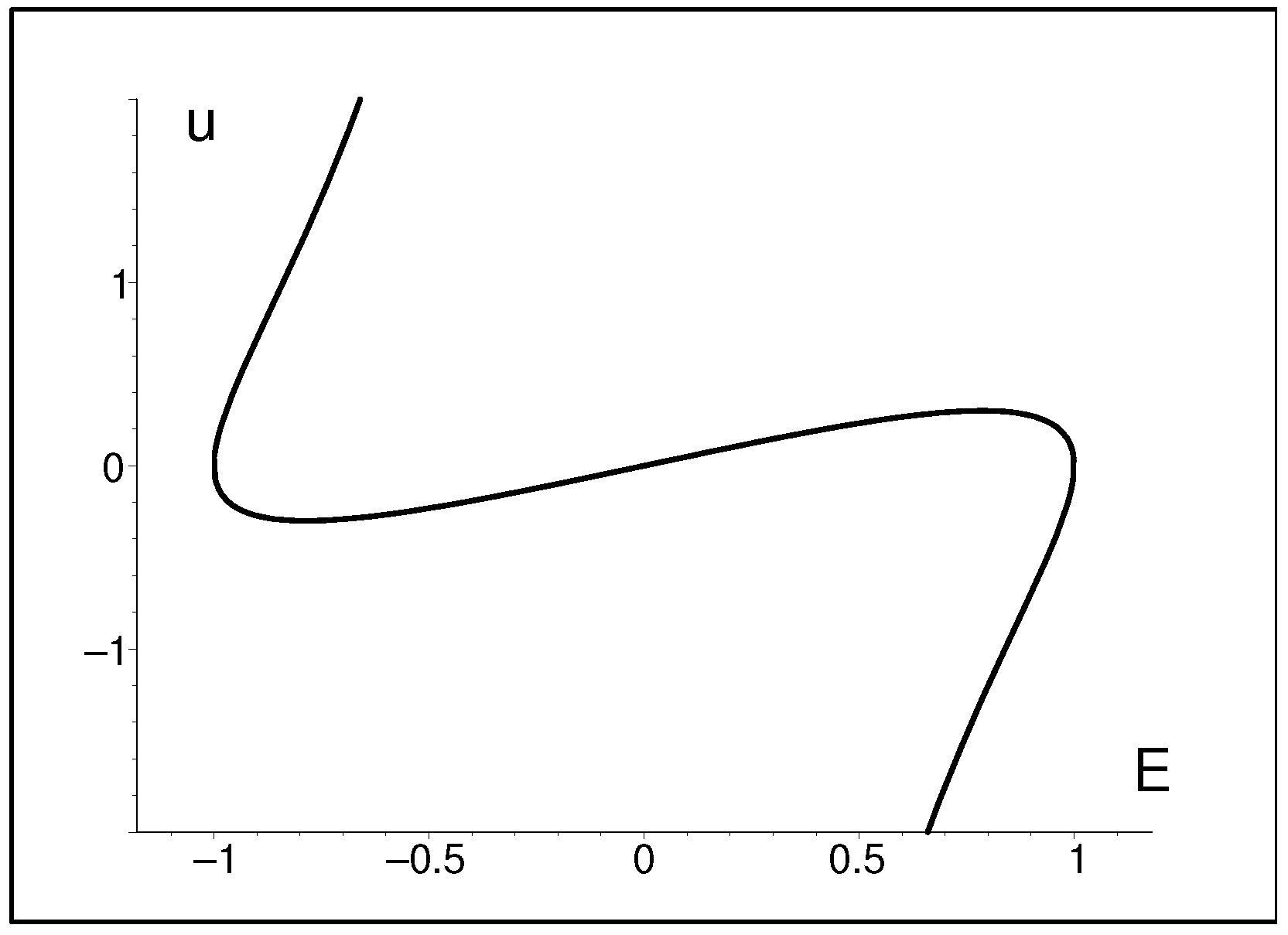
5.1. The First Nontrivial Model:
5.2. Benchmark Model with
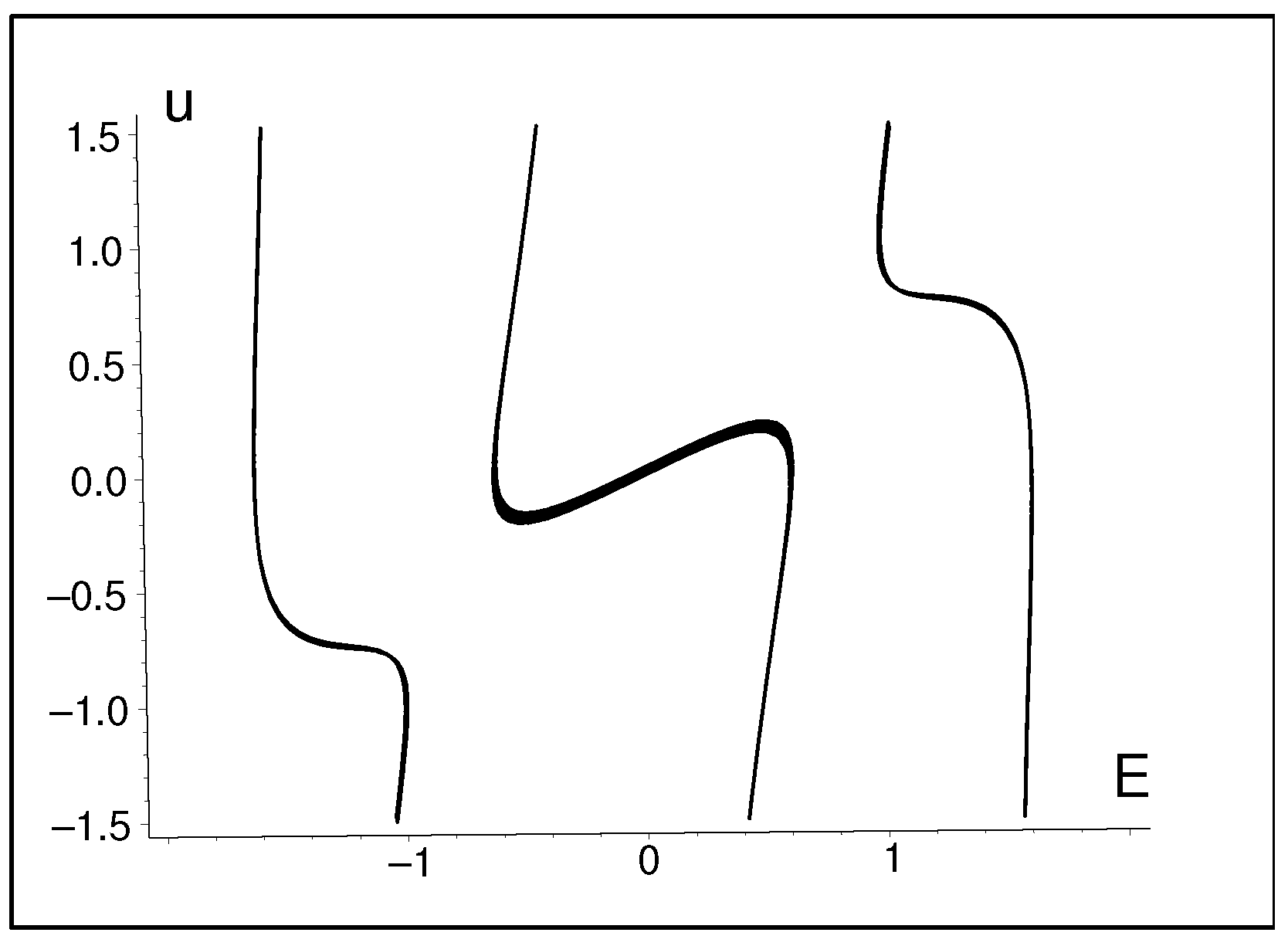
6. Beyond
6.1. Odd Versus Even Matrix Dimensions N
6.2. The Model Revisited
7. Beyond N = 5
8. Discussion
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. A Note on Non-Hermitian Degeneracies
Appendix A.1. Theoretical Framework
Appendix A.2. Phenomenology Behind Non-Hermitian Degeneracies
Appendix B. Closed Versus Open Systems
Appendix B.1. Closed Systems and Their Unitary Evolution
Appendix B.2. Unstable, Open Quantum Systems
Appendix C. Numerical Constructions
Appendix C.1. Complex Boundary Conditions in Square Well
Appendix C.2. Vicinity of Singularities
Appendix D. Quantum Physics near the Singularities
Appendix D.1. The Vicinity of the Singularity After Quantization
Appendix D.2. Singularities in Non-Stationary Dynamical Regime
References
- Arnold, V.I. Catastrophe Theory; Springer: Berlin, Germany, 1992. [Google Scholar]
- Messiah, A. Quantum Mechanics; North Holland: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: A status report. Class. Quantum Grav. 2004, 21, R53–R152. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Thiemann, T. Introduction to Modern Canonical Quantum General Relativity; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Bagarello, F.; Gazeau, J.-P.; Szafraniec, F.; Znojil, M. (Eds.) Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Scholtz, F.G.; Geyer, H.B.; Hahne, F.J.W. Quasi-Hermitian Operators in Quantum Mechanics and the Variational Principle. Ann. Phys. 1992, 213, 74–101. [Google Scholar] [CrossRef]
- Bender, C.M. Making Sense of Non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1018. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermitian Quantum Mechanics. Int. J. Geom. Meth. Mod. Phys. 2010, 7, 1191–1306. [Google Scholar] [CrossRef]
- Znojil, M. Quantum catastrophes: A case study. J. Phys. A Math. Theor. 2012, 45, 444036. [Google Scholar] [CrossRef]
- Znojil, M. Quantum singularities in a solvable toy model. J. Phys Conf. Ser. 2024, 29121, 012012. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis; Springer: New York, NY, USA, 1980. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover: New York, NY, USA, 1970. [Google Scholar]
- Znojil, M. Solvable non-Hermitian discrete square well with closed-form physical inner product. J. Phys. A Math. Theor. 2014, 47, 435302. [Google Scholar] [CrossRef]
- Dyson, F.J. General theory of spin-wave interactions. Phys. Rev. 1956, 102, 1217–1230. [Google Scholar] [CrossRef]
- Dieudonné, J. Quasi-Hermitian operators. In Proceedings of the International Symposium on Linear Spaces, Jerusalem, Israel, 5–12 July 1961; Pergamon: Oxford, UK, 1961; pp. 115–122. [Google Scholar]
- Brody, D.C. Biorthogonal quantum mechanics. J. Phys. A Math. Theor. 2013, 47, 035305. [Google Scholar] [CrossRef]
- Figueira de Morisson Faria, C.; Fring, A. Time evolution of non-Hermitian Hamiltonian systems. J. Phys. A Math. Gen. 2006, 39, 9269–9289. [Google Scholar] [CrossRef]
- Znojil, M. Time-dependent version of cryptohermitian quantum theory. Phys. Rev. D 2008, 78, 085003. [Google Scholar] [CrossRef]
- Znojil, M. Three-Hilbert-space formulation of Quantum Mechanics. Symm. Integ. Geom. Meth. Appl. SIGMA 2009, 5, 001. [Google Scholar] [CrossRef]
- Fring, A.; Moussa, M.H.Y. Unitary quantum evolution for time-dependent quasi-Hermitian systems with nonobservable Hamiltonians. Phys. Rev. A 2016, 93, 042114. [Google Scholar] [CrossRef]
- Znojil, M. Non-Hermitian interaction representation and its use in relativistic quantum mechanics. Ann. Phys. 2017, 385, 162–179. [Google Scholar] [CrossRef]
- Fring, A. An introduction to PT-symmetric quantum mechanics-time-dependent systems. J. Phys. Conf. Ser. 2023, 2448, 012002. [Google Scholar] [CrossRef]
- Fring, A.; Taira, T.; Tenney, R. Real energies and Berry phases in all PT regimes in time-dependent non-Hermitian theories. J. Phys. A Math. Theor. 2023, 56, 12LT01. [Google Scholar] [CrossRef]
- Rakhmanov, S.; Trunk, C.; Znojil, M.; Matrasulov, D. PT-symmetric dynamical confinement: Fermi acceleration, quantum force, and Berry phase. Phys. Rev. A 2024, 109, 053519. [Google Scholar] [CrossRef]
- Znojil, M. Discrete-coordinate crypto-Hermitian quantum system controlled by time-dependent Robin boundary conditions. Phys. Scr. 2024, 99, 035250. [Google Scholar] [CrossRef]
- Znojil, M. Broken Hermiticity phase transition in Bose-Hubbard model. Phys. Rev. A 2018, 98, 052102. [Google Scholar] [CrossRef]
- Znojil, M.; Geyer, H.B. Sturm-Schroedinger equations: Formula for metric. Pramana—J. Phys. 2009, 73, 299–306. [Google Scholar] [CrossRef]
- Schindler, J.; Li, A.; Zheng, M.-C.; Ellis, F.M.; Kottos, T. Experimental study of active LRC circuits with PT symmetries. Phys. Rev. A 2011, 84, 040101(R). [Google Scholar] [CrossRef]
- Li, J.-M.; Harter, A.K.; Liu, J.; de Melo, L.; Joglekar, Y.N.; Luo, L. Observation of parity-time symmetry breaking transitions in a dissipative Floquet system of ultracold atoms. Nat. Comm. 2019, 10, 855. [Google Scholar] [CrossRef]
- Christodoulides, D.; Yang, J.-K. (Eds.) Parity-Time Symmetry and Its Applications; Springer: Singapore, 2018. [Google Scholar]
- Bagchi, B.; Ghosh, R.; Sen, S. Exceptional point in a coupled Swanson system. EPL 2022, 137, 50004. [Google Scholar] [CrossRef]
- Trefethen, L.N.; Embree, M. Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Krejčiřík, D.; Siegl, P.; Tater, M.; Viola, J. Pseudospectra in non-Hermitian quantum mechanics. J. Math. Phys. 2015, 56, 103513. [Google Scholar] [CrossRef]
- Berry, M.V. Physics of Nonhermitian Degeneracies. Czech. J. Phys. 2004, 54, 1039–1047. [Google Scholar] [CrossRef]
- Heiss, W.D. Exceptional points - their universal occurrence and their physical significance. Czech. J. Phys. 2004, 54, 1091–1100. [Google Scholar] [CrossRef]
- Heiss, W.D. The physics of exceptional points. J. Phys. A Math. Theor. 2012, 45, 444016. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, G.; et al. Astrophysical Constants and Parameters. Phys. Rev. D 2019, 98, 030001. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Gurzadyan, V.G.; Penrose, R. On CCC-predicted concentric low-variance circles in the CMB sky. Eur. Phys. J. Plus. 2013, 128, 22. [Google Scholar] [CrossRef]
- Bojowald, M. Absence of a singularity in loop quantum cosmology. Phys. Rev. Lett. 2001, 86, 5227–5230. [Google Scholar] [CrossRef] [PubMed]
- Malkiewicz, P.; Piechocki, W. Turning Big Bang into Big Bounce: II. Quantum dynamics. Class. Quant. Gravity 2010, 27, 225018. [Google Scholar] [CrossRef]
- Wang, C.H.T.; Stankiewicz, M. Quantization of time and the big bang via scale-invariant loop gravity. Phys. Lett. B 2020, 800, 135106. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity-time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Guria, C.; Zhong, Q.; Ozdemir, S.K.; Patil, Y.S.S.; El-Ganainy, R.; Harris, J.G.E. Resolving the topology of encircling multiple exceptional points. Nat. Commun. 2024, 15, 1369. [Google Scholar] [CrossRef]
- Feinberg, J.; Riser, B. Pseudo-Hermitian random-matrix models: General formalism. Nucl. Phys. B 2022, 975, 115678. [Google Scholar] [CrossRef]
- Moise, A.A.A.; Cox, G.; Merkli, M. Entropy and entanglement in a bipartite quasi-Hermitian system and its Hermitian counterparts. Phys. Rev. A 2023, 108, 012223. [Google Scholar] [CrossRef]
- Bagchi, B.; Ghosh, R.; Sen, S. Analogue Hawking Radiation as a Tunneling in a Two-Level PT-Symmetric System. Entropy 2023, 25, 1202. [Google Scholar] [CrossRef]
- Koukoutsis, E.; Hizanidis, K.; Ram, A.K.; Vahala, G. Dyson maps and unitary evolution for Maxwell equations in tensor dielectric media. Phys. Rev. A 2023, 107, 042215. [Google Scholar] [CrossRef]
- Özdemir, Ş.; Rotter, S.; Nori, F.; Yang, L. Parity-time symmetry and exceptional points in photonics. Nat. Mater. 2019, 18, 783. [Google Scholar] [CrossRef]
- Graefe, E.M.; Günther, U.; Korsch, H.J.; Niederle, A.E. A non-Hermitian PT-symmetric Bose-Hubbard model: Eigenvalue rings from unfolding higher-order exceptional points. J. Phys. A Math. Theor. 2008, 41, 255206. [Google Scholar] [CrossRef]
- Henry, R.A.; Batchelor, M.T. Exceptional points in the Baxter-Fendley free parafermion model. Scipost Phys. 2023, 15, 016. [Google Scholar] [CrossRef]
- Liu, Y.X.; Jiang, X.P.; Cao, J.P.; Chen, S. Non-Hermitian mobility edges in one-dimensional quasicrystals with parity-time symmetry. Phys. Rev. B 2020, 101, 174205. [Google Scholar] [CrossRef]
- Janssen, D.; Dönau, F.; Frauendorf, S.; Jolos, R.V. Boson description of collective states. Nucl. Phys. A 1971, 172, 145–165. [Google Scholar] [CrossRef]
- Rotter, I. A non-Hermitian Hamilton operator and the physics of open quantum systems. J. Phys. A Math. Theor. 2009, 42, 153001. [Google Scholar] [CrossRef]
- Ramirez, R.; Reboiro, M.; Tielas, D. Exceptional Points from the Hamiltonian of a hybrid physical system: Squeezing and anti-Squeezing. Eur. Phys. J. D 2020, 74, 193. [Google Scholar] [CrossRef]
- Fisher, M.E. Yang-Lee edge singularity and φ3 field theory. Phys. Rev. Lett. 1978, 40, 1610–1613. [Google Scholar] [CrossRef]
- Bender, C.M.; Milton, K.A. Nonperturbative Calculation of Symmetry Breaking in Quantum Field Theory. Phys. Rev. 1997, D 55, R3255. [Google Scholar] [CrossRef]
- Jakubský, V.; Smejkal, J. A positive-definite scalar product for free Proca particle. Czech. J. Phys. 2006, 56, 985. [Google Scholar] [CrossRef]
- Dorey, P.; Dunning, C.; Tateo, R. From PT-symmetric quantum mechanics to conformal field theory. Pramana—J. Phys. 2009, 73, 217–239. [Google Scholar] [CrossRef]
- Bender, C.M. (Ed.) PT Symmetry in Quantum and Classical Physics; World Scientific: Singapore, 2018. [Google Scholar]
- Zezyulin, D.A.; Kartashov, Y.V.; Konotop, V.V. Metastable two-component solitons near an exceptional point. Phys. Rev. A 2021, 104, 023504. [Google Scholar] [CrossRef]
- Znojil, M. Few-Grid-Point Simulations of Big Bang Singularity in Quantum Cosmology. Symmetry 2025, 17, 972. [Google Scholar] [CrossRef]
- Buslaev, V.; Grecchi, V. Equivalence of unstable anharmonic oscillators and double wells. J. Phys. A Math. Gen. 1993, 26, 5541–5549. [Google Scholar] [CrossRef]
- Langer, H.; Tretter, C. A Krein space approach to PT symmetry. Czech. J. Phys. 2004, 54, 1113–1120. [Google Scholar]
- Heiss, W.D.; Müller, M.; Rotter, I. Collectivity, phase transitions, and exceptional points in open quantum systems. Phys. Rev. E 1998, 58, 2894. [Google Scholar] [CrossRef]
- Znojil, M. A return to observability near exceptional points in a schematic PT-symmetric model. Phys. Lett. B 2007, 647, 225–230. [Google Scholar] [CrossRef]
- Znojil, M. Unitarity corridors to exceptional points. Phys. Rev. A 2019, 100, 032124. [Google Scholar] [CrossRef]
- Feshbach, H. Unified theory of nuclear reactions. Ann. Phys. 1958, 5, 357–390. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Bender, C.M.; Wu, T.T. Anharmonic Oscillator. Phys. Rev. 1969, 184, 1231–1260. [Google Scholar] [CrossRef]
- Alvarez, G. Bender-Wu branch points in the cubic oscillator. J. Phys. A Math. Gen. 1995, 28, 4589–4598. [Google Scholar] [CrossRef]
- Bender, C.M.; Dunne, G.V. Large-order perturbation theory for a non-Hermitian PT-symmetric Hamiltonian. J. Math. Phys. 1999, 40, 4616–4621. [Google Scholar] [CrossRef]
- Ju, C.-Y.; Miranowicz, A.; Minganti, F.; Chan, C.-T.; Chen, G.-Y.; Nori, F. Einstein’s Quantum Elevator: Hermitization of Non-Hermitian Hamiltonians via a generalized vielbein Formalism. Phys. Rev. Res. 2022, 4, 023070. [Google Scholar] [CrossRef]
- Znojil, M.; Geyer, H.B. Construction of a unique metric in quasi-Hermitian quantum mechanics: Non-existence of the charge operator in a 2 × 2 matrix model. Phys. Lett. B 2006, 640, 52–56. [Google Scholar] [CrossRef]
- Ohmori, S.; Takahashi, J. Rigged Hilbert space approach for non-Hermitian systems with positive definite metric. J. Math. Phys. 2022, 63, 123503. [Google Scholar] [CrossRef]
- Acton, F.S. Numerical Methods that Work; Harper and Row: New York, NY, USA, 1970. [Google Scholar]
- Znojil, M. Generalized Bose-Hubbard Hamiltonians exhibiting a complete non-Hermitian degeneracy. Ann. Phys. 2019, 405, 325–339. [Google Scholar]
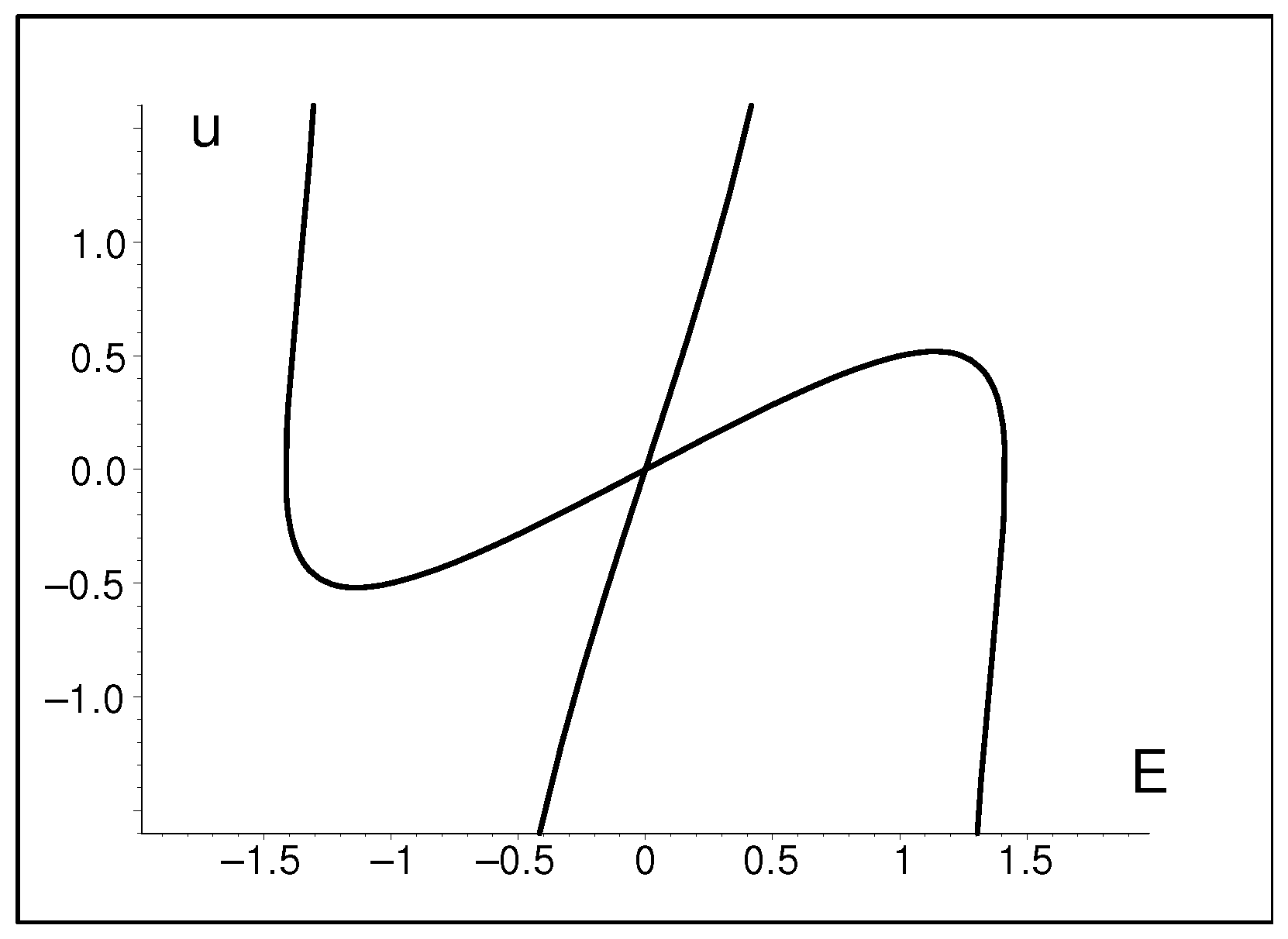

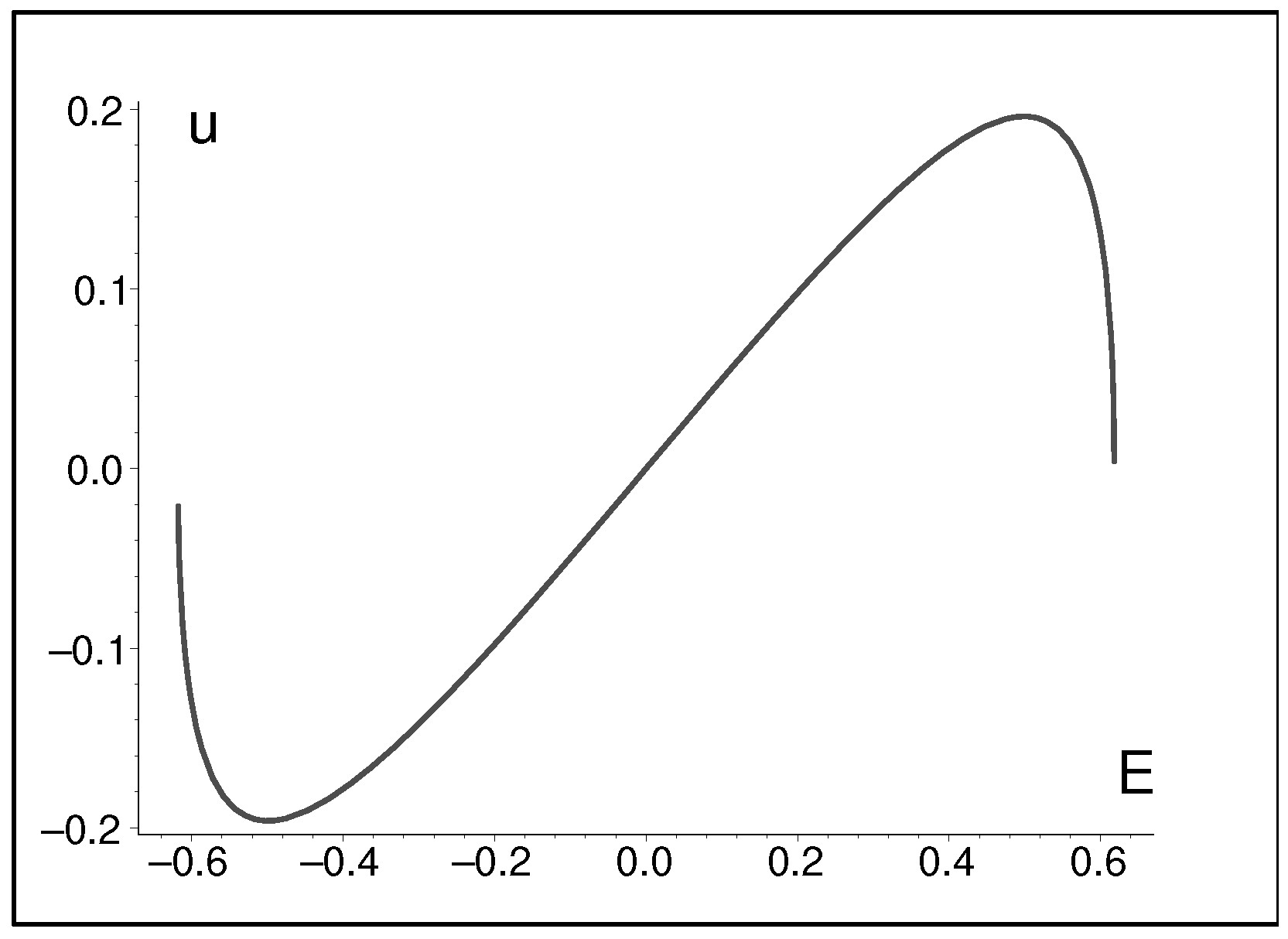


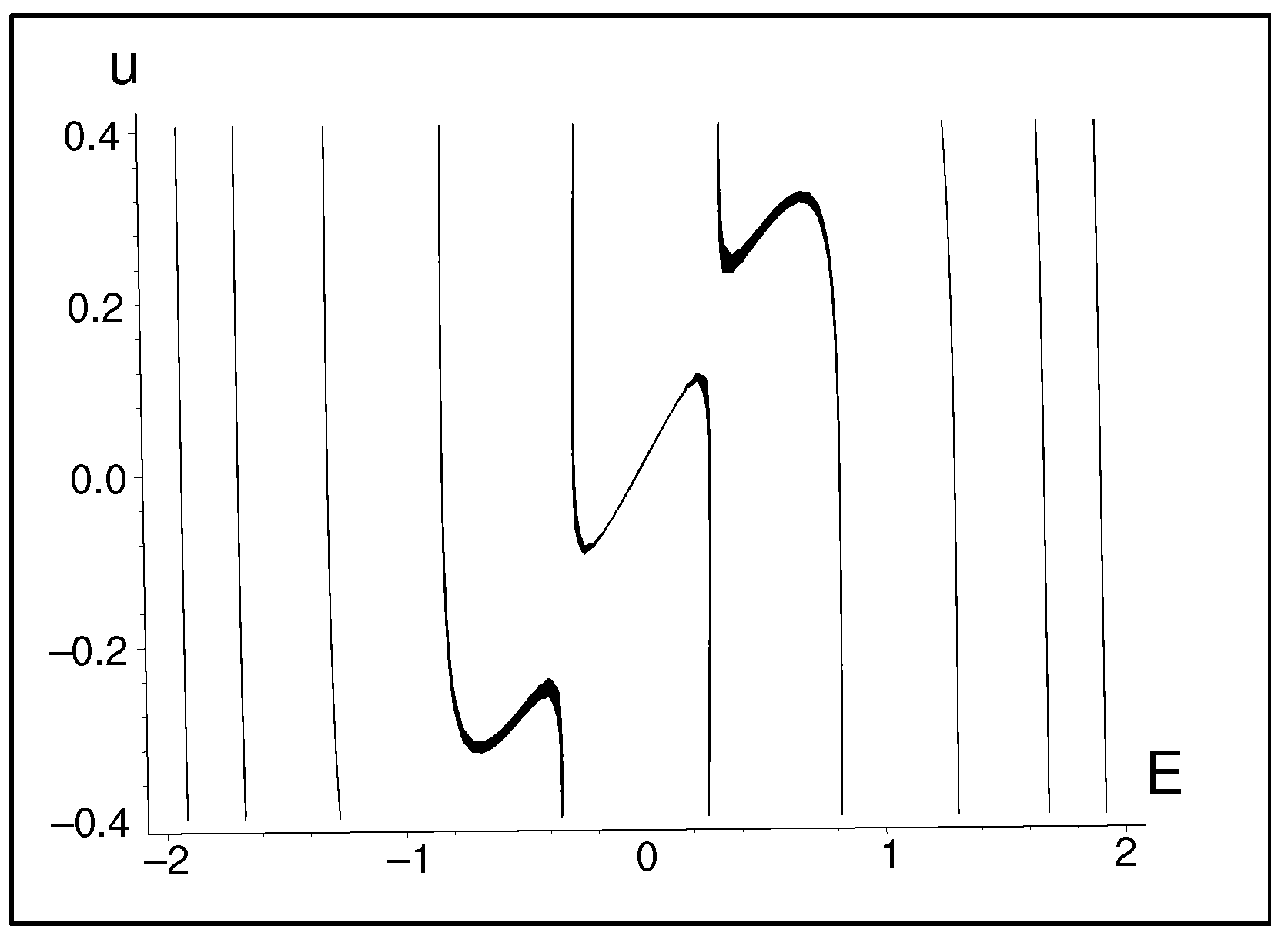
| N | |
|---|---|
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 |
| N | Denominator of |
|---|---|
| 6 | |
| 8 | |
| 9 |
| N | |
|---|---|
| 4 | |
| 5 | |
| 6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Znojil, M. Emergence and Localization of Exceptional Points in an Exactly Solvable Toy Model. Symmetry 2025, 17, 1630. https://doi.org/10.3390/sym17101630
Znojil M. Emergence and Localization of Exceptional Points in an Exactly Solvable Toy Model. Symmetry. 2025; 17(10):1630. https://doi.org/10.3390/sym17101630
Chicago/Turabian StyleZnojil, Miloslav. 2025. "Emergence and Localization of Exceptional Points in an Exactly Solvable Toy Model" Symmetry 17, no. 10: 1630. https://doi.org/10.3390/sym17101630
APA StyleZnojil, M. (2025). Emergence and Localization of Exceptional Points in an Exactly Solvable Toy Model. Symmetry, 17(10), 1630. https://doi.org/10.3390/sym17101630






