Abstract
Object detection in soccer scenes serves as a fundamental task for soccer video analysis and target tracking. This paper proposes WCC-YOLO, a symmetry-enhanced object detection framework based on YOLOv11n. Our approach integrates symmetry principles at multiple levels: (1) The novel C3k2-WTConv module synergistically combines conventional convolution with wavelet decomposition, leveraging the orthogonal symmetry of Haar wavelet quadrature mirror filters (QMFs) to achieve balanced frequency-domain decomposition and enhance multi-scale feature representation. (2) The Channel Prior Convolutional Attention (CPCA) mechanism incorporates symmetrical operations—using average-max pooling pairs in channel attention and multi-scale convolutional kernels in spatial attention—to automatically learn to prioritize semantically salient regions through channel-wise feature recalibration, thereby enabling balanced feature representation. Coupled with InnerShape-IoU for refined bounding box regression, WCC-YOLO achieves a 4.5% improvement in mAP@0.5:0.95 and a 5.7% gain in mAP@0.5 compared to the baseline YOLOv11n while simultaneously reducing the number of parameters and maintaining near-identical inference latency (δ < 0.1 ms). This work demonstrates the value of explicit symmetry-aware modeling for sports analytics.
1. Introduction
Football (soccer) boasts a vast global audience and a massive market. Utilizing computer vision techniques to perform object detection in football match videos—specifically, automatically identifying the positions of players and the ball—can provide a solid foundation for further object tracking. This has significant practical implications for match broadcasting and video data analysis.
Early methods for object detection in football scenes primarily relied on background subtraction [1], color space analysis [2], and HOG (Histogram of Oriented Gradients)- based detectors [3], among others. Although computationally efficient, these methods exhibit notable limitations in complex match scenarios, such as sensitivity to lighting variations and camera motion, as well as difficulties in handling dense player occlusions.
With advances in deep learning, convolutional neural network (CNN)-based object detection algorithms (e.g., the Faster R-CNN [4] and YOLO series [5,6,7]) have gradually become mainstream. These approaches employ end-to-end training to automatically learn multi-level features, achieving breakthrough performance in general scenarios. However, when applied to football match videos, existing deep learning-based detection models still have evident shortcomings, such as low recognition rates for distant players and the ball (small objects), as well as insufficient robustness in densely contested situations.
To bridge this gap, we draw inspiration from the field of signal processing, where wavelet transforms excel in multi-resolution analysis, and from the success of channel attention mechanisms in highlighting salient features. We hypothesize that integrating these principles into a modern detection framework can provide a targeted solution to the challenges of soccer video analysis. Following this hypothesis, this paper proposes WCC-YOLO, an improved YOLOv11 [8]-based object detection network for soccer scenarios. Inspired by the efficacy of symmetry principles in designing robust and efficient neural architectures, our main contributions include:
- (1)
- The proposed C3k2-WTConv module integrates wavelet convolution [9] into the C3k2 architecture, leveraging the orthogonal symmetry of quadrature mirror filters to achieve balanced frequency-space decomposition, enhancing multi-scale feature representation while reducing model parameters.
- (2)
- The introduced Channel Prior Convolutional Attention (CPCA) [10] mechanism incorporates symmetric operations (e.g., average-max pooling pairs and multi-scale convolutional kernels) to effectively direct feature focus toward critical regions, significantly improving detection accuracy without compromising inference speed.
- (3)
- The incorporation of the InnerShape-IoU loss function substantially improves bounding box generalization performance.
The remainder of this paper is organized as follows: Section 2 reviews related work on soccer object detection and wavelet transform in deep learning. Section 3 presents the principles of wavelet convolution, the network architecture of our proposed model and the detailed configurations of its modules. Section 4 provides experimental validation and discussion, including comprehensive ablation studies. Finally, Section 5 concludes this paper and outlines directions for future research.
2. Related Works
2.1. Object Detection in Soccer Scenes
The evolution of object detection in soccer scenes has transitioned from traditional image processing techniques to modern deep learning paradigms. Historically, traditional methods primarily relied on low-level features such as background subtraction [1], color space analysis [2,11,12], and hand-crafted descriptors like HOG [3,13,14]. While computationally efficient, these methods are inherently fragile, exhibiting significant performance degradation under challenging conditions like occlusions, varying lighting, and camera motion. Although some studies attempted to address these issues, for instance, by proposing a two-stage detection algorithm based on particle swarm optimization to partially resolve occlusion problems [15], the overall limitations remained largely unsolved until the rise in deep learning.
The dominance of deep learning, led by convolutional neural network (CNN)-based detectors, has set new benchmarks in general object detection [4,5,6,7]. However, the initial translation of these successes to the soccer domain often involved the direct application of models pre-trained on generic datasets [16,17], which struggled with domain-specific challenges. Subsequent research diversified into multiple strategies. Some works focused on closing the domain gap through techniques like self-supervised adaptation and knowledge distillation [18]. Another line of work addressed efficiency demands via lightweight architecture design [19] and efficient cascaded networks [20]. The persistent challenge of detecting small players was directly tackled by approaches like PassNet, which built upon pre-trained detectors like YOLOv3 [21] for multi-view analysis [22]. More recently, Transformer-based frameworks were explored for their ability to model global context [23,24], and other studies introduced advanced optimization techniques like Pseudo-IoU for improved sample screening [25]. Despite these advances, the core limitations of reliably detecting small objects (like the ball) and robustly handling severe occlusions remain largely unresolved, continuing to hinder automated analysis systems
2.2. Wavelet Transforms in Deep Learning
The Wavelet Transform (WT) [26] is a well-established multi-resolution analysis tool. Its integration into deep learning has been explored for enhancing feature representation and computational efficiency. Previous works have utilized WT as a pooling operator [27,28], for feature map compression [29], and as a replacement for standard sampling operations in encoder–decoder networks like U-Net [30,31]. It has also been incorporated into generative models to improve output quality [32,33]. These studies demonstrate the potential of wavelet theory in designing more efficient and effective neural networks, yet its application specifically for addressing small object detection in complex sports scenarios remains underexplored.
3. Methods
3.1. Wavelet Convolution
3.1.1. The Wavelet Transform as Convolutions
The wavelet transform is a powerful multi-resolution analysis tool that decomposes a signal into different frequency components [26,34]. For image processing, the two-dimensional Haar wavelet transform is particularly efficient and can be implemented through convolutional operations [35].
Given an input image or feature map , a single-level Haar wavelet transform along one spatial dimension (width or height) can be implemented by applying a set of depth-wise convolutional filters followed by downsampling.
The one-dimensional low-pass (ℎlow) and high-pass (ℎhigh) filter kernels for the Haar wavelet are defined as:
The corresponding two-dimensional filters are obtained through the outer product (or Kronecker product), resulting in the following four fundamental convolutional kernels that form an orthonormal basis:
Here, represents a low-pass filter, while , , and constitute a set of high-pass filters, capturing horizontal, vertical, and diagonal details, respectively. The two-dimensional wavelet transform for each input channel c is then implemented as a depth-wise convolution with a stride of 2 using this bank of filters:
where . The output consists of four subbands for each channel c. The spatial resolution of each output channel is halved. represents the low-frequency approximation component, while , , and correspond to the horizontal, vertical, and diagonal high-frequency detail components, respectively.
The kernels defined in Equation (2) form an orthonormal basis, a property known as quadrature mirror filtering in wavelet theory. This precise mathematical symmetry ensures that the filter bank can perfectly reconstruct the original signal from its subbands, which is the fundamental basis for using the inverse transform in our decoding process.
Since the kernels in Equation (2) form an orthonormal basis, the Inverse Wavelet Transform (IWT) can be implemented through transposed convolution:
The cascade wavelet decomposition is achieved by recursively decomposing the low-frequency components. Each level of decomposition is expressed as:
where i is the current level and .
3.1.2. Convolution in the Wavelet Domain
The concept of performing convolution directly on wavelet coefficients has been explored in signal processing and deep learning [28]. Our wavelet convolution (WConv) module builds upon this principle.
The wavelet convolution is implemented by first applying the wavelet transform (WT) to filter and downsample the input’s low- and high-frequency components, then performing small-kernel depth-wise convolutions on the different frequency maps, and finally reconstructing the output through the inverse wavelet transform (IWT). This process can be formally represented as:
where denotes a convolutional operation applied in the wavelet domain. Here, X denotes the input tensor, while F is implemented as a depth-wise convolution with a learnable weight tensor W. This operation not only accomplishes frequency-domain-separated convolution but also effectively enlarges the receptive field with respect to the input, as illustrated in Figure 1.
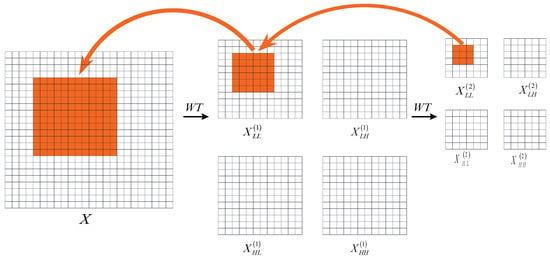
Figure 1.
Convolution in the wavelet domain yields an enlarged receptive field. In this example, when applying a 3 × 3 convolution kernel to the low-frequency components () in the second-level wavelet decomposition, this 9-parameter operation effectively processes lower-frequency information corresponding to a 12 × 12 region in the original input space X [9]. Reproduced with permission from Springer Nature Switzerland. License Number: 1564697-1.
The aforementioned single-level composite operation can be further extended by applying the cascade principle from Equation (5), with the specific procedure as follows:
where is the input, represents all three high-frequency maps at level i as described in Section 3.1.1.
Since both the wavelet transform and its inverse are linear operations, we integrate the outputs from different frequency bands through the following procedure:
where denotes the hierarchically aggregated outputs beginning at decomposition level i.
To provide a clearer and more concise implementation perspective of the aforementioned wavelet convolution process (particularly corresponding to Equation (6)), we further outline the detailed procedure for a single-level decomposition and reconstruction in Algorithm 1.
| Algorithm 1: Wavelet Convolution (WConv) |
| Input: Input tensor convolution kernel size k Output: Output tensor 1: // Step 1: Decomposition via Wavelet Transform (WT) 2: ← HaarWT(X) ▷ Using kernels in Equation (2) ) ▷ 4: // Step 2: Frequency-domain Convolution ←DepthwiseConv2D(Z,Wdw,kernel_size=k) ▷ Wdw is a learnable kernel ) ▷ Processed subbands 7: // Step 3: Reconstruction via Inverse Wavelet Transform (IWT) 8: Y ▷ Using transposed convolution 9: return Y |
3.2. Network Architecture
We propose WCC-YOLO, an improved YOLOv11n network, with its architecture shown in Figure 2. The network consists of three components: a backbone network, a neck network, and a detection head.
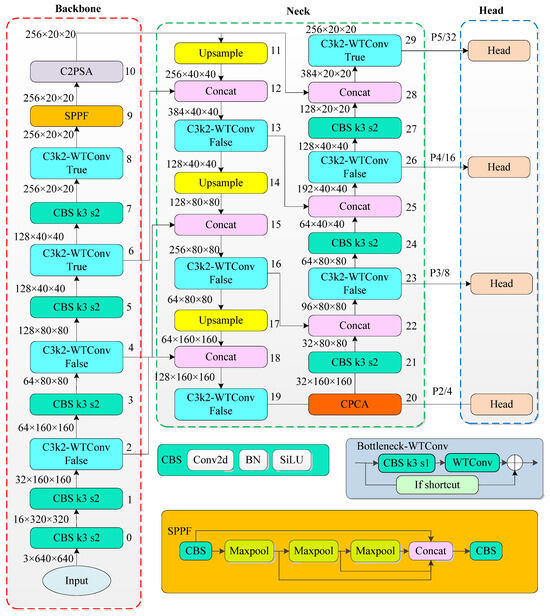
Figure 2.
The Network Architecture of WCC-YOLO.
The backbone network includes the standard convolution module (CBS), the C3k2-WTConv module, the spatial pyramid pooling module (SPPF), and the C2PSA module. The CBS module comprises a convolutional layer, batch normalization (BN), and a SiLU activation function, performing downsampling, feature extraction, and processing. The C3k2-WTConv module, an improved version of the original C3k2 combined with wavelet convolution, is a key innovation of this network, and its detailed structure will be elaborated in Section 3.2. The SPPF module, a canonical component in the YOLO series, expands the receptive field through multi-scale pooling, enabling fusion of spatial features across different granularities. The C2PSA module combines the CSP structure with the PSA attention mechanism, enabling efficient feature map processing and enhanced focus on critical regions. The neck network employs a hierarchical FPN + PAN architecture for multi-scale feature fusion, effectively aggregating both high-level semantic and low-level spatial features.
The proposed architecture differs from the original YOLOv11n in four key aspects:
- (1)
- A novel C3k2-WTConv module is designed to replace the original C3k2 module;
- (2)
- An additional P2 detection branch is introduced specifically to enhance small object detection performance;
- (3)
- The CPCA mechanism is incorporated into the Neck network;
- (4)
- The state-of-the-art Inner ShapeIoU is adopted for bounding box regression.
3.3. C3k2-WTConv Module
The main advantages of wavelet convolution (WTConv) are as follows: (1) By employing hierarchical wavelet decomposition, WTConv can significantly expand the receptive field of CNNs without substantially increasing the number of parameters. (2) The WTConv layer exhibits greater sensitivity to low-frequency information in images, thereby enhancing the CNN’s responsiveness to shape rather than texture.
Building upon these advantages, we integrate wavelet convolution to propose a C3k2-WTConv module, whose architecture is illustrated in Figure 3. The key modification involves replacing the second standard convolution in the C3K2 Bottleneck module with wavelet convolution (WTConv). This replacement is not merely a structural swap but is motivated by the goal of embedding the mathematical symmetries of the wavelet transform (as detailed in Section 3.1) directly into the network architecture, thereby providing a powerful inductive bias. Specifically, the orthogonal mirror symmetry of the wavelet filters ensures a balanced and lossless separation of features into frequency subbands. This prevents an information bottleneck and guarantees that both coarse-grained (low-frequency) and fine-grained (high-frequency) features are preserved and processed with equal importance, inherently enhancing the model’s multi-scale perception capability.
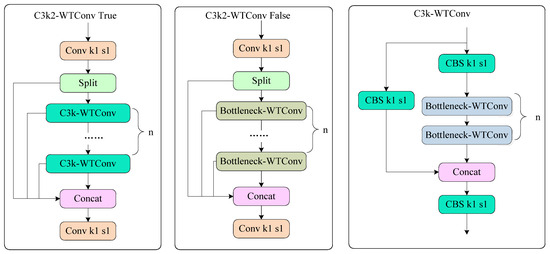
Figure 3.
The Architecture of C3k2-WTConv module.
Beyond the inherent properties of WTConv, the C3k2-WTConv architecture itself contributes to the model’s robustness through its design. Similarly to the C3k2 module, this module features two distinctive characteristics. First, it employs parallel convolution branches where the input feature map is split into two pathways: one maintains a direct mapping to preserve shallow features, while the other processes deeper features through multiple configurable Bottleneck or C3k blocks with variable kernel sizes, followed by feature concatenation. Second, the module offers exceptional parametric flexibility through several key parameters: the c3k parameter for selecting between C3k blocks or standard Bottleneck structures, the n parameter controlling block repetitions, the g parameter regulating group convolution, and the e parameter adjusting channel expansion ratios. This sophisticated parameterization enables an optimal balance between computational efficiency and model performance, making the module particularly versatile for various computer vision tasks.
Furthermore, the architecture of the C3k2-WTConv module exhibits a notable form of structural symmetry. As illustrated in Figure 3, the input feature map is symmetrically split into two parallel pathways. This design creates a symmetric processing flow: one branch prioritizes the preservation of original information through a direct identity mapping, while the other branch focuses on learning new feature representations through a sequence of transformative operations (Bottleneck-WTConv or C3k-WTConv blocks). The final concatenation step then symmetrically merges the outputs from both branches, ensuring a balanced integration of low-level, high-fidelity features and high-level, semantically rich features. This symmetric design mitigates the degradation of gradient information and enhances feature diversity, which is crucial for detecting objects across a wide range of scales and appearances in complex soccer scenes. Thus, the C3k2-WTConv module leverages symmetry at both the mathematical and architectural levels to form a more powerful and efficient foundation for multi-scale feature learning.
3.4. Channel Prior Convolutional Attention Mechanism(CPCA)
As show in Figure 4, the CPCA mechanism comprises two core modules: channel attention and spatial attention. The channel attention module analyzes and weights the importance of each channel in the feature maps to enhance critical features, while the spatial attention module extracts key spatial information to provide guidance for the former, enabling collaborative optimization of the feature maps.
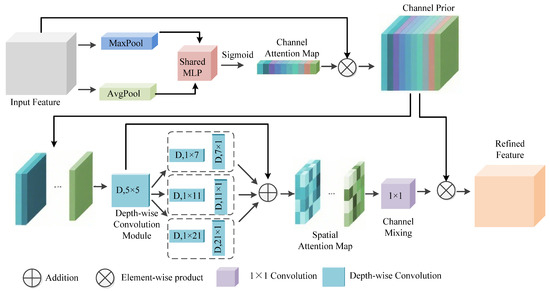
Figure 4.
The Channel Prior Convolutional Attention Mechanism (CPCA) [10]. Reproduced with permission from Springer Nature Switzerland. License Number: 1654867-1.
The CPCA mechanism incorporates symmetry through dual-perspective feature aggregation at both channel and spatial levels. The channel attention module uses symmetric pooling pathways—average pooling extracts global contextual features while max pooling highlights salient local features—which are then fused through a shared MLP to maintain feature equilibrium. The spatial attention module adopts architectural symmetry through parallel multi-scale depth-wise convolutions (kernel sizes 7, 11, 21), ensuring balanced receptive fields across scales. Furthermore, the multi-scale depth-wise convolution module incorporates structural symmetry through factorized kernels. For instance, the employment of 1 × 7 followed by 7 × 1 convolutions constitutes a spatially symmetric decomposition, efficiently approximating a 7 × 7 receptive field while significantly reducing computational complexity. This design maintains a balance in directional sensitivity, enabling the model to capture long-range dependencies equally along both horizontal and vertical axes.
In the channel attention module, the feature map is first processed, where C denotes the number of channels, and H and W represent the height and width of the feature map, respectively. Average pooling and max pooling operations are applied to extract the mean and maximum values for each channel, computed as:
These operations capture spatial features from complementary perspectives: average pooling reflects global contextual features, while max pooling highlights salient local features.
Next, and are fed into a shared multilayer perceptron (MLP) M, with input/output dimensionality of C and hidden layer dimensionality of C/r (where r is the reduction ratio). The processed outputs and are then summed to produce the channel importance descriptor S:
Subsequently, the Sigmoid activation function is applied to S to generate the channel attention map :
Here, quantitatively indicates the importance of each corresponding channel. Finally, the channel attention map is element-wise multiplied with the original input feature map to produce the refined feature map for subsequent model processing:
In the spatial attention module, the spatial attention map is first generated through Equation (14):
Here, denotes depth-wise convolution, which thoroughly explores spatial relationships among features. (where i ∈ {1,2,3}) represents different parallel branches. A multi-scale architecture is adopted, employing convolutional kernels of varying sizes to extract features at different scales. The outputs are then channel-mixed via 1 × 1 convolution to refine the spatial attention map. Finally, the detection-ready features are obtained via Equation (15):
3.5. The InnerShape-Iou Loss Function
Shape-IoU [36] can focus on the shape and scale of the bounding box itself to calculate losses, thereby improving accuracy. Meanwhile, Inner-IoU [37] enhances convergence speed through scale-factor-controlled generation of auxiliary bounding boxes for loss computation. In our detection framework, we implement an integrated approach that combines both Inner-IoU and Shape-IoU mechanisms, referred to as InnerShape-IoU.
The computational principle of InnerShape-IoU will be explained below with reference to Figure 5, where and b represent the ground-truth box and anchor box, respectively. The center points of both the ground-truth (GT) box and inner GT box are denoted as (), while those of the anchor box and inner anchor box are represented by (). The width and height of the GT box are and , respectively, and the corresponding dimensions of the anchor box are w and ℎ. The scaling factor, denoted as ratio, typically takes values within the range [0.5, 1.5].
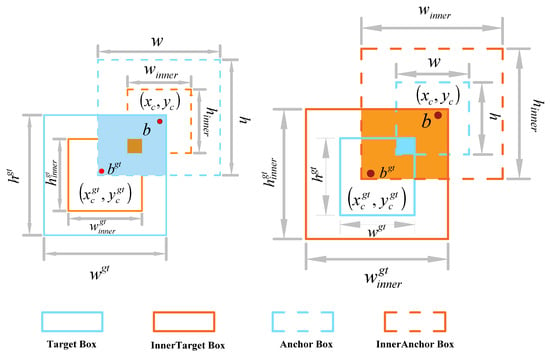
Figure 5.
Description of Inner-IoU and Shape-IoU [37].
The Inner-IoU is derived through the following computational framework:
The computational principle of Shape-IoU is described as follows:
Here, scale denotes the scaling factor, which correlates with target object sizes in the dataset, while ww and hh represent the horizontal and vertical weighting coefficients, respectively. These coefficients are determined by the geometric shape of the ground-truth (GT) box. The denotes the distance loss, which quantifies the normalized displacement between the predicted bounding box and ground-truth (GT) box centers along both horizontal (x-axis) and vertical (y-axis). The term represents the shape loss, measuring the geometric dissimilarity between the predicted box and GT box shapes.
The final loss function formula, which integrates both Inner-IoU and Shape-IoU, is computed as follows:
4. Experiment
4.1. Dataset
The dataset used in this study is the Soccer Detection dataset [38], which is publicly available on GitHub. This dataset is derived from video streams of professional soccer matches, though the precise original sensor information is not provided by the curators. It consists of 2549 RGB images with a resolution of 1280 × 720 pixels, capturing diverse soccer match scenarios under various lighting conditions and camera angles.
The dataset is partitioned into 1782 images for training, 515 for validation, and 252 for testing, following the original split without modification. The detection targets include three categories: goal (goalposts), ball, and player. The images were annotated in YOLO format, containing bounding boxes for these objects. The variety and challenges present in this dataset make it suitable for evaluating the robustness of object detection models in complex sports environments.
4.2. Evaluation Metrics
Following the evaluation protocol of the YOLO series, we adopt Precision (Pr), Recall (Re), mAP@0.5, and mAP@0.5:0.95 as the primary metrics for model assessment. Among these, mAP@0.5:0.95 serves as the main indicator for detection accuracy. Additionally, the number of parameters and GFLOPs are used to measure model complexity, while the end-to-end latency per image (ImgLatency, including pre-processing, inference, and post-processing) is employed to evaluate detection speed.
4.3. Experimental Environment and Parameter Settings
The experimental hardware setup includes an NVIDIA GeForce RTX 3090 GPU, an Intel i9-10900X CPU, and 32 GB RAM. The software environment runs on Windows 10 OS with Python 3.10 and PyTorch 1.13.1+cu117.
During training, the input image resolution is fixed at 640 × 640 pixels. The model is trained for 300 epochs with the following settings: optimizer set to ‘auto’, batch size of 16, initial learning rate of 0.01, momentum of 0.937, and weight decay of 0.0005. A warmup phase is applied for the first 3 epochs, followed by cosine learning rate decay for smoother gradient descent.
4.4. Experiment Results
This study presents a comprehensive experimental comparison of WCC-YOLO against the YOLOv5 to YOLOv11 series models at both nano (n) or tiny scale. Detailed results from a single representative training run for all models are provided in Table 1, following the common practice for broad benchmarking. To ensure statistical robustness and to validate the observed trends, we conducted three independent training runs for the most representative models (YOLOv8n, YOLOv9-t, YOLOv11n, and our WCC-YOLO). The averaged results from these runs are presented in Table 2 and form the basis of our conclusive performance claims. The low standard deviations observed (e.g., <0.01 for mAP) confirm that the performance improvements are consistent and robust across different random initializations.

Table 1.
Comparison of different models (representative results from a single training run).

Table 2.
Statistical performance comparison of key models over 3 independent training runs.
The improved WCC-YOLO model demonstrates remarkable advantages by achieving significantly higher detection accuracy while maintaining a compact model size. Based on the statistically robust results in Table 2, WCC-YOLO shows improvements of 5.7% in mAP@0.5 (from the baseline YOLOv11n’s 0.827 to our 0.874) and 4.5% in mAP@0.5:0.95 (from 0.534 to 0.558).
WCC-YOLO also demonstrates significant detection accuracy advantages compared to other models. Trends from the single-run comparison (Table 1) indicate substantial performance improvements over other mainstream models, with gains of approximately 8.3%, 3.9%, 3.7%, 2.4%, and 7.3% in mAP@0.5:0.95 over YOLOv5, v7, v8 [8], v9 [39], and v10 [40], respectively. For the mAP@0.5 metric, the corresponding improvements are 4.3%, 1.7%, 4.3%, 5.4%, and 6.7% against the same baseline models. Additionally, WCC-YOLO achieved the highest precision and recall rates among all models. It is noteworthy that for YOLOv8n and YOLOv9-t, these encouraging trends are confirmed by the rigorous statistical comparison in Table 2. Additionally, WCC-YOLO achieved the highest precision and recall rates among all models.
Comparative experiments reveal the following key findings. (1) Although YOLOv5 possesses the fewest parameters, it exhibits the lowest inference speed. (2) YOLOv7 incurs the highest parameter count and computational cost (GFLOPs) yet delivers inferior accuracy. (3) YOLOv10 attains the fastest inference speed at the expense of marked accuracy degradation. (4) Relative to WCC-YOLO, YOLOv9 yields no advantages in accuracy, parameter efficiency, or inference latency. (5) YOLOv8 surpasses WCC-YOLO solely in inference speed while demonstrating significantly lower accuracy.
The evaluation of the proposed model must be contextualized within its target domain of real-time soccer analytics. For these applications, detection accuracy (mAP) is the primary metric, as it directly determines system reliability by minimizing missed detections and false alarms of critical targets (e.g., players or the ball) in complex scenarios. While computational cost and latency are important, they are secondary considerations provided that real-time performance is satisfactorily achieved. The latency of our model (2.3 ms) is well within the typical requirement for processing 30 FPS video streams (~33 ms per frame). Therefore, the observed improvement in accuracy is of paramount importance, and the associated computational overhead represents a justifiable trade-off for this specific domain where accuracy is prioritized.
Collectively, these results indicate that the proposed WCC-YOLO model achieves a significant improvement in accuracy for soccer analytics applications, with a commensurate increase in computational cost that is acceptable given the application’s prioritization of accuracy and the fact that the latency remains well within real-time requirements.
4.5. Visualization and Detailed Performance Analysis
4.5.1. Visualization of Detection Results
To qualitatively evaluate the performance of WCC-YOLO, we present detection results on two challenging scenarios from the test set, as shown in Figure 6.

Figure 6.
Detection results on a soccer scene. (a) Daytime scene with predictions (class labels and confidence scores). (b) Daytime scene with bounding boxes only (to show detection completeness). (c) Night scene with predictions (class labels and confidence scores). (d) Night scene with bounding boxes only (to show detection completeness).
Figure 6a,b depict a dense daytime scene with multiple occlusions. Figure 6a shows the predictions with class labels and confidence scores. It demonstrates the model’s accurate classification, though some distant players are detected with moderate confidence scores (e.g., 0.5–0.6), indicating the inherent challenge of the scenario. Figure 6b presents the same result with bounding boxes only to clearly illustrate the completeness of detection without visual clutter, confirming that no objects are missed despite the congestion.
Figure 6c,d demonstrate the model’s performance in a night match setting with artificial lighting, which presents difficulties such as low contrast and shadows. Figure 6c provides a qualitative overview of the predictions in these conditions. The observed confidence scores are generally moderate, frequently falling below 0.7, which is consistent with the performance in the daytime scene and reflects the added challenge of poor lighting. Figure 6d unambiguously shows that all players are successfully detected, underscoring the model’s primary strength of robust detection completeness. The ability to detect all objects across these varying conditions, even with varying confidence, highlights the effectiveness of our approach. The consistency in confidence scores between day and night scenes suggests that distance and occlusion may be stronger factors affecting prediction confidence than lighting conditions alone.
4.5.2. Per-Class Performance Breakdown
A per-class breakdown of the Average Precision (AP), as detailed in Table 3, provides crucial insights into the specific strengths of our model that are not apparent from the overall mAP alone. This analysis focuses on the most representative baseline models (YOLOv8n, YOLOv9-t, YOLOv11n) and our proposed WCC-YOLO for a clear and concise comparison.

Table 3.
Per-class Average Precision (AP) on the Soccer Detection test set.
The analysis reveals the specific contribution of each class to the overall performance gain reported in Section 4.4:
- (1)
- Dramatic Improvement on the Critical “Sports Ball” Class: The most significant advancement is observed on the sports ball class—the smallest and most challenging object. Our method elevates the AP@0.5 to 0.701, which constitutes a substantial increase of 19.2% over the strongest baseline (YOLOv8n, 0.588) and a 31% gain over the baseline YOLOv11n (0.535). This leap in performance quantitatively confirms that our proposed innovations—specifically the P2 detection head and enhanced feature representation—are highly effective for small object detection, directly addressing a core challenge in soccer analytics.
- (2)
- Sustained High Performance on Larger Objects: For the larger goal and person classes, all models (including baselines) already perform at a very high level (AP@0.5 > 0.95), nearing the performance ceiling for these categories. Our method successfully maintains this superior performance, with AP scores on par with the best baselines. This indicates that the architectural complexities introduced for small object detection do not compromise the model’s capability on larger, less challenging objects.
In conclusion, the per-class analysis precisely attributes the overall performance gains reported earlier to a dramatic improvement in small object (ball) detection, while assuring maintained performance on other classes. This underscores the targeted effectiveness of our approach.
4.6. Ablation Study
To validate the effectiveness and rationality of the proposed modules, this section conducts ablation experiments to analyze the contribution of each component to model performance and explores the optimal placement of key modules.
4.6.1. Impact of the Improved Module on Model Performance
This section systematically evaluates the impact of the proposed enhancement modules (P2 branch, C3k2-WTConv module, and CPCA mechanism) through ablation experiments. As shown in Table 4, the experimental results demonstrate the following conclusions:

Table 4.
Impact of Improved Module on Model Performance (n scale).
- (1)
- Effectiveness of the P2 Branch.
After integrating the P2 detection branch into the original YOLOv11 model, the detection accuracy improves significantly. Specifically, it achieves 5.5% higher mAP@0.5 and 3.0% gain in mAP@0.5:0.95, with only marginal increases in parameter count and inference time.
- (2)
- Effectiveness of the C3k2-WTConv Module.
By introducing WTConv in the C3K2 module, the model achieves reduced parameter count and computational cost while improving accuracy, with mAP@0.5 and mAP@0.5:0.95 increasing by 2.7% and 1.7%, respectively.
- (3)
- Combined Effectiveness of P2 Branch and C3k2-WTConv.
When integrating both the P2 branch and C3k2-WTConv, the model combines their advantages. YOLOv11n-P2-WTConv achieves more significant accuracy improvements with 5.7% higher mAP@0.5 and 4.1% higher mAP@0.5:0.95. Notably, it maintains fewer parameters than the original YOLOv11n, with only a marginal increase in GFLOPs and a negligible 0.1ms increase in inference time.
- (4)
- Further Improvement with CPCA and InnerShape-IoU.
Finally, integrating both the CPCA mechanism and Inner-Shape IoU loss function further improves detection accuracy. The CPCA module enables the model to achieve the highest mAP@0.5, while the Inner-Shape IoU contributes to the best mAP@0.5:0.95 performance. Remarkably, these improvements are accomplished with nearly no additional parameters or increased inference time.
4.6.2. Impact of C3K2-WTConv Module Placement on Model Performance
To determine the optimal configuration, we conducted ablation studies on the placement of our core innovation module, C3K2-WTConv. The experimental results are presented in Table 5. The term “all” indicates replacing all C3k2 modules in both backbone and neck networks with C3k2-WTConv. “Backbone” refers to replacing only the C3k2 modules in the backbone network, while “Backbone (P4 + P5)” specifically denotes replacement at layers 6 and 8 (P4 and P5 layers) of the backbone network, as illustrated in Figure 1. The experimental results demonstrate that the “all” configuration achieves the best performance, and is consequently selected as our final network architecture.

Table 5.
Impact of C3K2-WTConv Module Placement on Model Performance.
4.6.3. Impact of CPCA Mechanism Placement on Model Performance
To select the optimal configuration, we conducted ablation studies on the placement of CPCA mechanism. The experimental results in Table 6 demonstrate that when applying the CPCA module before the P2 detection head in the Neck network, the model achieves optimal performance across all three metrics: mAP@0.5, mAP@0.5:0.95, and Recall, while maintaining the smallest parameter count. This configuration naturally emerges as our final choice due to its comprehensive advantages.

Table 6.
Impact of CPCA Module Placement on Model Performance.
4.6.4. Impact of Different Attention Mechanism on Model Performance
To evaluate the impact of different attention mechanisms on model performance, we conducted comprehensive comparisons among a series of state-of-the-art attention modules, including Efficient Multi-Scale Attention (EMA), Context Anchor Attention (CAA), and six other advanced mechanisms (as detailed in Table 7). The experimental results demonstrate that the CPCA mechanism achieves optimal performance across all four key metrics: Precision, Recall, mAP@0.5, and mAP@0.5:0.95. Additionally, the Context Anchor Attention (CAA) module also delivers competitive performance.

Table 7.
Impact of Different Attention Mechanisms on Model Performance.
5. Conclusions
In this paper, we propose WCC-YOLO, an enhanced object detection model tailored for soccer scenes, based on YOLOv11. A core innovation of our work is the explicit incorporation of symmetry principles into the network design. This is realized through three main contributions: First, the novel C3k2-WTConv module, inspired by wavelet transform theory, exploits the orthogonal symmetry of quadrature mirror filters to achieve balanced multi-scale feature representation while reducing model complexity. Second, the Channel Prior Convolutional Attention (CPCA) mechanism utilizes symmetric operations (e.g., average-max pooling pairs) for optimized feature recalibration, enabling the model to focus on semantically salient regions without sacrificing inference speed. Third, by introducing a P2 detection head, the model complements these feature-level symmetries with an architectural symmetry in the detection pyramid, significantly improving small object detection performance to address the challenge of recognizing distant players and the ball. Further improvements in localization accuracy were achieved through the integration of InnerShape-IoU loss, which refines bounding box regression.
Extensive experiments on the Soccer Detection dataset demonstrate that WCC-YOLO outperforms existing YOLO variants (v5 to v11) in soccer scenarios, achieving a 4.5% improvement in mAP@0.5:0.95 (from 0.534 to 0.558) and a 5.7% gain in mAP@0.5 (from 0.827 to 0.874) compared to the baseline YOLOv11n, while maintaining near-identical inference latency (δ < 0.1ms) and reducing parameter count. These results validate the efficacy of symmetry-aware design in developing robust models capable of handling complex match conditions, including occlusions and lighting variations.
Despite the promising results, this work has several limitations. The most significant limitation is the generalization ability of the model across different soccer datasets. To assess this, we evaluated our model on the Football dataset [48]. We observed a severe performance degradation for all models, including the baselines (e.g., mAP dropping from ~60% to approximately zero). This observation confirms a profound domain shift, likely caused by fundamental differences in the following: (1) Visual characteristics: (e.g., image resolution, lighting conditions, camera angles). (2) Annotation protocols: (e.g., the definition of a ‘player’ bounding box may vary significantly between datasets). This phenomenon underscores a common but critical challenge in sports AI—models trained on one benchmark often fail to generalize to others due to a lack of standardization [49]. Therefore, the performance claims in this study are most accurately interpreted within the context of the Soccer Detection dataset.
In future work, we will prioritize the following directions to address these limitations and extend the current research:
- (1)
- Enhancing Generalization: A primary focus will be on exploring domain adaptation and generalization techniques to mitigate the performance drop across datasets, which is the key challenge identified above.
- (2)
- Extending to Multi-Object Tracking: The robust detection capabilities of our model provide a strong foundation for extension to multi-object tracking (MOT) in dynamic sports scenarios, enabling holistic video analysis.
- (3)
- Enabling Edge Deployment: We will explore lightweight optimizations and model compression techniques to facilitate the real-time deployment of our system on edge devices, such as embedded systems at sporting venues.
Author Contributions
Conceptualization, Y.W. and G.Y.; methodology, Y.W. and G.Y.; software, L.G. and X.G. and C.W.; validation, L.G. and X.G.; formal analysis, Y.W.; investigation, L.G. and Y.W.; resources, Y.W. and X.G.; data curation, L.G. and X.G.; writing—original draft preparation, Y.W. and G.Y.; writing—review and editing, Y.W. and G.Y.; visualization, Y.W. and C.W.; supervision, G.Y.; project administration, G.Y.; funding acquisition, Y.W. and G.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Open Fund Project of the Sports Culture Research Base (Huanggang Normal University) under the General Administration of Sport of China (grant no.202530304).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yoon, H.S.; Bae, Y.J.; Yang, Y.K. A Soccer Image Sequence Mosaicking and Analysis Method Using Line and Advertisement Board Detection. ETRI J. 2002, 24, 443–454. [Google Scholar] [CrossRef]
- Vandenbroucke, N.; Macaire, L.; Postaire, J.-G. Color Image Segmentation by Pixel Classification in an Adapted Hybrid Color Space. Application to Soccer Image Analysis. Comput. Vis. Image Underst. 2003, 90, 190–216. [Google Scholar] [CrossRef]
- Gerke, S.; Singh, S.; Linnemann, A.; Ndjiki-Nya, P. Unsupervised Color Classifier Training for Soccer Player Detection. In Proceedings of the 2013 Visual Communications and Image Processing (VCIP), Kuching, Malaysia, 17–20 November 2013. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar] [CrossRef]
- Ultralytics YOLO Repository. Available online: https://github.com/ultralytics/yolov5/releases (accessed on 8 October 2024).
- Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. YOLOv7: Trainable Bag-of-Freebies Sets New State-of-the-Art for Real-Time Object Detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 7464–7475. [Google Scholar]
- Ultralytics YOLO Repository. Available online: https://github.com/ultralytics/ultralytics (accessed on 10 March 2025).
- Finder, S.E.; Amoyal, R.; Treister, E.; Freifeld, O. Wavelet Convolutions for Large Receptive Fields. In Computer Vision—ECCV 2024; Leonardis, A., Ricci, E., Roth, S., Russakovsky, O., Sattler, T., Varol, G., Eds.; Springer Nature: Cham, Switzerland, 2025; pp. 363–380. [Google Scholar] [CrossRef]
- Huang, H.; Chen, Z.; Zou, Y.; Lu, M.; Chen, C.; Song, Y.; Zhang, H.; Yan, F. Channel Prior Convolutional Attention for Medical Image Segmentation. Comput. Biol. Med. 2024, 178, 108784. [Google Scholar] [CrossRef]
- Kim, H.; Nam, S.; Kim, J. Player Segmentation Evaluation for Trajectory Estimation in Soccer Games. In Proceedings of the Image and Vision Computing, Palmerston North, New Zealand, 26–28 November 2003; pp. 159–162. [Google Scholar]
- Nunez, J.R.; Facon, J.; de Souza Brito, A. Soccer Video Segmentation: Referee and Player Detection. In Proceedings of the 15th International Conference on Systems, Signals and Image Processing, Bratislava, Slovakia, 25–28 June 2008. [Google Scholar]
- Mačkowiak, S. Segmentation of Football Video Broadcast. Int. J. Electron. Telecommun. 2013, 59, 75–84. [Google Scholar] [CrossRef][Green Version]
- Baysal, S.; Duygulu, P. Sentioscope: A Soccer Player Tracking System Using Model Field Particles. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 1350–1362. [Google Scholar] [CrossRef]
- Manafifard, M.; Ebadi, H.; Moghaddam, H. A Survey on Player Tracking in Soccer Videos. Comput. Vis. Image Underst. 2017, 159, 19–46. [Google Scholar] [CrossRef]
- Hsu, H.K.; Hung, W.C.; Tseng, H.Y.; Yao, C.J.; Tsai, Y.H.; Maneesh, S.; Yang, M.H. Progressive Domain Adaptation for Object Detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 749–757. [Google Scholar]
- Inoue, N.; Furuta, R.; Yamasaki, T.; Aizawa, K. Cross-Domain Weakly-Supervised Object Detection Through Progressive Domain Adaptation. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5001–5009. [Google Scholar] [CrossRef]
- Hurault, S.; Ballester, C.; Haro, G. Self-supervised Small Soccer Player Detection and Tracking. In Proceedings of the 3rd International Workshop on Multimedia Content Analysis in Sports, Seattle, WA, USA, 16 October 2020; pp. 9–18. [Google Scholar]
- Komorowski, J.; Kurzejamski, G.; Sarwas, G. FootAndBall: Integrated Player and Ball Detector. arXiv 2019, arXiv:191205445. [Google Scholar]
- Lu, K.; Chen, J.; Little, J.J.; He, H. Lightweight Convolutional Neural Networks for Player Detection and Classification. Comput. Vis. Image Underst. 2018, 172, 77–87. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar] [CrossRef]
- Sorano, D.; Carrara, F.; Cintia, P.; Falchi, F.; Pappalardo, L. Automatic Pass Annotation from Soccer Video Streams Based on Object Detection and LSTM. In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Valletta, Malta, 27–29 February 2020; pp. 475–490. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end Object Detection with Transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Qi, M.; Zheng, K.D. Soccer Video Object Detection Based on Deep Learning with Attention Mechanism. Intell. Comput. Appl. 2022, 12, 143–145+154. [Google Scholar]
- He, Y.Y. Improved YOLOX-S-based Video Target Detection Method for Football Matches. J. Sci. Teach. Coll. Univ. 2024, 44, 30–35. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Duan, Y.; Liu, F.; Jiao, L.; Zhao, P.; Zhang, L. SAR Image Segmentation Based on Convolutional-Wavelet Neural Network and Markov Random Field. Pattern Recognit. 2017, 64, 255–267. [Google Scholar] [CrossRef]
- Williams, T.; Li, R. Wavelet Pooling for Convolutional Neural Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Finder, S.E.; Zohav, Y.; Ashkenazi, M.; Treister, E. Wavelet Feature Maps Compression for Image-to-image CNNs. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2022. [Google Scholar]
- Liu, P.; Zhang, H.; Zhang, K.; Lin, L.; Zuo, W. Multi-level Wavelet-CNN for Image Restoration. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 773–782. [Google Scholar]
- Alaba, S.; Ball, J. WCNN3D: Wavelet Convolutional Neural Network-based 3d Object Detection for Autonomous Driving. Sensors 2022, 18, 7010. [Google Scholar] [CrossRef]
- Guth, F.; Coste, S.; De Bortoli, V.; Mallat, S. Wavelet Score-based Generative Modeling. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2022. [Google Scholar]
- Phung, H.; Dao, Q.; Tran, A. Wavelet Diffusion Models are Fast and Scalable Image Generators. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 10199–10208. [Google Scholar]
- Mallat, S.; Peyré, G. A Wavelet Tour of Signal Processing: The Sparse Way; Elsevier Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Publishing House of Electronics Industry: Beijing, China, 2010. [Google Scholar]
- Zhang, H.; Zhang, S. Shape-IoU: More Accurate Metric Considering Bounding Box Shape and Scale. arXiv 2023, arXiv:2312.17663v2. [Google Scholar]
- Zhang, H.; Xu, C.; Zhang, S. Inner-IoU: More Effective Intersection over Union Loss with Auxiliary Bounding Box. arXiv 2023, arXiv:2311.02877v4. [Google Scholar]
- Soccer-Detection Dataset Repository. Available online: https://github.com/Qunmasj-Vision-Studio/Soccer-Detectiin118 (accessed on 10 March 2025).
- Wang, C.Y.; Yeh, I.H.; Mark Liao, H.Y. YOLOv9: Learning What You Want to Learn Using Programmable Gradient Information. In Computer Vision—ECCV 2024; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2025; Volume 15089, pp. 1–21. [Google Scholar] [CrossRef]
- Wang, A.; Chen, H.; Liu, L.; Chen, K.; Lin, Z.; Han, J.; Ding, G. YOLOv10: Real-Time End-to-End Object Detection. arXiv 2024, arXiv:2405.14458v1. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Computer Vision—ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–19. [Google Scholar]
- Xu, W.; Wan, Y. ELA: Efficient Local Attention for Deep Convolutional Neural Networks. arXiv 2024, arXiv:2403.01123v1. [Google Scholar] [CrossRef]
- Cai, X.; Lai, Q.; Wang, Y.; Wang, W.; Sun, Z.; Yao, Y. Poly Kernel Inception Network for Remote Sensing Detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition 2024, Seattle, WA, USA, 17–21 June 2024; pp. 27706–27716. [Google Scholar] [CrossRef]
- Ouyang, D.; He, S.; Zhang, G.; Luo, M. Efficient Multi-Scale Attention Module with Cross-Spatial Learning. arXiv 2023, arXiv:2305.13563, 2023. [Google Scholar]
- Lau, K.W.; Po, L.M.; Rehman, Y.A.U. Large Separable Kernel Attention: Rethinking the Large Kernel Attention Design in CNN. Expert Syst. Appl. 2024, 236, 121352. [Google Scholar] [CrossRef]
- Wan, D.; Lu, R.; Shen, S.; Xu, T.; Lang, X.; Ren, Z. Mixed Local Channel Attention for Object Detection. Eng. Appl. Artif. Intell. 2023, 123, 106442. [Google Scholar] [CrossRef]
- Baidu Inc. Football Dataset; Baidu AI Studio: Beijing, China, 2023; Available online: https://aistudio.baidu.com/datasetdetail/254098 (accessed on 8 September 2025).
- Torralba, A.; Efros, A.A. Unbiased Look at Dataset Bias. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 1521–1528. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).