Robust Filtered-x LMS Algorithm Based on Adjustable Softsign Framework for Active Impulsive Noise Control

Abstract

For active control of impulsive noise, the conventional filtered-x least mean square (FxLMS) algorithm has poor noise reduction performance. To address this issue, this paper designs a robust cost function by embedding the cost function of the FxLMS algorithm into the framework of the adjustable Softsign function, thereby designing a robust Softsign-FxLMS (SFxLMS) algorithm for ANC systems. Furthermore, the parameter λ of the SFxLMS algorithm significantly influences its robustness and convergence speed. Therefore, a variable λ-parameter SFxLMS (VSFxLMS) algorithm is designed to improve the performance of the ANC system. Simulation studies indicate that the proposed SFxLMS algorithm and VSFxLMS algorithm exhibit stronger robustness, faster convergence rates, and better tracking performance compared to several robust FxLMS algorithms. Moreover, the symmetric properties of the proposed Softsign function contribute to balanced error suppression in both positive and negative directions, enhancing the robustness and stability of the ANC system under asymmetric impulsive noise conditions.

1. Introduction

Recent years have seen a sharp rise in noise pollution in both our daily lives and workplaces due to the rapid economic growth and widespread use of mechanized equipment. A key technique for controlling low-frequency noise is active noise control (ANC). As seen in Figure 1, it accomplishes noise cancellation [1] by producing anti-noise via the ANC controller. There are usually three types of ANC methods: feedforward ANC systems, which are commonly used for broadband noise cancellation, feedback ANC systems, which are commonly used for narrowband noise interference, and hybrid ANC systems, which are affected by both broadband noise and uncorrelated narrowband interference [2,3].

Due to their excellent performance and ease of implementation, the filtered-x least mean square (FxLMS) algorithm and the filtered-x normalized least mean square (FxNLMS) algorithm have been widely used in ANC systems of various structures [4]. In order to improve the noise reduction performance of ANC controllers, some improved FxLMS algorithms have been designed. For example, the error reused FxLMS (ErFxLMS) algorithm [5] was proposed by introducing information on past errors. To suppress cyclostationary input noise, a combination of filtered-x normalized least mean square (FxNLMS) algorithm and FxLMS algorithms was proposed in [6]. For multi-noise environments, hybrid ANC systems have superior processing capabilities [7]. In [8], a variable step-size FxLMS (VSS-FxLMS) algorithm was proposed in hybrid ANC systems. Moreover, a new hybrid ANC system was designed in [9] based on online secondary-path modelling (OSPM) with input power control.

However, both the conventional FxLMS algorithm and its enhanced version exhibit poor convergence in impulsive noise control. To address this limitation, researchers have developed several robust ANC algorithms [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. In [12], the filtered-x logarithmic error least mean square (FxlogLMS) algorithm was developed, utilizing the squared logarithm of the absolute value of the error signal as the cost function. A robust filtered-x least mean square (RFxLMS) algorithm [13] has been developed for the active control of impulsive noise in nonlinear systems by using the logarithmic form of the error square as the cost function. The variable tap-length method [16] is commonly used to model unknown devices or paths to obtain the optimal number of filter coefficients. In [17], a variable tap-length filtered-x least mean M-estimation (FxLMM) algorithm based on sub-band adaptive filtering technology has been designed. In [19], a modified FxLMS (MFxLMS) algorithm was designed by employing the technique of data reuse, which provides better robustness and faster convergence compared to the normalized step-size FxLMS (NSS-FxLMS) algorithm [20]. Owing to the superior robustness of maximum correntropy criterion (MCC) in handling impulsive noise [21], a robust filtered-x MCC (FxMCC) algorithm [22] was presented for nonlinear ANC systems. For ANC systems with impulsive noise interference, two robust filtered-x recursive least square (RFxRLS) algorithms were proposed in [23]. In [24], the filtered-x least cosine hyperbolic (FxLCH) algorithm was proposed by minimizing the logarithmic hyperbolic cosine cost function. By minimizing the square of the arctangent of the error signal, an enhanced filtered-x arctangent LMS (FxatanLMS) algorithm has been designed in [25]. A modified filtered-x affine-projection-like MCC (MFxAPLMCC) algorithm based on the correntropy framework with data reuse was proposed [26]. It has better noise reduction performance compared to the FxGMCC algorithm [27]. Based on generalized versoria function, the filtered-x maximum versoria criterion (FxMVC) algorithm [28] has been developed. In addition, the convex combination method is used to further improve the convergence performance of the algorithm. A robust filtered-x tanh LMS (FxtanhLMS) algorithm [31] has been presented which minimizes the squared hyperbolic tangent of the error signal. A robust Swish filtered-x sign algorithm (Swish-FxSA) has been proposed for diffusion ANC systems based on the Swish function framework [32]. While traditional optimization methods such as particle swarm optimization (PSO) [33] have been employed in ANC system [34], they often lack adaptability to non-stationary and impulsive noise environments. In contrast, the proposed SFxLMS algorithm offers a model-free, gradient-based adaptive framework that inherently handles impulsive noise without requiring offline optimization. This article defines a robust cost function by embedding the cost function of the FxLMS algorithm into the Softsign framework, and proposes a Softsign-FxLMS (SFxLMS) algorithm to eliminate the interference of impulsive noise in feedforward ANC systems. The concept of symmetry plays a crucial role in the design of robust adaptive filters, particularly in handling impulsive noise, which often exhibits asymmetric characteristics. By leveraging the symmetric and saturation properties of the Softsign function, the proposed algorithm ensures balanced adaptation dynamics, which is essential for maintaining stability and convergence in non-Gaussian noise environments. In addition, in order to further improve the convergence performance of the algorithm, an SFxLMS algorithm with variable λ-parameter is proposed. Simulation results show that the proposed SFxLMS algorithm exhibits rapid convergence, low steady-state misalignment, and excellent tracking performance.

The rest of the paper has the following structure: In Section 2, we introduce the feedforward ANC system model. In Section 3, we design a robust Softsign cost function framework and propose SFxLMS and VSFxLMS algorithms. Section 4 explores the convergence range of the SFxLMS algorithm, comparing its computational complexity with that of other ANC algorithms. Section 5 evaluates the performance of the proposed SFxLMS and VSFxLMS algorithms, while Section 6 provides a conclusion.

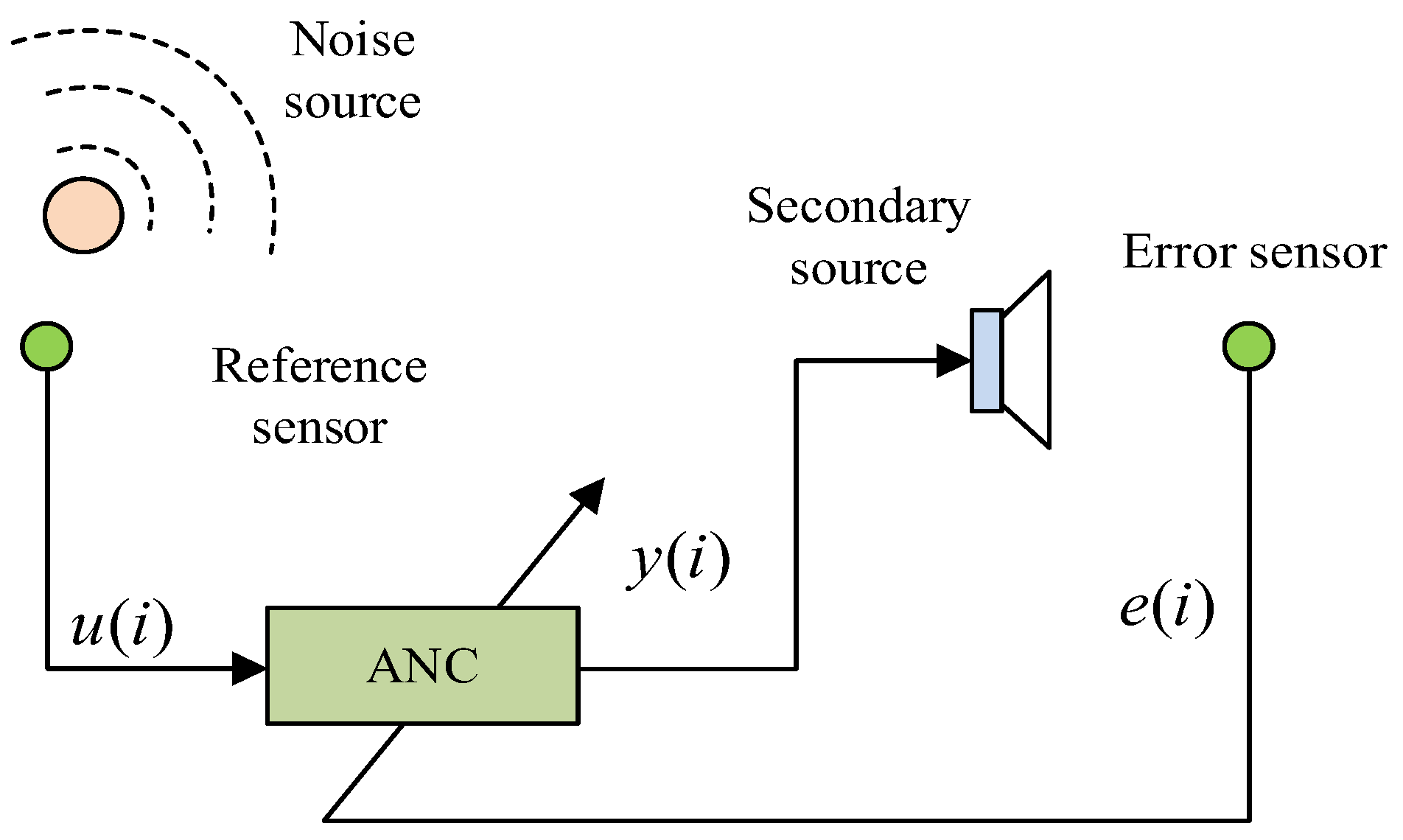
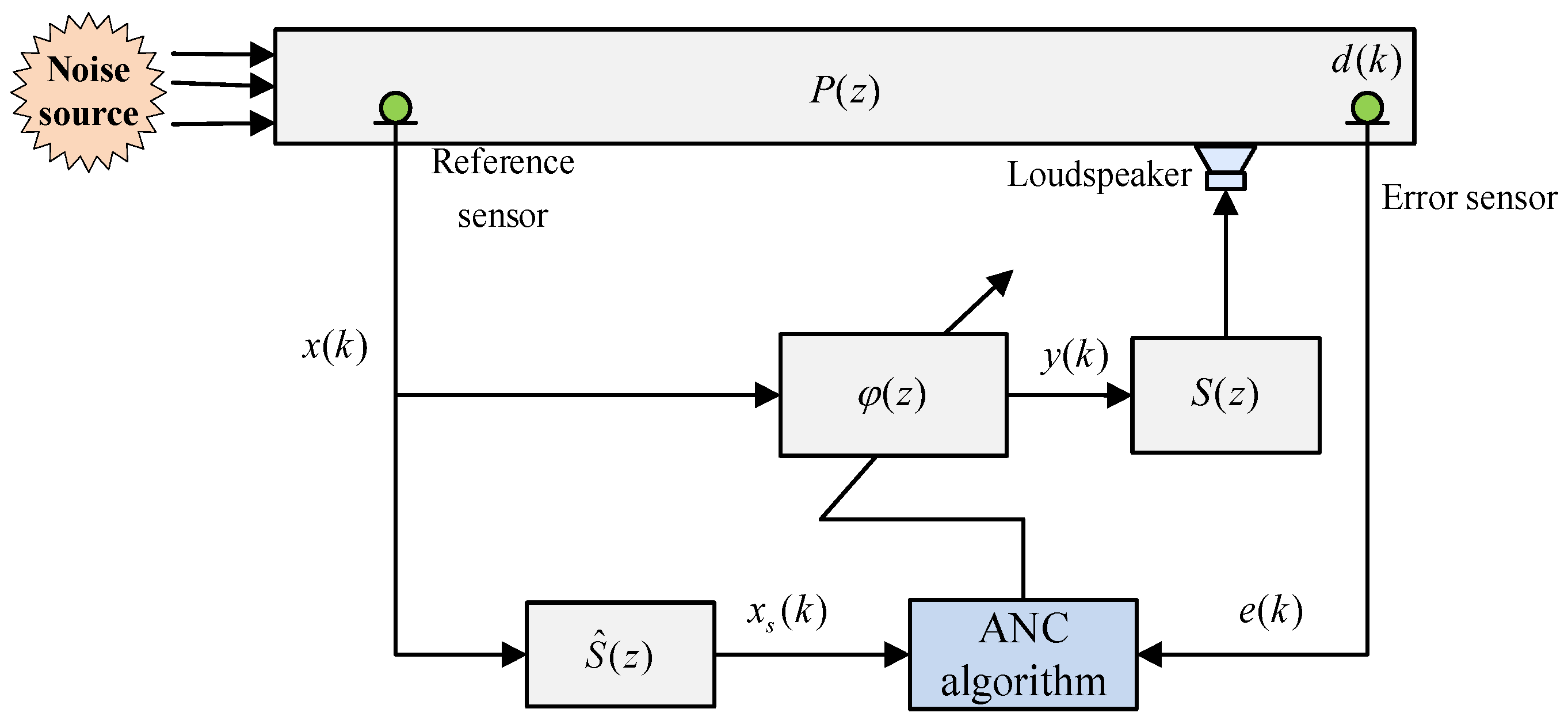
2. Feedforward ANC System Model

Figure 2 shows the block diagram depicting the feedforward ANC system. The reference input $x(k)$ is measured by sensors located near the noise source, $P(z)$ and $S(z)$ are the primary and secondary channels, respectively, while $d(k)$ denotes the noise cancelled by the ANC controller. $\widehat{S}(z)$ is the estimated value of $S(z)$ [35].

The output signal $y(k)$ from the ANC controller is

$$y(k)={\phi }^{\mathrm{T}}(k)x(k)$$

(1)

where $\phi (k)$ is the weight vector of the filter, and $x(k)$ is the reference input vector.

Therefore, the error signal $e(k)$ of the ANC system is expressed as

$$e(k)=d(k)-y(k)\ast s(k)$$

(2)

where $\ast$ denotes the discrete convolution operator.

3. Proposed Algorithms

3.1. Robust Cost Function Framework

By utilizing the saturation property of the Softsign function, this paper introduces a new cost function framework called the Softsign framework, in which the standard cost function $J(k)$ is embedded in the Softsign framework as

$$\xi (k)\triangleq \mathbb{E}\left[{\displaystyle \frac{1}{\lambda }}\hslash \left[\lambda J(k)\right]\right]\approx {\displaystyle \frac{1}{\lambda }}\hslash \left[\lambda J(k)\right]$$

(3)

where $\lambda >0$, $\hslash [•]$ is the improved Softsign function, and its mathematical expression is

$$\hslash (x)={\displaystyle \frac{x}{(1+{\left|x\right|}^{\beta }{)}^{1/\beta }}},\hspace{1em}\beta >0$$

(4)

Taking the gradient of the cost function in (3), we get

$${\mathrm{\nabla }}_{\phi }\xi (k)={\displaystyle \frac{\partial \xi (k)}{\partial \phi (k)}}\hspace{1em}={\displaystyle \frac{{\mathrm{\nabla }}_{\phi }J(k)}{{\left(1+\lambda {\left|J(k)\right|}^{\beta }\right)}^{(1+\beta )/\beta }}}$$

(5)

Hence, the weight update of the proposed robust Softsign ANC algorithm can be written as

$$\begin{array}{ll}\phi (k+1)& =\phi (k)-\eta {\mathrm{\nabla }}_{\phi }\xi (k)\\ & =\phi (k)-\eta {\displaystyle \frac{{\mathrm{\nabla }}_{\phi }J(k)}{{\left(1+\lambda {\left|J(k)\right|}^{\beta }\right)}^{(1+\beta )/\beta }}}\end{array}$$

(6)

3.2. The Proposed Softsign-FxLMS (SFxLMS) Algorithm

The conventional cost function of the FxLMS algorithm is defined as

$$J_{\mathrm{LMS}}(k)=\mathbb{E}\left[e^2(k)\right]\approx e^2(k)$$

(7)

Its weight vector update formula is therefore as follows:

$$\begin{array}{ll}\phi (k+1)& =\phi (k)-{\displaystyle \frac{\eta }{2}}{\displaystyle \frac{\partial J_{\mathrm{LMS}}(k)}{\partial \phi (k)}}\\ & =\phi (k)+\eta e(k)x_s(k)\end{array}$$

(8)

where $\eta$ denotes the step-size, $x_s(k)=x(k)\ast \widehat{s}(k)$.

If there is impulsive noise in the reference input, it will result in a very large error, and the stability of the FxLMS algorithm will be reduced. By incorporating the cost function of the FxLMS algorithm into the improved Softsign framework and using (6), we can obtain the update formula for the Softsign-FxLMS (SFxLMS) algorithm

$$\phi (k+1)=\phi (k)+\eta f\left[e(k)\right]x_s(k)$$

(9)

where $f\left[e(k)\right]=e(k)/{[1+\lambda {\left|e^2(k)\right|}^{\beta }]}^{(1+\beta )/\beta }$ represents nonlinear error function. As depicted in Figure 3, when the error $e(k)$ is significantly large, $f\left[e(k)\right]$ draws near 0, the SFxLMS algorithm stops its update process, this characteristic enables the effective suppression of interference induced by impulsive noise. On the other hand, when the error $e(k)$ is extremely small, $f\left[e(k)\right]$ gets close to $e(k)$, which converts the SFxLMS algorithm into the traditional FxLMS algorithm.

3.3. The Proposed Variable λ-Parameter SFxLMS (VSFxLMS) Algorithm

In the impulsive noise environment, the value of λ not only affects the robustness of the SFxLMS algorithm, but also its convergence speed. Therefore, based on the gradient method, this paper proposes the SFxLMS algorithm with variable λ-parameter, which is updated as follows

$$g(k)=\chi g(k-1)+(1-\chi ){\displaystyle \frac{e(k)x_s(k)}{{\left(1+\lambda {\left|e^2(k)\right|}^{\beta }\right)}^{(1+\beta )/\beta }}}$$

(10)

$$\lambda (k)=\gamma \exp \left(-{\displaystyle \frac{1}{\delta ‖g(k)‖}}\right)$$

(11)

where $g(k)$ is the smoothed gradient vector, and $\chi$ is set to be close to 1, $\gamma$ and $\delta$ are positive parameters.

In addition, the setting of parameter $\gamma$ greatly affects the value of $\lambda (k)$. When the impulsive noise intensity increases sharply, we expect $\lambda (k)$ to increase rapidly, thereby improving the robustness of the algorithm.

$$\gamma (k)=\exp \left(-{\displaystyle \frac{1}{\sigma ‖x_s(k)‖}}\right)$$

(12)

where $\sigma$ is the positive parameter.

To avoid anomalies in λ-parameter during updates, we can usually add constraints

$$\lambda (k)=\left\{\begin{array}{l}{\lambda }_{\max },\hspace{1em}\mathrm{if} \lambda (i)>{\lambda }_{\max }\\ {\lambda }_{\min },\hspace{1em}\mathrm{if} \lambda (i)<{\lambda }_{\min }\\ \lambda (k), \hspace{1em}\mathrm{otherwise}\end{array}\right.$$

(13)

where $0<{\lambda }_{\min }<{\lambda }_{\max }$, and the proposed VSFxLMS algorithm is detailed in Algorithm 1.

Algorithm 1 Proposed VSFxLMS Algorithm

Initializations:    $\phi (0)=g(0)=0$

Parameters:      $\delta$, $\chi$, $\beta$, $\sigma$, $\eta$, $0<{\lambda }_{\min }<{\lambda }_{\max }$

Adaptive process:       for k = 0, 1, 2, …         $d(k)=x(k)\ast p(k)$         $x(k)={\left[x(k),x(k-1),\dots ,x(k-K+1)\right]}^{\mathrm{T}}$         $y(k)={\phi }^{\mathrm{T}}(k)x(k)$         $e(k)=d(k)-y(k)\ast s(k)$         $x_s(k)=x(k)\ast \widehat{s}(k)$         $g(k)=\chi g(k-1)+(1-\chi ){\displaystyle \frac{e(k)x_s(k)}{{\left(1+\lambda {\left|e^2(k)\right|}^{\beta }\right)}^{(1+\beta )/\beta }}}$         $\lambda (k)=\gamma \exp \left(-{\displaystyle \frac{1}{\delta ‖g(k)‖}}\right)$         $\gamma (k)=\exp \left(-{\displaystyle \frac{1}{\sigma ‖x_s(k)‖}}\right)$         $\lambda (k)=\left\{\begin{array}{l}{\lambda }_{\max },\hspace{1em}\mathrm{if} \lambda (k)>{\lambda }_{\max }\\ {\lambda }_{\min },\hspace{1em}\mathrm{if} \lambda (k)<{\lambda }_{\min }\\ \lambda (k),\hspace{1em} \mathrm{otherwise}\end{array}\right.$         $\phi (k+1)=\phi (k)+\eta {\displaystyle \frac{e(k)x_s(k)}{{\left(1+\lambda (k){\left|e^2(k)\right|}^{\beta }\right)}^{(1+\beta )/\beta }}}$       end

4. Performance Analysis

4.1. Stability Analysis

This section analyzes the convergence range of the SFxLMS algorithm. Based on (9), the equation of the SFxLMS algorithm can be rewritten as

$$\phi (k+1)=\phi (k)+\eta f\left[e(k)\right]x_s(k)$$

(14)

where $f\left[e(k)\right]=e(k)/{[1+\lambda {\left|e^2(k)\right|}^{\beta }]}^{(1+\beta )/\beta }$. Let ${\phi }^{\ast }$ be the optimal weight vector of the ANC controller. The weight error vector is expressed as follows

$$\epsilon (k)={\phi }^{\ast }-\phi (k)$$

(15)

Applying the weighted error vector to Equation (14) yields the following:

$$\epsilon (k+1)=\epsilon (k)-\eta f\left[e(k)\right]x_s(k)$$

(16)

Taking the square of the l₂-norm for Equation (16), then calculate the expectation to obtain

$$\varpi (k+1)=\varpi (k)+{\eta }^2\mathbb{E}\left\{f^2\left[e(k)\right]{‖x_s(k)‖}^2\right\}-2\eta \mathbb{E}\left\{f\left[e(k)\right]{\epsilon }^{\mathrm{T}}(k)x_s(k)\right\}$$

(17)

where $\varpi (k)=\mathbb{E}\left[{‖\epsilon (k)‖}^2\right]$.

Since the SFxLMS algorithm always satisfies $\varpi (k+1)-\varpi (k)<0$ during convergence, the step-size range is obtained as

$$0<\eta <{\displaystyle \frac{2\mathbb{E}\left\{f\left[e(k)\right]e(k)\right\}}{\mathbb{E}\left\{f^2\left[e(k)\right]{‖x_s(k)‖}^2\right\}}}$$

(18)

where ${\epsilon }^{\mathrm{T}}(k)x_s(k)=e(k)$.

4.2. Computational Complexity

Active noise control (ANC) techniques necessitate efficient noise attenuation and convergence, while also being straightforward, effective, and easily implementable. Consequently, assessing the computational complexity of the devised ANC algorithm is essential.

Table 1. Computational Complexity.

Algorithms	Multiplications/Divisions	Additions/Subtractions
FxLMS	$2K+2L+1$	$2K+2L-2$
FxlogLMS	$2K+2L+3$	$2K+2L-2$
RFxLMS	$2K+2L+5$	$2K+2L-1$
Swish-FxSA	$2K+2L+8$	$2K+2L+1$
FxtanhLMS	$2K+2L+9$	$2K+2L+4$
SFxLMS	$2K+2L+5$	$2K+2L-1$

K is the length of the ANC controller; L represents the length of the secondary channel.

indicates that the computational complexity of the proposed SFxLMS approach is analogous to that of prior ANC algorithms.

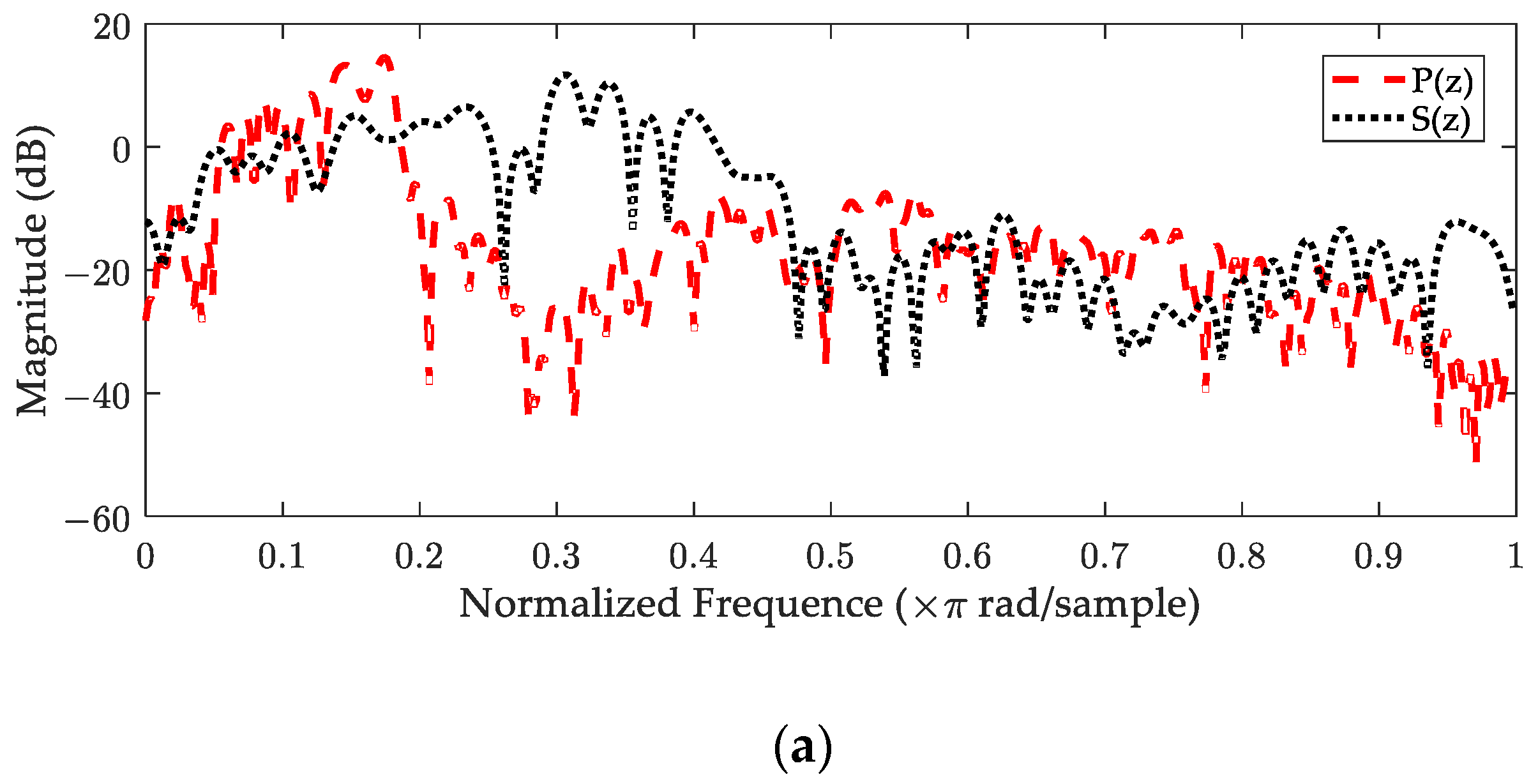
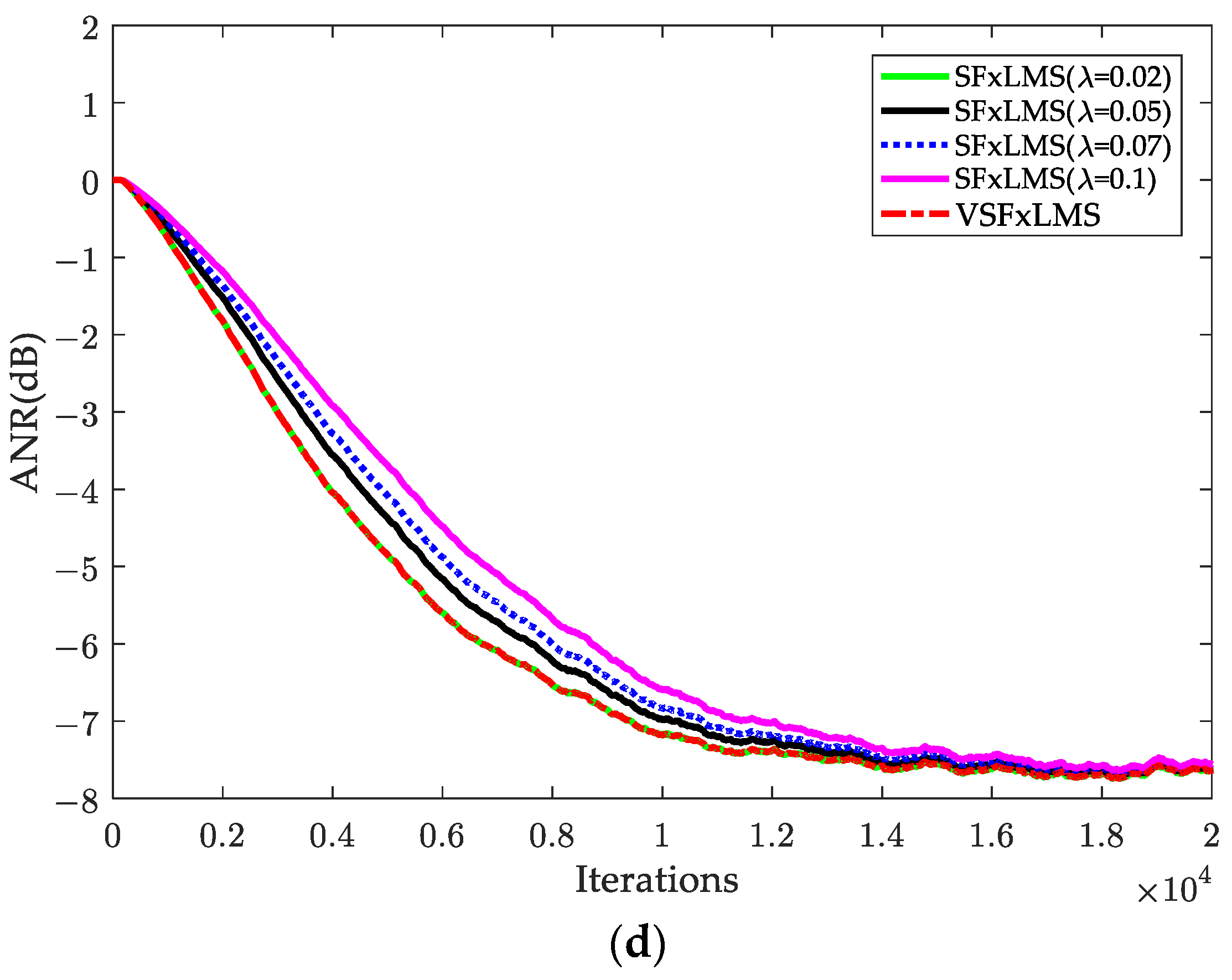
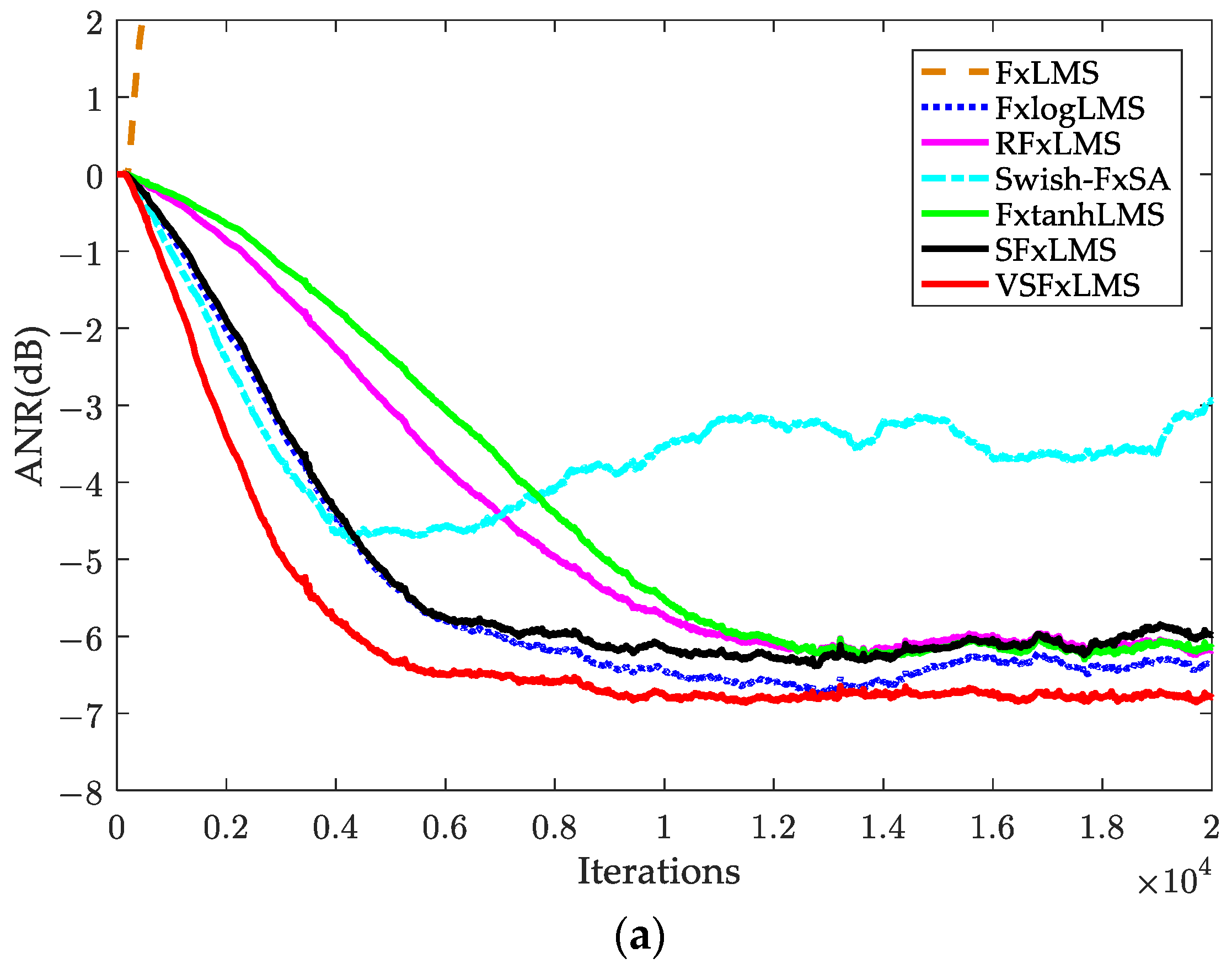
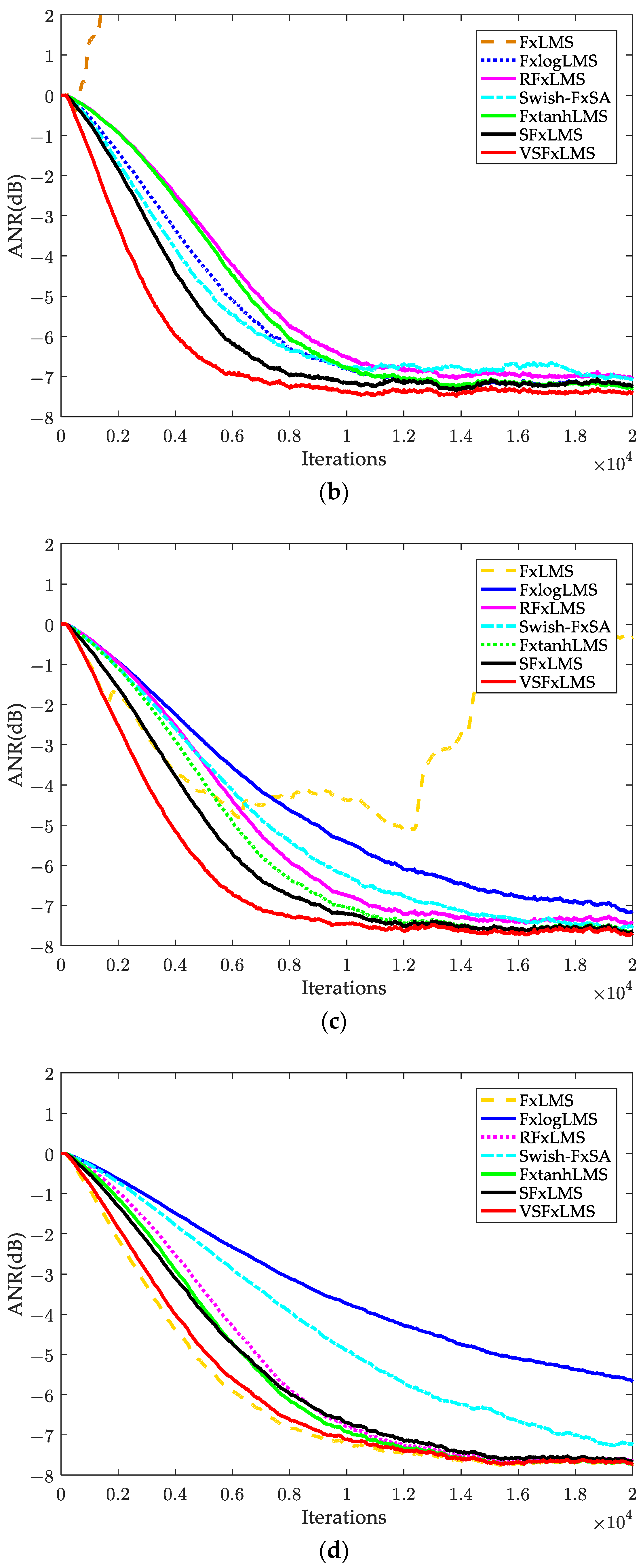
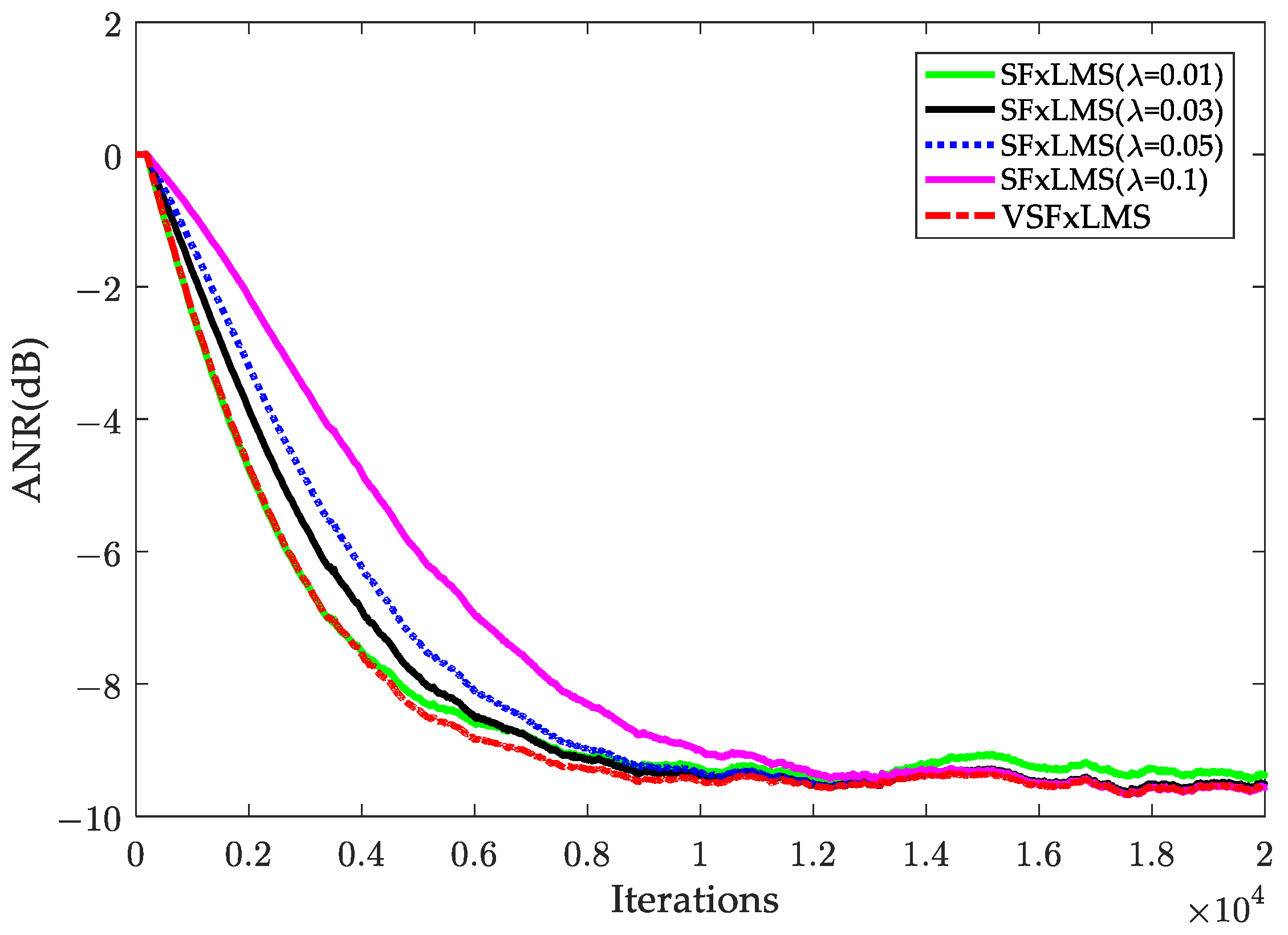
5. Computer Simulations

In the following simulation, $K=128$, $P(z)$ and $S(z)$ are modelled by FIR filters of lengths $M=256$ and $L=100$, respectively, and their amplitude and phase responses are illustrated in Figure 4. This research uses average noise reduction (ANR) to assess the efficacy of several ANC algorithms for noise cancellation.

$$\mathrm{ANR}=20{\log }_{10}\left({\displaystyle \frac{{\mathrm{H}}_e(k)}{{\mathrm{H}}_d(k)}}\right)$$

(19)

where ${\mathrm{H}}_e(k)=\xi {\mathrm{H}}_e(k-1)+\left(1-\xi \right)\left|e(k)\right|$, ${\mathrm{H}}_d(k)=\xi {\mathrm{H}}_d(k-1)+\left(1-\xi \right)\left|d(k)\right|$, and ${\mathrm{H}}_e(0)=0$, ${\mathrm{H}}_d(0)=0$, $\xi =0.999$.

Figure 4 depicts the frequency response of the primary path P(z) and secondary path S(z) used in the simulations. The variations in amplitude and phase across frequencies simulate real-world acoustic paths, which are crucial for evaluating the robustness and convergence behaviour of the proposed ANC algorithms in a realistic scenario.

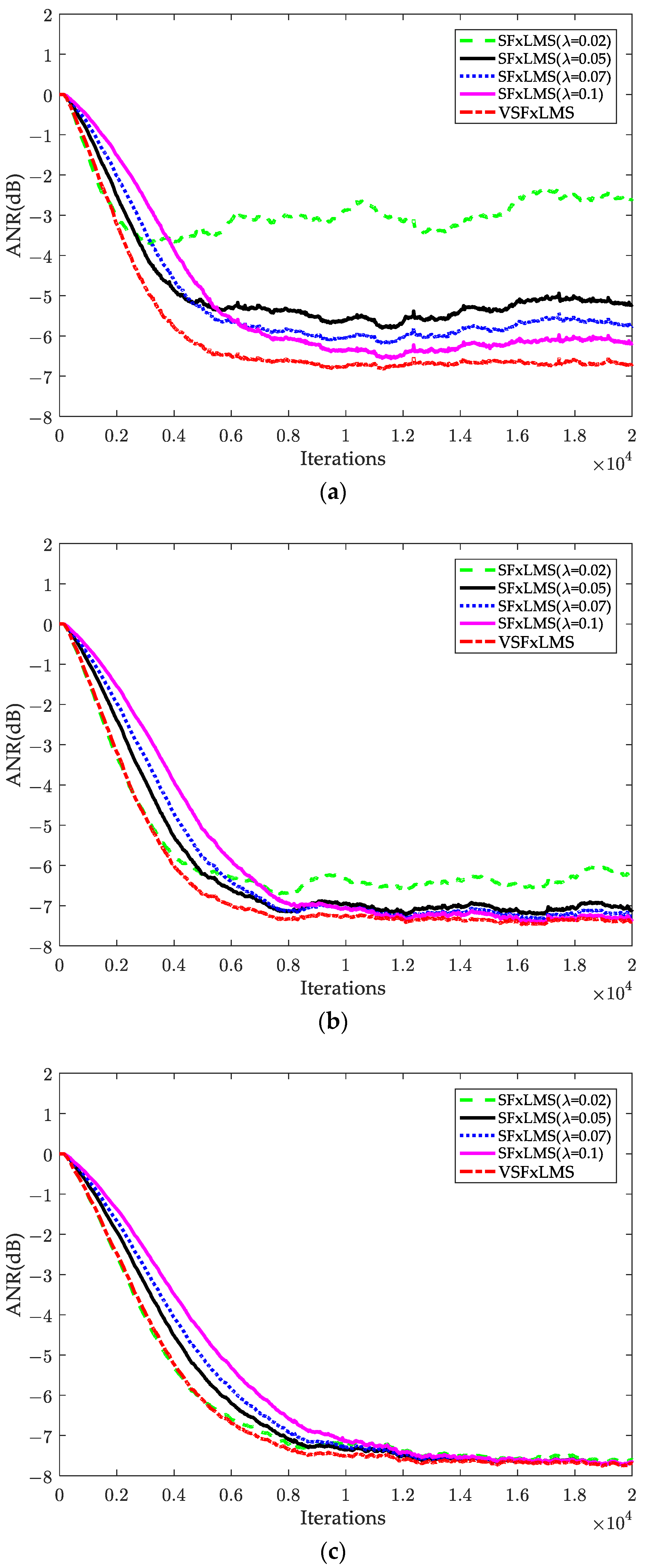
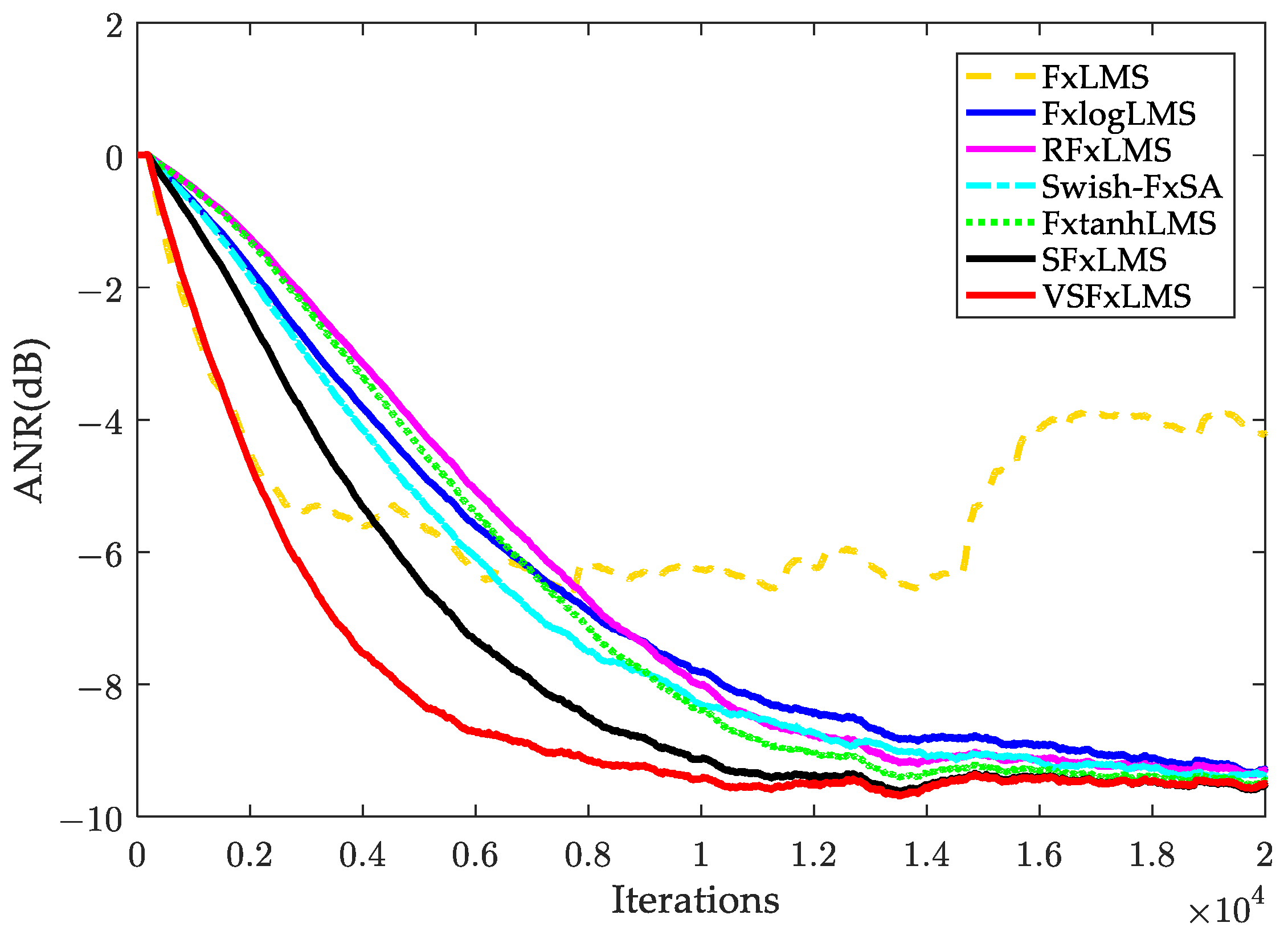
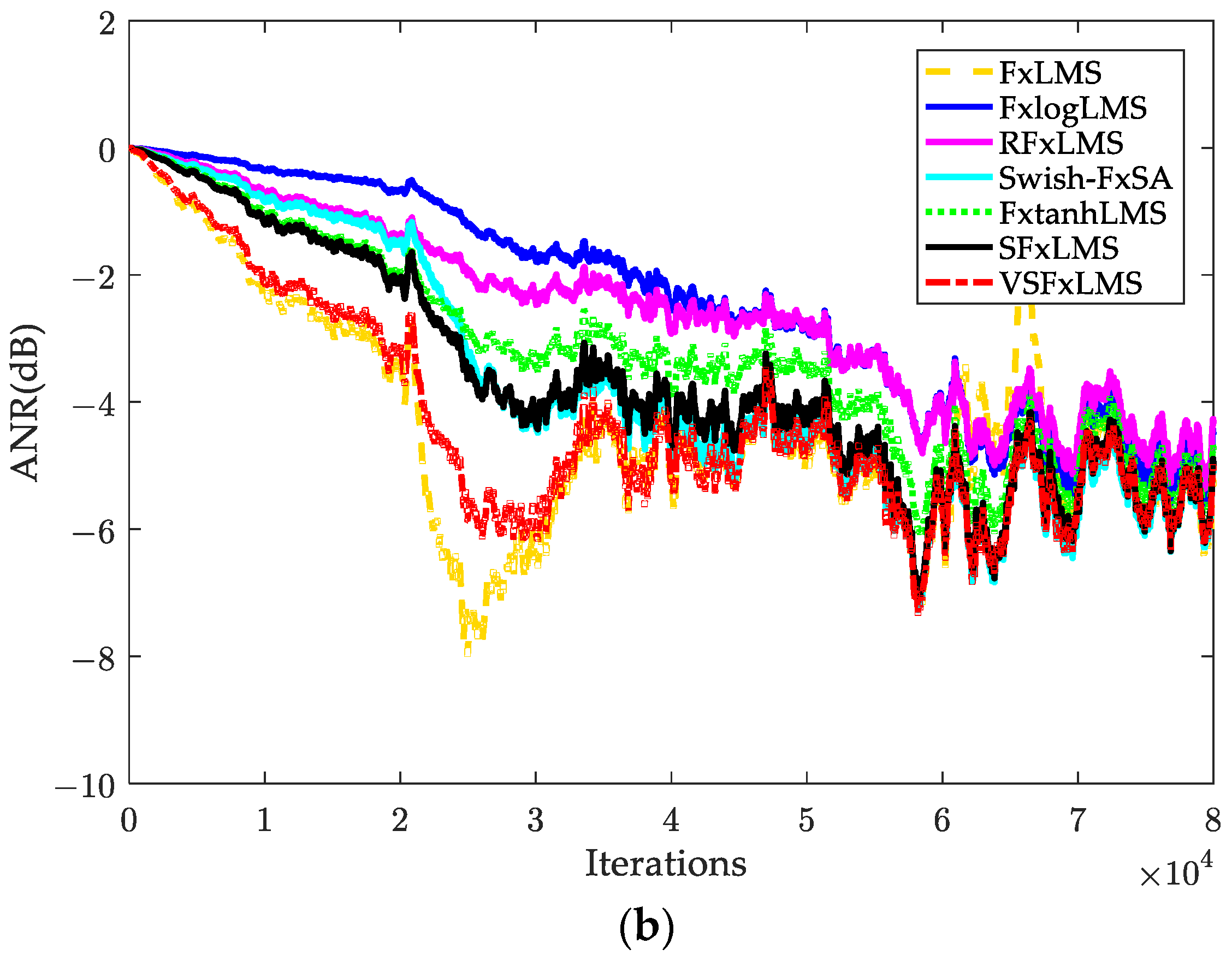
5.1. Impulsive Noise

The impulsive noise in the simulation experiments is exposed to standard symmetric α-stable (SαS) distribution noise [36], with a characteristic function that is described as

$$\vartheta (t)=\exp \left(-{\left|t\right|}^{\alpha }\right)$$

(20)

As shown in Figure 5, this is the probability density function of Equation (20). The characteristic exponent α in the SαS distribution governs the impulsiveness of the noise. A smaller value of α indicates a heavier tail and more frequent large-amplitude pulses, while α = 2.0 corresponds to Gaussian noise. By testing with increasing values of α, we can evaluate the performance transition of the algorithm from a highly impulsive environment to a Gaussian environment.

In the subsequent simulations, we test the suggested ANC algorithms’ effectiveness in reducing noise by employing impulsive noise that adheres to the standard SαS distribution with parameters α = 1.4, α = 1.6, α = 1.8, and α = 2.0 (Gaussian noise), respectively. The weight vector update formulas for different ANC algorithms are displayed in

Table 2. Update Formula for Algorithm.

Algorithms	Weight Vector Update
FxLMS	$\phi (k+1)=\phi (k)+\eta e(k)x_s(k)$
FxlogLMS [12]	$\phi (k+1)=\phi (k)+\eta \mathrm{sign}[e(k)]{\displaystyle \frac{\log \left|e(k)\right|}{\left|e(k)\right|}}{x}_s(k)$
RFxLMS [13]	$\phi (k+1)=\phi (k)+\eta \left[{\displaystyle \frac{e(k)}{e^2(k)+2{\sigma }^2}}\right]x_s(k)$
Swish-FxSA [32]	$\phi (k+1)=\phi (k)+\eta \mathrm{sign}[e(k)]{\displaystyle \frac{\left[1+[1-\beta \left|e(k)\right|]\exp [-\beta \left|e(k)\right|]\right]}{{\left[1+\exp [-\beta \left|e(k)\right|]\right]}^2}}{x}_s(k)$
FxtanhLMS [31]	$\phi (k+1)=\phi (k)+\eta \tanh \left(\lambda e(k)\right)\left[1-{\tanh }^2\left(\lambda e^2(k)\right)\right]x_s(k)$
SFxLMS	$\phi (k+1)=\phi (k)+\eta {\displaystyle \frac{e(k)x_s(k)}{{\left[1+\lambda {\left|e^2(k)\right|}^{\beta }\right]}^{(1+\beta )/\beta }}}$

, and the following simulation parameters are used for these algorithms: FxLMS algorithm with $\eta =0.0001$, RFxLMS algorithm with $\eta =0.0001$ and $\sigma =0.05$, FxlogLMS algorithm with $\eta =0.0002$, Swish-FxSA algorithm with $\eta =0.0001$ and $\beta =0.8$, FxtanhLMS algorithm with $\eta =0.0003$ and $\lambda =0.6$, SFxLMS algorithm with $\eta =0.0001$ and $\lambda =0.08$, and VSFxLMS algorithm with $\eta =0.0001$, $\delta =\sigma =0.01$, $\beta =1$, $\chi =0.9$, ${\lambda }_{\max }=0.5$, and ${\lambda }_{\min }=0.01$. The parameters for each algorithm were tuned via a grid search to ensure fair comparison and optimal performance under each noise scenario.

In order to evaluate the noise reduction effectiveness of the proposed SFxLMS algorithm about parameter λ, as depicted in Figure 6, an increase in λ leads to reduced residuals of the SFxLMS algorithm. Nonetheless, this simultaneously results in a decrease in convergence velocity. Conversely, as λ decreases, the convergence rate of the SFxLMS algorithm increases, albeit its residuals rise. For example, as shown in Figure 6a, for impulsive noise (α = 1.4), the VSFxLMS algorithm achieves a steady-state ANR of approximately −6.8 dB, which is 1.2 dB lower than the SFxLMS (λ = 0.05) algorithm, while maintaining a convergence speed of under 10,000 iterations. Furthermore, when Gaussian noise is introduced (i.e., α = 2.0), the steady-state ANR of SFxLMS algorithm is close to −7.7 dB at different λ values, while VSFXLMS has similar noise reduction but faster convergence speed.

Figure 7a,d illustrate that the noise reduction efficacy of the FxLMS algorithm is significantly influenced by impulse noise, and its convergence performance deteriorates with smaller values of α, potentially resulting in non-convergence. As the value of α incrementally rises, the convergence efficacy of the FxLMS algorithm progressively improves. In Figure 7b, it indicates that the proposed VSFxLMS algorithm achieves a steady-state ANR of −7.4 dB under impulse noise (α = 1.6), which is superior to SFxLMS (−7.2 dB), RFxLMS (−7.0 dB), FxlogLMS (−7.1 dB), FxtanhLMS (−7.2 dB), and Swish-FxSA (−6.8 dB). In terms of convergence speed, the designed VSFxLMS and SFxLMS algorithms are faster than other robust algorithms. Furthermore, under changing intensities of impulsive noise, the VSFxLMS algorithm with time-variable parameters exhibits a superior convergence rate and reduced residual error in comparison to the SFxLMS algorithm.

5.2. Sinusoidal Impulsive Noise

The reference signal $x(k)$ for the ANC system utilizes mixed noise [27] to further validate the noise reduction efficacy of the proposed SFxLMS algorithm. This is demonstrated as follows:

$$x(k)=\sqrt{2}\sin \left({\displaystyle \frac{2\pi \times k\times 500}{8000}}\right)+v(k)$$

(21)

where $v(k)$ represents the impulsive noise according to the conventional SαS distribution, with α fixed at 1.8.

Figure 8 demonstrates the efficacy of the proposed SFxLMS algorithm in noise reduction across various λ values. The noise reduction efficacy of the SFxLMS algorithm correlates with the value of λ. A smaller value of the parameter λ results in a more rapid convergence of the SFxLMS algorithm. The decrease in residuals of the SFxLMS algorithm is correlated with the increase in parameter λ. This work proposes a variable λ-parameter SFxLMS algorithm, termed the VSFxLMS algorithm, which demonstrates accelerated convergence and reduced residual error.

The efficacy of noise reduction for the suggested SFxLMS and VSFxLMS algorithms is demonstrated in Figure 9. The standard FxLMS algorithm has suboptimal convergence performance when subjected to impulsive noise disturbances. The convergence and noise reduction efficacy of the suggested SFxLMS and VSFxLMS algorithms surpass those of the FxLMS, FxlogLMS, RFxLMS, and FxtanhLMS algorithms.

5.3. Real Audio: Traction Substation Noise

In this section, a real noise signal example is used to validate the efficacy of the proposed SFxLMS algorithm. Figure 10a illustrates the waveform of real audio traction substation noise, sampled at a frequency of 8 kHz. Figure 10b illustrates that the suggested SFxLMS algorithm surpasses other robust ANC algorithms regarding noise reduction efficacy and convergence velocity. However, because the substation noise signal’s power increases significantly at 20,000 samples, we observe that although the FxLMS algorithm has a faster rate of convergence, it suffers from a larger steady-state misalignment. The linear update rule of the FxLMS algorithm contributes to its faster initial convergence, but its lack of robustness against impulsive disturbances causes higher steady-state misalignment when the noise power surges suddenly, as observed at about 20,000 samples.

5.4. Verification of Tracking Capability

In this simulation, we assessed the tracking capability of different ANC algorithms, assuming a sudden change in the primary path at iteration 20,000. Figure 11 illustrates that the Swish–FxSA algorithm demonstrates enhanced tracking performance relative to the FxlogLMS, RFxLMS and FxtanhLMS algorithms in the presence of SαS (α = 1.8) impulsive noise. The proposed SFxLMS algorithm also performs well. However, the VSFxLMS algorithm demonstrates superior tracking capability in the event of sudden changes to the primary path.

6. Conclusions

In summary, the proposed SFxLMS and VSFxLMS algorithms demonstrate superior performance in impulsive noise control, partly owing to the symmetric structure of the Softsign-based cost function, which provides balanced error handling and enhanced robustness. This article proposes a robust FxLMS algorithm based on the Softsign function framework. Furthermore, a variable λ-parameter algorithm was designed to enhance the performance of the ANC system. Despite the algorithm performing well in simulation experiments, there are still certain limitations. Although its computational complexity is comparable to other robust algorithms, it may pose challenges in real-time applications with strict latency requirements. In addition, the regulation of hyperparameters such as β, σ, δ, etc., still relies on experience. Future work will focus on using metaheuristic algorithms to achieve automatic parameter optimization, and deploying the proposed methods on embedded hardware for practical scenarios such as traction substations and manufacturing factories.