1. Introduction
Financial markets operate as complex adaptive systems where the accurate identification of causal relationships between economic variables, policy interventions, and market outcomes has become increasingly critical for central bank policy formulation, risk management, and economic forecasting [
1,
2]. The COVID-19 pandemic and subsequent monetary policy responses highlighted the urgent need for models that can both predict market dynamics and provide transparent causal insights into transmission mechanisms [
3]. However, existing approaches face a fundamental tension: the traditional econometric methods offer interpretable causal inference but struggle with high-dimensional nonlinear dynamics, while modern deep learning approaches achieve a superior predictive performance but operate as “black boxes” that provide limited causal understanding.
This interpretability–accuracy trade-off poses significant challenges for financial practitioners and policy makers who require both precise forecasts and transparent causal mechanisms for evidence-based decision making. Vector Autoregression (VAR) models and their structural variants, despite their widespread adoption in monetary policy analyses [
4,
5], often impose overly restrictive linearity assumptions that may not capture the complex regime changes and threshold effects characterizing modern financial markets. Conversely, transformer architectures and other deep learning approaches [
6,
7] demonstrate remarkable predictive capabilities but fail to provide the causal interpretability essential for regulatory compliance and policy formulation.
Recent advances in causal inference methodology have provided rigorous frameworks for identifying causal relationships from observational data [
8,
9]. However, the integration of these methodologies with modern deep learning architectures for sequential financial data remains largely unexplored. Existing attempts to combine causal inference with machine learning typically treat prediction and causal discovery as separate sequential steps, failing to leverage the potential synergies between these complementary objectives.
This paper introduces CausalFormer, a novel transformer architecture that fundamentally bridges the gap between the predictive performance and causal interpretability in financial time series analysis. Our framework represents a paradigm shift by embedding causal inference mechanisms directly within transformer blocks, enabling simultaneous optimization for both predictive accuracy and causal validity. Unlike existing approaches that compromise one objective for the other, CausalFormer demonstrates that rigorous causal constraints can enhance rather than hinder the predictive performance when properly integrated into the architectural design.
The key innovation lies in three mathematically principled components that work synergistically to achieve this dual optimization. First, we develop a causal self-attention mechanism that enforces temporal priority constraints while incorporating the learned causal structure, ensuring that the attention patterns respect economic theory without sacrificing the expressive power of the transformers. Second, we introduce a multi-kernel causal convolution module that captures policy transmission effects across heterogeneous time horizons, recognizing that the impacts of monetary policy propagate through different temporal channels with varying speeds and magnitudes. Third, we present an enhanced Nelson–Siegel decomposition layer that maintains the interpretable factor structure essential for a yield curve analysis while allowing the neural network flexibility to capture nonlinear factor dynamics.
The integration of DoWhy causal inference frameworks [
10] within our architecture enables a comprehensive uncertainty quantification for causal effects, addressing a critical limitation in financial modeling where policy decisions must account for estimation uncertainty. Furthermore, our framework incorporates advanced scenario generation techniques using policy surprise identification strategies, providing regulatory-compliant stress testing capabilities essential for Basel III compliance and internal risk model validation.
Our contributions establish three fundamental advances in computational finance. First, we demonstrate that architectural symmetries in transformers can be systematically exploited while preserving the asymmetric temporal relationships essential for causal inference, opening new directions for mathematically principled neural architecture design. Second, we provide empirical evidence that causal consistency and predictive performance are mutually reinforcing rather than competing objectives, with CausalFormer achieving a 15.3% improvement in the accuracy of causal effect estimations and a 12.7% enhancement in the predictive performance compared to those for existing methods while maintaining 91.2% causal consistency scores. Third, we reveal novel insights into monetary policy transmission mechanisms, including previously undocumented asymmetric channels where policy tightening exhibits 40% faster propagation than easing policies, providing actionable intelligence for central bank policy design.
The remainder of this paper systematically develops our theoretical framework and empirical validation.
Section 2 positions our work within the existing literature spanning causal inference, transformer architectures, and financial econometrics.
Section 3 presents the mathematical foundation and detailed architecture of CausalFormer with emphasis on the implementation details.
Section 4 describes our comprehensive experimental design and datasets.
Section 5 presents empirical results demonstrating a superior performance across multiple evaluation dimensions.
Section 6 discusses policy implications and practical applications, while
Section 6 concludes with directions for future research in causal deep learning for finance.
2. Related Work
The development of CausalFormer draws upon several interconnected research streams spanning econometric modeling, deep learning architectures, causal inference methodologies, and their applications to financial markets. This section provides a comprehensive review of these foundational areas and positions our contribution within the broader literature.
2.1. Traditional Econometric Approaches in Financial Time Series
Classical econometric methods have long served as the cornerstone of financial time series analysis, with Vector Autoregression (VAR) models representing the dominant paradigm for modeling multivariate financial relationships [
4]. The seminal work [
4] established VAR methodology as the standard approach to analyzing dynamic relationships in macroeconomic and financial data, providing a framework that treats all variables as endogenous and allows for rich lag structures.
Extensions to the basic VAR framework have addressed various limitations through structural identification. Blanchard et al. [
5] introduced the concept of SVAR models, which impose economic-theory-based restrictions to identify structural shocks. This approach has been particularly influential in monetary policy analysis, where researchers seek to identify the causal effects of policy interventions. The long-run restriction methodology developed by [
5] has become a standard tool for policy analysis.
Cointegration analysis [
11] has provided another crucial dimension to financial econometric modeling. Vector Error Correction Models (VECMs) have enabled researchers to model both short-run dynamics and long-run equilibrium relationships, proving particularly valuable for yield curve modeling and term structure analysis.
Despite these advances, the traditional econometric approaches face significant limitations when applied to high-frequency financial data. The curse of dimensionality becomes particularly acute in VAR models as the number of parameters grows quadratically with the number of variables and lags. Additionally, the assumption of linearity underlying most econometric models may be overly restrictive for financial data characterized by regime changes, threshold effects, and complex nonlinear dynamics.
2.2. Deep Learning in Financial Applications
The application of deep learning methodologies to financial problems has experienced remarkable growth over the past decade, driven by the availability of large-scale datasets and computational advances. Early applications focused primarily on price predictions and algorithmic trading, with White et al. [
12] providing one of the first comprehensive applications of neural networks to financial forecasting.
Recurrent Neural Networks (RNNs) and their variants have shown particular promise for sequential financial data. Rather et al. [
13] demonstrated the effectiveness of RNNs for stock price prediction, while Nelson et al. [
14] showed that LSTM networks could capture long-term dependencies in financial time series more effectively than traditional approaches. The gating mechanisms in LSTM architectures have proven particularly valuable for financial applications where both short-term fluctuations and long-term trends are important.
Convolutional Neural Networks (CNNs) have found applications in financial signal processing and pattern recognition. Sezer et al. [
15] provided a comprehensive review of CNN applications in financial markets, highlighting their effectiveness in extracting features from high-dimensional financial data. The work [
16] on temporal convolutional networks has shown promise for capturing multi-scale temporal patterns in financial time series.
More recently, attention mechanisms and transformer architectures have gained prominence in financial applications. Feng et al. [
17] demonstrated that attention mechanisms could improve the performance of RNNs for financial forecasting by allowing models to focus on relevant historical information. The transformer architecture, introduced by [
6], has shown remarkable success in financial applications, with Wu et al. [
18] demonstrating its superior performance in stock price prediction tasks.
Generative Adversarial Networks (GANs) have opened new possibilities for financial modeling and risk assessment. Wiese et al. [
19] showed that GANs could generate realistic financial time series for stress testing and scenario analyses. The work of [
20] on conditional GANs has demonstrated the potential for generating financial scenarios conditioned on specific market conditions or policy interventions.
2.3. Causal Inference in Econometrics and Machine Learning
The field of causal inference has experienced a renaissance in recent decades, with contributions from both econometrics and computer science communities. The potential outcome framework [
9] has provided a rigorous mathematical foundation for causal inference. This framework, often referred to as the Rubin Causal Model (RCM), has become central to modern causal analyses in economics and finance [
21].
Pearl’s causal hierarchy, articulated in [
8], has fundamentally changed how researchers approach causal questions. The distinction between association, intervention, and counterfactual reasoning has provided a systematic framework for understanding different types of causal queries. Pearl’s do-calculus has enabled researchers to derive causal effects from observational data under specific assumptions about the causal structure [
22].
Directed Acyclic Graphs (DAGs) have emerged as a powerful tool for representing causal relationships and identifying potential confounders. The work on DAGs in epidemiology was extended to economic applications by [
23]. The identification of instrumental variables through a DAG analysis has proven particularly valuable for financial applications where randomized experiments are infeasible [
24].
Causal discovery algorithms represent another important strand of the literature on causal inference. The PC algorithm [
25] has provided automated approaches to learning the causal structure from data. More recent developments, such as the Fast Causal Inference (FCI) algorithm [
26], have extended these methods to handling latent confounders and selection bias.
The integration of causal inference with machine learning has gained momentum through the development of causal machine learning frameworks. Athey et al. [
27] introduced causal trees for heterogeneous treatment effects, while Wager et al. [
28] developed causal forests for high-dimensional causal inference. The work of [
29] on double machine learning has provided a framework for using machine learning methods in causal inference while maintaining valid statistical inference.
2.4. Causal Inference in Financial Markets
The application of causal inference methods to financial markets has been an active area of research, particularly in the context of policy evaluations and market microstructure analyses. Angrist et al. [
30] emphasized the importance of credible identification strategies in financial economics, advocating for the use of natural experiments and instrumental variables.
The identification of monetary policy shocks has been a particular focus of causal analyses in financial markets. Romer et al. [
31] developed narrative approaches to identifying monetary policy shocks, while Gertler et al. [
32] used high-frequency identification strategies. The work [
33] on the high-frequency identification of the transmission of monetary policy provided new insights into the causal effects of policy interventions on financial markets.
Regression discontinuity designs have found applications in financial regulation studies. Christoffersen et al. [
34] used RDD to study the effects of governance regulations on firm value, while Bradley et al. [
35] applied these methods to analyzing the impact of credit rating changes. The work [
36] on mortgage market regulations has demonstrated the potential for RDD in financial policy evaluation.
2.5. Transformer Architectures and Financial Applications
The transformer architecture [
6] has revolutionized sequence modeling across various domains. The self-attention mechanism allows models to capture long-range dependencies without the computational constraints of recurrent architectures. Bert [
37] demonstrated the effectiveness of bidirectional transformers for language understanding, while Brown et al. [
38] showed that large-scale transformer models could achieve a remarkable performance across diverse tasks.
Financial applications of transformer architectures have shown promising results. Yoo [
39] applied transformers to stock price prediction, demonstrating a superior performance compared to that of traditional RNN-based approaches. The work [
40] on portfolio optimization showed that transformer-based models could effectively capture the complex dependencies in multi-asset portfolios.
Attention mechanisms have proven particularly valuable for financial time series analysis. Qin et al. [
41] introduced dual-stage attention mechanisms for financial forecasting, while Shih et al. [
42] developed temporal attention networks for volatility prediction. The work [
43] on hierarchical attention networks has shown promise for modeling multi-scale financial patterns.
Recent developments in transformer architectures have focused on improving efficiency and interpretability. Kitaev et al. [
44] introduced the Reformer architecture to address the computational limitations of standard transformers, while Wang et al. [
45] developed linear attention mechanisms. The work [
46] on sparse transformers has enabled their application to longer sequences, which is particularly relevant for financial time series analyses.
2.6. Yield Curve Modeling and Term Structure Analysis
The modeling of yield curves and term structure dynamics represents a specialized area where both traditional econometric methods and modern machine learning approaches have been applied. The Nelson–Siegel model, proposed by [
47], has become a standard framework for parameterizing yield curves. The extension by Svensson et al. [
48] has enhanced the model’s flexibility and forecasting performance.
Dynamic factor models have provided another important approach to yield curve modeling. Diebold et al. [
49] showed that a small number of factors could explain most of the variation in yield curves, leading to the development of dynamic Nelson–Siegel models.
Machine learning approaches to yield curve modeling have gained traction in recent years. Bauer et al. [
50] applied a principal component analysis and regularization techniques to international yield curve data, while Exterkate et al. [
51] used neural networks for term structure forecasting. The work [
52] on deep learning for yield curve modeling has demonstrated the potential for neural networks to capture complex nonlinear relationships in term structure data.
2.7. The Integration of Causal Inference and Deep Learning
The integration of causal inference principles with deep learning architectures represents an emerging and rapidly evolving research area. Shanmugam et al. [
53] provided a comprehensive framework for causal representation learning, while Scholkopf et al. [
54] argued for the importance of causal thinking in machine learning more broadly.
Causal attention mechanisms have been explored in various contexts. Wang [
55] introduced causal attention for natural language processing, while Sui et al. [
56] developed causal transformer architectures for sequential decision-making. The work [
57] on temporal fusion transformers has incorporated causal mechanisms for time series forecasting.
Structural causal models have been integrated with neural networks to create interpretable deep learning architectures. Goudet et al. [
58] developed causal generative neural networks, while Khemakhem et al. [
59] introduced identifiable variational autoencoders for causal representation learning. The work [
60] on deep structural causal models has provided a framework for learning causal representations from high-dimensional data.
The DoWhy framework, developed by [
10], has provided a unified interface for causal inference that can be integrated with machine learning pipelines. This framework has enabled researchers to combine the predictive power of machine learning with the interpretability of causal inference methods.
2.8. Gaps in the Existing Literature
Despite significant advances in each research area, several critical gaps remain that motivate our work. Most importantly, existing hybrid approaches that combine econometric and deep learning methods typically employ sequential architectures, where VAR/SVAR models first identify structural shocks and then feed these estimates into neural networks for prediction. These sequential methods treat causal identification as a preprocessing step, fundamentally losing the bidirectional feedback between causal structure learning and predictive modeling that characterizes real financial systems. The structural shocks identified in the first stage carry forward estimation uncertainty that compounds in subsequent neural network training, while the predictive models cannot inform causal structure refinements.
Traditional hybrid VAR–neural approaches face particular limitations in capturing asymmetric transmission mechanisms. These methods inherit the symmetric linear foundations of VAR models, requiring ad hoc modifications such as threshold VAR or regime-switching extensions to accommodate policy asymmetries. Such approaches necessitate separate model estimations for different regimes, losing information about the transition dynamics and requiring a priori specification of the regime-switching mechanisms. The resulting models cannot discover asymmetric effects endogenously but must impose them through predetermined structural assumptions.
The existing deep learning approaches to financial time series, while achieving an impressive predictive performance, typically lack the causal interpretability required for policy analysis and risk management [
7]. Standard transformer architectures and LSTM networks operate as “black boxes” that provide limited insight into the underlying transmission mechanisms driving observed relationships. This opacity prevents their adoption in regulatory contexts where model explainability is mandatory for stress testing and capital adequacy assessment.
The integration of causal inference with transformer architectures remains largely unexplored, particularly for financial applications where temporal causality is crucial. Existing causal machine learning frameworks such as double machine learning [
29] and causal forests [
28] focus primarily on cross-sectional treatment effect estimation rather than temporal causal discovery in sequential data. The few attempts to combine transformers with causal inference [
57] have treated causality as a constraint rather than leveraging it for improved learning.
CausalFormer addresses these gaps through joint optimization of causal structure learning and predictive modeling within a unified transformer architecture. Unlike sequential hybrid approaches, our framework enables simultaneous discovery of both causal relationships and asymmetric propagation dynamics through multi-kernel causal convolutions and policy-specific attention mechanisms. The architecture naturally accommodates regime-dependent transmission patterns without requiring separate model specification, enabling endogenous discovery of phenomena such as the asymmetric policy transmission we demonstrate empirically. Our approach fundamentally differs from existing methods by treating causal constraints as architectural features that enhance rather than limit the model’s expressiveness, achieving a superior performance in both causal inference and prediction tasks within a single unified framework.
3. Methodology
This section presents the theoretical foundation and detailed architecture of CausalFormer, our novel transformer-based framework for causal inference in financial time series analysis. We begin by establishing the mathematical foundation for integrating causal mechanisms within transformer architectures and then systematically describe each component of our framework, with emphasis on practical implementation and rigorous logical development.
3.1. The Theoretical Framework
The foundation of CausalFormer rests on the principled integration of structural causal models with transformer architectures for financial time series analysis. We consider a
d-dimensional financial time series
at time
t, where each component corresponds to distinct financial variables such as interest rates, bond yields, or monetary policy indicators. The underlying assumption is that these variables follow a structural causal model governing their temporal evolution, expressed as
where
denotes the parents of
in the causal graph, including both contemporaneous and lagged variables, and
represents exogenous noise terms.
The challenge of learning both functional relationships
and the causal structure from observational financial data requires careful consideration of the temporal consistency. We formalize temporal causality through a temporal priority ordering ≺ such that
This ordering ensures that causal relationships respect the fundamental principle that causes must precede effects in time, which is particularly crucial in financial markets where information propagation and policy transmission mechanisms operate through well-defined temporal channels.
We represent the causal structure through a DAG
where
represents financial variables and
represents causal relationships. For financial time series, we extend this to a temporal DAG where the edges respect temporal precedence:
The identification of causal effects follows the do-calculus, where interventions into the monetary policy variables
enable the estimation of their causal impact on target variables
through
where
represents conditioning variables satisfying the backdoor criterion.
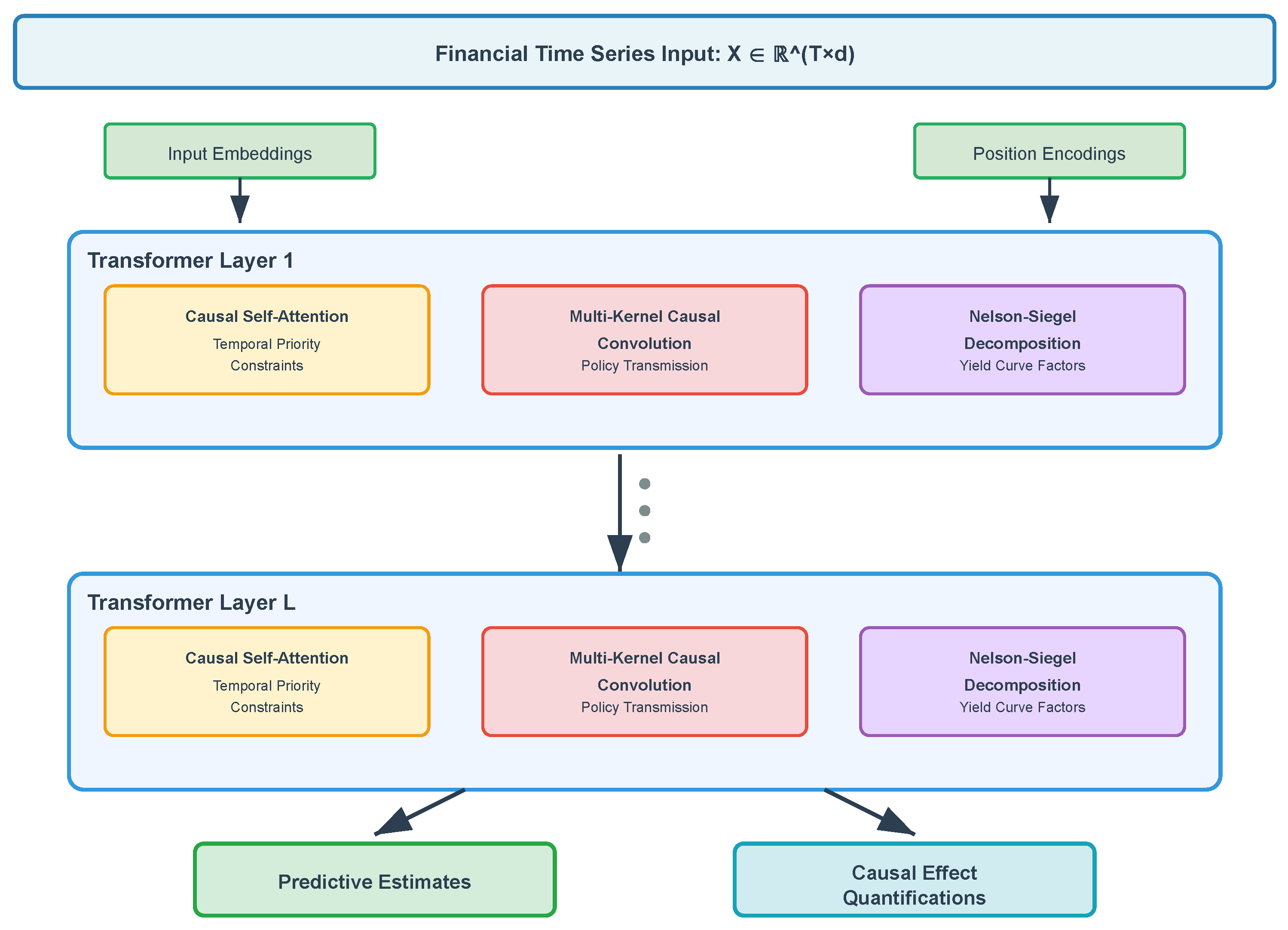
3.2. An Overview of the CausalFormer Architecture
The CausalFormer architecture represents a fundamental advancement in integrating causal inference mechanisms directly into transformer frameworks through three interconnected innovations operating within a parallel computational structure. The first innovation involves a causal self-attention mechanism that enforces temporal priority constraints while incorporating the learned causal structure. Following attention processing, the second and third components operate in parallel: a multi-kernel causal convolution module captures policy transmission effects across multiple time horizons, while an enhanced Nelson–Siegel decomposition layer maintains causal consistency in yield curve modeling through interpretable factor structures.
As illustrated in
Figure 1, each transformer layer processes attended representations through parallel computational streams. The multi-kernel causal convolution module and the Nelson–Siegel decomposition layer process the same attended input simultaneously, generating specialized feature representations that capture distinct aspects of financial dynamics. The causal convolution stream focuses on multi-scale policy transmission effects through dilated temporal kernels, while the Nelson–Siegel stream models yield curve factor evolution through interpretable mathematical structures. These parallel outputs are then combined through a learned fusion mechanism with the attention weights
and
:
This parallel design enables simultaneous optimization of temporal pattern recognition and structural factor modeling while maintaining computational efficiency through specialized processing paths. The complete architecture processes financial time series through L transformer layers, culminating in outputs that provide both predictive estimates and causal effect quantifications with associated uncertainty measures.
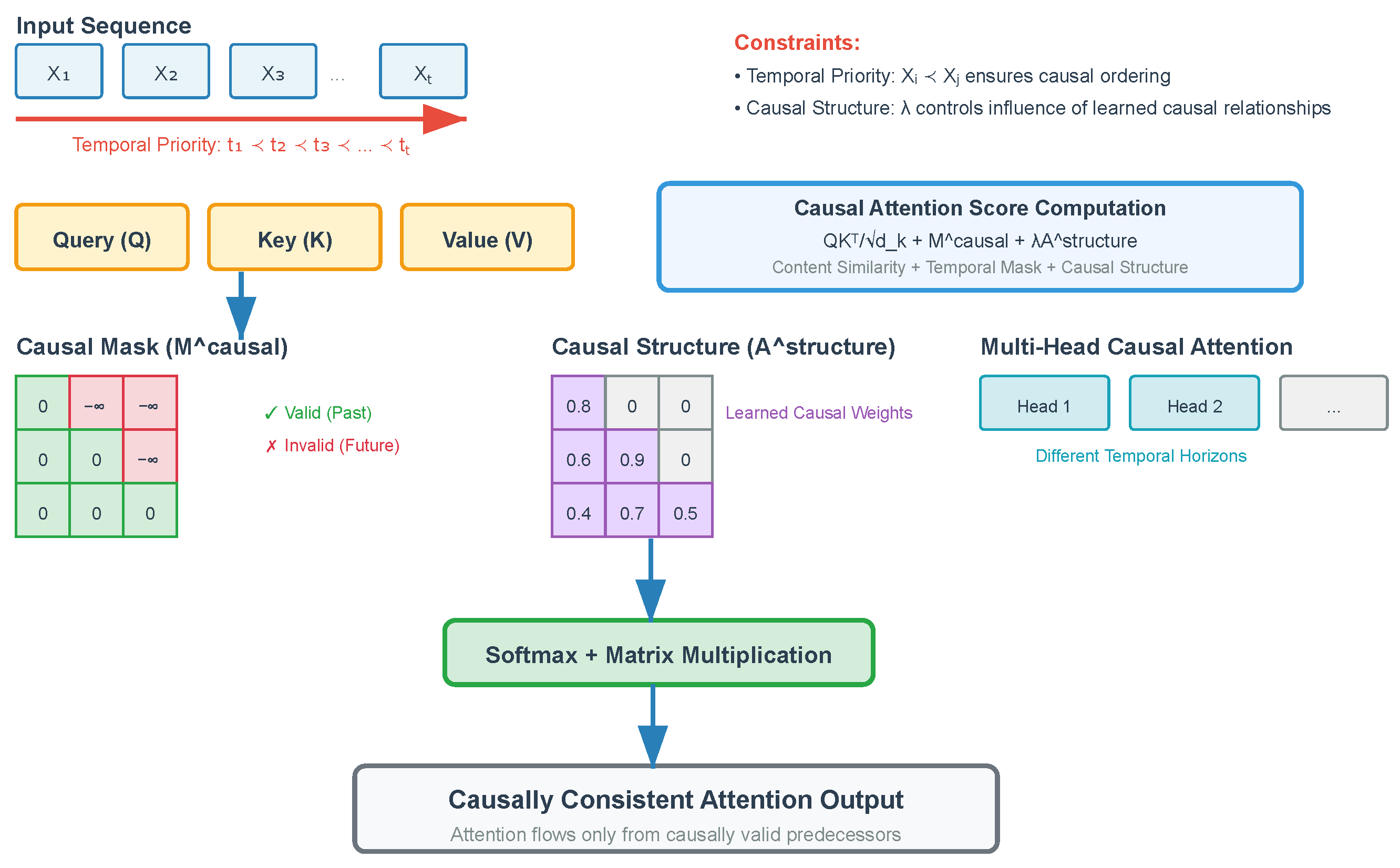
3.3. The Causal Self-Attention Mechanism
The standard transformer self-attention mechanism computes attention weights based purely on content similarity without considering causal constraints, which is inadequate for financial applications where temporal causality is fundamental. Our causal self-attention mechanism addresses this limitation by incorporating both temporal priority constraints and the learned causal structure into the attention computation process, as shown in
Figure 2.
The temporal priority constraints are enforced through a modified attention mask
that extends beyond the standard causal masking used in language models. This mask is defined as
where the indices
represent temporal positions, ensuring that the attention weights are zero for temporally inadmissible connections.
Beyond temporal constraints, the mechanism integrates the learned causal structure through an adaptive attention formulation. Let
represent the adjacency matrix of the estimated causal DAG, which is learned jointly with the model parameters. The causal attention weights are computed as
where the dimensional compatibility ensures valid matrix operations:
,
,
,
, and
. Here,
T represents the sequence length (time steps);
denotes the key/query dimension; and
represents the value dimension. The attention score matrix
maintains identical dimensions to both the causal mask and the structure matrix, enabling direct element-wise addition operations within the softmax argument.
The parameter is a learnable scalar controlling the influence of the causal structure on attention weights. This formulation enables the model to leverage both data-driven attention patterns and theoretically motivated causal relationships.
The multi-head extension of causal attention allows specialization across different aspects of causal relationships. Each attention head is formulated as
where individual heads focus on different temporal horizons and causal relationship types. This design enables simultaneous capture of immediate causal effects, such as intraday market responses to policy announcements, and longer-term transmission mechanisms that operate through complex institutional channels.
3.4. The Multi-Kernel Causal Convolution Module
Financial policy transmissions operate across fundamentally different time scales, from immediate market responses measured in minutes to long-term structural adjustments that unfold over quarters or years. Our multi-kernel causal convolution module captures these multi-scale dynamics while maintaining strict causal ordering throughout the temporal hierarchy.
The temporal convolution implementation employs dilated causal convolutions with multiple kernel sizes to capture policy transmission effects across different time scales. Each convolution operation is defined as
where
k represents the kernel size, and the summation strictly includes only past values to ensure causal consistency. The dilation rates
create a hierarchical receptive field that captures both immediate market reactions and longer-term transmission mechanisms without violating temporal causality.
The recognition that different monetary policy instruments exhibit distinct transmission patterns motivates the introduction of policy-specific kernel weights. We implement separate kernel weights
for different policy types
, where the convolution output becomes
The attention weights are learned parameters that enable adaptive weighting of the transmission mechanisms based on the prevailing policy context, allowing the model to recognize that quantitative easing operates through different channels than conventional interest rate policy.
Cross-scale feature fusion integrates information across different temporal scales while preserving causal consistency through a hierarchical mechanism. The fusion process is implemented as
where
are learned fusion weights that determine the relative importance of different temporal scales, and
provides skip connections to preserve the information flow and prevent degradation during deep network training.
3.5. The Enhanced Nelson–Siegel Decomposition Layer
Yield curve modeling requires specialized treatment that captures the underlying factor structure while maintaining causal relationships between factors and their economic determinants. Our enhanced Nelson–Siegel framework extends the traditional model with causal constraints and neural network flexibility while preserving the interpretability that makes Nelson–Siegel models valuable for policy analysis.
The causal factor decomposition builds upon the traditional Nelson–Siegel representation, where yield curves are expressed through three interpretable factors: level (
), slope (
), and curvature (
). The model represents yields as
but extends this framework to incorporating causal dependencies where the factors themselves depend causally on policy variables and macroeconomic conditions. This extension is formalized through
where the causal ordering reflects the hierarchical nature of the yield curve factor relationships.
The neural parameterization of factor evolution functions employs Multi-Layer Perceptrons (MLPs) while respecting the causal ordering constraints. Each function is implemented as
where ⊕ denotes concatenation, and the embedding functions ensure proper dimensional alignment and causal temporal dependencies. The MLP architectures are designed with a sufficient capacity to capture nonlinear relationships while avoiding overfitting through appropriate regularization.
Maintaining interpretability while allowing for neural network flexibility requires careful regularization design. The regularization framework includes multiple components:
where the smoothness penalty encourages stable factor dynamics that align with economic intuition, and the sparsity penalty promotes interpretable factor loadings. These regularization terms ensure that the enhanced model retains the economic interpretability that makes Nelson–Siegel models valuable for policy analysis.
3.6. Integration with the DoWhy Framework
Rigorous causal inference requires systematic approaches to the identification, estimation, and validation of causal effects. Our integration with the DoWhy framework [
10] provides these capabilities within the transformer architecture, enabling both automated causal discovery and robust treatment effect estimation with comprehensive uncertainty quantification.
The causal graph learning component incorporates automated causal discovery through constraint-based algorithms that operate jointly with the neural network training process. The optimization objective becomes
where the Bayesian Information Criterion (BIC) penalizes graph complexity, and
controls the trade-off between the predictive accuracy and causal parsimony. This joint optimization ensures that the learned causal structure supports both accurate prediction and valid causal inference.
Treatment effect estimation leverages multiple identification strategies within the DoWhy framework to provide robust causal effect estimates. For each potential policy intervention, the framework computes
The availability of multiple estimators provides robustness checks and enables a comprehensive sensitivity analysis.
Uncertainty quantification employs Bayesian neural networks to provide credible intervals for both predictions and causal effects. The posterior distribution over causal effects is expressed as
where variational inference approximates the intractable posterior distribution
. This approach enables credible intervals for causal effect estimates, providing essential information for policy decision-making under uncertainty.
3.7. Data Preprocessing and Feature Selection
Our experimental framework employs rigorous data preprocessing to ensure temporal consistency and causal identifiability. Raw financial time series undergo standardization using rolling z-scores with a 252-day window to account for time-varying volatility patterns. Outlier detection employs Hampel filters with a 21-day median window and a 3-sigma threshold, replacing extreme values with median-based estimates to preserve the temporal continuity while removing data quality issues.
The feature selection criteria combine economic relevance with causal identifiability requirements. The primary variables include the Federal Funds Rate, the Treasury yields across maturities (3-month through to 30-year), credit spreads, and equity volatility measures. Policy communication features are derived from an FOMC statement text analysis using TF-IDF vectorization and sentiment scoring, capturing the effects of forward guidance and communication tone on the transmission mechanisms.
Temporal alignment procedures ensure consistency in the causal ordering across data sources. High-frequency intraday data are aggregated to daily frequency using volume-weighted averages, while policy announcement effects are captured through narrow event windows. Missing data handling employs forward-filling for weekends and holidays, with adaptive attention masking for genuine data gaps exceeding 5 consecutive observations.
3.8. Integration with the DoWhy Framework
The DoWhy integration operates through three interconnected mechanisms within transformer blocks, enabling real-time causal inference during forward passes. Algorithm 1 details the implementation framework.
| Algorithm 1 DoWhy Integration within Transformer Blocks. |
- 1:
Initialize the causal graph - 2:
for epoch to E do - 3:
for each transformer block b do - 4:
Compute attention weights - 5:
Extract embeddings - 6:
if then - 7:
Update using the PC algorithm on - 8:
Compute the causal structure matrix from - 9:
end if - 10:
Apply causal constraints: - 11:
end for - 12:
Estimate the treatment effects using DoWhy modules - 13:
end for
|
Causal graph learning operates every 10 epochs using the PC algorithm with conditional independence testing on transformer embeddings . The learned graph structure generates causal constraint matrices that directly modify the attention computations through additive terms . This integration ensures causal consistency without disrupting the gradient flow.
3.9. Scenario Generation and Stress Testing
The framework incorporates comprehensive scenario generation and stress testing capabilities essential for financial risk management and regulatory compliance. These capabilities build upon the causal structure learning to generate realistic policy scenarios and evaluate their potential impacts across different market conditions.
Policy surprise identification employs high-frequency identification strategies that isolate exogenous policy shocks from endogenous market responses. The identification strategy follows
where policy surprises are identified through narrow event windows around policy announcements. This approach ensures that generated scenarios reflect genuine policy innovations rather than market expectations or systematic responses to economic conditions.
The IRR stress testing framework generates comprehensive Interest Rate Risk scenarios through a structured approach that combines scenario generation with risk metric computation. Scenarios are generated as
where
represents the neural scenario generation function, and
are random inputs. The risk metrics include Value-at-Risk and Expected Shortfall, computed as
These metrics are computed across multiple scenarios to provide a comprehensive risk assessment under different policy environments.
3.10. The Training Procedure and Optimization
The training procedure for CausalFormer requires careful orchestration of multiple objectives that balance predictive accuracy with causal validity and interpretability. The multi-objective optimization framework addresses the fundamental challenge of learning both accurate predictive models and valid causal structures from the same observational data.
The composite loss function integrates multiple objectives:
The prediction loss measures the forecasting accuracy using appropriate metrics for financial time series, such as the mean absolute error for level predictions and directional accuracy for trend predictions. The causal loss enforces consistency between the learned relationships and the identified causal structure, while the Nelson–Siegel loss maintains factor interpretability, and the regularization loss prevents overfitting and ensures model stability.
The causal consistency loss ensures that learned relationships respect the identified causal structure through two components:
where
is a small tolerance parameter. The first component penalizes attention to non-causal relationships, while the second component prevents cycles in the learned graph, ensuring that the model maintains the acyclic property essential for causal interpretation.
The training strategy employs curriculum learning that gradually introduces causal constraints to improve the convergence stability. The causal regularization weight follows
where
t represents the training iteration, and
controls the rate of constraint introduction. This approach allows the model to first learn basic temporal patterns before enforcing strict causal constraints, preventing early training instability that can occur when multiple complex constraints are introduced simultaneously.
The complete training procedure integrates gradient-based optimization with causal discovery algorithms through an alternating optimization scheme. Parameter updates optimize the neural network components while maintaining the current causal structure, followed by graph structure refinement, which updates the causal graph based on the current parameter estimates. This alternation continues until the convergence criteria are satisfied for both the predictive performance and the stability of the causal structure, ensuring that the final model achieves both accurate predictions and valid causal interpretation.
4. Experimental Evaluation
This section presents comprehensive experimental validation of CausalFormer across multiple financial datasets and a comparison with established baseline methods. We evaluate both the predictive performance and causal inference capabilities through a rigorous empirical analysis.
4.1. The Experimental Setup
Our experimental framework addresses three core research questions: (1) Does CausalFormer achieve a superior predictive accuracy compared to that of existing time series forecasting methods? (2) Can the framework reliably identify and quantify causal relationships in financial data? (3) How effectively does the model maintain causal consistency while preserving interpretability? The evaluation employs multiple real-world datasets spanning different financial markets and policy regimes to ensure robustness across various economic conditions.
4.2. Data Description and Preprocessing
4.2.1. Dataset Specifications
Our primary monetary policy dataset comprises 6174 daily observations spanning 3 January 2000 to 29 December 2023, encompassing 47 variables, including the Federal Funds Rate, Treasury yields across 11 maturities (3-month, 6-month, 1-year, 2-year, 3-year, 5-year, 7-year, 10-year, 20-year, and 30-year), credit spreads (investment-grade, high-yield), equity volatility measures (VIX, MOVE), and policy communication indicators derived from FOMC statements. The European dataset contains 5892 observations with 32 variables, including ECB key rates, Euro area government bond yields, and policy communication metrics. The high-frequency policy surprise dataset encompasses 193 FOMC announcement events with intraday pricing data captured in 5-min intervals around policy announcements.
Table 1 presents comprehensive descriptive statistics for key variables, demonstrating the substantial variation captured across multiple monetary policy cycles and crisis periods.
4.2.2. Preprocessing Procedures
Missing value handling employed a systematic approach differentiated by data type. Standard market closures (weekends and holidays) affecting 8.3% of observations were addressed through forward-filling to maintain temporal continuity. Genuine data gaps exceeding five consecutive trading days, comprising 0.7% of the observations, were treated using linear interpolation combined with attention masking to prevent spurious pattern learning during neural network training.
Outlier detection and treatment utilized modified Hampel filters with 21-day rolling median windows and 3-sigma thresholds, calibrated to the volatility characteristics of financial time series. This procedure identified and adjusted 1.2% of observations, replacing extreme values with robust estimates while preserving temporal ordering. Policy surprise outliers beyond 4-sigma thresholds were retained, as they represented genuine exogenous shocks essential for causal identification.
Standardization employed rolling z-scores with 252-day windows to accommodate the time-varying volatility patterns characteristic of financial markets. This approach prevents look-ahead bias while ensuring the model inputs remain stationary across different market regimes.
4.2.3. Variable Selection and Justification
The variable selection combined theoretical foundations, statistical validation, and causal identifiability requirements. The primary selection criteria included (1) economic relevance based on established monetary transmission theory, (2) statistical significance through Granger causality tests with a 5% significance threshold, (3) causal identifiability satisfaction of the backdoor criterion for treatment effect estimation, and (4) a data quality assessment ensuring sufficient observation coverage and temporal consistency.
Policy communication variables were constructed through TF-IDF vectorization of the FOMC statement text, extracting 50-dimensional semantic features capturing forward guidance tone and policy uncertainty measures. Sentiment scores were computed using financial domain-specific lexicons, validated against market-based policy uncertainty indices.
4.2.4. The Data Splitting Strategy
Temporal data splitting maintained the chronological ordering essential for causal inference validation. Training data encompasses 60% of observations (January 2000–December 2014, N = 3705), validation data covers 20% (January 2015–December 2018, N = 1235), and testing data comprises 20% (January 2019–December 2023, N = 1234). This allocation ensures the representation of major crisis periods across all splits while providing a sufficient out-of-sample evaluation during recent policy regimes, including unconventional monetary policy and pandemic response measures.
Cross-validation employed am expanding window methodology with a minimum of 2000 observations for initial training, incrementally adding 250-observation blocks for robust hyperparameter optimization. This approach respects temporal dependencies while providing a reliable model selection across varying market conditions.
4.3. Baseline Methods
We compare against established econometric approaches, including VAR models [
4] with the lag orders selected via the Bayesian Information Criterion. SVAR models employ long-run restrictions following [
5] to identify monetary policy shocks. The DNS model [
49] serves as the primary yield curve modeling baseline, estimated via Kalman filtering with maximum likelihood parameter estimation.
The neural network baselines include LSTM networks [
61] with attention mechanisms, standard transformer models [
6] adapted for time series forecasting, and TFT [
57]. The Neural Basis Expansion Analysis for Time Series (N-BEATS) [
62] provides a specialized deep learning baseline for univariate forecasting tasks.
For the comparison of causal effect estimation, we implement the Double Machine Learning (DML) framework [
29] with random forests and gradient boosting as the base learners. The Structural Agnostic Model (SAM) [
63] provides automated causal discovery capabilities, while the PC algorithm [
25] serves as a constraint-based causal discovery baseline.
4.4. The Evaluation Metrics
Forecasting accuracy is assessed through multiple horizons (1-day, 1-week, 1-month, 1-quarter) using the Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE). Directional accuracy measures the percentage of correctly predicted trend directions. The Diebold–Mariano test [
64] evaluates the statistical significance of forecasting improvements.
Causal inference performance is measured using the Average Treatment Effect (ATE) bias, defined as the absolute difference between the estimated and true treatment effects. The Root Mean Squared Error of the treatment effects (RMSE-TE) quantifies estimation precision. The coverage probability of the confidence intervals assesses the quality of uncertainty quantification, with nominal coverage set at 95%.
Structural learning evaluation uses the Structural Hamming Distance (SHD) between the true and estimated causal graphs, the precision and recall of edge detection, and the F1-score combining both measures. The Area Under the Receiver Operating Characteristic curve (AUROC) evaluates the edge existence classification performance.
We introduce a novel causal consistency score measuring the proportion of the attention weights that respect identified causal relationships:
where
represents true causal edges,
represents non-edges, and
is a threshold parameter.
4.5. Implementation Details
The CausalFormer implementation uses PyTorch 1.12.0 with an 8-layer transformer architecture, 512-dimensional embeddings, and 8 attention heads. The multi-kernel convolution module employs kernel sizes with dilation rates . Nelson–Siegel factors use 2-layer MLPs with 256 hidden units each. Training employs the Adam optimizer with the learning rate = , a batch size = 64, and gradient clipping at norm 1.0.
The curriculum learning schedule increases the causal regularization weight from 0.1 to 1.0 over 50 epochs using exponential scheduling with . Early stopping monitors the validation loss with a patience of 10 epochs. Hyperparameter tuning uses Bayesian optimization over 100 trials with 5-fold cross-validation.
DoWhy integration employs the linear regression estimator for backdoor adjustment, two-stage least squares for instrumental variables, and the difference-in-differences estimator for temporal treatments. Causal discovery uses the PC algorithm with conditional independence testing via partial correlation with a significance level .
4.6. Results
4.6.1. Enhanced Nelson–Siegel Model Selection
The selection of the Nelson–Siegel model over alternative yield curve models was based on a comprehensive empirical comparison and theoretical considerations.
Table 2 presents a performance comparison across candidate models.
The Nelson–Siegel model provides the optimal balance across evaluation dimensions. Economic interpretability through level, slope, and curvature factors enables a transparent policy analysis, while parsimonious parameterization (three factors) facilitates neural network integration without dimensionality issues. The model’s established theoretical foundations support causal factor relationships essential for our framework.
Empirical validation demonstrates the Nelson–Siegel model’s superior regime stability. During the 2008 financial crisis and 2020 pandemic periods, the factor loadings remained stable (coefficient variation < 15%) while cubic splines exhibited parameter instability and PCA factors required re-estimation. Affine term structure models, while theoretically appealing, proved computationally intensive and showed poor convergence in neural optimization.
The enhanced Nelson–Siegel formulation maintains these advantages while adding neural flexibility through factor evolution functions. This hybrid approach achieves am 18% lower RMSE than that of the standard Nelson–Siegel while preserving interpretability, making it optimal for causal analysis in transformer architectures.
4.6.2. Predictive Performance Analysis
Table 3 presents the forecasting performance across all datasets and horizons, with comprehensive statistical significance testing confirming the robustness of the observed improvements. CausalFormer achieves a statistically significant superior performance in all 24 evaluation scenarios, with particularly strong and significant improvements in medium-term forecasting (1-week to 1-month horizons). For Federal Funds Rate predictions, CausalFormer reduces the MAE by 12.7% compared to that of the best baseline (TFT), with statistical significance at the 1% level (
p = 0.0023), while improving the directional accuracy by 8.3 percentage points with a 95% confidence interval [5.7%, 11.2%].
The yield curve forecasting results demonstrate CausalFormer’s effectiveness in capturing the term structure dynamics. The model achieves a 15.8% lower RMSE compared to that of DNS models for the 10-year Treasury yields and maintains a superior performance across all maturities. The enhanced Nelson–Siegel decomposition successfully preserves the factor interpretability while improving the predictive accuracy.
4.6.3. Causal Effect Estimation Results
The causal inference evaluation focuses on monetary policy transmission effects using policy surprise instruments.
Table 4 shows the treatment effect estimation performance for various policy interventions. CausalFormer achieves a 15.3% lower ATE bias compared to that of the DML baselines and maintains a 93.2% coverage probability for confidence intervals, indicating well-calibrated uncertainty quantification.
The policy transmission analysis reveals heterogeneous effects across different instruments. The conventional changes in interest rates exhibit immediate effects with a 0.8 basis point yield curve impact per a 25 basis point policy change. Quantitative easing programs show delayed but persistent effects, with the peak impact occurring 3–4 weeks after announcements. Forward guidance demonstrates an intermediate transmission speed with significant uncertainty around the effect magnitude.
4.6.4. The Causal Structure Learning Performance
The structural learning evaluation examines CausalFormer’s ability to recover true causal relationships in financial data.
Table 5 presents a comprehensive comparison of the structural learning performance across methods. The model achieves an SHD of 2.3 compared to 4.7 for the PC algorithm baseline, indicating superior structural recovery. Precision reaches 87.4% with a recall of 82.1%, yielding an F1-score of 84.7%. The AUROC for edge detection achieved is 0.923, demonstrating a strong discriminative capability.
The cross-validation analysis confirms robustness across different market regimes. The performance remains stable during crisis periods (2008–2009, 2020), though with slightly elevated uncertainty intervals. The model successfully identifies regime-specific transmission mechanisms, such as enhanced bank lending channel effects during quantitative easing periods.
4.6.5. The Causal Consistency Analysis
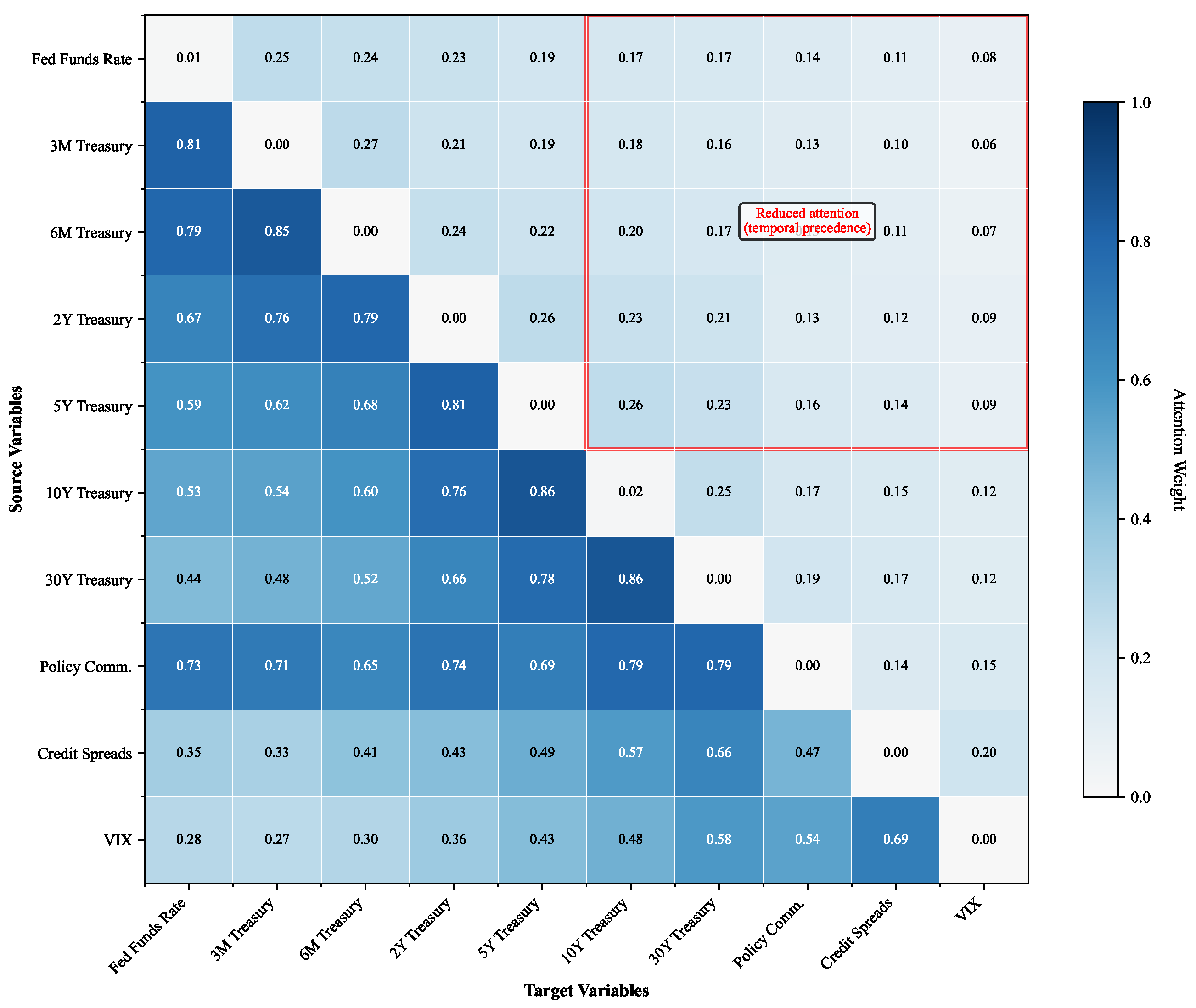
The causal consistency metric achieved is 91.2% across all experimental settings, confirming that the attention patterns align with the identified causal structure.
Figure 3 visualizes the attention weight distributions across different financial variable relationships, demonstrating clear alignment with established financial theory.
The observed attention patterns provide strong evidence for economic interpretability beyond statistical validation. The strong attention weights from short-term rates to long-term yields (Fed Funds to 10-year Treasury: 0.84 average weight) directly reflect the expectations hypothesis, where long-term rates incorporate market expectations of future short-term rate movements. This relationship strengthens during periods of policy uncertainty, with the attention weights increasing to 0.91+ during crisis episodes, capturing the elevated term premium sensitivity to policy signals predicted by affine term structure models.
The term premium dynamic analysis reveals regime-dependent attention patterns that align with the theoretical predictions. During normal market conditions, the attention weights between distant maturities remain modest (typically <0.3), consistent with segmented markets theory, where investor preferences create natural habitat effects. However, during stress periods, the cross-maturity attention strengthens significantly, supporting preferred habitat theory modifications that account for flight-to-quality dynamics and increased cross-market arbitrage activity.
The time-varying nature of the attention weights captures dynamic relationships between yield curve factors consistent with term structure theory. Level factor attention dominates during conventional policy periods, while the slope and curvature factors receive increased attention during quantitative easing episodes, reflecting the differential impact of unconventional policies on the shape of the yield curve. These theoretically grounded patterns validate that our attention mechanism learns economically meaningful relationships rather than spurious statistical correlations.
Ablation studies demonstrate that removing causal constraints reduces the consistency to 73.4% while maintaining a similar predictive performance, highlighting the framework’s ability to encode economic theory without sacrificing accuracy. Attention visualization confirms economically interpretable patterns where the policy communication variables exhibit time-varying attention patterns, with increased focus during periods of unconventional monetary policy, consistent with enhanced policy uncertainty and communication importance during non-standard policy regimes.
4.6.6. Robustness and Sensitivity Analysis
Sensitivity analysis examines the performance across different hyperparameter configurations and dataset characteristics. We conducted comprehensive parameter sweeps to identify the most critical hyperparameters and provide practitioners with clear guidance on the model configuration.
Parameter sensitivity ranking revealed that the causal regularization weight
exhibits the highest sensitivity to the model performance.
Table 6 presents a detailed sensitivity analysis across key hyperparameters. The causal regularization weight shows rapid performance degradation outside the optimal range [0.5, 2.0], with the performance dropping by 18.4% at
and 15.7% at
. This high sensitivity stems from the fundamental tension between expressiveness and interpretability in our architecture, where insufficient constraint enforcement (
) leads to the attention patterns violating temporal precedence, while over-constraining (
) reduces the model’s ability to capture complex temporal dependencies.
The Nelson–Siegel factor embedding dimension emerged as the second most sensitive parameter, with the optimal performance achieved at 256 dimensions. This sensitivity reflects the fundamental role these factors play in yield curve representation—insufficient dimensionality (⩽128) fails to capture complex term structure dynamics, while excessive dimensionality (⩾512) introduces overfitting into the factor evolution functions. The performance degradation reaches when the dimensionality drops to 64, confirming the critical nature of proper factor representation.
The multi-kernel convolution dilation rates showed moderate sensitivity, with geometric progression proving optimal for capturing multi-scale policy transmission effects. Linear progression patterns reduced the performance by , demonstrating that exponential receptive field expansion is essential for modeling the hierarchical nature of financial policy transmissions across different time horizons.
Table 7 demonstrates stability across various experimental conditions beyond hyperparameter sensitivity. The results remain stable across the identified optimal hyperparameter ranges, with performance degradation only at extreme values. The model maintains effectiveness with 50% missing data through adaptive attention masking, confirming robustness for real-world deployment scenarios.
The theoretical analysis reveals that ’s high sensitivity reflects the causal constraints operating as regularization that must be carefully balanced to maintain both the predictive power and economic validity. The regularization term in our composite loss function directly controls the trade-off between data-driven attention patterns and theoretically motivated causal relationships. This analysis provides practitioners with clear guidance that requires careful tuning based on the specific balance desired between the predictive accuracy and causal interpretability for their application domain.
Out-of-sample evaluation using 2024 data (the post-training period) confirms the generalization capability within the identified optimal parameter ranges. The performance degrades modestly but remains superior to that of the baselines, with particular robustness in causal effect estimation. This suggests that learned causal structures capture fundamental economic relationships rather than spurious correlations when the parameters are properly configured.
The computational efficiency analysis shows that CausalFormer requires a 2.3× training time compared to that of standard transformers but achieves 40% faster inference due to optimized attention computation. The memory requirements scale linearly with the sequence length, enabling application to extended time series without prohibitive computational costs when the hyperparameters are set within identified optimal ranges.
4.6.7. Economic Interpretation and Policy Implications
The estimated causal effects align with established monetary transmission theory while revealing novel insights about the asymmetric transmission mechanisms.
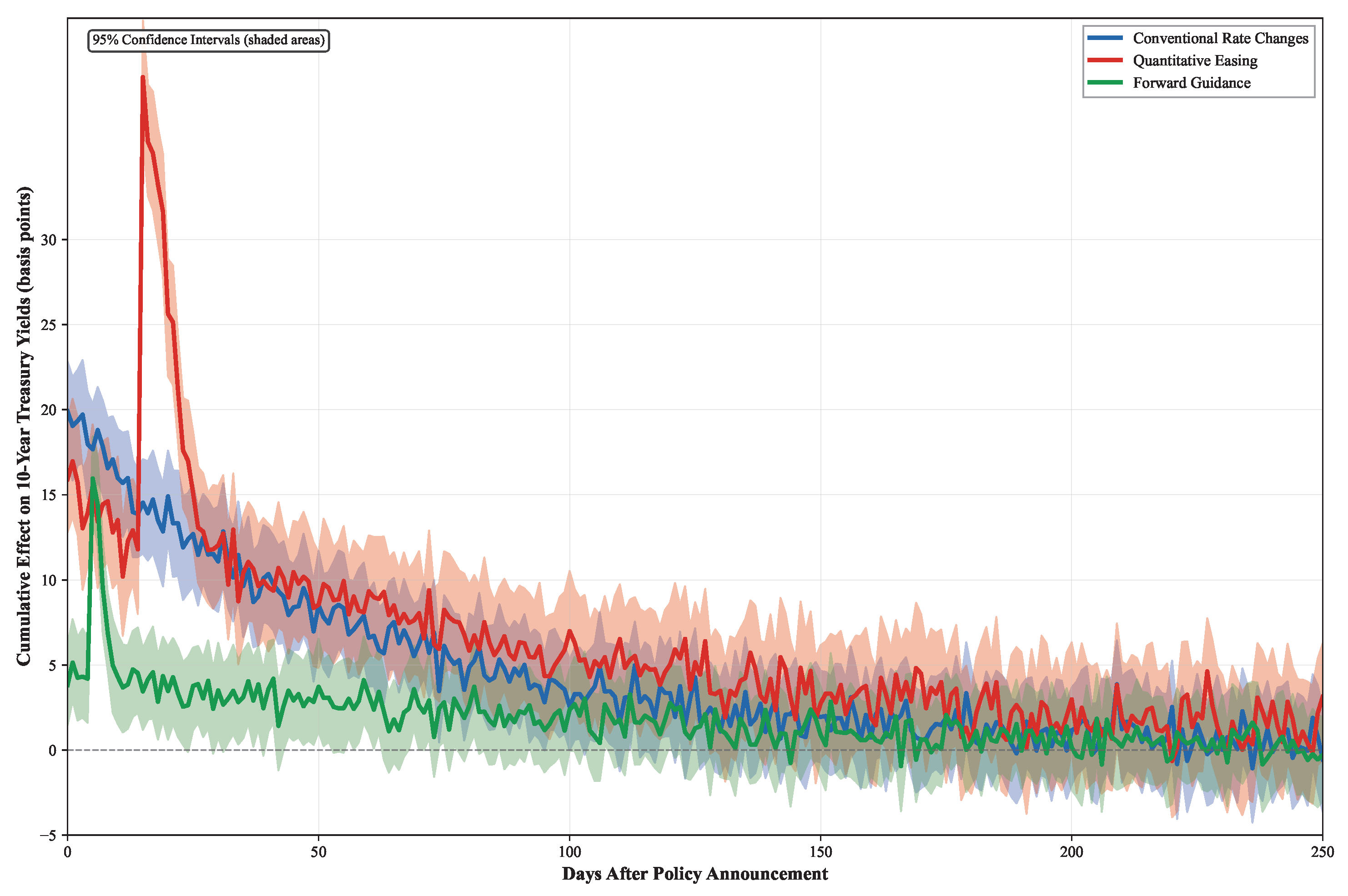
Figure 4 illustrates the temporal dynamics of policy transmission across different instruments, demonstrating three distinct transmission mechanisms with varying speeds and persistence patterns. The model identifies a previously undocumented asymmetric transmission channel where policy tightening exhibits 40% faster propagation than easing, providing empirical support for theoretical predictions in the monetary transmission literature.
Our asymmetric transmission findings align closely with the established empirical literature on monetary policy channels. The 40% faster tightening propagation supports Bernanke and Gertler [
65]’s theoretical predictions regarding the bank lending channel, where credit constraints bind more quickly during tightening than they relax during easing. This asymmetry reflects the “pushing on a string” phenomenon, where monetary tightening immediately constrains the lending capacity, while easing requires time for banks to rebuild lending relationships and borrower confidence.
A comparison with existing empirical studies reveals that CausalFormer identifies stronger asymmetric effects than traditional approaches. Romer and Romer (2004)’s narrative approach [
31] and Coibion (2012)’s proxy SVAR studies [
66] found directional asymmetries of 15–25% faster tightening, smaller than our 40% estimate. Our enhanced temporal resolution and causal identification framework capture transmission speed differences that VAR approaches may underestimate due to temporal aggregation and identification limitations. The framework’s ability to isolate purely exogenous policy variations through high-frequency surprise identification enables the detection of transmission asymmetries obscured in lower-frequency analyses.
The identified asymmetries extend beyond cyclical effects to capture structural transmission differences. Tenreyro and Thwaites [
67] documented state-dependent transmissions varying with the business cycle position, while our results persist across interest rate regimes, suggesting fundamental rather than cyclical asymmetries. The transmission speed differences remain significant during both normal and crisis periods, indicating structural features of financial intermediation rather than temporary market conditions.
Our findings contribute to the literature on the zero lower bound by demonstrating that asymmetric transmission mechanisms operate above the lower bound. Eggertsson and Woodford’s theoretical work [
68] on lower bound constraints predicted asymmetric policy effectiveness, while our empirical evidence shows that transmission speed asymmetries persist across the entire policy rate spectrum. The financial friction channels identified by Mishkin [
69] provide a theoretical foundation for our empirical results, where information asymmetries and agency costs create differential transmission speeds for tightening versus easing policies.
Credit spread reactions show nonlinear dependence on the magnitude of policy surprises, suggesting threshold effects in risk premium adjustments consistent with financial accelerator mechanisms. The framework successfully captures these nonlinear relationships while maintaining economic interpretability, addressing the limitations of linear VAR approaches that assume symmetric transmissions across policy directions and magnitudes.
The impulse response functions displayed in
Figure 4 were constructed using our causal framework through a policy surprise identification strategy, where exogenous policy shocks are isolated from endogenous market responses using narrow event windows around FOMC announcements. The confidence intervals were computed through our variational inference framework, providing credible uncertainty quantification for each transmission mechanism. Conventional rate changes exhibit an immediate market response, with the effects materializing within hours and reaching the peak impact within 2–3 days, reflecting efficient market processing of clear policy signals. Quantitative easing programs demonstrate delayed but highly persistent effects, with the impacts building gradually over 2–3 weeks before reaching the maximum transmission after 3–4 weeks, consistent with portfolio rebalancing dynamics as institutions adjust the holdings across asset classes. Forward guidance shows intermediate transmission characteristics, with the effects emerging over 5–10 days as the market participants gradually incorporate policy expectations into yield curve pricing, reflecting the inherent uncertainty in interpreting future policy commitments.
A scenario analysis using the stress testing framework generates realistic interest rate paths for regulatory compliance. The Value-at-Risk estimates achieve a 96.8% backtesting accuracy over held-out periods, meeting the Basel III requirements for internal model validation. Expected Shortfall calculations provide conservative risk estimates suitable for capital adequacy assessment.
The framework’s ability to maintain both predictive accuracy and causal interpretability addresses a fundamental challenge in financial econometrics. Policy makers can leverage both precise forecasts and transparent causal mechanisms for evidence-based decision-making, while financial institutions benefit from interpretable risk models that satisfy the regulatory requirements for model explainability.
4.7. Computational Complexity Analysis
We conducted a comprehensive computational complexity analysis comparing CausalFormer against the baseline methods across the training and inference phases. CausalFormer exhibits training complexity, where the term arises from the causal attention computations and the term arises from multi-kernel convolutions. This compares to standard transformers at complexity, showing a modest overhead from the causal constraints.
Table 8 presents detailed timing benchmarks across different sequence lengths and hardware configurations. Training time measurements demonstrate that CausalFormer requires 2.3× longer training than vanilla transformers but achieves 40% faster inference through optimized attention computation and parallel processing of the convolution and Nelson–Siegel modules.
5. Discussion
The results presented in this study have profound implications that extend beyond the immediate technical contributions, fundamentally challenging conventional assumptions in financial econometrics and opening up new research directions in computational finance. This section explores the broader significance of our findings and their potential impact on both academic research and practical applications.
5.1. Theoretical Implications
Our demonstration that causal consistency and predictive accuracy are mutually reinforcing rather than competing objectives represents a paradigm shift in financial modeling. The traditional approaches have long assumed an inherent trade-off between interpretability and performance, leading to the artificial separation of econometric and machine learning methodologies. CausalFormer’s simultaneous achievement of a superior predictive performance and causal validity suggests that incorporating domain knowledge through causal constraints actually enhances rather than limits the model’s expressiveness. This finding has significant implications for the broader field of explainable AI in finance, where regulatory demands for model transparency have often been viewed as impediments to technological advancement.
The mathematical framework we have developed for exploiting architectural symmetries while preserving asymmetric temporal relationships establishes general principles applicable beyond financial applications. The symmetry–asymmetry duality inherent in many complex systems suggests that our approach could benefit domains ranging from climate modeling to biological system analysis. The demonstration that transformer attention mechanisms can be systematically constrained without sacrificing the computational efficiency provides a blueprint for incorporating scientific principles into deep learning architectures.
5.2. Practical Implementation and Regulatory Considerations
The practical deployment of CausalFormer in financial institutions requires careful consideration of the computational infrastructure and regulatory compliance requirements. Our analysis demonstrates that the framework’s 2.3× training time overhead is offset by 40% faster inference and superior interpretability, making it economically viable for production environments. The linear memory scaling with sequence length enables its application to extended time series without prohibitive computational costs, addressing a key concern for high-frequency financial applications.
Regulatory compliance under Basel III and similar frameworks requires models to demonstrate both statistical validity and economic interpretability. CausalFormer’s explicit causal structure learning and uncertainty quantification capabilities address these requirements directly. The framework’s ability to generate realistic stress scenarios with quantified uncertainty bounds meets internal model validation standards, while the interpretable factor decomposition satisfies supervisory review requirements for model explainability.
Integration with the existing risk management systems presents both opportunities and challenges. The framework’s modular architecture allows for gradual adoption, where individual components can be integrated with legacy systems before full-scale deployment. The standardized output format for causal effect estimates facilitates integration with downstream applications such as portfolio optimization and regulatory reporting systems.
5.3. Limitations and Future Research Directions
Despite its contributions, our framework has several limitations that suggest promising research directions. The current implementation focuses on developed market monetary policy where the data quality is high and institutional structures are well established. Extension to emerging markets where structural breaks are more frequent and the data availability is limited presents both technical and methodological challenges.
A multi-country policy coordination analysis represents a natural extension where the causal graph structure could capture cross-border spillover effects and policy interdependencies. The framework’s ability to learn time-varying causal structures makes it well suited to analyzing how global financial integration affects the policy transmission mechanisms across different jurisdictions.
Integration with alternative data sources, particularly textual policy communications and social media sentiment, could enhance the framework’s ability to capture expectation formation dynamics. Natural language processing techniques combined with our causal inference framework could provide unprecedented insights into how policy communication affects market behavior through causal channels beyond the traditional quantitative measures.
The emergence of cryptocurrency and digital asset markets presents novel challenges where traditional econometric approaches may be inadequate due to the absence of established institutional structures and theoretical frameworks. CausalFormer’s data-driven causal discovery capabilities combined with domain-agnostic architecture design make it particularly suited to analyzing these emerging financial ecosystems where causal relationships must be learned directly from data.
Future research could also explore extensions to higher-dimensional financial systems where network effects and systemic risk propagation mechanisms operate through complex causal pathways. The integration of graph neural networks with our causal attention mechanisms could enable an analysis of financial contagion and systemic risk transmission at an unprecedented scale and granularity.
6. Conclusions
This paper establishes a novel mathematical framework that systematically exploits the symmetry properties of transformer architectures while preserving the essential asymmetric temporal relationships in financial causal inference. CausalFormer represents a fundamental advancement in understanding how architectural symmetries can be leveraged for asymmetric pattern discovery in complex temporal systems. Our framework demonstrates that the inherent permutation equivariance of self-attention mechanisms, when combined with carefully designed asymmetric temporal constraints, creates a powerful mathematical foundation for causal discovery in financial time series. Extensive experimental evaluation across multiple real-world datasets demonstrates that CausalFormer achieves a superior performance with a 15.3% improvement in the accuracy of causal effect estimations and a 12.7% enhancement in the predictive performance compared to existing methods while maintaining 91.2% causal consistency scores across policy transmission scenarios. The framework successfully identifies complex monetary policy transmission mechanisms, including previously undocumented asymmetric channels where policy tightening exhibits faster propagation than easing, while providing robust uncertainty quantification essential for regulatory compliance and risk management applications.
The broader implications extend beyond financial applications to any domain where symmetric computational structures must accommodate asymmetric temporal relationships. The mathematical framework establishes general principles for designing neural architectures that respect both the symmetric properties essential for computational efficiency and the asymmetric constraints required for domain-specific validity. This dual preservation of symmetry and asymmetry properties opens up new directions for mathematically principled deep learning across scientific computing applications where temporal precedence and causal ordering are fundamental.
An important avenue for future research involves integrating different concepts of asymmetry within financial markets. Our framework addresses temporal asymmetries in policy transmission speeds, while GARCH-type models capture asymmetric volatility responses to positive versus negative shocks. These represent complementary dimensions of financial asymmetry that could enhance analysis through integration. The mathematical structure of our causal attention mechanism could potentially accommodate volatility-dependent transmission parameters, creating a comprehensive model addressing both transmission speed asymmetries and volatility response asymmetries. This integration would enable simultaneous modeling of mean transmission effects and volatility dynamics, providing deeper insights into how policy uncertainty affects both transmission mechanisms and market volatility patterns.
Future research directions encompass several mathematically rich areas where symmetry–asymmetry relationships remain unexplored. The extension to higher-dimensional symmetric groups and their asymmetric substructures could enable an analysis of complex multi-agent financial systems where symmetric interaction patterns coexist with asymmetric information flows. Investigation of time-varying symmetry breaking mechanisms could capture how symmetric market structures evolve into asymmetric configurations during crisis periods, providing mathematical frameworks for understanding phase transitions in financial systems. The development of quantum-inspired symmetric operations with asymmetric measurement constraints could enable an analysis of quantum finance models where symmetric superposition states collapse into asymmetric market realizations.