Analysis of Symmetrical Three-Point Bending and Springback Process of Pipes
Abstract
1. Introduction
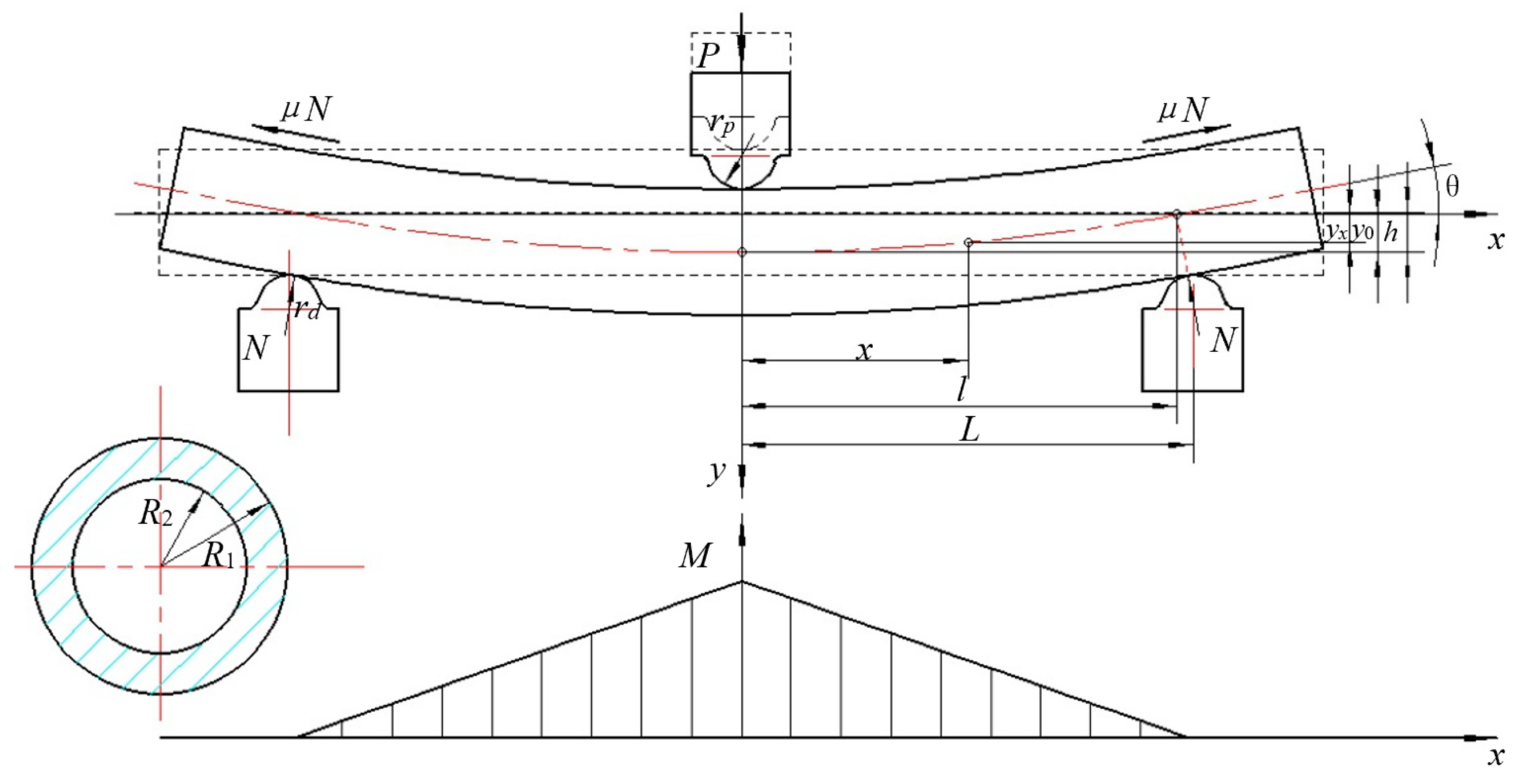
2. Basic Assumptions and Mechanical Models
2.1. Basic Assumptions
- The cross-sections of the pipes remain planar after bending and deformation, with no distortion occurring.
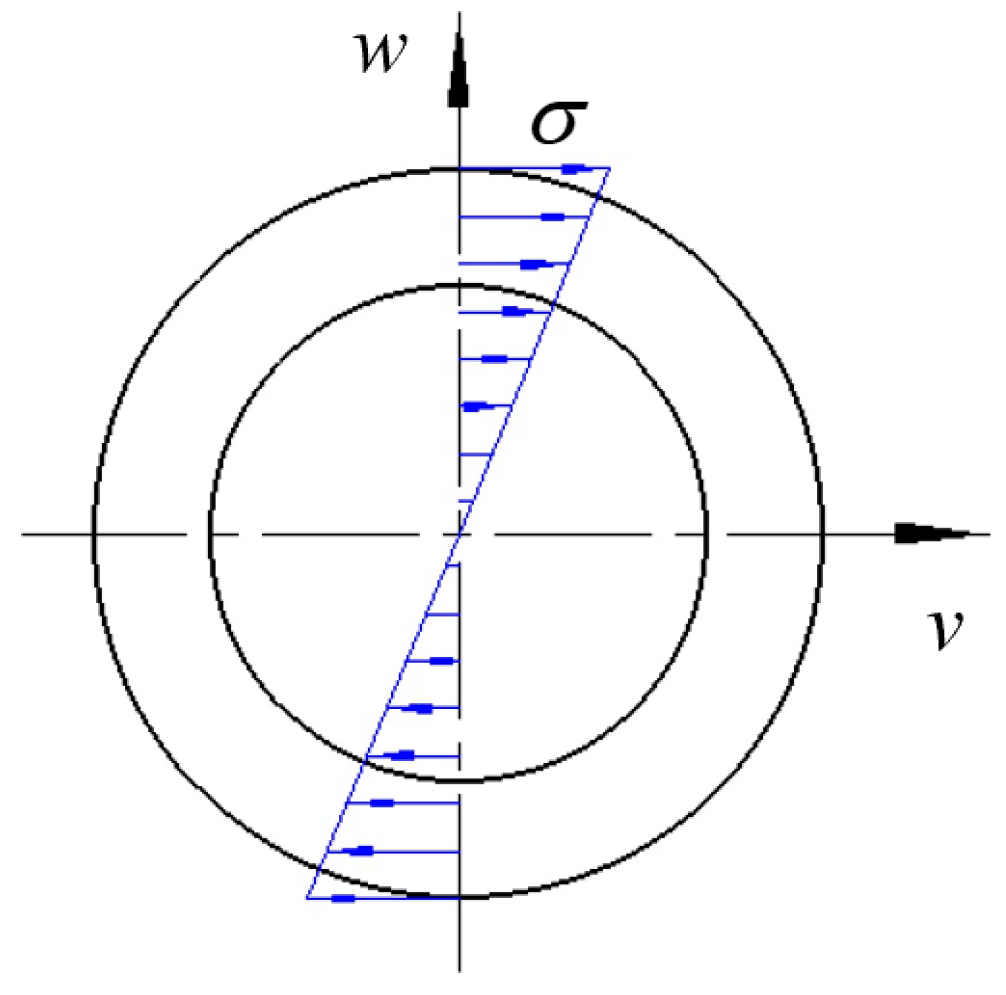
- Throughout the deformation process, the stress state at any point on any cross-section of the pipe is either uniaxial tension or uniaxial compression.
- The conventional elastic–plastic material model posits that the pipe is a continuous and homogeneous elastic–plastic body, where elastic deformation follows Hooke’s law for linear elasticity and plastic flow adheres to the unloading principles of stable material conditions and classical elastoplastic theory.
- The small-deformation assumption implies a linear distribution of strain across the cross-section, as
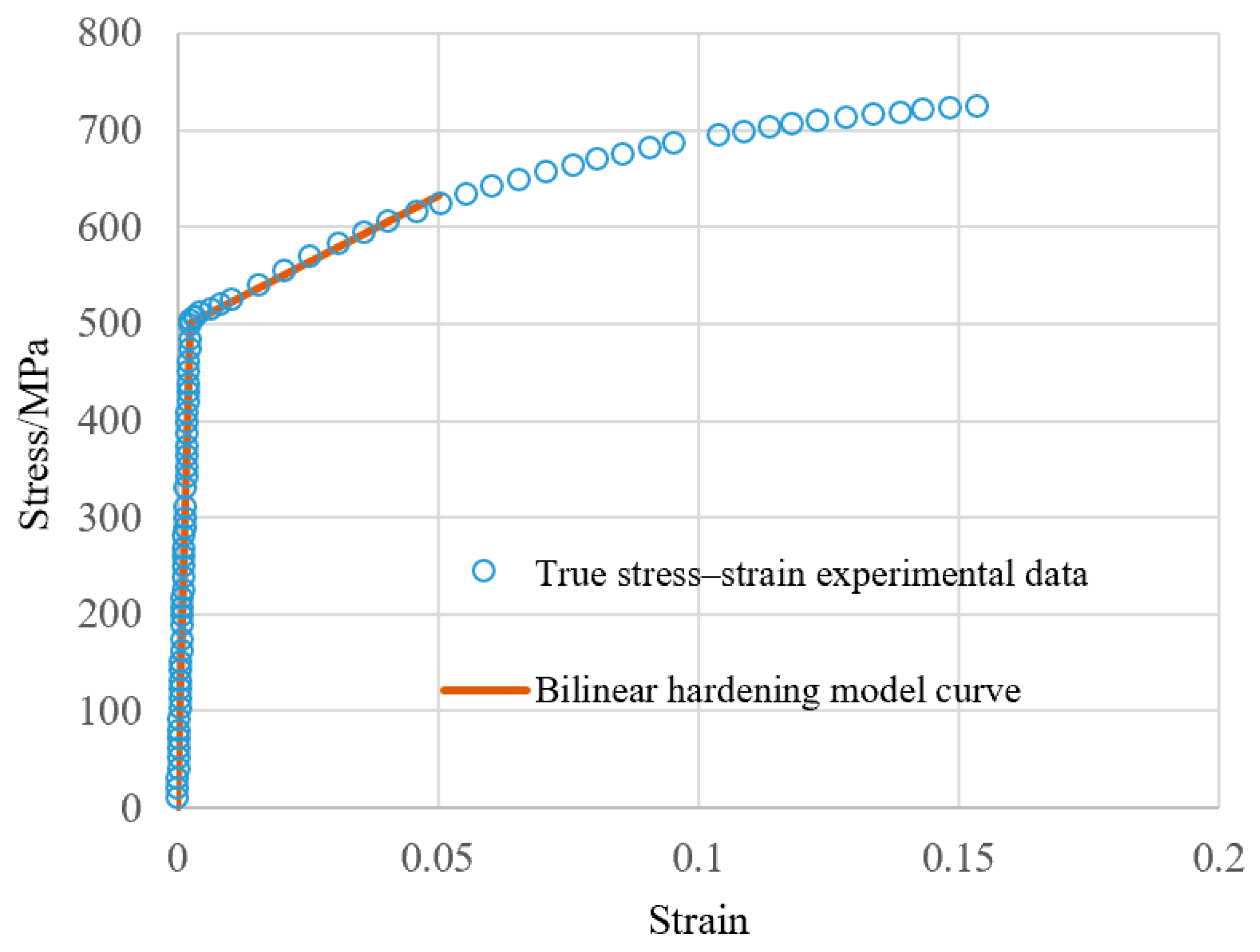
2.2. Material Model
2.3. Symmetrical Three-Point Bending Mechanical Model of Pipes
3. Analysis of Fully Elastic Bending Stage
4. Analysis of Elastic–Plastic Bending Stage
4.1. Analysis of Bending Process
- 1.
- Elastic–plastic deformation zone
- 2.
- Elastic deformation zone
4.2. Analysis of the Springback Process
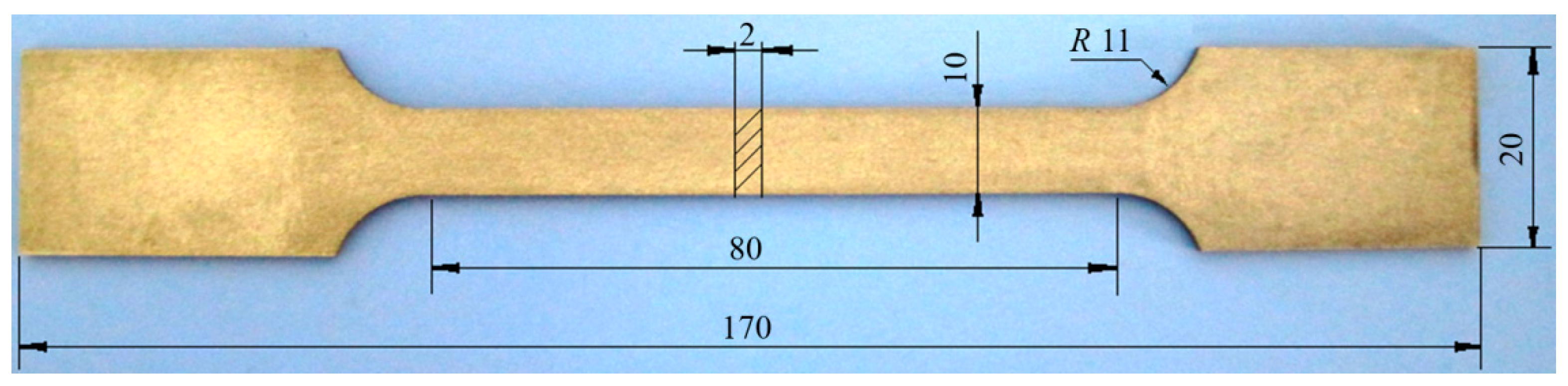
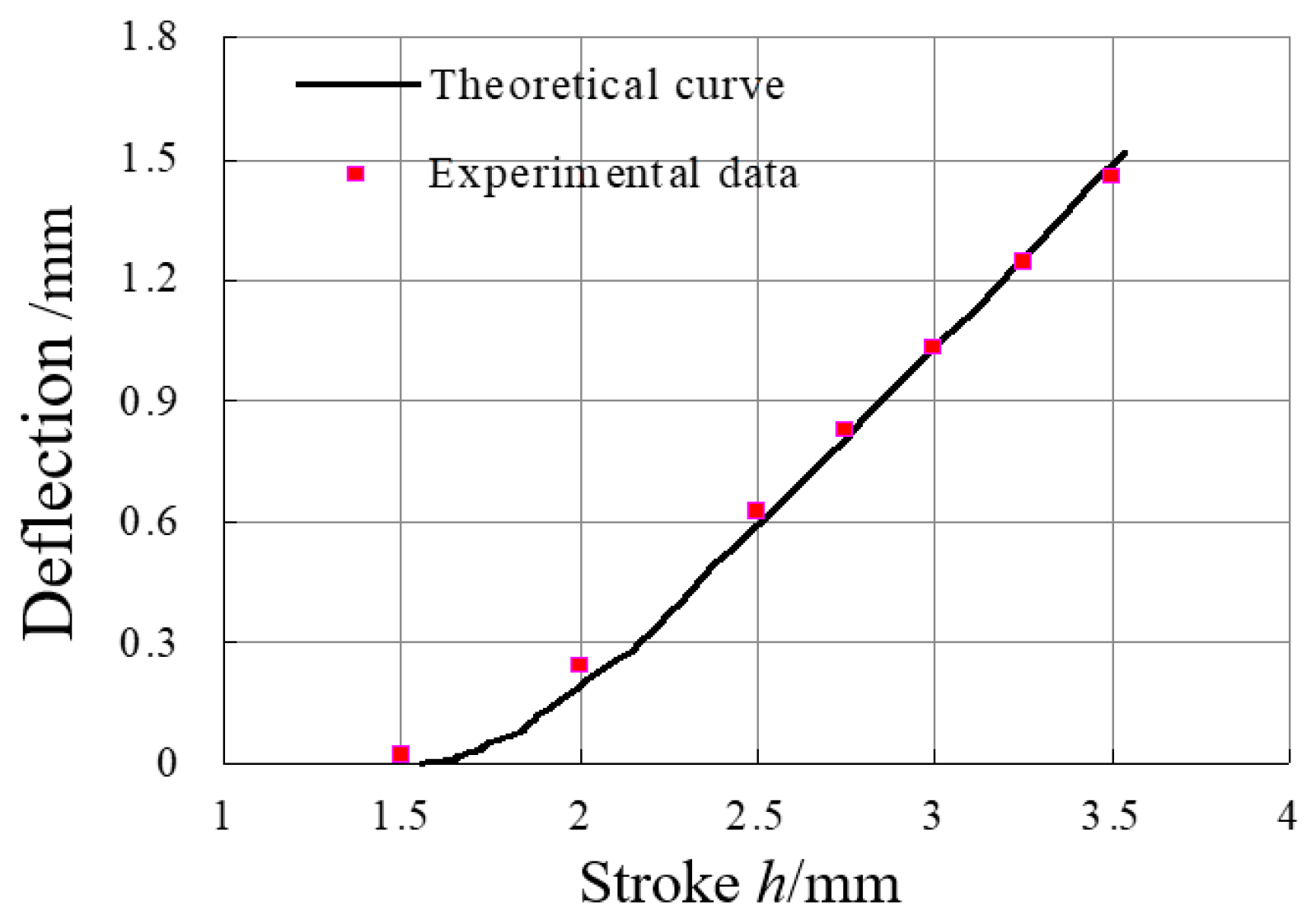
5. Experimental Validation
5.1. Material Properties of the Experimental Pipes
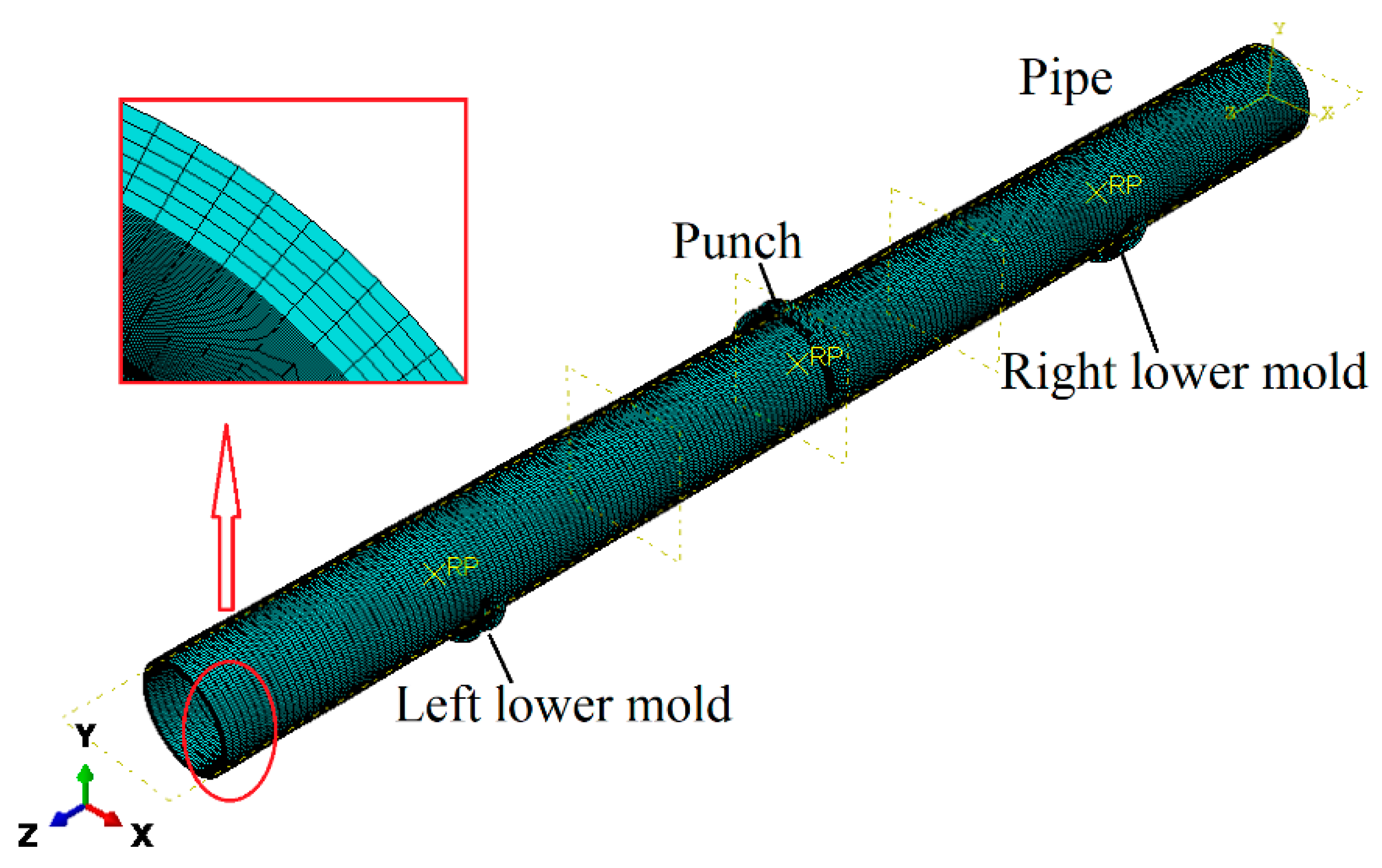
5.2. Experimental Molds and Equipment
5.3. Finite Element Simulation Model
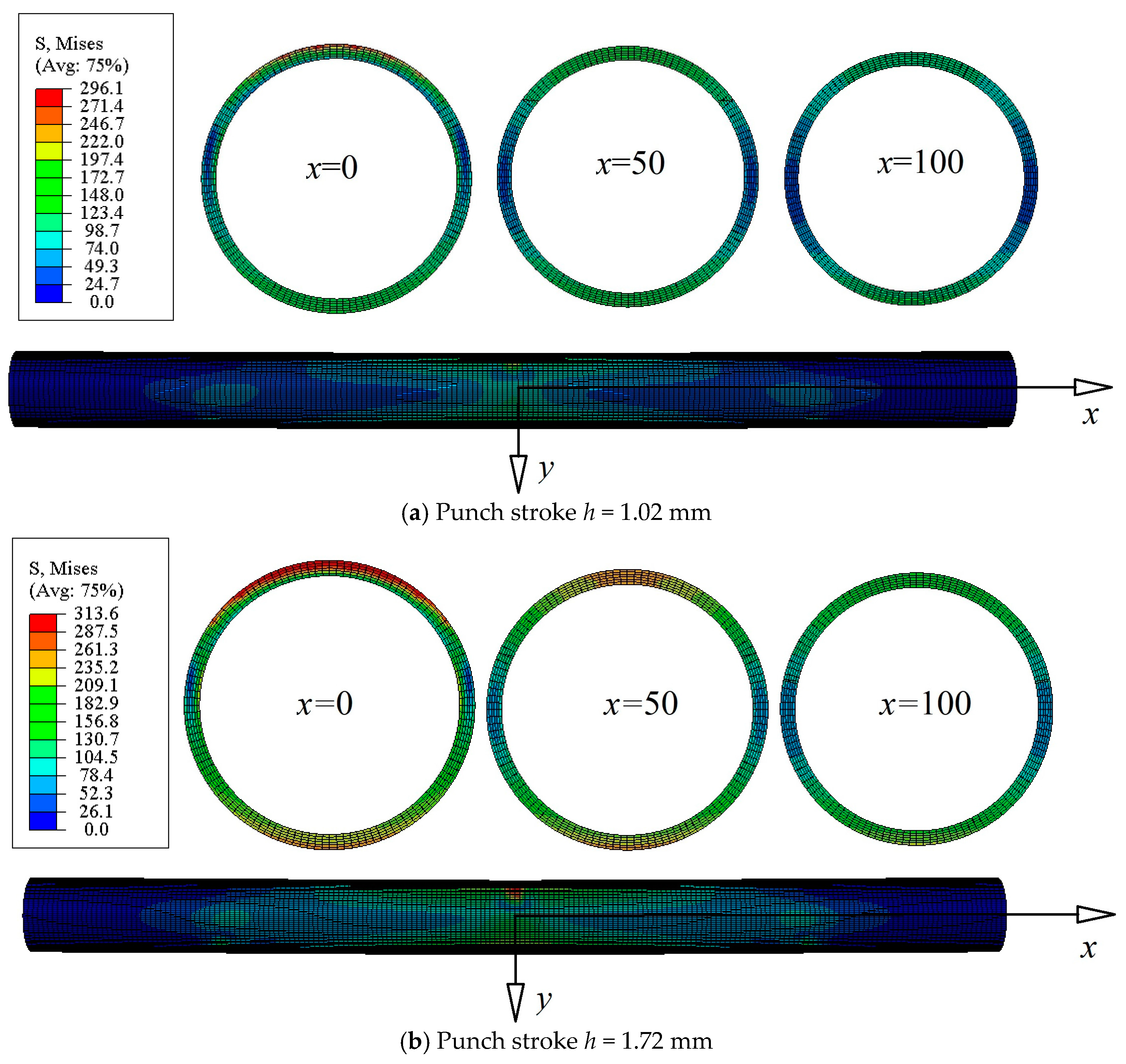
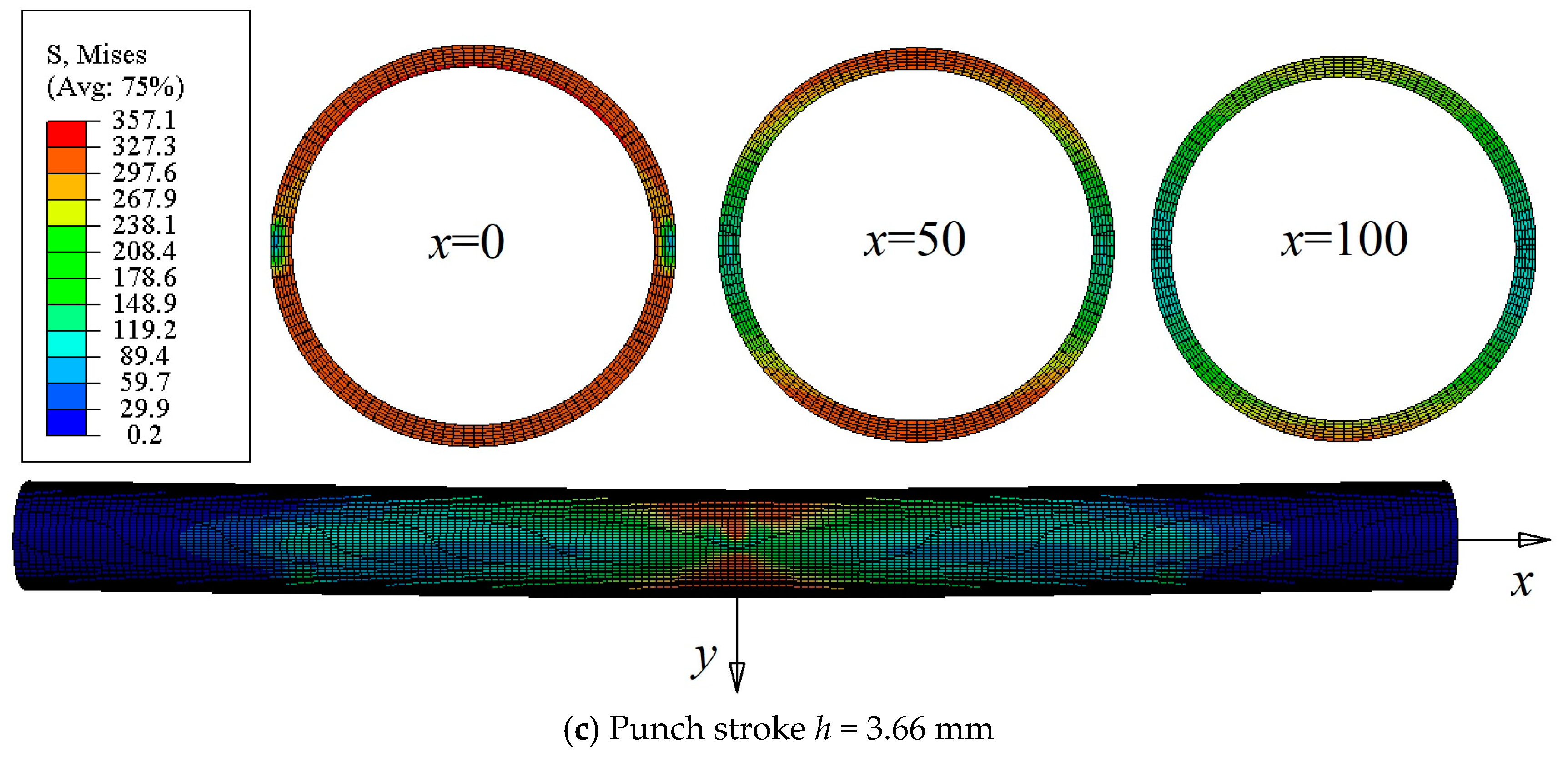
5.4. Results and Discussion
6. Conclusions
- Based on the assumption of small deformation, a mechanical model of symmetrical three-point bending and its springback process for pipes was developed using a bilinear hardening material model. This model incorporates the effects of mold parameters, material performance parameters, and other factors on pipe forming, aligning with the actual conditions of pipe pressure straightening.
- The finite element analysis and physical simulation experiment results of smaller pipes have confirmed the accuracy and reliability of the theoretical model. The establishment of this model not only enhances the accuracy of single-pressure straightening but also provides a theoretical foundation for the online identification of material performance parameters during the straightening process.
- Theoretical analysis and experimental results both indicate that the relationship between the maximum deflection after springback and the stroke of the indenter is very close to linear, offering a convenient method to establish an intelligent straightening control system for identifying springback laws.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- American Petroleum Institute. ANSI/API Specification 5L, Specification for Line Pipe, 45th ed.; American Petroleum Institute: Washington, DC, USA, 2012. [Google Scholar]
- Wang, C.; Yu, G.; Zhao, J.; Liu, W. Pure-Bend and Over-Bend Straightening Theory for In-Plane Curved Beams with Symmetrical Section and Straightening Mechanism Analysis. Metals 2022, 12, 1362. [Google Scholar] [CrossRef]
- Ling, H.; Yang, C.; Feng, S.; Lu, H. Predictive model of grinding residual stress for linear guideway considering straightening history. Int. J. Mech. Sci. 2020, 176, 105536. [Google Scholar] [CrossRef]
- Kaiser, R.; Hatzenbichler, T.; Buchmayr, B.; Antretter, T. Simulation of the roller straightening process with respect to residual stresses and the curvature trend. Mater. Sci. Forum 2014, 768–769, 456–463. [Google Scholar] [CrossRef]
- Zhao, J.; Yin, J.; Ma, R.; Ma, L. Springback equation of small curvature plane bending. Sci. China Technol. Sci. 2011, 54, 2386–2396. [Google Scholar] [CrossRef]
- Song, Y. Load-deflection model for T-section rail press straightening process under lateral loads. Clust. Comput. 2018, 22, 2955–2961. [Google Scholar] [CrossRef]
- Lu, H.; Zang, Y.; Zhang, X.; Zhang, Y.; Li, L. A General Stroke-Based Model for the Straightening Process of D-Type Shaft. Processes 2020, 8, 528. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, H.; Ling, H.; Lian, Y.; Ma, M. Analytical Model of a Multi-Step Straightening Process for Linear Guideways Considering Neutral Axis Deviation. Symmetry 2018, 10, 316. [Google Scholar] [CrossRef]
- Kim, S.-C.; Chung, S.-C. Synthesis of the multi-step straightness control system for shaft straightening processes. Mechatronics 2002, 12, 139–156. [Google Scholar] [CrossRef]
- Wang, K.; Wang, B.; Yang, C. Research on the multi-step straightening for the elevator guide rail. Procedia Eng. 2011, 16, 459–466. [Google Scholar] [CrossRef][Green Version]
- Wang, J.; Afshan, S.; Gkantou, M.; Theofanous, M.; Baniotopoulos, C.; Gardner, L. Flexural behaviour of hot-finished high strength steel square and rectangular hollow sections. J. Constr. Steel Res. 2016, 121, 97–109. [Google Scholar] [CrossRef]
- Song, F.; Yang, H.; Li, H.; Zhan, M.; Li, G. Springback prediction of thick-walled high-strength titanium tube bending. Chin. J. Aeronaut. 2013, 26, 1336–1345. [Google Scholar] [CrossRef]
- Oliveira, M.; Alves, J.; Chaparro, B.; Menezes, L. Study on the influence of work-hardening modeling in springback prediction. Int. J. Plast. 2007, 23, 516–543. [Google Scholar] [CrossRef]
- Li, L.; Zhang, C.G. Effects of Heat Treatment Process on Microstructure and Mechanical Properties of X70 Pipeline Steel. Hot Work. Technol. 2025, 54, 64–68. [Google Scholar]
- Wang, C.; Zhang, Z.; Zhai, R.; Yu, G.; Zhao, J. Cross-sectional distortion of LSAW pipes in over-bend straightening process. Thin-Walled Struct. 2018, 129, 85–93. [Google Scholar] [CrossRef]


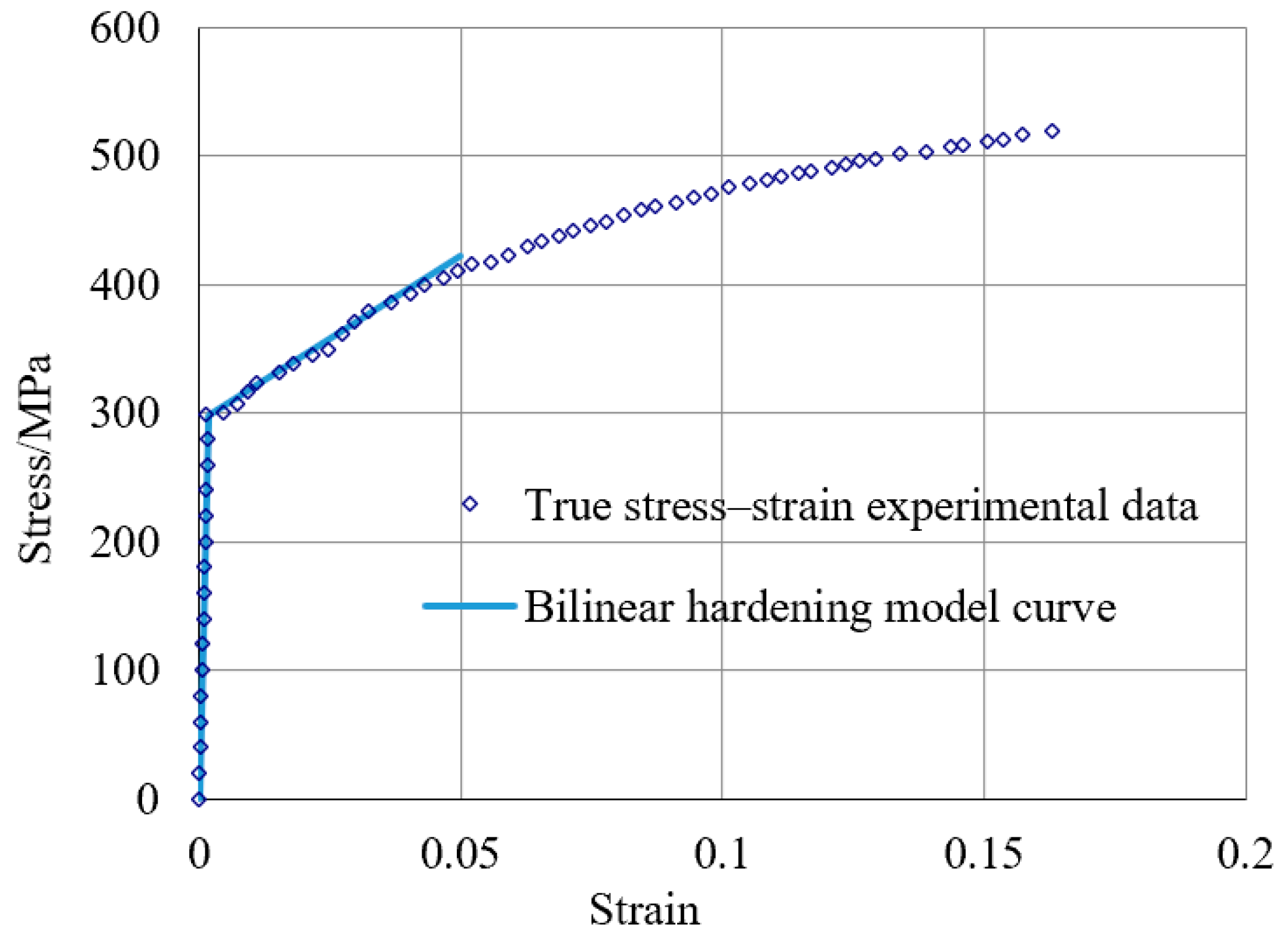


| Pipes Grade | E/GPa | D/MPa | /MPa |
|---|---|---|---|
| 20 | 172 | 2564 | 298.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Zhao, J.; Ma, R.; Li, J. Analysis of Symmetrical Three-Point Bending and Springback Process of Pipes. Symmetry 2025, 17, 95. https://doi.org/10.3390/sym17010095
Song X, Zhao J, Ma R, Li J. Analysis of Symmetrical Three-Point Bending and Springback Process of Pipes. Symmetry. 2025; 17(1):95. https://doi.org/10.3390/sym17010095
Chicago/Turabian StyleSong, Xiaokang, Jun Zhao, Rui Ma, and Jian Li. 2025. "Analysis of Symmetrical Three-Point Bending and Springback Process of Pipes" Symmetry 17, no. 1: 95. https://doi.org/10.3390/sym17010095
APA StyleSong, X., Zhao, J., Ma, R., & Li, J. (2025). Analysis of Symmetrical Three-Point Bending and Springback Process of Pipes. Symmetry, 17(1), 95. https://doi.org/10.3390/sym17010095






