NHSH: Graph Hybrid Learning with Node Homophily and Spectral Heterophily for Node Classification
Abstract
1. Introduction
- We design a graph hybrid-learning framework based on Node Homophily and Spectral Heterophily (NHSH) that can effectively aggregate the local and global information of nodes and improve the accuracy of node classification.
- The homophilic node extraction module combines graph convolutional network (GCN) and dynamic attention mechanism to find neighboring nodes with the same type as the central node to extract local features and obtain node homophily information. The heterophilic spectrum extraction module aggregates low- and high-frequency information from neighbors through low- and high-frequency filters to extract the global features of the nodes. The node feature fusion module uses the local topology information of the nodes to automatically generate fusion coefficients and dynamically update the final node features in graphs.
- Extensive experiments are implemented on eight benchmark datasets, demonstrating that the proposed network obtains competitive performances with eight state-of-the-art approaches in terms of quantitative comparisons.
2. Related Works
2.1. Spectral-Based Graph Convolutional Networks
2.2. Spatial-Based Graph Convolutional Networks
2.3. Homophily and Heterophily
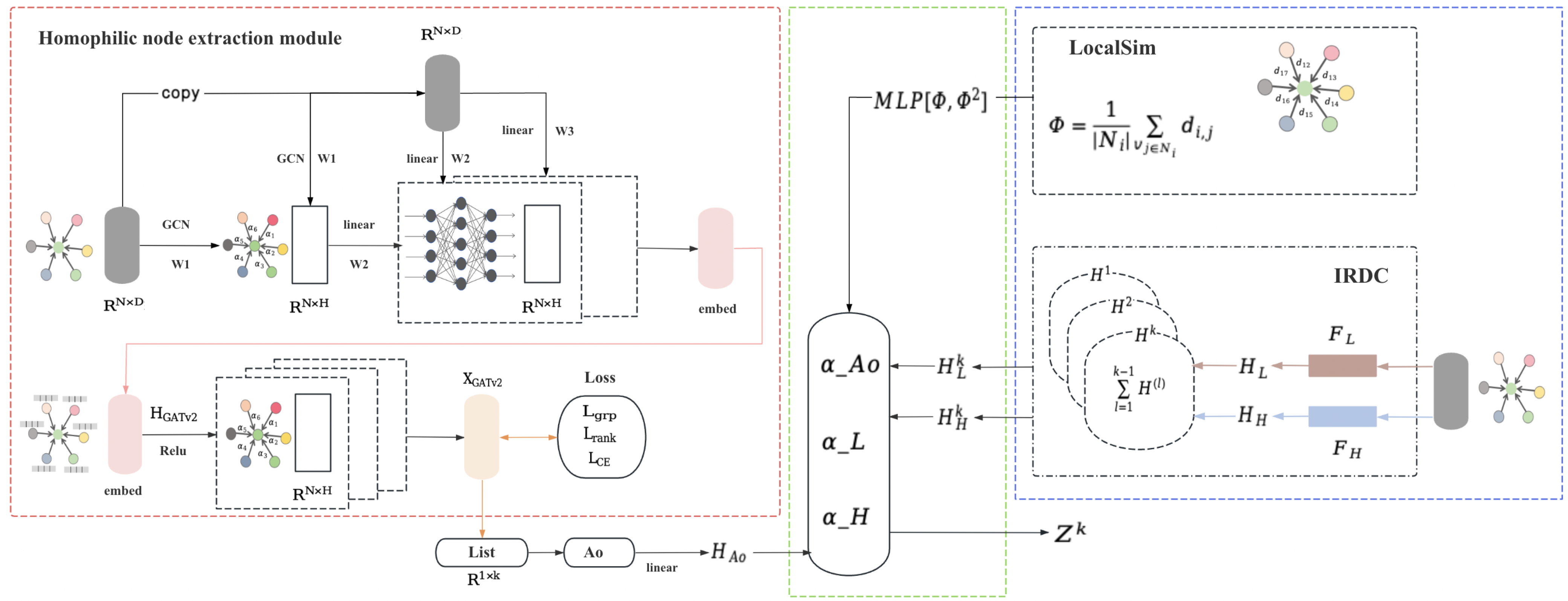
3. Proposed Method
3.1. Overview
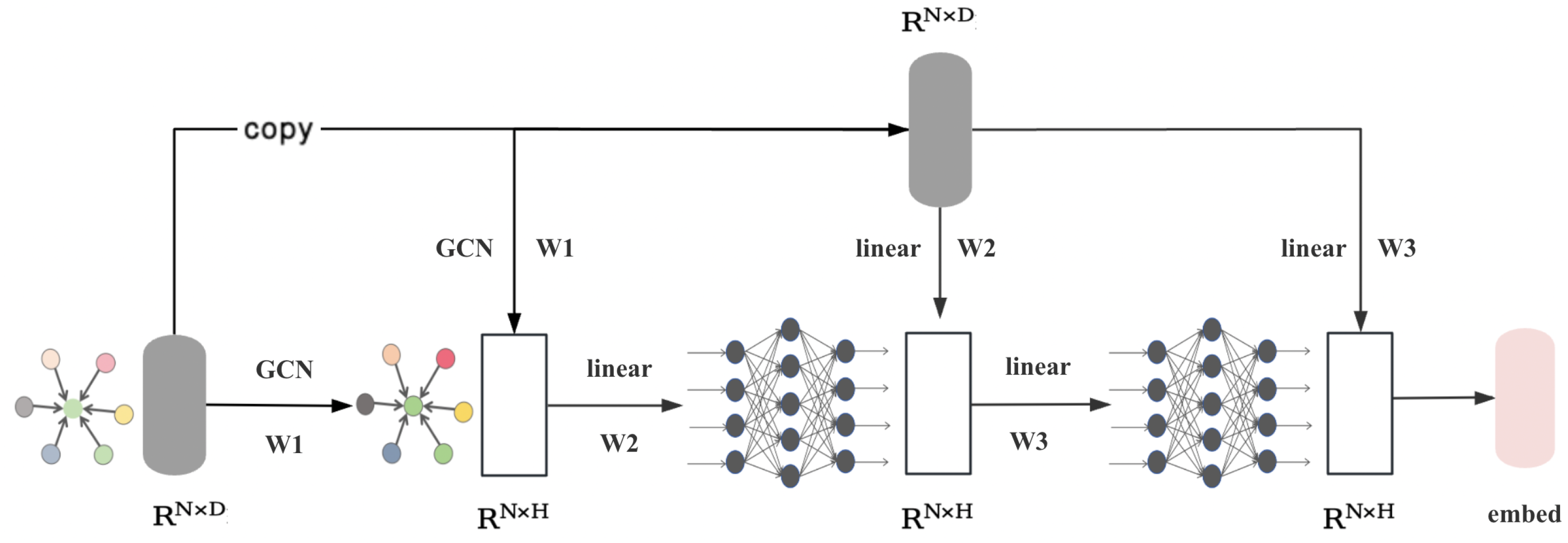
3.2. Homophilic Node Extraction
3.3. Heterophilic Spectrum Extraction
3.4. Node Feature Fusion
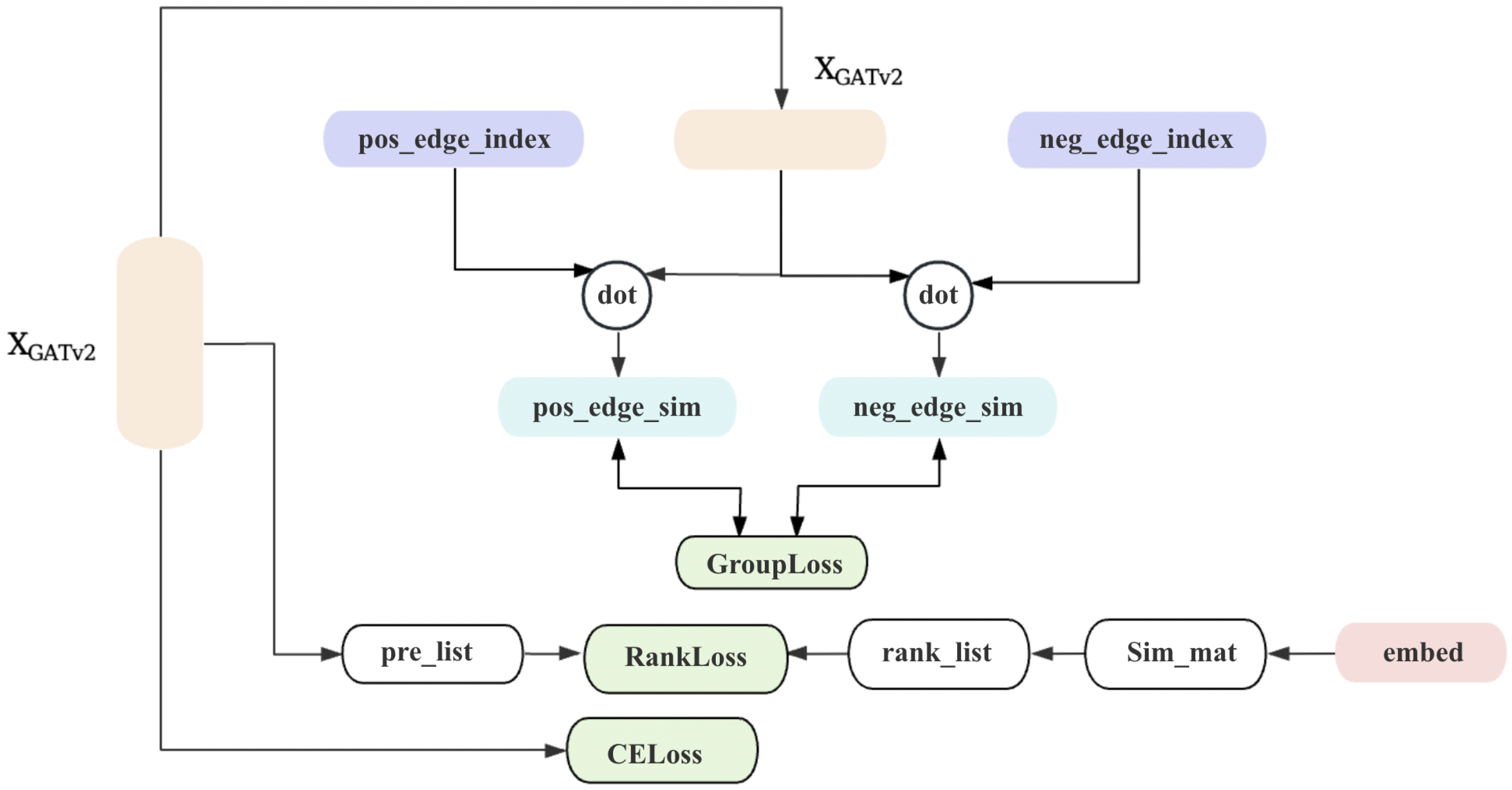
3.5. Loss Function
4. Experiments
4.1. Experimental Details and Datasets
4.2. Comparison with State-of-the-Art Methods
4.3. Ablation Studies
4.3.1. Analysis of the Homophilic Node Extraction
4.3.2. Analysis of the Heterophilic Spectrum Extraction
4.3.3. Analysis of the Node Feature Fusion
4.3.4. Analysis of the Loss Function
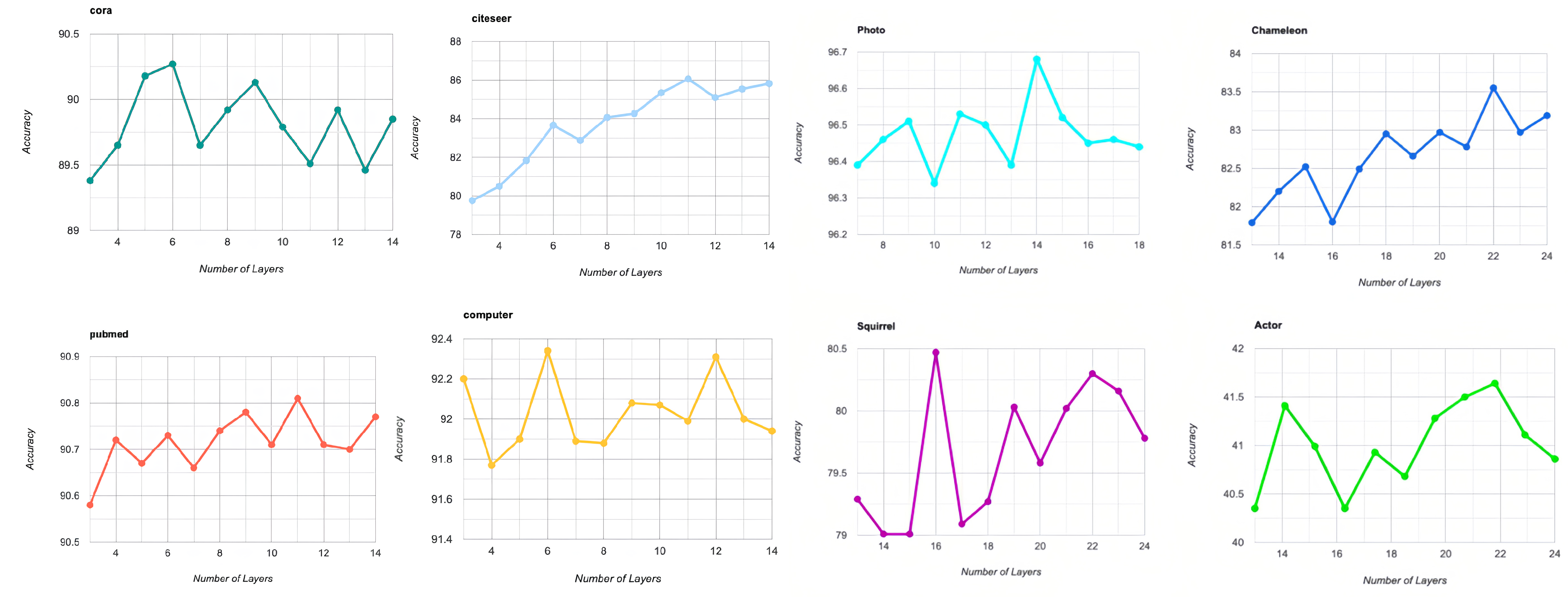
4.3.5. Analysis of the Hyperparameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HNE | homophilic node extraction |
| HSE | heterophilic spectrum extraction |
| NFF | node feature fusion |
| GNN | Graph Neural Networks |
| GCN | Graph Convolutional Network |
| GAT | Graph Attention Networks |
| GATv2 | A Dynamic Graph Attention Variant |
| GOAL | Graph Complementary Learning |
| LSGNN | Local Similarity Graph Neural Network |
Notations
| Undirected graphs | |
| Feature matrix | |
| Adjacency matrix | |
| Diagonal matrix | |
| Adjacency matrix with self-loops | |
| Diagonal matrix with self-loops | |
| The normalized Laplacian matrix | |
| Identity matrix |
References
- Pan, C.H.; Qu, Y.; Yao, Y.; Wang, M.J.S. HybridGNN: A Self-Supervised Graph Neural Network for Efficient Maximum Matching in Bipartite Graphs. Symmetry 2024, 16, 1631. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Wu, L.; Lin, H.; Liu, Z.; Liu, Z.; Huang, Y.; Li, S.Z. Homophily-enhanced self-supervision for graph structure learning: Insights and directions. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 12358–12372. [Google Scholar] [CrossRef]
- Khoushehgir, F.; Noshad, Z.; Noshad, M.; Sulaimany, S. NPI-WGNN: A Weighted Graph Neural Network Leveraging Centrality Measures and High-Order Common Neighbor Similarity for Accurate ncRNA–Protein Interaction Prediction. Analytics 2024, 3, 476–492. [Google Scholar] [CrossRef]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wang, Y.; Xiang, S.; Pan, C. Improving the Homophily of Heterophilic Graphs for Semi-Supervised Node Classification. In Proceedings of the 2023 IEEE International Conference on Multimedia and Expo (ICME), Brisbane, Australia, 10–14 July 2023. [Google Scholar]
- Li, J.; Zheng, R.; Feng, H.; Li, M.; Zhuang, X. Permutation equivariant graph framelets for Heterophilous graph learning. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 11634–11648. [Google Scholar] [CrossRef]
- Chen, R. Preserving Global Information for Graph Clustering with Masked Autoencoders. Mathematics 2024, 12, 1574. [Google Scholar] [CrossRef]
- Huang, W.; Guan, X.; Liu, D. Revisiting homophily ratio: A relation-aware Graph Neural Network for homophily and heterophily. Electronics 2023, 12, 1017. [Google Scholar] [CrossRef]
- Oishi, Y.; Kaneiwa, K. Multi-Duplicated Characterization Of Graph Structures Using Information Gain Ratio For Graph Neural Networks. IEEE Access 2023, 11, 34421–34430. [Google Scholar] [CrossRef]
- Park, H.S.; Park, H.M. Enhancing Heterophilic Graph Neural Network Performance Through Label Propagation in K-Nearest Neighbor Graphs. In Proceedings of the 2024 IEEE International Conference on Big Data and Smart Computing (BigComp), Bangkok, Thailand, 18–21 February 2024. [Google Scholar]
- Guan, X.; Wang, D.; Xiong, C.; Li, S.; Chen, Y. PBGAN: Path Based Graph Attention Network for Heterophily. In Proceedings of the 2022 26th International Conference on Pattern Recognition (ICPR), Montreal, QC, Canada, 21–25 August 2022. [Google Scholar]
- Sun, J.; Zhang, L.; Zhao, S.; Yang, Y. Improving your graph neural networks: A high-frequency booster. In Proceedings of the 2022 IEEE International Conference on Data Mining Workshops (ICDMW), Orlando, FL, USA, 28 November–1 December 2022. [Google Scholar]
- Wang, Y.; Hu, L.; Cao, X.; Chang, Y.; Tsang, I.W. Enhancing Locally Adaptive Smoothing of Graph Neural Networks Via Laplacian Node Disagreement. IEEE Trans. Knowl. Data Eng. 2023, 36, 1099–1112. [Google Scholar] [CrossRef]
- Gu, M.; Yang, G.; Zhou, S.; Ma, N.; Chen, J.; Tan, Q.; Bu, J. Homophily-enhanced structure learning for graph clustering. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Wu, F.; Souza, A.; Zhang, T.; Fifty, C.; Yu, T.; Weinberger, K. Simplifying graph convolutional networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Lingam, V.; Ragesh, R.; Iyer, A.; Sellamanickam, S. Simple truncated svd based model for node classification on heterophilic graphs. arXiv 2021, arXiv:2106.12807. [Google Scholar]
- Xu, B.; Shen, H.; Cao, Q.; Cen, K.; Cheng, X. Graph convolutional networks using heat kernel for semi-supervised learning. arXiv 2020, arXiv:2007.16002. [Google Scholar]
- Wang, X.; Zhang, M. How powerful are spectral graph neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022. [Google Scholar]
- He, M.; Wei, Z.; Xu, H. Bernnet: Learning arbitrary graph spectral filters via bernstein approximation. Adv. Neural Inf. Process. Syst. 2021, 34, 14239–14251. [Google Scholar]
- Chien, E.; Peng, J.; Li, P.; Milenkovic, O. Adaptive universal generalized pagerank graph neural network. arXiv 2020, arXiv:2006.07988. [Google Scholar]
- Awasthi, A.K.; Garov, A.K.; Sharma, M.; Sinha, M. GNN model based on node classification forecasting in social network. In Proceedings of the 2023 International Conference on Artificial Intelligence and Smart Communication (AISC), Greater Noida, India, 27–29 January 2023. [Google Scholar]
- Shetty, R.D.; Bhattacharjee, S.; Thanmai, K. Node Classification in Weighted Complex Networks Using Neighborhood Feature Similarity. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 3982–3994. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Pan, J.; Lin, H.; Dong, Y.; Wang, Y.; Ji, Y. MAMF-GCN: Multi-scale adaptive multi-channel fusion deep graph convolutional network for predicting mental disorder. Comput. Biol. Med. 2022, 148, 105823. [Google Scholar] [CrossRef] [PubMed]
- Gasteiger, J.; Bojchevski, A.; Günnemann, S. Predict then propagate: Graph neural networks meet personalized pagerank. arXiv 2018, arXiv:1810.05997. [Google Scholar]
- Pei, H.; Wei, B.; Chang, K.C.C.; Lei, Y.; Yang, B. Geom-gcn: Geometric graph convolutional networks. arXiv 2020, arXiv:2002.05287. [Google Scholar]
- Abu-El-Haija, S.; Perozzi, B.; Kapoor, A.; Alipourfard, N.; Lerman, K.; Harutyunyan, H.; Galstyan, A. Mixhop: Higher-order graph convolutional architectures via sparsified neighborhood mixing. In Proceedings of the international Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Roy, K.K.; Roy, A.; Rahman, A.M.; Amin, M.A.; Ali, A.A. Node embedding using mutual information and self-supervision based bi-level aggregation. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021. [Google Scholar]
- Zhu, J.; Rossi, R.A.; Rao, A.; Mai, T.; Lipka, N.; Ahmed, N.K.; Koutra, D. Graph neural networks with heterophily. Proc. Aaai Conf. Artif. Intell. 2021, 35, 11168–11176. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, X.; Shah, N.; Tang, J. Is homophily a necessity for graph neural networks? arXiv 2021, arXiv:2106.06134. [Google Scholar]
- Chen, D.; Lin, Y.; Li, W.; Li, P.; Zhou, J.; Sun, X. Measuring and relieving the over-smoothing problem for graph neural networks from the topological view. Proc. Aaai Conf. Artif. Intell. 2020, 34, 3438–3445. [Google Scholar] [CrossRef]
- Bo, D.; Wang, X.; Shi, C.; Shen, H. Beyond low-frequency information in graph convolutional networks. Proc. Aaai Conf. Artif. Intell. 2021, 35, 3950–3957. [Google Scholar] [CrossRef]
- Brody, S.; Alon, U.; Yahav, E. How attentive are graph attention networks? arXiv 2021, arXiv:2105.14491. [Google Scholar]
- Chen, Y.; Luo, Y.; Tang, J.; Yang, L.; Qiu, S.; Wang, C.; Cao, X. LSGNN: Towards general graph neural network in node classification by local similarity. arXiv 2023, arXiv:2305.04225. [Google Scholar]
- Zheng, X.; Zhang, M.; Chen, C.; Zhang, Q.; Zhou, C.; Pan, S. Auto-heg: Automated graph neural network on heterophilic graphs. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023. [Google Scholar]
- Taud, H.; Mas, J.F. Multilayer perceptron (MLP). In Geomatic Approaches for Modeling Land Change Scenarios; Springer: Cham, Switzerland, 2018; pp. 451–455. [Google Scholar]
- Chen, M.; Wei, Z.; Huang, Z.; Ding, B.; Li, Y. Simple and deep graph convolutional networks. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020. [Google Scholar]
- Zheng, Y.; Zhang, H.; Lee, V.; Zheng, Y.; Wang, X.; Pan, S. Finding the missing-half: Graph complementary learning for homophily-prone and heterophily-prone graphs. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
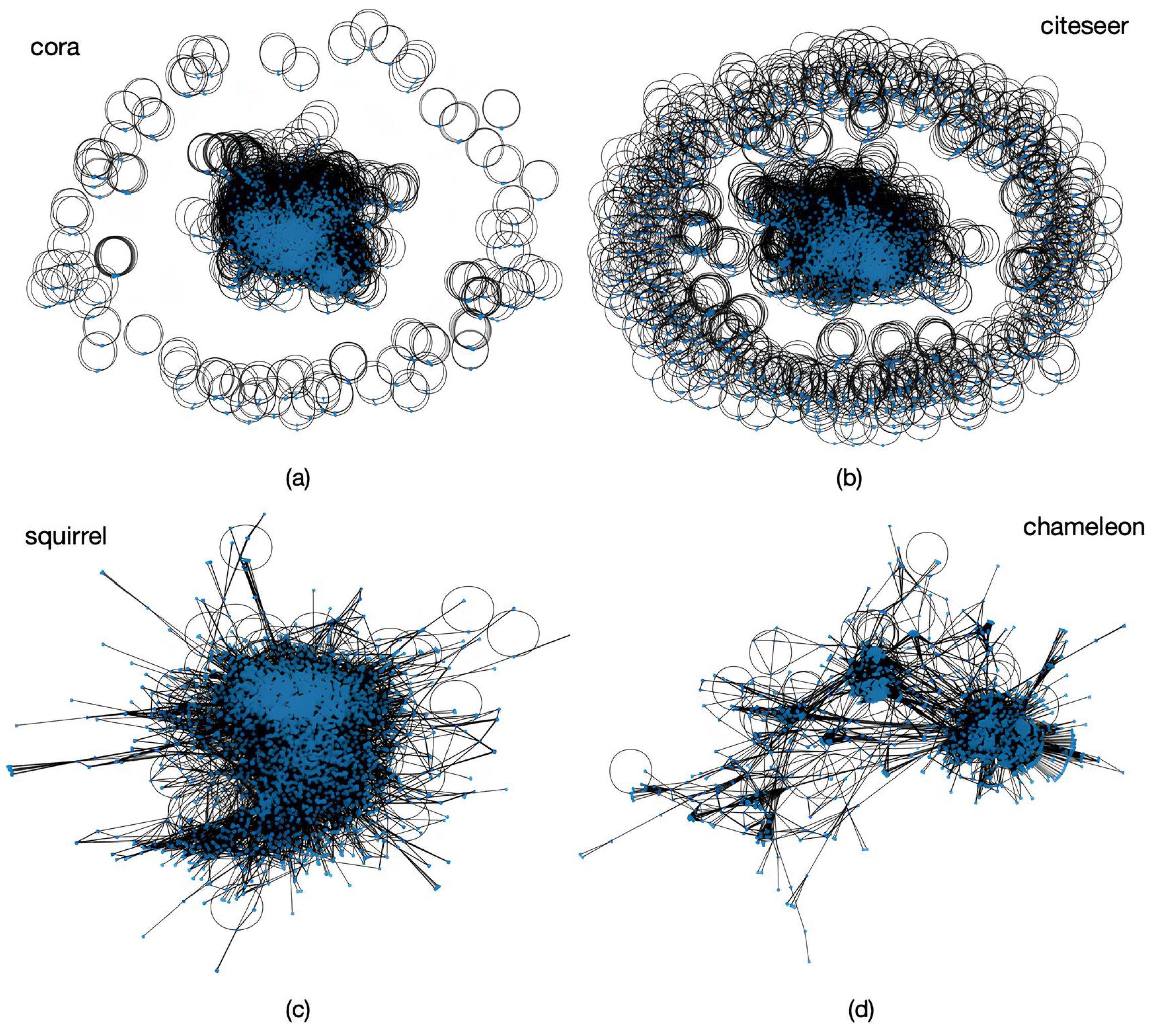


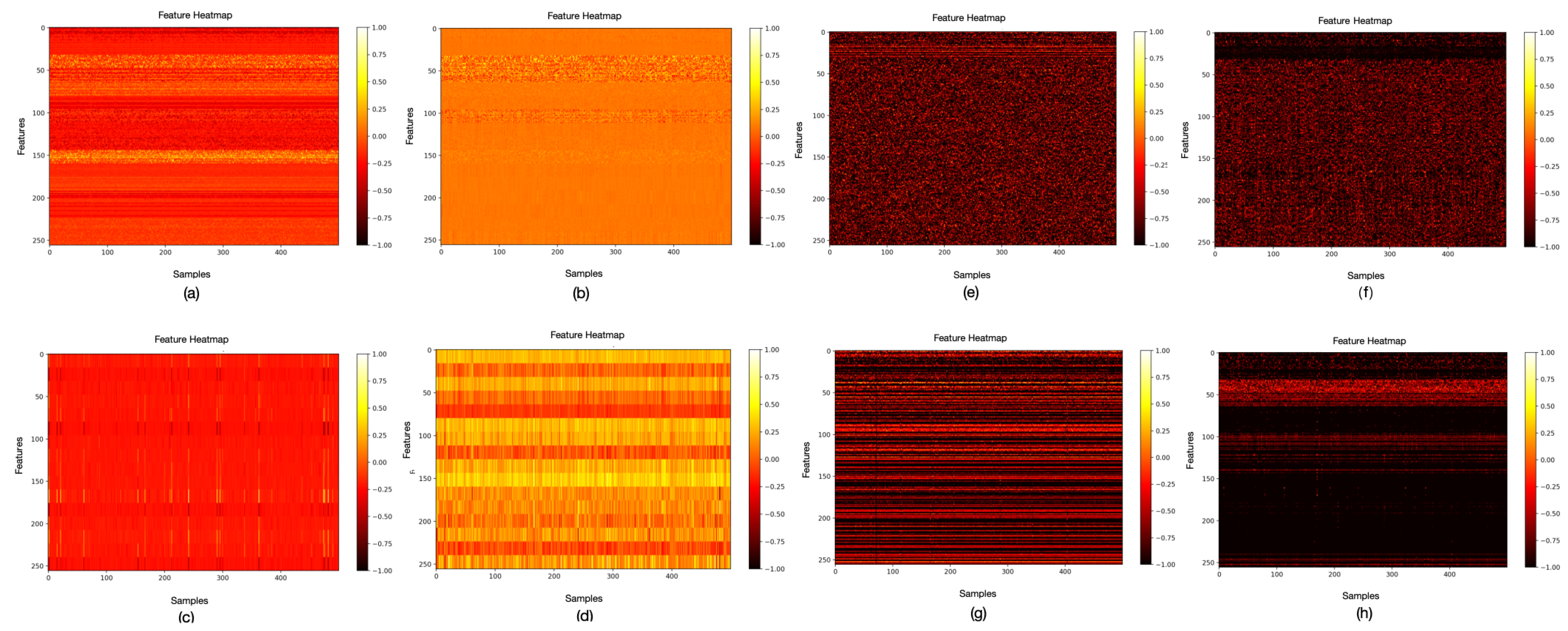
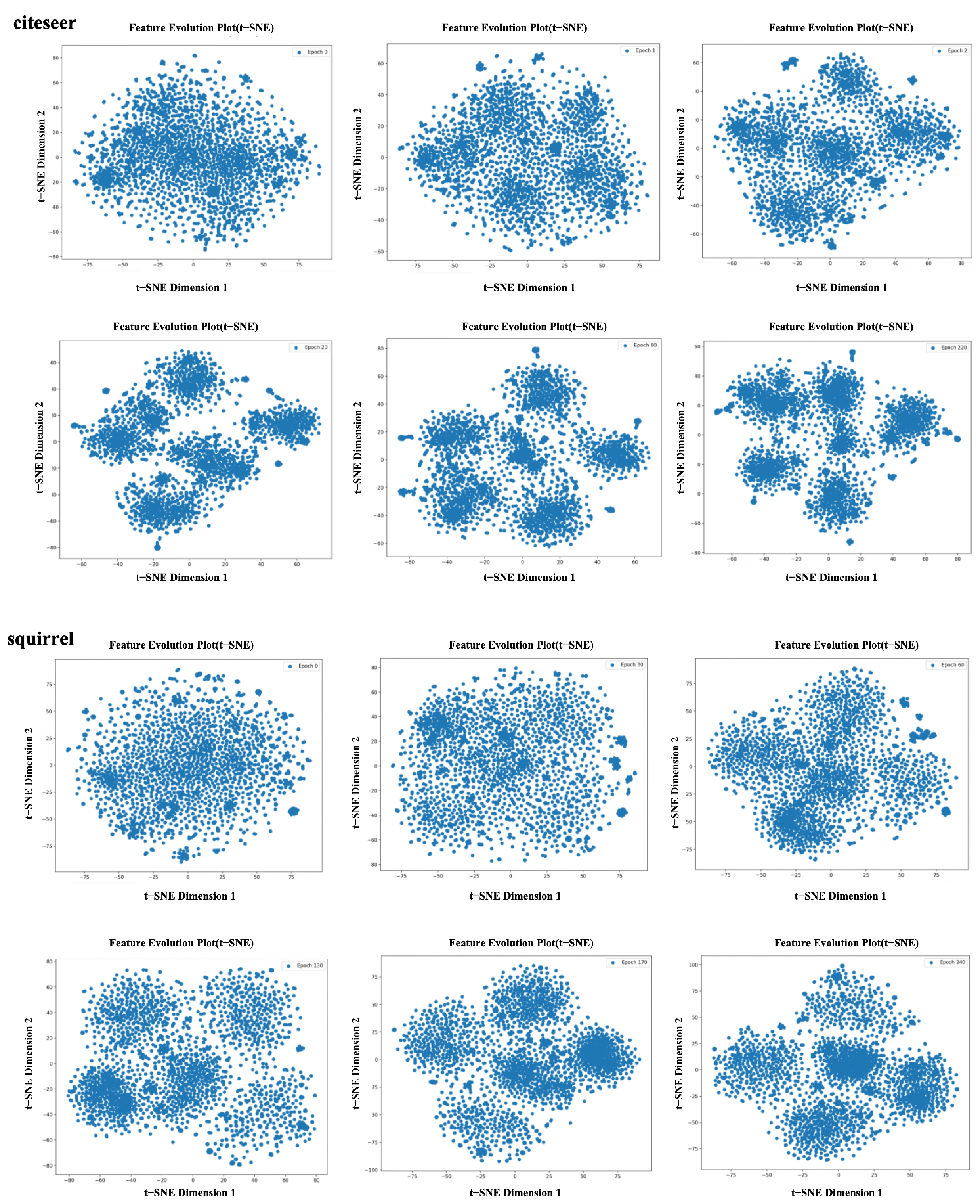
| References | Problems Areas | Proposed Methods | Similarities with NHSH | Differences with NHSH |
|---|---|---|---|---|
| [1,2,3,4,5,15] | Homophilic graph | By integrating semantic and contextual information, the node aggregation problem in homophilic graphs is effectively addressed through the learning of node embeddings. | Both leverage the structural information of the graph, utilizing its structural symmetry to enhance the quality of node representations for improved node classification. | NHSH not only focuses on the node aggregation problem in homophilic graphs but also combines local homophilic information with global spectral heterophilic information, enabling better handling of the complexity of heterophilic graphs. |
| [6,7,8,9,10,11,12] | Heterophilic graph | A graph convolution or multi-hop aggregation strategy is employed to update node features, enabling better handling of the complex connectivity patterns in heterophilic graphs. | Both focus on effectively aggregating and updating node features in heterophilic graphs, aiming to improve information aggregation strategies and minimize the risk of node feature loss. | |
| [13,14] | Heterophilic graph | Focusing on the filter-based method, which uses low-frequency and high-frequency information to process different features of nodes in the graph. | Both propose the aggregation of node features using filters. |
| Homophily | Heterophily | |||||||
|---|---|---|---|---|---|---|---|---|
| Cora | Citeseer | PubMed | Computer | Photo | Chameleon | Squirrel | Actor | |
| Classes | 7 | 6 | 5 | 10 | 8 | 5 | 5 | 5 |
| Features | 1433 | 3703 | 500 | 767 | 745 | 2325 | 2089 | 932 |
| Nodes | 2708 | 3327 | 19,717 | 13,752 | 7650 | 2277 | 5201 | 7600 |
| Edges | 5278 | 4552 | 44,324 | 491,722 | 238,162 | 31,371 | 198,353 | 26,659 |
| Cora | Citeseer | PubMed | Computer | Photo | Chameleon | Squirrel | Actor | |
|---|---|---|---|---|---|---|---|---|
| MLP | 72.09 | 71.67 | 87.47 | 83.59 | 90.49 | 46.55 | 30.67 | 28.75 |
| GCN | 87.50 | 75.11 | 87.20 | 83.55 | 89.30 | 62.72 | 47.26 | 29.98 |
| GAT | 88.25 | 75.75 | 85.88 | 85.36 | 90.81 | 62.19 | 51.80 | 28.17 |
| APPNP | 88.36 | 76.03 | 86.21 | 88.32 | 94.44 | 50.88 | 33.58 | 29.82 |
| GPR-GNN | 88.65 | 75.70 | 88.53 | 87.63 | 94.60 | 67.96 | 49.52 | 30.78 |
| JKNET | 86.99 | 75.38 | 88.64 | 86.97 | 92.68 | 64.63 | 44.91 | 28.48 |
| GOAL | 88.75 | 77.15 | 89.25 | 91.33 | 95.60 | 71.65 | 60.53 | 36.46 |
| LSGNN | 88.49 | 76.71 | 90.23 | 90.45 | 95.02 | 79.04 | 72.81 | 36.18 |
| Running Times(s) | 0.24 | 0.50 | 2.16 | 1.17 | 0.73 | 0.39 | 1.31 | 1.48 |
| NHSH | 90.69 | 83.20 | 90.70 | 91.99 | 96.46 | 86.81 | 83.18 | 39.65 |
| Local Structure Embedded | Feature Extraction | Cora | Citeseer | Chameleon | Squirrel | Actor | Photo | Computers | PubMed |
|---|---|---|---|---|---|---|---|---|---|
| Linear | GCN | 0.8416 | 0.7341 | 0.7461 | 0.6102 | 0.2114 | 0.9207 | 0.8100 | 0.7779 |
| GCN | GCN | 0.8663 | 0.7915 | 0.7721 | 0.6680 | 0.2439 | 0.9273 | 0.8448 | 0.8544 |
| Linear | GAT | 0.7920 | 0.7396 | 0.7718 | 0.6036 | 0.2259 | 0.9188 | 0.8383 | 0.7668 |
| Linear | GATv2 | 0.8309 | 0.7420 | 0.7882 | 0.6296 | 0.2145 | 0.9268 | 0.8345 | 0.7722 |
| GCN | GAT | 0.8779 | 0.7928 | 0.8017 | 0.7208 | 0.2504 | 0.9339 | 0.8743 | 0.8590 |
| GCN | GATv2 | 0.9055 | 0.8230 | 0.8169 | 0.7282 | 0.3098 | 0.9438 | 0.8764 | 0.8848 |
| Cora | Citeseer | Chameleon | Squirrel | Actor | Photo | Computers | PubMed | |
|---|---|---|---|---|---|---|---|---|
| 79.48 | 71.68 | 78.44 | 73.16 | 37.87 | 92.81 | 88.59 | 89.71 | |
| 87.58 | 76.62 | 73.90 | 64.32 | 37.91 | 93.43 | 91.77 | 89.87 | |
| + | 89.20 | 78.85 | 76.31 | 73.64 | 38.26 | 95.36 | 91.85 | 90.31 |
| Cora | Citeseer | Chameleon | Squirrel | Actor | Photo | Computers | PubMed | |
|---|---|---|---|---|---|---|---|---|
| 87.79 ± 1.41 | 76.95 ± 1.90 | 75.11 ± 1.20 | 71.59 ± 2.05 | 37.17 ± 1.09 | 95.36 ± 0.77 | 91.34 ± 0.51 | 89.84 ± 0.47 | |
| NHSH | 89.46 ± 1.23 | 82.09 ± 1.11 | 85.81 ± 1.00 | 82.40 ± 0.78 | 39.05 ± 0.60 | 95.89 ± 0.57 | 91.46 ± 0.53 | 90.13 ± 0.57 |
| loss_rank | loss_group | loss_ce | Cora | Citeseer | Chameleon | Squirrel | Actor | Photo | Computers | PubMed |
|---|---|---|---|---|---|---|---|---|---|---|
| ✓ | × | × | 0.2661 | 0.4200 | 0.2294 | 0.2794 | 0.2515 | 0.2769 | 0.2631 | 0.4049 |
| × | ✓ | × | 0.8445 | 0.8183 | 0.7258 | 0.7057 | 0.3016 | 0.9191 | 0.7548 | 0.8791 |
| × | × | ✓ | 0.2930 | 0.2106 | 0.3142 | 0.2219 | 0.2258 | 0.2780 | 0.3125 | 0.3453 |
| × | ✓ | ✓ | 0.9137 | 0.8070 | 0.7552 | 0.7162 | 0.2800 | 0.9366 | 0.8543 | 0.8769 |
| ✓ | × | ✓ | 0.4781 | 0.3571 | 0.6848 | 0.2248 | 0.2029 | 0.8405 | 0.6540 | 0.8227 |
| ✓ | ✓ | × | 0.8905 | 0.8222 | 0.7408 | 0.6817 | 0.2806 | 0.9443 | 0.8170 | 0.8632 |
| ✓ | ✓ | ✓ | 0.9055 | 0.8230 | 0.8169 | 0.7282 | 0.3098 | 0.9438 | 0.8764 | 0.8848 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Dai, W.; Liu, X.; Kang, M.; Ji, R. NHSH: Graph Hybrid Learning with Node Homophily and Spectral Heterophily for Node Classification. Symmetry 2025, 17, 115. https://doi.org/10.3390/sym17010115
Liu K, Dai W, Liu X, Kang M, Ji R. NHSH: Graph Hybrid Learning with Node Homophily and Spectral Heterophily for Node Classification. Symmetry. 2025; 17(1):115. https://doi.org/10.3390/sym17010115
Chicago/Turabian StyleLiu, Kang, Wenqing Dai, Xunyuan Liu, Mengtao Kang, and Runshi Ji. 2025. "NHSH: Graph Hybrid Learning with Node Homophily and Spectral Heterophily for Node Classification" Symmetry 17, no. 1: 115. https://doi.org/10.3390/sym17010115
APA StyleLiu, K., Dai, W., Liu, X., Kang, M., & Ji, R. (2025). NHSH: Graph Hybrid Learning with Node Homophily and Spectral Heterophily for Node Classification. Symmetry, 17(1), 115. https://doi.org/10.3390/sym17010115





