Directional Invariants of Doubly Periodic Tangles
Abstract
1. Introduction
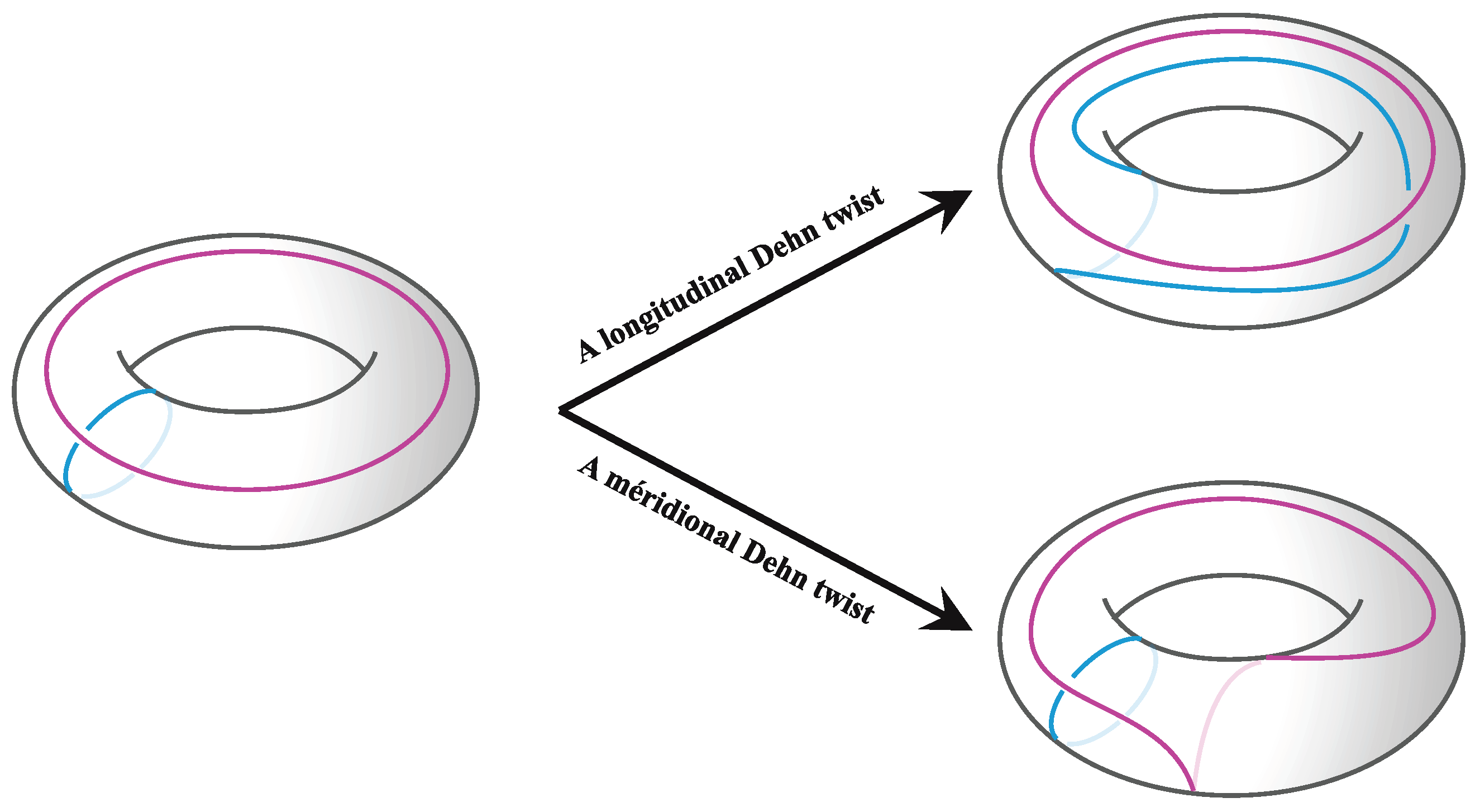
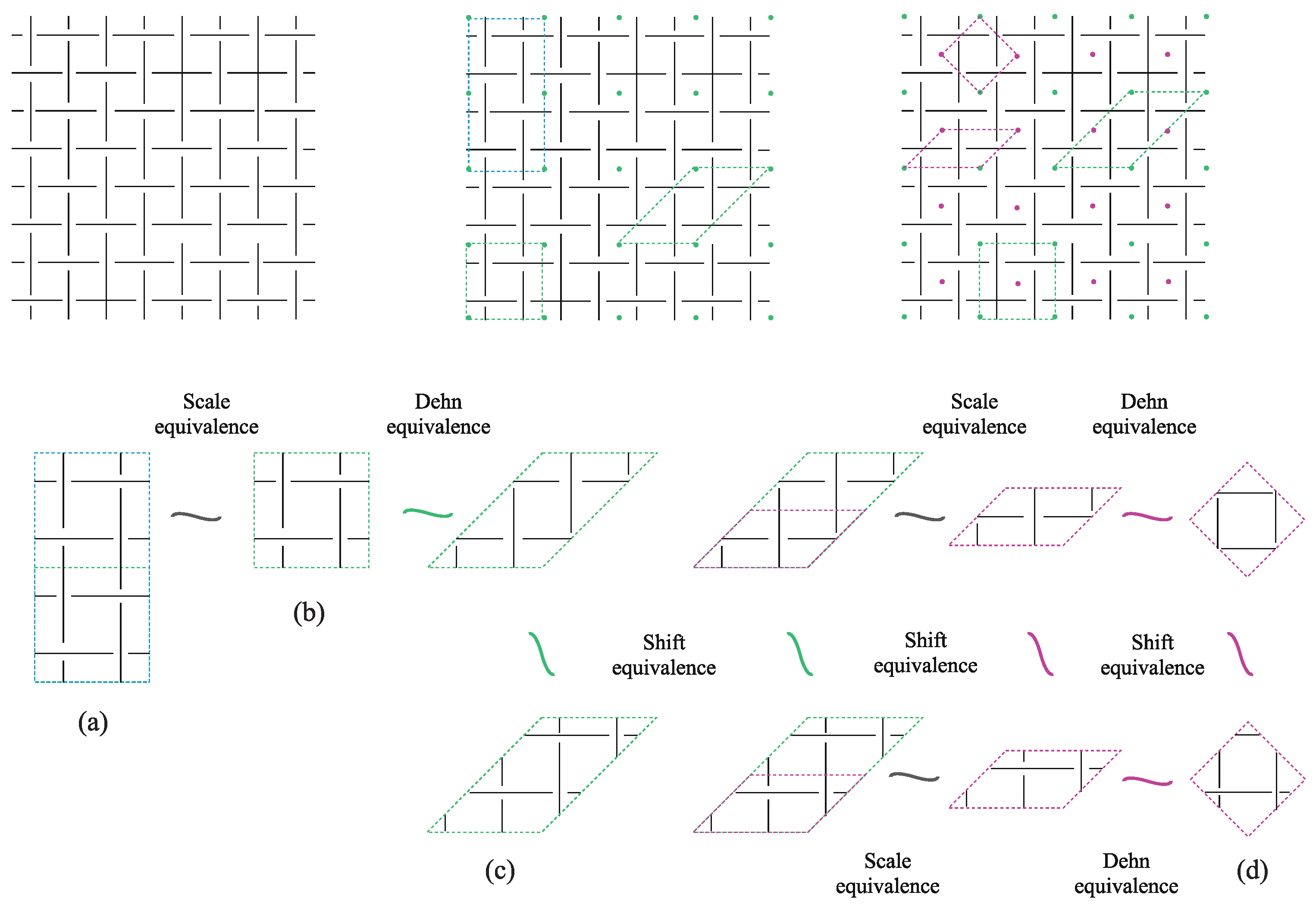
2. Preliminaries on Equivalence of DP Tangles
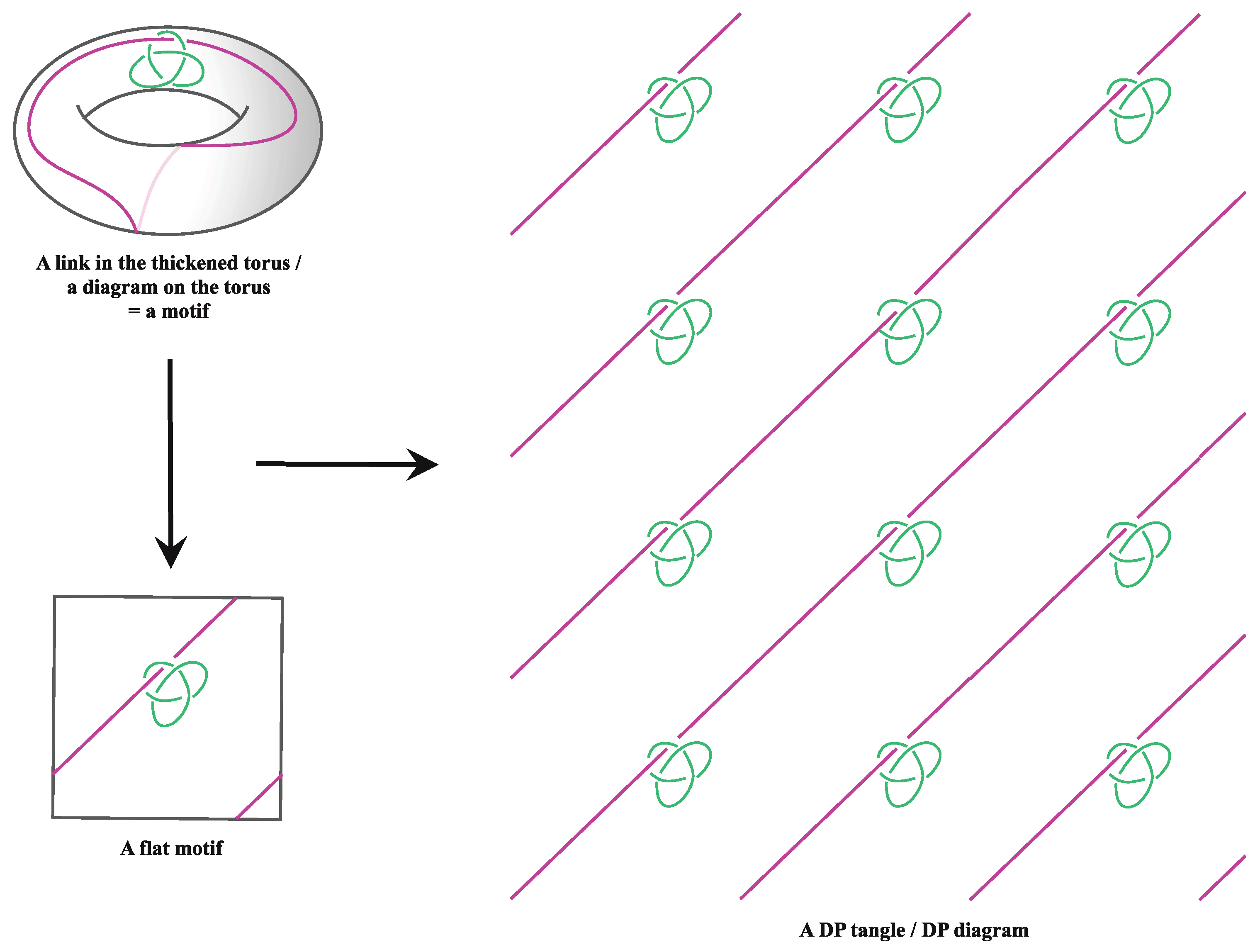
2.1. DP Tangles and Motifs
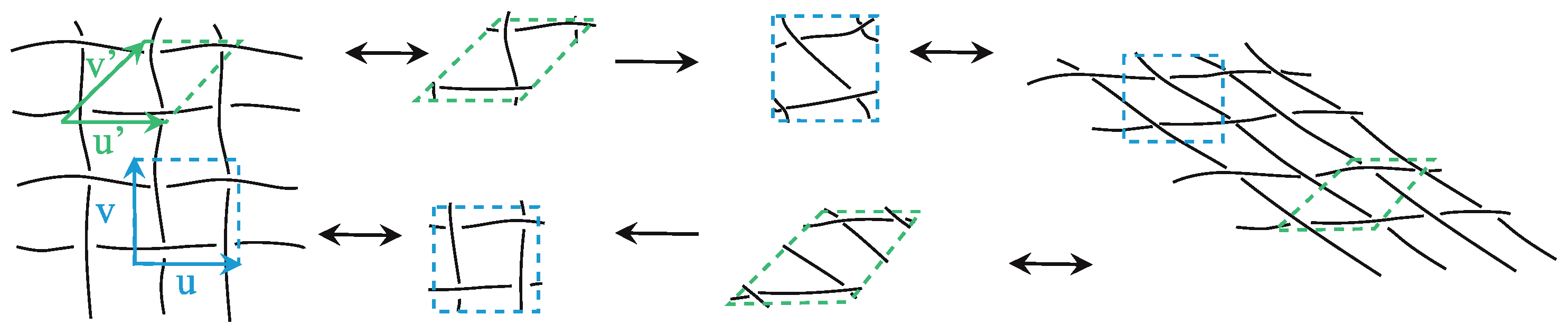
2.2. Equivalence of DP Tangles and Their Motifs
3. Interlinked Compounds and the Class of a Motif
3.1. The Class of an Interlinked Compound
- i.
- μ forms a split sublink of τ, that is, a sublink that can split from the rest of τ by isotopy;
- ii.
- μ cannot split into separate sublinks under isotopy.
- a.
- μ can be enclosed, up to motif isotopy, in a three-ball in . Then, it is referred to as a null-homotopic compound of τ and it lifts in to a disjoint union of null-homotopic compounds.
- b.
- μ can be enclosed, up to motif isotopy, in an essential thickened ribbon in . In this case μ is referred to as a ribbon compound of τ and it lifts in to an infinite disjoint union of identical ribbon compounds in .
- c.
- μ cannot be enclosed in either a three-ball or a thickened ribbon in , under any motif isotopy. In this case μ is referred to as a cover compound of τ and it lifts in to a single cover compound in .
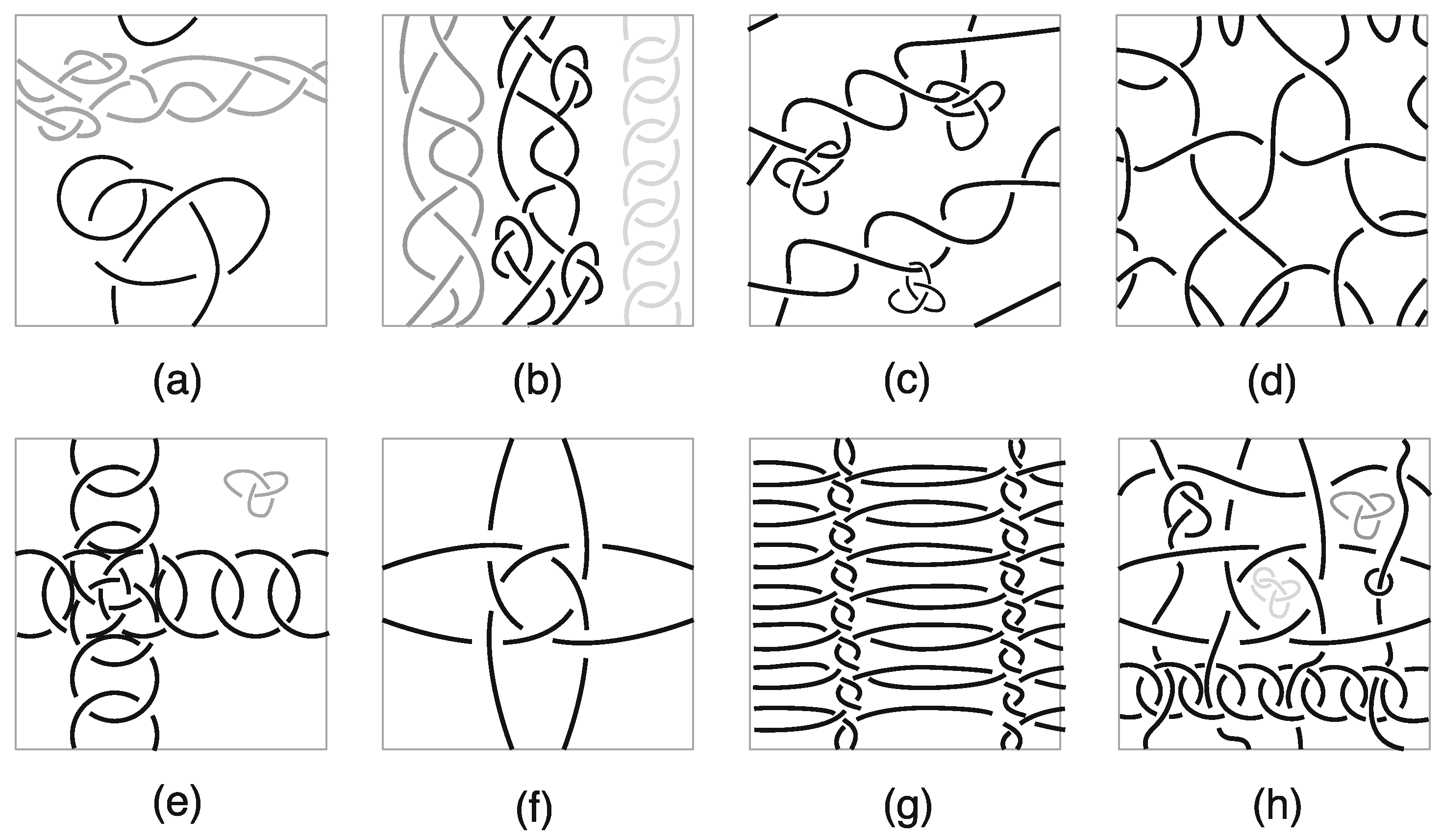
3.2. Subclasses of Interlinked Compounds
- is an essential ribbon compound if it consists of only essential closed curves in . An example is demonstrated by each one of the three interlinked compounds of motif (b) in Figure 7.
- is a chain-link ribbon compound if it consists of an interlinked combination of only null-homotopic components. An example is the interlinked compound in Figure 7c.
- is a chain–essential ribbon compound if it consists of essential curves interlinked with chain-links (see for example Figure 7d).
- is a null–essential ribbon compound if it consists of an essential ribbon compound interlinked with a null-homotopic compound (see for example Figure 7e).
- is a null–chain ribbon compound if it consists of a chain-link ribbon compound interlinked with a null-homotopic compound (see for example Figure 7f).
- If is a combination of all the above, we shall be refer to as a mixed ribbon compound (for an illustration see Figure 7g).
- is a polycatenane compound if it consists of only interlinked null-homotopic components. In particular, polycatenane compounds can be distinguished as follows:
- *
- is a chain–polycatenane compound if it can be defined as the interlinkage of at least two chain-link ribbon compounds. An example is illustrated in Figure 7h;
- *
- is a null–chain–polycatenane compound if it consists of a chain-polycatenane compound interlinked with at least one null-homotopic compound, as illustrated in Figure 7i;
- *
- is a full-polycatenane compound if it consists of null-homotopic components only, without null-homotopic compounds, as the examples illustrated in Figure 7j,k;
- *
- is a null–full-polycatenane compound if it consists of a full-polycatenane compound interlinked with at least one null-homotopic compound, as the example illustrated in Figure 7l;
- *
- is a chain–full-polycatenane compound if it consists of a full-polycatenane compound interlinked with at least one chain-link compound, as the examples illustrated in Figure 7m;
- *
- is a null–chain–full-polycatenane compound if it is a combination of all the above classes of polycatenanes, as the example illustrated in Figure 7n.
- If contains essential closed curves, then we have the following possibilities:
- *
- is an essential cover compound if it consists of an interlinked combination of (only) essential ribbon compounds. This case is exemplified by the interlinked compound of motifs (o), (p), and (q) in Figure 7.
- *
- is a null–essential cover compound if it consists of essential cover compounds interlinked with null-homotopic compounds (see for example Figure 7r);
- *
- is a chain–essential cover compound if it consists of closed curves interlinked with chain-links (see for example Figure 7s);
- *
- is a null–chain–essential cover compound if it consists of essential closed curves interlinked with chain-links and null-homotopic compounds (see for example Figure 7t);
- *
- is a essential–full-polycatenane cover compound if it consists of essential curves interlinked with a full-polycatenane (see examples in Figure 7u,v);
- *
- is a null–essential–full-polycatenane cover compound if it consists of essential curves interlinked with a full-polycatenane and with null-homotopic compounds (see for example Figure 7w);
- *
- is a chain–essential–full-polycatenane cover compound if it consists of essential curves interlinked with chain links and with a full-polycatenane (see for example Figure 7x);
- *
- If is a combination of all the above, we shall be refer to as mixed cover compound (see for example Figure 7y).
3.3. The Class of a Motif
4. Directional Invariants and Axis-Motifs of DP Tangles
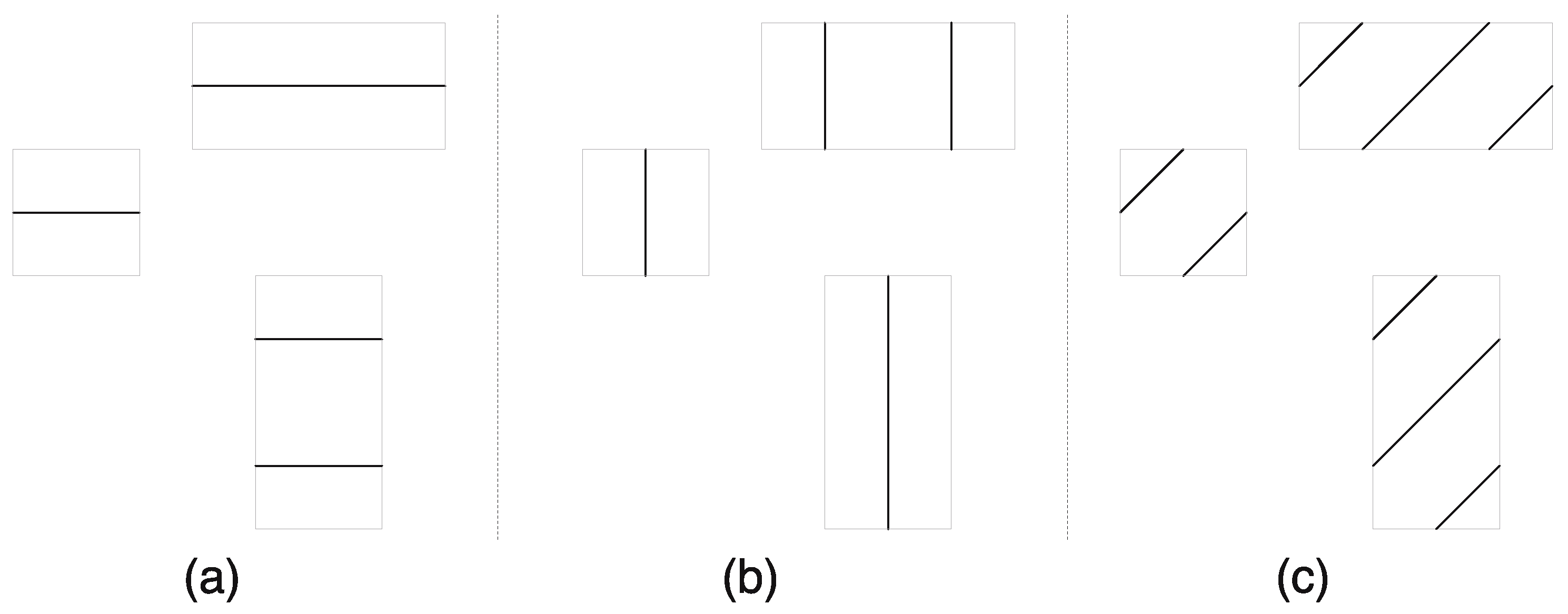
4.1. The Notion of Directions
- -
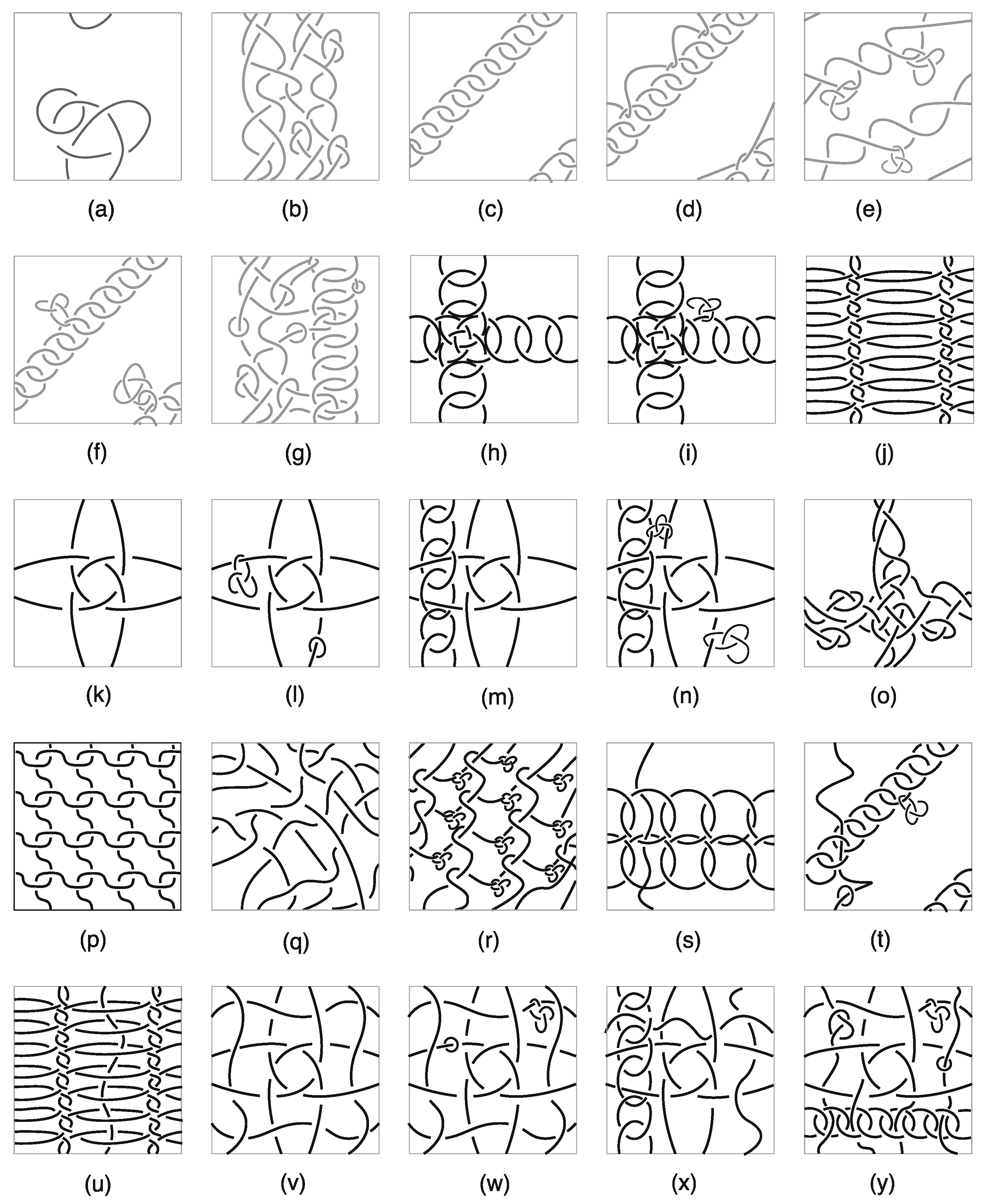
- The motifs (a), (l), (n), (t), (w), and (y) contains two isolated knots, while motifs (e) and (f) contain three isolated knots.
- -
- The motifs (b) and (o) contain five essential components, while motifs (p), (v), and (w) contain four essential components and motif (q) contains six essential components.
- -
- The motifs (c), (d), (f), (g), (m), (n), (t), (x), and (y) contain one chain link while the motifs (h) and (s) contain two chain links.
- -
- The motifs (j)–(n) and (u)–(y) contain a full polycatenane.
- a.
- If e is an isolated knot, thus homotopic to the trivial knot, then e is said to have direction .
- b.
- If e is an essential component, homotopic to an -torus knot, then e is said to have direction .
- c.
- If e is a chain-link, whose centerline curve is isotopic to an -torus knot, then e is said to have direction .
- d.
- If e is a full polycatenane, then e is said to have direction .
- N.
- If μ is a null-homotopic compound of τ, then μ is said to have direction .
- R.
- If μ is a ribbon compound of τ, whose centerline curve is isotopic to an -torus knot, then μ is said to have direction .
- C.
- If μ is a cover compound of τ, then we distinguish the following cases:
- 1.
- If μ is an essential cover compound, a chain–polycatenane compound or a chain–essential cover compound, then μ is an interlinkage of a finite set of distinct ribbon compounds , such that for all has direction . Then μ is said to have direction .
- 2.
- If μ is a null–essential cover compound or null–chain cover compound or null–chain–essential cover compound, then μ satisfies conditions (N) and (1) and is thus said to have direction .
- 3.
- If μ is a full polycatenane, then μ is said to have direction .
- 4.
- If μ is a null–full-polycatenane, then μ satisfies conditions (N) and (3) and is thus said to have direction .
- 5.
- If μ is a chain–full-polycatenane or a essential–full cover compound or a chain–essential-full cover compound, then μ satisfies conditions (1) and (3) and is thus said to have direction .
- 6.
- If μ is a null–chain–full cover compound, a null–essential–full cover compound or a mixed cover compound, then μ satisfies conditions (N), (1), and (3), and is thus said to have direction .
4.2. Axis-Motifs
- a.
- If e has direction , then the axis of e is a trivial knot, preserving possible intersections with longitude-meridian and their orders.
- b.
- If e has direction , then the axis of e is an -torus knot.
- c.
- If e has direction , then the axis of e is a flat link of as many trivial components as the components of e, preserving the intersections with longitude-meridian and their orders.
- a.
- If μ is a null-homotopic compound of τ defined as a link of c knots, then the axis of μ is a trivial link of c components.
- b.
- If μ is a ribbon compound of τ defined as a link of k elements with direction and c isolated knots, where , then the axis of μ consists of a -torus link and of a trivial link of c components.
- c.
- If μ is a cover compound of τ, then the axis of μ is the set of the axes of all its elements.
- -
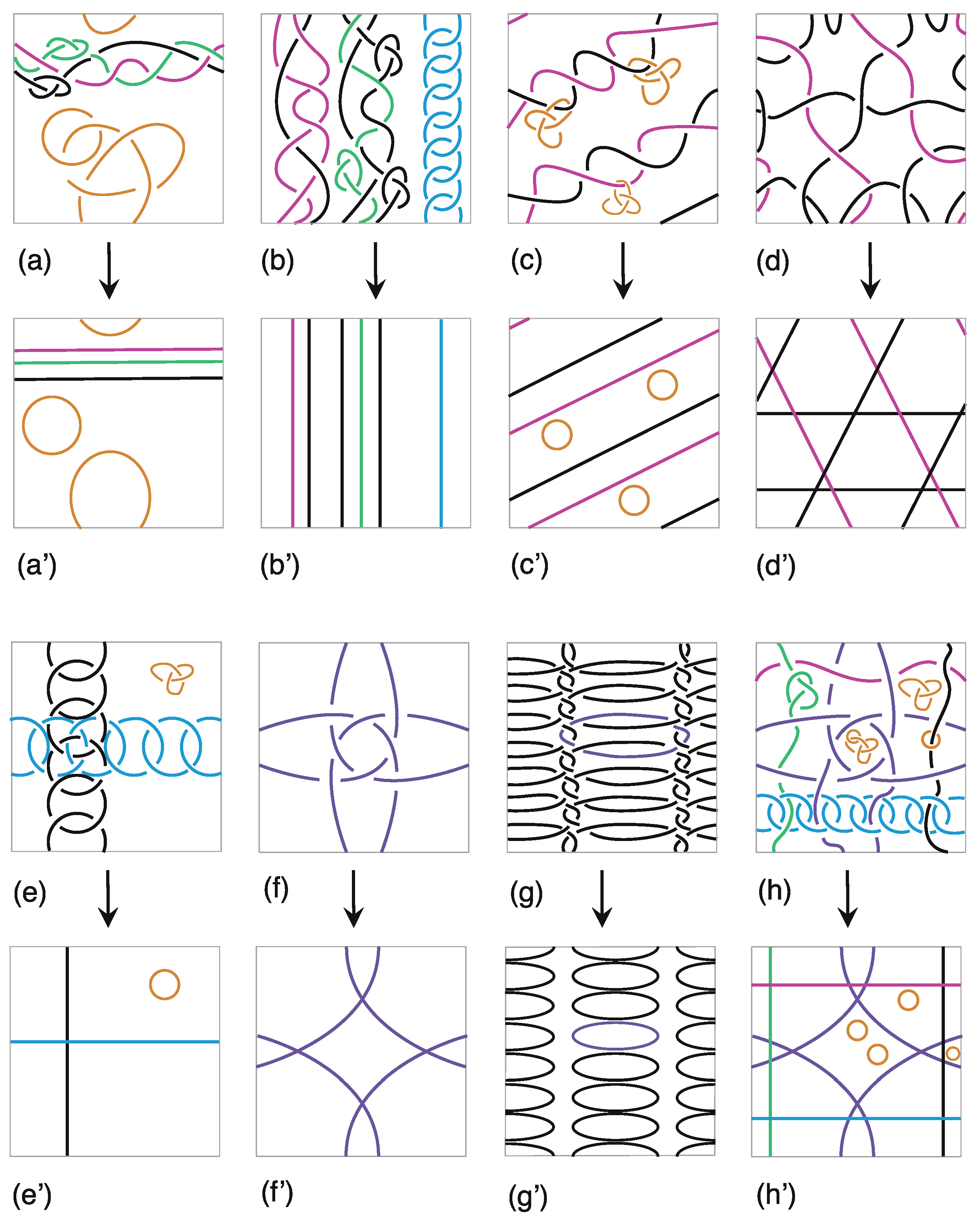
- Motif (a) contains two isolated knots and three essential components of the same direction. So, its direction is the set of two distinct elements, and its corresponding axis-motif (a′) contains two trivial knots and a -torus link.
- -
- Motif (b) contains three disjoint ribbon compounds; the leftmost consists of two essential components, the middle one contains three essential component, and the rightmost is a chain-link. The three compounds have the same direction, thus the motif has direction the singleton , and its corresponding axis-motif (b′) is a -torus link.
- -
- Motif (c) contains a null–essential ribbon compound made of two essential components and three isolated knots. So, it has direction and its corresponding axis-motif (c′) contains a -torus link and three trivial knots.
- -
- Motif (d) contains an essential cover compound made of three essential components. It has direction and its corresponding axis-motif (d′) contains a -torus knot, a -torus knot and a -torus knot.
- -
- Motif (e) contains a chain–polycatenane cover compound made of two interlinked chain-links and a null-homotopic compound consisting of a single knot. It has direction and its corresponding axis-motif (e′) contains a -torus knot, a -torus knot, and a trivial knot.
- -
- Motif (f) contains a full-polycatenane cover compound made of one knot. It has direction and its corresponding axis-motif (f′) contains one non-contractible trivial knot.
- -
- Motif (g) contains a full-polycatenane cover compound made of fourteen components. It has direction and its corresponding axis-motif (g′) consists of fourteen trivial knots, preserving the longitude/meridian intersections.
- -
- Motif (h) contains a cover compound consisting of an interlinkage of a full-polycatenane of one knot, a chain-link, three essential curves (pink, green, black), and a trivial knot. It also contains two null-homotopic compounds of one and two components, respectively. It has direction and its corresponding axis-motif (h′) contains a -torus link, a -torus link, four trivial knots, and one non-contractible trivial knot.
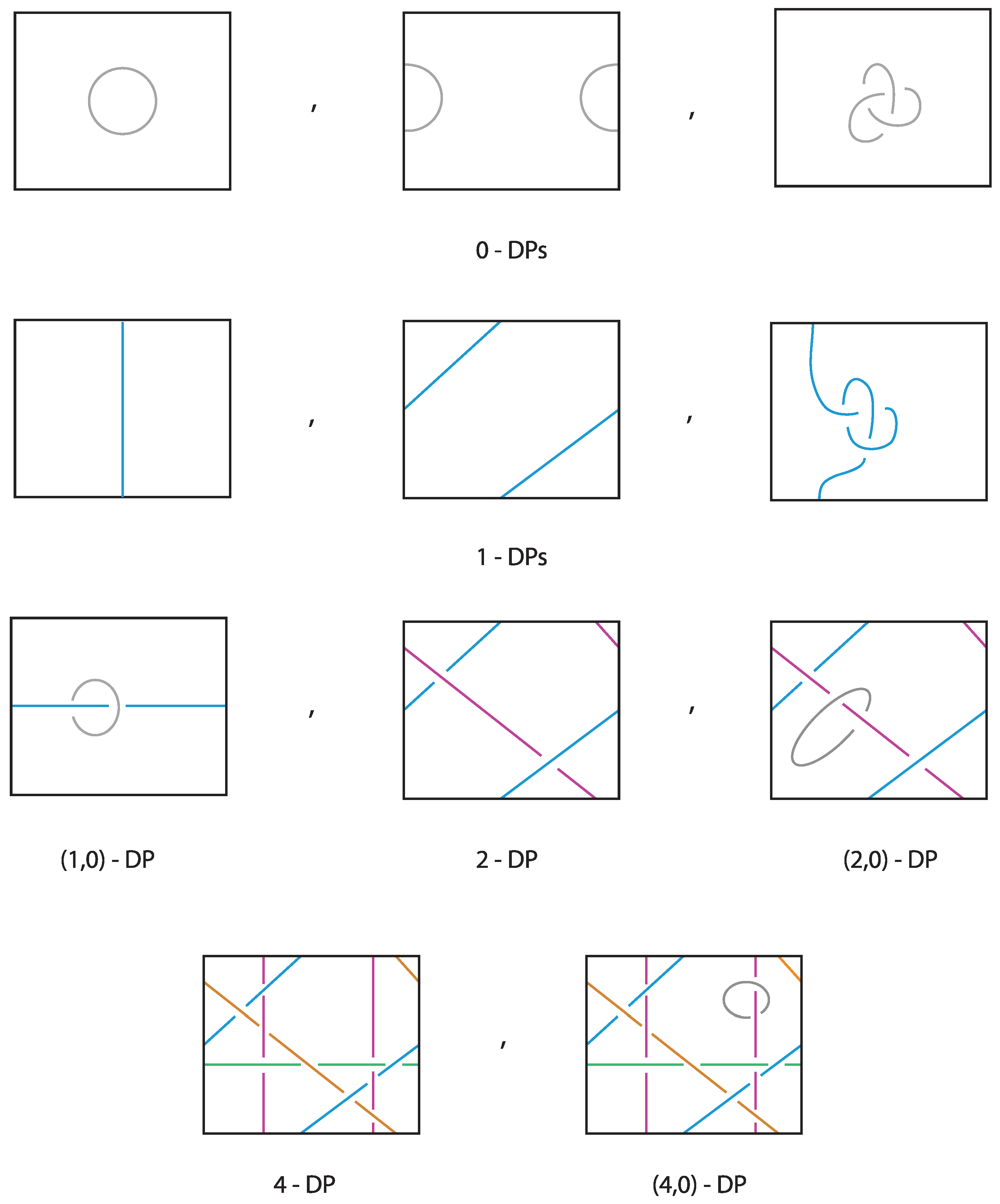
4.3. Directional Types of DP Tangles
- -
- If τ has direction , then τ and are said to be of type 0 or a 0-motif and a 0-DP tangle, respectively.
- -
- If τ has direction , then τ and are said to be of type ∞ or a ∞-motif and a ∞-DP tangle, respectively.
- -
- If τ has a set of direction of cardinality N that does not contains nor , then τ and is said to be of type N or a N-motif and a N-DP tangle, respectively.
- -
- If τ has direction , then τ and are said to be of type or a -motif and a -DP tangle, respectively.
- -
- If τ has a set of direction of cardinality , containing but not , then τ and is said to be of type or a -motif and a -DP tangle, respectively.
- -
- If τ has a set of direction of cardinality , containing but not , then τ and is said to be of type or a -motif and a -DP tangle, respectively.
- -
- If τ has a set of direction of cardinality , containing and , then τ and is said to be of type or a -motif and a -DP tangle, respectively.
5. Comparing Invariants and Computing Examples
- -
- The crossing number, defined as the minimal number of crossings in a motif of a DP tangle , among all possible minimal motifs of .
- -
- The number of components, defined as the number of component in any minimal motif of a DP tangle.
- -
- The axis number, which refers to the number of directions in this paper.
- *
- Motif 3 differs from motifs 1 and 2 only by its class;
- *
- Motif 4 differs from motifs 5 and 6 by its number of directions, its directional type, and its class;
- *
- Motifs 7 and 8 differ by their number of directions, their directional type, and their class;
- *
- Motif 11 differs from motifs 9 and 10 by its directional type and its set of subclasses;
- *
- Motifs 12 and 13 differ by their directional type and their set of subclasses;
- *
- Motifs 13 and 14 only differ by their class;
- *
- Motif 15 differs from motifs 13 and 14 by its directional type and its class;
- *
- Motifs 16 and 17 differ by their number of directions, their directional type, and their set of subclasses;
- *
- Motif 18 differs from motifs 19 and 20 by its number of directions, its directional type, and its class and set of subclasses;
- *
- Motifs 19 and 20 only differ by their set of subclasses.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Panagiotou, E.; Millett, K.C.; Lambropoulou, S. Quantifying Entanglement for Collections of Chains in Models with Periodic Boundary Conditions. Procedia IUTAM 2013, 7, 251–260. [Google Scholar]
- Panagiotou, E. The linking number in systems with Periodic Boundary Conditions. J. Comput. Phys. 2015, 300, 533–573. [Google Scholar]
- Panagiotou, E.; Millett, K.C. Linking matrices in systems with periodic boundary conditions. J. Phys. A Math. Theor. 2018, 51, 225001. [Google Scholar]
- Markande, S.G.; Matsumoto, E. Knotty Knits are Tangles in Tori. Proc. Bridg. 2020, 103–112. [Google Scholar]
- Fukuda, M.; Kotani, M.; Mahmoudi, S. Classification of doubly periodic untwisted (p,q)-weaves by their crossing number and matrices. J. Knot Theory Ramif. 2023, 32, 2350032. [Google Scholar]
- Liu, Y.; O’Keeffe, M.; Treacy, M.M.J.; Yaghi, O.M. The geometry of periodic knots, polycatenanes and weaving from a chemical perspective: A library for reticular chemistry. Chem. Soc. Rev. 2018, 47, 4642–4664. [Google Scholar] [PubMed]
- O’Keeffe, M.; Treacy, M.M.J. Crystallographic descriptions of regular 2-periodic weavings of threads, loops and nets. Acta Cryst. A 2020, 76, 110–120. [Google Scholar]
- Bond, J.R.; Kofman, L.; Pogosyan, D. How filaments of galaxies are woven into the cosmic web. Nature 1996, 380, 603–606. [Google Scholar]
- Hong, S.; Dey, A. Network Analysis of Cosmic Structures: Network Centrality and Topological Environment. Mon. Not. R. Astron. Soc. 2015, 450, 1999–2015. [Google Scholar]
- Hong, S.; Coutinho, B.; Dey, A.; Barabási, A.-L.; Vogelsberger, M.; Hernquist, L.; Gebhardt, K. Discriminating Topology in Galaxy Distributions using Network Analysis. Mon. Not. R. Astron. Soc. 2016, 459, 2690–2700. [Google Scholar]
- Grishanov, S.A.; Meshkov, V.R.; Omelchenko, A.V. Kauffman-type polynomial invariants for doubly periodic structures. J. Knot Theory Ramif. 2007, 16, 779–788. [Google Scholar]
- Grishanov, S.; Meshkov, V.; Omelchenko, A. A topological study of textile structures. Part I: An introduction to topological methods. Text. Res. J. 2009, 79, 702–713. [Google Scholar]
- Grishanov, S.; Meshkov, V.; Omelchenko, A. A topological study of textile structures. Part II: Topological invariants in application to textile structures. Text. Res. J. 2009, 79, 822–836. [Google Scholar]
- Grishanov, S.A.; Meshkov, V.R.; Vassiliev, V.A. Recognizing textile structures by finite type knot invariants. J. Knot Theory Ramif. 2009, 18, 209–235. [Google Scholar]
- Grishanov, S.A.; Vassiliev, V.A. Invariants of links in 3-manifolds and splitting problem of textile structures. J. Knot Theory Ramif. 2011, 20, 345–370. [Google Scholar]
- Morton, H.R.; Grishanov, S.A. Doubly periodic textile structures. J. Knot Theory Ramif. 2009, 18, 1597–1622. [Google Scholar]
- Bright, M.; Kurlin, V. Encoding and topological computation on textile structures. Comput. Graph. 2020, 90, 51–61. [Google Scholar]
- Barkataki, K.; Panagiotou, E. The Jones polynomial in systems with periodic boundary conditions. J. Phys. A Math. Theor. 2024, 57, 155202. [Google Scholar]
- Diamantis, I.; Lambropoulou, S.; Mahmoudi, S. Equivalences of doubly periodic tangles. arXiv 2023, arXiv:2310.00822. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diamantis, I.; Lambropoulou, S.; Mahmoudi, S. Directional Invariants of Doubly Periodic Tangles. Symmetry 2024, 16, 968. https://doi.org/10.3390/sym16080968
Diamantis I, Lambropoulou S, Mahmoudi S. Directional Invariants of Doubly Periodic Tangles. Symmetry. 2024; 16(8):968. https://doi.org/10.3390/sym16080968
Chicago/Turabian StyleDiamantis, Ioannis, Sofia Lambropoulou, and Sonia Mahmoudi. 2024. "Directional Invariants of Doubly Periodic Tangles" Symmetry 16, no. 8: 968. https://doi.org/10.3390/sym16080968
APA StyleDiamantis, I., Lambropoulou, S., & Mahmoudi, S. (2024). Directional Invariants of Doubly Periodic Tangles. Symmetry, 16(8), 968. https://doi.org/10.3390/sym16080968









