Geometric Interpretation of a Non-Linear Extension of Quantum Mechanics

Abstract

We recently introduced a particular non-linear generalization of quantum mechanics that has the property that it is exactly solvable in terms of the eigenvalues and eigenfunctions of the Hamiltonian of the usual linear quantum mechanics problem. In this paper, we suggest that the two components of the wave function represent the system described by the Hamiltonian H in two different asymptotic regions of spacetime and we show that the non-linear terms can be viewed as giving rise to gravitational effects.

1. Introduction

In a previous paper [1], we introduced a new extension of quantum mechanics in which a pair of state vectors in Hilbert space, $\left|\psi \right.〉$ and $\left|\varphi \right.〉$, are coupled together non-linearly. The system has the feature that if the underlying linear system is solvable, then the non-linear extension is also solvable.

In this paper, we address a major issue that was left unresolved in [1]: how to interpret the pair of state vectors that we associate with a dynamical system. The Schwarzschild solution in general relativity exhibits two distinct asymptotic regions connected by a non-traversable throat. Inspired by this circumstance, we conjecture that the two state vectors should represent the system in two separate asymptotic regions of spacetime.

To investigate how this might work, in this paper we study the simple example of a particle in $1+1$ dimensions. We choose the Hamiltonian to be that of a free particle, thereby concentrating only on the gravitational effects, which we ascribe to the non-linear couplings in our theory.

Normal general relativity is “top-down” in the sense that one solves Einstein’s equations for the metric and uses that information to determine the geodesics along which particles move. Our approach is “bottom-up”: we start with the geodesics and use that information to infer the metric. The geodesics, in turn, are determined from suitable expectation values in the underlying extension of quantum mechanics that we have postulated. By requiring that freely falling particles travel on geodesics, we are automatically incorporating a significant element of the equivalence principle.

In a two-dimensional spacetime, the Einstein tensor vanishes identically. Had we been relying on Einstein’s equations, we would have had nothing to work with. Also, there is no direct analog of the 4D Schwarzschild solution, since the latter is Ricci flat, and, in 2D, if the Ricci tensor vanishes, so does the Riemann tensor, rendering the spacetime flat.

Nevertheless, by starting with the geodesics, we find non-trivial 2D metrics, some of which possess the two independent asymptotic regions that we seek. We discover one case that has the exact same singularity and asymptotic structure as the Schwarzschild solution. The metrics that we find all have constant curvature. Thus, they are solutions of Jackiw–Teitelboim gravity [2,3], a much-studied surrogate for general relativity in two dimensions. We note, however, that the metrics that we obtain are not fundamental fields that need to be quantized; they are derived quantities that emerge from the underlying extended quantum mechanical system.

The equations of motion for the two state vectors are

$$i\frac{\mathcal{\partial }}{\mathcal{\partial }t}\left|\psi \right.〉=H\left|\psi \right.〉+g\left|\varphi \right.〉〈\varphi |\psi 〉.$$

(1)

and

$$i\frac{\mathcal{\partial }}{\mathcal{\partial }t}\left|\varphi \right.〉=H\left|\varphi \right.〉+g^{*}\left|\psi \right.〉〈\psi |\varphi 〉.$$

(2)

Here, H is the Hamiltonian of the system of interest, whatever that may be, and g is a coupling constant that is in general complex, with $g^{*}$ its complex conjugate. Note that the non-linear terms are universal, in that they are the same regardless of the dynamics described by H, unlike in some other recently proposed schemes [4].

As shown in [1], if we are given an orthonormal pair of solutions of the ordinary Schrödinger equation,

$$i\frac{\mathcal{\partial }}{\mathcal{\partial }t}\left|A\right.〉=H\left|A\right.〉,i\frac{\mathcal{\partial }}{\mathcal{\partial }t}\left|B\right.〉=H\left|B\right.〉,\langle A|B\rangle =0,$$

(3)

with

$$\left|A\right.〉=\sum _n{A}_n{e}^{-i{E}_{n}t}\left|n\right.〉,\left|B\right.〉=\sum _n{B}_n{e}^{-i{E}_{n}t}\left|n\right.〉,$$

(4)

then a solution to the non-linear equations is

$$\begin{array}{ccc}\hfill \left|\psi \right.〉& & ={\gamma }^{1/2}\left[e^{ig{\omega }_{0}t}sinh\vartheta \left|A\right.〉+e^{-ig{\omega }_{0}t}cosh\vartheta \left|B\right.〉\right]\hfill \\ \hfill \left|\varphi \right.〉& & ={{\gamma }^{*}}^{1/2}\left[-e^{i{g}^{*}{\omega }_{0}t}sinh\vartheta \left|A\right.〉+e^{-i{g}^{★}{\omega }_{0}t}cosh\vartheta \left|B\right.〉\right].\hfill \end{array}$$

(5)

Here, $\gamma =\langle \varphi |\psi \rangle ={\omega }_0{(cosh2{\omega }_{0}bt)}^{ig/b}$, up to an inessential constant phase. The parameter b is the imaginary part of g, which we represent as $g=a+ib$, and ${\omega }_0$ and $\vartheta$ are two additional parameters that characterize the solution beyond whatever information is resident in the states $\left|A\right.〉$ and $\left|B\right.〉$. Note that $\left|\gamma \right|={\omega }_0{(cosh2{\omega }_{0}bt)}^{-1}.$

The derivation of these results and more details about the properties of the solution can be found in [1]. What [1] does not contain, however, is an interpretation of the pair of state vectors that are used to characterize the system of interest. (The situation is somewhat reminiscent of that facing ordinary wave mechanics in the spring of 1926. At that time, Schrödinger was busy solving his eponymous equation, but he struggled to give an acceptable meaning to the wave function. When Max Born suggested the probability interpretation in the summer of 1926, Schrödinger was repelled, and indeed never reconciled himself to the Copenhagen interpretation, as dramatically expressed in the famous cat experiment that he introduced in 1935).

In this theory, there are two state vectors, obeying a pair of coupled non-linear equations, but only one underlying dynamical system, specified by a Hamiltonian H. As mentioned above, in this paper, we shall explore one possible interpretation that is inspired by some properties of the Schwarzschild solution in general relativity.

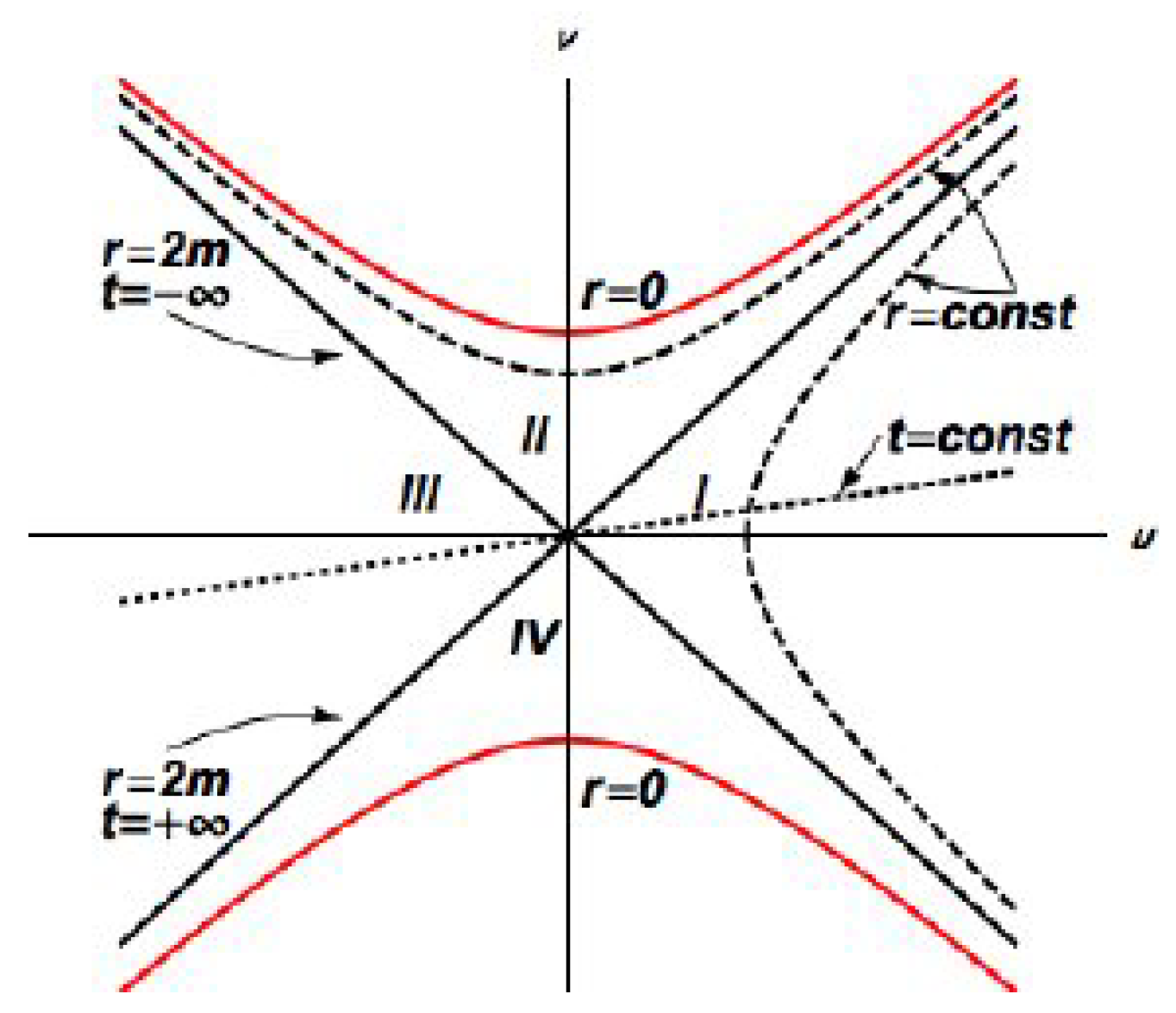
As is well known, the Schwarzschild solution is richer than first appears. When a coordinate transformation is made from the Schwarzschild coordinates to Kruskal–Szekeres coordinates, the apparent singularity at the event horizon disappears, and the spacetime is revealed to have four distinct regions, two of which contain singularities and two of which are asymptotic, singularity-free regions connected by a non-traversable throat.

We therefore suggest that $\left|\psi \right.〉$ and $\left|\varphi \right.〉$ can represent the system described by H in two different asymptotic regions of spacetime. A small note of encouragement is that, if one looks at Schwarzschild coordinates in the two asymptotic regions, time runs in opposite directions. In [1], we found that, assuming that H is time-reversal-invariant, our non-linear system also possesses a time-reversal invariance that involves interchanging $\left|\psi \right.〉$ and $\left|\varphi \right.〉$.

In the next section, we pursue some consequences of this suggestion in the context of a simple example that shows how the curvature of space can arise in our non-linear extension of quantum mechanics.

2. Geometry from Non-Linear Quantum Mechanics

Let us consider a system in two spacetime dimensions that consists of a single free particle, by which we mean that the Hamiltonian depends only on the momentum P and not on the position X. For any states $\left|A\right.〉$ and $\left|B\right.〉$ evolving according to the usual Schrödinger equation, it then follows that

$$\left.〈A\left(t\right)\right|X\left|B\left(t\right)\right.〉=\alpha t+\beta .$$

(6)

(The second time derivative of the left-hand side is the matrix element of the operator $[H,[H,X\left]\right]$, which vanishes if H depends only on P.)

If $\left|A\right.〉=\left|B\right.〉$, $\alpha$ and $\beta$ must be real parameters. Otherwise, they will in general be complex.

Letting $\left|\psi \left(t\right)\right.〉$ represent our system in some region of spacetime, we can compute the trajectory function

$$X\left(t\right)=\langle \psi \left(t\right)\left|X\right|\psi \left(t\right)\rangle /\langle \psi \left(t\right)\left|\psi \right(t)\rangle .$$

(7)

using Equation (5). Note that $〈\psi \left(t\right)|\psi \left(t\right)〉=\frac{1}{2}(N+\tau \left(t\right))$, where $N=2{\omega }_{0}cosh\left(2\vartheta \right)$. and $\tau \left(t\right)=2{\omega }_{0}tanh2{\omega }_{0}bt$. Even for a free particle, $X\left(t\right)$ is no longer simply a linear function.

From Equation (5), the numerator on the right-hand side of Equation (7) involves the matrix elements $<A\left|X\right|A>,<B\left|X\right|B>$ and $<A\left|X\right|B>$. From Equation (6), the first two each contribute two real constants, while the third contributes four. Hence, there are a total of eight real constants, so we can write

$$X\left(t\right)=\frac{2}{\Delta }\left[(k_{1}t+k_2)cosh\left(by\right)+(k_{3}t+k_4)sinh\left(by\right)+(k_{5}t+k_6)cos\left(ay\right)+(k_{7}t+k_8)sin\left(ay\right)\right].$$

(8)

Here, $y=2{\omega }_{0}t$ and $\Delta =Ncosh\left(by\right)+2{\omega }_{0}sinh\left(by\right)$. Note that we have the relation

$$Ncosh\left(by\right)/\Delta +2{\omega }_{0}sinh\left(by\right)/\Delta =1.$$

(9)

so there are really only seven independent constants in this expression.

We suggest that the deviation from linearity can be interpreted as a gravitational effect. The question that we want to answer is, if the trajectory functions defined by Equation (7) are geodesics of some metric, what is that metric? In two spacetime dimensions, there are three independent components of the metric and six of the affine connection. These numbers grow rapidly with dimension, so it may be challenging to extend our analysis to higher dimensions. Demanding that the various $X\left(t\right)$ determined from Equation (8) are geodesics for all possible choices of the eight $k_i$ is too restrictive: no metric in 2D will exist. Instead, we ask that they be geodesics for specific choices of the parameters. In this paper, we shall examine two possibilities, which we call the one-function and two-function cases. It is not clear to us whether there are any possibilities beyond these two cases for which solutions exist.

3. The Problem

The general problem that we face is inverse to the usual one. In general relativity, typically, one is given the metric either as a solution of Einstein’s equation or in some other way. From the metric, one calculates the connection using Christoffel’s formula:

$${\Gamma }_{jk}^i=\frac{1}{2}{g}^{il}\left(g_{jl,k}+g_{lk,j}-g_{jk,l}\right).$$

(10)

and then determines the geodesics $x^i\left(\tau \right)$ by solving the equation

$$\frac{d^2{x}^i}{d{\tau }^2}+{\Gamma }_{jk}^i\frac{d{x}^j}{d\tau }\frac{d{x}^k}{d\tau }=0.$$

(11)

Here, we are given a set of trajectories $\left\{x^i(t;k_j)\right\}$, where t is the parameter along the particular curve and the $k_j$ label the various curves, and we seek metrics for which these curves are geodesics. The generic equation for the trajectories in our non-linear model of quantum mechanics is given by Equation (8).

Determining a metric from its geodesics is an old problem whose history stretches back to the mists of the nineteenth century. A modern treatment of this problem has been given by Matveev [5], which also includes a cornucopia of references. We will follow the procedure outlined in [5].

In principle, one has to solve the geodesic equation, but this time for the ${\Gamma }_{jk}^i$ given the $x^i$. Then, one integrates the compatibility conditions ${\nabla }_i{g}_{jk}=0$ to determine the metric. However, there are some complications and subtleties to overcome.

First, we need an extra term in the geodesic equation because the parameter t that we are using is not, in general, the proper time. The more general form of the equation is

$${\ddot{x}}^i+{\Gamma }_{jk}^i{\dot{x}}^j{\dot{x}}^k=\widehat{g}\left(\left\{{\dot{x}}^j\right\}\right){\dot{x}}^i$$

(12)

where the over dot denotes differentiation with respect to t, and $\widehat{g}$ is an arbitrary function that encodes the relation between t and the proper time $\tau$. We shall assume that it is possible to choose coordinates such that $t=x^0$. The $i=0$ component of the geodesic equation reads

$$\widehat{g}={\Gamma }_{00}^0+2\sum _{j\ne 0}{\Gamma }_{j0}^0{\dot{x}}^j+\sum _{j,k\ne 0}{\Gamma }_{jk}^0{\dot{x}}^j{\dot{x}}^k.$$

(13)

We insert this expression into the remaining equations to obtain, for $i\ne 0$,

$${\ddot{x}}^i+{\Gamma }_{00}^i+2\sum _{j\ne 0}{\Gamma }_{j0}^i{\dot{x}}^j+\sum _{j,k\ne 0}{\Gamma }_{jk}^i{\dot{x}}^j{\dot{x}}^k={\dot{x}}^i\left[{\Gamma }_{00}^0+2\sum _{j\ne 0}{\Gamma }_{j0}^0{\dot{x}}^j+\sum _{j,k\ne 0}{\Gamma }_{jk}^0{\dot{x}}^j{\dot{x}}^k\right].$$

(14)

In 2D, this equation becomes

$${\ddot{x}}^1+(2{\Gamma }_{10}^1-{\Gamma }_{00}^0){\dot{x}}^1+({\Gamma }_{11}^1-2{\Gamma }_{10}^0){\left({\dot{x}}^1\right)}^2-{\Gamma }_{11}^0{\left({\dot{x}}^1\right)}^3+{\Gamma }_{00}^1=0.$$

(15)

It would be nice if, given a sufficient number of trajectories $x^i$, one could completely determine the connection coefficients ${\Gamma }_{jk}^i$. But, that is never the case because the geodesic equations possess a “gauge invariance”, ${\Gamma }_{jk}^i\to {\Gamma }_{jk}^i-{\delta }_j^i{\varphi }_k-{\delta }_k^i{\varphi }_j$, where the ${\varphi }_j$ are arbitrary. This transformation will only change the value of the function $\widehat{g}$, leaving the form of the geodesic equation unaltered.

In 2D, there are six components of the connection, and the geodesic equations will determine the four gauge-invariant combinations ${\Gamma }_{11}^0,(2{\Gamma }_{10}^1-{\Gamma }_{00}^0),{\Gamma }_{00}^1,({\Gamma }_{11}^1-2{\Gamma }_{10}^0)$, leaving the remaining two arbitrary. The compatibility equations ${\nabla }_i{g}_{jk}=0$ are not gauge-invariant, so they require more input than we seem to have available.

One can circumvent this difficulty by working with auxiliary functions, related to the metric, that are gauge-invariant. In 2D, these can be taken to be

$$a_{ij}={\left|Det\left(g\right)\right|}^{-2/3}{g}_{ij}.$$

(16)

The $a_{ij}$ obey the following equations:

$$\begin{array}{c}\hfill {\mathcal{\partial }}_t{a}_{00}+2K_0{a}_{01}-\frac{2}{3}{K}_1{a}_{00}=0,\\ \hfill 2{\mathcal{\partial }}_t{a}_{01}+{\mathcal{\partial }}_x{a}_{00}+2K_0{a}_{11}+\frac{2}{3}{K}_1{a}_{01}-\frac{4}{3}{K}_2{a}_{00}=0,\\ \hfill {\mathcal{\partial }}_t{a}_{11}+2{\mathcal{\partial }}_x{a}_{01}+\frac{4}{3}{K}_1{a}_{11}-\frac{2}{3}{K}_2{a}_{01}-2K_3{a}_{00}=0,\\ \hfill {\mathcal{\partial }}_x{a}_{11}+\frac{2}{3}{K}_2{a}_{11}-2K_3{a}_{01}=0,\end{array}$$

(17)

where

$$K_0=-{\Gamma }_{00}^1,K_1={\Gamma }_{00}^0-2{\Gamma }_{01}^1,K_2=-{\Gamma }_{11}^1+2{\Gamma }_{01}^0,K_3={\Gamma }_{11}^0.$$

(18)

The procedure is to solve these equations for the $a_{ij}$ and then to determine the $g_{ij}$ from

$$g_{ij}=\frac{a_{ij}}{{\left|Det\left(a\right)\right|}^2}.$$

(19)

One can then solve for all the ${\Gamma }_{jk}^i$ and verify that the input information conveyed by the $K_i$ is reproduced. Analogous equations exist in higher dimensions, but, in the analysis to follow, we shall concentrate on 2D for simplicity.

4. Solution of the One Function Case

In this section, we consider what we call the one-function case, in which we choose a particular combination $f\left(t\right)$ of the general $X\left(t\right)$ with fixed $k_i$ (for example, all $k_i$ vanish except one), and then demand that any multiple of that combination be a geodesic. In Section 6 we shall consider the two-function case, which will involve two combinations of $f_1\left(t\right)$ and $f_2\left(t\right)$.

From Equation (15), we obtain the geodesic equation for $x^1=f\left(t\right)$:

$$\ddot{f}+{\Gamma }_{00}^1+2{\Gamma }_{10}^1\dot{f}+{\Gamma }_{11}^1{\dot{f}}^2=\dot{f}({\Gamma }_{00}^0+2{\Gamma }_{10}^0\dot{f}+{\Gamma }_{11}^0{\dot{f}}^2)$$

(20)

Since f contains an arbitrary multiplicative constant, we require that the coefficients of powers of f must vanish separately. This leads to

$${\Gamma }_{00}^1=0;{\Gamma }_{11}^1-2{\Gamma }_{10}^0=0,{\Gamma }_{11}^0=0;{\Gamma }_{00}^0-2{\Gamma }_{10}^1=\frac{\ddot{f}}{\dot{f}},$$

(21)

so that

$$\ddot{f}+(2{\Gamma }_{10}^1-{\Gamma }_{00}^0)\dot{f}=0.$$

(22)

It will be useful to define

$$h\left(t\right)=\frac{\ddot{f}}{\dot{f}}$$

(23)

For our problem, the $K_i$ used in Matveev (Equation (17) of Ref. [5]) are given by

$$K_0=0;K_1=h\left(t\right);K_2=K_3=0.$$

(24)

From Equation (17), we obtain the Liouville system [6] (note that this is R. Liouville, not his more famous namesake, J. Liouville, after whom the Liouville equation is named)

$$\begin{array}{c}\hfill {\mathcal{\partial }}_t{a}_{00}-\frac{2}{3}h\left(t\right)a_{00}=0,\\ \hfill 2{\mathcal{\partial }}_t{a}_{01}+{\mathcal{\partial }}_x{a}_{00}+\frac{2}{3}h\left(t\right)a_{01}=0,\\ \hfill {\mathcal{\partial }}_t{a}_{11}+2{\mathcal{\partial }}_x{a}_{01}+\frac{4}{3}h\left(t\right)a_{11}=0,{\mathcal{\partial }}_x{a}_{11}=0.\end{array}$$

(25)

It follows that $a_{11}$ is independent of x, $a_{01}$ is at most linear in x, and $a_{00}$ is at most quadratic in x. So, we write

$$a_{11}=p_0\left(t\right);a_{01}=q_0\left(t\right)+q_1\left(t\right)x;a_{00}=r_0\left(t\right)+r_1\left(t\right)x+r_2\left(t\right)x^2.$$

(26)

We see that only the gauge-invariant combinations enter into Equation (25). Thus, one only needs $h\left(t\right)$ to solve for the $g_{ij}$ and then one can determine all six nonzero ${\Gamma }_{jk}^i$ directly from the $g_{ij}$.

Once we determine the $a_{ij}$, the $g_{ij}$ are given by

$$g_{ij}=\frac{a_{ij}}{{\left|Det\left(a\right)\right|}^2}$$

(27)

Inserting Equation (26) into the equations for $a_{ij}$ and equating the coefficients of each power of x separately to zero, we obtain six equations, which divide into a single equation for $r_0\left(t\right)$, a pair of equations for $r_1\left(t\right)$ and $q_0\left(t\right)$, and three equations for $r_2\left(t\right),q_1\left(t\right)$, and $p_0\left(t\right)$. They are as follows:

$$\begin{array}{ccc}& & {\dot{r}}_0-\frac{2}{3}h\left(t\right)r_0=0,\hfill \\ & & {\dot{r}}_1-\frac{2}{3}h\left(t\right)r_1=0;2{\dot{q}}_0+r_1+\frac{2}{3}h\left(t\right)q_0=0,\hfill \\ & & {\dot{r}}_2-\frac{2}{3}h\left(t\right)r_2=0;{\dot{p}}_0+\frac{4}{3}h\left(t\right)p_0+2q_1=0;{\dot{q}}_1+\frac{2}{3}h\left(t\right)q_1+r_2=0.\hfill \end{array}$$

(28)

Now, $h\left(t\right)=\frac{\ddot{f}}{\dot{f}}$, which is of the form $\frac{\dot{g}}{g}$. Since, for any function $s\left(t\right)$ and any constant $\alpha$,

$$\dot{s}+\alpha \frac{\dot{g}}{g}s=g^{-\alpha }\frac{d}{dt}\left(g^{\alpha }s\right),$$

(29)

we immediately obtain

$$r_i\left(t\right)={\overline{r}}_i{\left(\dot{f}\right)}^{2/3},i=0,1,2$$

(30)

where the ${\overline{r}}_i$ are constants. We can proceed to integrate the remaining equations in terms of three more constants of integration $c_i$. We then find, for the $a_{ij}$,

$$\begin{array}{ccc}\hfill a_{00}& & =\dot{f}{\left(t\right)}^{2/3}\left({\overline{r}}_0+{\overline{r}}_{1}x+{\overline{r}}_2{x}^2\right)\hfill \\ \hfill a_{01}& & =\left(-\frac{c_1{\overline{r}}_1}{2}-c_2{\overline{r}}_{2}x-f\left(t\right)(\frac{{\overline{r}}_1}{2}+{\overline{r}}_{2}x)\right)/\dot{f}{\left(t\right)}^{1/3}.\hfill \\ \hfill a_{11}& & ={\overline{r}}_2(c_3+2c_{2}f\left(t\right)+f^2\left(t\right))/\dot{f}{\left(t\right)}^{4/3}.\hfill \end{array}$$

(31)

One can simplify the expressions for $a_{ij}$ by the change in variables:

$$x\to X-\alpha ;f\left(t\right)\to T-\beta$$

(32)

We can eliminate the linear dependence on x in $a_{00}$ and the linear dependence of $a_{11}$ on $f\left(t\right)$ by choosing

$$\alpha =\frac{{\overline{r}}_1}{2{\overline{r}}_2};\beta =c_2.$$

(33)

We then have that

$$\begin{array}{ccc}\hfill a_{00}& & ={\overline{r}}_2(a^{\prime }+X^2)\dot{f}{\left(t\right)}^{2/3},a_{01}=-\frac{{\overline{r}}_2(b^{\prime }+TX)}{\dot{f}{\left(t\right)}^{1/3}}\hfill \\ \hfill a_{11}& & ={\overline{r}}_2\frac{(T^2+c^{\prime })}{\dot{f}{\left(t\right)}^{4/3}}\hfill \end{array}$$

(34)

where

$$a^{\prime }=\frac{{\overline{r}}_0}{{\overline{r}}_2}-\frac{{\overline{r}}_1^2}{4{\overline{r}}_2^2},b^{\prime }=\frac{(c_1-c_2){\overline{r}}_1}{2{\overline{r}}_2},c^{\prime }=c_3-c_2^2.$$

(35)

Calculating the determinant, we find that

$$\begin{array}{ccc}\hfill Det\left[a\right]& & =\frac{{\overline{r}}_2^2(-b^{\prime 2}+a^{\prime }(c^{\prime }+T^2)-2b^{\prime }TX+c^{\prime }{X}^2)}{{\dot{f}\left(t\right)}^{2/3}}\hfill \\ & & =\frac{{\overline{r}}_2^2[-{(b^{\prime }+TX)}^2+(c^{\prime }+T^2)(a^{\prime }+X^2)]}{{\dot{f}\left(t\right)}^{2/3}}\hfill \end{array}$$

(36)

The metric in the original coordinates $(t,x=f(t\left)\right)$ can be written as

$$g_{\alpha \beta }=\frac{1}{{\overline{r}}_2^3{D}^2}\left(\begin{array}{cc}(a^{\prime }+X^2)\dot{f}{\left(t\right)}^2& -(b^{\prime }+TX)\dot{f}\left(t\right)\\ -(b^{\prime }+TX)\dot{f}\left(t\right)& (c^{\prime }+T^2)\end{array}\right)$$

(37)

where

$$D=-{(b^{\prime }+TX)}^2+(c^{\prime }+T^2)(a^{\prime }+X^2).$$

(38)

Now, we have in the original coordinates $x^{\alpha }$,

$$d{s}^2=g_{\alpha \beta }d{x}^{\alpha }d{x}^{\beta }$$

(39)

Now, since $T=f\left(t\right)+c_2$,

$$dT=\dot{f}\left(t\right)dt;dX=dx$$

(40)

If we change the coordinates to $T,X$, due to the invariance of $d{s}^2$, the factors of $\dot{f}\left(t\right)$ in $g_{\alpha \beta }$ get absorbed into the definition of $dT$. Letting $X^{\alpha }=\{T,X\}$, one has

$$d{s}^2=h_{\alpha \beta }d{X}^{\alpha }d{X}^{\beta }$$

(41)

where, now,

$$h_{\alpha \beta }=\frac{1}{{\overline{r}}_2^3{D}^2}\left(\begin{array}{cc}(a^{\prime }+X^2)& -(b^{\prime }+TX)\\ -(b^{\prime }+TX)& (c^{\prime }+T^2)\end{array}\right).$$

(42)

The inverse metric is given by

$$h^{\alpha \beta }={\overline{r}}_2^{3}D\left(\begin{array}{cc}(c^{\prime }+T^2)& (b^{\prime }+TX)\\ (b^{\prime }+TX)& (a^{\prime }+X^2)\end{array}\right).$$

The nonzero connections calculated from Equation (10) are given by:

$$\begin{array}{ccc}\hfill {\Gamma }_{00}^0& & =2\frac{(b^{\prime }X-a^{\prime }T)}{D};{\Gamma }_{10}^0=\frac{(b^{\prime }T-c^{\prime }X)}{D}\hfill \\ \hfill {\Gamma }_{10}^1& & =\frac{(b^{\prime }X-a^{\prime }T)}{D};{\Gamma }_{11}^1=2\frac{(b^{\prime }T-c^{\prime }X)}{D}.\hfill \end{array}$$

(43)

Note that, in this coordinate system, both $K_1$ and $K_2$ are zero. Previously, $K_1=-\frac{\ddot{f}}{\dot{f}}$.

The Ricci curvature is given by

$$\frac{1}{D^2}\left(\begin{array}{cc}\left(a^{\prime }+X^2\right)\left(a^{\prime }{c}^{\prime }-{b^{\prime }}^2\right)& \left({b^{\prime }}^2-a^{\prime }{c}^{\prime }\right)(b^{\prime }+TX)\\ \left({b^{\prime }}^2-a^{\prime }{c}^{\prime }\right)(b^{\prime }+TX)& -\left(c^{\prime }+T^2\right)\left({b^{\prime }}^2-a^{\prime }{c}^{\prime }\right)\end{array}\right).$$

(44)

We can factor out $(a^{\prime }{c}^{\prime }-b^{\prime 2})$ to obtain

$$\begin{array}{ccc}\hfill R_{\alpha \beta }& & =\frac{(a^{\prime }{c}^{\prime }-b^{\prime 2})}{D^2}\left(\begin{array}{cc}(a^{\prime }+X^2)& -(b^{\prime }+TX)\\ -(b^{\prime }+TX)& (c^{\prime }+T^2)\end{array}\right)\hfill \\ & & =(a^{\prime }{c}^{\prime }-b^{\prime 2}){\overline{r}}_2^3{h}_{\alpha \beta }.\hfill \end{array}$$

(45)

We see that the Ricci curvature is proportional to the metric h as it must be in two dimensions. The scalar curvature is given by

$$R=2{\overline{r}}_2^3\left(a^{\prime }{c}^{\prime }-b^{\prime 2}\right).$$

(46)

5. Geometry of the One-Function Solution

In the previous section, we determined the metric in the one-function case in terms of six constants of integration. One of these is an inessential overall constant, which we choose arbitrarily. Two of them are absorbed in a change of variables from the original x and t to X and T:

$$X=x+\alpha ;T=f\left(t\right)+\beta$$

(47)

Here, by construction, the geodesics are $x=kf\left(t\right)+k_0$, or, what is the same thing,

$$X=kT+X_0,$$

(48)

i.e., straight lines in the $(X,T)$ plane. The remaining three constants play a significant role in determining the metric, which, in $(X,T)$ coordinates, has the form

$$h_{\alpha \beta }=\frac{1}{{\overline{r}}_2^3{D}^2}\left(\begin{array}{cc}{p}_{00}& p_{01}\\ p_{10}& p_{11}\end{array}\right),$$

(49)

with $p_{00}=X^2+a^{\prime }$; $p_{01}=p_{10}=-(XT+b^{\prime })$; $p_{11}=T^2+c^{\prime }$. Here, $D=p_{00}{p}_{11}-p_{01}^2=a^{\prime }{T}^2+c^{\prime }{X}^2-2b^{\prime }XT+a^{\prime }{c}^{\prime }-b^{\prime 2}$.

Setting ${\overline{r}}_2=1$, the Ricci scalar $R=2(a^{\prime }{c}^{\prime }-b^{\prime 2})$, which is twice the Gaussian curvature. Our space is one of constant curvature, which can be negative, positive, or zero depending on the choice of parameters.

We see that $Det\left|h\right|=D^{-3}$, so the curve $D=0$, along which $h_{\alpha \beta }$ is singular, separates a region of a Euclidean signature from one of a Minkowski signature. No singularity exists if we choose $a^{\prime }>0$, $c^{\prime }>0$, and $a^{\prime }{c}^{\prime }-b^{\prime 2}\ge 0$, in which case the entire plane has a Euclidean signature. Since we are interested in spacetime, not Euclidean space, we consider cases for which D can vanish. We shall regard the curve $D=0$ as separating the physical space $D<0$ from the $D>0$ region, which we take to be unphysical (although not everyone agrees (see [7])).

To proceed, we choose our parameters to bring our 2D model into a form similar to that used in a standard analysis of the radial geodesics of the Schwarzschild metric [8]. We take ${\overline{r}}_2=1$, $a^{\prime }=c^{\prime }=0$, and $b^{\prime }<0$, and, furthermore, we make a linear change of variables, $T=v+u;X=v-u$, in terms of which, the spacetime interval becomes

$$d{s}^2=\frac{2}{D^2}\left[(2u^2+|b^{\prime }\left|\right)d{v}^2-\left(4uv\right)dudv+(2v^2-|b^{\prime }\left|\right)d{u}^2\right]$$

(50)

with $D=|b^{\prime }\left|\right[2(v^2-u^2)-|b^{\prime }\left|\right]$. Thus, the singular curve is a hyperbola, as shown in Figure 1. We write a typical geodesic as $v=\xi (u-u_0)$. Along the geodesic, $dv=\xi du$, which implies that

$$d{s}^2=\frac{2K}{D^2}d{u}^2,$$

(51)

where $K={\xi }^2(2u_0^2+|b^{\prime }\left|\right)-|b^{\prime }|$. Thus, we find that the condition for a null geodesic is

$${\xi }^2=\frac{|b^{\prime }|}{2u_0^2+\left|b^{\prime }\right|}$$

(52)

The condition that a geodesic be tangent to the hyperbola $(v^2-u^2)=\left(\right|b^{\prime }\left|\right)/2$ is

$$\xi =\frac{dv}{du}=\frac{u}{v},$$

(53)

which, after some algebra, is seen to be the same as the condition for a null geodesic; that is, all null geodesics are tangent to the singular hyperbola, and all lines tangent to the singular hyperbola are null. The parameter $\xi$, which measures velocity (actually inverse velocity, since we are regarding v as the time-like parameter) depends on the particular null geodesic, reaching its maximum of 1 for $u_0=0$.

Through any point, one can draw two null geodesics. In regions I and III of the figure, one of these is tangent to the upper branch, and one to the lower. In region II, both are tangent to the upper branch, and in region IV, both are tangent to the lower branch. The origin $(u,v)=(0,0)$ is special in that each of the two null geodesics is asymptotically tangent to both the upper and lower branches.

The time-like geodesics are those with $K>0$. Inside a typical light cone in regions I and III, there will be some geodesics that intersect both the past and future singularities, there will be others that originate in the past singularity but escape to infinity in the future, and there will be still others that come from infinity in the past and intersect the future singularity. There are no time-like geodesics that escape to infinity in both the past and the future, which is the same as saying that there are none that travel between regions I and III. The throat is not traversable for time-like geodesics.

On the other hand, space-like ($K<0$) geodesics that intersect the line segment $(0,v)$ with $-|b^{\prime }|/2<v<(|b^{\prime }\left|\right)/2$ do travel through the throat between regions I and III.

If we take the view that the “white hole” singularity is not physical because a black hole should form from non-singular data in the past, we can concentrate on the part of the spacetime with $v>0$. Then, the special null geodesics through the origin act as an event horizon, since all time-like geodesics in region II end in the singularity, whereas, in regions I and III, there are at least some time-like geodesics that can escape to infinity.

6. Two Different Two-Function Cases

The one-function case has the advantage of simplicity but the disadvantage that the function itself can be eliminated from the metric by a change in coordinates so that all one-function metrics are essentially the same. They are governed by the parameters that we have called $a^{\prime },b^{\prime },c^{\prime }$, but these are constants of integration that have nothing to do with the function that we started with. It is therefore of interest to examine more complicated cases. Given the constraints imposed by the geodesic equation, it is unlikely that one can make use of the full set of independent functions inherent in the trajectory of Equation (8). However, there are at least two ways to introduce a pair of functions, which we will now describe.

6.1. Case A

The simplest way to introduce a second function is to choose the set of trajectories to be of the form

$$X\left(t\right)=k{f}_1\left(t\right)+f_2\left(t\right)$$

(54)

and require these to be geodesics for all values of the parameter k. We insert this form into Equation (14) and equate powers of k. We find the conditions

$${\Gamma }_{11}^0=0;{\Gamma }_{11}^1-2{\Gamma }_{01}^0=0;{\Gamma }_{00}^0-2{\Gamma }_{01}^1=\frac{\ddot{f_1}}{{\dot{f}}_1};{\Gamma }_{00}^1=\frac{w}{{\dot{f}}_1},$$

(55)

so that $K_3=K_2=0$. $K_1=\frac{\ddot{f_1}}{{\dot{f}}_1}$ and $K_0=-\frac{w}{{\dot{f}}_1}$, where we have defined $w={\ddot{f}}_1{\dot{f}}_2-{\ddot{f}}_2{\dot{f}}_1$. We can then use these as the input to Equation (17) for the quantities $a_{ij}$. The $a_{ij}$ equations reduce to

$$\begin{array}{ccc}\hfill & & {\mathcal{\partial }}_t{a}_{00}-2K_0{a}_{01}-\frac{2}{3}{K}_1{a}_{00}=0,\hfill \\ & & 2{\mathcal{\partial }}_t{a}_{01}+{\mathcal{\partial }}_x{a}_{00}+2K_0{a}_{11}=0,\hfill \\ & & {\mathcal{\partial }}_t{a}_{11}+2{\mathcal{\partial }}_x{a}_{01}+\frac{4}{3}{K}_1{a}_{11}=0,\hfill \\ & & {\mathcal{\partial }}_x{a}_{11}=0.\hfill \end{array}$$

(56)

As in the one-function case, $a_{11}$ is independent of x, $a_{01}$ is at most linear in x, and $a_{00}$ is at most quadratic in x. We can therefore use the same parameterization as in the one-function case Equation (26) but, of course, the equations for the six functions of time will be different. We find the following set of equations:

$$\begin{array}{c}\hfill {\dot{r}}_2-\frac{2}{3}\frac{{\ddot{f}}_1}{{\dot{f}}_1}{r}_2=0;{\dot{q}}_1+\frac{1}{3}\frac{{\ddot{f}}_1}{{\dot{f}}_1}{q}_1+r_2=0,\\ \hfill {\dot{p}}_0+\frac{4}{3}\frac{{\ddot{f}}_1}{{\dot{f}}_1}{p}_0+2q_1=0;{\dot{r}}_1-\frac{2}{3}\frac{{\ddot{f}}_1}{{\dot{f}}_1}{r}_1-\frac{2}{{\dot{f}}_1}w{q}_1=0,\\ \hfill 2\left({\dot{q}}_0+\frac{1}{3}\frac{{\ddot{f}}_1}{{\dot{f}}_1}{q}_0\right)+r_1-\frac{2}{{\dot{f}}_1}w{p}_0=0;{\dot{r}}_0-\frac{2}{3}\frac{{\ddot{f}}_1}{{\dot{f}}_1}{r}_0-\frac{2}{{\dot{f}}_1}w{q}_0=0,\end{array}$$

(57)

If we set $f_2=0$, we recover the equations for the one-function case, as expected.

We define the functions $u,v,w$ by

$$u\left(t\right)=\frac{{\dot{f}}_2}{{\dot{f}}_1},v={\dot{f}}_1{f}_2-{\dot{f}}_2{f}_1,w={\ddot{f}}_1{\dot{f}}_2-{\ddot{f}}_2{\dot{f}}_1.$$

(58)

We see that we can relate $f_2,f_1,u,v$ using $f_2=u{f}_1+\frac{v}{{\dot{f}}_1}$, or $u{f}_1-f_2=-\frac{v}{{\dot{f}}_1}$. Using Equation (29), we can solve these equations sequentially starting with the equation for $r_2$. We find that the following functional forms for the six independent functions satisfy Equation (57):

$$\begin{array}{ccc}\hfill r_2\left(t\right)& & ={\overline{r}}_2{\left({\dot{f}}_1\right)}^{2/3},\hfill \\ \hfill q_1\left(t\right)& & ={\left({\dot{f}}_1\right)}^{-1/3}({\overline{q}}_1-{\overline{r}}_2{f}_1\left(t\right)),\hfill \\ \hfill p_0\left(t\right)& & ={\left({\dot{f}}_1\right)}^{-4/3}({\overline{p}}_0-2{\overline{q}}_1{f}_1\left(t\right)+{\overline{r}}_2{f}_1{\left(t\right)}^2),\hfill \\ \hfill r_1\left(t\right)& & ={\left({\dot{f}}_1\right)}^{2/3}({\overline{r}}_1-2{\overline{q}}_{1}u\left(t\right)-2{\overline{r}}_2\frac{v\left(t\right)}{{\dot{f}}_1}),\hfill \\ \hfill q_0\left(t\right)& & =\frac{1}{2}{\left({\dot{f}}_1\right)}^{-1/3}\left[{\overline{q}}_0+2{\overline{r}}_{2}v\left(t\right)\frac{f_1}{{\dot{f}}_1}-2{\overline{p}}_{0}u\left(t\right)-{\overline{r}}_1{f}_1+2{\overline{q}}_1(u\left(t\right)f_1\left(t\right)-v\left(t\right)/{\dot{f}}_1)\right],\hfill \\ \hfill r_0\left(t\right)& & ={\left({\dot{f}}_1\right)}^{2/3}\left[{\overline{r}}_0-{\overline{q}}_{0}u\left(t\right)+{\overline{r}}_2{\left(\frac{v\left(t\right)}{{\dot{f}}_1}\right)}^2+{\overline{p}}_0{u}^2\left(t\right)-{\overline{r}}_{1}v\left(t\right)/{\dot{f}}_1+2u\left(t\right){\overline{q}}_{1}v\left(t\right)/{\dot{f}}_1\right].\hfill \end{array}$$

(59)

In terms of this solution, we have Equation (26):

$$a_{11}=p_0\left(t\right);a_{01}=q_0\left(t\right)+q_1\left(t\right)x;a_{00}=r_0\left(t\right)+r_1\left(t\right)x+r_2\left(t\right)x^2.$$

(60)

We find that $\left|Det\right(a\left)\right|$ can be written as

$$\begin{array}{ccc}& & \left|Det\left(a\right)\right|=\frac{1}{4{\left({\dot{f}}_1\right)}^{2/3}}\times \hfill \\ & & \left[e_2-4e_{4}x-4e_1{x}^2-e_3{f}_1{\left(t\right)}^2+4(e_4+2e_{1}x)f_2\left(t\right)-4e_1{f}_2{\left(t\right)}^2+2f_1\left(t\right)(e_5-2e_{6}x+2e_6{f}_2\left(t\right))\right].\hfill \end{array}$$

(61)

where

$$\begin{array}{ccc}& & e_1={\overline{q}}_1^2-{\overline{p}}_0{\overline{r}}_2,e_2=-{\overline{q}}_0^2+4{\overline{p}}_0{\overline{r}}_0,e_3={\overline{r}}_1^2-4{\overline{r}}_0{\overline{r}}_2,e_4={\overline{q}}_0{\overline{q}}_1-{\overline{p}}_0{\overline{r}}_1\hfill \\ & & e_5=-4{\overline{q}}_1{\overline{r}}_0+{\overline{q}}_0{\overline{r}}_1,e_6={\overline{q}}_1{\overline{r}}_1-{\overline{q}}_0{\overline{r}}_2.\hfill \end{array}$$

(62)

The metric is given by Equation (27).

The affine connections satisfy the gauge-invariant conditions in Equation (55). The Ricci curvature has the property that

$$R_{\mu \nu }=\frac{1}{2}R{g}_{\mu \nu }.$$

(63)

where the scalar curvature R is a constant and is given by

$$\begin{array}{ccc}\hfill R& & =2{\overline{r}}_0\left({\overline{p}}_0{\overline{r}}_2-{\left({\overline{q}}_1\right)}^2\right)+{\overline{q}}_0{\overline{q}}_1{\overline{r}}_1-\frac{1}{2}\left({\overline{p}}_0{\left({\overline{r}}_1\right)}^2+{\overline{r}}_2{\left({\overline{q}}_0\right)}^2\right)\hfill \\ & & =-2{\overline{r}}_0{e}_1+\frac{1}{2}{\overline{r}}_1{e}_4+\frac{1}{2}{\overline{q}}_0{e}_6.\hfill \end{array}$$

(64)

We can re-express the metric by changing the time coordinate from t to T via

$$f_1\left(t\right)=T-T_0.$$

(65)

Just as with the one-function case, this will absorb the pre-factors of ${\dot{f}}_1\left(t\right)$. In addition, we have the relation

$$\frac{{\dot{f}}_2}{{\dot{f}}_1}=\frac{d{f}_2\left(T\right)}{dT}=f_2^{\prime }\left(T\right),$$

(66)

which also implies that

$$\frac{v}{{\dot{f}}_1}=f_2\left(T\right)-(T-T_0)f_2^{\prime }\left(T\right)$$

(67)

Using these, we find that the metric now depends on $f_2\left(T\right)$ and $f_2^{\prime }\left(T\right)$, as well as explicitly on the coordinates x and T. As we see from Equation (64), the Ricci scalar is a constant, so it does not provide evidence as to whether the dependence on $f_2$ has real geometrical significance or is merely a coordinate artifact.

6.2. Case B

A second way to involve two functions is to demand that

$$x^1\left(t\right)={\kappa }_1{f}_1\left(t\right)+{\kappa }_2{f}_2\left(t\right)$$

(68)

is a geodesic for an arbitrary choice of the constants ${\kappa }_i$. At first, this does not seem possible, because the terms linear in the ${\kappa }_i$ in the geodesic equation impose the condition

$$({\kappa }_1{\dot{f}}_1+{\kappa }_2{\dot{f}}_2)({\Gamma }_{00}^0-2{\Gamma }_{10}^1)={\kappa }_1{\ddot{f}}_1+{\kappa }_2{\ddot{f}}_2.$$

(69)

which can hold for all ${\kappa }_i$ only if ${\ddot{f}}_1/{\dot{f}}_1={\ddot{f}}_2/{\dot{f}}_2$. But, that implies that ${\dot{f}}_2=\beta {\dot{f}}_1$ for some constant $\beta$, and hence $f_2\left(t\right)=\beta f_1\left(t\right)+{\beta }_0$, so we are essentially back to the one-function case. However, this ignores the possibility that the ${\Gamma }_{jk}^i$ can depend on x as well as on t. We rewrite Equation (68) as

$${\kappa }_2=\frac{x-{\kappa }_1{f}_1\left(t\right)}{f_2\left(t\right)},$$

(70)

where we now treat x as the coordinate, not the given function of t (this should be valid as long as we are on the geodesic). We substitute this expression into the geodesic equation and equate powers of ${\kappa }_1$.

The terms cubic and quadratic in ${\kappa }_1$ lead as before to the conditions

$${\Gamma }_{11}^0=0;{\Gamma }_{11}^1-2{\Gamma }_{01}^0=0.$$

(71)

But, the terms linear in ${\kappa }_1$ and independent of ${\kappa }_1$ yield new conditions, which can be solved and lead to

$${\Gamma }_{00}^0-2{\Gamma }_{10}^1=\frac{{\ddot{f}}_1{f}_2-{\ddot{f}}_2{f}_1}{{\dot{f}}_1{f}_2-{\dot{f}}_2{f}_1}$$

(72)

and

$${\Gamma }_{00}^1=\left(\frac{{\ddot{f}}_1{\dot{f}}_2-{\ddot{f}}_2{\dot{f}}_1}{{\dot{f}}_1{f}_2-{\dot{f}}_2{f}_1}\right)x$$

(73)

Letting

$$v={\dot{f}}_1{f}_2-{\dot{f}}_2{f}_1,w={\ddot{f}}_1{\dot{f}}_2-{\ddot{f}}_2{\dot{f}}_1,$$

(74)

we have

$${\Gamma }_{00}^0-2{\Gamma }_{10}^1=\frac{\dot{v}}{v};{\Gamma }_{00}^1=\frac{w}{v}x.$$

(75)

Using this information, we find that, once again, $a_{11}$ is independent of x, $a_{01}$ is at most linear in x, and $a_{00}$ is at most quadratic in x. So, we can continue to use the same parameterization of the $a_{ij}$ in terms of $p,q,r$, Equation (26). In this case, we find the equations for the $a_{ij}$, i.e., Equation (17) can be written as

$$\begin{array}{ccc}\hfill & & {\dot{r}}_0-\frac{2}{3}\frac{\dot{v}}{v}{r}_0=0;\hfill \\ & & {\dot{r}}_1-\frac{2}{3}\frac{\dot{v}}{v}{r}_1-2\frac{w}{v}{q}_0=0;{\dot{q}}_0+\frac{1}{3}\frac{\dot{v}}{v}{q}_0+\frac{1}{2}{r}_1=0;\hfill \\ & & {\dot{r}}_2-\frac{2}{3}\frac{\dot{v}}{v}{r}_2-2\frac{w}{v}{q}_1=0;{\dot{q}}_1+\frac{1}{3}\frac{\dot{v}}{v}{q}_1+r_2-\frac{w}{v}{p}_0=0;\hfill \\ & & {\dot{p}}_0+\frac{4}{3}\frac{\dot{v}}{v}{p}_0+2q_1=0.\hfill \end{array}$$

(76)

If we set $w=0$, then $f_2\left(t\right)=\beta f_1\left(t\right)+{\beta }_0$, and hence $v={\beta }_0{\dot{f}}_1$, so these equations reduce to the one-function case.

We can solve the equations for $r_1$ and $q_0$ by first introducing new variables that scale out the v dependence:

$$A_1=v^{1/3}{q}_0;B_1=v^{-2/3}{r}_1$$

(77)

Then, we have that $A_1$ and $B_1$ satisfy the equations

$${\dot{A}}_1+\frac{1}{2}v{B}_1=0;{\dot{B}}_1-\frac{2w}{v^2}{A}_1=0.$$

(78)

Making the ansatz

$$A_1=\mathcal{F}\left(t\right)=\left(\alpha f_1+\beta f_2\right),$$

(79)

where $\alpha$ and $\beta$ are arbitrary constants; one finds immediately that

$$B_1=-2\frac{\dot{\mathcal{F}}}{v}$$

(80)

The ansatz for $\mathcal{F}$ satisfies the following equation:

$$\ddot{\mathcal{F}}v-\dot{\mathcal{F}}\dot{v}+\mathcal{F}w=0.$$

(81)

Thus, we have

$$q_0=v^{-1/3}\left(\alpha f_1+\beta f_2\right),r_1=-2v^{-1/3}\left(\alpha {\dot{f}}_1+\beta {\dot{f}}_2\right)$$

(82)

To solve for the remaining three variables, we again rescale $p_0$, $r_2$, and $q_1$ by introducing

$$A_2=v^{4/3}{p}_0;B_2=v^{-2/3}{r}_2;C=v^{1/3}{q}_1.$$

(83)

We now have the rescaled equations

$$\dot{A_2}+2vC=0;{\dot{B}}_2-\frac{2w}{v^2}C=0;\dot{C}+v{B}_2-\frac{w}{v^2}{A}_2=0.$$

(84)

The variables $A_2,B_2,C$ satisfy the constraint.

$$\frac{d}{dt}\left(A_2{B}_2-C^2\right)=0.$$

(85)

Making the assumption that $A_2,B_2$, and C depend on t only through the functions $f_1,f_2,{\dot{f}}_1,\dot{f_2}$, one finds the solution

$$\begin{array}{ccc}\hfill A_2& & =\left(m_1{f}_1^2+m_2{f}_1{f}_2+m_3{f}_2^2\right)\hfill \\ \hfill B_2& & =\frac{1}{v^2}\left(m_1{\dot{f_1}}^2+m_2{\dot{f}}_1{\dot{f}}_2+m_3{\dot{f_2}}^2\right)\hfill \\ \hfill C& & =-\frac{1}{v}\left(m_1{f}_1{\dot{f}}_1+m_3{f}_2{\dot{f}}_2+\frac{1}{2}{m}_2({\dot{f}}_1{f}_2+\dot{f_2}{f}_1)\right).\hfill \end{array}$$

(86)

Here, $m_1,m_2$, and $m_3$ are the three arbitrary constants of the solution. They enter into the solution of the constraint equation Equation (85):

$$A_2{B}_2-C^2=m_1{m}_3-\frac{1}{4}{m}_2^2$$

(87)

The original variables $p_0,r_2,q_1$ can be written as

$$\begin{array}{ccc}\hfill p_0& & =v^{-4/3}\left(m_1{f}_1^2+m_2{f}_1{f}_2+m_3{f}_2^2\right)\hfill \\ \hfill r_2& & =v^{-4/3}\left(m_1{\dot{f_1}}^2+m_2{\dot{f}}_1{\dot{f}}_2+m_3{\dot{f_2}}^2\right)\hfill \\ \hfill q_1& & =-v^{-4/3}\left(m_1{f}_1{\dot{f}}_1+m_3{f}_2{\dot{f}}_2+\frac{1}{2}{m}_2({\dot{f}}_1{f}_2+\dot{f_2}{f}_1)\right).\hfill \end{array}$$

(88)

where now the constraint is given by

$$v^{2/3}\left(p_0{r}_2-q_1^2\right)=m_1{m}_3-\frac{1}{4}{m}_2^2$$

(89)

In terms of this solution, we have Equation (17):

$$a_{11}=p_0\left(t\right);a_{01}=q_0\left(t\right)+q_1\left(t\right)x;a_{00}=r_0\left(t\right)+r_1\left(t\right)x+r_2\left(t\right)x^2.$$

(90)

The metric is given by Equation (27).

We find that $\left|Det\right(a\left)\right|$ can be written as

$$\begin{array}{ccc}& & \left|Det\left(a\right)\right|=\frac{1}{4v^{2/3}}\times D\hfill \\ & & D=\left[n_1{x}^2+x(n_2{f}_1+n_3{f}_2)+4(n_4{f}_1^2+n_6{f}_2^2+n_5{f}_1{f}_2)\right].\hfill \end{array}$$

(91)

where

$$\begin{array}{ccc}& & n_1=-m_2^2+4m_1{m}_3,n_2=-4m_2\alpha +8m_1\beta ,n_3=-8m_3\alpha +4m_2\beta \hfill \\ & & n_4=m_1{\overline{r}}_0-{\alpha }^2,n_5=m_2{\overline{r}}_0-2\alpha \beta ,n_6=m_3{\overline{r}}_0-{\beta }^2.\hfill \end{array}$$

(92)

From this, we find that the affine connection components are, in general, of the form

$$\frac{f(i,j,k)}{v\left(t\right)D}$$

(93)

where $f(i,j,k)$ is linear in the $n_i$, quadratic in x, and also quadratic in the variables $\left(f_i,{\dot{f}}_i,{\ddot{f}}_i\right)$. The gauge-invariant components obey Equation (75).

The Ricci scalar is given by

$$\begin{array}{ccc}\hfill R& & =-\frac{1}{2}{m}_2^2{\overline{r}}_0+2m_1{m}_3{\overline{r}}_0-2m_3{\alpha }^2+2m_2\alpha \beta -2m_1{\beta }^2\hfill \\ & & =\frac{1}{2}{\overline{r}}_0{n}_1+\frac{1}{4}(n_3\alpha -n_2\beta ).\hfill \end{array}$$

(94)

In case B, we can repeat the process of making a coordinate transformation to eliminate the dependence on one of the functions. Unlike in case A, the functions $f_1\left(t\right)$ and $f_2\left(t\right)$ are on equal footing, so it is equivalent to choose either one. Taking, as before, $f_1\left(t\right)=T-T_0$, we can proceed to re-express the metric coefficients as functions of $f_2\left(T\right),f_2^{\prime }\left(T\right),x$, and T. Here, too, the Ricci scalar is a constant, this time given in Equation (94).

7. Conclusions

The investigations reported in this paper were motivated by an attempt to interpret the non-linear extension of quantum mechanics introduced in a previous work. We have assumed that one of the two state vectors represents the system in a particular region of space, such as region I in the spacetime discussed in Section 5. Then, the other state vector should represent the system in region III. To see how this might work, we compare the trajectories generated by the two state vectors. In Equation (8), we represented the trajectory associated with $\left|\psi \right.〉$ as

$$X_{\psi }\left(t\right)=\frac{2}{\Delta }\left[(k_{1}t+k_2)cosh\left(by\right)+(k_{3}t+k_4)sinh\left(by\right)+(k_{5}t+k_6)cos\left(ay\right)+(k_{7}t+k_8)sin\left(ay\right)\right].$$

(95)

Here, $y=2{\omega }_{0}t$ and $\Delta =Ncosh\left(by\right)+2{\omega }_{0}sinh\left(by\right)$.

Using Equation (5), we can perform a similar calculation for the trajectory associated with $\left|\varphi \right.〉$ to obtain

$$X_{\varphi }\left(t\right)=\frac{2}{{\Delta }^{\prime }}\left[(k_{1}t+k_2)cosh\left(by\right)-(k_{3}t+k_4)sinh\left(by\right)-(k_{5}t+k_6)cos\left(ay\right)-(k_{7}t+k_8)sin\left(ay\right)\right].$$

(96)

where, now,

$${\Delta }^{\prime }=Ncosh\left(by\right)-2{\omega }_{0}sinh\left(by\right).$$

(97)

So, we have

$$X_{\psi }(-k_1,k_2,-k_3,,k_4,k_5,-k_6,-k_7,k_8;-t)=X_{\varphi }(k_1,k_2,k_3,,k_4,k_5,k_6,k_7,k_8;t).$$

(98)

In the simple 2D examples that we have considered, we have sought geodesics in which the parameters analogous to the $k_i$ are freely variable, in which case the metrics derived from $X_{\chi }$ would be the same as those derived from $X_{\psi }$ once the substitution $t\to -t$ is made. There would then be no obstacle to interpreting $\left|\psi \right.〉$ and $\left|\varphi \right.〉$ as representing the system in two disjoint regions, with quantum-mechanical time (i.e., the time appearing in Equations (1) and (2)) flowing in opposite directions in the two regions. This is a quite different scenario from what was discussed in the work of Aharonov and collaborators, refs. [9,10], in trying to use a two-component Schrödinger equation to have time-symmetric quantum mechanics (see also [11]).

Of course, the limited investigations that we have conducted, in two-dimensional spacetime, do not address the issue of whether our interpretation will survive in more complicated situations. To gain further insight, it will be necessary to pursue the same set of ideas in higher dimensions, where Einstein’s equations have dynamical content.

The reader may wonder how our proposed extension of quantum mechanics relates to the scheme introduced by Weinberg [12]. In both cases, the intent is to explore the possibility of adding non-linear terms to the usual linear quantum mechanics, but our approach is not a special case of Weinberg’s scheme. Unlike Weinberg, we introduce a pair of state vectors, and, furthermore, Weinberg imposes the constraint that the norm of his wave function is constant in time. In our case, the individual norms $<\psi |\psi >$ and $<\varphi |\varphi >$ vary in time, although the sum of the two does remain constant.

The take-away message of our work is that the non-linear extension of quantum mechanics induces a modification in the time dependence of the expectation values of operators, in particular, position operators, which, in the classical regime, represent the world-lines of the associated particles. If we further assume that, for free particles, these trajectories are geodesics of some metric, then we are led to imagine that gravity is a manifestation of the underlying non-linearity of quantum mechanics. (In a totally different context using the functional Schrödinger equation in a gauge theory of non-linear quantum mechanics, H-T Elze made the assertion that “gravity, in this picture, appears as a manifestation of the nonlinearity of quantum mechanics” [13]). These geodesics are the actual observables of gravity. In most, if not all, situations, the metric itself is a quantity inferred from the behavior of particles that are assumed to travel on geodesics.

To pursue this idea further, we need to extend our investigations beyond two dimensions. It will also be useful to probe more deeply into the meaning of the non-linear extension introduced in [1] and perhaps find interesting generalizations thereof. In particular, in [1], we did not succeed in exhibiting a variational principle from which our Equations (1) and (2) could be derived when $g\ne g*$ (we were able to derive them by introducing a dissipation function, but it is not clear if that was necessary). A variational principle that does not rely on a dissipation function would provide additional understanding and new ways to analyze the consequences of what we have carried out.