1. Introduction
In recent decades, a noteworthy surge in scholarly endeavors has been witnessed, focusing on addressing the stabilization challenges associated with flexible spacecraft systems [
1,
2]. This surge is evidenced by a growing body of research. The increased interest in this field is primarily driven by the growing recognition of the substantial advantages that flexible spacecraft systems offer in the realm of space activities. A closer examination of attitude control systems for flexible spacecraft reveals a complex and demanding landscape. These systems exhibit intricate dynamics, characterized by robust interconnections between flexible and rigid modes [
3,
4]. Moreover, the precise values of key parameters governing these nonlinearities, along with several other system parameters, often elude accurate measurement and characterization. These inherent nonlinearities and uncertainties not only present a formidable challenge in designing control strategies but also exert a discernible impact on the overall system performance.
A well-established approach to addressing such complex nonlinearities involves the utilization of fuzzy system models [
5,
6]. Fuzzy models excel in their capacity to approximate unparameterized functions with nonlinearity through a linearly parametrized representation, thereby achieving suitably small approximation errors [
7,
8]. In recent years, this methodology has yielded numerous effective control strategies tailored to address the intricate dynamics of various nonlinear systems. These advances are primarily rooted in the T–S fuzzy model framework. In the research conducted by [
9], the focus was on addressing the complexities of event-triggered control through the application of an
strategy to a truck-trailer model. The study utilized the T–S fuzzy model approach to ensure system stability. Academic work [
10] employed a sophisticated Lyapunov technique to design an output feedback controller for an interval type 2 T–S fuzzy system, considering the impact of external disturbances. It is vital to underscore the significance of actuators in control systems, as their failure can lead to subpar performance or even cause the system to become unstable. This is especially critical in the context of space vehicles, where the emphasis on reliability is extremely high. A decrease in the working efficiency of space vehicles due to actuator issues could potentially result in fatal accidents. As a result, there is an increasing focus on developing dependable control systems that can counteract actuator faults, ensuring robustness and high reliability, not just in space vehicles but also in industrial systems. However, it is important to note that many existing reliable control methodologies are based on the assumption that faults are deterministic. In practical scenarios, faults can exhibit both predictable and random characteristics, often due to elements such as wear and tear or harm to control parts. To address this intricacy, contemporary studies have investigated diverse strategies to handle unpredictable actuator faults. For example, in the paper [
11], researchers tackled the problem of output feedback
control in nonlinear spatially distributed systems affected by Markovian jump-type actuator faults. A robust feedback control strategy for T–S fuzzy systems, affected by sensor multiplicative errors, was developed using the dynamic parallel distributed compensation technique [
12]. A new T–S fuzzy controller was developed, tailored specifically for spacecraft dealing with random actuator defects. The researchers in [
13,
14] aimed to tackle the issues brought about by actuator faults by implementing a restriction condition, specifically to acheive
performance. Conversely, in another methodology [
15], a distinct stabilization technique was employed to address the problems caused by actuator faults. This approach incorporated an innovative iterative linearization algorithm for the design of controller gains. Furthermore, in the research conducted by [
16], the issue of finite-time control in a nonlinear flexible spacecraft system affected by random errors was investigated. However, the said study mainly employs Jensen’s inequality and transforms time-varying delays into maximum limits, which brings about substantial conservatism. Hence, it is essential to investigate novel techniques to enhance the application of time-varying delays [
17,
18].
In addition, the traditional
stabilization strategy is often utilized to scrutinize the preferred behavior of considered dynamics and investigate the asymptotic properties of controlled system trajectories, generally assuming an infinite time stability theory [
19,
20]. In practical scenarios, the focus often lies on the behavior of dynamic systems within a specific, limited time frame. For instance, there might be situations where the impact of external disturbances requires a guarantee that the system’s states stay within acceptable boundaries during this finite period [
21,
22]. In these scenarios, the principle of finite-time boundedness gains paramount significance. The past several years have seen a surge in attention towards this principle, backed by extensive studies and related refs. [
23,
24,
25]. In this research, the method of free-weighting matrices is commonly employed, typically necessitating the inclusion of auxiliary matrices. Yet, it is vital to recognize that the adaptability of these supplementary matrices is intrinsically limited, suggesting a possible scope for improvement.
This paper investigates finite-time fuzzy fault-tolerant control for spacecraft mechanisms under the influence of actuator malfunctions, employing the T–S fuzzy paradigm. Unlike traditional methods, actuator malfunctions are represented as random signals following a stochastic Markov process, offering a comprehensive solution to concerns related to timeliness. A generalized reciprocally convex inequality with tunable parameters is introduced, which includes existing results as special cases. By integrating this enhanced inequality with flexible independent parameters, this novel controller design methodology formulates a less conservative
performance analysis condition in a mean-square sense compared with some existing works [
13,
14]. The effectiveness of this approach is empirically validated through a numerical example involving a fuzzy spacecraft system, demonstrating the practical applications and benefits of the proposed methodology. To enhance the flexibility of the control approach, a set of versatile parameters is incorporated. This novel controller design technique permits individual modification of these variables, offering a higher level of autonomy and personalization relative to current approaches. Significantly, these adaptable variables are predetermined, distinct from the unidentified slack matrices observed in prior research [
13,
16]. When compared with previous literature like [
13,
16], this control strategy demonstrates enhanced usability and efficacy.
The rest of this paper is organized as follows.
Section 2, gives the system description and preliminaries. In
Section 3, the main results are given.
Section 4 provides a numerical example, and
Section 5 concludes the paper.
Notation: The sum of A and its transpose is denoted as or . The symbol ⨂ is used to denote the Kronecker product for matrices. Unless explicitly stated, matrices are assumed to have compatible dimensions.
2. System Description and Preliminaries
Figure 1 illustrates the overall closed-loop dynamical system’s structure. The motion and forces of the pliable spacecraft are characterized by differential equations. To represent the rotational state of the spacecraft, quaternion notation is introduced. We set
and the quaternion vector can be defined as
. It is important to note that the constraint
must be satisfied. The dynamic model of this nonlinear spacecraft model can be denoted as follows:
where for
, let us define
as the diagonal matrix
and the diagonal matrix
is defined as
. Here,
denotes the damping ratio for the
i mode,
v signifies the rotation angle about the Euler axis. The frequency for the
ith mode is denoted by
, and
(for
) is associated with the pitch, yaw, and axis angular velocities, in that order. The matrix
is responsible for coupling, and
denotes the total count of mode frequencies. The system’s control input is denoted by
, and
signifies an external disruption variable.
To simplify the representation, we can define a consolidated disturbance term since
,
, and
are interrelated. This consolidated disturbance term can be expressed as follows:
Recalling (3) and (4), one has
where
is a positive definite matrix,
indicates the coupling matrix with a sufficiently small norm.
Given that the condition
holds true for
. The state vector can be defined as follows:
. Here,
denotes the quaternion, and
signifies the angular rate, both are viewed as the regulated outputs. By amalgamating Equations (
1) through (
5), the dynamic system is obtained by an “IF-THEN” fuzzy principle.
Rule
i: IF
,
, …,
, THEN
We define
, and
are recognized as T–S fuzzy sets. Here, the expression of the system matrices, denoted as
,
, and
can be delineated in the subsequent manner:
Hence, the T–S fuzzy system can be delineated as
where
Remark 1. It should be clarified that the set of fuzzy rules employed in this study is meticulously designed to cover all possible operational scenarios of the nonlinear spacecraft system. Consequently, each rule is crafted to address distinct conditions, ensuring that the control logic is exhaustive in the sense that at least one rule is always applicable, as seen in [13,14,21]. For instance, within the context of Rule 1, should the premise conditions not be met, the system seamlessly transitions to assess subsequent rules. This approach guarantees that the system’s response is consistently governed by the most pertinent rule, thereby preserving the integrity and performance of the control system. The sensor grid intercepts system output signals, employing an output feedback technique for the formulation of the controller. In actual systems, the output vector is periodically sampled at set via a sampling device. This discretely sampled output signal is then directed into the input interface of the sensor network. In controller design, signals from the system’s output are captured by the sensor network using an output feedback method. It is important to note that at a specific sampling point, say , the value of stays constant during the time interval . Therefore, the signal that the sensors receive during this interval, i.e., for , is consistently represented by .
It is important to underscore that the components of the adjacency matrix should be positive for the edges present in the graph, which is expressed as for all . Moreover, for nodes belonging to , the diagonal elements of the matrix are determined as .
The ideal control input is
the output of the
sensor is given by
and
. Here,
denotes the output matrix of the
-th sensor, and
satisfies the corresponding limit.
This paper considers a situation where the sampling intervals are not periodic but remain bounded. This means that between successive sampling points, one has . Define to represent the elapsed time from the previous sampling point . It is crucial to observe that complies with the condition and for all instances, barring the distinct sampling point .
Taking into account randomized failures, we have
Here,
can be seen in (
7),
is a bounded actuator fault. For scalar
,
can be denoted as
. Moreover, the fault matrices can be defined as
and
, where
for
. The stochastic Markov process can be denoted by
, which satisfies
and transition rates can be denoted as follows:
where
and
.
In order to streamline the symbols, we establish
,
, and likewise for
with
in
. In addition, in Equation (
8), we set the constraints
, where
and
respectively denote the lower and upper bounds of
. Defining
,
,
, and
,
can be depicted as the amalgamation of
and
scaled by
, where
is defined as
with
.
By amalgamating (
6) and (
8), we put forth the subsequent fuzzy FTC methodology. This controller, under the influence of the sampled-data input, is architected as follows:
Rule
i: IF
,
, …,
, THEN
where
is the required controller.
Setting
and
, combining (
10) and (
6), we can derive the following dynamical system:
Furthermore, by recognizing that
, model (
11) can be rewritten as
where
and
In our pursuit of addressing the challenge of fuzzy FTC control with stochastic actuator faults, our chief aim is to architect a fuzzy fault-tolerant controller that meets the subsequent performance benchmarks:
(i) Given the positive scalars
, and a positive definite matrix
Z, we can ascertain that system (
12) demonstrates FTSDB in relation to the parameters
, provided certain prerequisites are met:
(ii) For positive values of
and
, if the subsequent condition is satisfied, then system (
12) attains the
performance level:
By defining
and imposing the constraint
, we construct a strategy that employs the captured output from an individual sensor and its adjacent sensors. This innovative technique presents a distinctive condition for preserving system stability and concurrently attaining
performance. Furthermore, we develop a procedure for formulating controller gains that satisfy these particular criteria.
4. Numerical Example
We consider the spacecraft dynamics (
1), as referenced from [
13]. Most of the energy linked to elastic oscillation is focused in the modes of low frequency. As a result, it becomes crucial to focus solely on the initial four elastic modes. The vector of natural frequencies for these modes is denoted as
rad/s, and the associated damping ratios are
. Following this,
and
are defined accordingly.
and
is given as
By choosing three operating points, setting , , and , the flexible spacecraft can be formulated as follows:
Rule 1: IF
,
, THEN
Rule 2: IF
,
, THEN
Rule 3: IF
,
, THEN
The determination of lower and upper membership functions proceeds as such: when
j assumes values of
if
Remark 8. Note that the selection of the membership function in this paper is predicated on the determination of the specific values of χ, aligning with the inherent characteristics of the flight systems under consideration. Actually, the choice of the membership function is congruent with the nature of the problem at hand. For instance, Gaussian membership functions, owing to their smoothness and symmetry, are frequently utilized for data that exhibit properties of normal distribution. This selection criterion ensures that the analytical approach is not only consistent with the system’s attributes but also optimally equipped to handle the statistical nuances of the data involved.
Taking into account the aforementioned triad of operational points, we can ascertain the values of the matrices
,
, and
for
, subject to the effect of the external disturbance
. The matrices are depicted in
Figure 2. For the purpose of ensuring stability in the flexible spacecraft system, the matrix
is given as follows:
The matrices corresponding to the sensor output are defined as follows:
,
, and
. For
and
, we examine the subsequent trio of scenarios:
(2) Compromised operational condition with a degree of functionality impairment.
The transition rate matrix corresponding to the Markov process is presented below:
Setting
,
,
, and applying Theorem 2, we find that the maximum permissible upper bound for
is calculated to be
. This value surpasses the previously reported upper bound of
in [
16], highlighting the benefits and enhancements introduced by the parameters proposed in this paper. Moreover, setting
with other parameters unchanged, and applying Theorem 2, we find that the maximum permissible upper bound for
is calculated to be
, which shows the advantages of the introduced GRCI. Additionally, predicated on the stipulation outlined in Equation (
35), Theorem 2 furnishes the feedback gains in the following manner:
where
Initiating the system with
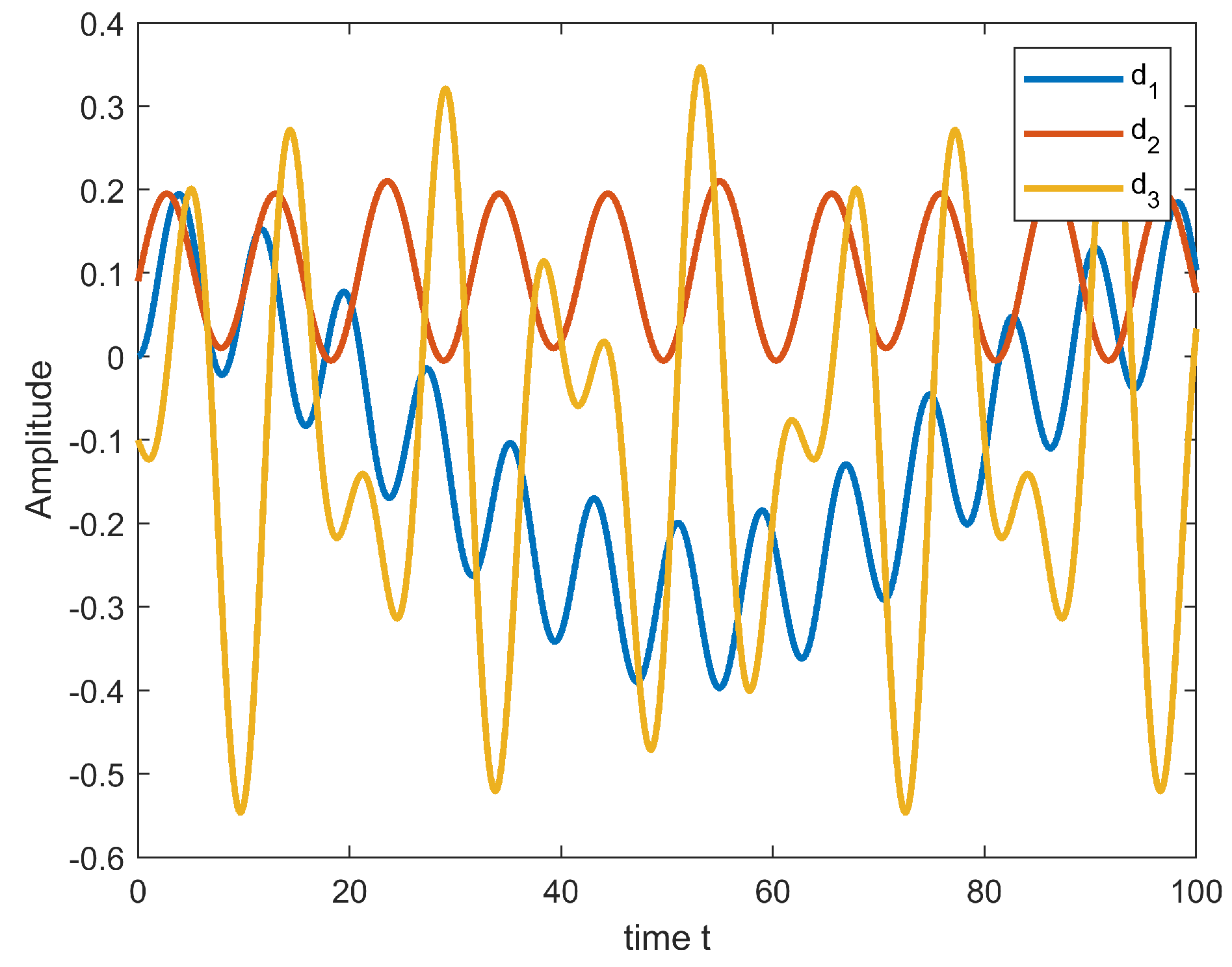
, the state responses of the closed-loop fuzzy system can be visualized in
Figure 3. The illustrations emphasize the efficacy of the control design methodology, particularly in managing a stochastic Markovian process.
Remark 9. It should be pointed out that, in Figure 3, disturbances typically represent environmental influences, such as wind speed, pressure changes, and temperature variations, all of which can affect the performance and control of the aircraft system. In this paper, the disturbances we chose mainly serve to validate the effectiveness of the proposed method. The two sinusoidal waves can simulate periodic changes in wind speed, pressure, or temperature. It is worth noting that this paper does not consider the issue of disturbance amplitude, as the current disturbances are sufficient to demonstrate the advantages of our method. Additionally, actuator faults and disturbances are two different focus points in the system we consider, and their cumulative effects can impact the system’s robustness. Therefore, these disturbances are closely related to actuator faults, see Figure 1.