Abstract
While there are well-known synthetic methods in the literature for finding the image of a point under circular inversion in -normed geometry (Euclidean geometry), there is no similar synthetic method in Minkowski geometry, also known as the geometry of finite-dimensional Banach spaces. In this study, we have succeeded in creating a synthetic construction of the circular inversion in -normed spaces, which is one of the most fundamental examples of Minkowski geometry. Moreover, this synthetic construction has been given using the Euclidean circle, independently of the -norm.
1. Introduction
The main geometrical methods in the sciences go back to ancient times and are based on lines and circles. The ubiquitous contemporary use of Fourier methods in physics and engineering is mathematically equivalent to the methods used by Ptolemy [1].
Euclidean geometry has mainly evolved into Riemannian geometry, with local Euclidean geometry in tangent spaces [2]. Another extension is into Minkowski–Finsler geometry, also referred to as Riemannian geometry without the quadratic restriction [3]. Just as Euclidean geometry in two dimensions is based on using the circle as the basic figure for the isotropic determination of distances, Lamé curves (also referred to as supercircles and superellipses) form the basis of the simplest definitive Minkowski–Finsler geometries. Generalizing superellipses to any symmetry (Gielis transformations) extends the methods that the natural sciences have to describe various natural anisotropies for different symmetries s (, etc., or any real value), as observed in starfish or diatoms [4]. By applying Gielis transformations to the most “natural” curves and surfaces of Euclidean geometry, e.g., circles under closed curves and logarithmic spirals under non-closed curves in two dimensions, one obtains many shapes observed in nature, biology, crystallography, physics, and other fields [4,5].
Over the past decade, these curves and transformations have been used successfully to model of a wide variety of natural shapes, from plant leaves and tree rings to starfish and avian eggs [6]. Further applications of Finsler geometry involving superellipses or Gielis curves in the natural sciences are found in forest ecology [7,8], seismic ray paths in anisotropic media [9], and the spreading of wildfires [10]. This has inspired various researchers to study inversions, using classical inversion over a circle (Figure 1) [11], or with Lamé–Gielis curves as inversion circles [12,13].
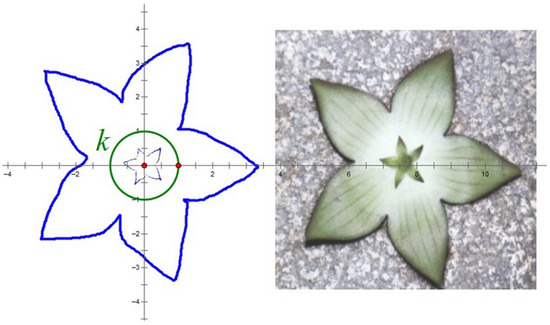
Figure 1.
Huernia flowers and how the outer edges of the corolla (blue) are obtained by the inversion of the sepals (light blue) over the green circle k (see [11] for details).
Inversions are area-preserving transformations, whereby the area of a rectangle formed by two distances from the center is equal to the area of the square on the radius of the circle (see [14] for more details). This is very similar to the parabola, a machine for transforming rectangles into squares with the same area. In Euclidean geometry, parabolas, ellipses, and hyperbolas are related directly to the application of areas in Euclid’s Book II. Since the basic shapes of our simplest Minkowski–Finsler geometries are a one-step generalization of the classic conic sections, it is of great interest to return to the methods used in ancient times. While, in Euclidean geometry, the image of a point under circular inversion can be found by a synthetic method, in another type of geometry that stands next to and is a relative of Euclidean geometry (called Minkowki geometry), synthetic methods for circular inversion are not well known.
The concept of Euclidean distance can be generalized to any linear space by the introduction of a norm. In this sense, the geometry that reveals, with the help of norms, infinite-dimensional Banach spaces is called Minkowski geometry (we refer the reader to [15,16,17] for a wider treatment of this). This is often confused with spacetime geometry, also called Minkowski geometry. Hermann Minkowski (1864–1909) was a pioneer in both geometries, and the general structure of Minkowski space was introduced by Minkowski while working on some problems in number theory [18]. However, considering that Riemann mentioned the -norm in [19], it can be said that the first step towards Minkowski geometry was taken by Riemann. A norm on a vector space V is a function for which the following hold for any V, and :
i. (positive definite, );
ii. (positive homogeneity);
iii. (triangle inequality).
A normed space is a set V with a norm defined on V. The most important thing that explains the relationship between normed spaces and metric spaces is the following proposition:
Lemma 1.
A normed linear space is a metric space with the distance
Proof.
The metric properties (non-negative and symmetry) of are quite obvious from the norm axioms. From the triangular inequality property of the norm,
for any or . □
Also, the most well-known examples of normed spaces are the -normed space and -normed space, whose definitions are given below.
Let be a vector in the n-dimensional real vector space . The -norm is defined as
Also, the pair is called the -normed or p-normed space. The -norm is defined by
where , , and . The pair is called the -normed space (we refer the reader to [20,21,22] for a wider treatment).
In Figure 2a, the brown circle represents the unit circle according to the norm and the red circle represents the circle according to the norm as , while the other blue circles represent the circle according to various -norms. Similarly, in Figure 2b, the brown circle represents the circle according to the norm and the red circle represents the circle according to the -norm as , while the other blue circles represent the circle according to various -norms. Also, Figure 2 shows that the unit balls are convex with a non-empty interior and centrally symmetric sets according to the and -norms. However, norms that have unit balls that are centrically symmetric but not mirror symmetric can be defined as follows (see Figure 3):
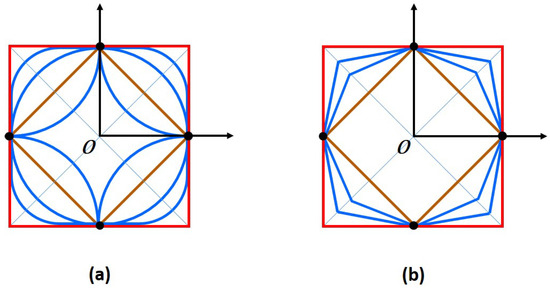
Figure 2.
(a) Unit circles for varying p-norms, (b) unit circles for varying -norms.
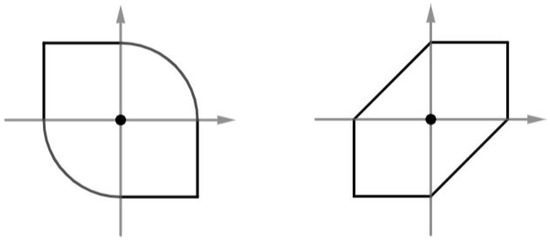
Figure 3.
Unit circles in terms of the norms , respectively.
As a result, it is clear from the definition of a norm that the unit ball has the following characteristics:
(i) The unit ball is a closed and bounded set;
(ii) The unit ball is centrally symmetric;
(iii) The unit ball is convex.
Conversely, if B is a set satisfying the properties i, ii, and iii, then the function
is a norm on , for which B is the unit ball.
It should be noted here that the convex distance function induced by the convex set D,which has a non-empty interior and is not necessarily centrally symmetric, is defined via by
However, it is obvious that the convex distance function has the properties
and (homogeneity) such that, for any vectors , and , the distance function does not have to satisfy the symmetry property, which is one of the axioms of metric space. The distance function satisfies the symmetric axiom if and only if D is centrally symmetric (see [16,17] for more details). Thus, is a norm and the distance function is a metric on . The pair is called Minkowski geometry. Thanks to translation invariance and homogeneity, all points in any Minkowski geometry have the same status, and all geometric objects are centered at the origin. Furthermore, the open balls are rescaled, translated versions of the unit ball . As a result, the fact that the norms can be interpreted and understood entirely with the help of the shapes of the unit balls shows that the structure of Minkowski geometry can be completely determined by the unit ball, which is a centrally symmetrical convex body.
The idea of examining the invariance of concepts, including the concept of distance in Euclidean geometry, in Minkowski geometry when the Euclidean norm is replaced by an arbitrary Minkowski norm is quite interesting. However, this trade-off can cause even very elementary and simple questions to be very difficult to answer, and an answer may not even be found. One example is the following question: while in Euclidean geometry the image of a point under circular inversion can be found by a synthetic method due to the unit ball having perfect symmetry, can a synthetic method be constructed for a Minkowski geometry whose unit ball is centrally symmetric but not perfect?
2. Literature Review and Motivation
Although the emergence of inversion is not known for certain in the literature, there are some studies [12,23] that indicate that it was first introduced by Apollonius of Perga (225–190 ). The first systematic research on inversion began with Jakob Steiner (1796–1863), who made many geometric discoveries using this transformation in the 1820s (see [12,23] for details). Later, Mario Pieri [24] developed the subject axiomatically and systematically in the early . In What is Mathematics? [14] by Richard Courant and Herbert Robbins, a detailed description is given of inversion, including Peaucellier’s linkage, converting circular into rectilinear motion using the theory of inversion.
When research on inversion is examined, it is seen that the main source is the frequently cited book Inversion theory and conformal mapping, written by David E. Blair [25]. Additionally, Gerard A. Venema, in the 10th chapter of his book titled Fundamentals of Geometry [26], has presented almost all the properties of circular inversion in a very simple and understandable way. At present, except for the references [27,28,29], it is very difficult to find documents in the literature containing significant results regarding inversion theory in addition to the results in the essential studies mentioned above. In [27,28,29], José Luis Ramírez and Gustavo N. Rubiano have introduced the concept of elliptical inversion, which is the generalization of the circular (or spherical) inversion concept, and obtained important results.
In the studies mentioned so far, inversion has been limited to Euclidean geometry. However, the finding of some important but not surprising results regarding inversion in -, -, and -normed spaces, respectively, in references [30,31,32] is evidence that inversion theory is also becoming popular in non-Euclidean geometries.
Especially in the normed spaces and , an inversion in a circle (or sphere) of radius r centered at the point O is a map of an arbitrary point X found by inverting the length of the displacement vector and multiplying by . If X and are inverse points according to this circular inversion, then the circular inversion with respect to the - and p-norm are defined as follows, respectively:
In Euclidean geometry, it can be easily obtained from the definition of inversion that a circular inversion will have the following properties:
i. The inverse of a circle (not through the center of inversion) is a circle;
ii. The inverse of a circle through the center of inversion is a line;
iii. The inverse of a line (not through the center of inversion) is a circle through the center of inversion;
vi. A circle orthogonal to the circle of inversion is its own inverse;
v. A line through the center of inversion is its own inverse;
vi. angles are preserved under inversion.
However, it can be easily seen from the - and p-circular inversion definitions given in (1) that none of the above-defined properties, except for v, remain invariant in the normed spaces and (see [31,33] for more details).
Although inversion is a subject that has been known about and studied for a long time, it has been limited to Euclidean logic. It is particularly surprising that inversion theory has hardly been studied within the framework of Minkowski geometry. As far as we know, only references [34,35,36] can be given as examples of inversion studies in Minkowski geometry. So, there is good motivation for researchers to investigate which geometric features known in Euclidean geometry and related to inversion will remain invariant in Minkowski geometry. In this sense, our main motivation will be to develop a synthetic method to find the inverse of a point under circular inversion in Minkowski geometry. In order to construct this synthetic method, which has not been given before in the literature, in the next section we will take a short journey into circular inversion with the - and -norms in Minkowski geometry.
3. A Visit to Circular Inversion in Minkowski Geometries and
Let us consider the circle . The inverse of an arbitrary point P, different from the center of symmetry of the circle O, with respect to the circle C is the point , such that
A circular inversion is sometimes referred to as a “reflection” relative to the circle. Obviously, if the inverse of point P is point , then the inverse of point is point P. Moreover, from Equation (2), it is clear that, except for the center of the inversion circle O, circular inversion will map the points inside the inversion circle to points outside the circle, or the points inside the circle to points outside. The points on the inversion circle C remain fixed under circular inversion. It should be noted that the center of the inversion circle O cannot be mapped to any point of the plane. However, points close to O are mapped to points far from O, and points far from O are mapped to points close to O. Thus, it would be meaningful to make a mapping between point at infinity and point O under circular inversion. Inversion mapping, which is one of the most important representatives of the conformal functions that generally map circles or lines onto (the same or different) circles or lines and preserves the angles between intersecting curves, is defined as follows (see [25] for more details):
Definition 1.
Let the circle be given. The inversion, according the circle C, is the mapping , defined as follows for all
such that is the point lying on the ray and . Additionally, and .
According to the above definition, in the plane equipped with the Manhattan norm (which is given by ) and the Euclidean norm (which is given by ), circular inversion is formally defined as (see [31,33,37,38] for more details)
for and .
According to this definition, it is clear that finding the inverse of a point analytically will lead to tedious operations. In this sense, the following simple synthetic method, which is well known in the literature, has been proposed to find the inverse of a point according to the Euclidean norm .
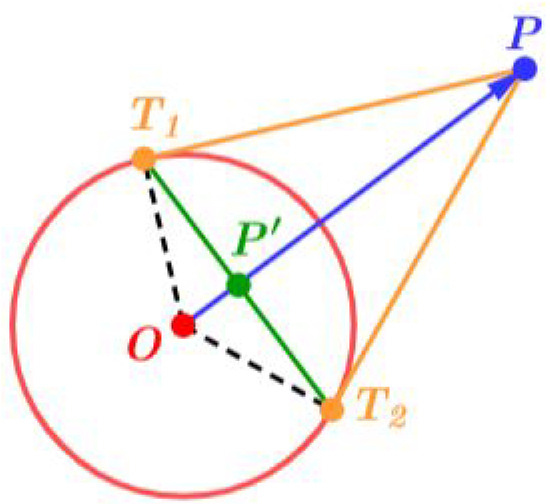
Figure 4.
A standard construction for Euclidean circular inversion.
Step 1: Draw the tangent lines from point P to inversion circle C;
Step 2: Label the point where the tangent lines touch circle C as and ;
Step 3: The point where line segment intersects the ray is the inverse of P.
The inverse of a point in Euclidean geometry can be easily found by the above well-known synthetic method since the unit ball has perfect symmetry. However, a synthetic method for Minkowski geometry, in which the unit ball is centrally symmetric but does not necessarily have perfect symmetry, is not available in the literature. In order to create a synthetic method for circular inversion in Minkowski geometry, we will consider p- and -normed spaces, which are the most classical examples of Minkowski geometry. If we manage to generate a synthetic method for Manhattan (or taxicab) geometry, which corresponds to the special case of or in p- and -normed spaces, we can attempt to generalize this method to Minkowski geometry. Thus, the method we will give for Manhattan geometry in the next section will illuminate our way forward in this difficult journey regarding the synthetic method we want to give for Minkowski geometry. Here, we should immediately point out that the effort to develop a synthetic method for circular inversion in Minkowski geometry is a motivation for our future work. In this study, we will be content with only the norm .
4. Main Result
4.1. Notation and Preliminary
We will denote the metric induced by the -norm as , which is called the taxicab or Manhattan metric, and formulate it as . Similarly, the metric induced by the -norm is formulated as . The similarity of triangles will be denoted by “∼”. Also, from the definition of the metric , the following proposition is quite clear (see [39] for more details).
Lemma 2.
Let L be a line through the points and in the analytical plane. If L has slope m, and is not a vertical line,
If L is a vertical line, then .
4.2. Synthetic Construction of Circular Inversion in -Normed Space
Let be an normed circle with the radius and center O.
If P is an exterior point to , then the point Q, which is the intersection of the circle by the ray is determined. Afterward, an Euclidean circle C is constructed with the radius and centered at the point O. Let the points where the tangent lines drawn from the point P to the Euclidean circle touch the Euclidean circle be labeled and . Thus, the point where the line segment intersects the ray is the inverse of the desired point (see Figure 5).
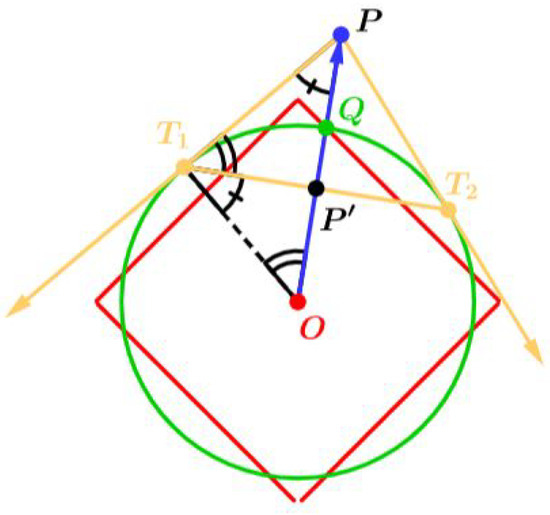
Figure 5.
A new construction for circular inversion in terms of the -norm.
Indeed, it is simply observed that , hence
Therefore,
Using the relation given in Lemma 2, which allows conversion between the Euclidean metric and the taxicab metric , we obtain that
By making simplifications to the above equation, we find that
If point P is taken outside the circle, only the roles of points P and will change. Therefore, the synthetic construction is the same.
Theorem 1
(Main Theorem). Let be a -normed circle with the radius and center O in the Minkowski plane . Then, the image of a point P under inversion with respect to is
where and are the points made by the tangents drawn from point P to a Euclidean circle with radius , such that and the center at O touch the Euclidean circle.
5. Conclusions
Open problem: In Minkowski geometry with an -norm (Euclidean geometry), the image of a point under circular inversion can be found by a synthetic method. Similarly, can a synthetic method be constructed to find the image of a point under circular inversion in Minkowski geometry (geometry that emerges through norms in a finite-dimensional Banach space)?
The fact that circles corresponding to the norm in Minkowski geometry are centrally symmetric but do not always have mirror symmetry makes this question quite difficult. In this work, we have succeeded in providing a synthetic method for circular inversion in -normed spaces. Based on the method given here, we will try to generalize this method to Minkowski geometry, regardless of the norm, in our future work.
Author Contributions
Conceptualization, T.E., A.O.Ş. and J.G.; methodology, T.E., A.O.Ş. and J.G.; software, T.E., A.O.Ş. and J.G.; validation, T.E., A.O.Ş. and J.G.; formal analysis, T.E., A.O.Ş. and J.G.; investigation, T.E., A.O.Ş. and J.G.; resources, T.E., A.O.Ş. and J.G.; data curation, T.E., A.O.Ş. and J.G.; writing—original draft preparation, T.E., A.O.Ş. and J.G.; writing—review and editing, T.E., A.O.Ş. and J.G.; visualization, T.E., A.O.Ş. and J.G.; supervision, T.E., A.O.Ş. and J.G.; project administration, T.E., A.O.Ş. and J.G.; funding acquisition, T.E., A.O.Ş. and J.G.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Russo, L. The Forgotten Revolution: How Science Was Born in 300 BC and Why It Had to be Reborn; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Cartan, E. Géométrie Euclidienne et géométrie Riemannienne; Scientia: Bristol, UK, 1931; English translation in Beyond Geometry-Classic papers from Riemann to Einstein Dover Publications, 2007; Volume 49, pp. 393–402. [Google Scholar]
- Chern, S.S. Finsler Geometry Is Just Riemannian Geometry without the Quadratic Restriction. Not. AMS 1996, 43, 959–963. [Google Scholar]
- Verstraelen, L. A concise mini history of geometry. Kragujev. J. Math. 2014, 38, 5–21. [Google Scholar] [CrossRef]
- Koiso, M.; Palmer, B. Equilibria for anisotropic energies and the Gielis Formula. Forma Soc. Sci. Form Jpn. 2008, 23, 1–8. [Google Scholar]
- Gielis, J.; Shi, P.; Beirinckx, B.; Caratelli, D.; Ricci, P.E. Lamé-Gielis curves in biology and geometry. In Proceedings of the 2021 International Conference Riemannian Geometry and Applications (RIGA), Bucharest, Romania, 15–17 January 2021. [Google Scholar]
- Antonelli, P.L.; Miron, R. Lagrange and Finsler Geometry: Applications to Physics and Biology; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013; Volume 76. [Google Scholar]
- Antonelli, P.L.; Rutz, S.F. Finslerian diffusions in forest ecology: Retrospective and open problems. Nonlinear Stud. Int. J. 2014, 21, 631–639. [Google Scholar]
- Yajima, T.; Nagahama, H. Finsler geometry of seismic ray path in anisotropic media. Proc. R. Soc. Math. Phys. Eng. Sci. 2009, 465, 1763–1777. [Google Scholar] [CrossRef]
- Javaloyes, M.Á.; Pendás-Recondo, E.; Sánchez, M. Gielis Superformula and Wildfire models. arXiv 2024, arXiv:2406.06831. [Google Scholar]
- Mladinić, P.; Radović, N. Geometrija Prirode; Proven Grupa: Zagreb, Croatia, 2018. [Google Scholar]
- Ramírez, J.L.; Rubiano, G.N.; Zlobec, B.J. Generating fractal patterns by using p-circle inversion. Fractals 2015, 23, 1550047. [Google Scholar] [CrossRef]
- Spichal, L. About the inversion of the rectangular hyperbolas on the supercircles. Symmetry Sci. Cult. 2024, 35, 127–139. [Google Scholar]
- Courant, R.; Robbins, H. What Is Mathematics? Oxford University Press: Oxford, UK, 1941. [Google Scholar]
- Martini, H.; Swanepoel, K.; Weiß, G. The geometry of Minkowski spaces—A survey. Part I. Expo. Math. 2001, 19, 97–142. [Google Scholar] [CrossRef]
- Martini, H.; Swanepoel, K. The geometry of Minkowski spaces—A survey. Part II. Expo. Math. 2004, 22, 93–144. [Google Scholar] [CrossRef]
- Balestro, V.; Martini, H. Minkowski Geometry—Some Concepts and Recent Developments. In Surveys in Geometry I; Papadopoulos, A., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 49–94. [Google Scholar]
- Minkowski, H. Sur les propriétés des nombres entiers qui sont dérivées de l’intuition de l’espace. Nouv. Ann. Math. J. Candidats Aux Écoles Polytech. Norm. 1896, 15, 393–403. [Google Scholar]
- Riemann, B. Uber die Hypothesen, welche der Geometrie zu Grunde liegen. Abh. Königlichen Ges. Wiss. Göttingen 1868, 13, 133–152. [Google Scholar]
- Gelişgen, Ö.; Kaya, R. On α-distance in three dimensional space. Appl. Sci. 2006, 8, 65–69. [Google Scholar]
- Gelişgen, Ö.; Kaya, R. Generalization of α-distance to n-dimensional space. KoG 2006, 10, 33–35. [Google Scholar]
- Gelişgen, Ö.; Kaya, R. On αi-distance in n-dimensional space. Appl. Sci. 2008, 1, 88–93. [Google Scholar]
- Kozai, K.; Libeskind, S. Circle Inversions and Applications to Euclidean Geometry. Lecturer Notes. 2009. Available online: http://jwilson.coe.uga.edu/MATH7200/InversionCompanion/inversion/inversionSupplement.pdf (accessed on 1 June 2024).
- Pieri, M. Nuovi principia di geometria della inversion. Giornal Mat. Battagl. 1911, 49, 49–96. [Google Scholar]
- Blair, D.E. Inversion Theory and Conformal Mapping; American Mathematical Society: Providence, RI, USA, 2000. [Google Scholar]
- Venema, G.A. The Foundations of Geometry, 2nd ed.; Pearson Education: Boston, MA, USA, 2012. [Google Scholar]
- Ramírez, J.L.; Rubiano, G.N. Elliptic inversion of two-dimensional objects. Int. J. Geom. 2014, 3, 12–27. [Google Scholar]
- Ramírez, J.L.; Rubiano, G.N. A geometrical construction of inverse points with respect to an ellipse. Int. J. Math. Educ. Sci. Technol. 2014, 4, 1254–1259. [Google Scholar] [CrossRef]
- Ramírez, J.L.; Rubiano, G.N. A generalization of the spherical inversion. Int. J. Math. Educ. Sci. Technol. 2017, 48, 132–149. [Google Scholar] [CrossRef]
- Sezgin, N. Öklidyen Düzlemde ve Taksi Düzlemde Evritim Üzerine. Master’s Thesis, Eskişehir Osmangazi University, Eskişehir, Türkiye, 2014. (In Turkish). [Google Scholar]
- Gelişgen, Ö.; Ermiş, T. Some properties of inversions in alpha plane. Forum Geom. 2019, 19, 1–9. [Google Scholar]
- Can, Z.; Yüca, G. On the circular inversion in maximum plane. Ikonion J. Math. 2020, 2, 26–34. [Google Scholar]
- Rubiano, G.N. Circle Inversion [A Modern Visual Perspective], e-Book. 2022. Available online: https://www.researchgate.net/profile/Gustavo-Rubiano/research (accessed on 1 June 2024).
- Spirova, M. On Miquel’s theorem and inversions in normed planes. Monatshefte Math. 2010, 161, 335–345. [Google Scholar] [CrossRef]
- Kovačevič, N. Inversion in Minkowskischer geometrie. Math. Pannonica 2010, 21, 89–113. [Google Scholar]
- Stiles, W.J. On inversions in normed linear spaces. Proc. Am. Math. Soc. 1969, 20, 505–508. [Google Scholar] [CrossRef]
- Gelişgen, Ö.; Ermiş, T. Inversions and fractal patterns in alpha plane. Int. Electron. J. Geom. 2023, 16, 398–411. [Google Scholar] [CrossRef]
- Şen, A.O. lp-normlu Uzaylarda Inversiyon Dönüşümünün Özellikleri. Master’s Thesis, Eskisehir Osmangazi University, Eskişehir, Türkiye, 2022. (In Turkish). [Google Scholar]
- Kaya, R. Area formula for taxicab triangles. Pi Mu Epsil. J. 2006, 12, 219–220. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).