Homogeneous Projective Coordinates for the Bondi–Metzner–Sachs Group
Abstract
1. Introduction
2. Homogeneous Coordinates on the 2-Sphere
3. Bondi–Sachs Metric in Homogeneous Coordinates
4. Asymptotic Killing Fields
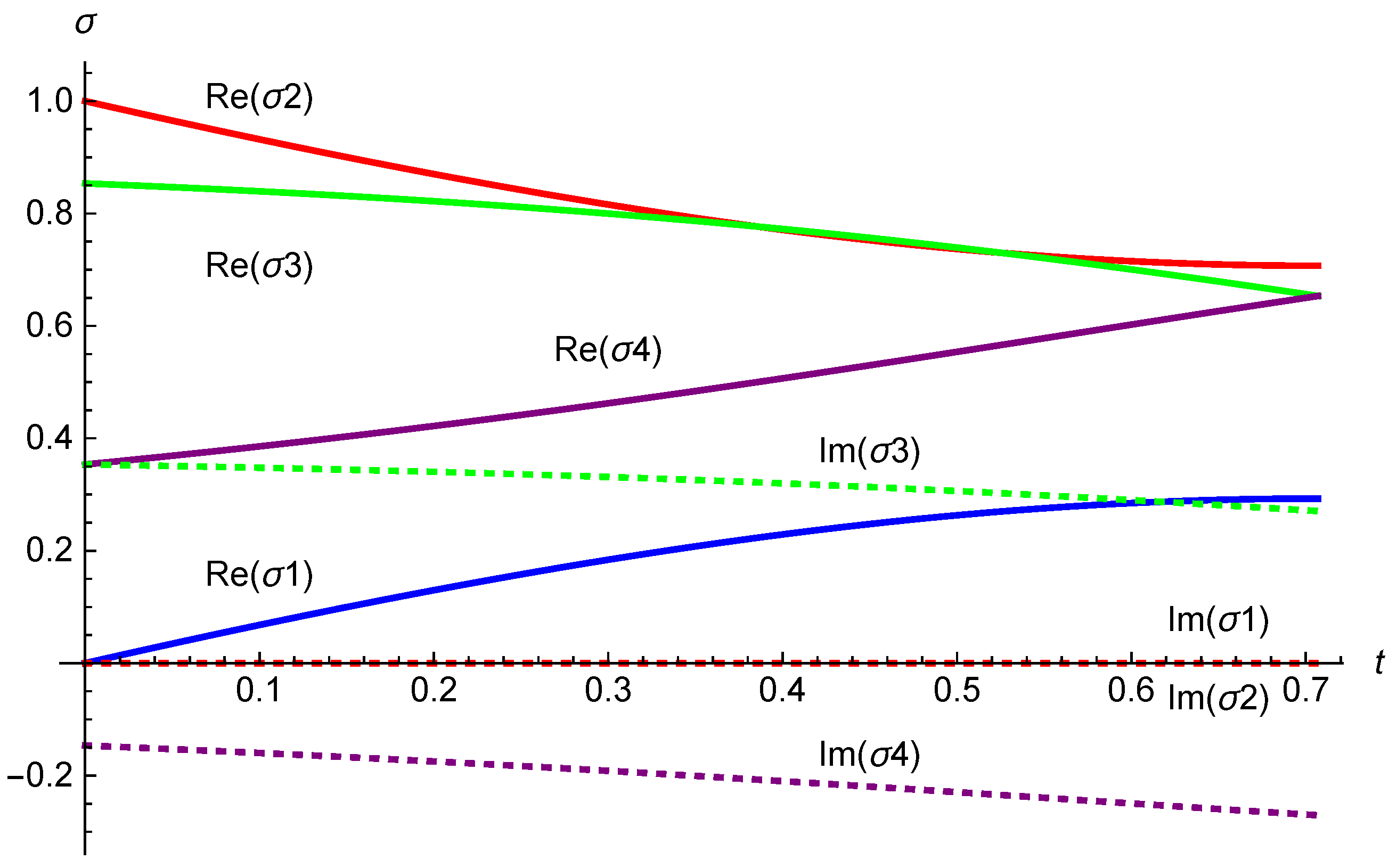
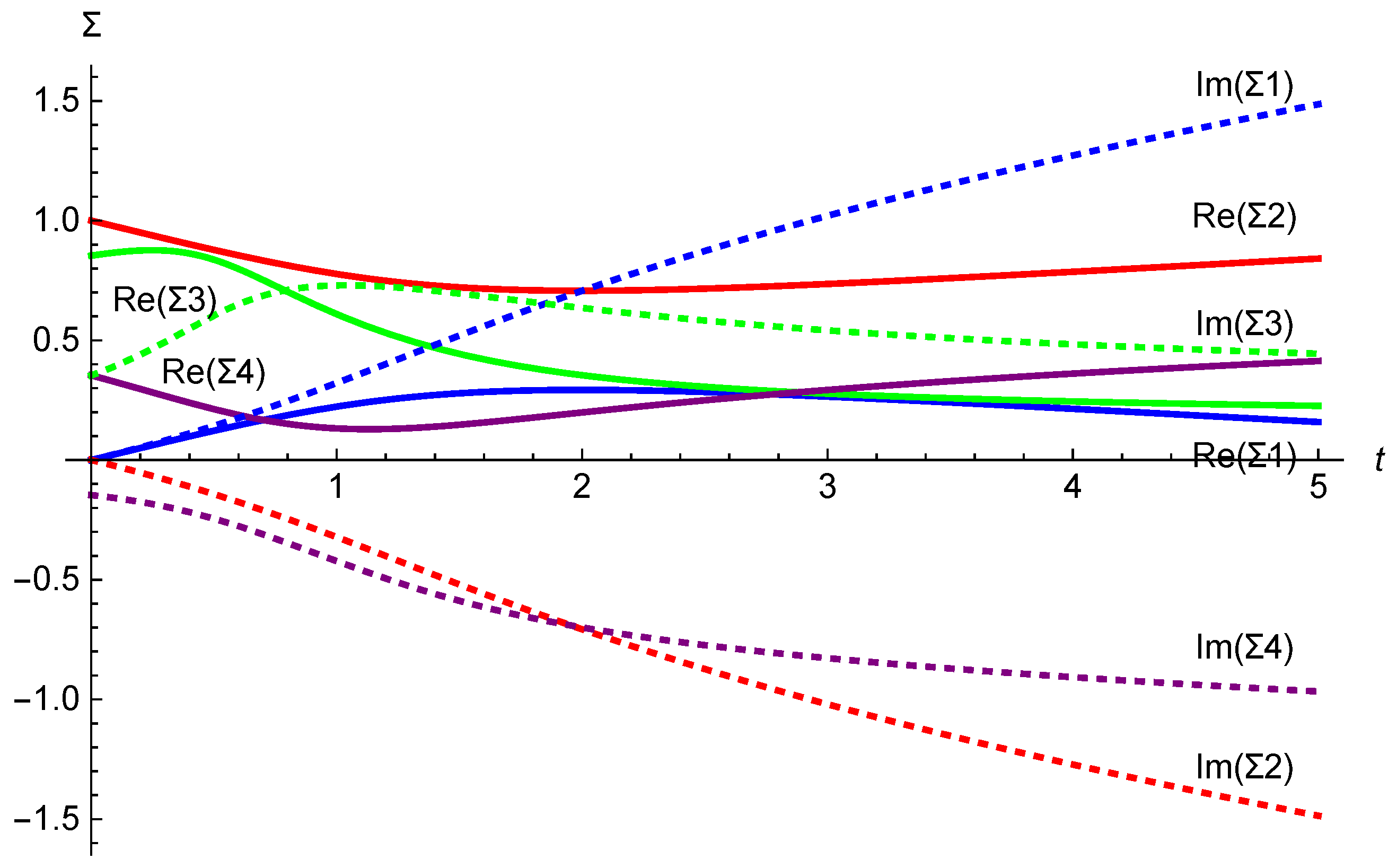
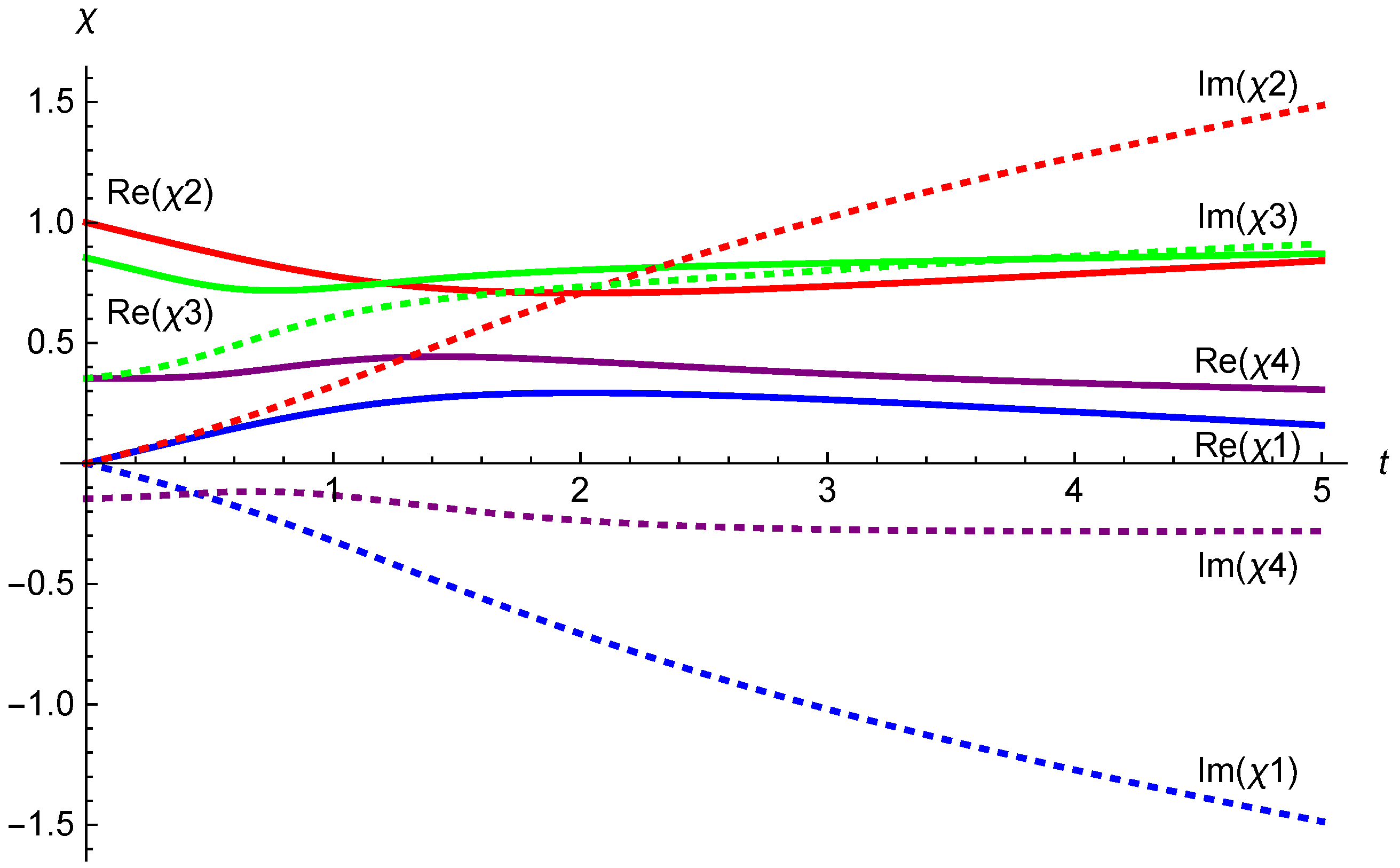
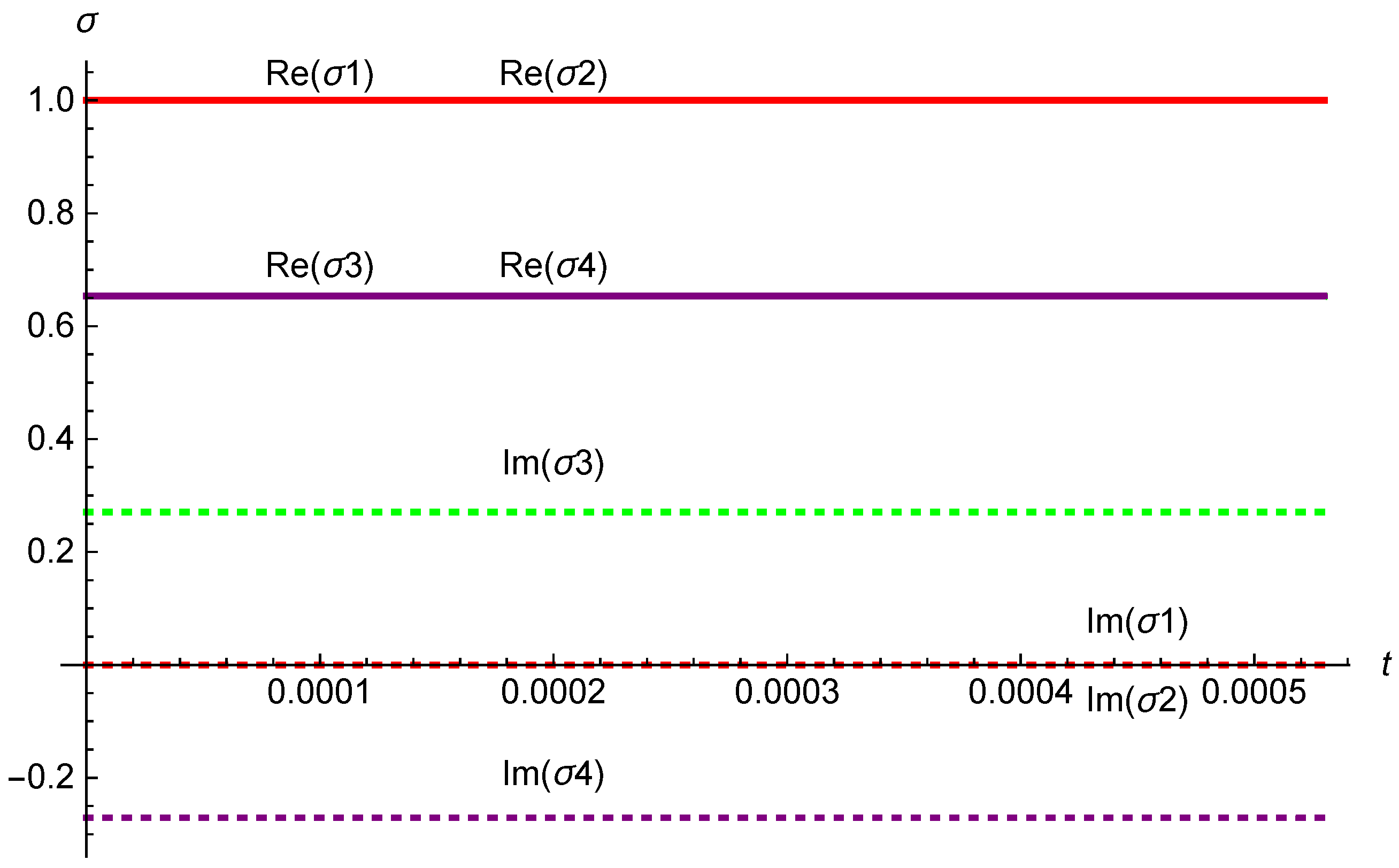
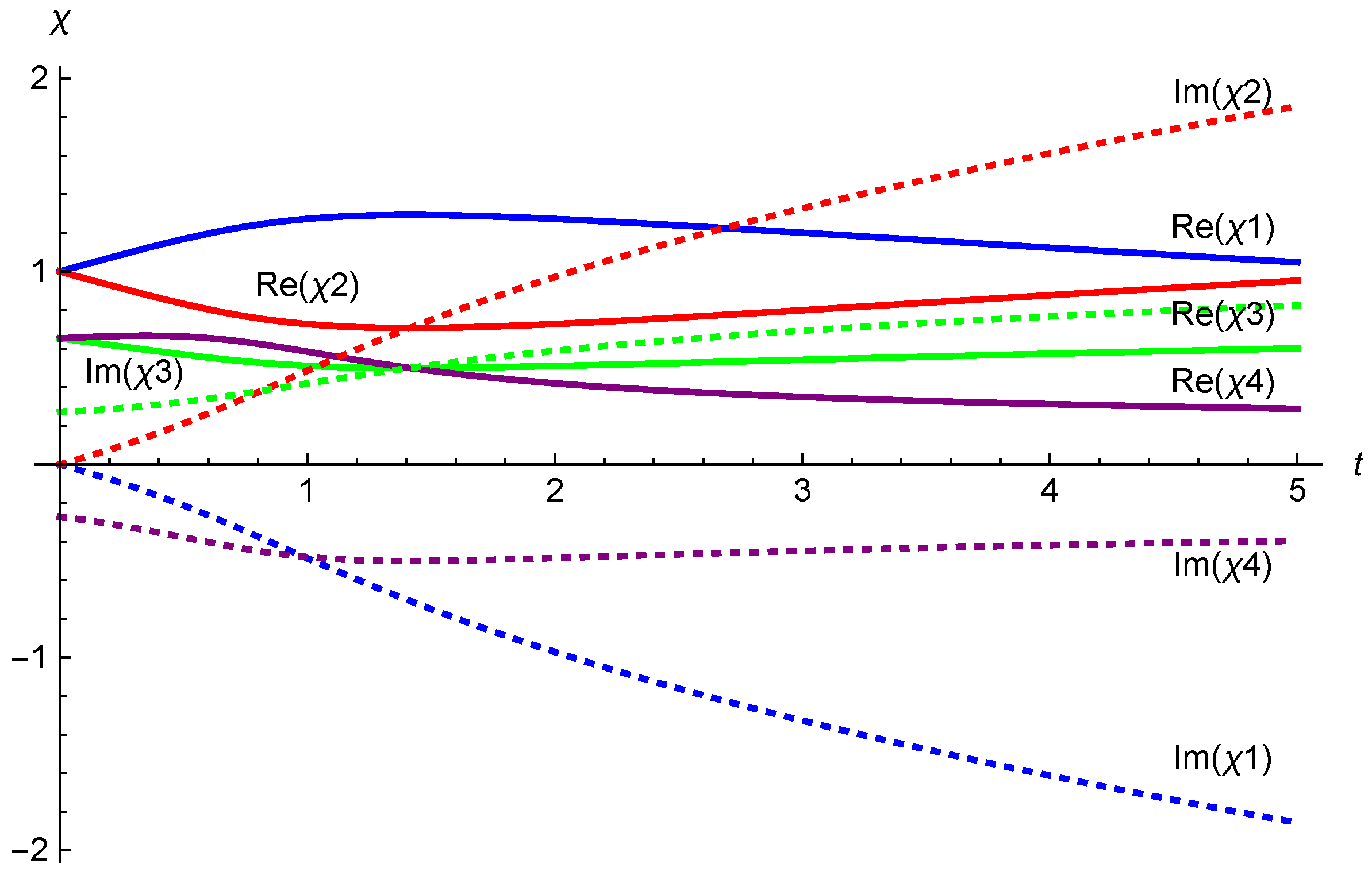
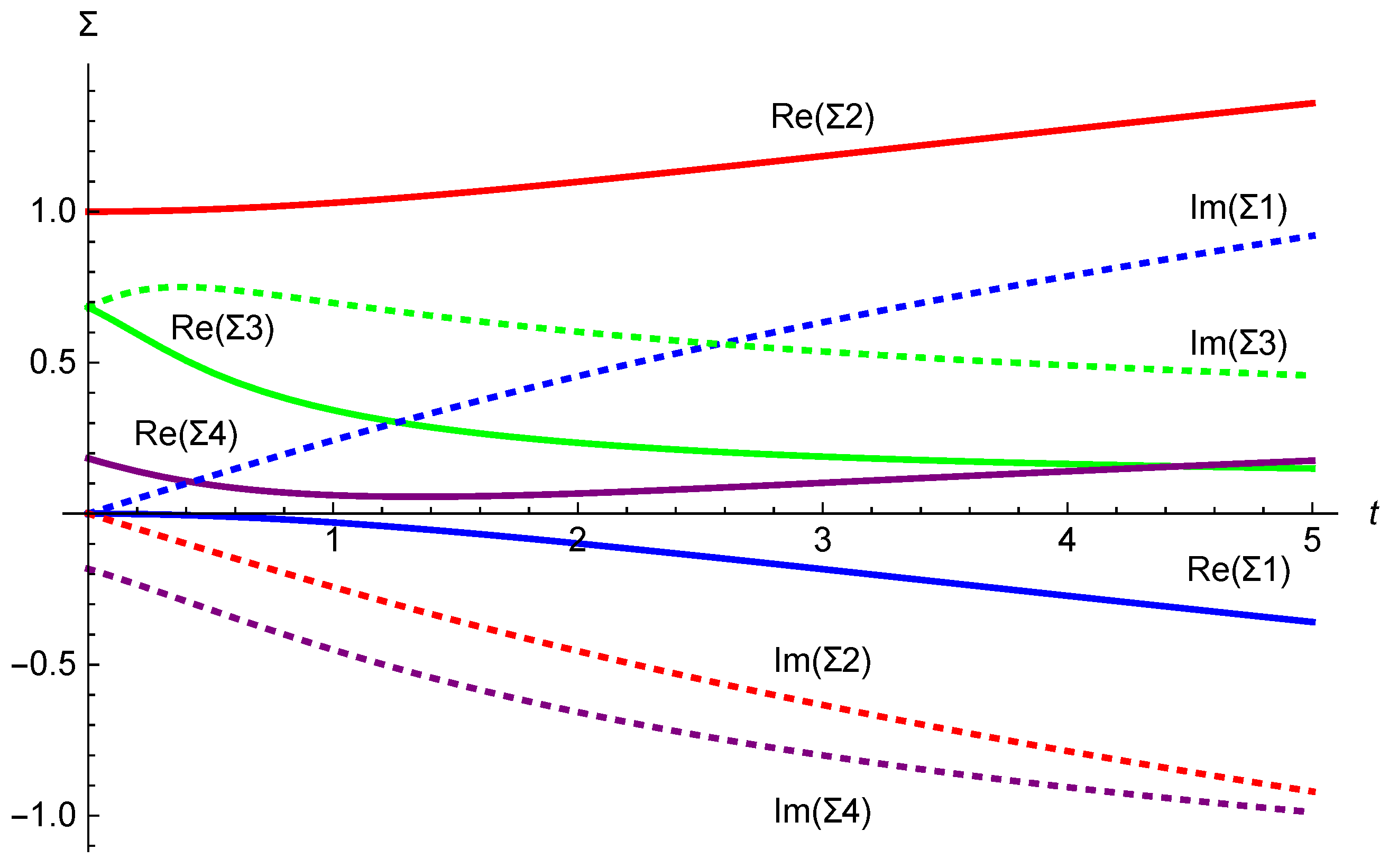
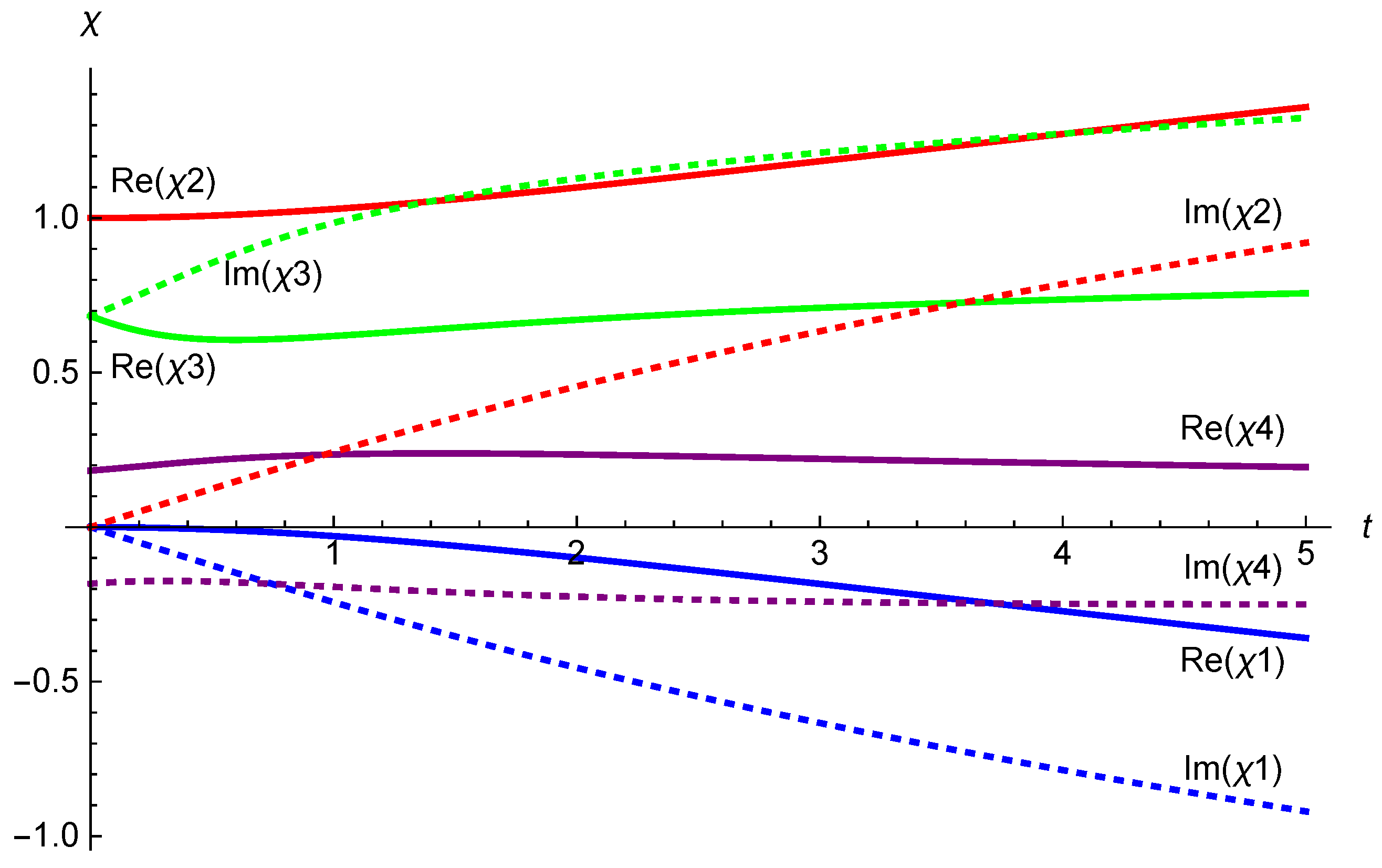
5. Flow of Supertranslation Vector Fields
6. Concluding Remarks and Open Problems
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Use of Homogeneous Coordinates
Appendix B. Lie Brackets of Asymptotic Killing Fields
References
- Bondi, H.; van der Burg, M.G.J.; Metzner, A.W.K. Gravitational waves in general relativity. VII. Waves from axi-symmetric isolated systems. Proc. R. Soc. Lond. A 1962, 269, 21. [Google Scholar]
- Sachs, R.K. Gravitational waves in general relativity. VIII. Waves in asymptotically flat space-time. Proc. R. Soc. Lond. A 1962, 270, 103. [Google Scholar]
- Sachs, R.K. Asymptotic symmetries in gravitational theory. Phys. Rev. 1962, 128, 2851. [Google Scholar] [CrossRef]
- Hawking, S.W.; Perry, M.A.; Strominger, A. Soft hair on black holes. Phys. Rev. Lett. 2016, 116, 231301. [Google Scholar] [CrossRef] [PubMed]
- Hawking, S.W.; Perry, M.A.; Strominger, A. Superrotation charge and supertranslation hair on black holes. J. High Energy Phys. 2017, 2017, 161. [Google Scholar] [CrossRef]
- Haco, S.; Hawking, S.W.; Perry, M.A.; Strominger, A. Black hole entropy and soft hair. J. High Energy Phys. 2018, 2018, 98. [Google Scholar] [CrossRef]
- McCarthy, P.J. Representations of the Bondi-Metzner-Sachs group I. Determination of the representations. Proc. R. Soc. Lond. A 1972, 330, 517. [Google Scholar]
- McCarthy, P.J. Structure of the Bondi-Metzner-Sachs group. J. Math. Phys. 1972, 13, 1837. [Google Scholar] [CrossRef]
- McCarthy, P.J. Representations of the Bondi-Metzner-Sachs group II. Properties and classification of representations. Proc. R. Soc. Lond. A 1973, 333, 317. [Google Scholar]
- McCarthy, P.J.; Crampin, M. Representations of the Bondi-Metzner-Sachs group III. Poincaré spin multiplicities and irreducibility. Proc. R. Soc. Lond. A 1973, 335, 321. [Google Scholar]
- McCarthy, P.J.; Crampin, M. Representations of the Bondi-Metzner-Sachs group IV. Cantoni representations are induced. Proc. R. Soc. Lond. A 1976, 351, 55. [Google Scholar]
- Barnich, G.; Troessaert, C. Finite BMS transformations. J. High Energy Phys. 2016, 2016, 167. [Google Scholar] [CrossRef]
- Alessio, F.; Esposito, G. On the structure and applications of the Bondi-Metzner-Sachs group. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1830002. [Google Scholar] [CrossRef]
- Henneaux, M.; Troessaert, C. BMS group at spatial infinity. The Hamiltonian (ADM) approach. J. High Energy Phys. 2018, 2018, 147. [Google Scholar] [CrossRef]
- Barnich, G.; Nguyen, K.; Ruzziconi, R. Geometric action of extended Bondi-Metzner-Sachs group in four dimensions. J. High Energy Phys. 2022, 2022, 154. [Google Scholar] [CrossRef]
- Chowdhury, C.; Anupam, A.; Kundu, A. Generalized BMS algebra in higher even dimensions. Phys. Rev. D 2022, 106, 126025. [Google Scholar] [CrossRef]
- Fuentealba, O.; Henneaux, M.; Matulich, J.; Troessaert, C. Bondi-Metzner-Sachs group in five spacetime dimensions. Phys. Rev. Lett. 2022, 128, 051103. [Google Scholar] [CrossRef] [PubMed]
- Prinz, D.; Schmeding, A. Lie theory for asymptotic symmetries in general relativity: The BMS group. Class. Quantum Grav. 2022, 39, 065004. [Google Scholar] [CrossRef]
- Mirzaiyan, Z.; Esposito, G. On the nature of Bondi-Metzner-Sachs transformations. Symmetry 2023, 15, 947. [Google Scholar] [CrossRef]
- Weiss, D.A. A microscopic analogue of the BMS group. J. High Energy Phys. 2023, 2023, 136. [Google Scholar] [CrossRef]
- He, T.; Lysov, V.; Mitra, P.; Strominger, A. BMS supertranslations and Weinberg’s soft graviton theorem. J. High Energy Phys. 2015, 2015, 151. [Google Scholar] [CrossRef]
- Strominger, A. Lectures on the Infrared Structure of Gravity and Gauge Theory; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Pasterski, S. Implications of superrotations. Phys. Rep. 2019, 829, 1. [Google Scholar] [CrossRef]
- Himwich, E.; Mirzaiyan, Z.; Pasterski, S. A note on the subleading soft graviton. J. High Energy Phys. 2021, 2021, 172. [Google Scholar] [CrossRef]
- Compère, G.; Gralla, S.E. An asymptotic framework for gravitational scattering. Class. Quantum Grav. 2023, 40, 205018. [Google Scholar] [CrossRef]
- Fotopoulos, A.; Stieberger, S.; Taylor, T.R.; Zhu, B. Extended super BMS algebra of celestial CFT. J. High Energy Phys. 2020, 2020, 198. [Google Scholar] [CrossRef]
- Donnay, L.; Ruzziconi, R. BMS flux algebra in celestial holography. J. High Energy Phys. 2021, 2021, 40. [Google Scholar] [CrossRef]
- Donnay, L.; Fiorucci, A.; Herfray, Y.; Ruzziconi, R. Carrollian perspective on celestial holography. Phys. Rev. Lett. 2022, 129, 071602. [Google Scholar] [CrossRef]
- Donnay, L.; Fiorucci, A.; Herfray, Y.; Ruzziconi, R. Bridging Carrollian and celestial holography. Phys. Rev. D 2023, 107, 126027. [Google Scholar] [CrossRef]
- Bagchi, A.; Divakar, P.; Dutta, S. Holography in flat spacetimes: The case for Carroll. arXiv 2023, arXiv:2311.11246. [Google Scholar]
- Chen, B.; Hu, Z. Bulk reconstruction in flat holography. J. High Energy Phys. 2024, 2024, 064. [Google Scholar] [CrossRef]
- Hao, Z.; Taylor, M. Flat holography and celestial shockwaves. J. High Energy Phys. 2024, 2024, 090. [Google Scholar] [CrossRef]
- Stewart, J.M. Advanced General Relativity; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Caccioppoli, R. Teoria delle Funzioni di Più Variabili Complesse; Carbone, L., Esposito, G., Dell’Aglio, L., Tomassini, G., Eds.; Memorie dell’Accademia di Scienze Fisiche e Matematiche: Napoli, Italy, 2022; Volume 10. [Google Scholar]
- Beltrametti, M.C.; Carletti, E.; Gallarati, D.; Bragadin, G.M. Letture su Curve, Superfici e Varietà Proiettive Speciali. Introduzione alla Geometria Algebrica; Bollati Boringhieri: Torino, Italy, 2003. [Google Scholar]
- Barnich, G.; Troessaert, C. Aspects of the BMS/CFT correspondence. J. High Energy Phys. 2010, 2010, 062. [Google Scholar] [CrossRef]
- Tamburino, L.A.; Winicour, J.H. Gravitational fields in finite and conformal Bondi frames. Phys. Rev. 1966, 150, 1039. [Google Scholar] [CrossRef]
- Della Sala, G.; Saracco, A.; Simioniuc, A.; Tomassini, G. Lectures on Complex Analysis and Analytic Geometry; Scuola Normale Superiore: Pisa, Italy, 2006. [Google Scholar]
- Barnich, G.; Troessaert, C. BMS charge algebra. J. High Energy Phys. 2011, 2011, 105. [Google Scholar] [CrossRef]
- Freidel, L.; Oliveri, R.; Pranzetti, D.; Speziale, S. The Weyl BMS group and Einstein’s equations. J. High Energy Phys. 2021, 2021, 170. [Google Scholar] [CrossRef]
- Geiller, M.; Zwikel, C. The partial Bondi gauge: Further enlarging the asymptotic structure of gravity. arXiv 2022, arXiv:2205.11401. [Google Scholar] [CrossRef]
- Penrose, R.; Rindler, W. Spinors and Space-Time. 1: Two-Spinor Calculus and Relativistic Fields; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esposito, G.; Vitale, G.F. Homogeneous Projective Coordinates for the Bondi–Metzner–Sachs Group. Symmetry 2024, 16, 867. https://doi.org/10.3390/sym16070867
Esposito G, Vitale GF. Homogeneous Projective Coordinates for the Bondi–Metzner–Sachs Group. Symmetry. 2024; 16(7):867. https://doi.org/10.3390/sym16070867
Chicago/Turabian StyleEsposito, Giampiero, and Giuseppe Filiberto Vitale. 2024. "Homogeneous Projective Coordinates for the Bondi–Metzner–Sachs Group" Symmetry 16, no. 7: 867. https://doi.org/10.3390/sym16070867
APA StyleEsposito, G., & Vitale, G. F. (2024). Homogeneous Projective Coordinates for the Bondi–Metzner–Sachs Group. Symmetry, 16(7), 867. https://doi.org/10.3390/sym16070867





