Hypergolic Ignition by Off-Center Binary Collision of Monoethanolamine-NaBH₄ and Hydrogen Peroxide Droplets

Abstract

Hypergolic ignition of H₂O₂ and MEA-NaBH₄ by off-center collision of their droplets was experimentally studied, focusing on the characteristics and mechanism of droplet mixing, droplet heating and evaporation, and gas-phase ignition. The whole collision ignition process was divided into five stages, which were compared, respectively, with that of head-on collision. Under the condition of a slightly off-center collision (for cases where B < 0.35), H₂O₂ droplets penetrate MEA-NaBH₄ droplets after the collision and coalesce with it, but the internal H₂O₂ drop inside the MEA-NaBH₄ droplet does not form a stable sphere. Instead, it rotates and expands inside the mixed droplet. With B increasing to 0.59, the droplets no longer coalesce after collision but separate away, forming satellite droplets. In such cases, multi-ignition mode is observed. When B increases to a certain extent, specifically, 0.85, a grazing collision is observed such that no mass transfer exists during the interaction of droplets, which leads to ignition failure. A theoretical model quantifying droplet swelling rate was established to calculate the volume change of the droplet. It was found that the swelling can be attributed to the flash boiling of superheated internal H₂O₂ fluid. Meanwhile, the ignition delay time was found to linearly decrease with B at various Wes until the extent where the chemical reaction takes over control, leading to an almost constant time delay defined as RDT. Additionally, the regime of ignition modes corresponding to different droplet mixing features is summarized in the We-B parametric space.

1. Introduction

Hypergolic bipropellants have found wide implementation in propulsion systems that require multi-starts [1,2,3]. IN fact, hypergolic propellants are usually applied in upper-stage rocket propulsion systems as well as the orbital attitude adjustment power system. Ignition of the hypergols is achieved spontaneously once the fuel and oxidizer make contact with each other at the start condition. It was evidenced in previous studies that the physical mixing between the propellants imposes an essential influence on ignition properties [4,5]. For realistic propulsion systems, the hypergolic fuel and oxidizer make contact primarily in terms of the interaction of their small droplets downstream of the injector [6,7].

To imitate such type of mixing, the authors established an experimental apparatus where a pair of freely moving droplets collide and mix with each other. The ignition of bipropellants of white fuming nitric acid (WFNA) and N,N,N′,N′-tetraacetylethylenediamine-mine (TMEDA) was first examined as reported in [4,8,9,10]. The development of the ignition process was fully interpretated, and the dependence of ignition delay on collisional dynamic parameters, i.e., the Weber number (We, ratio of inertial force to droplet surface tension), droplet size ratio (Δ), and impact parameter, (B, measuring the degree of off-center collision effect, where B = 0 represents head-on collision and 0 < B < 1 represents the off-center collisions) was explicitly established. By comparison, the characteristics of the ignition process were found to phenomenally correspond to the types of interactions and mixing patterns appearing in non-reactive droplet collisions under different dynamic conditions. For instance, Qian [11] and Ashgriz [12] identified the presence of various collision outcomes in the predominant parameter space of f(We,Δ,B), namely, (a) bouncing away without any contact, (b) coalescence in a largest extent of mixing, and (c) separation after some certain level of mass transfer in their experiments for water and hydrocarbon droplets.

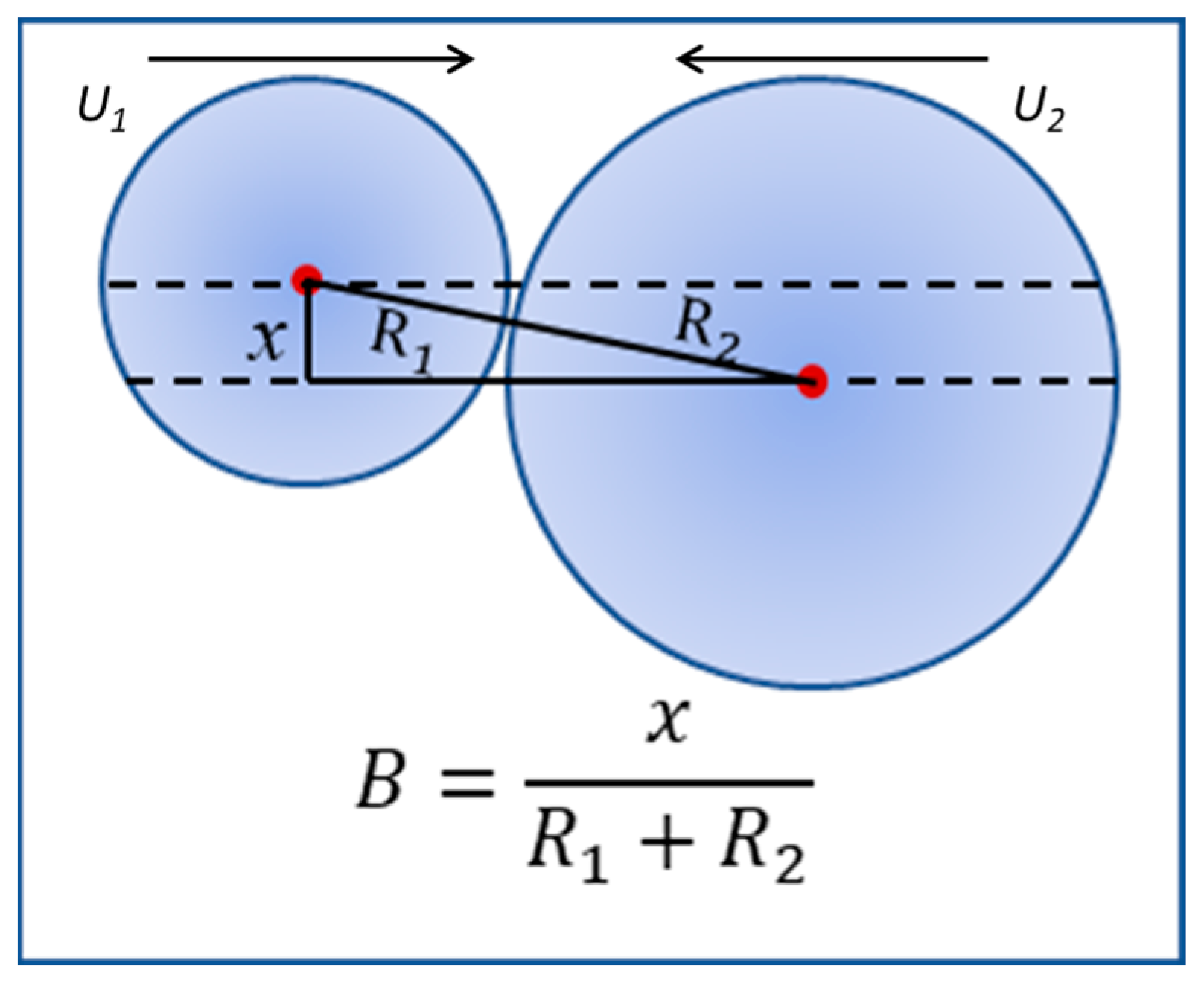
For the scenario of atomization and a spray zone upstream of the combustion, the off-center collisions where the value of B is other than 0 should be statistically predominant between the fuel and oxidizer droplets. The off-center effect is quantified by the impact parameter that is defined as B = x/(R₁ + R₂) as depicted in Figure 1. The droplet velocity of collisions between droplets is defined as U₁ and U₂. According to previous studies [11,13,14], in off-center collisions, the symmetry of droplet interactions that exists in head-on collisions is broken down in off-center collisions, which makes the process of droplet collision and mixing more complicated. Brenn [15] studied the off-center effect on the volume of liquid filaments and satellite droplets through the isopropanol droplet collision experiment system: when the off-center effect is low, the volume of liquid filaments is small and the length is short due to the viscous dissipation between the collision droplets; with the increase of the impact parameter, the volume and length of the liquid filament reach the maximum value, corresponding to a certain We value and droplet size. As the impact parameter continues to increase, the interaction between the liquid micelles reduces the volume of the liquid filament. Sarwasva [16] performed a high-fidelity numerical simulation of binary droplet off-center collisions by numerical simulation. The effect of cavity formation in the liquid bridge (connecting the end droplets) on the ligament characteristics was studied. The study found that the drainage of mass from smaller droplets to larger droplets is more significant for lower-diameter-ratio collisions. Despite the fruitful results, droplet collision and mixing features during off-center collisions by a pair of hypergolic droplets during ignition are still rarely reported.

In previous studies, the issue of the flame structure of hypergolic ignition has presented itself as a problem of interest. Among the related works, the flame configuration by hypergolic jet impingement [17,18] was studied. And the structure of flame of the gelled propellant was recorded employing the OH planar laser-induced fluorescence (PLIF) [19,20,21]. Despite the fruitful results reported, the effects of the configuration of the droplet during mixing, heating, and gasification periods on the flame structure still remain unexplored. Moreover, the physical properties affective in droplet collision, such as viscosity and surface tension, for different types of hypergols vary in a wide range of values, which may present distinct mixing manners. The assembly of comprehensive knowledge of the relation between hypergolic mixing pattern and the subsequent ignition structure thereby necessitates the study of the collision of droplets with disparate physical properties.

The reason for the lack of direct observations or measurements of the configuration and internal structure of hypergolic droplets during the ignition period in previous studies lies in the fact that the hypergolic droplets are usually severely veiled by the large number of opaque gaseous species evaporating out from the droplet [4]. The loss of details of the droplets makes it hardly possible to explicitly establish a quantitative relationship between the collision and mixing process and the ignition properties. To solve this problem, we have established an experimental setup that allows for the observation of mixing details inside the coalesced droplets of the bi-propellants of Monoethanolamine (MEA) mixing with sodium borohydride (NaBH₄) and hydrogen peroxide (H₂O₂) [22]. In this work, internal drop rebounding, dual-bell-shaped swelling droplets, and ‘waist’ ignition mode are observed and interpretated. However, whether such features still exist and affect in the predominant off-center collisions or not has not been discovered.

This study follows our previous work [22], while placing the emphasis on the effects of droplet mixing, droplet heating and vaporization, hypergolic ignition delay time and the structural characteristics by off-center collision of the MEA-NaBH₄ and H₂O₂ droplets. The bipropellants herein are employed as the pair of H₂O₂ and MEA under the following considerations. First, as the saturated vapor pressure of MEA is much lower than that of WFNA and TMEDA, the dark vapors that block the droplet can be significantly suppressed. Moreover, the increased viscosity of MEA is regarded as a prevailing property among hypergols, especially when referring to the gelling ones by polymer media [23,24,25]. The principles of the ignition properties of MEA-NaBH₄/H₂O₂ must, therefore, maintain applicability in a large variety of types of hypergols. Indeed, the theoretical results of hypergolic ignition induced by off-center collisions of the bi-propellant droplets would be of great significance in calculation and design to the realistic propulsion system. First, theoretical quantification of each pre-ignition stage provides a precise prediction of the total ignition delay time, which has been regarded as a crucial property for hypergolic ignitions. Second, the distribution pattern of droplet collision outcomes and ignition modes in the We-B parametric space where the range of We is 20~100 and the range of B is 0~1.0 has been quantified so that the atomization characteristics and spatial ignition feature can be referenced in the atomization system design in the realistic propulsion system. Also, the pair of MEA-NaBH₄/H₂O₂ has been treated as the promising ‘green’ hypergols since they are very friendly to human beings [26,27,28,29,30].

Under the above considerations, the present work is organized as follows. The recipe of the adopted hypergolic propellants and the experimental apparatus are depicted in Section 2. Experimental observations and a theoretical analysis of the droplet and flame pre- and post-ignition are presented in Section 3, followed by the concluding remarks.

2. Experimental Setup and Materials

2.1. Materials

As depicted above, in the present study, the two droplet components used in this study are composed of H₂O₂ as oxidant and MEA as liquid fuel. NaBH₄ particles are dissolved in MEA as a superb reducibility recipe. When the fuel is mixed with the oxidant, NaBH₄ will first react with H₂O₂ to release a large amount of heat, which will then be used to achieve gas-phase ignition.

The purity of the H₂O₂ liquid used is 92 wt%, and the fuel mixture consists of 91 wt% MEA and 9 wt% NaBH₄. Values of physical properties of the ingredients are shown in

Table 1. Relevant physical properties (density, viscosity, surface tension, and boiling temperature) of H₂O₂, MEA, and NaBH₄ at room temperature.

	ρ (To Water)	μ (mpa∙s)	σ (mN/m)	Tb (K, 1 atm)
H2O2	1.45	1.3	80.4	423
MEA	1.0	15.95	49.0	443
NaBH4	1.04	−	−	−

. The fraction of 9 wt% is taken to be greater than the critical spontaneous combustion fraction of 7 wt% in the previous experiment in order to guarantee the spontaneous combustion at the operating condition [20]. The NaBH₄ particles were added to the fuel liquid by an ultrasonic stirrer to avoid NaBH₄ deliquescence. Before the experiment, all the materials used in the experiment were placed in a desiccative environment for one week to ensure that there was no sediment.

2.2. Experimental Setup and Measurement Methodology

Binary collision of free H₂O₂ and MEA–NaBH₄ mixture droplets was realized by upgrading the experimental apparatus employed for WFNA and TMEDA droplets [8]. The specific experimental device is shown in the Figure 2; fuel mixture droplets were produced using a fixed needle-shaped nozzle, while H₂O₂ droplets were produced using a set of micro-electromagnetic nozzles from Fritz Gyger AG. In order to suppress the self-decomposition of H₂O₂, the liquid tank was maintained in an ice bath, and the conveying pipe was placed under shading throughout the experiment. The collision was adjusted by precisely adjusting the setting of the XYZ−α stage with a spatial resolution of 2 μm. The frequency of collision and ignition events was intentionally controlled to 3 Hz to avoid interference from adjacent events.

The pressure of the fuel and oxidant droplets’ collision is the ambient pressure, and the operating pressure in the fuel and oxidant tank did not exceed 100 kPa. The initial temperatures of fuel and oxidant are ambient temperature and ice point, respectively. The initial temperature of oxidizer H₂O₂ was close to 0 °C, since the H₂O₂ was maintained in an ice bath to avoiding severe self-decomposition.

2.3. Measurement Methods

For the measurement, a high-speed camera (5000 fps) was used to record the entire process of droplet collision and combustion. The exposure time was 5 μs, which was proved to be able to obtain the droplet movement.

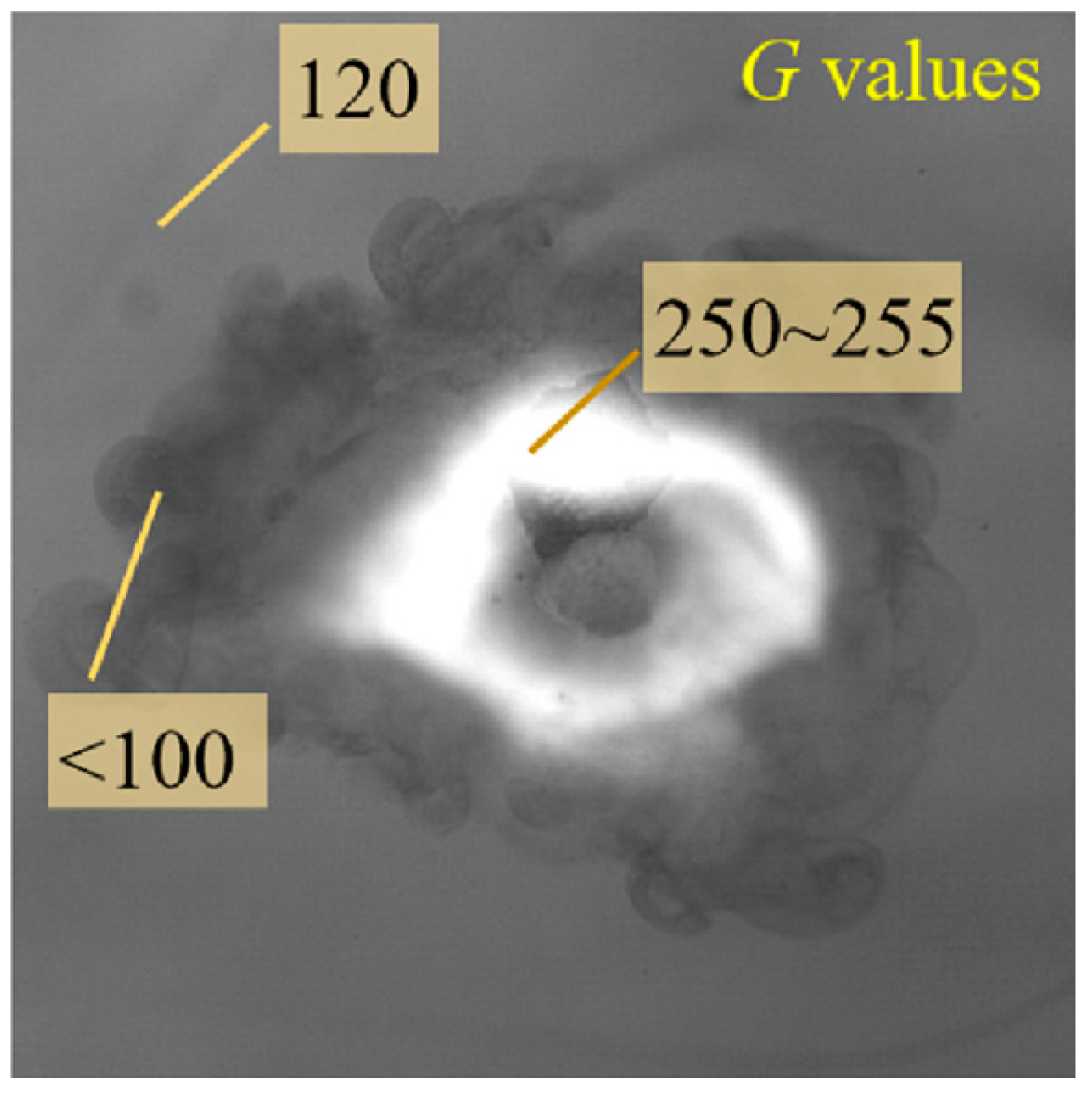
The size and speed of the injected droplets and the ignition event were measured and detected via a program applying the information of gray-level value (G) in the recorded images. In specific, the droplet area is recognized from the background (with an average gray-level value of G_n) by virtue of the large discrepancy of the brightness between them in the image. Specifically, a narrow interface area Δx is identified in the image, where G increases sharply from the minimum value representing the edge of the droplet to a higher level comparable to the average gray level G_n (G/G_n equals nearly to 1.0). The real edge of the droplet is located at a specific point within Δx to obtain the shape of the droplet.

The grayscale image of the shadow photo is stored at a resolution of 8 bits per sample pixel, which results in 256 different gray levels of the gray shadow. The lowest level, 0, indicates the darkest, and the highest level, 255, indicates the brightest. When the average gray level is set to 100, the gray level less than 100 represents the dark gas species, and the region higher than 250 (less than 255) is considered to be a luminous flame, as shown in Figure 3. The accuracy of gray threshold selection has been tested and verified in our previous studies [31]. When the flame is identified, the uncertainty is less than 0.1 ms.

In present study, the collision Weber number is defined as We = ρ_odU²D_od/σ_od, where ρ_od, D_od, and σ_od are the oxidant density, droplet diameter, and surface tension coefficient, respectively. U is the relative velocity. The use of the physical parameters of oxidants is for the purpose of concise description and convenient calculation. The Weber number range in this paper is 20~100, which is the range that researchers often pay attention to in the study of droplet collision. The value of We in this paper is adjusted by adjusting the relative velocity of the droplet, and the relative velocity of the droplet is controlled by the gas supply. For droplets of different sizes, the droplet size ratio is Δ = D_f/D_od, where D_f is the droplet diameter of the fuel mixture and D_od is the droplet diameter of the oxidant. Considering that binary droplets of different sizes will lead to more coalescence, and when too-small droplets impact large droplets, the mixing between two colliding droplets will be accelerated. In this paper, the droplet size ratio is controlled in the range of 1.0–2.5. Meanwhile, the size of the fuel droplets is fixed in the experiment, and the size of the oxidant droplets changes with the different conditions.

3. Results and Discussion

3.1. Ignition Process by Off-Center Droplet Collisions

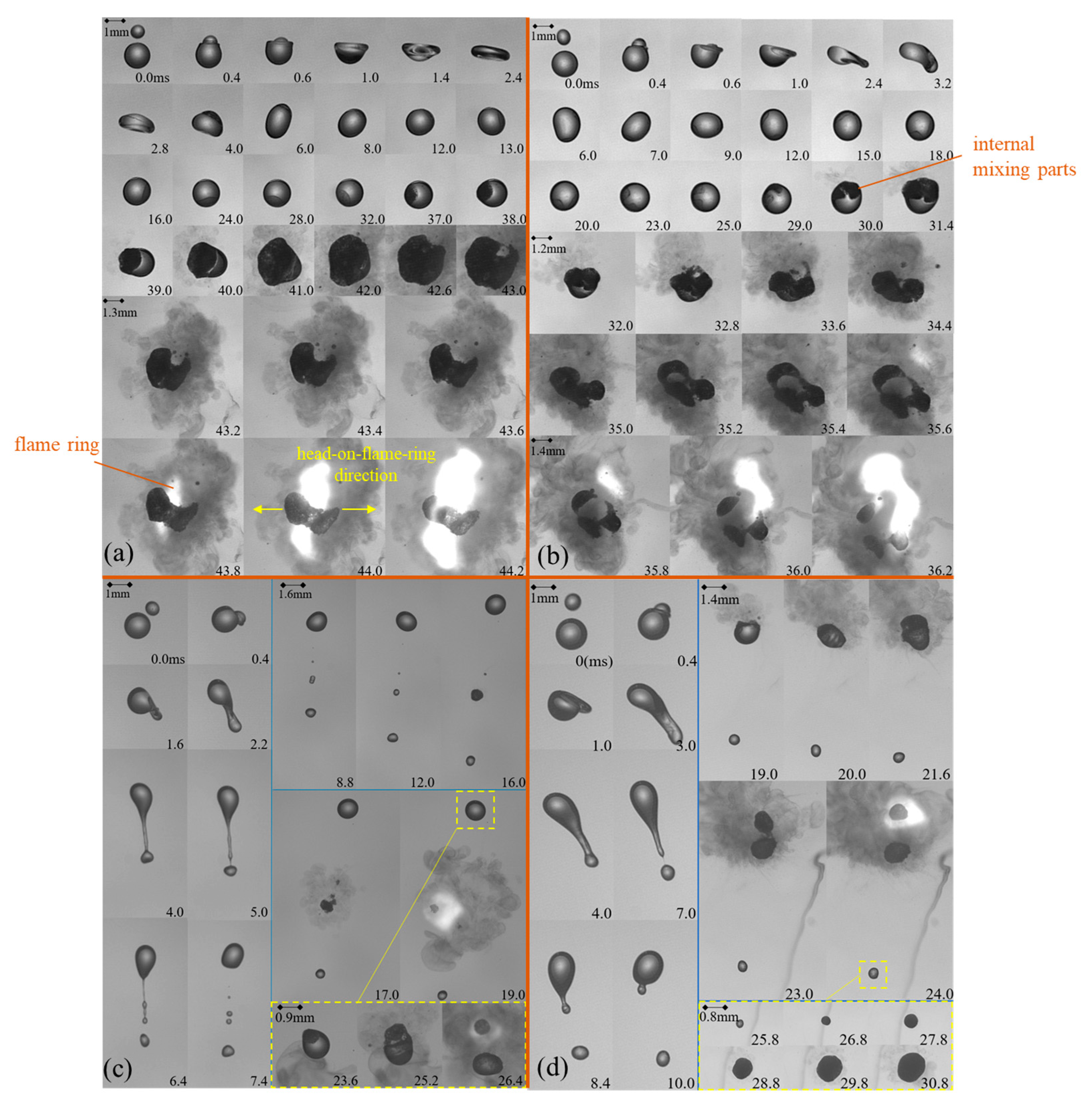
For a clear illustration, representative collisions at We = 31 and Δ = 1.8 but with various impact parameters covering off-center coalescence as well as stretching separation cases are selected and shown in Figure 4. The time-sequence images are arranged sketching the main features during the entire ignition process. The length scale in each focused frame, as shown in the corresponding image, is adjusted accordingly to display details of the droplets, vapor, and flame. Consistent with our previous work, the ignition induced by off-center collision herein is also divided into five stages, namely, stage I: droplet collision and deformation; stage II: occurrence and development of inter-mixing structure; stage III: droplet swelling; and stages IV and V: gas-phase ignition and flame propagation. These five stages occur in turn over time.

The off-center collision when B = 0.16 is shown in Figure 4a. In stage I, after collision between the two droplets, a large extent of deformation is observed, which is similar to that happening in head-on collisions. Meanwhile, discrepancy exhibits at the same time that the deformation morphology in off-center collisions becomes asymmetric due to the existence of angular momentum between the two colliding droplets. In such a situation, the two interacting droplets start to rotate at a period of nearly 13 ms with each other after collision. Nevertheless, the interaction and deformation of the droplets are very similar to those of the non-reactive droplets, indicating that the chemical reaction is negligible during stage I.

In stage II, an opaque structure is generated and observed inside the merged droplet at 16.0 ms. It develops rapidly all the way to the moment of 38 ms. It is found that this dark zone rotates almost at the same rate with that in stage I. The opaque structure is therefore considered to be an oxidizer mass that is reacting with the fuel, and the opaque substance is the solid-phase products of the exothermal chemical reactions.

In stage III, the opaque structure develops sharply so that the surface tension cannot maintain the droplet shape anymore. The opaque, condensed phase products break through the droplet surface and dark vapor releases out. In addition, at a certain moment around 39 ms, the droplet suddenly begins to expand itself, which is characterized by volume expansion. The swelling of the droplet happens so quickly that within 4 ms, the volume of the droplet enlarges several times compared to that at 39 ms. As the droplet expands, a remarkable amount of dark vapor is detected, and the droplet deforms severely from the spherical shape.

In stages IV and V, an obvious ‘dual-bell’-shaped droplet can be observed at 43.6 ms, which is similar to that formed in head-on collision. A corresponding ring-shaped flame is then first detected at 43.8 ms around the waist of the two parts of the droplet, which herein is defined as ‘waist-ignition’ mode. However, since droplet rotation existed during the off-center collision, the ‘dual-bell’ droplet is found deviating from the colliding direction when comparing the images at 43.6 ms and 0 ms when the two droplets are just about to collide to each other. The bright flame initiates surrounding the droplet waist orientating perpendicular to the polar direction of the ‘dual-bell’ droplet. The bright flame develops rapidly after ignition along the waist of the droplet and envelops the droplet.

The off-center collision and ignition process when B = 0.35 is shown in Figure 4b. The droplets still show asymmetric deformation after the collision, and the deformation is more serious. It can be observed that in this case, the internal mixing structure is also deformed, as seen from 23.0 ms to 30.0 ms. The larger angular momentum makes the mixing region move along the curvature inside the high-viscosity merged droplet. The internal mixing region is elongated and then separates into two parts, as indicated in the image at 30.0 ms, due to the effect of interfacial tension. Herein, the mixing region and the droplet interface are still rotating. The droplet starts to swell at 31.4 ms, and at 34.4 ms, it is observed that the merged droplet deformed severely, and the surface broke down with vapor and satellite droplets puffing out from the cracked area. As shown at 35.2 ms, the originally merged droplet disintegrated into three parts. The bright flame was firstly observed at 35.6 ms among the dark vapor just near the cracked surface area. The bright area expanded rapidly while the three parts separated away, forming three independent segments. It is shown that the bright flame developed mainly at the cracked surface area since the flammable gaseous species were largely puffed out from the breakup droplet.

As B continues increasing to 0.47, stretching separation occurs after the droplet collision as in Figure 4c. In such case, a liquid bridge is generated at the interface of the two interacting droplets. Owing to the sufficiently large off-center effect, the droplets stretch away, and the liquid ligament breaks down under the effect of surface tension into several tiny satellite droplets, as shown from 6.4 to 76.4 ms. The stretching process, with no doubt, enhances mass transformation between the fuel and oxidizer, and so does the surface tension gradience between the droplets, which is known as the Marangoni effect. Thereby, the bright flame occurs for the first time surrounding one of the satellite droplets at 19.0 ms, which is much earlier than it does in the cases with B = 0.16 and 0.35. As the oxidizer mass is transferred onto the fuel droplet when the droplets graze with each other, the remaining fuel will react with the oxidizer mass, leading eventually to another ignition surrounding the fuel droplet at 26.4 ms. However, the brightness of the flame is much weaker than that which occurs at the satellite droplet because of the limited amount of the oxidizer left on the fuel droplet.

When B increases to the value of 0.59, stretching separation is still observed after the collision, as shown in Figure 4d. Nevertheless, a discrepancy exists when comparing to the case where B = 0.47. Since the collision is more off-center, there would be a smaller portion of the droplets participating in the mass transfer during the interaction between them. This results in an even smaller volume of the satellite droplet compared with that at B = 0.47, where the satellite droplet’s mass is already small. Such insufficient mass leads to failure of the ignition eventually despite the mass transfer during the grazing between the droplets, since for hypergolic ignition, the cold environment acts as a heat sink, which has been demonstrated crucial to the ignition, especially when the droplets are small in size [9]. Meanwhile, for the large fuel droplet, similar to case B = 0.47, a certain amount of oxidizer mass will be trapped during the grazing, which in turn leads to the ignition at 24.0 ms. Note that the fuel droplet separates into two parts during the ignition under the mechanism of large droplets’ size ratio effect as discussed in our previous work [22].

According to the results of the droplet collision in We-B parametric space, the two droplets bounce away as the impact parameter increases to extremely large values. For the droplets in the present study, the off-center bouncing collision appears at B = 0.85, We = 31, and Δ = 1.8, as shown in Figure 5. The two droplets in such case both deform to some extent when they are interacting with each other. As the larger the droplet, the greater inertia it holds, the large fuel mixer droplet is observed to deform less than it does for the smaller oxidizer droplet. Moreover, the large level of viscosity would dissipate the kinetic energy quickly after the interaction of the droplets. One essential property of the bouncing collision is that there is no mass transfer between the two interacting droplets. This characteristic is also demonstrated here, since an internal mixing structure does not emerge inside the two droplets after collision, nor do the changes in droplet volume as is shown in cases at other Bs in Figure 4. The droplets thereby fail to ignite, as shown in Figure 5.

3.2. Intermixing and Droplet Swelling in Off-Center Collisions

The origin of the intermixing structure inside the fuel droplet can be traced back to the moment when the two droplets completed the coalescence. During the internal mixing period, the smaller oxidizer droplet rotates and deforms inside the larger fuel droplet. Since the chemical reaction rate is negligible at this time, the observed changes in the internal structure can be fully considered as the recovery of the mass of the deformed oxidant.

To reveal the underlying mechanism of the internal mass restoration and to quantify the relaxation of a single droplet immersed in a viscous fuel liquid environment, the recovery time (τ_c) of droplet collision is calculated using the optimized Equation (1) in the previous study [22]. The formula discards the wavenumber-related information and creates appropriate scaling to construct an ad hoc model.

$$\frac{1}{{\tau }_c}=\frac{\sqrt{{\beta }^{*}{\mu }_i{\mu }_o{\rho }_i{\rho }_o}}{R\Gamma {\left(\sqrt{{\mu }_i{\rho }_i}+\sqrt{{\mu }_o{\rho }_o}\right)}^2}+\frac{{{\mu }_i}^2{\rho }_i+{{\mu }_o}^2{\rho }_o+{\mu }_i{\rho }_i\left|{\rho }_i-{\rho }_o\right|}{R^2\Gamma {\left(\sqrt{{\mu }_i{\rho }_i}+\sqrt{{\mu }_o{\rho }_o}\right)}^2}$$

(1)

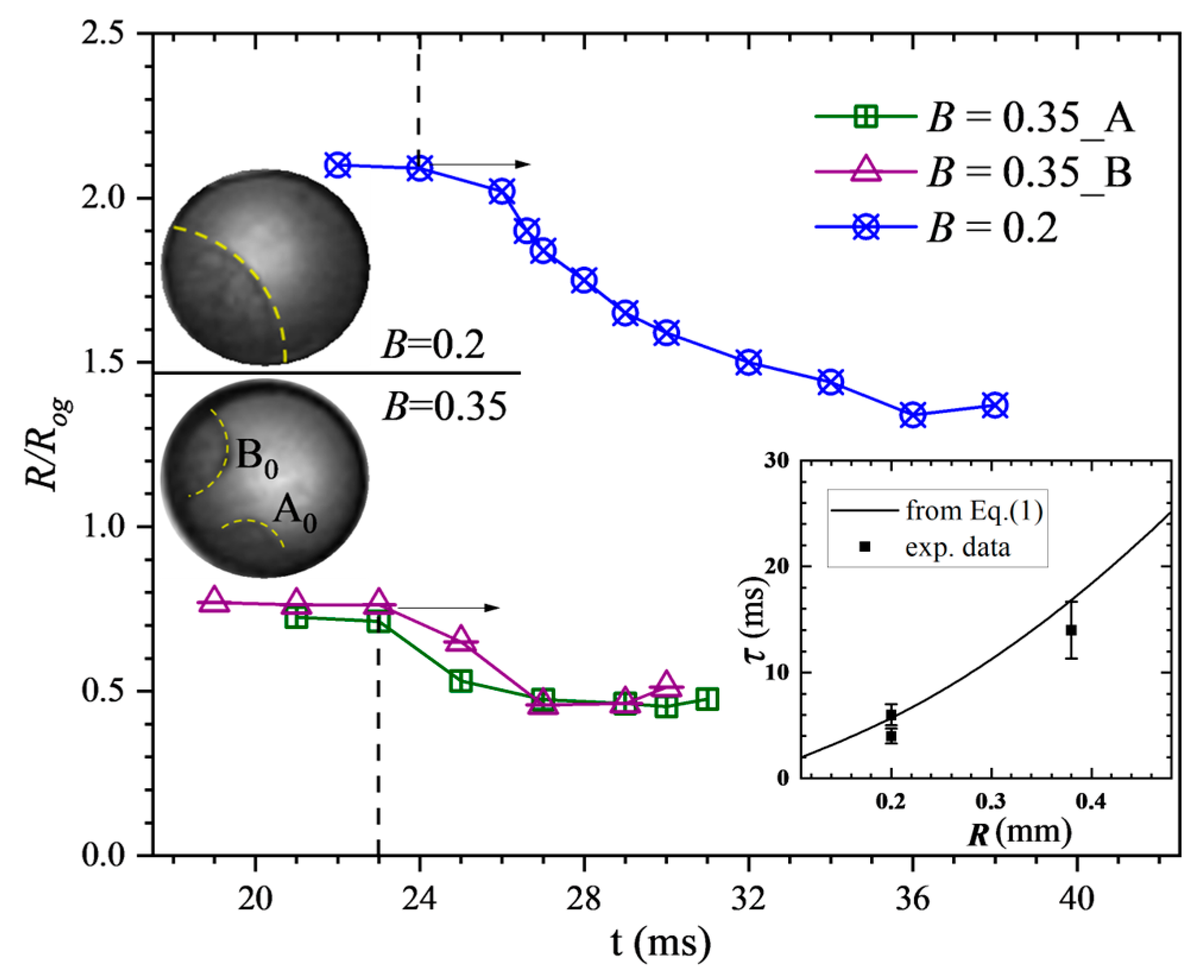
where τ_c is the calculated rebounding time; Γ = (ρ_o + ρ_i)/2 is the correlated density; i and o represent fuel and oxidant, respectively; and β* = (γ/ΓR³)^1/2 is the frequency of droplet natural oscillation driven by interfacial tension. The interfacial tension herein is simplified by the model of γ = σ_i − σ_o.

Figure 6 shows the development of the interface curvature of the mixing structure inside the merged droplet at B = 0.2 and B = 0.35. It is found that for the two cases, the values of the normalized curvature (R/R₀) maintained large levels (relatively flat shape) at the beginning of the mixing process. The internal mixing mass then started to restore its shape so that the curvature values began to decrease, as shown in the figure. As in case B = 0.35, the internal mixing mass separated into two independent pieces, and both the shape restorations were recorded corresponding to Part A₀ and B₀, respectively. The final values of all the mixing boundary curvatures are around 1.3 for B = 0.2 and 0.5 for the two parts in case B = 0.35 where the restorations are considered already completed. The time interval from the beginning of restoration, which is quantified as the initiation of the decrease of the normalized curvature value to the completion of the restoration that is quantified by the cease of the decrease, is defined as the restoration time of the internal mixing structure. As shown from the subfigure in Figure 6, the measured restoration times for all the cases fit well to the calculation values from Equation (1), which in turn verifies that for all the off-center collisions, the internal mixing is driven by interfacial tension between the oxidizer and fuel substance.

Droplet swellings are observed for all the representative off-center collision cases at the mixing droplets in cases B = 0.2 and B = 0.35 or at the separated droplet parts in cases B = 0.47 and B = 0.59. According to the results of head-on droplet collision in our previous study [22], droplet swelling is under the mechanism of bubbles generating inside the mixing droplet due to the flash vaporization of the substance with a lower boiling point within the droplet. The bubbles develop and merge into larger ones at the mixing boundary. Flammable gaseous species inside the bubbles would puff out when the droplet surface broke down, forming ‘dual-bell’-shaped droplets. For a quantitative description of the swelling process, one theoretical model has been established based on the balance of heat generation by the superheating of the internal boiling oxidizer and the energy needed to maintain the growth of the bubbles [32]. Such model is expressed by

$$R_{\mathrm{bubble}}=2\lambda {\left(\frac{3}{\alpha \pi }\right)}^{1/2}\frac{T_{\infty }-T_b}{L{\rho }_v}{t}^{1/2}$$

(2)

where ρ_v is the equilibrium vapor density at the boiling temperature, L is the latent heat, α is the thermal diffusivity of the liquid, λ is the liquid thermal conductivity, and T_∞ and T_b are the boiling temperatures of MEA and H₂O₂, respectively. The term T_∞ − T_b can be regarded as a measure of the level of superheating of the inner liquid. The volume of the measured droplet should be equal to the sum of the volumes of the internal inflating bubbles and the original droplet, so it gives

$${\left(\frac{R}{R_{og}}\right)}^3={\left(\frac{R_{\mathrm{bubble}}}{R_{og}}\right)}^3+1$$

(3)

Substituting Equation (2) into Equation (3), an expression of droplet volume at different times in the expansion process can be obtained as

$${\left(\frac{R}{R_{og}}\right)}^3=k{t}^{3/2}+1$$

(4)

where the factor $k=7.47{\left[\frac{\lambda \left(T_{\infty }-T_b\right)}{{\alpha }^{1/2}L{\rho }_v{R}_{og}}\right]}^3$.

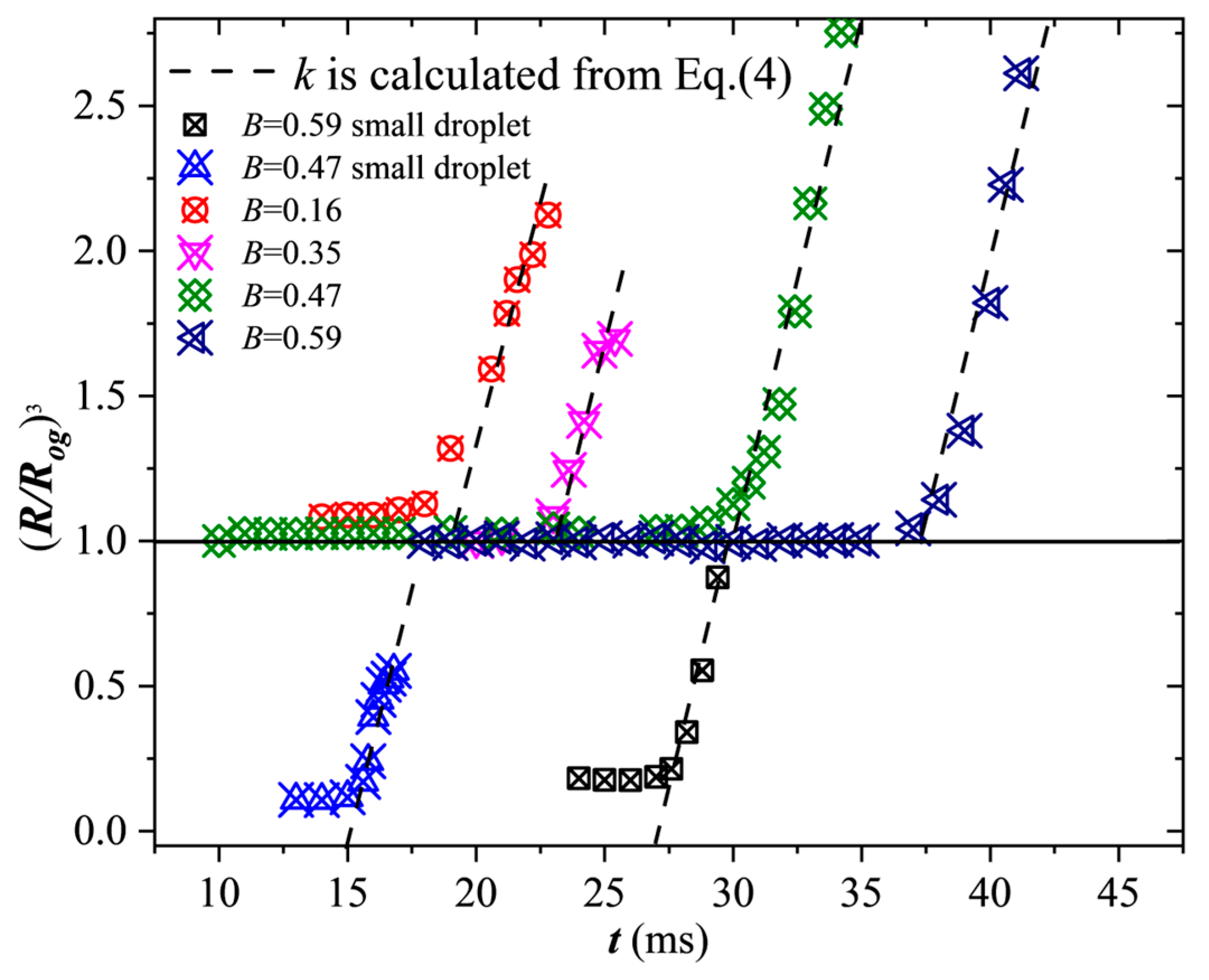
In order to verify that the bubble generation mechanism still works for the droplet swelling in off-center collisions, droplet swelling rates quantified by ${\left(R/R_{og}\right)}^3$ were measured. For B = 0.47 and B = 0.59, the expansions of the two separated parts of the droplet were measured independently. A comparison of the measured swelling rates and the calculated results via Equation (4) are shown in Figure 7. It can be seen from the figure that the droplet volume first remains constant, which corresponds to droplet collision and internal mixing periods. The droplets then expand moderately, during which the droplet volumes increase but are limited to 1.2 times larger than the original value. Such slight expansion is owed to the resistance from inertia.

In each collision case, there exists a rapid expansion at a rate of k which is defined in Equation (4). It is found that the larger the B, the later the initiation of the rapid swelling process. For all the representative cases, the calculated value of k agrees well with the experimental data. Since Equation (4) is based on the mechanism of rapid vapor accumulation trapped inside the bubbles, such agreement between the experimental results and the theoretical result in turn verifies the conclusion that the expansion is controlled by the flash evaporation of the superheated H₂O₂ liquid within the merged droplet. The vapor inside the bubble can be used as an oxidant when the bubble is blown out to participate in the gas-phase ignition.

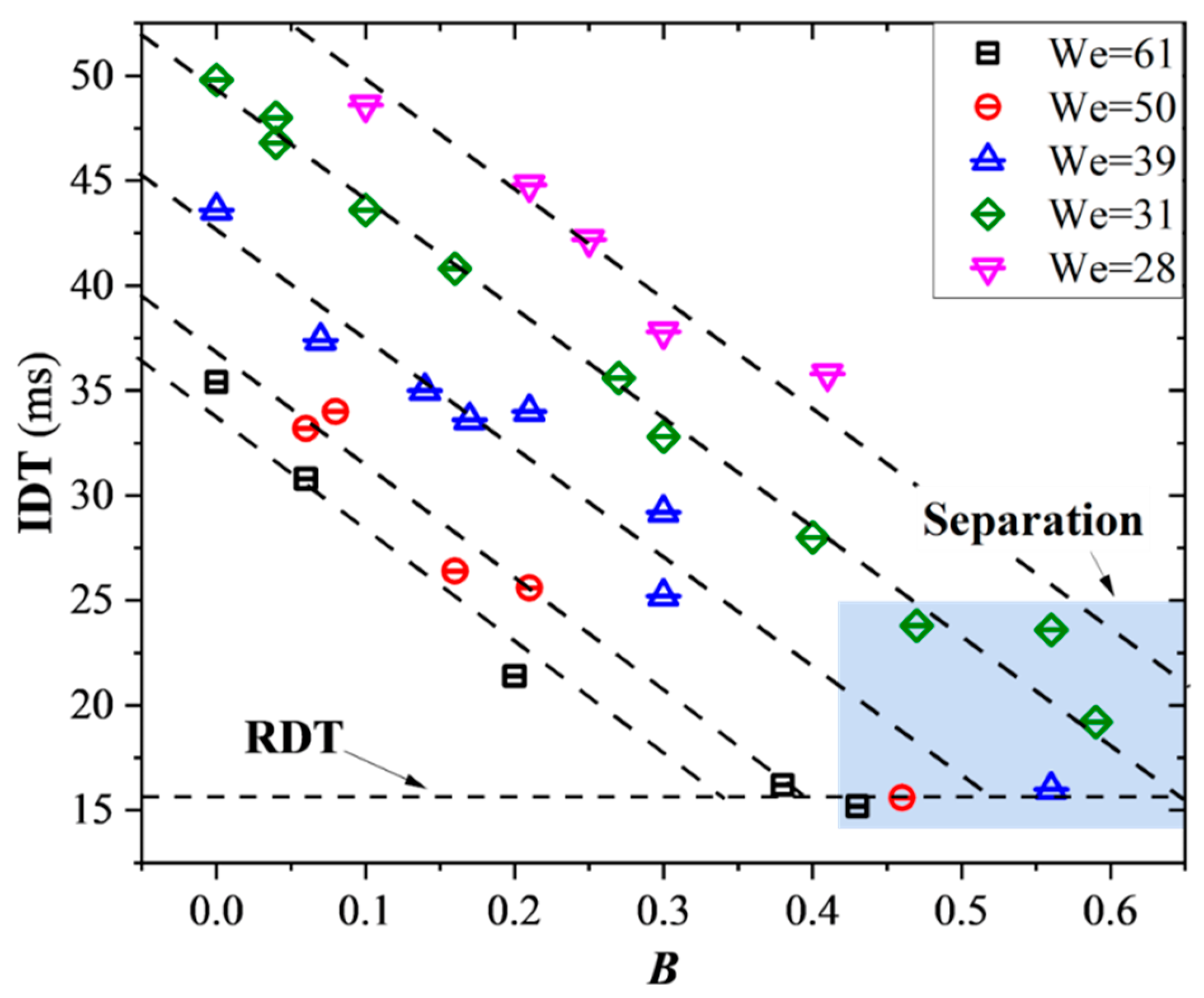
3.3. Ignition Delay Time at Off-Center Collisions

Ignition delay time (IDT) is regarded as one of the most important parameters quantifying the hypergolic ignition process. In the present study, the IDT is systematically studied with respect to the collision Weber number, an impact parameter including both the head-on collision (B = 0) and the off-center collision (0 < B < 1). The specific effect of B on ignition delay under different Wes and Bs is illustrated in the Figure 8. It is found that at different Wes, IDT generally decreases with the increase of B until a certain low value where if B continues to increase, IDT will no longer change, as shown in the horizontal dashed line in the figure. This value is defined as the reaction delay time (RDT). Under this situation, the ignition time delay will not be affected by the collision dynamic parameters but mainly be controlled by the chemical reaction rate of the two droplet substances. The inclined dashed lines in the figure indicate a linear dependence between the IDT and B. Specifically, when B increases to a certain value, the droplets will separate after the collision, known as the stretching separation, but the separation behavior of the droplets does not affect its linear dependence.

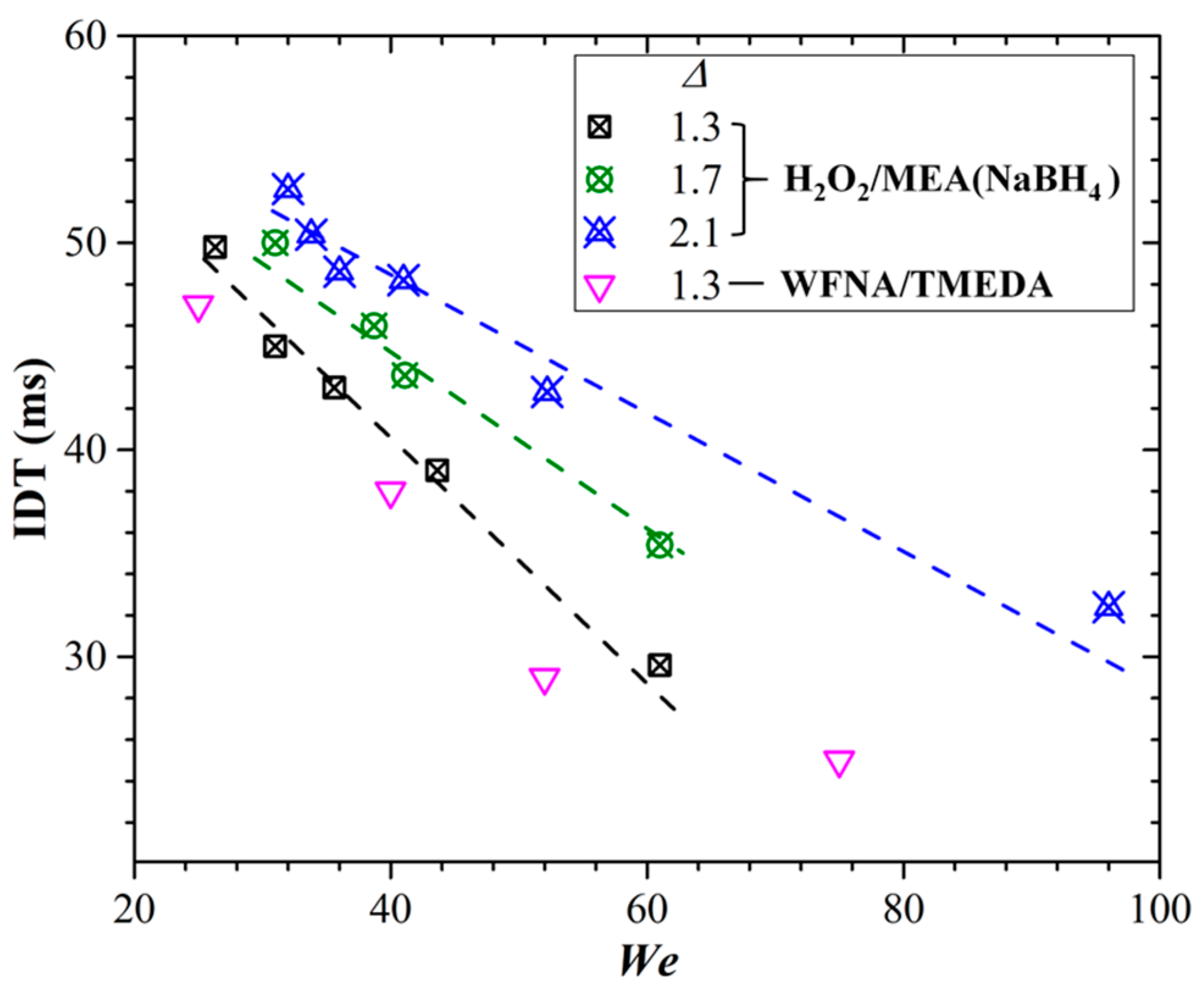
Figure 9 shows the dependence of IDT on We at different Δs for the bi-propellants of H₂O₂/MEA(NaBH₄) and WFNA/TMEDA in a previous study [4]. Generally, the IDT of H₂O₂/MEA(NaBH₄) is greater than that of WFNA/TMEDA. This is because of the great viscosity of H₂O₂/MEA(NaBH₄) droplets after collision. The resistance of viscosity makes the mixing inside the droplets insufficient, resulting in a delayed heat release and subsequent vaporization process. In addition, for both pairs of propellants of H₂O₂/MEA(NaBH₄) and WFNA/TMEDA, the IDT will decrease with the increase of We since a larger We signifies more kinetic collision energy for the interaction and mixing between the droplets. Meanwhile, for the droplet size ratio, it is found that IDT decreases with the increase of Δ due to the large discrepancy of the oxidizer/fuel mass ratio.

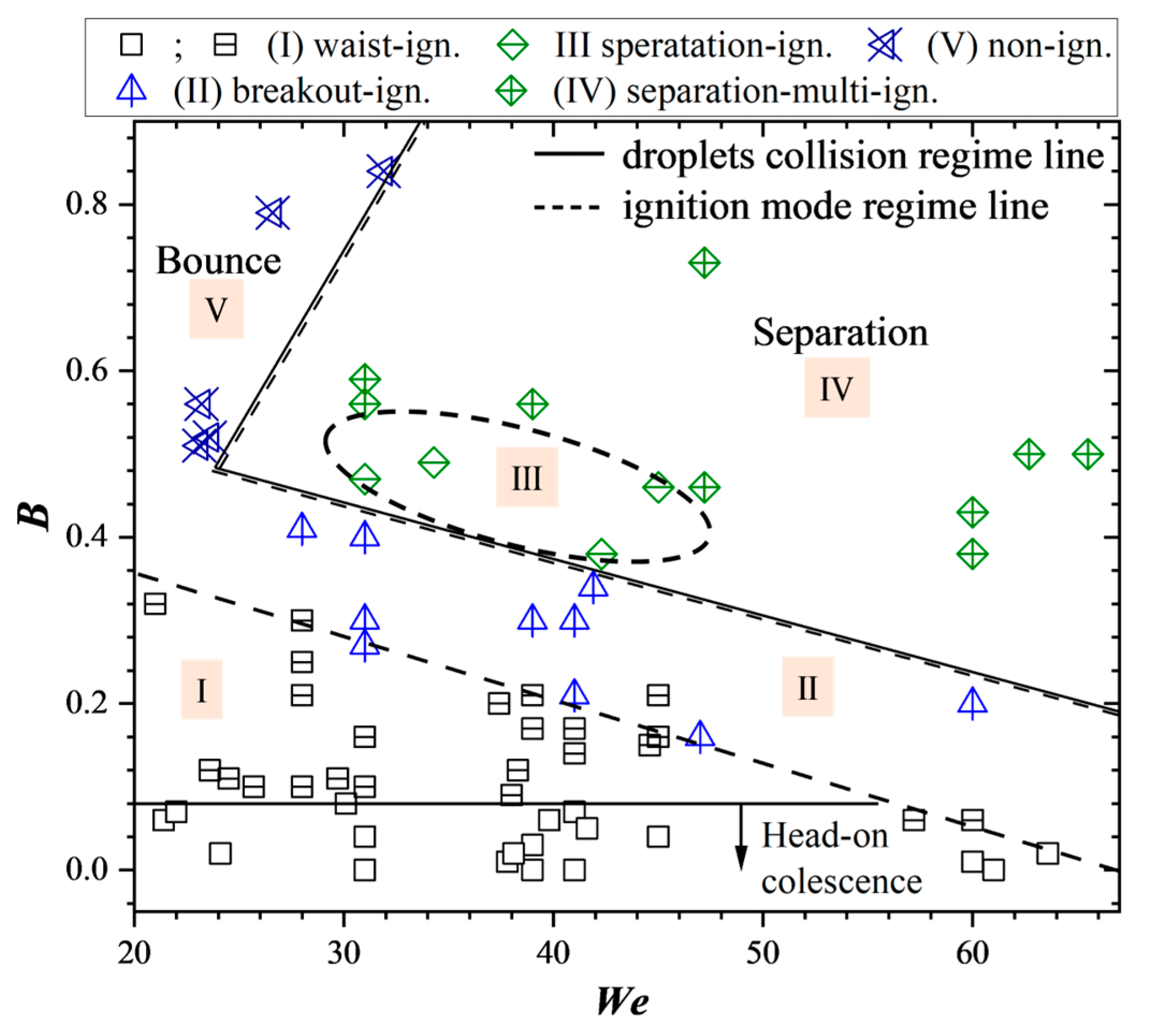
3.4. Ignition Modes in We-B Parametric Space

As for the structural characteristics of hypergolic ignition at various off-center collision conditions, the mixing and reacting droplet feature is crucial since it is decisive to the mass and heat transfer processes of the combustible gaseous species. As depicted in Section 3.1, the merged droplet turns into different interaction modes and shapes according to the collision impact parameter B. With the increase of B, the mixing droplet successively turns into the ‘dual-bell’ shape as in head-on collision, the break-down droplet, in stretching separation with the generation of satellite droplets and off-center bouncing droplets with no mass transfer. Accordingly, the ignition mode is categorized into different modes in the We-B parametric space. Droplet mixing and ignition modes are shown in Figure 10 with the solid line and dashed line quantifying the regime boundaries of the interaction and ignition modes, respectively. As illustrated in the figure, the ignition is categorized into I, waist-ignition corresponding to the ‘dual-bell’-shaped droplet; II, breakout-ignition when the droplet surface breaks down with inner species puffing out; separation ignition mode in which there exists two sub-modes, namely, III, single ignition, and IV, multi-ignition mode; and V, non-ignition mode where the bouncing collision predominates.

As seen from Figure 10, for the entire range of Wes, the binary droplets behave just as the head-on collisions with B < 0.08, which results in the regime of waist-ignition mode. The breakout ignition boundary line decreases along the We axis when B increases, and this is because for larger kinetic colliding energy, droplets will obtain more initiating angular momentum to rotate themselves to break down the droplet surface. It is found that the regime lines quantifying the stretching separation collision and the separation ignition coincide together which in turn verifies that the ignition mode is entirely affected by the droplets’ collision and mixing mode, and the same as to the bouncing collision and non-ignition mode. In the stretching separation regime, for most cases, multi-ignition mode is observed in experiments where the bright flame can be detected at both the satellite droplets and the remaining reacting droplet. Nevertheless, there also exists a special sub-regime with moderate values of We and B, where the stretching separation collisions are identified but the ignition can be detected merely one time around the reacting droplet. The possible explanation lies in the interaction and mixing performance between the droplets at such collisional parameters.

4. Conclusions

In the present study, hypergolic ignition by off-center collisions of H₂O₂ and MEA(NaBH₄) droplets was experimentally studied. The effects of the collision Weber number, impact parameter B, and droplet size ratio on the ignition process and on the temporal and structural characteristics of the hypergolic ignition were discussed and analyzed. Droplet internal mixing was described and interpreted by a theory based on linear instability analysis. The droplet swelling process during vaporization was analyzed in detail and the flash vaporization of the superheated inner oxidizer mass was theoretically verified to be the controlling mechanism of droplet swelling. In addition, the development of ignition delay time in function of collision We, B, and Δ was systematically studied. Multiple ignition modes illustrating the structural features of the reacting droplet and the bright flame were defined and interpreted in the collisional parametric space.

The conclusions of the results in the present study are as follows:

(1) According to the characteristics of droplets and flames, the five stages of ignition by off-center collision are defined. In stage I droplet collision, the fuel and oxidizer droplets behave as if they are non-reactive ones. In stage II, the deformed H₂O₂ droplets rotate around the geometric center in the MEA fuel mixture droplets and then exhibit different swelling characteristics in stage III at different Bs. Stages IV and V are gaseous ignition and flame propagation, during which a bright flame is detected to initiate with a certain structure and propagate among the flammable vapor species.

(2) Internal mixing and droplet swelling processes were illustrated in detail and theoretically interpreted. The development of the curvature of the internal mixing boundary was measured and calculated. The agreement between experimental data and theoretical results revealed that the controlling mechanism of the internal mixing is the interfacial tension between the two-mixing substance. Droplet swelling was interpreted by comparing the measured volumetric expansion rate and the calculated values via the equation formulated based on the balance between the energy sustaining bubble growth inside the droplet and the heat generation by the superheating of the internal boiling oxidizer. It was verified that in such way, droplet swelling is caused by the flash vaporization of the superheated substance inside the droplet.

(3) Ignition delay time was systematically studied in collisional We, B, and Δ space. It was found that the IDT decreases with the increase of B at various Wes until some certain level where the reaction rate takes over the dominant mechanism of the ignition process. In this situation, the ignition time delay turns out to be independent of the droplets’ collision and mixing patterns. When comparing it to the traditional bi-propellant pair of WFNA/TMEDA, IDT for H₂O₂/MEA is overall larger than the former. The underlying reason is the high-viscous dissipation from MEA which impedes the internal mixing rate and hence delays the subsequent heating and vaporization processes.

(4) The collision results in the We-B space were categorized into coalescence, stretching separation, and off-center bouncing collision. With the increase of B, multiple ignition modes, namely, waist ignition, breakout-ignition, separation-single-ignition, separation-multi-ignition, and non-ignition modes were observed and identified. Both the collision and ignition mode regimes were sketched. The specific results of the collisional and ignition modes include the following: the breakout ignition boundary line decreases along We axis when B increases; the regime lines quantifying the stretching separation collision and the separation ignition coincide together; and the stretching separation regime contains the separation-single-ignition and separation-multi-ignition sub-modes.

Off-center droplets are considered the common cases in the dense spray zone. Understanding the interaction and mixing between the droplets during pre-ignition is essential to explain the heat and mass transfer and the subsequent ignition process. The collisional and ignition modes’ regime has been established in the present study. Nevertheless, theoretical prediction of all the regime boundaries is of great significance in engineering applications, which certainly merits future efforts.