Characterizations of Minimal Dominating Sets in γ-Endowed and Symmetric γ-Endowed Graphs with Applications to Structure-Property Modeling

Abstract

Claude Berge (1987) introduced the concept of k-extendable graphs, wherein any independent set of size k is inherently a constituent of a maximum independent set within a graph $H=(V,E)$. Graphs possessing the property of being 1-extendable are termedas Berge graphs. This introduction gave rise to the notion of well-covered graphs and well-dominated graphs. A graph is categorized as well-covered if each of its maximal independent sets is, in fact, a maximum independent set. Similarly, a graph attains the classification of well-dominated if every minimal dominating set (DS) within it is a minimum dominating set. In alignment with the concept of k-extendable graphs, the framework of $(k,\gamma )$-endowed graphs and symmetric $(k,\gamma )$-endowed graphs are established. In these graphs, each DS of size k encompasses a minimum DS of the graph. In this article, a study of $\gamma$-endowed dominating sets is initiated. Various results providing a deep insight into $\gamma$-endowed dominating sets in graphs such as those characterizing the ones possessing a unique minimum DS are proven. We also introduce and study the symmetric $\gamma$-endowed graphs and minimality of dominating sets in them. In addition, we give a solution to an open problem in the literature. which seeks to find a domination-based parameter that has a correlation coefficient of $\rho >0.9967$ with the total $\pi$-electronic energy of lower benzenoid hydrocarbons. We show that the upper dominating number $\Gamma \left(H\right)$ studied in this paper delivers a strong prediction potential.

1. Introduction

All the undefined notations and terminologies have been introduced in Section 2.

Domination-related graphical parameters have immense applications in computer science, engineering and chemistry. The earliest domination-related parameters were reported in the book by Ore [1]. Over the years, diverse variants of the domination number in graphs have been proposed and studied. Some of the variants include the locating-dominating number, k-domination number and the Roman domination number, among others. There is a rich amount of the literature which has been published on the domination theory of graphs. For instance, Atakul [2] investigated the domination exponential and stability in certain families of graphs. Li [3] derived some upper/lower bounds on the Roman domination numbers of graphs. Hernández-Ortiz et al. [4] studied the weak Roman domination in certain infinite families of rooted product graphs. Cabrera-Martínez & Peiró [5] investigated the $\left\{k\right\}$-domination number of graphs with $k=2.$ For a detailed survey of the mathematical results on the domination theory of graphs, we refer the reader to Haynes et al. [6].

Well-covered graphs constitute an important class of graphs introduced by Ravindra [7] back in 1977. They have been extensively studied since then. For instance, Favaron [8] extended the notion of well-covered graphs and introduced very well-covered graphs. Finbow et al. [9] characterized well-covered graphs with a girth greater than or equal to 5. King [10] classified a subclass of well-covered networks. For the well-coveredness of product graphs with such strong products of graphs, Topp & Volkmann [11] published some results. Recently, in 2018, Cartesian product graphs with well-covered properties were investigated by Hartnell et al. [12].

Well-dominated and k-extendable graphs form another structurally important class of graphs. In 1992, Anunchuen & Caccetta [13] introduced and studied critically k-extendable graphs. Well-dominated graphs first appeared in a seminal paper by Finbow et al. [14], who introduced them in the context of well-covered graphs. The well-dominated properties of a graph have an extensive amount of published results. Topp & Volkmann [15] in 1990 studied the well-coveredness and well-dominated properties of uniclycic as well as block graphs. Zverovich & Zverovich [16] proposed locally independent well-dominated and locally well-dominated graphs and showed some structural results. Gözüpek et al. [17] investigated the well-dominated property of graphs obtained from the lexicographic product of two graphs. Graphs which are $\{C_4,C_5\}$-free have been studied in the context of well-dominated properties by Levit & Tankus [18]. Alizadeh & Gözüpek [19] investigated bipartite graphs H, which are almost well-dominated having $\delta \left(H\right)\ge 2$ (the minimum degree in H of at least 2). For a survey on well-dominated graphs, we suggest the readers turn to a survey by Anderson et al. [20]. Recently, in 2023, Rall [21] studied the well-dominated properties of strong, direct and Cartesian product graphs.

There have been numerous recent developments on well-dominated, well-covered and k-extendable graphs. For instance, in addition to introducing the classical well-dominated graphs, Anderson et al. [22] introduced the edge version of the well-dominated graphs. Kuenzel & Rall [23] in 2024 classified the well-dominated Cartesian product of graphs. In their seminal paper, Crupi et al. [24] investigated very well-covered graphs by algebraic structures such as Betti splittings. By putting certain conditions on $\Delta$ (largest degree) and $\delta$ (smallest degree), Levit & Tankus [25] investigated well-covered graphs. Alves et al. [26] solved the graph sandwich problem in the context of partitions and well-coveredness. Regarding k-extendable graphs, Gan et al. [27] studied the k-extendability of Cayley graphs generated by transpositions. Feng et al. [28] investigated Hamiltonian cycle properties in k-extendable non-bipartite graphs with high connectivity. For implementation of machine learning by employing graph theory such as graph neural networks, we refer to [29,30,31,32,33].

In this paper, by extending the concept of k-extendable graphs, we introduce $(k,\gamma )$-endowed graphs. We characterize minimal dominating sets in $(k,\gamma )$-endowed graphs and study their well-dominated property. We also introduce and study the symmetric $\gamma$-endowed graphs and prove some structurally important results. In this work, an open problem (from Khan [34]) asking to find a domination-dependent graphical descriptor delivering a correlation coefficient of $\rho >0.9967$ with the total $\pi$-electronic energy $E_{\pi }$ of lower benzenoid hydrocarbons (BHs) has been solved. Section 6 shows that the upper domination number studied in this paper delivers a correlation coefficient $\rho =0.99905>0.9967$ with $E_{\pi }$ of lower BHs. A regression model is also proposed with a detailed statistical analysis for structure–property studies of the $E_{\pi }$ of lower BHs.

2. Preliminaries

Consider a simple graph $H=(V,E),$ where the number of vertices adjacent to a given vertex $v\in V\left(H\right)$ is denoted by $deg\left(v\right).$ The graph’s minimum and maximum degrees are represented by $\delta \left(H\right)$ and $\Delta \left(H\right),$ respectively. The set of vertices adjacent to v in H is designated as $N\left(v\right),$ and the closed neighborhood of v is defined as $N\left[v\right]=N\left(v\right)\cup \left\{v\right\}.$ The complement of a graph $H,$ denoted as $\overline{H},$ is characterized by vertices being adjacent only if they are non-adjacent in $H.$ For a subgraph G of $H,$ its vertex and edge sets are denoted as $V\left(G\right)\subseteq V\left(H\right)$ and $E\left(G\right)\subseteq E\left(H\right),$ respectively. Two subsets $V_1,V_2\subseteq V\left(H\right)$ satisfying $V_1\bigcup V_2=V\left(H\right)$ and $V_1\bigcap V_2=\varphi$ form a bipartition $(V_1,V_2),$ if for any $xy\in E\left(H\right)$ we have $x\in V_1$ and $y\in V_2$ or vice versa. Various well-known graph structures are hereby identified, including the n-dimensional complete graph $K_n$, cycle graph $C_n$, path graph $P_n$ and the $(m,n)$-dimensional complete bipartite graph $K_{m,n}$. Note that the start graph is merely the complete bipartite graph $K_{1,n}$. In a connected graph, it is noteworthy that every pair of vertices is connected by a path. A subset $T\subset V\left(H\right)$ is said to be an independent set if no pair of vertices of T are adjacent in H. The maximum cardinality of an independent set is called the independence number ${\beta }_0\left(H\right)$ of H. For basic definitions, we refer the reader to [35,36].

A subset T within the vertex set $V\left(H\right)$ is termed a dominating set (DS) of graph H if, for each vertex v in the complement of T there exists a vertex u in T such that u and v are adjacent. It is noteworthy that any superset of a dominating set of H also qualifies to be a dominating set of H [6,37]. Moreover, a dominating set T of H is categorized as a minimal dominating set of H if no proper subset of T possesses the property of being a dominating set of H. Minimal DSs of a graph have been characterized by Ore in his famous Ore’s theorem. A vertex $z\in V\left(H\right)$ is said to be a private neighbour ($pn$) of $y\in T\subset V\left(H\right)$ with respect to T denoted by $pn[z,T]$ if $z\in N\left[y\right]-N[T-\{y\left\}\right]$. A DS T is minimal if and only if the private neighboured set of any vertex of T is non-empty. Note that any DS of H contains a minimal DS of H.

The smallest (resp. largest) cardinality of a minimal DS in graph H is termed as the domination number ($\gamma \left(H\right)$) (resp. upper domination number ($\Gamma \left(H\right)$). A DS is characterized as an independent DS if all the vertices in it are independent (i.e., mutually non-adjacent). The cardinality of the smallest independent DS is defined as the independent domination number and is represented by $i\left(H\right).$ For instance, in the star graph $K_{1,n}$ where $n\ge 2,$ the set of pendant vertices qualifies to be a DS, however, it does not encompass a minimal DS.

Berge [38] initiated the study of independent sets being contained in maximum independent sets. The natural curiosity is to start a similar study of DSs comprising a minimum DS. The minimum cardinality of such DSs are called $\gamma$-sets. Some dominating sets of a graph contain a minimum dominating sets while some may not. Claude Berge in 1980 defined k-extendable graphs as those in which any independent set of cardinality k is part of a maximum independent set of the graph. Graphs which are 1-extendable are called Berge graphs. This has led to the concepts of well-covered and well-dominated graphs. Analogous to k-extendable graphs, the concept of $(k,\gamma )$-endowed graphs is being introduced in this paper.

In $(k,\gamma )$-endowed graphs, every dominating set of cardinality k contains a minimum dominating set of the graph. Alternatively, a dominating set of a graph H containing a minimum dominating set of H is called a $\gamma$-endowed dominating set of H. If that set is of cardinality k then it is called a $(k,\gamma )$-endowed dominating set. If in a graph H, minimal dominating sets of cardinality greater than $\gamma \left(H\right)$ exist, such sets will not qualify to be $\gamma$-endowed. Moreover if $\gamma \left(H\right)=\Gamma \left(H\right)$, then every dominating set of H contains a minimum dominating set of $H.$ This is one extreme. The other extreme is that for every positive integer $\gamma \left(H\right)<k<\Gamma \left(H\right)$, there exists a minimal dominating set of H of cardinality k. The former concept is well-known and named as well-dominated graphs. In this article, we discuss the results related to $(k,\gamma )$-endowed graphs.

3. $(\mathbf{k},\gamma )$-Endowed Graphs

Let us define the concept of a $(k,\gamma )$-endowed graph.

Definition 1.

Let k be a positive integer. A simple graph H is called a $(k,\gamma )$-endowed graph if every dominating set of cardinality k in H contains a minimum dominating set of H.

Remark 1.

• Note that every n-vertex graph possesses the $(n,\gamma )$-endowed property as well as the $(\gamma ,\gamma )$-endowed property.
• If H is $(k,\gamma )$-endowed, then k inherently satisfies $k\ge \gamma \left(H\right).$
• If the domination number $\gamma \left(H\right)$ in graph H is less than its upper domination number $\Gamma \left(H\right),$ then H does not exhibit the $(\Gamma ,\gamma )$-endowed property.

We discuss the $(k,\gamma )$-endowed property of some standard graph families.

Example 1.

• $K_n$ is k-endowed for all $K,1\le k\le n.$
• $K_{1,n}$ is k-endowed for all k except when $k=n,1\le k\le n+1.$
• $P_{3n}$ is trivially γ-endowed.
• $C_{3n}(n\ge 2)$ is trivially γ-endowed.
• $K_{m,n}$ is $(k,\gamma )$-endowed for every $k,2\le k\le m+n$ except when $k\in \{m,n\}.$
• Let $D_{r,s}$ be the double star which is constructed by adjoining the centers of two stars $K_{1,s}$ and $K_{1,r}$. Let $r\le s.$ $D_{r,s}$ is $(k,\gamma )$-endowed for all k such that $2\le k\le r$ and $k=r+s+2$ and not $(k,\gamma )$-endowed for $r+1\le k\le r+s+1.$
• In the case of the Peterson graph $P,\gamma \left(P\right)=3,{\beta }_0\left(P\right)=4$ and P is $(k,\gamma )$-endowed, if $k\ne 4,3\le k\le 10.$
• $K_n-e$ is $(k,\gamma )$-endowed for all $k\ne 2,$ $k=1,2,\dots ,n$.
• Assume that $G=(C,I)$ is a complete split graph. Then, H is $(k,\gamma )$-endowed for all k except when $l=\left|I\right|.$

Remark 2.

Let $H=P_n$ when $n\ge 5$. We have $\gamma \left(P_n\right)=\lceil \frac{n}{3}\rceil$ (for any three consecutive vertices of $P_n,$ one vertex contributes to the DS), ${\beta }_0\left(P_n\right)=\lceil \frac{n}{2}\rceil$ and $i\left(P_n\right)=\lfloor \frac{n}{2}\rfloor$. Since $n\ge 5,$ $\gamma \left(P_n\right)<{\beta }_0\left(P_n\right).$ Therefore, $P_n$ is not k-endowed when $k={\beta }_0\left(H\right).$ If $n\ge 8,$ $P_n$ is not k-endowed when $k={\beta }_0\left(P_n\right)$ and $k=i\left(P_n\right).$ Moreover,

• When $n=6,\gamma \left(P_6\right)=2,{\beta }_0\left(P_6\right)=i\left(P_6\right)=3.$
• When $n=7,\gamma \left(P_n\right)=3,{\beta }_0\left(P_7\right)=4,i\left(P_7\right)=3.$

Example 2.

The graph $K_{1,n}$ is $(k,\gamma )$-endowed for every $k,1\le k\le n-1.$ It is not $(n,\gamma )$-endowed though. Note that the above example shows that a graph H may be $(k,\gamma )$-endowed for some positive integer k but may not be $(l,\gamma )$-endowed for some $l>k.$ There exists a graph H in which H is $(k,\gamma )$-endowed but not $(l,\gamma )$-endowed for all $l,$ where $k<l\le n-1.$ Figure 1 presents a graph H possessing $\gamma \left(H\right)=2$. Moreover, H is not $(k,\gamma )$-endowed for any $t,3\le t\le 5.$

Figure 1. The graph H with $\gamma \left(H\right)=2$. Moreover, H is not $(t,\gamma )$-endowed for any $t,3\le t\le 5.$

• Open Problem: Under what conditions on H, the property of being $(k,\gamma )$-endowed, is it implied that H is $(l,\gamma )$-endowed for all $l,k\le l\le n?$

Observation 1.

• If H has a γ-fixed vertex u, i.e., that is every γ-set (a DS of cardinality γ) of H contains u which is not an isolated vertex, then H is not $(k,\gamma )$-endowed for all k, in which the existence of a DS of cardinality k is not containing $u.$ In particular, H is not $\left(\right(n-1),\gamma )$-endowed (when H is of order n).
• If H has t full degree vertices, then H is $(k,\gamma )$-endowed if $k=1$ or $n-t+1\le k\le n.$ Also, if S is the set of all full degree vertices then for any k such that $\gamma (⟨H-S⟩)\le k\le n-\left|S\right|,$ H is not $(k,\gamma )$-endowed.
• If $\gamma \left(H\right)<i\left(H\right)$ and $\Gamma \left(H\right)<n$ then H is not $(k,\gamma )$-endowed when $k=i\left(H\right),{\beta }_0\left(H\right)$ and $\Gamma \left(H\right).$
• Assume H is not $(k,\gamma )$-endowed. Then, $H\cup t{K}_1$ is not $\left(\right(k+t),\gamma )$-endowed.
• If H has a minimal DS of cardinality $k>\gamma$, then H is not $(k,\gamma )$-endowed.

4. Graphs with Unique Minimum DS

In this section, we study unique minimum dominating sets in $(k,\gamma )$-endowed graphs.

Proposition 1.

Consider a simple graph H possessing no isolated members. If H has a unique minimum DS, then H is not $(k,\gamma )$-endowed for any $k,$ where $n-\gamma \left(H\right)\le k\le n-1$.

Proof. 

Suppose T is the minimum DS of $H.$ As H possesses no isolated members, $V-T$ is a DS of T and $|V-T|=n-\gamma \left(H\right).$ Hence H is not $(k,\gamma )$-endowed if $k=n-\gamma \left(H\right).$ Also, for any $k,$ $n-\gamma \left(H\right)\le k\le n-1,$ $(V-T)\cup T_1$ where $T_1$ is a subset of T of cardinality $k-(n-\gamma (H\left)\right)$ is a DS of H not containing $T.$ Hence H is not $(k,\gamma )$-endowed if $n-\gamma \left(H\right)\le k\le n-1.$ □

Proposition 2.

Let H be a graph without isolated members. Let $T=\{u_1,u_2,\cdots ,u_k\}$ be a unique minimum DS of $H.$ Every vertex $u_i\in T$ has at least two $pn$ in $V-T$ with respect to $T.$ (That is, $\left|pn\right(u,D)\cap (V-T\left)\right|\ge 2$).

Proof. 

Assume that $u_i$ lacks a pendant neighbor ($pn$) in the set $V-T$ with respect to $T.$ In this scenario, $u_i$ is an isolated member in the induced subgraph $⟨T⟩.$ As $u_i$ is not an isolated member in the original graph $H,$ there must exist a vertex $v\in N\left(u_i\right)\cap (V-T).$ Let $T_1=u_1,u_2,\dots ,u_{i-1},v,u_{i+1},\dots ,u_k.$ Note that any $u_i$’s neighbor (resp. the vertices $u_i$) is dominated by $T_1-\left\{v\right\}$ (resp. v). Consequently, $T_1$ qualifies as a minimum DS of $H,$ leading to a contradiction.

Hence, it is established that every vertex $u_i$ in T must have a pendant neighbor in $V-T.$ Now, let us consider the case where $u_i$ possesses exactly one pendant neighbor in $V-T$ concerning $T.$ Denote the sole pendant neighbor of $u_i$ as $v.$ Form the set $T_2=u_1,u_2,\dots ,u_{i-1},v,u_{i+1},\dots ,u_k.$ In this configuration, v dominates $u_i,$ and any neighbor of $u_i$ (excluding v) is dominated by $T_2-\left\{v\right\}.$ Therefore, $T_2$ constitutes a minimum DS of $H,$ resulting in a contradiction.

Consequently, it can be concluded that each vertex $u_i$ must have at least two pendant neighbors in $V-T$ with respect to T. □

Remark 3.

Let H be a graph without isolated members. Assume $T=\{u_1,\cdots ,u_k\}$ is a unique minimum DS of H. Let $\alpha ={\displaystyle \underset{1\le i\le k}{min}}\left|pn\right(u_i,T\left)\right|$ and $\left|pn\right(u_i,T\left)\right|=\alpha .$ Then $(T-\left\{u_i\right\})\cup pn(u_i,T))$ is a DS of H of cardinality $k+\alpha -1\ge k+1,$ since $\alpha \ge 2$).

Proposition 3.

Suppose H is a graph possessing no isolated members. Assume $T=\{u_1,\cdots ,u_k\}$ is a unique minimum DS of $H.$ Then, $\gamma \left(⟨pn(u_i,T)⟩\right)\ge 2.$

Proof. 

Suppose for some $i,\gamma (⟨pn(u,T)⟩)=1.$ Let $x\in pn(u_i,T)$ and let $\left\{x\right\}$ be a DS of $\gamma \left(⟨pn(u_i,T)⟩\right).$ Then, $(T-\left\{u_i\right\})\cup \left\{x\right\}$ is a DS of H with number of members $\gamma \left(H\right),$ a contradiction. Therefore, $\gamma \left(⟨pn(u_i,T)⟩\right)\ge 2.$ □

Corollary 1.

The induced graph $⟨pn(u_i,T)⟩$ has no full degree vertex for every $u_i\in T.$

Remark 4.

• Let H be a graph without isolated members. Assume $T=\{u_1,\cdots ,u_k\}$ is a unique minimum DS of $H.$ Let $\gamma ⟨(V-T)⟩=a$. Then, for any $k_1$ such that $a\le k_1\le n-k,$ there exists a DS of cardinality $k_1.$ These DSs do not contain $T.$ Therefore, H is not $(k_1,\gamma )$-endowed for all $k_1$ with $\gamma (⟨V-T)⟩)\le k_1\le n-k.$
• There exists a graph with the unique minimum DS which is not $\left(\right(\gamma +2),\gamma )$-endowed and which is $\left(\right(\gamma +1),\gamma )$-endowed. For example, consider $H=K_{1,3};\gamma \left(H\right)=1,$ then H is not $(3,\gamma )$-endowed, however, H is $(2,\gamma )$-endowed.
• There exists a graph with a unique minimum DS which is $(\gamma +1,\gamma )$-endowed and which is not $\left(\gamma \right(H)+2,\gamma )$-endowed and $\left|V\right(H\left)\right|-\left(\gamma \right(H)+2)$ is large. Let $H=T_3, k-1, k\ge 4.$ Then, H has a unique minimum DS and $\gamma \left(H\right)=2.$ Moreover, H is $(3,\gamma )$-endowed, H is not $(k,\gamma )$-endowed for all $k,4\le k\le k+4.$ Hence, $\left|V\right(H\left)\right|-\left(\gamma \right(H)+2)=k+4-4=k.$
• Let H be a graph without isolated members. Let $T=\{u_1,u_2,\cdots ,u_{\gamma }\}$ be a unique minimum DS of H. Let $min\gamma \left(⟨pn(u_i,T)⟩\right)=a,$. Then, H is not a $(k,\gamma )$-endowed for k satisfying $\gamma \left(H\right)+a-1\le k\le n-1.$
• Consider $H=K_{n_1,n_2,\cdots ,n_k}$ where $n_1<n_2<\cdots <n_k.$ Then, H is not $(k,\gamma )$-endowed for $k=n_1,n_2,\cdots ,n_k$ and H is $(k,\gamma )$-endowed for all $k\ne n_1,n_2,\cdots ,n_k$ and $2\le k\le n.$

Proposition 4.

Assume $a\in {\mathbb{Z}}^{+}$ to be the minimum satisfying $\gamma \left(H\right)<a$ and H contains a minimal DS of cardinality $a.$ Then, H is a $(k,\gamma )$-endowed for all $k,$ $\gamma \left(H\right)\le k\le a-1.$

Proof. 

Let T be a DS of cardinality $k,$ $\gamma \left(H\right)\le k\le a-1,$ by hypothesis, T is not minimal and T cannot contain a minimal DS other than a $\gamma$-set. Therefore, T is a $(k,\gamma )$-endowed. □

Corollary 2.

Under the hypothesis of the above remark and assuming $a\ne \gamma \left(H\right)+1,$ H is not trivially γ-endowed.

Remark 5.

There exists a graph H with a unique minimum DS such that every DS of cardinality $\gamma \left(H\right)+1$ contains the unique minimum DS.

Example 3.

• The star $K_{1,n}$.
• For the graph H in Figure 2, any DS of cardinality 5 contains T. There exists a DS of cardinality 6, namely $\{v_1,v_2,v_3,v_{14},v_{15},v_{16}\}$ which does not contain $T.$ Therefore, H is not a $(6,\gamma )$-endowed. In fact, H is not $(k,\gamma )$-endowed for any k such that $6\le k\le 15.$

Figure 2. The graph H in Example 3.

Remark 6.

Let H be the graph without isolated members. Let T be the unique minimum DS of $H.$ Let $T=\{u_1,u_2,\cdots ,u_{\gamma \left(H\right)}\}$ and $k=min\{pn[u_i,T]:1\le i\le \gamma \}$. Moreover, let $T_1=\{u_1,u_2,\cdots ,u_{i-1},u_{i+1},\cdots ,u_{\gamma \left(H\right)}\}\cup pn(u_i,T)$ where $pn(u_i,T)=k.$ Therefore, H is not $\left(\right(\gamma \left(H\right)-1)+k,\gamma )$-endowed. Therefore, H is not $(k,\gamma )$-endowed for all $k,$ such that $\gamma \left(H\right)-1+k\le -1+n.$

Theorem 1.

Suppose H is a graph without isolated members with a unique minimum DS $T.$ Let $\ell ={\displaystyle \underset{u_i\in T}{min}}\{\left(pn(u_i,T)\right\}$. Then, H is $({\ell }_1,\gamma )$-endowed for $\gamma \left(H\right)\le {\ell }_1\le \gamma \left(⟨V-T⟩\right)-1$ and not $({\ell }_1,\gamma )$-endowed if $\gamma \left(⟨V-T⟩\right)\le {\ell }_1\le n-1$ provided $|V-T|=\ell -1+\gamma \left(H\right).$ If $|V-T|>\ell -1+\gamma \left(H\right),$ and $\ell \gamma \left(H\right)>\ell -1+\gamma \left(H\right)$, then H is $({\ell }_1,\gamma )$-endowed if $\gamma \left(H\right)\le {\ell }_1\le \gamma \left(H\right)+\ell -2$ and not $({\ell }_1,\gamma )$-endowed if $\gamma \left(H\right)+\ell -1\le {\ell }_1\le n-1$.

Proof. 

Let T be a unique minimum DS of $H.$ Let $\ell =min\left\{\right|pn(u_i,T)|:u_i\in T\}.$ Suppose $|V-T|=n-\gamma \left(H\right)<\gamma \left(H\right)+\ell -1$. Since any vertex of T has at least ℓ $pn$s in $V-T,$ $|V-T|\ge \ell \gamma \left(H\right).$ Therefore, $\ell \gamma \left(H\right)\le |V-T|=n-\gamma \left(H\right)<\gamma \left(H\right)+\ell -1.$ $(\ell -1)\gamma \left(H\right)<\ell -1.$ Since $\ell \ge 2,$ that is $\gamma \left(H\right)<1,$ a contradiction.

Case (i):$|V-T|=\gamma \left(H\right)+\ell -1.$ Therefore, $\ell \gamma \left(H\right)\le \gamma +\ell -1,$ that is $(\ell -1)\le \gamma \left(H\right)\le \ell -1.$ $\ell \ge 2,$ $\gamma \le 1$ Therefore, $\gamma \left(H\right)=1.$ Let $s=\gamma (⟨V-T⟩).$ If $1\le t\le s-1,$ then any DS of cardinality t contains T. Therefore, for all ${\ell }_1$, such that $1\le {\ell }_1\le \gamma \left(⟨V-T⟩\right)-1,$H is $({\ell }_1,\gamma )$-endowed. Therefore, for all ${\ell }_1$ such that $\gamma \left(⟨V-T⟩\right)\le {\ell }_1\le n-1,$H is not $({\ell }_1,\gamma )$-endowed.

Subcase (i):$\ell \gamma \left(H\right)<\gamma \left(H\right)+\ell -1<|V-T|.$ Then $(\ell -1)\gamma \left(H\right)<\ell -1.$ Therefore, $\gamma \left(H\right)<1$ (since $\ell \ge 2$), a contradiction.

Subcase (ii):$\ell \gamma \left(H\right)+\ell -1<|V-T|.$ Then, $(\ell -1)\gamma \left(H\right)=\ell -1.$ Therefore, $\gamma \left(H\right)=1.$ Proceeding as in case (i), we obtain the result.

Subcase (iii):$\ell \gamma \left(H\right)+\ell -1.$ Then, $(\ell -1)\gamma \left(H\right)>\ell -1.$ Therefore, $\gamma \left(H\right)>1$. That is, $\gamma \left(H\right)\ge 2.$ If $\gamma \left(H\right)\le {\ell }_1\le \gamma +\ell -2$ then any ${\ell }_1$ DS of H must contain $T.$

Suppose $T_1$ is a DS of H of cardinality ${\ell }_1\le \gamma +\ell -2.$ Suppose $T_1$ does not contain $T.$ Then, for any vertex in $V-T_1,$ $pn$ of that vertex belong to $T_1.$ Suppose $T_1$ does not contain t vertices of $T,t\ge 0.$ Therefore, $H_1$ contains $2t\ell$ vertices from $V-T.$ Therefore, $|T_1|=\gamma \left(H\right)-t+2t\ell \le \gamma \left(H\right)+\ell -2.$ Therefore, $2t\ell -t\le \ell -2.$ Since $\ell \ge 2,$ $2(2t-1)\le \ell (2t-1)\le t-2.$ Therefore, $4t-2\le t-2,$ therefore, $3t\le 0,$ thus, $t=0.$ Hence, $D_1$ contains every vertex of $T.$ Thus, H is $({\ell }_1,\gamma )$-endowed for $\gamma \left(H\right)\le {\ell }_1\le \gamma \left(H\right)+\ell -2.$ If $\gamma \left(H\right)+\ell -1\le {\ell }_1\le n-1$ then there exists a DS of cardinality ${\ell }_1$ not containing a vertex $u\in T$ for which $\left|pn\right(u,T\left)\right|=\ell .$ Hence, H is not $({\ell }_1,\gamma )$-endowed for ${\ell }_1$ with $\gamma \left(H\right)+\ell -1\le {\ell }_1\le n-1.$ □

Corollary 3.

Let $r,s\ge 2,r\le s$. Then, $D_{r,s}$ is $({\ell }_1,\gamma )$-endowed if $2\le {\ell }_1\le r$ and is not $({\ell }_1,\gamma )$-endowed if $r+1\le {\ell }_1\le n-1.$

Proof. 

Since $\gamma \left(D_{r,s}\right)=2$ and $D_{r,s}$ has a unique minimum DS T consisting of the two centers, say, $u_1$ and $u_2.$ $pn(u_1,T)=r$ if $u_1$ supports r pendant vertices. $\ell =min\{pn(u_1,T),pn(u_2,T)\}=min(r,s)=r.$ $\gamma +\ell -1=r+2-1=r+1.$ $\gamma \ell =2r.$ Since $r\ge 2,$ $\gamma \ell >\gamma +\ell -1.$ Also $|V-T|=r+s+2-2=r+s>r+1,$ since $s\ge 2.$ Therefore, by Theorem 1, $D_{r,s}$ is $({\ell }_1,\gamma )$-endowed if $r\le {\ell }_1\le r+\ell -2$ and is not $({\ell }_1,\gamma )$-endowed if $\gamma +\ell -1\le {\ell }_1\le n-1.$ That is, $D_{r,s}$ is $({\ell }_1,\gamma )$-endowed if $2\le {\ell }_1\le r$ and is not $({\ell }_1,\gamma )$-endowed if $r+1\le {\ell }_1\le n-1.$ □

Remark 7.

$D_{r,s}$ is trivially γ-endowed if $2=r\le s.$

Theorem 2.

Suppose H is a graph without isolated members. Assume u is a γ-fixed member of H. Let $k=min\left\{\right|pn(u,T)|:T$ is a γ-set of $H\}$. Then, H is not $(k_1,\gamma )$-endowed for all $k_1,\gamma +k-1\le k_1\le n-1.$

Proof. 

Suppose T is a minimum DS of H satisfying $\left|pn\right(u,T\left)\right|$ is minimum. Let $\left|pn\right(u,T\left)\right|=k$ and $pn(u,T)=\{v_1,v_2,\cdots ,v_k\}.$ Then, $T_1=(T-\left\{u\right\})\cup \{v_1,v_2,\cdots ,v_k\}$ is a DS of H. Since $u\in T_1,$ we have that $T_1$ does not contain any $\gamma$-set of H. Therefore, H is not $(\gamma +k-1,\gamma )$-endowed and hence H is not $(k_1,\gamma )$-endowed for all $k_1,$ $\gamma +k-1\le k_1\le n-1.$ □

Here we have a subsequent corollary to Theorem 2.

Corollary 4.

When $k=2,$ H is trivially γ-endowed.

Theorem 3.

Let H be a graph without isolated members in which $\gamma \left(H\right)<i\left(H\right)<{\beta }_0\left(H\right).$ Suppose there exists a minimum independent DS T in which at least one vertex, say u, has a $pn$ in $V-T$ with respect to $T.$ Then, H is not $(k,\gamma )$-endowed for $k=i$ and $i+1.$

Proof. 

Suppose T is a minimum independent DS of H. Then, $\left|T\right|=i\ge 2.$ Moreover, by hypothesis, existence of a $u\in T$ is ensured, satisfying $pn(u,T)=Ø.$ Let $v\in pn(u,T)$ and $T_1=T\cup \left\{v\right\}$. Suppose $T_1$ contains a minimum DS, say S of H. Clearly, $S\not\subset T.$ Therefore, $v\in S.$ Since $\left|S\right|=\gamma \left(H\right)<i\left(H\right),$ $|S\cap T|\le i-2.$ Let $u_1,u_2\in T-S.$ Since $v\in pn(u,T),$v can dominate at most one of $u_1,u_2.$ Since $S-\left\{v\right\}$ contains independent vertices of $T,$ no vertices of $S-\left\{v\right\}$ can dominate $u_1$ as well as $u_2,$ a contradiction, since S is a DS of $H.$ Therefore, $T_1$ does not contain any minimum DS of $H.$ Therefore, H is not $\left(\right(i\left(H\right)+1),\gamma )$-endowed. □

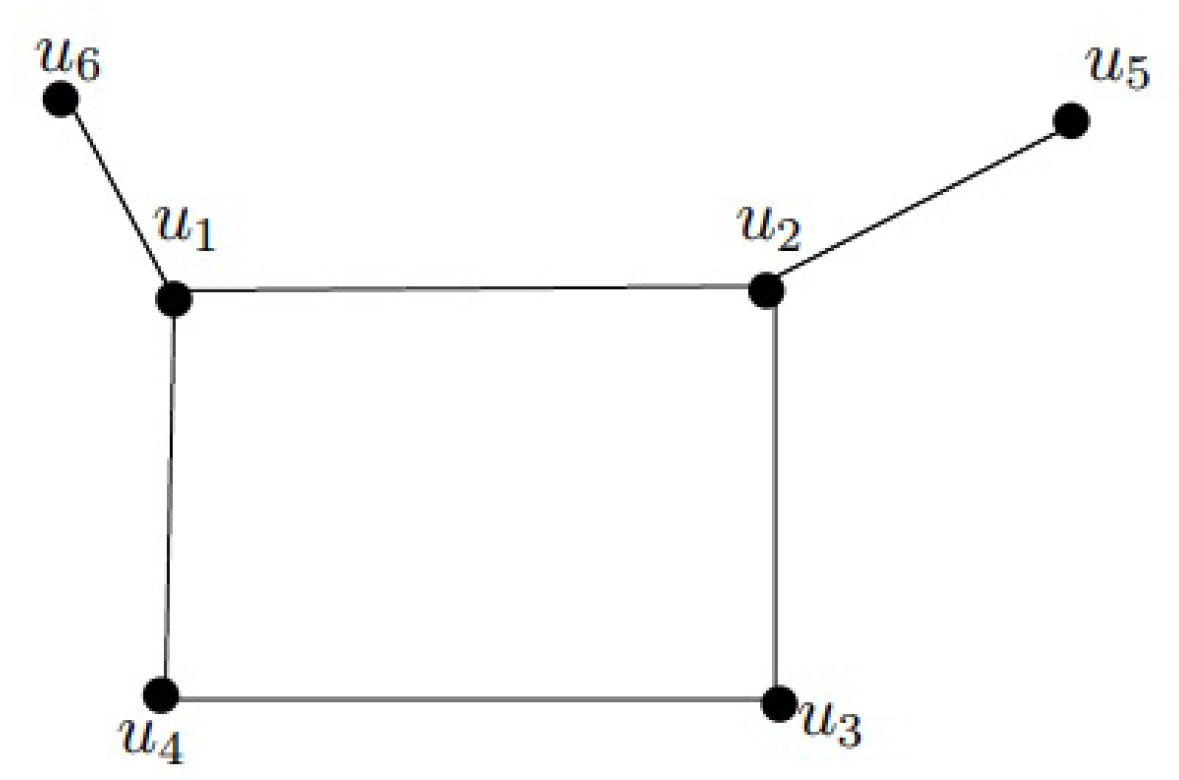
Remark 8.

• Consider $K_{m,n}$ where $m\ge n\ge 3$, then $\gamma \left(H\right)=2$ and $i\left(H\right)=min\{m,n\}=n=3$. The partite set with n elements constitutes a minimum independent DS and no vertex of this set has a $pn$ in the complement.
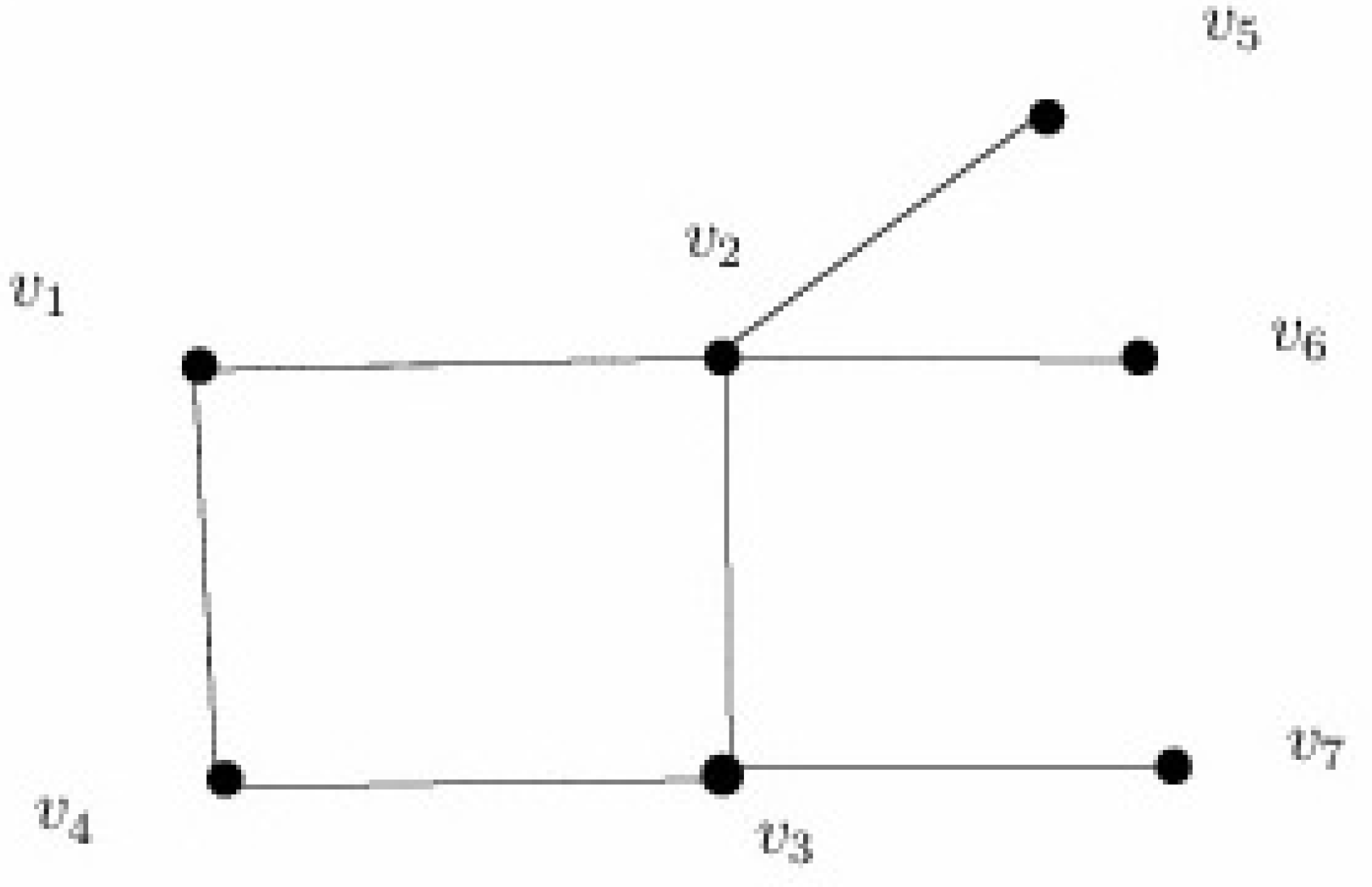
• For the graph H in Figure 3, $\{v_2,v_3\}$ is the only minimum DS of H and $\{v_2,v_4,v_7\}$ is a minimum independent DS of H. Therefore, $i\left(H\right)=3.$ The subsets $\{v_2,v_4,v_5,v_7\},\{v_2,v_4,v_7\}$ and $\{v_2,v_4,v_5,v_6,v_7\}$ are a DS of H not containing any γ-set of H. Therefore, H is not $(k,\gamma )$-endowed for $k=3,4$ and 5. See Figure 3.

Figure 3. The graph H in Remark 8.

Proposition 5.

Suppose H is a graph having no isolated members in which $\gamma \left(H\right)<i\left(H\right).$ Suppose there exists a minimum independent DS named $T=\{u_1,u_2,\cdots ,u_{i\left(H\right)}\}$ satisfying $|pn[u_j,T]|=|t_j|,$ $1\le j\le i\left(G\right).$ Let $t_j\ge 2$ for $j=j_1,j_2,\cdots ,j_r,$ $r\ge 1.$ Then, H is not $(k,\gamma )$-endowed for $k=i,i+1,\cdots ,i+{\displaystyle \sum _{j\in (j_1,j_2,\cdots ,j_r)}}{t}_j.$

Proof. 

Assume $T=\{u_1,u_2,\cdots ,u_{i\left(H\right)}\}$ is a minimum independent DS of H. Let $|pn[u_j,T]|=|t_j|,1\le j\le i\left(H\right).$ Let $t_j\ge 2$ for $j=j_1,j_2,\cdots ,j_r,r\ge 1$ and $S=T\cup \{{\displaystyle \bigcup _{j\in (j_1,j_2,\cdots ,j_r)}}pn[u_j,T]\}.$ Suppose S contains a $\gamma$-set of H, say, $S_1=\{x_1,x_2,\cdots ,x_r\}.$ Since T is a minimum independent DS of $H.$ Then, T is minimal DS of $H.$ Therefore, $S_1\not\subset T$ and $S_{11}=S_1\cap T,$ $S_{12}=S_1\cap (S-T).$ Moreover, let $T^{\prime }=T-(S_1\cap T).$ Therefore, $S_{12}$ dominates $T^{\prime }.$ Also $|T^{\prime }|\le |S_{12}|$ (since every vertex of $S_{12}$ is a $pn$ of some vertex of $T).$ $i\left(H\right)=\left|T\right|=|T^{\prime }|+|S_{11}|\le |S_{12}|+|S_{11}|=|S_1|=\gamma \left(H\right).$ Therefore, $i\left(H\right)=\gamma \left(H\right),$ a contradiction, since $\gamma \left(H\right)<i\left(H\right).$ □

Remark 9.

Assume T is a minimal independent DS of $H.$ Let $\gamma \left(H\right)<i\left(H\right)\le \left|T\right|={\beta }_0\left(H\right).$ Assume $T=\{u_1,u_2,\cdots ,u_r\}$ satisfies $|pn[u_j,T]|=t_j,1\le j\le r.$ Let $t_j\ge 2$ for $j=j_1,j_2,\cdots ,j_s,$ $s\ge 1.$ Then, H is not $(k,\gamma )$-endowed for $k=r,r+1,\cdots ,r+{\displaystyle \sum _{j\in (j_1,j_2,\cdots ,j_r)}}{t}_j.$

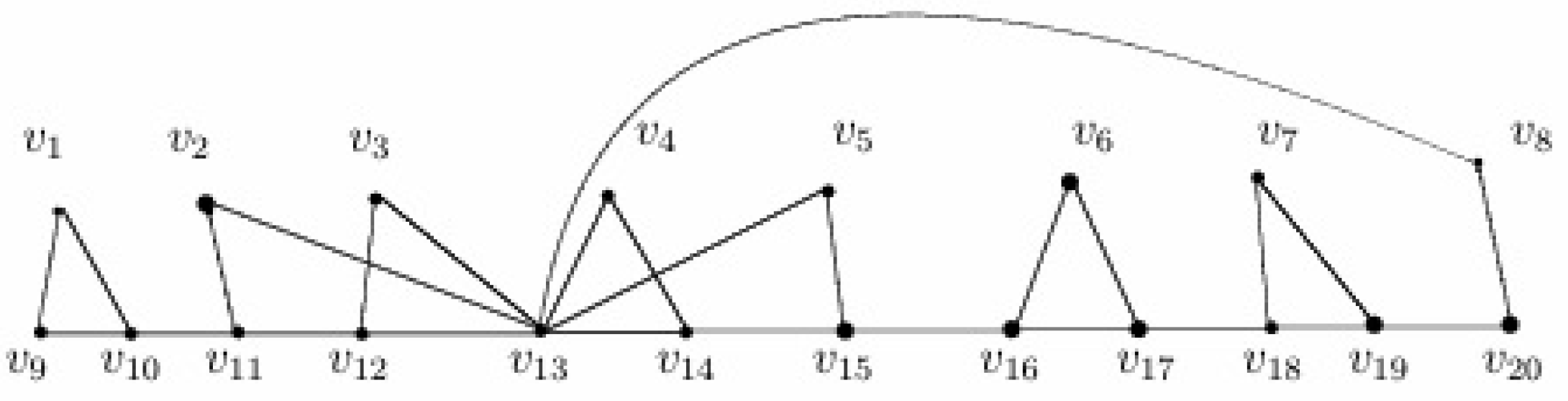
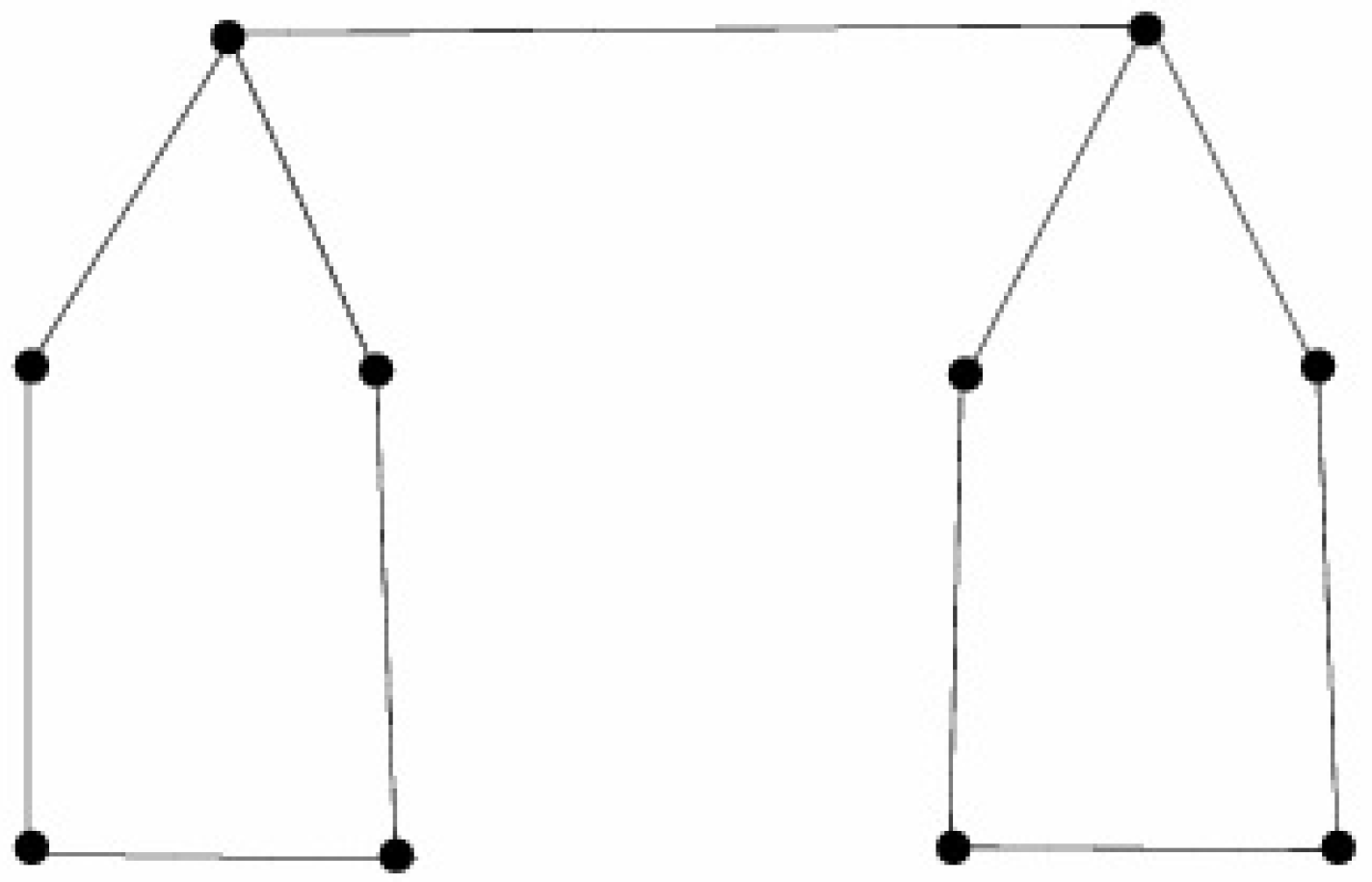
Remark 10.

Existence of a graph H is depicted in Figure 4 with $\gamma \left(H\right)<{\beta }_0\left(H\right)$ and H is not $(k,\gamma )$-endowed for all k. We have the following:

• ${\beta }_0\left(H\right)\le k\le \left|V\left(H\right)\right|-1;$
• γ-set: $D=\{v_{10},v_{13},v_{16},v_{19}\}.$ $\gamma \left(H\right)=4.$ ${\beta }_0$-set: $\{v_1,\dots ,v_8\},$ ${\beta }_0\left(H\right)=8.$
• $pn[u_j,D]=\{v_9,\dots ,v_{12},v_{14},\dots ,v_{20}\}$
• ${\displaystyle \sum _{j\in (j_1,j_2,\cdots ,j_r)}}{t}_j=11.$

Figure 4. The graph H in Remark 10.

Theorem 4.

Assume an n-vertex graph H comprises a minimal DS of cardinality $n-1$, then

(i)

$\gamma \left(H\right)=n-1$ if H has exactly $(n-2)$ isolated members.

(ii)

$\gamma \left(H\right)=n-t$ if H has exactly $(n-t-1)$ isolated members and the remaining vertices form a star.

Proof. 

Let T be a minimal DS of cardinality $n-1.$ Let $\gamma \left(H\right)=\{u_1,u_2,\cdots ,u_n\}$ and let $T=\{u_1,u_2,\cdots ,u_{n-3}\}.$ Then, $u_n$ is adjacent to some point of D, say, $u_i,1\le i\le n-1$.

Case (i):T is independent. Then, H is $K_{1,t}\cup (n-t-1)K_1$ where $1\le t\le n-1.$ Thus, $\gamma \left(H\right)=1+n-t-1=n-t.$

Case (ii):T is not independent. Let WLOG assume that $u_1\sim u_2$. Then, $u_n$ is adjacent with exactly one of $u_1,u_2\in T$ (since T is minimal). Therefore, $H=P_3\cup (n-3)K_1.$ This implies that $\gamma \left(H\right)=n-2=n-t$ where $t=2$ and $H=K_{1,t}\cup (n-t-1)K_1.$ □

Corollary 5.

• Consider a graph H with an order of $n.$ The graph H possesses a minimal DS of cardinality $n-1$ if and only if H can be expressed as $K_{1,t}\cup (n-t-1)K_1,$ where $1\le t\le n-1.$
• Let H be a graph of order n with a minimal DS of cardinality $n-1.$ In such a case, H is trivially γ-endowed if and only if H takes the form $K_{1,t}\cup (n-t-1)K_1,$ where $t\in \{1,2\}$. Alternatively, if H is an n-vertex graph with $\gamma \left(H\right)=n-1,$ then H is trivially γ-endowed if and only if H is either $K_2\cup (n-2)K_1$ or $K_{1,2}\cup K_1.$

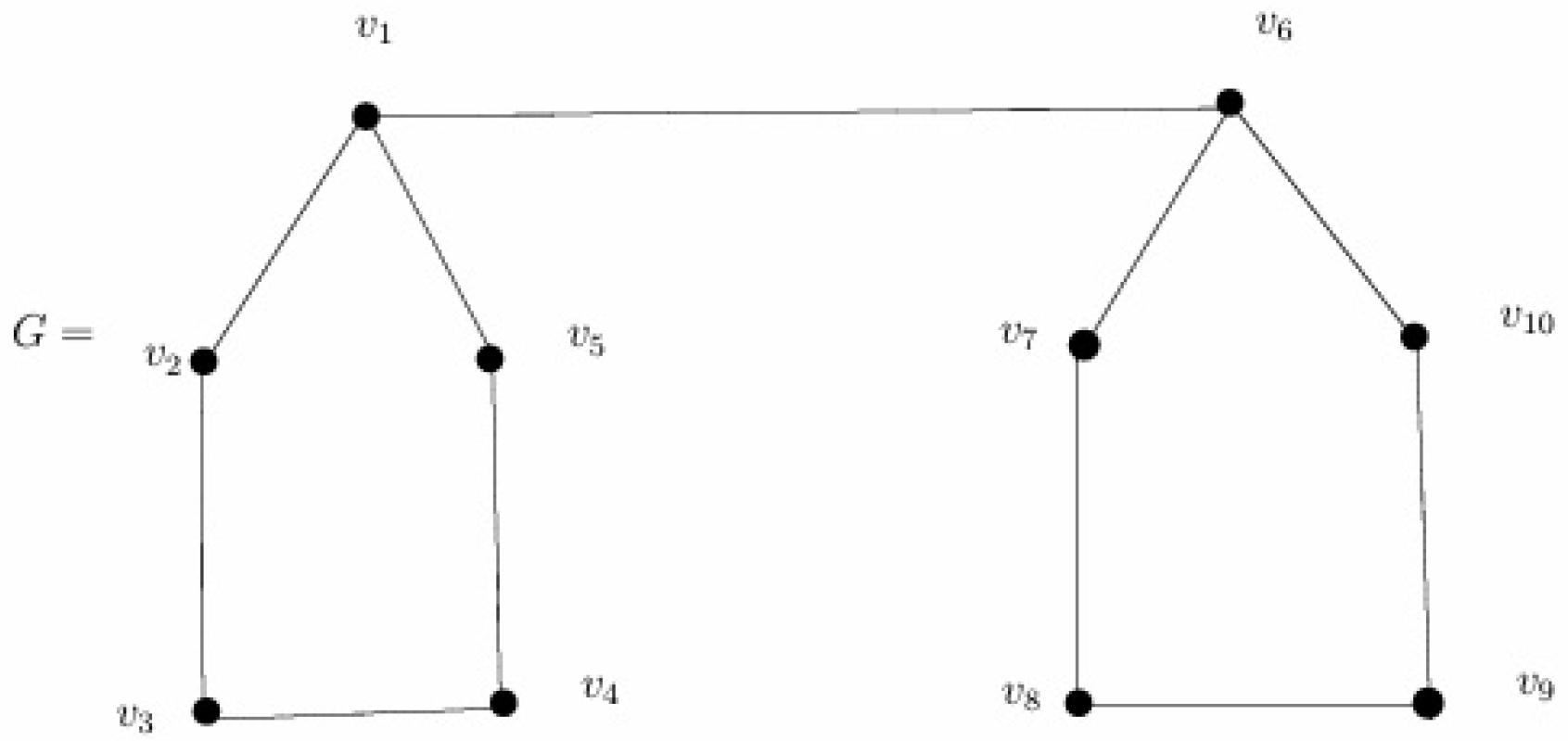
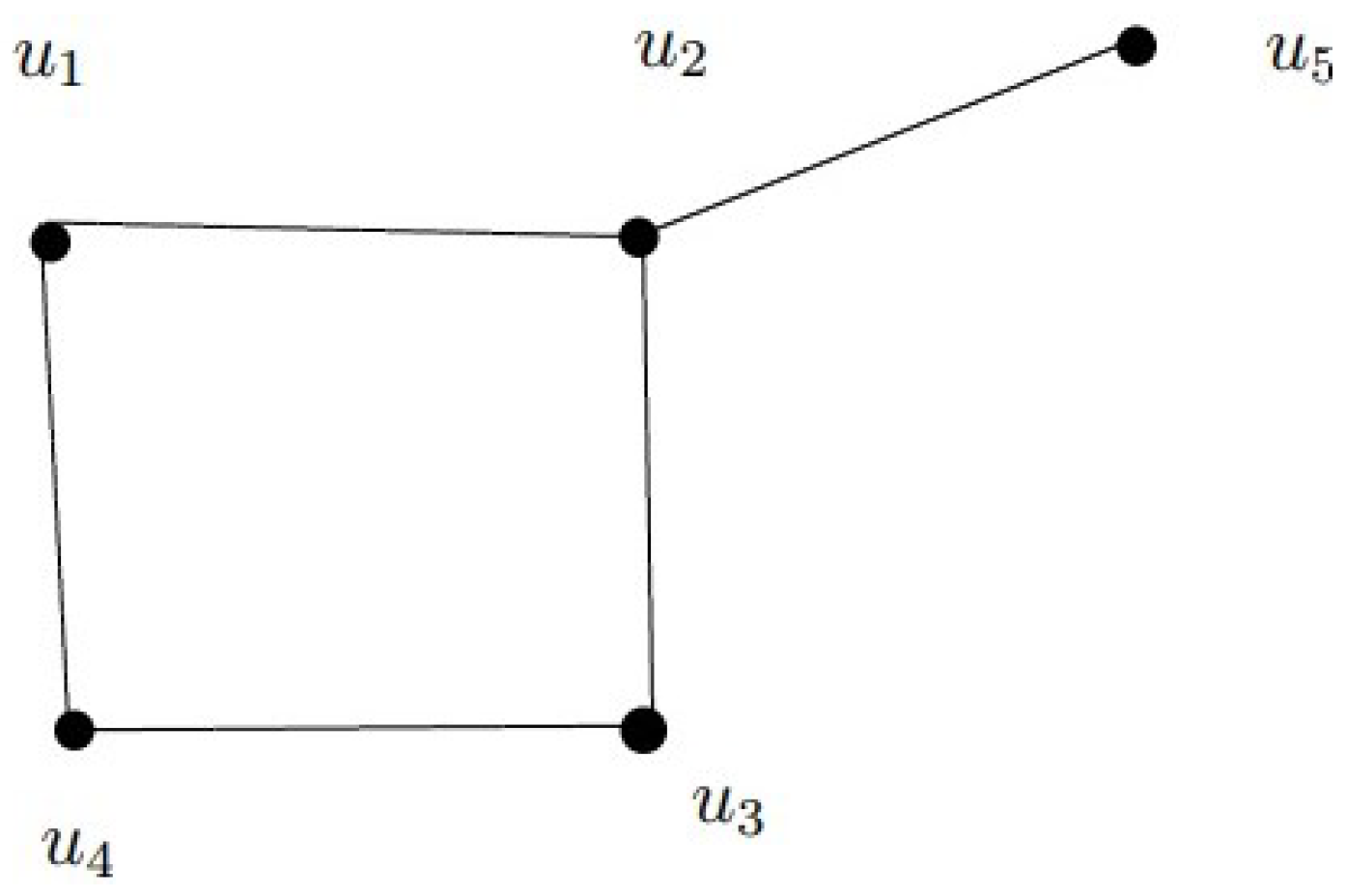
Example 4.

Figure 5 presents a graph H with $\gamma \left(H\right)=2,\Gamma \left(H\right)=n-2$.

Figure 5. The graph H with $\gamma \left(H\right)=2,\Gamma \left(H\right)=n-2.$

Remark 11.

Example 4 implies that there are graphs H in which $\gamma \left(H\right)={\beta }_0\left(G\right)$ and $\Gamma \left(H\right)={\beta }_0\left(H\right)+1$ and H is $(k,\gamma )$-endowed for all $k,$ $\gamma \left(H\right)\le k\le n$ except when $k=\Gamma \left(H\right).$

Example 5.

Figure 6 exhibits a graph H having $\gamma \left(H\right)=4={\beta }_0\left(H\right)$ and $\Gamma \left(H\right)=5.$

Figure 6. The graph H with $\gamma \left(H\right)=4={\beta }_0\left(H\right)$ and $\Gamma \left(H\right)=5.$ Moreover, $\{v_3,v_4,v_6,v_7,v_{10}\}$ is a $\gamma \left(H\right)$- set of $H.$ Thus, H is $(k,\gamma )$-endowed for all $k\ge 6.$

Theorem 5.

Let $u,v\in V\left(H\right)$ be such that any minimum DS of H either contains u or v. Suppose there exists a DS of cardinality $\gamma +1$ not containing u and $v.$ Then, H is almost trivially γ-endowed, that is, H is not $(k,\gamma )$-endowed for all $k,$ $\gamma \left(H\right)+1\le k\le n-2.$

Proof. 

Let T be a DS of cardinality $\gamma \left(H\right)+1$ not containing u and v. For any w not equal to $u,v$, we have that $T\cup \left\{w\right\}$ is a DS of cardinality $\gamma \left(H\right)+2$ and it does not contain any minimum DS of $H.$ In general, if $v_1,v_2,\cdots ,v_{\left(\gamma \right(H)+3)}\notin T\cup \{u,v\},$ the set $T\cup \{v_1,v_2,\cdots ,v_{\gamma \left(H\right)+3}\}$ is a DS of cardinality $n-2$ and this does not contain any minimum DS. Thus, H is not $(k,\gamma )$-endowed for all $k,$ $\gamma \left(H\right)+1\le k\le n-2.$ □

Corollary 6.

Suppose $u,v\in V\left(H\right)$ exist, satisfying the condition that any minimum DS of H either contains u or contains v and there exists a DS of cardinality $\gamma \left(H\right)+1$ not containing u and v. Moreover, if H is not $\left(\right(n+1),\gamma )$-endowed, then H is trivially γ-endowed.

Observation 2.

If H is $(k,\gamma )$-endowed for all $k,$ $\gamma \left(H\right)\le k\le n$ except for exactly one value of $k,$ say, l then in the sequence $\gamma \left(H\right)\le i\left(G\right)\le {\beta }_0\left(H\right)\le \Gamma \left(H\right),$ there are only two distinct values, as well as any minimal DS of H or a Γ-set (a minimum DS with cardinality $\Gamma \left(H\right)$) of $H.$ The following two graphs satisfy the above property:

(i)

Let $H=K_{2,4}.$ Then, $\gamma =2,{\beta }_0\left(H\right)=\Gamma \left(H\right)=4$ and H is $(k,\gamma )$-endowed for all $k,$ $2\le k\le 6$ except for $k=4.$

(ii)

Assume the graph H is obtained from $2C_5$ by joining one vertex of one $C_5$ with exactly one vertex of another $C_5$. See Figure 7.

Figure 7. The graph H having $\gamma \left(H\right)=4={\beta }_0\left(H\right)$ and $\Gamma \left(H\right)=5.$ Note that H is $(k,\gamma )$-endowed for all $k,$ $4\le k\le 10$ except when $k=5.$

Consider $C_n,n\cong 1,2(mod3).$ Suppose $n=3t+1$ or $3t+2.$ Then, $\gamma \left(C_n\right)=t+1=\frac{n+2}{3}$ or $\frac{n+1}{3}.$ Moreover,

$${\beta }_0\left(H\right)=\left\{\begin{array}{cc}\frac{n-1}{2}\hfill & n\mathit{is}\mathit{odd}\hfill \\ \frac{n}{2}\hfill & n\mathit{is}\mathit{even}.\hfill \end{array}\right.$$

For this class of graphs H, the graph H is $(k,\gamma )$-endowed for all $k,\gamma \left(H\right)\le k\le n$ except for $k={\beta }_0\left(C_n\right)=\Gamma \left(C_n\right).$

5. Symmetric $\gamma$-Endowed Graphs

First, we define the symmetric $\gamma$-endowed graphs.

Definition 2.

A graph H is said to be symmetric γ-endowed if for every $k,$ $\gamma \left(H\right)\le k\le n,$ H is $(k,\gamma )$-endowed.

Let us illustrate this concept by studying it for standard families.

Example 6.

• $K_n,\overline{K_n},\overline{\left(\frac{n}{2}\right)K_2},C_n(n\cong 1mod3)$ are symmetric γ-endowed.
• $K_{1,n},C_{3n}(n\ge 2)$ are not symmetric γ-endowed.

Observation 3.

A graph H is symmetric γ-endowed if and only H is well-dominated.

Proof. 

Let H be well-dominated. Then, we have $\Gamma \left(H\right)=\gamma \left(H\right).$ Let T be any DS of H of cardinality $k\ge \gamma \left(H\right).$ Then, D contains a minimal DS of $H.$ But, any minimal DS of H is a minimum DS of $H.$ Therefore, H is $(k,\gamma )$-endowed. Therefore, H is symmetric $\gamma$-endowed. Conversely, if H is symmetric $\gamma$-endowed then $\Gamma \left(H\right)=\gamma \left(H\right)$ and hence H is well-dominated. □

Proposition 6.

The polygon $C_n$ is symmetric γ-endowed if and only if $n=4,5,7,10$ and 13. Moreover, $\gamma \left(C_n\right)=\lceil \frac{n}{3}\rceil$ and ${\beta }_0\left(C_n\right)=\lfloor \frac{n}{2}\rfloor .$

Proof. 

If $n\cong 0(modk)$ and $n\ge 12,\lfloor \frac{n}{2}\rfloor -\lceil \frac{n}{3}\rceil \ge 2$ and hence there exists a DS of cardinality $\lceil \frac{n}{3}\rceil +1$ which does not contain a minimum DS. If $n\cong 1$ or 2 (mod k) and $n\ge 16,$ then $\lfloor \frac{n}{2}\rfloor -\lceil \frac{n}{3}\rceil \ge 2.$ There exists a DS of cardinality $\lceil \frac{n}{3}\rceil +1$ which does not contain a minimum DS. It can be easily verified that $C_6,C_9$ and $C_{12}$ are not $\gamma$-endowed. The same goes for $C_8,C_{11},$ and $C_{14}$. □

Observation 4.

A complete bipartite graph is not symmetric γ-endowed.

Lemma 1.

Let H be a simple graph in which $\Gamma \left(H\right)=\gamma \left(H\right)+1$. Suppose H is $\left(\right(\gamma +2),\gamma )$-endowed, then H is $(k,\gamma )$-endowed for all $k\ge \gamma \left(H\right)+2.$

Proof. 

Let T be a DS of H of cardinality $k\ge \gamma \left(H\right)+2.$ Then, T contains a minimal DS of H. Suppose D does not contain a minimal DS of $H.$ Then, T contains a $\Gamma \left(H\right)$-set S of $H.$ Since $\left|T\right|\ge \Gamma \left(H\right)+1,$ $|T-S|\ge 1.$ Let $u\in T-S.$ Then, $S\cup \left\{u\right\}$ is a DS of cardinality $\gamma \left(H\right)+2.$ By hypothesis, $S\cup \left\{u\right\}$ is $\gamma$-endowed. There exists a $\gamma$-endowed set, say $T_1$, which is contained in $S\cup \left\{u\right\}$ and hence contained in $T.$ □

As a converse to Lemma 1, we have:

Lemma 2.

Let H be a simple graph which is not well-dominated. Suppose H is $(k,\gamma )$-endowed for all $k\ge \gamma \left(H\right)+2$ then $\gamma \left(H\right)=\Gamma \left(H\right)+1$.

Proof. 

Since H is $(k,\gamma )$-endowed for all $k\ge \gamma \left(H\right)+2,$ $\Gamma \left(H\right)=\gamma \left(H\right)$ or $\gamma \left(H\right)+1.$ Since H is not well-dominated, $\gamma \left(H\right)\ne \Gamma \left(H\right).$ Therefore, $\Gamma \left(H\right)=\gamma \left(H\right)+1.$ □

Proposition 7.

Let H be a simple graph. H is $(k,\gamma )$-endowed for all k except $k=\gamma \left(H\right)+1$ if and only if $\Gamma \left(H\right)=\gamma \left(H\right)+1$ and H is $(\gamma +2,\gamma )$-endowed.

Proof. 

If $\Gamma \left(H\right)=\gamma \left(H\right)+1$ and H is $(\gamma +2,\gamma )$-endowed then by the Lemma 2, H is $(k,\gamma )$-endowed for all k except $k=\gamma \left(H\right)+1.$

Conversely, if H is $(k,\gamma )$-endowed for all $k,\gamma \left(H\right)\le k\le n$ except for $k=\gamma \left(H\right)+1,$ then $\Gamma \left(H\right)=\gamma \left(H\right)+1$ and clearly H is $\left(\right(\gamma +2),\gamma )$-endowed. □

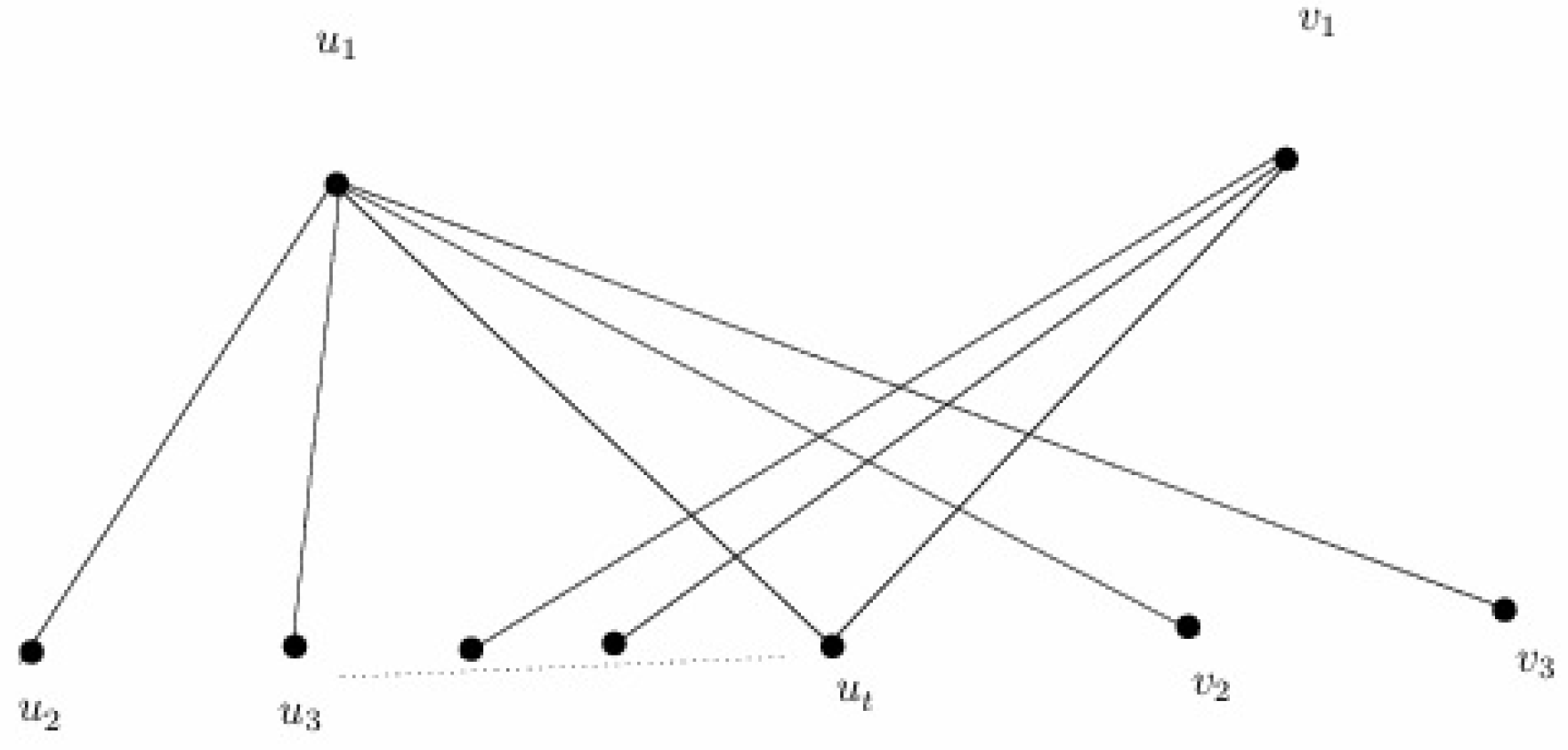
Remark 12.

There are graphs in which $\Gamma \left(H\right)=\gamma \left(H\right)+1$ and H is not $\left(\right(\gamma \left(H\right)+2),\gamma )$-endowed. For a graph H in Figure 8, consider that $\{u_1,u_2\}$ is the unique minimum DS of H Moreover, $\{u_2,u_4,u_6\},\{u_1,u_3,u_5\},\{u_3,u_5,u_6\},\{u_4,u_5,u_6\}$ are Γ-sets of $H.$ Any four or five element DS of H contains either $\{u_1,u_2\}$ or any of the Γ-set of this graph is not $\left(\right(\gamma \left(H\right)+2),\gamma )$-endowed since $\{u_3,u_4,u_5,u_6\}$ is a DS of cardinality $4=\gamma \left(H\right)+2$ and this set does not contain the unique minimum DS of $H.$

Figure 8. A graph in which any of the $\Gamma$-sets of this graph are not $\left(\right(\gamma \left(H\right)+2),\gamma )$-endowed.

Theorem 6.

Let H be a simple graph which is $(k,\gamma )$-endowed for all k except $k=\gamma \left(H\right)+1.$ Then, for any $\gamma \left(H\right)$- set T of H and for any $u\in V-T,$ the existence of two vertices $v_1,v_2\in T$ is ensured, satisfying $pn[\{v_1,v_2\},T]\subset N\left(u\right).$

Proof. 

By hypothesis, $\Gamma \left(H\right)=\gamma \left(H\right)+1.$ Let D be a $\gamma \left(H\right)$- set of $H.$ Then, by using the hypothesis that “$T\cup \left\{u\right\}$ is a DS”, we obtain that H contains a $\gamma$-endowed set, say $T_1$. We have that $T_1=(T-\{v_1,v_2\})\cup \left\{u\right\}$ where $v_1,v_2\in T$ that is, for any $u\in V-T$. This implies that there exists two vertices $v_1,v_2\in T$ such that $pn[\{v_1,v_2\},T]\subset N\left(u\right).$ □

Example 7.

Consider the graph H in Figure 9. The sets $\{u_2,u_4\},\{u_2,u_1\},\{u_2,u_3\},\{u_4,u_5\}$ are the γ-endowed sets of H. $T=\{u_1,u_3,u_5\}$ is a $\gamma \left(H\right)$- set of $H.$ $u_2,u_4\in V-T.$ $T_1=\{u_1,u_2\}$ is a γ-endowed set of $H.$ $T_2=\{u_4,u_5\}$ is a γ-endowed set of $H.$ Moreover, $pn[\{u_3,u_5\},T]=\{u_3,u_5\}\subset N\left(u\right).$

Figure 9. The graph H with $pn[\{u_1,u_3\},T]=\{u_1,u_3\}\subset N\left(u\right)$.

Example 8.

There exists a graph H with $\Gamma \left(H\right)=\gamma \left(H\right)+3$ and H is $\left(\gamma \right(H)+2,\gamma )$-endowed. See Figure 10.

Figure 10. The graph H is $\left(\gamma \right(H)+2,\gamma )$-endowed.

Let $H=K_{1,4},\gamma \left(H\right)=1,\Gamma \left(H\right)=4.$ Therefore $\Gamma \left(H\right)=\gamma \left(H\right)+3.$ Any DS of cardinality D with $\left|D\right|\le 3$ containing the central vertex is, in fact, a minimum DS. Therefore, H is $(k,\gamma )$-endowed for $k=1,2,3$ and 5. Therefore, H is $(\gamma +2,\gamma )$-endowed.

Example 9.

In $K_{2,5}$, we have $\gamma \left(H\right)=2,\Gamma \left(H\right)=5$ and H is $(k,\gamma )$-endowed for all $k,2\le k\le 7$ except when $k=5.$ In this graph, we have $\Gamma \left(H\right)=\gamma \left(H\right)+3$ and H is $(\gamma +2,\gamma )$-endowed.

6. Application of $\gamma$ in QSPR Models

This section investigates a significant applicability of the upper domination number within the context of QSPR studies of benzenoid hydrocarbons (BHs).

The total $\pi$-electron ($E_{\pi }$) energy in BHs that can be modelled through structure–property relationships has emerged as an active research field. Notably, Luči’c et al. [39] demonstrated a close interrelation between product/sum-connectivity descriptors, which exhibit significant accuracy in predicting $E_{\pi }$ for BHs. Their study focused on a selection of 30 BHs as test molecules. Subsequently, their work was expanded by Luči’c et al. to encompass generalized versions of these connectivity descriptors denoted as ${\chi }_{\alpha }$ and ${\chi }_{\alpha }^s$, identifying optimal values (${\chi }_{-0.2661}$ and ${\chi }_{-0.5601}^s$) that offer superior predictive capabilities for $E_{\pi }$ in BHs. Furthermore, Hayat and coauthors [40] (and Hayat et al. [41]) investigated the estimation ability of valency-related (and distance-dependent) indices commonly observed in BHs. For insights into the effectiveness of eigenvalue-dependent spectral descriptors in $E_{\pi }$ prediction for BHs, readers are directed to [42,43]. Additionally, recent advancements in QSPR models for chemical/physical characteristics in biomolecular networks as well as nano-structures have been discussed in [44,45,46,47,48]. For the predictive potential of graphical indices for thermodynamic properties of benzenoid hydrocarbons, we refer the reader to [49,50,51,52]. For the structure–property modeling of different chemical properties of a specific set of test molecules, the reader is referred to [53,54,55].

In a recent work, Khan [34] carried out a comparison analysis of seven domination-dependent graphical descriptors (excluding $\Gamma$), aiming to establish correlations with the $E_{\pi }$ of lower BHs. Among these parameters, the work by Khan [34] showcased that the paired-domination number ${\gamma }_p$ exhibits the most significant capability, showing a high correlation number of $\rho =0.9967$. The following question was raised by concluding the investigation.

Problem 7.

Find a domination-dependent graphical descriptor γ for which the correlation coefficient $\rho (E_{\pi },\gamma )$ of lower BHs exceeds $\rho >0.9967$?

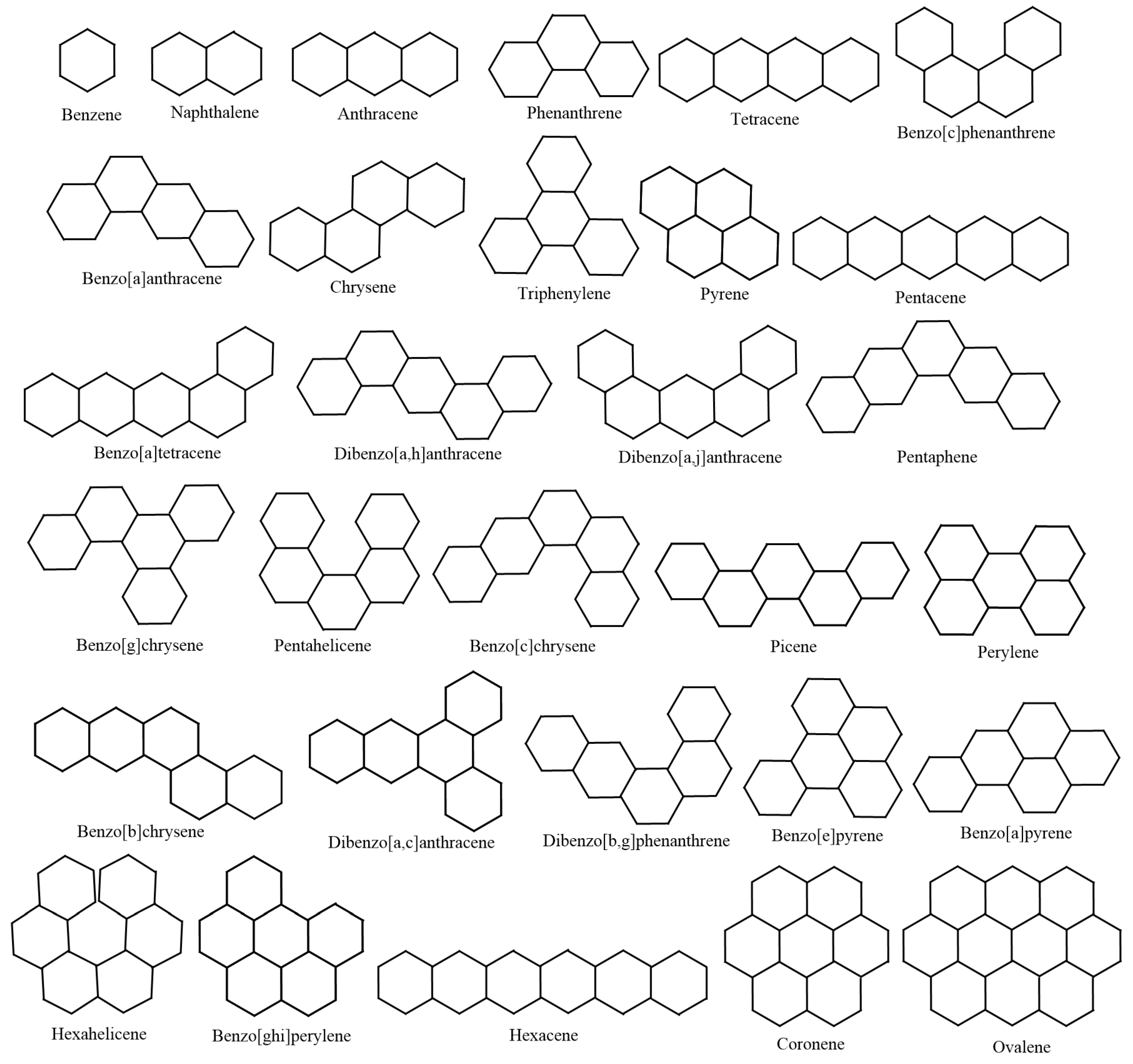
This section addresses Problem 7 and demonstrates that the upper domination number $\Gamma$ yields an enhanced correlative capability, with $E_{\pi }$ of BHs exhibiting $\rho (E_{\pi },\Gamma )=0.99905>0.9967$. To demonstrate this, 30 lower BHs as suggested by Khan [34] were opted. Figure 11 displays the BHs investigated in this analysis.

Figure 11. Graphical structures of the test molecules which have been considered.

Subsequently, we determine the locating–dominating number $\Gamma$ for the 30 BHs depicted in Figure 11. The values of the locating–dominating number $\Gamma$ and $E_{\pi }\left(\beta \right)$, measured in units of $\beta$, are presented in Table 1 for the 30 lower BHs shown in Figure 11. Utilizing Table 1’s data, we conducted thorough regression and correlation analyses. Initially, the correlation coefficient valuing $\rho =0.99905$ was calculated, which is considerably higher than the minimum value of $\rho =0.9967$. Subsequently, a comprehensive statistical data investigation was carried out. The most significant data-fitting regression model suggested by data analysis is linear. The subsequent details include a regression equation with 95% estimated confidence values and other important statistical values derived from Table 1.

$$E_{\pi }\left(\beta \right)=2.{911}_{\pm 0.0490}\Gamma -1.{003}_{\pm 0.5066},\rho =0.99905,s=0.3134,r^2=0.9981.$$

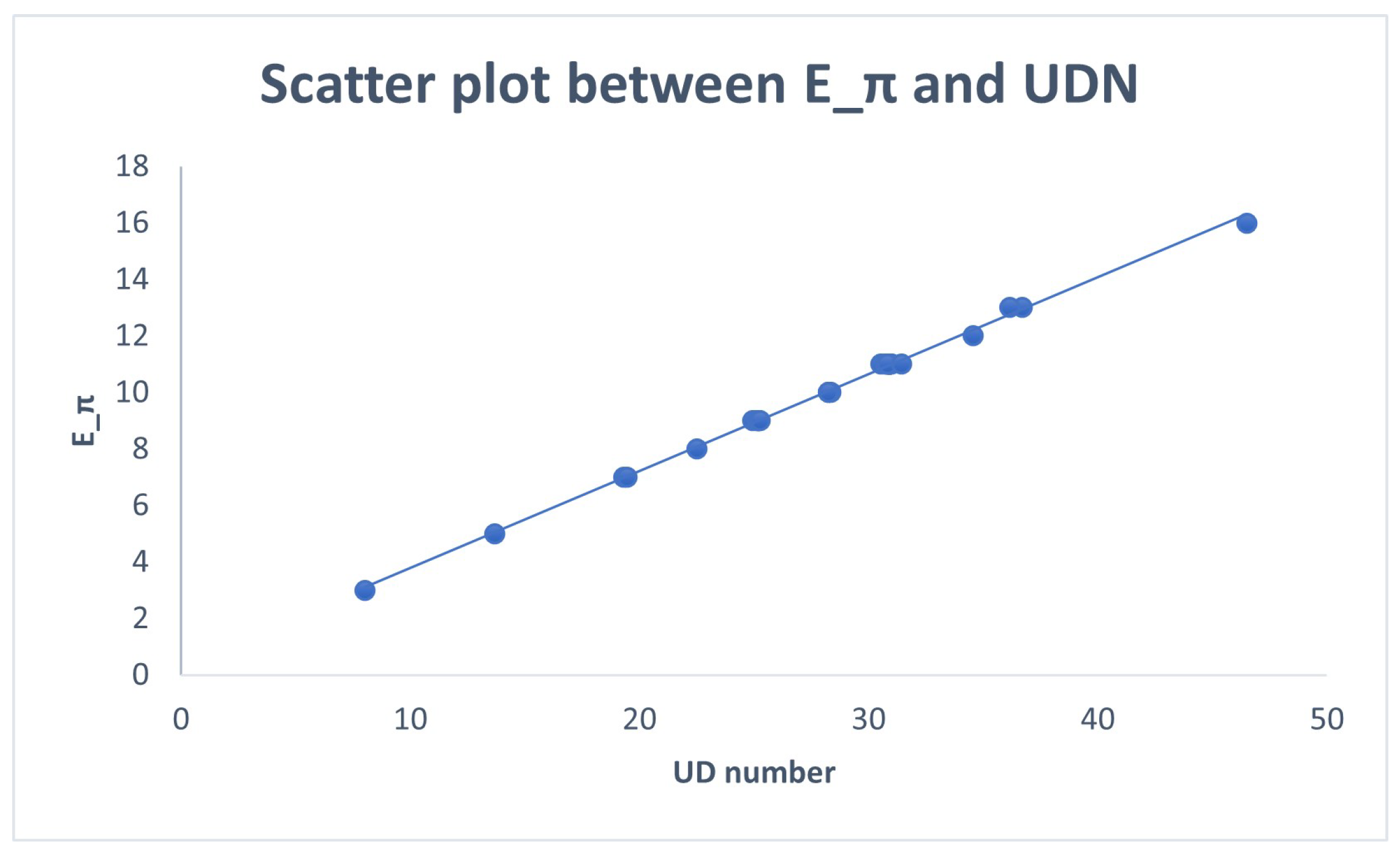
Subsequently, we present the scatter plot depicting the relationship between $\Gamma$ and $E_{\pi }$ for 30 lower BHs. Refer to Figure 12.

Figure 12. Scatter plot for $\Gamma$ and $E_{\pi }$ for 30 lower BHs.

Table 1. $E_{\pi }\left(\beta \right)$ and the upper domination number of 30 lower BHs (View Figure 11).

Molecule	${\mathit{E}}_{\mathit{\pi }}\left(\mathit{\beta }\right)$	$\mathit{\Gamma }$
Benzene	8	3
Naphthalene	13.6832	5
Phenanthrene	19.4483	7
Anthracene	19.3137	7
Pyrene	22.5055	9
Tetracene	24.9308	9
Benzo[a]anthracene	25.1012	9
Benzo[c]phenanthrene	25.1875	9
Chrysene	25.1922	9
Triphenylene	25.2745	9
Benzo[e]pyrene	28.3361	10
Perylene	28.2453	10
Benzo[a]pyrene	28.222	10
Benzo[a]tetracene	30.7255	11
Pentacene	30.544	11
Benzo[ghi]perylene	31.4251	11
Dibenzo[a,j]anthracene	30.8795	11
Dibenzo[a,h]anthracene	30.8805	11
Benzo[g]chrysene	30.999	11
Pentaphene	30.7627	11
Benzo[c]chrysene	30.9386	11
Pentahelicene	30.9362	11
Benzo[b]chrysene	30.839	11
Picene	30.9432	11
Dibenzo[b,g]phenanthrene	30.8336	11
Dibenzo[a,c]anthracene	30.9418	11
Coronene	34.5718	12
Hexacene	36.1557	13
Hexahelicene	36.6814	13
Ovalene	46.4974	16

Table 1. $E_{\pi }\left(\beta \right)$ and the upper domination number of 30 lower BHs (View Figure 11).

Molecule	${\mathit{E}}_{\mathit{\pi }}\left(\mathit{\beta }\right)$	$\mathit{\Gamma }$
Benzene	8	3
Naphthalene	13.6832	5
Phenanthrene	19.4483	7
Anthracene	19.3137	7
Pyrene	22.5055	9
Tetracene	24.9308	9
Benzo[a]anthracene	25.1012	9
Benzo[c]phenanthrene	25.1875	9
Chrysene	25.1922	9
Triphenylene	25.2745	9
Benzo[e]pyrene	28.3361	10
Perylene	28.2453	10
Benzo[a]pyrene	28.222	10
Benzo[a]tetracene	30.7255	11
Pentacene	30.544	11
Benzo[ghi]perylene	31.4251	11
Dibenzo[a,j]anthracene	30.8795	11
Dibenzo[a,h]anthracene	30.8805	11
Benzo[g]chrysene	30.999	11
Pentaphene	30.7627	11
Benzo[c]chrysene	30.9386	11
Pentahelicene	30.9362	11
Benzo[b]chrysene	30.839	11
Picene	30.9432	11
Dibenzo[b,g]phenanthrene	30.8336	11
Dibenzo[a,c]anthracene	30.9418	11
Coronene	34.5718	12
Hexacene	36.1557	13
Hexahelicene	36.6814	13
Ovalene	46.4974	16

7. Conclusions

The concept of $(k,\gamma )$-endowed graphs has been put forward. Furthermore, we characterized the graphs with unique minimum D-sets. In the last section, we introduced and studied symmetric $\gamma$-endowed graphs. In the second part of the paper, we found a domination-based parameter which showcases a correlation value of $\rho =0.99905$ with $E_{\pi }\left(\beta \right)$ of lower BHs, thus answering an open problem in [34]. The following problems are naturally raised from the findings of this study.

• Open Problems:

Problem 8.

Characterize graphs such that H is $(k,\gamma )$-endowed for all $k,$ satisfying $\gamma \left(H\right)\le k\le \gamma \left(H\right)-1$ and not $(k,\gamma )$-endowed for all k with $\gamma \left(H\right)\le k\le n-1.$

Problem 9.

Characterize graphs H with $\gamma \left(H\right)=\gamma \left(H\right)+1$ such that H is not $(k,\gamma )$-endowed for all $k,$ $\gamma \left(H\right)\le k\le n-1.$

The search for identifying the optimal domination-related parameter to predict $E_{\pi }\left(\beta \right)$ is still ongoing. Therefore, we encounter the following issue.

Problem 10.

Find a graphical descriptor γ for which the correlation coefficient $\rho (E_{\pi },\gamma )$ of BHs exceeds $\rho =0.99905$?