Strange Things in Bottom-to-Strange Decays: The Standard Model Turned Upside Down?
Abstract
1. Introduction
2. Theoretical Formalism
3. Experimental Aspects
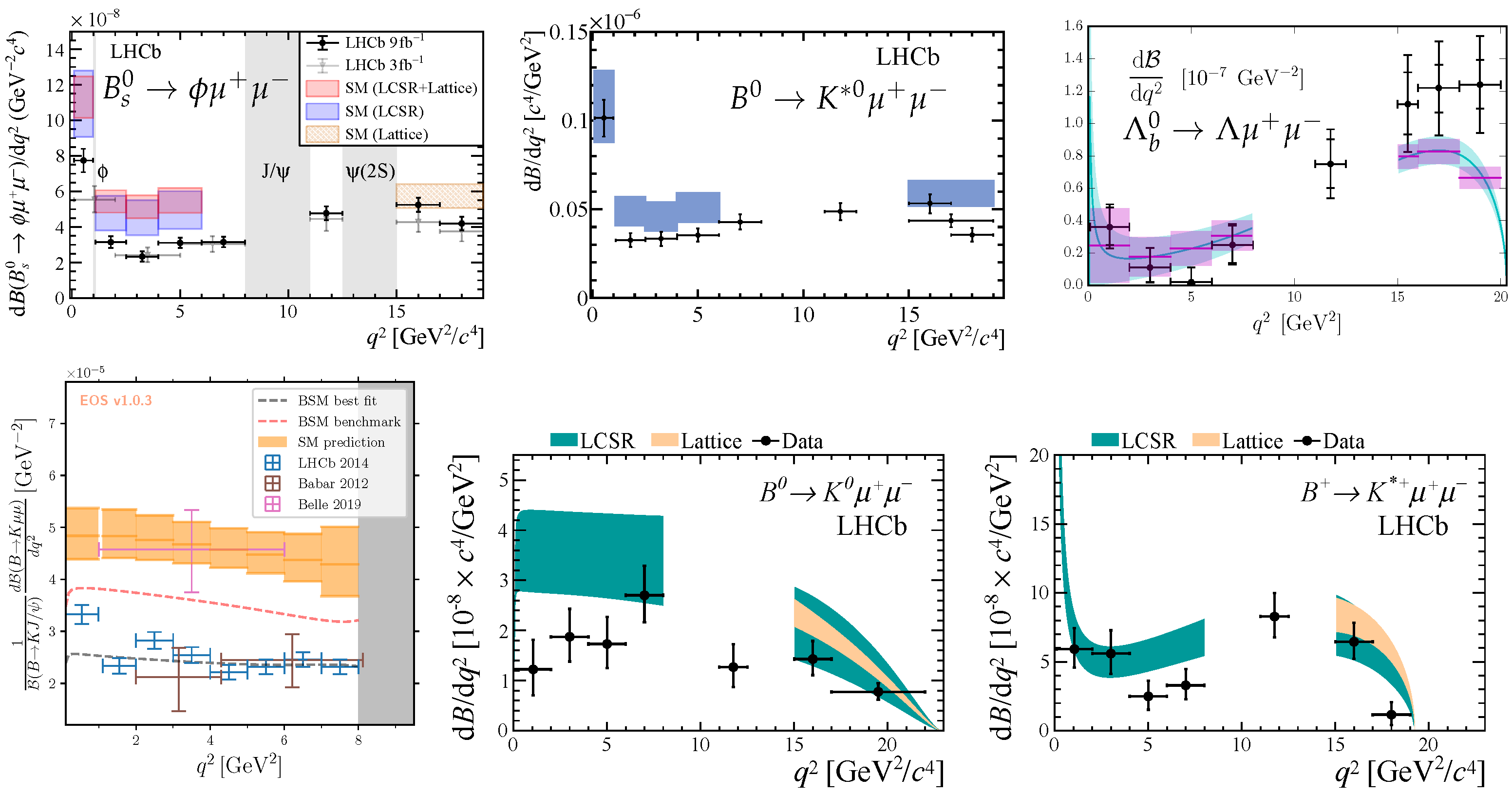
4. Branching Fraction Measurements
5. Angular Analyses
5.1. Binned Angular Analyses
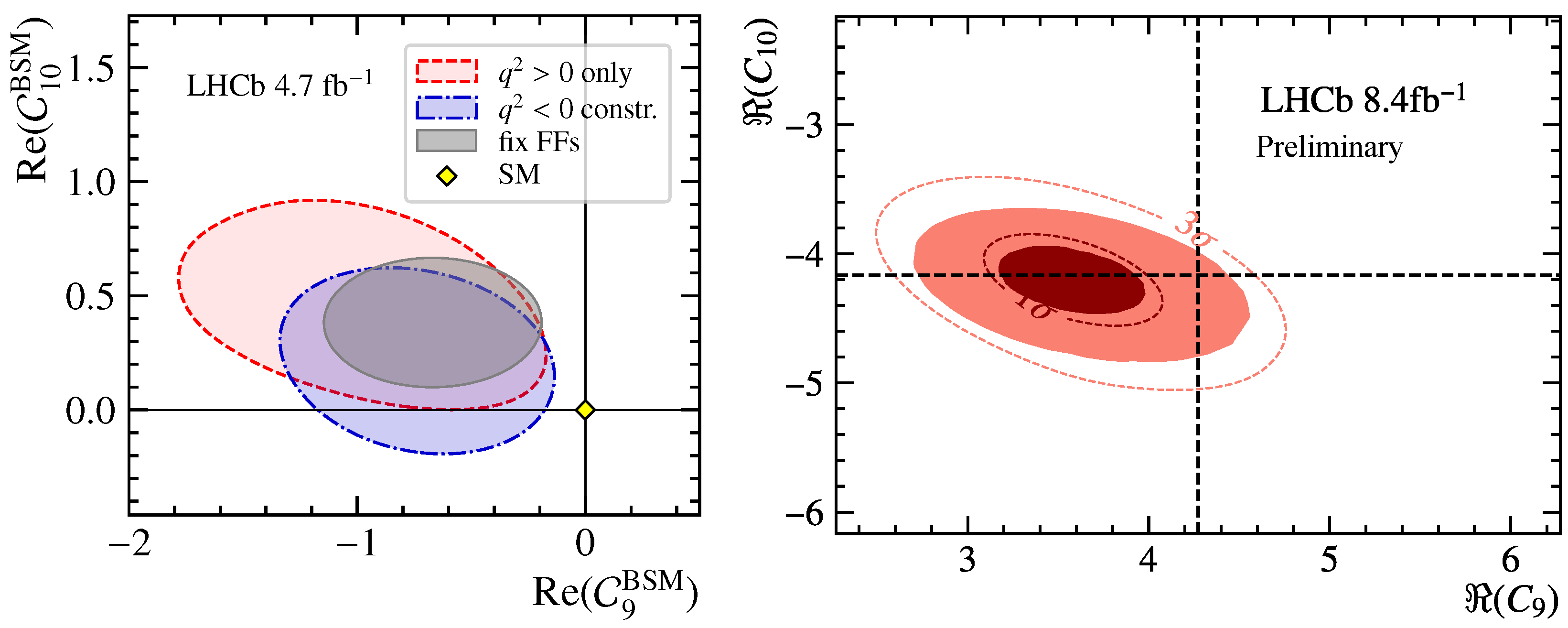
5.2. Unbinned Angular Analyses
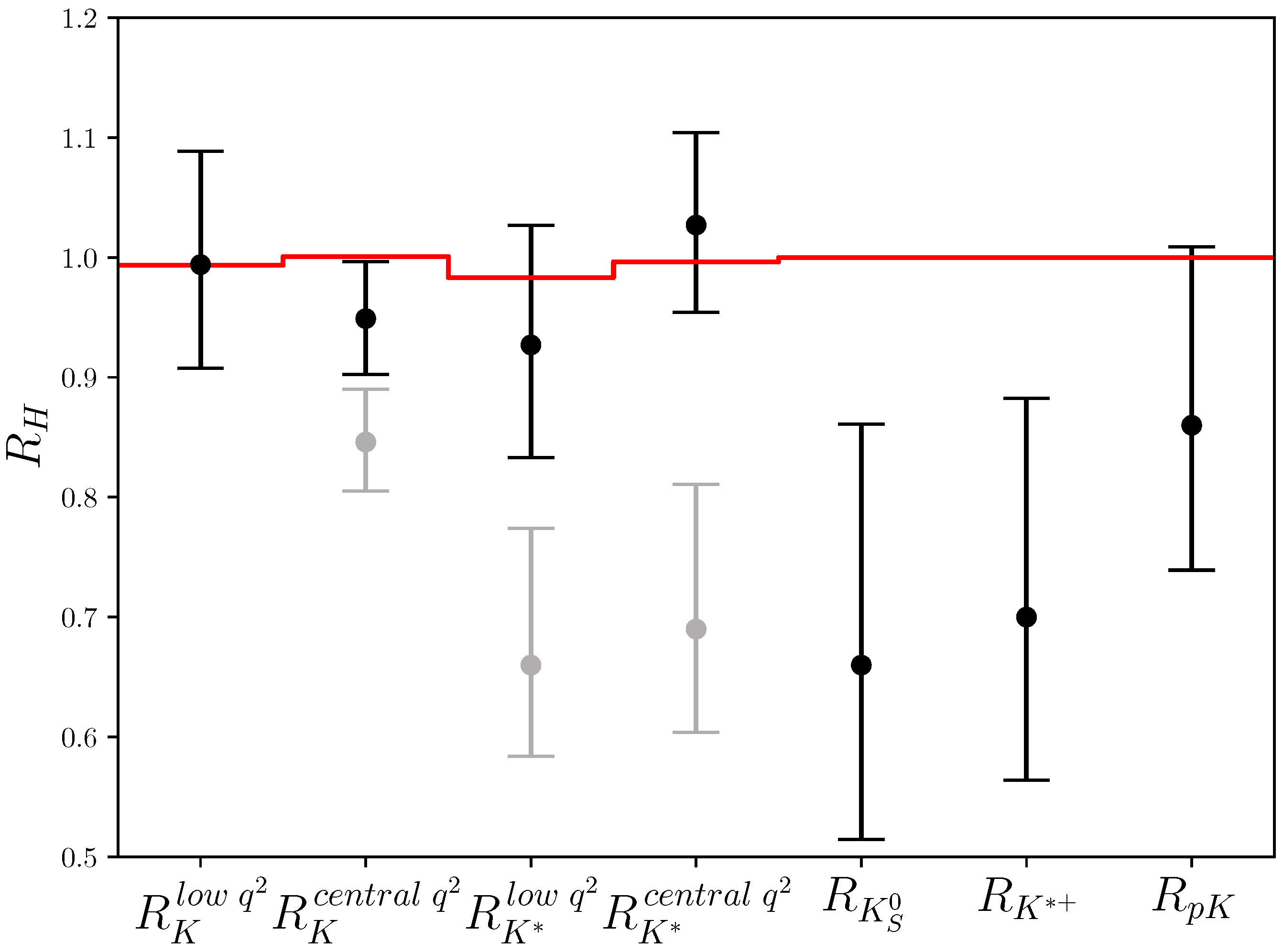
6. Tests of Lepton Flavour Universality
7. Discussion
8. Future Directions and Conclusions
- The new physics models put forward for explaining the anomalies predict a two-order of magnitude enhancement of the decay rate relative to the SM [68]. This prediction originates from connecting the anomalies with LFU tests in and decays that exhibit a tension with SM predictions [69,70,71,72,73,74,75,76,77]. Searches for processes are challenging at LHCb due to the presence of neutrinos stemming from the subsequent decays even for much-enhanced signal decay rates. The Belle II experiment is ideally suited for such measurements owing to the knowledge of the collision energy and the hermetic detector design that allows for the detection of the presence of neutrinos through missing energy in the collision.
- Larger datasets will also enable precise measurements of new physics effects that give rise to violation in transitions. By analysing and decays separately, searches for complex-valued Wilson coefficients, and therefore sources of violation beyond the SM, can be pursued. The presence of a significant violation in transitions would be a clear indication of new physics.
- Angular analyses of and similar decays in ever-narrowing bins of can provide significant insight into the potential effect of hadronic contributions. New-physics effects in should be consistent across different bins, in contrast to potential unaccounted hadronic effects. Similarly, new-physics effects in should be consistent across different helicity amplitudes, in contrast to amplitudes [78]. Measurements in small bins with high precision from the current and future runs of the LHC therefore have the potential to decouple new physics from unaccounted hadronic effects.
- Decays mediated via transitions have an extra suppression (CKM suppression) in the SM with respect to their counterpart. This additional suppression makes transitions even more sensitive probes of new physics and stand to benefit the most from the large datasets collected over the following decades. If the deviations in transitions are due to new physics with different quark couplings compared to the SM (i.e., not minimally flavour-violating), then large effects may be present in transition. So far, only two modes have been observed [79,80]. Additional data will allow for a broad physics program of measurements, including angular analyses, LFU tests, and violation measurements. Testing the different amounts of violation between and decays can provide useful input on potential unaccounted contributions owing to an approximate SM symmetry between and amplitudes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SM | Standard Model |
| FCNC | Flavour-Changing Neutral Current |
| LHC | Large Hadron Collider |
| CKM | Cabbibo–Kobayashi–Maskawa |
| QCD | Quantum Chromodynamics |
| LFU | Lepton Flavour Universality |
References
- Glashow, S.L.; Iliopoulos, J.; Maiani, L. Weak Interactions with Lepton-Hadron Symmetry. Phys. Rev. D 1970, 2, 1285–1292. [Google Scholar] [CrossRef]
- Albrecht, H.; Andam, A.; Binder, U.; Böckmann, P.; Gläser, R.; Harder, G.; Nippe, A.; Schäfer, M.; Schmidt-Parzefall, W.; Schröder, H.; et al. Observation of B0-B0 Mixing. Phys. Lett. B 1987, 192, 245–252. [Google Scholar] [CrossRef]
- Tumasyan, A.; Adam, W.; Andrejkovic, J.; Bergauer, T.; Chatterjee, S.; Damanakis, K.; Dragicevic, M.; Escalante Del Valle, A.; Hussain, P.; Jeitler, M.; et al. Measurement of the →μ+μ− decay properties and search for the B0→μ+μ− decay in proton-proton collisions at = 13 TeV. Phys. Lett. B 2023, 842, 137955. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Measurement of the →μ+μ− decay properties and search for the B0→μ+μ− and →μ+μ−γ decays. Phys. Rev. D 2022, 105, 012010. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abbott, D.C.; Abdinov, O.; Abeloos, B.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; et al. Study of the rare decays of and B0 mesons into muon pairs using data collected during 2015 and 2016 with the ATLAS detector. J. High Energy Phys. 2019, 2019, 98. [Google Scholar] [CrossRef]
- Altmannshofer, W.; Straub, D.M. New physics in b→s transitions after LHC run 1. Eur. Phys. J. C 2015, 75, 382. [Google Scholar] [CrossRef]
- Beaujean, F.; Bobeth, C.; van Dyk, D. Comprehensive Bayesian analysis of rare (semi)leptonic and radiative B decays. Eur. Phys. J. C 2014, 74, 2897, Erratum in Eur. Phys. J. C 2014, 74, 3179. [Google Scholar] [CrossRef] [PubMed]
- Descotes-Genon, S.; Matias, J.; Virto, J. Understanding the B→K*μ+μ− Anomaly. Phys. Rev. D 2013, 88, 074002. [Google Scholar] [CrossRef]
- Algueró, M.; Capdevila, B.; Descotes-Genon, S.; Matias, J.; Novoa-Brunet, M. b→sℓ+ℓ− global fits after RKS and RK*+. Eur. Phys. J. C 2022, 82, 326. [Google Scholar] [CrossRef]
- Algueró, M.; Biswas, A.; Capdevila, B.; Descotes-Genon, S.; Matias, J.; Novoa-Brunet, M. To (b)e or not to (b)e: No electrons at LHCb. Eur. Phys. J. C 2023, 83, 648. [Google Scholar] [CrossRef]
- Descotes-Genon, S.; Hurth, T.; Matias, J.; Virto, J. Optimizing the basis of B→K*ll observables in the full kinematic range. J. High Energy Phys. 2013, 2013, 137. [Google Scholar] [CrossRef]
- Hiller, G.; Kruger, F. More model-independent analysis of b→s processes. Phys. Rev. D 2004, 69, 074020. [Google Scholar] [CrossRef]
- Khodjamirian, A.; Mannel, T.; Pivovarov, A.A.; Wang, Y.M. Charm-loop effect in B→K(*)ℓ+ℓ− and B→K*γ. J. High Energy Phys. 2010, 2010, 89. [Google Scholar] [CrossRef]
- Alves, A.A.; Andrade, L.M.; Barbosa-Ademarlaudo, F.; Bediaga, I.; Cernicchiaro, G.; Guerrer, G.; Lima, H.P.; Machado, A.A.; Magnin, J.; Marujo, F.; et al. The LHCb Detector at the LHC. JINST 2008, 3, S08005, Also published by CERN Geneva in 2010. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Hmayakyan, G.; Khachatryan, V.; Sirunyan, A.M.; Adolphi, R.; Anagnostou, G.; Brauer, R.; Braunschweig, W.; Esser, H.; Feld, L.; et al. The CMS experiment at the CERN LHC. The Compact Muon Solenoid experiment. JINST 2008, 3, S08004, Also published by CERN Geneva in 2010. [Google Scholar] [CrossRef]
- Aad, G.; Bentvelsen, S.; Bobbink, G.J.; Bos, K.; Boterenbrood, H.; Brouwer, G.; Buis, E.J.; Buskop, J.J.F.; Colijn, A.P.; Dankers, R.; et al. The ATLAS Experiment at the CERN Large Hadron Collider. JINST 2008, 3, S08003, Also published by CERN Geneva in 2010. [Google Scholar] [CrossRef]
- Kou, E.; Urquijo, P.; Altmannshofer, W.; Beaujean, F.; Bell, G.; Beneke, M.; Bigi, I.I.; Bishara, F.; Blanke, M.; Bobeth, C.; et al. The Belle II Physics Book. Prog. Theor. Exp. Phys. 2019, 2019, 123C01. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Measurements of the S-wave fraction in B0→K+π−μ+μ− decays and the B0→K*(892)0μ+μ− differential branching fraction. J. High Energy Phys. 2016, 2016, 47, Erratum in J. High Energy Phys. 2017, 2017, 142. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Differential branching fractions and isospin asymmetries of B→K(*)μ+μ− decays. J. High Energy Phys. 2014, 2014, 133. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Branching Fraction Measurements of the Rare →ϕμ+μ− and → (1525)μ+μ−-Decays. Phys. Rev. Lett. 2021, 127, 151801. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Differential branching fraction and angular analysis of →Λμ+μ− decays. J. High Energy Phys. 2015, 2015, 115, Erratum in J. High Energy Phys. 2018, 2018, 145. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Angular analysis of the decay B0→K*0μ+μ− from pp collisions at = 8 TeV. Phys. Lett. B 2016, 753, 424–448. [Google Scholar] [CrossRef]
- Aubert, B.; Barate, R.; Bona, M.; Boutigny, D.; Couderc, F.; Karyotakis, Y.; Lees, J.; Poireau, V.; Tisserand, V.; Zghiche, A.; et al. Measurements of branching fractions, rate asymmetries, and angular distributions in the rare decays B→Kℓ+ℓ− and B→K*ℓ+ℓ−. Phys. Rev. D 2006, 73, 092001. [Google Scholar] [CrossRef]
- Hayrapetyan, A.; Erbacher, R.; Carrillo Montoya, C.A.; Newbold, D.M.; Carvalho, W.; Karunarathna, N.; Górski, M.; Sommerhalder, M.; Lindsey, C.; Parmar, N.; et al. Test of lepton flavor universality in B±→ K±μ+μ− and B±→ K±e+e− decays in proton-proton collisions at = 13 TeV. arXiv 2024, arXiv:2401.07090. [Google Scholar]
- Detmold, W.; Meinel, S. Λb→Λℓ+ℓ− form factors, differential branching fraction, and angular observables from lattice QCD with relativistic b quarks. Phys. Rev. D 2016, 93, 074501. [Google Scholar] [CrossRef]
- Gubernari, N.; Reboud, M.; van Dyk, D.; Virto, J. Improved theory predictions and global analysis of exclusive b→sμ+μ− processes. J. High Energy Phys. 2022, 2022, 133. [Google Scholar] [CrossRef]
- Bharucha, A.; Straub, D.M.; Zwicky, R. B→Vℓ+ℓ− in the Standard Model from light-cone sum rules. J. High Energy Phys. 2016, 2016, 98. [Google Scholar] [CrossRef]
- Horgan, R.R.; Liu, Z.; Meinel, S.; Wingate, M. Lattice QCD calculation of form factors describing the rare decays B→K*ℓ+ℓ− and Bs→ϕℓ+ℓ−. Phys. Rev. D 2014, 89, 094501. [Google Scholar] [CrossRef]
- Parrott, W.G.; Bouchard, C.; Davies, C.T.H. B→K and D→K form factors from fully relativistic lattice QCD. Phys. Rev. D 2023, 107, 014510. [Google Scholar] [CrossRef]
- Bobeth, C.; Hiller, G.; van Dyk, D. More Benefits of Semileptonic Rare B Decays at Low Recoil: CP Violation. J. High Energy Phys. 2011, 2011, 67. [Google Scholar] [CrossRef]
- Bobeth, C.; Hiller, G.; van Dyk, D.; Wacker, C. The Decay B→Kℓ+ℓ− at Low Hadronic Recoil and Model-Independent ΔB = 1 Constraints. J. High Energy Phys. 2012, 2012, 107. [Google Scholar] [CrossRef]
- Huber, T.; Hurth, T.; Jenkins, J.; Lunghi, E.; Qin, Q.; Vos, K.K. Phenomenology of inclusive →Xsℓ+ℓ− for the Belle II era. J. High Energy Phys. 2020, 2020, 88. [Google Scholar] [CrossRef]
- Iwasaki, M.; Itoh, K.; Aihara, H.; Abe, K.; Abe, K.; Adachi, I.; Asano, Y.; Aushev, T.; Bahinipati, S.; Bakich, A.M.; et al. Improved measurement of the electroweak penguin process B→Xsl+l−. Phys. Rev. D 2005, 72, 092005. [Google Scholar] [CrossRef]
- Lees, J.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.; Kolomensky, Y.G.; et al. Measurement of the B→Xsl+l− branching fraction and search for direct CP violation from a sum of exclusive final states. Phys. Rev. Lett. 2014, 112, 211802. [Google Scholar] [CrossRef]
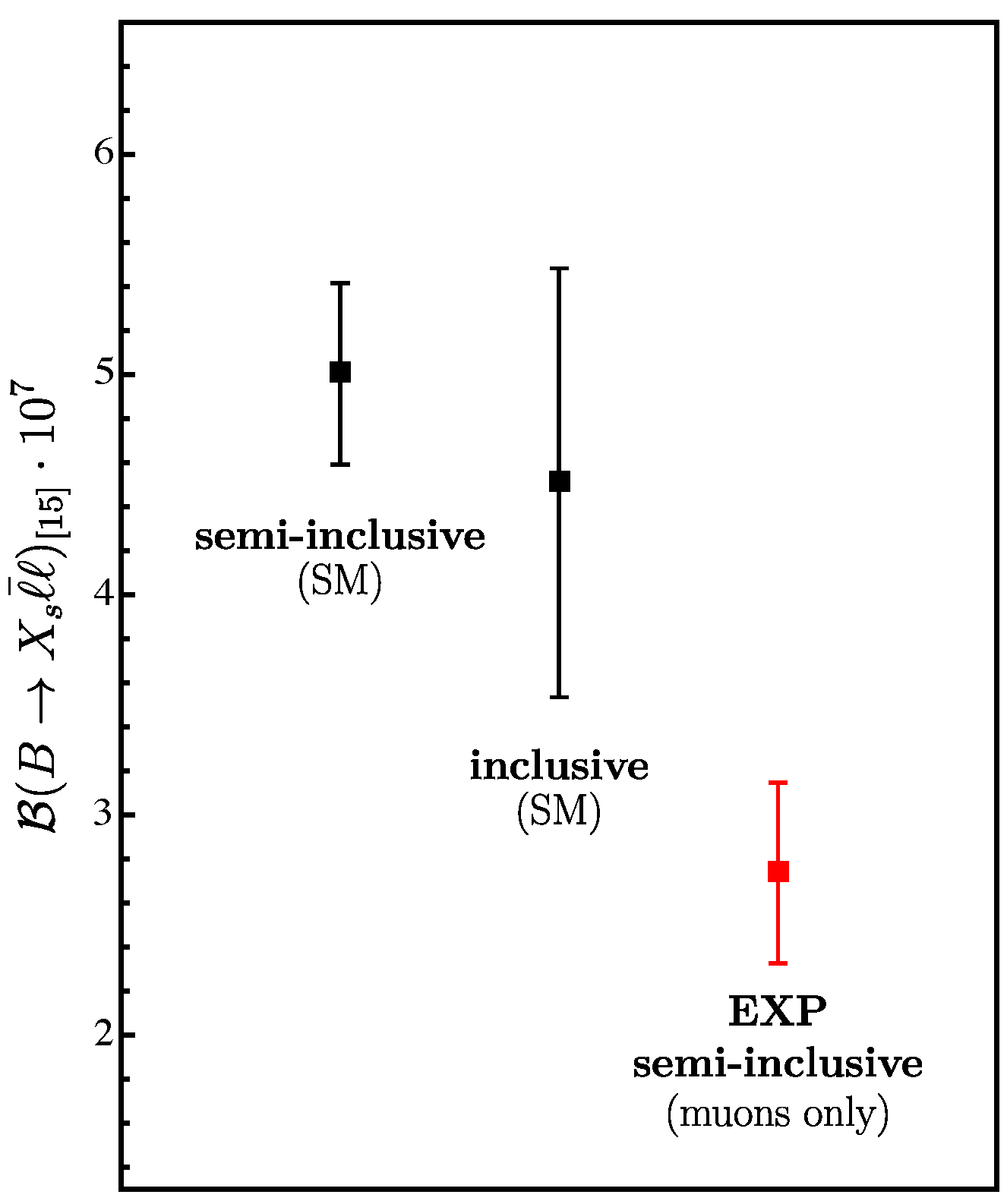
- Isidori, G.; Polonsky, Z.; Tinari, A. Semi-inclusive b→s transitions at high q2. arXiv 2023, arXiv:2305.03076. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Measurement of the phase difference between short- and long-distance amplitudes in the B+→K+μ+μ− decay. Eur. Phys. J. C 2017, 77, 161. [Google Scholar] [CrossRef]
- Adachi, I.; Adamczyk, K.; Aggarwal, L.; Ahmed, H.; Aihara, H.; Akopov, N.; Aloisio, A.; Ky, N.A.; Asner, D.; Atmacan, H.; et al. Evidence for B+→K+ Decays. arXiv 2023, arXiv:2311.14647. [Google Scholar]
- Parrott, W.G.; Bouchard, C.; Davies, C.T.H. Standard Model predictions for B→Kℓ+ℓ−, B→K and B→K using form factors from Nf = 2 + 1 + 1 lattice QCD. Phys. Rev. D 2023, 107, 014511, Erratum in Phys. Rev. D 2023, 107, 119903. [Google Scholar] [CrossRef]
- Chen, K.F.; Mombächer, T.; de Sanctis, U. Analysis of →μ+μ− decays at the LHC. arXiv 2024, arXiv:2402.09901. [Google Scholar]
- Frau, G.; Langenbruch, C. Charged Lepton-Flavour Violation. Symmetry 2024, 16, 359. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Measurement of CP-Averaged Observables in the B0→K*0μ+μ− Decay. Phys. Rev. Lett. 2020, 125, 011802. [Google Scholar] [CrossRef]
- Aaboud, M.; Angelozzi, I.; Bentvelsen, S.; Berge, D.; Bobbink, G.J.; Brenner, L.; Colijn, A.P.; de Groot, N.; de Jong, P.J.; Ferrari, P.; et al. Angular analysis of →K*μ+μ− decays in pp collisions at = 8 TeV with the ATLAS detector. J. High Energy Phys. 2018, 2018, 47. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Measurement of angular parameters from the decay B0→K*0μ+μ− in proton-proton collisions at = 8 TeV. Phys. Lett. B 2018, 781, 517–541. [Google Scholar] [CrossRef]
- Wehle, S.; Niebuhr, C.; Yashchenko, S.; Adachi, I.; Aihara, H.; Al Said, S.; Asner, D.; Aulchenko, V.; Aushev, T.; Ayad, R.; et al. Lepton-Flavor-Dependent Angular Analysis of B→K*ℓ+ℓ−. Phys. Rev. Lett. 2017, 118, 111801. [Google Scholar] [CrossRef] [PubMed]
- Aaij, R.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Strong constraints on the b→sγ photon polarisation from B0→K*0e+e− decays. J. High Energy Phys. 2020, 2020, 81. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Angular Analysis of the B+→K*+μ+μ− Decay. Phys. Rev. Lett. 2021, 126, 161802. [Google Scholar] [CrossRef] [PubMed]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Escalante Del Valle, A.; Fruehwirth, R.; Jeitler, M.; Krammer, N.; Lechner, L.; et al. Angular analysis of the decay B+→ K*(892)+μ+μ− in proton-proton collisions at = 8 TeV. J. High Energy Phys. 2021, 2021, 124. [Google Scholar] [CrossRef]
- Aaij, R.; Abdelmotteleb, A.S.W.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Agapopoulou, C.; Aidala, C.A.; Aiola, S.; et al. Angular analysis of the rare decay →ϕμ+μ−. J. High Energy Phys. 2021, 2021, 43. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Angular analysis of charged and neutral B→Kμ+μ− decays. J. High Energy Phys. 2014, 2014, 82. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Angular analysis of the decay B+→ K+μ+μ− in proton-proton collisions at = 8 TeV. Phys. Rev. D 2018, 98, 112011. [Google Scholar] [CrossRef]
- Descotes-Genon, S.; Hofer, L.; Matias, J.; Virto, J. On the impact of power corrections in the prediction of B→K*μ+μ− observables. J. High Energy Phys. 2014, 2014, 125. [Google Scholar] [CrossRef]
- Bobeth, C.; Chrzaszcz, M.; van Dyk, D.; Virto, J. Long-distance effects in B→K*ℓℓ from analyticity. Eur. Phys. J. C 2018, 78, 451. [Google Scholar] [CrossRef]
- Gubernari, N.; Reboud, M.; van Dyk, D.; Virto, J. Dispersive analysis of B → K(*) and Bs→ ϕ form factors. J. High Energy Phys. 2023, 2023, 153. [Google Scholar] [CrossRef]
- Aaij, R.; Abdelmotteleb, A.S.W.; Beteta, C.A.; Abudinén, F.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Adlarson, P.; Agapopoulou, C.; Aidala, C.A.; et al. Amplitude analysis of the B0→K*0μ+μ− decay. Phys. Rev. D 2023, 102, 112003. [Google Scholar] [CrossRef]
- Hadavizadeh, T. b→sℓℓ Decays at LHCb; Conference Talk on Behalf of the LHCb Collaboration Moriond QCD 2024. Available online: https://cds.cern.ch/record/2894566/files/Hadavizadeh.pdf (accessed on 9 May 2024).
- Aaij, R.; Abdelmotteleb, A.; Abellan Beteta, C.; Abudinén, F.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Adlarson, P.; Afsharnia, H.; Agapopoulou, C.; et al. Measurement of lepton universality parameters in B+→K+ℓ+ℓ− and B0→K*0ℓ+ℓ− decays. Phys. Rev. D 2023, 108, 032002. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Test of lepton universality in beauty-quark decays. Nat. Phys. 2022, 18, 277–282, Addendum: Nat. Phys. 2023, 19, 1517. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Test of lepton universality with →pK−ℓ+ℓ− decays. J. High Energy Phys. 2020, 2020, 40. [Google Scholar] [CrossRef]
- Aaij, R.; Abdelmotteleb, A.S.W.; Abellán Beteta, C.; Abudinén, F.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Agapopoulou, C.; Aidala, C.A.; et al. Tests of lepton universality using B0→ ℓ+ℓ− and B+→K*+ℓ+ℓ− decays. Phys. Rev. Lett. 2022, 128, 191802. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Test of lepton universality with B0→K*0ℓ+ℓ− decays. J. High Energy Phys. 2017, 2017, 55. [Google Scholar] [CrossRef]
- Wehle, S.; Adachi, I.; Adamczyk, K.; Aihara, H.; Asner, D.; Atmacan, H.; Aulchenko, V.; Aushev, T.; Ayad, R.; Babu, V.; et al. Test of Lepton-Flavor Universality in B→K*ℓ+ℓ− Decays at Belle. Phys. Rev. Lett. 2021, 126, 161801. [Google Scholar] [CrossRef]
- Lees, J.; Poireau, V.; Tisserand, V.; Tico, J.G.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.; et al. Measurement of Branching Fractions and Rate Asymmetries in the Rare Decays B→K(*)l+l−. Phys. Rev. D 2012, 86, 032012. [Google Scholar] [CrossRef]
- Choudhury, S.; Sandilya, S.; Trabelsi, K.; Giri, A.; Aihara, H.; Al Said, S.; Asner, D.; Atmacan, H.; Aulchenko, V.; Aushev, T.; et al. Test of lepton flavor universality and search for lepton flavor violation in B→Kℓℓ decays. J. High Energy Phys. 2021, 2021, 105. [Google Scholar] [CrossRef]
- Hurth, T.; Mahmoudi, F.; Neshatpour, S. B anomalies in the post RK(*) era. Phys. Rev. D 2023, 108, 115037. [Google Scholar] [CrossRef]
- Greljo, A.; Salko, J.; Smolkovič, A.; Stangl, P. Rare b decays meet high-mass Drell-Yan. J. High Energy Phys. 2023, 2023, 87. [Google Scholar] [CrossRef]
- Isidori, G.; Lancierini, D.; Owen, P.; Serra, N. On the significance of new physics b→sℓ+ℓ− decays. Phys. Lett. B 2021, 822, 136644. [Google Scholar] [CrossRef]
- Ciuchini, M.; Fedele, M.; Franco, E.; Paul, A.; Silvestrini, L.; Valli, M. Constraints on lepton universality violation from rare B decays. Phys. Rev. D 2023, 107, 055036. [Google Scholar] [CrossRef]
- Capdevila, B.; Crivellin, A.; Descotes-Genon, S.; Hofer, L.; Matias, J. Searching for New Physics with b→sτ+τ− processes. Phys. Rev. Lett. 2018, 120, 181802. [Google Scholar] [CrossRef] [PubMed]
- Lees, J.; Poireau, V.; Tisserand, V.; Tico, J.G.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.; et al. Evidence for an excess of →D(*)τ−τ decays. Phys. Rev. Lett. 2012, 109, 101802. [Google Scholar] [CrossRef] [PubMed]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; Kolomensky, Y.G.; et al. Measurement of an excess of →D(*)τ−τ decays and implications for charged Higgs bosons. Phys. Rev. D 2013, 88, 072012. [Google Scholar] [CrossRef]
- Sato, Y.; Iijima, T.; Adamczyk, K.; Aihara, H.; Asner, D.; Atmacan, H.; Aushev, T.; Ayad, R.; Aziz, T.; Babu, V.; et al. Measurement of the branching ratio of 0→D*+τ−τ relative to 0→D*+ℓ−ℓ decays with a semileptonic tagging method. Phys. Rev. D 2016, 94, 072007. [Google Scholar] [CrossRef]
- Huschle, M.; Kuhr, T.; Heck, M.; Goldenzweig, P.; Abdesselam, A.; Adachi, I.; Adamczyk, K.; Aihara, H.; Al Said, S.; Arinstein, K.; et al. Measurement of the branching ratio of →D(*)τ−τ relative to →D(*)ℓ−ℓ decays with hadronic tagging at Belle. Phys. Rev. D 2015, 92, 072014. [Google Scholar] [CrossRef]
- Caria, G.; Urquijo, P.; Adachi, I.; Aihara, H.; Said, S.A.; Asner, D.; Atmacan, H.; Aushev, T.; Babu, V.; Badhrees, I.; et al. Measurement of (D) and (D*) with a semileptonic tagging method. Phys. Rev. Lett. 2020, 124, 161803. [Google Scholar] [CrossRef] [PubMed]
- Hirose, S.; Iijima, T.; Adachi, I.; Adamczyk, K.; Aihara, H.; Al Said, S.; Asner, D.; Atmacan, H.; Aushev, T.; Ayad, R.; et al. Measurement of the τ lepton polarization and R(D*) in the decay →D*τ−τ with one-prong hadronic τ decays at Belle. Phys. Rev. D 2018, 97, 012004. [Google Scholar] [CrossRef]
- Aaij, R.; Abdelmotteleb, A.S.W.; Beteta, C.A.; Abudinén, F.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Adlarson, P.; Afsharnia, H.; Agapopoulou, C.; et al. Test of lepton flavor universality using B0→D*−τ+ντ decays with hadronic τ channels. Phys. Rev. D 2023, 108, 012018. [Google Scholar] [CrossRef]
- Aaij, R.; Abdelmotteleb, A.S.; Beteta, C.A.; Abudinén, F.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Adlarson, P.; Afsharnia, H.; Agapopoulou, C.; et al. Measurement of the ratios of branching fractions (D*) and (D0). Phys. Rev. Lett. 2023, 131, 111802. [Google Scholar] [CrossRef] [PubMed]
- Amhis, Y.; Banerjee, S.; Ben-Haim, E.; Bertholet, E.; Bernlochner, F.U.; Bona, M.; Bozek, A.; Bozzi, C.; Brodzicka, J.; Chobanova, V.; et al. Averages of b-hadron, c-hadron, and τ-lepton properties as of 2021. Phys. Rev. D 2023, 107, 052008. [Google Scholar] [CrossRef]
- Bordone, M.; Isidori, G.; Mächler, S.; Tinari, A. Short- vs. long-distance physics in B→K(*)ℓ+ℓ−: A data-driven analysis. arXiv 2024, arXiv:2401.18007. [Google Scholar]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; Alkhazov, G.; et al. Observation of the suppressed decay →pπ−μ+μ−. J. High Energy Phys. 2017, 2017, 29. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Adametz, A.; Adeva, B.; Adinolfi, M.; Adrover, C.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; et al. First observation of the decay B+→π+μ+μ−. J. High Energy Phys. 2012, 2012, 125. [Google Scholar] [CrossRef]



| ✔✔ | ✔ | X | |
| ✔✔ | ✔✔ | X | |
| ✔✔ | ✔✔ | ✔✔ | |
| ✔ | ✔ | ✔✔ | |
| ✔ | ✔ | ✔✔ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andersson, M.; Marshall, A.M.; Petridis, K.A.; Smith, E. Strange Things in Bottom-to-Strange Decays: The Standard Model Turned Upside Down? Symmetry 2024, 16, 638. https://doi.org/10.3390/sym16060638
Andersson M, Marshall AM, Petridis KA, Smith E. Strange Things in Bottom-to-Strange Decays: The Standard Model Turned Upside Down? Symmetry. 2024; 16(6):638. https://doi.org/10.3390/sym16060638
Chicago/Turabian StyleAndersson, Martin, Alexander Mclean Marshall, Konstantinos A. Petridis, and Eluned Smith. 2024. "Strange Things in Bottom-to-Strange Decays: The Standard Model Turned Upside Down?" Symmetry 16, no. 6: 638. https://doi.org/10.3390/sym16060638
APA StyleAndersson, M., Marshall, A. M., Petridis, K. A., & Smith, E. (2024). Strange Things in Bottom-to-Strange Decays: The Standard Model Turned Upside Down? Symmetry, 16(6), 638. https://doi.org/10.3390/sym16060638





