An Online Review-Driven Picture Fuzzy Multi-Criteria Group Decision-Making Approach for Evaluating the Online Medical Service Quality of Doctors
Abstract
1. Introduction
1.1. Research Gaps and Motivations
1.2. Contributions
- (1)
- The NPFSs mentioned and explained above are used to describe DMs’ preference information.
- (2)
- Aczel–Alsina operations for normal picture fuzzy numbers (NPFNs) are defined and the corresponding properties are discussed.
- (3)
- The normal picture fuzzy Aczel–Alsina aggregation operators, including the normal picture fuzzy Aczel–Alsina weighted average operator (NPFAAWA) and normal picture fuzzy Aczel–Alsina weight geometric (NPFAAWG) operator, are developed. The corresponding properties are also explored as well. The two proposed operators involving a variable parameter can make the corresponding operations more flexible compared to other existing operators.
- (4)
- The online review-driven weight determination method is constructed. Then, the evaluation criteria and their corresponding weights for OMSQD are obtained objectively.
- (5)
- The extend COPRAS method based on normal picture fuzzy Aczel–Alsina aggregation operators is proposed, which can be more effective to evaluate OMSQD problems.
2. Literature Review
2.1. Fuzzy Sets and Extensions
2.2. Picture Fuzzy Sets and Normal Picture Fuzzy Sets
2.3. COPRAS Method
3. Preliminaries
- (1)
- If , then ;
- (2)
- If , then
- if , then ;
- If , then
- if , then ;
- If , then
- if , then ;
- If , then .
4. Normal Picture Fuzzy Aczel–Alsina Aggregation Operators
4.1. Aczel–Alsina Operations for NPFNs
4.2. Normal Picture Fuzzy Aczel–Alsina Aggregation Operators
- (a)
- For the positive membership degree of ,
- (b)
- For the neutral membership degree of ,
- (c)
- For the negative membership degree of , we can also obtain
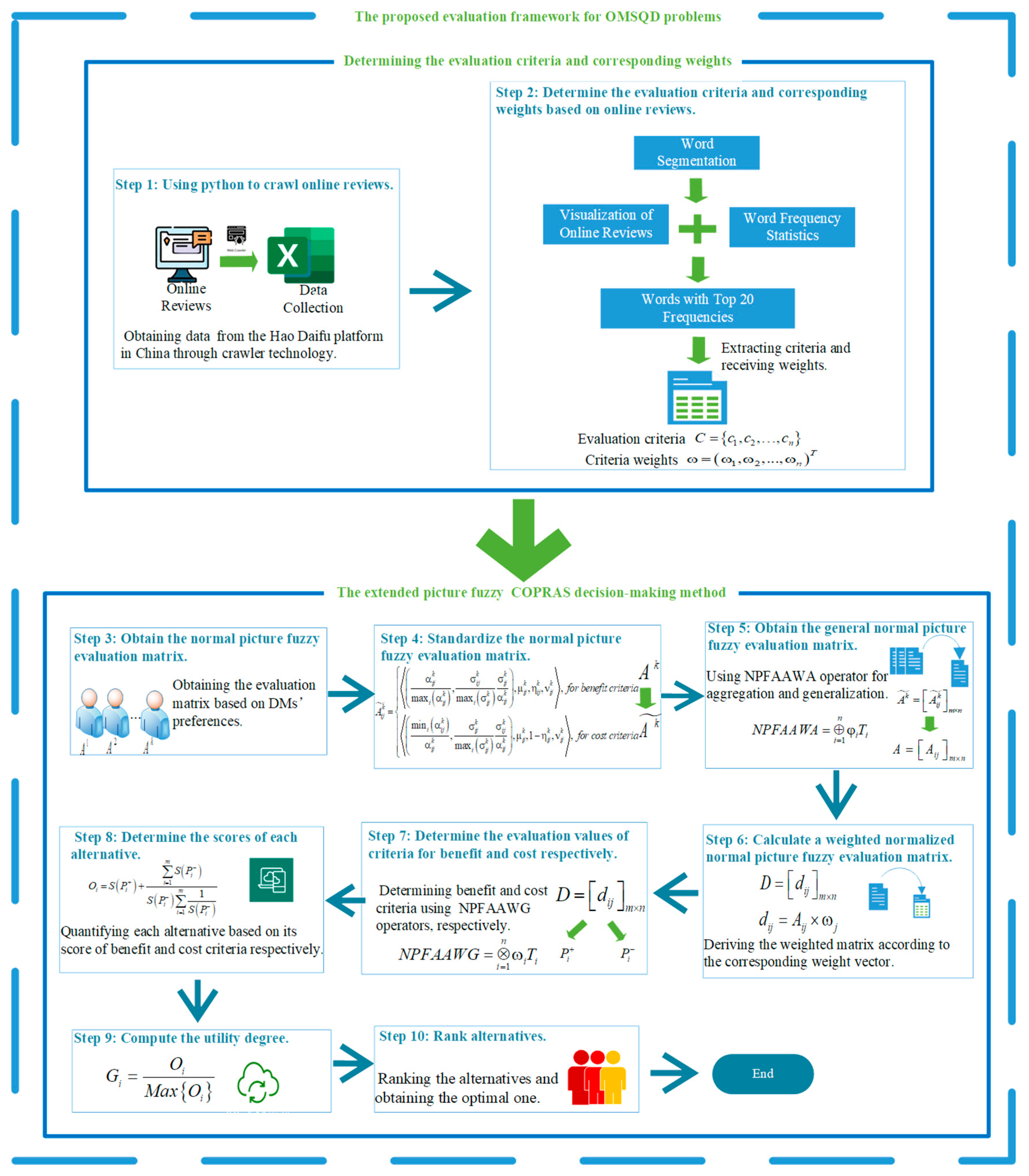
5. Determining the Evaluation Criteria and Corresponding Weights for OMSQD
5.1. Online Review Collection
| Algorithm 1: | Crawl website reviews and visualize online comments. | |
| Input: Online URL set | ||
| Output: Online Review set | ||
| 1 | request and parse | |
| 2 | get_page_num | |
| 3 | For URL in_set R | |
| 4 | request and parse | |
| 5 | get_each_page_link_url_meta | |
| 6 | return metas | |
| 7 | for metas in url-metas | |
| 8 | request and parse | |
| 9 | if url_meta.class=’description’ | |
| 10 | get url-meta.text | |
| 11 | get url-meta.id | |
| 12 | save (id, text) | |
| 13 | end | |
| 14 | end | |
| 15 | end | |
| 16 | close | |
5.2. Text Preprocessing
5.2.1. Word Segmentation
| Algorithm 2: | Word Segmentation | |
| Input: Online Review set , Stopwordslist | ||
| Output: Word Segmentation result R | ||
| 1 | For S in review set | |
| 2 | sentence_depart = jieba.cut (S. strip ()) | |
| 3 | #Introduce a deactivation glossary | |
| 4 | outstr. append(sentence_depart) | |
| 5 | For word in Word Segmentation result: | |
| 6 | stopwords = Stopwordslist () | |
| 7 | if word in stopwords then | |
| 8 | R. remove(word) | |
| 9 | end if | |
| 10 | end for each | |
| 11 | return R close | |
5.2.2. Visualization of Online Reviews
5.3. Feature Extraction
6. An extended Picture Fuzzy MCGDM Method Based on COPRAS for Evaluating OMSQD
- Step 1.
- Determine the evaluation criteria and corresponding weight based on online reviews.
- Step 2.
- Obtain the normal picture fuzzy evaluation matrix.
- Step 3.
- Standardize the normal picture fuzzy evaluation matrix.
- Step 4.
- Obtain the general normal picture fuzzy evaluation matrix.
- Step 5.
- Calculate a weighted normalized normal picture fuzzy evaluation matrix.
- Step 6.
- Determine the evaluation values of the criteria for benefit and cost.
- Step 7.
- Determine the scores of each alternative:where
- Step 8.
- Compute the utility degree.
- Step 9.
- Rank the alternatives.
7. A Case Study
7.1. The Evaluation Processes
- Step 1.
- Determine the evaluation criteria and corresponding weight based on online reviews.
- Step 2.
- Obtain the normal picture fuzzy evaluation matrix.
- Step 3.
- Standardize the normal picture fuzzy evaluation matrix.
- Step 4.
- Obtain the general normal picture fuzzy evaluation matrix.
- Step 5.
- Calculate a weighted normalized normal picture fuzzy evaluation matrix.
- Step 6.
- Determine the evaluation values of the criteria for benefit and cost.
- Step 7.
- Determine the scores of each alternative.
- Step 8.
- Compute the utility degree.
- Step 9.
- Ranking all alternatives.
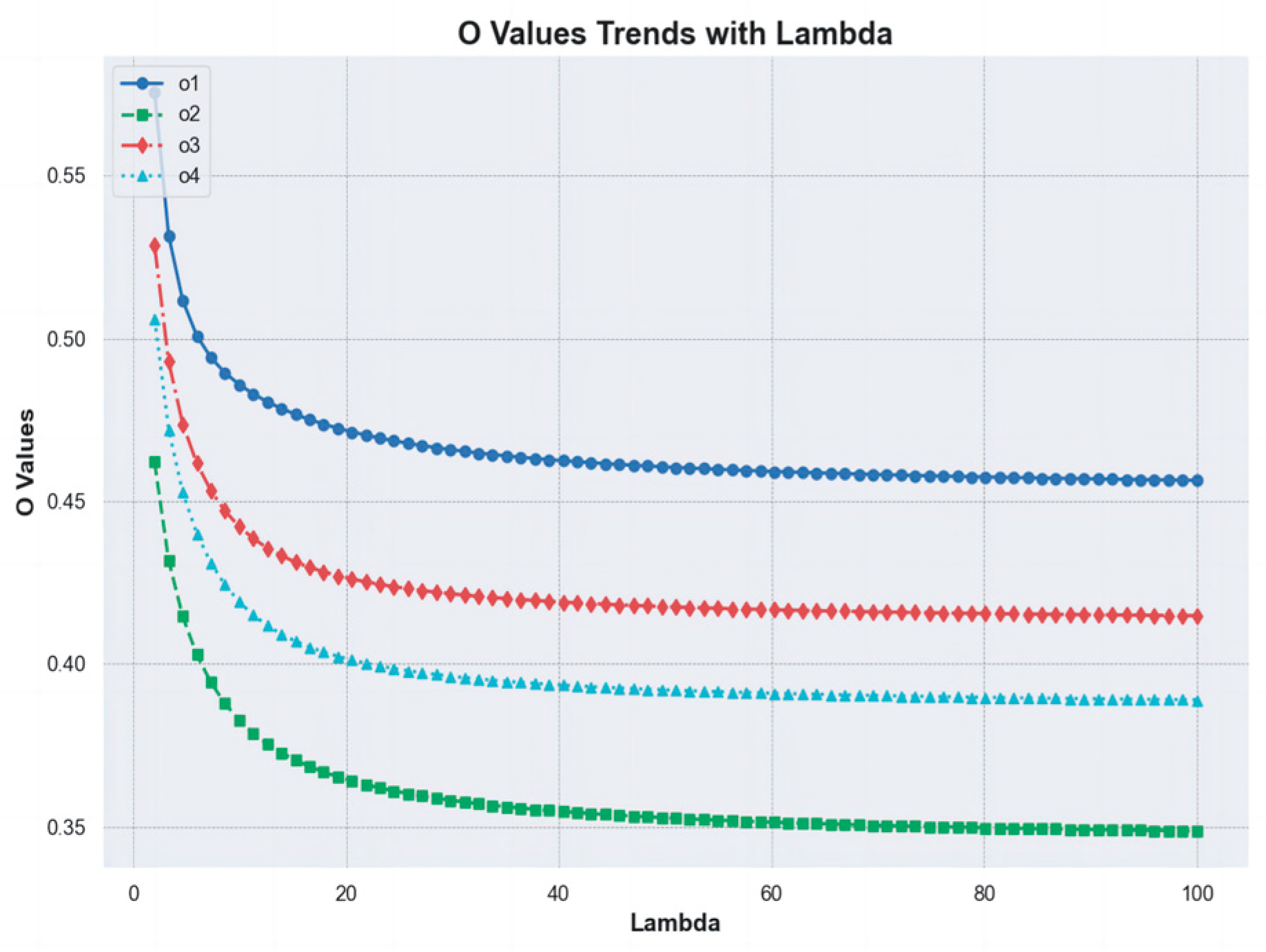
7.2. Sensitivity Analysis
7.3. Comparative Analysis
- (1)
- Comparison analysis with picture fuzzy MCGDM or MCDM methods based on aggregation operators.
- (2)
8. Discussion and Managerial Implications
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, P.; Yang, Y.L.; Weng, J.; Jiang, F. Construction of a competency evaluation indicator system for internet medical practitioners in China. Med. Soc. 2023, 36, 82–87. [Google Scholar]
- Turk, A.; Fleming, J.; Powell, J.; Atherton, H. Exploring UK doctors’ attitudes towards online patient feedback: Thematic analysis of survey data. Digit. Health 2020, 6, 2055207620908148. [Google Scholar] [CrossRef]
- Xiong, H.X.; Xiang, Y.; Meng, X.; Xiao, B. Doctor service evaluation based on user review mining in online health community. Inf. Sci. 2024. Available online: https://link.cnki.net/urlid/22.1264.G2.20240126.1758.004 (accessed on 29 January 2024).
- Gong, J.B.; Wang, L.L.; Sun, S.T. A hybrid multi-layer architecture for doctor recommendation in medical social networks. J. Comput. Sci. Technol. 2015, 30, 1073–1081. [Google Scholar] [CrossRef]
- Aczél, J.; Alsina, C. Characterizations of some classes of quasilinear functions with applications to triangular norms and to synthesizing judgements. Aequationes Math. 1982, 25, 313–315. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Wang, S.; Wen, J.; Li, H.; Rao, C.; Zhao, X. A novel fuzzy comprehensive evaluation model for application effect of connected vehicle system in a tunnel scenario. Int. J. Fuzzy Syst. 2022, 24, 1986–2004. [Google Scholar] [CrossRef]
- Li, Z.; Liu, A.; Miao, J.; Yang, Y. A three-phase method for spherical fuzzy environment and application to community epidemic prevention management. Expert Syst. Appl. 2023, 211, 118601. [Google Scholar] [CrossRef]
- Gundogdu, F.K.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
- Alcantud, J.C.R. Complemental fuzzy sets: A semantic justification of q-rung orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. Publ. IEEE Neural Netw. Counc. 2023, 31, 4262–4270. [Google Scholar] [CrossRef]
- Zadeh, L.A. A note on z-numbers. Inf. Sci. 2011, 181, 2923–2932. [Google Scholar] [CrossRef]
- Xiao, Q.; Gao, M.; Chen, L.; Jiang, J. Dynamic multi-attribute evaluation of digital economy development in China: A perspective from interaction effect. Technol. Econ. Dev. Econ. 2023, 29, 1728–1752. [Google Scholar] [CrossRef]
- Rao, C.; Wei, X.; Xiao, X.P.; Shi, Y.; Goh, M. Oversampling method via adaptive double weights and Gaussian kernel function for the transformation of unbalanced data in risk assessment of cardiovascular disease. Inf. Sci. 2024, 665, 120410. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Traneva, V.; Tranev, S. Intuitionistic fuzzy model for franchisee selection. In Intelligent and Fuzzy Systems; Kahraman, C., Tolga, A.C., Cevik, O.S., Cebi, S., Oztaysi, B., Sari, I.U., Eds.; INFUS 2022; Lecture Notes in Networks and Systems; Springer: Cham, Swizerland, 2022; Volume 504. [Google Scholar]
- Ting, Y.C. A circular intuitionistic fuzzy assignment model with a parameterized scoring rule for multiple criteria assessment methodology. Adv. Eng. Inform. 2024, 61, 102479. [Google Scholar]
- Dworniczak, P. Some applications of intuitionistic fuzzy sets for the determination of a sociometric index of acceptance. Cybern. Inf. Technol. 2012, 12, 70–77. [Google Scholar] [CrossRef][Green Version]
- Davvaz, B.; Sadrabadi, E.H. An application of intuitionistic fuzzy sets in medicine. Int. J. Biomath. 2016, 9, 81–95. [Google Scholar] [CrossRef]
- Ejegwa, P.A.; Anum, M.T.; Isife, K.I. A new method of distance measure between intuitionistic fuzzy sets and its application in admission procedure. J. Uncertain Syst. 2024. [Google Scholar] [CrossRef]
- Anum, M.T.; Zhang, H.; Ejegwa, P.A.; Feng, Y. Tendency coefficient-based weighted distance measure for intuitionistic fuzzy sets with applications. In Proceedings of the 2024 12th International Conference on Intelligent Control and Information Processing (ICICIP), Nanjing, China, 8–10 March 2024; pp. 54–61. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Gupta, R.; Kumar, S. Novel similarity measure between hesitant fuzzy set and their applications in pattern recognition and clustering analysis. J. Eng. Appl. Sci. 2024, 71, 1–26. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wu, X.H. Novel multi-criteria decision-making approaches based on hesitant fuzzy sets and prospect theory. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 621–643. [Google Scholar] [CrossRef]
- Wang, L.; Ni, M.; Zhu, L. Correlation measures of dual hesitant fuzzy sets. J. Appl. Math. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Karaaslan, F.; Ozlu, S. Correlation coefficients of dual type-2 hesitant fuzzy sets and their applications in clustering analysis. Int. J. Intell. Syst. 2020, 35, 1200–1229. [Google Scholar] [CrossRef]
- Sindhu, M.S.; Rashid, T. Selection of alternative based on linear programming and the extended fuzzy TOPSIS under the framework of dual hesitant fuzzy sets. Soft Comput. 2023, 27, 1985–1996. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the IFSA World Congress & Nafips Meeting IEEE, Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Li, R.; Ejegwa, P.A.; Li, K.; Agaji, I.; Feng, Y.; Onyeke, I.C. A new similarity function for Pythagorean fuzzy sets with application in football analysis. AIMS Math. 2024, 9, 4990–5014. [Google Scholar] [CrossRef]
- Khan, M.J.; Alcantud, J.C.R.; Kumam, W.; Kumam, P.; Alreshidi, N.A. Expanding Pythagorean fuzzy sets with distinctive radii: Disc Pythagorean fuzzy sets. Complex Intell. Syst. 2023, 9, 7037–7054. [Google Scholar] [CrossRef]
- Senapati, T.; Yager, R.R. Fermatean fuzzy sets. J. Ambient Intell. Humaniz. Comput. 2020, 11, 663–674. [Google Scholar] [CrossRef]
- Wang, H.; Tuo, C.; Wang, Z.; Feng, G.; Li, C. Enhancing similarity and distance measurements in Fermatean fuzzy sets: Tanimoto-Inspired measures and decision-making applications. Symmetry 2024, 16, 277. [Google Scholar] [CrossRef]
- Ejegwa, P.A.; Wanzenke, T.D.; Ogwuche, I.O. A robust correlation coefficient for Fermatean fuzzy sets based on spearman’s correlation measure with application to clustering and selection process. J. Appl. Math. Comput. 2024, 70, 1747–1770. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R. Interval-valued Fermatean fuzzy sets with multi-criteria weighted aggregated sum product assessment-based decision analysis framework. Neural Comput. Appl. 2022, 34, 8051–8067. [Google Scholar] [CrossRef]
- Ranitovic, M.G.; Petojevic, A. Lattice representations of interval-valued fuzzy sets. Fuzzy Sets Syst. 2014, 236, 50–57. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning I. Inf. Sci. 1975, 3, 199–249. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Ali, Z.; Yang, M.S. On circular q-rung orthopair fuzzy sets with Dombi aggregation operators and application to symmetry analysis in artificial intelligence. Symmetry 2024, 16, 260. [Google Scholar] [CrossRef]
- Cuong, B.C.; Kreinovitch, V. Picture fuzzy sets—A new concept for computational intelligence problems. In Proceedings of the 2013 Third World Congress on Information and Communication Technologies, Hanoi, Vietnam, 15–18 December 2013; pp. 1–6. [Google Scholar]
- Son, L.H. Measuring analogousness in picture fuzzy sets: From picture distance measures to picture association measures. Fuzzy Optim. Decis. Mak. 2017, 16, 359–378. [Google Scholar] [CrossRef]
- Long, H.F.; Luo, M.X. Picture fuzzy aggregation operators and their application to multi-attribute decision making. J. China Jiliang Univ. 2021, 031, 524–530. [Google Scholar]
- Tian, C.; Peng, J.J.; Zhang, S.; Wang, J.Q.; Goh, M. A sustainability evaluation framework for WET-PPP projects based on a picture fuzzy similarity-based VIKOR method. J. Clean. Prod. 2021, 289, 125130. [Google Scholar] [CrossRef]
- Singh, S.; Ganie, A.H. Applications of picture fuzzy similarity measures in pattern recognition, clustering, and MADM. Expert Syst. Appl. 2021, 168, 114264. [Google Scholar] [CrossRef]
- Verma, R.; Rohtagi, B. Novel similarity measures between picture fuzzy sets and their applications to pattern recognition and medical diagnosis. Granul. Comput. 2022, 7, 761–777. [Google Scholar] [CrossRef]
- Wei, G.; Gao, H. The generalized dice similarity measures for picture fuzzy sets and their applications. Informatica 2018, 29, 107–124. [Google Scholar] [CrossRef]
- Tian, C.; Peng, J.J.; Zhang, S.; Zhang, W.Y.; Wang, J.Q. Weighted picture fuzzy aggregation operators and their applications to multi-criteria decision-making problems. Comput. Ind. Eng. 2019, 137, 106037. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.; Wang, J.; Li, L. Picture fuzzy normalized projection-based VIKOR method for the risk evaluation of construction project. Appl. Soft Comput. 2018, 64, 216–226. [Google Scholar] [CrossRef]
- Wei, G.W.; Alsaadi, F.E.; Hayat, T.; Alsaedi, A. Projection models for multiple attribute decision making with picture fuzzy information. Int. J. Mach. Learn. Cybern. 2016, 9, 713–719. [Google Scholar] [CrossRef]
- Arya, V.; Kumar, S. A novel TODIM-VIKOR approach based on entropy and Jensen–Tsalli divergence measure for picture fuzzy sets in a decision-making problem. Int. J. Intell. Syst. 2020, 35, 2140–2180. [Google Scholar] [CrossRef]
- Kadian, R.; Kumar, S. A new picture fuzzy divergence measure based on Jensen–Tsallis information measure and its application to multicriteria decision making. Granul. Comput. 2022, 7, 113–126. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy cross-entropy for multiple attribute decision making problems. J. Bus. Econ. Manag. 2016, 17, 491–502. [Google Scholar] [CrossRef]
- Han, E.D. Picture fuzzy multi-attribute decision-making method with unknown attribute weights and its application. Appl. Res. Comput. 2021, 38, 3657–3672. [Google Scholar]
- Arya, V.; Kumar, S. A picture fuzzy multiple criteria decision-making approach based on the combined TODIM-VIKOR and entropy weighted method. Cogn. Comput. 2021, 13, 1172–1184. [Google Scholar] [CrossRef]
- Peng, J.J.; Chen, X.G.; Long, Q.Q.; Zhang, S.Z. A picture fuzzy evaluation framework based on a novel approach incorporating bidirectional projection measures and the VIKOR method. Artif. Intell. Rev. 2023, 56 (Suppl. S2), 2235–2261. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 713–724. [Google Scholar] [CrossRef]
- Khan, S.; Abdullah, S.; Ashraf, S. Picture fuzzy aggregation information based on Einstein operations and their application in decision making. Math. Sci. 2019, 13, 213–229. [Google Scholar] [CrossRef]
- Jana, C.; Senapati, T.; Pal, M.; Yager, R.R. Picture fuzzy Dombi aggregation operators: Application to MADM process. Appl. Soft Comput. J. 2019, 74, 99–109. [Google Scholar] [CrossRef]
- Phu, N.D.; Hung, N.N.; Ahmadian, A.; Salahshour, S. Limit properties in the metric semi-linear space of picture fuzzy numbers. Soft Comput. 2022, 26, 5481–5496. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.J.; Chen, X.G.; Tian, C.; Zhang, Z.Q.; Song, H.Y.; Dong, F. Picture fuzzy large-scale group decision-making in a trust-relationship-based social network environment. Inf. Sci. 2022, 608, 1675–1701. [Google Scholar] [CrossRef]
- Yang, M.S.; Ko, C.H. On a class of fuzzy c-numbers clustering procedures for fuzzy data. Fuzzy Sets Syst. 1996, 84, 49–60. [Google Scholar] [CrossRef]
- Li, D.Y.; Liu, C.Y. Study on the universality of the normal cloud model. Eng. Sci. 2005, 3, 28–34. [Google Scholar]
- Yang, Z.L.; Li, X.; Garg, H.; Qi, M. A cognitive information-based decision-making algorithm using interval-valued q-rung picture fuzzy numbers and Heronian mean Operators. Cogn. Computer. 2021, 13, 357–380. [Google Scholar] [CrossRef]
- Akram, M.; Shahzadi, G.; Alcantud, J.C.R. Multi-attribute decision-making with q-rung picture fuzzy information. Granul. Comput. 2022, 7, 197–215. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Sarka, V. The new method of multi-criteria complex proportional assessment of projects. Technol. Econ. Dev. Econ. 1994, 3, 131–139. [Google Scholar]
- Unvan, Y.A.; Ergenc, C. Financial performance analysis with the fuzzy COPRAS and entropy-COPRAS approaches. Comput. Econ. 2022, 59, 1577–1605. [Google Scholar] [CrossRef]
- Soltani, M.; Barekatain, B.; Hendesi, F. FSCN: A novel forwarding method based on Shannon entropy and COPRAS decision process in named data networking. J. Supercomput. 2023, 79, 15324–15357. [Google Scholar] [CrossRef]
- Torabzadeh Khorasani, S. Green supplier evaluation by using the integrated fuzzy AHP model and fuzzy COPRAS. Process Integr. Optim. Sustain. 2018, 2, 17–25. [Google Scholar] [CrossRef]
- Hezer, S.; Gelmez, E.; Zceylan, E. Comparative analysis of TOPSIS, VIKOR and COPRAS methods for the COVID-19 Regional Safety Assessment. J. Infect. Public Health 2021, 14, 775–786. [Google Scholar] [CrossRef] [PubMed]
- Allah, M.M.A.; Abd El-baky, M.A.; Alshahrani, H.; Sebaey, T.A.; Hegazy, D.A. Multi attribute decision making through COPRAS on tensile properties of hybrid fiber metal laminate sandwich structures for aerospace and automotive industries. J. Compos. Mater. 2023, 57, 3757–3773. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Peldschus, F. Multi-attribute assessment of road design solutions by using the COPRAS method. Balt. J. Road Bridge Eng. 2007, 2, 195–203. [Google Scholar]
- Ch, B.M.; Anand, C.J.; Padmaja, M. Selection of best web site by applying COPRAS-G method. Int. J. Comput. Sci. Inf. Technol. 2010, 1, 138–146. [Google Scholar]
- Kumar, R.; Kumar, S.; Agbulut, U.; Guerel, A.E.; Alwetaishi, M.; Shaik, S.; Saleel, C.A.; Lee, D. Parametric optimization of an impingement jet solar air heater for active green heating in buildings using hybrid CRITIC-COPRAS approach. J. Therm. Sci. 2024, 197, 108760. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Garg, H.; Peng, R.; Wu, S.; Huang, L. Group decision algorithm for aged healthcare product purchase under q-rung picture normal fuzzy environment using Heronian mean operator. Int. J. Comput. Intell. Syst. 2020, 13, 1176–1197. [Google Scholar] [CrossRef]
- Li, X.; Ju, Y.B.; Ju, D.W.; Zhang, W.K.; Dong, P.W.; Wang, A.H. Multi-attribute group decision making method based on EDAS under picture fuzzy environment. IEEE Access 2019, 7, 141179–141192. [Google Scholar] [CrossRef]
- Kahraman, C. Proportional picture fuzzy sets and their AHP extension: Application to waste disposal site selection. Expert Syst. Appl. 2024, 238, 122354. [Google Scholar] [CrossRef]
- Tian, C.; Peng, J.J. An integrated picture fuzzy ANP-TODIM multi-criteria decision-making approach for tourism attraction recommendation. Technol. Econ. Dev. Econ. 2020, 26, 331–354. [Google Scholar] [CrossRef]
- Peng, J.J.; Chen, X.G.; Tan, H.; Sun, J.Y.; Long, Q.Q.; Jiang, L.L. A heterogeneous picture fuzzy SWARA-MARCOS evaluation framework based on a novel cross-entropy measure. Int. J. Syst. Sci. 2024, 55, 1528–1552. [Google Scholar] [CrossRef]
- Mao, J.; Wang, W.; Cao, D. Exploration on the mechanism of examination and encouragement of medical quality control center. Jiangsu Health Syst. Manag. 2023, 34, 331–334. [Google Scholar]
- Shen, X.; Zhang, T.T.; Chen, B.; Chen, M. Design of a satisfaction evaluation indicator system based on patients’ experience of medical services. J. Zhejiang Univ. (Med. Sci.) 2014, 43, 240–244. [Google Scholar]
- Cao, B.L. Internet-based medical treatment: Online doctor-patient communication, effect and influence. J. Shenzhen Univ. Humanit. Soc. Sci. 2021, 38, 119–130. [Google Scholar]


| Comments | Word Segmentation Results |
|---|---|
| 腰椎间盘突出,感谢冯医生实施的微创手术治疗,腰椎间盘严重脱出,效果很好 “Lumbar disc herniation, thanks to Dr. Feng for the minimally invasive surgical treatment. The lumbar disc is severely herniated, and the effect is very good” | 腰椎间盘 突出 感谢 冯 医生 实施 的 微创 手术 治疗 腰椎间盘 严重 脱出 效果 很 好 Lumbar disc herniation, Thanks to Dr. Feng, the minimally, invasive surgery, the treatment, lumbar disc, severely herniated, is very good |
| 非常感谢滕主任!温州有您这样责任心强,技术高,亲切感十足,乐于助人的医生真是件庆幸的事,金华父老乡亲好羡慕啊! “Thanks to Dr. Teng! Wenzhou is really fortunate to have such a strong sense of responsibility, high technology, full of cordiality, and helpful doctors. Jinhua parents and villagers are so envious!” | 非常感谢 滕 主任 温州 有 您 这样 责任心 强 技术 高 亲切感 十足 乐于助人 医生 真是 件 庆幸 事 金华 父老乡亲 好羡慕 Thanks to Dr. Teng, Wenzhou, such a strong sense, responsibility, high technology, cordiality, helpful, doctors, Jinhua, parents and villagers, are so envious |
| 我觉得滕医生有经验,有知识,有医德,非常感谢他对我老爸的这次治疗。 “I think that Dr. Teng has experience, knowledge and medical ethics. I am very grateful to him for this treatment for my father.” | 我 觉得 滕 医生 有 经验 有 知识 有 医德 非常感谢 对 我 老爸 这次 治疗 I think, Dr. Teng, has, experience, knowledge, medical ethics, I, am very grateful, treatment, my father |
| Category | Keywords (English) | Keywords (中) | Sum | Weight |
|---|---|---|---|---|
| Professional skills | Director (2667) | 主任 (2667) | 12,062 | 0.46 |
| Surgery (4369) | 手术 (4369) | |||
| Medicine (1556) | 医术 (1556) | |||
| Treatment (1390) | 治疗 (1390) | |||
| Meniscus (703) | 半月板 (703) | |||
| Knee (689) | 膝关节 (689) | |||
| Lumbar (688) | 腰椎间盘 (688) | |||
| Communication skills | Description (846) | 描述 (846) | 4662 | 0.18 |
| Pathology (1435) | 病情 (1435) | |||
| Case (1146) | 情况 (1146) | |||
| Examine (1235) | 看病 (1235) | |||
| Service attitude | gratefulness (1433) | 感谢 (1433) | 6159 | 0.23 |
| Patience (1345) | 耐心 (1345) | |||
| Attitude (1256) | 态度 (1256) | |||
| Superb (799) | 精湛 (799) | |||
| Thanks (790) | 谢谢 (790) | |||
| medical ethics (572) | 医德 (572) | |||
| Results and follow- up | Rehabilitation (1516) | 康复 (1516) | 3218 | 0.13 |
| Post operation (1087) | 术后 (1087) | |||
| Care (615) | 照顾 (615) |
| Professional Skills | Communication Skills | |
|---|---|---|
| Service Attitude | Results and Follow-up | |
| Professional Skills | Communication Skills | |
|---|---|---|
| Service Attitude | Results and Follow-up | |
| Professional Skills | Communication Skills | |
|---|---|---|
| Service Attitude | Results and Follow-up | |
| Professional Skills | Communication Skills | |
|---|---|---|
| Service Attitude | Results and Follow-up | |
| Professional Skills | Communication Skills | |
|---|---|---|
| Service Attitude | Results and Follow-up | |
| Professional Skills | Communication Skills | |
|---|---|---|
| Service Attitude | Results and Follow-up | |
| Professional Skills | Communication Skills | |
|---|---|---|
| Service Attitude | Results and Follow-up | |
| Professional Skills | Communication Skills | |
|---|---|---|
| Service Attitude | Results and Follow-up | |
| References | Aggregation Operators | Final Rankings |
|---|---|---|
| Wei [54] | Weighted geometric operator | |
| Jana [56] | Picture fuzzy Dombi weighted average operator () | |
| Jana [56] | Picture fuzzy Dombi weighted geometric operator () | |
| Jana [56] | Picture fuzzy Dombi weighted geometric operator () | |
| Li [73] | Picture fuzzy weighted interaction averaging operator | |
| Cengiz et al. [74] | Proportional picture fuzzy weighted averaging (PPFWA) operator | |
| The proposed method | NPFAAWA and NPFAAWG operators |
| References | Measures | Final Rankings |
|---|---|---|
| Wang [46] | Projection-based VIKOR | |
| Tian and Peng [75] | Distance-based TODIM ( = 1 and = 2.25) | |
| Peng et al. [53] | Bidirectional projection and VIKOR | |
| Peng et al. [76] | Cross-entropy measure | |
| The proposed method | NPFAAWA and NPFAAWG operators |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, K.; Peng, J. An Online Review-Driven Picture Fuzzy Multi-Criteria Group Decision-Making Approach for Evaluating the Online Medical Service Quality of Doctors. Symmetry 2024, 16, 639. https://doi.org/10.3390/sym16060639
Shi K, Peng J. An Online Review-Driven Picture Fuzzy Multi-Criteria Group Decision-Making Approach for Evaluating the Online Medical Service Quality of Doctors. Symmetry. 2024; 16(6):639. https://doi.org/10.3390/sym16060639
Chicago/Turabian StyleShi, Kaiwen, and Juanjuan Peng. 2024. "An Online Review-Driven Picture Fuzzy Multi-Criteria Group Decision-Making Approach for Evaluating the Online Medical Service Quality of Doctors" Symmetry 16, no. 6: 639. https://doi.org/10.3390/sym16060639
APA StyleShi, K., & Peng, J. (2024). An Online Review-Driven Picture Fuzzy Multi-Criteria Group Decision-Making Approach for Evaluating the Online Medical Service Quality of Doctors. Symmetry, 16(6), 639. https://doi.org/10.3390/sym16060639





