PSD and Cross-PSD of Responses of Seven Classes of Fractional Vibrations Driven by fGn, fBm, Fractional OU Process, and von Kármán Process
Abstract
1. Introduction
2. Seven Classes of Fractional Vibrators
2.1. Motion Equations
2.2. Frequency Transfer Functions
2.3. Impulse Response Functions
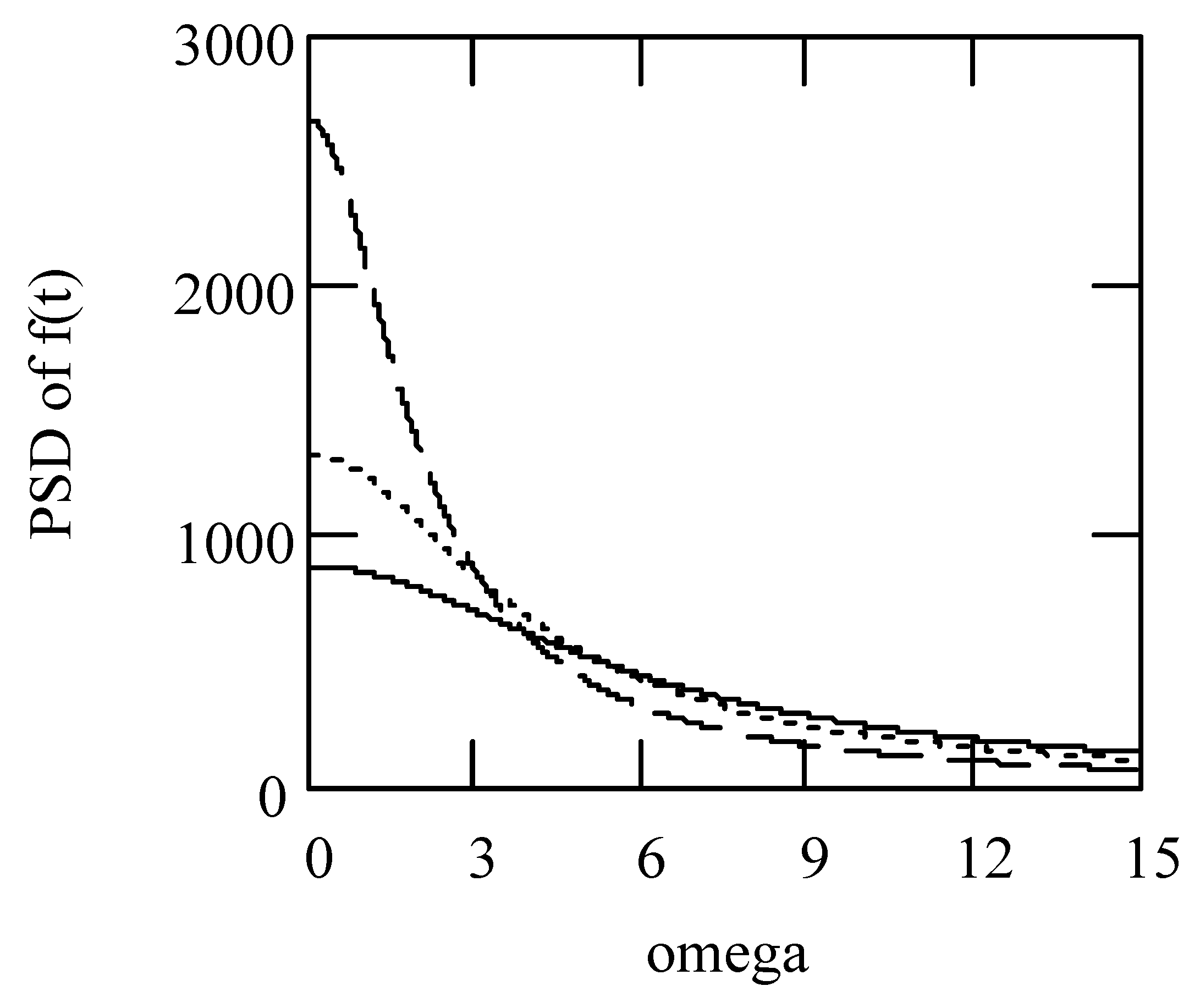
3. PSD and Cross-PSD Responses to Seven Classes of Fractional Vibrations Driven by fGn
3.1. Background
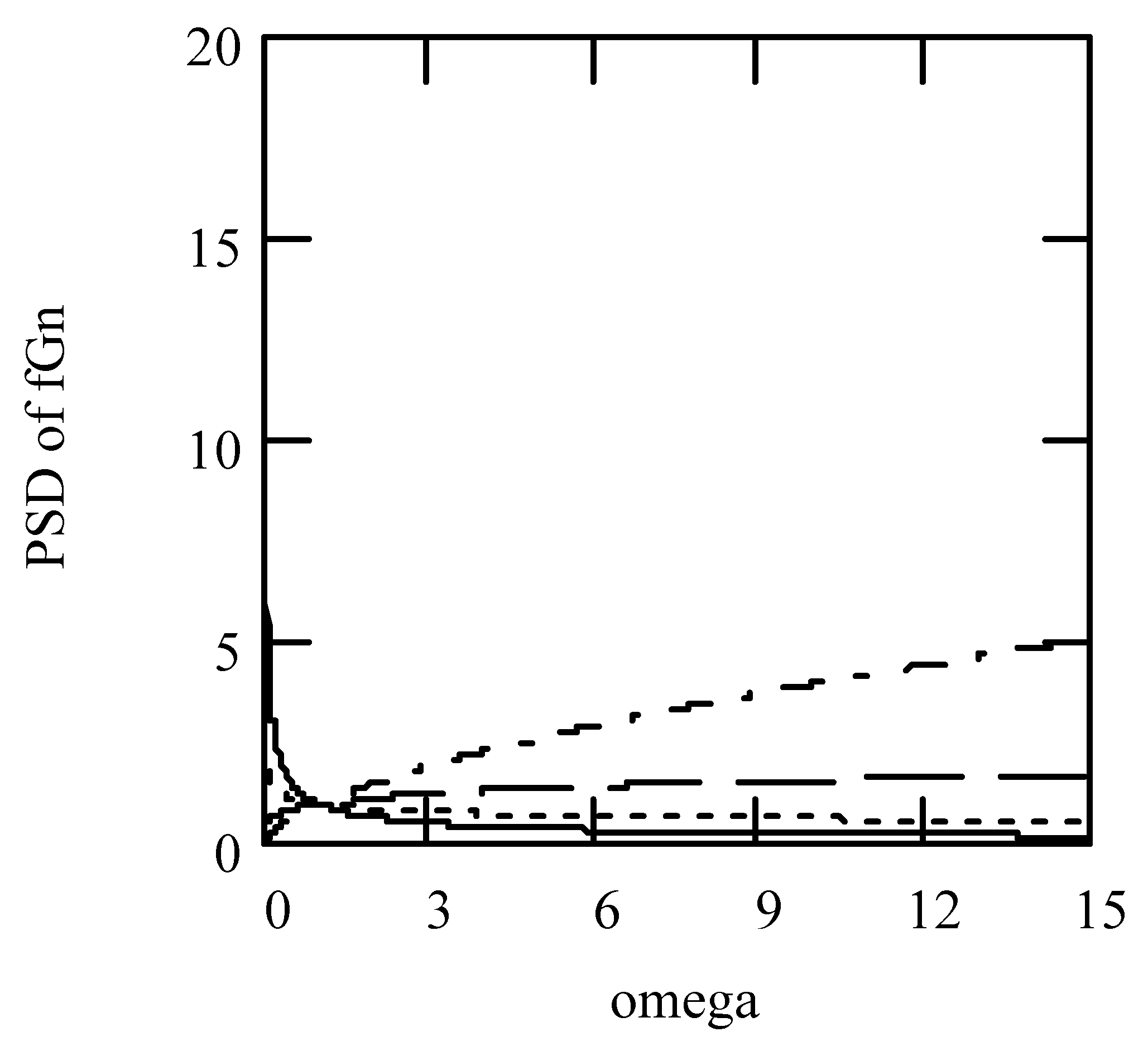
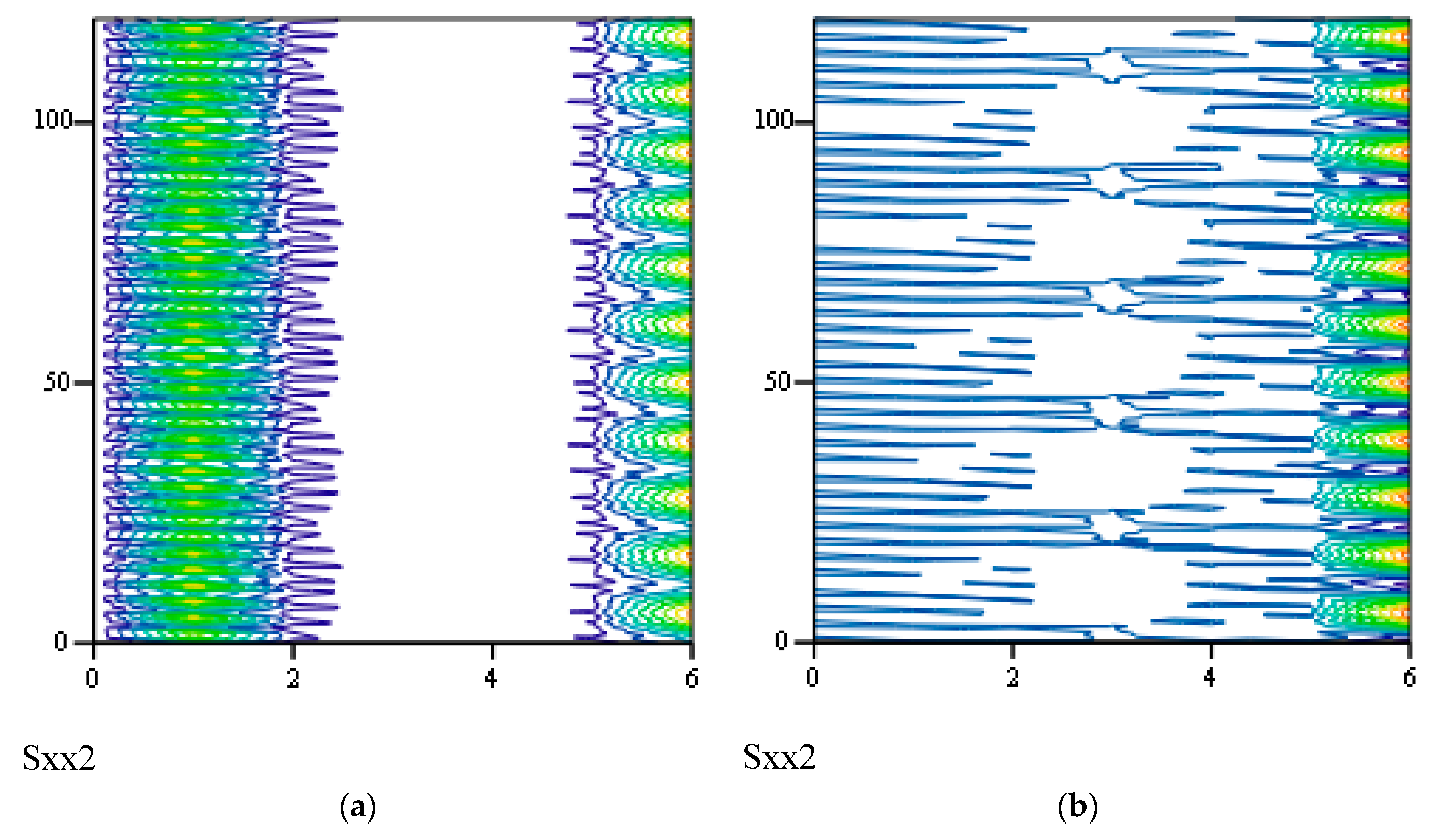
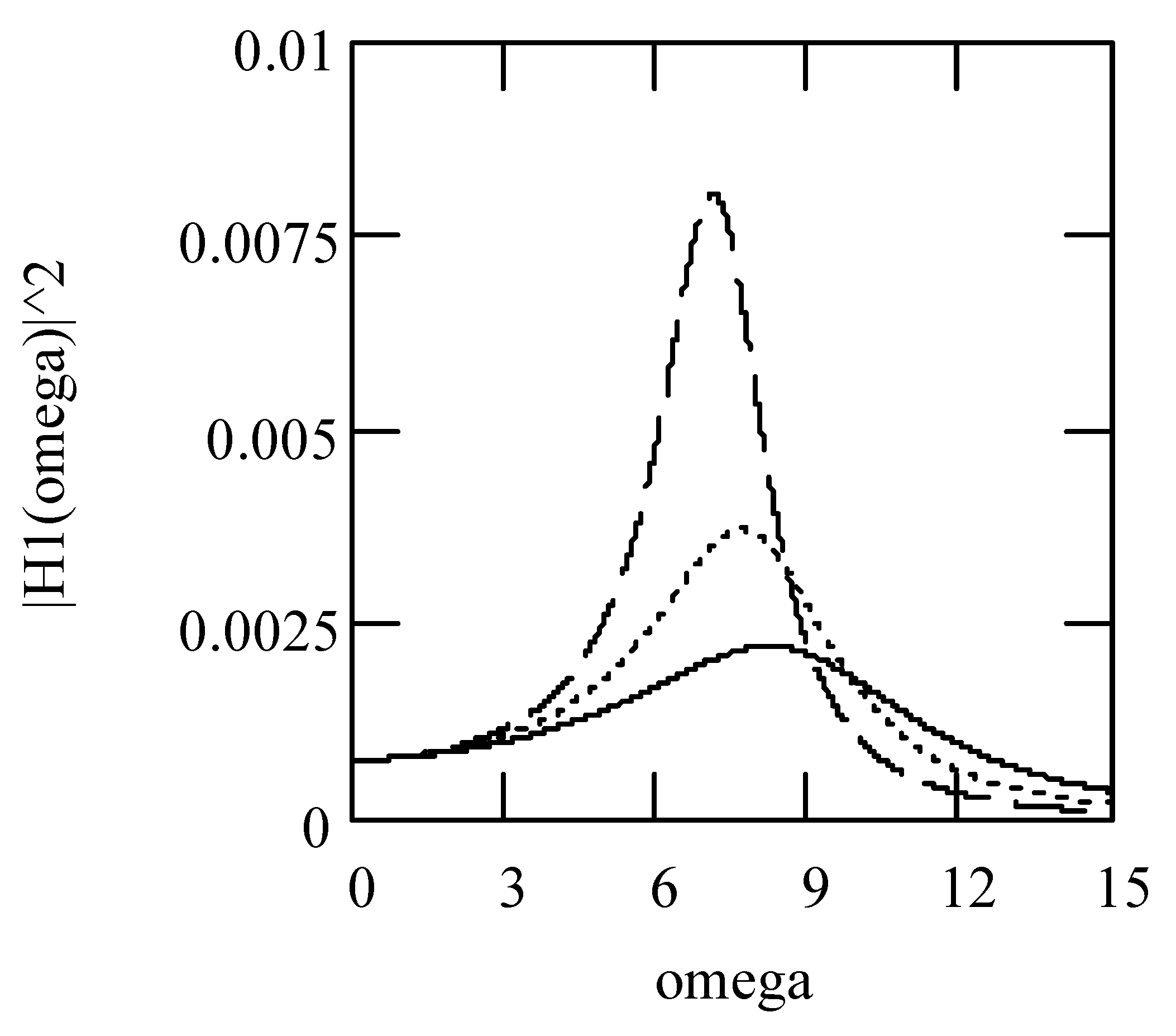
3.2. Responses of Class I Fractional Vibrators Driven by fGn
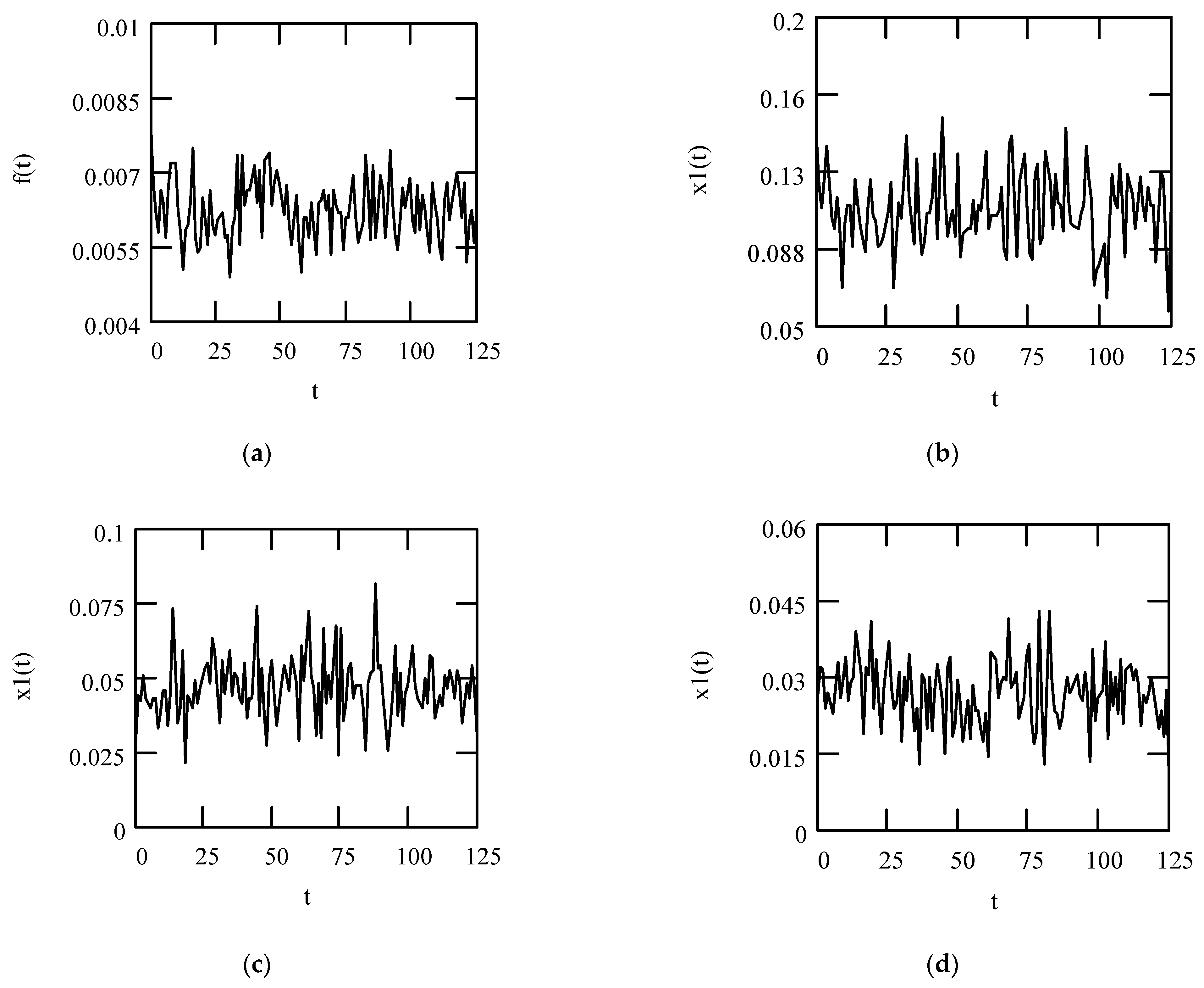
3.2.1. Computations
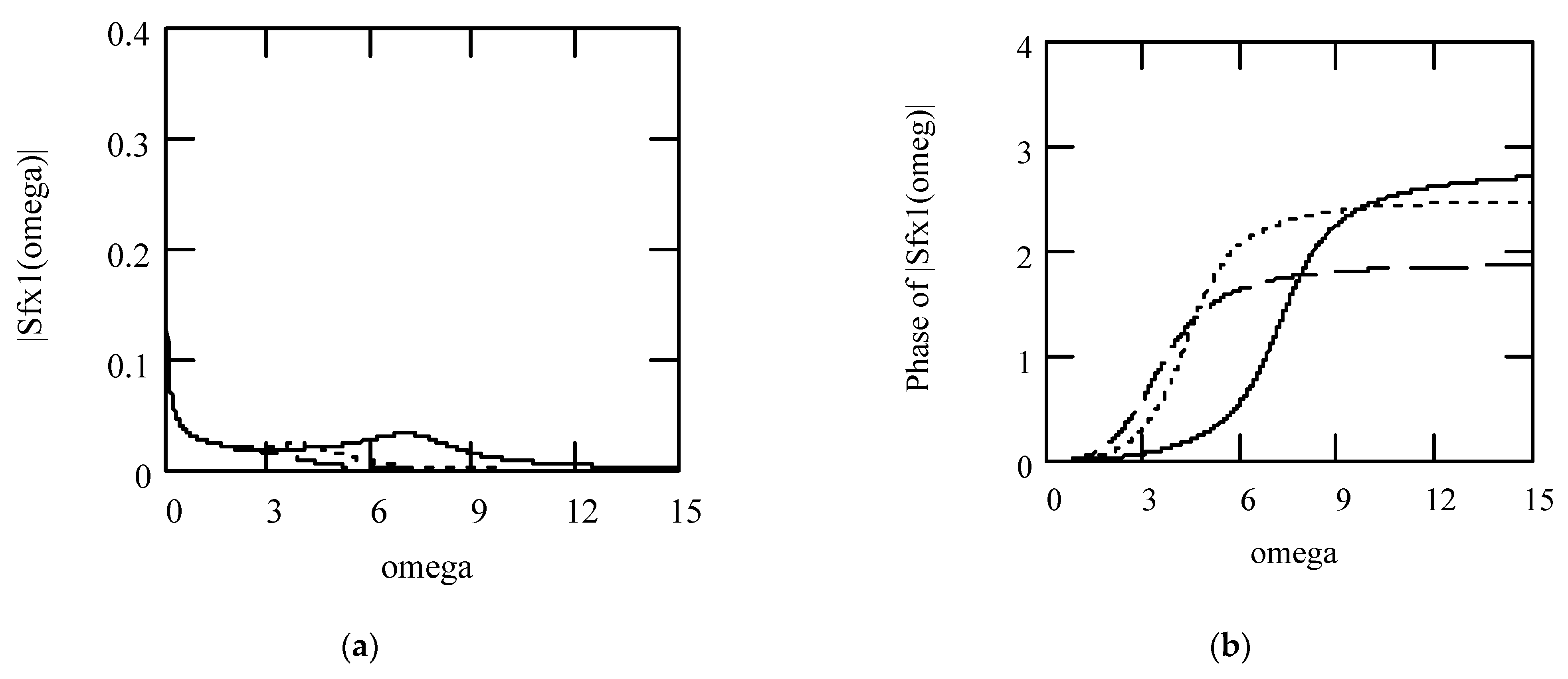
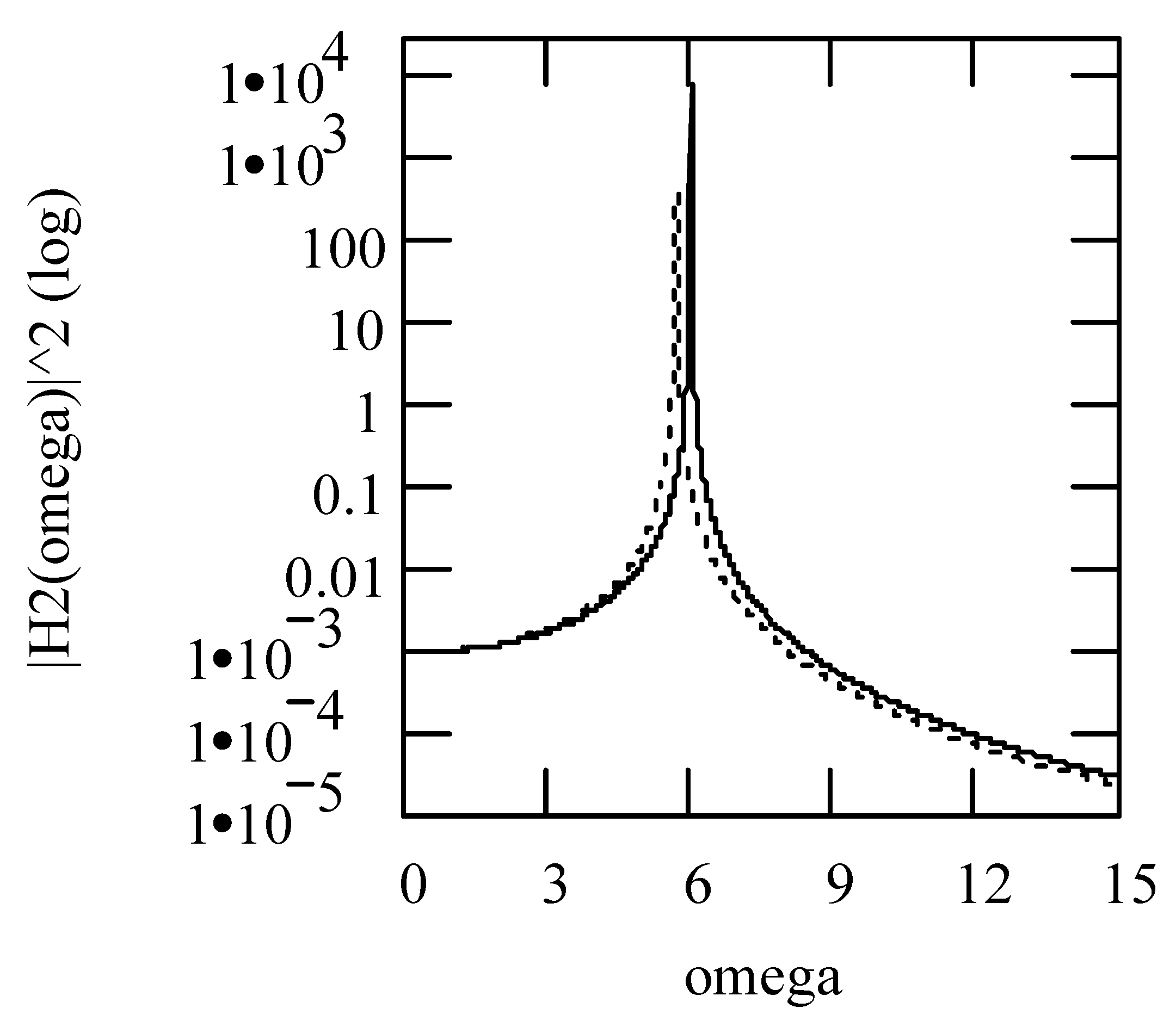
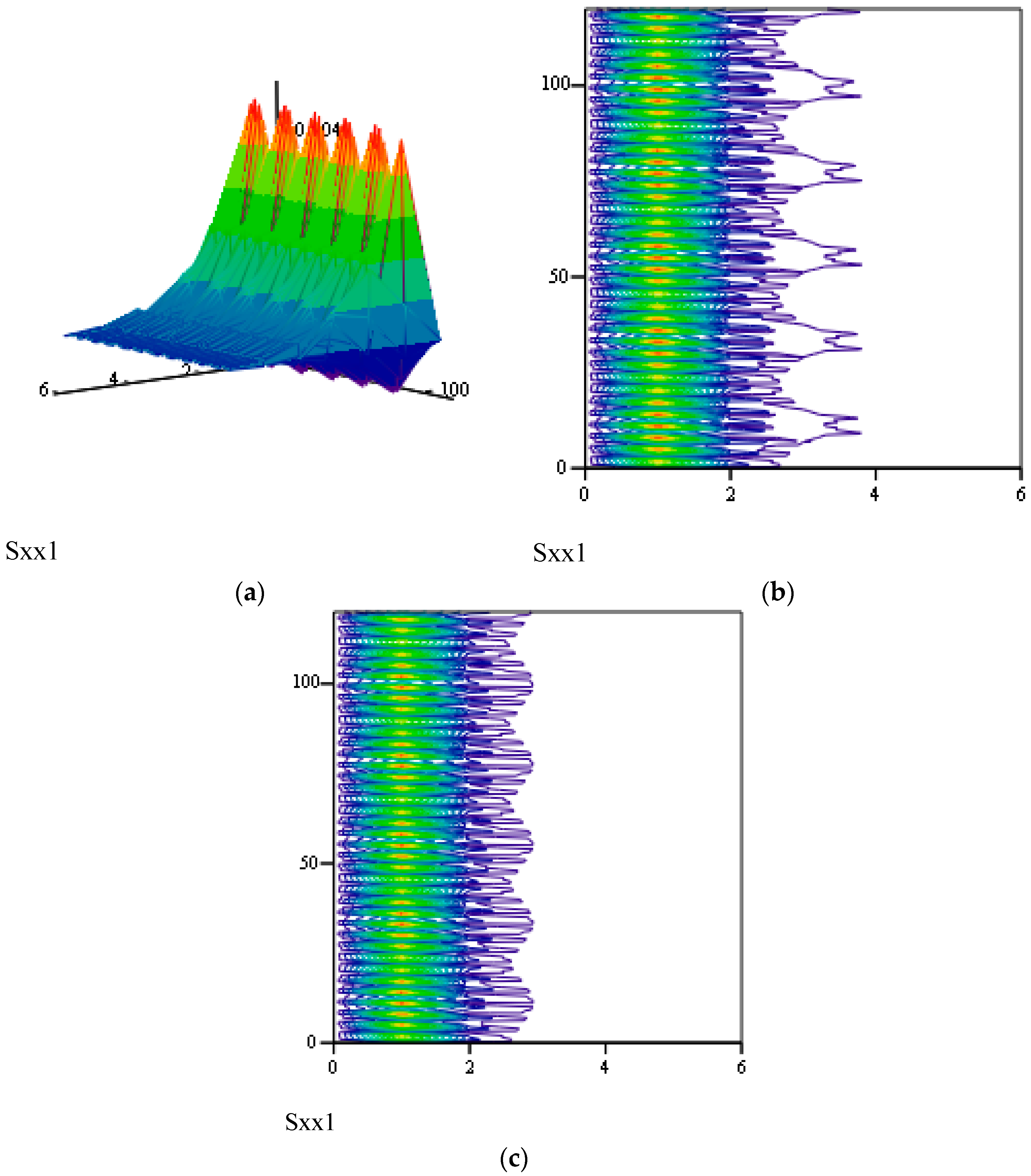
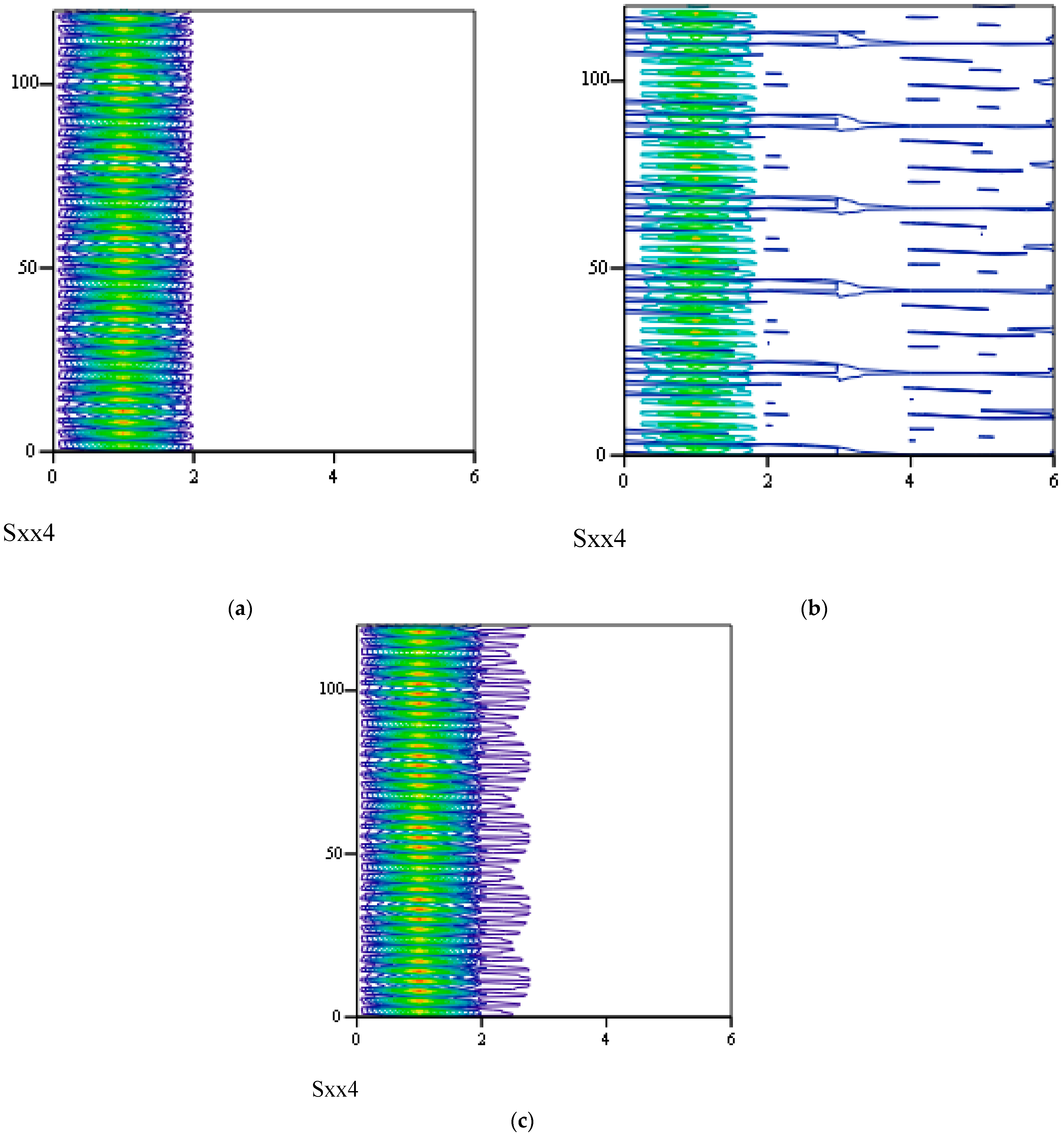
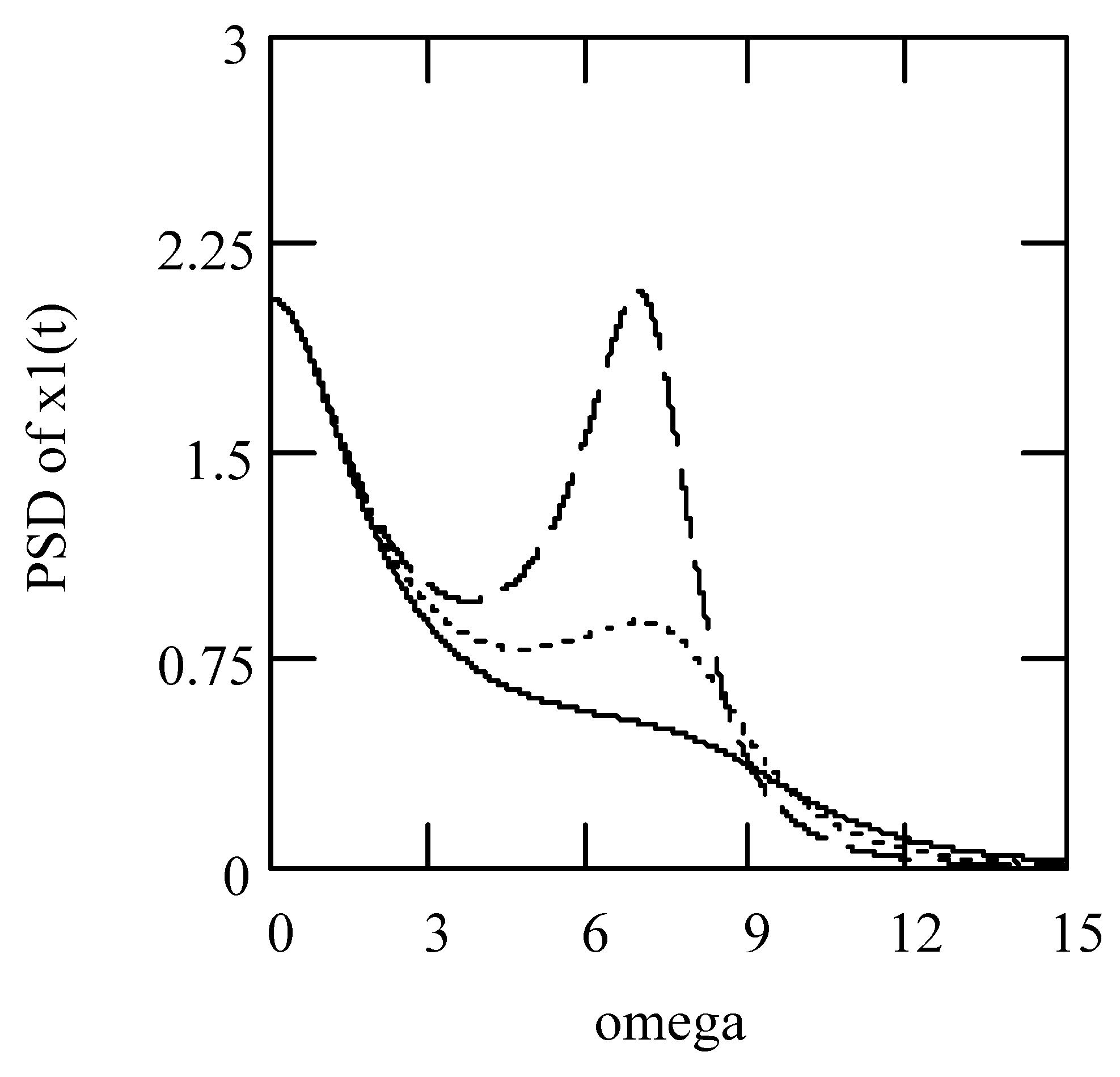
3.2.2. Effects of α on Responses
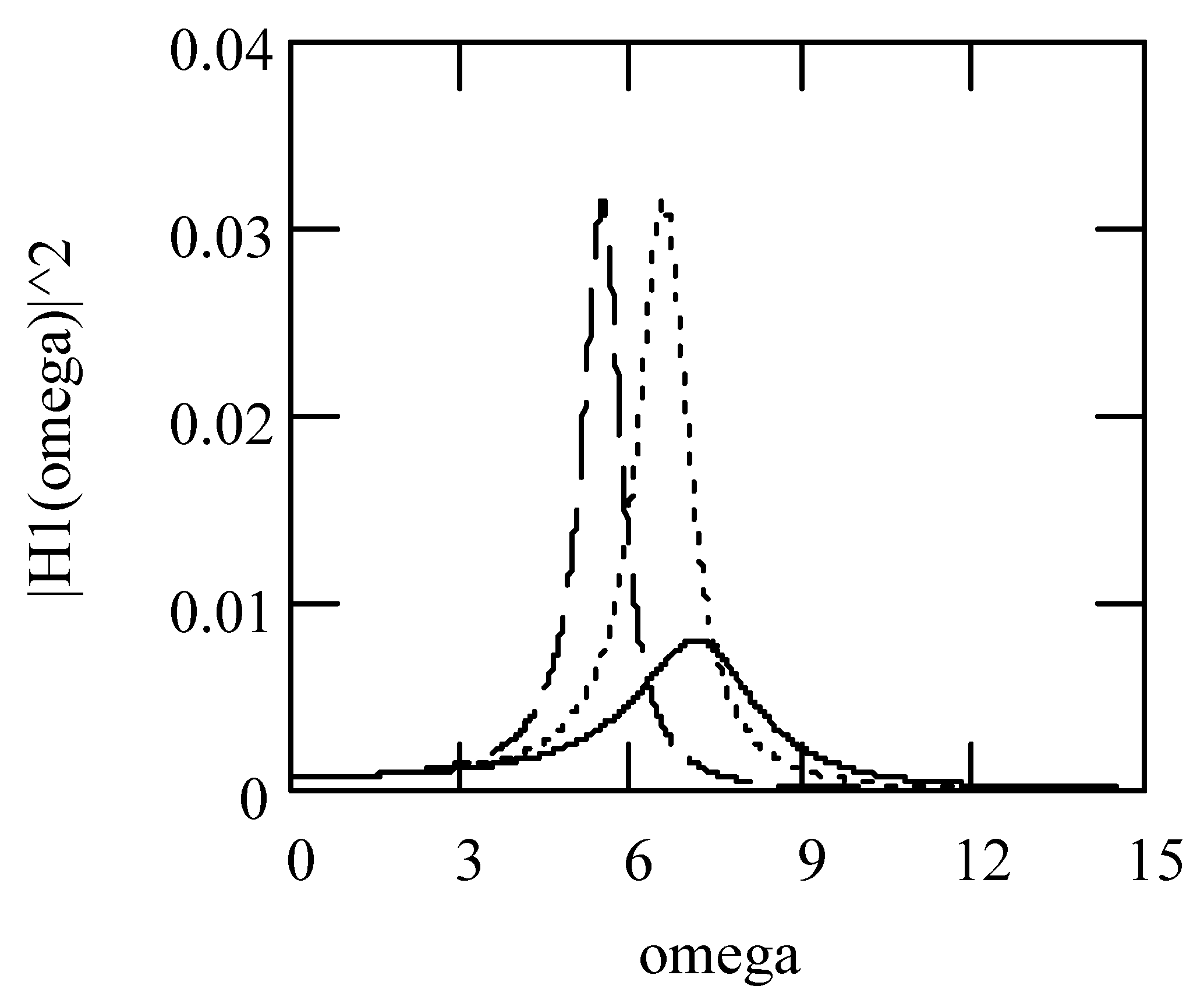
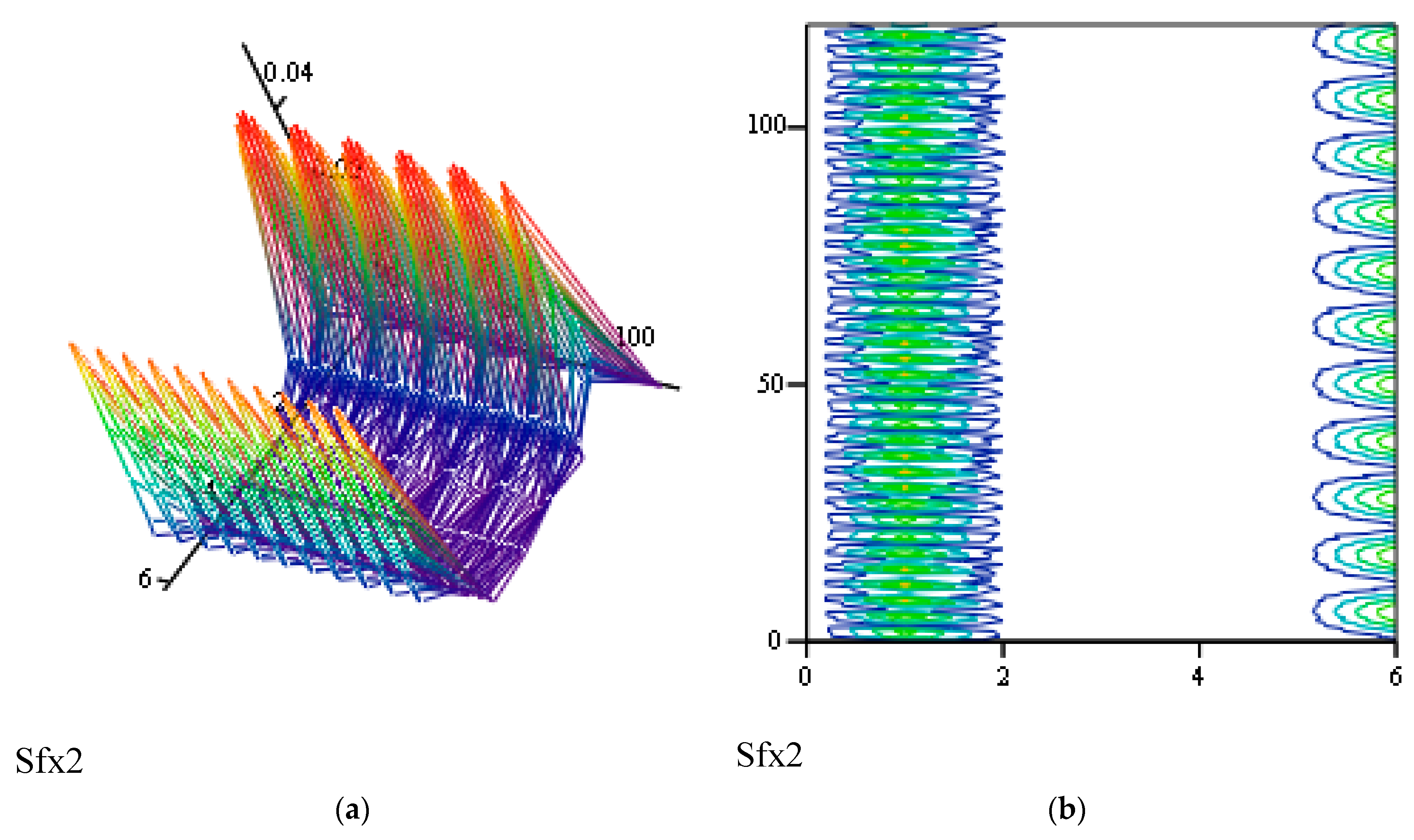
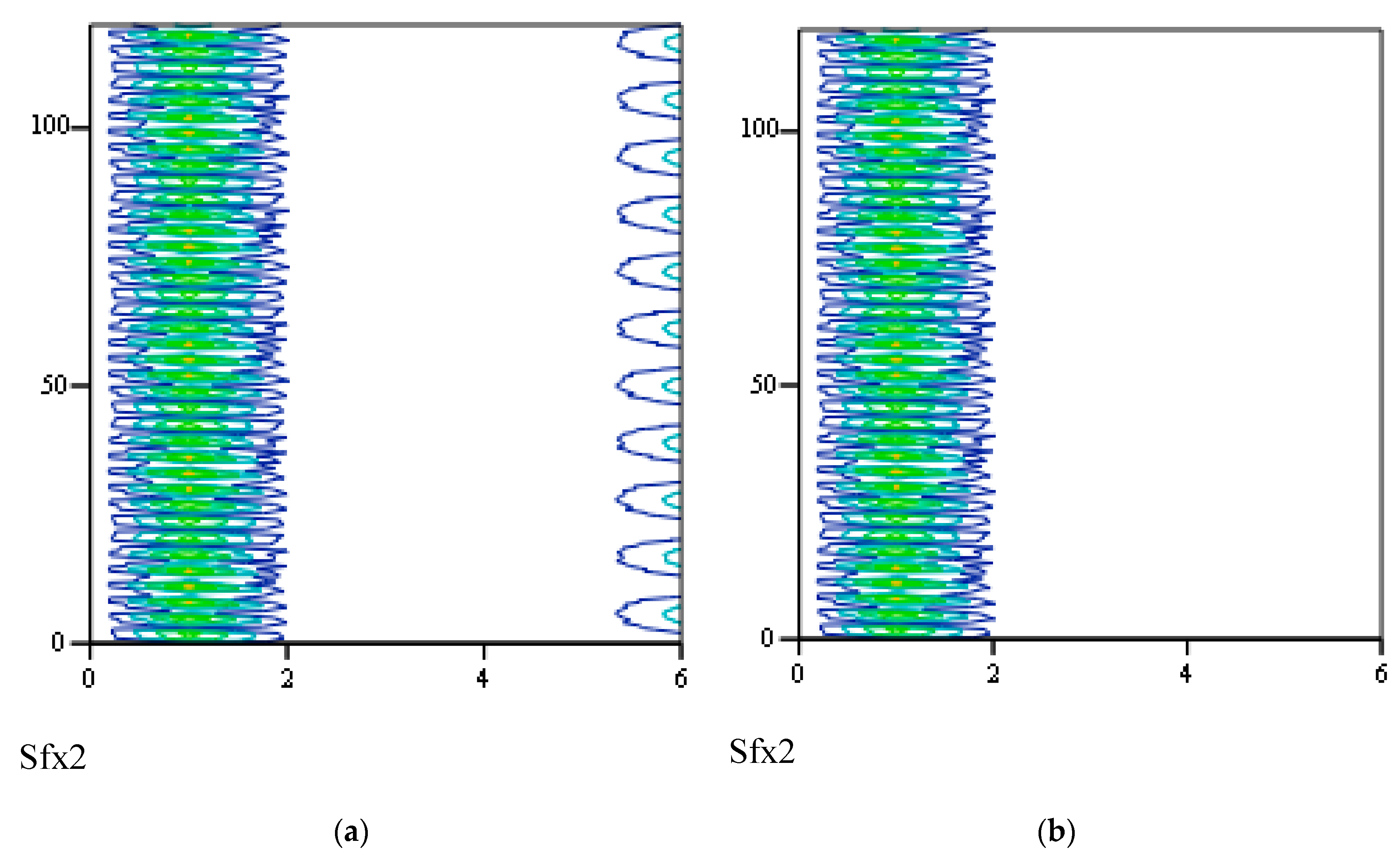
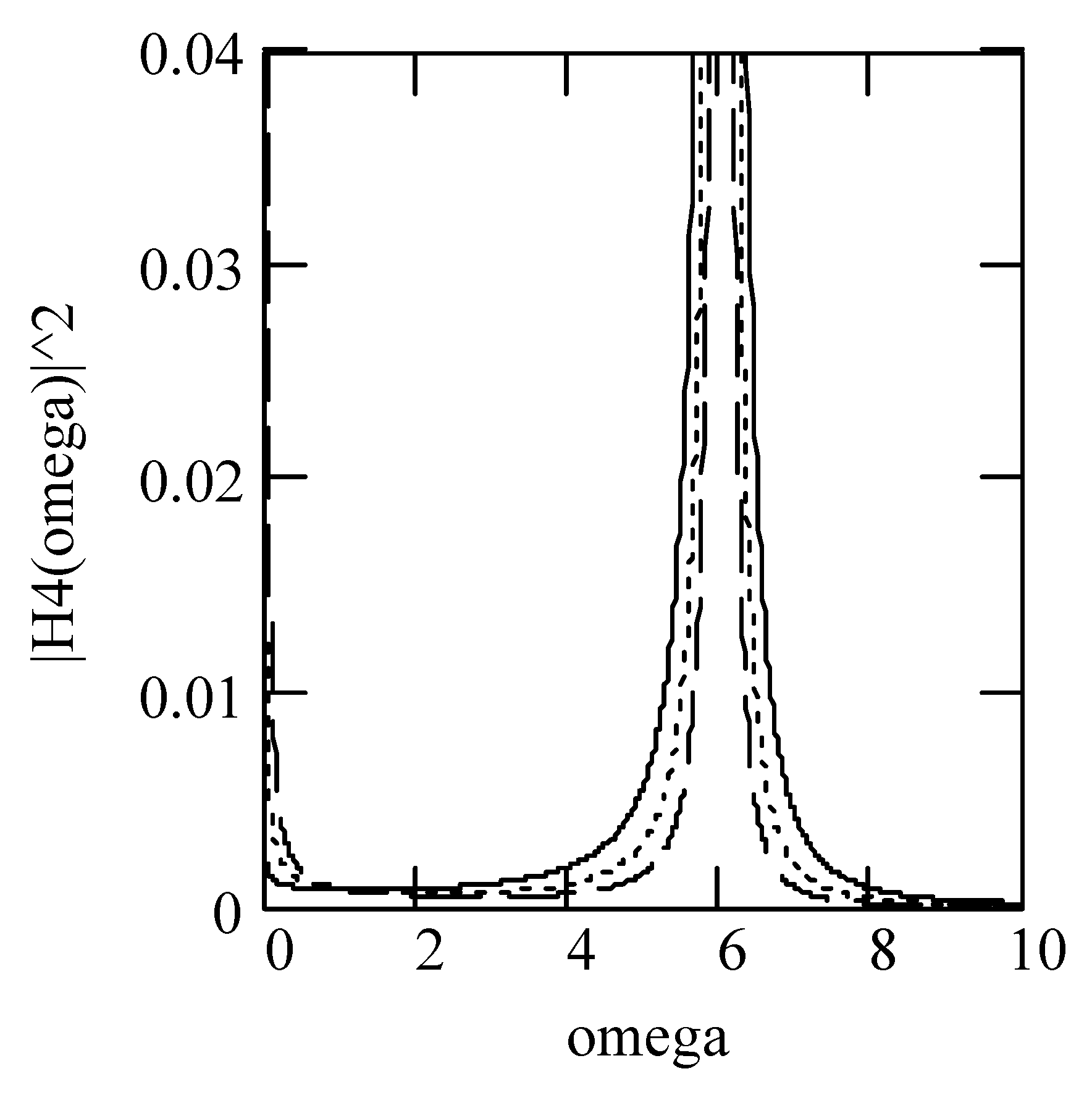
3.3. Responses of Class II Fractional Vibrators Driven by fGn
3.3.1. Computation Methods
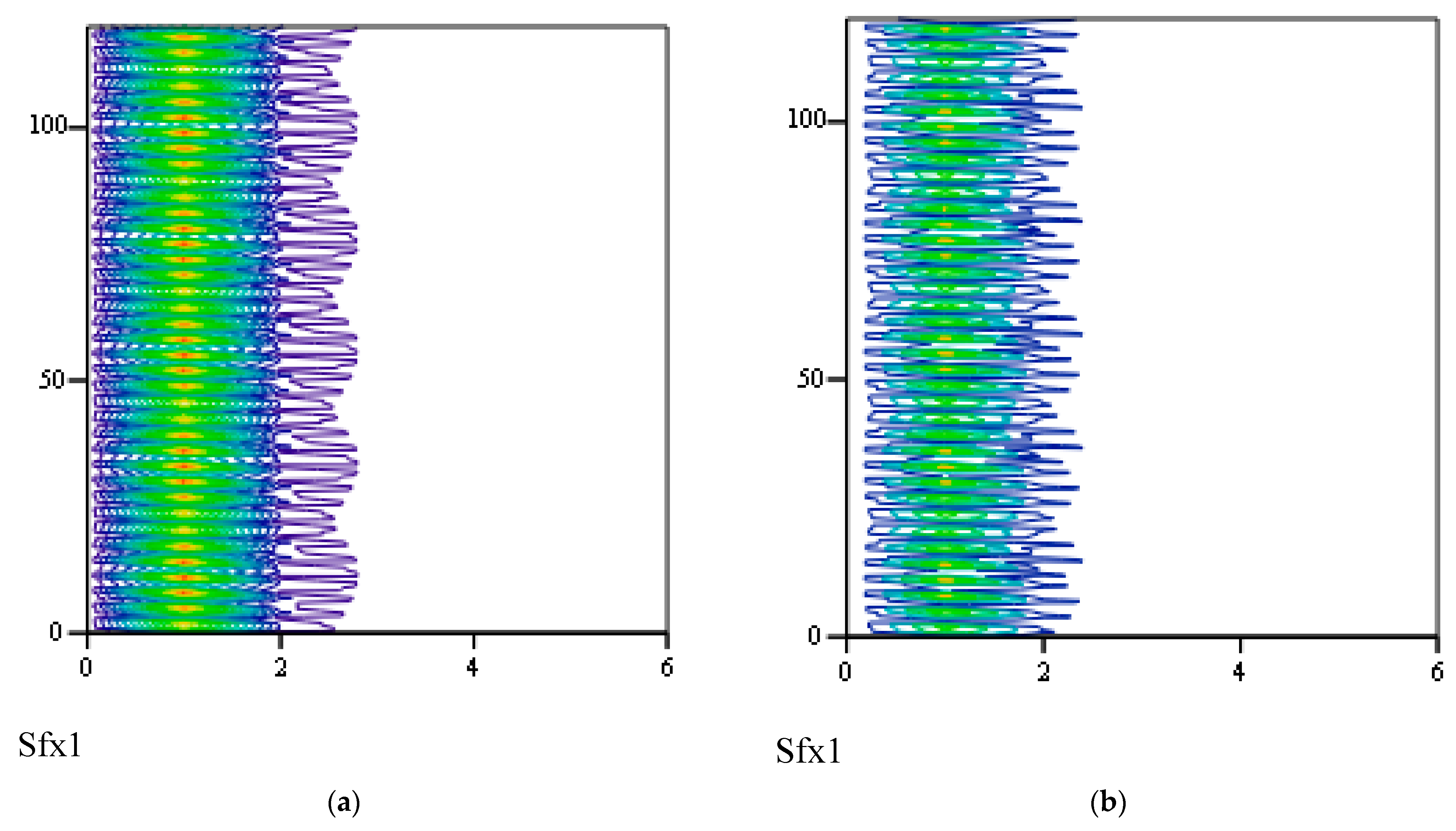
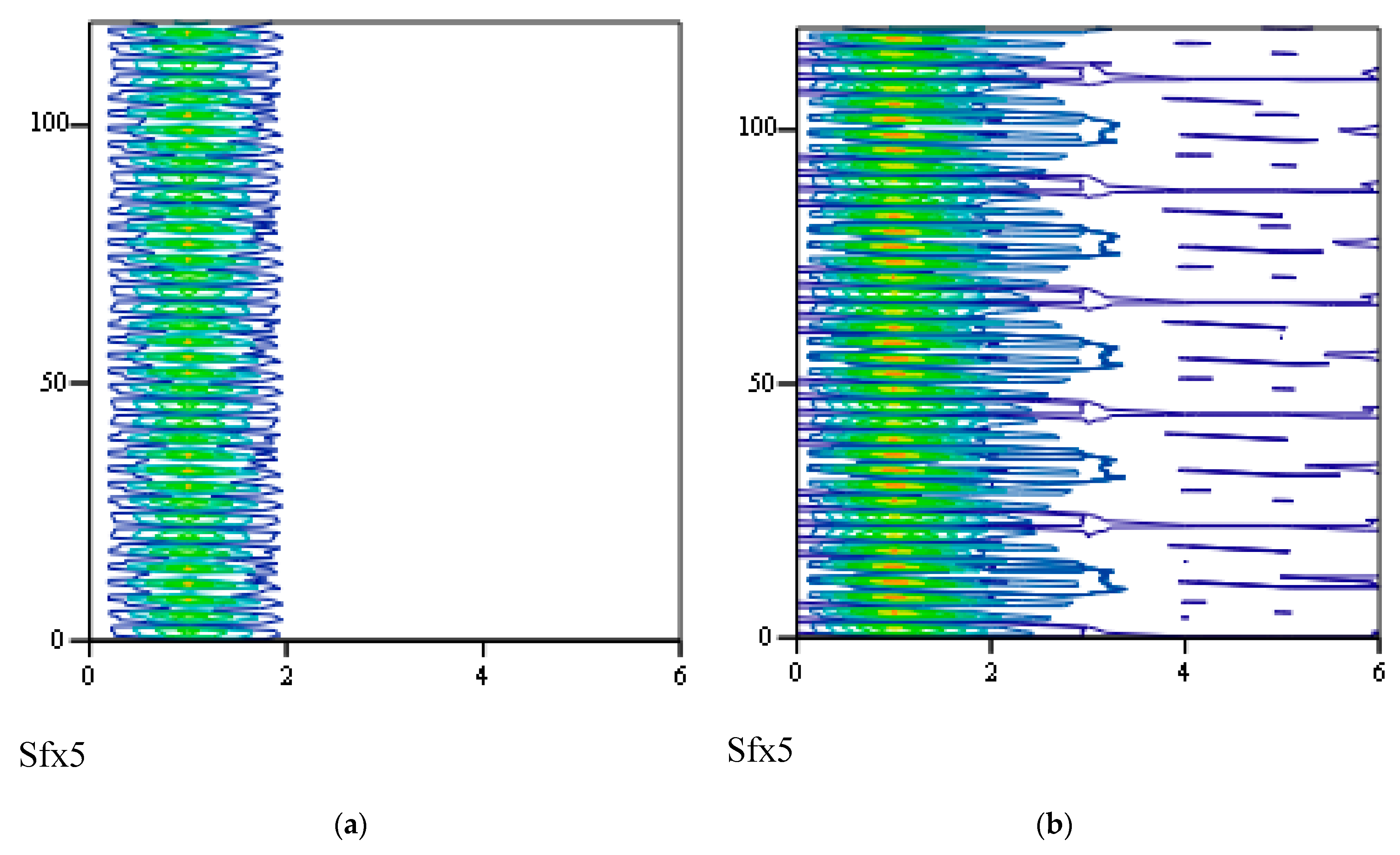
3.3.2. Effects of β on Responses
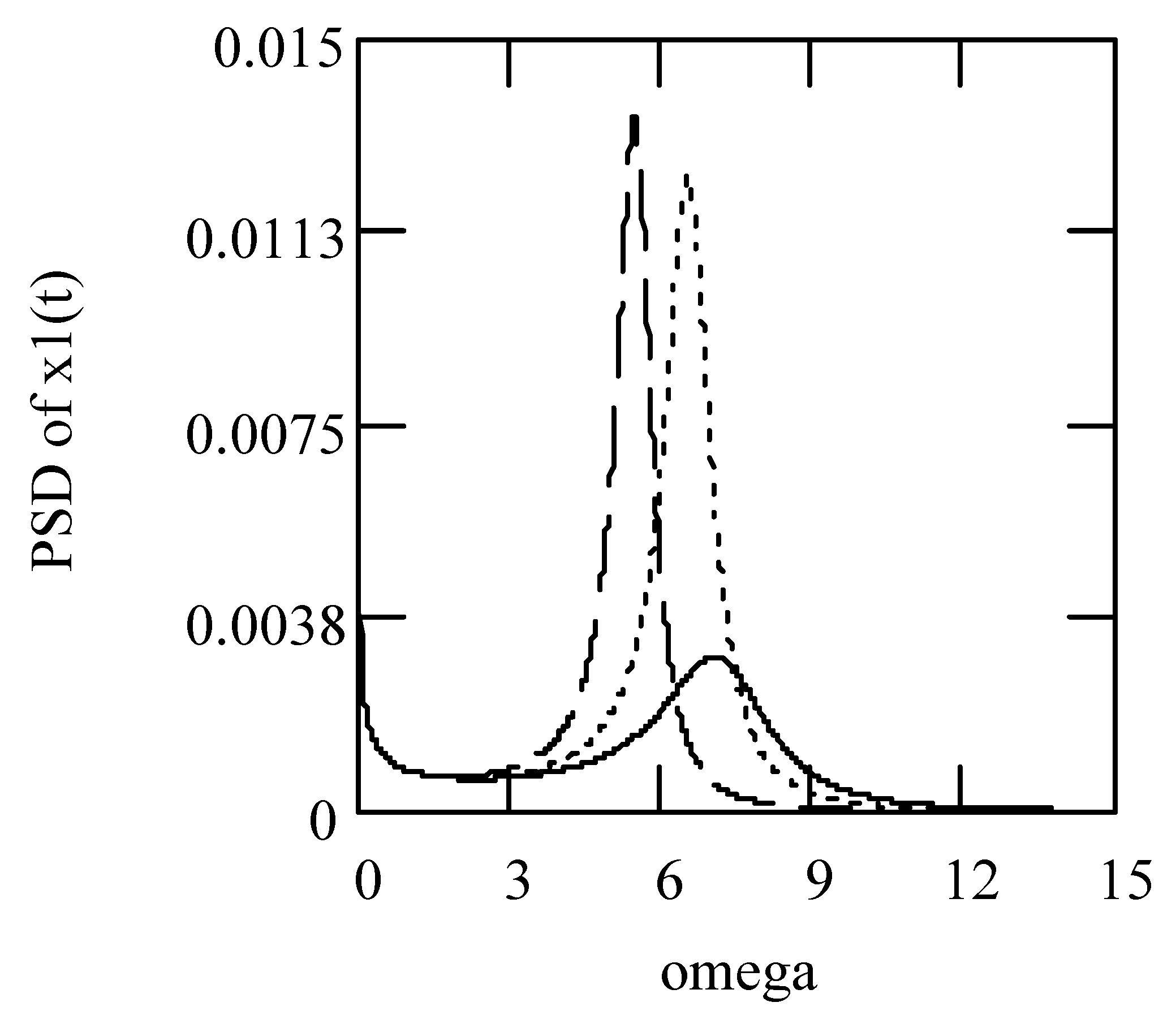
3.4. Responses of Class III Fractional Vibrators Driven by fGn
3.4.1. Computations
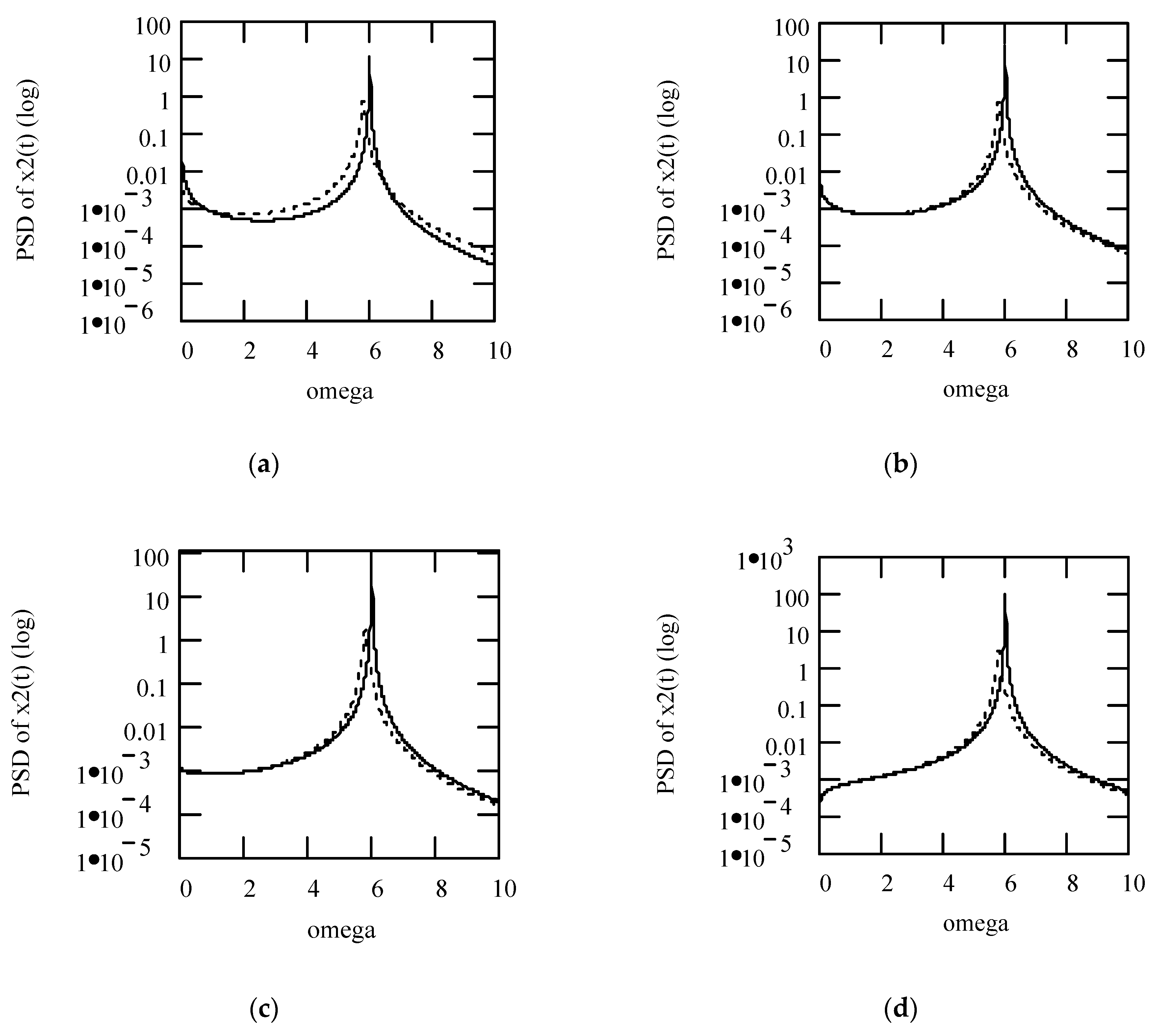
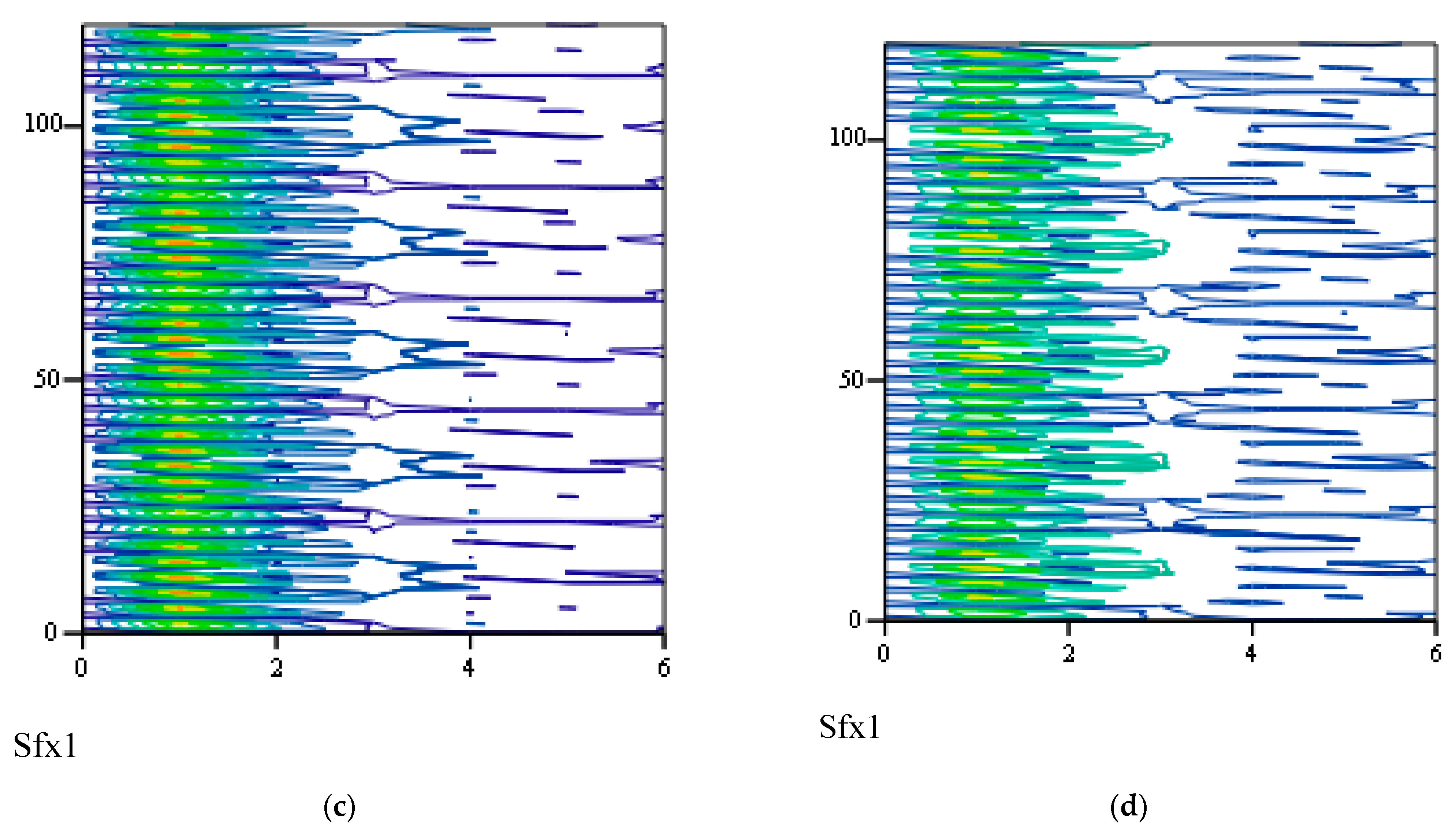
3.4.2. Effects of α and β on Responses
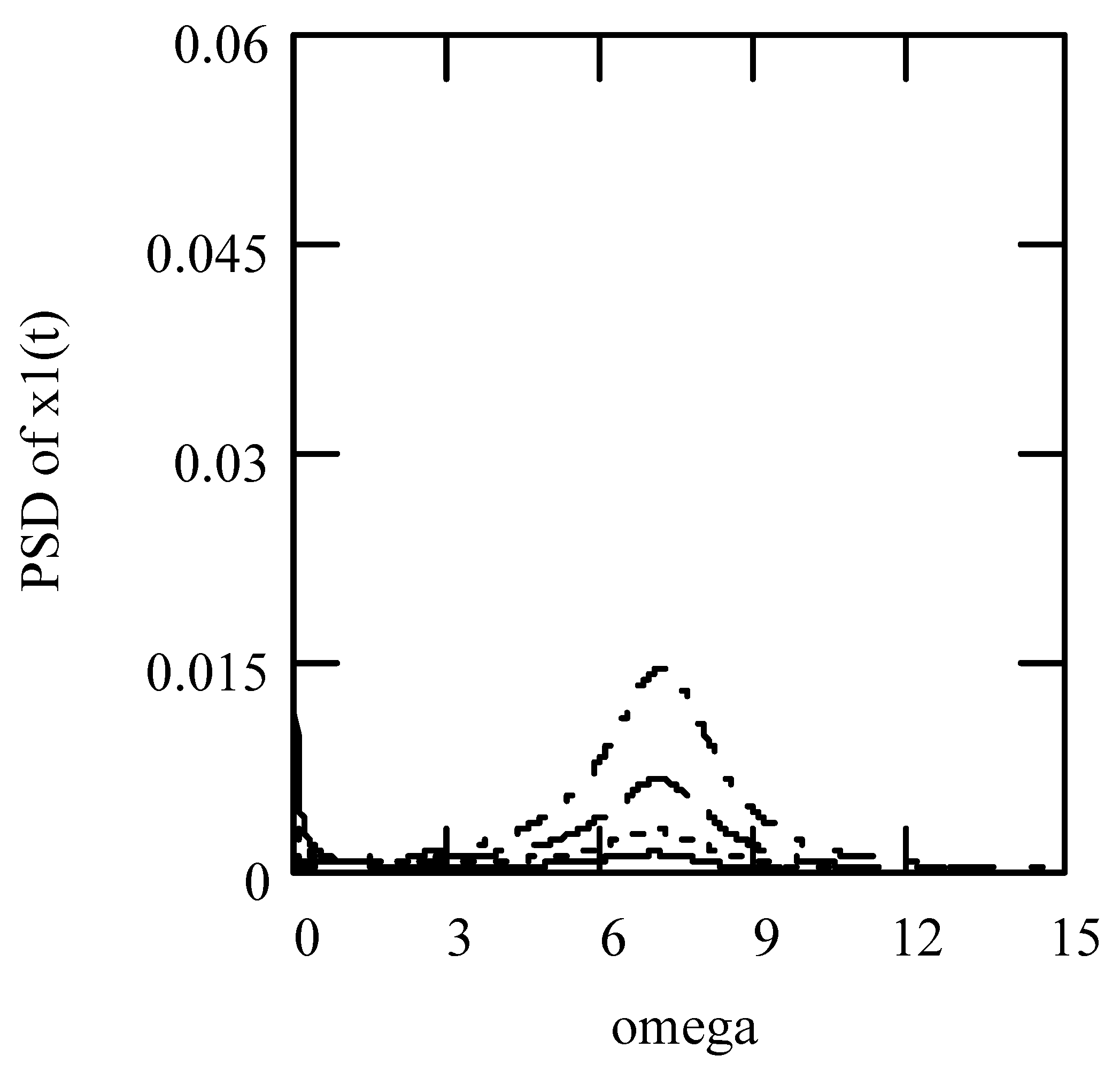
3.5. Responses of Class IV Fractional Vibrators Driven by fGn
3.5.1. Computations
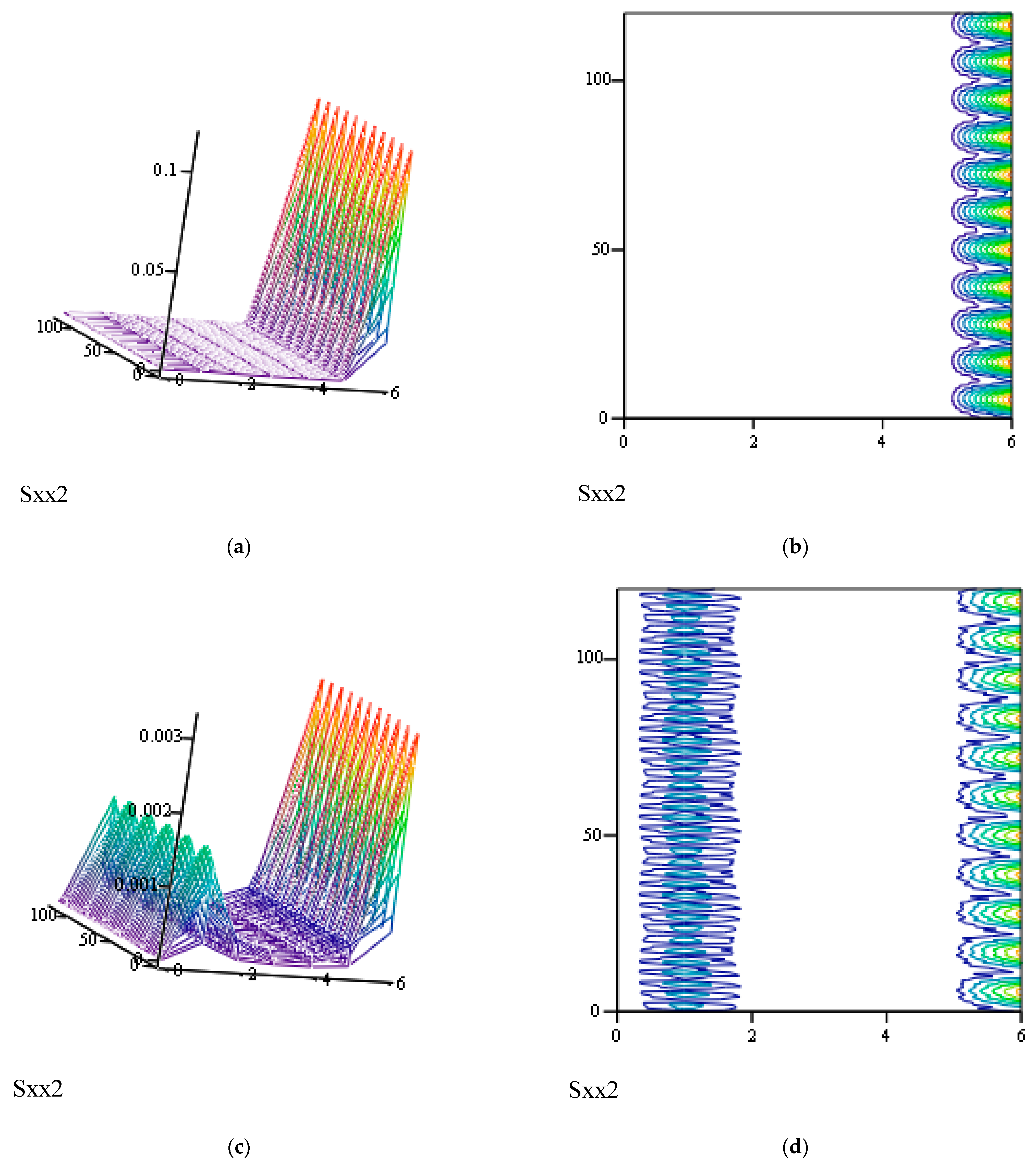
3.5.2. Effects of α and λ on Responses
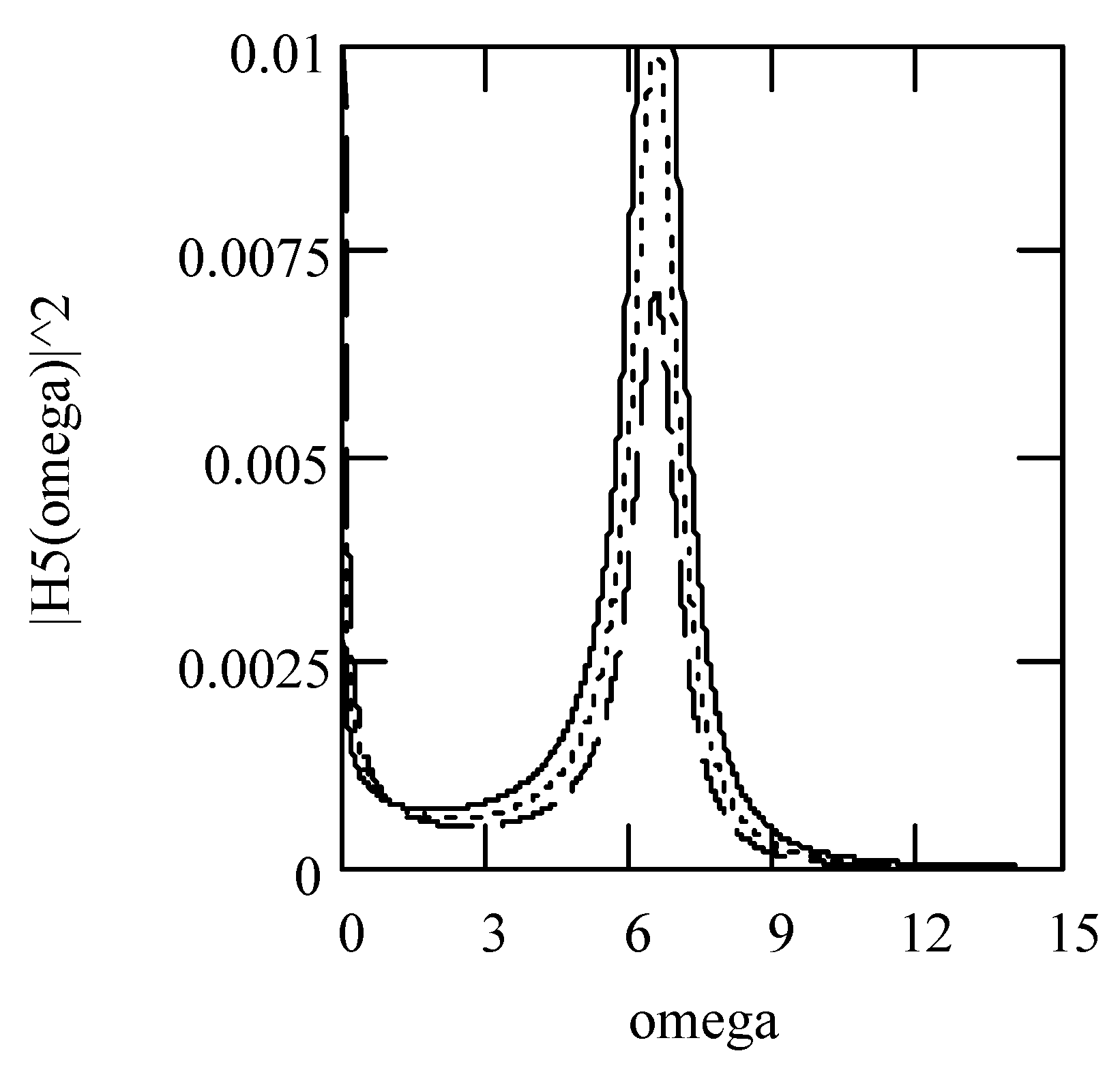
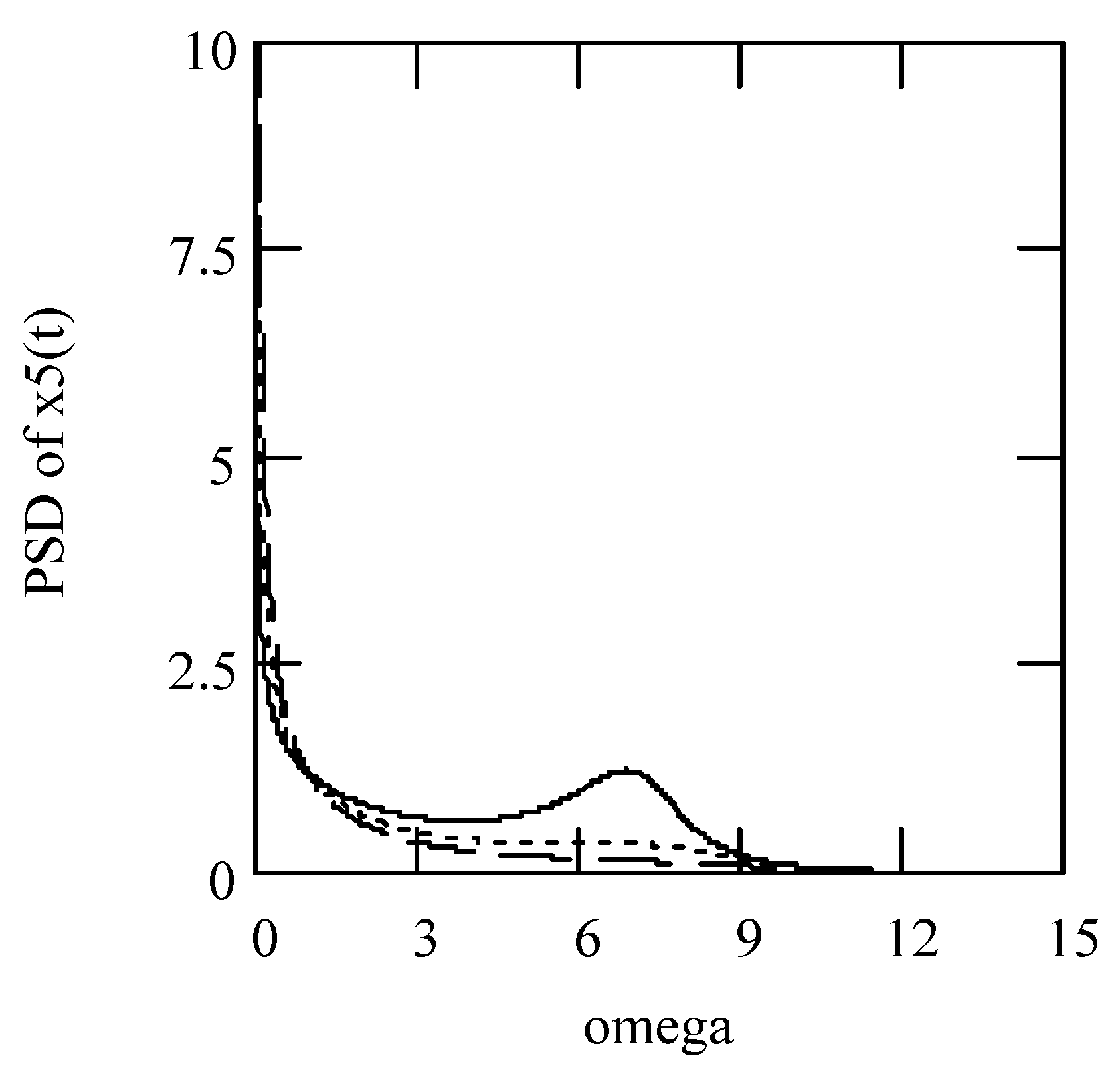
3.6. Responses of Class V Fractional Vibrators Driven by fGn
3.6.1. Computation Methods
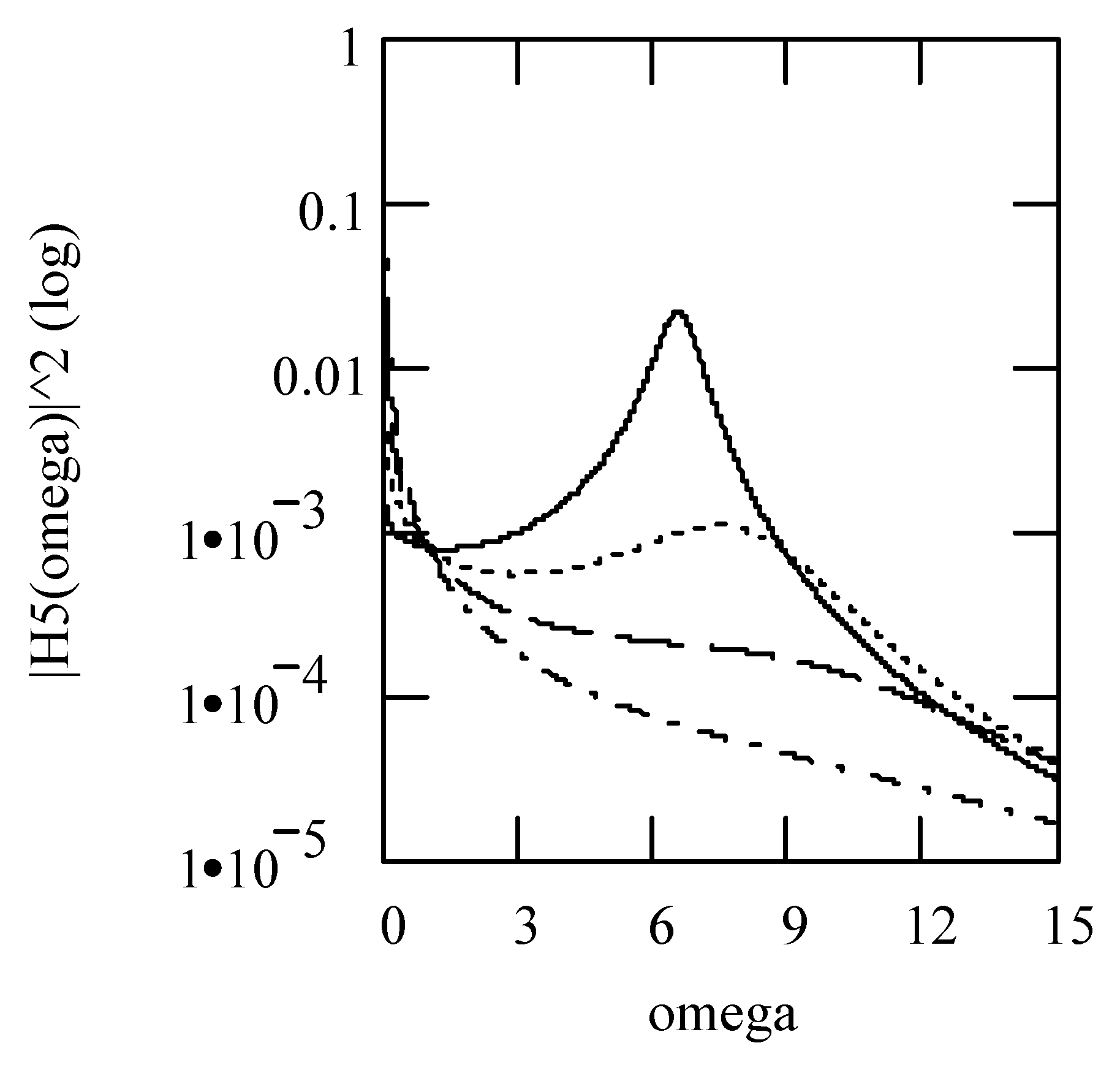
3.6.2. Effects of λ on Responses
3.7. Responses of Class VI Fractional Vibrators Driven by fGn
3.7.1. Computations
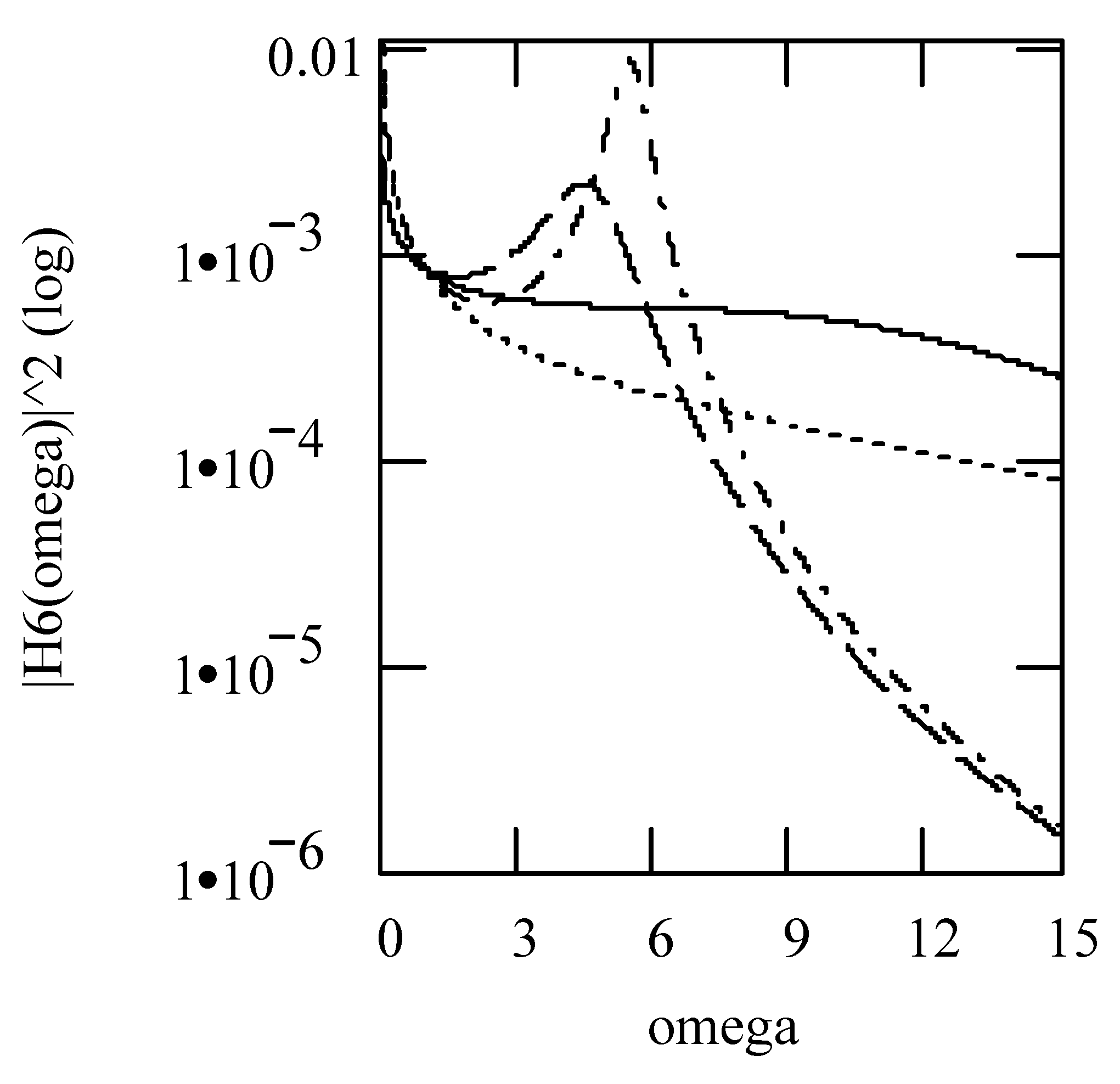
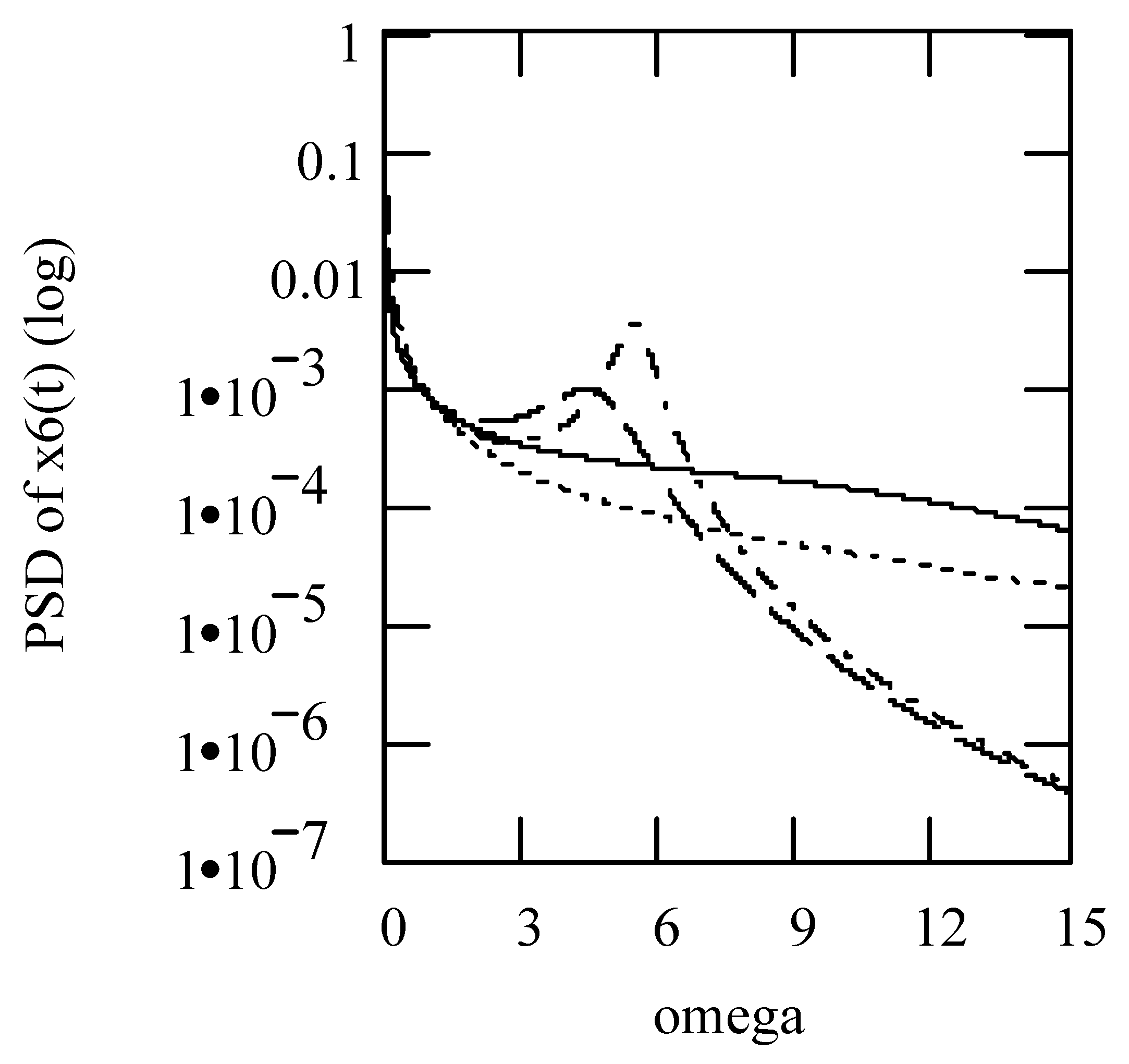
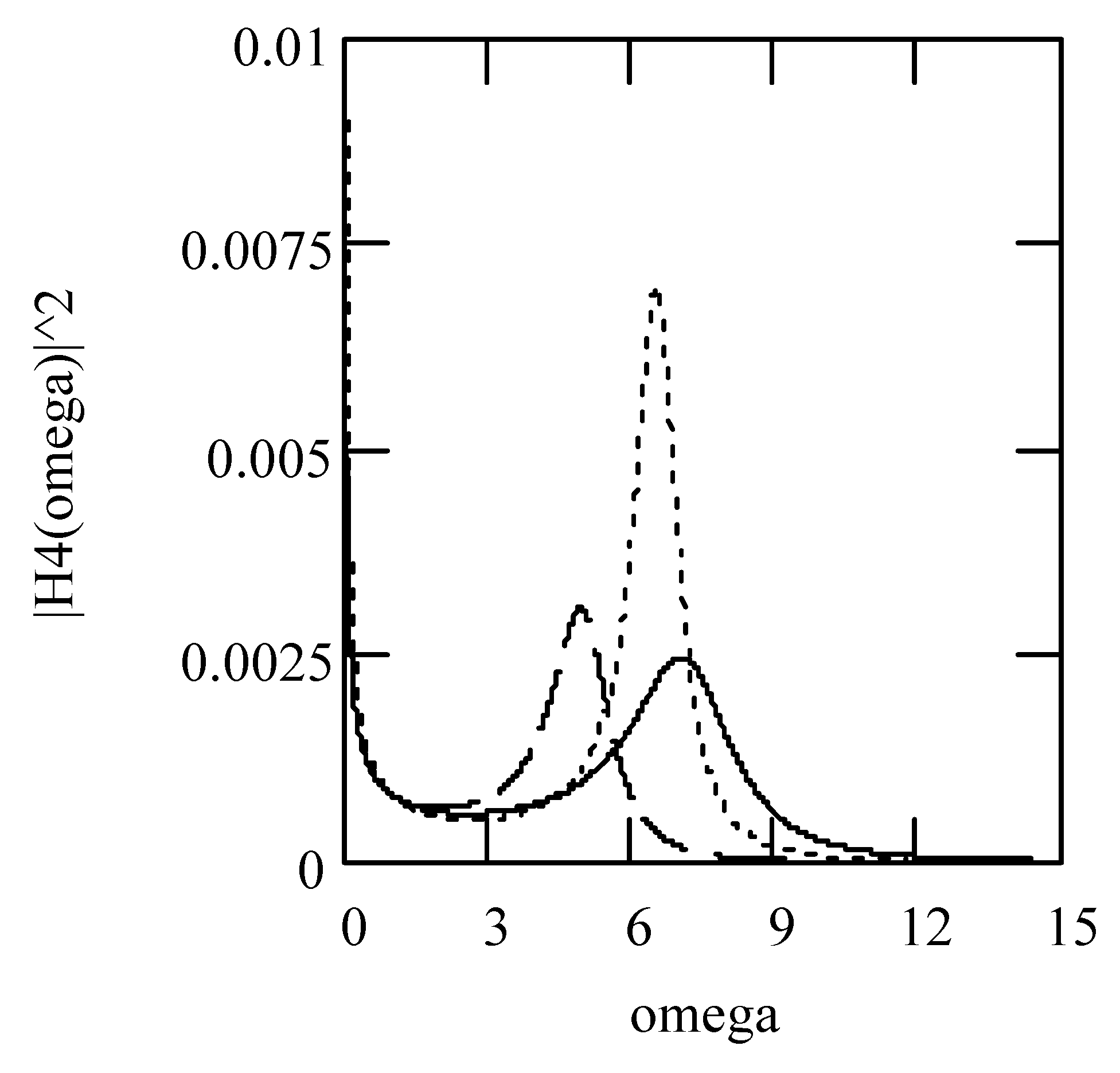
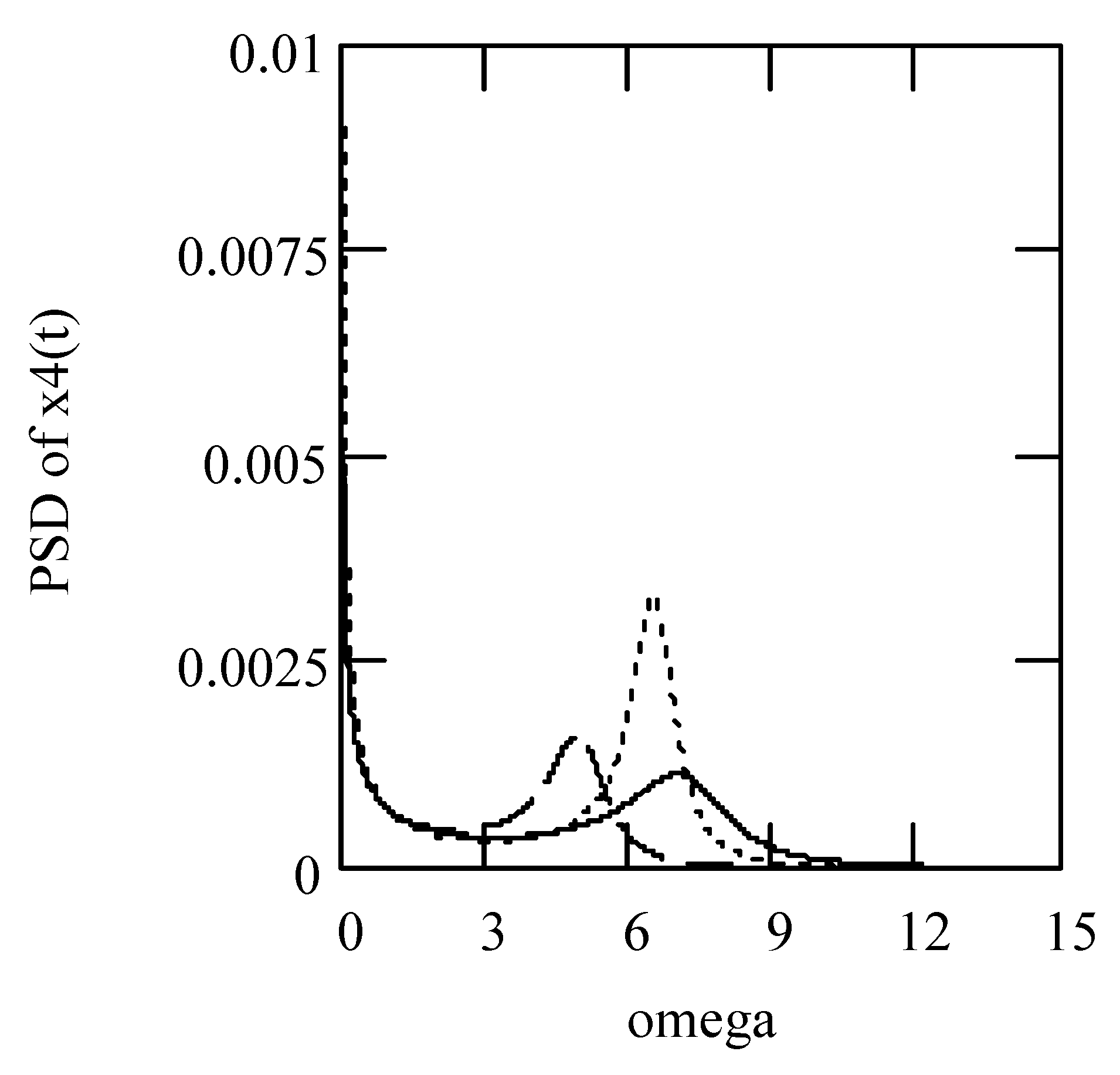
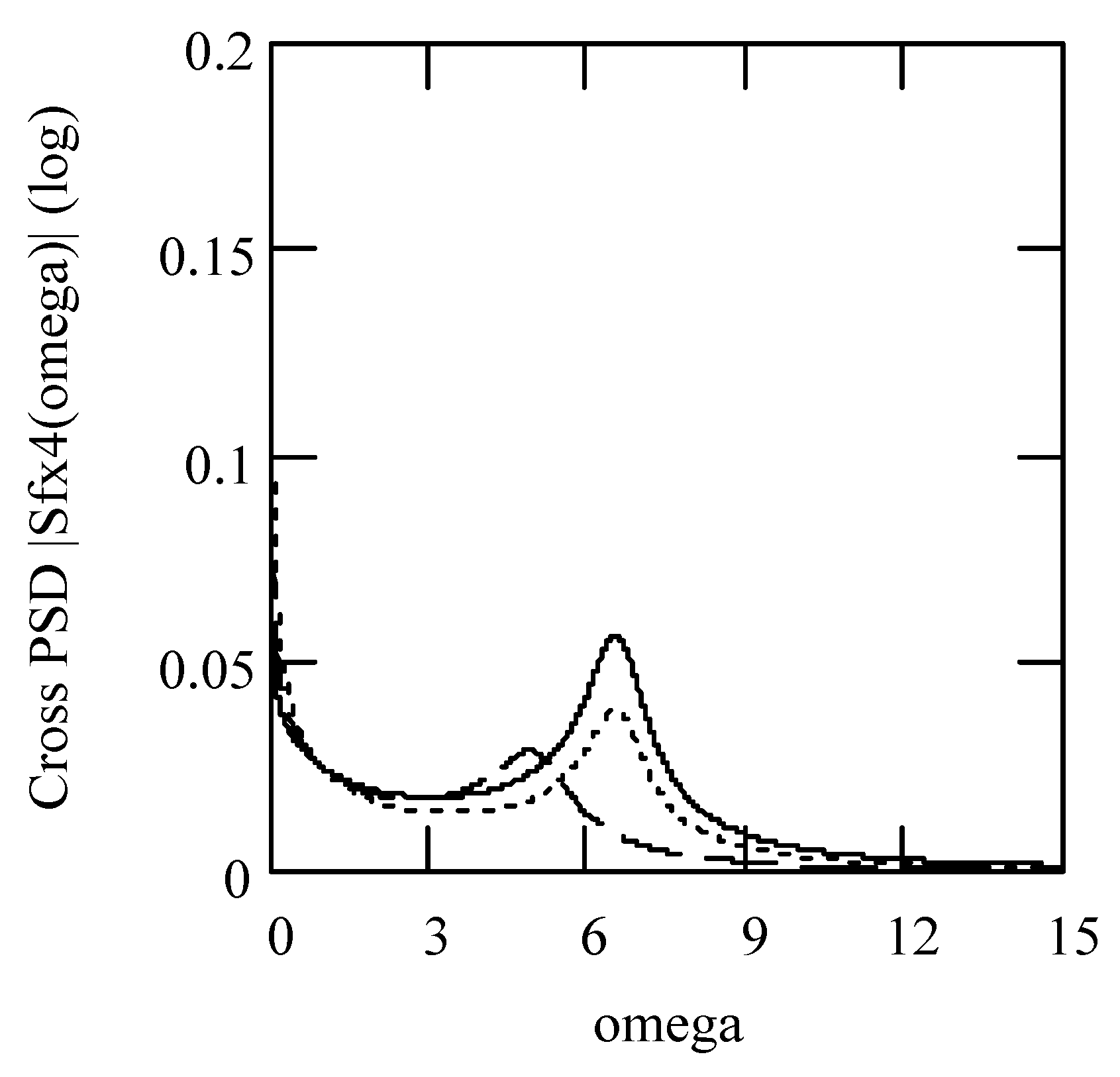
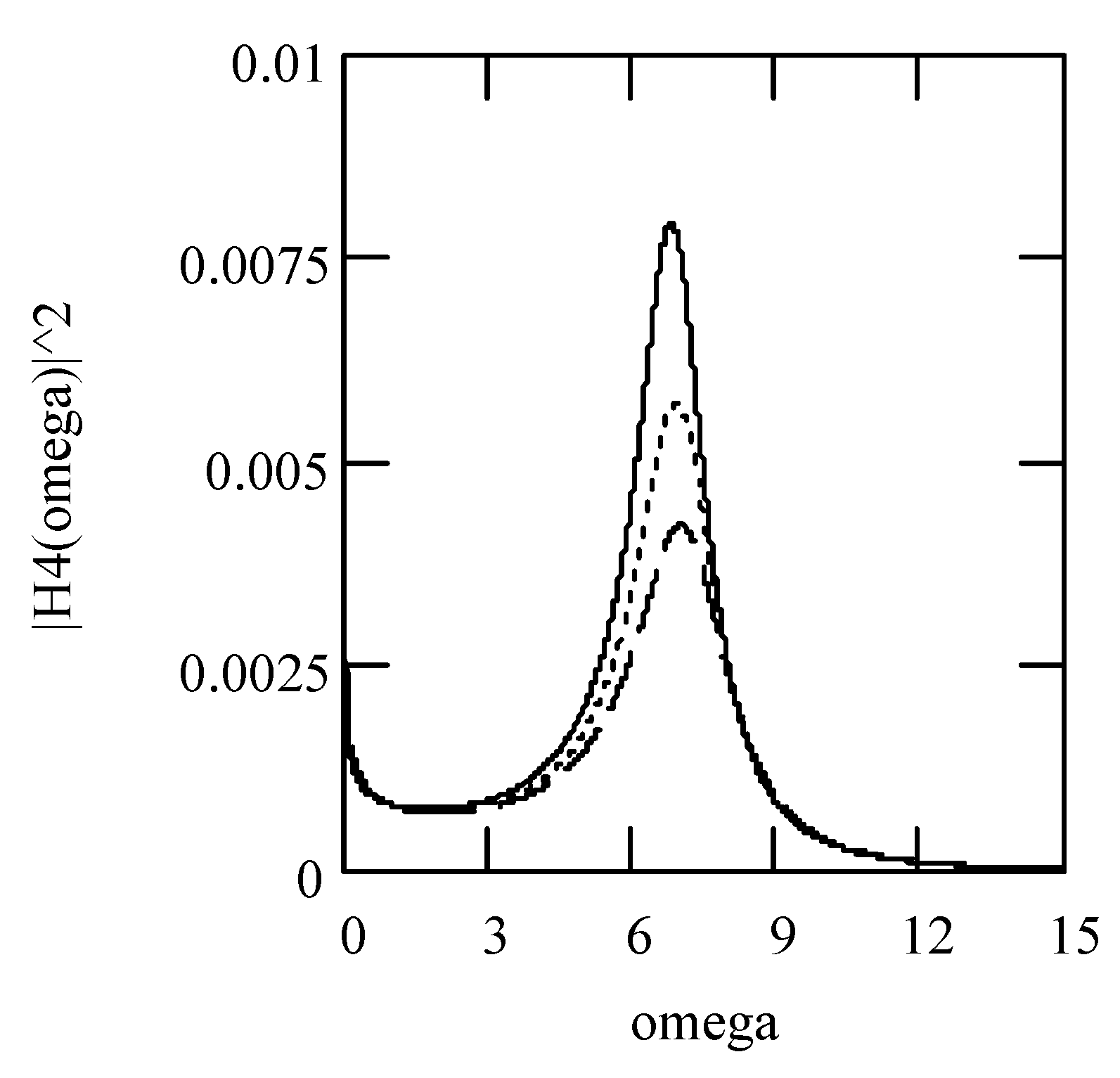
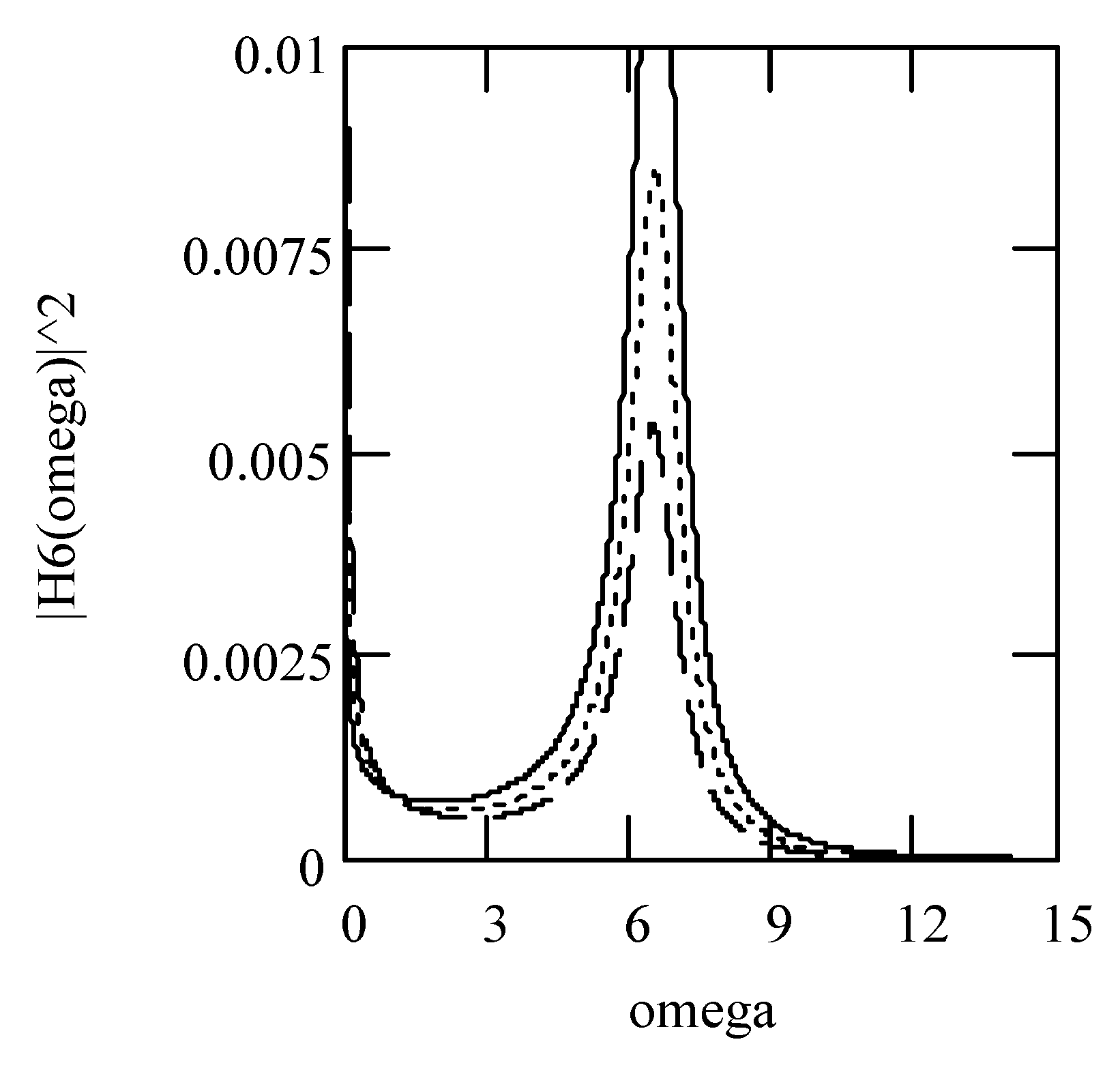
3.7.2. Effects of α, β, λ on Responses
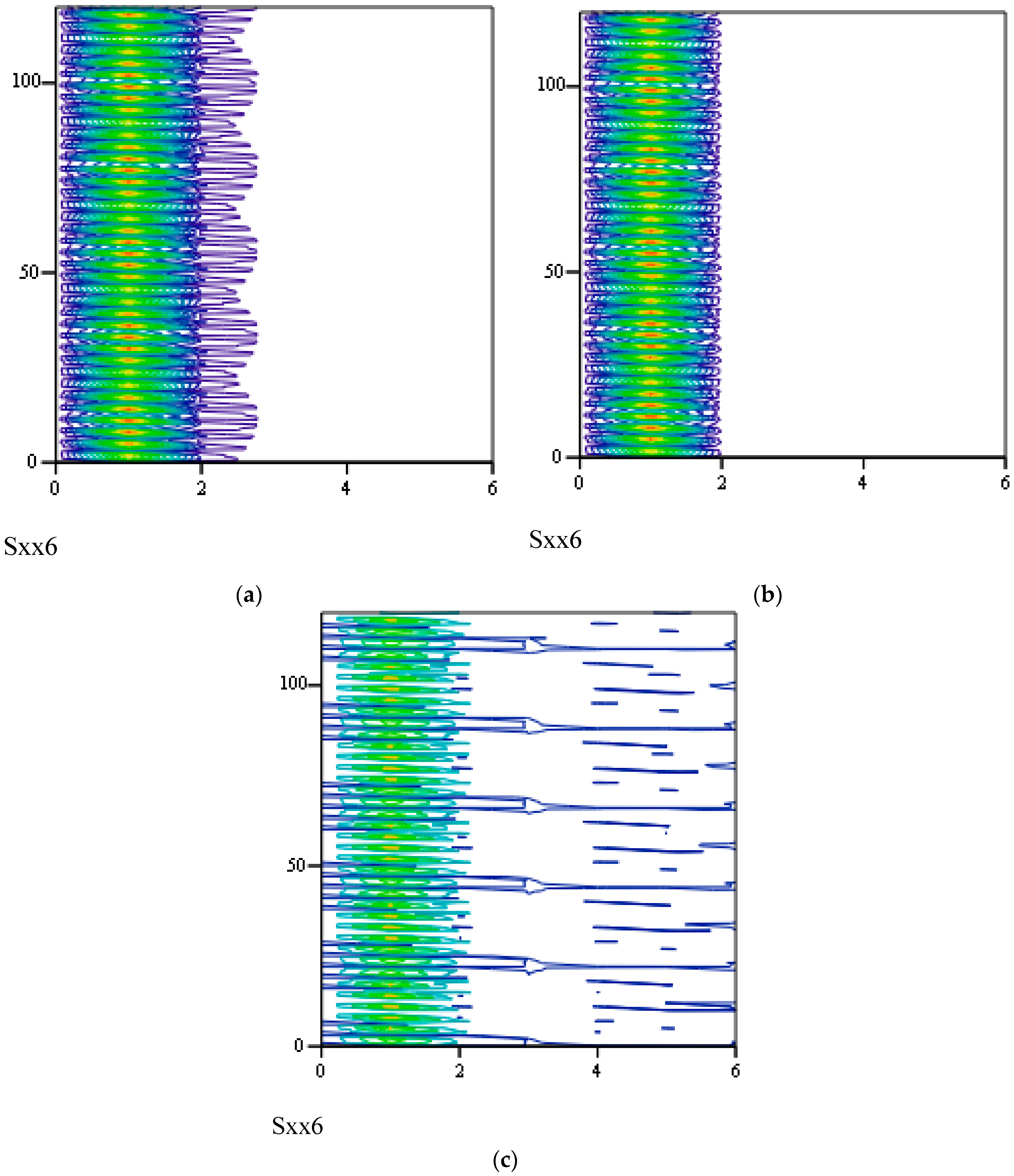
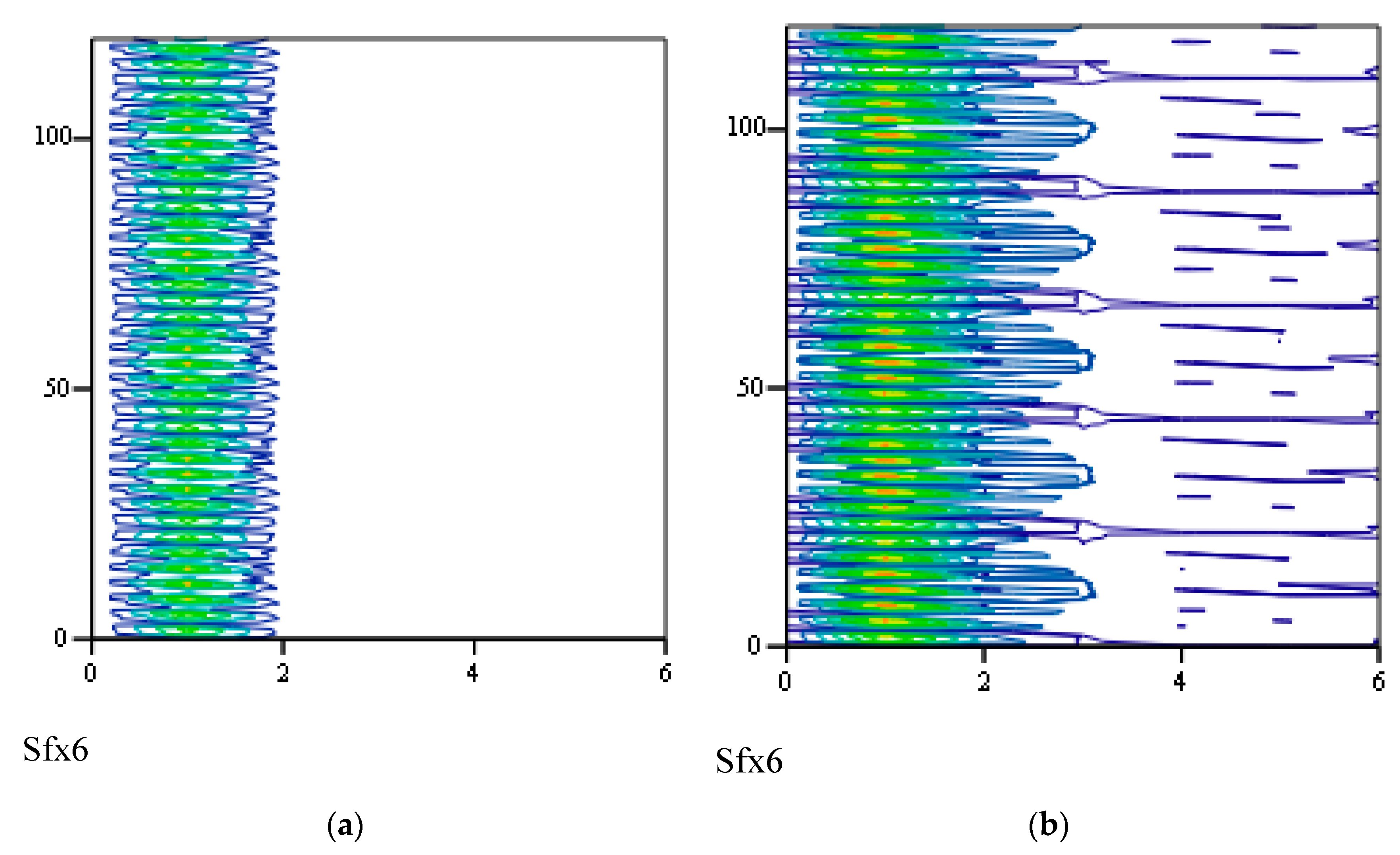
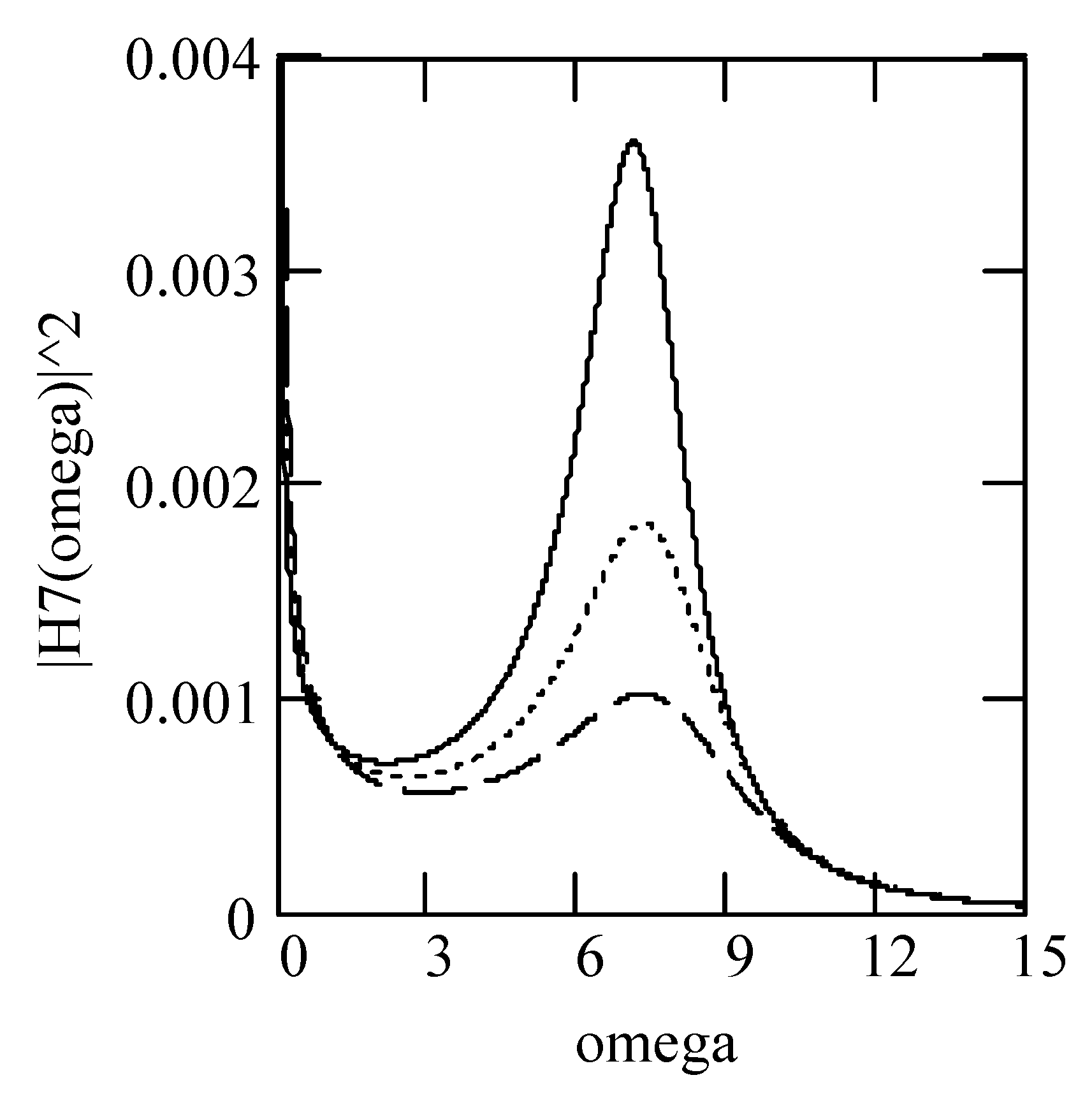
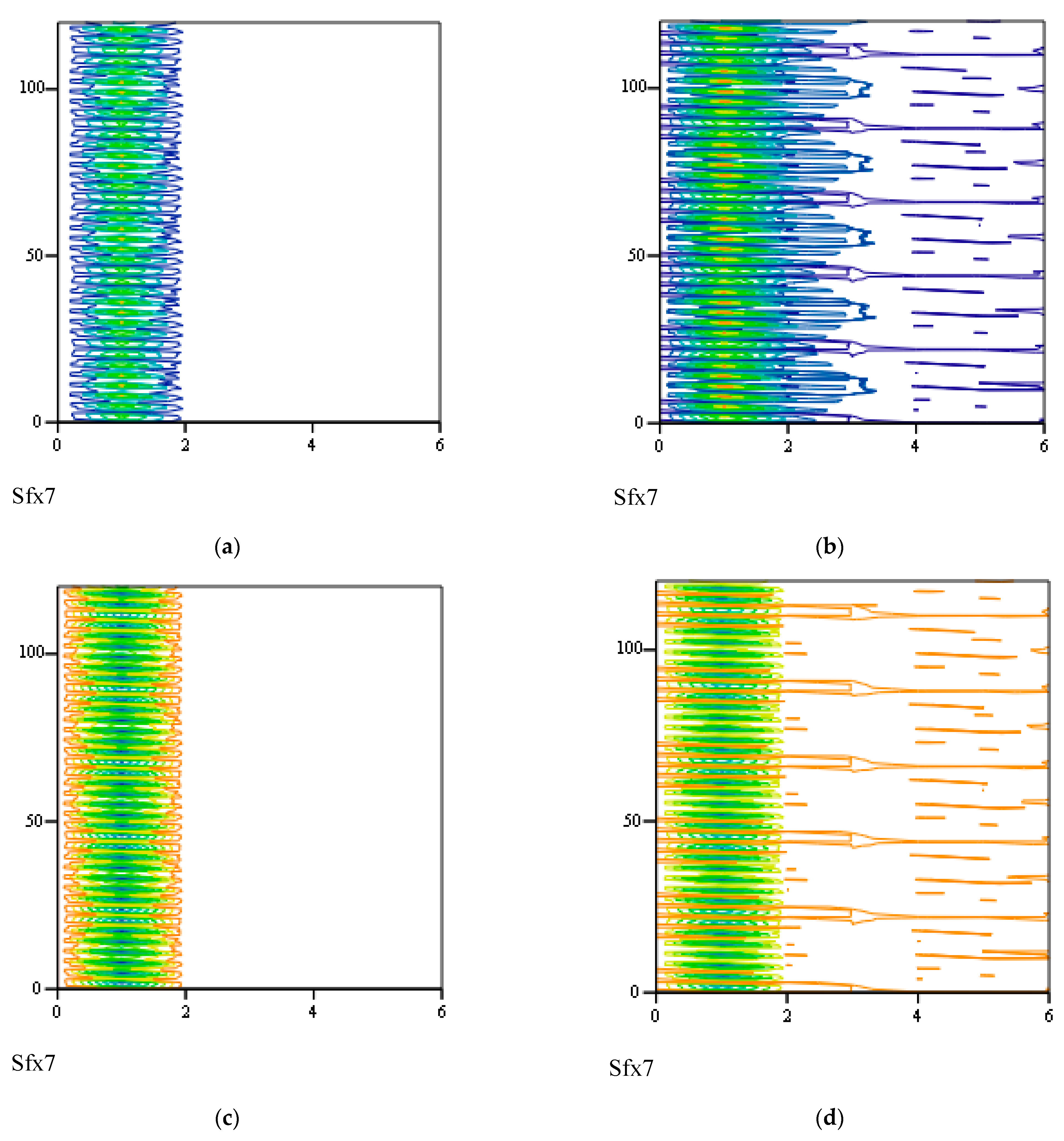
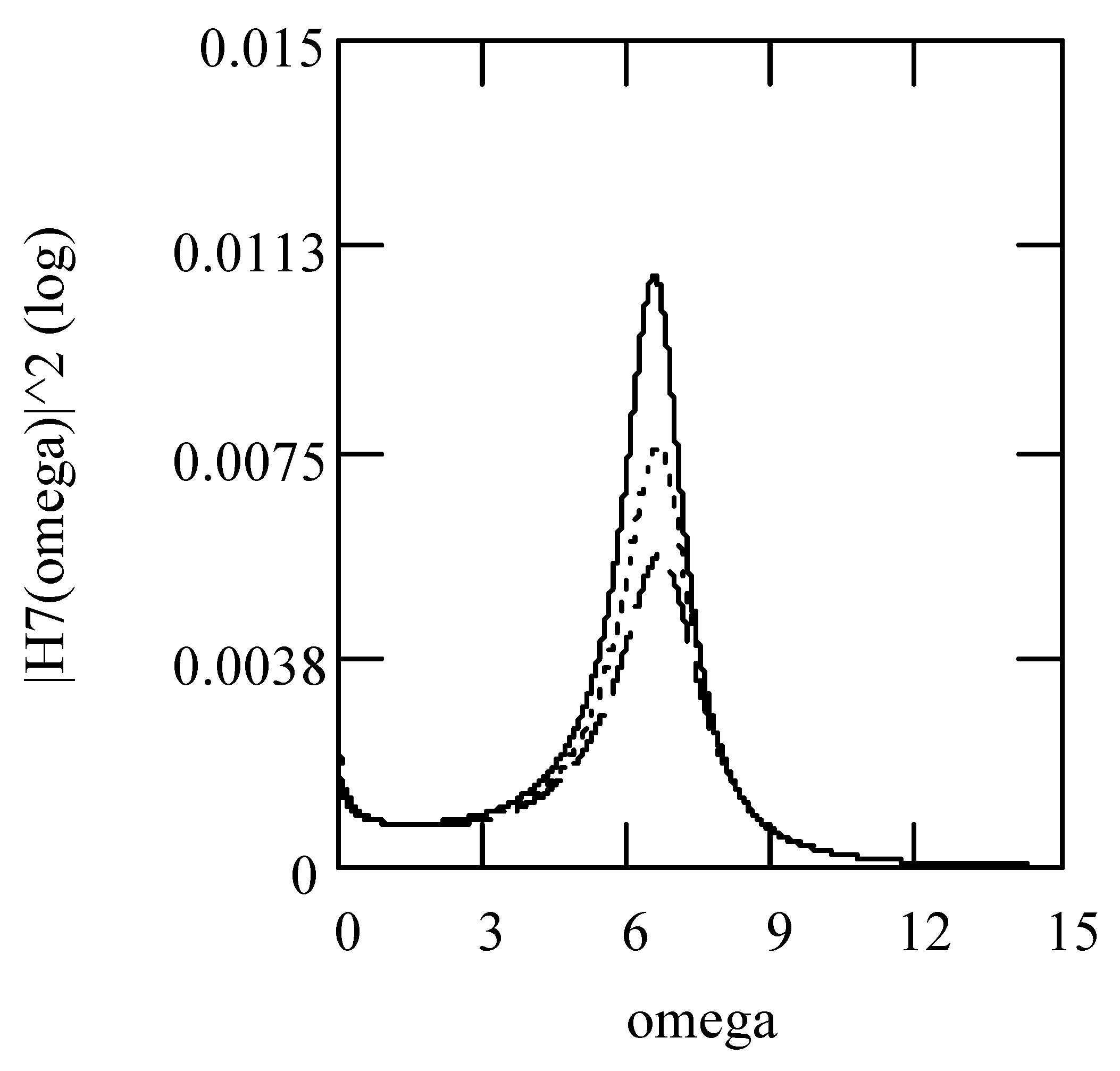
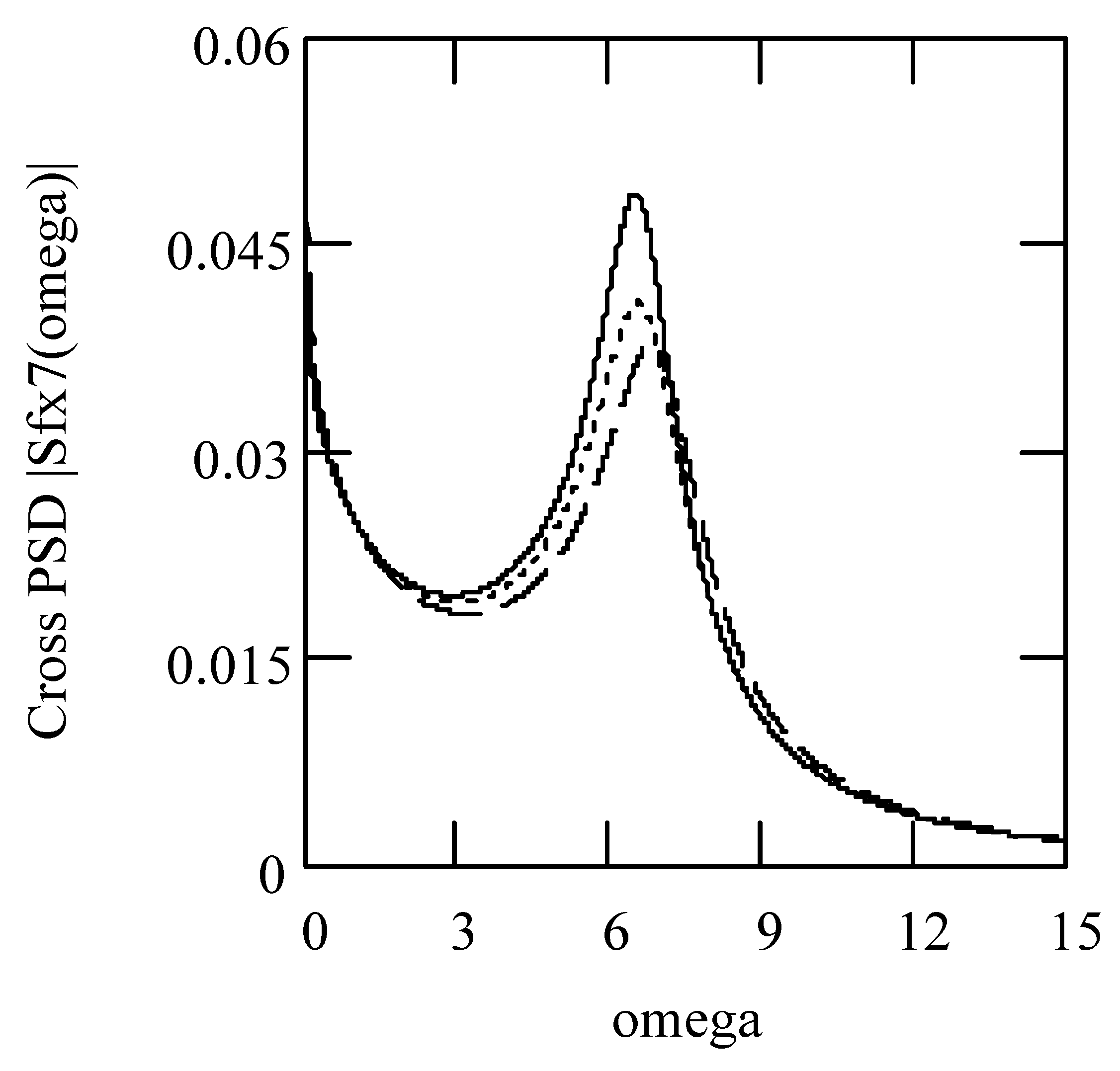
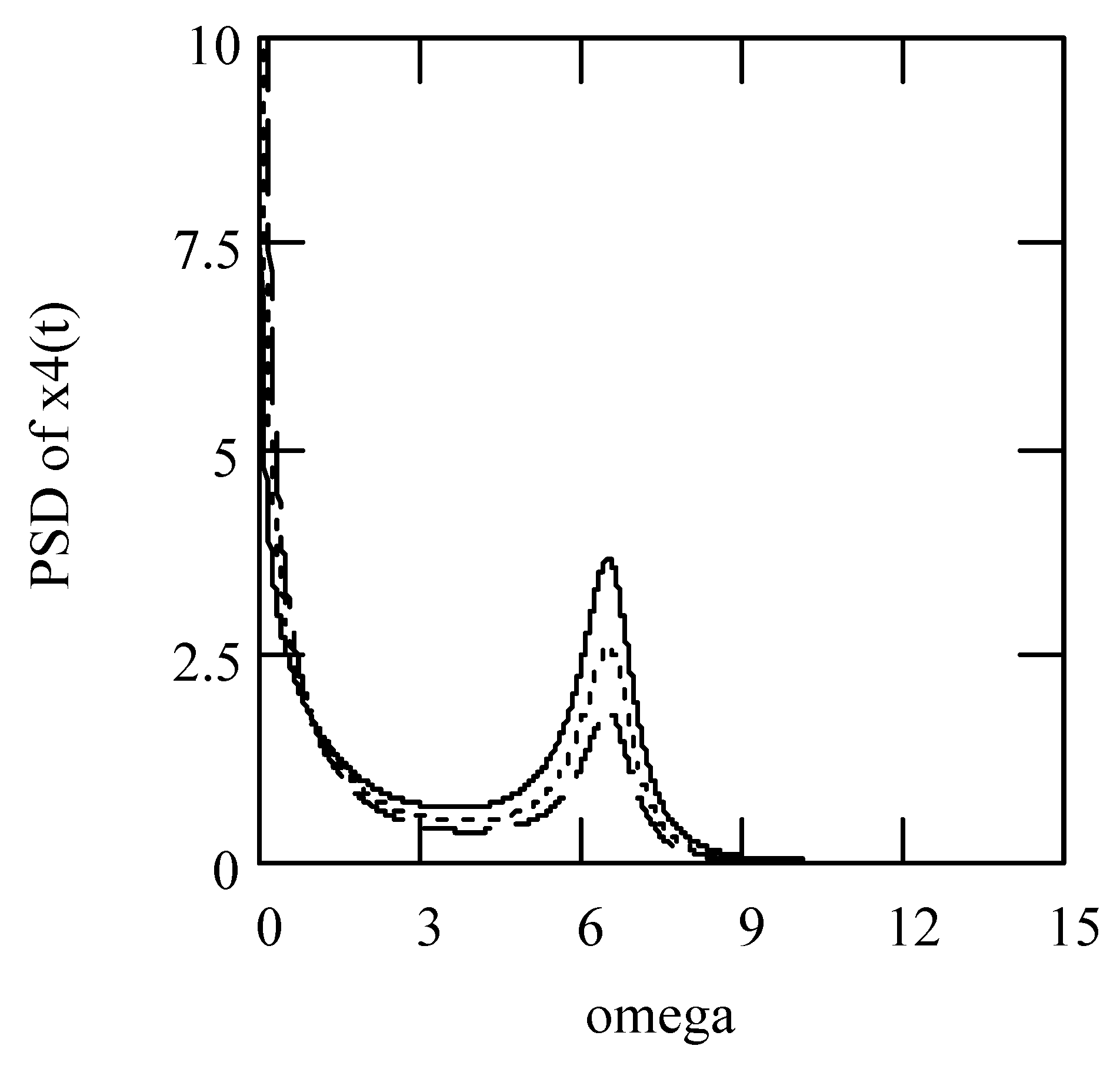
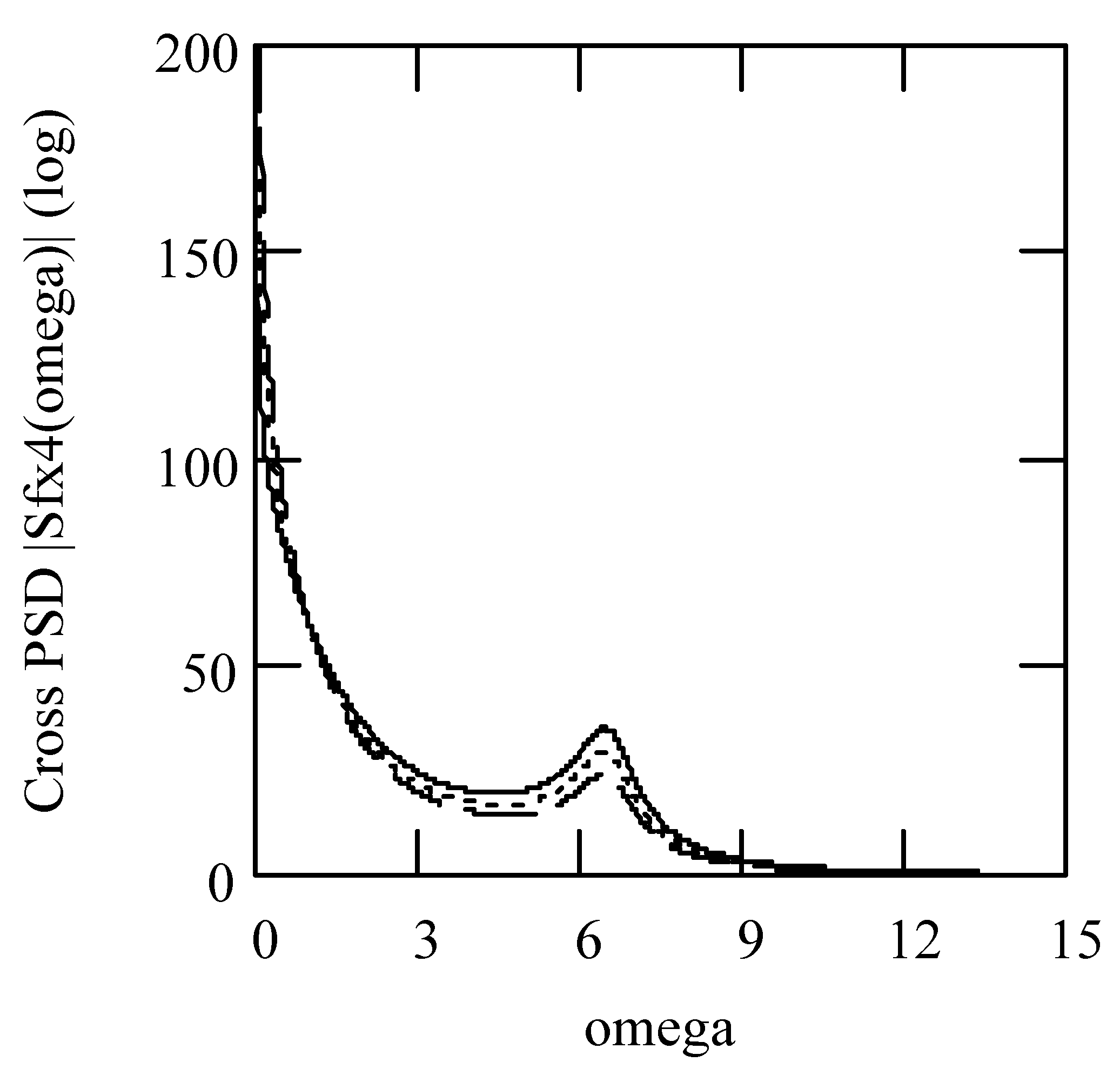
3.8. Responses of Class VII Fractional Vibrators Driven by fGn
3.8.1. Computations
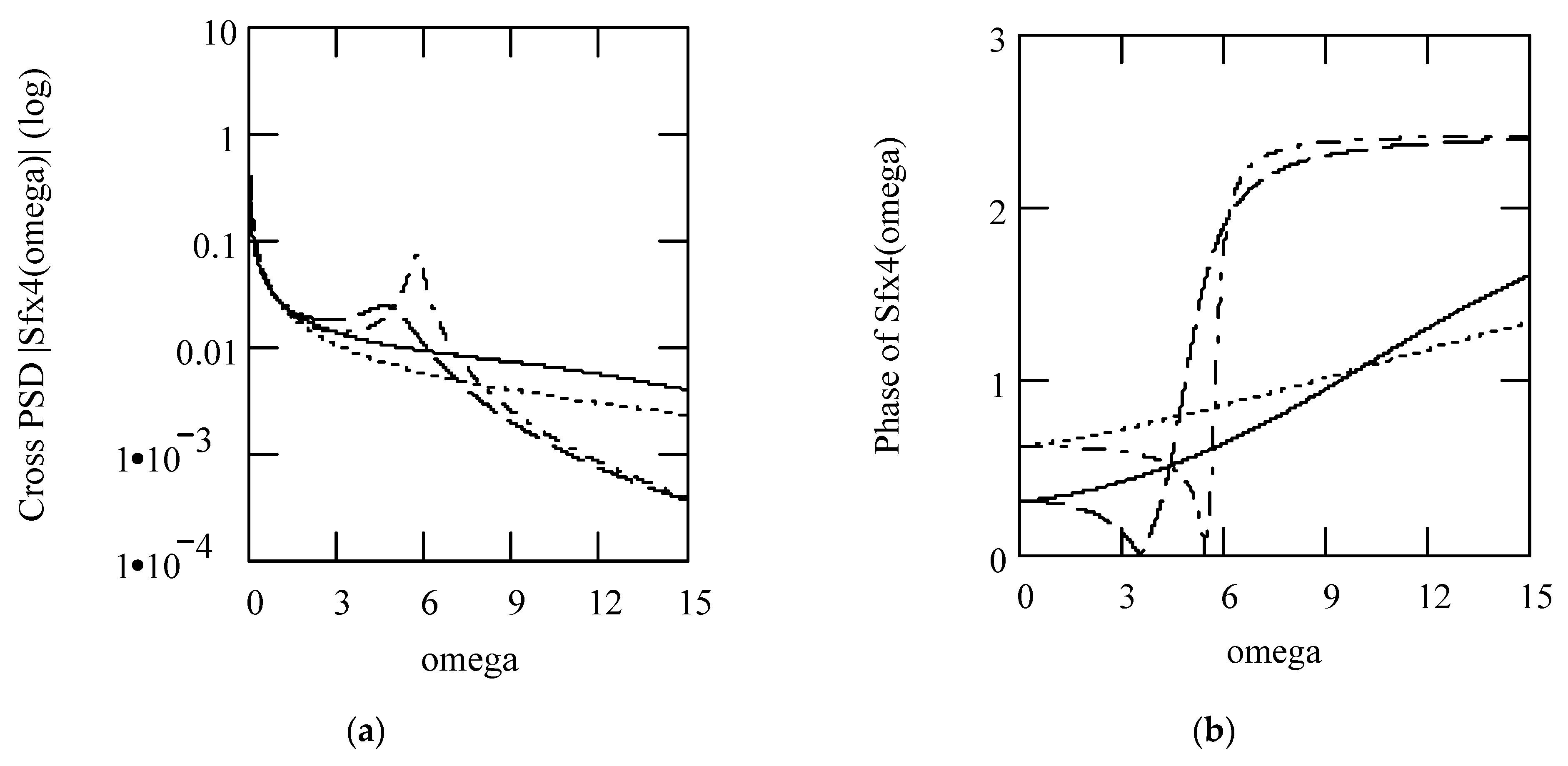
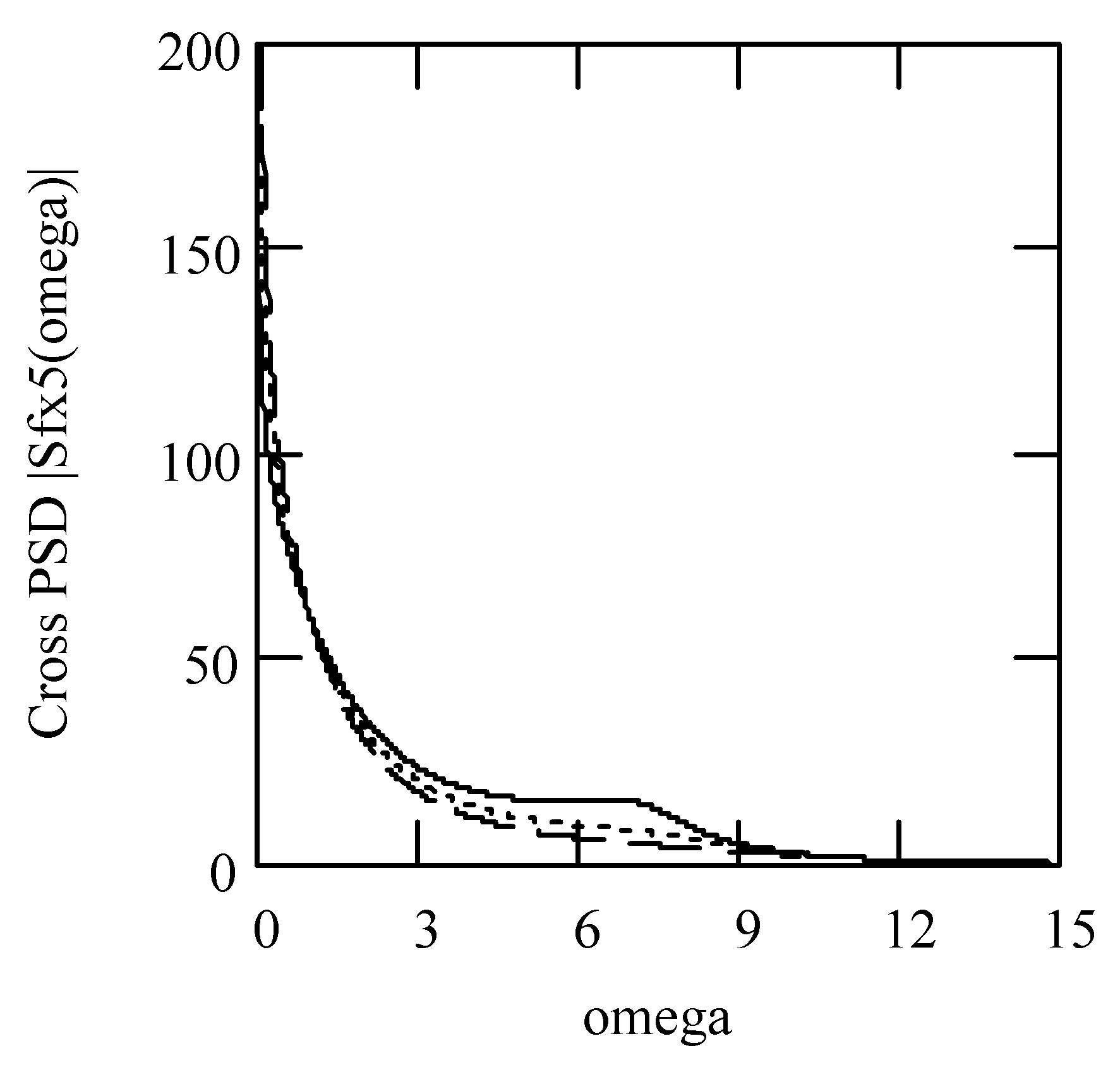
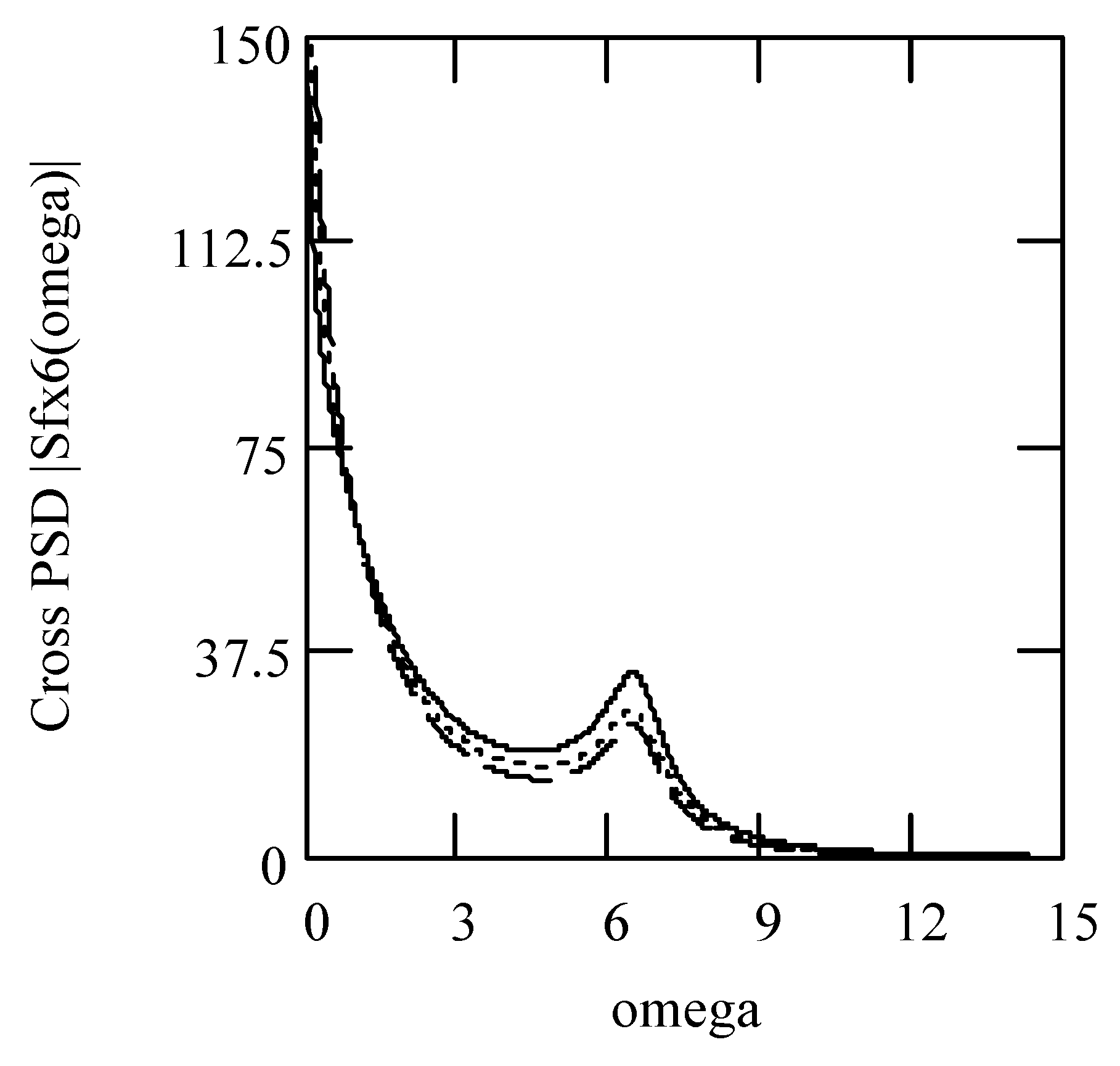
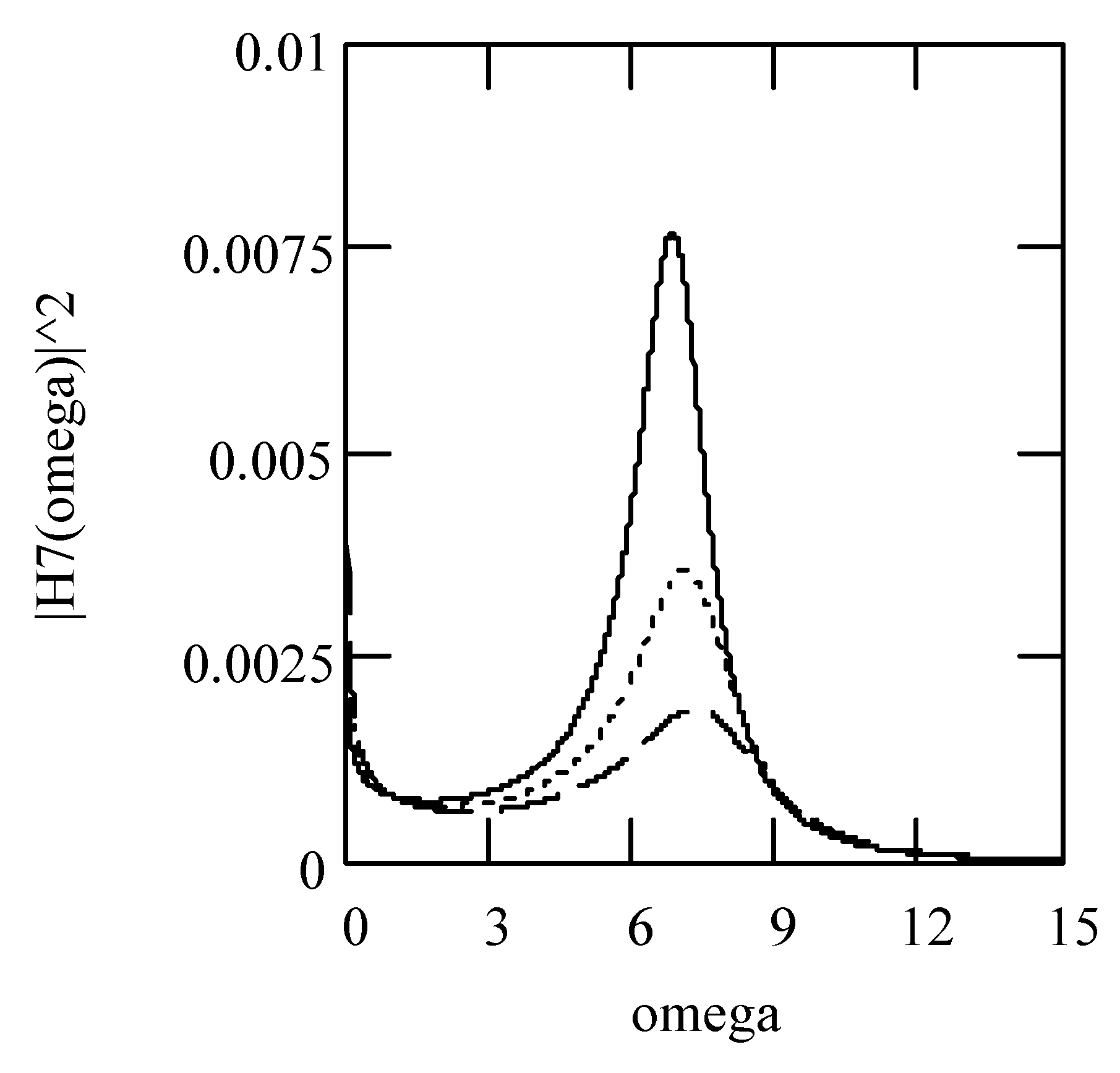
3.8.2. Effects of β, λ on Responses
3.9. Summary
4. PSD and Cross-PSD Responses to Seven Classes of Fractional Vibrations Driven by fBm
4.1. Background
4.2. Responses of Class I Fractional Vibrators Driven by fBm
4.2.1. Computations
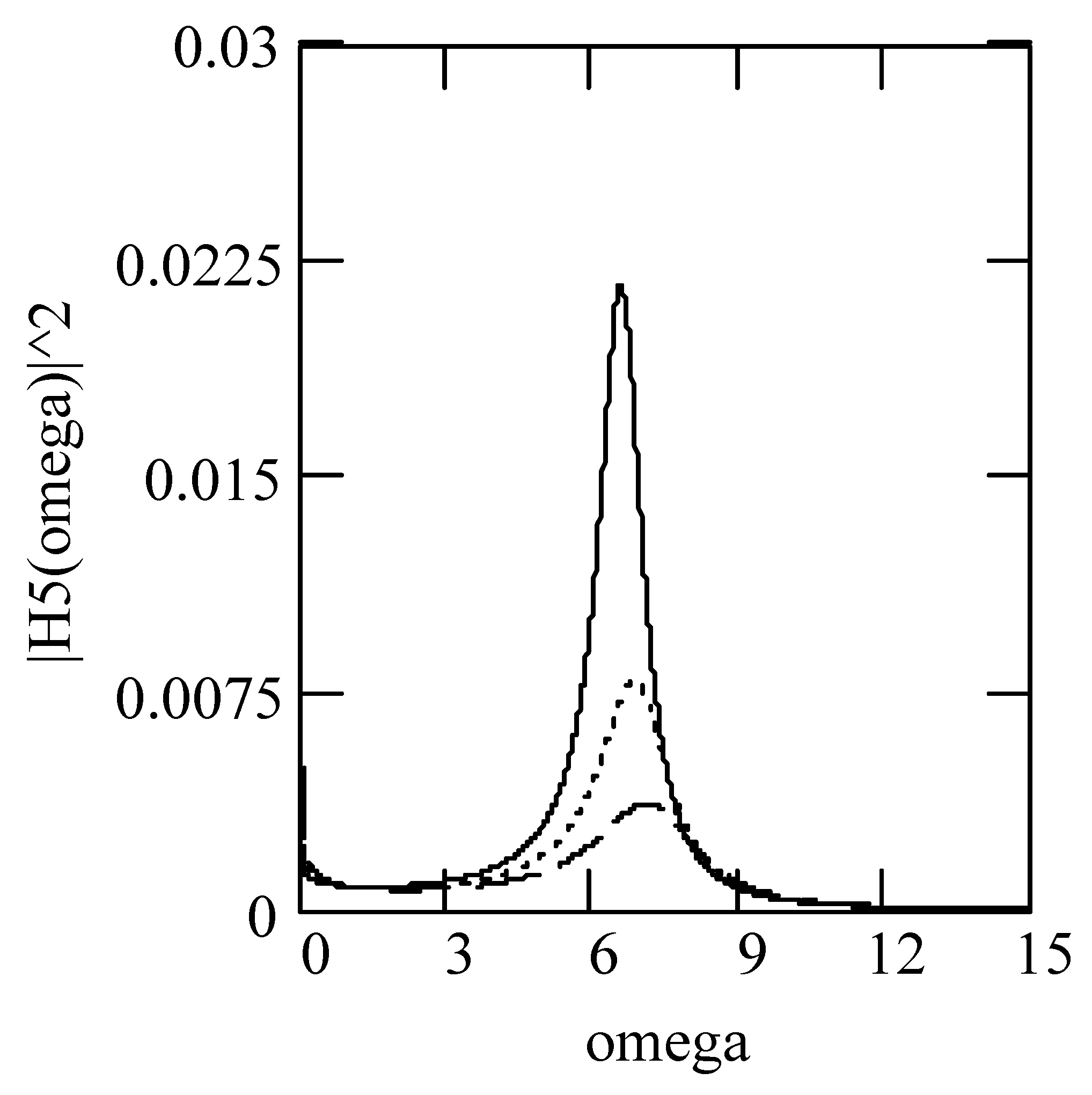
4.2.2. Effects of α on Responses
4.3. Responses of Class II Fractional Vibrators Driven by fBm
4.3.1. Computations
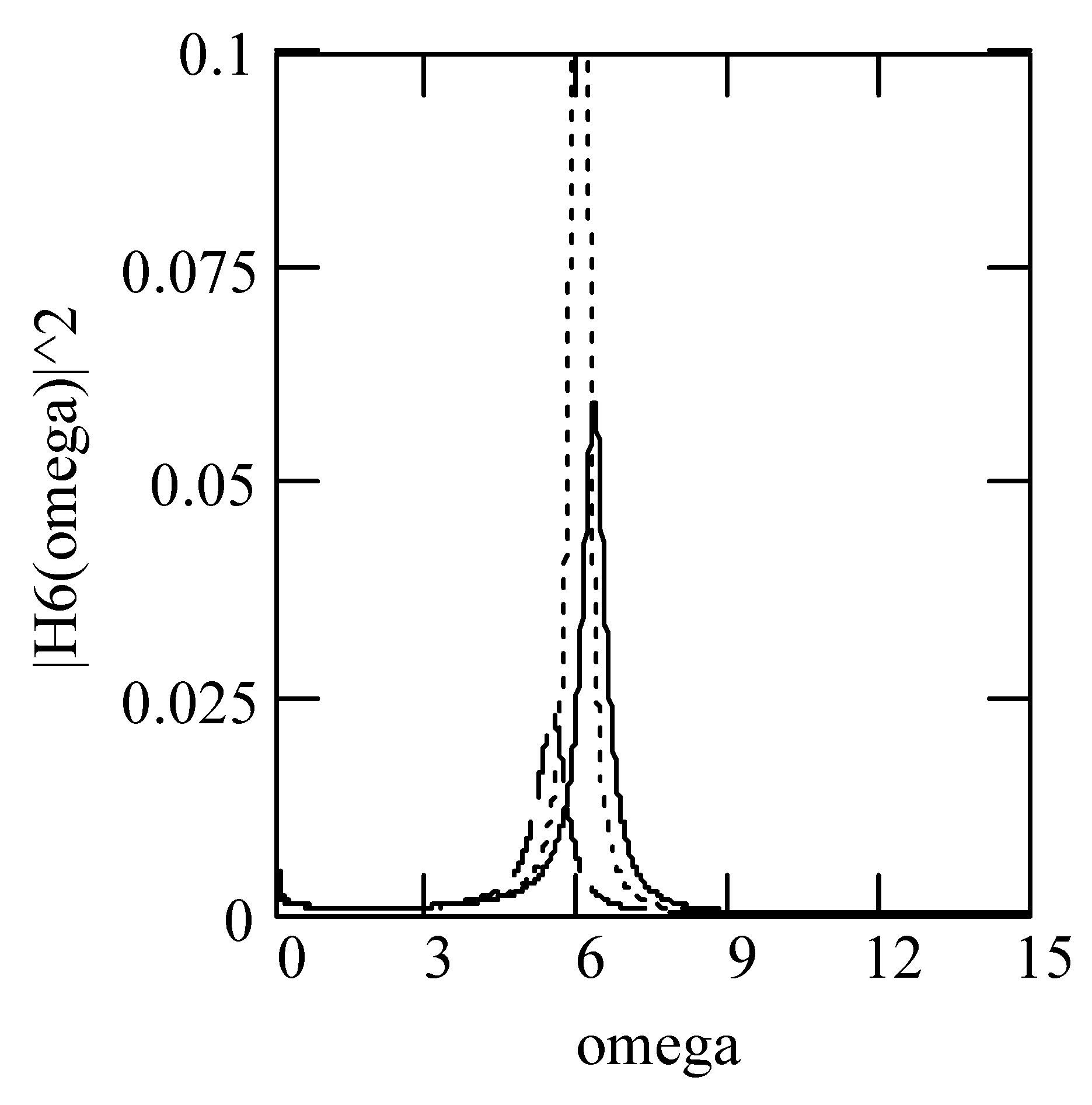
4.3.2. Effects of β on Responses
4.4. Responses of Class III Fractional Vibrators Driven by fBm
4.4.1. Computations
4.4.2. Effects of α and β on Responses
4.5. Responses of Class IV Fractional Vibrators Driven by fBm
4.5.1. Computations
4.5.2. Effects of α and λ on Responses
4.6. Responses of Class V Fractional Vibrators Driven by fBm
4.6.1. Computation Methods
4.6.2. Effects of λ on Responses
4.7. Responses of Class VI Fractional Vibrators Driven by fBm
4.7.1. Computations
4.7.2. Effects of α, β, λ on Responses
4.8. Responses of Class VII Fractional Vibrators Driven by fBm
4.8.1. Computations
4.8.2. Effects of β, λ on Responses
4.9. Summary
5. PSD and Cross-PSD Responses to Seven Classes of Fractional Vibrations Driven by Fractional OU Processes
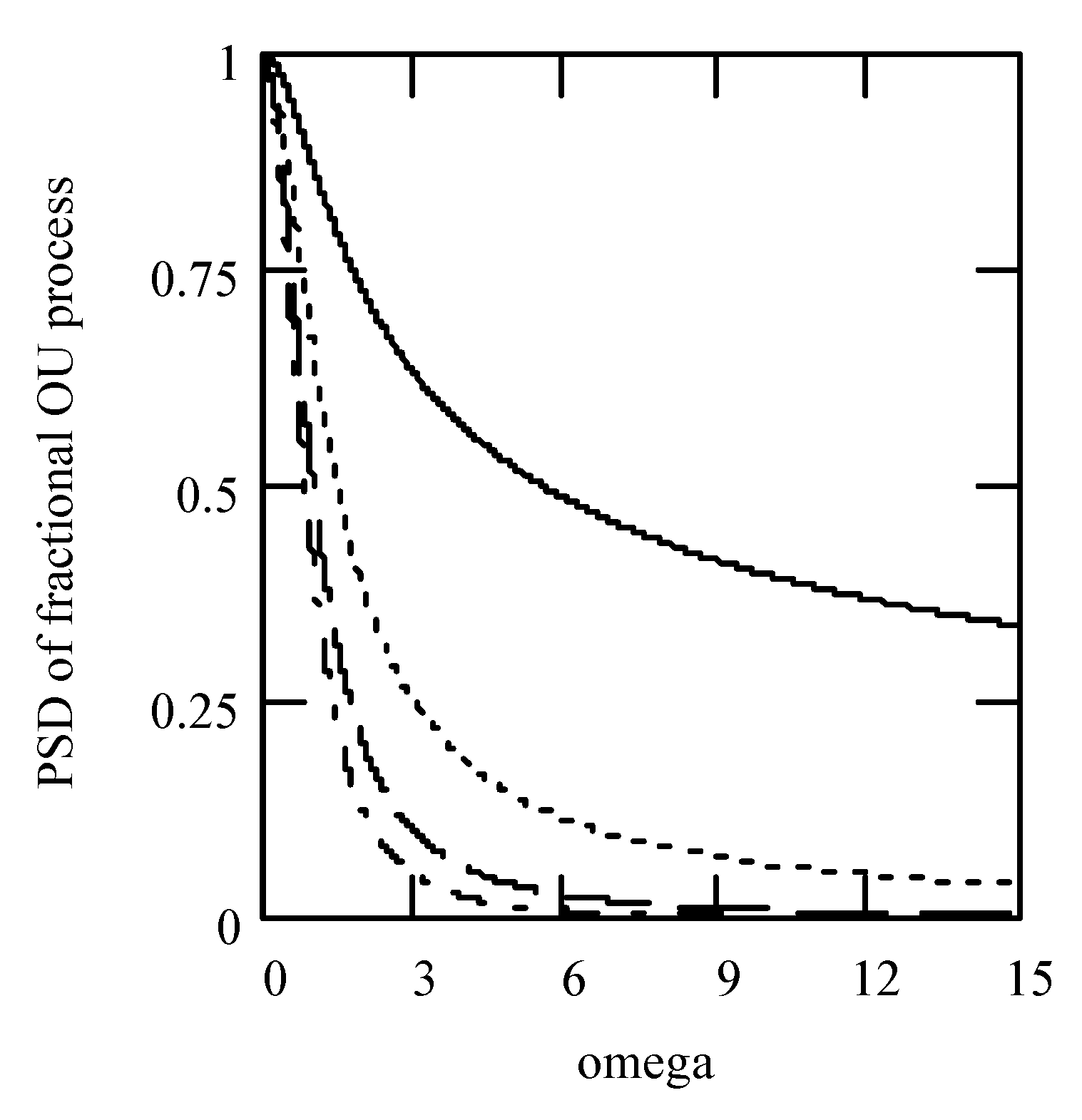
5.1. Background
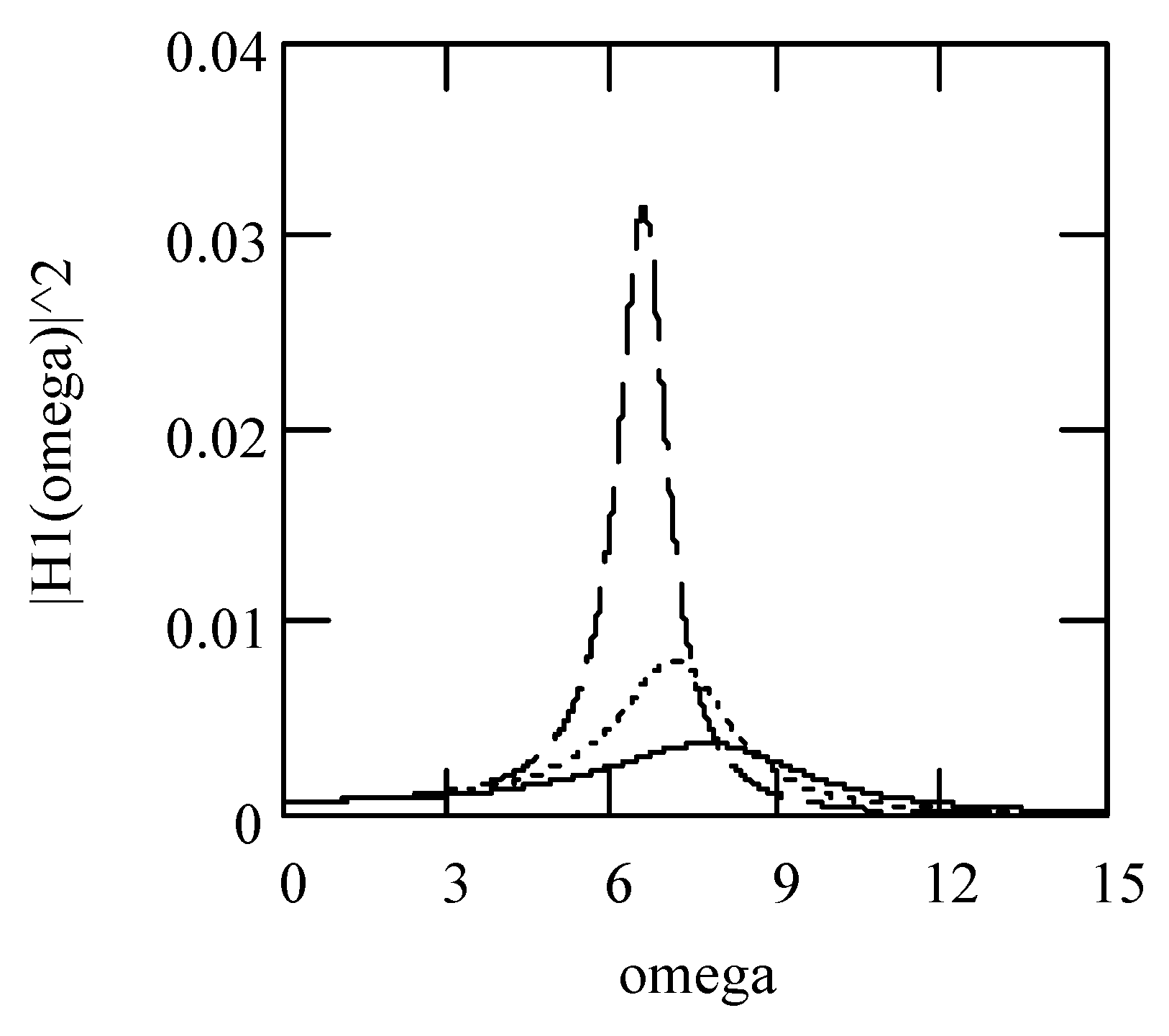
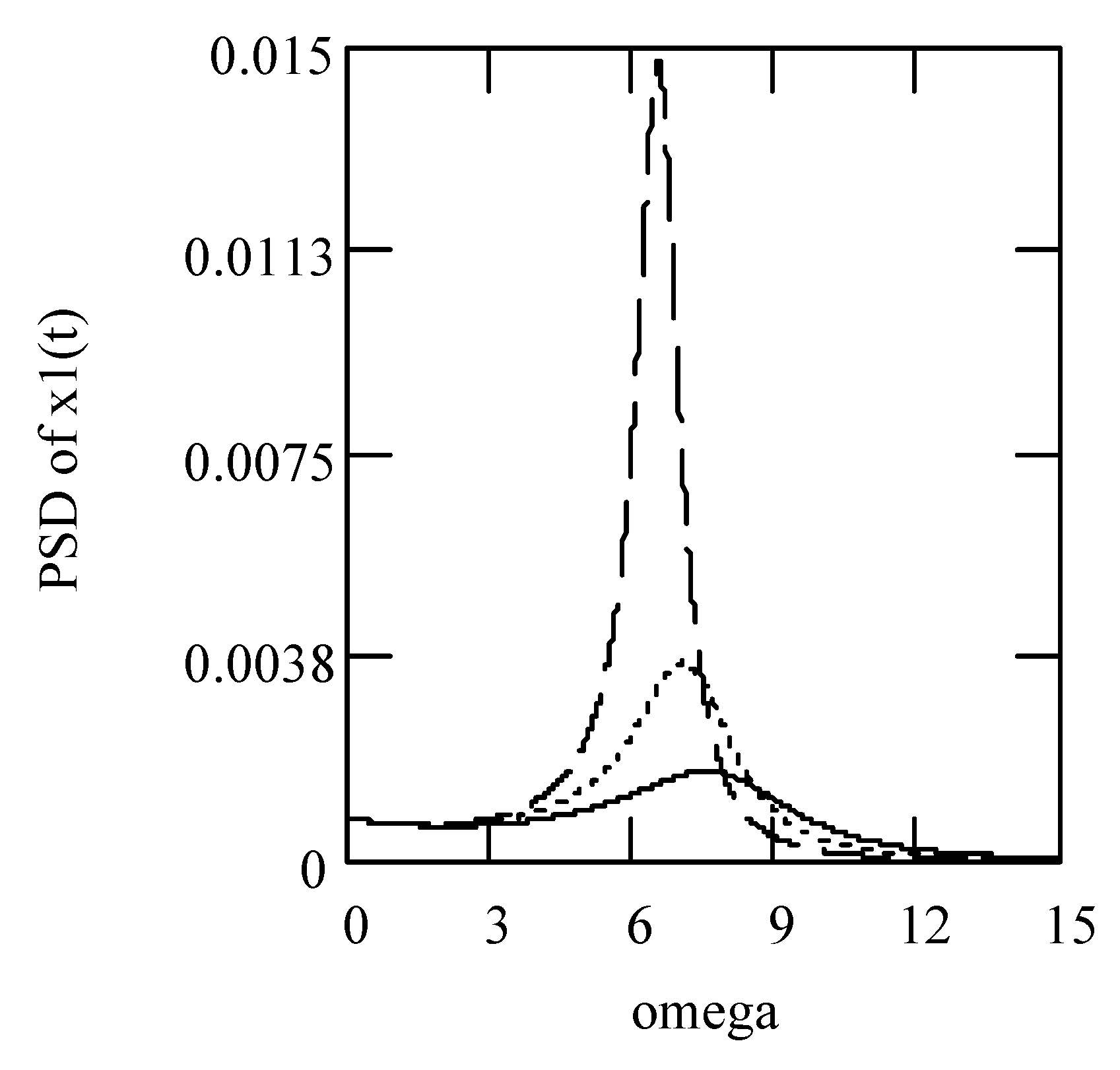
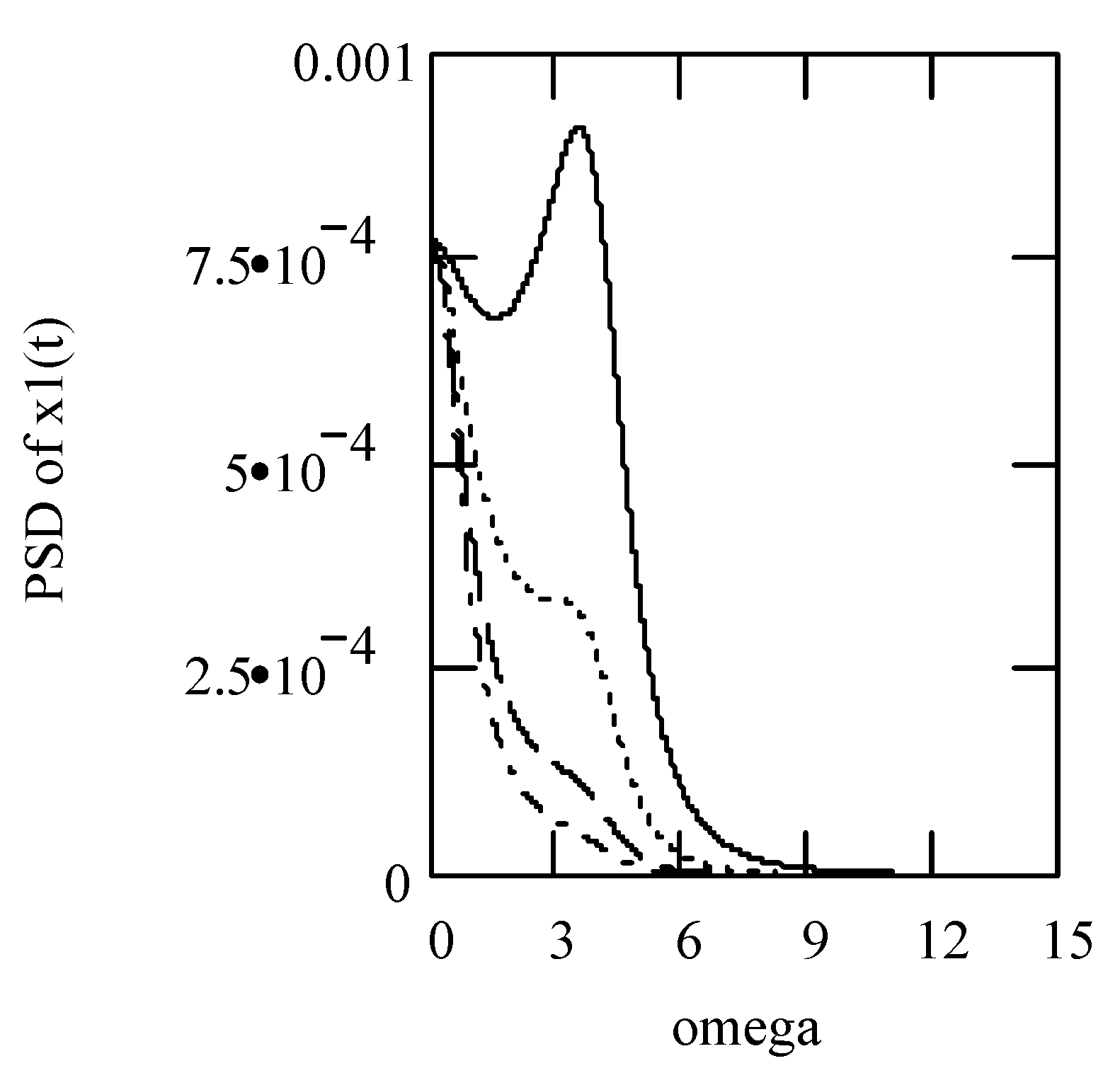
5.2. Responses of Class I Fractional Vibrators Driven by Fractional OU Processes
5.2.1. Computations
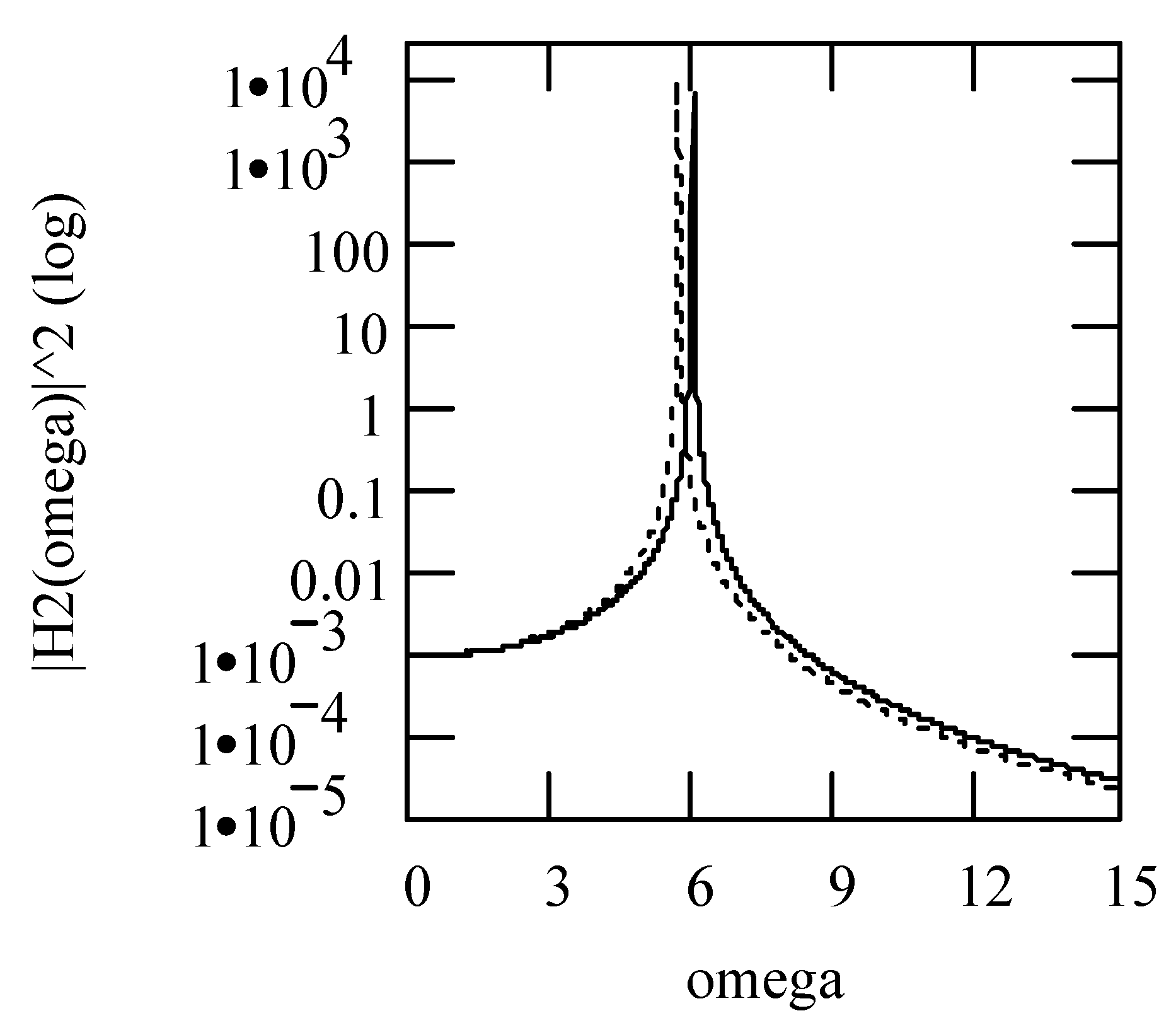
5.2.2. Effects of α on Responses
5.3. Responses of Class II Fractional Vibration Systems Driven by Fractional OU Processes
5.3.1. Computation Methods
5.3.2. Effects of β on Responses
5.4. Responses of Class III Fractional Vibrators Driven by Fractional OU Processes
5.4.1. Computations
5.4.2. Effects of α and β on Responses
5.5. Responses of Class IV Fractional Vibration Systems Driven by Fractional OU Processes
5.5.1. Computations
5.5.2. Effects of α and λ on Responses
5.6. Responses of Class V Fractional Vibrators Driven by Fractional OU Processes
5.6.1. Computation Methods
5.6.2. Effects of λ on Responses
5.7. Responses of Class VI Fractional Vibrators Driven by Fractional OU Processes
5.7.1. Computations
5.7.2. Effects of α, β, λ on Responses
5.8. Responses of Class VII Fractional Vibrators Driven by Fractional OU Processes
5.8.1. Computations
5.8.2. Effects of β, λ on Responses
5.9. Summary
6. PSD and Cross-PSD Responses to Seven Classes of Fractional Vibrations Driven by the von Kármán Process
6.1. Background
6.2. Responses of Class I Fractional Vibrators Driven by von Kármán Process
6.2.1. Computations
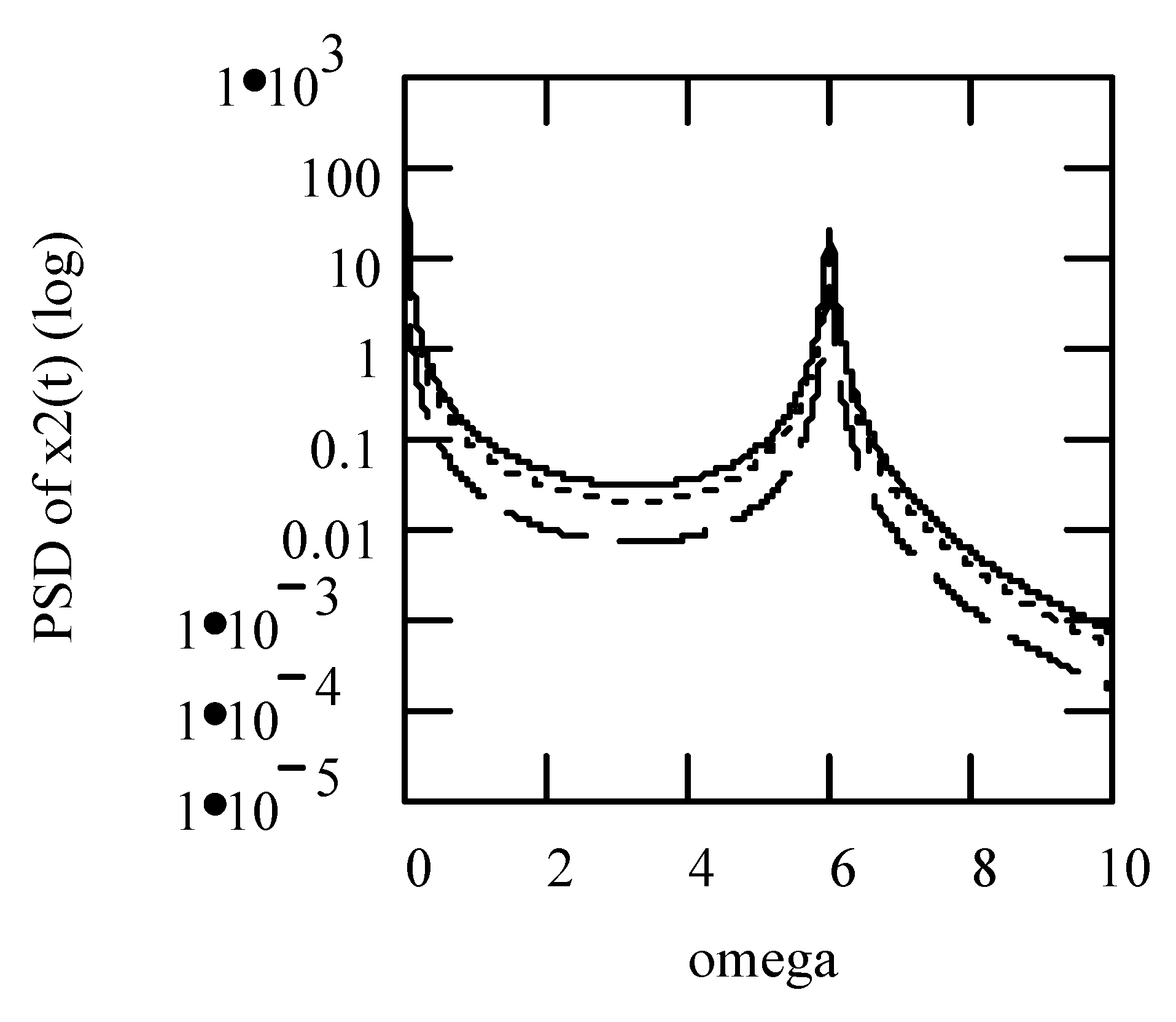
6.2.2. Effects of α on Responses
6.3. Responses of Class II Fractional Vibration Systems Driven by von Kármán Process
6.3.1. Computation Methods
6.3.2. Effects of β on Responses
6.4. Responses of Class III Fractional Vibrators Driven by von Kármán Process
6.4.1. Computations
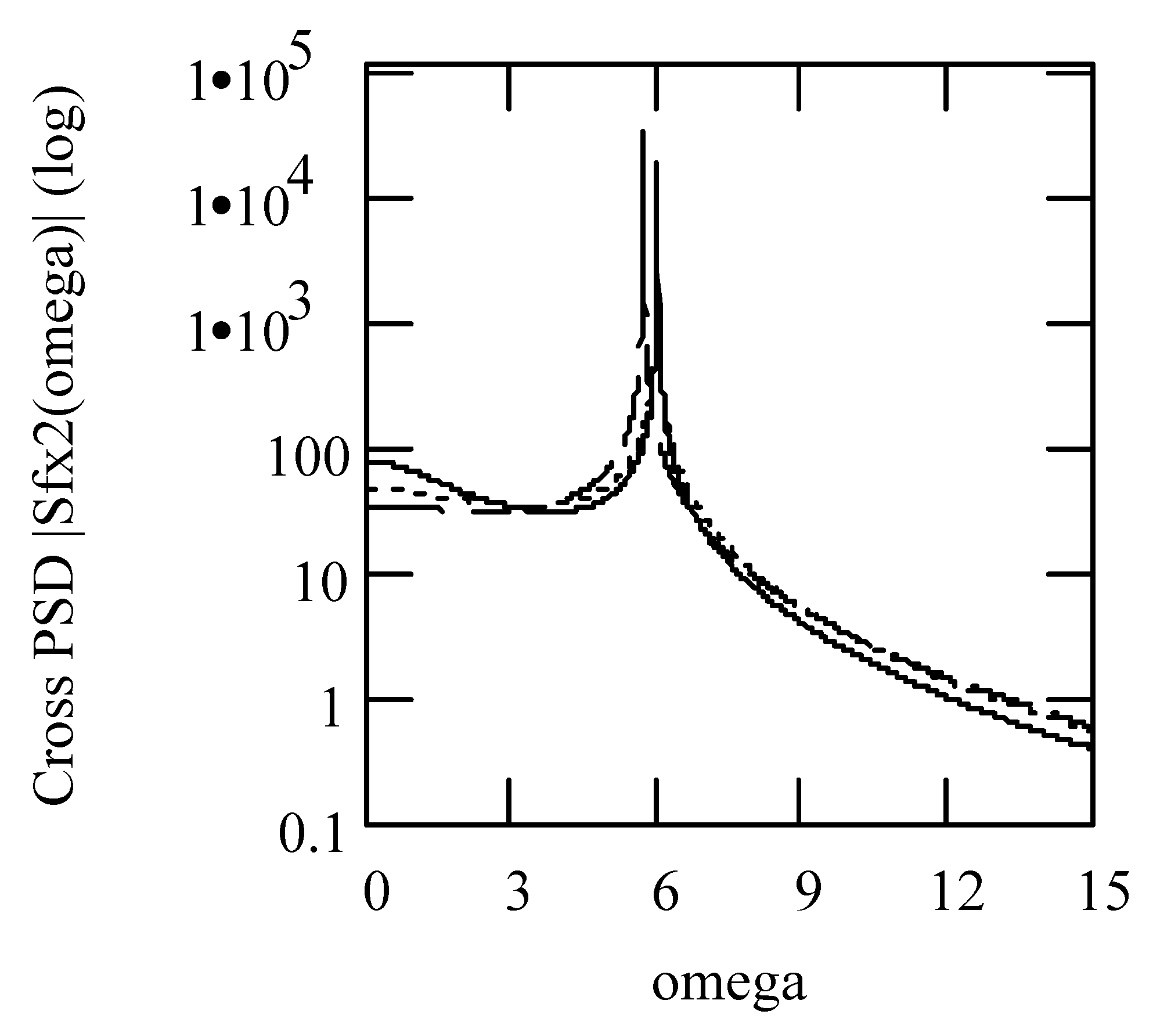
6.4.2. Effects of α and β on Responses
6.5. Responses of Class IV Fractional Vibration Systems Driven by the von Kármán Process
6.5.1. Computations
6.5.2. Effects of α and λ on Responses
6.6. Responses of Class V Fractional Vibrators Driven by von Kármán Process
6.6.1. Computation Methods
6.6.2. Effects of λ on Responses
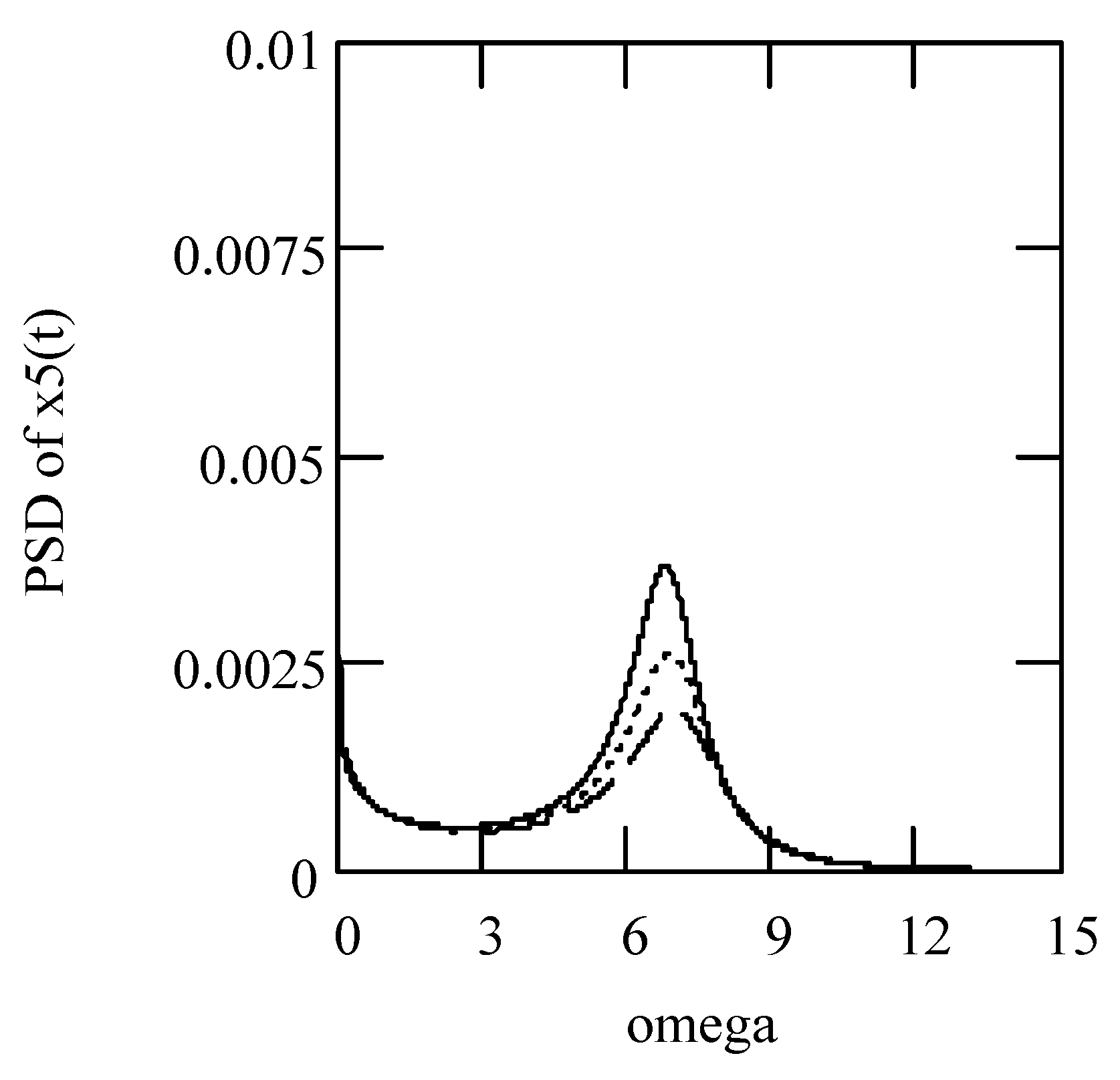
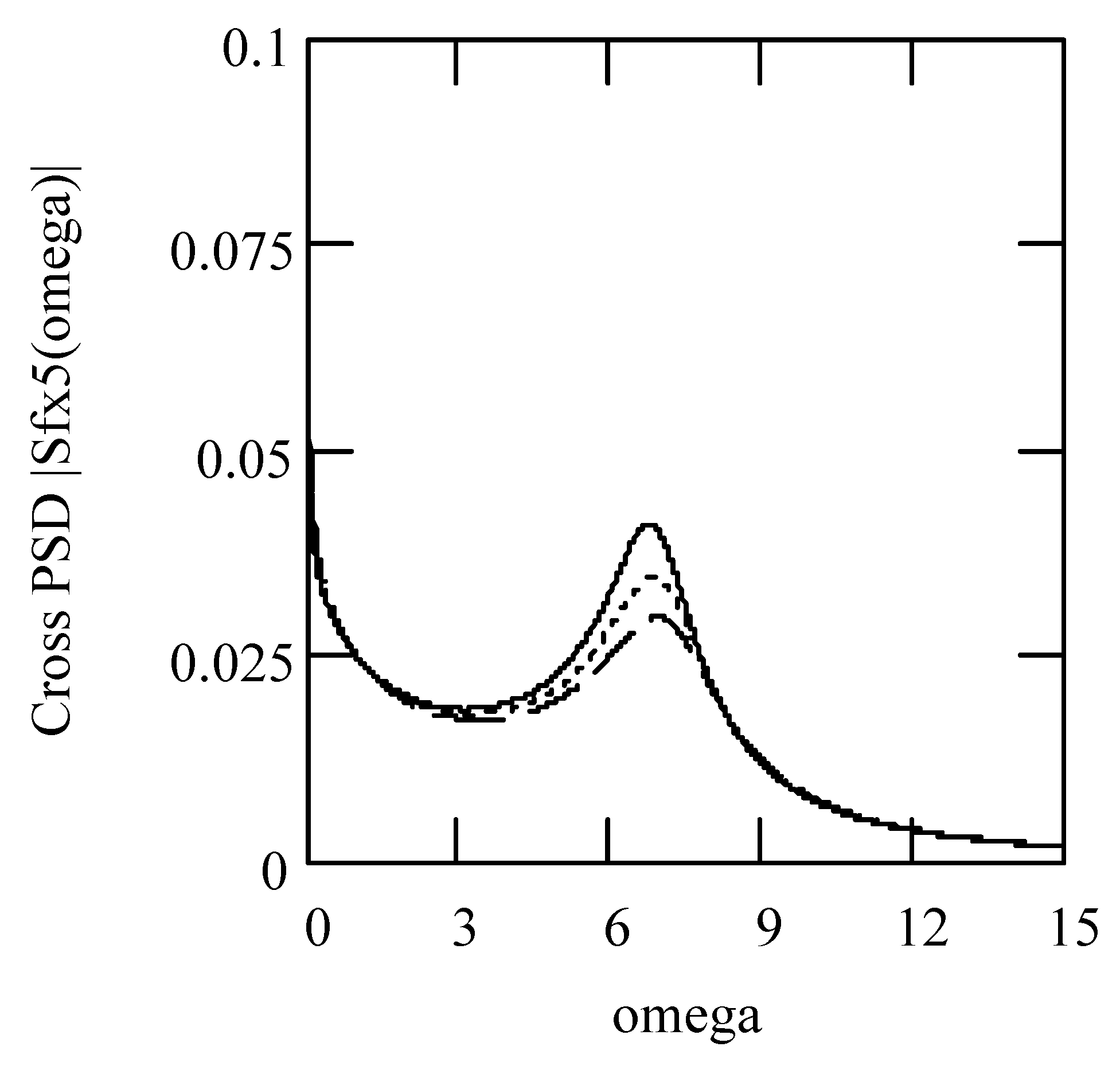
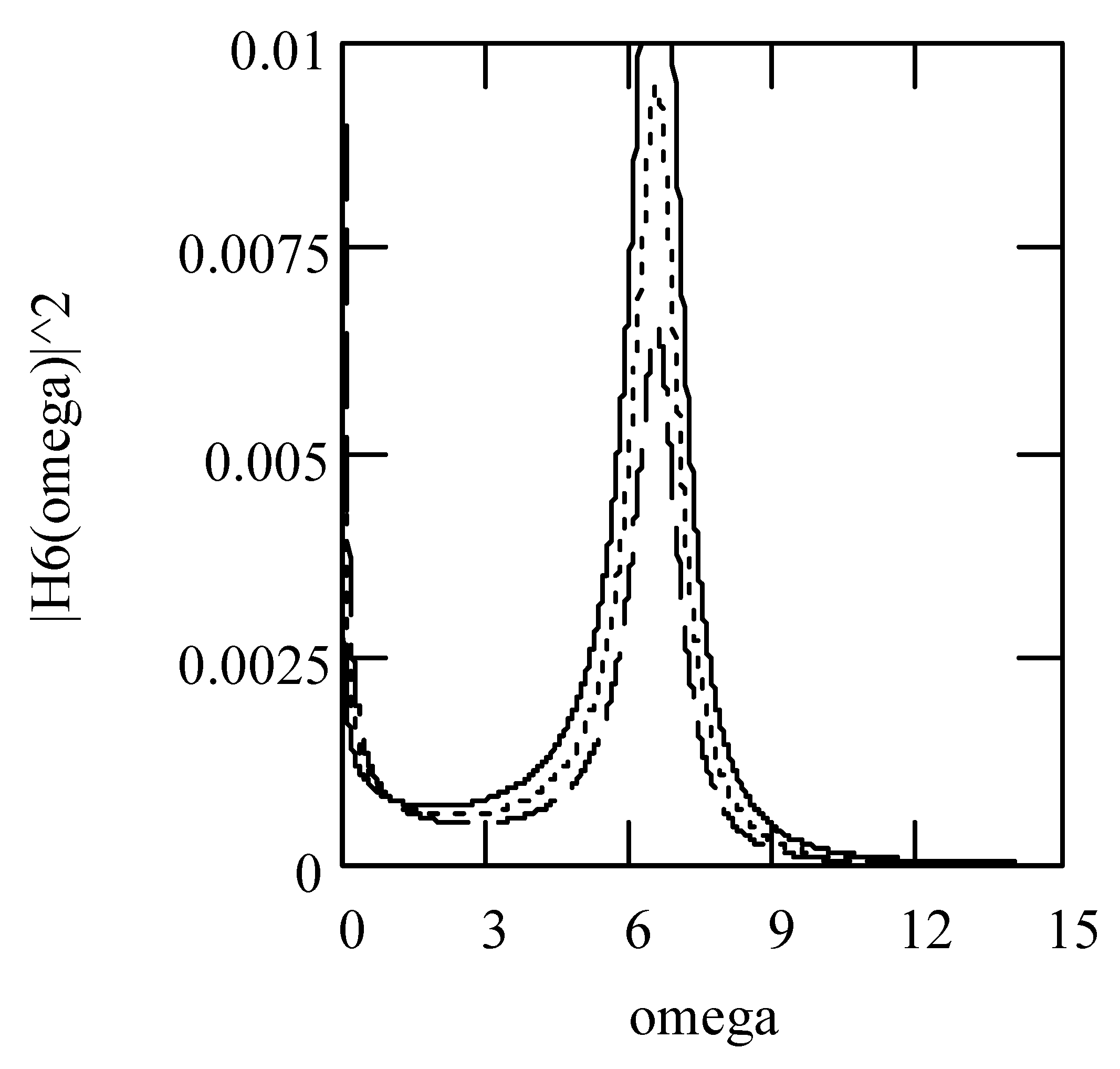
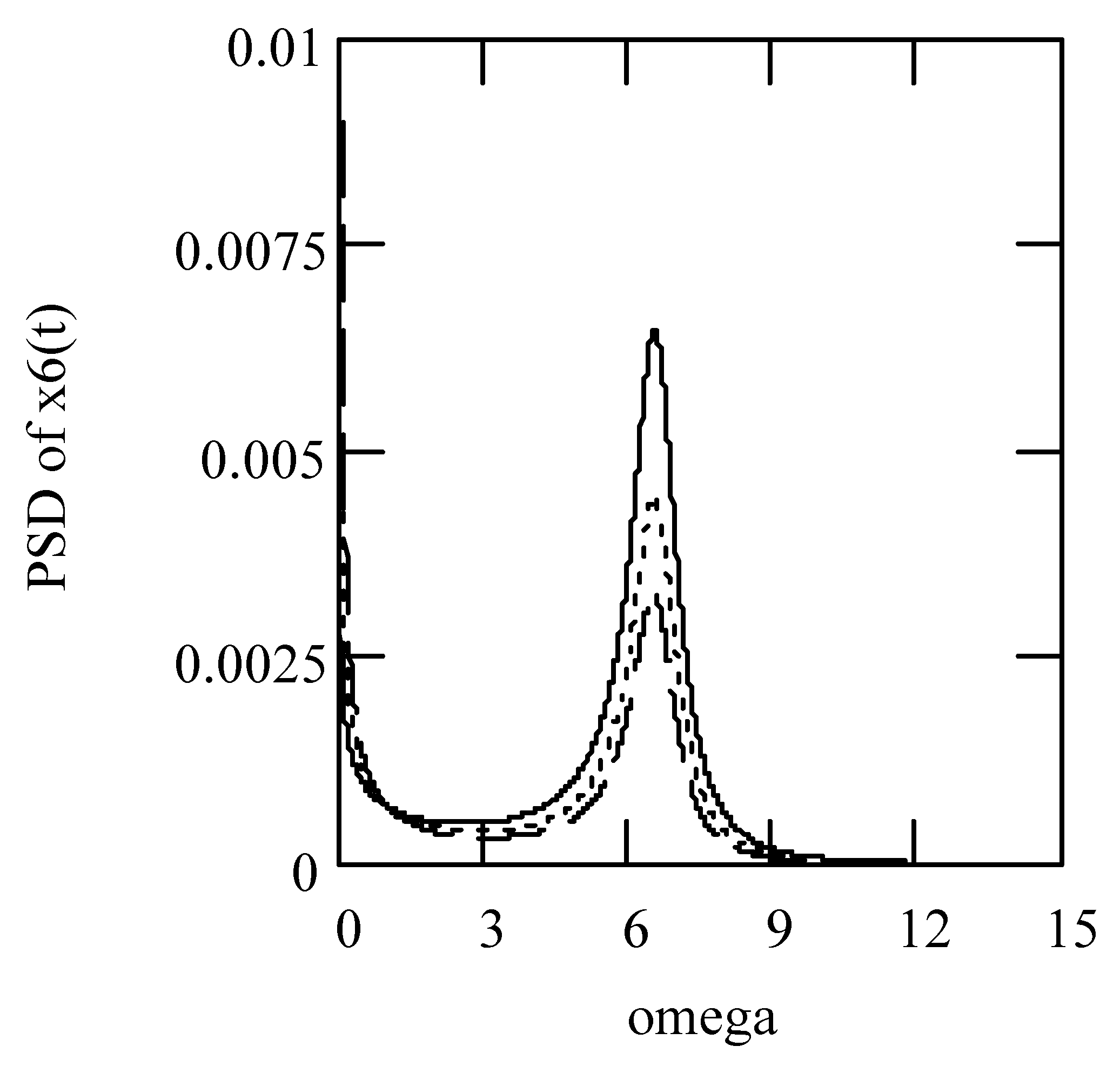
6.7. Responses of Class VI Fractional Vibrators Driven by von Kármán Process
6.7.1. Computations
6.7.2. Effects of α, β, λ on Responses
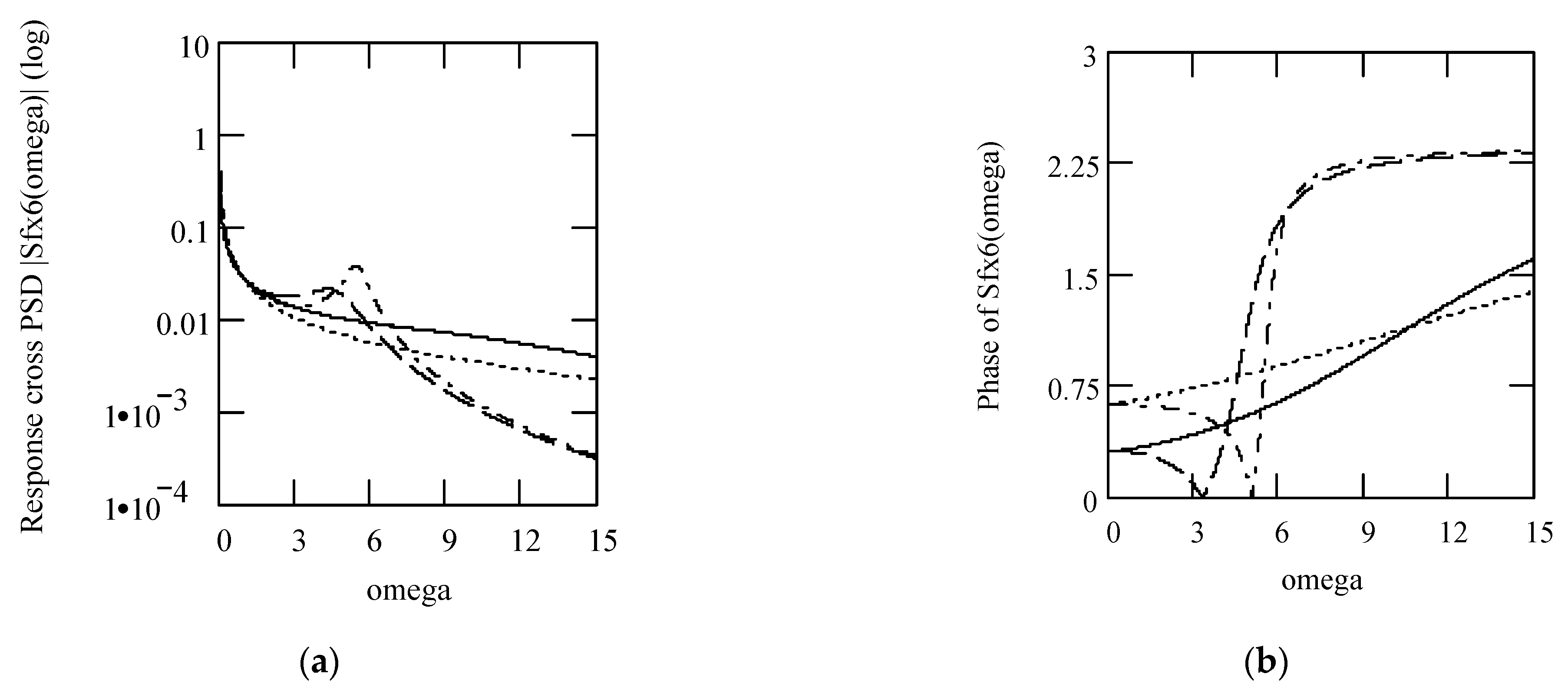
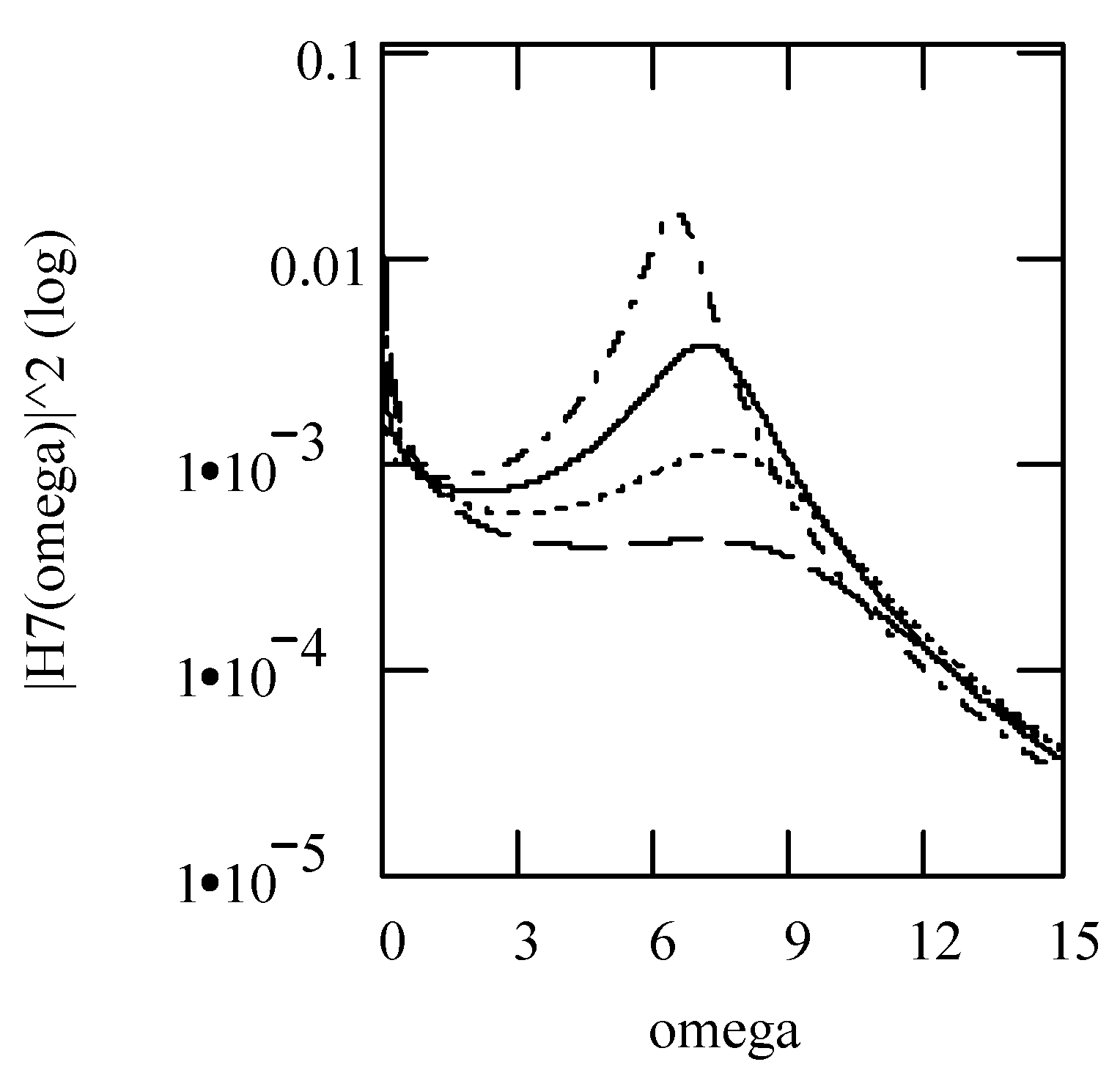
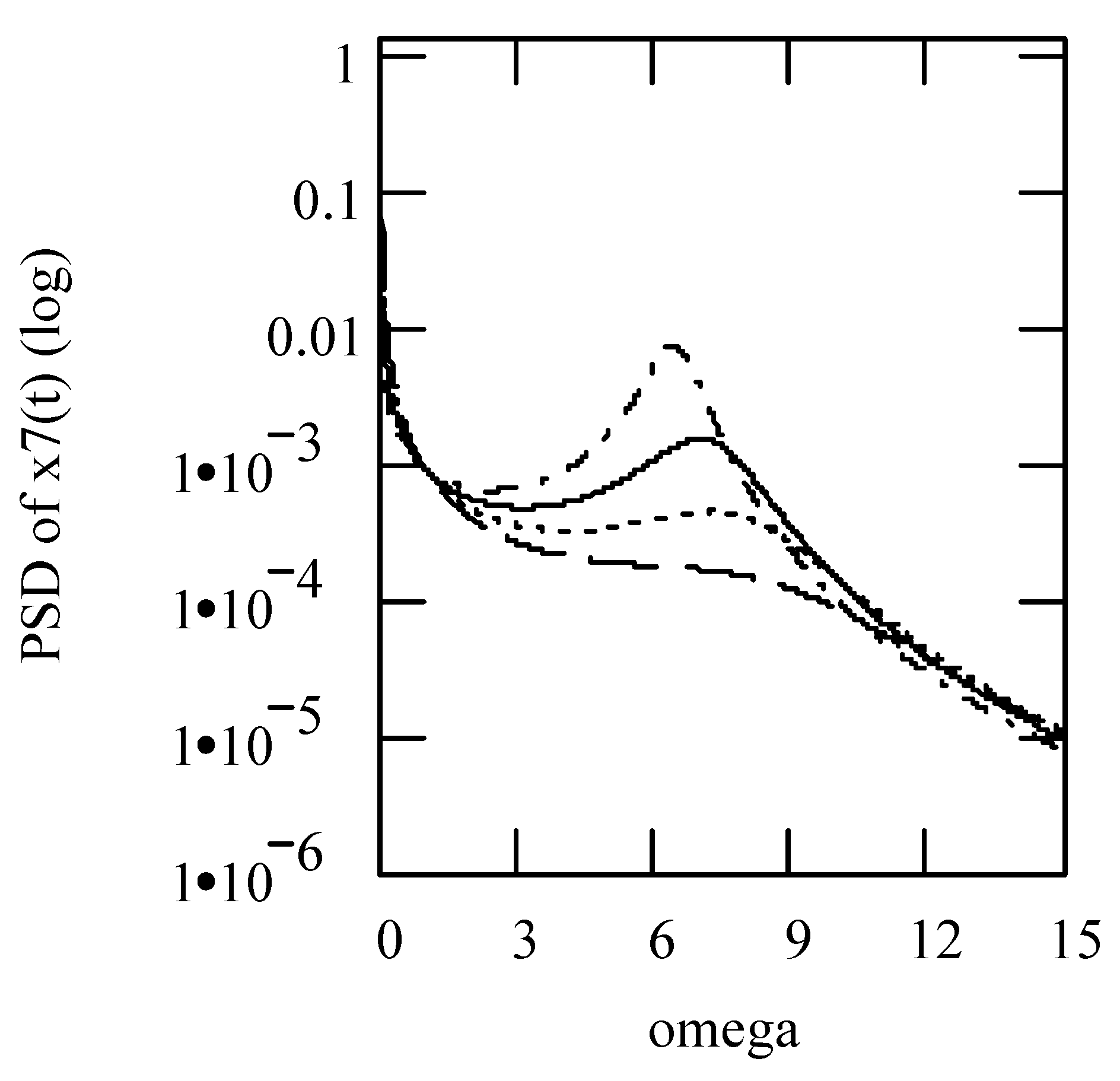
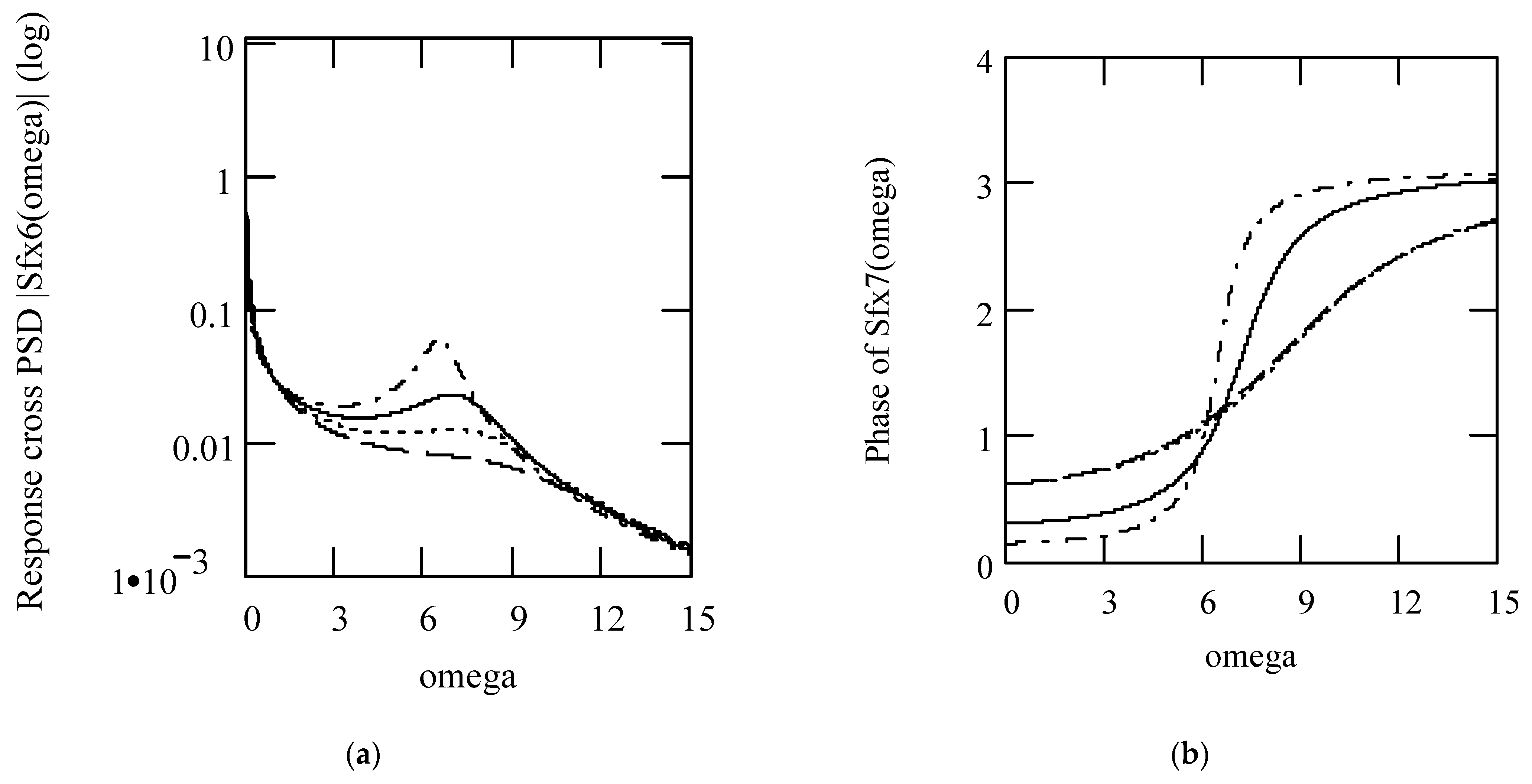
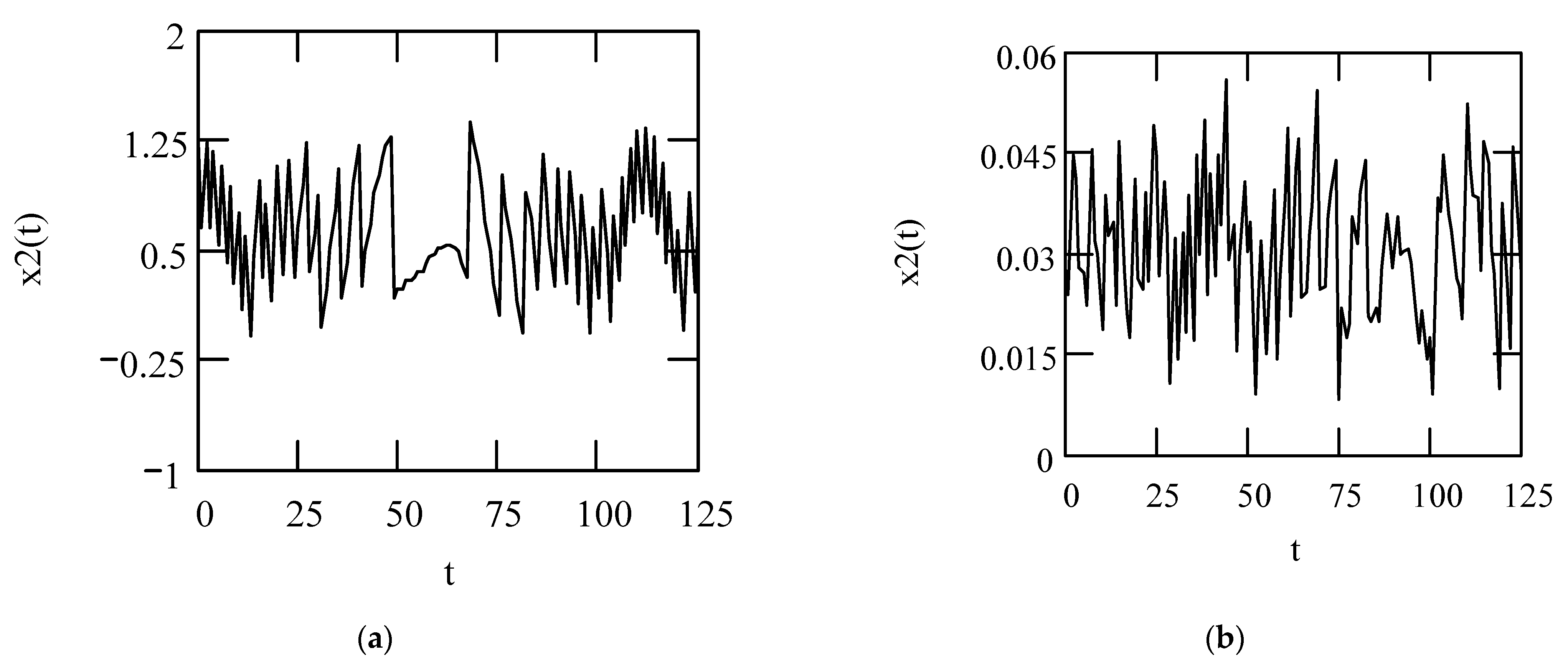
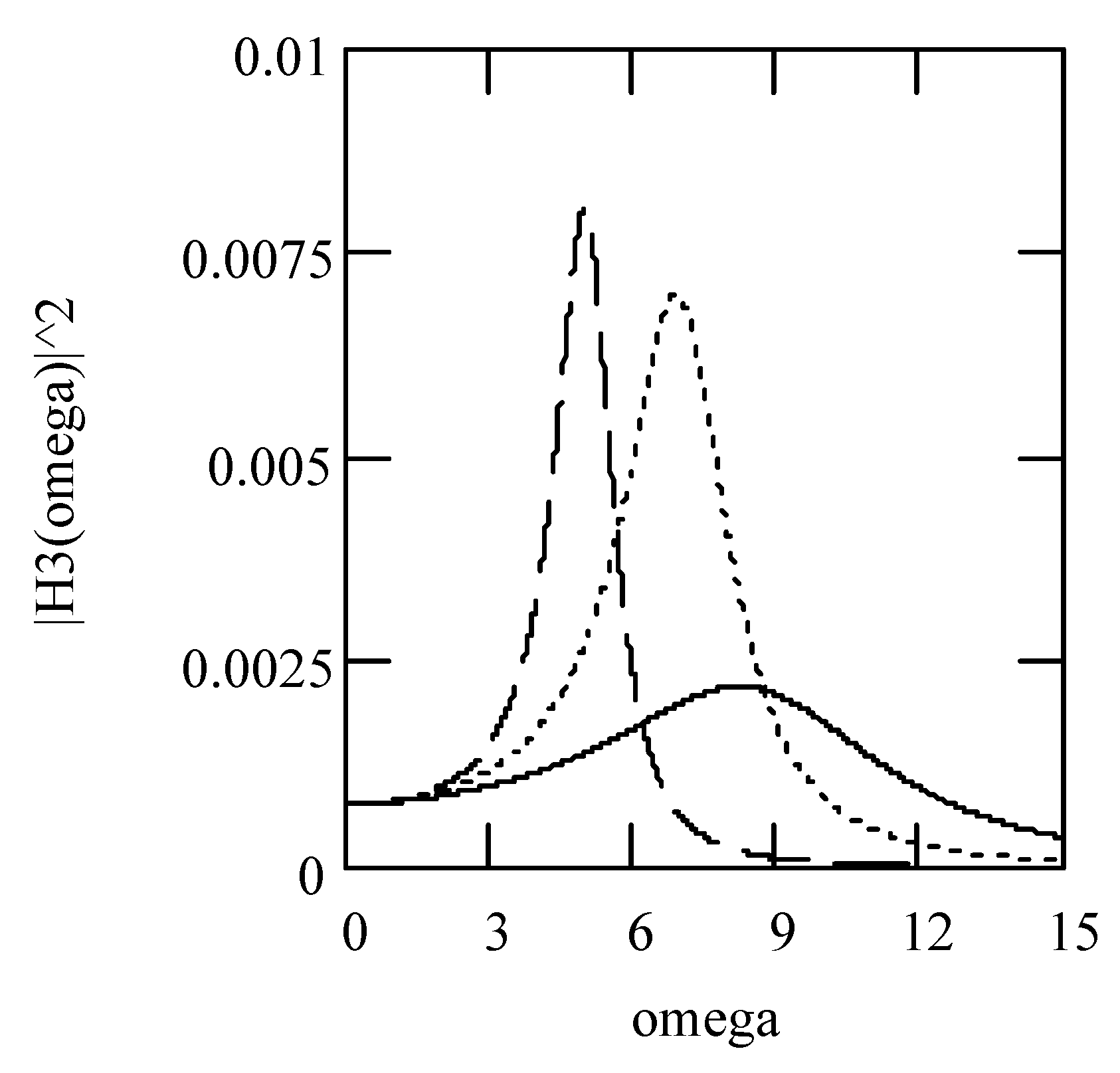
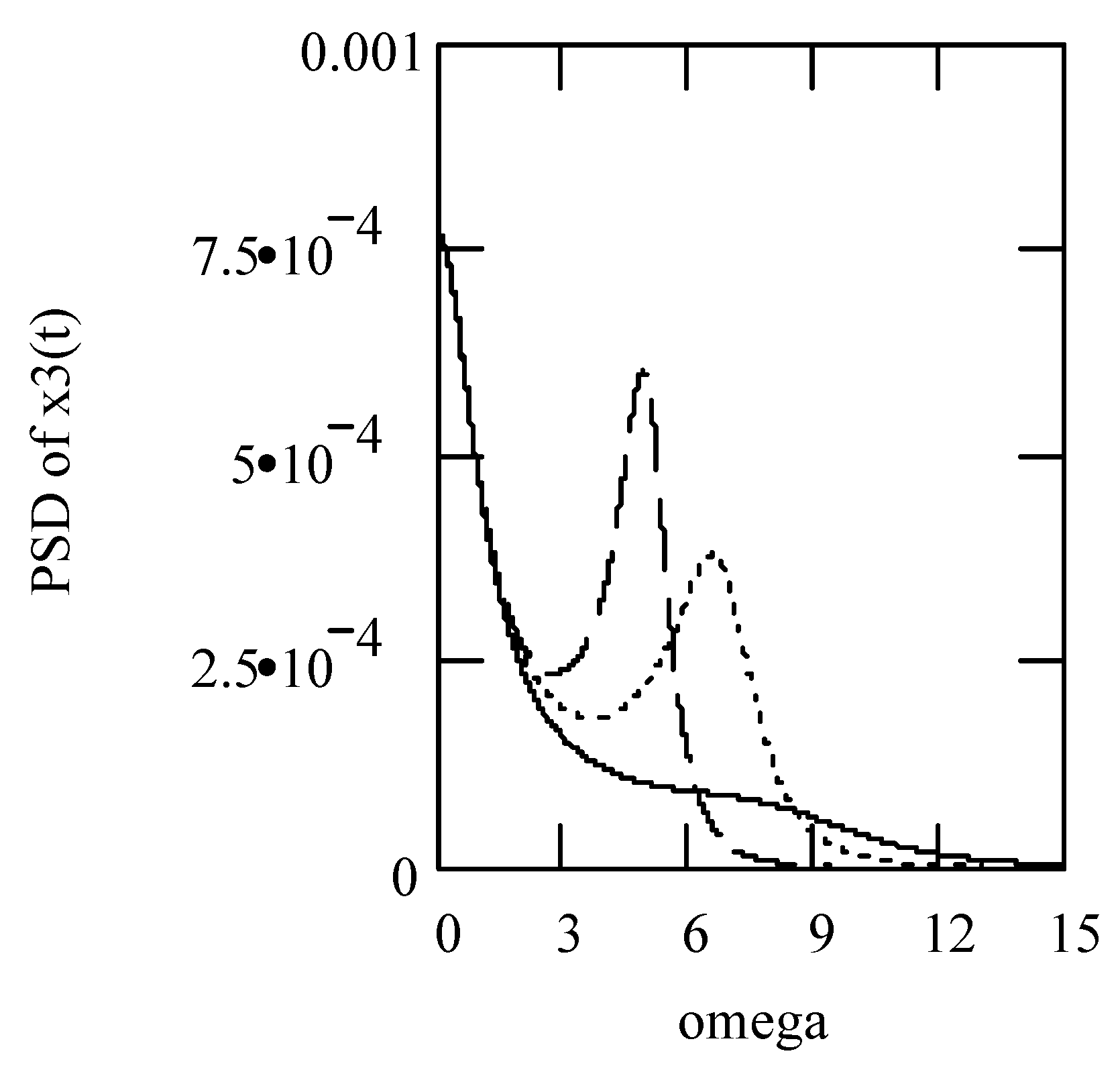
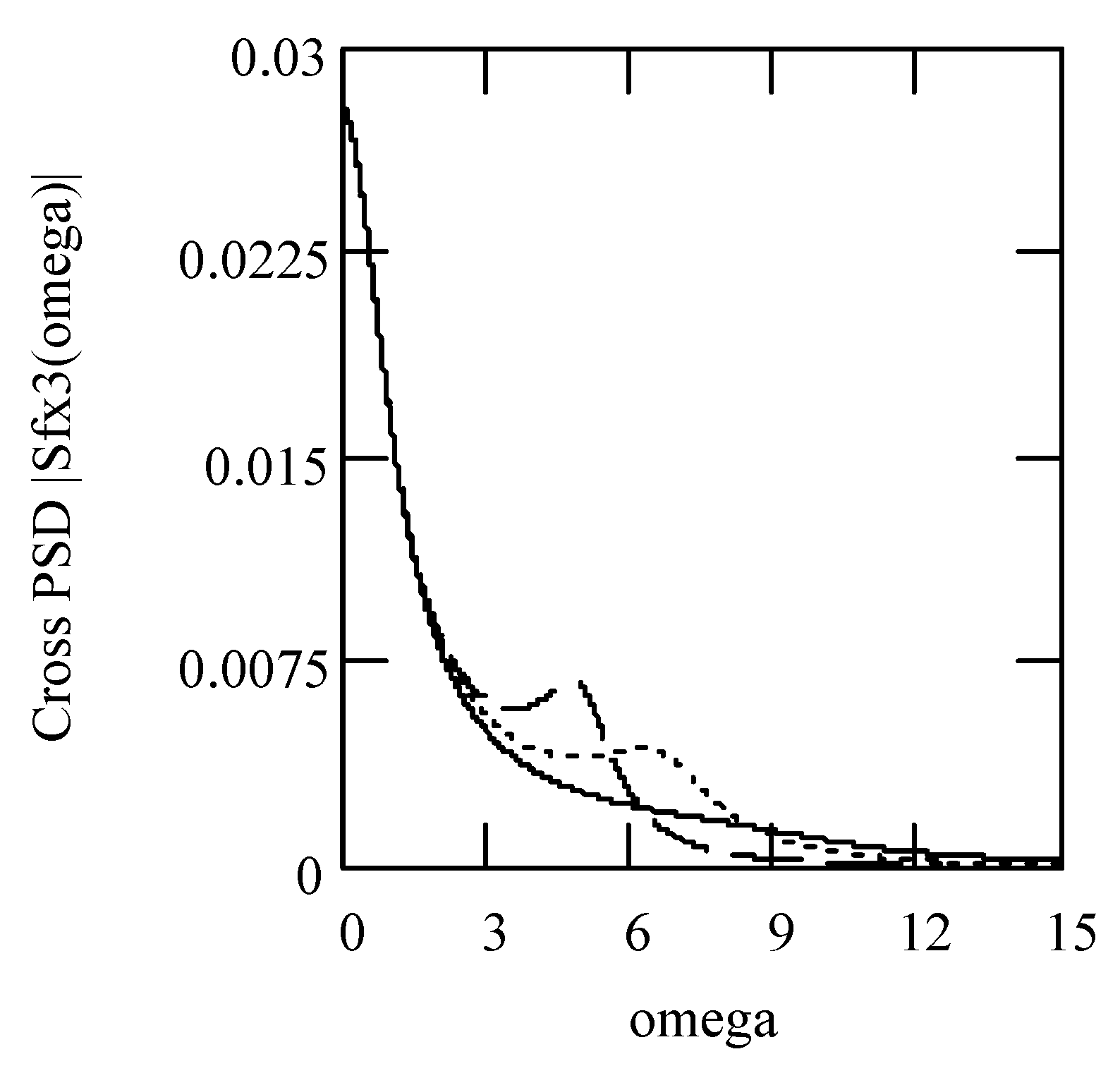
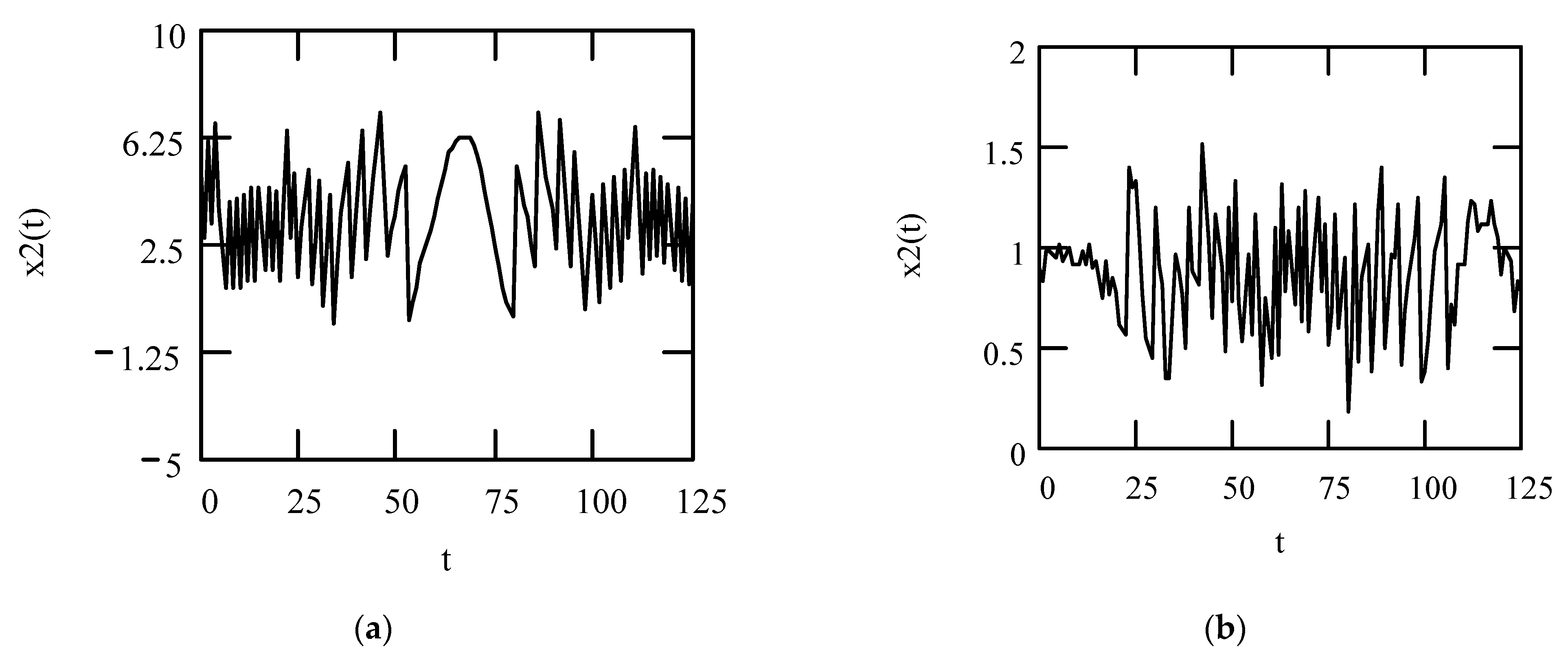
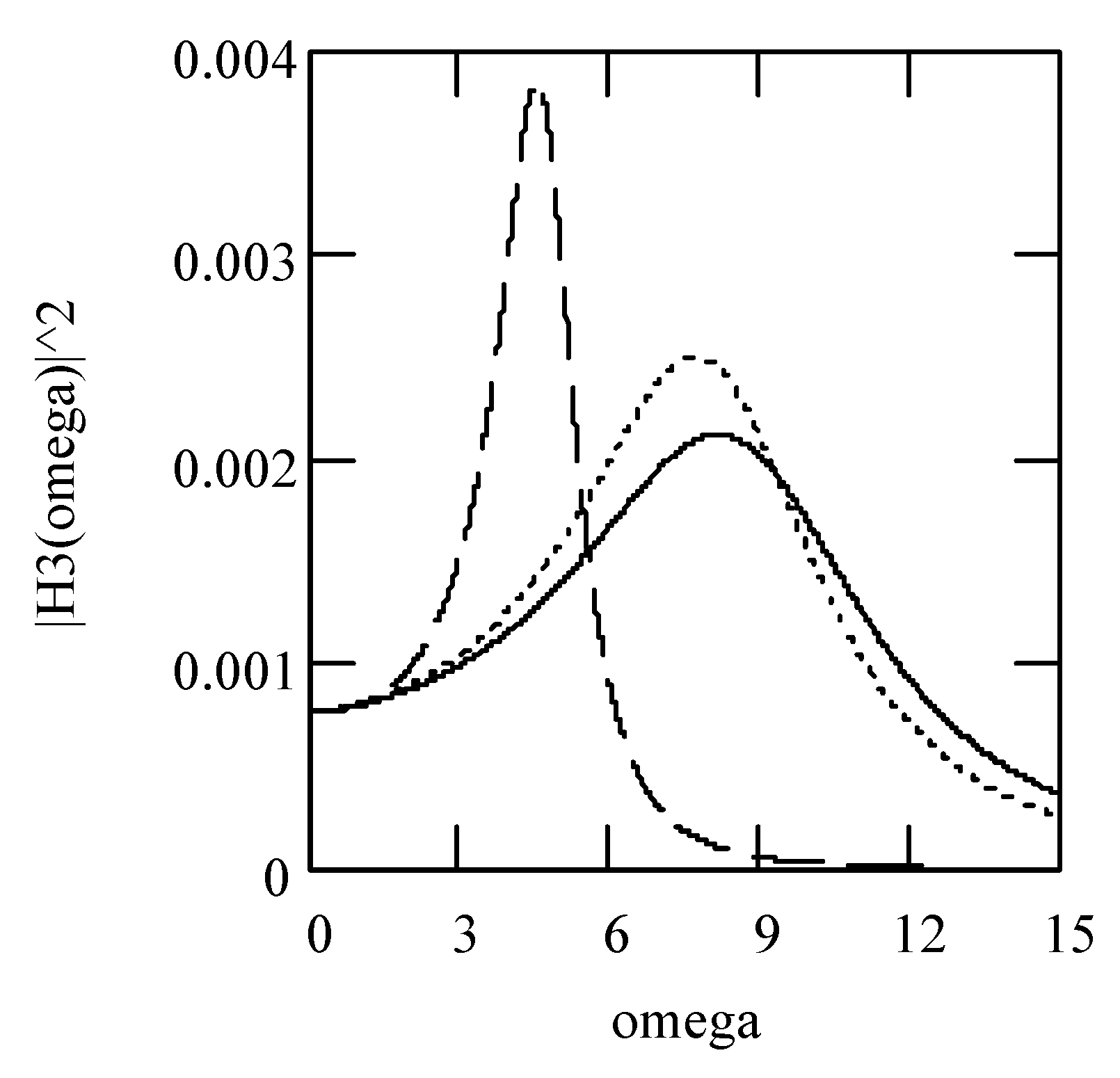
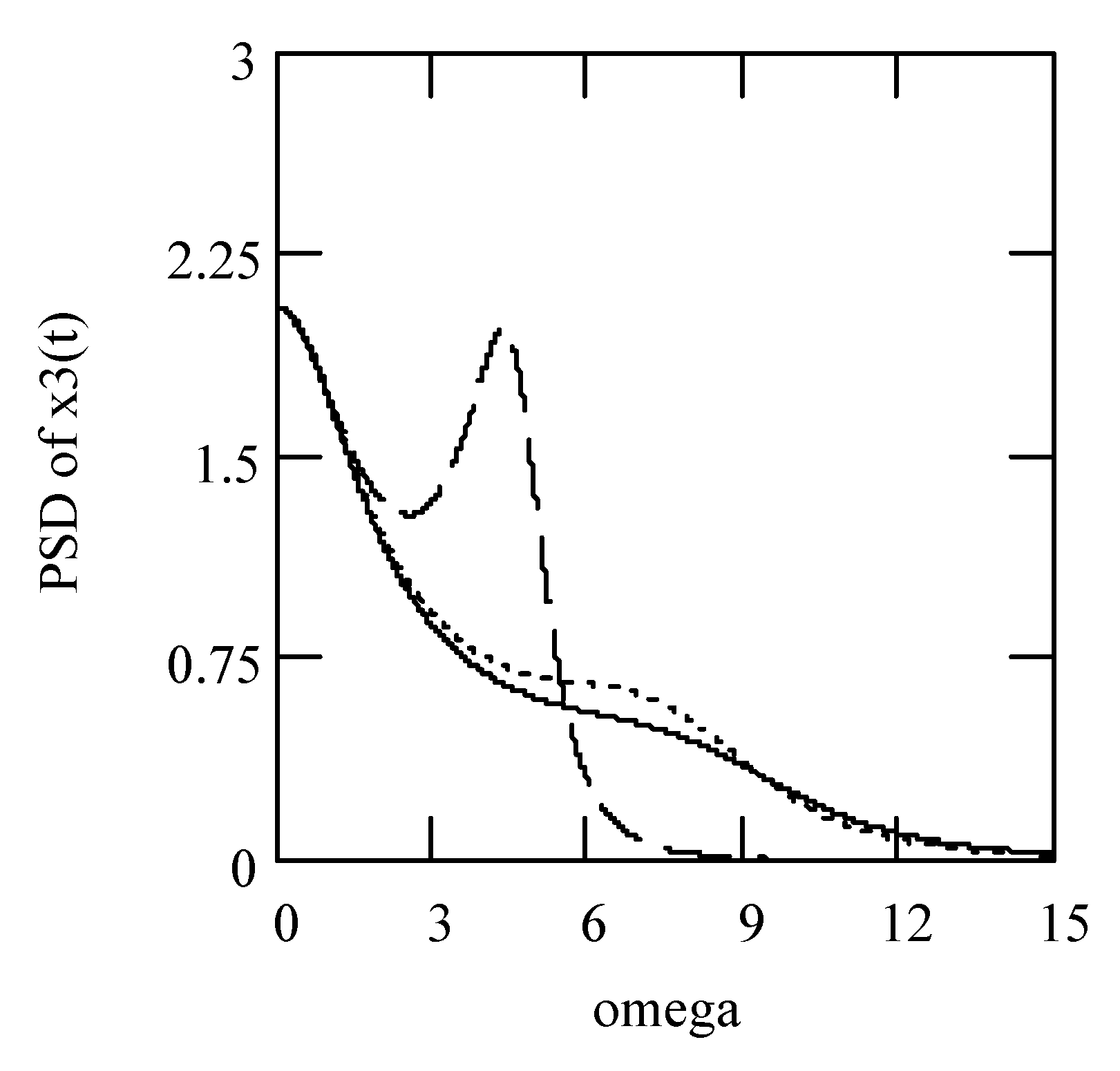
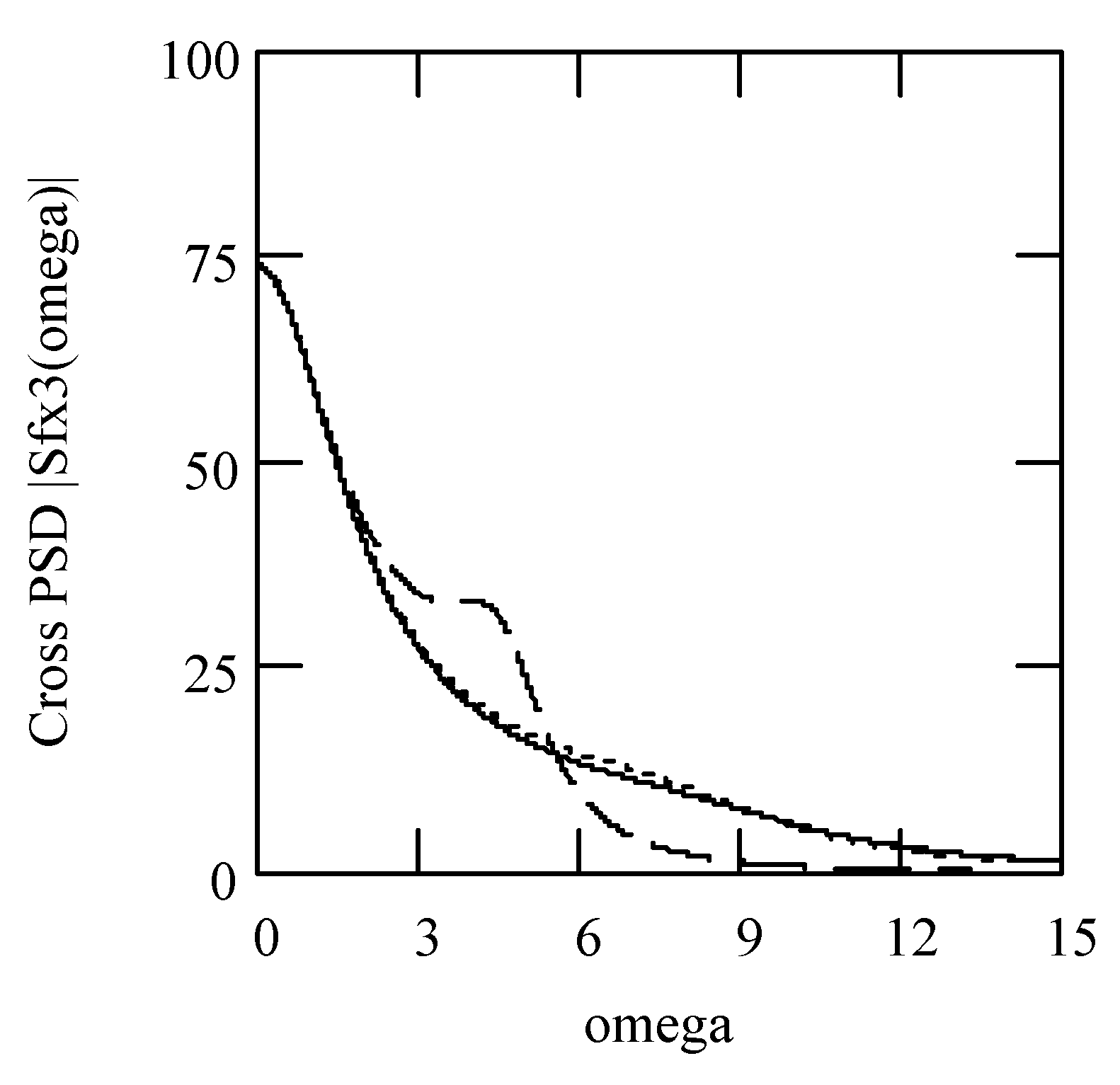
6.8. Responses of Class VII Fractional Vibrators Driven by the von Kármán Process
6.8.1. Computations
6.8.2. Effects of β, λ on Responses
6.9. Summary
7. Discussions and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013; Volume II. [Google Scholar]
- Achar, B.N.N.; Hanneken, J.W.; Clarke, T. Damping characteristics of a fractional oscillator. Physical A 2004, 339, 311–319. [Google Scholar] [CrossRef]
- Achar, B.N.N.; Hanneken, J.W.; Clarke, T. Response characteristics of a fractional oscillator. Physical A 2002, 309, 275–288. [Google Scholar] [CrossRef]
- Achar, B.N.N.; Hanneken, J.W.; Enck, T.; Clarke, T. Dynamics of the fractional oscillator. Physical A 2001, 297, 361–367. [Google Scholar] [CrossRef]
- Duan, J.-S. The periodic solution of fractional oscillation equation with periodic input. Adv. Math. Phys. 2013, 2013, 869484. [Google Scholar] [CrossRef]
- Coccolo, M.; Seoane, J.M.; Sanjuán, M.A.F. Fractional damping induces resonant behavior in the Duffing oscillator. Commun. Nonlinear Sci. Numer. Simul. 2024, 133, 107965. [Google Scholar] [CrossRef]
- Sidorov, V.; Shitikova, M.V.; Badina, E.; Detina, E.A. Review of nonlocal-in-time damping models in the dynamics of structures. Axioms 2023, 12, 676. [Google Scholar] [CrossRef]
- Di Paola, M.; Heuer, R.; Pirrotta, A. Fractional visco-elastic Euler–Bernoulli beam. Int. J. Solids Struct. 2013, 50, 3505–3510. [Google Scholar] [CrossRef]
- Pirrotta, A.; Cutrona, S.; Di Lorenzo, S.; Di Matteo, A. Fractional visco-elastic Timoshenko beam deflection via single equation. Int. J. Numer. Methods Eng. 2015, 104, 869–886. [Google Scholar] [CrossRef]
- Lewandowski, R.; Wielentejczyk, P. Nonlinear vibration of viscoelastic beams described using fractional order derivatives. J. Sound Vib. 2017, 399, 228–243. [Google Scholar] [CrossRef]
- Spanos, P.D.; Malara, G. Nonlinear vibrations of beams and plates with fractional derivative elements subject to combined harmonic and random excitations. Probab. Eng. Mech. 2020, 59, 103043. [Google Scholar] [CrossRef]
- Blaszczyk, T. A numerical solution of a fractional oscillator equation in a non-resisting medium with natural boundary conditions. Rom. Rep. Phys. 2015, 67, 350–358. [Google Scholar]
- Blaszczyk, T.; Ciesielski, M. Fractional oscillator equation—Transformation into integral equation and numerical solution. Appl. Math. Comput. 2015, 257, 428–435. [Google Scholar] [CrossRef]
- Blaszczyk, T.; Ciesielski, M.; Klimek, M.; Leszczynski, J. Numerical solution of fractional oscillator equation. Appl. Math. Comput. 2011, 218, 2480–2488. [Google Scholar] [CrossRef]
- Blaszczyk, T.; Siedlecki, J.; Sun, H.G. An exact solution of fractional Euler-Bernoulli equation for a beam with fixed-supported and fixed-free ends. Appl. Math. Comput. 2021, 396, 125932. [Google Scholar] [CrossRef]
- Al-Rabtah, A.; Ertürk, V.S.; Momani, S. Solutions of a fractional oscillator by using differential transform method. Comput. Math. Appl. 2010, 59, 1356–1362. [Google Scholar] [CrossRef]
- Zurigat, M. Solving fractional oscillators using Laplace homotopy analysis method. Ann. Univ. Craiova Math. Comput. Sci. Ser. 2011, 38, 1–11. [Google Scholar]
- Rossikhin, Y.A.; Shitikova, M.V. Analysis of the viscoelastic rod dynamics via models involving fractional derivatives or operators of two different orders. Shock Vib. Dig. 2004, 36, 3–26. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Application of fractional calculus for dynamic problems of solid mechanics: Novel trends and recent results. Appl. Mech. Rev. 2010, 63, 010801. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Application of fractional operators to the analysis of damped vibrations of viscoelastic single-mass systems. J. Sound Vib. 1997, 199, 567–586. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Classical beams and plates in a fractional derivative medium, Impact response. In Encyclopedia of Continuum Mechanics; Springer: Berlin, Germany, 2020; Volume 1, pp. 294–305. [Google Scholar]
- Rossikhin, Y.A. Reflections on two parallel ways in progress of fractional calculus in mechanics of solids. Appl. Mech. Rev. 2010, 63, 010701. [Google Scholar] [CrossRef]
- Shitikova, M.V.; Kandu, V.V.; Krusser, A.I. On nonlinear vibrations of an elastic plate on a fractional viscoelastic foundation in a viscoelastic medium in the presence of the one-to-one internal resonance. J. Sound Vib. 2023, 549, 117564. [Google Scholar] [CrossRef]
- Shitikova, M.V. Impact response of a thin shallow doubly curved linear viscoelastic shell rectangular in plan. Math. Mech. Solids 2022, 27, 1721–1739. [Google Scholar] [CrossRef]
- Shitikova, M.V. Fractional operator viscoelastic models in dynamic problems of mechanics of solids: A review. Mech. Solids 2022, 57, 1–33. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A.; Anukool, W. Vlasov equation, waves and dispersion relations in fractal dimensions: Landau damping and the toroidal ion temperature gradient instability problem. Waves Random Complex Media 2022, 1–21. [Google Scholar] [CrossRef]
- Banerjee, J.R. An exact method for free vibration of beams and frameworks using frequency-dependent mass, elastic and geometric stiffness matrices. Comput. Struct. 2024, 292, 107235. [Google Scholar] [CrossRef]
- Sofi, A. Nonlinear vibrations of beams with fractional derivative elements crossed by moving loads. Int. J. Non-Linear Mech. vol. 2024, 159, 104567. [Google Scholar] [CrossRef]
- Sofi, A.; Muscolino, G. Improved pseudo-force approach for Monte Carlo Simulation of non-linear fractional oscillators under stochastic excitation. Probab. Eng. Mech. 2023, 71, 103403. [Google Scholar] [CrossRef]
- Molina-Villegas, J.C.; Ortega, J.E.B.; Martínez, G.M. Closed-form solution for non-uniform Euler—Bernoulli beams and frames. Eng. Struct. 2023, 292, 116381. [Google Scholar] [CrossRef]
- Parovik, R.I. Quality factor of forced oscillations of a linear fractional oscillator. Tech. Phys. 2020, 65, 1015–1019. [Google Scholar] [CrossRef]
- Li, M.; Lim, S.C.; Chen, S.Y. Exact solution of impulse response to a class of fractional oscillators and its stability. Math. Probl. Eng. 2011, 2011, 657839. [Google Scholar] [CrossRef]
- Li, M.; Lim, S.C.; Cattani, C.; Scalia, M. Characteristic roots of a class of fractional oscillators. Adv. High Energy Phys. 2013, 2013, 853925. [Google Scholar] [CrossRef]
- Li, M. Three classes of fractional oscillators. Symmetry 2018, 10, 91. [Google Scholar] [CrossRef]
- Li, M. Theory of Fractional Engineering Vibrations; De Gruyter: Berlin, Germany; Boston, MA, USA, 2021. [Google Scholar]
- Li, M. Fractional Vibrations with Applications to Euler-Bernoulli Beams; CRC Press: Boca Raton, UK, 2023. [Google Scholar]
- Mandelbrot, B.B. Gaussian Self-Affinity and Fractals; Springer: New York, NY, USA, 2001. [Google Scholar]
- Mandelbrot, B.B. Multifractals and 1/f Noise; Springer: New York, NY, USA, 1998. [Google Scholar]
- Beran, J. Statistics for Long-Memory Processes; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar]
- Levy-Vehel, J.; Lutton, E. Fractals in Engineering; Springer: Berlin, Germany, 2005. [Google Scholar]
- Véhel, J.L.; Rams, M. Large deviation multifractal analysis of a class of additive processes with correlated non-stationary increments. IEEE/ACM Trans. Netw. 2013, 21, 1309–1321. [Google Scholar] [CrossRef]
- Bender, C.; Lebovits, J.; Véhel, J.L. General transfer formula for stochastic integral with respect to multifractional Brownian motion. J. Theor. Prob. 2024, 37, 905–932. [Google Scholar] [CrossRef]
- Guével, R.L.; Lévy-Véhel, J. Hausdorff, large deviation and Legendre multifractal spectra of Lévy multistable processes. Stoch. Process. Their Appl. 2020, 130, 2032–2057. [Google Scholar] [CrossRef]
- Lebovits, J.; Lévy-Véhel, J.; Herbin, E. Stochastic integration with respect to multifractional Brownian motion via tangent fractional Brownian motions. Stoch. Process. Their Appl. 2014, 124, 678–708. [Google Scholar] [CrossRef]
- Corlay, S.; Lebovits, J.; Lévy-Véhel, J. multifractional stochastic volatility models. Math. Financ. 2014, 24, 364–402. [Google Scholar] [CrossRef]
- Ayache, A.; Roueff, F.; Xiao, Y. Linear fractional stable sheets: Wavelet expansion and sample path properties. Stoch. Process. Their Appl. 2009, 119, 1168–1197. [Google Scholar] [CrossRef]
- Park, H.; Xiao, Y.; Yang, X. Uniform dimension results for the inverse images of symmetric Lévy processes. J. Theor. Probab. 2020, 33, 2213–2232. [Google Scholar] [CrossRef]
- Luks, T.; Xiao, Y. Multiple points of operator semistable Lévy processes. J. Theor. Probab. 2020, 33, 153–179. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, Y. A class of fractional Brownian fields from branching systems and their regularity properties. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 2013, 16, 1350023. [Google Scholar] [CrossRef]
- Flandrin, P. On the spectrum of fractional Brownian motions. IEEE Trans. Inf. Theory 1989, 35, 197–199. [Google Scholar] [CrossRef]
- Flandrin, P. Wavelet analysis and synthesis of fractional Brownian motion. IEEE Trans. Inf. Theory 1992, 38, 910–917. [Google Scholar] [CrossRef]
- Zao, L.; Coelho, R.; Flandrin, P. Speech Enhancement with EMD and Hurst-based mode selection. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 897–909. [Google Scholar] [CrossRef]
- Borgnat, P.; Amblard, P.-O.; Flandrin, P. Scale Invariances and Lamperti Transformations for Stochastic Processes. J. Phys. A Math. Theor. 2005, 38, 2081–2101. [Google Scholar] [CrossRef][Green Version]
- Borgnat, P.; Flandrin, P.; Amblard, P.-O. Stochastic discrete scale invariance. IEEE Signal Process. Lett. 2002, 9, 181–184. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Casillas-Pérez, D.; Del Ser, J.; Casanova-Mateo, C.; Cuadra, L.; Piles, M.; Camps-Valls, G. Persistence in complex systems. Phys. Rep. 2022, 957, 1–73. [Google Scholar] [CrossRef]
- Levin, Y.; Pakter, R.; Rizzato, F.B.; Teles, T.N.; Benetti, F.P.C. Nonequilibrium statistical mechanics of systems with long-range interactions. Phys. Rep. 2014, 535, 1–60. [Google Scholar] [CrossRef]
- Marković, D.; Gros, C. Power laws and Self-Organized Criticality in Theory and Nature. Phys. Rep. 2014, 536, 41–74. [Google Scholar] [CrossRef]
- Eliazar, I.I.; Shlesinger, M.F. Fractional motions. Phys. Rep. 2013, 527, 101–129. [Google Scholar] [CrossRef]
- Campa, A.; Dauxois, T.; Ruffo, S. Statistical mechanics and dynamics of solvable models with long-range interactions. Phys. Rep. 2009, 480, 57–159. [Google Scholar] [CrossRef]
- Pinchas, M.; Avraham, Y. Performance of the modified clock skew estimator and its upper bound for the IEEE 1588v2 (PTP) case under packet loss and fractional Gaussian noise environment. Front. Phys. 2023, 11, 222735. [Google Scholar]
- Pinchas, M.; Avraham, Y. A novel clock skew estimator and its performance for the IEEE 1588v2 (PTP) case in fractional Gaussian noise/generalized fractional Gaussian noise environment. Front. Phys. 2021, 9, 796811. [Google Scholar]
- Mirás-Avalos, J.M.; Trigo-Córdoba, E.; da Silva-Dias, R.; Varela-Vila, I.; García-Tomillo, A. Multifractal behaviour of the soil water content of a vineyard in northwest Spain during two growing seasons. Nonlinear Process. Geophys. 2016, 23, 205–213. [Google Scholar] [CrossRef]
- Kaulakys, B.; Alaburda, M.; Ruseckas, J. 1/f noise from the nonlinear transformations of the variables. Mod. Phys. Lett. B 2015, 29, 1550223. [Google Scholar] [CrossRef]
- Lubashevsky, I.A. Truncated Lévy flights and generalized Cauchy processes. Eur. Phys. J. B 2011, 82, 189–195. [Google Scholar] [CrossRef]
- Starchenko, V. Images fractal compression algorithms. Comput.-Integr. Technol. Educ. Sci. Prod. 2023, 53, 215–221. (In Ukrainian) [Google Scholar]
- Gorev, V.N.; Gusev, A.Y.; Korniienko, V.I.; Shedlovska, Y.I. Generalized fractional Gaussian noise prediction based on the Walsh functions. Radio Electron. Comput. Sci. Control 2023, 3, 48. [Google Scholar] [CrossRef]
- Sheluhin, O.; Rybakov, S.; Vanyushina, A. Modified algorithm for detecting network attacks using the fractal dimension jump estimation method in online mode. Proc. Telecommun. Univ. 2022, 8, 117–126. (In Russian) [Google Scholar] [CrossRef]
- Sousa-Vieira, M.E.; Fernández-Veiga, M. Efficient generators of the generalized Fractional Gaussian noise and Cauchy processes. Fract. Fract. 2023, 7, 455. [Google Scholar] [CrossRef]
- Beskardes, G.D.; Weiss, C.J.; Everett, M.E. Estimating the power-law distribution of Earth electrical conductivity from low-frequency, controlled-source electromagnetic responses. Geophys. J. Int. 2017, 208, 639–651. [Google Scholar] [CrossRef]
- Ercan, A.; Kavvas, M.L. Time-space fractional governing equations of one-dimensional unsteady open channel flow process: Numerical solution and exploration. Hydrol. Process. 2017, 31, 2961–2971. [Google Scholar] [CrossRef]
- Lee, M.; Genton, M.G.; Jun, M. Testing self-similarity through Lamperti transformations. J. Agric. Biol. Environ. Stat. 2016, 21, 426–447. [Google Scholar] [CrossRef]
- Li, M. Fractal time series—A tutorial review. Math. Probl. Eng. 2010, 2010, 157264. [Google Scholar] [CrossRef]
- Li, M. Multi-Fractal Traffic and Anomaly Detection in Computer Communications; CRC Press: Boca Raton, UK, 2022. [Google Scholar]
- Li, M. Fractal Teletraffic Modeling and Delay Bounds in Computer Communications; CRC Press: Boca Raton, UK, 2022. [Google Scholar]
- Li, Z.; Yan, L. Harnack inequalities for SDEs driven by subordinator fractional Brownian motion. Stat. Probab. Lett. 2018, 134, 45–53. [Google Scholar] [CrossRef]
- Gao, H.; Guo, R.; Jin, Y.; Yan, L. Large time behavior on the linear self-interacting diffusion driven by sub-fractional Brownian motion I: Self-repelling case. Front. Phys. 2021, 9, 795210. [Google Scholar] [CrossRef]
- Guo, H.; Gao, R.; Jin, Y.; Yan, L. Large time behavior on the linear self-interacting diffusion driven by sub-fractional Brownian motion II: Self-attracting case. Front. Phys. 2021, 9, 791858. [Google Scholar] [CrossRef]
- Gao, L.; Sun, X. Almost periodic solutions to impulsive stochastic delay differential equations driven by fractional Brownian motion with 0.5 < H < 1. Front. Phys. 2021, 9, 783125. [Google Scholar]
- Pei, W.; Zhang, Z. Stability of hybrid SDEs driven by fBm. Front. Phys. 2021, 9, 783434. [Google Scholar] [CrossRef]
- Barth, A.; Stüwe, T. Weak convergence of Galerkin approximations of stochastic partial differential equations driven by additive Lévy noise. Math. Comput. Simul. 2018, 143, 215–225. [Google Scholar] [CrossRef]
- Kim, K.-H.; Park, D. A Sobolev space theory for time-fractional stochastic partial differential equations driven by Lévy processes. J. Theor. Probab. 2024, 37, 671–720. [Google Scholar] [CrossRef]
- Noupelah, A.J.; Tambue, A.; Woukeng, J.L. Strong convergence of a fractional exponential integrator scheme for finite element discretization of time-fractional SPDE driven by fractional and standard Brownian motions. Commun. Nonlinear Sci. Numer. Simul. 2023, 125, 107371. [Google Scholar] [CrossRef]
- Massing, T. Approximation and error analysis of forward–backward SDEs driven by general Lévy processes using shot noise series representations. ESAIM Probab. Stat. 2023, 27, 694–722. [Google Scholar] [CrossRef]
- Lee, C.Y. Local nondeterminism and local times of the stochastic wave equation driven by fractional-colored noise. J. Fourier Anal. Appl. 2022, 28, 26. [Google Scholar] [CrossRef]
- Fa, K.S.; Pianegonda, S.; da Luz, M.G.E. Broad class of nonlinear Langevin equations driven by multiplicative Ornstein–Uhlenbeck noise: Generalized n-moment and generalized second Einstein relation. Physical A 2023, 622, 128807. [Google Scholar] [CrossRef]
- Freundlich, J.; Sado, D. Dynamics of a mechanical system with a spherical pendulum subjected to fractional damping: Analytical analysis. Nonlinear Dyn. 2023, 111, 7961–7973. [Google Scholar] [CrossRef]
- Burlon, A. On the numerical solution of fractional differential equations under white noise processes. Probab. Eng. Mech. 2023, 73, 103465. [Google Scholar] [CrossRef]
- Wang, W.; Yan, Z.; Liu, X. The escape problem and stochastic resonance in a bistable system driven by fractional Gaussian noise. Phys. Lett. A 2017, 381, 2324–2336. [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, X.Y. Stochastic control for linear systems driven by fractional noises. SIAM J. Control Optim. 2005, 43, 2245–2277. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Caraballo, T. The continuity, regularity and polynomial stability of mild solutions for stochastic 2D-Stokes equations with unbounded delay driven by tempered fractional Gaussian noise. Stoch. Dyn. 2022, 22, 2250022. [Google Scholar] [CrossRef]
- Li, M.; Lim, S.C. A rigorous derivation of power spectrum of fractional Gaussian noise. Fluct. Noise Lett. 2006, 6, C33–C36. [Google Scholar] [CrossRef]
- Li, M.; Chi, C.-H. A correlation-based computational method for simulating long-range dependent data. J. Frankl. Inst. 2003, 340, 503–514. [Google Scholar] [CrossRef]
- He, J.; Xing, Z.; Guo, Q. Spectral collocation method for stochastic differential equations driven by fractional Brownian motion. Fluct. Noise Lett. 2023, 22, 2350019. [Google Scholar] [CrossRef]
- He, J.; Guo, Q. An explicit method for the self-interacting diffusion driven by fractional Brownian motion under global Lipschitz conditions. Appl. Math. Lett. 2022, 134, 108379. [Google Scholar] [CrossRef]
- Liu, X. Strong approximation for fractional wave equation forced by fractional Brownian motion with Hurst parameter H ∈ (0, 0.5). J. Comput. Appl. Math. 2023, 432, 115285. [Google Scholar] [CrossRef]
- Tuan, N.H.; Caraballo, T.; Thach, T.N. New results for stochastic fractional pseudo-parabolic equations with delays driven by fractional Brownian motion. Stoch. Process. Their Appl. 2023, 161, 24–67. [Google Scholar] [CrossRef]
- Tuan, N.H.; Foondun, M.; Thach, T.N.; Wang, R. On backward problems for stochastic fractional reaction equations with standard and fractional Brownian motion. Bul. Sci. Math. 2022, 179, 103158. [Google Scholar] [CrossRef]
- Sharma, N.; Selvamuthu, D.; Natarajan, S. Variable annuities valuation under a mixed fractional Brownian motion environment with jumps considering mortality risk. Appl. Stoch. Models Bus. Ind. 2022, 38, 1019–1038. [Google Scholar] [CrossRef]
- Fan, X.; Huang, X.; Suo, Y.; Yuan, C. Distribution dependent SDEs driven by fractional Brownian motions. Stoch. Process. Their Appl. 2022, 151, 23–67. [Google Scholar] [CrossRef]
- Zhang, S.-Q.; Yuan, C. Stochastic differential equations driven by fractional Brownian motion with locally Lipschitz drift and their implicit Euler approximation. Proc. R. Soc. Edinb. Sect. A Math. 2021, 151, 1278–1304. [Google Scholar] [CrossRef]
- Shahnazi-Pour, A.; Moghaddam, B.P.; Babaei, A. Numerical simulation of the Hurst index of solutions of fractional stochastic dynamical systems driven by fractional Brownian motion. J. Comput. Appl. Math. 2021, 386, 113210. [Google Scholar] [CrossRef]
- Araya, H.; León, J.A.; Torres, S. Numerical scheme for stochastic differential equations driven by fractional Brownian motion with ¼ < H < 1/2. J. Theor. Probab. 2020, 33, 1211–1237. [Google Scholar]
- Gairing, J.; Imkeller, P.; Shevchenko, R.; Tudor, C. Hurst Index estimation in stochastic differential equations driven by fractional Brownian motion. J. Theor. Probab. 2020, 33, 1691–1714. [Google Scholar] [CrossRef]
- Xu, P.; Huang, J.; Zeng, C. Ergodicity of stochastic Rabinovich systems driven by fractional Brownian motion. Physical A 2020, 546, 122955. [Google Scholar] [CrossRef]
- Heydari, M.H.; Avazzadeh, Z.; Mahmoudi, M.R. Chebyshev cardinal wavelets for nonlinear stochastic differential equations driven with variable-order fractional Brownian motion. Chaos Solitons Fractals 2019, 124, 105–124. [Google Scholar] [CrossRef]
- Heydari, M.H.; Mahmoudi, M.R.; Shakiba, A.; Avazzadeh, Z. Chebyshev cardinal wavelets and their application in solving nonlinear stochastic differential equations with fractional Brownian motion. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 98–121. [Google Scholar] [CrossRef]
- Pavliotis, G.A. Stochastic Processes and Applications, Diffusion Processes, the Fokker-Planck and Langevin Equations; Texts in Applied Mathematics; Springer: New York, NY, USA, 2014; Volume 60. [Google Scholar]
- Coffey, W.T.; Kalmykov, Y.P.; Waldron, J.T. The Langevin Equation with Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering, 2nd ed.; World Scientific: Singapore, 2004. [Google Scholar]
- West, B.J.; Geneston, E.L.; Grigolini, P. Maximizing information exchange between complex networks. Phys. Rep. 2008, 468, 1–99. [Google Scholar] [CrossRef]
- Lim, S.C.; Li, M.; Teo, L.P. Langevin equation with two fractional orders. Phys. Lett. A 2008, 372, 6309–6320. [Google Scholar] [CrossRef]
- Lim, S.C.; Li, M.; Teo, L.P. Locally self-similar fractional oscillator processes. Fluct. Noise Lett. 2007, 7, L169–L179. [Google Scholar] [CrossRef]
- Shao, Y. The fractional Ornstein-Uhlenbeck process as a representation of homogeneous Eulerian velocity turbulence. Physical D 1995, 83, 461–477. [Google Scholar] [CrossRef]
- Cheridito, P.; Kawaguchi, H.; Maejima, M. Fractional Ornstein-Uhlenbeck processes. Electron. J. Probab. 2003, 8, 1–14. [Google Scholar] [CrossRef]
- Magdziarz, M. Fractional Ornstein–Uhlenbeck processes, Joseph effect in models with infinite variance. Physical A 2008, 387, 123–133. [Google Scholar] [CrossRef]
- Gehringer, J.; Li, X.-M. Functional Limit Theorems for the fractional Ornstein–Uhlenbeck process. J. Theor. Probab. 2022, 35, 426–456. [Google Scholar] [CrossRef]
- Patel, H.G.; Sharma, S.N. Some evolution equations for an Ornstein–Uhlenbeck process-driven dynamical system. Fluct. Noise Lett. 2012, 11, 1250020. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures, 2nd ed.; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Holmes, J.D. Wind Loading of Structure, 2nd ed.; Taylor & Francis: London, UK; New York, NY, USA, 2007. [Google Scholar]
- Crandall, S.H.; Mark, W.D. Random Vibration in Mechanical Systems; Elsevier Inc.: New York, NY, USA; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Elishakoff, I.; Lyon, R.H. (Eds.) Random Vibration Status and Recent Developments; Elsevier: New York, NY, USA, 1986. [Google Scholar]
- Rothbart, H.A.; Brown, T.H., Jr. Mechanical Design Handbook, 2nd ed.; Measurement, Analysis and Control of Dynamic Systems; McGraw–Hill: New York, NY, USA, 2006. [Google Scholar]
- Jensen, J.J. (Ed.) Load and Global Response of Ships; Elsevier: Oxford, UK; Academic Press: Oxford, UK, 2001; Volume 4. [Google Scholar]
- Harris, C.M. Shock and Vibration Handbook, 5th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Lalanne, C. Mechanical Vibration and Shock, 2nd ed.; Random Vibration; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 3. [Google Scholar]
- Lalanne, C. Mechanical Vibration and Shock, 2nd ed.; Fatigue Damage; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 4. [Google Scholar]
- Lalanne, C. Mechanical Vibration and Shock, 2nd ed.; Specification Development; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 5. [Google Scholar]
- Li, M. An iteration method to adjusting random loading for a laboratory fatigue test. Int. J. Fatigue 2005, 27, 783–789. [Google Scholar] [CrossRef]
- Li, M. Experimental stability analysis of test system for doing fatigue test under random loading. J. Test. Eval. 2006, 34, 364–367. [Google Scholar]

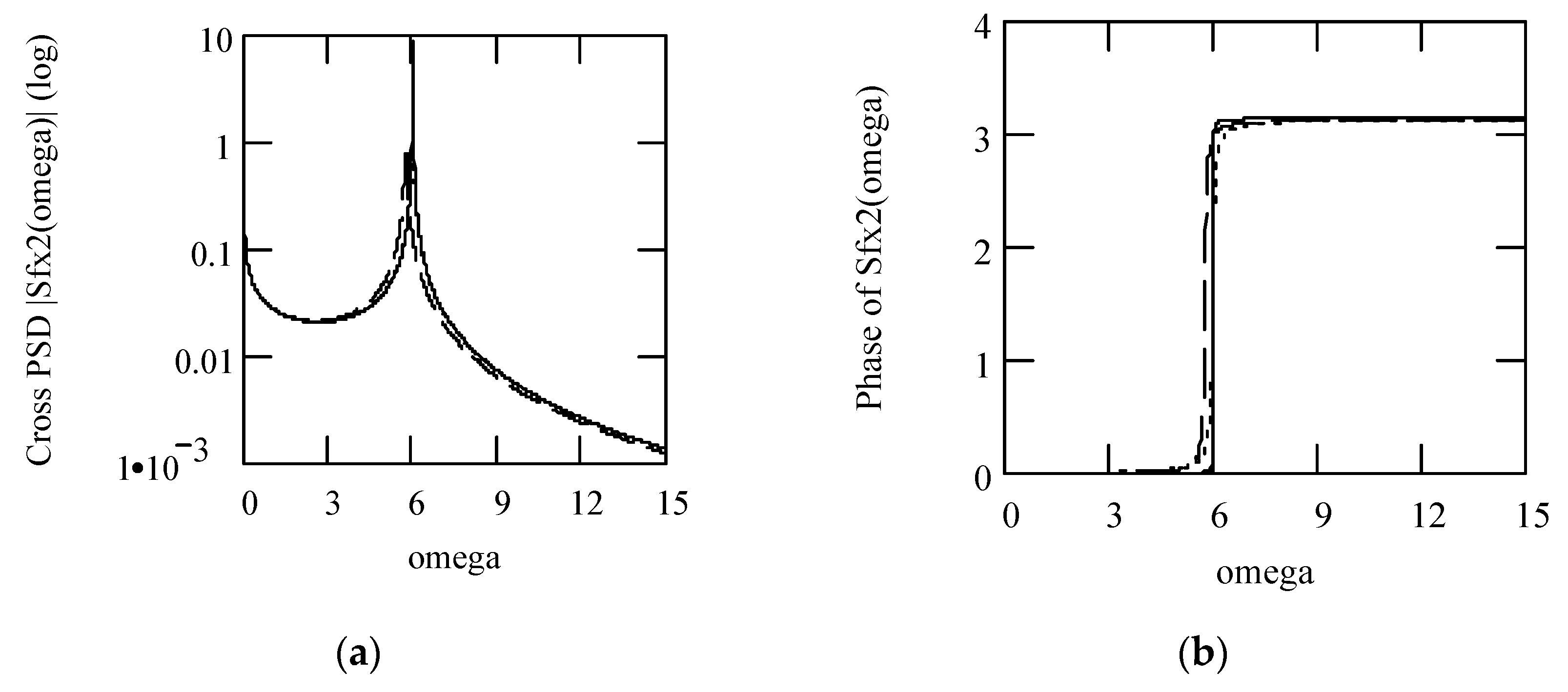


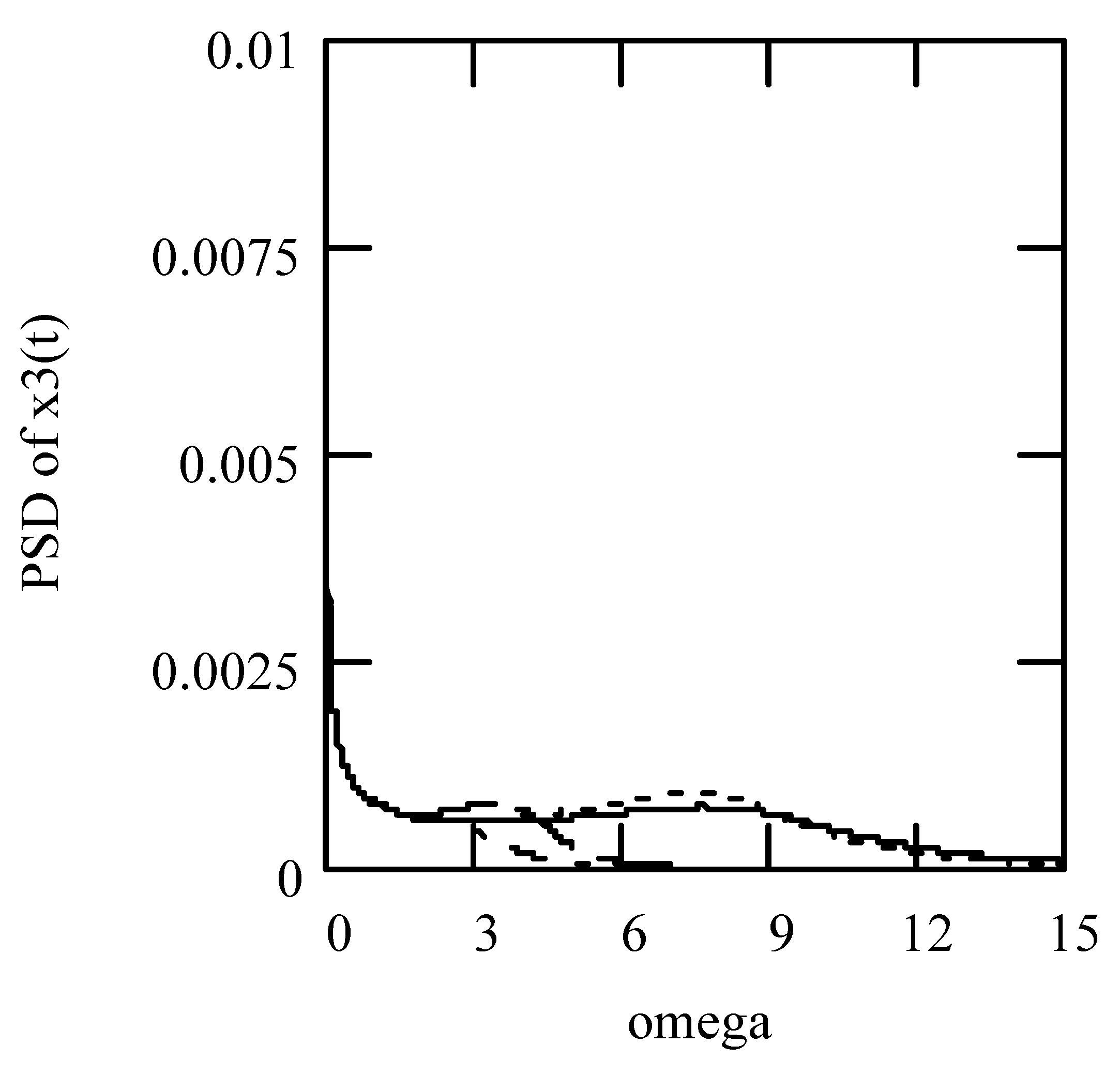
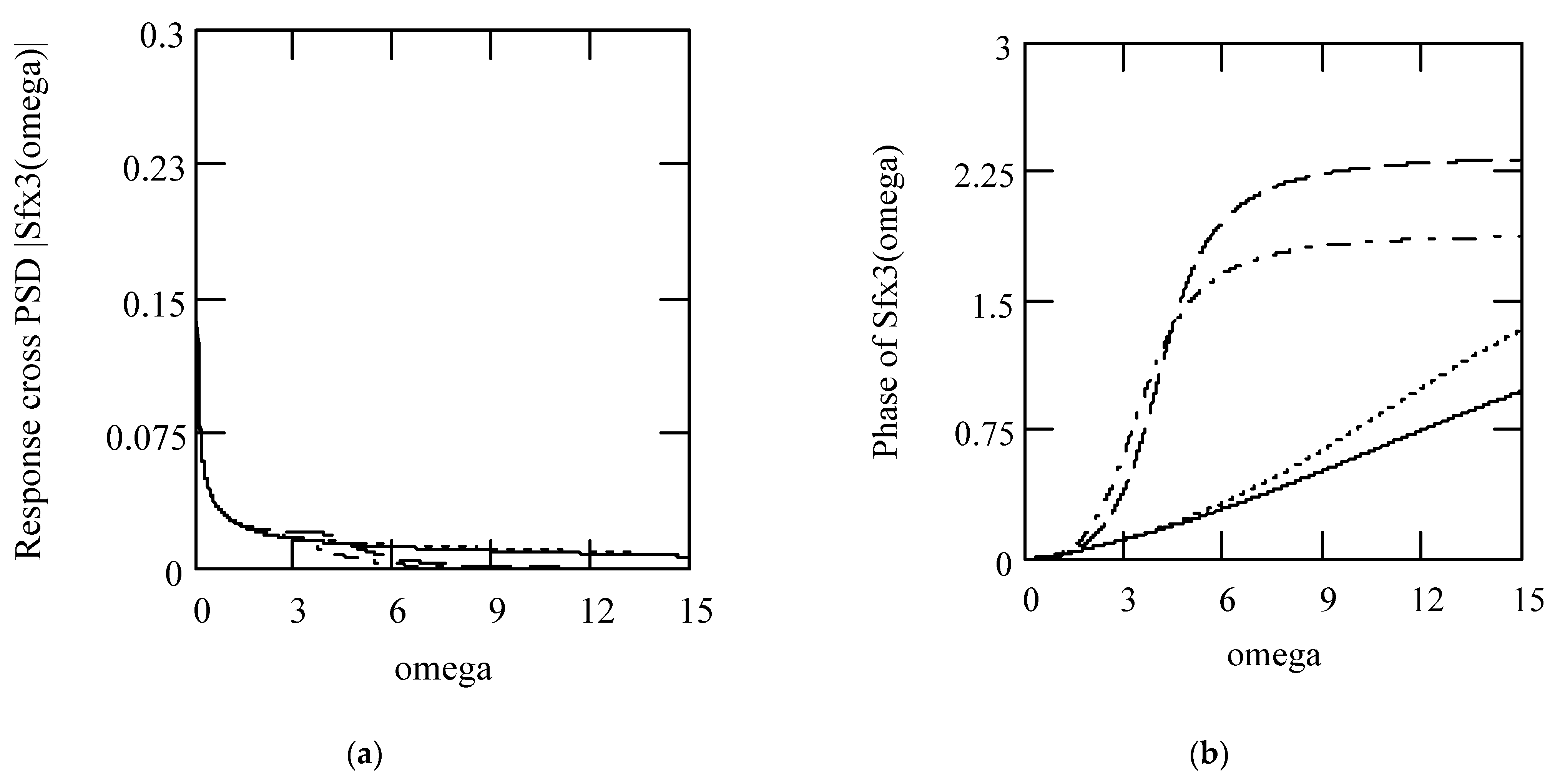
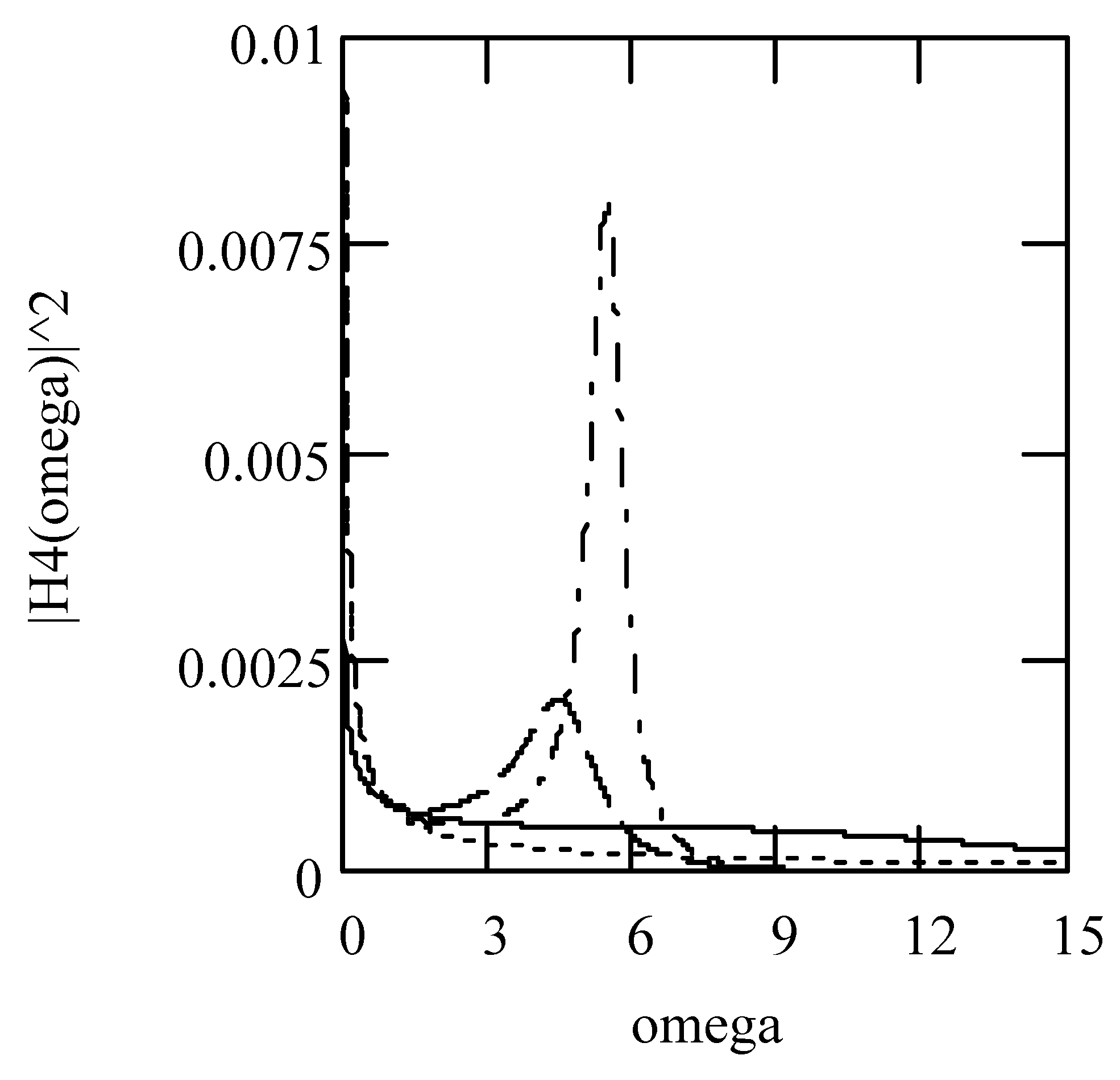














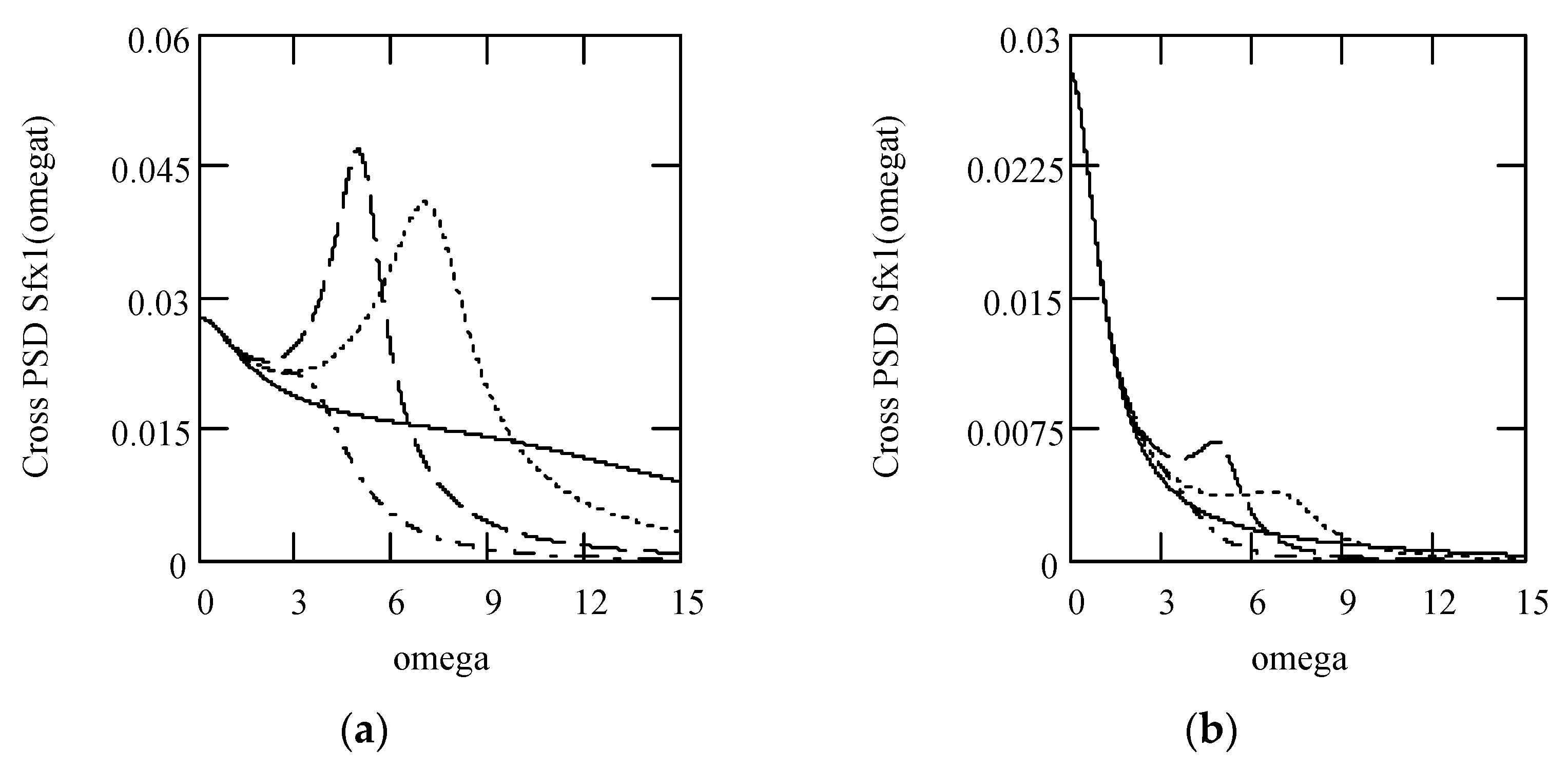
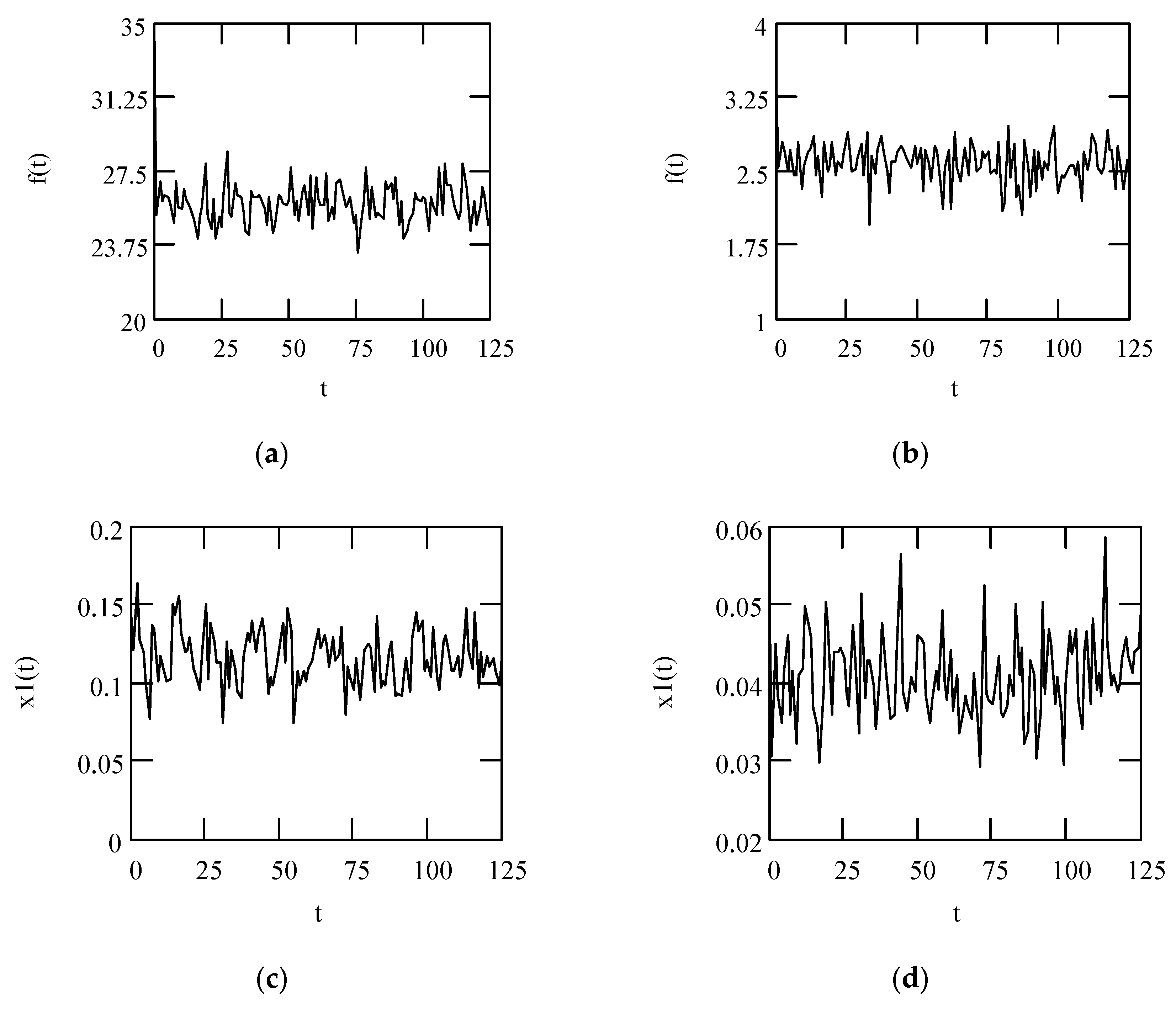

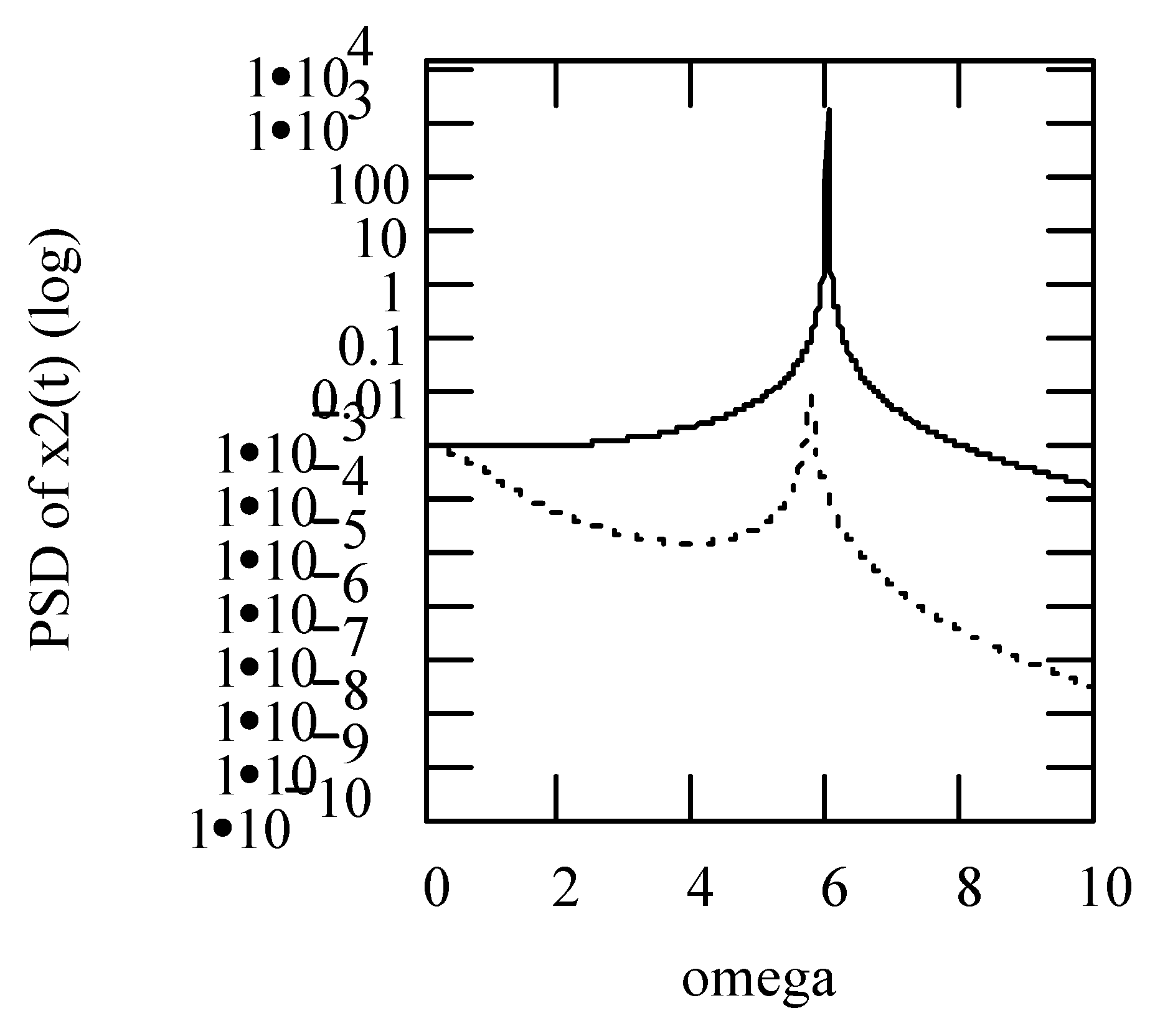
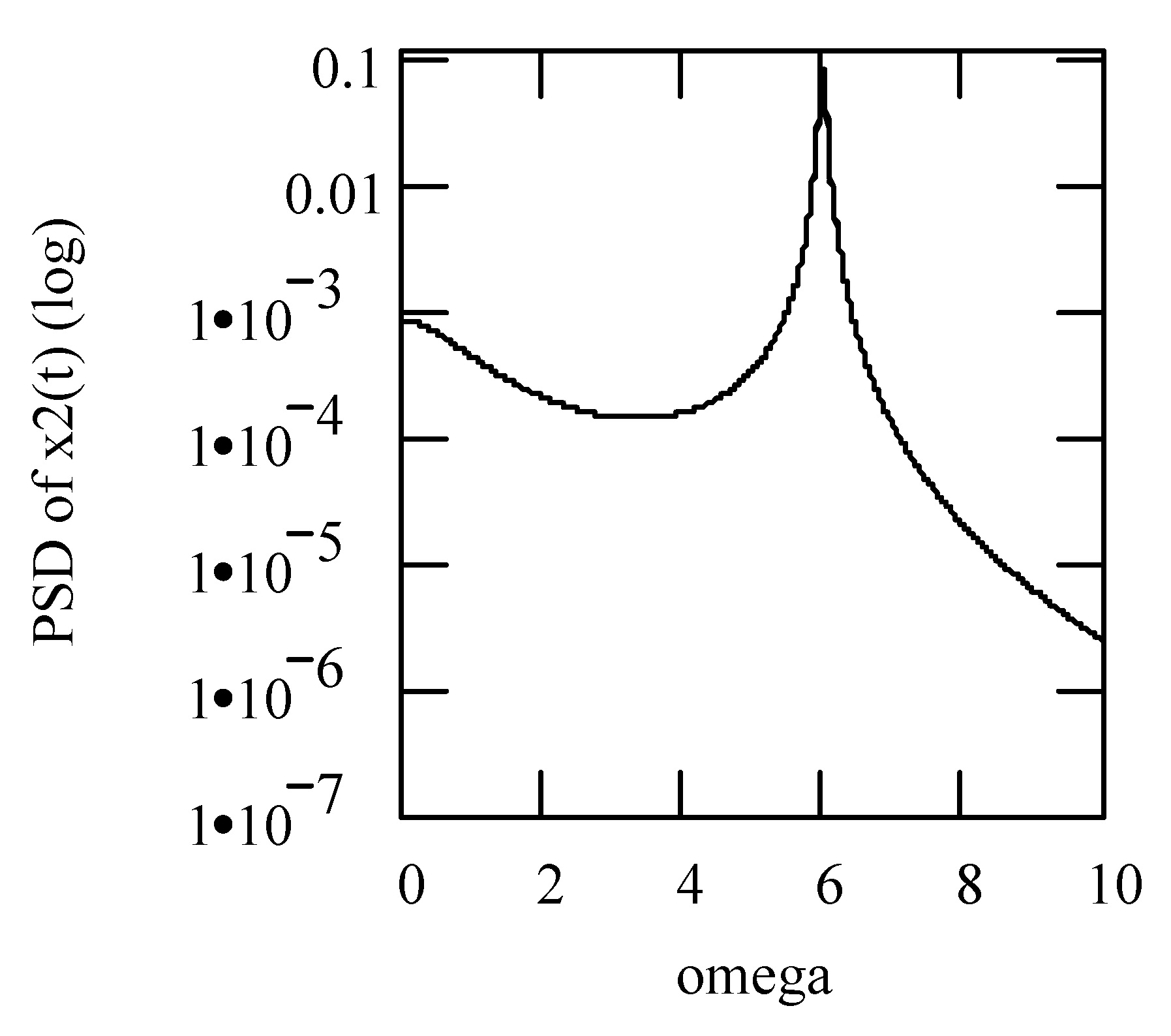









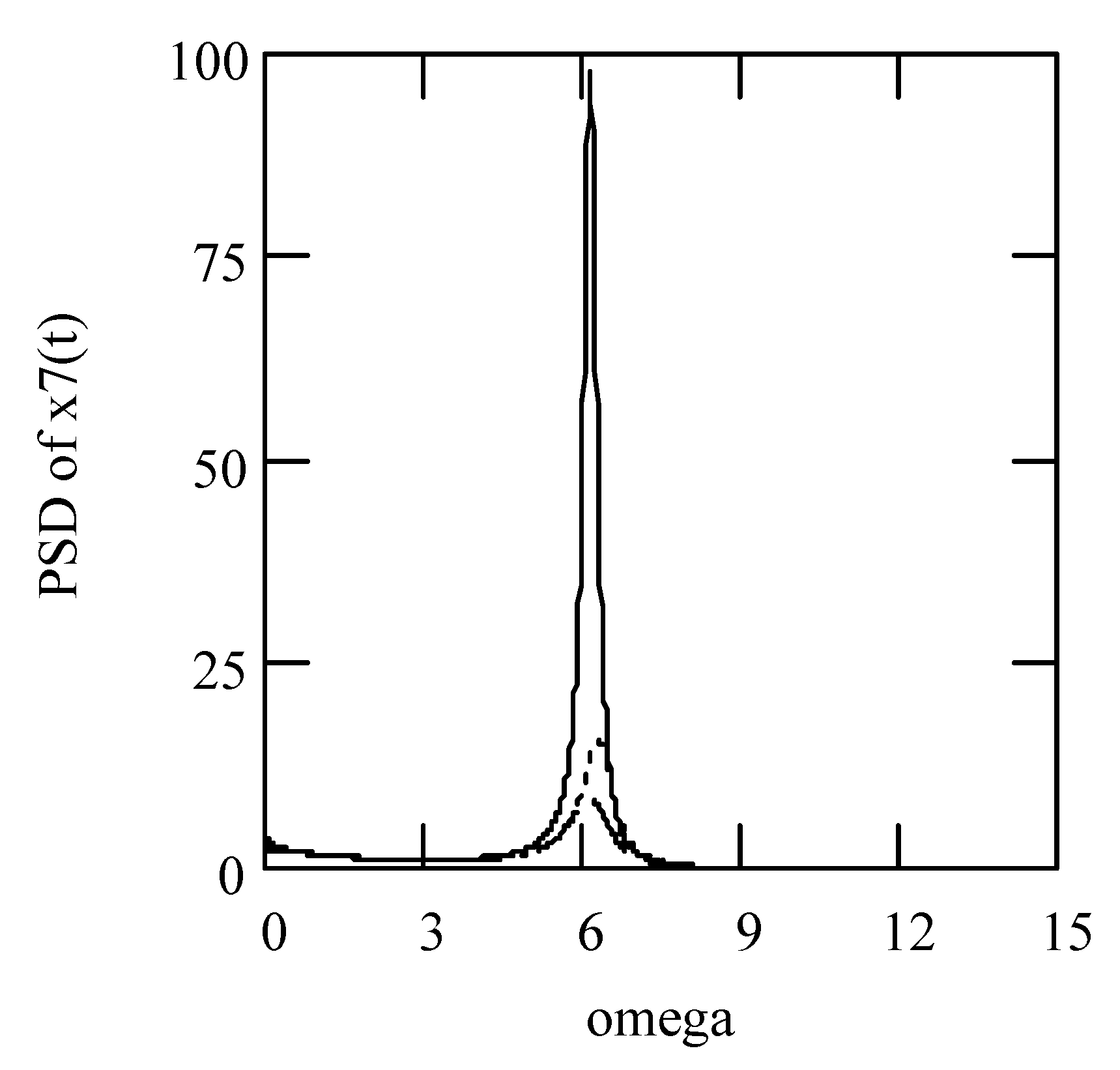
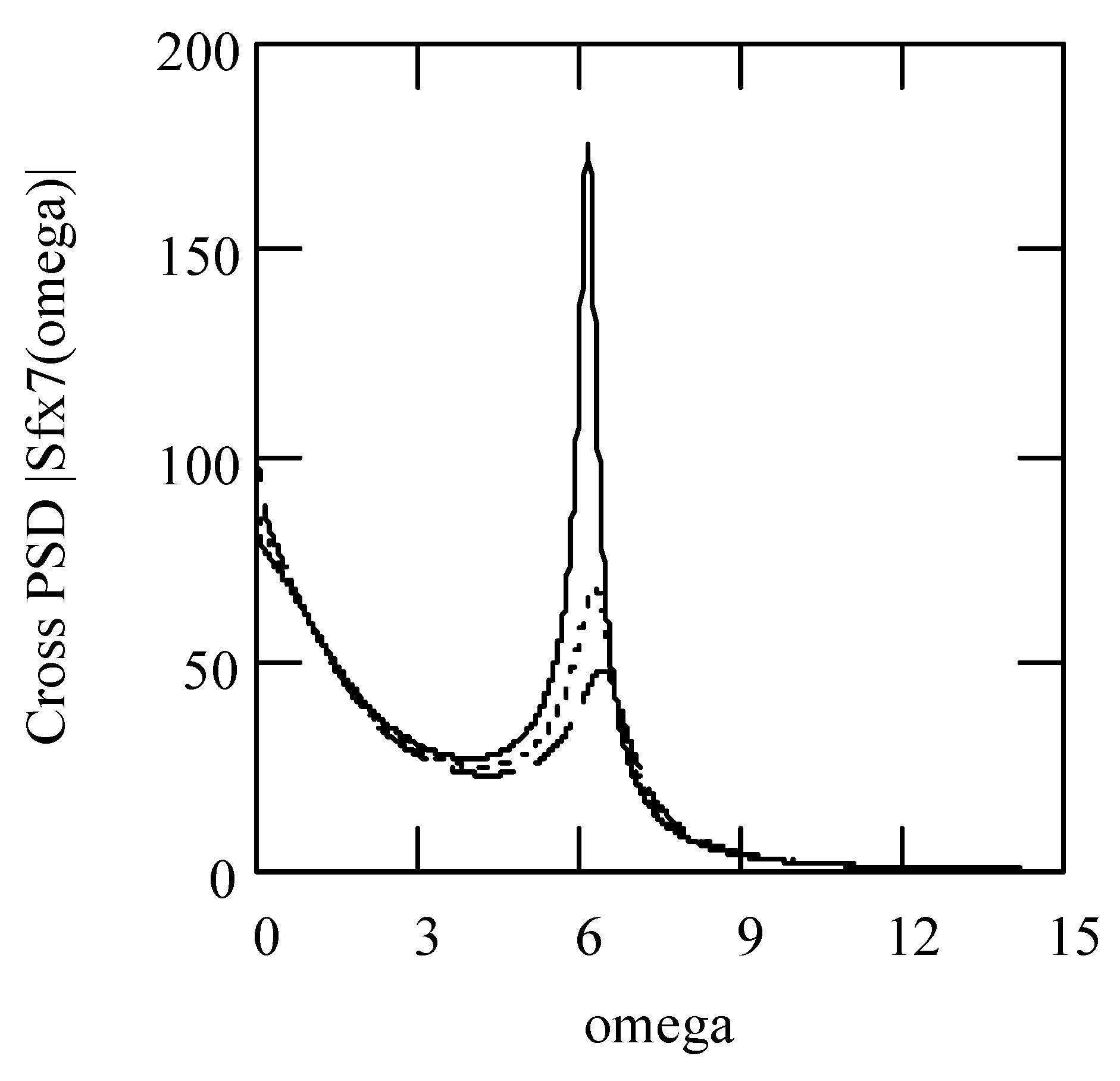
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M. PSD and Cross-PSD of Responses of Seven Classes of Fractional Vibrations Driven by fGn, fBm, Fractional OU Process, and von Kármán Process. Symmetry 2024, 16, 635. https://doi.org/10.3390/sym16050635
Li M. PSD and Cross-PSD of Responses of Seven Classes of Fractional Vibrations Driven by fGn, fBm, Fractional OU Process, and von Kármán Process. Symmetry. 2024; 16(5):635. https://doi.org/10.3390/sym16050635
Chicago/Turabian StyleLi, Ming. 2024. "PSD and Cross-PSD of Responses of Seven Classes of Fractional Vibrations Driven by fGn, fBm, Fractional OU Process, and von Kármán Process" Symmetry 16, no. 5: 635. https://doi.org/10.3390/sym16050635
APA StyleLi, M. (2024). PSD and Cross-PSD of Responses of Seven Classes of Fractional Vibrations Driven by fGn, fBm, Fractional OU Process, and von Kármán Process. Symmetry, 16(5), 635. https://doi.org/10.3390/sym16050635





