FGeo-TP: A Language Model-Enhanced Solver for Euclidean Geometry Problems

Abstract

The application of contemporary artificial intelligence techniques to address geometric problems and automated deductive proofs has always been a grand challenge to the interdisciplinary field of mathematics and artificial intelligence. This is the fourth article in a series of our works, in our previous work, we established a geometric formalized system known as FormalGeo. Moreover, we annotated approximately 7000 geometric problems, forming the FormalGeo7k dataset. Despite the fact that FGPS (Formal Geometry Problem Solver) can achieve interpretable algebraic equation solving and human-like deductive reasoning, it often experiences timeouts due to the complexity of the search strategy. In this paper, we introduced FGeo-TP (theorem predictor), which utilizes the language model to predict the theorem sequences for solving geometry problems. The encoder and decoder components in the transformer architecture naturally establish a mapping between the sequences and embedding vectors, exhibiting inherent symmetry. We compare the effectiveness of various transformer architectures, such as BART or T5, in theorem prediction, and implement pruning in the search process of FGPS, thereby improving its performance when solving geometry problems. Our results demonstrate a significant increase in the problem-solving rate of the language model-enhanced FGeo-TP on the FormalGeo7k dataset, rising from 39.7% to 80.86%. Furthermore, FGeo-TP exhibits notable reductions in solution times and search steps across problems of varying difficulty levels.

1. Introduction

The utilization of computers to solve mathematical problems has long been an intriguing and highly challenging endeavor. With the continuous evolution of artificial intelligence technology, various methods have emerged for solving mathematical problems across different domains. This has led to the creation of solvers specifically designed for arithmetic [1], algebraic [2,3,4], and theorem proving [5,6]. In this context, artificial intelligence plays a significant role in computational optimization and strategy selection optimization, while there has been relatively limited research on plane geometry problems, recent years have witnessed the emergence of corresponding studies, such as inter-GPS [7], GeoQA [8], and uniGEO [9]. These approaches have each introduced their own datasets and demonstrated the solving capabilities of their solvers. However, these studies often suffer from some flaws, such as opaque solver solving processes, lack of real-time interaction, and difficulty in expanding the solving framework. In our previous research, FormalGeo [10], we designed Formal Geometric Problem Solver (FGPS) and FormalGeo7k dataset to perfectly solve these problems. The FGPS employs both forward and backward search methods with various strategies for automated problem-solving. It is capable of executing traceable and interpretable algebraic equation solving and relationship reasoning.

The FormalGeo7k dataset comprises 6981 SAT-level geometry problems, each accompanied by a complete natural language description, geometric shapes, formal language annotations, and theorem sequence annotations. Different from GeoQA and uniGEO, inter-GPS annotates geometric images themselves, yet utilizes Euclidean coordinate annotations, leading to the inability of reflecting the symmetry of the images in its annotations. FormalGeo7K adopts the topological mapping method, describing the relative information between points, which ensures that basic transformations, such as rotation or scaling of the figures, do not affect the topological information of the figures themselves, thus preserving their symmetry. One of the examples is illustrated in Figure 1. When annotated theorem sequences are provided, FGPS can serve as an interactive assistant to help humans verify the problem-solving process. In the absence of provided annotated theorem sequences, FGPS can employ various heuristic search methods to solve problems autonomously.

Experiments conducted on the FormalGeo7k dataset indicate that FGPS achieved a maximum solving rate of 39.7% with the forward random search method. Both forward and backward search methods showed success rates of less than 40% in solving correct answers within a limited time frame; however, this may not elicit excitement. To achieve true artificial intelligence automated reasoning in solving plane geometry problems, auxiliary measures are needed to enhance the speed and effectiveness of FGPS.

The provision or absence of theorem sequences significantly impacts the solving efficacy of FGPS, prompting the urgent need for FGPS to generate theorem sequences autonomously. Analogous to humans annotating theorem sequences after attempting to comprehend geometric problems, we aspire for FGPS to emulate this process, discerning the relationship between geometric problem information and theorem sequences. We envision inputting geometric problem information and obtaining corresponding theorem sequences, a concept closely resembling the sequence-to-sequence language model.

Inspired by existing works, we found that language models can effectively comprehend the annotations of geometric information in the FormalGeo7k dataset. In the dataset, the formalized representation of geometric conditions takes the form of statements such as “Equal(LengthOfLine(AD), 8)” indicating the length of line segment AD is 8. Our formalization is easily comprehensible by both humans and computers. Therefore, we propose integrating FGPS with language models, leveraging the inferential capabilities of language models to train them in predicting theorem sequences required for geometric problem-solving. Formalized condition sequences and predicted theorem sequences exhibit a symmetrical input–output relationship, motivating our exploration of the transformer, an encoder–decoder architecture characterized by inherent symmetry in language modeling. We employ various language models for the prediction and selection of the most effective result among them, as the predicted theorem sequence to be incorporated into the FGPS solving process. The specific approach involves predicting the theorems that may be required for a given geometric problem before FGPS initiates its theorem search. The solver can execute the predicted theorems first, incorporating the conclusions obtained through theorem execution into the set of conditions. This ensures a reduction in the steps and time required for the solver to utilize the forward or backward search strategies.

In summary, our contributions are three-fold, as follows:

• We introduce a groundbreaking approach that amalgamates FGPS with language models, redefining the FGPS’ search process for plane geometry problem-solving;
• Through the utilization of multiple language models, we have achieved unprecedented levels of theorem sequence prediction accuracy on the FormalGeo7k dataset;
• The implementation of FGeo-TP (FGPS and theorem predictor) has led to a substantial leap in problem-solving success rates, markedly diminishing the search time and steps required—a testament to the efficacy of our method.

2. Related Work

2.1. Datasets for Geometry Problem Solving

In recent years, numerous exemplary planar geometry datasets have emerged. However, we contend that the formalization methods employed in these datasets lack uniformity. This includes datasets such as Geometry3K [7], GeoQA, and PGDP5K [11]. Each of these datasets employs distinct formalization methods for annotating geometric problem-solving. Geometry3K annotates information in problem statements using both diagram formal language and text formal language but does not provide annotations for solution information. PGDP5K is designed to construct a formal language dataset through geometric image analysis. However, these approaches lack concrete mathematical theoretical support, leading to a deficiency in ensuring completeness. The GeoQA dataset encompasses nearly 5000 planar geometry problems, predominantly focused on numerical calculations involving angles and lengths. However, it lacks data related to geometric relationship proofs. Moreover, the answer annotations in these datasets often manifest as multiple-choice questions, introducing the possibility of solvers randomly selecting the correct answer.

In contrast, our FormalGeo7k dataset consists of 6981 SAT-level geometry problems, further expanded to 186,832 through data augmentation. Each problem in the dataset includes a comprehensive natural language description, geometric shapes, formal language annotations, and theorem sequence annotations. Importantly, our dataset does not adopt a multiple-choice question format but instead presents authentic planar geometry problems akin to those encountered by secondary school students in routine assessments. The answer types encompass numerical values, geometric relationships, and combinations thereof.

2.2. Geometry Problem Solving

The history of computer-aided geometric problem-solving can be traced back to the previous century. Gelernter et al., employed a backward search method to address formalized problems [12], and Nevins utilized the forward chaining method [13]. Search-based methods often prove only a limited number of planar geometry theorems due to their high computational complexity. Wen-Tsun proposed Wu’s Method [14], which transforms geometry problems into algebraic equation-solving problems but is confined to the algebraic domain. Zhang introduced the point elimination method based on geometric invariants [15], generating concise and meaningful readable proofs for a large number of geometry problems. However, this method is restricted by the types of geometric invariant points.

In recent years, Seo et al., established the first automated system, Geos [16], which translates the text and images of geometry problems into a logical language. However, its high dependence on manually annotated rules limits its generalization. GeoQA transforms the process of solving geometry problems into a sequence of programs composed of variables and operators, resulting in problems with a lower readability compared to formal languages. Lu et al., proposed Inter-GPS, achieving high accuracy across multiple geometry datasets. However, Inter-GPS is limited to numerical calculation problems and cannot handle geometry relationship proofs.

In our prior work, FGPS can reason through all geometry problems in the FormalGeo7k dataset, providing detailed solution processes. Specifically, for a given planar geometry problem, FGPS can output a complete solution process, including the mathematical theorems used in each step, which the conditions of the problem are involved in the theorem application, and the new geometric conditions generated after applying the theorems. FGPS can emulate the step-by-step problem-solving process as a secondary school student approaching planar geometry problems. Moreover, FGPS is not limited to numerical calculation problems and can effectively handle geometry relationship proof problems.

2.3. Pre-Training Model in NLP

In the field of natural language processing (NLP), pre-trained models play a crucial role by enabling NLP models to achieve excellent performance without the need to train from scratch. Instead, these models can undergo fine-tuning directly on the pre-trained counterparts, streamlining the training process and yielding outstanding results [17,18]. In the work of MWp-bert [19], pre-trained models were employed for solving mathematical word problems. GeoQA+ [20] utilized pre-trained models to transform the textual information of geometric problems, thereby augmenting the dataset. Inter-GPS used pre-trained models to predict theorems; however, the Geometry3K dataset in Inter-GPS did not have manually annotated theorem sequences required for solving problems. Instead, they were randomly sampled, leading to potentially non-optimal theorem sequences. Furthermore, it could only predict theorems for 1500 questions and not for all questions in the dataset.

The transformer [21] is a neural network model used for sequence-to-sequence [22] learning, which classic encoder–decoder architecture has shown excellent results in NLP tasks. Inspired by this success, we propose using the transformer architecture to comprehend the formal statements and predict the theorems required for geometric problem solvers.

The formalized conditional statements in FormalGeo7k’s geometry problems are easily understandable, not completely detached from the computer’s comprehension of English text. Since the transformer demonstrates remarkable effectiveness in understanding English text, we consider employing the encoder–decoder architecture of the transformer to learn the relationship between conditional formalized statements and theorems. For the seq2seq task, we conducted a comparative analysis of various language models to determine their performance.

3. Geometry Problem Solver

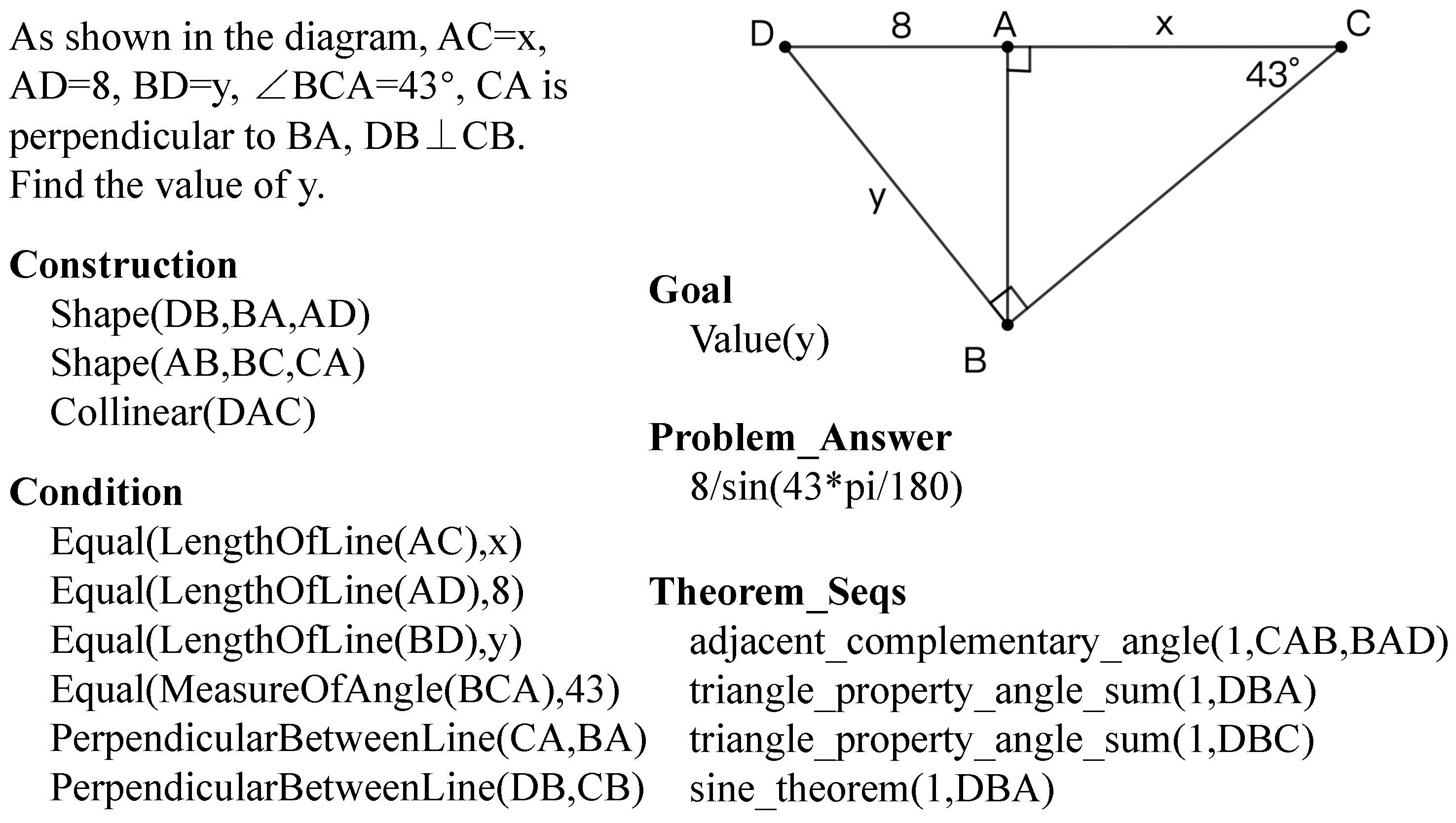
3.1. FGPS

In our previous work [10], we implemented FGPS for the inference and solution of all problems in the FormalGeo7k dataset. However, this was contingent on the annotated theorem sequences provided in the FormalGeo7k dataset. When the solution theorem sequence is not provided, FGPS resorts to using built-in methods to search for theorem solutions. During the search process, FGPS constructs a search tree containing the sequence of theorem applications for solving a given problem. We utilized both forward search (FW) and backward search (BW) methods. FW starts from known conditions, continually searching for available theorems to generate new conditions until the solving objective is reached. In contrast, BW starts from the solving objective, decomposes it into multiple sub-goals, and seeks the conditions required for each sub-goal, determining whether the current sub-goal is solvable. This process repeats until all sub-goals are resolved.

Additionally, we employed the following four search strategies: breadth-first search (BFS), depth-first search (DFS), random search (RS), and beam search (BS). BFS traverses each node of the search tree in a level-wise manner, DFS recursively selects nodes from shallow to deep, RS randomly selects nodes for expansion at each stage, and BS selects a specified number of nodes (K) at each expansion stage, striking a balance between BFS and RS.

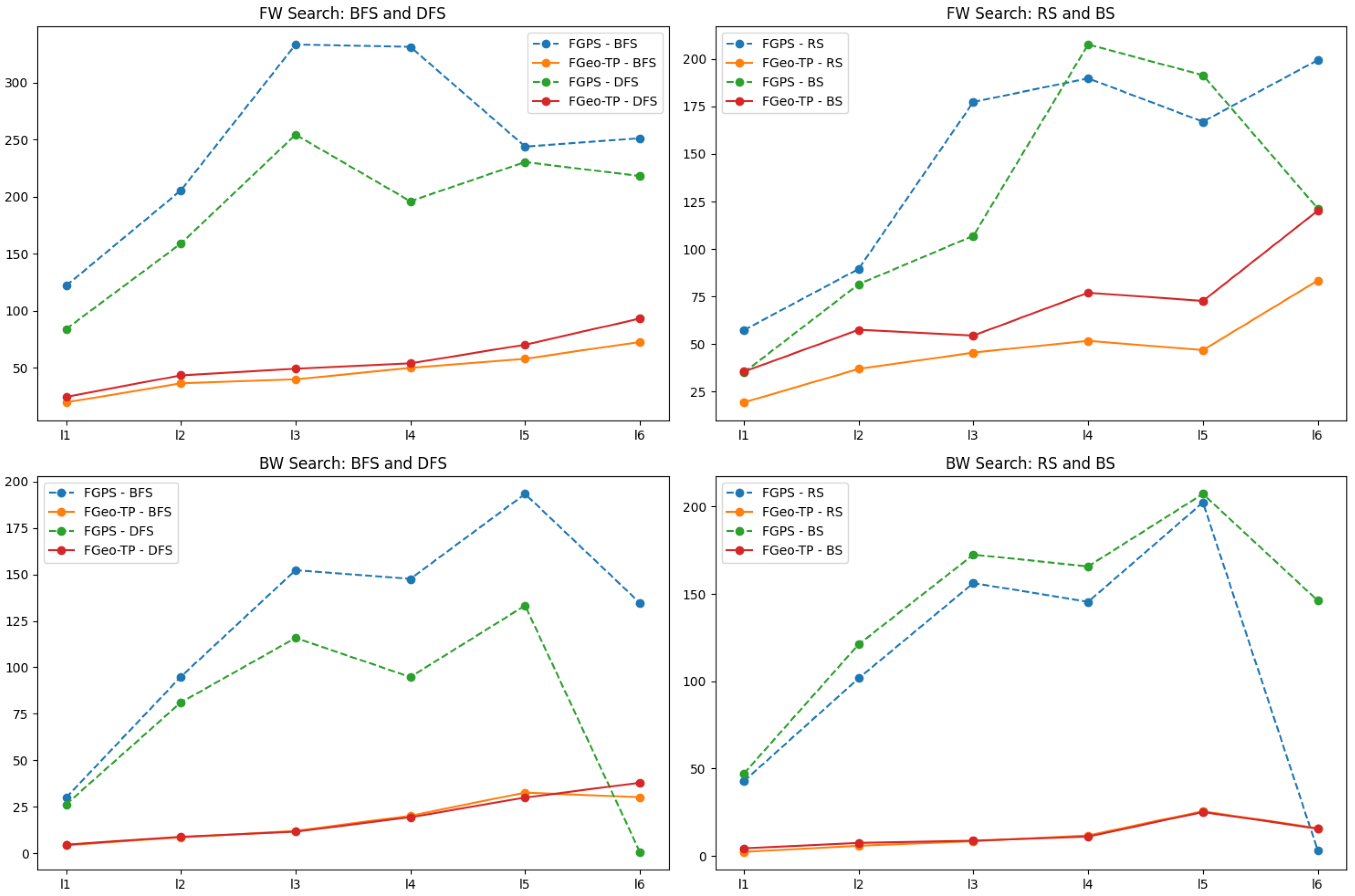
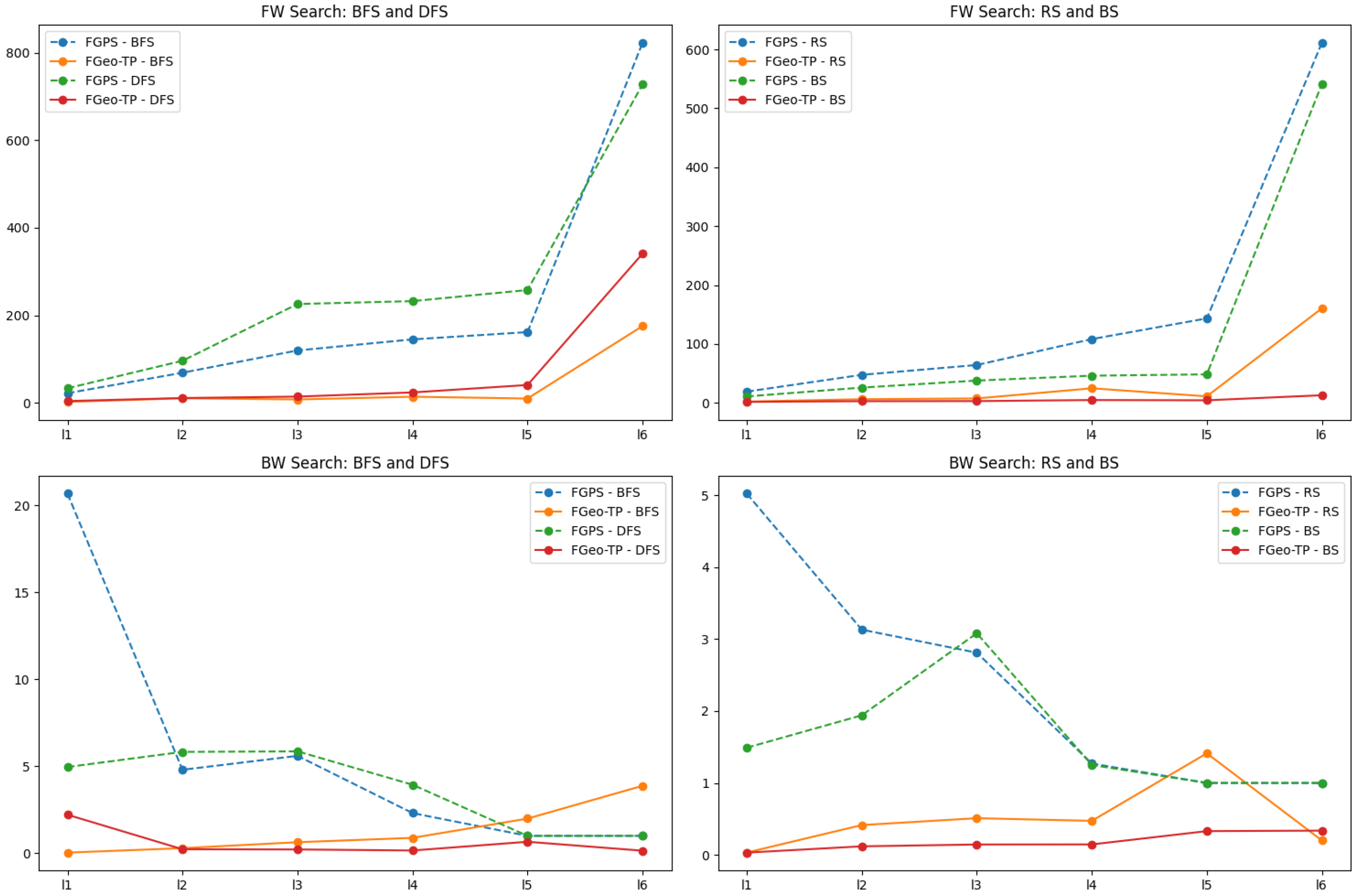
In cases where the search time exceeded 600 s, indicating a timeout for problem-solving, the search results are presented in

Table 1. The search results(%) of FGPS.

Method	Strategy	Solved	Unsolved	Timeout
FW	BFS	38.86	7.42	53.72
FW	DFS	36.16	9.80	54.05
FW	RS	39.71	9.07	51.22
FW	BS	25.28	38.72	36.00
BW	BFS	35.44	2.68	61.88
BW	DFS	33.73	2.42	63.84
BW	RS	34.05	2.65	63.30
BW	BS	34.39	12.86	52.74

The bold data indicates the best results in the search results of FGPS.

. Notably, the forward random search method achieved the highest success rate of 39.7%, while the backward depth-first search method exhibited the lowest unsolved rate of 2.42%. We observed that a substantial portion of problem-solving tasks were not entirely unsolvable but rather failed due to prolonged solving times, leading to timeout. Hence, there is a need for optimizations and pruning of the FGPS solving process to achieve a higher success rate in problem-solving.

In line with the habitual problem-solving practices of humans, a high school student, accustomed to regular problem-solving, typically skims through the problem conditions when faced with a plane geometry question. With this initial scan, the student can often make an approximate inference regarding the primary knowledge points being tested by the question. Therefore, our aim is for FGPS to emulate this cognitive process. To achieve this, we have incorporated a theorem predictor ahead of the solver in our methodology. This modification enables FGPS to select more suitable theorems for application, rather than attempting to utilize all available theorems.

3.2. FGeo-TP

FGPS experienced a high percentage of timeouts in searching the FormalGeo7k dataset, primarily because, during the search process, each step involves exploring a large number of theorems for potential matches. To optimize the solver’s solving process, we introduced a theorem predictor. Before FGPS initiates the theorem search, the theorem predictor guides FGPS, reducing the search complexity. The augmented FGPS, incorporating the theorem predictor, is denoted as FGeo-TP (theorem predictor). The architecture of FGeo-TP is illustrated in Figure 2.

In contrast to directly inputting the formalized language into FGPS, FGeo-TP requires the formalized language to be simultaneously input into the theorem predictor. The theorem predictor outputs the corresponding theorem sequence, and FGPS receives both the formalized language and the predicted theorem sequence.

In the theorem predictor, we anticipate the input and output to be the formalized language from FormalGeo7k and the required theorem sequence for each problem. As the length of the formalized language and the theorems varies for each problem, a Seq2Seq model is considered suitable. We opted to use the well-established transformer architecture for implementing both the encoder and decoder.

The formalized conditional language in FormalGeo7k consists of geometric relationship predicates, geometric form predicates, free variables, or numbers. This differs significantly from popular natural language corpora in the field of natural language processing. Therefore, pre-training the transformer model with our corpus is essential for the subsequent comprehension of formalized language by the model. To enhance readability, the formalized geometric relationship and form predicates in FormalGeo7k are composed of English words or concatenations of English words. This can be treated as word-level tokenization in the encoder, while free variables and numbers are considered character-level tokenization. Hence, there is no need to update the existing vocabulary. Due to the specificity of theorem names, a slight change in a single word may render FGPS unable to recognize them. To prevent out-of-vocabulary situations in the decoder, we convert theorem names into their corresponding numerical representations and represent the theorem sequence as a one-dimensional array containing only integers.

We performed fine-tuning on the transformer pre-trained model using annotated training and validation datasets. The fine-tuned model was then evaluated on the test set to assess the prediction results. In fine-tuning tasks, the optimization was carried out using the negative log-likelihood loss to refine the generated objectives.

$$\mathit{Loss}=-\frac{1}{N}\sum _{i=1}^{N}logP\left(y_i\right|y_1,\dots ,y_{i-1},\mathit{input})$$

(1)

Here, N represents the length of the sequence, representing the number of theorems in the target sequence. $logP\left(y_i\right|y_1,\dots ,y_{i-1},\mathit{input})$ represents the conditional probability of predicting theorem $y_i$ given the historical predictions $y_1,\dots ,y_{i-1}$ and the input formalized language.

To achieve higher matching degrees, we employed beam search, selecting the union of multiple theorem sequences with higher probabilities to enhance the degree of matching.

$$B_n=\underset{y_1,\dots ,y_{n-1},y_n}{argtopk}\left[P\left(y_n\right|y_1,\dots ,y_{n-1},\mathit{input})\right]$$

(2)

$B_n$ represents the set of the top k predicted theorem sequences when predicting the next theorem. Each predicted theorem sequence has the form [$y_1,\dots ,y_{n-1},y_n$], where $y_n$ is the theorem added in that step. The input is the formalized geometry problem conditions. This process continues until the predefined sequence length is reached or an end token is encountered. In the experiments, we set the maximum sequence length to 20, and the number of top predicted theorem sequences is 5.

$$S_{\mathit{tp}}=B_{n_1}\cup B_{n_2}\cup \dots \cup B_{n_k}$$

(3)

$S_{tp}$ represents the final predicted theorem sequence, while $B_{n_1},B_{n_2},\dots ,B_{n_k}$ denotes the set of the top-k predicted theorem sequences when the last theorem prediction is completed. The experimental findings indicate that even when merging multiple predicted theorem sequences, the final predicted theorem sequence’s length does not experience a significant increase.

After FGeo-TP executes the predicted theorem sequence, the conclusions are deduced based on the original problem conditions. We integrate these conclusions with the initial problem conditions to form a new set of conditions. If the problem-solving objective is still unresolved with this updated set, FGeo-TP employs a search method based on the new condition set to identify a solution. FGPS demonstrates a quick use of the theorem, thus, the use of predicted theorem sequences by FGeo-TP does not impose a significant burden on reasoning. On the contrary, it can reduce FGPS’ search for subsequent theorems. Through these steps, our objective is to streamline the solver’s search process and implement pruning in the solver’s solving procedure.

4. Experiment

4.1. Description of the Dataset

The FormalGeo7k dataset is aggregated from diverse sources, including Geometry3K, GeoQA, GeoQA+, and online repositories, which consists of 6981 SAT-level geometry problems. We meticulously curated, classified, deduplicated, and standardized the problem statements. Creating the FormalGeo7k dataset was a substantial undertaking, which involved approximately 16 trained master’s students over a period of around 13 weeks.

Furthermore, the construction of the FormalGeo7k dataset is guided by studies in geometry ontology and geometry representation theory. These methodologies address questions regarding what content should be formalized and how it should be formalized. The dataset includes geometric shapes, formal language annotations, and theorem sequence annotations for each problem. The theorems involve relational reasoning, logical operations, and algebraic calculations. Therefore, the FormalGeo7k dataset encompasses all the information and problem-solving processes for planar geometry problems. Specific data examples can be referred to in Figure 1. For specific construction methods, please refer to FormalGeo [10].

The sound construction methods enable the theorem predictor to effectively learn the relationship between formal language and theorems. For example, if a formal statement contains both “perpendicular” and the lengths of sides, the theorem predictor may predict the “Pythagorean theorem”. The theorem predictor’s prediction of theorems is not limited to specific conditions within the individual problems but rather encompasses the learning of relationships between geometric knowledge and theorems, endowing it with generalization capabilities.

4.2. Theorem Sequence Prediction

We utilized data from the FormalGeo7k dataset for training purposes. Initially, we randomly shuffled the 6981 geometry problems, allocating them to training, validation, and test sets in a ratio of 0.7:0.15:0.15. Furthermore, the training epochs were set to 20, with an initial learning rate of $3\times {10}^{-5}$. The loss function employed was the negative log-likelihood loss, and the optimizer used was Adam. For the theorem prediction model, we attempted to compare various pre-trained language models based on the transformer architecture.

It is worth noting that our initial experiments did not directly assess the problem-solving effectiveness of FGeo-TP. Instead, we began by evaluating the accuracy of predicting theorems for various pre-trained language models. After trying out numerous transformer pre-trained models, we eventually settled on BART and T5. BART [23] and T5 [24] are both excellent transformer architecture models, with BART being particularly suitable for sequence generation tasks, and T5 having greater versatility due to its “Text-to-Text” approach. BART-base utilizes a 6-layer encoder and decoder, while BART-large uses 12 layers. Beside that, mT5 [25] builds upon T5 by incorporating training data from a more diverse range of languages, whereas FLan-T5 [26] fine-tunes the instructions on top of T5 to achieve “One Model for All Tasks”. FLan-T5-base employs a 12-layer encoder–decoder architecture, while FLan-T5-large utilizes a 24-layer architecture.

We trained the models using formal language annotations and theorem sequences annotations from the FormalGeo7k dataset as input and output, respectively. We recorded the matching accuracy between the predicted theorem sequences and the annotated theorem sequences. We define the matching degree as the ratio of the accurately predicted theorems in the predicted sequence to the number of theorems required for the problem. For instance, if a problem’s theorem sequence includes 10 theorems and the predicted theorem sequence contains 8 of them, we consider the sequence matching degree to be 80%. Furthermore, ultimately, we obtained experimental results as shown in

Table 2. Prediction matching degree.

Model	Average (%)	Complete (%)
mT5	33.73	17.51
FLAN-T5-base	59.37	33.59
FLAN-T5-large	74.61	55.22
BART-base	86.29	70.77
BART-large	84.16	67.33

.

Where “average” represents the average matching degree of predicted theorem sequences for all questions. When the matching degree is 100% (i.e., the predicted theorem sequence contains all the theorems required for that question), we consider the question solved with complete theorem sequence prediction, denoted as prediction complete. The “complete” in the table signifies the percentage of questions with a predicted matching degree of 100% in the FormalGeo7k dataset.

According to the experimental results, we observed that, for the FormalGeo7k dataset, the BART-base pre-trained model performs the best. Of course, both BART-large and T5-large also exhibit good predictive performance. Since our ultimate goal is to integrate the predicted theorem sequences into FGPS to achieve the best problem-solving results, we choose to use the BART-base pre-trained model in the solver’s solving process. This aims to explore the true problem-solving rate for the FormalGeo7k dataset.

4.3. Experimental Results of FGeo-TP

Our experimental setup comprised 2 Intel i9-10900X, 1 AMD Ryzen 9 5900X, and 1 AMD Ryzen 9 7950X(The Intel processors were sourced from Intel Corporation, Santa Clara, California, USA. The AMD processors were sourced from Advanced Micro Devices, Inc., Sunnyvale, California, USA.). The maximum search depth for the search algorithm was set to 15, with a beam size of 20, and a timeout of 600 s for each problem. The entire experiment lasted approximately one day under multi-process handling. For the solving methods and strategies employed by FGeo-TP, we employed both the FW and BW methods, as well as the BFS, DFS, RS, and BS search strategies.

Table 3. The search results (%) for FGeo-TP.

Method	Strategy	Solved	Unsolved	Timeout
FW	BFS	68.16	1.96	29.88
FW	DFS	67.36	1.87	30.76
FW	RS	68.76	2.01	29.23
FW	BS	60.06	4.40	35.54
BW	BFS	80.12	1.81	18.07
BW	DFS	79.55	2.14	18.31
BW	RS	80.86	1.78	17.36
BW	BS	79.06	2.23	18.71

The bold data indicates the best results in the search results of FGeo-TP.

presents the solving rates, unsolved rates, and timeout rates of these methods on the FormalGeo7k dataset.

The experimental results reveal that FGeo-TP achieves a maximum solving rate of 80.86%, doubling the average solving rate compared to FGPS. Additionally, the maximum unsolved rate is only 4.4%. Based on these results, we can confidently assert that FGeo-TP exhibits a significant potential for solving geometric problems.

From the table, it is evident that FGeo-TP generally exhibits a higher solved rate in the backward search method compared to the forward search. However, in the case of FGPS, the solving results show the opposite situation. This discrepancy arises because, in the backward search method, each update of the final goal state is accompanied by updates to multiple child node states, consuming considerable time. When FGeo-TP provides new reasoning conditions, it significantly reduces the backward search process, thereby decreasing the timeout rate and improving the solving rate. For the forward search, the expansion of the initial condition set leads to an expansion of theorem selection paths, resulting in less optimization in areas with higher time complexity.

At the same time, we observe that the solving rate of FGeo-TP is lower than the matching degree of the theorem predictor for theorem sequences. Upon comparing the predicted theorem sequences with the actual solving theorem sequences, we find differences in the theorem order and the quantity of theorem uses. In geometric problem-solving, the same theorems with different usage orders may lead to different outcomes in solution success. Similarly, a question may require the repeated use of a particular theorem, while the theorem predictor only predicts whether this theorem should be used without considering the frequency of use. Therefore, there is still room for improvement in the theorem predictor, and FGeo-TP may achieve even better solving performance.

4.4. Solving Time and Step

Based on the required length of theorem sequences for problem resolution, we have categorized the questions in FormalGeo7k into the following difficulty levels: $l_1$ ($\mathrm{length}\le 2$), $l_2$ ($3\le \mathrm{length}\le 4$), $l_3$ ($5\le \mathrm{length}\le 6$), $l_4$ ($7\le \mathrm{length}\le 8$), $l_5$ ($9\le \mathrm{length}\le 10$), and $l_6$ ($\mathrm{length}\ge 11$). The corresponding quantities of questions for each difficulty level are 2407, 1898, 1247, 824, 313, and 292, respectively. To investigate whether FGeo-TP optimizes the search space based on FGPS problem-solving, we compared the solving time and solution steps of the two for problems of varying difficulty levels. The experimental results on FormalGeo7k are illustrated in Figure 3 and Figure 4. The detailed data can be found in the

Table A1. Experimental results.

Solver	Metric	Method	Strategy	Total	${\mathit{l}}_1$	${\mathit{l}}_2$	${\mathit{l}}_3$	${\mathit{l}}_4$	${\mathit{l}}_5$	${\mathit{l}}_6$
* FGPS	time(s)	FW	BFS	185.05	121.97	205.51	333.33	331.26	243.92	251.11
		FW	DFS	132.35	84.11	158.91	254.29	196.02	230.39	218.05
		FW	RS	92.21	57.38	89.55	177.34	189.74	166.96	199.31
		FW	BS	58.76	35.11	81.52	106.92	207.55	191.40	121.36
		BW	BFS	57.67	30.00	94.97	152.26	147.55	193.21	134.65
		BW	DFS	46.45	26.34	81.17	115.83	94.85	133.23	0.85
		BW	RS	65.82	42.79	101.71	156.27	145.50	202.37	3.37
		BW	BS	75.55	47.16	121.17	172.50	165.80	207.28	146.26
	step	FW	BFS	58.44	21.85	68.67	119.56	144.80	161.44	822.18
		FW	DFS	87.16	33.15	95.95	225.57	232.25	257.59	727.17
		FW	RS	41.89	19.14	47.63	64.32	108.26	143.41	611.00
		FW	BS	18.64	10.99	25.97	37.86	46.19	48.44	541.00
		BW	BFS	15.14	20.68	4.80	5.60	2.31	1.00	1.00
		BW	DFS	5.17	4.96	5.83	5.86	3.94	1.00	1.00
		BW	RS	4.34	5.02	3.13	2.81	1.27	1.00	1.00
		BW	BS	1.67	1.49	1.94	3.08	1.25	1.00	1.00
FGeo-TP	time(s)	FW	BFS	32.10	19.83	36.51	40.11	50.05	58.05	72.76
		FW	DFS	38.62	24.70	43.55	49.30	54.06	70.34	93.30
		FW	RS	33.19	19.39	37.00	45.57	51.79	46.86	83.45
		FW	BS	49.67	35.55	57.56	54.53	77.04	72.71	120.13
		BW	BFS	9.44	4.99	8.63	12.14	20.27	32.75	30.29
		BW	DFS	9.59	4.74	8.96	11.74	19.46	30.07	37.99
		BW	RS	6.08	2.34	5.91	8.43	11.78	25.65	15.91
		BW	BS	7.28	4.46	7.48	8.71	11.10	25.18	15.65
	step	FW	BFS	8.90	2.07	10.27	7.61	13.87	9.68	175.24
		FW	DFS	15.10	3.88	10.81	14.12	23.63	40.62	340.67
		FW	RS	8.83	2.23	6.25	7.55	24.76	11.13	160.41
		FW	BS	2.69	1.74	2.87	3.04	4.84	4.39	12.98
		BW	BFS	0.39	0.04	0.29	0.63	0.88	1.99	3.88
		BW	DFS	1.05	2.21	0.23	0.22	0.16	0.66	0.15
		BW	RS	0.30	0.03	0.41	0.51	0.47	1.41	0.20
		BW	BS	0.10	0.03	0.12	0.14	0.15	0.33	0.34

* The experimental data for FGPS is derived from the FormalGeo [10].

(Appendix A).

From the figure, it is evident that, both in terms of solving time and solution steps, FGeo-TP exhibits a superior performance compared to FGPS across the majority of difficulty levels for the given problems. Regarding the solving time, FGPS exhibits randomness due to its reliance on unstable searches. In contrast, FGeo-TP, with the integration of theorem prediction, bases its subsequent search space on the given theorems. Consequently, the relationship between solving time and problem difficulty aligns more closely with human problem-solving behavior, reducing the overall average solving time to a quarter of the original.

Under the guidance of theorem prediction, FGeo-TP rapidly identifies the direction for problem-solving, exhibiting significantly fewer solution steps than FGPS, especially in lower difficulty problems. However, as the complexity of the problems increases, the length of the necessary theorem sequences for solving these problems also extends, leading to a gradual weakening in the effectiveness of theorem prediction. This decline can be attributed to the following two main factors: Firstly, with the rise in problem difficulty, the search space for solutions grows exponentially, outpacing the rate at which theorem prediction can reduce this search space. Secondly, as the theorem sequences become longer, the accuracy of the theorem prediction decreases, consequently diminishing its utility in problem-solving.

4.5. The Combined Approach of FGeo-TP and FGPS

In the analysis of the problem-solving results using FGeo-TP, unexpected phenomena were observed. For certain problems, FGeo-TP failed to yield a solution, while the original FGPS successfully solved them. Consequently, additional experiments were conducted. Building upon FGeo-TP, a hybrid approach was employed, where, in case of timeouts, the search strategy was switched back to FGPS. The experimental outcomes, derived from the collaborative problem-solving efforts of FGeo-TP and FGPS, are presented in

Table 4. The average solving results(%) for FGeo-TP and the combined approach of FGeo-TP and FGPS.

Method	FW				BW
Strategy	BFS	DFS	RS	BS	BFS	DFS	RS	BS
FGeo-TP	68.16	67.36	68.76	60.06	80.12	79.55	80.86	79.06
FGeo-TP+FGPS	71.56	72.14	73.48	65.07	81.09	80.67	81.86	80.41

.

Based on the experimental results, it is observed that, for the forward search, the combined approach of FGeo-TP and FGPS leads to an average improvement in the problem-solving rate of approximately 3–5% compared to FGeo-TP alone. Similarly, for the backward search, the combined FGeo-TP and FGPS approach yields an average improvement in the problem-solving rate of around 1% compared to FGeo-TP alone. Further investigation was conducted to explore this anomalous phenomenon.

After comparing a considerable amount of experimental data, we identified the underlying reasons for the observed outcomes. The initial condition set of FGPS consists of the formal language annotations annotated in FormalGeo7k. These annotations include information provided by the problem statement, typically in limited quantity. Consequently, when FGPS selects a search path, it matches the available theorems based on the current condition set, placing feasible theorem sequences in a queue. Various search strategies will select different theorems from the queue for application. After applying a theorem, new conditions are obtained, and adding these conditions to the condition set generates a new condition set. The new set can once again match a batch of available theorem sequences, which are subsequently added to the previous theorem sequences.

Therefore, we observe that if FGeo-TP predicts the inclusion of non-essential theorems, the initial condition set may contain unnecessary conditions. This results in the generation of unnecessary condition sequences, diluting the probability of the solver selecting the correct theorem sequence. This significantly increases the prediction time, leading to timeouts. However, BFS is not affected by the addition of new theorems and continues to run the initially matched theorem sequences, ensuring that the desired theorems will be executed. From the experimental results of the combined approach of FGeo-TP and FGPS, it is evident that only the FW method and BFS strategy shows a modest improvement of 3%, while the other three strategies show an improvement of around 5%. This observation indicates that BFS is less influenced by redundant theorems. In the backward search, the effectiveness of the combined approach of FGeo-TP and FGPS has shown a modest improvement of 1% compared to using FGeo-TP alone. The possible reason for this is the introduction of unnecessary conditions, leading to an increase in the redundant algebraic equations during the solving process. Consequently, excessive and futile computations occur during equation solving, resulting in extended computation time and timeouts.

5. Correlation Analysis

In the previous analysis, we primarily focused on comparing the solving rates and solving times of FGeo-TP and FGPS on the dataset, revealing the superiority of FGeo-TP. However, besides these straightforward comparisons, we aimed to uncover the subtle relationships that might not be immediately apparent. We hypothesize that different strategies may influence the timeout rates of FGeo-TP solutions. However, intuitively discerning the relationship between timeout rates and different strategies can prove challenging. Therefore, we sought a method to ascertain the correlation or independence between timeout rates and strategies, leading us to opt for the chi-square test [27].

The chi-square test is a statistical method used to determine whether the observed data deviates significantly from the expected data, allowing for the rejection of the null hypothesis. Initially, we need to conduct the following hypothesis test: Null Hypothesis (H0): The strategy is independent of the timeout rate. Alternative Hypothesis (H1): There is a relationship between the strategy and the timeout rate. we organized the raw number data from Table 3 into a $4\times 2$ contingency table. The first column represents the proportions of non-timeouts (both solved and unsolved), while the second column represents the proportions of timeouts, as illustrated in

Table 5. The number of search results for FGeo-TP.

Strategy	Non-Timeout	Timeout
BFS	10,614	3348
DFS	10,536	3426
RS	10,710	3252
BS	10,175	3787

.

To proceed, we computed the expected frequency matrix using the formula:

$$E_{ij}=\frac{R_i\times C_j}{N}$$

(4)

where $E_{ij}$ denotes the expected frequency at the intersection of the i-th row and j-th column, $R_i$ represents the total for the i-th row (row sum), $C_j$ represents the total for the j-th column (column sum), and N is the total sum of all values in the table (i.e., the sum of all row and column totals).

After obtaining the expected frequency matrix, we proceeded to calculate the chi-square statistic using the formula:

$${\chi }^2=\sum _{i,j}\frac{{(O_{ij}-E_{ij})}^2}{E_{ij}}$$

(5)

where $O_{ij}$ denotes the observed frequency at the intersection of the i-th row and j-th column, $E_{ij}$ denotes the expected frequency for the i-th row and j-th column under the null hypothesis, and the summation symbol ∑ indicates summation over all rows i and columns j.

Finally, we determined the degrees of freedom using the formula:

$$df=(r-1)\times (c-1)$$

(6)

r and c, respectively, represent the number of rows and columns in the contingency table.

Using the data from Table 5 and Equations (4)–(6), we derive the chi-square statistic yield is 62.99 and the degrees of freedom is 3. Consulting the chi-square distribution critical values table, at a significance level of $\alpha$ = 0.05, consulting the table yields a critical value of 7.815. Since the chi-square statistic (62.99) is greater than the critical value (7.815), we reject the null hypothesis and accept the alternative hypothesis. Therefore, at the significance level of 0.05, there is sufficient evidence to support the association between the strategy and the timeout rate, which also validates our hypothesis.

6. Conclusions

We combined a language model with FGPS to enhance the automatic problem-solving capability for plane geometry problems. Initially, we experimented with multiple pre-trained language models and selected the BART-base as the optimal model due to its high theorem sequence prediction match rate of 86.29%. Subsequently, we integrated the theorem predictor into the FGPS solving process, resulting in the development of FGeo-TP. The experimental results indicate that FGeo-TP achieves a problem-solving success rate of 80.86% on the FormalGeo7k dataset, surpassing the solving rate of using FGPS alone by more than twice. Moreover, FGeo-TP’s problem-solving process rapidly identifies the direction of solution, significantly reducing the number of problem-solving steps, and cutting the average problem-solving time to a quarter of the original. However, for real-time data, we still require manual annotation of the problems before the system can solve them. Additionally, the current version of FGeo-TP does not perform well in predicting the theorem solutions for more challenging geometry problems such as IMO questions. Currently, we are exploring the automated problem annotation methods and will refine the dataset for IMO-level geometry problems in the future.