Reply to Zheng, X.; Palffy-Muhoray, P. Comment on “Choi, M.G. Computing the Closest Approach Distance of Two Ellipsoids. Symmetry 2020, 12, 1302”

Abstract

In this paper, we address the comment provided by Zheng and Palffy-Muhoray regarding our previous work on computing the closest approach distance of two ellipsoids. Additionally, we present experimental results that assess the numerical error bounds in the authors’ own implementation of the analytic solution for the closest approach distance of two ellipses. We report very rare cases where the closest approach distances of two ellipses are erroneously calculated as zero, which is impossible given that the radii of the ellipses are not zero.

1. Introduction

Computing the closest approach distance of two ellipsoids in their inter-center direction is crucial for collision handling in simulations involving ellipsoidal bodies [1,2,3]. In our previous work [4], we presented two practical methods by formulating a set of equations for externally contacting two ellipsoids and efficiently solving them using hybrid approaches. One method is the hybrid Newton method, suitable for high-accuracy applications, and the other is the hybrid fixed-point iteration method, ideal for real-time applications like computer games when coupled with a stopping criterion based on the relative spatial error.

We demonstrated the robustness and efficiency of the proposed methods in various experiments. The robustness and efficiency depend significantly on the ratio between the radii of an ellipse. In our second experiment, one million pairs of ellipsoids were randomly generated, while restricting the ratio within each $\gamma$, which increases from 1 to 200. This was carreid out to assess the robustness and efficiency of various methods. In this experiment, we excluded the cross-section search [5,6] due to efficiency and robustness issues. It exhibited inefficiency, as the number of solver iterations remained relatively high even with a moderate tolerance of ${10}^{-8}$; the maximum reached 41 iterations, with an average of approximately 40.5. Additionally, it lacked robustness, as the error was unacceptably high in some cases; the maximum error in the closest approach distance reached up to $30\%$.

We attributed these issues to numerical errors within the implementation [6] of the analytic solution for the closest approach distance of two ellipses [7]. Therefore, we added the following statements at the beginning of the paragraph explaining the second experiment: “The error in the analytic method for the closest approach distance of two ellipses increased as $\gamma$ increased [7]. Correspondingly, the error in the cross-section search [5] also increased, regardless of the number of solver iterations in the golden section search that found the angle of the cross-section, resulting in the closest approach distance of two ellipsoids”. These statements were not intended to imply that there are errors in the derivation of the analytic solution.

Recently, Zheng and Palffy-Muhoray wrote a comment [8] claiming that these statements are incorrect in that their analytic method has no error. However, to ensure error-free arithmetic for an analytic solution, symbolic computation is required. Since our methods are intended for real-time applications such as computer games, symbolic computation is impractical. Consequently, errors in scientific computation are inevitable. For these reasons, we chose to use ‘the error in the analytic method’ as a concise term for referring to the numerical error, including numerical truncation and approximation errors, in an implementation of an analytic solution on a modern computer, as their conjecture in the middle of the comment.

Zheng and Palffy-Muhoray also claimed, in their comment, that their cross-section search is error-free. It is important to note that even when using symbolic computation for their analytic solution, their cross-section search is not error-free due to the use of the golden section search. Numerical error is inevitable in the golden section search, although the error could be sufficiently small with a sufficiently small tolerance. However, while examining the numerical error in their implementation of the analytic solution, we found that the implementation produces some unexpected results. In our previous work [4], we initially thought that this was due to the numerical error. However, further investigation revealed that there are very rare cases in which the closest approach distance of two ellipses is reported as zero, which is impossible given that the radii of the ellipses are not zero. Details will be addressed in Section 2 along with an empirical analysis of the numerical error.

2. Experimental Results

All experiments were conducted using a MacBook Pro laptop computer with an Apple M2 Max CPU, and we utilized the C++ implementation of the hybrid Newton method [4]. Initially, for both the analytic solution for the ellipses [7] and the cross-section search for ellipsoids [5], we relied on the implementation found on Wikipedia. However, following further investigation prompted by the comment [8], we confirmed that it is the authors’ own implementation [6].

The first experiment aimed to assess the numerical error bounds in the 2D analytic solution method [6,7]. Since we only had reliable solution methods for a pair of ellipsoids, we embedded an ellipse in 3D by duplicating its minimum radius and constraining its center to the $xy$-plane. As described in [4], we generated ten million pairs of ellipses randomly, with the ratio between the radii of each ellipse restricted to less than $\gamma =7$ and the ratio between the maximum radii in a pair of ellipses restricted to less than $\Gamma =3$. This dataset, comprising ten million pairs, is denoted as ${\mathcal{D}}_7$.

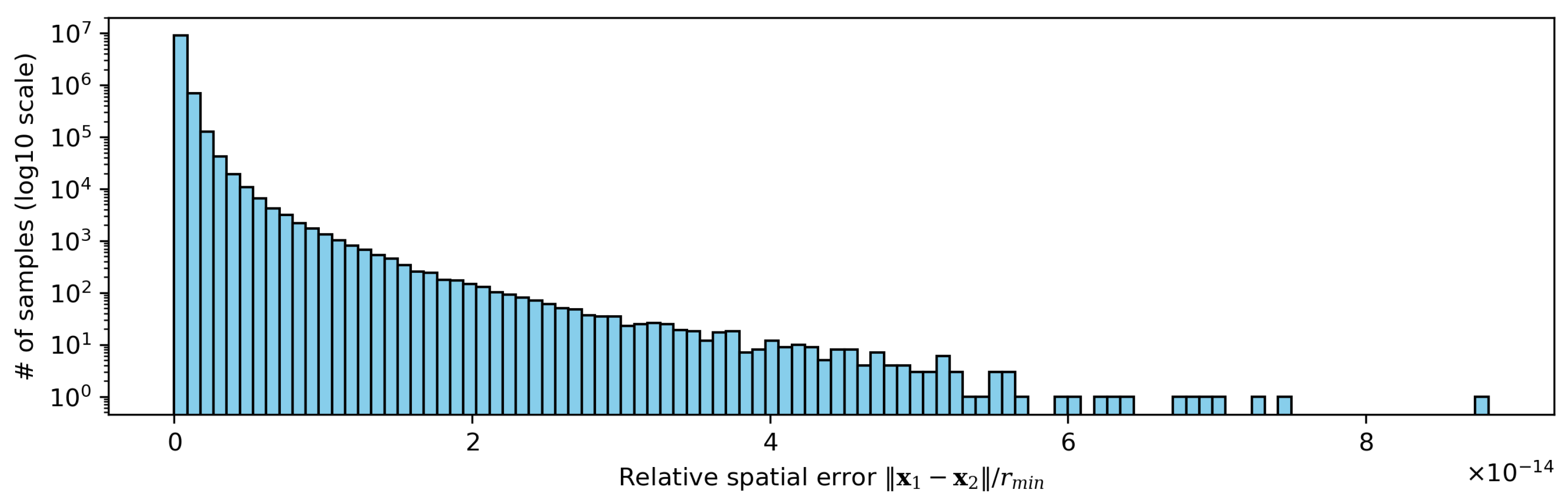
To obtain solutions for ${\mathcal{D}}_7$ that can be considered sufficiently reliable as the ground truth, we employed the hybrid Newton method with a stopping criterion of ${ϵ}_u={10}^{-15}$, as described in Equation (13) of [4]. The solution set for ${\mathcal{D}}_7$ is denoted as ${\mathcal{S}}_7$. Figure 1 illustrates the distribution of $\parallel {\mathbf{x}}_1-{\mathbf{x}}_2\parallel /r_{min}$ in ${\mathcal{S}}_7$, representing the relative spatial error between two contact points ${\mathbf{x}}_1$ and ${\mathbf{x}}_2$ with respect to the minimum radius $r_{min}$, as introduced in Equation (14) of [4]. The maximum error was $8.82\times {10}^{-14}$, the minimum was 0, the average was $3.76\times {10}^{-16}$, and the standard deviation was $7.12\times {10}^{-16}$. This implies that the spatial error was ${10}^{-13}$ times smaller than the minimum radius, indicating that the solution set ${\mathcal{S}}_7$ can be considered sufficiently reliable as the ground truth.

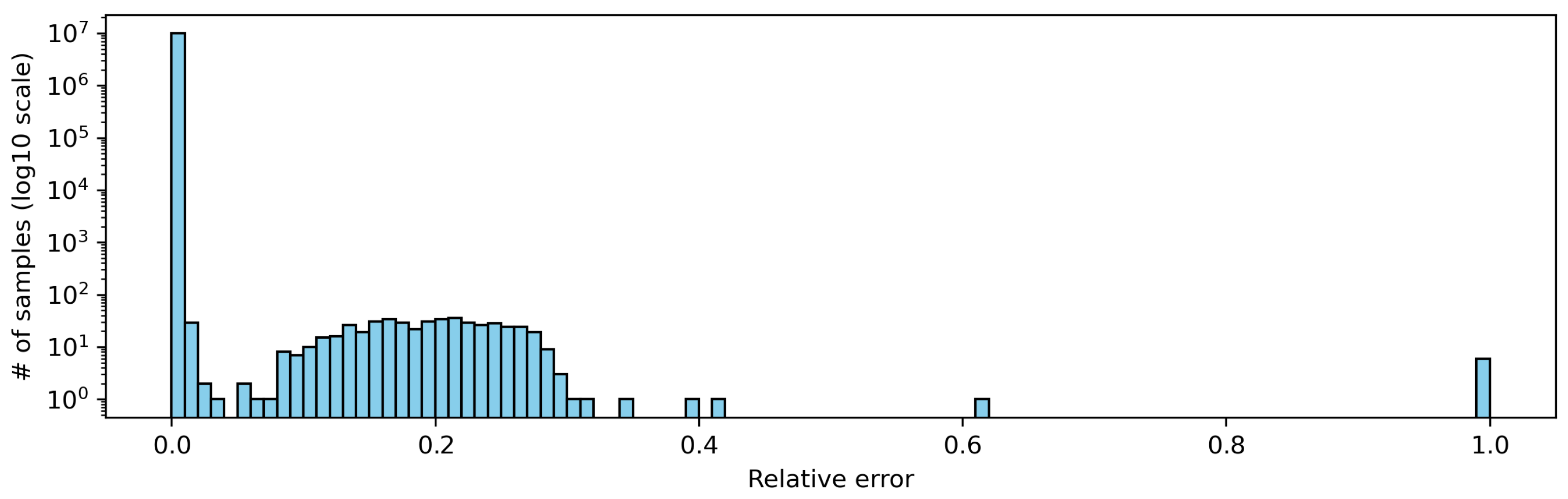
We applied the 2D analytical solution method [6,7] to dataset ${\mathcal{D}}_7$. Figure 2 shows the distribution of the relative errors with respect to ${\mathcal{S}}_7$. The maximum error was $1.0$, the minimum was 0, the average was approximately $1.07\times {10}^{-5}$, and the standard deviation was approximately $1.63\times {10}^{-3}$. Solutions with a relative error of $1.0$ are invalid because they have 100% error. Upon closer examination of these cases, we discovered that the reported closest approach distances were erroneously calculated as zero, which is impossible given that the radii of the ellipses were not zero. For instance, suppose that one ellipse has radii $a_1$ and $b_1$ and an angle ${\theta }_1$ and the other has radii $a_2$ and $b_2$ and an angle ${\theta }_2$ in radians, with an inter-center direction along the x-axis, where the specific values are as follows:

$$\begin{array}{cccccc}\hfill a_1& =1,\hfill & \hfill b_1& =0.58176609694640,\hfill & \hfill {\theta }_1& =2.48871845392908,\hfill \\ \hfill a_2& =0.97421946282229,\hfill & \hfill b_2& =0.30611919061817,\hfill & \hfill {\theta }_2& =0.72646529157362.\hfill \end{array}$$

Then, the closest approach distance is approximately 1.60. However, in the 2D analytical solution method, a zero distance was erroneously calculated. More specifically, within the distance2d() function, the last call to the complex square root function csqrt(), which computes the value of dp as a double float type, was passed with a negative real number as an argument, resulting in a zero distance. Interestingly, when using three decimal places only in the above specific values, a non-zero distance was reported and the error became 29%. Additionally, when swapping the values of the two ellipses, the error became less than ${10}^{-13}\%$.

To further observe the behavior of the solutions, we conducted a second experiment, in which the closest approach distances were computed for each of the 1 million pairs of ellipses generated randomly with $\gamma$ increasing from 2 to 200, while $\Gamma$ remained fixed at 3. We denote this dataset as ${\mathcal{D}}_{\gamma }$. The solution set ${\mathcal{S}}_{\gamma }$ for this dataset was obtained using the hybrid Newton method with ${ϵ}_u={10}^{-15}$. 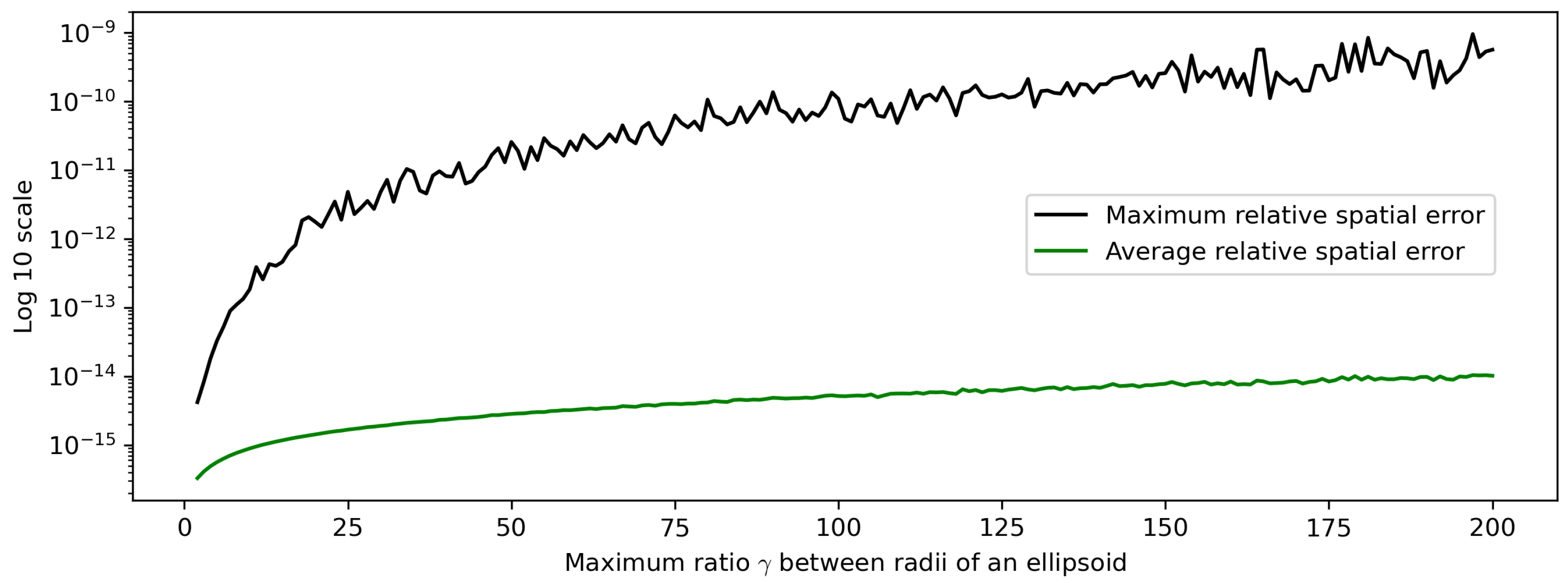Figure 3 shows the maximum and average of the relative spatial errors. As $\gamma$ increases, the maximum error also increases, reaching up to ${10}^{-9}$. However, this error is still sufficiently small to consider ${\mathcal{S}}_{\gamma }$ reliable enough as the ground truth.

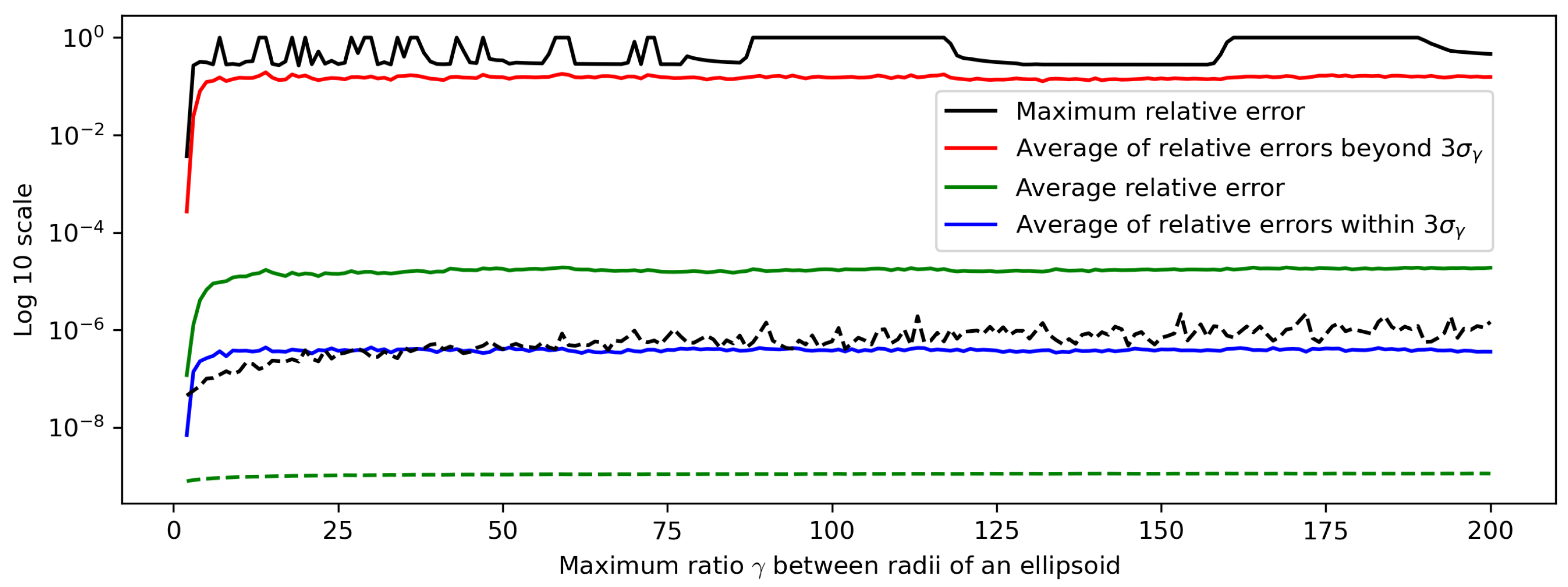
We applied the 2D analytical solution method along with the hybrid Newton method, using ${ϵ}_u={10}^{-8}$, to dataset ${\mathcal{D}}_{\gamma }$. Figure 4 shows the maximum and average of the relative errors with respect to ${\mathcal{S}}_{\gamma }$. The solid black line represents the maximum relative errors of the 2D analytic solution method. It clearly highlights the existence of solutions with excessively large relative errors, which result from erroneously calculated closest approach distances of nearly zero.

There are a small number of solutions with large relative errors, as shown in Figure 2, which can be thought of as outliers resulting from erroneous computation. To effectively filter out the outliers, we employed a three-sigma rule across $\gamma$ values. The errors beyond $3{\sigma }_{\gamma }$ from the average were removed. Here, ${\sigma }_{\gamma }$ represents the standard deviation of the errors for each $\gamma$. The solid blue line represents the average of the filtered errors. It is approximately two orders of magnitude lower than the solid green line, representing the average of the original errors, and five orders of magnitude lower than the red line, representing the average of the outliers. This indicates that there are a small number of solutions with large relative errors across $\gamma$ values. Dashed lines are for the hybrid Newton method with ${ϵ}_u={10}^{-8}$. We added the dashed black and green lines for comparison but omitted the red and blue ones because they are meaningless in this case.

3. Conclusions

In summary, ‘the error in the analytic method’ refers to the numerical error in the analytic method, as conjectured by Zheng and Palffy-Muhoray. However, we were unable to clarify the issues regarding the behavior of the numerical error in the cross-section search because there seem to be exceptional cases or other factors in their implementation of the analytic solution, which result in excessively large errors, including erroneously calculated closest approach distances of zero, as described in Section 2. We hope that Zheng and Palffy-Muhoray will rectify the issues in their implementation of the analytic solution for ellipses. Once rectified, we can proceed with further experiments to investigate the behavior of the numerical error in the cross-section search for ellipsoids.