1. Introduction
Active power symmetry and power balance refer to the balance between the power provided by the power supplier and the power consumed by the load in the power system. This is the key to the stable operation of a power system. Unbalanced power will lead to problems such as deviations in frequency from normal values, affecting power quality. Therefore, it is very important to maintain the active power symmetry of the microgrid and power system through load frequency control (LFC) methods. The need for renewable energy sources such as wind and solar power is accentuated by the ongoing environmental impacts of fossil fuels and their greenhouse gas emissions. Distributed generation (DG) is increasingly being recognized as a vital approach for utilizing these cleaner energy sources. The efficient operation of DG systems facilitates the use of diverse renewable energies, although their intermittent nature and the integration of auxiliary storage devices introduce operational challenges to the grid [
1]. The evolution of microgrid technology, operating in both islanded and grid-connected modes, addresses these issues by harmoniously combining DGs, storage devices, and converters to enhance power reliability and quality [
2]. This technology significantly contributes to energy sustainability, grid stability, and the reduction in environmental pollution. Furthermore, advancements in load frequency control, crucial for maintaining grid stability, have paralleled the development of advanced control theory [
3]. Recent research has led to the development of adaptive control methods, capable of responding to changing system conditions, thus enhancing frequency regulation performance in power systems. This includes the implementation of model reference adaptive PI controllers [
4], adaptive fuzzy logic control [
5], and adaptive neuro-fuzzy inference systems [
6], each offering unique advantages in optimizing grid operations.
Sliding mode variable structure control represents a nonlinear control technique, distinguished by its adaptability to system uncertainties. This method, proficient in handling system uncertainties, robustly adjusts to parameter changes and external disturbances, ensuring system stability. Particularly in power systems, where disturbances can affect frequency and other states, this control strategy excels by adjusting controller gain in response to frequency shifts and generator outputs, effectively mitigating load variations [
7]. However, challenges like system chattering arise due to the oscillatory nature of the frequency response trajectory around the sliding mode surface. Innovations in decentralized sliding mode control for multi-area power systems have been developed, utilizing local state information to stabilize system jitter [
8]. Additionally, the integration of disturbance observers in controller designs enhances the prediction accuracy for uncertain disturbances, reducing controller conservatism, diminishing system jitter, and improving response speed [
9].
Robust control methods in power systems are designed using the boundary information of system uncertainties, allowing them to effectively address power system uncertainties without pre-identifying the characteristics of perturbations [
10]. Recent literature has discussed the development of a robust load frequency controller based on Riccati’s equation, which effectively stabilizes power systems against parameter variations and external disturbances [
11]. Another study proposed a robust gate-adaptive load frequency control method, combining robust and eye-adaptive control for different ranges of parameter variations [
12]. Model predictive control (MPC) is increasingly utilized for managing power system constraints due to its direct handling capabilities and wide industrial applications [
13,
14,
15,
16,
17]. These studies have predominantly focused on traditional energy storage systems, with recent shifts towards incorporating renewable energy sources like wind and photovoltaic power in system frequency regulation. The stochastic nature and diversity of new power generation units, including those with low inertia, present new challenges for system frequency controllers.
Artificial intelligence methods have made remarkable progress in recent years, enabling their application in various domains due to their high adaptability. However, a power system is subject to uncertainty and stochastic disturbances, such as fluctuations in renewable energy sources, load variations, and network failures, which pose challenges for traditional LFC methods to adapt to complex operating environments, resulting in frequency deviations and increased control costs. To address this issue, some researchers have attempted to apply deep reinforcement learning to LFC, using deep neural networks to learn the system’s dynamic model and control strategy to achieve adaptive control and multi-objective optimization of the system.
Reinforcement learning has been applied in all control layers of microgrids, but most of them are focused on energy management and optimal economic allocation for tertiary control. Liu et al. [
18] used reinforcement learning for domestic residential heating and hot water installations to effectively control the energy costs of building energy systems. In [
19], a microgrid model of wind power generation and battery storage was established, and Q-learning algorithm was used to predict the environment of wind power generation, achieve the optimal scheduling of energy storage, and improve the utilization rate of wind power generation. Dai et al. [
20] combined a reinforcement learning algorithm with a distributed optimization method based on multiplier splitting to achieve the optimal power output of different DGs at each moment without knowing the actual power generation cost function. A microgrid with multiple distributed power sources can be regarded as a multi-intelligent system, and although the model-free reinforcement learning approach has a natural advantage, its application in the control field is still very limited, and most applications tend to be converted to a single-intelligence problem to solve. Therefore, the application of reinforcement learning in the secondary control of microgrids still has a great potential. Esmaeili et al. [
21] used a reinforcement learning algorithm to improve the PID controller and realized the adaptive control of the microgrid frequency. Adibi et al. [
22] applied reinforcement learning to the secondary frequency control of lossy microgrids, effectively dealing with time-varying loads, load impedance, and other common general interference situations. Yu et al. [
23] proposed an optimal CPS control strategy based on a Q-learning algorithm under CPS, which was able to optimize the output action commands of the CPS control system online to improve the control system’s anti-interference abilities. Bhongade et al. [
24] applied a three-layer feedforward neural network to the design of an automatic power generation controller and adopted the back propagation algorithm for training. The feasibility of the proposed strategy was verified through simulation in a multi-area AGC system considering superconducting magnetic energy storage units. In [
25], a deep reinforcement learning algorithm with action-weighted optimization and state-of-the-art experience replay was proposed for the stochastic perturbation problem brought by large-scale clean energy.
The efficacy of deep reinforcement learning in power system control, particularly in load frequency control (LFC), is impeded by its reliance on extensive datasets, which are often constrained by the limited, incomplete, or unreliable nature of power system data. This limitation impacts the performance and generalization capacity of deep reinforcement learning, leading to increased frequency bias and higher generation costs in LFC applications. Proximal policy optimization (PPO), a policy-gradient-based deep reinforcement learning algorithm, addresses these issues. It introduces an effective clipping objective function that ensures policy updates are both monotonic and constrained, enhancing efficiency and scalability. The application of the PPO algorithm in LFC optimizes controller parameters, facilitating adaptive control and multi-objective optimization in power systems. PPO, a policy-gradient-based deep reinforcement learning algorithm, addresses the computational complexity and scalability challenges of the trust region policy optimization (TRPO) algorithm. It offers a simple yet effective clipping objective function to ensure policy update monotonicity and constraints, enhancing algorithmic efficiency and scalability. Utilized in load frequency control, PPO optimizes controller parameters for adaptive control and multi-objective optimization in power systems. This approach is particularly suited for islanded microgrid load frequency control but faces challenges in generalization and robustness. The paper introduces a Knowledge Aggregation Proximal Policy Optimization method, combining a priori knowledge and deep neural networks. This method enhances the reinforcement learning process by balancing exploration and exploitation and considering factors like frequency stability and control cost. The effectiveness of this approach is demonstrated through simulations on a four-unit islanded microgrid system, highlighting its potential in the adaptive control and multi-objective optimization of microgrids. This paper introduces two novel contributions to the field of microgrid control:
(1) A Knowledge-Data-Driven Load Frequency Control (KDD-LFC) method is developed. In traditional LFC, it is difficult to achieve adaptive and multi-objective frequency control for complex islanded microgrids [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17]. This method combines the application of prior knowledge models with the capabilities of deep neural networks to achieve adaptive control and multi-objective optimization in microgrid systems.
(2) A new algorithm named Knowledge Aggregation Proximal Policy Optimization (KA-PPO) is created. Traditional DRL lacks robustness and is difficult to adapt to complex islanded microgrid environments [
18,
19,
20,
21,
22,
23,
24,
25]. This KA-PPO leverages traditional methods for generating prior knowledge, which is then incorporated into the experience pool. Subsequently, it employs a near-end strategy optimization technique to learn the state representation and behavioral strategies of the microgrid.
The structure of this paper is organized as follows:
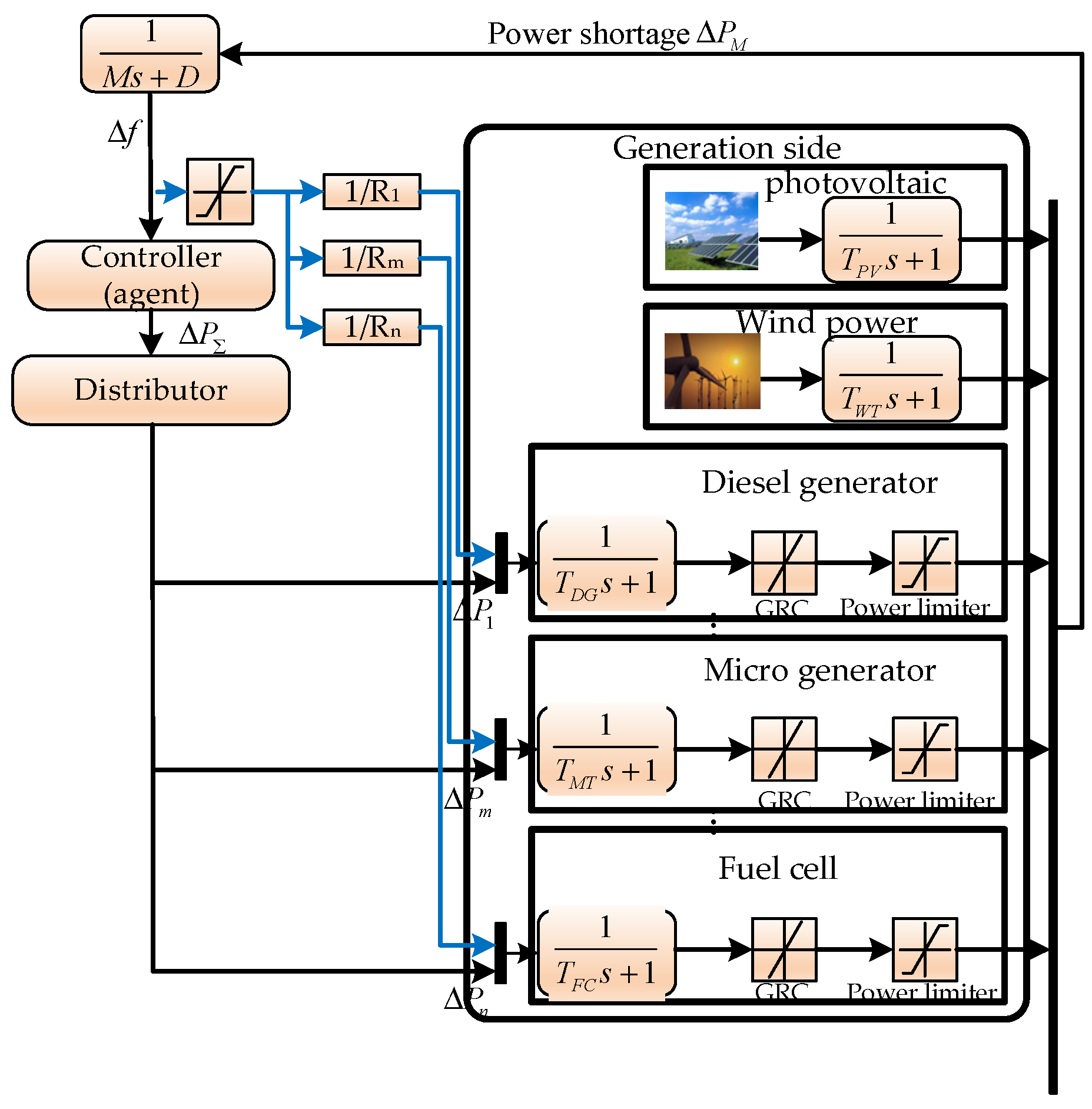
Section 2 details the model of the islanded microgrid system.
Section 3 introduces a novel method, outlining its comprehensive framework. In
Section 4, case studies are conducted to evaluate the effectiveness of the proposed method. Finally,
Section 5 concludes the paper, summarizing key insights and discussing the primary findings of the research.
3. Knowledge-Aggregation-Based Proximal Policy Optimization Method
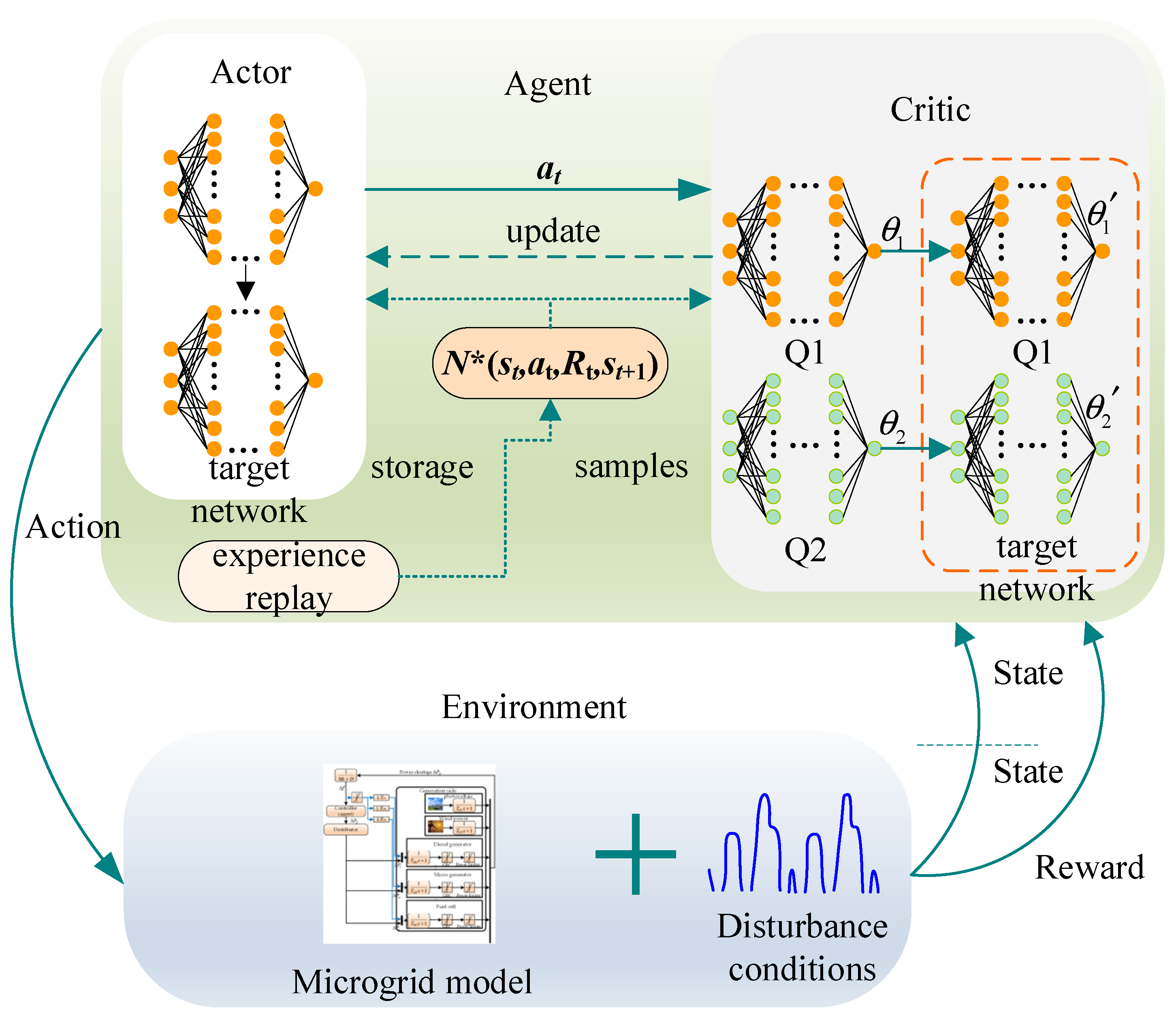
Deep reinforcement learning (DRL) is a powerful, model-free, adaptive control method ideal for load frequency control (LFC) of islanded microgrids. It excels at handling complex, high-dimensional, nonlinear continuous action spaces, enhancing control accuracy and responsiveness. DRL’s ability to directly learn from data reduces modeling difficulties and errors. Furthermore, it adapts to dynamic changes and uncertainties within system operations. Knowledge aggregation, which merges a priori and data-driven knowledge, significantly augments DRL’s learning efficiency and robustness. It guides DRL’s learning process, enhances generalization, and updates knowledge, leading to improved control performance. The proposed KA-PPO algorithm in this paper combines traditional methods for generating prior knowledge with advanced learning strategies, effectively balancing exploration and utilization. This method integrates aspects like frequency stability, tracking performance, and control cost into its reward function, achieving comprehensive, end-to-end control for the microgrid.
3.1. PPO Algorithm in Load Frequency Control
The PPO algorithm effectively overcomes the limitations of previous reinforcement learning algorithms, addressing issues such as low data utilization efficiency and poor robustness in traditional policy gradient methods, as well as the complexity associated with the trust region policy optimization (TRPO) algorithm. PPO’s main advantages include its ease of deployment, reduced variance during iterations, user-friendliness, and enhanced robustness in training. It solves the challenge of determining the optimal learning rate in policy gradient methods by using a ratio that limits the update range of new strategies, reducing sensitivity to large training steps. In islanded microgrid load frequency control, the critic’s Q-function, which assesses action quality, is modeled in a specific manner to enhance control performance.
The PPO algorithm first adopts the generalized advantage estimation (GAE) as the advantage function to estimate the advantage; then, it selects the loss function of the network parameter θ in the Actor network structure as well as the restriction on the KL scatter term during the process of updating the parameter θ; it also selects the loss function of the network parameter Φ in the criterion network structure. Finally, a new working process of the primary and secondary network structures is proposed.
The proximal policy optimization (PPO) algorithm, while effective, faces a challenge concerning the need for the frequent resampling of data in the environment for each parameter update, leading to a slow update process. This requirement to sample extensive data over extended periods is time-consuming and costly. To enhance training speed and enable data reuse, a strategy involving resampling has been proposed to transition from an on-policy to an off-policy approach. This method, outlined in Equation (12), aims to streamline the learning process, thus addressing the inherent inefficiencies of the PPO algorithm in certain tasks.
where
p(
x) is the sampling function for
but is unknown for
p(
x), and
q(
x) is the known sampling function.
The PPO algorithm is designed to allow strategies to choose actions with a higher “advantage”, i.e., a much higher cumulative reward than predicted by the evaluator. The core purpose of the PPO algorithm is the improvement of the PG algorithm. PPO adds an additional constraint to make
and
similar during training, so that the trained
θ and
θ′ are more similar. Proximal policy optimization (PPO) has two main variants based on constraint methods: PPO-penalty and PPO-clip. PPO-penalty adjusts its penalty value by monitoring the KL’s divergence, ensuring the new policy is not too far from the old one. On the other hand, PPO-clip does not directly incorporate KL divergence in the likelihood function but applies a clipping mechanism to the objective function. This clipping limits the range of policy updates, contributing to PPO-clip’s effectiveness. PPO-clip is often preferred over PPO-penalty for its superior performance and ease of implementation. The optimization objective function of PPO-clip is designed to balance exploration and exploitation efficiently.
where
ε is the hyperparameter, which is usually set to 0.1 or 0.2.
The proximal policy optimization (PPO) algorithm incorporates both on-policy and off-policy approaches. The key distinction lies in the alignment of the policy used for interacting with the environment and the policy used for learning. In the off-policy approach, the model’s strategy for action selection in the environment differs from the strategy used during Q-value updates. The latter always chooses actions that maximize state benefits, indicating a divergence between learning and sampling strategies. Conversely, the on-policy approach denotes a scenario where the learning and sampling strategies are identical, ensuring consistency between environmental interaction and policy learning.
The Actor network in the PPO algorithm learns the policy by taking the current state as the input and producing the action probability distribution as the output. The training process of the intelligent agent consists of the following steps: first, the Actor network outputs the action probability distribution; second, the action is sampled from the action probability distribution; third, the environmental state is obtained after executing the action; and finally, the Actor network’s parameters are updated using the gradient ascent method.
The Actor network loss is shown in Equation (15):
where
πθ is the stochastic strategy and
is the estimate of the dominant
function at the
t moment.
The Critic network’s function in the PPO algorithm is to compute
v(
st) and
At, whose current states are used as inputs to the algorithm, and the output of the algorithm is the predicted state values. The Critic network updates the parameters of the network by minimizing a loss function, which is shown in Equation (14) as follows:
where
is the state value predicted by the Critic network,
is the update target obtained by the GAE algorithm, and
is shown in Equation (17) as follows:
where
denotes the timing difference error.
The general PPO algorithm is not satisfactory at learning efficiency and convergence, and it is difficult to adapt to the complex islanded microgrid load frequency control environment. In this paper, a PPO algorithm based on knowledge aggregation is proposed. The samples obtained from other controllers are input into the PPO network as a priori knowledge information, aiming to reduce the training time and interactive data required by the policy learning algorithm and, at the same time, improve the frequency regulation performance and generalization.
3.2. Knowledge-Aggregation Methods and the KA-PPO Algorithm
In reinforcement learning, various kinds of prior knowledge can facilitate the agent’s strategy learning and enhance the final quality of the strategy. However, the methods for the integration and utilization of prior knowledge in reinforcement learning differ depending on their forms of expression. Reinforcement learning relies on the sample data generated by the interaction between the agent and the environment. The agent explores the environment and uses the obtained data to guide its strategy learning, which constitutes the general learning process of reinforcement learning. In this process, enhancing exploration will motivate the agent to try some uncertain actions, so as to gain a more comprehensive understanding of the environment and the task and to prevent the policy from falling into a local optimum prematurely. However, enhancing exploration will also reduce the learning efficiency to some extent, and may incur unnecessary costs and computational resources due to meaningless exploration. Enhancing data utilization will prompt the agent to focus on actions that are likely to bring high cumulative returns, thus maximizing the use of the available data samples and accelerating the convergence process of the policy. The learning process is shown in
Figure 2. Nevertheless, such a choice may cause the policy learning to fall into local optima, affecting the final performance of decision-making tasks. Therefore, how to balance the factors of exploration and exploitation according to different task scenarios is an important challenge for reinforcement learning.
Reinforcement learning with knowledge integration refers to the use of some prior or external knowledge to guide or assist the agent’s learning in the process of reinforcement learning, so as to improve the efficiency and performance of learning. This prior knowledge can take various forms, such as the demonstrations of experts, the strategies of scripts, the design of reward functions, and the division of state space. Prior knowledge can help the agent to narrow the search space, reduce the exploration cost, avoid wrong behaviors, accelerate convergence, adapt to changes in the environment, and so on.
Reinforcement learning with knowledge aggregation refers to a combination of imitation learning and reinforcement learning. This type of algorithm stores expert examples in the example replay area and co-trains the behavior policy model with state–action pairs collected from the environment in a certain ratio, so that the agent can both absorb the expert experience and explore the environment beyond the limitations of the expert’s experience. The KA-PPO algorithm needs to optimize the TD-error, the loss of supervised learning, and the L2 regular term at the same time, as shown in Equation (18).
Since the knowledge aggregation reinforcement learning is based on expert example data, the learning efficiency of the agent is significantly improved and the interpretability of the system is enhanced, which has received much attention in the industrial field.
The KA-PPO design employs imitation learning. Each knowledge aggregation module consists of a controller and a distributor. During training, each integrator generates a reasonable result based on its own controller and distributor, converts it to a sample, and adds it to the experience pool. This enriches the public experience pool with valuable samples.
The controller in the knowledge aggregation module uses PI, PSO-PI, FOPI, PSO-tuned fuzzy-PI, and fuzzy-PI algorithms. Due to the frequent occurrence of large disturbances, the controller’s objective for the integrators is shown below.
The learning process of the KA-PPO algorithm is as follows: First, the information obtained from the knowledge aggregation module is converted into samples according to MDP and used as the a priori knowledge input to the experience pool. Next, the state of the islanded microgrid is inputted to the PPO network, which consists of multiple fully-connected layers. The PPO network then outputs the action distribution for the current state, i.e., the probability of each possible action.
4. Case Studies
To verify the effectiveness of the proposed methodology, we establish an LFC model for the Sansha isolated microgrid of the China Southern Power Grid, which contains both multiple small and medium-sized distributed FM resources and conventional FM units (gas turbines, diesel generators), based on actual data. In the case study, we include not only the KDD-LFC based on the KA-PPO algorithm, but also three deep reinforcement learning algorithm-based KDD-LFCs and three conventional algorithm-based LFCs. The algorithms included for comparison are soft actor–critic (SAC) algorithm-based LFC [
23], twin delayed deep deterministic policy gradient (TD3)-based LFC [
24], deep deterministic policy gradient (DDPG)-based LFC [
23], genetic algorithm fuzzy PI controller (GA-fuzzy-PI) [
22], Takagi–Sugeno fuzzy PI controller (TS-fuzzy-PI) [
25], and GA optimized PI (GA-PI) [
21]. We use a computer with two CPUs with 2.10 GHz Intel Xeon Platinum processors and 16 GB of memory to run the simulation models and procedures that we present in this paper. The simulation software package that we employ is MATLAB/Simulink version 9.8.0 (R2020a).
4.1. Case 1: Step Disturbance and Renewable Disturbance
In Case 1, we add three large-scale load step perturbations and persistent stochastic perturbations in PV and WT energy, with a total perturbation time of 7200 s.
As shown in
Table 1, KA-PPO can reduce the deviation in frequency by 12.30–82.83% and the generation cost by 0.0028–0.072% compared with other algorithms. The KDD-LFC with deterministic optimal control policies learned from pre-training can be deployed for online operation to achieve intelligent control of the power system. To simulate the load surge that often occurs in power systems and evaluate the control performance of different controllers, continuous step disturbances with amplitudes of 500 MW, 1000 MW, and 1500 MW (with an evaluation period of 7200 s) are applied as test signals and compared with six other controllers that have also been pre-trained: the proportional–integral controller (PI), proportional–integral–derivative (PID) controller, fuzzy controller (FC), neural network controller (NN), deep deterministic policy gradient algorithm (DDPG), and dual deep q network algorithm (DDQN). In this paper, we use the Knowledge-Aggregation-based Proximal Policy Optimization (KA-PPO) algorithm as the main controller with the following features.
Regarding the output accuracy of the action values, the KA-PPO controller enhances the algorithm’s convergence speed and stability by using knowledge aggregation to increase its prior knowledge and applying more prior knowledge to guide its learning process. This algorithm stores expert examples in the replay buffer and samples them with state–action pairs collected from the environment at a certain ratio to co-train the behavior policy model. Thus, the agent can not only learn from the expert experience, but also explore the environment and overcome the limitations of the expert’s experience, achieving a better control effect. Other deep reinforcement learning algorithms lack this function and can only obtain more samples for learning through trial and error. Such samples are not diverse, which lowers the agent’s learning efficiency, and the algorithms are prone to fall into local optima and struggle to adapt to complex environmental changes. Therefore, as shown in
Figure 3, the KA-PPO algorithm achieves a better frequency control effect, and its frequency deviation does not exhibit large overshooting and oscillation, and it returns to stability after only a small amount of overshooting. However, the other deep reinforcement learning algorithms have difficulty in obtaining good performance due to their poor performance. Their frequency deviation oscillates and overshoots, and this overshooting and oscillation severely affect the algorithm’s power generation cost. Moreover, repeated adjustments increase the power generation cost of the other deep reinforcement learning algorithms.
Among other conventional control algorithms, fuzzy rule-based controllers can adaptively regulate the controller’s output and adjust and recover in time after the output overshoots. However, since the fuzzy rules are manually formulated, their control accuracy is very low, which causes their frequency to oscillate still. Other optimization-based controllers lack adaptive tuning and thus suffer from different frequency fluctuations and performance under different load perturbations, which severely impairs the frequency control performance, resulting in frequency overshooting and difficulty in controlling it.
4.2. Case 2: Step Disturbance and Renewable Disturbance
This paper presents a smart distribution network model that addresses the challenge of integrating new and distributed energy sources into the grid on a large scale, while maintaining the stability of large grid systems. The proposed model integrates a diverse array of alternative energy sources, including wind power, small-scale hydroelectric systems, micro gas turbines, fuel cells, solar power, and biomass energy. This multifaceted approach to energy generation leverages the unique benefits of each source, aiming to enhance efficiency, reduce environmental impact, and promote sustainability. By diversifying the energy portfolio, the model addresses the growing demand for clean energy solutions and mitigates reliance on traditional fossil fuels. This paper investigates the control performance of KA-PPO in a highly stochastic environment based on this model. Due to the high uncertainty in the output of electric vehicles and wind and solar energy, they are treated as stochastic load disturbances in this paper and are excluded from control. This paper employs finite bandwidth white noise to simulate random wind speeds as an input to the wind turbine and obtain its output. Similarly, this paper uses the simulated variation in solar irradiance throughout the day to obtain the output of the solar power generation model.
Our objective is to investigate how the power system can handle the stochastic fluctuations in load when a large number of new energy sources are integrated into the grid. For this purpose, we introduce random white noise as a load disturbance in the smart distribution network model to evaluate the control effect of the KA-PPO strategy in this complex environment. The KA-PPO algorithm can deal with the random disturbances effectively and produce accurate tracking results.
Table 2 presents the statistics of the simulation experiment, where the generation cost indicates the total regulation cost of all generating units in 24 h. The distribution network data reveal that the deviation in frequency of the other algorithms is 11.61–80.64% higher than that of the KA-PPO algorithm, while the generation cost of the KA-PPO algorithm is reduced by 0.067–0.085%. The analysis of control performance metrics demonstrates that the KA-PPO algorithm surpasses other intelligent algorithms in terms of economy, adaptability, and coordinated optimal control performance. We also performed experimental verification of various disturbances such as step waves, square waves, and random waves. The experimental results indicate that KA-PPO has strong convergence ability and high-speed learning efficiency. Particularly in random environments, it exhibits excellent adaptability. It not only mitigates random disturbances, but also improves the dynamic control performance in the interconnected grid environment. Under the control of the total power command, the complementary and synergistic optimal operation of multiple energy sources is accomplished in each time period.
4.3. Case 3: Large-Scale Renewable Disturbance
In this study, Case 3 is introduced, incorporating large-scale renewable energy disturbances, to rigorously evaluate the robustness of the proposed algorithm. This addition aims to simulate realistic conditions under which the algorithm’s performance can be assessed against significant fluctuations in renewable energy output, reflecting scenarios such as sudden changes in wind speed or solar irradiance. Through this strategic inclusion, the research endeavors to provide a comprehensive analysis of the algorithm’s capability to maintain stability and efficiency in the face of dynamic and unpredictable renewable energy patterns. This approach not only enhances the validity of the algorithm’s application in real-world settings but also substantiates its resilience and adaptability to accommodate the inherent variability in renewable energy sources, thereby contributing valuable insights into its potential for optimizing energy distribution and grid stability.
This study aims to explore the capacity of the power system to manage stochastic load fluctuations as a consequence of integrating a substantial number of novel energy sources into the electrical grid. To achieve this, we have introduced random white noise to act as a load disturbance within the smart distribution network model. This methodology is deployed to assess the efficacy of the KA-PPO strategy under such complex conditions. The KA-PPO algorithm demonstrates a proficient capability in addressing random disturbances, delivering precise tracking outcomes. The simulation experiment’s results are summarized in
Table 3, showcasing the total regulation costs incurred by all generating units over a 24 h period as a measure of generation cost. Data on the distribution network elucidate that the deviation in frequency with other algorithms is 17.11–87.22% higher than that achieved using the KA-PPO algorithm. Simultaneously, the generation cost associated with the KA-PPO algorithm shows a reduction of 0.066–0.083%. This critical analysis of control performance metrics highlights the KA-PPO algorithm’s superiority over other intelligent algorithms in delivering economic efficiency, adaptability, and coordinated optimal control performance.
Further experimental validation was conducted to assess the algorithm’s response to various disturbances, including step waves, square waves, and random waves. These experimental findings underscore the KA-PPO’s robust convergence capabilities and expedited learning efficiency, which is particularly pronounced in environments characterized by randomness. The algorithm’s exceptional adaptability is not only pivotal in counteracting random disturbances but also in enhancing the dynamic control performance within the interconnected grid. The KA-PPO algorithm facilitates the complementary and synergistic optimal operation of multiple energy sources across different time intervals, under the directive of total power command. This orchestration underscores the potential of the KA-PPO algorithm to significantly contribute to the stability and efficiency of power systems amidst the increasing integration of renewable energy sources.
5. Conclusions
This manuscript delineates several significant contributions to the realm of microgrid management and optimization. Initially, it introduces the Knowledge-Driven Deep Learning for Load Frequency Control (KDD-LFC) methodology. This sophisticated approach amalgamates prior knowledge models with advanced deep neural network architectures to facilitate adaptive control and achieve multi-objective optimization within microgrid systems. The incorporation of established knowledge into deep learning frameworks allows for a more nuanced and effective control strategy, catering to the dynamic and complex nature of microgrid operations.
Furthermore, the study pioneers a cutting-edge algorithm designated as Knowledge-Augmented Proximal Policy Optimization (KA-PPO). This algorithm ingeniously integrates conventional methodologies to harvest prior knowledge as a form of experiential data, which is subsequently assimilated into the experience pool. Utilizing this enriched dataset, KA-PPO employs an end-to-end policy optimization technique to intricately learn the state representation and behavioral strategies pertinent to microgrid management. This dual-phase approach not only capitalizes on the strengths of traditional and deep learning methodologies but also enhances the algorithm’s capability to navigate and optimize the multifaceted microgrid environment.
Empirical validation of the proposed KDD-LFC method and KA-PPO algorithm is conducted through rigorous simulation experiments. These experiments utilize the load frequency control (LFC) model of the Sansha isolated microgrid, operated by the China Southern Power Grid. The outcomes of these simulations unequivocally demonstrate the superiority and efficacy of the proposed solutions. When benchmarked against a suite of prevalent deep reinforcement learning algorithms (such as soft actor–critic (SAC), twin delayed dDPG (TD3), and deep deterministic policy gradient (DDPG)) and conventional control strategies (including genetic algorithm-enhanced fuzzy-PI (GA-fuzzy-PI), Takagi–Sugeno (TS) fuzzy-PI, and GA-PI algorithms), KA-PPO exhibits remarkable performance in minimizing deviations in frequency and reducing generation costs.
Looking ahead, the trajectory of future work is set to pivot towards the practical application and real-world implementation of the proposed algorithm. This endeavor will aim to transcend theoretical validation and simulation experiments, focusing on the deployment and operational efficacy of KA-PPO within live microgrid environments. Such applied research will not only underscore the practical viability of the algorithm but also contribute to its refinement and optimization for broader utility in the field of microgrid management.