Computational Design of an In-Line Coaxial-to-Circular Waveguide Adapter with More Than an Octave Bandwidth
Abstract
1. Introduction
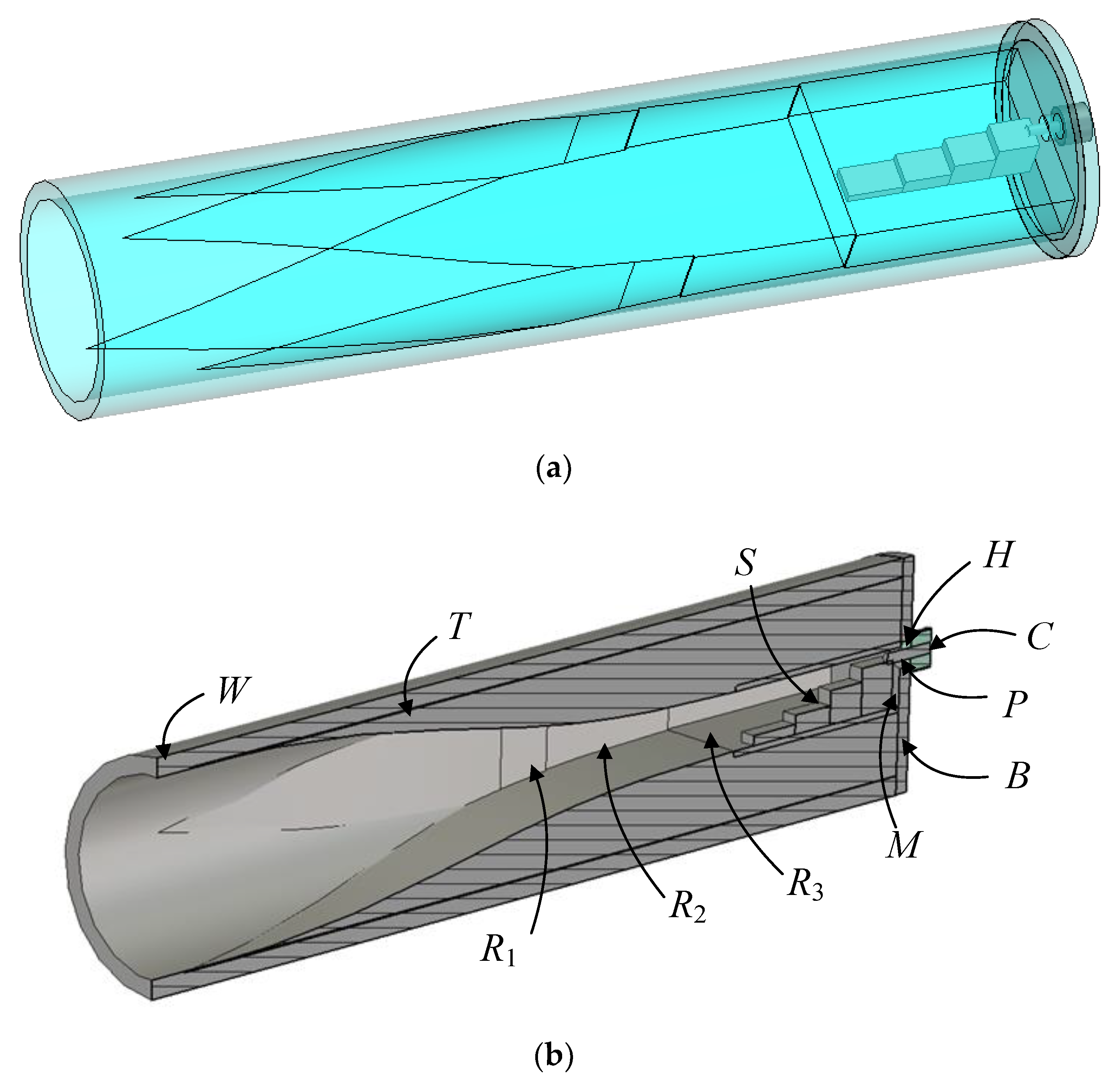
2. Adapter Design Methodology
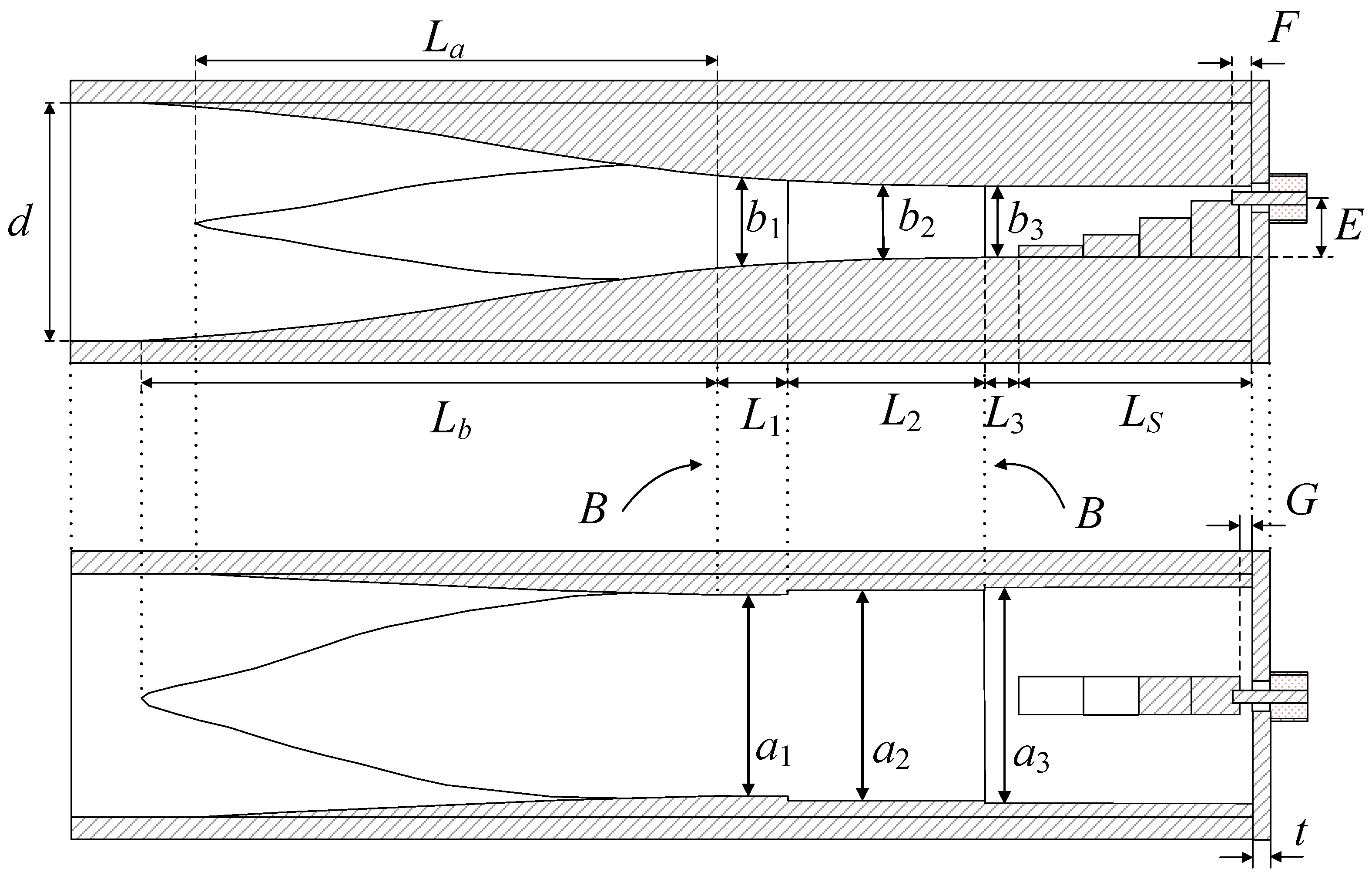
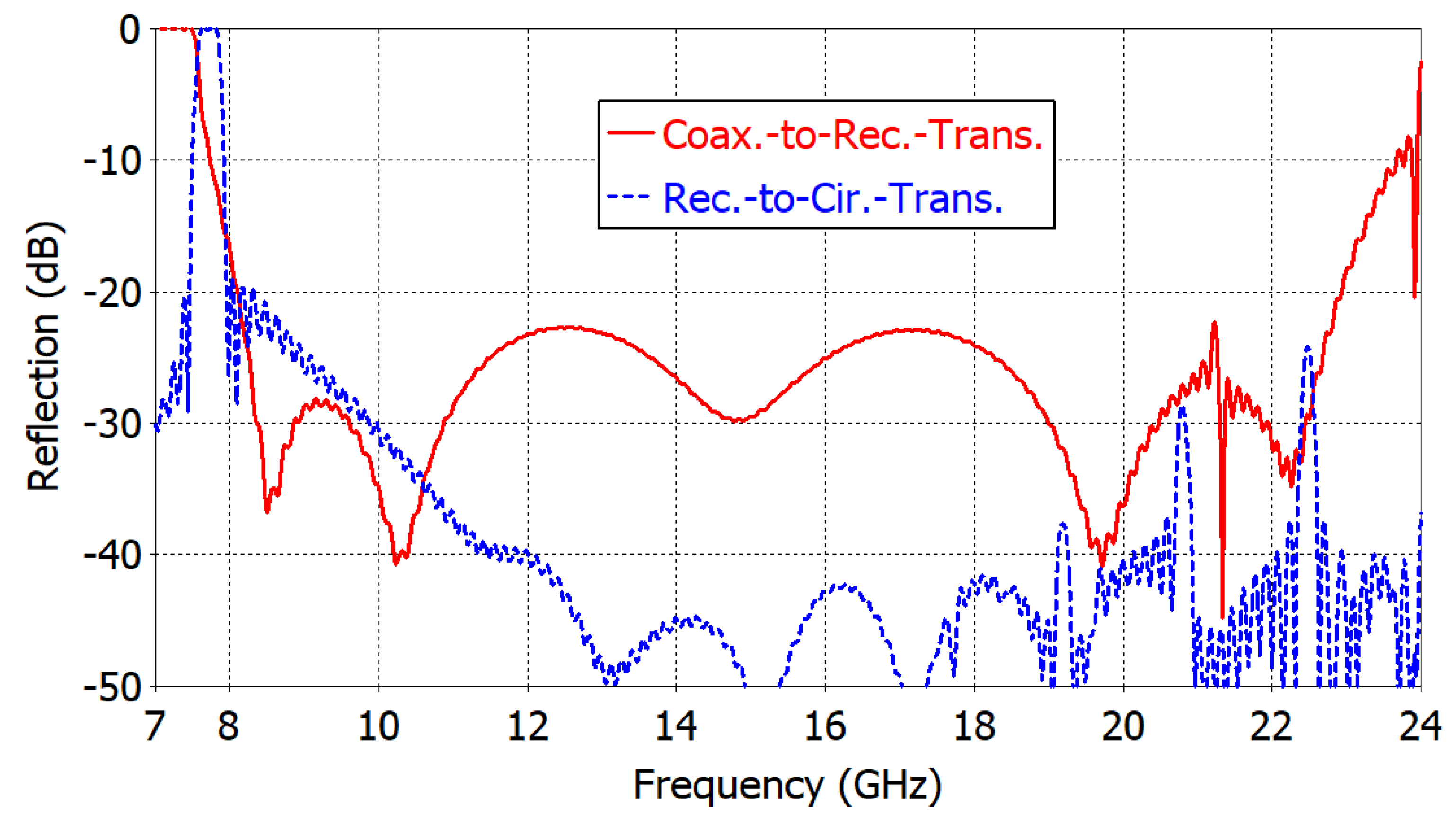
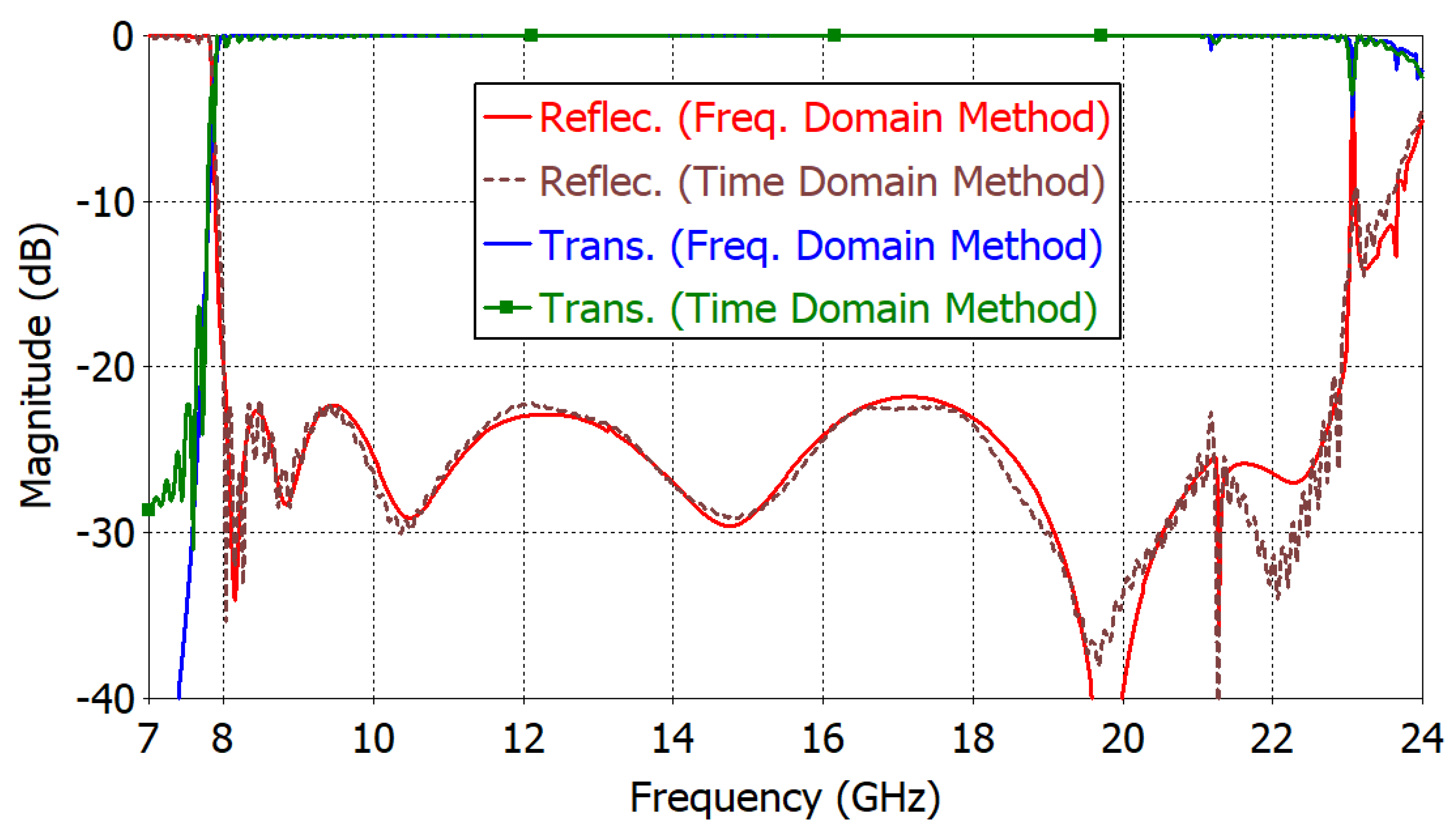
3. Simulation-Based Design of the Adapter
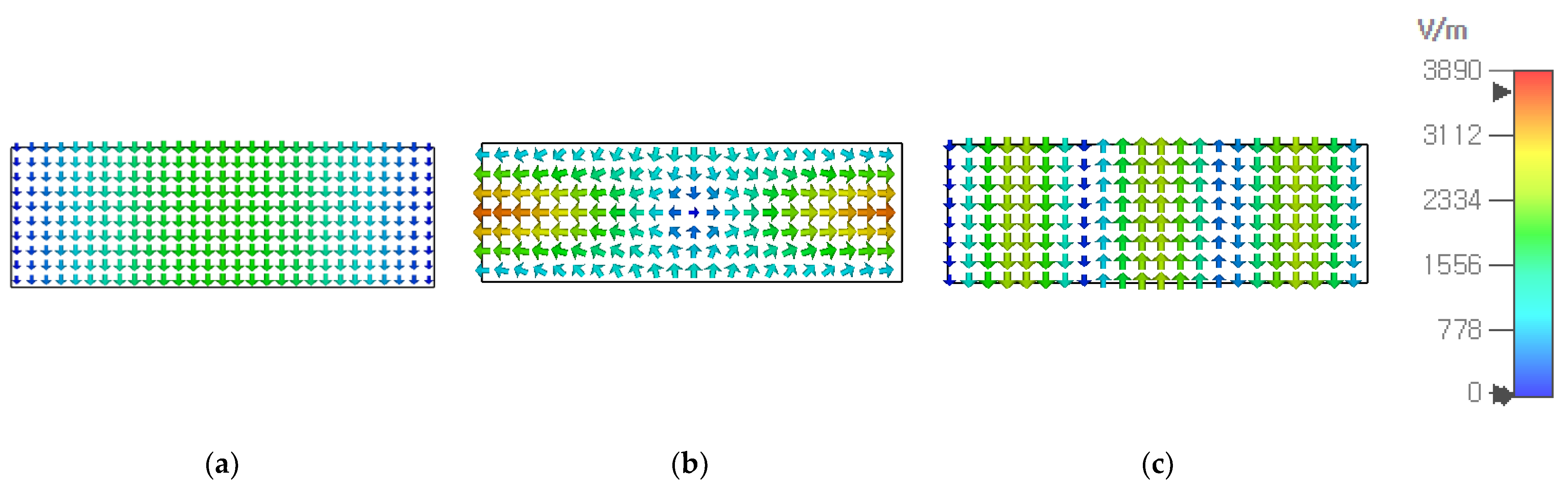
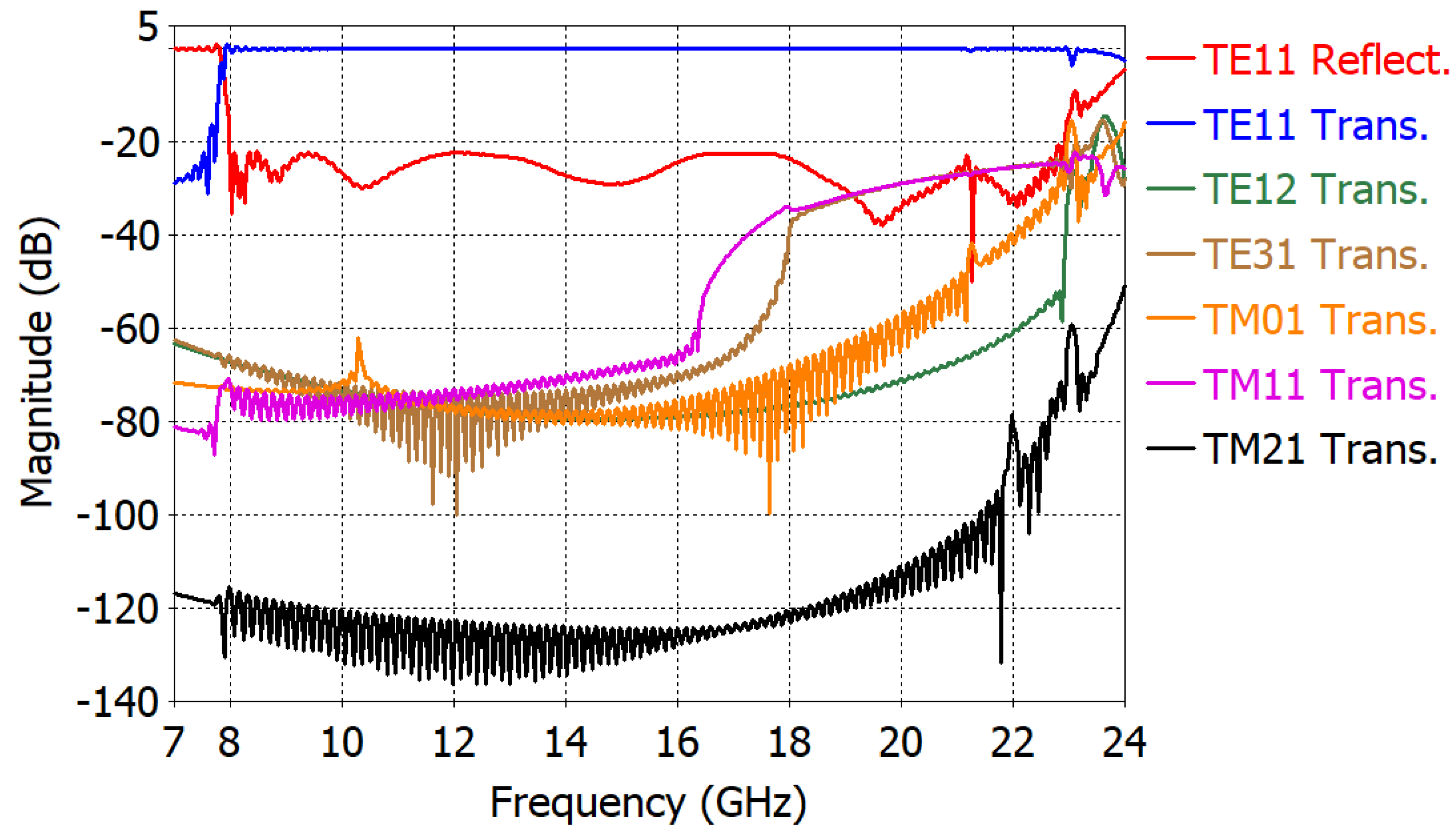
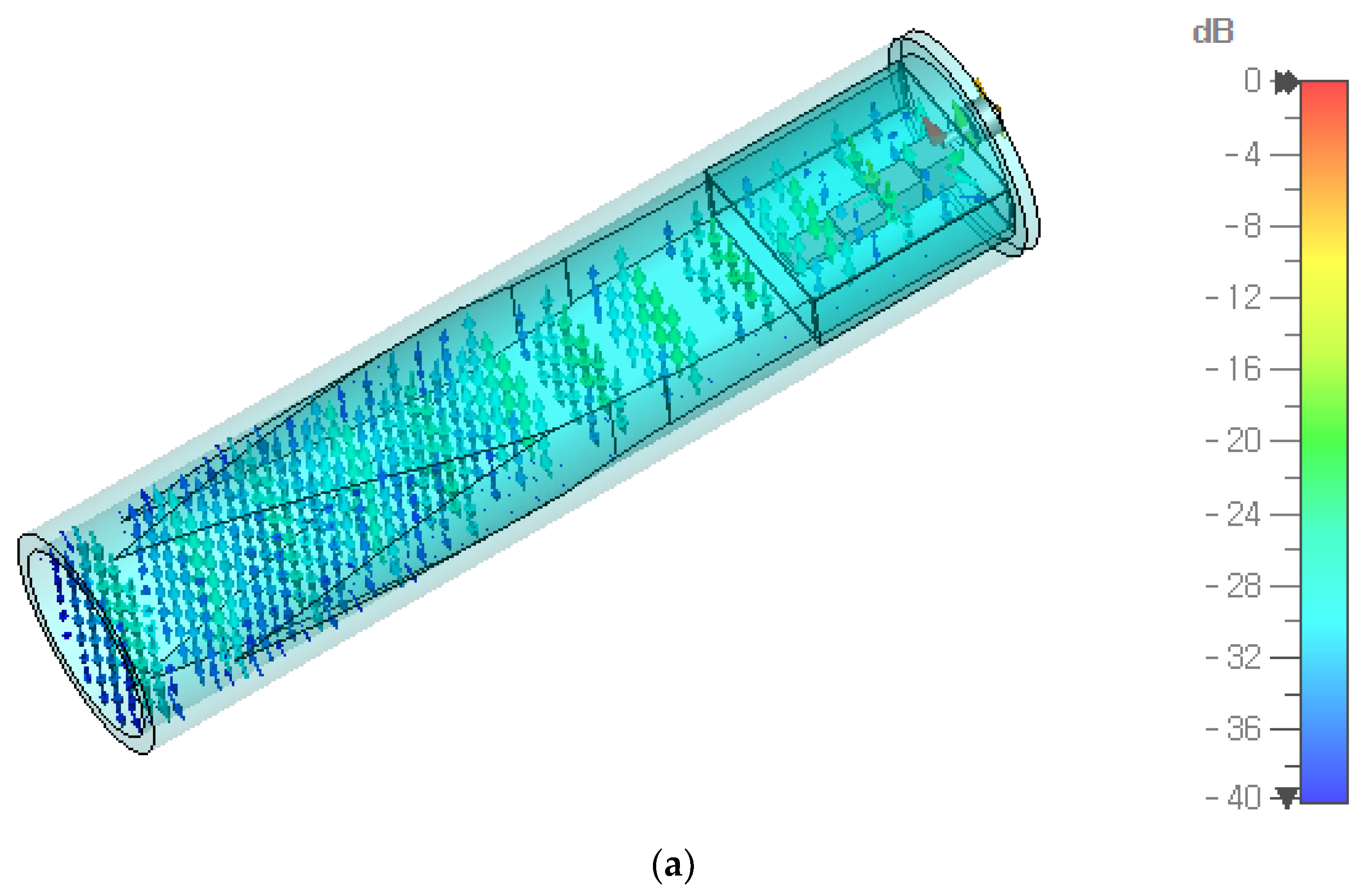
4. Analysis of the Dominant and Higher-Order Modes
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chakrabarty, S.B.; Singh, V.K.; Sharma, S.B. TM01 mode transducer using circular and rectangular waveguides. Int. J. RF Microw. Comp. Aided Eng. 2010, 20, 259–263. [Google Scholar] [CrossRef]
- Chittora, A.; Singh, S.; Sharma, A.; Mukherjee, J. Design of wideband coaxial-TEM to circular waveguide TM 01 mode transducer. In Proceedings of the 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016. [Google Scholar]
- Zhang, L.J.; Choi, S.G.; Ahn, B.C.; Bang, J.H.; Kim, D.H.; Choi, Y.T. Simplified feed prime focus reflector antenna. Microw. J. 2016, 59, 108–114. [Google Scholar]
- Jadhav, R.P.; Dongre, J.V.; Heddallikar, A. Design of X-band conical horn antenna using coaxial feed and improved design technique for bandwidth enhancement. In Proceedings of the 2017 International Conference on Computing, Communication, Control and Automation (ICCUBEA), Pune, India, 17–18 August 2017. [Google Scholar]
- Mallahzadeh, A.R.; Dastranj, A.A. Double-ridged conical horn antenna for 2–18 GHz. Electromagnetics 2008, 28, 450–461. [Google Scholar] [CrossRef]
- Solak, B.; Secmen, M.; Tekin, A. The design of a high gain dual-polarized quad-ridged circular horn antenna for wideband EMC test applications. Appl. Comput. Electromag. Soc. J. 2018, 33, 1009–1017. [Google Scholar]
- Göttmann, O.; Kaatze, U.; Petong, P. Coaxial to circular waveguide transition as high-precision easy-to-handle measuring cell for the broad band dielectric spectrometry of liquids. Meas. Sci. Technol. 1996, 7, 525. [Google Scholar] [CrossRef]
- Tantawi, S.G.; Nantista, C.D.; Bowden, G.B.; Fant, K.S.; Kroll, N.M.; Vlieks, A.E.; Chin, Y.H.; Hayano, H.; Vogel, V.F.; Nielson, J. Evaluation of the TE12 mode in circular waveguide for low-loss, high-power RF transmission. Rev. Mod. Phys. 2000, 3, 082001. [Google Scholar]
- De Ronde, F.C. Ideal w.g. to coax transitions using a fbm monopole. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, New York, NY, USA, 25–27 May 1988. [Google Scholar]
- Bialkowski, M.E. Analysis of a coaxial-to-waveguide adaptor including a discended probe and a tuning post. IEEE Trans. Microw. Theory Tech. 1995, 43, 344–349. [Google Scholar] [CrossRef]
- Bang, J.H.; Ahn, B.C. Coaxial-to-circular waveguide transition with broadband mode-free operation. Electron. Lett. 2014, 50, 1453–1454. [Google Scholar] [CrossRef]
- Simone, M.; Fanti, A.; Lodi, M.; Pisanu, T.; Mazzarella, G. An in-line coaxial-to-waveguide transition for Q-band single-feed-per-beam antenna systems. Appl. Sci. 2021, 11, 2524. [Google Scholar] [CrossRef]
- Cano, J.L.; Mediavilla, A. Octave bandwidth in-line rectangular waveguide-to-coaxial transition using oversized mode conversion. Electron. Lett. 2017, 53, 1370–1371. [Google Scholar] [CrossRef]
- Zhu, Q.C.; Williamson, A.G.; Neve, M.J. Design of coaxial line-to-circular waveguide transitions. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Boston, MA, USA, 7–12 June 2009. [Google Scholar]
- Park, K.; Jeong, J. Design of Ku-band circular waveguide-to-coaxial adapter. In Proceedings of the 2018 Progress in Electromagnetics Research Symposium, Toyama, Japan, 1–4 August 2018. [Google Scholar]
- Schönfeld, F.; Weihreter, E.; Tasi, Y.C.; Chu, K.R. Layout of a broadband circular waveguide to coaxial transition. In Proceedings of the 5th European Particle Accelerator, Sitges, Spain, 10–14 June 1996. [Google Scholar]
- Yamamoto, T.; Urabe, K.; Tsuda, H. Analysis of coaxial-to-circular waveguide transition. In Proceedings of the IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014. [Google Scholar]
- Xia, L.; Li, J.L.; Ji, Z.; Gao, S.S. An in-line coaxial-to-circular waveguide transition at X band. J. Elecr. Eng. 2020, 71, 55–59. [Google Scholar] [CrossRef]
- Tribak, A.; Zbitou, J.; Sanchez, A.M.; Touhami, N.A. Ultra-broadband high efficiency mode converter. Prog. Electromag. Res. C 2013, 36, 145–158. [Google Scholar] [CrossRef]
- Yun, J.Y.; Nho, J.W.; Lee, C.H.; Park, Y.G.; Ahn, B.C. Design of a circular waveguide to coaxial cable transition employing a printed dipole (in Korean). J. Korean Inst. Inf. Tech. 2017, 15, 65–71. [Google Scholar]
- Marcuvitz, N. Waveguide Handbook; McGraw-Hill: New York, NY, USA, 1951; pp. 66–80. [Google Scholar]
- Das, B.N.; Sanyal, G.S. Coaxial-to-waveguide transition (end-launcher type). Proc. Inst. Electr. Eng. 1976, 123, 984–986. [Google Scholar] [CrossRef]
- Kim, D.-H.; Yang, D.-Y. Analysis and design of multiple-stepped coaxial coupling launcher for wideband rectangular waveguide excitation. J. Electr. Eng. Technol. 2021, 16, 2149–2155. [Google Scholar] [CrossRef]
- Niemann, F.L. Transitions from coaxial line to waveguide. In Microwave Transmission Circuits; Ragan, G.L., Ed.; McGraw-Hill: New York, NY, USA, 1948; pp. 314–361. [Google Scholar]
- Dix, J.C. Design of waveguide/coaxial transition for the band 2.5–4.1 Gc/s. Proc. Inst. Electr. Eng. 1963, 110, 253–255. [Google Scholar] [CrossRef]
- Gaudio, J.G.; Station, J.; Debski, T.R. Broadband Waveguide to Coaxial Line Transition. U.S. Patent 3,737,812, 5 June 1973. [Google Scholar]
- Chan, K.K.; Martin, R.; Chadwick, K. A broadband end launched coaxial-to-waveguide transition for waveguide phased arrays. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Atlanta, GA, USA, 21–26 June 1998. [Google Scholar]
- Levy, R.; Hendrick, L.-W. Analysis and synthesis of in-line coaxial-to-waveguide adapters. In Proceedings of the 2002 IEEE MTT-S International Microwave Symposium Digest, Seattle, WA, USA, 2–7 June 2002. [Google Scholar]
- Durga, M.; Tomar, S.; Singh, S.; Suthar, L. Millimeter wave in-line coaxial-to-rectangular waveguide transition. In Proceedings of the 2011 IEEE Applied Electromagnetics Conference (AEMC), Kolkata, India, 18–22 December 2011. [Google Scholar]
- Carmel, N.; Elmakayes, D.; Matzner, H. Investigation of a coax-to-waveguide transition element. In Proceedings of the 2011 IEEE International Conference on Microwaves, Communications, Antennas and Electronic Systems, Tel Aviv-Yafo, Israel, 7–9 November 2011. [Google Scholar]
- Gatti, R.V.; Rossi, R.; Dionigi, M. In-line stepped ridge coaxial-to-rectangular waveguide transition with capacitive coupling. Int. J. RF Microw. Comput. Aided Eng. 2018, 29, e21626. [Google Scholar] [CrossRef]
- Ye, J.; Zhang, H.; Chu, R. Analysis of a new method to design a coaxial-to-rectangular waveguide transition. In Proceedings of the 2019 International Applied Computational Electromagnetics Society Symposium-China (ACES), Nanjing, China, 8–11 August 2019. [Google Scholar]
- Bilik, V. High-power in-line waveguide to coaxial adapter. In Proceedings of the 2020 30th International Conference Radioelektronika (RADIOELEKTRONIKA), Bratislava, Slovakia, 15–16 April 2020. [Google Scholar]
- Shu, Y.; Ren, L. Novel waveguide connectors to simplify microwave and millimeter wave component packaging. In Proceedings of the 2022 IEEE/MTT-S International Microwave Symposium-IMS 2022, Denver, CO, USA, 19–24 June 2022. [Google Scholar]



| Waveguide | Modes/Cutoff Frequency (GHz) |
|---|---|
| W | TE11, TM11, TE12/7.88, 16.39, 22.80 |
| R1 | TE10, TE11, TE30/7.87, 17.68, 23.61 |
| R2 | TE10, TE11, TE30/7.70, 20.17, 23.10 |
| R3 | TE10, TE11, TE30/7.54, 24.03, 22.61 |
| C | TEM, TE11, TE21/0.00, 26.27, 48.09 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| a1, b1, L1 | 19.05, 8.04–9.47, 6.73 | d, Lb, F, E | 22.31, 55.04, 1.91, 5.62 |
| a2, b2, L2 | 19.47, 6.57–8.04, 18.22 | La, LS, t, G | 48.19, 21.96, 1.57, 1.06 |
| a3, b3, L3 | 19.89, 6.57, 2.89 | Ridge width/height | 3.62/1.12, 2.14, 3.8, 5.33 |
| Coax. cable | 1.27/4.11, εr = 2.08 | Probe hole | Dia. = 2.95, Len. = 1.57 |
| Work | Type | Frequency (GHz) | Reflection (dB) | Ratio Bandwidth | Complexity |
|---|---|---|---|---|---|
| [11] | Right-angle | 7.34–17.77 | −20 | 2.42 | Low (conical probe and tapered transformer) |
| [16] | Right-angle | 0.7–3.0 | −10 | 4.29 | Medium (double ridge) |
| [19] | In-line | 9.2–16.2 | −20 | 1.76 | High (coaxial-to-rectangular-to-circular) |
| [20] | In-line | 13.6–17.9 | −15 | 1.32 | Medium (dielectrically filled; contains air gap) |
| This work | In-line | 8.00–22.95 | −20 | 2.87 | Medium (stepped ridge and spline taper converter) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altanzaya, E.; Heo, J.; Xu, S.; Lee, C.-S.; Ahn, B.-C.; Kim, S.-S.; Choi, S.-G. Computational Design of an In-Line Coaxial-to-Circular Waveguide Adapter with More Than an Octave Bandwidth. Symmetry 2024, 16, 304. https://doi.org/10.3390/sym16030304
Altanzaya E, Heo J, Xu S, Lee C-S, Ahn B-C, Kim S-S, Choi S-G. Computational Design of an In-Line Coaxial-to-Circular Waveguide Adapter with More Than an Octave Bandwidth. Symmetry. 2024; 16(3):304. https://doi.org/10.3390/sym16030304
Chicago/Turabian StyleAltanzaya, Erdenesukh, Jiwon Heo, Songyuan Xu, Chan-Soo Lee, Bierng-Chearl Ahn, Sung-Soo Kim, and Seong-Gon Choi. 2024. "Computational Design of an In-Line Coaxial-to-Circular Waveguide Adapter with More Than an Octave Bandwidth" Symmetry 16, no. 3: 304. https://doi.org/10.3390/sym16030304
APA StyleAltanzaya, E., Heo, J., Xu, S., Lee, C.-S., Ahn, B.-C., Kim, S.-S., & Choi, S.-G. (2024). Computational Design of an In-Line Coaxial-to-Circular Waveguide Adapter with More Than an Octave Bandwidth. Symmetry, 16(3), 304. https://doi.org/10.3390/sym16030304








