Correction: Klimchitskaya et al. Nonequilibrium Casimir–Polder Interaction between Nanoparticles and Substrates Coated with Gapped Graphene. Symmetry 2023, 15, 1580

Galina L. Klimchitskaya; Constantine C. Korikov; Vladimir M. Mostepanenko; Oleg Yu. Tsybin

doi:10.3390/sym16030274

,

and

¹

Central Astronomical Observatory at Pulkovo of the Russian Academy of Sciences, 196140 Saint Petersburg, Russia

²

Peter the Great Saint Petersburg Polytechnic University, 195251 Saint Petersburg, Russia

³

Huawei Noah’s Ark Laboratory, Krylatskaya str. 17, 121614 Moscow, Russia

⁴

Kazan Federal University, 420008 Kazan, Russia

Symmetry2024, 16(3), 274;https://doi.org/10.3390/sym16030274

This article belongs to the Section Physics

Version Notes

Order Reprints

The authors wish to make the following corrections in their paper [1].

1. Equation (28) is replaced with

\begin{matrix} {\tilde{Π}}_{00}^{(1)} (t, \tilde{Δ}, τ_{g}) = \frac{8 α}{{\tilde{v}}_{F}^{2} t^{2}} \int_{\tilde{Δ}}^{\infty} d z Ψ (z, τ_{g}) [1 + \frac{1}{2} \sum_{λ = \pm 1} λ \frac{{\tilde{v}}_{F}^{2} t^{2} - {(z + λ)}^{2}}{\sqrt{[{\tilde{v}}_{F}^{2} t^{2} - {(z + λ)}^{2}] ({\tilde{v}}_{F}^{2} t^{2} - 1) + {\tilde{v}}_{F}^{2} t^{2} {\tilde{Δ}}^{2}}}], \\ {\tilde{Π}}^{(1)} (t, \tilde{Δ}, τ_{g}) = \frac{8 α}{{\tilde{v}}_{F}^{2} t^{2}} \int_{\tilde{Δ}}^{\infty} d z Ψ (z, τ_{g}) [1 + \frac{1}{2} \sum_{λ = \pm 1} λ \frac{{(z + λ)}^{2} ({\tilde{v}}_{F}^{2} t^{2} - 1) - {\tilde{v}}_{F}^{2} t^{2} {\tilde{Δ}}^{2}}{\sqrt{[{\tilde{v}}_{F}^{2} t^{2} - {(z + λ)}^{2}] ({\tilde{v}}_{F}^{2} t^{2} - 1) + {\tilde{v}}_{F}^{2} t^{2} {\tilde{Δ}}^{2}}}] . \end{matrix}

(28)

This equation differs from Equation (28) in Ref. [1] by the additional multiple

- λ

under the summation signs, which is responsible for the correct choice of branches of the square root in denominators when performing the analytic continuation of the polarization tensor to the real frequency axis.

This error does not influence the main results of the Ref. [1] but makes a quantitative impact on Figures 5 and 6.

2. Section 4, paragraph 8, starting from the words “As shown in Figure 5a,b”, should be formulated as:

As shown in Figure 5a,b, the quantity

F_{r}

, unlike

F_{M}

, substantially depends on the value of

Δ

at both

T_{g} = 77

and 500 K. The point is that, for

T_{g} < T_{E}

, the contributions to

F_{r}

from the regions (14) and (15) are positive, i.e., decrease the force magnitude. The opposite situation occurs for

T_{g} > T_{E}

, i.e., the contributions of Equations (14) and (15) to

F_{r}

are negative, leading to the increase in force magnitude.

Section 4, paragraph 10, the text starting with “In so doing, …” should be omitted, as well the full paragraphs 11 and 12.

The corrected Figure 5 is

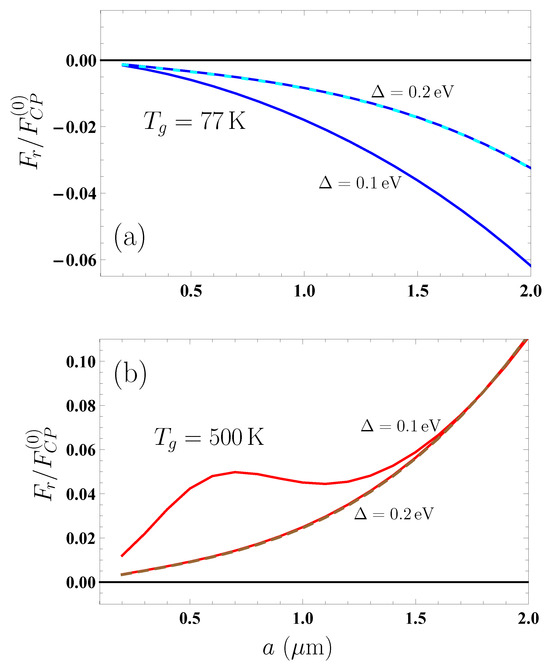
Figure 5. The ratio of the second contribution to the nonequilibrium Casimir–Polder force acting on a nanoparticle from a SiO₂ plate coated by a graphene sheet (a) at

T_{g} = 77

K and (b)

T_{g} = 500

K to the equilibrium one from an ideal metal plane at

T_{p} = T_{E} = 0

is shown as the function of separation (a) by the two lines for

Δ = 0.1

and 0.2 eV, where the latter coincides with that for an uncoated plate shown by the dashed line, and (b) by the two solid lines for

Δ = 0.1

and 0.2 eV, where the latter coincides with that for an uncoated plate shown by the dashed one.

3. Next, Figure 6 should be corrected, and in the third paragraph from the bottom in Section 4 the values of the ratio

F_{neq} / F_{neq}^{{SiO}_{2}}

equal to 1.03 and 1.35 at separations

a = 0.2

and 2 μm for a graphene sheet with Δ = 0.1 eV should be replaced with 1.05 and 0.94.

The authors state that the scientific conclusions are unaffected. This correction was approved by the Academic Editor. The original publication has also been updated.

The corrected Figure 6 is

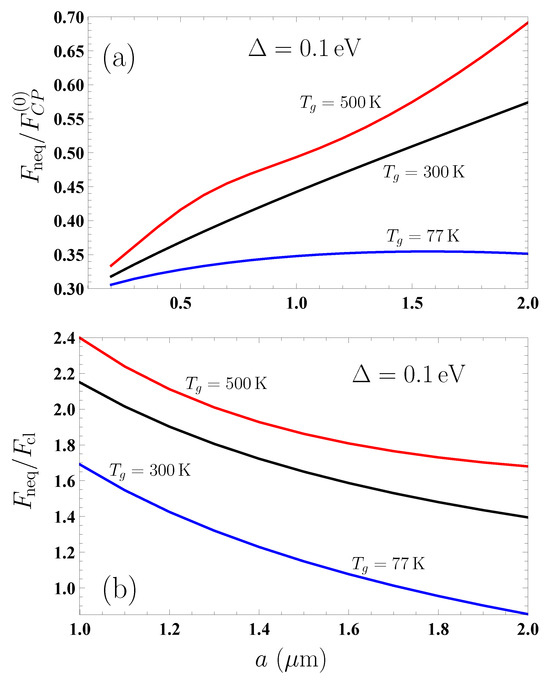
Figure 6. The ratio of the nonequilibrium Casimir–Polder force acting on a nanoparticle from a SiO₂ plate coated by a graphene sheet with Δ = 0.1 eV to the equilibrium one from an ideal metal plane (a) at

T_{p} = T_{E} = 0

and (b) at

T_{p} = T_{E} = 300

K (the classical limit) is shown as the function of separation. The bottom and top lines are for the graphene plate temperatures

T_{g} = 77

K and 500 K, respectively. The middle lines demonstrate similar ratio, where

T_{g} = T_{E} = 300

K.

Funding

The work of O.Yu.T. was funded by the Russian Science Foundation Grant No. 21-72-20029, https://rscf.ru/project/21-72-20029/. G.L.K. was partially funded by the Ministry of Science and Higher Education of Russian Federation (“The World-Class Research Center: Advanced Digital Technologies”, contract No. 075-15-2022-311 dated 20 April 2022). The research of V.M.M. was partially carried out in accordance with the Strategic Academic Leadership Program “Priority 2030” of the Kazan Federal University.

Reference

Klimchitskaya, G.L.; Korikov, C.C.; Mostepanenko, V.M.; Tsybin, O.Y. Nonequilibrium Casimir–Polder Interaction between Nanoparticles and Substrates Coated with Gapped Graphene. Symmetry 2023, 15, 1580. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Correction: Klimchitskaya et al. Nonequilibrium Casimir–Polder Interaction between Nanoparticles and Substrates Coated with Gapped Graphene. Symmetry 2023, 15, 1580

Funding

Reference

Article Metrics

Citations

Article Access Statistics