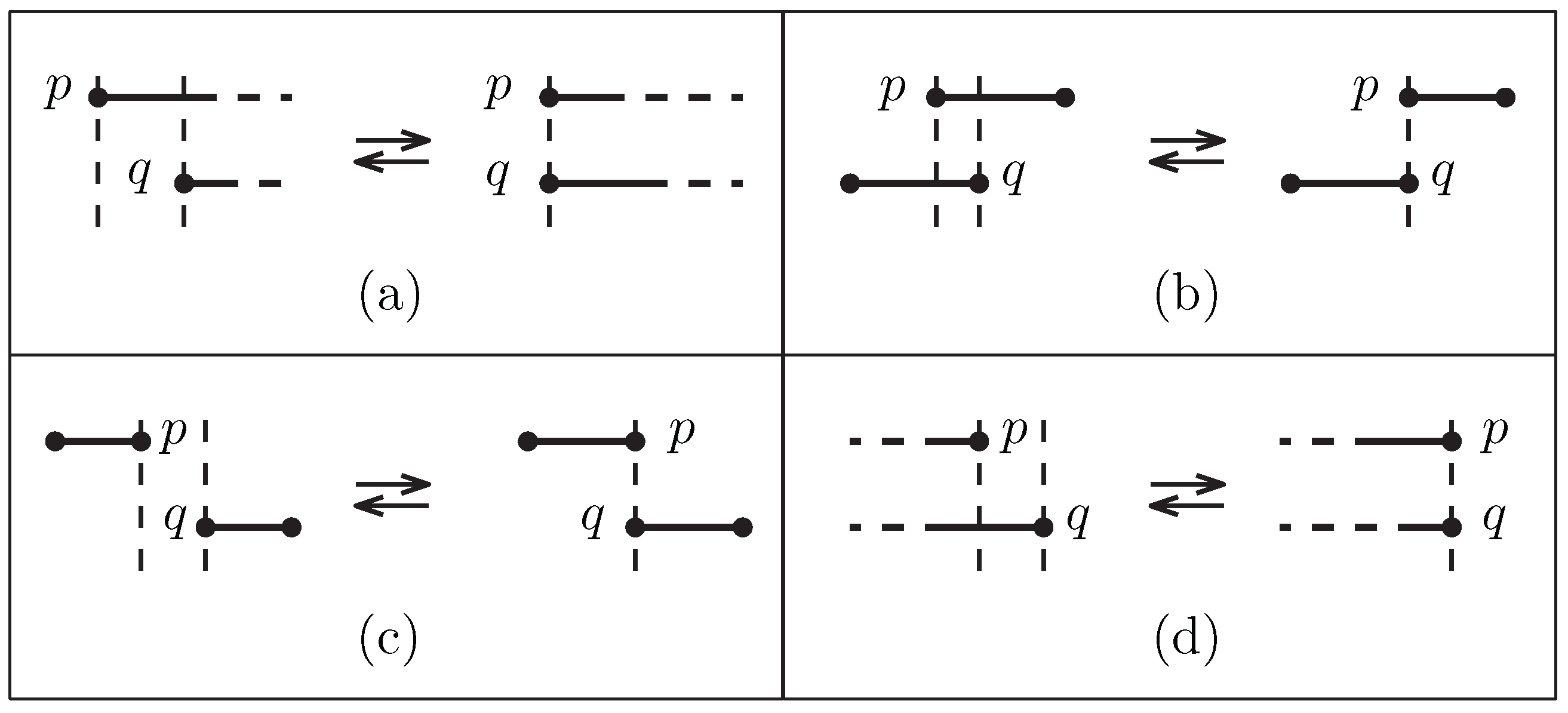Maximum Coverage by k Lines

Abstract

Given a set of n disks in the plane, we study the problem of finding k lines that together intersect the maximum number of input disks. We consider three variants of this problem with the following constraints on the solution: (1) no constraint on the lines, (2) the k lines should be parallel and (3) the k lines should pass through a common point. For $k=2$, we give $O(n^{3}logn)$-time algorithms for all three cases. For any fixed $k\ge 3$, we give an $O\left(n^{3k/2}\right)$-time algorithm for (1). For variants (2) and (3), the running times of our algorithms vary from $O\left(n^4\right)$ to $O\left(n^6\right)$.

1. Introduction

Given a set of n disks in the plane, we study the problem of finding k lines that together intersect the maximum number of input disks. In other words, we want to maximize the number of disks that intersect at least one output line. We study two other variants of this problem, where the k output lines should be parallel, and where the k lines should pass through a common point. The problems that we consider in this paper are the following. (See Figure 1).

Problem 1

(Maximum Coverage by k Lines). Given a set of n disks in the plane and a positive integer k, find k lines that together intersect the maximum number of input disks.

Problem 2

(Maximum Coverage by k Parallel Lines). Given a set of n disks in the plane and a positive integer k, find k parallel lines that together intersect the maximum number of input disks.

Problem 3

(Maximum Coverage by k Lines through a Point). Given a set of n disks in the plane and a positive integer k, find k lines that together intersect the maximum number of input disks and pass through a common point.

In this paper, we give algorithms for the three above problems. We will assume that k is a constant. A summary of our results is given in

Table 1. The running times of our algorithms for Problem 1, 2 and 3 for a constant k. Space usage is $O\left(n\right)$ if not explicitly stated.

	Problem 1	Problem 2	Problem 3
$k=1$	$O\left(n^2\right)$ time, $O\left(n^2\right)$ space
$k=2$	$O(n^{3}logn)$ time	$O(n^{3}logn)$ time	$O(n^{3}logn)$ time
		$O\left(n^3\right)$ time, $O(nlogn)$ space
$k=3$	$O\left(n^{3k/2}\right)$ time	$O\left(n^4\right)$ time	$O(n^{5}logn)$ time
			$O\left(n^5\right)$ time, $O\left(n^2\right)$ space
$k\ge 4$	$O\left(n^{3k/2}\right)$ time	$O\left(n^4\right)$ time	$O\left(n^6\right)$ time

. In particular, for $k=1$, Problem 1, 2 and 3 coincide, and we give an $O\left(n^2\right)$-time algorithm. Given a set of points in the plane, the problem of finding a line that covers the maximum number of points is 3SUM-hard [1], so an $O\left(n^{\alpha }\right)$-time algorithm for any $\alpha <2$ is currently out of reach for Problem 1, 2 and 3, even when $k=1$.

Related Work

The one-dimensional version of our problem, where we want to find a set of k points that intersect the maximum number of input intervals, is known as the partial interval hitting set problem [2]. Jansen et al. [3] and Chrobak et al. [4] gave an $O\left(k{n}^2\right)$-time algorithm.

Dumitrescu and Jiang [5] showed that the problem of hitting the maximum number of input points with k lines is APX-hard. In this paper, we consider the more general problem of hitting the maximum number of disks in the plane using k lines. To the best of our knowledge, the problem of finding k lines that together intersect the maximum number of input disks (or other geometric figures) has not been studied yet.

In the most general, combinatorial setting, we are given a collection of subsets of a larger set, and we want to find k such subsets whose union is the largest. This problem is known as the maximum coverage problem, and the simple greedy algorithm provides a $1-1/e$ approximation of the optimum [6]. Another maximum coverage problem was studied by Jin et al. They considered the problem of covering a maximum number of input points by k copies of the same rectangle or disk [7]. They provide linear-time approximation schemes, and give references to related problems.

The combinatorics of intersections between lines and balls have also been studied. In particular, Ha et al. showed that, for n disjoint spheres, if $n\ge 7$, then at most three different permutations of the spheres can appear along a line that crosses them all [8].

One motivation for studying maximum coverage by lines is to find line patterns in a two-dimensional dataset. Input disks may represent data points, each given with an imprecision that is equal to their radii. Other computational geometry problems have been studied under this imprecision model, such as the Hausdorff distance [9], the Delaunay triangulation [10] and the discrete Fréchet distance [11].

Our problem of finding line patterns is related to edge detection, which is a fundamental problem in image processing and computer vision, where the goal is to extract edges, lines or junctions from images [12]. Therefore, our algorithms could find applications in 3D reconstruction or image registration, by identifying the main lines or edges in the image. Our algorithms for lines through a point, or parallel lines, could help find symmetries in such an image.

Our algorithms could also be used for a facility location problem wherein one wants to place line facilities that are close to a set of demand regions; for instance, we may want to place k satellites at different orbits, that together cover the largest possible number of population centers. Line facility location has been studied by Cheung and Daescu, in the context of weighted regions [13].

2. Preliminaries and Notations

2.1. Partial Interval Hitting Set

In Section 4 and Section 5, we use a reduction to the partial interval hitting set problem [2]. Given a set of n closed intervals $I_j=[s_j,t_j]$ for $j=1,\dots ,n$ on the real line, and a positive integer $\gamma$, the partial interval hitting set problem, shortly $\mathsf{PIHS}$, is to find a set H of $\gamma$ points that together hit the maximum number of intervals. We say that a point q hits an interval I if $q\in I$.

Chrobak et al. ([4] Section 3.1) gave a dynamic-programming algorithm for this problem which runs in $O\left(\gamma n^2\right)$ time. Their algorithm uses $O\left(n^2\right)$ space for pre-computing $O\left(n^2\right)$ values. We show in Section 6 that we can reduce the space usage to $O\left(\gamma n\right)$ while keeping the same time bound. In addition, when $\gamma =2$, we show that we can maintain the solution for intervals with moving endpoints in $O\left(n\right)$ time per event using $O\left(n^2\right)$ space.

2.2. Notations

We denote by $\mathcal{D}$ a set of n closed disks in the plane. We will consider that a point is a disk of radius 0. We will assume that $\bigcap \mathcal{D}=\varnothing$, as otherwise, a trivial solution to our problem is to take a line that intersects $\bigcap \mathcal{D}$.

The orientation $\theta$ of a line is the angle that it forms with horizontal. More precisely, it is the angle swept from a horizontal line to ℓ in counterclockwise direction. Therefore, we have $\theta \in [0,\pi )$. Given an orientation $\theta \ne \pi /2$, and a disk $D\in \mathcal{D}$, the lowest line with orientation $\theta$ that is not below any point of D is called the upper tangent to D with orientation $\theta$. Similarly, the highest line with orientation $\theta$ that is not above any point of D is called the lower tangent to D with orientation $\theta$. When $\theta =\pi /2$, the upper tangent to D is the leftmost vertical line that is not to the left to any point of D, and the lower tangent to D is the rightmost vertical line that is not to the right to any point of D. A line is said to be tangent to D if it is either the lower or the upper tangent to D for some orientation. A line that is tangent to two different disks in $\mathcal{D}$ is called a common tangent of $\mathcal{D}$.

Given a directed line $\overrightarrow{\ell }$ in the plane, the orientation of $\overrightarrow{\ell }$ denotes the angle swept from the x-axis to $\overrightarrow{\ell }$ in the counterclockwise direction. The orientation of a directed line is in $[0,2\pi )$. Given a disk D and an angle $\theta \in [0,2\pi )$, the directed line tangent to D with orientation $\theta$ is the directed line with orientation $\theta$ that intersects the boundary of D and that has no point of D to its right.

For a disk D and a line ℓ tangent to it, we refer to the process of rotating ℓ around D while keeping it tangent to D as rotating ℓ tangentially around D.

We say that two disks $D_1$ and $D_2$ cross if $D_1\cap D_2\ne \varnothing$, and neither $D_1\subset D_2$ nor $D_2\subset D_1$. In this case, $D_1$ and $D_2$ have two common tangents. Two disks in $\mathcal{D}$ have at most four common tangents, which happens when $D_1$ and $D_2$ are disjoint and have a positive radius. Two disks are said to be tangent if their boundaries intersect at exactly one point. We allow disks to be points, and hence have radius 0.

3. Maximum Coverage by k Lines

Given a set $\mathcal{D}$ of n disks in the plane and a positive integer k, we would like to find k lines that together intersect the maximum number of input disks. In this section, we give efficient algorithms for this problem by reducing it to the problem of computing the depth of a collection of boxes, which is related to Klee’s problem [14].

3.1. A First Algorithm

We begin with the observation below.

Lemma 1.

Let ℓ be a line tangent to a disk $D\in \mathcal{D}$. Suppose that there is no common tangent between D and any other disk in $\mathcal{D}$. Then, there is a common tangent ${\ell }^{\prime }$ between two disks in $\mathcal{D}$ such that any disk intersected by ℓ is intersected by ${\ell }^{\prime }$.

Proof. 

As there is no common tangent between D and any other disk in $\mathcal{D}$, each disk in $\mathcal{D}$ is either contained in D or contains D. There must be more than one disk contained in D, as otherwise, D or the disk that it contains, if it exists, is a subset of $\bigcap \mathcal{D}$, which we assumed to be empty (see Section 2.2), a contradiction.

There must be a pair of disks $D_1$ and $D_2$ that are both contained in D, and either cross or are disjoint. Otherwise, the j disks contained in D would form a chain of inclusions $D_{i_1}\subset D_{i_2}\subset \cdots \subset D_{i_j}$, and we would have $D_{i_1}\subset \bigcap \mathcal{D}$. This is a contradiction, as we assumed that $\bigcap \mathcal{D}=\varnothing$.

We take ${\ell }^{\prime }$ to be a common tangent to $D_1$ and $D_2$. Then, ${\ell }^{\prime }$ intersects all the disks that contain $D_1$, and since ℓ only intersects these disks, the set of disks intersected by ${\ell }^{\prime }$ is a superset of those intersected by ℓ. □

It follows that we can choose the k lines of our solution to be common tangents between disks in $\mathcal{D}$:

Lemma 2.

There exists an optimal set of k lines, each of which is a common tangent of $\mathcal{D}$.

Proof. 

Let ${\ell }_1$ be a line in an optimal set of k lines. We translate ${\ell }_1$ in a direction orthogonal to itself until it first becomes tangent to some disk $D_1\in \mathcal{D}$. Let ${\ell }_2$ denote this translated line.

Suppose that there is a common tangent between $D_1$ and some other disk in $\mathcal{D}$. We rotate ${\ell }_2$ tangentially around $D_1$ until it first becomes a line ${\ell }_3$ tangent to some other disk $D_2$. Then, the set of disks intersected by ${\ell }_3$ contains the set of disks intersected by ${\ell }_1$. Therefore, we can replace ${\ell }_1$ with ${\ell }_3$ in our optimal solution.

On the other hand, if there is no common tangent between $D_1$ and any other disk in $\mathcal{D}$, then by Lemma 2, we can replace ${\ell }_1$ in our solution with a line ${\ell }^{\prime }$ that is a common tangent. We repeat this process until all the lines in our solution are common tangents. □

Therefore, the maximum intersection problem can be solved as follows. We first compute all the common tangents of $\mathcal{D}$. Among these $O\left(n^2\right)$ lines, we choose k of them and count the number of disks that are intersected by the chosen lines. Then, we return the k lines that intersect the largest number of disks. It takes $O\left(n^{2k+1}\right)$ time in total. In the two sections below, we present more efficient algorithms.

3.2. Maximum Coverage by One Line

In this section, we assume that $k=1$. We give an $O\left(n^2\right)$-time algorithm to solve the maximum coverage problem, which improves on the $O\left(n^3\right)$-time algorithm described above. By Lemma 2, we only need to find a common tangent of $\mathcal{D}$ that intersects the maximum number of disks in $\mathcal{D}$. Using the duality transformation, we can find an optimal line and the set of disks intersected by this line in $O\left(n^2\right)$ time as follows:

Theorem 1.

Given a set $\mathcal{D}$ of n disks in the plane, we can find a line that intersects the maximum number of disks in $O\left(n^2\right)$ time.

Proof. 

We use a standard point-line duality transformation ([15] Chapter 8). A line $\ell :y=ax-b$ in the primal plane corresponds to a point ${\ell }^{*}=(a,b)$ in the dual plane. For a disk D, let ${\mathcal{U}}_D$ be the set of all upper tangents to D. Then, the set of points ${\mathcal{U}}_D^{*}=\{{\ell }^{*}:\ell \in {\mathcal{U}}_D\}$ forms a curve in the dual plane. Analogously, we define ${\mathcal{V}}_D$ to be the set of all lower tangents to D and consider the curve ${\mathcal{V}}_D^{*}$ formed by the points $\{{\ell }^{*}:\ell \in {\mathcal{V}}_D\}$. We compute these two dual curves for all disks in $\mathcal{D}$ and compute the arrangement of them. As these curves are algebraic curves of constant degree, their arrangement $\mathcal{A}$ has a $O\left(n^2\right)$ size, and we can compute $\mathcal{A}$ in $O\left(n^2\right)$ time [16].

Let $D\in \mathcal{D}$. We rotate an upper tangent ℓ of D tangentially around D and update the number of disks intersected by ℓ each time it becomes tangent to another disk, or ceases to be tangent to it. In the dual plane, this simply means that we follow the dual curve ${\mathcal{U}}_D^{*}$ in $\mathcal{A}$, and add or remove the disk corresponding to any dual curve that we cross. Therefore, it can be achieved in $O\left(1\right)$ time per vertex of $\mathcal{A}$ that is along ${\mathcal{U}}_D^{*}$, and an additional $O\left(n\right)$ time to find the number of disks that are intersected when we start rotating ℓ.

We perform the same traversal for each disk in $\mathcal{D}$, and we perform it for lower tangents as well. In total, it takes time $O\left(n^2\right)$ as $\mathcal{A}$ has a size $O\left(n^2\right)$. During this traversal, we record the best line that was found so far, and we return it after all the traversals are completed. □

3.3. Maximum Coverage by $k\ge 2$ Lines

By Lemma 2, there is a subset $\overline{\mathcal{D}}=\{D_1,\cdots ,D_k\}\subseteq \mathcal{D}$ of size k and an optimal solution ${\ell }_1,\cdots ,{\ell }_k$ such that each line ${\ell }_i$ is tangent to $D_i$. We show that, if we know $\overline{\mathcal{D}}$, we are able to find an optimal solution by reducing the problem to the depth problem [17]: Given a set of n boxes in ${\mathbb{R}}^d$, find a point $p\in {\mathbb{R}}^d$ that maximizes the number of boxes containing p. It is known that the depth problem can be solved in $O(nlogn)$ time when $d=2$ [18], and in $O\left(n^{d/2}\right)$ time when $d>2$ using linear space [17].

Lemma 3.

Given a subset $\overline{\mathcal{D}}=\{D_1,\cdots ,D_k\}\subset \mathcal{D}$ of size k, we can find k lines ${\ell }_1,\cdots ,{\ell }_k$ such that each line ${\ell }_i$ is tangent to $D_i$ and the number of intersected disks in $\mathcal{D}$ is maximized in $O(nlogn)$ time when $k=2$ and in $O\left(n^{k/2}\right)$ time when $k\ge 3$.

Proof. 

We first show that finding k such tangent lines can be reduced to the depth problem. For a disk $D\in \overline{\mathcal{D}}$, let $\overrightarrow{\ell }\left(\theta \right)$ be the directed line tangent to D with orientation $\theta$. Let $D^{\prime }$ be another disk in $\mathcal{D}\backslash \overline{D}$. While increasing $\theta$ from 0 to $2\pi$, the tangent $\overrightarrow{\ell }\left(\theta \right)$ intersects $D^{\prime }$ in at most two intervals of angles in $[0,2\pi ]$. We say that these intervals are induced by $(D,D^{\prime })$.

For each disk $D^{\prime }\in \mathcal{D}\backslash \overline{\mathcal{D}}$, we compute the intervals induced by $(D,D^{\prime })$ for every $D\in \overline{\mathcal{D}}$. Then, there are at most $2k$ such intervals corresponding to $D^{\prime }$.

Let $i\in \{1,\cdots ,l\}$ and let $S_i,S_i^{\prime }$ be the intervals induced by $(D_i,D^{\prime })$, where $S_i^{\prime }$ is possibly empty. We associate to these intervals $S_i$ and $S_i^{\prime }$ the slab consisting of the points $({\theta }_1,\cdots ,{\theta }_k)\in {[0,2\pi ]}^k$ such that $min{S}_i\le {\theta }_i\le max{S}_i$, and if $S_i^{\prime }\ne \varnothing$, the slab consisting of the points that satisfy $min{S}_i^{\prime }\le {\theta }_i\le max{S}_i^{\prime }$. These slabs are orthogonal to the ${\theta }_i$-axis. As $k=O\left(1\right)$, the union of these slabs for all disks in $\overline{\mathcal{D}}$ has constant complexity. More precisely, the union of these slabs is the union of $O\left(1\right)$ interior-disjoint boxes. (See Figure 2). We replace the union of the slabs by these boxes.

We repeat this for every disk $D^{\prime }\in \mathcal{D}\backslash \overline{\mathcal{D}}$ and obtain $O\left(n\right)$ boxes. Then, for any sequence of angles $({\theta }_1,\cdots ,{\theta }_k)$ of the directed tangent lines, the number of boxes containing $({\theta }_1,\cdots ,{\theta }_k)$ is the number of disks in $\mathcal{D}\backslash \overline{D}$ intersected by the k tangent lines. Therefore, finding an optimum solution for a fixed $\overline{\mathcal{D}}$ reduces to the depth problem for $O\left(n\right)$ boxes.

One issue here is that we should count only once the boundary between two boxes corresponding to the same disk $D^{\prime }$, but in degenerate cases where the boundaries of two boxes overlap, we need to count twice their common boundary. The maximum depth algorithm by Chan [17] can handle this situation. □

For every subset of k distinct disks of $\mathcal{D}$, we find a set of k lines such that each line is tangent to a different disk in this subset, and that together intersect the maximum number of disks in $\mathcal{D}$. Among those $O\left(n^k\right)$ sets of lines, we choose one with the largest number of intersected disks, which is an optimal solution. It follows that:

Theorem 2.

Given a set of n disks in the plane and a positive integer k, we can find k lines that together intersect the maximum number of disks in $\mathcal{D}$ in $O(n^{3}logn)$ time for $k=2$ and in $O\left(n^{3k/2}\right)$ time for $k\ge 3$, using $O\left(n\right)$ space.

4. Maximum Coverage by k Parallel Lines

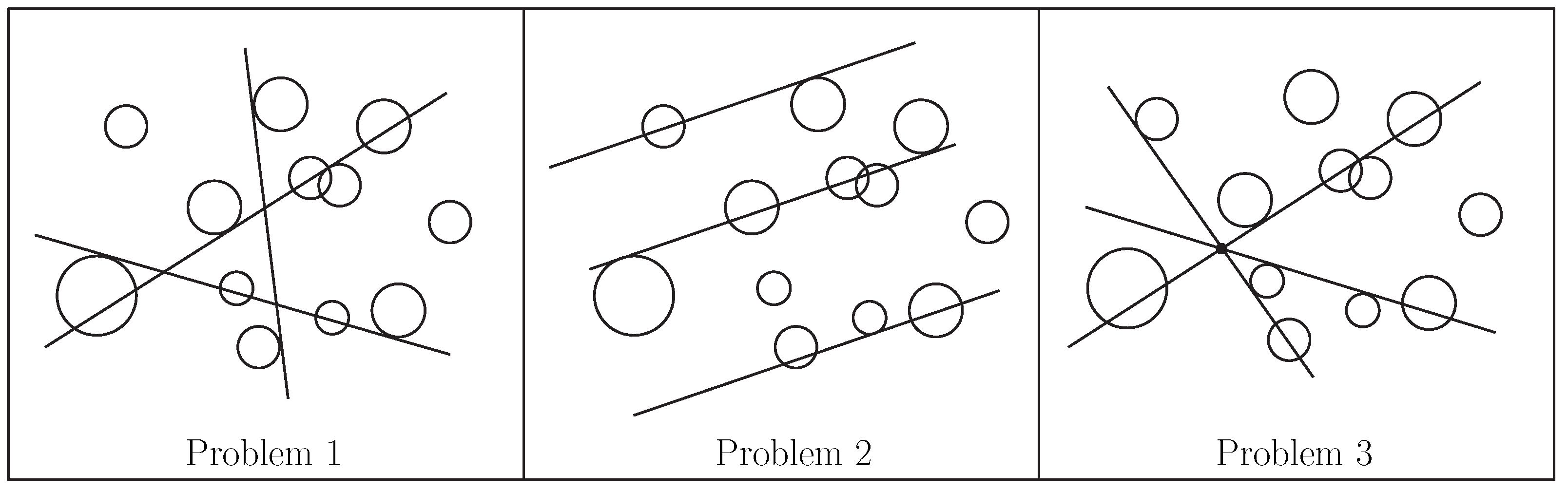
Given a set $\mathcal{D}$ of n disks in the plane and an integer $k\ge 2$, we would like to find k parallel lines that together intersect the maximum number of disks in $\mathcal{D}$. We first show that this problem can be solved by reducing it to the partial interval hitting set problem. Then, we show how to improve the running time for small k.

We begin with an observation about optimal sets of k parallel lines. Given an optimal set $\{{\ell }_1,\dots ,{\ell }_k\}$ of k parallel lines, it is always possible to translate a line of this optimal solution so that the line becomes tangent to an input disk, while keeping the same set of intersected disks. Therefore, we may assume that each line ${\ell }_i$ is tangent to a disk $D_i$, for $i=1,\dots ,k$.

For each $i\in \{1,\cdots ,k\}$, we may assume that there exists a common tangent between $D_i$ and some other disk in $\mathcal{D}$. Otherwise, for each $D\in \mathcal{D}\backslash \left\{D_i\right\}$, we must have $D\subset D_i$ or $D_i\subset D$. Therefore, without loss of generality, the disks $D_1,\cdots ,D_k$ form a chain of inclusion $D_1\subset \cdots \subset D_k$. In addition, all the other disks are either contained in $D_1$ or contain $D_k$. No disk in $\mathcal{D}\backslash \{D_1,\cdots ,D_k\}$ can be contained in $D_1$, as otherwise we could improve the solution by translating ${\ell }_1$ until it crosses this disk. It follows that $D_1=\bigcap \mathcal{D}$, contradicting our assumption that $\bigcap \mathcal{D}=\varnothing$.

We then rotate ${\ell }_i$ tangentially around $D_i$ simultaneously for all $i=1,\dots ,k$ until one of the k lines becomes tangent to another disk or ceases to be tangent to it. Let ${\ell }_1^{\prime },\dots ,{\ell }_k^{\prime }$ denote the k lines after the rotation. As the set of disks intersected by ${\ell }_i^{\prime }$ contains the set of disks intersected by ${\ell }_i$ for all $i=1,\dots ,k$, we can replace our optimal set of parallel lines with $\{{\ell }_1^{\prime },\dots ,{\ell }_k^{\prime }\}$. Thus we have the following observation.

Observation 1.

There exists an optimal set of k parallel lines such that every line is tangent to an input disk and at least one of them is a common tangent of $\mathcal{D}$.

Once we know the direction of an optimal set of lines, we project the disks in $\mathcal{D}$ onto a line orthogonal to this direction. We obtain n closed intervals on this line. The problem of finding k lines with this orientation that intersect the maximum number of disks is equivalent to the problem of finding k points that together intersect the maximum number of intervals, which is the $\mathsf{PIHS}$ problem. In Section 6, Lemma 6, we show that it can be solved in $O\left(n^2\right)$ time using $O\left(n\right)$ space.

By Observation 1, we have $O\left(n^2\right)$ possible orientations. So we can solve the maximum intersection problem by k parallel lines in $O\left(n^4\right)$ time as k is a constant. When $k=2$, we give two different algorithms which improve the running time and we provide a space-time trade-off.

Improvements for $k=2$

Let $D_1$ and $D_2$ be two disks in $\mathcal{D}$. Let ${\ell }_1$ and ${\ell }_2$ be two parallel lines such that ${\ell }_i$ is tangent to $D_i$ for $i=1,2$. For $i=1,2$, we maintain an array of $O\left(n\right)$ Booleans that records for each disk in $\mathcal{D}$ whether it is intersected by ${\ell }_i$, and we keep a counter for the number of disks in $\mathcal{D}$ which are intersected by ${\ell }_1$ or ${\ell }_2$. Now we simultaneously rotate the two lines tangentially around $D_1$ and $D_2$, respectively.

Whenever ${\ell }_1$ becomes tangent to a disk other than $D_1$, an element of the boolean list for ${\ell }_1$ needs to be updated and the number of intersected disks may change. The same holds for ${\ell }_2$ and $D_2$. We call this an event. As any two disks have at most 4 common tangents, there are $O\left(n\right)$ events in total. We precompute them, and sort them according to the orientation of the common tangents that they correspond to in $O(nlogn)$ time.

For each event, the number of disks in $\mathcal{D}$ intersected by ${\ell }_1$ or ${\ell }_2$ increases or decreases by at most one, and we can update the boolean lists and compute the number of intersected disks in $O\left(1\right)$ time. There are $O\left(n\right)$ events in total, so it takes $O\left(n\right)$ time.

We repeat this for every pair of disks in $\mathcal{D}$ and find an event where the number of intersected disks is maximized. By Observation 1, the two parallel lines ${\ell }_1$ and ${\ell }_2$ corresponding to this event is an optimal solution. Thus, we obtain the following result.

Lemma 4.

Given a set $\mathcal{D}$ of n disks in the plane, we can find two parallel lines that together intersect the maximum number of disks in $\mathcal{D}$ in $O(n^{3}logn)$ time using $O\left(n\right)$ space.

We can improve the running time to $O\left(n^3\right)$ time using $O(nlogn)$ space as follows.

• Let $T=\lfloor logn\rfloor$. Partition the disks into $\lceil n/T\rceil$ disjoint groups, each consisting of T disks, except possibly the last group containing less than T disks. Let $\mathcal{G}=\{G_1,\dots ,G_{\lceil n/T\rceil }\}$ be the set of groups.
• For every subset of $\mathcal{S}\subseteq \mathcal{G}$ of size at most two,

  (a)

  Let ${\mathcal{D}}_{\mathcal{S}}=\bigcup \mathcal{S}$. For each disk $D\in {\mathcal{D}}_{\mathcal{S}}$, compute the sorted list of the other disks in $\mathcal{D}$ intersected by the tangent line rotating around D in $O(nlogn)$ time. It takes $O(Tnlogn)$ time for all disks in ${\mathcal{D}}_{\mathcal{S}}$.

  (b)

  For a fixed pair $D_1,D_2\in {\mathcal{D}}_{\mathcal{S}}$, we can find the maximum number of disks intersected by ${\ell }_1$, ${\ell }_2$ in $O\left(n\right)$ time as the ordering of the events has been precomputed. So over all the pairs $D_1,D_2\in {\mathcal{D}}_{\mathcal{S}}$, it takes $O\left(n{T}^2\right)$ time to find optimal lines ${\ell }_1$, ${\ell }_2$.

We consider $O\left({(n/T)}^2\right)$ subsets of $\mathcal{G}$, and we spend $O(Tnlogn)+O\left(n{T}^2\right)$ time for each subset. Thus we spend $O((n^{3}logn)/T+n^3)$ time in total, which is $O\left(n^3\right)$ time.

Theorem 3.

Given a set of n disks in the plane and a positive integer k, we can find k parallel lines that together intersect the maximum number of disks in $\mathcal{D}$ in $O\left(n^4\right)$ time using $O\left(n\right)$ space. For $k=2$, we can find such two parallel lines in $O(n^{3}logn)$ time using $O\left(n\right)$ space and in $O\left(n^3\right)$ time using $O(nlogn)$ space.

5. Maximum Coverage by k Lines through a Point

Concurrent lines are lines that meet at a common point, called their concurrency point. Given a set $\mathcal{D}$ of n disks in the plane and a positive integer k, we want to find k concurrent lines that together intersect the maximum number of disks in $\mathcal{D}$. We can solve this problem in $O\left(n^2\right)$ time by Theorem 1 for $k=1$.

For $k=2$, a simple modification of the algorithm from Theorem 2 gives a solution in $O(n^{3}logn)$ time. The idea is the following. We use the plane-sweep algorithm by Asano and Imai to compute the depth of our set of rectangles [18]. We need to rule out the solutions consisting of two parallel lines, which correspond to points along the diagonal $x=y$ in our arrangement of rectangles. So at each event $x=x_i$ of the sweep, we add a negative weight $-2$ to the point $(x_i,x_i)$, which guarantees that it will not be returned as an optimal solution.

Therefore, we consider the case where $k\ge 3$, and we make the assumption that no two intersecting lines together intersect all the disks in $\mathcal{D}$, as otherwise we can simply solve the problem using our algorithm for $k=2$.

Lemma 5.

Suppose that no two intersecting lines together intersect all the disks in $\mathcal{D}$. Then there exists an optimal set of k lines for $k\ge 3$ such that every line is tangent to an input disk and at least two of them are common tangents of $\mathcal{D}$.

Proof. 

Let ${\mathcal{L}}^{*}=\{{\ell }_1^{*},\dots ,{\ell }_k^{*}\}$ be an optimal solution to our problem. Let $p^{*}$ be their concurrency point. When we rotate a line ${\ell }_i^{*}$ about $p^{*}$, as ${\ell }_i^{*}$ does not intersect all the disks in $\mathcal{D}$, it must at some point become tangent to a disk in $\mathcal{D}$. So we rotate each line ${\ell }_i^{*}$ clockwise until it first becomes tangent to some disk in $\mathcal{D}$, obtaining a line ${\ell }_i$. Then $\mathcal{L}=\{{\ell }_1,\cdots ,{\ell }_k\}$ is still an optimal solution, and each line ${\ell }_i$ is tangent to a disk $D_i\in \mathcal{D}$.

We move the intersection point $p=\bigcap \mathcal{L}$ along ${\ell }_1$, while rotating each ${\ell }_i$, $i\ge 2$ tangentially around $D_i$. By our assumption, no line parallel to ${\ell }_1$ intersects all the disks in $\mathcal{D}$. So ${\ell }_i$ must become tangent to some disk in $\mathcal{D}\backslash \left\{D_i\right\}$ at some point for every $i\ge 2$. Let $p^{\prime }$ be the point corresponding to the first such event, when p moves in either direction along ${\ell }_1$. Then we obtain a new optimal solution ${\mathcal{L}}^{\prime }=\{{\ell }_1^{\prime },\cdots ,{\ell }_k^{\prime }\}$ such that ${\ell }_j^{\prime }$ is a common tangent of $\mathcal{D}$ for some j with $2\le j\le k$. If ${\ell }_1$ is a common tangent of $\mathcal{D}$, we are done. Otherwise, we apply the same argument as above to ${\ell }_j^{\prime }$, obtaining a second common tangent. □

By Lemma 5, there exists an optimal set of k lines whose concurrency point is the intersection of two common tangents of $\mathcal{D}$. For every pair of common tangents $(\ell ,{\ell }^{\prime })$, we consider the point of intersection as a candidate for being the concurrency point of an optimal solution. Thus we have $O\left(n^4\right)$ candidates for being the concurrency point of an optimal solution.

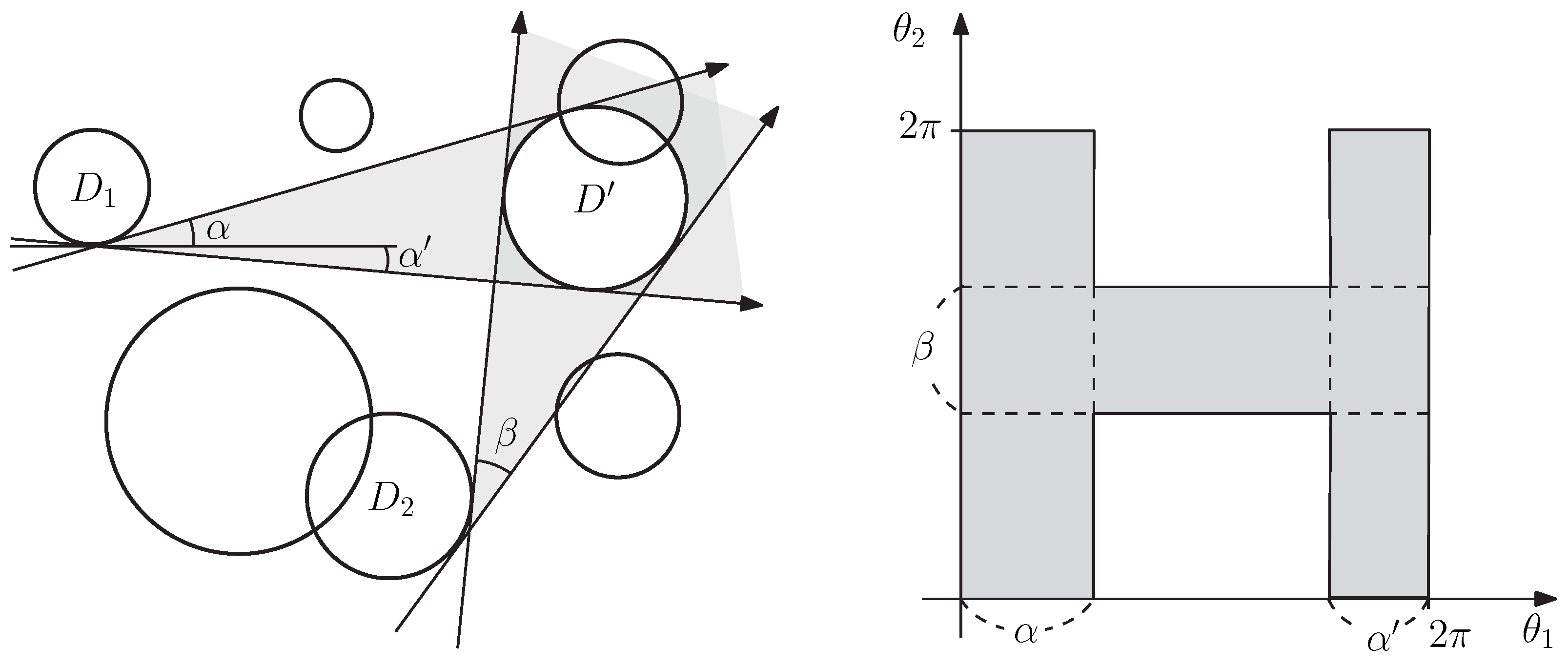
Once we pick a concurrency candidate p, we can reduce our problem to the partial interval hitting set problem. Let ℓ and ${\ell }^{\prime }$ be the two common tangents that intersect at p. Without loss of generality, we assume that ℓ is parallel to the x-axis. Let $\overline{\mathcal{D}}$ be the set of disks in $\mathcal{D}$ which are intersected by neither ℓ nor ${\ell }^{\prime }$. For every disk D in $\overline{\mathcal{D}}$, let $I_D\in [0,\pi )$ be the interval of angles $\theta$ such that the line through p with orientation $\theta$ intersects D. Note that $I_D$ is a closed interval in $[0,\pi )$. Now we solve $\mathsf{PIHS}$ for these intervals $I_D$ for $D\in \overline{\mathcal{D}}$, and $\gamma =k-2$. Let $\mathsf{\Gamma }=\{{\theta }_1,\dots ,{\theta }_{k-2}\}$ denote an optimal solution for the problem. Let ${\mathcal{L}}_p$ denote the set of $k-2$ lines of orientation ${\theta }_1,\dots ,{\theta }_{k-2}$ passing through p. Since ${\mathcal{L}}_p$ is a set of $k-2$ lines that pass through p and that together intersect the maximum number of disks in $\overline{\mathcal{D}}$, ${\mathcal{L}}_p\cup \{\ell ,{\ell }^{\prime }\}$ is an optimal set of k lines if ℓ and ${\ell }^{\prime }$ are contained in an optimal solution. Therefore, we can compute an optimal set of k concurrent lines by repeating this process for every concurrency candidate.

For $k=3$, we solve $\mathsf{PIHS}$ for $\gamma =1$, so we need to find a point that hits the maximum number of intervals, which can be done in $O(nlogn)$ time by a simple scan after sorting the endpoints of the intervals. For $k\ge 4$, Chrobak et al. ([4] Section 3.1) show that $\mathsf{PIHS}$ can be solved in $O\left(n^2\right)$ time, and we show that it can be done using only $O\left(n\right)$ space in Section 6. Thus we can solve this problem in $O(n^{5}logn)$ time and $O\left(n\right)$ space for $k=3$, and in $O\left(n^6\right)$ time and $O\left(n\right)$ space for $k\ge 4$.

We now show how the running time can be reduced to $O\left(n^5\right)$ for $k=3$, using $O\left(n^2\right)$ space. Our approach is based on a result presented in Section 6 that shows how to update a solution to $\mathsf{PIHS}$ for a set of intervals with moving endpoints where an event occurs when two endpoints collide or separate. We show in Lemma 7 that the solution can be updated in $O\left(n\right)$ time per event.

Let ℓ denote a common tangent of $\mathcal{D}$, and assume without loss of generality that ℓ is parallel to the x-axis. We show that we can find two lines ${\ell }_1$ and ${\ell }_2$ such that their intersection point lies on ℓ, and the number of disks in $\mathcal{D}$ intersected by $\{\ell ,{\ell }_1,{\ell }_2\}$ is maximized, in $O\left(n^3\right)$ time. As the set of disks intersected by ℓ does not change for a fixed line ℓ, we do not take this set of disks into consideration.

Let ${\overline{\mathcal{D}}}_{\ell }$ denote the set of disks in $\mathcal{D}$ that do not intersect ℓ. For a point p on ℓ, let ${\mathcal{I}}_p$ be the collection of intervals which are defined for ${\overline{\mathcal{D}}}_{\ell }$ around p in the same manner as we explained in the reduction step above. We solve $\mathsf{PIHS}$ for ${\mathcal{I}}_p$ and $\gamma =2$, and let $\{{\theta }_1,{\theta }_2\}$ be the solution. Let ${\ell }_{{\theta }_1}$ and ${\ell }_{{\theta }_2}$ denote the two lines through p with orientations ${\theta }_1$ and ${\theta }_2$, respectively. These two lines together intersect the maximum number of disks in ${\overline{\mathcal{D}}}_{\ell }$ while passing through p.

Now suppose that we move p along ℓ. The endpoints of the intervals in ${\mathcal{I}}_p$ will move along the real line. A solution to $\mathsf{PIHS}$ changes only if an event occurs, as otherwise the ordering of endpoints of the interval remains the same. The key point is that an event occurs only if p is on a concurrency candidate for ℓ. The reason is that, for a point $q\in \ell$, there exists two intervals in ${\mathcal{I}}_q$ such that two endpoints from distinct intervals lie on the same point if and only if there exists a line which passes through q and is tangent to two disks in $\mathcal{D}$.

There are $O\left(n^2\right)$ concurrency candidates along ℓ in total, and they can be precomputed and sorted along ℓ in $O(n^{2}logn)$ time. From the pairs of disks which determine each concurrency candidate on ℓ, the corresponding event can also be found directly. We handle all the events in order and store the best two lines, ${\ell }_{{\theta }_1^{*}}$ and ${\ell }_{{\theta }_2}^{*}$, which together intersect the maximum number of disks in ${\overline{\mathcal{D}}}_{\ell }$. In Section 6, Lemma 7, we show how to handle each event in $O\left(n\right)$ time. Thus, we can find ${\ell }_{{\theta }_1^{*}}$ and ${\ell }_{{\theta }_2}^{*}$ in $O\left(n^3\right)$ time in total.

We repeat this for every common tangent of $\mathcal{D}$. By Lemma 5, there always exists an optimal set of k lines such that one of the lines is a common tangent to two disks in $\mathcal{D}$. Thus, the best set of k lines found during the repetition is an optimal solution. Hence, we have just proved the following theorem.

Theorem 4.

Given a set of n disks in the plane and a positive integer k, we can find k lines that pass through a common point and that together intersect the maximum number of disks in $O\left(n^6\right)$ time using $O\left(n\right)$ space. When $k=3$, we can solve this problem in $O(n^{5}logn)$ time using $O\left(n\right)$ space, and $O\left(n^5\right)$ time using $O\left(n^2\right)$ space.

6. On the Partial Interval Hitting Set Problem

As we mentioned above, given n closed intervals $I_j=[s_j,t_j]$, $j=1,\dots ,n$ on the real line, and a positive integer $\gamma$, the partial hitting set problem is to find a set H of $\gamma$ points on the real line that together hit the maximum number of intervals. We say that a point q hits an interval I if $q\in I$ [2]. It is easy to see that, after shifting the solution points to the right until they each meet a right endpoint, that we may assume that the points in the solution are the right endpoints of $\gamma$ input intervals.

Chrobak et al. ([4] Section 3.1) gave a dynamic-programming algorithm for this problem that runs in $O\left(\gamma n^2\right)$ time. We give a sketch of their algorithm. First, it sorts the intervals using their right endpoints and relabels them so that $t_1\le t_2\le \dots \le t_n$. Let $T_{h,b}$ be the maximum number of input intervals that can be hit by a subset $H\subseteq \{t_1,t_2,\dots ,t_b\}$ such that $\left|H\right|\le h$ and $t_b\in H$, where $h\in \{1,2,\dots \gamma \}$ and $b\in \{1,2,\dots ,n\}$. Let $w_{a,b}$ be the number of intervals $I_i$ such that $t_a<s_i\le t_b\le t_i$, namely the intervals that are hit by $t_b$ but not by $t_a$. We first set $T_{1,b}$ to the number of intervals that contain $t_b$. Similarly, we set $T_{h,1}$ to the number of intervals that contain $t_1$. Then, for every $h=2,3,\dots ,\gamma$ and for every $b=2,3,\dots ,n$, we can compute $T_{h,b}$ using the recurrence relation $T_{h,b}={max}_{a<b}\{T_{h-1,a}+w_{a,b}\}$.

The output value is ${max}_b{T}_{\gamma ,b}$. Chrobak et al. use $O\left(n^2\right)$ space as their algorithm precomputes all values $w_{a,b}$ in time $O\left(n^2\right)$. We show how the space usage can be reduced to $O\left(\gamma n\right)$ without increasing the time bound.

Lemma 6.

Given n closed intervals on the real line, and a positive integer γ, we can find a set of γ points on the line that together hit the maximum number of intervals in $O\left(\gamma n^2\right)$ time using $O\left(\gamma n\right)$ space.

Proof. 

We first compute the sorted list of the interval endpoints in increasing order. We let $T_{h,1}$ be the number of intervals that contain $t_1$ for $h=1,\dots ,\gamma$. These values can be computed in $O\left(n\right)$ time. For a fixed b with $1<b\le n$, $T_{h,b}$ can be computed for all $h=1,\dots ,\gamma$ in $O\left(\gamma n\right)$ time once $T_{h,i}$ and $w_{i,b}$ are computed for all $h=1,\dots ,\gamma$ and all $i=1,\dots ,b-1$.

We show that $w_{i,b+1}$ for all $i=1,\dots ,b$ can be computed in (amortized) $O\left(n\right)$ time once $w_{i,b}$ is computed for all $i=1,\dots ,b-1$. For any fixed b with $1\le b<n$, let $S_b$ be the number of intervals $I_i$ such that $t_b<s_i\le t_{b+1}$, and let $E_b$ be the number of intervals $I_i$ such that $t_i=t_b$. Let $E_b^a$ be the number of intervals $I_i$ such that $t_a<s_i<t_i=t_b$. For any integers $a,b$ with $1\le a<b\le n$, $w_{a,b+1}=w_{a,b}+S_b-E_b^a$. Thus, $S_b$ and $E_b^i$ for all $i=1,\dots ,b-1$ must be computed in advance when we compute $w_{i,b+1}$ from $w_{i,b}$ for all $i=1,\dots ,b-1$. By scanning the sorted list of interval endpoints, we can compute $S_b$ in $O\left(S_b\right)$ time and $E_b^i$ for all $i=1,\dots ,b-1$ in $O(n·E_b)$ time. So we can compute $w_{i,b+1}$ for all $i=1,\dots ,b-1$ in $O(S_b+n·E_b)$ time. Additionally, we set $w_{b,b+1}=S_b$.

For every $b=2\dots ,n$, we compute $w_{a,b}$ for all $a<b$ and then compute $T_{h,b}$ for all h. It takes $O(S_{b-1}+n·E_{b-1}+\gamma n)$ time for every $b=2,\dots ,n$. As ${\sum }_b{S}_b=n$ and ${\sum }_b{E}_b=n$, it takes $O\left(\gamma n^2\right)$ time in total using $O\left(\gamma n\right)$ space. □

We now consider the case where the interval endpoints move along the real line, so each endpoint p is given as a function $p\left(t\right)$ of the time $t\in \mathbb{R}$. For two intervals $I_i$ and $I_j$$(i\ne j)$, let p and q denote two endpoints such that $p\in \{s_i,t_i\}$ and $q\in \{s_j,t_j\}$. Let $t_0\in \mathbb{R}$. If $p\left(t_0^{-}\right)\ne q\left(t_0^{-}\right)$, that is, if for any $t<t_0$ that is close enough to $t_0$ we have $p\left(t\right)\ne q\left(t\right)$, and then $p\left(t_0\right)=q\left(t_0\right)$, we say that p and qcollide. On the other hand, if $p\left(t_0\right)=q\left(t_0\right)$ and $p\left(t_0^{+}\right)\ne q\left(t_0^{+}\right)$, that is, if for any $t>t_0$ that is close enough to $t_0$ we have $p\left(t\right)\ne q\left(t\right)$, then we say that p and q separate. We say that an event occurs when two endpoints collide or separate. An event at time $t_0$ is one of the following types:

($\mathsf{LL}$)

Two points p and q, which are both left endpoints of intervals, collide or separate. (See Figure 3a).

($\mathsf{LR}$)

Two points p and q, where p is the left endpoint of an interval and q is the right endpoint of another interval, satisfy $p\left(t_0^{-}\right)<q\left(t_0^{-}\right)$ and collide at $t_0$, or p and q separate at $t_0$ and $p\left(t_0^{+}\right)<q\left(t_0^{+}\right)$. (See Figure 3b).

($\mathsf{RL}$)

Two points p and q, where p is the right endpoint of an interval and q is the left endpoint of another interval, satisfy $p\left(t_0^{-}\right)<q\left(t_0^{-}\right)$ and collide at $t_0$, or p and q separate at $t_0$ and $p\left(t_0^{+}\right)<q\left(t_0^{+}\right)$. (See Figure 3c).

($\mathsf{R}$)

Two points p and q, which are both right endpoints of intervals, collide or separate. (See Figure 3d).

Lemma 7.

At each event, we can update an optimal solution to $\mathsf{PIHS}$ for $\gamma =2$ in $O\left(n\right)$ time after $O\left(n^2\right)$-time preprocessing using $O\left(n^2\right)$ space.

Proof. 

Let $\mathcal{W}$ denote the table which stores all $w_{a,b}$, and let $\mathcal{T}$ denote the table which stores all $T_{h,b}$. For $\gamma =2$, we show that an event where two interval endpoints p and q collide or separate can be handled in $O\left(n\right)$ time so that all elements of $\mathcal{W}$ and $\mathcal{T}$ store correct values reflecting the situation right after the event. We first assume that no three intervals endpoints coincide at any time. At the end of this proof, we explain how to handle these degenerate cases.

For an event of type $\mathsf{LL}\mathrm{or}\mathsf{LR}$, the set of intervals which are hit by a right endpoint does not change at all. Thus nothing in $\mathcal{W}$ and $\mathcal{T}$ needs to change.

For an event of type $\mathsf{RL}$, let $I_i$ and $I_j$ be the two intervals involved in the event such that $t_i=p$ and $s_j=q$. Then at this event, the set of intervals that are hit by $t_i$ will change, and the set of intervals hit by any other point does not change. The number of intervals hit by $t_i$ increases by 1 for the case where p and q collide, and this number decreases by 1 for the other case where p and q separate. It follows that among all $T_{1,b}$ for $b=1,\dots ,n$, $T_{1,i}$ is the only element which changes. The update of $T_{1,i}$ can be done in $O\left(1\right)$ time. Among all $T_{2,b}$ for $b=1,\dots ,n$, however, more than one element can change. We show that we can compute the changes in $O\left(n\right)$ time in total. For both cases where the points collide or separate, $w_{a,b}$ changes only if $a=i$ or $b=i$ in the following way. The value $w_{a,i}$ increases or decreases by 1 for all $a=1,\dots ,i-1$. The value $w_{i,b}$ increases or decreases by 1 if $t_b\le t_j$ for $b=i+1,\dots ,n$. Thus we can update $\mathcal{W}$ in $O\left(n\right)$ time in total.

The observation that $w_{a,b}$ changes only if $a=i$ or $b=i$ implies that $T_{2,b}$ changes only if $T_{1,i}+w_{i,b}$ becomes larger than its original value for $b=i+1,\dots ,n$. This can be checked in $O\left(1\right)$ time for every $b=i+1,\dots ,n$ once $T_{1,i}$ and $w_{i,b}$ were computed. Using additional $O\left(n\right)$ time, we update $T_{2,i}$ using the recurrence relation. Thus we can update $\mathcal{T}$ in $O\left(n\right)$ time in total. Then we can report a new solution by computing ${max}_b{T}_{2,b}$.

For an event of type $\mathsf{RR}$, let $I_i$ and $I_j$ be the two intervals involved in the event such that $t_i=p$, $t_j=q$, and $p<q$ holds right after the event if p and q separate at this event. If $i>j$, which happens only for the case where p and q separate, we just switch the labels of two intervals so that $i<j$ holds. Then $I_j$ is the only interval such that the set of intervals which are hit by its right endpoint changes by this event. The size of the set increases by 1 for the case where p and q collide, and the size of the set decreases by 1 for the case where p and q separate. It follows that among all $T_{1,b}$ for $b=1,\dots ,n$, $T_{1,j}$ is the only element which changes. The update of $T_{1,j}$ can be done in $O\left(1\right)$ time. Among all $T_{2,b}$ for $b=1,\dots ,n$, however, more than one element can change. We show that we can compute the changes in $O\left(n\right)$ time in total. For both cases where points collide or separate, $w_{a,b}$ changes only if $b=j$. More precisely, the value $w_{a,j}$ increases or decreases by 1 if $t_a<s_i$. Thus we can update $\mathcal{W}$ in $O\left(n\right)$ time in total.

The observation that $T_{1,j}$ is the only element which changes among all $T_{1,b}$ for $b=1,\dots ,n$ implies that $T_{2,b}$ changes only if $T_{1,j}+w_{j,b}$ becomes larger than its original value for $b=j+1,\dots ,n$. This can be checked in $O\left(1\right)$ time for every $b=j+1,\dots ,n$ once $T_{1,j}$ and $w_{j,b}$ were computed. Using additional $O\left(n\right)$ time, we update $T_{2,j}$ using the recurrence relation. Thus we can update $\mathcal{T}$ in $O\left(n\right)$ time in total. Then we can report a new solution by computing ${max}_b{T}_{2,b}$.

We now explain how to handle degenerate cases where more than 2 endpoints collide or separate at the same time t. So we have several events of the type LL, LR, RL or RR occurring at time t. In this case, we first separately handle in an arbitrary order each of the events where two points collide, in the way that is described above. Then we obtain the solution at time t with maximum coverage. After this, we handle in an arbitrary order all the events where two points separate at time t. □

7. Discussion and Conclusions

We addressed the problem of finding k lines that together intersect the maximum number of input disks. We considered two other variants, where the k output lines should be parallel, and where the k lines should pass through a common point. We presented the first algorithms for these problems.

For $k=1$, the three problems coincide, and we give an $O\left(n^2\right)$ time algorithm by applying a geometric dualization. As this problem is 3SUM-hard even for covering points, an $O\left(n^{\alpha }\right)$-time algorithm for any $\alpha <2$ is currently out of reach.

For the problem of finding $k\ge 2$ lines that together intersect the maximum number of input disks, we first show that there exists an optimal set of k lines, each of which is tangent to two input disks. Using this observation, we show that the problem can be reduced to the problem of computing the depth of a set of boxes. The running time of our algorithm is $O(n^{3}logn)$ when $k=2$ and is $O\left(n^{3k/2}\right)$ time when $k\ge 3$.

For the problem of finding k parallel lines that together intersect the maximum number of input disks for $k\ge 2$, it can be reduced to the Partial Interval Hitting Set problem once the direction of the output lines is fixed. We first give $O\left(n^4\right)$-time algorithm by observing that there exists an optimal set of k parallel lines such that every line is tangent to an input disk and at least one of them is tangent to two input disks in $\mathcal{D}$. Then we reduce the time complexity when $k=2$, at the expense of increasing the space usage by a logarithmic factor.

Our results are the first nontrivial results of these three problems, which are maximum coverage problems in geometric settings. One natural question is to extend our results to other geometric settings, for instance to covering balls by lines in ${\mathbb{R}}^3$. Another possible direction for further work is to consider approximation algorithms. The maximum coverage problem for arbitrary sets is known to be NP-hard, and the straightforward greedy algorithm gives a $(1-1/e)$-approximation of the optimum. Can we find better approximation algorithms in geometric settings?