A Discrete-Time Current Control Method for the High-Speed Permanent Magnet Motor Drive Using the Modular Multilevel Converter
Abstract
1. Introduction
- (1)
- The symmetrical discrete-time model of the MMC for a HSPMM drive is established. Compared with the traditional discrete PI current controller, the proposed discrete-time current regulator can achieve significant dynamic performance at high speed regions.
- (2)
- The energy balance model for MMC is illustrated, the design of energy balance controller is introduced.
- (3)
- The proposed methods are realized and verified during the dynamic and steady states, and the motor speed reached up to 15 kr/min.
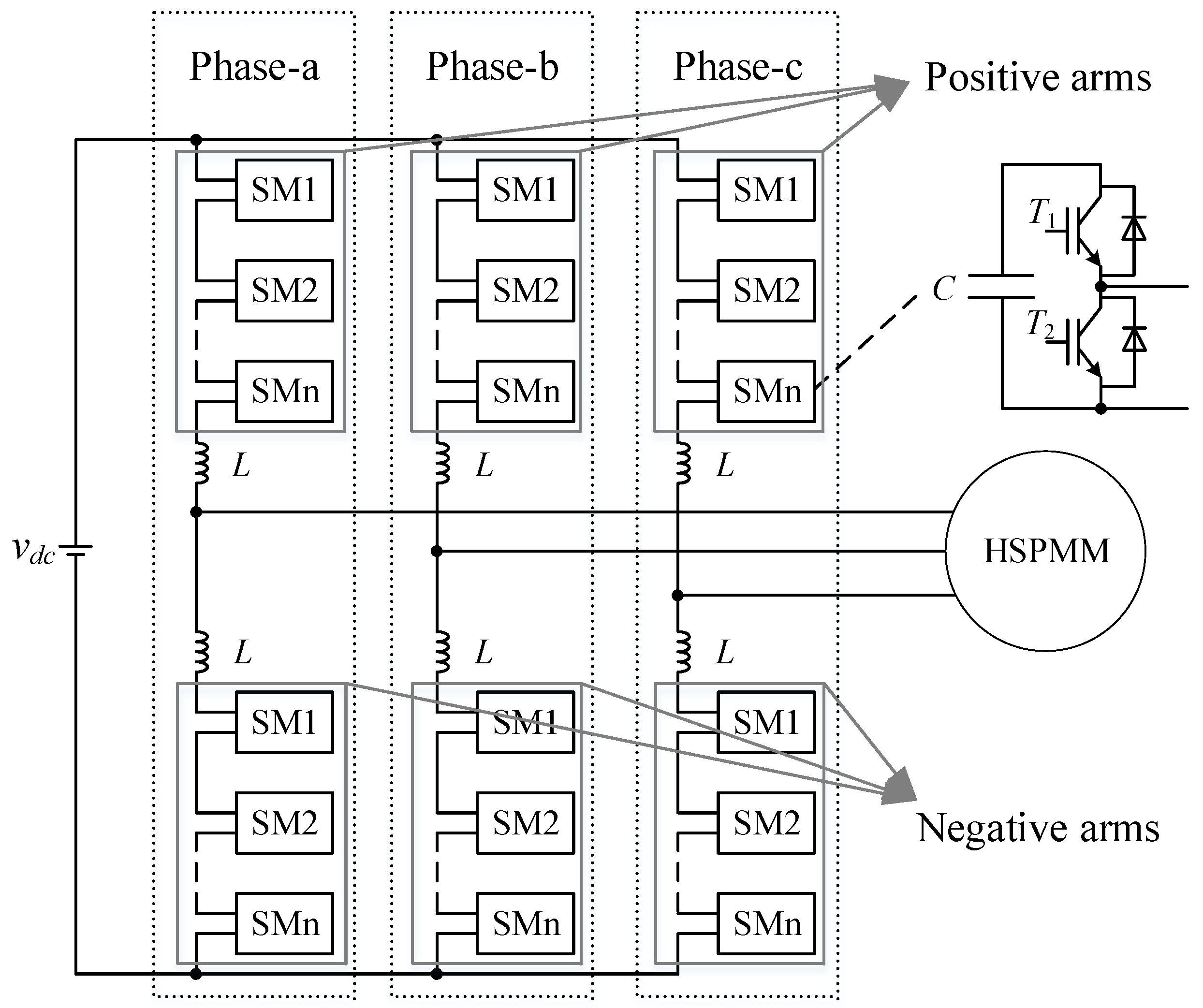
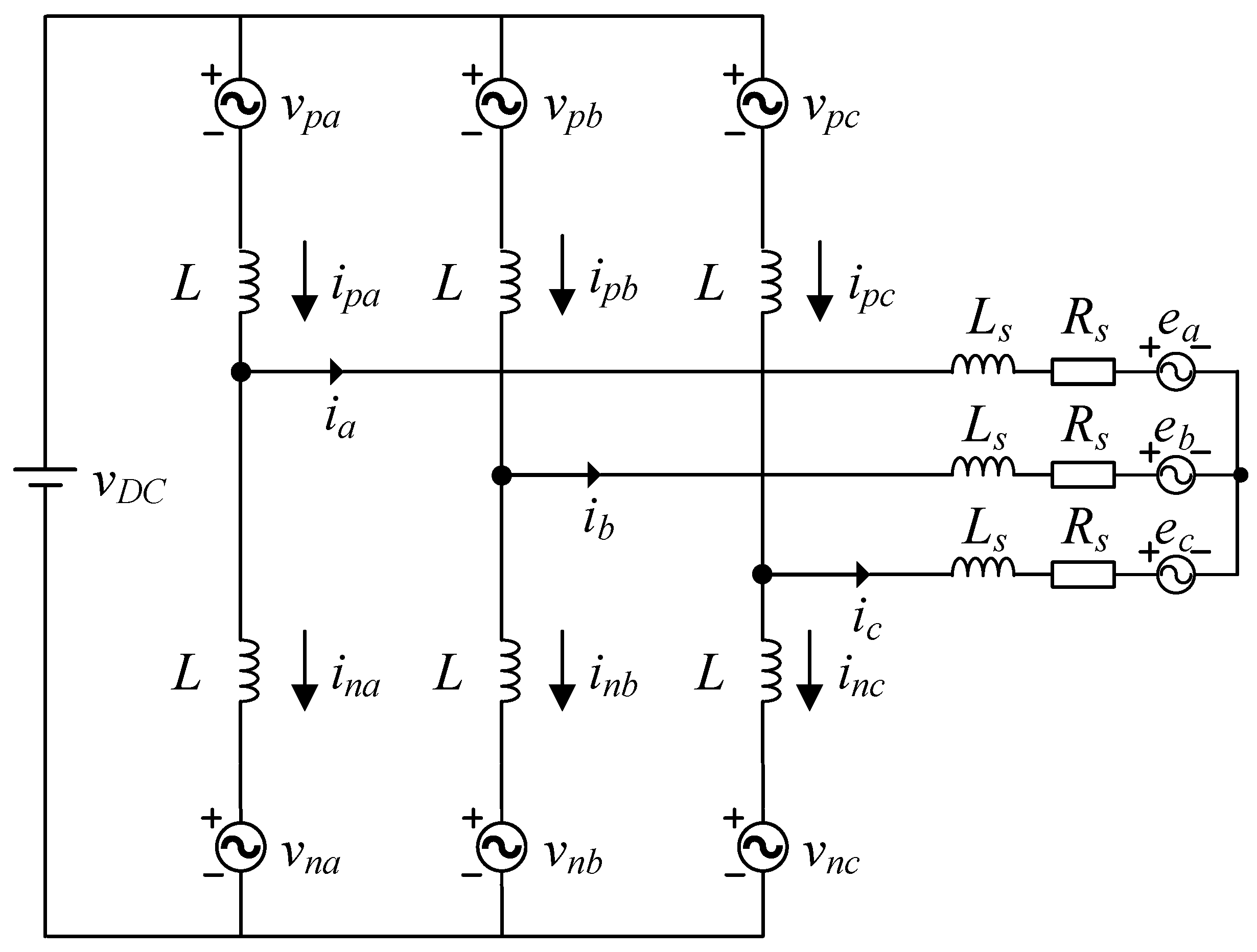
2. MMC Topology and Circuit Architecture
2.1. MMC Topology Structure
2.2. Circuit Structure
3. Discrete-Time Current Control Scheme
3.1. Discrete-Time Model
3.2. Conventional PI Method
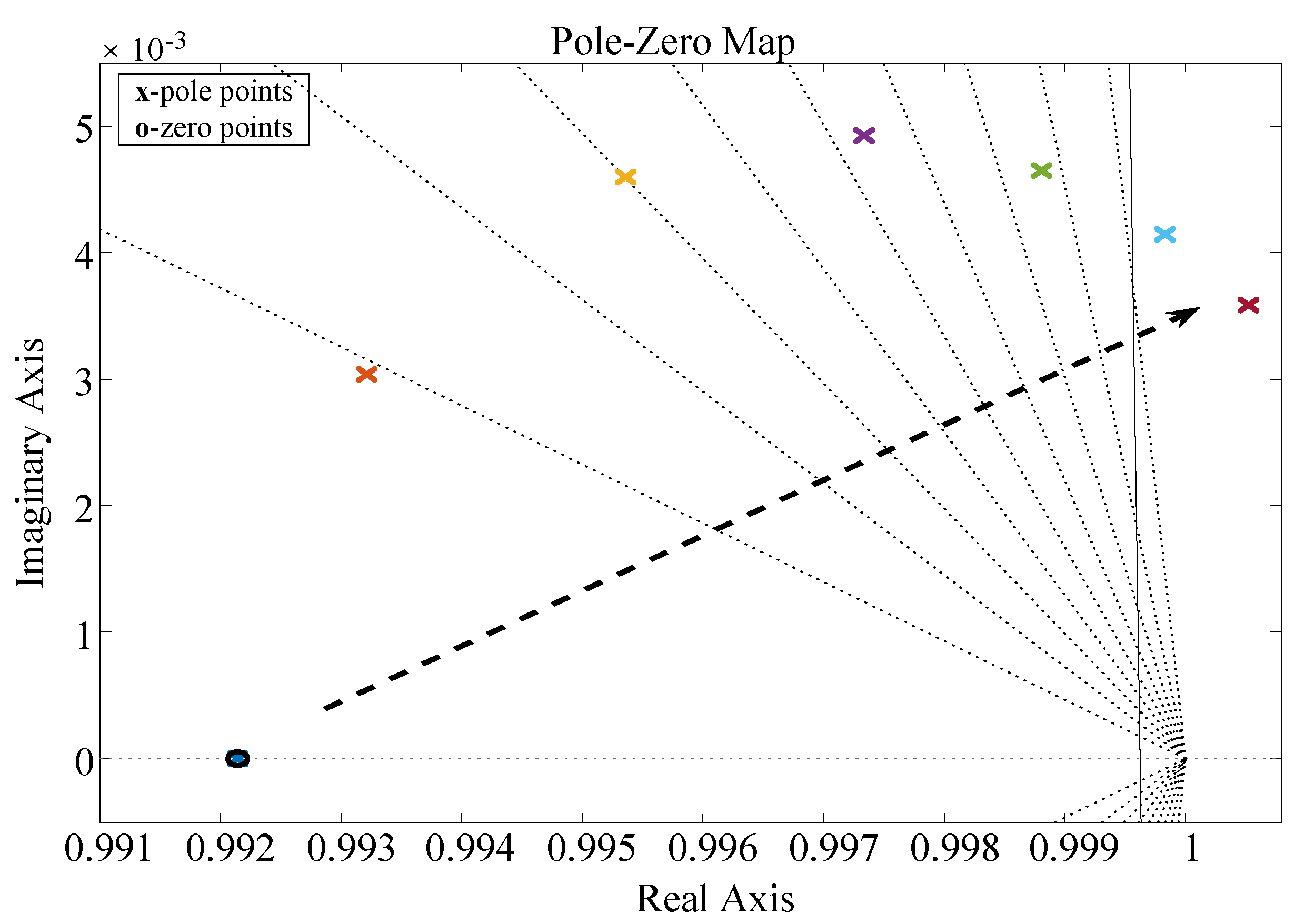
3.3. Controller Design of Discrete-Time Current
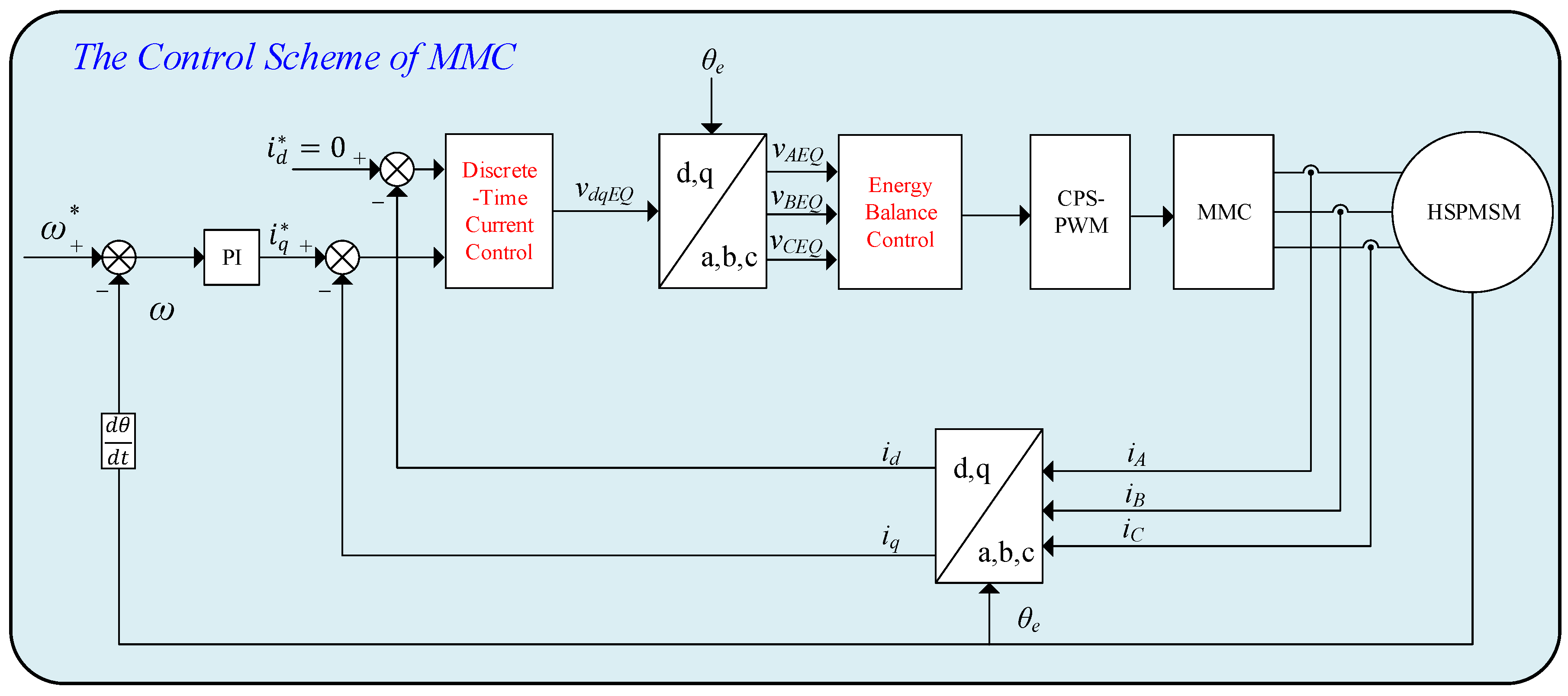
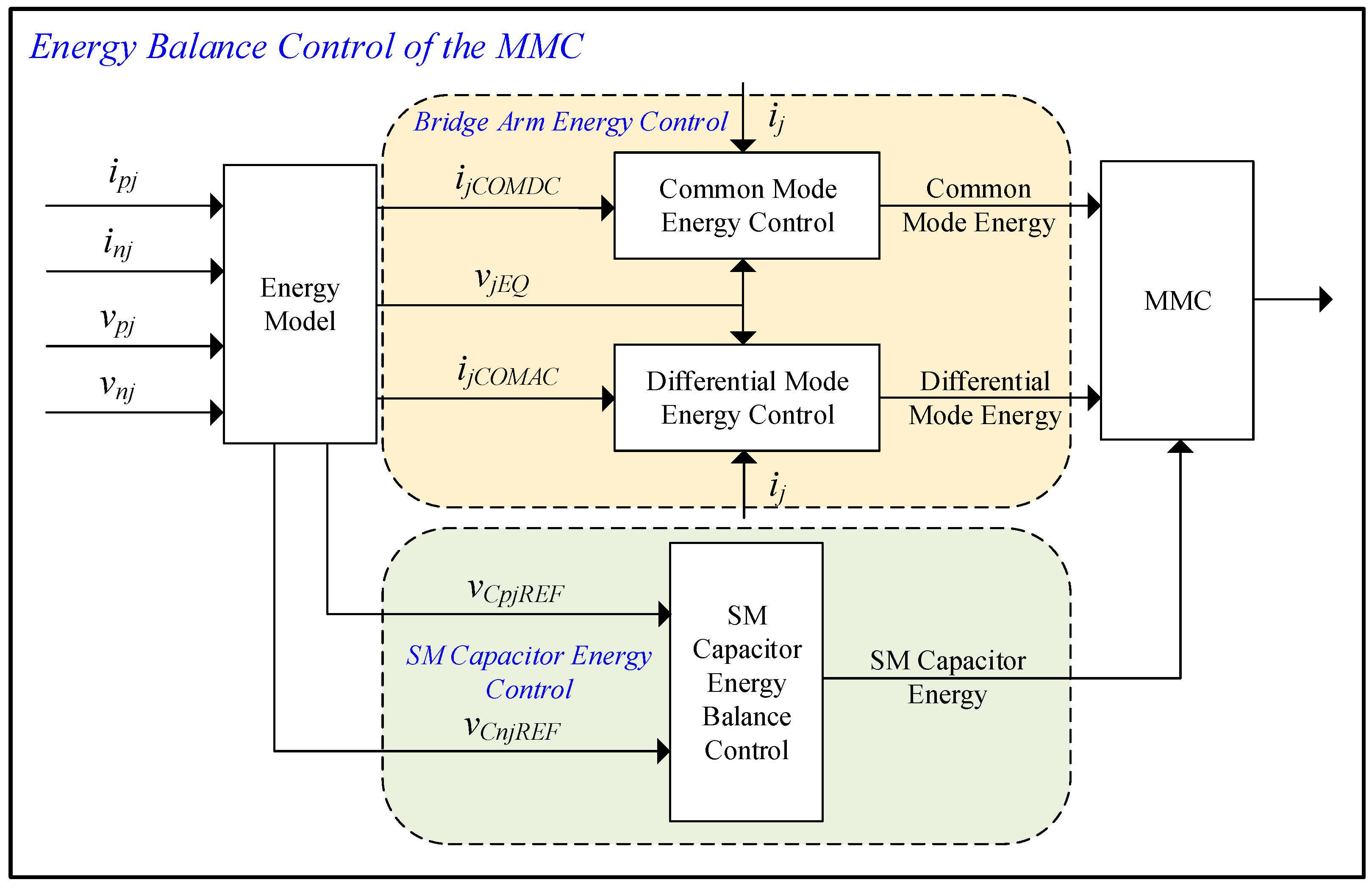
4. Energy Balance Control of the MMC
4.1. Energy Model Analysis
4.2. SM Capacitor Energy Model
4.3. Bridge Arm Energy Model
4.4. Energy Balance Controller Design
4.4.1. Control Scheme of Bridge Arm Energy
4.4.2. SM Capacitor Energy Control
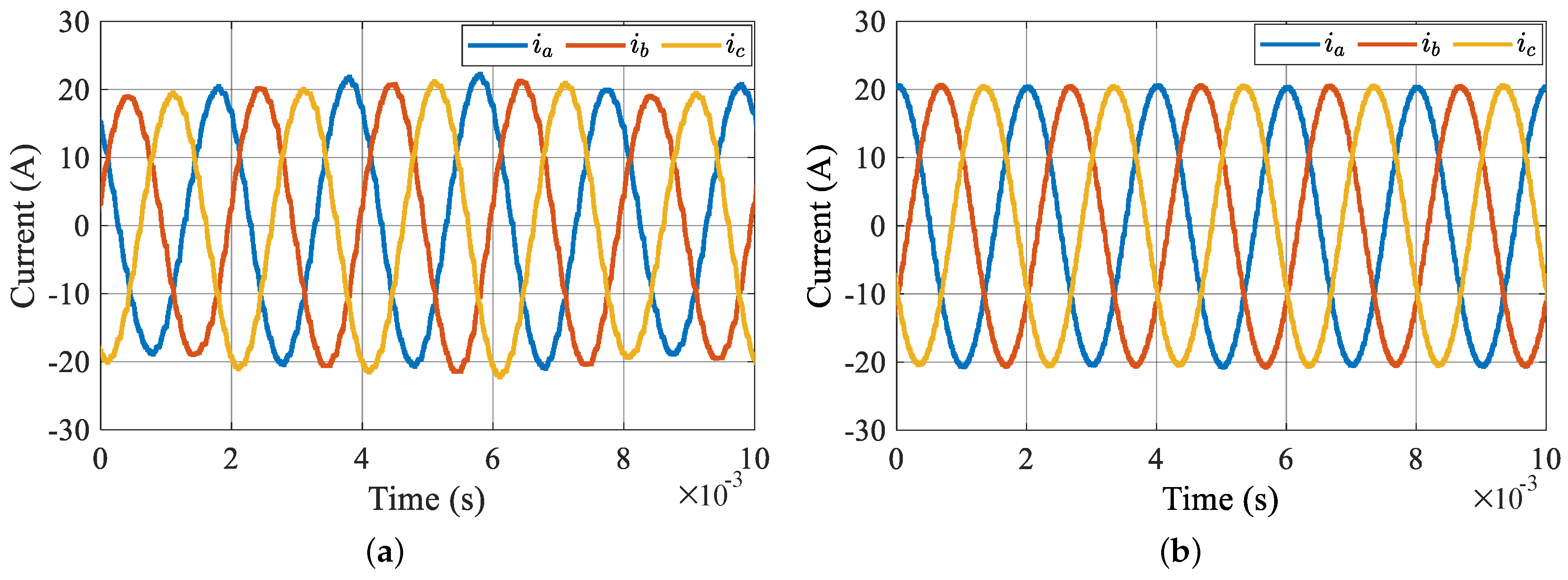
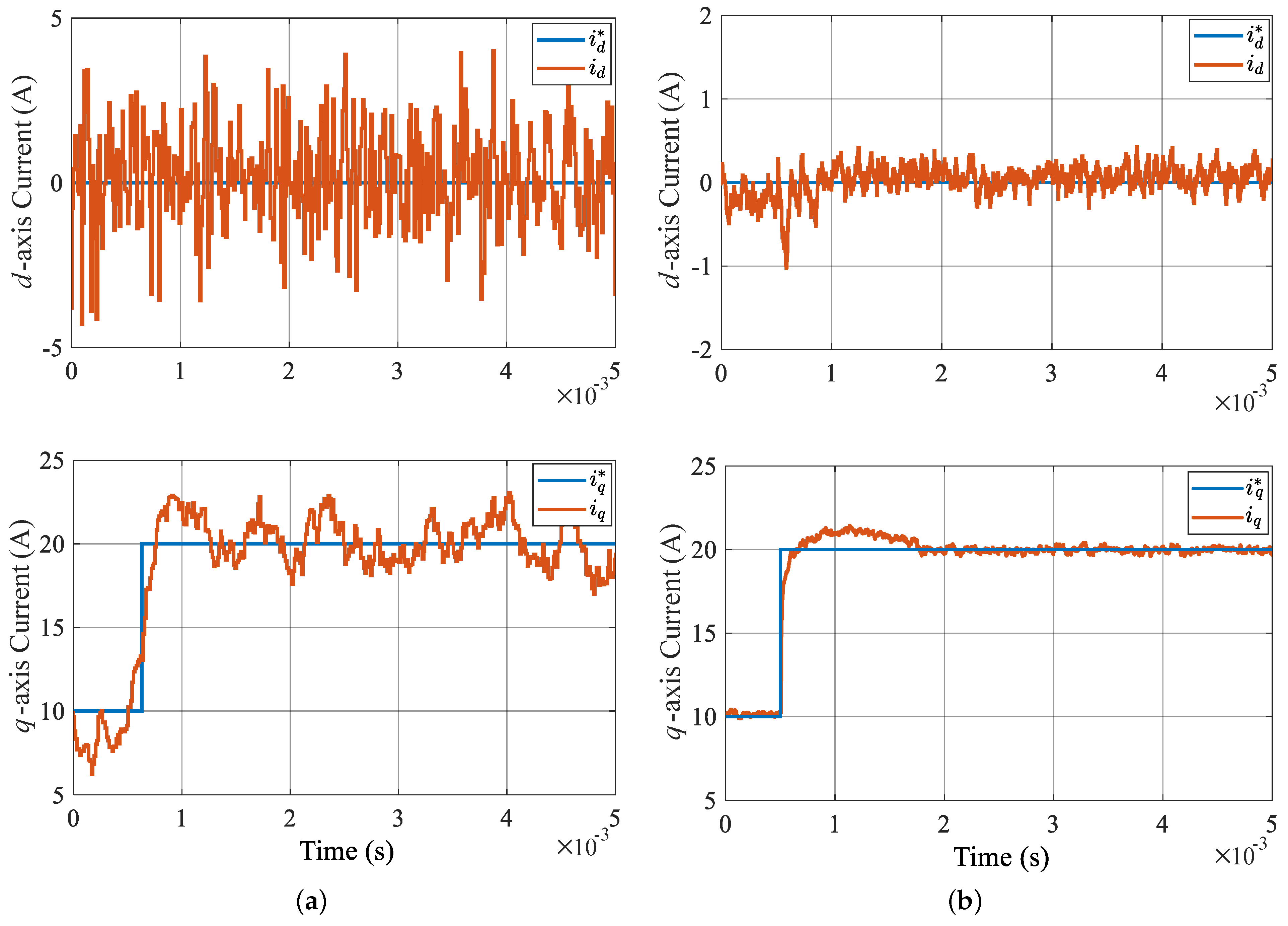
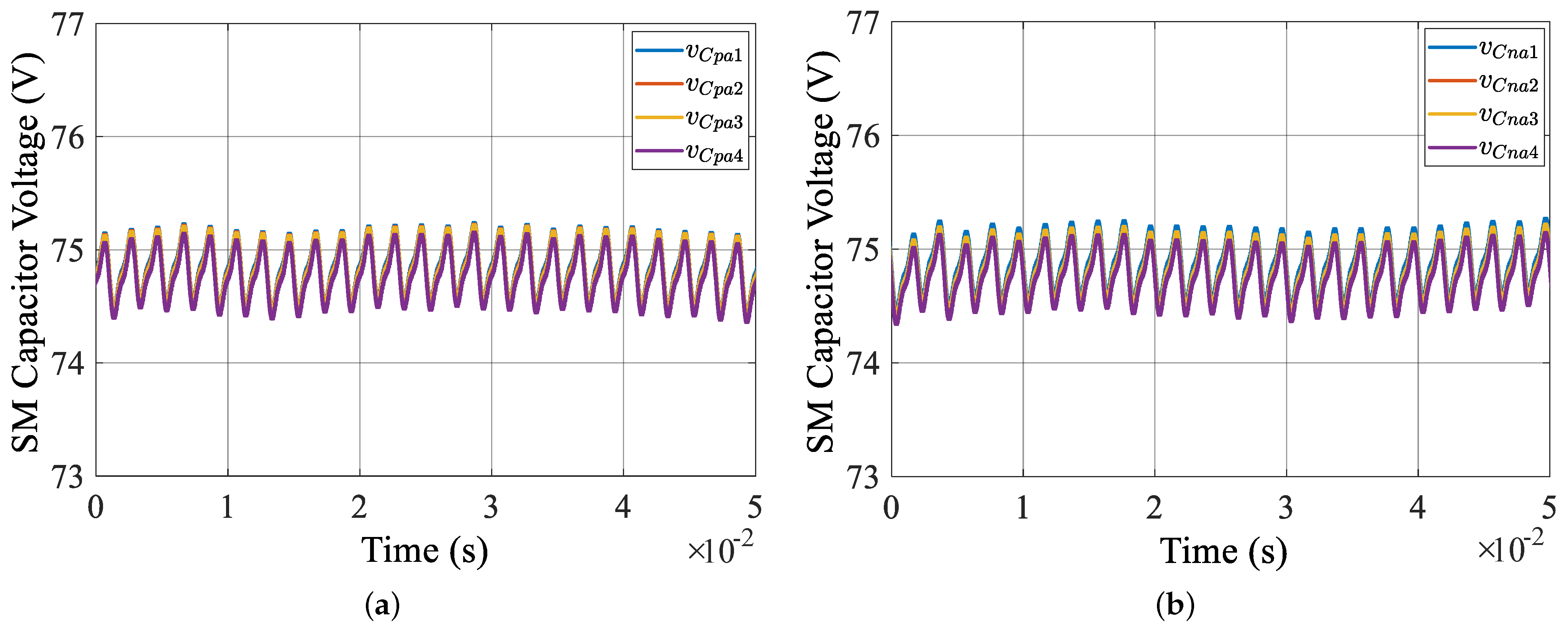
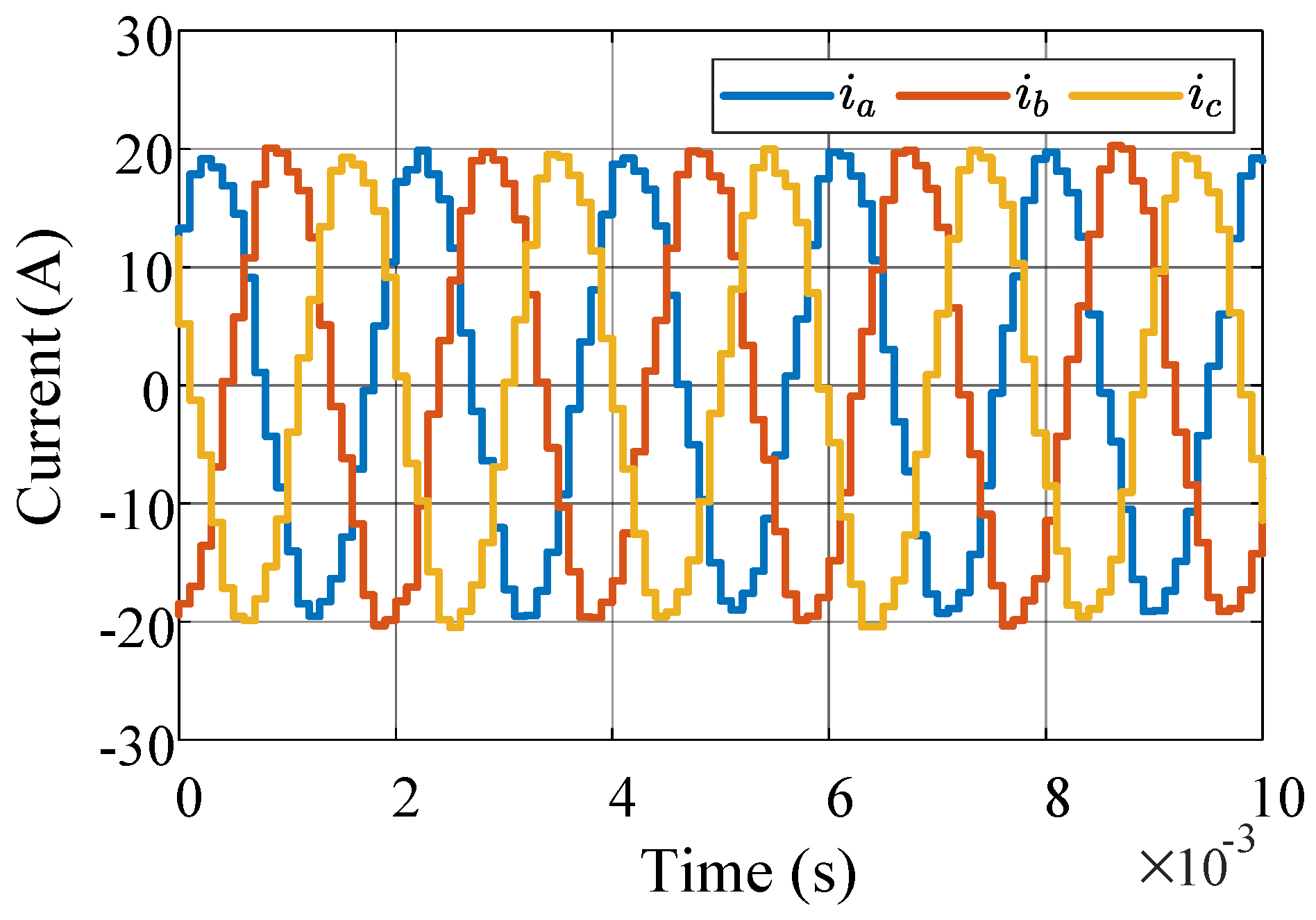
5. Simulation Analysis
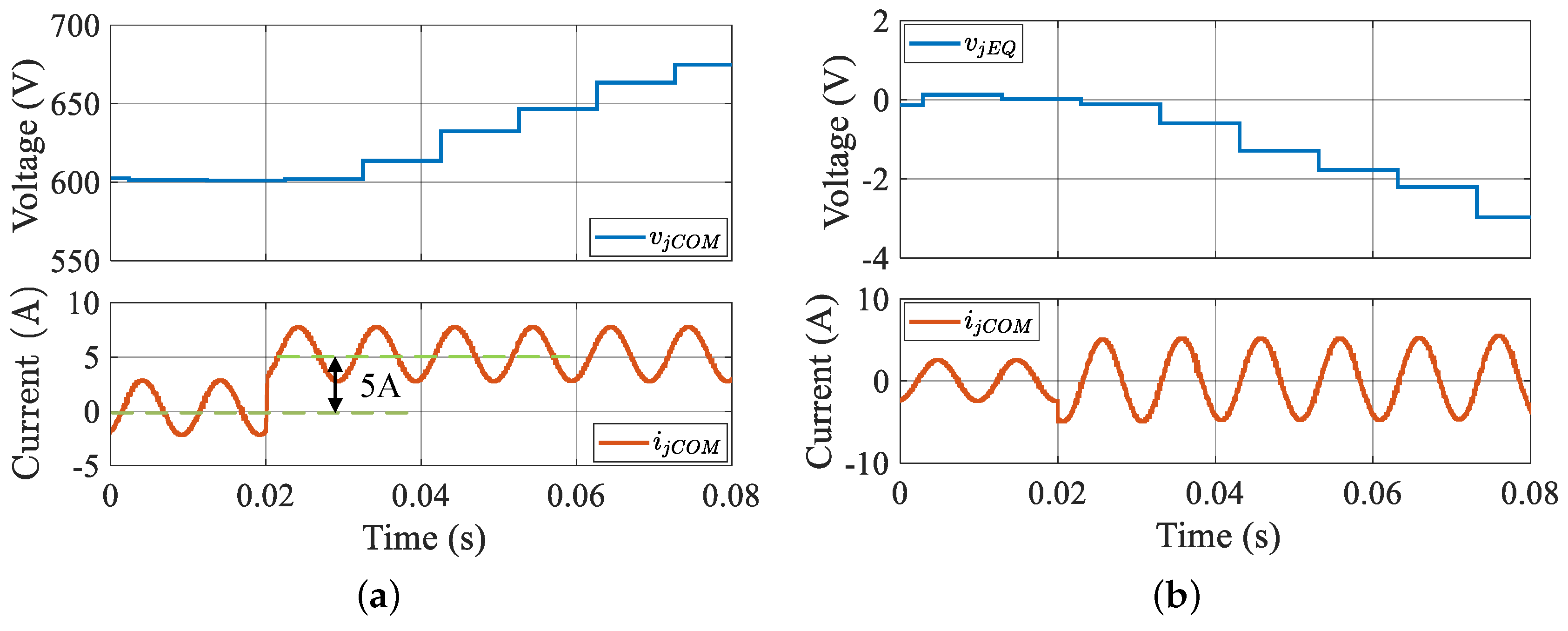
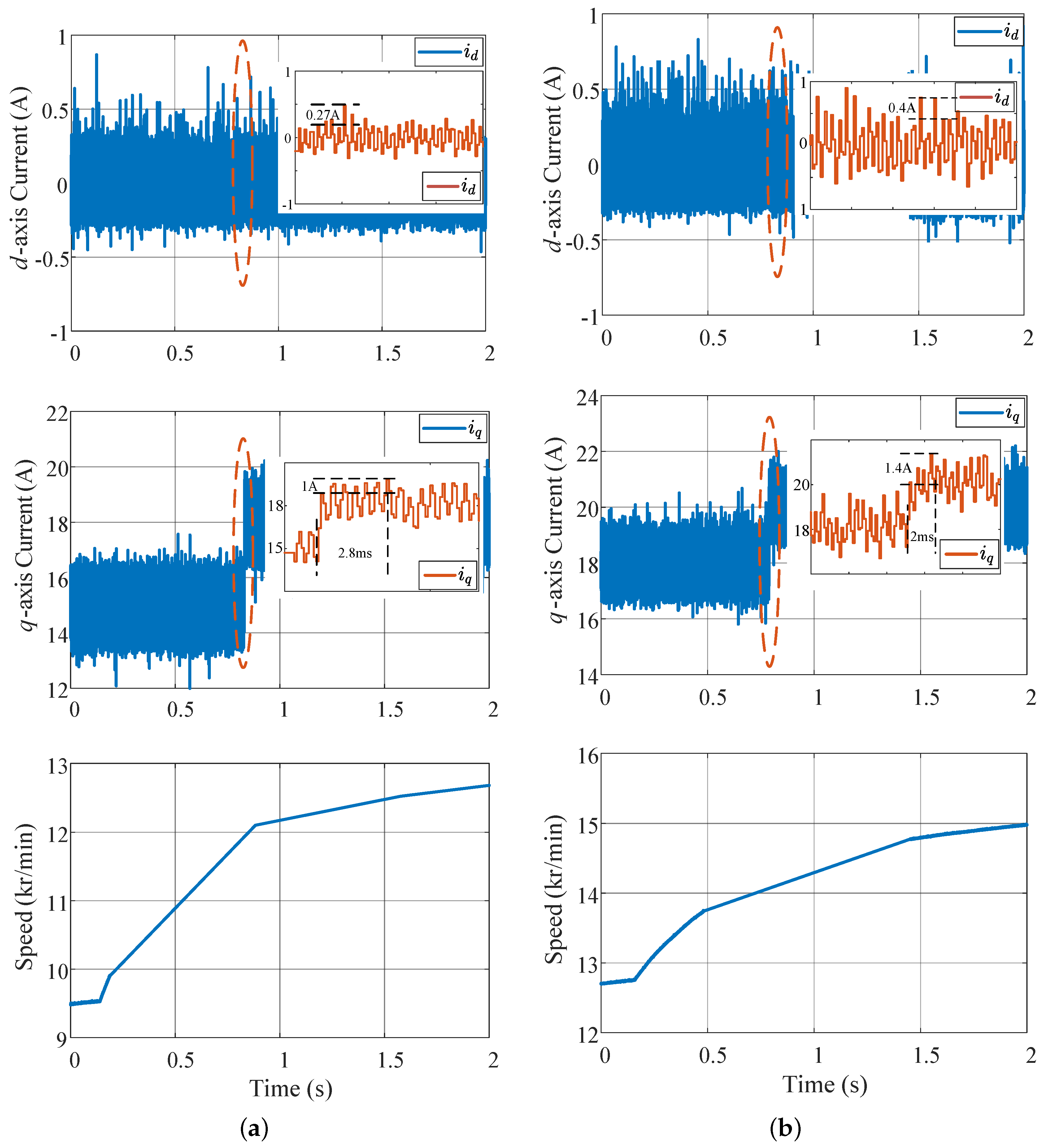
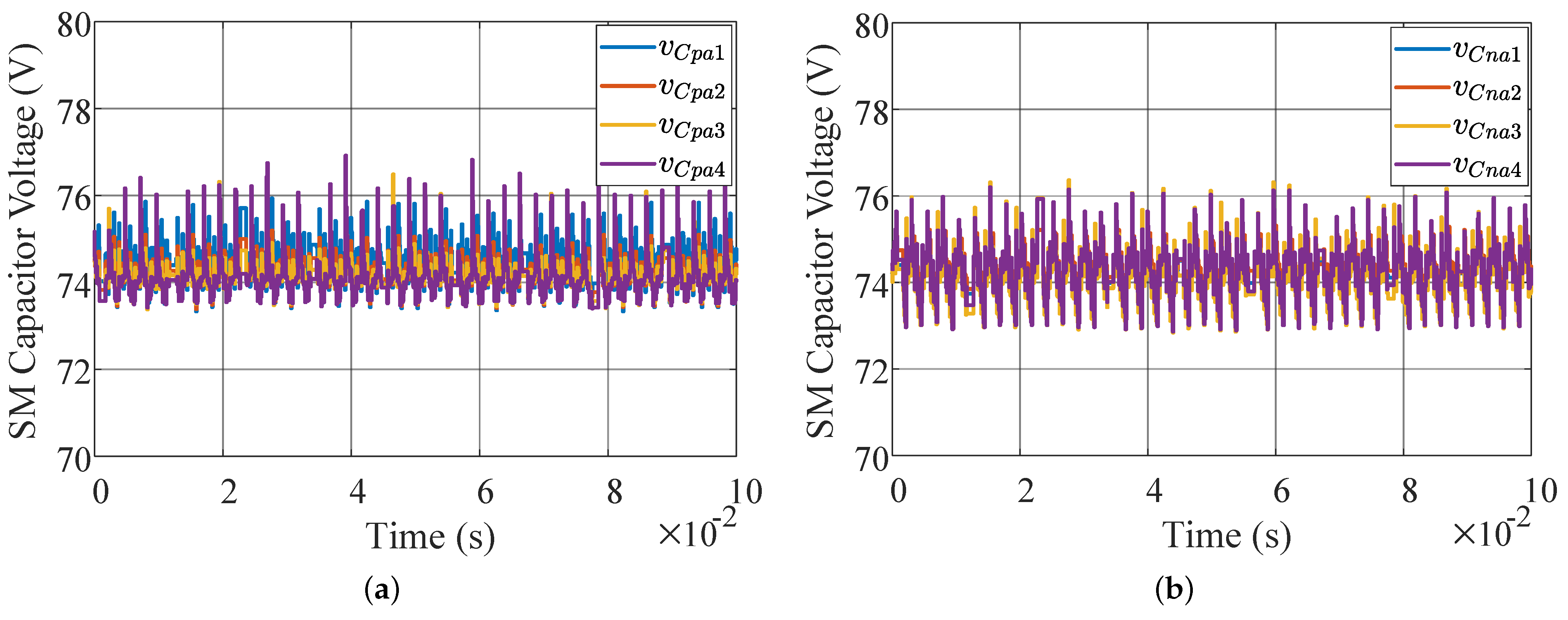
6. Experimental Verifications
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gerada, D.; Mebarki, A.; Brown, N.; Gerada, C.; Cavagnino, A.; Boglietti, A. High-Speed Electrical Machines: Technologies, Trends, and Developments. IEEE Trans. Ind. Electron. 2014, 61, 2946–2959. [Google Scholar] [CrossRef]
- Lusignani, D.; Barater, D.; Franceschini, G.; Buticchi, G.; Galea, M.; Gerada, C. A high-speed electric drive for the more electric engine. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 4004–4011. [Google Scholar] [CrossRef]
- Zhao, N.; Zhu, Z.Q.; Liu, W. Rotor Eddy Current Loss Calculation and Thermal Analysis of Permanent Magnet Motor and Generator. IEEE Trans. Magn. 2011, 47, 4199–4202. [Google Scholar] [CrossRef]
- Dong, J.; Huang, Y.; Jin, L.; Lin, H. Comparative Study of Surface-Mounted and Interior Permanent-Magnet Motors for High-Speed Applications. IEEE Trans. Appl. Supercond. 2016, 26, 5200304. [Google Scholar] [CrossRef]
- Perisse, F.; Werynski, P.; Roger, D. High frequency behavior of AC machine: Application of turn insulation aging diagnostic. In Proceedings of the Conference Record of the 2006 IEEE International Symposium on Electrical Insulation, Toronto, ON, Canada, 11–14 June 2006; pp. 555–559. [Google Scholar] [CrossRef]
- Wada, K.; Tsuji, K.; Muto, H.; Yashiro, O. Effect of cabling and grounding configuration on surge voltages in inverter-fed motors. In Proceedings of the 2006 IEEE Conference on Electrical Insulation and Dielectric Phenomena, Kansas City, MO, USA, 15–18 October 2006; pp. 602–606. [Google Scholar] [CrossRef]
- Narayanasamy, B.; Sathyanarayanan, A.S.; Luo, F.; Chen, C. Reflected Wave Phenomenon in SiC Motor Drives: Consequences, Boundaries, and Mitigation. IEEE Trans. Power Electron. 2020, 35, 10629–10642. [Google Scholar] [CrossRef]
- Langmaack, N.; Balasubramanian, S.; Mallwitz, R.; Henke, M. Comparative Analysis of High Speed Drive Inverter Designs using different Wide-Band-Gap Power Devices. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Chang, L.; Alvi, M.; Lee, W.; Kim, J.; Jahns, T.M. Efficiency Optimization of PWM-Induced Power Losses in Traction Drive Systems with IPM Machines Using Wide Bandgap-Based Inverters. IEEE Trans. Ind. Appl. 2022, 58, 5635–5649. [Google Scholar] [CrossRef]
- Xu, Y.; Yuan, X.; Ye, F.; Wang, Z.; Zhang, Y.; Diab, M.; Zhou, W. Impact of High Switching Speed and High Switching Frequency of Wide-Bandgap Motor Drives on Electric Machines. IEEE Access 2021, 9, 82866–82880. [Google Scholar] [CrossRef]
- Hatua, K.; Jain, A.K.; Banerjee, D.; Ranganathan, V.T. Active Damping of Output Filter Resonance for Vector-Controlled VSI-Fed AC Motor Drives. IEEE Trans. Ind. Electron. 2012, 59, 334–342. [Google Scholar] [CrossRef]
- Yao, Y.; Peng, F.; Huang, Y. Position and Capacitor Voltage Sensorless Control of High-Speed Surface-Mounted PMSM Drive with Output Filter. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 2374–2381. [Google Scholar] [CrossRef]
- Wang, M.; Xu, Y.; Zou, J. Sliding mode control with open-switch fault diagnosis and sensorless estimation based on PI observer for PMSM drive connected with an LC filter. IET Power Electron. 2020, 13, 2334–2341. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, Y.; Peng, F.; Dong, J.; Zhu, Z. Discrete-Time Dynamic-Decoupled Current Control for LCL-Equipped High-Speed Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2022, 69, 12414–12425. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Perez, M.A.; Leon, J.I. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Raju, M.N.; Sreedevi, J.; Mandi, R.P.; Meera, K.S. Modular multilevel converters technology: A comprehensive study on its topologies, modelling, control and applications. IET Power Electron. 2019, 12, 149–169. [Google Scholar] [CrossRef]
- Picas, R.; Zaragoza, J.; Pou, J.; Ceballos, S.; Konstantinou, G.; Capella, G.J. Study and Comparison of Discontinuous Modulation for Modular Multilevel Converters in Motor Drive Applications. IEEE Trans. Ind. Electron. 2019, 66, 2376–2386. [Google Scholar] [CrossRef]
- Ke, Z.; Pan, J.; Sabbagh, M.A.; Na, R.; Zhang, J.; Wang, J.; Xu, L. Capacitor Voltage Ripple Estimation and Optimal Sizing of Modular Multi-Level Converters for Variable-Speed Drives. IEEE Trans. Power Electron. 2020, 35, 12544–12554. [Google Scholar] [CrossRef]
- Li, B.; Han, L.; Mao, S.; Zhou, S.; Qu, Z.; Xu, D. Decoupled Modulation Scheme for Modular Multilevel Converters in Medium-Voltage Applications. IEEE Trans. Power Electron. 2020, 35, 11430–11441. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Wang, G.; Sun, W.; Xu, D.; Wang, W. A Modified Modular Multilevel Converter with Reduced Capacitor Voltage Fluctuation. IEEE Trans. Ind. Electron. 2015, 62, 6108–6119. [Google Scholar] [CrossRef]
- Dekka, A.; Wu, B.; Zargari, N.R.; Fuentes, R.L. Dynamic Voltage Balancing Algorithm for Modular Multilevel Converter: A Unique Solution. IEEE Trans. Power Electron. 2016, 31, 952–963. [Google Scholar] [CrossRef]
- Kolluri, S.; Gorla, N.B.Y.; Panda, S.K. Capacitor Voltage Ripple Suppression in a Modular Multilevel Converter Using Frequency-Adaptive Spatial Repetitive-Based Circulating Current Controller. IEEE Trans. Power Electron. 2020, 35, 9839–9849. [Google Scholar] [CrossRef]
- Samajdar, D.; Bhattacharya, T. Capacitor Voltage Ripple Optimization in Modular Multilevel Converter Using Synchronous Reference Frame Energy Ripple Controller. IEEE Trans. Power Electron. 2022, 37, 7883–7895. [Google Scholar] [CrossRef]
- Kumar, Y.S.; Poddar, G. Balanced Submodule Operation of Modular Multilevel Converter-Based Induction Motor Drive for Wide-Speed Range. IEEE Trans. Power Electron. 2020, 35, 3918–3927. [Google Scholar] [CrossRef]
- Zhao, F.; Xiao, G.; Zhu, T.; Zheng, X.; Wu, Z.; Zhao, T. A Coordinated Strategy of Low-Speed and Start-Up Operation for Medium-Voltage Variable-Speed Drives with a Modular Multilevel Converter. IEEE Trans. Power Electron. 2020, 35, 709–724. [Google Scholar] [CrossRef]
- Pan, J.; Ke, Z.; Al Sabbagh, M.; Li, H.; Potty, K.A.; Perdikakis, W.; Na, R.; Zhang, J.; Wang, J.; Xu, L. 7-kV 1-MVA SiC-Based Modular Multilevel Converter Prototype for Medium-Voltage Electric Machine Drives. IEEE Trans. Power Electron. 2020, 35, 10137–10149. [Google Scholar] [CrossRef]
- Pan, J.; Ke, Z.; Li, X.; Zhao, Y.; Zhang, J.; Wang, J.; Xu, L. Integrated Control and Performance Analysis of High-Speed Medium-Voltage Drive Using Modular Multilevel Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3692–3704. [Google Scholar] [CrossRef]
- Xia, T.; Peng, F.; Huang, Y. A Novel Energy Balance Control Method for a Modular Multilevel Converter in a High-Speed PMSM Drive Application. Energies 2023, 16, 5022. [Google Scholar] [CrossRef]
- Bae, B.H.; Sul, S.K. A compensation method for time delay of full-digital synchronous frame current regulator of PWM AC drives. IEEE Trans. Ind. Appl. 2003, 39, 802–810. [Google Scholar] [CrossRef]



| Parameter | Symbol | Value |
|---|---|---|
| Rated mechanical speed | n | 15 kr/min |
| Pole pairs | 2 | |
| PM flux linkage | 0.04 Wb | |
| Rate current | I | 20 A |
| Stator resistance | 0.01385 | |
| Stator inductance | 0.1256 mH |
| Parameter | Symbol | Value |
|---|---|---|
| Number of SM per arm | N | 4 |
| Number of IGBT half bridge | / | 24 |
| Submodule capacitance | C | 4 mF |
| DC voltage | 300 V | |
| Bridge arm inductance | L | 0.1 mH |
| Switching frequency | 10 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, T.; Peng, F.; Huang, Y. A Discrete-Time Current Control Method for the High-Speed Permanent Magnet Motor Drive Using the Modular Multilevel Converter. Symmetry 2024, 16, 200. https://doi.org/10.3390/sym16020200
Xia T, Peng F, Huang Y. A Discrete-Time Current Control Method for the High-Speed Permanent Magnet Motor Drive Using the Modular Multilevel Converter. Symmetry. 2024; 16(2):200. https://doi.org/10.3390/sym16020200
Chicago/Turabian StyleXia, Tianqi, Fei Peng, and Yunkai Huang. 2024. "A Discrete-Time Current Control Method for the High-Speed Permanent Magnet Motor Drive Using the Modular Multilevel Converter" Symmetry 16, no. 2: 200. https://doi.org/10.3390/sym16020200
APA StyleXia, T., Peng, F., & Huang, Y. (2024). A Discrete-Time Current Control Method for the High-Speed Permanent Magnet Motor Drive Using the Modular Multilevel Converter. Symmetry, 16(2), 200. https://doi.org/10.3390/sym16020200







