1. Introduction and Preliminaries
Special functions have significant applications in statistics, economics, physics, and other applied sciences. For this reason, such functions attract the attention of mathematicians and other researchers. In particular, functions that are special solutions of some differential equations attract much more attention than other functions. Some of these functions are hypergeometric, Bessel, Struve, and Lommel functions, and so on. In the last century, a number of important studies have been carried out on the special functions mentioned above.
A particular solution of the next differential equation
is known as a Bessel function of the first kind and is denoted by
. The solution of the differential Equation (
1) implies that
has the following representation:
where
represents Euler’s gamma function. For comprehensive knowledge on this function, interested readers can refer to [
1]. In addition, the modified Bessel function of the first kind
is a private solution of the differential equation
Also, the function
has the following infinite series representation:
Another significant property of the mentioned functions is having some natural generalizations. In the literature, there exist certain natural generalizations of the Bessel functions. One of the most important of them is the generalized
k-Bessel function, and it has the following infinite series representation (see [
2]):
for
. Here,
stands for the
k-gamma function, which is defined by (see [
3])
for
. It is known that
reduces to
for
. On the other hand, the generalized
k-Bessel function reduces to
and
for
and
, respectively (see [
2]). In addition, it is known from [
2] that the function
is a solution of the following differential equation:
for
and
.
The Pochammer
s-symbol is defined by
for
and
. For other useful properties of the Pochammer
s-symbol and
k-gamma function, one can refer to [
3].
The outcome of this paper is as follows. In the rest of this section, certain basic concepts in geometric function theory and useful lemmas for the proofs are given.
Section 2 is devoted to the geometric properties such as starlikeness and convexity generalized
k-Bessel functions. Also, we determine some conditions on the parameters such that the generalized
k-Bessel function belongs to the some subclasses of analytic functions defined in [
4]. In
Section 3, we deal with Hardy class of generalized
k-Bessel functions. Also, some corollaries are indicated at the end of
Section 2 and
Section 3.
Let
show the open unit disk and
be the collection of all holomorphic functions on
. Let
indicate the class of all holomorphic functions
normalized by
which satisfy
. Also, it is known that the function
f does not take the same value twice in a set; then,
f is called univalent in this set. By
, we indicate the collection of functions belonging to class
that are univalent in
. The class
has various subclasses consisting of functions which have nice geometric properties. The starlike functions’ class
and convex functions’ class
are known as famous subclasses of
. In fact, the functions in
and
map
onto a starlike domain with respect to the origin and a convex domain, respectively. In addition, for
, the class
denotes the class of starlike functions of order
in
, while the class
denotes the class of convex functions of order
in
. It is well known that
and
are also subclasses of
. The classes
and
reduce to the classes
and
for
, respectively. Analytic characterizations of the classes
and
may be given as follows:
and
In addition to the above significant function classes, there exist certain subclasses of the classes
and
in the literature. Two of them are the classes
and
, and they are defined in [
4] as follows:
and
The classes and reduce to and for , respectively. Also, we simplify and by and for , respectively.
The Hadamard product of the series
is defined by
The Hardy class of all holomorphic functions inside
is shown by
. A regular function
f in
is said to belong to the Hardy class
for
if the set
is bounded, where
It is known from [
5] that
is a Banach space with the norm defined by
for
. Furthermore, it is known that
denotes the family of bounded analytic functions in
, and the set
shows the collection of power series
such that
Additionally,
is a subset of
for
; see [
5]. Also, for the Hardy space
, the following is a significant result (see [
5]):
In the last fifty years, several scholars proved certain important results about some geometric properties of the functions in the class
; see, for example, [
6,
7,
8]. These geometric properties include univalence, starlikeness, convexity and close to convexity. Then, the same geometrical properties of certain special functions like Bessel, hypergeometric, Mittag–Leffler, and Wright are investigated by researchers using the results of [
6,
7,
8]. Additionally, some requirements for the convex, starlike, and close-to-convex functions are determined by Eenigenburg and Keogh in [
9] such that these functions belong to the Hardy space
. Utilizing the results in [
6,
7,
8,
9], the Hardy space of the hypergeometric function [
10], generalized Bessel function [
4], Struve functions [
11,
12], Lommel function [
13], Mittag–Leffler function [
14], Wright function [
15], Dini function [
16], hyper-Bessel function [
17],
q-Bessel function [
18], Rabotnov fractional exponential function [
19], and so on are studied by the researchers.
Inspired by the above studies, the main objective of this paper is to present certain conditions on the parameters such that the generalized
k-Bessel function
is starlike of order
and convex of order
on disk
, respectively. It is important to emphasize here that specific examples of the given functions map the open unit disk onto some domains consisting of symmetric points with respect to the real axis. Further, we determine certain conditions for the Hadamard product
such that
and
, where
f is an regular function in
. In addition, we show that the function
is in the class
under certain conditions. Moreover, we show that the function
is in the Hardy space
and bounded analytic function class
under some conditions, respectively. Finally, at the end of the every subsection, we indicate certain corollaries for normalized Bessel and modified Bessel functions.
Some Key Preliminary Lemmas in Geometric Function Theory
The following useful lemmas will be used in order to prove our main results:
Lemma 1 ([
7])
. Let and . Ifthen . Lemma 2 ([
7])
. Let and . Ifthen Lemma 3 ([
9])
. Let . If is not of the formfor some and then the following statements hold:- a.
There exist such that .
- b.
If then there exist such that .
- c.
If then .
Lemma 4 ([
20])
. Suppose that . Then, . The value of ς is the best possible. Additionally, in order to prove the assertions, the following series sums
and
will be used. It is important to note that the series sums given by (
5)–(
7) can easily be obtained by the derivation or integration of (
4). Also, the following inequalities
will be useful in the proofs.
2. Certain Properties of Generalized k-Bessel Functions
In this part of the paper, we present certain geometrical properties of the function .
Theorem 1. Let , , , , , and . Ifthen . Proof of Theorem 1. Suppose that the hypothesis of the theorem holds true. Due to Lemma 1, the function
is starlike of order
if
Using the sums (
4) and (
5) and the inequalities given by (
8)–(10), one can check that
The expression (
12) is bounded above by
under the condition (
11). Thus, the proof follows. □
Replacing in Theorem 1, we deduce the following, respectively.
Corollary 1. Suppose that , and the inequalityholds true. where and denote the classical Bessel function of the first kind order ρ and the modified Bessel function of the first kind order ρ, respectively.
It is well known that the functions
and
generalize trigonometric and hyperbolic functions for some private values of
, respectively. For
and
, we have the following (see [
21]):
and
Utilizing this fact, we can give the following examples regarding Corollary 1.
Example 1. - i.
If , , then . Also, both and .
- ii.
If , , then, . Also, both and .
Theorem 2. Let , , , , , and . Ifthen . Proof of Theorem 2. Assume that the hypothesis of the theorem holds true. To show that
is convex of order
, it is enough to prove that
For this purpose, considering the sums (
5) and (
6) and the inequalities (
8)–(10), one can obtain that
But the expression (
14) is bounded above by
under the assumption given by (
13). So, the proof is completed by applying Lemma 2. □
Taking in Theorem 2 we deduce the following, respectively.
Corollary 2. Suppose that , and Putting certain values of in Corollary 2, we obtain the following examples:
Example 2. - i.
If , , then . Also, both and .
- ii.
If , , then . Also, both and .
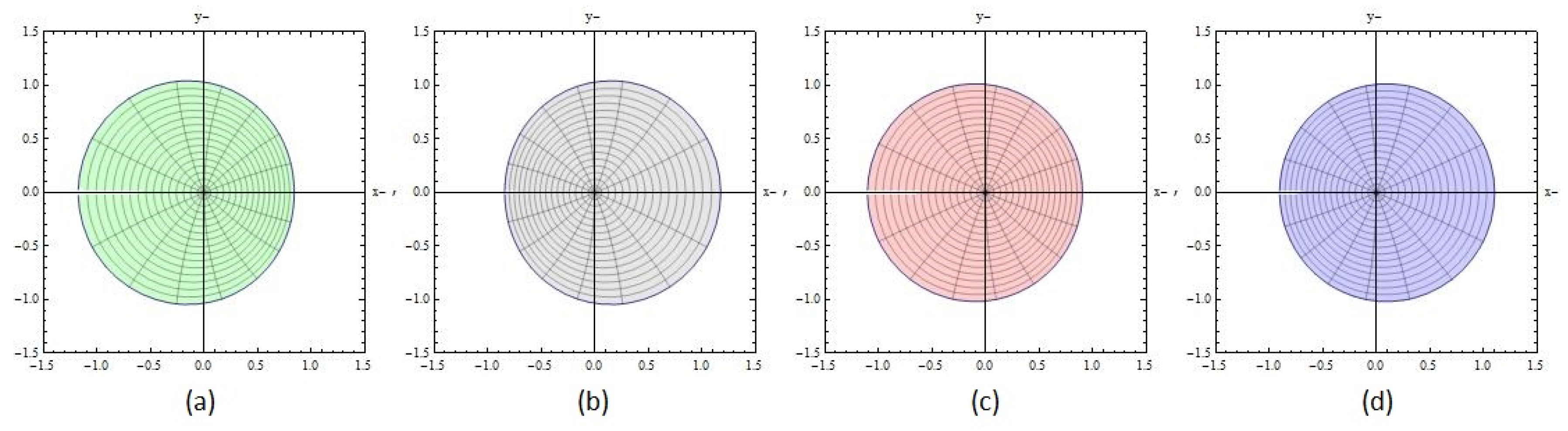
Figure 1 shows the mappings of functions
over
provided in Examples 1–4. It is clear that the image domains shown here are symmetrical with respect to the real axis.
Theorem 3. Let , , , , and . Ifthen the function . Proof of Theorem 3. In order to show that
, we need to prove that
for
and
. For this purpose, considering the function
, we will show that
. Then, using the inequalities (
8) and (9) and geometric series sum, one can easily deduce
But under the assumption given by (
16), the expression given in (
17) is bounded above by 1. This means that
. □
If we replace and in Theorem 3, we have the following results, respectively.
Corollary 3. Assume that , , , and .
- i.
If , then .
- ii.
If , then .
Example 3. Certain special values of ρ in Corollary 3 imply the following:
- i.
Let . If , then
- ii.
Let . If , then while for .
- iii.
Let . If , then while for .
Considering in Theorem 3, we obtain the following.
Corollary 4. Let , , and Example 4. The following are the examples of Corollary 4 for special values of ρ:
- a.
Let . Then, and for , while for .
- b.
Let . Then, and for , while for .
- c.
Let . Then, and for , while for .
Taking and in Corollary 4, we have the following results, respectively.
Corollary 5. Let and .
Example 5. The following are the examples of Corollary 5 for certain values of ρ:
- a.
Let . Then, for , while for .
- b.
Let . Then, is in both classes and for , while is in both classes and for .
- c.
Let . Then, is in both classes and for , while is in both classes and for .
Theorem 4. Let , , , , and . Ifthen the function . Proof of Theorem 4. To show that
, we have to prove that
for
and
. Hence, we consider the function
and show that
. In fact, it may be easily checked that
It can be easily seen that the expression given in (
19) is bounded above by 1 under the condition given by (
18). This completes the proof. □
If we replace and in Theorem 4, we have the following results, respectively:
Corollary 6. Assume that , , , and . If
- i.
, then .
- ii.
, then .
Example 6. The following are the examples of Corollary 6 for certain values of ρ:
- a.
Let . Then, is in both classes and for , while is in both classes and for .
- b.
Let . Then, is in both classes and for , while is in both classes and for .
Considering in Theorem 4, we obtain the following.
Corollary 7. Let , , and - i.
If , then
- ii.
If , then
Example 7. The following are the examples of Corollary 7 for certain values of ρ:
- a.
Let . Then, , and both and are in the class for and , respectively.
- b.
Let . Then, , and both and are in the class for and , respectively.
Taking and in Corollary 7, we give the following special cases.
Corollary 8. Let and .
- i.
If , thenand - ii.
If , then