Abstract
In this paper, we study certain geometric properties such as the starlikeness of order and the convexity of order of the generalized k-Bessel function. In addition, we establish several requirements for the parameters so that the generalized k-Bessel function belongs to some subclasses of analytic functions. Furthermore, as an application of the geometric properties, we establish certain results concerning the Hardy spaces of the generalized k-Bessel function. On the other hand, we present some corollaries concerning the classical Bessel function and the modified Bessel function . To support our geometric results, we present some specific examples of functions that map the open unit disk onto the symmetric domains with respect to the real axis.
Keywords:
analytic function; convex functions of order ζ; starlike functions of order ζ; generalized k-Bessel functions; Hardy space MSC:
30C45; 33E20; 30H05; 30H10
1. Introduction and Preliminaries
Special functions have significant applications in statistics, economics, physics, and other applied sciences. For this reason, such functions attract the attention of mathematicians and other researchers. In particular, functions that are special solutions of some differential equations attract much more attention than other functions. Some of these functions are hypergeometric, Bessel, Struve, and Lommel functions, and so on. In the last century, a number of important studies have been carried out on the special functions mentioned above.
A particular solution of the next differential equation
is known as a Bessel function of the first kind and is denoted by . The solution of the differential Equation (1) implies that has the following representation:
where represents Euler’s gamma function. For comprehensive knowledge on this function, interested readers can refer to [1]. In addition, the modified Bessel function of the first kind is a private solution of the differential equation
Also, the function has the following infinite series representation:
Another significant property of the mentioned functions is having some natural generalizations. In the literature, there exist certain natural generalizations of the Bessel functions. One of the most important of them is the generalized k-Bessel function, and it has the following infinite series representation (see [2]):
for . Here, stands for the k-gamma function, which is defined by (see [3])
for . It is known that reduces to for . On the other hand, the generalized k-Bessel function reduces to and for and , respectively (see [2]). In addition, it is known from [2] that the function is a solution of the following differential equation:
for and .
The Pochammer s-symbol is defined by
for and . For other useful properties of the Pochammer s-symbol and k-gamma function, one can refer to [3].
The outcome of this paper is as follows. In the rest of this section, certain basic concepts in geometric function theory and useful lemmas for the proofs are given. Section 2 is devoted to the geometric properties such as starlikeness and convexity generalized k-Bessel functions. Also, we determine some conditions on the parameters such that the generalized k-Bessel function belongs to the some subclasses of analytic functions defined in [4]. In Section 3, we deal with Hardy class of generalized k-Bessel functions. Also, some corollaries are indicated at the end of Section 2 and Section 3.
Let show the open unit disk and be the collection of all holomorphic functions on . Let indicate the class of all holomorphic functions normalized by
which satisfy . Also, it is known that the function f does not take the same value twice in a set; then, f is called univalent in this set. By , we indicate the collection of functions belonging to class that are univalent in . The class has various subclasses consisting of functions which have nice geometric properties. The starlike functions’ class and convex functions’ class are known as famous subclasses of . In fact, the functions in and map onto a starlike domain with respect to the origin and a convex domain, respectively. In addition, for , the class denotes the class of starlike functions of order in , while the class denotes the class of convex functions of order in . It is well known that and are also subclasses of . The classes and reduce to the classes and for , respectively. Analytic characterizations of the classes and may be given as follows:
and
In addition to the above significant function classes, there exist certain subclasses of the classes and in the literature. Two of them are the classes and , and they are defined in [4] as follows:
and
The classes and reduce to and for , respectively. Also, we simplify and by and for , respectively.
The Hadamard product of the series
is defined by
The Hardy class of all holomorphic functions inside is shown by . A regular function f in is said to belong to the Hardy class for if the set is bounded, where
It is known from [5] that is a Banach space with the norm defined by
for . Furthermore, it is known that denotes the family of bounded analytic functions in , and the set shows the collection of power series such that Additionally, is a subset of for ; see [5]. Also, for the Hardy space , the following is a significant result (see [5]):
In the last fifty years, several scholars proved certain important results about some geometric properties of the functions in the class ; see, for example, [6,7,8]. These geometric properties include univalence, starlikeness, convexity and close to convexity. Then, the same geometrical properties of certain special functions like Bessel, hypergeometric, Mittag–Leffler, and Wright are investigated by researchers using the results of [6,7,8]. Additionally, some requirements for the convex, starlike, and close-to-convex functions are determined by Eenigenburg and Keogh in [9] such that these functions belong to the Hardy space . Utilizing the results in [6,7,8,9], the Hardy space of the hypergeometric function [10], generalized Bessel function [4], Struve functions [11,12], Lommel function [13], Mittag–Leffler function [14], Wright function [15], Dini function [16], hyper-Bessel function [17], q-Bessel function [18], Rabotnov fractional exponential function [19], and so on are studied by the researchers.
Inspired by the above studies, the main objective of this paper is to present certain conditions on the parameters such that the generalized k-Bessel function
is starlike of order and convex of order on disk , respectively. It is important to emphasize here that specific examples of the given functions map the open unit disk onto some domains consisting of symmetric points with respect to the real axis. Further, we determine certain conditions for the Hadamard product such that and , where f is an regular function in . In addition, we show that the function is in the class under certain conditions. Moreover, we show that the function is in the Hardy space and bounded analytic function class under some conditions, respectively. Finally, at the end of the every subsection, we indicate certain corollaries for normalized Bessel and modified Bessel functions.
Some Key Preliminary Lemmas in Geometric Function Theory
The following useful lemmas will be used in order to prove our main results:
Lemma 1
([7]). Let and . If
then .
Lemma 2
([7]). Let and . If
then
Lemma 3
([9]). Let . If is not of the form
for some and then the following statements hold:
- a.
- There exist such that .
- b.
- If then there exist such that .
- c.
- If then .
Lemma 4
([20]). Suppose that . Then, . The value of ς is the best possible.
2. Certain Properties of Generalized k-Bessel Functions
In this part of the paper, we present certain geometrical properties of the function .
Theorem 1.
Let , , , , , and . If
then .
Proof of Theorem 1.
Suppose that the hypothesis of the theorem holds true. Due to Lemma 1, the function is starlike of order if
Replacing in Theorem 1, we deduce the following, respectively.
Corollary 1.
Suppose that , and the inequality
holds true.
- i.
- If , then
- ii.
- If , then
where and denote the classical Bessel function of the first kind order ρ and the modified Bessel function of the first kind order ρ, respectively.
It is well known that the functions and generalize trigonometric and hyperbolic functions for some private values of , respectively. For and , we have the following (see [21]):
and
Utilizing this fact, we can give the following examples regarding Corollary 1.
Example 1.
- i.
- If , , then . Also, both and .
- ii.
- If , , then, . Also, both and .
Theorem 2.
Let , , , , , and . If
then .
Proof of Theorem 2.
Assume that the hypothesis of the theorem holds true. To show that is convex of order , it is enough to prove that
Taking in Theorem 2 we deduce the following, respectively.
Corollary 2.
Suppose that , and
- i.
- If , then
- ii.
- If , then
Putting certain values of in Corollary 2, we obtain the following examples:
Example 2.
- i.
- If , , then . Also, both and .
- ii.
- If , , then . Also, both and .
Figure 1 shows the mappings of functions over provided in Examples 1–4. It is clear that the image domains shown here are symmetrical with respect to the real axis.
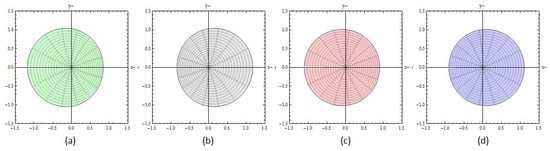
Figure 1.
(a) , (b) , (c) , (d) .
Theorem 3.
Let , , , , and . If
then the function .
Proof of Theorem 3.
In order to show that , we need to prove that for and . For this purpose, considering the function , we will show that . Then, using the inequalities (8) and (9) and geometric series sum, one can easily deduce
If we replace and in Theorem 3, we have the following results, respectively.
Corollary 3.
Assume that , , , and .
- i.
- If , then .
- ii.
- If , then .
Example 3.
Certain special values of ρ in Corollary 3 imply the following:
- i.
- Let . If , then
- ii.
- Let . If , then while for .
- iii.
- Let . If , then while for .
Considering in Theorem 3, we obtain the following.
Corollary 4.
Let , , and
- i.
- If , then
- ii.
- If , then
Example 4.
The following are the examples of Corollary 4 for special values of ρ:
- a.
- Let . Then, and for , while for .
- b.
- Let . Then, and for , while for .
- c.
- Let . Then, and for , while for .
Taking and in Corollary 4, we have the following results, respectively.
Corollary 5.
Let and .
- i.
- If , thenand
- ii.
- If , thenand
Example 5.
The following are the examples of Corollary 5 for certain values of ρ:
- a.
- Let . Then, for , while for .
- b.
- Let . Then, is in both classes and for , while is in both classes and for .
- c.
- Let . Then, is in both classes and for , while is in both classes and for .
Theorem 4.
Let , , , , and . If
then the function .
Proof of Theorem 4.
To show that , we have to prove that for and . Hence, we consider the function and show that . In fact, it may be easily checked that
If we replace and in Theorem 4, we have the following results, respectively:
Corollary 6.
Assume that , , , and . If
- i.
- , then .
- ii.
- , then .
Example 6.
The following are the examples of Corollary 6 for certain values of ρ:
- a.
- Let . Then, is in both classes and for , while is in both classes and for .
- b.
- Let . Then, is in both classes and for , while is in both classes and for .
Considering in Theorem 4, we obtain the following.
Corollary 7.
Let , , and
- i.
- If , then
- ii.
- If , then
Example 7.
The following are the examples of Corollary 7 for certain values of ρ:
- a.
- Let . Then, , and both and are in the class for and , respectively.
- b.
- Let . Then, , and both and are in the class for and , respectively.
Taking and in Corollary 7, we give the following special cases.
Corollary 8.
Let and .
- i.
- If , thenand
- ii.
- If , thenand
3. Hardy Space of Generalized k-Bessel Functions
Theorem 5.
Assume that , , , , and . Also, the inequality (13) holds true:
- i.
- If , then
- ii.
- If , then
Proof of Theorem 5.
It is known from Theorem 2 that the function under the hypothesis conditions. Also, from the infinite series representation of the Gauss hypergeometric function, it can be easily seen that
and
where and . One can obviously see that the function is not in the forms of (20) for and (21) for , respectively. Now, in view of Lemma 3, the proof is completed. □
Theorem 5 reduces to the following result for .
Corollary 9.
Let us suppose that , and the inequality (15) holds true. Then, we have the following:
- i.
- The functions and for .
- ii.
- The functions and for .
Example 8.
Taking certain values of ρ in Corollary 9, we obtain the following:
- i.
- Let . Then, and the functions and are in the class .
- ii.
- Let . Then, and the functions and are in the class .
Theorem 6.
Let suppose that , , , , and . If the function of the form (2) is in the class and , then the function
Proof of Theorem 6.
By definition of the class , the hypothesis condition implies that . Further, suppose that , which implies . Also, it is known from Corollary 3 that the function Applying Lemma 4, we conclude that which implies and so we get Now, from the relation given by (3), we deduce for and for , or equivalently, for all . In addition, by using the inequalities (8) and (9) and basic calculations, we conclude
Moreover, it is known from [22] that if the function , then for By utilizing this fact and the series sum rule given by (7), we may write that
Hence, the function is convergent in under assumption. On the other hand, it is known from [5] that implies that is continuous on which is the closure of . Due to being a compact set, is a bounded function on . So, the proof follows. □
Theorem 7.
Let , , , , , and . If , and the inequality (16) holds true, then .
Proof of Theorem 7.
By definition of the class , the assumption yields . In addition, it is known from Theorem 3 that . Since , applying Lemma 4, we deduce , which implies that □
4. Conclusions
In this paper, several geometric properties of the generalized k-Bessel function are established. As application of the convexity properties, certain sufficient conditions are established so that the mentioned function belongs to the Hardy space of analytic functions. Moreover, for the Hadamard product of the generalized k-Bessel function and the analytic function, several results are presented such that the mentioned functions are in the previously defined classes of analytic functions. Furthermore, by specializing the parameters, some direct consequences are given for the classical Bessel function and the modified Bessel function.
In the future, uniform convexity, starlikeness, and convexity associated with the exponential function, as well as Bernoulli’s lemniscate may be studied for generalized k-Bessel functions.
Author Contributions
Conceptualization, İ.A. and L.-I.C.; methodology, İ.A. and L.-I.C.; software, İ.A.; validation, İ.A. and L.-I.C.; formal analysis, İ.A. and L.-I.C.; investigation, İ.A. and L.-I.C.; resources, İ.A.; writing—original draft preparation, İ.A. and L.-I.C.; writing—review and editing, İ.A. and L.-I.C.; visualization, İ.A.; funding acquisition, L.-I.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Mondal, S.R.; Akel, M.S. Differential equation and inequalities of the generalized k-Bessel functions. J. Inequal. Appl. 2018, 2018, 175. [Google Scholar] [CrossRef]
- Díaz, R.; Pariguan, E. On hypergeometric functions and Pochhammer k-symbol. Divulg. Math. 2007, 15, 179–192. [Google Scholar]
- Baricz, Á. Bessel transforms and Hardy space of generalized Bessel functions. Mathematica 2006, 48, 127–136. [Google Scholar]
- Duren, P.L. Theory of Spaces—A Series of Monographs and Textbooks in Pure and Applied Mathematics; Academic Press: New York, NY, USA; London, UK, 1970; Volume 38. [Google Scholar]
- Owa, S.; Nunokawa, M.; Saitoh, H.; Srivastava, H.M. Close-to-convexity, starlikeness, and convexity of certain analytic functions. App. Math. Letter. 2002, 15, 63–69. [Google Scholar] [CrossRef]
- Silverman, H. Univalent functions with negative coefficients. Proc. Am. Math. Soc. 1975, 51, 109–116. [Google Scholar] [CrossRef]
- Singh, R.; Singh, S. Some sufficient conditions for univalence and starlikeness. Colloq. Math. 1982, 47, 309–314. [Google Scholar] [CrossRef][Green Version]
- Eenigenburg, P.J.; Keogh, F.R. The Hardy class of some univalent functions and their derivatives. Mich. Math. J. 1970, 17, 335–346. [Google Scholar] [CrossRef]
- Ponnusamy, S. The Hardy space of hypergeometric functions. Complex Var. Elliptic Equ. 1996, 29, 83–96. [Google Scholar] [CrossRef]
- Yağmur, N.; Orhan, H. Hardy space of generalized Struve functions. Complex Var. Elliptic Equ. 2014, 59, 929–936. [Google Scholar] [CrossRef]
- Sarkar, S.; Das, S.; Mondal, S.R. Geometric properties of normalized Galué type Struve function. Symmetry 2024, 16, 211. [Google Scholar] [CrossRef]
- Yağmur, N. Hardy space of Lommel functions. Bull. Korean Math. Soc. 2015, 52, 1035–1046. [Google Scholar] [CrossRef]
- Prajapat, J.K.; Maharana, S.; Bansal, D. Radius of Starlikeness and Hardy Space of Mittag-Leffer Functions. Filomat 2018, 32, 6475–6486. [Google Scholar] [CrossRef]
- Raza, M.; Din, M.U.; Malik, S.N. Certain geometric properties of normalized Wright functions. J. Funct. Spaces 2016, 2016, 1896154. [Google Scholar] [CrossRef]
- Din, M.U.; Raza, M.; Hussain, S.; Darus, M. Certain geometric properties of generalized Dini functions. J. Funct. Spaces 2018, 2018, 2684023. [Google Scholar] [CrossRef]
- Aktaş, İ. Certain geometric properties of a normalized hyper-Bessel function. Facta Univ. Ser. Math. Inform. 2020, 35, 179–186. [Google Scholar] [CrossRef]
- Aktaş, İ. On some geometric properties and Hardy class of q-Bessel functions. AIMS Math. 2020, 5, 3156–3168. [Google Scholar] [CrossRef]
- Raza, M.; Breaz, D.; Musthag, S.; Cotîrlǎ, L.I.; Tawfiq, F.M.O.; Rapeanu, E. Geometric properties and Hardy spaces of Rabotnov fractional exponential functions. Fractal Fract. 2024, 8, 5. [Google Scholar] [CrossRef]
- Stankiewich, J.; Stankiewich, Z. Some applications of Hadamard convolutions in the theory of functions. Ann. Univ. Mariae-Curie-Sklodowska 1986, 40, 251–265. [Google Scholar]
- Baricz, Á. Generalized Bessel Functions of the First Kind; Springer: Berlin, Germany, 2010. [Google Scholar]
- MacGregor, T.H. Functions whose derivative has a positive real part. Trans. Amer. Math. Soc. 1962, 104, 532–537. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).