Wave Solutions for a (2 + 1)-Dimensional Burgers–KdV Equation with Variable Coefficients via the Functional Expansion Method
Abstract
1. Introduction
2. Basics on the Solving Method
2.1. Description of the Functional Expansion Method
2.2. An Auxiliary Equation of the Reaction–Diffusion Type
3. Multiple Wave Solutions of the vcBKdV Equation
3.1. The Functional Expansion of the vcBKdV Equation
3.2. Explicit vcBKdV Wave Solutions
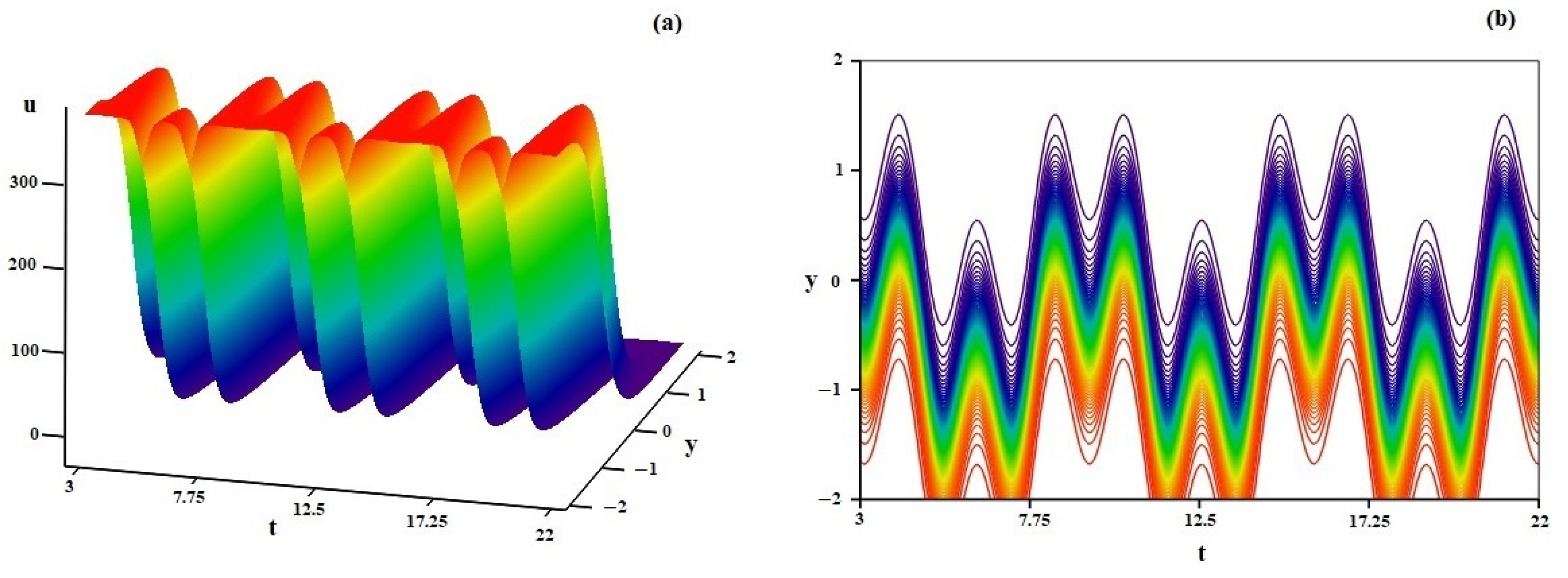
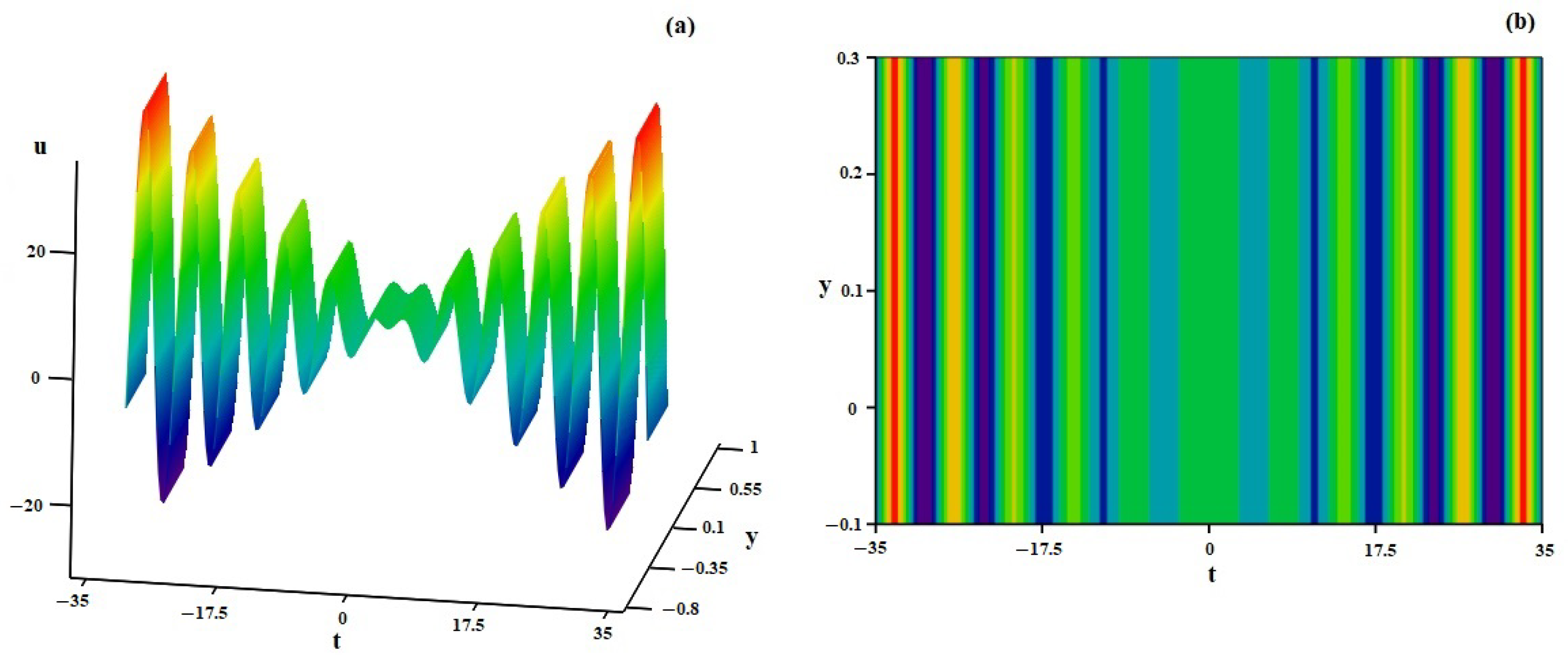
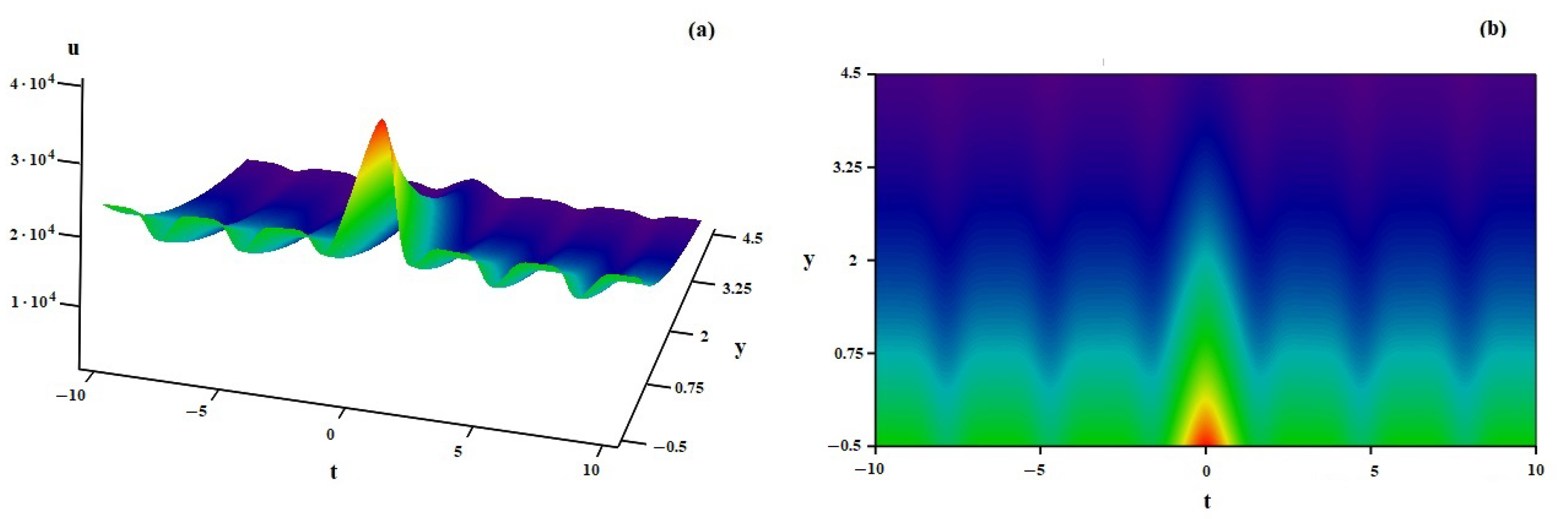
4. Discussion of Some Specific Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gerdjikov, V.S.; Stefanov, A.A. Riemann–Hilbert Problems, Polynomial Lax Pairs, Integrable Equations and Their Soliton Solutions. Symmetry 2023, 15, 1933. [Google Scholar] [CrossRef]
- Bettelheim, E.; Smith, N.R.; Meerson, B. Inverse scattering method solves the problem of full statistics of nonstationary heat transfer in the Kipnis-Marchioro-Presutti model. Phys. Rev. Lett. 2022, 128, 1130602. [Google Scholar] [CrossRef]
- Babalic, C.N. Complete integrability and complex solitons for generalized Volterra system with branched dispersion. Int. J. Mod. Phys. B 2020, 34, 2050274. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; University Press: Cambridge, UK, 2004. [Google Scholar]
- Babalic, C.N.; Carstea, A.S. On various integrable discretizations of a general twocomponent Volterra system. Phys. A Math. Theor. 2013, 46, 145205. [Google Scholar] [CrossRef]
- Babalic, C.N.; Carstea, A.S. Bilinear approach to the supersymmetric Gardner equation. Theor. Math. Phys. 2016, 188, 1172–1180. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Symmetry Methods to Partial Differential Equations; Springer: New York, NY, USA, 1986. [Google Scholar]
- Xu, M.J.; Tian, S.F.; Tu, J.M.; Zhang, T.T. Lie symmetry analysis, conservation laws, solitary and periodic waves for a coupled Burger equation. Superlattice Microst. 2017, 101, 415–428. [Google Scholar] [CrossRef]
- Bruzón, M.S.; Recio, E.; Garrido, T.M.; Márquez, A.P. Conservation laws, classical symmetries and exact solutions of the generalized KdV-Burgers-Kuramoto equation. Open Phys. 2017, 15, 433–439. [Google Scholar] [CrossRef]
- Tu, J.M.; Tian, S.F.; Xu, M.J.; Zhang, T.T. On Lie symmetries, optimal systems and explicit solutions to the Kudryashov–Sinelshchikov equation. Appl. Math. Comput. 2016, 275, 345–352. [Google Scholar] [CrossRef]
- Cimpoiasu, R. Generalized conditional symmetries and related solutions of the Grad-Shafranov equation. Phys. Plasmas 2014, 21, 042118. [Google Scholar] [CrossRef]
- Su, k.; Cao, J. Third-Order Conditional Lie–Bäcklund Symmetries of Nonlinear Reaction-Diffusion Equations. Adv. Math. Phys. 2017, 2017, 2825416. [Google Scholar] [CrossRef]
- Henneaux, M.; Teitelboim, C. Quantization of Gauge Systems; Princeton University Press: Princeton, NJ, USA, 1992. [Google Scholar]
- Constantinescu, R.; Ionescu, C. Gauge fixing procedure in the extended BRST theory. The example of the abelian two form. Ann. Phys. 2006, 15, 169–176. [Google Scholar] [CrossRef]
- Ionescu, C. The sp (3) BRST Hamiltonian formalism for the Yang-Mills fields. Mod.Phys.Lett. A. 2008, 23, 737–750. [Google Scholar] [CrossRef]
- Constantinescu, R.; Ionescu, C. Multidifferential complexes and their application to gauge theories. Int. J. Mod. Phys. A 2006, 21, 6629–6640. [Google Scholar] [CrossRef]
- Fan, E. Extended Tanh-function method and its applications to nonlinear equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Abazari, R. Application of extended tanh function method on KdV-Burgers equation with forcing term. Rom. J. Phys. 2014, 59, 3–11. [Google Scholar]
- Vahidi, J.; Zabihi, A.; Rezazadeh, H.; Ansari, R. New extended direct algebraic method for the resonant nonlinear Schrödinger equation with Kerr law nonlinearity. Optik 2021, 227, 165936. [Google Scholar] [CrossRef]
- Biswas, A. Solitary waves for power-law regularized long-wave equation and R (m, n) equation. Nonlinear Dyn. 2010, 59, 423–426. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Baleanu, D.; Machado, J.A.T.; Osman, M.S.; Rezazadeh, H.; Arshed, S.; Günerhan, H. Traveling wave solutions to nonlinear directional couplers by modified Kudryashov method. Phys. Scr. 2020, 95, 075217. [Google Scholar] [CrossRef]
- Liu, G.T.; Fan, T.Y. New applications of developed jacobi elliptic function expansion methods. Phys. Lett. A 2005, 345, 161–166. [Google Scholar] [CrossRef]
- Lu, D.; Hong, B.; Tian, L. New explicit exact solutions for the generalized coupled Hirota–Satsuma KdV system. Comput. Math. Appl. 2007, 53, 1181–1190. [Google Scholar] [CrossRef]
- Wang, X.; Li, J. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Kudryashov, N.A. A note on the G′/G-expansion method. Appl. Math. Comput. 2010, 217, 1755–1758. [Google Scholar]
- Ionescu, C.; Constantinescu, R. Solving Nonlinear Second-Order Differential Equations through the Attached Flow Method. Mathematics 2022, 10, 2811. [Google Scholar] [CrossRef]
- Zhang, C.Y. Integrable properties of a variable-coefficient Korteweg–de Vries model from Bose–Einstein condensates and fluid dynamics. J. Phys. A-Math. Gen. 2006, 39, 14353. [Google Scholar] [CrossRef]
- Mhlanga, I.E.; Khalique, C.M. A study of a generalized Benney–Luke equation with time-dependent coefficients. Nonlinear Dyn. 2017, 90, 1535. [Google Scholar] [CrossRef]
- Kumar, R.; Gupta, R.K.; Bhatia, S.S. Lie symmetry analysis and exact solutions for a variable coefficient generalised Kuramoto-Sivashinsky equation. Rom. Rep. Phys. 2014, 66, 923–928. [Google Scholar]
- Li, Z.; Zhang, X. New exact kink solutions and periodic form solutions for a generalized Zakharov–Kuznetsov equation with variable coefficients. Commun. Nonlinear Sci. 2010, 15, 3418–3422. [Google Scholar] [CrossRef]
- Meng, G.Q.; Gao, Y.T.; Yu, X.; Shen, Y.J.; Qin, Y. Painlev’e analysis, Lax pair, Bäcklund transformation and multi-soliton solutions for a generalized variable coefficient KdV-mKdV equation in fluids and plasmas. Phys. Scr. 2012, 85, 055010. [Google Scholar] [CrossRef]
- Kumar, V.; Gupta, R.K.; Jiwari, R. Painlevé Analysis, Lie Symmetries and exact solutions for variable coefficients Benjamin-Bona-Mahony-Burger (BBMB)equation. Commun. Theor. Phys. 2013, 60, 175–182. [Google Scholar] [CrossRef]
- Gupta, R.K.; Singh, K. Symmetry analysis and some exact solutions ofcylindrically symmetric null fields in general relativity. Commun. Nonlinear Sci. Numer. Simul. 2011, 6, 4189–4196. [Google Scholar] [CrossRef]
- Serkin, V.N.; Hasegawa, A.; Belyaeva, T.L. Nonautonomous matter-wave solitons near the Feshbach resonance. Phys. Rev. A 2010, 81, 023610. [Google Scholar] [CrossRef]
- Cimpoiasu, R. Multiple explicit solutions of the 2D variable coefficients Chafee–Infante model via a generalized expansion method. Mod. Phys. Lett. B 2021, 35, 2150312. [Google Scholar] [CrossRef]
- Serkin, V.N.; Hasegawa, A.; Belyaeva, T.L. Nonautonomous solitons in external potentials. Phys. Rev. Lett. 2007, 98, 074102. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Chang, L.; Liu, H. Solutions for a Class of Nonlinear PDE with Variable Coefficients Using ET and ETEM. J. Appl. Math. Phys. 2019, 7, 2685–2700. [Google Scholar] [CrossRef]
- Cimpoiasu, R.; Constantinescu, R. Invariant solutions of the Eckhaus-Kundu model with nonlinear dispersion and non-Kerr nonlinearities. Waves Random Complex Media 2021, 31, 331–341. [Google Scholar] [CrossRef]
- Cimpoiasu, R. Multiple invariant solutions of the 3 D potential Yu-Toda-Sasa-Fukuyama equation via symmetry technique. Complex. Int. J. Mod. Phys. B 2020, 34, 2050188. [Google Scholar] [CrossRef]
- Bluman, G.W.; Cole, J.D. The general similarity solution of the heat equation Complex. J. Math. Mech. 1969, 18, 025–1042. [Google Scholar]
- Clarkson, P.; Kruskal, M. New similarity reductions of the Boussinesq equation. J. Math. Mech. 1989, 30, 2201–2213. [Google Scholar] [CrossRef]
- Ozisik, M.; Bayram, M.; Secer, A.; Cinar, M.; Yusuf, A.; Sulaiman, T. Optical solitons to the (1+2)-dimensional Chiral non-linear Schrodinger equation. Opt. Quant. Electron. 2022, 54, 558. [Google Scholar] [CrossRef]
- Ozisik, M.; Secer, A.; Bayram, M. On solitary wave solutions for the extended nonlinear Schrödinger equation via the modified F-expansion method. Opt. Quant. Electron. 2023, 55, 215. [Google Scholar] [CrossRef]
- Vaganan, B.M.; Priya, T.S. Exact analytic, regular perturbation and numerical solutions of symmetry reductions of a (2+1)-dimensional KdV–Burgers equation. J. Math. Mech. 2013, 14, 1265–1275. [Google Scholar]
- Cimpoiasu, R. Symmetry reductions and new wave solutions for the 2D Burgers-Korteweg-de Vries equation. Rom. J. Phys. 2014, 59, 617–624. [Google Scholar]
- Lou, S.Y.; Tang, X.Y.; Lin, J. Similarity and conditional similarity reductions of a (2+1)-dimensional KdV equation via a direct method. J. Math. Phys. 2000, 41, 8286–8303. [Google Scholar] [CrossRef]
- Kheiri, H.; Moghaddam, M.R.; Vafaei, V. Application of the G′/G-expansion method for the Burgers, Burgers–Huxley and modified Burgers–KdV equations. Pramana J. Phys. 2011, 76, 831–842. [Google Scholar] [CrossRef]
- Helal, M.A. Soliton solution of some nonlinear partial differential equations and its applications in fluid mechanics. Appl. Math. Comput. 2002, 13, 1917–1929. [Google Scholar] [CrossRef]
- Dehghan, M. Application of the Adomian decomposition method for two-dimensional parabolic equation subject to nonstandard boundary specifications. Appl. Math. Comput. 2004, 157, 549–560. [Google Scholar] [CrossRef]
- Jeffrey, A.; Mohamad, M.N.B. Exact solutions to the KdV–Burgers’ Equation. Motion 1991, 14, 369–375. [Google Scholar] [CrossRef]
- Tanwar, D.V.; Wazwaz, A.-M. Lie symmetries and exact solutions of KdV-Burgers equation with dissipation in dusty plasma. Qual. Theor. Dyn. Syst. 2022, 21, 164. [Google Scholar] [CrossRef]
- Cimpoiasu, R.; Cimpoiasu, V.; Constantinescu, R. Nonlinear dynamical systems in various space-time dimensions. Rom. J. Phys. 2010, 55, 25–35. [Google Scholar]
- Abd-el-Malek, M.B.; Amin, A.M. Lie Group Method for Solving the Generalized Burgers’, Burgers’-KdV and KdV Equations with Time-Dependent Variable Coefficients. Symmetry 2015, 7, 1816–1830. [Google Scholar] [CrossRef]
- Kumar, V.; Kaur, L.; Kumar, A.; Koksal, M.E. Lie symmetry based-analytical and numerical approach for modified Burgers-KdV equation. Results Phys. 2018, 8, 1136–1142. [Google Scholar] [CrossRef]
- Akbar, M.A.; Ali, N.H.M.; Zayed, E.M.E. A generalized and improved-expansion method for nonlinear evolution equations. Math. Probl. Eng. 2012, 2012, 459879. [Google Scholar] [CrossRef]
- Naher, H.; Abdullah, F.A. Further extension of the generalized and improved G′/G-expansion method for nonlinear evolution equation. J. Assoc. Arab. Univ. Basic Appl. Sci. 2016, 19, 52–58. [Google Scholar] [CrossRef]
- Zhang, S. A generalized auxiliary equation method and its application to the (2+1)-dimensional KdV equations. Appl. Math. Comput. 2007, 188, 1–6. [Google Scholar] [CrossRef]
- Wen-An, L.; Hao, C.; Guo-Cai, Z. The (w/g)-expansion method and its application to vakhnenko equation. Chin. Phys. B 2009, 18, 400–404. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Pradhan, B.; Sagidullayeva, Z.; Myrzakulov, R.; Dev, A.N. Exact solutions for the Bogoyavlensky-Konopelchenko equation with variable coefficients with an efficient technique. Alex. Eng. J. 2023, 72, 287–293. [Google Scholar] [CrossRef]
- Gepreel, K.A. Exact solutions for nonlinear integral member of kadomtsev-petviashvili hierarchy differential equations using the modified (w/g)-expansion. Comput. Math. Appl. 2016, 72, 2072–2083. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cimpoiasu, R.; Constantinescu, R. Wave Solutions for a (2 + 1)-Dimensional Burgers–KdV Equation with Variable Coefficients via the Functional Expansion Method. Symmetry 2024, 16, 96. https://doi.org/10.3390/sym16010096
Cimpoiasu R, Constantinescu R. Wave Solutions for a (2 + 1)-Dimensional Burgers–KdV Equation with Variable Coefficients via the Functional Expansion Method. Symmetry. 2024; 16(1):96. https://doi.org/10.3390/sym16010096
Chicago/Turabian StyleCimpoiasu, Rodica, and Radu Constantinescu. 2024. "Wave Solutions for a (2 + 1)-Dimensional Burgers–KdV Equation with Variable Coefficients via the Functional Expansion Method" Symmetry 16, no. 1: 96. https://doi.org/10.3390/sym16010096
APA StyleCimpoiasu, R., & Constantinescu, R. (2024). Wave Solutions for a (2 + 1)-Dimensional Burgers–KdV Equation with Variable Coefficients via the Functional Expansion Method. Symmetry, 16(1), 96. https://doi.org/10.3390/sym16010096






