Jacobi Stability for T-System
Abstract
1. Introduction
2. Preliminary Results
3. SODE Formulation of the T-System
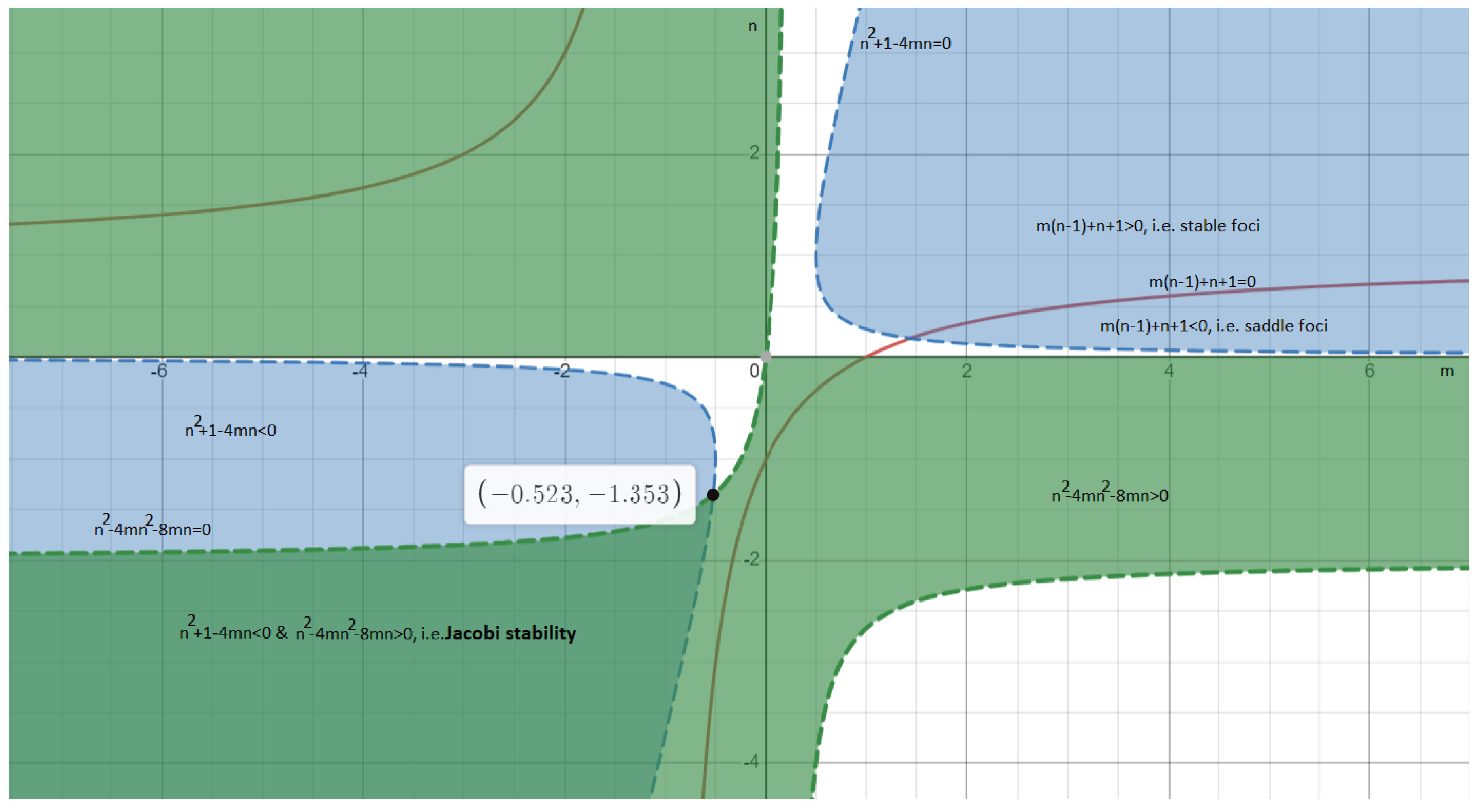
4. Jacobi Stability Analysis of the T-System
Dynamics of the Deviation Vector for the T-System
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Kosambi–Cartan–Chern Geometric Theory and Jacobi Stability
- If , then the geodesics “add up together” (i.e., Jacobi stability of the geodesics occurs);
- If , then the geodesics “disperse” (i.e., no Jacobi stability of the geodesics occurs).
References
- Tigan, G. Bifurcation and the stability in a system derived from the Lorentz system. In Proceedings of the Third Internationl Colloquium: Mathematics in Engineering and Numerical Physics, Bucharest, Romania, 7–9 October 2004; Balkan Society of Geometers, Geometry Balkan Press: Bucharest, Romania, 2005; pp. 265–272. Available online: http://www.mathem.pub.ro/proc/bsgp-12/K12-TIG.PDF (accessed on 10 September 2023).
- Tigan, G. Analysis of a dynamical system derived from the Lorenz system. Sci. Bull. Politeh. Univ. Timis. 2005, 50, 61–72. [Google Scholar]
- Tigan, G.; Opriş, D. Analysis of a 3D chaotic system. Chaos Solitons Fractals 2008, 36, 1315–1319. [Google Scholar] [CrossRef]
- Van Groder, R.A.; Roy Choudhury, S. Analytical Hopf bifurcation and stability analysis of T-system. Commun. Theor. Phys. 2011, 55, 609–616. [Google Scholar] [CrossRef]
- Tigan, G.; Constantinescu, D. Heteroclinic orbits in T and Lu systems. Chaos Solitons Fractals 2009, 42, 20–23. [Google Scholar] [CrossRef]
- Algaba, A.; Fernandez-Sanchez, F.; Merino, M.; Rodríguez-Luis, A. On Shilnikov analysis on homoclinic and heteroclinic orbits of the T-system. J. Comput. Nonlinear Dyn. 2013, 8, 027001. [Google Scholar] [CrossRef]
- Zhang, R. Bifurcation analysis for T-system with delayed feedback and its applications to control of chaos. Nonlinear Dyn. 2013, 72, 629–641. [Google Scholar] [CrossRef]
- Constantinescu, D.; Tigan, G.; Zhang, X. Coexistence of Chaotic Attractor and Unstable Limit Cycles in a 3D Dynamical System. Available online: https://open-research-europe.ec.europa.eu/articles/1-50/v1 (accessed on 2 May 2023).
- Constantinescu, D. On the Bifurcations of a 3D Symmetric Dynamical System. Symmetry 2023, 15, 923. [Google Scholar] [CrossRef]
- Llibre, J.; Zhang, X. Invariant algebraic surfaces of the Lorenz system. J. Math. Phys. 2002, 43, 1622–1645. [Google Scholar] [CrossRef]
- Liu, X.; Hong, L.; Yang, L. Fractional-order complex T-system: Bifurcations, chaos control and synchronization. Nonlinear Dyn. 2014, 75, 589–602. [Google Scholar] [CrossRef]
- Lorentz, E. Deterministic nonperiodic flows. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Chua, L.O. Nonlinear circuits. IEEE Trans. Circ. Syst. 1984, 31, 69–87. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G. New Chaotic Attractor Coined. Int. J. Bifurc. Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Yan, Z. Hopf bifurcation in the Lorenz-type chaotic system. Chaos Solitons Fractals 2007, 31, 1135–1142. [Google Scholar] [CrossRef]
- Tee, L.S.; Salleh, Z. Dynamical Analysis of a Modified Lorenz System. J. Math. 2013, 2013, 820946. [Google Scholar] [CrossRef][Green Version]
- Harko, T.; Ho, C.Y.; Leung, C.S.; Yip, S. Jacobi stability analysis of Lorenz system. Int. J. Geom. Methods Mod. Phys. 2015, 12, 1550081. [Google Scholar] [CrossRef]
- Munteanu, F.; Ionescu, A. Analyzing the Nonlinear Dynamics of a Cubic Modified Chua’s Circuit System. In Proceedings of the 2021 International Conference on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 27–29 May 2021; pp. 1–6. [Google Scholar]
- Munteanu, F. Analyzing the Jacobi Stability of Lü’s Circuit System. Symmetry 2022, 14, 1248. [Google Scholar] [CrossRef]
- Gupta, M.K.; Yadav, C.K. Jacobi stability of modified Chua circuit system. Int. J. Geom. Methods Mod. Phys. 2017, 14, 1750089. [Google Scholar] [CrossRef]
- Thom, R. Stabilité Structurelle et Morphogénèse; Essai d’une Théorie Générale des Modèles; Benjamin, W.A., Ed.; Publisher Benjamin-Cummings: Reading, MA, USA, 1972; 362p. (In French) [Google Scholar]
- Zeeman, E.C. Catastrophe Theory. Sci. Am. 1976, 234, 65–83. [Google Scholar] [CrossRef]
- Antonelli, P.L.; Ingarden, R.S.; Matsumoto, M. The Theories of Sprays and Finsler Spaces with Application in Physics and Biology; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 1993. [Google Scholar]
- Antonelli, P.L. Equivalence Problem for Systems of Second Order Ordinary Differential Equations, Encyclopedia of Mathematics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Antonelli, P.L. Handbook of Finsler Geometry; Kluwer Academic Publishers: Boston, MA, USA, 2003. [Google Scholar]
- Antonelli, P.L.; Bucătaru, I. New results about the geometric invariants in KCC-theory. An. St. Univ.” Al. I. Cuza” Iasi. Mat. NS 2001, 47, 405–420. [Google Scholar]
- Bao, D.; Chern, S.S.; Shen, Z. An Introduction to Riemann–Finsler Geometry; Graduate Texts in Mathematics; Springer: New York, NY, USA, 2000; Volume 200. [Google Scholar]
- Udrişte, C.; Nicola, R. Jacobi stability for geometric dynamics. J. Dyn. Syst. Geom. Theor. 2007, 5, 85–95. [Google Scholar] [CrossRef]
- Sabău, S.V. Systems biology and deviation curvature tensor. Nonlinear Anal. Real World Appl. 2005, 6, 563–587. [Google Scholar] [CrossRef]
- Sabău, S.V. Some remarks on Jacobi stability. Nonlinear Anal. 2005, 63, 143–153. [Google Scholar] [CrossRef]
- Bohmer, C.G.; Harko, T.; Sabau, S.V. Jacobi stability analysis of dynamical systems—Applications in gravitation and cosmology. Adv. Theor. Math. Phys. 2012, 16, 1145–1196. [Google Scholar] [CrossRef]
- Harko, T.; Pantaragphong, P.; Sabau, S.V. Kosambi–Cartan–Chern (KCC) theory for higher order dynamical systems. Int. J. Geom. Methods Mod. Phys. 2016, 13, 1650014. [Google Scholar] [CrossRef]
- Gupta, M.K.; Yadav, C.K. Rabinovich-Fabrikant system in view point of KCC theory in Finsler geometry. J. Interdiscip. Math. 2019, 22, 219–241. [Google Scholar] [CrossRef]
- Munteanu, F. A Study of the Jacobi Stability of the Rosenzweig–MacArthur Predator–Prey System through the KCC Geometric Theory. Symmetry 2022, 14, 1815. [Google Scholar] [CrossRef]
- Munteanu, F.; Grin, A.; Musafirov, E.; Pranevich, A.; Şterbeţi, C. About the Jacobi Stability of a Generalized Hopf–Langford System through the Kosambi–Cartan–Chern Geometric Theory. Symmetry 2023, 15, 598. [Google Scholar] [CrossRef]
- Munteanu, F. On the Jacobi Stability of Two SIR Epidemic Patterns with Demography. Symmetry 2023, 15, 1110. [Google Scholar] [CrossRef]
- Kosambi, D.D. Parallelism and path-space. Math. Z. 1933, 37, 608–618. [Google Scholar] [CrossRef]
- Cartan, E. Observations sur le memoire precedent. Math. Z. 1933, 37, 619–622. [Google Scholar] [CrossRef]
- Chern, S.S. Sur la geometrie dn systeme d’equations differentielles du second ordre. Bull. Sci. Math. 1939, 63, 206–249. [Google Scholar]
- Miron, R.; Hrimiuc, D.; Shimada, H.; Sabău, S.V. The Geometry of Hamilton and Lagrange Spaces; Book Series Fundamental Theories of Physics (FTPH 118); Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Miron, R.; Bucătaru, I. Finsler–Lagrange Geometry. Applications to Dynamical Systems; Romanian Academy: Bucharest, Romania, 2007. [Google Scholar]
- Munteanu, F. On the semispray of nonlinear connections in rheonomic Lagrange geometry. In Finsler and Lagrange Geometries, Proceedings of the Finsler–Lagrange Geometries Conference, Iaşi, Romania, 26–31 August 2002; Springer: Dordrecht, The Netherlands, 2003; pp. 129–137. [Google Scholar]
- Yamasaki, K.; Yajima, T. Lotka–Volterra system and KCC theory: Differential geometric structure of competitions and predations. Nonlinear Anal. Real World Appl. 2013, 14, 1845–1853. [Google Scholar] [CrossRef]
- Abolghasem, H. Stability of circular orbits in Schwarzschild spacetime. Int. J. Pure Appl. Math. 2013, 12, 131–147. [Google Scholar]
- Abolghasem, H. Jacobi stability of Hamiltonian systems. Int. J. Pure Appl. Math. 2013, 87, 181–194. [Google Scholar] [CrossRef]
| Case | Conditions | Equilibrium Point Type |
|---|---|---|
| 1 | O is the only one equilibrium point | |
| O is asymptotically stable iff , and | ||
| or O is unstable iff or or ( and ). | ||
| 2 | O, , are three equilibrium points, | |
| O is asymptotically stable iff , and | ||
| or O is unstable iff or or ( and ) | ||
| and is asymptotically stable iff and , | ||
| otherwise is unstable. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munteanu, F. Jacobi Stability for T-System. Symmetry 2024, 16, 84. https://doi.org/10.3390/sym16010084
Munteanu F. Jacobi Stability for T-System. Symmetry. 2024; 16(1):84. https://doi.org/10.3390/sym16010084
Chicago/Turabian StyleMunteanu, Florian. 2024. "Jacobi Stability for T-System" Symmetry 16, no. 1: 84. https://doi.org/10.3390/sym16010084
APA StyleMunteanu, F. (2024). Jacobi Stability for T-System. Symmetry, 16(1), 84. https://doi.org/10.3390/sym16010084






