Detecting Phase Transitions through Non-Equilibrium Work Fluctuations
Abstract
1. Introduction
2. Theory and Methods
2.1. Work and Free Energy for Markov Chains
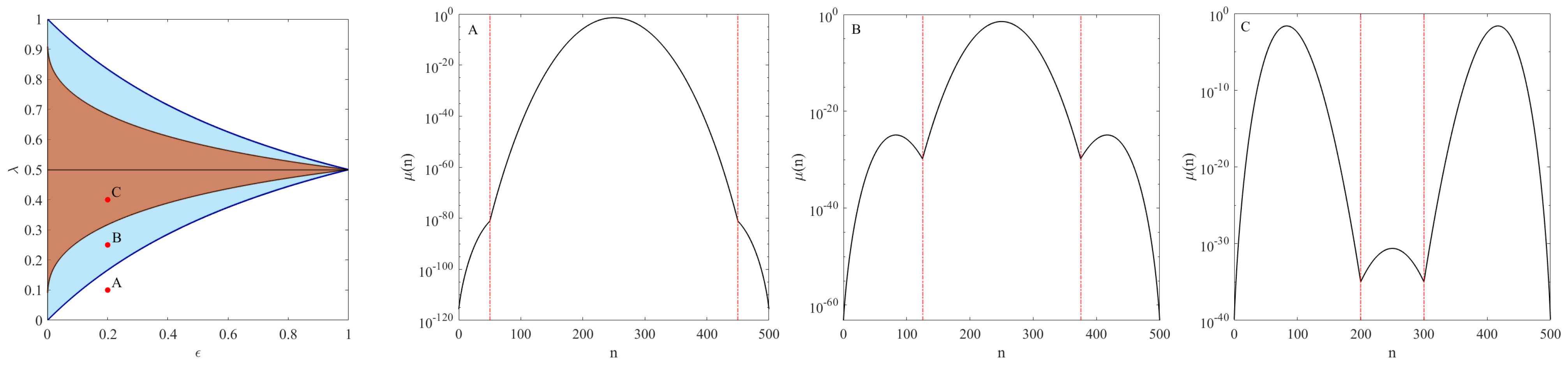
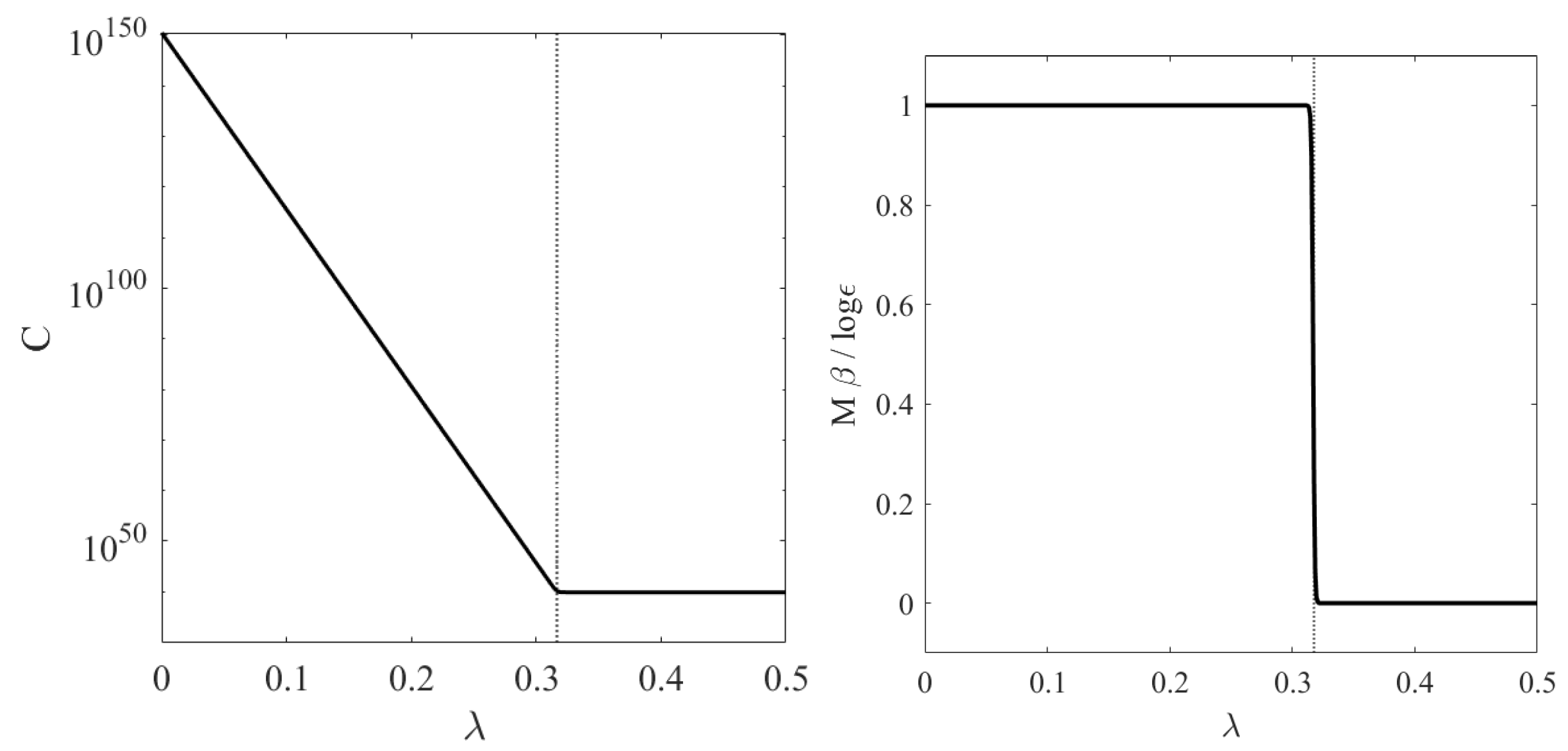
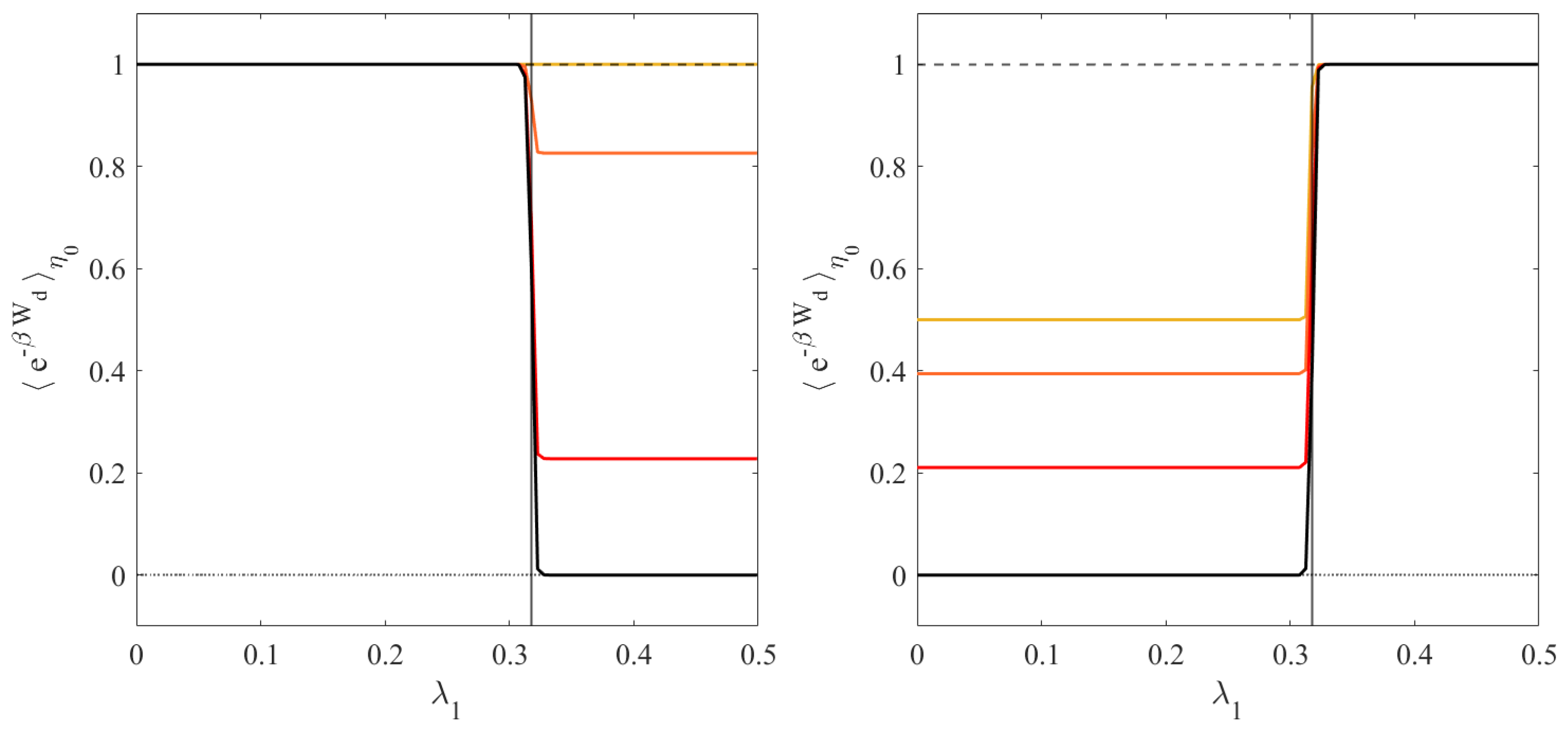
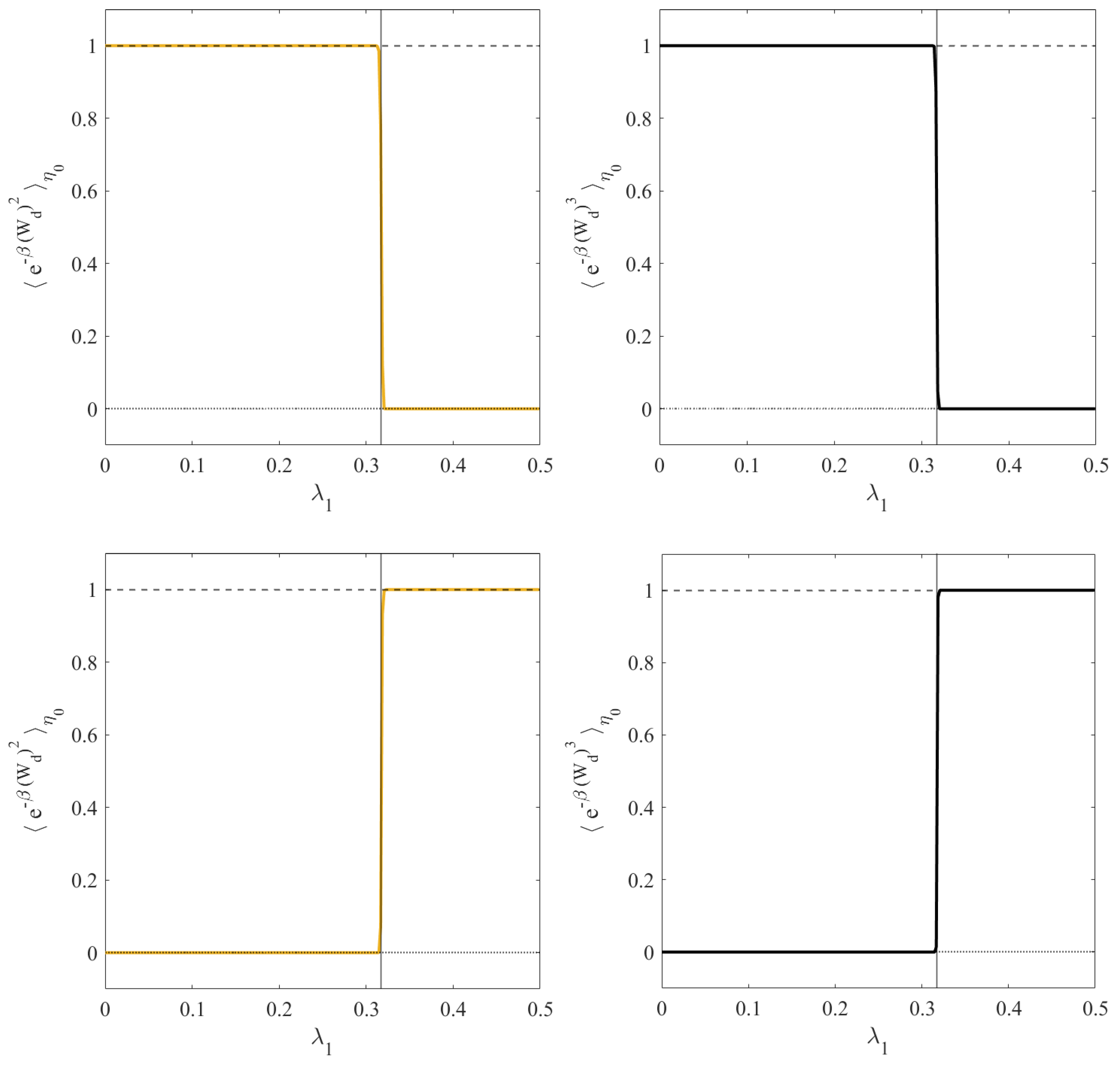
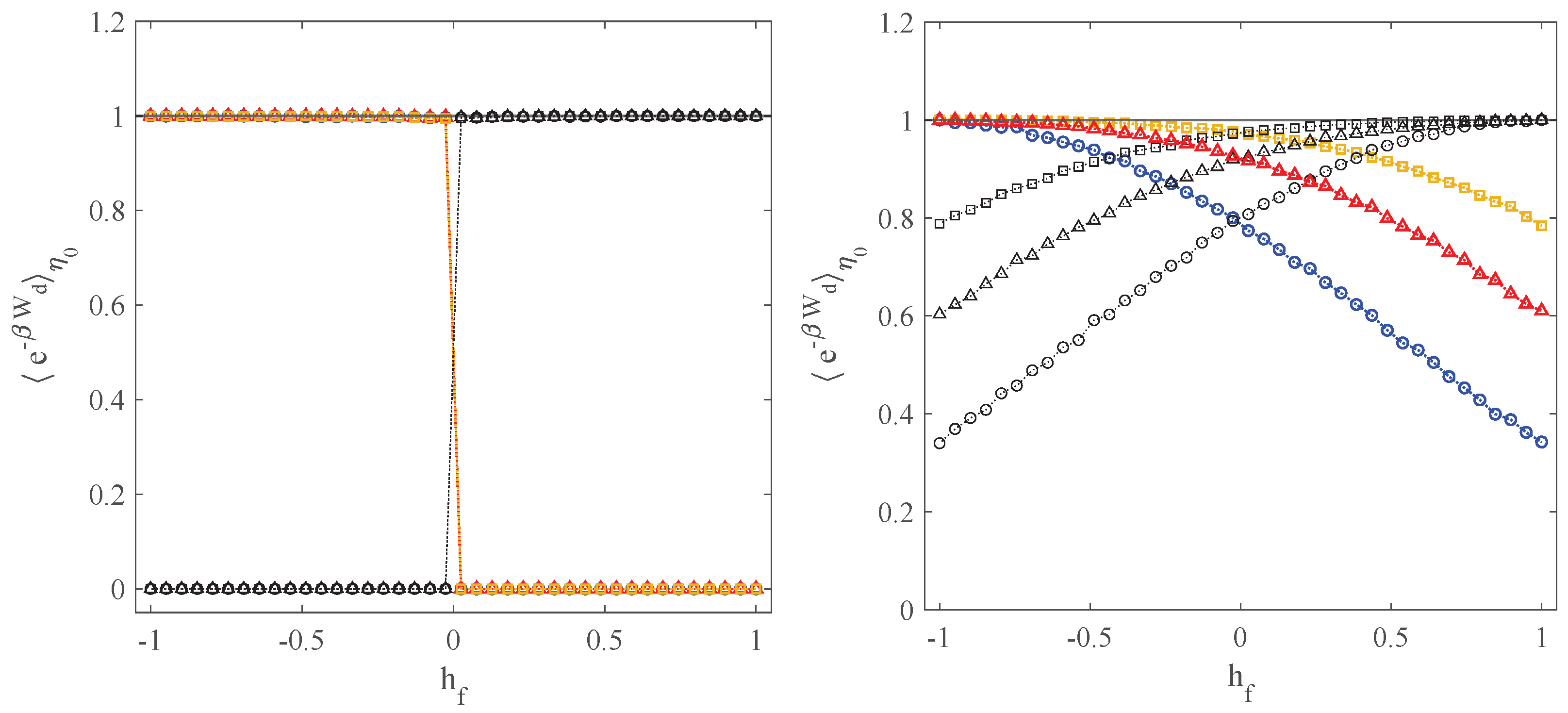
2.2. State Space Truncation and Absolute Irreversibility
3. The Models
3.1. The Urn Model
3.2. The 2D Ising Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bennett, C.H. Efficient estimation of free energy differences from monte carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Widom, B. Some topics in the theory of fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-temperature equation of state by a perturbation method. ii. Polar gases. J. Chem. Phys. 1955, 23, 1915–1922. [Google Scholar] [CrossRef]
- Evans, D.J.; Searles, D.J. The fluctuation theorem. Adv. Phys. 2002, 52, 1529. [Google Scholar] [CrossRef]
- Evans, D.J.; Cohen, E.G.D.; Morriss, G.P. Probability of second law violations in shearing steady states. Phys. Rev. Lett. 1993, 71, 2401. [Google Scholar] [CrossRef] [PubMed]
- Jepps, O.G.; Rondoni, L. A dynamical-systems interpretation of the dissipation function, T-mixing and their relation to thermodynamic relaxation. J. Phys. A Math. Theor. 2016, 49, 154002. [Google Scholar] [CrossRef]
- Jarzynski, C. Non-equilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Crooks, G.E. Non-equilibrium measurements of free energy differences for microscopically reversible markovian systems. J. Stat. Phys. 1998, 90, 1481–1487. [Google Scholar] [CrossRef]
- Crooks, G.E. Path-ensemble averages in systems driven far from equilibrium. Phys. Rev. E 2000, 61, 2361–2366. [Google Scholar] [CrossRef]
- Hatano, T.; Sasa, S. Steady-state thermodynamics of langevin systems. Phys. Rev. Lett. 2001, 86, 3463. [Google Scholar] [CrossRef]
- Marconi, U.M.B.; Puglisi, A.; Rondoni, L.; Vulpiani, A. Fluctuation–dissipation: Response theory in statistical physics. Phys. Rep. 2008, 461, 111–195. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef]
- Cohen, E.G.D.; Mauzerall, D. A note on the jarzynski equality. J. Stat. Mech. Theory Exp. 2004, 2004, P07006. [Google Scholar] [CrossRef]
- Vilar, J.M.G.; Rubi, J.M. Failure of the work-hamiltonian connection for free-energy calculations. Phys. Rev. Lett. 2008, 100, 020601. [Google Scholar] [CrossRef] [PubMed]
- Talkner, P.; Hänggi, P. Open system trajectories specify fluctuating work but not heat. Phys. Rev. E 2016, 94, 022143. [Google Scholar] [CrossRef] [PubMed]
- Peliti, L. On the work—Hamiltonian connection in manipulated systems. J. Stat. Mech. Theory Exp. 2008, 2008, P05002. [Google Scholar] [CrossRef]
- Vilar, J.M.G.; Rubi, J.M. Vilar and rubi reply. Phys. Rev. Lett. 2008, 101, 098902. [Google Scholar] [CrossRef]
- Ciliberto, S. Experiments in stochastic thermodynamics: Short history and perspectives. Phys. Rev. X 2017, 7, 021051. [Google Scholar] [CrossRef]
- Liphardt, J.; Dumont, S.; Smith, S.B.; Tinoco, I.; Bustamante, C. Equilibrium information from non-equilibrium measurements in an experimental test of jarzynski’s equality. Science 2002, 296, 1832–1835. [Google Scholar] [CrossRef]
- Monge, A.M.; Manosas, M.; Ritort, F. Experimental test of ensemble inequivalence and the fluctuation theorem in the force ensemble in dna pulling experiments. Phys. Rev. E 2018, 98, 032146. [Google Scholar] [CrossRef]
- Peliti, L. Comment on “failure of the work-hamiltonian connection for free-energy calculations”. Phys. Rev. Lett. 2008, 101, 098903. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, C.; Liphardt, J.; Ritort, F. The Non-equilibrium Thermodynamics of Small Systems. Phys. Today 2005, 58, 43–48. [Google Scholar] [CrossRef]
- Lua, R.C.; Grosberg, A.Y. Practical applicability of the jarzynski relation in statistical mechanics: A pedagogical example. J. Phys. Chem. B 2005, 109, 6805–6811. [Google Scholar] [CrossRef] [PubMed]
- Crooks, G.E.; Jarzynski, C. Work distribution for the adiabatic compression of a dilute and interacting classical gas. Phys. Rev. E 2007, 75, 021116. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Stochastic and macroscopic thermodynamics of strongly coupled systems. Phys. Rev. X 2017, 7, 011008. [Google Scholar] [CrossRef]
- Hansen, N.; Van Gunsteren, W.F. Practical aspects of free-energy calculations: A review. J. Chem. Theory Comput. 2014, 10, 2632–2647. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in monte carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Pohorille, A.; Jarzynski, C.; Chipot, C. Good practices in free-energy calculations. J. Phys. Chem. B 2010, 114, 10235–10253. [Google Scholar] [CrossRef]
- Wu, D.; Kofke, D.A. Phase-space overlap measures. ii. Design and implementation of staging methods for free-energy calculations. J. Chem. Phys. 2005, 123, 084109. [Google Scholar] [CrossRef]
- Colangeli, M.; Di Francesco, A.; Rondoni, L. Finite Reservoirs Corrections to Hamiltonian Systems Statistics and Time Symmetry Breaking. Symmetry 2023, 15, 1268. [Google Scholar] [CrossRef]
- Hack, P.; Gottwald, S.; Braun, D.A. Jarzyski’s Equality and Crooks’ Fluctuation Theorem for General Markov Chains with Application to Decision-Making Systems. Entropy 2022, 42, 1731. [Google Scholar] [CrossRef]
- Ge, H.; Qian, M. Generalized Jarzynski’s equality in inhomogeneous Markov chains. J. Math. Phys. 2007, 48, 053302. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Vaikuntanathan, S. Non-equilibrium detailed fluctuation theorem for repeated discrete feedback. Phys. Rev. E 2010, 82, 061120. [Google Scholar] [CrossRef] [PubMed]
- Murashita, Y.; Funo, K.; Ueda, M. Non-equilibrium equalities in absolutely irreversible processes. Phys. Rev. E 2014, 90, 042110. [Google Scholar] [CrossRef] [PubMed]
- Murashita, Y.; Ueda, M. Gibbs paradox revisited from the fluctuation theorem with absolute irreversibility. Phys. Rev. Lett. 2017, 118, 060601. [Google Scholar] [CrossRef] [PubMed]
- Funo, K.; Murashita, Y.; Ueda, M. Quantum non-equilibrium equalities with absolute irreversibility. New J. Phys. 2015, 17, 075005. [Google Scholar] [CrossRef]
- Manikandan, S.K.; Elouard, C.; Jordan, A.N. Fluctuation theorems for continuous quantum measurements and absolute irreversibility. Phys. Rev. A 2019, 99, 022117. [Google Scholar] [CrossRef]
- Cirillo, E.N.; Colangeli, M.; Muntean, A.; Richardson, O.; Rondoni, L. Deterministic reversible model of non-equilibrium phase transitions and stochastic counterpart. J. Phys. A Math. Theor. 2020, 53, 305001. [Google Scholar] [CrossRef]
- Stroock, D.J. An Introduction to Markov Processes; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Billingsley, P. Probability and Measures; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Feller, W. An Introduction to Probability. Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 1968. [Google Scholar]
- Sekimoto, K. Stochastic Energetics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Hoang, D.-T.; Venkatesh, B.P.; Han, S.; Jo, J.; Watanabe, G.; Choi, M.-S. Scaling law for irreversible entropy production in critical systems. Sci. Rep. 2016, 6, 27603. [Google Scholar] [CrossRef]
- Kac, M. Probability and Related Topics in Physical Sciences, 1 of Lectures in Applied Mathematics; Interscience Publishers: Geneva, Switzerland, 1959. [Google Scholar]
- Cirillo, E.N.; Colangeli, M.; Richardson, O.; Rondoni, L. Deterministic model of battery, uphill currents, and nonequilibrium phase transitions. Phys. Rev. E 2021, 103, 032119. [Google Scholar] [CrossRef]
- Cirillo, E.N.; Colangeli, M.; Di Francesco, A.; Kröger, M.; Rondoni, L. Transport and nonequilibrium phase transitions in polygonal urn models. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 093127. [Google Scholar] [CrossRef] [PubMed]
- Cirillo, E.N.; Colangeli, M.; Kröger, M.; Rondoni, L. Nonequilibrium phase transitions in feedback-controlled three-dimensional particle dynamics. Phys. Rev. Res. 2023, 5, 043063. [Google Scholar] [CrossRef]
- Godreche, C.; Luck, J.M. Non-equilibrium dynamics of urn models. J. Phys. Condens. Mat. 2002, 14, 1601–1615. [Google Scholar] [CrossRef]
- Dette, H. On a generalization of the Ehrenfest urn model. J. Appl. Prob. 1994, 31, 930–939. [Google Scholar] [CrossRef]
- Ohkubo, J.; Yasuda, M.; Tanaka, K. Preferential urn model and nongrowing complex networks. Phys. Rev. E 2005, 72, 065104. [Google Scholar] [CrossRef] [PubMed]
- Siegmund, D.; Yakir, B. An urn model of diaconis. Annal. Prob. 2005, 33, 2036–2042. [Google Scholar] [CrossRef]
- Chen, M.-R.; Hsiau, S.-R. On a generalized q-urn model. Prob. Eng. Sci. 2015, 29, 99–115. [Google Scholar] [CrossRef]
- Idriss, S. Nonlinear unbalanced urn models via stochastic approximation. Meth. Comput. Appl. Prob. 2022, 24, 413–430. [Google Scholar] [CrossRef]
- Zhang, L.-X.; Hu, F.; Cheung, S.H.; Chan, W.S. Asymptotic properties of multicolor randomly reinforced Pólya urns. Adv. Appl. Prob. 2014, 46, 585–602. [Google Scholar] [CrossRef]
- Kao, Y.M.; Luan, P.G. Poincare cycle of a multibox Ehrenfest urn model with directed transport. Phys. Rev. E 2003, 67, 031101. [Google Scholar] [CrossRef]
- Chen, M.-R.; Kuba, M. On generalized Pólya urn models. J. Appl. Prob. 2013, 50, 1169–1186. [Google Scholar] [CrossRef]
- Bai, Z.D.; Hu, F.F.; Zhang, L.X. Gaussian approximation theorems for urn models and their applications. Annal. Appl. Prob. 2002, 12, 1149–1173. [Google Scholar] [CrossRef]
- Klein, M.J. Entropy and the Ehrenfest urn model. Physica 1956, 22, 569–575. [Google Scholar] [CrossRef]
- Thornblad, E. The dominating colour of an infinite Pólya urn model. J. Appl. Prob. 2016, 53, 914–924. [Google Scholar] [CrossRef][Green Version]
- Presutti, E. Scaling Limits in Statistical Mechanics and Microstructures in Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colangeli, M.; Di Francesco, A.; Rondoni, L. Detecting Phase Transitions through Non-Equilibrium Work Fluctuations. Symmetry 2024, 16, 125. https://doi.org/10.3390/sym16010125
Colangeli M, Di Francesco A, Rondoni L. Detecting Phase Transitions through Non-Equilibrium Work Fluctuations. Symmetry. 2024; 16(1):125. https://doi.org/10.3390/sym16010125
Chicago/Turabian StyleColangeli, Matteo, Antonio Di Francesco, and Lamberto Rondoni. 2024. "Detecting Phase Transitions through Non-Equilibrium Work Fluctuations" Symmetry 16, no. 1: 125. https://doi.org/10.3390/sym16010125
APA StyleColangeli, M., Di Francesco, A., & Rondoni, L. (2024). Detecting Phase Transitions through Non-Equilibrium Work Fluctuations. Symmetry, 16(1), 125. https://doi.org/10.3390/sym16010125







