Boundedness in the Bloch Space of Symmetric Domain for a Class of Multi-Valent Meromorphic Functions Given by a Fractional Integral

Abstract

Convolution operators have profited in various areas of science. They are utilized in the investigations of computing techniques. A new convolution operator linked to a specific class of multi-valent meromorphic functions in the punctured unit disk (symmetric domain) is formulated. This analysis uncovers certain properties on the connections as well as the power series. We study a novel class of holomorphic functions concerning the recommended new operator. The second part of the outcome concerns the boundedness of the suggested difference structure given by the proposed operator. We focus on the Bloch space of meromorphic functions in the open unit disk. In this case, we use the spherical derivative. To obtain the maximum value of the polar derivative of the polynomials created by their partial sums, we use their partial sums as applications of the suggested operator.

1. Background

The investigation of the operator theory is closely communicated via the themes of the functional theory. Numerous suggested operators are given in different spaces, including holomorphic function spaces. For occurrence, Beurling’s theorem describes the a function, quantity, or property which remains unchanged when a specified transformation is applied. Beurling realized the knowledge as the convolution of the independent variable on special spaces, such as Hardy space. The understanding in dealing with convolution operators is recognized in different operators, and explicitly in different subspaces of holomorphic functions. A key idea in mathematics and signal processing is the convolution operator, which mixes two functions to create a third. Asterisks $(\ast )$ are frequently used to indicate it. Special functions might be used as the input functions for convolution when applied to special functions. Special functions are mathematical operations that are extensively used in many fields of research and engineering. These operations have special characteristics that render them valuable in particular contexts. Specific instances of convolution employing special functions are as follows. (1) Convolution with Gaussians: The additional Gaussian function is the result of the convolution of two Gaussian functions. In signal processing, image processing, and statistics, this feature is frequently exploited. (2) The convolution of Bessel functions: In both science and engineering, Bessel functions, a family response to Bessel’s differential equation, are used in a variety of different contexts. Two Bessel functions are combined to create a third Bessel function [1]. The convolution operators go through the definition of all operators (derivative and integral) in the field of fractional calculus. Many image processing and computer vision techniques are based on the potent method of convolution. The knowledge of how filters and kernels can be used to extract data from images and carry out different operations requires knowledge of this fundamental idea. The fundamental principle of convolution in image processing is to move a tiny matrix (the kernel or filter) over the image while multiplying the values of the kernel by the corresponding image pixels in a pixel-by-pixel manner. The output of these multiplications is then added together to create the kernel’s central value, which is subsequently superimposed over the present location in the image. For each position in the image that is viable, this process is completed [2].

The notion of typical integer-order operators (such as addition, subtraction, multiplication, and division) is extended in mathematics by fractional operators to non-integer or fractional orders; fractional calculus especially makes extensive use of fractional operators in a variety of scientific and engineering domains. Mathematicians who study fractional calculus work to extend the idea of differentiation and integration to non-integer orders. It provides derivatives and integrals of fractional or non-integer orders that can be utilized to describe systems and processes with long-range dependency issues, memory impacts, and non-local actions (see [3]).

In all parts of the complex plane aside from isolated singularities, where it may have poles, meromorphic functions are defined and analytic (holomorphic). In its simplest form, it is a function that, with the exception of certain particular points where it contains poles, behaves smoothly and well practically everywhere in the complex plane. Meromorphic functions have certain intriguing characteristics, and they are important in the theory of functions of a complex variable and complex analysis. They are employed in the investigation of residue calculus, contour integrals, and numerous other facets of complex analysis. Rational, trigonometric, and exponential functions are a few prominent illustrations of meromorphic functions. For instance, the function $\phi \left(z\right)=1/z$ has a simple pole at the origin but is otherwise meromorphic throughout the complex plane. Similar to the last example, the function $\psi \left(z\right)=exp\left(z\right)$ does not have any singularities and is meromorphic across the whole complex plane (see [4]). The main well-known convolution operator, which is given by a special function (confluent hypergeometric function) is the Carlson–Shaffer operator [5]. This operator is suggested for the normalized analytic functions. Later, it was generalized utilizing different classes such as the multi-valent, meromorphic and meropmorphic multi-valent functions.

In this investigation, we continue to present a new convolution operator by using the generalized Mittag–Leffler function. The generalization is occurred by using the Prabhakar fractional integral operator. The suggested operator will be linked to a class of multi-valent meromorphic functions. Accordingly, we recommend a specific class of holomorphic functions based on the convolution operator studding its geometric presentation. Additionally, we explore the actual case of a structure enclosing the operator. We indicate that this operator can be formulated in a type of fractional differential equation. In order to ascertain the greatest value of the polar derivative of polynomials created by their partial sums, we choose to apply the suggested operator to their partial sums.

2. Preliminaries

We formulate a new convolution operator related to the special class of multi-valent meromorphic functions ${\prod }_k\left(\rho \right)$ involving the functions $\upsilon$ with the structure

$$\upsilon \left(z\right)=z^{-\rho }+\sum _{n=k}^{\infty }{\upsilon }_n{z}^{n-\rho },$$

(1)

whenever $k\in \mathbb{N}$ and $n-\rho \in \mathbb{N}$. A recapture of the function $\upsilon$ of Equation (1) is known as a meromorphic owning a pole at origin, such that $\upsilon \left(z\right)-z^{-\rho }$ is analytic in the open unit disk $\mathbb{K}$ (more details can be located in Komatu [6] or Hayman [7]). Consequently, our subclass of $\prod \left(\rho \right)$ can be realized by a subordination and other properties of the geometric function theory.

2.1. Definitions

• Two analytic functions $\upsilon , f\in {\prod }_k\left(\rho \right)$ are convoluted ( $\upsilon \ast f$) if

  $$(\upsilon \ast f)\left(z\right)=\left(z^{-\rho }+\sum _{n=k}^{\infty }{\upsilon }_n{z}^{n-\rho }\right)\ast \left(z^{-\rho }+\sum _{n=k}^{\infty }{a}_n{z}^{n-\rho }\right)$$

  $$=z^{-\rho }+\sum _{n=k}^{\infty }\left({\upsilon }_n{a}_n\right)z^{n-\rho }.$$
• The modified Mittag–Leffler function is presented via the formula [8,9,10]

  $${\mathsf{\Sigma }}_{a,b}^{\kappa }\left(z\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(\kappa \right)}_n}{\Gamma (bn+a)}}{\displaystyle \frac{z^n}{n!}},$$

  $$\left({\left(\kappa \right)}_0=1,{\left(\kappa \right)}_n=\kappa (\kappa +1)\dots (\kappa +n-1)\right)$$

  where ${\left(\kappa \right)}_n$ indicates the Pochhammer number, such that

  $${\mathsf{\Sigma }}_{a,b}^1\left(z\right):={\mathsf{\Sigma }}_{a,b}\left(z\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{z^n}{\Gamma (bn+a)}}.$$

2.2. Fractional Operators

For analytic functions, the Prabhakar fractional integral operator is formulated by the following structure [11,12]

$$\begin{array}{cc}\hfill \prod _{a,b}^{p,q}g\left(z\right)& ={\int }_0^z{(z-\chi )}^{b-1}{\mathsf{\Sigma }}_{a,b}^p\left[q{(z-\chi )}^a\right]g\left(\chi \right)d\chi \hfill \\ \hfill & =(g·{\varrho }_{a,b}^{p,q})\left(z\right),\hfill \end{array}$$

(2)

whenever the parameters are complex ($a,b,p,q\in \mathbb{C}$),

$$\left({\varrho }_{a,b}^{p,q}\right)\left(z\right):={\displaystyle \frac{{\mathsf{\Sigma }}_{a,b}^p\left(q{z}^a\right)}{z^{1-b}}}$$

and

$${\mathsf{\Sigma }}_{a,b}^p\left(z\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{\Gamma (p+n)}{\Gamma \left(p\right)\Gamma (an+b)}}\left({\displaystyle \frac{z^n}{n!}}\right).$$

For example, by letting $g\left(z\right)=z^{\ell -1}$ and using (2), a computation yields: [13]

$$\begin{array}{cc}\hfill \prod _{a,b}^{p,q}{z}^{\ell -1}& ={\int }_0^z{(z-\chi )}^{b-1}{\mathsf{\Sigma }}_{a,b}^p\left[q{(z-\chi )}^a\right]\left({\chi }^{\ell -1}\right)d\chi \hfill \\ \hfill & ={\displaystyle \frac{\Gamma (\ell ){\prod }_{a,b+\ell }^p\left(q{z}^a\right)}{z^{1-b-\ell }}}.\hfill \end{array}$$

(3)

The differential operator for the above Equation (3) can be written by [11]:

$${}_k{\Delta }_{a,b}^{p,q}g\left(z\right)=\frac{d^k}{d{z}^k}\left(\prod _{a,k-b}^{-p,q}g\left(z\right)\right),k\in \mathbb{N}.$$

2.3. Convolution Operator

Let $\upsilon \in {\prod }_k\left(\rho \right).$ Then, we define the following operator:

Definition 1.

Define a new functional operator, as follows: for $a,b,p,q\in \mathbb{C},z\in \mathbb{K},\Re \left(a\right),\Re \left(b\right)>0,{\Omega }_{a,b}^{p,q}:\mathbb{K}\to \mathbb{K};$ then, the operator admits the following structure:

$$\begin{array}{cc}\hfill {\Omega }_{a,b}^{p,q}\left(z\right)& :=\Gamma \left(b\right)z^{1-b-\rho }{\varrho }_{a,b}^{p,q}\left(z^{1/a}\right)\hfill \\ \hfill & =\Gamma \left(b\right)z^{-\rho }{\mathsf{\Sigma }}_{a,b}^p\left(q^{1/a}{\left(z^{1/a}\right)}^a\right)\hfill \\ \hfill & =\Gamma \left(b\right)\sum _{n=0}^{\infty }{\displaystyle \frac{\Gamma (p+n)}{\Gamma \left(p\right)\Gamma (an+b)}}{\displaystyle \frac{q^{n/a}{z}^{n-\rho }}{n!}}\hfill \\ \hfill & =\sum _{n=0}^{\infty }\left({\displaystyle \frac{\Gamma \left(b\right)\Gamma (p+n)q^{n/a}}{\Gamma \left(p\right)\Gamma (an+b)}}\right){\displaystyle \frac{z^{n-\rho }}{n!}}\hfill \\ \hfill & =z^{-\rho }+\sum _{n=1}^{\infty }\left({\displaystyle \frac{\Gamma \left(b\right)\Gamma (p+n)q^{n/a}}{\Gamma \left(p\right)\Gamma (an+b)}}\right){\displaystyle \frac{z^{n-\rho }}{n!}}\hfill \end{array}$$

(4)

For extended $k-$sum, (4) becomes

$${\Omega }_{a,b}^{p,q}\left(z\right)=z^{-\rho }+\sum _{n=k}^{\infty }\left({\displaystyle \frac{\Gamma \left(b\right)\Gamma (p+n)q^{n/a}}{\Gamma \left(p\right)\Gamma (an+b)}}\right){\displaystyle \frac{z^{n-\rho }}{n!}}.$$

We have the following outcome:

Proposition 1.

If $\upsilon \in {\prod }_k\left(\rho \right)$, then ${\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)=\left({\Omega }_{a,b}^{p,q}\ast \upsilon \right)\in {\prod }_k\left(\rho \right),$ where ∗ indicates the convolution product.

Proof. 

Let $\upsilon \in {\prod }_k\left(\rho \right).$ Then we have

$$\begin{array}{cc}\hfill \left({\Omega }_{a,b}^{p,q}\ast \upsilon \right)\left(z\right)& =\left(z^{-\rho }+\sum _{n=k}^{\infty }\left({\displaystyle \frac{\Gamma \left(b\right)\Gamma (p+n)q^{n/a}}{\Gamma \left(p\right)\Gamma (an+b)}}\right){\displaystyle \frac{z^{n-\rho }}{n!}}\right)\ast \left(z^{-\rho }+\sum _{n=k}^{\infty }{\upsilon }_n{z}^{n-\rho }\right)\hfill \\ \hfill & =\left(z^{-\rho }+\sum _{n=k}^{\infty }\left(q^{n/a}\right)z^{n-\rho }\right)\hfill \\ \hfill & \ast \left(z^{-\rho }+{\displaystyle \frac{\Gamma \left(b\right)}{\Gamma \left(p\right)}}\sum _{n=k}^{\infty }\left({\displaystyle \frac{\Gamma (p+n)}{\Gamma (an+b)}}\right){\displaystyle \frac{z^{n-\rho }}{n!}}\right)\ast \left(z^{-\rho }+\sum _{n=k}^{\infty }{\upsilon }_n{z}^{n-\rho }\right)\hfill \\ \hfill & =\left(z^{-\rho }+{\displaystyle \frac{q^{k/a}{z}^{k-\rho }}{(1-z{q}^{1/a})}}\right)\ast \left(z^{-\rho }+A{z}^{k-\rho }{}_2{\Psi }_2^{\ast }\left[\begin{array}{cc}(p+k,1)& (1,1)\\ (ak+b,a)& (k+1,1)\end{array};z\right]\right)\hfill \\ \hfill & \ast \left(z^{-\rho }+\sum _{n=k}^{\infty }{\upsilon }_n{z}^{n-\rho }\right):=z^{-\rho }+\sum _{n=k}^{\infty }{\Phi }_n{z}^{n-\rho },\hfill \end{array}$$

(5)

where $A:={\displaystyle \frac{\Gamma \left(b\right)\Gamma (p+k)}{\Gamma \left(p\right)\Gamma (ak+b)\Gamma (k+1)}},$ ${\Phi }_n=\left({\displaystyle \frac{\Gamma \left(b\right)\Gamma (p+n)q^{n/a}}{\Gamma \left(p\right)\Gamma (an+b)}}\right){\displaystyle \frac{{\upsilon }_n}{n!}}$ and ${}_p{\Psi }_q^{\ast }$ represents the normalized Fox–Wright function. □

The corresponding derivative of (5), ${\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)=\left({\Omega }_{a,b}^{p,q}\ast \upsilon \right)\left(z\right)$, can be formulated as follows:

$${\mathbb{L}}_{a,b}^{p,q}\upsilon \left(z\right)=z^{-\rho }+\sum _{n=k}^{\infty }{\displaystyle \frac{z^{n-\rho }}{{\Phi }_n}},z\in \mathbb{K},$$

where

$$\left({\mathbb{P}}_{a,b}^{p,q}\ast {\mathbb{L}}_{a,b}^{p,q}\right)\upsilon \left(z\right)=\left({\mathbb{L}}_{a,b}^{p,q}\ast {\mathbb{P}}_{a,b}^{p,q}\right)\upsilon \left(z\right)=\upsilon \left(z\right),z\in \mathbb{K}.$$

We propose the next concepts to study the ${\mathbb{P}}_{\alpha ,\beta }^{\gamma ,\omega }\varphi \left(z\right)$ geometrically. The function $\upsilon$ is subordinate to the function $\nu$ in ${\prod }_k\left(\rho \right)$, denoted by $\upsilon \prec \nu$; if for $\varpi ,\varpi \left(0\right)=0,\left|\varpi \right(z\left)\right|\le \left|z\right|<1,$ we have $\upsilon \left(z\right)=\nu \left(\varpi \right(z\left)\right)$ in $\mathbb{K}$ (see [14] or [15]).

Definition 2.

By setting $\beta <\alpha \in [-1,1]$ and $\gamma <0$, a function $\upsilon \in {\prod }_k\left(\rho \right)\in {}_k{\prod }_{a,b}^{p,q}(\alpha ,\beta ,\gamma ,\rho )$ if it admits the deference inequality, which is structured by

$${⨿}_{a,b}^{p,q}\left(z\right):=(1-\gamma )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime }\prec {\mathcal{W}}_{\alpha ,\beta }\left(z\right),$$

(6)

where

$$\begin{array}{cc}\hfill {\mathcal{W}}_{\alpha ,\beta }\left(z\right)& :={\displaystyle \frac{1+\alpha z}{1+\beta z}}\hfill \\ \hfill & =1+\sum _{n=1}^{\infty }{\displaystyle \frac{z^n{(-\beta )}^n(\beta -\alpha )}{\beta }}\hfill \\ \hfill & =1+\sum _{n=k}^{\infty }{\displaystyle \frac{z^{n-k+1}{(-\beta )}^{n-k+1}(\beta -\alpha )}{\beta }},z\in \mathbb{K}.\hfill \end{array}$$

We note that ${\mathcal{W}}_{\alpha ,\beta }\left(z\right)$ is a special type of the Möbius transformations, which are widely used in geometry, complex analysis, and other branches of mathematics. In areas like fluid dynamics, conformal mapping, and computer graphics, they are frequently used to transfer simple geometric structures to more complicated ones, examine the behavior of functions, and find solutions to issues. Protective geometry’s cross-ratio and Möbius transformations have a lot in common. It keeps its properties under Möbius transformations, making it an effective tool for examining the connections between points in a transformation. In general, Möbius transformations offer an effective foundation for comprehending and working with complex numbers and the geometric meanings of those numbers.

Note that (6) satisfies the following power series:

$${⨿}_{a,b}^{p,q}\left(z\right)=1+\sum _{n=k}^{\infty }\left(1-\gamma (1+{\displaystyle \frac{1}{\rho }})\right){\Phi }_n{z}^n.$$

The functional ${⨿}_{a,b}^{p,q}\left(z\right)$ will be studied in terms of the polar differentiation of the polynomial. The equality of Equation (6) represents the d’Alembert’s equation. For example, when ${⨿}_{a,b}^{p,q}\left(z\right)=1$ is a constant, we have the following solution (see Figure 1):

$$\begin{array}{cc}\hfill \left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]& =c_1{z}^{(\rho -\gamma \rho )/\gamma }+z^{-\rho },\hfill \end{array}$$

where $c_1$ is a constant. In addition, when ${⨿}_{a,b}^{p,q}\left(z\right)=(1+z)/(1-z),$ we have

$$\begin{array}{cc}\hfill \left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]& =c_1{z}^{(\rho -\gamma \rho )/\gamma }-{\displaystyle \frac{(2\rho z^{1-\rho }{}_2{F}_1(1,1-\frac{\rho }{\gamma },2-\frac{\rho }{\gamma },z)}{\gamma -\rho }}-{\displaystyle \frac{\rho z^{-\rho }}{\gamma -\rho }}+{\displaystyle \frac{\gamma z^{-\rho }}{\gamma -\rho }}\hfill \\ \hfill & =c_1{z}^{(\rho -\gamma \rho )/\gamma }-{\displaystyle \frac{(2\rho z^{1-\rho }{}_2{F}_1(1,1-\frac{\rho }{\gamma },2-\frac{\rho }{\gamma },z)}{\gamma -\rho }}+z^{-\rho },\hfill \end{array}$$

where ${}_2{F}_1\left(\right)$ indicates the hypergeometric function. The above examples show that $\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]\in {\Pi }_k\left(\rho \right).$

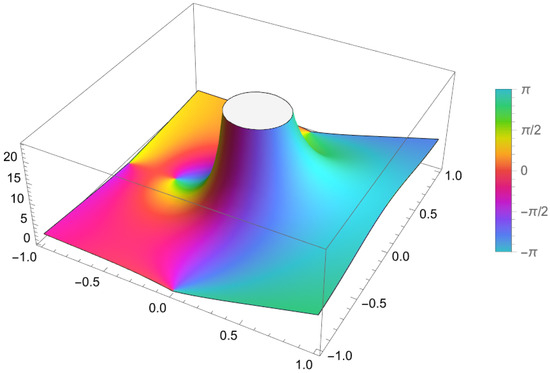
Figure 1. 3D complex plot of the solution $\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right],$ when $\gamma =1/2, \rho =2, c_1=1.$ (Mathematica 13.3).

The function

$${\mathcal{W}}_{\alpha ,\beta }\left(\phi \left(z\right)\right)=\frac{1+\alpha \phi \left(z\right)}{1+\beta \phi \left(z\right)}$$

with its special case, the function

$${\mathcal{W}}_{\alpha ,\beta }\left(z\right)={\displaystyle \frac{1+\alpha z}{1+\beta z}}$$

are of particular importance since ${\mathcal{W}}_{\alpha ,\beta }\left(\phi \left(z\right)\right)$ denotes the class of Caratheodory functions of the order $\frac{1 - \alpha }{1 - \beta }$, that is (more details can be located in Janowski [16] or Jahangiri et. al. [17]):

$$\Re \left\{{\mathcal{W}}_{\alpha ,\beta }\left(\phi \left(z\right)\right)\right\}>\frac{1-\alpha }{1-\beta }.$$

2.4. Lemmas

To deal with our results in the following part, we need the next preliminaries, which are given by Miller and Mocanu [15]. Define the general class of holomorphic functions with

$$\mathbb{H}[a,n]=\{h:h\left(z\right)=a+a_n{z}^n+a_{n+1}{z}^{n+1}+\cdots \},$$

where $a\in \mathbb{C}$ and n is a positive integer.

Lemma 1.

For analytic function $f_1\left(z\right)$ and a convex univalent function $f_2\left(z\right)$ in $\mathbb{K}$ satisfying $f_1\left(0\right)=f_2\left(0\right);$ if

$$f_1\left(z\right)+(1/\gamma )f_1^{\prime }\left(z\right)\prec f_2\left(z\right)$$

for $\gamma \in \mathbb{C}$, such that $\Re \left(\gamma \right)\ge 0,$ then

$$f_1\left(z\right)\prec f_2\left(z\right).$$

Lemma 2.

Set $\aleph \in \mathbb{R}$ such that

$$\Re \left(\hslash \left(z\right)+\aleph z{\hslash }^{\prime }\left(z\right)\right)>0.$$

Then,

$$\Re \left(\hslash \left(z\right)\right)>0.$$

In addition, if $\aleph >0$ such that $\hslash \in \mathbb{H}[1,n]$, then there are constants ${\lambda }_1>0$ and ${\lambda }_2>0$ satisfying the inequality

$$\hslash \left(z\right)+\aleph z{\hslash }^{\prime }\left(z\right)\prec {\left({\displaystyle \frac{1+z}{1-z}}\right)}^{{\lambda }_1}$$

which implies

$$\hslash \left(z\right)\prec {\left({\displaystyle \frac{1+z}{1-z}}\right)}^{{\lambda }_2}.$$

Lemma 3

([18]). Let $\hslash ,h\in \mathbb{H}[a,n]$, where h admits the convexity in $\mathbb{K}$ and for ${\mathbb{k}}_1,{\mathbb{k}}_2\in \mathbb{C},{\mathbb{k}}_2\ne 0,$ then

$${\mathbb{k}}_1\hslash \left(z\right)+{\mathbb{k}}_{2}z{\hslash }^{\prime }\left(z\right)\prec {\mathbb{k}}_{1}h\left(z\right)+{\mathbb{k}}_{2}z{h}^{\prime }\left(z\right)$$

yields

$$\hslash \left(z\right)\prec h\left(z\right).$$

Lemma 4

([19]). Let $h,p\in \mathbb{H}[a,n]$, where p admits the convexity in $\mathbb{K}$, where $h\left(z\right)+\mathbb{k}z{h}^{\prime }\left(z\right)$ admits the univalency, then

$$p\left(z\right)+\mathbb{k}z{p}^{\prime }\left(z\right)\prec h\left(z\right)+\mathbb{k}z{h}^{\prime }\left(z\right)$$

results in

$$p\left(z\right)\prec h\left(z\right).$$

Lemma 5

([20]). Let $\hslash ,\hslash ,g\in \mathbb{H}[a,n]$ and g admits the convexity in $\mathbb{K}$ such that $\hslash \prec g$ and $\hslash \prec g$, then

$$\mathbb{k}\hslash +(1-\mathbb{k})\hslash \prec g,\mathbb{k}\in [0,1].$$

3. Analytic Results

The inclusion result for the class ${}_k{\prod }_{a,b}^{p,q}(\alpha ,\beta ,\gamma ,\rho )$.

3.1. Inclusion Outcomes

Analytic continuation is a technique that allows analytic functions to often be extended beyond the boundaries of their originally specified domains. There is only one technique to extend an analytic function while maintaining its qualities, which makes this extension unique. The inclusion property is one of these attributes. The unique characteristics of analytic functions in a complex analysis are highlighted by these inclusion qualities. They make manipulating and analyzing these functions possible for mathematicians employing a range of techniques and theorems, thereby rendering them a key subject in the discipline. We have the following result:

Proposition 2.

Let $\upsilon \in {\prod }_k\left(\rho \right).$ If ${\gamma }_2<{\gamma }_1<0$, then

$${}_k\prod _{a,b}^{p,q}(\alpha ,\beta ,{\gamma }_2,\rho )\subset {}_k\prod _{a,b}^{p,q}(\alpha ,\beta ,{\gamma }_1,\rho ).$$

Proof. 

Set $\upsilon \in {}_k{\prod }_{a,b}^{p,q}(\alpha ,\beta ,{\gamma }_2,\rho ).$ Assume that

$$V\left(z\right)=z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right],z\in \mathbb{K}$$

is analytic in $\mathbb{K}$ with $V\left(0\right)=1.$ Then, we obtain the conclusion:

$$(1-{\gamma }_2)z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{{\gamma }_2}{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime }=V\left(z\right)-{\displaystyle \frac{{\gamma }_2}{\rho }}\left(z{V}^{\prime }\left(z\right)\right).$$

Accordingly, we have the inequality:

$$V\left(z\right)-{\displaystyle \frac{{\gamma }_2}{\rho }}\left(z{V}^{\prime }\left(z\right)\right)\prec {\displaystyle \frac{\alpha z+1}{\beta z+1}}.$$

In virtue of Lemma 1, where $\gamma :=-{\displaystyle \frac{{\gamma }_2}{\rho }}>0,$ we have

$$V\left(z\right)\prec {\displaystyle \frac{\alpha z+1}{\beta z+1}},z\in \mathbb{K}.$$

But, as $0<{\gamma }_1/{\gamma }_2<1$, and ${\mathcal{W}}_{\alpha ,\beta }\left(z\right)$ admits the convexity in $\mathbb{K}$, this leads to

$$\begin{array}{cc}\hfill & (1-{\gamma }_1)z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{{\gamma }_1}{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime }\hfill \\ \hfill & =(1-{\gamma }_1)V\left(z\right)-\left(\frac{{\gamma }_1}{\wp }\right)\left(z{V}^{\prime }\left(z\right)-\rho V\left(z\right)\right)+\left({\displaystyle \frac{{\gamma }_1}{{\gamma }_2}}V\left(z\right)-{\displaystyle \frac{{\gamma }_1}{{\gamma }_2}}V\left(z\right)\right)\hfill \\ \hfill & ={\displaystyle \frac{{\gamma }_1}{{\gamma }_2}}\left((1-{\gamma }_2)V\left(z\right)-\left(\frac{{\gamma }_2}{\rho }\right)(z{V}^{\prime }\left(z\right)-\rho V\left(z\right))\right)+\left(1-{\displaystyle \frac{{\gamma }_1}{{\gamma }_2}}\right)V\left(z\right)\hfill \\ \hfill & ={\displaystyle \frac{{\gamma }_1}{{\gamma }_2}}\left((1-{\gamma }_2)z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{{\gamma }_2}{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime }\right)+\left(1-{\displaystyle \frac{{\gamma }_1}{{\gamma }_2}}\right)V\left(z\right)\hfill \\ \hfill & \prec {\mathcal{W}}_{\alpha ,\beta }\left(z\right).\hfill \end{array}$$

Hence, through Definition 2, we obtain the conclusion $\upsilon \in {}_k{\prod }_{a,b}^{p,q}(\alpha ,\beta ,{\gamma }_1,\rho ).$ □

3.2. General Properties

At this point, we proceed to explore more properties of the suggested operator, including preserving the Janowski class of analytic functions and the sandwich theorem of the subordination and superordination. In general, we have the following:

Proposition 3.

Let

$$\Theta \left(z\right):=(1-\gamma )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime }.$$

Then

$${\sigma }_1(1+\rho )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]+[{\sigma }_1-{\sigma }_2(1+\rho )-{\sigma }_2]z^{1+\rho }{\left(\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]\right)}^{\prime }-{\sigma }_2{z}^{2+\rho }{\left(\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]\right)}^{\prime \prime }$$

$$\prec {\left({\displaystyle \frac{1+z}{1-z}}\right)}^{{\lambda }_1}\Rightarrow \Theta \left(z\right)\prec {\left({\displaystyle \frac{1+z}{1-z}}\right)}^{{\lambda }_2}$$

$$\left({\lambda }_1>0,{\lambda }_2>0,{\sigma }_1=1-\gamma ,{\sigma }_2={\displaystyle \frac{\gamma }{\rho }},\rho \ne 0\right).$$

Proof. 

A computation presents

$$\begin{array}{cc}\hfill \Theta \left(z\right)+z{\Theta }^{\prime }\left(z\right)& =(1-\gamma )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime }\hfill \\ \hfill & +z{\left((1-\gamma )z^{\wp }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{\gamma }{\wp }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime }\right)}^{\prime }\hfill \\ \hfill & ={\sigma }_1(1+\rho )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]+[{\sigma }_1-{\sigma }_2(1+\rho )-{\sigma }_2]z^{1+\rho }{\left(\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]\right)}^{\prime }\hfill \\ \hfill & -{\sigma }_2{z}^{2+\rho }{\left(\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]\right)}^{\prime \prime }\hfill \\ \hfill & \prec {\left({\displaystyle \frac{1+z}{1-z}}\right)}^{{\lambda }_1}.\hfill \end{array}$$

Thus, putting $c=1$ in Lemma 2 results in $\Theta \left(z\right)\prec {\left({\displaystyle \frac{1+z}{1-z}}\right)}^{{\lambda }_2}.$ □

Considering ${\lambda }_1={\lambda }_2=1,$ then we attain the next corollary:

Corollary 1.

Let $\Theta \left(z\right)$ be as in Proposition 3. If

$${\sigma }_1(1+\rho )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]+[{\sigma }_1-{\sigma }_2(1+\rho )-{\sigma }_2]z^{1+\rho }{\left(\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]\right)}^{\prime }-{\sigma }_2{z}^{2+\rho }{\left(\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]\right)}^{\prime \prime }$$

$$\prec \left({\displaystyle \frac{1+z}{1-z}}\right),$$

$$\left({\sigma }_1=1-\gamma ,{\sigma }_2={\displaystyle \frac{\gamma }{\rho }},\rho \ne 0\right)$$

holds, then $\upsilon \in {}_k{\prod }_{a,b}^{p,q}(1,-1,\gamma ,\rho ).$

Proof. 

Let ${\lambda }_1={\lambda }_2=1$ in Proposition 3. This results in

$$\Theta \left(z\right)\prec \left({\displaystyle \frac{1+z}{1-z}}\right)$$

and then

$$\upsilon \in {}_k\prod _{a,b}^{p,q}(1,-1,\gamma ,\rho ).$$

□

Lastly, we show some convolution properties concerning the class ${}_k{\prod }_{a,b}^{p,q}(\alpha ,\beta ,\gamma ,\rho )$.

Proposition 4.

Let $\upsilon \in {}_k{\prod }_{a,b}^{p,q}(\alpha ,\beta ,\gamma ,\rho )$ and $f\in {\prod }_k\left(\rho \right).$ Then

$$\upsilon \ast f\in {}_k\prod _{a,b}^{p,q}(\alpha ,\beta ,\gamma ,\rho )$$

whenever

$$\Re \left(z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}f\left(z\right)\right]\right)>0.5.$$

(7)

Proof. 

Employing the operations of the convolution multiplication [21,22], this yields

$$\begin{array}{cc}\hfill & (1-\gamma )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}(\upsilon \ast f)\left(z\right)\right]-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}(\upsilon \ast f)\left(z\right)\right]}^{\prime }\hfill \\ \hfill & =(1-\gamma )\left(z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]\ast z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}f\left(z\right)\right]\right)\hfill \\ \hfill & -\left(\frac{\gamma }{\rho }\right)\left(z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}f\left(z\right)\right]}^{\prime }\ast \left(z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}f\left(z\right)\right]\right)\right)\hfill \\ \hfill & =\left((1-\gamma )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}f\left(z\right)\right]}^{\prime }\right)\ast \left(z^{\rho }{\mathbb{P}}_{a,b}^{p,q}f\left(z\right)\right)\hfill \\ \hfill & =\Theta \left(z\right)\ast \left(z^{\rho }{\mathbb{P}}_{a,b}^{p,q}f\left(z\right)\right),\hfill \end{array}$$

where $\Theta \left(z\right)\prec {\mathcal{W}}_{\alpha ,\beta }\left(z\right)$. The assumption (7) provides $\left(z^{\rho }{\mathbb{P}}_{a,b}^{p,q}f\left(z\right)\right)$, which owns the Herglotz integral structure [21]

$$\left(z^{\rho }{\mathbb{P}}_{a,b}^{p,q}f\left(z\right)\right)={\int }_{\left|X\right|=1}{\displaystyle \frac{d\xi \left(X\right)}{1-Xz}};$$

here, $dX$ indicates the probability measure over $\left|X\right|=1$ and

$${\int }_{\left|X\right|=1}d\xi \left(X\right)=1.$$

Because ${\mathcal{W}}_{\alpha ,\beta }\left(z\right)$ is convex in $\mathbb{K}$, this implies that

$$\begin{array}{cc}\hfill & (1-\gamma )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}(\upsilon \ast f)\left(z\right)\right]-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}(\upsilon \ast f)\left(z\right)\right]}^{\prime }\hfill \\ \hfill & =\Theta \left(z\right)\ast \left(z^{\rho }{\mathbb{P}}_{a,b}^{p,q}f\left(z\right)\right)\hfill \\ \hfill & ={\int }_{\left|X\right|=1}\Theta \left(Xz\right)d\xi \left(X\right)\hfill \\ \hfill & \prec {\mathcal{W}}_{\alpha ,\beta }\left(z\right).\hfill \end{array}$$

Hence, $\upsilon \ast f\in {}_k{\prod }_{a,b}^{p,q}(\alpha ,\beta ,\gamma ,\rho ).$ □

Proposition 5.

Let $\upsilon \in {\prod }_k\left(\rho \right)$ be formulated by

$$\Theta \left(z\right):=(1-\gamma )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime }$$

$$=1+\sum _{n=1}^{\infty }{\theta }_n{z}^n.$$

Then, $\Re \left(\Theta \left(z\right)\right)>0$ implies

$$|{\theta }_n|\le 2\left({\int }_0^{2\pi }\left|e^{-i\theta n}\right|dX\left(\theta \right)\right),$$

here, again, $dX$ indicates any probability measure. In addition,

$$\Re \left(e^{i\vartheta }\Theta \left(z\right)\right)>0\Rightarrow \Theta \left(z\right)$$

admits the convexity in $\mathbb{K}.$

Proof. 

Firstly, we let

$$\Re (\Theta \left(z\right))=\Re \left(1+\sum _{n=1}^{\infty }{\theta }_n{z}^n\right)>0.$$

Thus, the Carathéodory theorem implies that

$$|{\theta }_n|\le 2{\int }_0^{2\pi }\left|e^{-i\theta n}\right|dX\left(\theta \right),$$

where $dX$ indicates any probability measure. Secondly, if

$$\Re \left(e^{i\vartheta }\Theta \left(z\right)\right)>0,z\in \mathbb{K},\vartheta \in \mathbb{R}$$

then in virtue of [22], there exists a number $\vartheta \in \mathbb{R}$ satisfying

$$\Theta \left(z\right)={\displaystyle \frac{\alpha z+1}{\beta z+1}},z\in \mathbb{K}.$$

But ${\displaystyle \frac{\alpha z+1}{\beta z+1}}$ admits the convexity in $\mathbb{K},$ which, by majority relation, results in $\Theta \left(z\right)$ admitting the convexity. □

Note that Proposition 5 yields the sufficient hypothesis for functions to lay in ${}_k{\prod }_{a,b}^{p,q}(\alpha ,\beta ,\gamma ,\rho ).$

Proposition 6.

Suppose that $\upsilon \in {\prod }_k\left(\rho \right),$ which is formulated in the functional

$$\mathcal{B}\left(z\right):=z^{\rho +1}\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right],z\in \mathbb{K}.$$

If the inequality

$$\mathcal{B}\left(z\right)\prec {\displaystyle \frac{z}{{(1+z)}^2}}$$

occurs, then $\mathcal{B}\left(z\right)\in {\mathbb{S}}^{\ast }$ and

$${\displaystyle \frac{1}{4}}{\left({\int }_0^z{\displaystyle \frac{\sqrt{\mathcal{B}\left(\eta \right)}}{\eta }}d\eta \right)}^2\prec {\left({tan}^{-1}\sqrt{z}\right)}^2$$

where

$$-{\displaystyle \frac{\pi }{2}}<-2{tan}^{-1}\sqrt{r}\le \Re \left({\int }_0^z{\displaystyle \frac{\sqrt{\mathcal{B}\left(\eta \right)}}{\eta }}d\eta \right)<2{tan}^{-1}\sqrt{r}\le {\displaystyle \frac{\pi }{2}}.$$

Proof. 

Set $\mathcal{B}\left(z\right)=z^{\rho +1}\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right],z\in \mathbb{K}.$ As a consequence, we can determine that

$$\mathcal{B}\left(z\right)=z+\sum _{n=2}^{\infty }{♭}_n{z}^n,z\in \mathbb{K}$$

is holomorphic. Clearly, we have

$$\begin{array}{cc}\hfill \mathcal{B}\left(z\right):& =4z-8{\displaystyle \frac{z^2}{3}}+{\displaystyle \frac{92}{45}}{z}^3+O\left(z^4\right).\hfill \end{array}$$

In view of the discussion in [15], p. 177, we obtain

$$\begin{array}{cc}\hfill p\left(z\right)& ={\displaystyle \frac{z}{{(1+z)}^2}}\hfill \\ \hfill & =z-2z^2+3z^3-4z^4+5z^5+O\left(z^6\right)\in {\mathbb{S}}^{\ast },z\in \mathbb{K}.\hfill \end{array}$$

Hence, by majority, we attain $\mathcal{B}\left(z\right)\in {\mathbb{S}}^{\ast }$. The last two results can be obtained from [15]—Corollary 3.6a.1. □

In the same manner, we conclude the next outcome.

Proposition 7.

Set $\upsilon \in {\prod }_k\left(\rho \right);$ and

$$\mathcal{B}\left(z\right)=z^{\rho +1}\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right].$$

If the inequality

$$\mathcal{B}\left(z\right)\prec {\displaystyle \frac{z}{{(1+z)}^2}}$$

is satisfied, then $\mathcal{B}\left(z\right)\in {\mathbb{S}}^{\ast }$ and

$${\displaystyle \frac{1}{4}}{\left({\int }_0^z{\displaystyle \frac{\sqrt{\mathcal{B}\left(\eta \right)}}{\eta }}d\eta \right)}^2\prec {\left({cot}^{-1}\sqrt{1/z}\right)}^2$$

where

$$-{\displaystyle \frac{\pi }{2}}<-2{cot}^{-1}\sqrt{1/r}\le \Re \left({\int }_0^z{\displaystyle \frac{\sqrt{\mathcal{B}\left(\eta \right)}}{\zeta }}d\eta \right)<2{cot}^{-1}\sqrt{1/r}\le {\displaystyle \frac{\pi }{2}}.$$

3.3. Sandwich Outcomes

In this part, we deal with the sandwich results:

Proposition 8.

Define the functional

$$\Theta \left(z\right)=(1-\gamma )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime }.$$

Let the following assumptions hold:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{-\left(z^{\rho }(z(\gamma z{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime \prime }+(2\gamma (\rho +1)-\rho ){\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime })+(\gamma -1)\rho (\rho +1)\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right])\right)}{\rho }}\hfill \\ \hfill & \prec p_2\left(z\right)+z{p}_2^{\prime }\left(z\right),\hfill \end{array}$$

(8)

where $p_2\left(0\right)=1$ and convex in $\mathbb{K}.$ Also, assume the univalency of $\Theta \left(z\right)$ in $\mathbb{K}$, such that

$$\Theta \in \mathbb{H}[p_1\left(0\right),1]\cap \mathbb{Q}.$$

Here, $\mathbb{Q}$ denotes the collection of injection functions g satisfying the limit

$$\underset{z\in \partial \mathbb{K}}{lim}g\left(z\right)\ne \infty ,z\in \mathbb{K}$$

and

$$\begin{array}{cc}\hfill & p_1\left(z\right)+z{p}_1^{\prime }\left(z\right)\hfill \\ \hfill & \prec {\displaystyle \frac{-\left(z^{\rho }(z(\gamma z{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime \prime }+(2\gamma (\rho +1)-\rho ){\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime })+(\gamma -1)\rho (\rho +1)\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right])\right)}{\rho }}.\hfill \end{array}$$

(9)

Then,

$$p_1\left(z\right)\prec \Theta \left(z\right)\prec p_2\left(z\right)$$

and $p_1\left(z\right)$ admits the best sub-dominant and $p_2\left(z\right)$ admits the best dominant.

Proof. 

Since

$$\begin{array}{cc}\hfill & \Theta \left(z\right)+z{\Theta }^{\prime }\left(z\right)=\hfill \\ \hfill & {\displaystyle \frac{-\left(z^{\rho }(z(\gamma z{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime \prime }+(2\gamma (\rho +1)-\rho ){\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime })+(\gamma -1)\rho (\rho +1)\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right])\right)}{\rho }}\hfill \end{array}$$

then the bi-subordination implies that

$$\begin{array}{cc}\hfill p_1\left(z\right)+z{p}_1^{\prime }\left(z\right)& \prec \Theta \left(z\right)+z{\Theta }^{\prime }\left(z\right)\hfill \\ \hfill & \prec p_2\left(z\right)+z{p}_2^{\prime }\left(z\right).\hfill \end{array}$$

Hence, combining Lemmas 3 and 4 results in the requested assertion. □

Proposition 9.

Let p be a univalent convex function in $\mathbb{K}$ such that $p\left(0\right)=1$ and

$$\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]\prec p\left(z\right)$$

and

$${\mathbb{L}}_{a,b}^{p,q}\upsilon \left(z\right)\prec p\left(z\right).$$

Then,

$${\mathbb{A}}_{a,b}^{p,q}\upsilon \left(z\right):=\mathbb{k}\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]+(1-\mathbb{k})\left[{\mathbb{L}}_{a,b}^{p,q}\upsilon \left(z\right)\right],\mathbb{k}\in [0,1].$$

Proof. 

By the property of $\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]$ and $\left[{\mathbb{L}}_{a,b}^{p,q}\upsilon \left(z\right)\right],$ eventually, we have ${\mathbb{A}}_{a,b}^{p,q}\upsilon \left(z\right)\in {\prod }_k\left(\rho \right).$ According to Lemma 5, the outcome is obtained. □

4. Boundedness Results

Meromorphic functions’ boundedness in the Bloch space depends on how they grow and behave close to singularities. A function that has an excessive number of poles or poles that are too close together may not meet the Bloch space’s boundedness constraint. Meromorphic functions are typically studied in a variety of function spaces, and this generally entails examining their development, polar distribution, activity around singularities, and interactions with other functions in the space. Depending on the precise definitions and conditions taken into account within the framework of the Bloch space, the outcomes might vary.

4.1. Boundedness in Bloch Space

The Bloch space is a function space that appears in the study of analytic functions on the unit disk. Although the Bloch space is bounded, all of its functions have finite norms, making it a well-defined and well-behaved function space. As a way to prevent excess growth or oscillation among locations in the functions that make up this space, Bloch spaces need to be constrained. The boundedness characteristic is useful in a wide range of challenging analytic and function theory problems and is often used in the study of numerous different holomorphic functions on specific domains. The Bloch space serves as an example of a function space that is utilized in complicated analysis. Any of these spaces have been recognized based on different criteria and requirements for the functions they contain. Every space differs from the others in terms of its features and purposes, providing beneficial assets for an investigation of holomorphic functions [23]. In this section, we deal with the boundedness of the meromorphic operator $\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right].$ It is well known that in the of study meromorphic functions in $\mathbb{K}$, it is natural to replace $|g^{\prime }\left(z\right)|$ in these expressions by the spherical derivative [24]

$$|g^{♯}\left(z\right)|={\displaystyle \frac{|g^{\prime }\left(z\right)|}{1+{\left|g\left(z\right)\right|}^2}}.$$

Definition 3.

The Bloch space $\left(\mathfrak{S}\right)$ admits a collection of analytic meromorphic function in $\mathbb{K}$, such that

$${\parallel g\parallel }_{\mathfrak{S}}=\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2\left)\right|g^{♯}\left(z\right)|<\infty .$$

In addition, consider the positive real valued function $\omega :[0,1)\to [0,\infty )$, then the weighted $\wp -$Bloch space ${\mathfrak{S}}_{\omega }^{\wp }$ admits a collection of analytic functions g in $\mathbb{K}$, such that

$${\parallel g\parallel }_{{\mathfrak{S}}_{\omega }^{\wp }}=\underset{z\in \mathbb{K}}{sup}{\displaystyle \frac{{(1-|z\left|\right)}^{\wp }}{\omega (1-|z\left|\right)}}\left|h^{♯}\left(z\right)\right|<\infty .$$

Additionally, the weighted logarithmic $\wp -$Bloch space ${\mathfrak{S}}_{\omega ,log}^{\wp }$ is a set of analytic meromorphic functions $h\in \mathbb{K}$ with the following norm:

$${\parallel g\parallel }_{{\mathfrak{S}}_{\omega ,log}^{\wp }}=\underset{z\in \mathbb{K}}{sup}\left({\displaystyle \frac{{(1-|z\left|\right)}^{\wp }}{\omega (1-|z\left|\right)}}\right)\left(log\left({\displaystyle \frac{1}{1-\left|z\right|}}\right)\right)\left|g^{♯}\left(z\right)\right|<\infty .$$

We will demonstrate below an assortment of requirements for the recommended operators to be members of the aforementioned Bloch spaces.

Theorem 1.

Consider the operator${\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)$. Then:

• ${\parallel \upsilon \parallel }_{\mathfrak{S}}\iff {\parallel {\mathbb{P}}_{a,b}^{p,q}\upsilon \parallel }_{\mathfrak{S}};$
• ${\parallel \upsilon \parallel }_{{\mathfrak{S}}_{\omega }^{\wp }}\iff {\parallel {\mathbb{P}}_{a,b}^{p,q}\upsilon \parallel }_{{\mathfrak{S}}_{\omega }^{\wp }};$
• ${\parallel \upsilon \parallel }_{{\mathfrak{S}}_{\omega ,log}^{\wp }}\iff {\parallel {\mathbb{P}}_{a,b}^{p,q}\upsilon \parallel }_{{\mathfrak{S}}_{\omega ,log}^{\wp }}.$

Proof. 

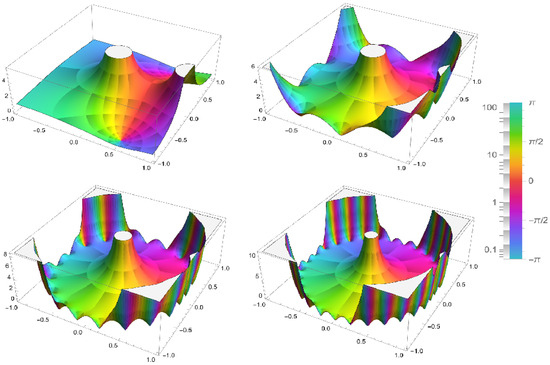
Obviously, by using Young’s inequality, we have

$$\begin{array}{cc}\hfill {|(f\ast g)}^{♯}|& ={\displaystyle \frac{{|(f\ast g)}^{\prime }|}{{1+|(f\ast g)}^2|}}={\displaystyle \frac{|(-\rho )(f^{\prime }\ast {\displaystyle \frac{g}{z}})|}{{1+|(f\ast g)}^2|}}\le \rho |(f^{\prime }\ast {\displaystyle \frac{g}{z}})|\hfill \\ \hfill & =\rho (1+|f^2|){\displaystyle \frac{|(f^{\prime }\ast {\displaystyle \frac{g}{z}})|}{{1+|\left(f\right)}^2|}}\le \rho |f^{♯}\left|\right|{\displaystyle \frac{g}{z}}\left|\right(1+|f^2\left|\right).\hfill \end{array}$$

Let $\upsilon \in \mathfrak{S}.$ Then it owns the inequality

$${\parallel \upsilon \parallel }_{\mathfrak{S}}=\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2\left)\right|{\upsilon }^{♯}\left(z\right)|<\infty .$$

Our point is to prove that ${\mathbb{P}}_{a,b}^{p,q}\upsilon \in \mathfrak{S}.$ Let

$$\begin{array}{c}\hfill K_1:=\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2)\left|{(-\rho )(1+|\upsilon |}^2)\left({\displaystyle \frac{z^{-\rho }+{\displaystyle \frac{q^{k/a}{z}^{k-\rho }}{(1-z{q}^{1/a})}}}{z}}\right)\right|\end{array}$$

(10)

$$\begin{array}{c}\hfill K_2:=\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2)\left|{(-\rho )(1+|\upsilon |}^2)\left({\displaystyle \frac{z^{-\rho }+A{z}^{k-\rho }{}_2{\Psi }_2^{\ast }\left[\begin{array}{cc}(p+k,1)& (1,1)\\ (ak+b,a)& (k+1,1)\end{array};z\right]}{z}}\right)\right|\end{array}$$

(11)

and

$$K:=max\{K_1,K_2\}.$$

In view of Proposition 1 and using some properties of the convolution product, a computation yields

$$\begin{array}{cc}\hfill \parallel {\mathbb{P}}_{a,b}^{p,q}{\upsilon \parallel }_{\mathfrak{S}}& =\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2\left)\right|{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \right]}^{♯}\left(z\right)|\hfill \\ \hfill & =\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2)\left|{\left[\left(z^{-\rho }+{\displaystyle \frac{q^{k/a}{z}^{k-\rho }}{(1-z{q}^{1/a})}}\right)\ast \left(z^{-\rho }+A{z}^{k-\rho }{}_2{\Psi }_2^{\ast }\left[\begin{array}{cc}(p+k,1)& (1,1)\\ (ak+b,a)& (k+1,1)\end{array};z\right]\right)\ast \upsilon \left(z\right)\right]}^{♯}\right|\hfill \\ \hfill & \le \underset{z\in \mathbb{K}}{sup}{(1-|z|}^2)\left|\left[\left({(-\rho )(1+|\upsilon |}^2){\displaystyle \frac{z^{-\rho }+{\displaystyle \frac{q^{k/a}{z}^{k-\rho }}{(1-z{q}^{1/a})}}}{z}}\right)\right.\right.\hfill \\ \hfill & \ast \left({(-\rho )(1+|\upsilon |}^2){\displaystyle \frac{z^{-\rho }+A{z}^{k-\rho }{}_2{\Psi }_2^{\ast }\left[\begin{array}{cc}(p+k,1)& (1,1)\\ (ak+b,a)& (k+1,1)\end{array};z\right]}{z}}\right)\ast \left.\left.{\upsilon }^{♯}\left(z\right)\right]\right|\hfill \\ \hfill & \le K^2\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2)\left|{\upsilon }^{♯}\left(z\right)\right|<\infty .\hfill \end{array}$$

Conversely, let ${\mathbb{P}}_{a,b}^{p,q}\upsilon \in \mathfrak{S}.$ Also, define the following convolution function

$$\Theta \left(z\right):=\left(z^{-\rho }+{\displaystyle \frac{q^{k/a}{z}^{k-\rho }}{(1-z{q}^{1/a})}}\right)\ast \left(z^{-\rho }+A{z}^{k-\rho }{}_2{\Psi }_2^{\ast }\left[\begin{array}{cc}(p+k,1)& (1,1)\\ (ak+b,a)& (k+1,1)\end{array};z\right]\right)$$

such that (see Figure 2)

$$[\Theta \left(z\right)]\ast {[\Theta \left(z\right)]}^{(-1)}=z^{-\rho }+{\displaystyle \frac{z^{k-\rho }}{1-z}},\left|z\right|<1$$

$$=z^{-\rho }+z^{k-\rho }(1+z+z^2+z^3+z^4+z^5+O\left(z^6\right))$$

and

$$\lambda :=\underset{\left|z\right|<1}{sup}{(1-|z|}^2)\left|{\displaystyle \frac{-\rho (1+|{[\upsilon \ast \Theta \left(z\right)]}^2\left|\right)}{z(1+|{\upsilon }^2\left|\right)}}{[\Theta \left(z\right)]}^{(-1)}\right|.$$

A computation implies that

$$\begin{array}{cc}\hfill {\parallel \upsilon \parallel }_{\mathfrak{S}}& =\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2{\left)\right|\left[\upsilon \left(z\right)\right]}^{♯}|=\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2)\left|{\left[\upsilon \left(z\right)\right]}^{♯}\ast \left(z^{-\rho }+{\displaystyle \frac{z^{k-\rho }}{1-z}}\right)\right|\hfill \\ \hfill & =\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2)\left|{\left[\upsilon \left(z\right)\right]}^{♯}\ast \left({\Theta \left(z\right)]\ast [\Theta \left(z\right)]}^{(-1)}\right)\right|\hfill \\ \hfill & \le \underset{z\in \mathbb{K}}{sup}{(1-|z|}^2)\left|{\left[\upsilon \left(z\right)\ast \Theta \left(z\right)\right]}^{♯}\right|\left|{\displaystyle \frac{-\rho (1+|{[\upsilon \ast \Theta \left(z\right)]}^2|)}{z(1+|{\upsilon }^2\left|\right)}}{[\Theta \left(z\right)]}^{(-1)}\right|\hfill \\ \hfill & \le \lambda \underset{z\in \mathbb{K}}{sup}{(1-|z|}^2)\left|{\left[\upsilon \left(z\right)\ast \Theta \left(z\right)\right]}^{♯}\right|\hfill \\ & =\lambda \parallel {\mathbb{P}}_{a,b}^{p,q}{\upsilon \parallel }_{\mathfrak{S}}<\infty .\hfill \end{array}$$

Similarly, by replacing the factors ${\displaystyle \frac{{(1-|z\left|\right)}^{\wp }}{\omega (1-|z\left|\right)}}$ and $\left({\displaystyle \frac{{(1-|z\left|\right)}^{\wp }}{\omega (1-|z\left|\right)}}\right)\left(log\left({\displaystyle \frac{1}{1-\left|z\right|}}\right)\right)$ instead of the factor $(1-|z{|}^2)$, respectively, the second and third relations are valid. □

Figure 2. 3D complex plot of the function $z^{-\rho }+{\displaystyle \frac{z^{k-\rho }}{1-z}}$ when $\rho =1, k=2, 10, 20, 30$, respectively.

Next, we deal with the Siegal domain.

4.2. Boundedness in Symmetrical Siegel Domain

A Siegel domain is a particular kind of sector in the complex vector space of symmetric matrices in the field of complex analysis and modular forms. In order to analyze modular forms, which are utilized in number theory, representation theory, and other branches of mathematics, these domains are utilized. A Siegel domain is a location in the framework of automorphic structures where the imaginary part of the symmetric matrices fulfills specific requirements.

Definition 4.

Define the set

$$\Pi =\{z\in \mathbb{K}:\Im (z)>0\}.$$

A Bloch analytic function $\varphi \in \mathcal{A}(\Pi )$, which achieves the norm

$${\parallel \varphi \parallel }_{\mathfrak{S}[\Pi ]}=\underset{z=x+iy\in \Pi }{sup}\left\{y\right|{\varphi }^{\prime }\left(z\right)\left|\right\}<\infty .$$

Theorem 2.

Consider the operator ${\mathbb{P}}_{a,b}^{p,q}\upsilon .$ Then,

$${\parallel \upsilon \parallel }_{\mathfrak{S}[\Pi ]}\iff {\parallel {\mathbb{P}}_{a,b}^{p,q}\upsilon \parallel }_{\mathfrak{S}[\Pi ]}.$$

Proof. 

Let $\upsilon \in \mathfrak{S}[\Pi ].$ Then it owns the inequality

$${\parallel \upsilon \parallel }_{\mathfrak{S}[\Pi ]}=\underset{z=x+iy\in \Pi }{sup}y\left|{\upsilon }^{♯}\left(z\right)\right|<\infty .$$

We herein prove that ${\mathbb{P}}_{a,b}^{p,q}\upsilon \in \mathfrak{S}[\Pi ].$ Assume that

$$\begin{array}{c}\hfill {{\rm Y}}_1:=\underset{z\in \mathbb{K}}{sup}{y(1-|z|}^2)\left|{(-\rho )(1+|\upsilon |}^2)\left({\displaystyle \frac{z^{-\rho }+{\displaystyle \frac{q^{k/a}{z}^{k-\rho }}{(1-z{q}^{1/a})}}}{z}}\right)\right|,y>0\end{array}$$

(12)

$$\begin{array}{c}\hfill {{\rm Y}}_2:=\underset{z\in \mathbb{K}}{sup}{y(1-|z|}^2)\left|{(-\rho )(1+|\upsilon |}^2)\left({\displaystyle \frac{z^{-\rho }+A{z}^{k-\rho }{}_2{\Psi }_2^{\ast }\left[\begin{array}{cc}(p+k,1)& (1,1)\\ (ak+b,a)& (k+1,1)\end{array};z\right]}{z}}\right)\right|,y>0\end{array}$$

(13)

and

$${\rm Y}:=max\{{{\rm Y}}_1,{{\rm Y}}_2\}.$$

By applying the properties of the convolution product, we obtain

$$\begin{array}{cc}\hfill & \parallel {\mathbb{P}}_{a,b}^{p,q}{\upsilon \parallel }_{\mathfrak{S}[\Pi ]}\hfill \\ \hfill & =\underset{z=x+iy\in \Pi }{sup}y\left|{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \right]}^{♯}\left(z\right)\right|,y>0\hfill \\ \hfill & =\underset{z\in \mathbb{K}}{sup}{y(1-|z|}^2)\left|{\left[\left(z^{-\rho }+{\displaystyle \frac{q^{k/a}{z}^{k-\rho }}{(1-z{q}^{1/a})}}\right)\ast \left(z^{-\rho }+A{z}^{k-\rho }{}_2{\Psi }_2^{\ast }\left[\begin{array}{cc}(p+k,1)& (1,1)\\ (ak+b,a)& (k+1,1)\end{array};z\right]\right)\ast \upsilon \left(z\right)\right]}^{♯}\right|\hfill \\ \hfill & \le \underset{z\in \mathbb{K}}{sup}{y(1-|z|}^2)\left|\left[\left({(-\rho )(1+|\upsilon |}^2){\displaystyle \frac{z^{-\rho }+{\displaystyle \frac{q^{k/a}{z}^{k-\rho }}{(1-z{q}^{1/a})}}}{z}}\right)\right.\right.\hfill \\ \hfill & \ast \left({(-\rho )(1+|\upsilon |}^2){\displaystyle \frac{z^{-\rho }+A{z}^{k-\rho }{}_2{\Psi }_2^{\ast }\left[\begin{array}{cc}(p+k,1)& (1,1)\\ (ak+b,a)& (k+1,1)\end{array};z\right]}{z}}\right)\ast \left.\left.{\upsilon }^{♯}\left(z\right)\right]\right|\hfill \\ \hfill & \le {{\rm Y}}^2\underset{z\in \mathbb{K}}{sup}{(1-|z|}^2)\left|{\upsilon }^{♯}\left(z\right)\right|<\infty .\hfill \end{array}$$

Thus, we have ${\mathbb{P}}_{a,b}^{p,q}\upsilon \in \mathfrak{S}[\Pi ].$

Conversely, assume that

$$u:=\underset{\left|z\right|<1}{sup}{y(1-|z|}^2)\left|{\displaystyle \frac{-\rho (1+|{[\upsilon \ast \Theta \left(z\right)]}^2\left|\right)}{z(1+|{\upsilon }^2\left|\right)}}{[\Theta \left(z\right)]}^{(-1)}\right|,$$

where

$$\Theta \left(z\right)=\left(z^{-\rho }+{\displaystyle \frac{q^{k/a}{z}^{k-\rho }}{(1-z{q}^{1/a})}}\right)\ast \left(z^{-\rho }+A{z}^{k-\rho }{}_2{\Psi }_2^{\ast }\left[\begin{array}{cc}(p+k,1)& (1,1)\\ (ak+b,a)& (k+1,1)\end{array};z\right]\right)$$

such that (see Figure 2)

$$[\Theta \left(z\right)]\ast {[\Theta \left(z\right)]}^{(-1)}=z^{-\rho }+{\displaystyle \frac{z^{k-\rho }}{1-z}},\left|z\right|<1.$$

Let ${\mathbb{P}}_{a,b}^{p,q}\upsilon \in \mathfrak{S}[\Pi ].$ Then, this leads to

$$\begin{array}{cc}\hfill {\parallel \upsilon \parallel }_{\mathfrak{S}}& =\underset{z\in \mathbb{K}}{sup}{y(1-|z|}^2{\left)\right|\left[\upsilon \left(z\right)\right]}^{♯}|=\underset{z\in \mathbb{K}}{sup}{y(1-|z|}^2)\left|{\left[\upsilon \left(z\right)\right]}^{♯}\ast \left(z^{-\rho }+{\displaystyle \frac{z^{k-\rho }}{1-z}}\right)\right|\hfill \\ \hfill & =\underset{z\in \mathbb{K}}{sup}{y(1-|z|}^2)\left|{\left[\upsilon \left(z\right)\right]}^{♯}\ast \left({\Theta \left(z\right)]\ast [\Theta \left(\xi \right)]}^{(-1)}\right)\right|\hfill \\ \hfill & \le \underset{z\in \mathbb{K}}{sup}{y(1-|z|}^2)\left|{\left[\upsilon \left(z\right)\ast \Theta \left(z\right)\right]}^{♯}\right|\left|{\displaystyle \frac{-\rho (1+|{[\upsilon \ast \Theta \left(z\right)]}^2\left|\right)}{z(1+|{\upsilon }^2\left|\right)}}{[\Theta \left(z\right)]}^{(-1)}\right|\hfill \\ \hfill & \le u\underset{z\in \mathbb{K}}{sup}{y(1-|z|}^2)\left|{\left[\upsilon \left(z\right)\ast \Theta \left(z\right)\right]}^{♯}\right|=u{\parallel {\mathbb{P}}_{a,b}^{p,q}\upsilon \parallel }_{\mathfrak{S}}<\infty .\hfill \end{array}$$

Thus, $\upsilon \in \mathfrak{S}[\Pi ].$ □

4.3. Polar Derivative of the Partial Sums

Definition 5.

Assume that $w\left(z\right)$ is an m-degree polynomial. Then, the polar differentiation of the polynomial $w\left(z\right)$ of degree m with respect to the point ζ is formulated by the structure

$${\Delta }_{\zeta }w\left(z\right)=mw\left(z\right)+(\zeta -z)w^{\prime }\left(z\right),z\in \mathbb{K},\zeta \in \mathbb{C}.$$

Note that the polynomial ${\Delta }_{\zeta }w\left(z\right)$ is at most of the degree $m-1$.

The geometrical relationship between a complex polynomial’s modulus on a circle and the location of this polynomial’s zeros either within or outside of this circle is one of the fascinating and rewarding topics in polynomial geometry (see [25]). Bernstein-type inequalities provide a lot of ideas in the field of polynomial inequalities. From Bernstein’s disparity, numerous conclusions can be drawn. We begin with a Bernstein-related finding (see [26]). Let $w\left(z\right)$ be an m-degree polynomial. Then, based on the widely recognized finding known as Bernstein’s inequality, we obtain:

$$\underset{\left|z\right|=1}{max}|w^{\prime }\left(z\right)|\le m\underset{\left|z\right|=1}{max}\left|w\left(z\right)\right|.$$

Our aim is to present a study on the functional ${⨿}_{a,b}^{p,q}\left(z\right)$ using the polar derivative concept of its polynomial, which is presented as follows:

$$w\left(z\right):={\left[{⨿}_{a,b}^{p,q}\right]}_m\left(z\right)=1+\sum _{n=k}^m\left(1-\gamma (1+{\displaystyle \frac{1}{\rho }})\right){\Phi }_n{z}^n.$$

Since

$${⨿}_{a,b}^{p,q}\left(z\right)=(1-\gamma )z^{\rho }\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}^{\prime },$$

then the polynomial $w\left(z\right)$ satisfies

$$w\left(z\right)=(1-\gamma )z^{\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m^{\prime },$$

where ${\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m$ is the m degree polynomial produced by the integral $\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right].$ A computation leads to

$$\begin{array}{cc}\hfill \left|w\left(z\right)\right|& =\left|(1-\gamma )z^{\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m-\left(\frac{\gamma }{\rho }\right)z^{1+\rho }{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m^{\prime }\right|\hfill \\ \hfill & \le (1-\gamma )\left|{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m\right|+{\displaystyle \frac{\gamma }{\rho }}\left|{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m^{\prime }\right|\hfill \\ \hfill & \le (1-\gamma )\left|{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m\right|+{\displaystyle \frac{\gamma }{\rho }}\left|{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m^{\prime }\right|.\hfill \end{array}$$

By taking the max value at $\left|z\right|=1,$ we obtain

$$\begin{array}{c}\hfill \underset{\left|z\right|=1}{max}\left|w\left(z\right)\right|\le \left(1+\gamma \left({\displaystyle \frac{m}{\rho }}-1\right)\right)\underset{\left|z\right|=1}{max}\left|{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m\right|,m\ge \rho .\end{array}$$

(14)

Assume that $\Xi :=\left(1+\gamma \left({\displaystyle \frac{m}{\rho }}-1\right)\right)$, then, we obtain the inequality

$$\begin{array}{c}\hfill \underset{\left|z\right|=1}{max}\left|w\left(z\right)\right|\le \Xi \underset{\left|z\right|=1}{max}\left|{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m\right|.\end{array}$$

(15)

Dewan et al. [27] considered the polynomial

$$h\left(z\right)=h_0+\sum _{n=k}^m{h}_n{z}^n,k\le m.$$

Then, in view of [27]—Theorem 2—the upper bound of the polar derivative is as follows:

$$\begin{array}{c}\hfill |{\Delta }_{\zeta }h\left(z\right)|\le {\displaystyle \frac{m}{2}}\left(\left(\right|\zeta |+1)\underset{z\in \partial \mathbb{K}}{max}\left|h\left(z\right)\right|-(1-|\zeta \left|\right)\underset{z\in \partial \bigsqcup }{min}\left|h\left(z\right)\right|\right),\left|\zeta \right|\le 1.\end{array}$$

(16)

In addition, by [27]—Theorem A:

$$\begin{array}{c}\hfill \underset{z\in \partial \mathbb{K}}{max}|{\Delta }_{\zeta }h\left(z\right)|\ge {\displaystyle \frac{m}{2}}\left(\left(\right|\zeta |-1)\underset{z\in \partial \mathbb{K}}{max}\left|h\left(z\right)\right|+\left(\right|\zeta |+1)\underset{z\in \partial \mathbb{K}}{min}\left|h\left(z\right)\right|\right),\left|\zeta \right|\ge 1.\end{array}$$

(17)

Through a direct application of Theorems 1 and 2, together with Equations (15) and (16), we seek the following result.

Theorem 3.

Consider the polynomial $w\left(z\right)={\left[{⨿}_{a,b}^{p,q}\right]}_m\left(z\right)$ of degree m. If $w\left(z\right)$ admits all its zeros in $\mathbb{K}$ and $\left|\zeta \right|\le 1$ then:

• $|{\Delta }_{\zeta }w\left(z\right)|\le |\zeta |+{\displaystyle \frac{m\Xi K^2}{2}}\left(\left(\right|\zeta |+1)\parallel {\mathbb{P}}_{a,b}^{p,q}{\upsilon \left(1\right)\parallel }_{\mathfrak{S}}-(1-|\zeta \left|\right)\mathfrak{M}\right)$, where $\upsilon \in \mathfrak{S};$
• $|{\Delta }_{\zeta }w\left(z\right)|\le |\zeta |+{\displaystyle \frac{m\Xi K^2}{2}}\left(\left(\right|\zeta |+1)\parallel {\mathbb{P}}_{a,b}^{p,q}{\upsilon \left(1\right)\parallel }_{{\mathfrak{S}}_{\omega }^{\wp }}-(1-|\zeta \left|\right)\mathfrak{M}\right)$, where $\upsilon \in {\mathfrak{S}}_{\omega }^{\wp };$
• $|{\Delta }_{\zeta }w\left(z\right)|\le |\zeta |+{\displaystyle \frac{m\Xi K^2}{2}}\left(\left(\right|\zeta |+1)\parallel {\mathbb{P}}_{a,b}^{p,q}{\upsilon \left(1\right)\parallel }_{{\mathfrak{S}}_{\omega ,log}^{\wp }}-(1-|\zeta \left|\right)\mathfrak{M}\right)$, where $\upsilon \in {\mathfrak{S}}_{\omega ,log}^{\wp }$;
• $|{\Delta }_{\zeta }w\left(z\right)|\le |\zeta |+{\displaystyle \frac{m\Xi {{\rm Y}}^2}{2}}\left(\left(\right|\zeta |+1)\parallel {\mathbb{P}}_{a,b}^{p,q}{\upsilon \left(1\right)\parallel }_{\mathfrak{S}[\Pi ]}-(1-|\zeta \left|\right)\mathfrak{M}\right),$ where $\upsilon \in \mathfrak{S}[\Pi ]$.

$$\left(\Xi =\left(1+\gamma \left({\displaystyle \frac{m}{\rho }}-1\right)\right),\left|z\right|<1,m\ge 1,\mathfrak{M}:=\underset{\left|z\right|=1}{min}\left\{\left|{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m\right|\right\}\right)$$

The lower bound of $w\left(z\right)$ is given in the application of Theorems 1 and 2 and Equations (15) and (17).

Theorem 4.

Consider the polynomial $w\left(z\right)={\left[{⨿}_{a,b}^{p,q}\right]}_m\left(z\right)$ of degree m. If $w\left(z\right)$ admits all its zeros in $\mathbb{K}$ and $\left|\zeta \right|\ge 1$then:

• ${max}_{\left|z\right|=1}\left|{\Delta }_{\zeta }w\left(z\right)\right|\ge 1+{\displaystyle \frac{\Xi m{K}^2}{2}}\left(\left(\right|\zeta |-1)\parallel {\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(1\right)\right]}_m{\parallel }_{\mathfrak{S}}+\left(\right|\zeta |+1)\mathfrak{M}\right)$, where $\upsilon \in \mathfrak{S};$
• ${max}_{\left|z\right|=1}\left|{\Delta }_{\zeta }w\left(z\right)\right|\ge 1+{\displaystyle \frac{\Xi m{K}^2}{2}}\left(\left(\right|\zeta |-1)\parallel {\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(1\right)\right]}_m{\parallel }_{{\mathfrak{S}}_{\omega }^{\wp }}+\left(\right|\zeta |+1)\mathfrak{M}\right)$, where $\upsilon \in {\mathfrak{S}}_{\omega }^{\wp };$
• ${max}_{\left|z\right|=1}\left|{\Delta }_{\zeta }w\left(z\right)\right|\ge 1+{\displaystyle \frac{\Xi m{K}^2}{2}}\left(\left(\right|\zeta |-1)\parallel {\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(1\right)\right]}_m{\parallel }_{{\mathfrak{S}}_{\omega ,log}^{\wp }}+\left(\right|\zeta |+1)\mathfrak{M}\right)$, where $\upsilon \in {\mathfrak{S}}_{\omega ,log}^{\wp }$;
• ${max}_{\left|z\right|=1}\left|{\Delta }_{\zeta }w\left(z\right)\right|\ge 1+{\displaystyle \frac{\Xi m{{\rm Y}}^2}{2}}\left(\left(\right|\zeta |-1)\parallel {\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(1\right)\right]}_m{\parallel }_{\mathfrak{S}[\Pi ]}+\left(\right|\zeta |+1)\mathfrak{M}\right),$ where $\upsilon \in \mathfrak{S}[\Pi ]$.

$$\left(\Xi =\left(1+\gamma \left({\displaystyle \frac{m}{\rho }}-1\right)\right),\left|z\right|<1,m\ge 1,\mathfrak{M}:=\underset{\left|z\right|=1}{min}\left\{\left|{\left[{\mathbb{P}}_{a,b}^{p,q}\upsilon \left(z\right)\right]}_m\right|\right\}\right).$$

5. Conclusions

Based on the above information, we suggested a generalized convolution operator defining the well-known Prabhakar fractional integral. We established the operator by utilizing the generalized meromorphic multi-valent analytic functions of a complex variable $0<\left|z\right|<1.$ We presented different kinds of properties, depending on the subordination, superordination and majorization concepts. As a consequence, we illustrated a list of sufficient conditions to obtain a geometric representation of the operator. Moreover, as an application, we used their partial sums to determine the highest value of the polar derivative of polynomials produced by their partial sums. The findings can be expanded in the future to various classes of analytic functions. Additionally, it can be expanded to include k-symbol fractional calculus and quantum calculus, by employing the generalized formula of gamma function.